应力-应变曲线
应力-应变曲线
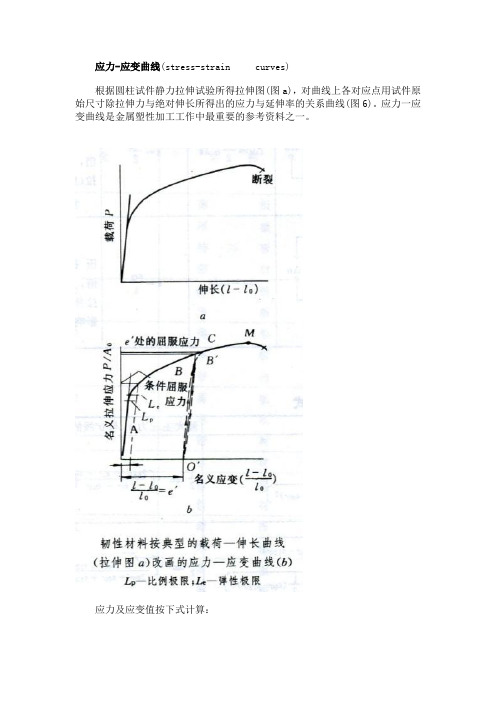
应力-应变曲线(stress-strain curves)根据圆柱试件静力拉伸试验所得拉伸图(图a)，对曲线上各对应点用试件原始尺寸除拉伸力与绝对伸长所得出的应力与延伸率的关系曲线(图6)。
应力一应变曲线是金属塑性加工工作中最重要的参考资料之一。
应力及应变值按下式计算：式中σi 表示拉伸图上任意点的应力值，δi为i点的延伸率，Pi及Δli为该点的拉力与绝对伸长值，F0及l为试件的断面积和计算长度。
试件受拉伸时，先产生弹性变形，这时应力应变成比例，当出现二者不能保持线性关系的点时，表示材料已屈服而将发生塑性变形，这时的应力定义为屈服应力或流变应力，用σs表示，其求法见屈服点。
拉伸时当试件计算长度上的均匀变形阶段结束而产生细颈时，变形将集中在细颈部分。
出现细颈前材料所能承受的应力名为强度极限或抗拉强度，用σb表示σb =Pmax/F式中Pmax为拉伸图上所记录的最大载荷值。
试件出现细颈后很快即断裂，断裂应力σfσf =Pf/Tf式中Pf 是断裂时的拉力，Ff是断口面积。
试件拉断时的延伸率δf(％)或断面收缩率ψ(％)是表示材料可承受最大塑性变形能力的指标：矾一牮×100(4)￡fPf=盐≯×100(5)』’0式中厶和Ff是将断开的试件对合后测定的试件长度和断口处的面积。
抗拉强度靠及延伸率d或断面收缩率妒是材料性能的两个基本指标，在工程上有着广泛的应用。
屈服应力民(或乱：)是金属塑性加工时变形体开始产生塑性变形所必需的最小应力，它是计算变形力的一个重要参数。
应力-应变曲线表征材料受外力作用时的行为。
材料受力后即发生弹性变形，这时应力应变呈简单的线性关系，继续增加作用力至一定大小后材料将出现塑性变形，以后变形与应力的关系复杂，当塑性变形至一定程度以后，试件破断则变形过程终结。
所以任何变形过程均包括弹性变形、塑性变形及破断3个典型阶段。
金属的塑性加工过程处于弹性变形与破断二者之间。
首先要创造一定的应力状态条件使金属能发生塑性变形，其次是安排一个使塑性变形尽可能大又不致发生破坏的热力学条件。
真实应力-应变曲线
§3.6 真实应力－应变曲线
应力－应变曲线反映变形体变形时应力随应变强化的规律。
初始屈服应力S
一般屈服应力( 流动应力S ,Y ) 真实应力：变形体内实际承受应力的大小。
影响流动应力的因素
材料属性， 温度， 应变， 应变速率
建立真实应力－应变曲线方法
拉伸试验，
压缩试验，
扭转试验
流动应力S 的公式表达形式
失稳点b，Fb = Fmax。
dF A0 edS Sed 0
dS Sd 0
dS
d
b
Sb
二、 压缩试验曲线
拉伸试验曲线：失稳，精确范围（ < 0.3）； 压缩试验曲线：摩擦（S ），精确范围（ 2）；
1、直接消除摩擦的圆柱体压缩法
S
P A
P A0e
ln H0
H
2、外推法 摩擦力影响和式样尺寸D0/H0 有关，根据不同的D0/H0 ， 外推出D0/H0 = 0时的S，得到 真实应力－应变曲线。
1 1
Fd F(0)
1、拉伸图和条件应力－应变曲线
0
F A0
l
l0
b d
c
Fb= Fmax
Fp Fc
三个变形阶段：
ph
特征点：弹性极限点p，屈服点c，失稳点b，断裂点k。
?
k
Δl()
2、真实应力－应变曲线 用真实应力与应变表示的曲线。
S( ) ; S( ) ; S( )
2 2t
24
1 3 平面应变问题
2
3
1 2 2 2 3 2 3 1 2
2 3
6 1 1.1551
S 800 0.25
8001.151 0.25 443
应力 应变 曲线
应力应变曲线
应力-应变曲线描述了材料在受到外部力作用下的应力和应变之间的关系。
应力（stress）指的是材料在单位面积上受到的力的大小，通常以强度（N/m^2）作为单位。
应力-应变曲线的横轴通常表示材料的应变（strain），应变指的是材料在受到力后产生的形变程度，通常以长度的相对变化或者角度的相对变化表示。
应力-应变曲线通常可以分为四个阶段：
1. 弹性阶段（Elastic region）：当材料受到小应力时，材料会表现出弹性行为，即应变与应力成正比。
在这个阶段，应力增加时材料会发生形变，但一旦外力消失，材料会恢复到原来的形状。
2. 屈服阶段（Yield Point）：当材料受到足够大的应力时，材料会超过其弹性限度，开始发生可见的形变。
这个阶段的应力-应变曲线通常表现为一个明显的曲线，材料开始变得塑性。
3. 塑性阶段（Plastic region）：在这个阶段，材料受到的应力继续增加，但应变的增加速度逐渐减慢。
材料开始发生不可逆的塑性变形。
4. 断裂阶段（Fracture point）：当材料受到过大的应力时，材料会发生断裂，即完全失去其机械性能。
应力-应变曲线的形状和材料的性质，结构和处理方式等因素密切相关。
不同材料（如金属、塑料、陶瓷等）的应力-应变曲线会有所不同，也受到温度、湿度等环境条件的影响。
这在工程设计和材料选择中具有重要的意义，可以帮助工程师评估材料的强度、延展性、可塑性和抗断裂性等性能。
应力-应变曲线
9-1 金属的应力－应变曲线 单向静拉伸试验
是应用最广泛的力学性能试验方法之一。 1）可揭示材料在静载下的力学行为（三种失效形式）： 即：过量弹性变形、塑性变形、断裂。 2）还可标定出材料的最基本力学性
能指标： 如：屈服强度、抗拉强度、伸长率、
断面收缩率等。
3
1、拉伸力－伸长曲线
2. 铸铁、陶瓷：只有第I阶段
3. 中、高碳钢：没有第II阶段
7
3、真应力S－真应变e 曲线
3、真应力S－真应变e 曲线：（流变曲线）
在实践的塑性变形中，试样的截面积与长度也在不断发生着变化，在研究 金属塑性变形时，为了获得真实的变形特性，应当按真应力和真应变来进 行分析。
流变曲线真实反映变形过程中，随应变量增大，材料性质的变化。
若应力足够大，位错可从溶质 原子簇中挣脱，载荷就下降。
若溶质原子足够快地扩散开， 就可将位错重新锁住，则须再 增大载荷才使变形继续下去。
23
4）第Ⅳ种类型：弹性－不均匀塑性－均匀塑性变形 许多体心立方铁基合金和有色合金，应力－应变曲线在弹性
与均匀塑性变形间有一狭窄一段属不均匀塑变区。即从弹性 向塑性变形的过渡明显。
L0
L1
L0
但是，各次拉伸真应变量e之和等于一次拉伸的真应变量。
ln L1 ln L2 ln L2
L0
L1
L0
14
5、不同类型材料典型的拉伸应力－应变曲线
1）第Ⅰ种类型：完全弹性 可用虎克定律描述其应力σ-应变ε成比例的材料特性。
E
E－材料的弹性模量（杨氏模量）
特点：具有可逆应力－应变曲线 和不出现塑性变形的特征。
工程应力－应变曲线
真应力-应变曲线介绍
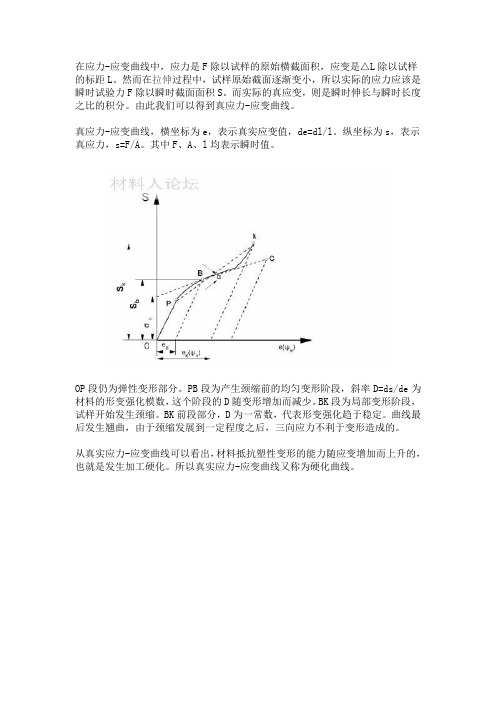
在应力-应变曲线中，应力是F除以试样的原始横截面积，应变是△L除以试样的标距L。
然而在拉伸过程中，试样原始截面逐渐变小，所以实际的应力应该是瞬时试验力F除以瞬时截面面积S。
而实际的真应变，则是瞬时伸长与瞬时长度之比的积分。
由此我们可以得到真应力-应变曲线。
真应力-应变曲线，横坐标为e，表示真实应变值，de=dl/l。
纵坐标为s，表示真应力，s=F/A。
其中F、A、l均表示瞬时值。
OP段仍为弹性变形部分。
PB段为产生颈缩前的均匀变形阶段，斜率D=ds/de为材料的形变强化模数，这个阶段的D随变形增加而减少。
BK段为局部变形阶段，试样开始发生颈缩。
BK前段部分，D为一常数，代表形变强化趋于稳定。
曲线最后发生翘曲，由于颈缩发展到一定程度之后，三向应力不利于变形造成的。
从真实应力-应变曲线可以看出，材料抵抗塑性变形的能力随应变增加而上升的，也就是发生加工硬化。
所以真实应力-应变曲线又称为硬化曲线。
应力应变曲线类型
应力-应变曲线是用来描述材料在受到外部力作用时，其应力和应变之间的关系的图形。
这些曲线可以用来了解材料的弹性和塑性行为，以及其破坏点等重要信息。
应力-应变曲线的类型可以分为几种常见的情况：
1. 弹性材料的应力-应变曲线：
-在弹性阶段，应力和应变成正比，遵循胡克定律。
-弹性材料在卸载后会完全恢复原始形状。
-典型的弹性曲线是线性上升的，没有明显的屈服点。
2. 塑性材料的应力-应变曲线：
-塑性材料在一定应力下会发生屈服，超过这一点后应变增加但应力基本稳定。
-塑性材料的曲线通常有明显的屈服点。
-塑性变形是不可逆的，材料在卸载后会有永久的变形。
3. 韧性材料的应力-应变曲线：
-韧性材料通常在屈服点之后继续延展，具有良好的抗断裂性能。
-曲线的下降部分较为缓和，表示能够吸收相对大的应变能量。
4. 脆性材料的应力-应变曲线：
-脆性材料通常在屈服点之后迅速断裂，没有明显的延展性。
-曲线的下降部分陡峭，表示应变能量较小，容易断裂。
应力-应变曲线的形状取决于材料的类型，因此不同的材料会具有不同的曲线类型。
这些曲线可以用来评估材料的性能、工程应用以及材料的破坏特性。
钢筋的应力—应变曲线分析
自开始加载至应力达到A点以前，应力应变成线性关系，A点称比例极限，OA段属于弹性工作阶段。
应力达到Bˊ点后，钢筋进入屈服阶段，产生很大的塑性形变，Bˊ点应力称为屈服强度（流限），在应力-应变曲线中呈现一水平段B〞B，称为流幅。
超过B点后，应力-应变关系重新表现为上升的曲线，B-C段为强化阶段。
曲线最高点C点的应力称为抗拉强度。
此后钢筋试件产生颈缩现象，应力应变关系成为下降曲线，应变继续增大，到D点钢筋被拉断。
D点所对应的横坐标称为伸长率，它标志钢筋的塑性。
伸长率越大，塑性越好。
钢筋塑性除用伸长率标志外，还用冷弯试验来检验。
冷弯就是把直径为D的钢辊转弯转α角而不发生裂纹。
钢筋塑性越好，钢辊直径D可越小，冷弯角α就越大。
屈服强度（流限）是软钢的主要强度指标。
在混凝土中的钢筋，当应力达到屈服强度后，荷载不增加，而应变会继续增大，使得混凝土开展过宽，构件变形过大，结构不能正常使用。
所以软钢钢筋的受拉强度限值以屈服强度为准，钢筋的强化阶段只作为一种安全储备考虑。
钢材中含碳量越高，屈服强度和抗拉强度就越高，伸长率就越小，流幅也相应缩短。
应力-应变曲线
项目部对工程工序施工质量实行班组初检、技术主管复检和专职质检工程师终检“三检”应力-应变曲线-计算公式stress-straincurve在工程中，应力和应变是按下式计算的应力-应变曲线应力（工程应力或名义应力）σ=P/A。
，应变（工程应变或名义应变）ε=（L-L。
）/L。
式中，P为载荷；A。
为试样的原始截面积；L。
为试样的原始标距长度；L 为试样变形后的长度。
应力-应变曲线-特点从此曲线上，可以看出低碳钢的变形过程有如下特点：当应力低于σe时，应力与试样的应变成正比，应力去除，变形消失，即试样处于弹性变形阶段，σe为材料的弹性极限，它表示材料保持完全弹性变形的最大应力。
当应力超过σe后，应力与应变之间的直线关系被破坏，并出现屈服平台或屈服齿。
如果卸载，试样的变形只能部分恢复，而保留一部分残余变形，即塑性变形，这说明钢的变形进入弹塑性变形阶段。
σs称为材料的屈服强度或屈服点，对于无明显屈服的金属材料，规定以产生0.2%残余变形的应力值为其屈服极限。
应力-应变曲线-塑性变形当应力超过σs后，试样发生明显而均匀的塑性变形，若使试样的应变增大，则必须增加应力值，这种随着塑性变形的增大，塑性变形抗力不断增加的现象称为加工硬化或形变强化。
当应力达到σb时试样的均匀变形阶段即告终止，此最大应力σb称为材料的强度极限或抗拉强度，它表示材料对最大均匀塑性变形的抗力。
在σb值之后，试样开始发生不均匀塑性变形并形成缩颈，应力下降，最后应力达到σk时试样断裂。
σk为材料的条件断裂强度，它表示材料对塑性的极限抗力。
应力-应变曲线-极限抗力上述应力-应变曲线中的应力和应变是以试样的初始尺寸进行计算的，事实上，在拉伸过程中试样的尺寸是在不断变化的，此时的真实应力S应该是瞬时载荷（P）除以试样的瞬时截面积（A），即：S=P/A；同样，真实应变e应该是瞬时伸长量除以瞬时长度de=dL/L。
而真应力-真应变曲线，它不像应力-应变曲线那样在载荷达到最大值后转而下降，而是继续上升直至断裂，这说明金属在塑性变形过程中不断地发生加工硬化，从而外加应力必须不断增高，才能使变形继续进行，即使在出现缩颈之后，缩颈处的真实应力仍在升高，这就排除了应力-应变曲线中应力下降的假象。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
应力-应变曲线MA 02139，剑桥麻省理工学院材料科学与工程系David Roylance2001年8月23日引言应力-应变曲线是描述材料力学性能的极其重要的图形。
所有学习材料力学的学生将经常接触这些曲线。
这些曲线也有某些细微的差别，特别对试验时会产生显著的几何变形的塑性材料。
在本模块中，将对表明应力-应变曲线特征的几个点作简略讨论，使读者对材料力学性能的某些方面有初步的总体了解。
本模块中不准备纵述“现代工程材料的应力-应变曲线”这一广阔的领域，相关内容可参阅参考文献中列出的博依（Boyer ）编的图集。
这里提到的几个专题——特别是屈服和断裂——将在随后的模块中更详尽地叙述。
“工程”应力-应变曲线在确定材料力学响应的各种试验中，最重要的恐怕就是拉伸试验1了。
进行拉伸试验时，杆状或线状试样的一端被加载装置夹紧，另一端的位移δ是可以控制的，参见图1。
传感器与试样相串联，能显示与位移对应的载荷)(δP 的电子读数。
若采用现代的伺服控制试验机，则允许选择载荷而不是位移为控制变量，此时位移)(P δ是作为载荷的函数而被监控的。
图1 拉伸试验在本模块中，应力和应变的工程测量值分别记作e σ和e ε，它们由测得的载荷和位移值，及试样的原始横截面面积和原始长度按下式确定0A 0L1 应力-应变试验及材料力学中几乎所有的试验方法都由制定标准的组织，特别是美国试验和材料学会(ASTM)作详尽的规定。
金属材料的拉伸试验由ASTM 试验E8规定；塑料的拉伸试验由ASTM D638规定；复合材料的拉伸试验由ASTM D3039规定。
当以应变e ε为自变量、应力e σ为函数绘制图形时，就得到如图2所示的工程应力-应变曲线。
图2 退火的多晶体铜在小应变区的工程应力-应变曲线（在许多塑性金属中，这一曲线具有典型性）在应力-应变曲线的初始部分（小应变阶段），作为合理的近似，许多材料都服从胡克定律。
于是应力与应变成正比，比例常数即弹性模量或杨氏模量，记作E :随着应变的增大，许多材料的应力与应变最终都偏离了线性的比例关系，该偏离点称为比例极限。
这种非线性通常与试样中由应力引起的“塑性”流动有关。
在此阶段，材料内部的分子或微观结构重新排列或调整，原子移动到新的平衡位置。
材料呈现塑性的机理是分子的活动性，对晶体材料，分子的活动性可由位错运动引起（在随后的模块中将深入讨论）。
若材料内部的分子缺少这种活动性，例如其内部微观结构会阻碍位错运动，则这种材料通常是脆性而不是塑性的。
脆性材料的应力-应变曲线，在其整个变形范围内都近似为直线，最后试验因断裂而终止，没有明显的塑性流动现象。
在图2中可见，塑性材料的应变超过比例极限后，要使应变再增加，所需的应力必须在超出比例极限后继续增加，这一现象称为应变硬化。
这些与塑性流动相关的微观结构重新调整通常在卸载后并不能逆转，因此比例极限往往就是材料的弹性极限，或者至少两者很接近。
弹性是指在卸除载荷后、材料完全并立即从强制的变形状态恢复原形的性能，弹性极限是指这样的应力值：当材料达到此应力值后，卸载后仍将保留永久的残余变形。
要确定由给定应力引起的残余变形，可从该应力在应力-应变曲线上达到的最高点，向应变轴画一条卸载直线，此直线的斜率与初始弹性加载直线的斜率相同，直线与应变轴的交点对应的应变值即残余应变值。
产生残余变形的原因是：材料卸载后弹性变形虽然消失，但已没有外力强迫分子结构恢复其初始位置。
与应力-应变曲线密切相关的术语是屈服应力，在这些模块中记作Y σ。
屈服应力是试样产生塑性变形所需的应力。
因为往往很难精确确定开始产生塑性变形时的应力值，故通常取产生特定量的永久应变时（通常为0.2%）的应力为屈服应力。
求“条件屈服应力”的作图过程如图2所示：从应变轴=e ε0.2%处作斜率为E 的直线，这就是会引起特定的永久变形的卸载线。
此直线与应力-应变曲线交点处的应力即条件屈服应力。
图3所示为铜的工程应力-应变曲线，已按比例放大，该图显示了变形从零开始直至试样断裂的全过程。
由图可见，在到达标为UTS （即拉伸强度极限，在这些模块中记为f σ）的点之前，应变硬化率2逐渐减少。
过了此点后，材料出现应变软化，对新加的应变的每一增量只需较小的应力。
图3 退火的多晶体铜完整的工程应力-应变曲线然而，材料从应变硬化到应变软化这一明显的改变，如同在应力-应变曲线的UTS 点看到的应力极值一样，毕竟是人为的作图过程的产物。
材料在屈服点以后，分子的流动使试样的横截面面积显著减小,因此材料实际承受的应力A A P t /=σ要大于按原始的横截面面积计算的工程应力(0/A P e =σ)。
所加载荷应等于真实应力与实际面积的乘积（A P t σ=），只要应变硬化引起的t σ的增大足以弥补横截面面积的减小，则载荷及相应的工程应力将继续随着应变的增大而上升。
但最终，由流动造成的横截面面积的减小要超过由应变硬化导致的真实应力的增大，于是载荷开始下跌。
这是一种几何效应，如果试验时画出的是真实应力、而不是工程应力的话，应力-应变曲线中将不出现最大值。
A 在拉伸强度极限处，载荷P 的微分为零，由此可给出在颈缩时真实应力与横截面面积之间的解析关系式：最后的式子表明：当横截面面积的缩减率等于真实应力的增加率时，载荷及相应的工程应力作为应变的函数，都将达到最大值。
在拉伸试验的实验报告中，记录得最多的材料性能可能就是拉伸强度极限。
尽管如此，由于上述几何尺寸的影响，拉伸强度极限并非对材料的直接测量值,应当慎用。
当设计涉及塑性金属时，通常宁愿用屈服应力Y σ，而不用拉伸强度极限。
不过，拉伸强度极限对脆性材料而言还是有效的设计依据，因为脆性材料不会出现因流动而使横截面面积缩减的现象。
2 应变硬化率是应力-应变曲线的斜率，也称为切线模量。
真实应力值在整个试样上并不是完全相同的，试样上总有一些区域（如表面上的划痕或某些其他缺陷）的局部应力最大。
一旦应力达到工程应力-应变曲线上的最大值时，在该部位材料的局部流动无法由进一步的应变硬化来弥补，于是该处的横截面面积进一步缩小。
这使局部应力变得更大，从而进一步加速了材料的流动。
这种局部的不断增加的材料流动很快导致在试样标距内的“颈缩”，如图4所示。
图4 拉伸试样的颈缩直到颈缩形成，整个试样的变形基本上是均匀的，但在颈缩后，所有随后的变形都在颈缩处发生。
颈缩处变得越来越小，局部真实应力不断地增大，直到试样被拉断。
这就是大部分塑性金属的失效模式。
当颈部收缩时，颈部变化的几何形状使该处的单轴应力状态变成复杂的应力状态——除正应力外，还有切应力分量。
试样最终常以锥杯状的断口断裂，如图5所示。
由图可见，材料的外层是剪切破坏，而内部是拉伸破坏。
当试样断裂时，断裂点的工程应变（记作f ε）将把颈缩区和非颈缩区的变形包括在一起。
由于材料在颈缩区的真实应变大于非颈缩区，f ε值将取决于颈缩区的长度与试样标距的比值。
所以，f ε不仅是材料性能的函数，而且是试样几何形状的函数，因而它只是对材料塑性的粗略测量值。
图5 塑性金属的锥杯状断裂图6所示为半晶质的热塑性塑料的工程应力-应变曲线，这种材料的响应与图3所示铜的响应很相似。
在图3中，响应显示了比例极限，随后在曲线的应力最大值处发生颈缩现象。
对塑料，通常称此应力的最大值为屈服应力，虽然塑性流动实际上在达到此应变前就已开始了。
但聚合物和铜的响应也有显著区别：聚合物的颈部不会持续收缩到试样被拉断，而是颈缩区的材料被拉长，直至达到“固有伸长比3”（固有伸长比是温度和试样加工工艺的函数）。
超过固有伸长比后，颈缩处的材料停止伸长，靠近颈缩处的新材料开始颈缩。
于是颈缩区域 不断扩展变长，直至蔓延到试样的整个标距，这一过程称为冷拉。
当拉伸由“六原子小基团”组成的聚乙烯时,不用试验机就可看到这一过程，如图7所示。
3 固有伸长比是冷拉区的长度与同一材料原始长度之比。
——译者注并非所有聚合物都能持续这一冷拉过程。
颈缩过程使材料的微观结构强化，当其破坏载荷大于使颈缩区外围未变形材料发生颈缩所需的载荷时，才会出现冷拉现象。
下文将对此作进一步的讨论。
图6 聚酰胺（尼龙）热塑性塑料的应力-应变曲线图7 聚乙烯材料的颈缩和冷拉“真实”的应力-应变曲线正如上节所述，超过弹性极限后，由于试样的尺寸与其原始值相比已有明显的改变，对这部分的工程应力-应变曲线必须谨慎地加以诠释。
使用真实应力A P t /=σ、而不是工程应力0/A P e =σ，可以更直接地度量材料在塑性流动范围内的响应。
与真实应力相对应的常用的应变度量方法，则是取应变的增量为位移的增量除以当前的长度：dL L通常称此为“真实”应变或“对数”应变。
在屈服及随后的塑性流动期间，材料流动引起的体积改变可忽略不计，因为长度增加的影响被横截面面积的减小抵消了。
在颈缩前，应变沿整个试样长度仍旧是相同的，体积不变的约束条件可写成：比值称为伸长比，记作0/L L λ。
应用这些关系式，容易导出拉应力和拉应变的真实值与工 程测量值之间的关系（见习题2）：在应变达到开始颈缩的值之前，应用这些方程，可从工程应力-应变曲线导出真实的应力-应变曲线。
图8重画了图3，并增添了按上述方程算得的真实的应力-应变曲线，以供对照。
图8 铜的工程应力-应变曲线与真实的应力-应变曲线的比较。
箭头指出了工程曲线上的UTS （拉伸强度极限）在“真实”曲线上的位置。
发生颈缩后，应变在试样的标距内是不均匀的，这时再对更大的工程应变值计算真实的应力-应变曲线就没有多大意义了。
但若在整个拉伸试验过程中，都对颈缩处的横截面面积进行监控，则可画出完整的真实应力-应变曲线。
因为由对数应变可得图9 用幂律表示铜的塑性应力-应变关系对塑性材料，其真实的应力-应变关系常可用简单的幂律关系来描述，如下式所示：根据图8所示的关系，用双对数坐标画出铜的真实应力-应变数据4，如图9所示。
图中，参数=0.474称为应变硬化参数,通常作为材料抗颈缩能力的度量。
塑性材料在室温下的n 值大致为0.02到0.5。
n “康西特莱（Considere ）作图法”利用真实应力-应变曲线的形状来量化不同材料在颈缩和冷拉过程中的差别。
该法以真实应力t σ为纵坐标、伸长比0/L L =λ为横坐标，重新画出拉伸时的应力-应变曲线。
在此λσ−t 曲线上找到真实应力为任意值t σ的点，过此点和坐标原点（原点处0=λ，不是1=λ）作割线，由式（6）可知，与t σ相对应的工程应力e σ即此割线的斜率。
图10 康西特莱作图法：（a ）真实的应力-应变曲线没有过原点的切线 ——无颈缩或冷拉过程；（b ）有一条过原点的切线——有颈缩而无冷拉过程；（c ）有两条过原点的切线——有颈缩和冷拉过程。
在真实的应力-应变曲线假设的许多可能形状中，考虑图10所示的向上凹、向下凹和S 形这三种情况。