高一物理变速直线运动速度与时间关系

合集下载

高一物理必修一重点知识点匀变速直线运动速度与时间的关系

高一物理必修一重点知识点：匀变速直线运动速度与时间的关系高一物理必修一重点知识点：匀变速直线运动速度与时间的关系一、【概念及公式】沿着一条直线，且加速度方向与速度方向平行的运动，叫做匀变速直线运动。

如果物体的速度随着时间均匀减小，这个运动叫做匀减速直线运动。

如果物体的速度随着时间均匀增加，这个运动叫做匀加速直线运动。

s(t)=1/2?at^2+v(0)t=【v(t)^2-v(0)^2】/(2a)={【v(t)+v(0)】/2}*t v(t)=v(0)+at其中a为加速度，v(0)为初速度，v(t)为t秒时的速度 s(t)为t秒时的位移速度公式：v=v0+at位移公式：x=v0t+1/2at2;位移---速度公式：2ax=v2;-v02;条件：物体作匀变速直线运动须同时符合下述两条：受恒外力作用合外力与初速度在同一直线上。

二、【规律】瞬时速度与时间的关系：V1=V0+at位移与时间的关系：s=V0t+1/2?at^2瞬时速度与加速度、位移的关系：V^2-V0^2=2as位移公式 X=Vot+1/2?at ^2=Vo?t(匀速直线运动)位移公式推导：⑴由于匀变速直线运动的速度是均匀变化的，故平均速度=(初速度+末速度)/2=中间时刻的瞬时速度而匀变速直线运动的路程s=平均速度*时间，故s=[(v0+v)/2]?t利用速度公式v=v0+at，得s=[(v0+v0+at)/2]?t=[v0+at/2]?t=v0?t+1/2?at^2⑵利用微积分的基本定义可知，速度函数(关于时间)是位移函数的导数，而加速度函数是关于速度函数的导数，写成式子就是ds/dt=v，dv/dt=a，d2s/dt2=a于是v=∫adt=at+v0，v0就是初速度，可以是任意的常数进而有s=∫vdt=∫(at+v0)dt=1/2at^2+v0?t+C，(对于匀变速直线运动)，显然t=0时，s=0，故这个任意常数C=0，于是有s=1/2?at^2+v0?t这就是位移公式。

高一物理必修1 匀变速直线运动的速度与时间的关系

(3)a3=-2m/s2
[讲解]除了用图象法来研究物体运动速度和时间的关系之外，我们还可
以用公式法来描述它。下面就来分析以下，如何用公式法来描述做匀变速
直线运动的物体的速度和时间的关系。
[提问]同学们观察图象，结合我们数学学过的知识，先猜想一下，做匀
变速直线运动的物体，某时刻速度和时间的关系应该如何表达？（如果学
容是物体的加速度，t 是时间间隔，v 则是 t 时刻末的速度（是瞬时速度）。
（2）
公式中有三个矢量，除时间 t 外都是矢量，所以，代入
数值计算时要特别注意方向性。物体做直线运动时，矢量的方向性可以在
选定正方向后，用正、负来体现，方向与规定正方向相同时，矢量取正值，
方向与规定方向相反时，矢量取负值。一般我们都去物体的运动方向或初
速度的方向为正。
［分析］结合图象进行说明。
[例题 1]汽车以 40km/h 的速度匀速行驶，现以 0.6m/s2 的加速度加速，
10s 后速度能达到多少？
[分析]首先我们必须明
确，研究的对象是汽车，研
究的过程是它加速后 10s 的
运动情况，要求物体 10s 后
速度能达到多少，也就是知
道初速度，加速度，时间，要求末速度，要注意的是，物体是加速的，也
课向，也即物体的加速度相等。堂 2.要学会从速度——时间图象上去理解运动的情况， v-t 图象的倾斜度表示物体的小加速度，物体做匀变速直线运动的速度——时间图象是一条倾斜的直线，它的倾斜结度（斜率）是不变的，也就是加速度不变。
3.从速度——时间图象上来理解速度与时间的关系式：v=v0+at，t 时刻的末速度 v 是在 v0 的基础上加上速度的变化量△v=at 得到。

2.2匀变速直线运动的速度与时间的关系教案-高一上学期物理人教版(2019)必修第一册

课题匀变速直线运动的速度与时间的关系共课时第课时课型新授教学目标1.根据实验得到的v-t图像是一条倾斜的直线，构建匀变速直线运动的模型，了解匀变速直线运动的特点。

2.能根据v-t图像得出匀变速直线运动的速度与时间的关系，理解公式的含义。

3.能应用匀变速直线运动的速度与时间的关系或图像分析和解决生产、生活中有关的实际物体。

4.践行社会主义核心价值观，培养学生科学精神、创新精神和爱国情怀。

重难点重：理解速度与时间的关系难：通过速度与时间的关系解决实际问题。

教学策略推理、讲授教学过程课前、课中反思复习引入教师提问：1.请同学们在下图中描绘物体以6m/s的匀速直线运动。

2.我们所描述的v-t图有什么特点？3.物体的加速度为多少？学生回答：略教师活动：对学生的回答进行点评与表扬。

教师进一步提问下图中a1、a2、a3的值分别为多少？学生活动：仔细的计算并且作答。

教师活动：及时的点评及表扬新课教学一：匀变速直线运动教师活动：补充与总结上述学生的回答。

总结：1.物理意义：沿着一条直线，且加速度不变的运动。

2.条件：（1）运动轨迹是直线（2）加速度恒定不变3. 分类：匀加速直线运动匀减速直线运动课堂练习：分析下列图像是不是匀变速运动思考与讨论教材图2.2-3 是一个物体运动的v-t 图像。

它的速度怎样变化？在相等的时间间隔内，即t ＝t′时，速度的变化量v′和v 总是相等的吗？物体在做匀变速运动吗？学生活动：积极思考，小组讨论，选取代表发言。

教师活动：对学生发言进行点评与总结总结：并画出相应图像。

1.在v-t图像中倾斜程度表示加速度大小。

倾斜程度逐渐变大，物体运动的加速度越来越大；倾斜程度直角变小，物体运动的加速度越来越小，最后为零，速度越来越大，最后匀速。

二：速度与时间的关系1.公式推导某质点作匀变速直线运动，已知该质点在初始时刻速度为v0，加速度为a，则t秒时的速度v是多少？教师提问：请同学们用初中数学直线公式表达该图像？学生回答：我们只记得y=kx+b教师提示：我们能不能用高中物理所学物理量来取代呢？学生回答：v=v 0+at教师提问：上面我们是从图像加数学得来的，那有没有物理的方法得到呢？请同学们用5分钟时间思考，如何小组讨论。

高一物理人教版2019必修第一册：匀变速直线运动的速度与时间的关系

(1)若汽车以0.6 m/s2的加速度加速，则10 s末速度能达到多少？
(2)若汽车刹车以0.6 m/s2的加速度减速，则10 s末速度能达到多少？
(3)若汽车刹车以3 m/s2的加速度减速，则10 s末速度为多少？
解:(1)取初速度方向为正方向则v0＝45km/h＝12.5 m/s
a1＝0.6 m/s2
向下。那么，经过3 s时物体的速度大小和方向是 ( B )
A．25 m/s，沿斜面向上
B．5 m/s，沿斜面向下
C．5 m/s，沿斜面向上
D．25 m/s，沿斜面向下解析：取初速度方向为正方向，则v0＝10 m/s，a＝－5 m/s2，由v＝v0＋at可得，当t＝3 s时，v＝－5 m/s， “－”表示速度方向沿斜面向下，故B正确。答案：B
刹车”的加速度取4～6 m/s2之间的某一值，则“全力自动刹车”的
最长时间为（）A. 5S/3
B.25S/3
C.2.5 s
D.12.5 s
【答案】C
5.一物体做直线运动的速度图象如图所示，则该物体（） A.先做匀加速运动，后做匀减速运动，
速度方向相同B.先做匀加速运动，后做匀减速运动，
速度方向相反C.先做匀减速运动，后做匀加速运动，
【答案】ABD
7.我国在西昌卫星发射中心用“长征三号丙”运载火箭，将第三颗北斗导航卫星送入预定轨道，这标志着北斗卫星导航系统工程建设又迈出了重要一步，卫星组网正按计划稳步推进.如图所示，发射过程中某段时间内火箭速度的变化规律为v＝（2t＋4） m/s，由此可知这段时间内（） A.火箭的初速度为4 m/sB.火箭的加速度为2 m/s2C.在3 s末，火箭的瞬时速度为12 m/sD.火箭做匀减速直线运动

高一物理练习题【匀变速直线运动的速度与时间的关系】

高一物理练习题【匀变速直线运动的速度与时间的关系】[A组基础达标练]1．对于匀变速直线运动的速度与时间关系式v＝v0＋at，以下理解正确的是()A．v0是时间间隔t开始的速度，v是时间间隔t内的平均速度B．v一定大于v0C．在时间间隔t内，at可以是速度的增加量，也可以是速度的减少量，以初速度方向为正方向时，在匀加速直线运动中at为正值，在匀减速直线运动中at为负值D．a与匀变速直线运动的v-t图像的倾斜程度无关解析：v0、v都是瞬时速度，at是速度的变化量，A错误；在匀加速直线运动中v>v0，在匀减速直线运动中v<v0，B错误；在v-t图像中，v-t图像的斜率表示加速度，D错误。

答案：C2．如图所示为我国的“和谐号”列车，“和谐号”到某站时匀减速进站，停靠一段时间后又匀加速(同方向)出站。

在如图所示的四个v-t图像中，正确描述了“和谐号”运动情况的是()解析：进站速度均匀减小，出站速度均匀增大，故A、D错误；进站、出站的运动方向相同，故B正确，C错误。

答案：B3．一辆沿直线匀加速行驶的汽车，经过路旁的两根电线杆共用5 s时间，汽车的加速度为2 m/s2，它经过第二根电线杆时的速度是15 m/s，则汽车经过第一根电线杆的速度为()A．2 m/s B．10 m/sC．2.5 m/s D．5 m/s解析：汽车沿直线匀加速行驶，加速度为2 m/s2，经过第二根电线杆时的速度是15 m/s，用时5 s，根据速度与时间的关系式v＝v0＋at得v0＝v－at＝(15－2×5) m/s＝5 m/s，D正确。

答案：D4．(多选)2021年10月14日，我国在太原卫星发射中心采用长征二号丁运载火箭成功发射首颗太阳探测科学技术试验卫星“羲和号”。

假若某段时间内火箭速度的变化规律为v ＝(8t＋16) m/s，由此可知这段时间内()A．火箭的初速度为8 m/sB．火箭的加速度为16 m/s2C．在3 s末，火箭的瞬时速度为40 m/sD．火箭做匀加速直线运动解析：在这段时间内，由速度的表达式可知，火箭的速度均匀增大，故火箭做匀加速直线运动，选项D正确；由匀变速直线运动的速度公式v＝v0＋at知，这段时间内火箭的初速度v0＝16 m/s，加速度a＝8 m/s2，选项A、B错误；将时间t＝3 s代入得v3＝40 m/s，选项C正确。

匀变速直线运动的速度与时间的关系ppt课件

根据 v＝v0 ＋at 得：
汽车 10 s 末的速度为 16 m/s，从刹车到停下来要用 2.67 s。
知识讲解
解题步骤： 1.认真审题，分析已知量和待求量； 2.弄清题意画示意图，明确初速度v0、末速度v、加速度a和时间 t及各量的正负号。 3.将已知量带入公式求未知量，若所求量是矢量，要说明方向。 4.对计算结果和结论进行验算。
知识讲解
解法二：直接解，再检验解：以初速方向为正方向，则 a＝-5 m/s2 vt =v0+at=20+（-5）×10m/s=-30m/s 汽车刹车过程是一个实际的运动过程，一旦车的速度减到0，汽车将保持静止状态，不后退，由结果可知，车实际已经停下来了，所以6s末 vt =0。
18
知识讲解
人教版高一物理必修 1 第一学期第二章 2.2匀变速直线运动的速度与时间的关系
第二章匀变速直线运动的研究
2.2 匀变速直线运动的速度与时间的关系
核心素养目标
1、物理观念：知道什么是匀变速直线运动，理解“匀”的含义是指加速度恒定． 2、科学思维：理解v t图像中图线与纵轴的交点、斜率的物理意义． 3、科学探究：会从加速度的定义式中推导速度和时间的关系，明白在v t图像中速度和时间的关系． 4、科学态度与责任：会用v＝v0＋at解释简单的匀变速直线运动问题．
分析：依题意，汽车加速和减速过程都是在做匀变速直线运动。第（1）问是已知加速的时间求末速度。第（2）问是已知末速度求减速的时间。两个问题都需要用匀变速直线运动的速度与时间关系式来求解。其中，第（2）问汽车加速度的方向跟速度、位移的方向相反，需要建立坐标系处理物理量之间的正负号问题。
知识讲解
解（1）汽车做匀加速直线运动。初速度 v0＝36 km/h ＝10 m/s，加速度 a＝0.6 m/s2 ，时间 t＝10 s

高一物理《速度和时间的关系》

这种运动就叫匀速直线运动。
2、x-t图象是一条倾斜的直线
3、匀速运动是速度（大小，方向）不变的运动
4、V-t图像是一条平行时间轴的直线
V-t图像表示物体匀速运动
假设向右为正方向
v/ms-1
2 0 -2
v/ms-1
2 0 -2
V=2m/s
4
t/s
4
t/s
V=-2m/s
假设向右为正方向
一、复习
1
前面我们学习了位移和时间的关
系，从物体运动的位移--时间图象我
们可以得出一些物体运动的相关信息。
x/m 1
2
由图象可以确定： ①运动的状态 ②速度的大小v1＞v2
0
t/s
匀速直线运动的x—t图象是倾斜的直线
我们可以看到图象法也是研究物体运动的一种方法和途径，下面我们来利用图象研究速度和时间的关系。
0
5 10 15
7、甲、乙两个质点同时同地向同一方向做直线运动，
它们的v一t图像如图所示，由图像可知( CD)
A．甲比乙运动快，所以乙追不上甲 B．在2 s末时两质点相遇 C.在2 s末后乙的速度大于甲的速度
D．乙会追上甲并超过甲
8、如图所示为一物体做匀变速直线运动的速度图线，根据
图线作出的以下判断中，正确的是（ A、物体始终沿正方向运动
）
BD
B、物体先沿负方向运动，在t=2秒后物体开始沿正方向运动
C、在t=2秒前物体位于出发点负方向上，在t=2秒后位于出发点正方向上
D、在t=2秒时，物体距出发点最远。
图象在t轴下方与坐标轴围成的面积表示位移是负的。
9、如图为质点在一段时间内运动的x—t 图象，画出在该时间内它的v—t图象.

高一物理必修一2.2《匀变速直线运动的速度与时间的关系》

注意：对于末速度为零的匀减速直线运动，也
可以采用逆向思维法，即把运动倒过来看成是初速度为零的匀加速直线运动。
例题3、某汽车正以12m/s的速度在路面上匀速行驶，前方出现紧急情况需刹车，加速度大小是3m/s2，求汽车5s末的速度。解：以初速方向为正方向注意：则v=v0+at=12+(-3) ×5m/s=-3m/s 刹车问题（与实际相符）正确解法：以初速方向为正方向当车速减为零时，v=v0+at=12-3t=0 解得t=4s
加速运动，a为正值。减速运动，a为负值。
3、明确初速度v0、末速度v、加速度a和时间t 及各量的正负号。
4、将已知量带入公式求未知量，若所求量是矢量，要说明方向。
注意：在解题过程中可适当运用图解法。
例题1、汽车以40km/h的速度匀速行驶，现以0.6m/s2 的加速度加速，10s后速度能达到多少？
即4s末汽车已刹车完毕，所以5末时
汽车处于静止状态，即速度为零。
总结
1.匀变速直线运动
分类
沿着一条直线，且加速度不变的运动。匀加速直线运动匀减速直线运动
2.匀变速直线运动的速度公式
v=v0Байду номын сангаасat
作业：课后第1、2题
t
v
o
例题：课堂讲义例1。
t
二、速度与时间的关系
设物体从运动开始0到时刻t，那么：时间的变化量就是△t＝t-0 速度的变化量就是△v＝v-v0 v
v v v0 a t t
Δν Δt
t
解得：v＝v0 +at
设t=0时速度为v0 t时刻的速度为v。
匀变速直线运动公式的说明
末速度

高一物理必修三《匀变速直线运动的速度与时间的关系》教案

【导语】现代⼈总结成功的⼏⼤要素：正确的思想、不懈的⾏动、伟⼤的性格、娴熟的技能、天赐的机会、宝贵的健康。

可见，想取得成功，不仅要吃“苦中苦”，也要相关条件的配合⽀持，那些光知道吃苦的⼈，那些吃了不值得吃的苦的⼈，那些把吃苦当成解决⼀切问题法宝的⼈，恐怕只能继续在“苦中苦”的怪圈⾥徘徊。

⽆忧考为⼤家整理了《⾼⼀物理必修三《匀变速直线运动的速度与时间的关系》教案》更多精彩内容，请持续关注本站！【篇⼀】教学准备教学⽬标知识与技能 1.知道匀变速直线运动的v—t图象特点，理解图象的物理意义. 2.掌握匀变速直线运动的概念，知道匀变速直线运动v—t图象的特点. 3.理解匀变速直线运动v—t图象的物理意义，会根据图象分析解决问题， 4.掌握匀变速直线运动的速度与时间关系的公式，能进⾏有关的计算. 过程与⽅法 1.培养学⽣识别、分析图象和⽤物理语⾔表达相关过程的能⼒. 2.引导学⽣研究图象、寻找规律得出匀变速直线运动的概念. 3.引导学⽣⽤数学公式表达物理规律并给出各符号的具体含义. 情感态度与价值观 1.培养学⽣⽤物理语⾔表达物理规律的意识，激发探索与创新*. 2.培养学⽣透过现象看本质、甩不同⽅法表达同⼀规律的科学意识. 教学重难点教学重点 1.理解匀变速直线运动v—t图象的物理意义 2.掌握匀变速直线运动中速度与时间的关系公式及应⽤. 教学难点 1.匀变速直线运动v—t图象的理解及应⽤. 2.匀变速直线运动的速度⼀时间公式的理解及计算. 教学⼯具多媒体、板书教学过程⼀、匀变速直线运动 1.基本知识 (1)定义：沿着⼀条直线运动，且加速度不变的运动. (2)分类 ①匀加速直线运动：速度随时间均匀增加的直线运动. ②匀减速直线运动：速度随时间均匀减⼩的直线运动. (3)图象：匀变速直线运动的v-t图象是⼀条倾斜的直线. 2.思考判断 (1)匀变速直线运动是速度均匀变化的直线运动.(√) (2)物体的加速度为负值时，不可能是匀加速直线运动.(×) (3)加速度不变的运动⼀定是匀变速直线运动.(×) 探究交流某物体的速度—时间图象如图所⽰，试说明物体做什么运动? 【提⽰】由于物体的v-t图象是⼀条倾斜直线，⾸先确定该物体做匀变速直线运动;⼜由于它的速度逐渐增⼤，所以说物体的运动性质为匀加速直线运动. ⼆、速度与时间的关系式 1.基本知识 (1)速度公式：v=v0+at. (2)对公式的理解：做匀变速直线运动的物体，在t时刻的速度v，就等于物体在开始时刻的速度v0，再加上在整个过程中速度的变化量at. 2.思考判断 (1)公式v=v0+at仅适⽤于匀加速直线运动.(×) (2)速度随时间不断增加的运动叫做匀加速直线运动.(×) (3)速度随时间均匀减⼩的直线运动，叫做匀减速直线运动.(√) 探究交流试根据匀变速直线运动的特点，分别通过v-t图象和加速度的定义式推导出速度v和时间t关系的数学表达式. 【提⽰】 (1)图象推导：由图可知末速度⼤⼩由初速度v0和t时间内增加的部分at组成，故v=v0+at. (2)加速度定义式推导：由得：v=v0+at. 三、对速度-时间图象的理解【问题导思】 1.上节课“探究⼩车的速度与时间的变化关系”中所画出的v-t图象是什么形状?图象的物理意义是什么? 2.v-t图线的倾斜程度具有什么含义? 3.速度图象中的纵截距和横截距代表什么意义? 1.匀速直线运动的v-t图象⼀条平⾏于时间轴的直线.从图象中可以直接读出速度的⼤⼩和⽅向. 2.匀变速直线运动的v-t图象如图所⽰，匀变速直线运动的v-t图象是⼀条倾斜的直线. (1)直线a反映了速度随着时间是均匀增加的，为匀加速直线运动的图象. (2)直线b反映了速度随着时间是均匀减⼩的，为匀减速直线运动的图象. (3)直线c反映了速度随着时间先均匀减⼩，后均匀增加，由于加速度不变，整个运动过程也是匀变速直线运动. 3.v-t图象应⽤误区警⽰：v-t图象的两点说明 1.只能描述直线运动，⽆法描述曲线运动. 2.v-t图象描述的是物体的速度随时间的运动规律，并不表⽰物体的运动轨迹. 例：如图所⽰为某质点的v-t图象，则下列说法中正确的是() A.在0～6s内，质点做匀变速直线运动 B.在6s～10s内，质点处于静⽌状态 C.在4s末，质点向相反⽅向运动 D.在t=12s末，质点的加速度为-1m/s2 【审题指导】解答该题主要是观察图线，通过图线的特点得出有关结论，观察图线时，需要注意： (1)速度的正、负问题. (2)速度的⼤⼩变化趋势. (3)图线斜率⼤⼩问题. (4)图线斜率的正负问题. 【答案】D 规律总结：v-t图象的意义 1.可求出物体在任⼀时刻的速度和物体达到某⼀速度所需要的时间. 2.图线的斜率等于物体的加速度. 3.图线在时间轴的上⽅表⽰物体向正⽅向运动，在时间轴的下⽅表⽰物体向负⽅向运动. 4.可判断物体的运动性质：在v-t图象中，倾斜直线表⽰物体做匀变速直线运动;平⾏于时间轴的直线表⽰物体做匀速直线运动;和时间轴重合的直线表⽰物体静⽌. 四、速度时间关系式的应⽤【问题导思】 1.汽车从静⽌匀加速运动，经时间t后的速度怎么求出?需要知道什么物理量? 2.速度公式v=v0+at中各量的含义是什么?它们是⽮量还是标量? 3.速度公式的适⽤条件是什么?应⽤其解题时应注意什么问题? 1.适⽤条件公式v=v0+at只适⽤于匀变速直线运动. 2.公式中各量的含义 (1)v0为开始时刻物体的瞬时速度，称为初速度，v为经时间t后物体的瞬时速度，称为末速度. (2)a为物体的加速度，为恒量，表明速度均匀变化，即相等时间内速度的变化量相等. 3.⽮量性 (1)公式中的v0、v、a均为⽮量，应⽤公式解题时，⼀般取v0的⽅向为正⽅向，a、v与v0的⽅向相同时取正值，与v0的⽅向相反时取负值.对计算结果中的正、负，应根据正⽅向的规定加以说明，如v>0，表明末速度与初速度v0同向;若a<0，表明加速度与v0反向. (2)a与v0同向时物体做匀加速直线运动，a与v0反向时物体做匀减速直线运动. 误区警⽰速度公式v=v0+at虽然是加速度定义式的变形，但两式的适⽤条件是不同的： 1.v=v0+at仅适⽤于匀变速直线运动. 2.可适⽤于任意的运动，包括直线运动和曲线运动. 例：在平直公路上，⼀辆汽车以108km/h的速度⾏驶，司机发现前⽅有危险⽴即刹车，刹车时加速度⼤⼩为6m/s2，求： (1)刹车后3s末汽车的速度⼤⼩; (2)刹车后6s末汽车的速度⼤⼩. 【审题指导】解答该题应把握以下两点： (1)刹车时为减速运动. (2)计算结果是否符合实际. 【答案】(1)12m/s(2)0 规律总结：求解汽车刹车问题时应注意的问题汽车刹车、飞机着陆、⽕车进站等实际减速运动，由于它们在速度减⼩为零后不再返回，此后它们就⼀直停留在某位置不动，故计算它们的速度时切不可盲⽬将所给时间代⼊速度公式.若所给时间⼩于刹车⽤时，则可将所给时间代⼊速度公式求解，若所给时间⼤于或等于刹车⽤时，则它们在所给时间速度为零. 五、加速度变化的v-t图象例：试说明如图所⽰的图象中物体的运动情况. 【答案】图甲中，物体运动的加速度越来越⼤，速度越来越⼤，表⽰物体做加速度越来越⼤的变加速直线运动. 图⼄中，物体运动的加速度越来越⼩，最后为0，速度越来越⼤，最后不变，表⽰物体做加速度越来越⼩的变加速直线运动，直到加速度为0，做匀速直线运动. 图丙中，物体运动的加速度越来越⼤，速度越来越⼩，最后为0，表⽰物体做加速度越来越⼤的变减速直线运动，直到速度减为0. 图丁中，物体运动的加速度越来越⼩，速度越来越⼩，表⽰物体做加速度越来越⼩的变减速直线运动. 规律总结：根据v-t图象判断加速度的变化图甲中，速度v随时间t的延长⽽增⼤，在时间轴上取两段相等的时间间隔Δt，对应的速度变化量Δv不同，⽽且Δv2>Δv1，所以物体做的不是匀加速直线运动.当Δt→0时，a=Δt/Δv表⽰Δt内任⼀时刻的瞬时加速度，此时a应为该时刻曲线切线的斜率.即v-t图象为曲线时，曲线上⾯某点的切线斜率等于该时刻物体的加速度.对甲图，随时间t的延长，切线斜率变⼤，即物体做加速度变⼤的加速运动. 同理可得，图⼄中的物体做加速度逐渐减⼩的变加速直线运动. 课后⼩结本节重点学习了对匀变速直线运动的理解和对公式v=vo+at的掌握.对于匀变速直线运动的理解强调以下⼏点： 1.任意相等的时间内速度的增量相同，这⾥包括⼤⼩⽅向，⽽不是速度相等. 2.从速度⼀时间图象上来理解速度与时间的关系式：v=vo+at，t时刻的末速度v是在初速度v0的基础上，加上速度变化量△v=at得到. 3.对这个运动中，质点的加速度⼤⼩⽅向不变，但不能说a与△v成正⽐、与△t成反⽐，a决定于△v和△t的⽐值. 4.a=△v/△t⽽不是a=v/t,a=△v/△t=(vt-v0)/△t即v=vo+at，要明确各状态的速度，不能混淆. 5.公式中v、vo、a都是⽮量，必须注意其⽅向. 板书 §2.2匀速直线运动的速度和时间的关系 1.匀变速直线运动 2.速度⼀时间图象 3.速度与时间的关系式v=v0+at 4.初速度vo再加上速度的变化量at就得到t时刻物体的末速度【篇⼆】教学准备教学⽬标知识与技能 1、掌握匀变速直线运动的概念、运动规律及特点。

高一物理匀变速直线运动的速度与时间的关系

解：由题意知 α=-6m/s2，
t=2s， υ=0m/s，由υ=υ0＋αt 得 υ0=υ-αt =0m/s-(-6m/s2)×2s =12m/s =43km/h ∴汽车的速度不能超过43km/h 根据V= V0 + a t，有
v v 0 0m/s 12m/s a t 1.5s 8m / s 2
2、关于直线运动的下述说法中正确的是 A.匀速直线运动的速度的恒定的，不随时间而改变 B.匀变速直线运动的瞬时速度随时间而改变 C.速度随时间不断增加的运动，叫匀加速直线运动（ ABD ）
D.速度随着时间均匀减小的运动，通常叫做匀减速直线运动
3、如图所示，两条直线表示两个物体的运动
特点，试分析两物体各做什么运动，两条直
0.6m/s2的加速度加速，10s后速度能达到多少？加速后经过多长时间汽车的速度达到80km/h？
解：由题意知初速度V0=40km/h =11m/s，加速度a=0.6m/s2，时间t＝10s,10s后的速度为V 由V=V0+at得 V=V0+at =11m/s+0.6m/s2× 10s =17m/s=62km/h 由V=V0+at得
纸带
V-t图象
v
o
t
பைடு நூலகம்
v
探究：
⑴图象的形状特点 ⑵速度如何变化的 ⑶加速度如何计算
o
t
v
v4
v3 v1 v0 0
探究：
}
∆v
v2
∆t
} ∆v
∆t
⑴图象的形状特点 ⑵速度如何变化的 ⑶加速度如何计算
}
t1
由于v-t图象是一条直线，无论∆t选在什么区间，对应的速度 v的变化量∆v与时间t的变化量∆t之比都是一样的，表示速度的变化量与所用时间的比值，即加速度。所以v-t图象是一倾斜的直线，是加速度不变的运动。

高一物理必修一人教版第二章2 匀变速直线运动的速度与时间的关系

今天这节课我们再进一步探究匀变速直线运动的速度
与时间的关系。
说出下图显示的物体的运动
甲乙
运动方向一定相反吗？
一、匀变速直线运动
引例：如图所示，一个小球沿
着光滑的斜面下滑，（点击右图）每隔1s 小球的位置分别
是A，B，C，D，对应的速度分
别是 vA = 0，vB = 0.5 m/s vC = 1.0 m/s，vD = 1.5 m/s 点击可重复观看
的速度: v=v0+at=(11+0.6×10×3.6)km/h=61.6km/h
例题3.火车在过桥时，需要提前减速。一列以72km/h
的速度匀速行驶的火车，在到达一座铁桥前100s开始减速，加速度的大小是0.1m/s2,那么，火车到达铁桥时的速度是多大？解:已知v0= 72km/h =20m/s,a=-0.1m/s2,t=100s, 所以vt=v0+at=20m/s+(-0.1m/s2×100s)=10m/s 答：火车到达铁桥时的速度是10m/s
1.下列关于匀变速直线运动的说法正确的是( D ) A.匀变速直线运动是运动快慢相同的运动
B.匀变速直线运动是速度变化量相同的运动
C.匀变速直线运动的a-t图象是一条倾斜直线 D.匀变速直线运动的v-t图象是一条倾斜直线
2.根据下表数据，画出v-t图象，说明做何运动？位置编号 0 1 2 3 4 5
Δt Δv Δt ′ Δv ′
1.物体运动的速度怎样变化? 2.在相等的时间间隔内,速度的变化量总
是相等吗?
3.物体在做匀加速运动吗?
t1
t2 t t4 3
t
例题2.汽车以40km/h的速度匀速行驶，现以0.6m/s2 的加速度加速，10s后速度能达到多少？

匀变速直线运动的速度与时间的关系(6大题型)24-25学年高一上学期物理同步题型(人教版必修一)教师

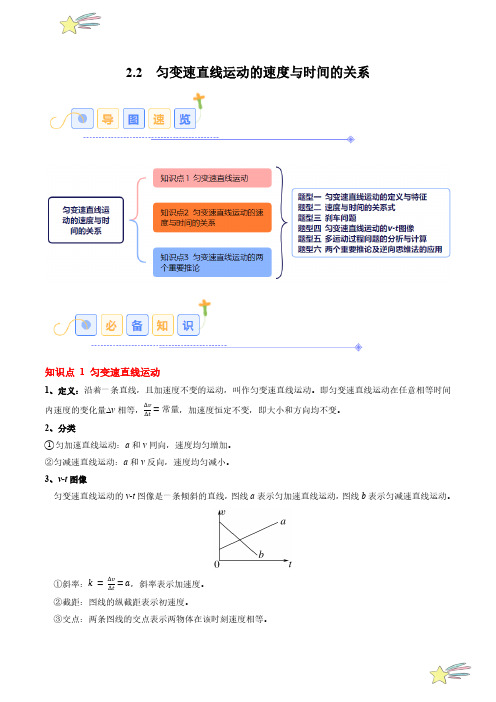
2.2 匀变速直线运动的速度与时间的关系知识点 1 匀变速直线运动1、定义：沿着一条直线，且加速度不变的运动，叫作匀变速直线运动。

即匀变速直线运动在任意相等时间=常量，加速度恒定不变，即大小和方向均不变。

内速度的变化量∆v相等，∆v∆t2、分类①匀加速直线运动：a和v同向，速度均匀增加。

②匀减速直线运动：a和v反向，速度均匀减小。

3、v-t图像匀变速直线运动的v-t图像是一条倾斜的直线，图线a表示匀加速直线运动，图线b表示匀减速直线运动。

=a，斜率表示加速度。

①斜率：k=∆v∆t②截距：图线的纵截距表示初速度。

③交点：两条图线的交点表示两物体在该时刻速度相等。

知识点2 匀变速直线运动的速度与时间的关系1、速度公式的推导2、速度公式v t =v 0+at3、对公式的理解①该公式仅适用于匀变速直线运动。

②公式是矢量式，习惯上规定初速度的方向为正方向。

③公式的特殊形式：当a =0时，v = v 0 ；当v 0 = 0时，v =at 。

④可逆思想：若物体做末速度为0的匀减速直线运动，则可以运用逆向思维，将其看成反向的初速度为0的匀加速直线运动。

知识点3 匀变速直线运动的两个重要推论1、某段时间内的平均速度等于初、末速度的平均值，即 v =12（v 0+v ）。

【证明】如图所示为匀变速直线运动的v -t 图像，图线与坐标轴所围的面积表示这段时间内的位移。

则t 时间内的位移为x =12（v 0+v ）t ，故平均速度v =xt =12（v 0+v t ）。

2、某段时间中间时刻的瞬时速度等于这段时间内的平均速度，即v t 2=v =12（v 0+v t ）。

【证明】0∼t 2 时间内，有v t 2=v 0+a ∙t2①t 2∼t 时间内，有v t =v t 2+a ∙t2②联立①②可得，v t 2=v =12（v 0+v t ）=v 。

1、刹车类问题求解刹车类问题时应注意，由于它们在速度减小为零后就会停留在某位置不动，所以计算它的末速度时不可盲目将所给时间代人公式计算。

匀变速直线运动速度时间公式

匀变速直线运动速度时间公式匀变速直线运动（Uniformly Accelerated Motion, UAM）是物理学中常见的一种运动形式。

在这种运动中，物体的加速度是常数，但速度是变化的。

与匀速直线运动相比，匀变速直线运动更为复杂。

为了描述这种运动，我们需要使用速度-时间关系式、位移-时间关系式和速度-位移关系式等等。

接下来，我将详细介绍匀变速直线运动的速度时间公式。

在匀变速直线运动中，加速度是常数，设为a；初速度是v0，最终速度是v，运动过程的时间是t，位移是s。

根据这些已知值，我们可以得到一些方程式来描述运动过程。

1.速度-时间关系式：v = v0 + at这个公式表明，物体的速度v是它的初始速度v0与加速度a乘以时间t的和。

该公式适用于任何时间点上的物体速度计算。

2.位移-时间关系式：s = v0t + (1/2)at^2这个公式描述了匀变速直线运动中物体的位移s和时间t之间的关系。

它由物体的初始速度v0、时间t和加速度a确定。

3.速度-位移关系式：v^2 = v0^2 + 2as这个公式表达了物体的最终速度v和位移s之间的关系。

它通过物体的初始速度v0、加速度a和位移s来计算最终速度v。

以上三个公式是匀变速直线运动中最常用的速度时间关系公式。

它们可以相互推导和证明，因此在解题时可以有选择地使用它们中的任意一个。

有了以上的速度时间关系公式，我们就可以用它们来计算物体在匀变速直线运动中的各种参数。

例如，如果我们知道初始速度v0、加速度a和时间t，我们可以用速度-时间关系式计算出最终速度v；如果我们知道初始速度v0、加速度a和位移s，我们可以用速度-位移关系式计算出最终速度v等等。

需要注意的是，在使用以上公式时需保持单位的一致性。

例如，如果加速度的单位为m/s^2，时间的单位为秒，那么速度的单位应为m/s，位移的单位应为米。

总结起来，匀变速直线运动速度时间公式包括速度-时间关系式、位移-时间关系式和速度-位移关系式。

高一物理 2.2 匀变速直线运动的速度与时间的关系教案新人教版

第二节匀变速直线运动的速度与时间的关系学习目标（一）课程要求1．理解匀变速直线运动的定义2．理解匀变速直线运动的v-t图象的特点3．掌握匀变速直线运动的速度与时间关系的公式v = v0+ at,并能利用公式解决实际问题（二）重、难点重点：1. 理解匀变速直线运动的定义2.理解匀变速直线运动的v-t图象特点。

3.匀变速直线运动的速度与时间关系的有关计算。

难点：1.匀变速直线运动定义的理解2.匀减速直线运动的速度与时间关系的有关计算。

强化基础1．下列运动图象中表示质点做匀变速直线运动的是（）2．关于匀减速直线运动的描述，下列说法中正确的是 ( )A．在任意相同的时间间隔内，速度变化均相同B．只有在连续相同的时间间隔内，速度变化才相同C．加速度是恒定的D．加速度越来越小3．关于匀变速直线运动中加速度的方向和正、负值问题，下列说法中错误．．的是( ) A．匀加速直线运动中加速度方向一定和初速度方向相同B．匀减速直线运动中加速度一定是负值C．匀加速直线运动中加速度也有可能取负值D．只有在规定了初速度方向为正方向的前提下，匀加速直线运动的加速度才取正值4．关于图2所示v－t图象，下列叙述正确的是 ( ) A．在t1到t2这段时间内，A的速度比B的速度增加得多，所以a A > a BB．当速度由v1增加到v2时， A用的时间少于B用的时间，所以a A > a BC．在同一时刻v A > v B，所以a A > a BD．A、B一定是从同一位置向同一方向做初速度为零的匀加速直线运动5．某物体做直线运动的v— t图象如图3所示，从图中可以看出，物体加速度和速度方向相同的时间间隔是( )A．只有0～2 sB．只有2 s～4 sC．0～2 s和6 s～8 sD．0～2 s和5 s～6 s6．一物体做匀变速直线运动的速度方程为v=(－2t+12)m/s。

（1）说明方程中各字母或数字的物理意义；（2）在图4中的直角坐标系中画出该物体运动的v-t图象。

高中物理高一物理《2.2-匀变速直线运动的速度与时间的关系》教案(必修一)

课题名称§2.2匀变速直线运动的速度与时间的关系课时数1课时课型问题解决课课程标准《普通高中物理课程标准》中对本节知识的具体内容标准如下：1.知道什么是匀变速直线运动；2.知道匀变速直线运动的v-t图像的特点，知道直线的倾斜程度反映匀变速直线运动的加速度；3.理解匀变速直线运动的速度与时间的关系式v=v0+at，并能用它来解决匀变速直线运动的相关问题。

学习目标1．知识与技能：(1)知道匀速直线运动t-υ图象，理解图像的物理意义。

(2)知道匀变速直线运动的t-υ图象,概念和特点。

(3)掌握匀变速直线运动的速度与时间关系公式v=v0+at,并会应用它进行计算。

2．过程与方法：(1)让学生初步了解探究学习的方法.(2)培养学生的逻辑推理能力,数形结合的能力,应用数学知识的解决物理问题的能力。

3．情感态度与价值观：(1)培养学生基本的科学素养。

(2)培养学生建立事物是相互联系的唯物主义观点。

(3)培养学生应用物理知识解决实际问题的能力。

重点重点：(1)匀变速直线运动的t-υ图象,概念和特点。

难点(2)匀变速直线运动的速度与时间关系的公式v =v0+at,并会应用它进行计算。

难点：应用t-υ图象推导出匀变速直线运动的速度与时间关系的公式v = v0 + at。

学习过程评价任务（内容、问题、试题）学习活动（方式、行为策略）一、匀变速直线运动【问题1】上一节中已经学习了关于速度时间图像的相关知识，请同学们根据自己描绘出的速度时间图像对小车的运动做定性描述。

并以此总结，我们能从速度时间图像中提取那些运动信息？小车的速度增加得有规律吗？【成功发现】：不难看出，速度图象中的一点表示某一时刻的速度；小车的速度图象是一条倾斜的直线，表明小车的速度不断增大，而且速度变化是均匀的；小车做的是加速度不变的直线运动。

[来源:]★沿着一条直线运动，且加速度保持不变的运动，叫做匀变速直线运动。

★在上图中可以看出，匀变速直线运动的速度时间图像是一条倾斜的直线。

高一物理匀变速直线运动的速度与时间的关系教案

芯衣州星海市涌泉学校2．2匀变速直线运动的速度与时间是是的关系学习目的:1.知道匀变速直线运动的根本规律。

2.掌握速度公式的推导，并可以应用速度与时间是是的关系式。

3.能识别不同形式的匀变速直线运动的速度-时间是是图象。

学习重点：1.推导和理解匀变速直线运动的速度公式。

2.匀变速直线运动速度公式的运用。

学习难点:对匀变速直线运动速度公式物理意义的理解。

主要内容:一、匀变速直线运动：沿着一条直线，且加速度不变的运动，叫做匀变速直线运动。

1．匀加速直线运动：2．匀减速直线运动：二、速度与时间是是的关系式1．公式：v=v0+at2．推导：①由加速度定义式变形：②也可以根据加速度的物理意义和矢量求和的方法推出：加速度在数值上等于单位时间是是内速度的改变量，且时间是是t内速度的改变量△v=at，设物体的初速度为v0，那么t秒末的速度为v=v0+△v=v0+at 3．物理意义：4．由数学知识可知，v是t的一次函数，它的函数图象是一条倾斜直线，直线斜率等于a，应用速度公式时，一般取v0方向为正方向，在匀加速直线运动中a＞0，在匀减速直线运动中a＜0。

【例一】汽车以40km/h的速度匀速行驶，现以0．6m/s2的加速度加速运动，问10s后汽车的速度能到达多少？【例二】一辆汽车做匀减速直线运动，初速度大小为15m/s，加速度大小为3m/s2，求：①汽车第3s末的瞬时速度大小？②汽车速度刚好为零时所经历的时间是是？【例三】辆汽车做匀减速直线运动，初速度大小为15m/s，加速度大小为3m/s2，求：①汽车第6s末的瞬时速度大小？②汽车末速度为零时所经历的时间是是？【例四】火车从A站驶往B站，由静止开始以0．2m／s2加速度作匀变速直线运动，经1分钟到达最大速度Vm后匀速行驶，途中经过一铁路桥，假设火车过桥最高限速为18km／h，火车减速的最大加速度为0．4m／s2，那么(1)火车的最高行驶速度为多少(2)火车过桥时应提早多长时间是是开始减速【例五】如下列图，在一光滑斜面上，有一小球以V0=5m/s沿斜面向上运动，经2s到达最高点，然后又沿斜面下滑，经3s到达斜面底端，小球在斜面上运动的加速度恒定，试求：(1)小球运动的加速度。

高一物理第二节匀变速直线运动速度和时间的关系人教实验版知识精讲

高一物理第二节匀变速直线运动速度和时间的关系人教实验版【本讲教育信息】一. 教学内容：第二节匀变速直线运动速度和时间的关系第三节匀变速直线运动位移和时间的关系二. 知识要点：1. 进一步理解匀变速直线运动的速度时间图象，学会利用图象表示物理规律。

2. 知道匀变速直线运动速度公式的推导方法。

3. 掌握匀变速直线运动的速度公式，会用公式解决有关运动问题。

4. 知道匀变速直线运动位移公式的推导方法。

5. 进一步理解匀变速直线运动的速度时间图象，会利用速度时间图象求位移。

6. 掌握匀变速直线运动的位移公式，会用公式解决有关运动问题。

三. 重点、难点解析：1. 匀变速直线运动的定义小车做直线运动的v—t图象是一条倾斜的直线，表示小车在任意相等的时间内速度的变化都一样，如下列图；小车的加速度不变。

这样的运动是变速运动中最简单的运动形式，叫做匀变速直线运动。

匀变速直线运动的类型：〔1〕匀加速直线运动：速度随时间均匀增加〔如汽车起步、飞机起飞、火车出站、石块自由下落等〕〔2〕匀减速直线运动：速度随时间均匀减小〔如汽车刹车、飞机着落、火车进站、石块竖直上抛等〕2. 匀变速直线运动的图象〔1〕匀变速直线运动的图线是一条倾斜的直线；在时间轴上方，匀加速直线运动图线是一条向上倾斜的直线〔如图2〕，匀减速直线运动图线是一条向下倾斜的直线〔如图3〕。

〔2〕从图线上可以确定物体在任一时刻的速度。

如：在图2中t=6s时刻物体的速度大小为8m/s，方向与规定的正方向一样。

〔3〕从图线上可以确定物体达到某一速度所对应的时刻〔或所需时间〕。

如：在图3中v=2.0 m/s 在t=2s 时刻〔或从0时刻起经历2s 时间〕。

〔4〕从图线上可以确定物体做匀变速直线运动的加速度。

如：在图2中，取t=0时刻到t=6s 时刻过程，时间t=6s ，初速度v 0=2m/s ，末速度v=8 m/s ，如此加速度a =tv v 0-=1 m/s 2，方向与正方向一样。

高一物理匀变速直线运动的速度与时间的关系

2 匀变速直线运动的速度与时间的关系一、匀变速直线运动在现实生活中，不同物体的运动快慢程度往往不同.就是同一物体的运动，在不同的过程中，运动情况也不一定相同.比如：火车出站时速度由零逐渐增大，速度达到一定值后匀速运动，进站时速度逐渐减小至零.整个过程中，运动情况不同.火车在不同阶段速度如何变化？加速度发生变化吗？火车出站时速度增加，其v-t 图象如同上节小车在重物牵引下运动的v-t 图象；在平直轨道上行驶时速度不变，v-t 图象是平行于t 轴的直线；进站时速度逐渐减小，三个阶段v-t 图象分别如图2-2-5甲、乙、丙所示：图2-2-51.在以上三个v-t 图象中，取相同时间Δt 看速度的变化量Δv 如何变化.发现图甲Δv ＞0，且数值相同，图乙Δv=0，图丙Δv ＜0且数值也相同.2.取相同时间间隔Δt ′＜Δt ，观察Δv 的变化，结论与上述相同.3.取相同时间间隔Δt ″＜Δt ′，观察Δv 的变化，仍得到上述结论.结论：在任意相等的时间内：图甲、图丙Δv 不变.由a=t v ∆∆知：加速度不变图乙Δv=0，说明做匀速直线运动.归纳：如果一个运动物体的v-t 图象是直线，则无论Δt 取何值，对应的速度变化量Δv 与Δt 的比值t v ∆∆都是相同的，由加速度的定义a=tv ∆∆可知，该物体做加速度恒定的运动. 课件展示：1.匀变速直线运动的定义：沿着一条直线，且加速度不变的运动.2.特点：（1）相等时间Δv 相等，速度均匀变化；（2）tv ∆∆=a 恒定，保持不变；（3）v-t 图象是一条倾斜直线. 3.分类⎩⎨⎧.,:.,:00越来越小反向与匀减速直线运动越来越大同向与匀加速直线运动v v a v v a课堂训练如图2-2-6所示为四个物体在一条直线上运动的v-t 图象，由图象可以看出，做匀加速直线运动的是（）图2-2-6解析：v-t 图象的斜率就是物体的加速度，A 中图象平行于时间轴，斜率为零，加速度为零，所以做匀速直线运动.B 图象斜率不变，加速度不变，是匀变速直线运动，且由图象可看出，物体的速度随时间减小，所以是做匀减速直线运动.C 图象斜率不变，加速度不变，做匀加速直线运动.D 图象的切线斜率越来越大，表示物体做加速度越来越大的变加速运动. 答案：C二、速度与时间的关系式解决物理问题的常用方法有两种，即图象法和数学分析法.我们可以通过对图象的分析判定物体是否做匀变速运动，做匀变速直线运动的定量描述是怎样的呢？（设计方案一）：利用例题用数学归纳法得出v-t 关系.例1火车原以10.0 m/s 的速度匀速行驶，后来开始做匀加速直线运动，加速度是0.2 m/s 2，从火车加速起第1 s 末、第2 s 末、第3 s 末……第t 秒末的速度分别是多少？解析：火车匀加速运动时，速度是均匀增大的.加速度是0.2 m/s 2，说明火车每1 s 速度增大0.2 m/s.v 1=10.0 m/s+0.2 m/s=10.2 m/sv 2=10.2 m/s+0.2 m/s=10.4 m/s=10.0 m/s+0.2 m/s+0.2 m/sv 3=10.4 m/s+0.2 m/s=10.6 m/s=10.0 m/s+0.2 m/s+0.2 m/s+0.2 m/s.由以上可类推：第t 秒末的速度应等于初速度加上t 秒内速度的增加，即为：v t =v 0+at. （设计方案二）利用加速度的定义式推导a=x v ∆∆=00--t v v =t 0v -v 解出v=v 0+at答案：v=v 0+at这就是匀变速直线运动的速度与时间的关系式.要点扫描1.速度公式反映了匀变速直线运动的瞬时速度随时间变化的规律，式中v 0是开始计时时的瞬时速度，v t 是经过时间t 后的瞬时速度.2.速度公式中v 0、v t 、a 都是矢量，在直线运动中，规定正方向后（常以v 0的方向为正方向），都可用带正、负号的代数量表示，因此，对计算出的结果中的正、负，需根据正方向的规定加以说明.若经计算后v t ＞0，说明末速度与初速度同向；若a ＜0，表示加速度与v 0反向.3.若初速度v 0=0，则v t =at ，瞬时速度与时间成正比.4.若初速度v 0的方向规定为正方向，减速运动的速度公式v t =v 0-at.当v t =0时，可求出运动时间t=v 0/a.5.利用v=v 0+at 计算未知量时，若物体做减速运动，且加速度a 已知，则代入公式计算时a 应取负数，如v 0=10 m/s ，以2 m/s 2做减速运动，则2 s 后的瞬时速度v t =10 m/s-2×2 m/s=（10-4） m/s=6 m/s.课堂训练汽车以40 km/h 的速度匀速行驶，现以0.6 m/s 2的加速度加速，10 s 后速度能达到多少？分析：此问题已知v 0、a 、t ，求v t ，因此可利用速度关系来求解.解析：设初速度的方向为正方向，v 0=40 km/h=6.340 m/s=11 m/s 因为加速，故a 与v 0同向，a=0.6 m/s 2，时间t=10 s10 s 后速度为：v=v 0+at=11 m/s+0.6 m/s 2×10 s=17 m/s.答案：17 m/s知识拓展刹车问题例2小明驾驶汽车以v=20 m/s 的速度匀速行驶，突然前面有紧急情况，（如图2-2-7所示）小明紧急刹车，加速度大小为4 m/s 2.求汽车6 s 末的速度.图2-2-7解析：在式子v=v 0+at 中有四个物理量，题目中出现了其中的三个，即v 0=20 m/s ，a=-4 m/s 2，t=6 s 代入公式中，解得：v=v 0+at=20+（-4）×6 m/s=-4 m/s意思是车正以4 m/s 的速度后退，这显然与实际现象违背.根据题意知，刹车一段时间（t=420 s=5 s ）后，汽车速度减为零，以后就会静止，不会后退，故所求速度v=0.答案：0总结：1.在实际生活中，汽车刹车停止后，不会做反向加速运动，而是保持静止.2.题目给出的时间比刹车时间长还是短？若比刹车时间长，汽车速度为零.若比刹车时间短，可利用公式v=v 0+at 直接计算，因此解题前先求出刹车时间t 0.3.刹车时间t 0的求法.由v=v 0+at ，令v=0，求出t 0便为刹车时间，即t 0=av 0. 4.比较t 与t 0，⎩⎨⎧+=<=>.,;0,t t 000at v v t t v 则若则若课堂训练某汽车在平直公路上以43.2 km/h 的速度匀速正常行驶，现因前方出现危险情况而紧急刹车，加速度的大小是6 m/s 2.问刹车后经过5 s ，汽车的速度变为多少？分析：此题与例题相似，解此类题目先求刹车时间t ，然后比较t 与t 0的关系得出结论. 解析：设汽车经时间t 0停止.v 0=43.2 km/h=12 m/s ，v=0，a=-6 m/s 2由v=v 0+at 得t 0=a 0v -v =6120-- s=2 s 则知汽车从刹车开始经过2 s 速度就减为零，故再经过3 s ，汽车速度仍为零. 答案：0三、对速度—时间图象的理解速度—时间图象描述物体的速度随时间的变化关系，从“v-t”图象中我们可获得如下信息：1.某时刻的瞬时速度.2.某段时间内速度变化量.3.加速度大小.4.位移的大小.为了加深对“v-t”图象的理解，说出如图2-8-示图线所代表的意义.图2-2-81.若图象过原点，说明物体做初速度为零的匀加速直线运动，如图①.2.图象不过原点，若与纵轴有截距，表示运动物体初速度为v0，如图②；若与横轴有截距，表示物体经过一段时间后从t0开始运动，如图③.3.两图线交点说明两物体在该时刻具有相同的速度.4.图线是直线说明物体做匀变速直线运动；图线是曲线则表示物体做变加速运动，如图④.5.图线⑤表示物体的速度逐渐减小，做匀减速运动.6.图线⑥在t轴下方表示物体运动的速度方向反向（与正方向相反）.7.图线与横轴t所围成的面积在数值上等于该物体在该段时间内的位移.8.图线的倾斜程度（即斜率），反映了速度改变的快慢，倾斜程度越大，表示速度改变得越快；倾斜程度越小，表示速度改变得越慢，如图线②比图线③速度改变得慢.说明：1.若图线⑤跨过t轴，表示在交点时刻速度减为零，之后做反向加速运动.如图2-2-9所示.图2-2-92.图线不表示物体的运动轨迹.课堂训练如图2-2-10所示，物体在各段时间内做何种运动？哪一段时间内加速度最大？图2-2-10分析：v-t图象的斜率等于加速度的大小，负斜率表示加速度方向与规定的正方向相反.解析：由v-t 图象的意义可知，物体在0——t 1、t 4——t 5时间内做匀加速运动；t 2——t 3、t 6——t 7时间内做匀减速直线运动；在t 1——t 2、t 5——t 6时间内做匀速直线运动.v-t 图象的斜率大小等于加速度大小，t 2——t 3段斜率最大，所以加速度最大.小结：速度大小的变化情况仅由速度和加速度方向的关系确定，不要认为加速度为负值，就做匀减速运动.思考与讨论：为什么v-t 图象只能反映直线运动的规律？因为速度是矢量，既有大小又有方向.物体做直线运动时，只可能有两个速度方向，规定了一个为正方向时，另一个便为负值，所以可用正、负号描述全部运动方向.当物体做一般曲线运动时，速度方向各不相同，不可能仅用正、负号表示所有的方向，所以不能画出v-t 图象.所以，只有直线运动的规律才能用v-t 图象描述，任何v-t 图象反映的也一定是直线运动规律.四、速度—时间关系的应用运动学问题往往有多种解法.解题时可灵活处理，以开拓思路，提高能力.本节课学习了速度—时间关系，利用此关系，我们来探究一道题目的解法.例3火车沿平直铁轨匀加速前进，通过某一路标时的速度为10.8 km/h ，1 min 后变成54 km/h ，又需经多少时间，火车的速度才能达到64.8 km/h ？分析：题中给出了火车在三个不同时刻的瞬时速度，分别设为v 1、v 2、v 3，火车的运动的示意图如图2-2-11所示.由v 1、v 2和时间t 1可以算出火车的加速度a ，再用速度公式就可算出t 2.还可以画出v-t 图，如图2-2-12所示.图2-2-11解法一：三个不同时刻的速度分别为v 1=10.8 km/h=3 m/sv 2=54 km/h=15 m/sv 3=64.8 km/h=18 m/s时间t 1=1 min=60 s据a=tv v 12-得加速度 a=60315-m/s 2=0.2 m/s 2 则时间t 2=a v v 23-=2.01518- s=15 s. 解法二：此运动加速度不变由于a=tv ∆，所以112t v v -=223t v v - 得所求时间t 2=1223v v v v --t 1=15 s.解法三：因为物体加速度不变，作出其v-t 图象如图2-2-12所示，由图中的相似三角形可知1213v v v v --=121t t t +图2-2-12代入数据315318--=60602t +，解得t 2=15 s. 答案：15 s规律方法总结：1.速度公式v t =v 0+at 的适用条件是匀变速直线运动，所以应用公式时必须首先对运动性质和运动过程进行判断和分析.2.分析物体的运动问题，要养成画运动草图的习惯，主要有两种草图：一是v-t 图象；二是运动轨迹.这样将加深对物体运动过程的理解，有助于发现已知量和未知量之间的相互关系.3.如果一个物体的运动包含几个阶段，就要分段分析，弄清物体在每段上的运动规律.如果全过程不是匀变速运动，但只要每一小段做匀变速运动，也可以在该小段应用匀变速速度公式求解.课堂训练发射卫星一般应用多级火箭，第一级火箭点火后，使卫星向上匀加速运动的加速度为50 m/s 2，燃烧30 s 后第一级脱离，第二级火箭没有马上点火，所以卫星向上做加速度为10 m/s 2的匀减速运动，10 s 后第二级火箭启动，卫星的加速度为80 m/s 2，这样经过1分半钟第二级火箭脱离时，卫星的速度多大？解析：整个过程中卫星的运动不是匀变速直线运动，但可以分为三个匀变速直线运动处理.第一级火箭燃烧完毕时的速度v 1=a 1t 1=50×30 s=1 500 m/s减速上升10 s 后的速度v 2=v 1-a 2t 2=1 500 s-10×10 s=1 400 m/s第二级火箭脱离时的速度v 3=v 2+a 3t 3=400 s+80×90 s=8 600 m/s.答案：8 600 m/s2 匀变速直线运动的速度与时间的关系匀变速直线运动速度与时间的关系⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧-=-=+=+=⎩⎨⎧-a v v t t v v a at v v atv v t v 0000::::::求运动时间求加速度求某时刻的速度应用公式倾斜的直线图象加速度恒定的直线运动定义匀变速直线运动。