最优化模型
多目标最优化数学模型

第六章 最优化数学模型§1 最优化问题1.1 最优化问题概念 1.2 最优化问题分类1.3 最优化问题数学模型 §2 经典最优化方法 2.1 无约束条件极值 2.2 等式约束条件极值 2.3 不等式约束条件极值 §3 线性规划 3.1 线性规划 3.2 整数规划§4 最优化问题数值算法 4.1 直接搜索法 4.2 梯度法 4.3 罚函数法§5 多目标优化问题 5.1 多目标优化问题 5.2 单目标化解法 5.3 多重优化解法 5.4 目标关联函数解法 5.5 投资收益风险问题第六章 最优化问题数学模型 §1 最优化问题1.1 最优化问题概念 (1)最优化问题在工业、农业、交通运输、商业、国防、建筑、通信、政府机关等各部门各领域的实际工作中,我们经常会遇到求函数的极值或最大值最小值问题,这一类问题我们称之为最优化问题。
而求解最优化问题的数学方法被称为最优化方法。
它主要解决最优生产计划、最优分配、最佳设计、最优决策、最优管理等求函数最大值最小值问题。
最优化问题的目的有两个:①求出满足一定条件下,函数的极值或最大值最小值;②求出取得极值时变量的取值。
最优化问题所涉及的内容种类繁多,有的十分复杂,但是它们都有共同的关键因素:变量,约束条件和目标函数。
(2)变量变量是指最优化问题中所涉及的与约束条件和目标函数有关的待确定的量。
一般来说,它们都有一些限制条件(约束条件),与目标函数紧密关联。
设问题中涉及的变量为n x x x ,,,21 ;我们常常也用),,,(21n x x x X 表示。
(3)约束条件在最优化问题中,求目标函数的极值时,变量必须满足的限制称为约束条件。
例如,许多实际问题变量要求必须非负,这是一种限制;在研究电路优化设计问题时,变量必须服从电路基本定律,这也是一种限制等等。
在研究问题时,这些限制我们必须用数学表达式准确地描述它们。
数学建模~最优化模型(课件)

投资组合优化
在风险和收益之间寻求平衡,通 过优化投资组合实现最大收益。
03
非线性规划模型
非线性规划问题的定义
目标函数
一个或多个非线性函数,表示 要最小化或最大化的目标。
约束条件
决策变量的取值受到某些限制 ,通常以等式或不等式形式给 出。
决策变量
问题中需要求解的未知数,通 常表示为x1, x2, ..., xn。
这是一种常用的求解整数规划问题的算法,通过不断将问题分解为更 小的子问题,并确定问题的下界和上界,逐步逼近最优解。
割平面法
该方法通过添加割平面来限制搜索区域,从而逼近最优解。
迭代改进法
该方法通过不断迭代和改进当前解,逐步逼近最优解。
遗传算法
这是一种基于生物进化原理的优化算法,通过模拟自然选择和遗传机 制来寻找最优解。
定义域
决策变量的取值范围,通常是 一个闭区间或开区间。
非线性规划问题的求解方法
梯度法
利用目标函数的梯度信息,通过迭代方法寻 找最优解。
共轭梯度法
结合梯度法和牛顿法的思想,通过迭代方法 寻找最优解。
牛顿法
利用目标函数的二阶导数信息,通过迭代方 法寻找最优解。
信赖域方法
在每次迭代中,通过限制搜索步长来保证求 解的稳定性。
02
线性规划模型
线性规划问题的定义
01
02
03
线性规划问题
在给定一组线性约束条件 下,求一组线性函数的最 大值或最小值的问题。
约束条件
包括资源限制、物理条件 等,通常以等式或不等式 形式给出。
目标函数
需要最大化或最小化的线 性函数,通常表示为决策 变量的线性组合。
线性规划问题的求解方法
数学建模最优化模型

数学建模最优化模型随着科学与技术的不断发展,数学建模已经成为解决复杂实际问题的一种重要方法。
在众多的数学建模方法中,最优化模型是一种常用的方法。
最优化模型的目标是找到最佳解决方案,使得一些目标函数取得最大或最小值。
最优化模型的基本思想是将实际问题抽象为一个数学模型,该模型包含了决策变量、约束条件和目标函数。
决策变量是需要优化的变量,约束条件是对决策变量的限制条件,目标函数是优化的目标。
最优化模型的求解方法可以分为线性规划、非线性规划和整数规划等。
线性规划是最优化模型中最基本的一种方法,其数学模型可以表示为:max/min c^T xs.t.Ax<=bx>=0其中,c是目标函数的系数向量,x是决策变量向量,A是约束条件的系数矩阵,b是约束条件的右边向量。
线性规划的目标是找到最优的决策变量向量x,使得目标函数的值最大或最小。
非线性规划是最优化模型中更为复杂的一种方法,其数学模型可以表示为:max/min f(x)s.t.g_i(x)<=0,i=1,2,...,mh_i(x)=0,i=1,2,...,p其中,f(x)是目标函数,g_i(x)是不等式约束条件,h_i(x)是等式约束条件。
非线性规划的求解过程通常需要使用迭代的方法,如牛顿法、拟牛顿法等。
整数规划是最优化模型中另一种重要的方法,其数学模型在线性规划的基础上增加了决策变量的整数限制。
max/min c^T xs.t.Ax<=bx>=0x是整数整数规划的求解通常更为困难,需要使用特殊的算法,如分支定界法、割平面法等。
最优化模型在实际问题中有着广泛的应用,如资源调度、生产计划、路线选择、金融投资等。
通过建立数学模型并求解,可以得到最优的决策方案,提高效益和效率。
总结起来,最优化模型是数学建模的重要方法之一、通过建立数学模型,将实际问题转化为数学问题,再通过求解方法找到最佳解决方案。
最优化模型包括线性规划、非线性规划和整数规划等方法,应用广泛且效果显著。
最优化模型(第五讲)

数学建模讲义主讲人:穆学文西安电子科技大学数学系Email:xdmuxuewen@ 最优化模型---最优化方法的概念参考书目1. 陈宝林。
最优化理论与算法。
清华大学出版社.2. 谢金星,薛毅。
优化建模与lindo/lingo优化软件. 清华大学出版社. 背景知识基本概念及其应用最优化问题举例最优化方法的概念优化问题的数学模型及其分类 最优解与极值点常用的数学软件§1背景知识•运筹学理论的一部分•最早起源于中国古代¾公元前6世纪孙武所著的《孙子兵法》¾孙膑“斗马术”,田忌与齐王赛马,博弈论¾运筹帷幄之中,决胜千里之外”。
这千古名句也可以说是对张良运筹思想的赞颂和褒奖。
•国外起源与发展¾1896年,V.Pareto首次从数学角度提出多目标优化问题,引进了Pareto最优的概念。
¾1935-38年,英国为了正确地运用新研制的雷达系统来对付德国飞机的空袭,在皇家空军中组织了一批科学家,进行新战术试验和战术效率评价的研究,并取得了满意的效果。
他们把自己从事的这种工作命名为“Operational Research”(背景知识(续)Operational Research(运筹学,或直译为作战研究)。
¾1939年,苏联的Л.В.Канторович总结了他对生产组织的研究,写了《生产组织与计划中的数学方法》一书,是线性规划应用于工业生产问题的经典著作¾1947年,G.B.Dantzig提出了单纯形方法后,线性规划便迅速形成为一个独立的分支。
并逐级发展起来。
¾英国运筹学会1948年成立(1948-53年是运筹学俱乐部,1953年11月起改名为学会)。
¾二次大战胜利后,美英各国不但在军事部门继续保留了运筹学的研究核心,而且在研究人员、组织的配备及研究范围和水平上,都得到了进一步的扩大和发展,同时筹学方法也向政府和业等部门扩展背景知识(续)运筹学方法也向政府和工业等部门扩展。
非线性最优化模型

案例二:生产调度优化的应用
总结词
生产调度优化是利用非线性最优化模型来安排生产计划 ,以提高生产效率和降低生产成本。
详细描述
生产调度问题需要考虑生产线的配置、工人的排班、原 材料的采购等多个因素。非线性最优化模型能够综合考 虑这些因素,并找到最优的生产调度方案,提高生产效 率,降低生产成本,并确保生产计划的可行性。
04
非线性最优化模型的实例分析
投资组合优化模型
投资组合优化模型
通过非线性最优化方法,确定最佳投资组合配置,以实现预期收 益和风险之间的平衡。
目标函数
最大化预期收益或最小化风险,通常采用夏普比率、詹森指数等 作为评价指标。
约束条件
包括投资比例限制、流动性约束、风险控制等。
生产调度优化模型
01
生产调度优化模型
非线性最优化模型
• 非线性最优化模型概述 • 非线性最优化模型的分类 • 非线性最优化模型的求解方法 • 非线性最优化模型的实例分析 • 非线性最优化模型的挑战与展望 • 非线性最优化模型的应用案例
01
非线性最优化模型概述
定义与特点
定义
非线性最优化模型是指用来描述具有 非线性特性的系统或问题的数学模型 。
多目标非线性优化模型
多目标
多目标非线性优化模型中存在多个目标函数,这些目标函 数之间可能存在冲突。
01
求解方法
常用的求解方法包括权重法、帕累托最 优解法、多目标遗传算法等,这些方法 通过迭代过程逐步逼近最优解。
02
03
应用领域
多目标非线性优化模型广泛应用于各 种领域,如系统设计、城市规划、经 济分析等。
通过非线性最优化方法,合理安 排生产计划和调度,以提高生产 效率和降低成本。
多目标最优化模型

缺点
计算复杂度高
求解速度慢
难以找到全局最优 解
对初始解依赖性强
多目标最优化模 型的发展趋势
算法改进
进化算法:如遗传算法、粒子群算法等,在多目标优化问题中表现出色,能够找到多个非支配解。
机器学习算法:如深度学习、强化学习等,在处理大规模、高维度多目标优化问题时具有优势,能 够自动学习和优化目标函数。
金融投资
风险管理:多目标最 优化模型用于确定最 优投资组合,降低风 险并最大化收益。
资产配置:模型用于 分配资产,以实现多 个目标,例如最大化 收益和最小化风险。
投资决策:模型帮助 投资者在多个投资机 会中选择最优方案, 以实现多个目标。
绩效评估:模型用于评 估投资组合的绩效,以 便投资者了解其投资组 合是否达到预期目标。
混合算法:将多种算法进行融合,形成新的优化算法,以适应不同类型和规模的多目标优化问题。
代理模型:利用代理模型来近似替代真实的目标函数,从而加速多目标优化问题的求解过程。
应用拓展
人工智能领域的应用
金融领域的应用
物流领域的应用
医疗领域的应用
未来研究方向
算法改进:研究更高效的求解多目标最优化问题的算法 应用拓展:将多目标最优化模型应用于更多领域,如机器学习、数据挖掘等 理论深化:深入研究多目标最优化理论,提高模型的可解释性和可靠性 混合方法:结合多种优化方法,提高多目标最优化模型的性能和适用范围
资源分配
电力调度:多目标最优化模型用于协调不同区域的电力需求和供应,实现电力资源的 合理分配。
金融投资:多目标最优化模型用于确定投资组合,以最小风险实现最大收益,优化金 融资源分配。
最优化模型

星期日 星期一 星期二 星期三 星期四 星期五 星期六
2、模型
决策变量:设x j为第j天开始休息的人数( j 1, 2,, 7)
目标函数: min x1 x2 x3 x4 x5 x6 x7 约束条件: x1 x2 x3 x4 x5 28 x2 x3 x4 x5 x6 15 x3 x4 x5 x6 x7 24 x4 x5 x6 x7 x1 25 x5 x6 x7 x1 x2 19 x6 x7 x1 x2 x3 31 x7 x1 x2 x3 x4 28 x1 , x2 , x3 , x4 , x5 , x6 , x7 0, 整数
例(挑选球员问题)某篮球教练要从8名业余队员中 挑选3名队员参加专业球队,使平均身高达到最高。 队员的号码、身高及所擅长的位置如下。要求:中 锋1人;后卫1人;前锋1人,但1号、3号与6号队员 中必须保留1人给业余队。
号码 1 2 3 4 5 6 7 8 身高(米) 1.92 1.91 1.90 1.86 1.85 1.83 1.80 1.79 位置 中锋 中锋 前锋 前锋 前锋 后卫 后卫 后卫 挑选变量 x1 x2 x3 x4 x5 x6 x7 x8
例(选址问题)设有n个市场,第j个市场的位置为(aj,bj), 对某种货物的需要量为qj, j=1,…,n,现计划建立m个仓库, 第i个仓库的容量为ci,i=1,…,m,试确定仓库的位置,使各 仓库到各市场的运输量与路程乘积之和最小. 解:设第i个仓库的位置为(xi,yi),运输量为wij.
min n m w ( x a ) 2 ( y b ) 2 i j i j j 1 i 1 ij n s.t. j 1 wij ci i 1, 2, , m m i 1 wij q j j 1, 2, , n wij 0 i 1, 2, , m j 1, 2, , n
最优化模型.

华北电力大学数理学院
School of mathematics & physics
一、简单优化问题
* p 利润U(p)达到最大值的最优价格 满足:
dU dI dC a bq 2bp 0 dp dp dp
得到:
q a p 2 2b
*
最优价格一部分是成本的一半,另一部分与“绝对需求” 成正比,与市场需求对价格的敏感系数成反比。
一、简单优化问题
3、模型求解及其结果分析
需求函数是售价的减函数,通常是根据实际销售
情况定出。现在,假设它是线性函数,即
x f ( p) a bp, a, b 0
其中, a--代表这种产品免费供应(p=0)时的社会需求
量,也称为绝对需求量;
幅度。它反映市场需求对价格的敏感程度。
dx b 表示价格上涨一个单位时销售量下降的 dp
(3) 由于市场需求变化,每千克A1产品的获利增加到30 元,是否应改变生产计划?
二、模型分析 生产计划就是每天生产多少A1和多少A2,获利润最大。或 者是每天用多少桶牛奶生产A1和用多少桶牛奶生产A2,获 利润最大。
当技术参数、价值系数为常数时,此为线性规划模型。
华北电力大学数理学院
School of mathematics & physics
二、数学规划模型
四、模型的建立
目标:设每天收入z元。则 z 24 3x1 16 4 x2
约束条件:
原料限制
劳动时间限制
x1 x2 50
12x1 8x2 480
设备能力限制
3x1 100
决策变量的非负性 x1 , x2 0
华北电力大学数理学院
最优化问题的数学模型
为凸集.
1,
0 证明: x , y 为超球中的任意两点, 设
则有:
x 1 y
r ???
x 1 y
r r r 1
即点 x 1 y 属于超球
所以超球为凸集.
注: 常见的凸集:空集,整个欧氏空间 超平面: H
T
aR
n
和实数
,
使得: T x a
a y , x D ,
xR a x
n T
即存在超平面 H y 与凸集 D .
严格分离点
注: 点与闭凸集的分离定理。
y.
D
定理
(点与凸集的分离定理)
是非空凸集,x D, 则存在 非零向量 a R n 使成立
DR
n
目标函数
R ( i 1, 2 , , p )
1
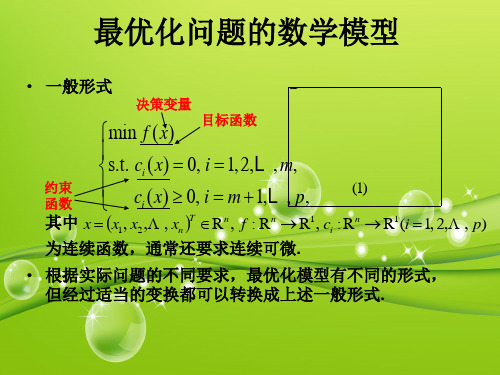
• 根据实际问题的不同要求,最优化模型有不同的形式, 但经过适当的变换都可以转换成上述一般形式.
最优化问题的分类
最优化问题
根据约束条件 分类
m in f ( x ), x R .
n
无约束最优化问题 约束最优化问题 等式约束最优化问题 不等式约束最优化问题 混合约束优化问题
设
a xa x
T T
x D . ( D代 表 D 的 闭 包 )
_ _
定理
(两个凸集的分离定理)
n
x
x
设 D1 , D2 是
且 R 的两个非空凸集, D1 D2 ,
则存在超平面分离 D1 和 D2 , 即存在非零向量 n a R 使得 aT x aT y , x D , y D . 1 2
最优化模型的建立与求解

最优化模型的建立与求解在现代社会中,各种资源的有限性和复杂性给企业和组织带来了难以解决的问题。
通过数学对各个问题进行建模,并对问题进行求解,是现代数学所解决的核心问题之一。
最优化模型的建立与求解,是一种有效的方法,可以帮助企业和组织更好地规划和管理资源。
一、最优化模型的概念与分类最优化模型是指根据给定的约束条件,通过建立数学模型,求解出最优的决策方案的过程。
按照求解的方式,最优化模型可以分为解析求解和数值求解。
解析求解是利用数学公式进行精确求解,其求解过程较为简单,但适用范围受限,只适用于一些简单的问题。
数值求解是通过计算机进行迭代计算得到方程的近似解或最优解的方法,较为适用于复杂的、高维度的问题,但是需要注意求解误差。
在实际的应用中,最常见的最优化模型有线性规划、整数规划、非线性规划、动态规划、图论等。
其中,线性规划是一种最基本的最优化模型。
其建模过程简单,使用广泛,并且可以通过现有的算法求解。
整数规划是指限制决策变量为整数的线性规划问题,其求解过程相对于线性规划较为复杂,但可以处理更加真实的实际问题。
非线性规划是指决策变量在一定条件下满足非线性约束的最优化模型。
动态规划和图论是一种最优化模型,在解决多阶段决策和网络设计等问题中起着重要的作用。
二、最优化模型的建立方法最优化模型的建立是将实际问题转化为数学公式的过程。
建立方法一般分为以下三步。
1. 确定决策变量和约束条件在建立最优化模型时,需要先明确问题的量化指标,即问题包含哪些参量,以及这些参量之间的关系。
在确定决策变量时,需要考虑决策变量的意义、类型、数量以及相互之间的约束关系。
在确定约束条件时,需考虑问题本身的实际情况,遵循可行性原则,不违反现实约束条件。
2. 确定目标函数目标函数是最优化模型中最重要的部分,它描述了最终优化的具体内容和目标。
在确定目标函数时,应优先考虑问题的核心目标,为保证目标函数的正确性,可能需要对其进行重新构造、转化和调整,以使其符合实际情况。
最优化问题数学模型

最优化问题数学模型在我们的日常生活和各种实际应用中,最优化问题无处不在。
从生产线上的资源分配,到物流运输中的路径规划,从金融投资中的资产配置,到工程设计中的参数选择,都需要找到最优的解决方案,以实现效率最高、成本最低、效益最大等目标。
而数学模型就是帮助我们解决这些最优化问题的有力工具。
那么,什么是最优化问题数学模型呢?简单来说,它是将实际问题转化为数学语言和表达式的一种方式,通过建立数学关系式,来描述问题中的各种约束条件和目标函数,然后运用数学方法和算法求解,找到最优的决策变量取值。
举个简单的例子,假设一家工厂要生产两种产品 A 和 B,生产 A 产品每件需要消耗 2 个单位的原材料和 3 个小时的工时,生产 B 产品每件需要消耗 3 个单位的原材料和 2 个小时的工时。
工厂共有 100 个单位的原材料和 80 个小时的工时可用,每件 A 产品的利润是 5 元,每件 B 产品的利润是 4 元。
那么,如何安排生产才能使工厂的总利润最大呢?为了建立这个问题的数学模型,我们首先定义决策变量:设生产 A 产品的数量为 x 件,生产 B 产品的数量为 y 件。
然后,我们确定目标函数,即要最大化的总利润:Z = 5x + 4y 。
接下来,考虑约束条件。
原材料的限制可以表示为:2x +3y ≤ 100 ;工时的限制可以表示为:3x +2y ≤ 80 ;还有非负约束:x ≥ 0 ,y ≥ 0 。
这样,我们就建立了一个简单的最优化问题数学模型。
通过求解这个模型,就可以得到最优的生产方案,即 x 和 y 的取值,使得总利润Z 最大。
最优化问题数学模型的类型多种多样,常见的有线性规划、非线性规划、整数规划、动态规划等。
线性规划是最简单也是应用最广泛的一种模型。
它的目标函数和约束条件都是线性的,就像我们上面的例子。
线性规划问题可以通过单纯形法等有效的算法在较短的时间内求解。
非线性规划则是目标函数或约束条件中至少有一个是非线性的。
最优化建模算法与理论

最优化建模算法与理论最优化建模算法与理论最优化建模是以一种有效的方式来求解优化问题的过程。
它是一种用于处理优化问题的综合算法,其中包括搜索算法、随机算法、组合算法等。
最优化建模的主要目标是通过有效的算法和理论,寻找最优解来解决优化问题。
本文将从以下几个方面讨论最优化建模中的算法和理论:一、基本最优化模型基本最优化模型是一种描述变量之间关系的模型,它一般用于求解优化问题。
基本最优化模型一般由目标函数、约束条件、决策变量等组成。
目标函数是描述求解问题的目标,约束条件是指处理问题的要求,决策变量是用于描述最优化问题的变量。
基本最优化模型一般可以用数学模型来表示,如线性模型、非线性模型等。
二、最优化搜索算法最优化搜索算法是用于最优化问题的一类算法,它可以在有限的时间内搜索出最优解,因此被用来求解最优化问题。
最优化搜索算法主要包括贪心算法、模拟退火算法、遗传算法等。
贪心算法是一种局部最优搜索算法,它通过从一个状态进行评估,不断的求解局部最优解,最终求得全局最优解。
模拟退火算法是一种基于概率的搜索算法,它通过增加概率来接受新的状态,从而最终接受最优解。
遗传算法是一种进化算法,它通过迭代的过程,不断的进化出更优的解。
三、最优化理论最优化理论是指用于求解最优化问题的一系列理论,它可以帮助我们更好地理解和分析最优化问题。
最优化理论主要包括多目标优化理论、随机优化理论、优化系统理论等。
多目标优化理论是指在求解多目标优化问题时,按照一定的准则,构造出最优解的理论。
随机优化理论是指在求解随机优化问题时,按照一定的准则,构造出最优解的理论。
优化系统理论是指在求解优化系统问题时,按照一定的准则,构造出最优解的理论。
四、应用最优化建模算法和理论已被广泛应用于各个领域。
在工程中,最优化建模算法和理论可用于解决结构优化、供应链管理等问题。
在管理学中,最优化建模算法和理论可用于解决生产调度、经营决策等问题。
在经济学中,最优化建模算法和理论可用于解决价格机制、资源分配等问题。
ppt4-最优化模型

【条件设置】 总成本必须是最小值; 月末库存 = 月初库存 + 本月生产量 – 需求量 月初库存 = 上月末库存 储存成本是每月末库存量之和与单位储存成本 之乘积; 各种生产方式每月的产量必须大于等于0; 每月的库存量不能小于0; 各种生产方式的月生产量不能大于其月生产能 力。
【例】 某移动通讯公司准备在一城市建立发射塔,该 城有4个地区,现有4个建塔位置,每个位置对各 地区的覆盖情况和费用如单元格区域 C2:G7 所示 (其中:1表示能覆盖该区域)。 ( 1 )假设在每个位置都建塔,计算每个地区被 覆盖的次数和建塔总费用。 ( 2 )用规划求解工具求解最优建塔位置(必须 确给保覆盖所有地区)和总费用的最小值。【发 射塔规划】
200
销地3 6 5
产地A 产地B
【例】 某农场主拥有两个农场,分别有 80 和 100 亩耕 地。他可用两个农场的全部耕地来种植玉米和小 麦。根据高层需求,他今年的生产指标是玉米 20000千克和小麦50000千克。两个农场的产量及 成本如下所示。该农场主应如何合理安排种植面 积。 【规划求解1】
P103
1、最优化问题分类 ▲根据有无约束条件可以分为: 有约束条件的最优化问题 即在资源限定的情况下求解最佳目标。 无约束条件的最优化问题 即在资源无限的情况下求解最佳目标。 ▲根据决策变量在目标函数与约束条件中出现的 形式可分为: 线性规划问题 目标函数与约束条件函数都是线性的。 非线性规划问题 目标函数与约束条件函数都是非线性的。
最优化模型
在生产、经营和管理中,经常遇到求最大值和 最小值的问题,如经济订货量等,这些都属于最 优化问题。 最优化问题是运筹学的一个重要分支,根据其 形式又分为: 数学规划 动态规划 网络规划
一、最优化问题概述 最优化问题就是在给定的条件下寻找最佳方案 的问题。最佳的含义包括两个方面: 在资源给定时寻找最好的目标 在目标确定下使用最少的资源
最优化模型

G (400) = G0 (400) = 600 × 0.30 + 600 × 8 400 + 0.2 × 0.30 × 400 2 = $204.00
C(Q) c 1 = 0.29 c 0 = 0.30 c 2 = 0.28
500
1000
Q
按量折扣模型
一致折扣模式下的最优订货策略: 一致折扣模式下的最优订货策略:
针对各个折扣价格计算对应的EOQ值
Q (0 ) =
Q (1) =
Q (2 ) =
2 Kλ = Ic0
2 Kλ = Ic1
2 Kλ = Ic2
经济订货批量(EOQ)模型 经济订货批量(EOQ)模型 (EOQ)
基本模型: 基本模型:
斜率 = λ 库存 I(t) I Q
T
时间 t
经济订货批量(EOQ)模型 经济订货批量(EOQ)模型 (EOQ)
基本模型: 基本模型: 每一周期的进货成本
C (Q ) = K + cQ
平均库存量
Q 2
单位时间库存成本
(2 ) = Q
2 × 23 × 600 = 702 0.2 × 0.28
按量折扣模型
分段折扣模型: 分段折扣模型:
(0 ) 和 Q
(1) 均为有效值 因为 Q (2 ) < 1000 ,所以 Q (2 ) 均为有效值;因为 Q 为无效值。 为无效值。 最优解可通过比较 G0 Q (0 ) 和 G1 Q (1) 的大小而获得。 的大小而获得。
最优化模型与算法

最优化模型与算法
最优化模型和算法是求解优化问题的基本工具,随着人工智能和机器
学习的发展,最优化模型和算法从物理、工程和管理等多个领域被广泛应用。
最优化模型通常是一种特殊的抽象模型,它可以用来把实际问题以数
学模型的形式表示出来,并依据一定的目标函数对这个模型的参数进行优化。
而最优化算法是根据最优化模型寻找最优解的一种算法。
从计算上来讲,最优化模型可分为精确求解和近似求解。
精确求解是
指找到原问题的最优解,它通常采用解析法,比如利用简单x法、线法等
简单算法求解;而近似求解是指通过迭代的过程找到最优解的近似值,它
通常需要采用启发式算法,比如梯度下降法、牛顿法等更复杂的算法求解。
优化过程中,选择合适的算法非常重要。
线性规划若是精确求解,可
以采用简单x法,比如简单的罗伯特-普林斯顿极值法;若是近似求解,
常用的有梯度优化算法、模拟退火算法等。
数学建模~最优化模型(课件ppt)

用MATLAB解无约束优化问题 解无约束优化问题
1. 一元函数无约束优化问题 一元函数无约束优化问题: min f ( x )
x1 ≤ x ≤ x 2
常用格式如下: 常用格式如下: (1)x= fminbnd (fun,x1,x2) ) (2)x= fminbnd (fun,x1,x2 ,options) ) (3)[x,fval]= fminbnd(…) ) , ( (4)[x,fval,exitflag]= fminbnd(…) ) , , ( (5)[x,fval,exitflag,output]= fminbnd(…) ) , , , ( 其中等式( )、( )、(5)的右边可选用( ) )、(4)、( 其中等式(3)、( )、( )的右边可选用(1)或(2) ) 的等式右边. 的等式右边 函数fminbnd的算法基于黄金分割法和二次插值法,它要求 函数 的算法基于黄金分割法和二次插值法, 的算法基于黄金分割法和二次插值法 目标函数必须是连续函数,并可能只给出局部最优解. 目标函数必须是连续函数,并可能只给出局部最优解
有约束最优化问题的数学建模
有约束最优化模型一般具有以下形式: 有约束最优化模型一般具有以下形式:
min
x
f (x)
或
max
x
f (x)
st. ...... .
st. ...... .
其中f(x)为目标函数,省略号表示约束式子,可以是 为目标函数,省略号表示约束式子, 其中 为目标函数 等式约束,也可以是不等式约束。 等式约束,也可以是不等式约束。
标准型为: 标准型为:min F ( X ) 命令格式为: 命令格式为 );或 (1)x= fminunc(fun,X0 );或x=fminsearch(fun,X0 ) ) ( ( (2)x= fminunc(fun,X0 ,options); ) ( ); 或x=fminsearch(fun,X0 ,options) ( ) (3)[x,fval]= fminunc(...); ) , ( ); 或[x,fval]= fminsearch(...) , ( ) (4)[x,fval,exitflag]= fminunc(...); ) , , ( ); 或[x,fval,exitflag]= fminsearch , , (5)[x,fval,exitflag,output]= fminunc(...); ) , , , ( ); 或[x,fval,exitflag,output]= fminsearch(...) , , , ( )
数学建模最优化模型例题

数学建模最优化模型例题好,咱们今天来聊聊数学建模和最优化模型这块儿。
数学建模,这名字听起来就挺高大上的,实际上,咱们日常生活中处处都是它的身影。
想象一下,早上起床,看到窗外阳光明媚,心里琢磨着今天去不去公园,顺便锻炼锻炼。
于是,你心里开始盘算,公园离家有多远,走路要多久,还是骑个单车比较快?这就是在用数学建模,算一算,看看哪个更划算。
再说说最优化模型,这就像是在挑选午饭一样。
你有一大堆选择,米饭、面条、快餐还是外卖,真是眼花缭乱。
你心里想,要是不吃太油腻的,又想吃得饱,还得好吃。
于是开始分析:今天外卖不如自己做,自己做的话,买啥材料比较好,怎么搭配更营养呢?这时候,你的脑子就像一个小计算机,开始进行各种选择。
想想,如果能把所有的选择变成一个数学问题,肯定能算出最优解,嘿,生活简直就像在解题一样,乐趣多多。
再说说商场里打折的那种,真是让人心痒痒的。
假如你打算买新鞋,满心期待。
可是一进商场,各种颜色、各种款式扑面而来,心里顿时就犯了选择困难症。
想要买的那双鞋打折了,可是另外一双颜色也不错,怎么办呢?这时候,最优化模型就可以帮你了。
想一想,你最看重什么,舒适、样式还是价格?用数学的眼光来审视,看看哪双鞋的性价比最高,没准儿就能找到那个最适合自己的了。
有些小伙伴可能会问了,数学建模到底有什么用呢?你知道吗,很多企业在决策的时候都离不开这些模型。
就拿快递公司来说,他们每天都要处理成千上万的包裹,怎么能保证包裹及时送到呢?他们需要用到最优化模型来安排路线,减少运输成本。
想象一下,如果没有这些模型,快递员可能跑了一大圈,最后才发现原来只需要直走就到了。
那可真是得不偿失,没准儿包裹还会晚到,这可就麻烦了。
数学建模的魅力就在于它能把复杂的问题简单化。
我们生活中遇到的各种难题,最终都可以转化为一个个数学问题。
你说这是不是挺神奇的?比如你要规划一次旅行,想去多少个地方,怎么安排最合适,住哪儿能便宜又舒服,这些全都可以用建模来解决。
第八讲网络最优化模型【共61张PPT】

第八讲 网络最优化模型
最短路模型
最短路模型的求解
求解最短路问题实际上就是找一条总长度最短的路 线,对于这样的最短路问题,可以建立0-1整数规划数学
模型求解(如下图)。
第八讲 网络最优化模型
最短路模型
最短路模型的求解
为简化求解过程,可以建立专门的最短路求解模型 ,用计算机求解:可以将图中各条边和每条边是的权数 直接录入到求解模型中,直接得到结果。因此可以称下 图就是一个最短路问题的数学表述模型。
条路,使两点间的总距离为最短。
第八讲 网络最优化模型
最短路模型
例8.1 如下图所示,某人每天从住处S开车到工作地T上
班,图中各弧旁的数字表示道路的长度(千米),试问 他从家出发到工作地,应选择哪条路线,才能使路上行 驶的总距离最短?
第八讲 网络最优化模型
最短路模型的基本特征
最短路模型
1、在网络中选择一条路,始于发点(源点),终于收点(目的
条道路及道路维修。工期和所需劳动力见下表。该公司共 有劳动力120人,任一工程在一个月内的劳动力投入不能超 过80人,问公司应如何分配劳动力以完成所有工程,是否能按
期完成?
工程 A.地下通道 B.人行天桥 C.新建道路 D.道路维修
工期和所需劳动力
工期 5~7月 6~7月 5~8月
8月
需要劳动力(人) 100 80 200 80
赵●
(v1)
e1
e3
钱● (v2)
●孙 (v3) e4
●李 (v4)
第八讲 网络最优化模型
基本概念
图
7、 回路 始点和终点重合的路叫做回路。上图中(v3,v5,v6
,v7,v4 ,v3)就是一条回路。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3)每件产品成本为q,产量x与成本q无关。
华北电力大学数理学院
School of mathematics & physics
一、简单优化问题
2、模型建立
总收入:I(p)=px 总支出:C(p)=qx 利 润:U= I(p)- C(p)= (p- q)x=(p-q)f(p)
x1 x2 50 s.t132x1x1180x02 480 x
x1, x2 , x 0
(4)
华北电力大学数理学院
School of mathematics & physics
f=[-72 -64 0]';a=[1 1 0;12 8 -1;3 0 0];b=[50,480,100]'; [x,z]=linprog(f,a,b,[],[],[0;0;0],[]) x = 33.3333,16.6667,104.3896 z = -3.4667e+003。收入:s=0时,3466.7
最优化模型概述
最大值或最小值 数学规划:线性规划(整数规划、0-1规划、目
标规划等),非线性规划 动态规划
华北电力大学数理学院
School of mathematics & physics
一、简单优化问题
案例1:产销平衡下的某种产品的最优价格,即使工厂利润最 大的价格。
1、模型假设
(1)售量为x,并与产量相等; (2)每件产品售价为p。在竞争市场的环境中售量x依赖于
得到: p* q a 2 2b
最优价格一部分是成本的一半,另一部分与“绝对需求” 成正比,与市场需求对价格的敏感系数成反比。
华北电力大学数理学院
School of mathematics & physics
一、简单优化问题
最大利润: U ( p*) b( a q )2 2b 2
边界收入: dI a 2bp* bq dp
当技术参数、价值系数为常数时,此为线性规划模型。
华北电力大学数理学院
School of mathematics & physics
二、数学规划模型
三、模型的假设
1、每天用 x1 桶牛奶生产A1,x2 桶牛奶生产A2;x1, x2
可以是任意的实数。 2、劳动时间、设备能力、利润均为与产量无关常数。 即技术参数、价值系数为常数
价格 y1 48元 ,所以企业应买进牛奶用于扩大生产。设再 增加x桶,其他条件不变,则有相应生产计划:
max z 72x1 64x2 35(50 x)
x1 x2 50 x s.t132x1x1180x02 480
x1, x2, x 0
(3)
x =[0.0000, 60.0000, 10.0000]’; z = -3.4900e+003 收入:3840 。即最多每天再多买进10桶!
案例3:奶制品的生产销售计划 一、问题的提出
案例2的A1,A2的生产条件、利润、资源都不变条件下,提高奶制 品深加工技术,增加工厂获利。用2小时和3元加工费,可将1千克A1加 工成0.8千克高级奶制品B1,也可将1千克A2加工成0.75千克高级奶制品 B2,每千克B1可获利44元,每千克B2可获利32元。生产的产品全能售出, 试着为该厂订制一个生产销售计划,使每天获利最大。并进一步讨论以 下问题:
3、生产的产品全能售出。
华北电力大学数理学院
School of mathematics & physics
四、模型的建立
目标:设每天净利润z元。则 z 24 x1 16 x2 44 x3 32 x4 3x5 3x6
约束条件:
原料限制 劳动时间限制 设备能力限制
3、生产的产品全能售出。
华北电力大学数理学院
School of mathematics & physics
二、数学规划模型
四、模型的建立
目标:设每天收入z元。则 z 24 3x1 16 4x2
约束条件:
原料限制
x1 x2 50
劳动时间限制
12 x1 8x2 480
设备能力限制
3x1 100
0<s<2时,
f=[-72 -64 s]';a=[1 1 0;12 8 -1;3 0 0];b=[50,480,100]'; [x,z]=linprog(f,a,b,[],[],[0;0;0],[]) x = 33.3333,16.6667,53.3333
z = -3.4133e+003。收入:3466.7
(1) 若投资30元可增加供应1桶牛奶,投资3元可增加1小时劳动时间, 是否应作这项投资?若每天投资150元,可赚回多少?
(2) 每千克高级奶制品B1,B2的获利经常有10%的波动,对制订的生 产销售计划有无影响?若每千克B1的获利下降10%,计划是否应作调 整?
华北电力大学数理学院
School of mathematics & physics
华北电力大学数理学院
School of mathematics & physics
二、数学规划模型
影子价格y,它由模型(1)的对偶问题决定:
min s bT y ATy c
s.t. y 0
L (2)
其中, y [y1, y2, y3]T 分别为出租(出售)单位资源 b1, b2 , b3 的附加值.
对第i种资源的估价——影子价格(
z* b j
)。在完全市
场经济的条件下,当某种资源的市场价低于影子价格时,
企业应买进该资源用于扩大生产;而当某种资源的市场价
高于企业影子价格时,则企业的决策者应把已有资源卖掉。
附加问题(3)是考虑当费用系数c变化时对最优解和最 优值有没有影响?找出使最优解不变的区间。
华北电力大学数理学院
要
点
School of mathematics & physics
爱因斯坦的一句名言: 想象力比知识更重要!因为
知识是有限的,而想象力包括世 界的一切,是知识的源泉。
最优优化模型
School of mathematics & physics
华北电力大学数理学院
School of mathematics & physics
21 f
0 3360 20 f
4
显然,当-48+2f<=0,-2-(1/4)f<=0时,最优解不变!即
c1 72 8,72 24 64,96 时,最优解不变!
现在 c1 30 3 90 ,所以不用改变生产计划!ematics & physics
决策变量的非负性 x1, x2 0
华北电力大学数理学院
School of mathematics & physics
二、数学规划模型
综上可得: max z 72x1 64x2
x1 x2 50 s.t132x1x1180x02 480
x1, x2 0
max z cT x
s.t.
Ax b x LB
1
1
劳动时间(h)
12
8
设备甲能力(kg)
3
0
设备乙能力(kg)
0
4
资源
50 480 100 inf
根据市场需求,生产的A1,A2产品全部能售出,且每千克A1 产品获利24元,每千克A2产品获利16元。试为该厂订一个 生产计划,使每天获利最大。并进一步讨论以下问题:
华北电力大学数理学院
School of mathematics & physics
华北电力大学数理学院
School of mathematics & physics
解附加问题(2):在每位临时工人的工资不超过每小时2元 的条件下,可以聘用临时工人以增加劳动时间。
设小时工资为s(0=<s<=2)元,其他条件不变的条件下,再 增加x小时,则有相应生产计划:
max z 72x1 64x2 s(480 x)
(1)
华北电力大学数理学院
School of mathematics & physics
二、数学规划模型
五、模型求解及结果分析
[X,z]=LINPROG(f,A,b,Aeq,beq,LB,UB) 用于解:
min f'*x subject to: A*x <= b
Aeq*x = beq. LB <= X <= UB. f=[-72;-64];A=[1 1;12 8;3 0];b=[50;480;100]; [x,z]=linprog(f,A,b,[],[],[0;0],[])
x = 20.0000, 30.0000; z =-3.3600e+003
即按每天用20桶牛奶生产A1,用30桶牛奶生产A2,获最大 收益:z=3360元。
华北电力大学数理学院
School of mathematics & physics
二、数学规划模型
附加问题的讨论:
附加问题(1)和(2)是要不要扩大生产?这取决于
数学模型为:
max U(p)
华北电力大学数理学院
School of mathematics & physics
一、简单优化问题
3、模型求解及其结果分析
需求函数是售价的减函数,通常是根据实际销售 情况定出。现在,假设它是线性函数,即
x f ( p) a bp, a,b 0
其中, a--代表这种产品免费供应(p=0)时的社会需求
二、数学规划模型
(1) 若用35元可以买到1桶牛奶,是否应作这项投资?若 投资,每天最多购买多少桶牛奶?
(2) 若可以聘用临时工人以增加劳动时间,付给临时工 人的工资最多是每小时几元?
