过程能力图
minitab过程能力分析图制作

2
过程能力分析分类
计量型
-------表现为正态概率和非正态概率分布型,是一组连续性数据
计数型
-------表现为Poisson(泊松)计数型和二次(元)型,依次形成缺 陷数U图为基础的报告和不良数P图为基础的报告,是各自独立的 一组数据
3
过程能力分析------计量型
例题:我们研究一个冲压件孔直径是否符合规定要求(规定值 f10+0.1/0,满足客户Ppk≥1.33要求。
13
过程能力分析------计数型
Step2. 点击“统计”--“质量工具”--“能力分析”--“二项B“。
14
过程能力分析------计数型
Step3. 出现的”能力分析(二项分布)“工具栏内,在”缺陷 数“,双击”C3“,输入“不合格数”;在”实际样本量) “中双击”C2“,输入“数量”;单击”选项“。
10
过程能力分析------计量型
Step7. 报告分析(略)
11
过程能力分析------计数型
例题:我们研究11月份焊接件生产和检查数量。从发现的不合格数 ,来探讨焊接件的过程能力。
12
过程能力分析------计数型
Step1. 我们将一个月1-30日采集的数据输入工作表
连续输入1日-30日的数据
4
过程能力分析------计量型
Step1. 按要求测量得到一组数据后,输入工作表
连续输入60个数据
5
过程能力分析------计量型
Step2. 点击“统计”--“质量工具”--“能力分析”--“”正态“。
6
过程能力分析------计量型
Step3. 出现的”能力分析(正态分布)“工具栏内,在”单列“中双 击”C2“,填入”实测值“;在”子组大小(Z)“中输入”5“ ;在”规格下限“中输入10;在”规格上限“中输入10.1,单击 ”确定“。
过程能力与过程能力指数分析

过程能力与过程能力指数过程能力过程能力以往也称为工序能力。
过程能力是指过程加工质量方面的能力,它是衡量过程加工内在一致性的,是稳态下的最小波动。
而生产能力则是指加工数量方面的能力,二者不可混淆。
过程能力决定于质量因素,而与公差无关。
当过程处于稳态时,产品的计量质量特性值有99.73%落在μ±3σ的范围内,其中μ为质量特性值的总体均值,σ为质量特性值的总体标准差,也即有99.73%的产品落在上述6σ范围内,这几乎包括了全部产品。
故通常用6倍标准差(6σ)表示过程能力,它的数值越小越好。
过程能力指数(一)双侧公差情况的过程能力指数对于双侧公差情况,过程能力指数C p的定义为:C p= T =TU-TL (公式1);6σ 6σ式中,T为技术公差的幅度,T U、T L分别为上、下公差限,σ为质量特性值分布的总体标准差。
当σ 未知时,可用σˆ1=R/d2或σˆ2=s/c4估计,其中R为样本极差,R为其平均值,s占为样本标准差,s为其平均值,d2、c4为修偏系数,可查国标《常规控制图》GB/T4091—2001表。
注意,估计必须在稳态下进行,这点在国标GB/T4091—2001《常规控制图》中有明确的规定并再三强调,不可忽视。
在过程能力指数计算公式中,T反映对产品的技术要求,而σ反映过程加工的一致性,所以在过程能力指数C p中将6σ与T比较,就反映了过程加工质量满足产品技术要求的程度。
根据T与6σ的相对大小可以得到过程能力指数C p。
如下图的三种典型情况。
C p值越大,表明加工质量越高,但这时对设备和操作人员的要求也高,加工成本也越大,所以对于C p值的选择应根据技术与经济的综合分析来决定。
当T=6σ,C p=1,从表面上看,似乎这是既满足技术要求又很经济的情况。
但由于过程总是波动的,分布中心一有偏移,不合格品率就要增加,因此,通常应取C p大于1。
各种分布情况下的C p值一般,对于过程能力指数制定了如下表所示的评价参考。
过程能力的确认方法

99.5 99.73
从表一可以看出,只有当测量次数 n →∞ 时,对应 KPt =3时的置信概率 p 才为 99.73%也就是说,只有这时 t- 分布才趋于正态分布。这说明,当 t- 分布 时,对应置信系数 KPt=3(即 ± 3 为极限误差),其置信概率并不永远是 99.73%,而是随测量次数的减少而降低。
1
μ= n
n
∑ X i ,(n→∞ )
i=1
n
√ δ=
1 ∑ (Xi - μ) 2
n
i=1
,(n→∞ )
在进行有限次测量时,上述参数的估计值分别为:
n
?= = 1 Xn
∑ X i ,(n 为有限
次) i=1
n
√ e=
1
____
∑
n-1 ( X i -
X )2
i=1
,(n 为有限次 )
上述估计值 ?、e可以作为 t- 分布的参数值。 2.t- 分布时,置信概率与测量次数的关系。 对于正态分布,当置信系数 KPt =3 时,对应置信区间(- 3δ 、+ 3δ )
表三 过程能力指数C P(或C Pt ) 评价表
一、过程确认与过程能力 7.5.2 条款要求对特殊过程实施确认,并明确提出:“确认应证实这些过程 实现所策划的结果的能力。”所谓过程能力,就是在受控条件下,保证过程能够 生产合格产品的能力。 任何过程的运行都会受到许多因素的影响,这些影响因素大致可分为两大 类:一是系统性影响因素,二是随机性影响因素。 系统性影响因素能使过程产生系统性波动, 这类波动的数值较大或具有一定 的规律性,这是我们所不期望的, 应该力加避免。 所谓使过程在受控条件下运行, 就是要对系统性因素实施有效控制,不允许过程在系统性因素的影响下运行。 随机性影响因素能使过程产生随机性波动, 这种波动的数值比较小, 从微观 上说波动没有规律, 是很多微弱影响因素综合作用的结果。 这类波动无法 (或不 值得)从技术的角度加以克服, 只能利用统计学的规律对其进行研究。 大多数随 机波动服从统计学的正态分布规律。 综上所述, 当过程受控并消除了系统性波动, 在随机状态下运行, 就可以用 随机状态的正态分布规律讨论过程的能力。
运用Minitab进行过程能力(Process+Capability)_1

过程能力概述(Process CapabilityOverview)在过程处于统计控制状态之后,即生产比较稳定时,你很可能希望知道过程能力,也即满足规格界限和生产良品的能力。
你可以将过程变差的宽度与规格界限的差距进行对比来片段过程能力。
在评价其能力之前,过程应该处于控制状态,否则,你得出的过程能力的估计是不正确的。
你可以画能力条形图和能力点图来评价过程能力,这些图形可以帮助你评价数据的分布并验证过程是否受控。
你还可以计算过程指数,即规范公差与自然过程变差的比值。
过程指数是评价过程能力的一个简单方法。
因为它们无单位,你可以用能力统计量来比较不同的过程。
一、选择能力命令(Choosing a capability command)Minitab提供了许多不同的能力分析命令,你可以根据数据的属性及其分布来选择适当的命令。
你可以为以下几个方面进行能力分析:⏹正态或Weibull概率模型(适合于测量数据)⏹很可能来源于具有明显组间变差的总体的正态数据⏹二项分布或泊松概率分布模型(适合于属性数据或计数数据)注:如果你的数据倾斜严重,你可以利用Box-Cox转换或使用Weibull 概率模型。
在进行能力分析时,选择正确的分布是必要的。
例如:Minitab提供基于正态和Weibull概率模型的能力分析。
使用正态概率模型的命令提供更完整的一系列的统计量,但是你的数据必须近似服从正态分布以保证统计量适合于这些数据。
举例来说,Analysis (Normal) 利用正态概率模型来估计期望的PPM。
这些统计量的结实依赖于两个假设:数据来自于稳定的过程,且近似服从的正态分布。
类似地,Capability Analysis (Weibull) 利用Weibull 分布模型计算PPM。
在两种情况下,统计的有效性依赖于假设的分布的有效性。
如果数据倾斜严重,基于正态分布的概率会提供对实际的超出规格的概率做比较差的统计。
这种情况下,转化数据使其更近似于正态分布,或为数据选择不同的概率模型。
6 Sigma_定义衡量阶段_过程能力Process Capability

评估过程能力时,短期研究是为了看一下一个过程可以有多 好。
数据在一个较短时期内收集,此时过程只受偏差的随机原因影响。
长期研究是为了获知过程实际的长期性能。
数据收集的时间相当长,这段时间内的过程基线受所有主要原因 (包括随机与非随机)的影响(例如:数据是从不同组、批、班 次、季节等中收集来的。)
12
短期和长期过程的标准差 • 短期研究
由于这是一个短期研究,过程西格玛水平 = 2.84。
30
Cp,Cpk 与 Pp,Ppk
统计控制的过程 Cp Cpk
统计控制
之外的过程 Pp Ppk
通常,长期研究对象是统计控制之外的过程。
在这些情况下,应使用 Pp 和 Ppk。
过程稳定时(在统计控制中),过程能力的预测要可靠得多!
31
Pp 和 Ppk
z下限
X - LSL s ˆ 178.6 - 160.0 = = 5.17 3 .6 =
23
估计超出规定的百分比
从Z表中我们发现 Z = 0.94 对应于比例 = 0.1736 这可转化为17.36% 缺陷项 或 173,600 PPM
189.4
控制下限 = 160
167.8
178.6
Z 上限 = 0.94
天内支付。
• 每20天记录一次已支付发票数和逾期 (超过45天)支付数。 • 二项分布适用于这些数据。 • 过程能力怎么样?
过程能力与过程能力指数

其中,标准差的计算为:
中心无偏过程能力示意图 这是产品质量标准要求的公差双侧对称分布,其公 差中心M与过程质量特性分布中心μ相重合的情形。
3、有偏时计算公式
当过程平均不在规格限的中心,CP不能真实反映过程满足顾 客的要求,但能反映过程的潜在能力。因此,实际过程能力指数 有:
CPK也可以用以下公式计算:
2、公式: 以过程实际质量特征值分布的6倍标准差表示 B=6σ
二、过程能力定义的缘由
当过程处于稳态时,产品的计量特性值有99.73%落在 μ±3σ的范围内,其中μ为质量特性的总体平均值,σ为质量特性 的总体标准差,也即有的产品落在上述6σ范围内,这几乎包括了 全部产品。故通常用6倍标准差(6σ)表示过程能力,它的数值 越小越好。
五、CP CPK 与不合格率P的关系
六、过程能力等级评定
七、案例分析--尺寸理论设计短期能力
尺寸理论设计长期能力
尺寸理论设计长期能力
尺寸实际成型短期能力
尺寸实际成型长期能力
三、过程能力指数
1、定义:--它是评估过程加工质量满足设计要求(技术 标准)的程度。 它包括: A、CP(PP)----用来衡量制程精密程度,它是假设均值与 目标值重合为前提的,所以不能真实反映过程满足设计的要求。 但能反映过程的潜在能力。
B、CPK(PPK)----用来衡量制程的质量水平,它Байду номын сангаас虑了集 中程度和散布程度所以可以真实反映过程满足设计要求的程度。
过程能力分析minitab版

过程能力概述(Process CapabilityOverview)在过程处于统计控制状态之后,即生产比较稳定时,你很可能希望知道过程能力,也即满足规格界限和生产良品的能力。
你可以将过程变差的宽度与规格界限的差距进行对比来片段过程能力。
在评价其能力之前,过程应该处于控制状态,否则,你得出的过程能力的估计是不正确的。
你可以画能力条形图和能力点图来评价过程能力,这些图形可以帮助你评价数据的分布并验证过程是否受控。
你还可以计算过程指数,即规范公差与自然过程变差的比值。
过程指数是评价过程能力的一个简单方法。
因为它们无单位,你可以用能力统计量来比较不同的过程。
一、选择能力命令(Choosing a capability command)Minitab提供了许多不同的能力分析命令,你可以根据数据的属性及其分布来选择适当的命令。
你可以为以下几个方面进行能力分析:⏹正态或Weibull概率模型(适合于测量数据)⏹很可能来源于具有明显组间变差的总体的正态数据⏹二项分布或泊松概率分布模型(适合于属性数据或计数数据)注:如果你的数据倾斜严重,你可以利用Box-Cox转换或使用Weibull 概率模型。
在进行能力分析时,选择正确的分布是必要的。
例如:Minitab提供基于正态和Weibull概率模型的能力分析。
使用正态概率模型的命令提供更完整的一系列的统计量,但是你的数据必须近似服从正态分布以保证统计量适合于这些数据。
举例来说,Analysis (Normal) 利用正态概率模型来估计期望的PPM。
这些统计量的结实依赖于两个假设:数据来自于稳定的过程,且近似服从的正态分布。
类似地,Capability Analysis (Weibull) 利用Weibull 分布模型计算PPM。
在两种情况下,统计的有效性依赖于假设的分布的有效性。
如果数据倾斜严重,基于正态分布的概率会提供对实际的超出规格的概率做比较差的统计。
这种情况下,转化数据使其更近似于正态分布,或为数据选择不同的概率模型。
过程能力分析

二)过程能力分析1、过程能力过程能力指产品生产得每个过程对产品质量得保证程度,反映得就是处于稳定生产状态下得过程得实际加工能力,记为B。
获取产品生产得过程能力,就是质量管理中收集样本得目得之一,以便了解过程得生产能力如何,即生产合格品得能力究竟如何。
如果生产能力过低,必需采取措施加以改进。
过程能力越高,稳定性越高,生产能力也强。
过程能力得高低可以用标准差σ得大小来衡量。
σ越小则过程越稳定,过程能力越强;σ越大过程越不稳定,过程能力越弱。
当生产过程稳定,且产品得技术标准为双侧时,B=6σ(见图11—10)。
过程能力包括长期过程能力与短期过程能力。
短期过程能力就是指仅由偶然因素所引起得部分变异,它实际上反映了短期变异情况。
长期过程能力就是指由偶然因素与异常因素所引起得总变异,它实际反映了长期变异情况。
过程能力只与标准差有关,而与产品得技术要求无关,只表示一个过程固有得最佳性能。
标准差决定于质量因素,即人、机、料、法、环,与规范无关。
为了反映与衡量过程能力满足技术要求得程度,引进一个新指标,即过程能力指数。
[例题6] 过程能力得高低可以用标准差σ得大小来衡量。
σ越小则()。
A、过程标准越高B、过程越稳定C、过程越不稳定D、过程能力越强E、过程能力越弱答案:BD2.过程能力指数过程能力指数反映过程加工中质量满足产品技术要求得程度,也即产品得控制范围满足顾客要求得程度。
过程能力指数=技术要求/过程能力(11—14)过程能力指数越大,说明过程能力越满足技术要求,产品质量越有保证。
对于产品特性值分布得平均值μ与规范中心M重合即无偏移时用Cp衡量,对于产品特性值分布得平均值μ与规范中心M不重合即有偏差时用Cpk衡量。
①无偏移双侧规范情况得短期过程能力对于双侧规范情况,无偏移短期过程能力指数Cp得计算公式如下:大得情况,即0≤K<1。
3.过程能力指数与产品不合格率得关系当生产过程处于稳定状态时,过程能力指数Cp与不合格品率P相对应。
CPK(过程能力分析方法)

过程能力分析过程能力也称工序能力,是指过程加工方面满足加工质量的能力,它是衡量过程加工内在一致性的,最稳态下的最小波动。
当过程处于稳态时,产品的质量特性值有99.73%散布在区间[μ-3σ,μ+3σ],(其中μ为产品特性值的总体均值,σ为产品特性值总体标准差)也即几乎全部产品特性值都落在6σ的范围内﹔因此,通常用6σ表示过程能力,它的值越小越好。
为什么要进行过程能力分析进行过程能力分析,实质上就是通过系统地分析和研究来评定过程能力与指定需求的一致性。
之所以要进行过程能力分析,有两个主要原因。
首先,我们需要知道过程度量所能够提供的基线在数量上的受控性;其次,由于我们的度量计划还相当"不成熟",因此需要对过程度量基线进行评估,来决定是否对其进行改动以反映过程能力的改进情况。
根据过程能力的数量指标,我们可以相应地放宽或缩小基线的控制条件。
工序过程能力分析工序过程能力指该工序过程在5M1E正常的状态下,能稳定地生产合格品的实际加工能力。
过程能力取决于机器设备、材料、工艺、工艺装备的精度、工人的工作质量以及其他技术条件。
过程能力指数用Cp、Cpk表示。
非正态数据的过程能力分析方法当需要进行过程能力分析的计量数据呈非正态分布时,直接按普通的计数数据过程能力分析的方法处理会有很大的风险。
一般解决方案的原则有两大类:一类是设法将非正态数据转换成正态数据,然后就可按正态数据的计算方法进行分析;另一类是根据以非参数统计方法为基础,推导出一套新的计算方法进行分析。
遵循这两大类原则,在实际工作中成熟的实现方法主要有三种,现在简要介绍每种方法的操作步骤。
非正态数据的过程能力分析方法1:Box-Cox变换法非正态数据的过程能力分析方法2:Johnson变换法非正态数据的过程能力分析方法3:非参数计算法当第一种、第二种方法无法适用,即均无法找到合适的转换方法时,还有第三种方法可供尝试,即以非参数方法为基数,不需对原始数据做任何转换,直接按以下数学公式就可进行过程能力指数CP和CPK的计算和分析。
02_ 过程能力分析(常规控制图)
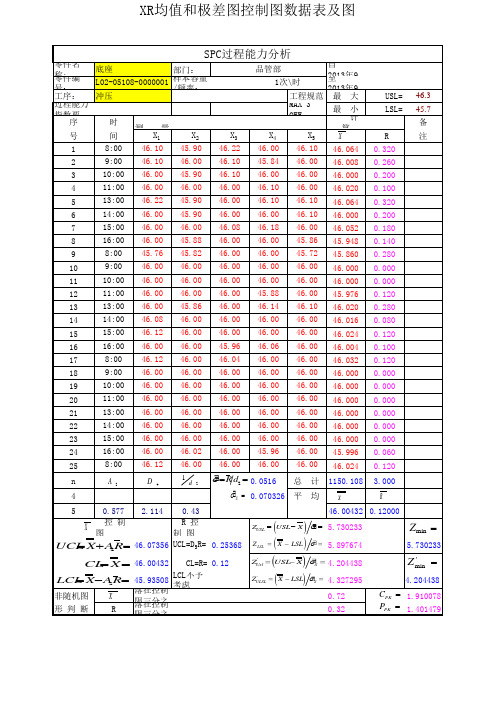
UCL
C L
LCL U C CL L
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
R ¼ Í
0.350
0.300 0.250 0.200 0.150 0.100 0.050
0.000
1
2
3
4
5
6
7
8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
R
价 图 能 力 指 数 数据整理者(签名): 数据分析者(签名): 审批者(签名):
计算控制限的日期:
评
X
图
没超出控制上限的点。 有超出控制下限的点,请检查过程纪录,用因果图查明原因,并订出纠正措施。 #REF! 没有明显的非随机图形。 有超出控制上限的点,请检查过程纪录,用因果图查明原因,并订出纠正措施。 #REF! 有明显的非随机图形,请查明情况,并订出纠正措施。 Cpk: 能力指数过剩,考虑是否降低成本。 PPK: 能力指数符合要求
R
MAX 3 OFF 最 数 据 X2 45.90 46.00 45.90 46.00 45.90 45.90 46.00 45.88 45.82 46.00 46.00 46.00 45.86 46.00 46.00 46.00 46.00 46.00 46.00 46.00 46.00 46.00 46.00 46.02 46.00
X
46.064 46.008 46.000 46.020 46.064 46.000 46.052 45.948 45.860 46.000 46.000 45.976 46.020 46.016 46.024 46.004 46.032 46.000 46.000 46.000 46.000 46.000 46.000 45.996 46.024 1150.108
如何用MINITAB进行过程能力分析

过程能力概述一旦过程处于统计控制状态,并且是连续生产,那么你可能想知道这个过程是否有能力满足规范的限制,生产出好的零件(产品),通过比较过程变差的宽度和规范界限的宽度可以确定过程能力。
在评估过程能力之前,过程必须受控。
如果过程不受控,你将得到不正确的过程能力值。
.你能通过画能力柱状图和能力图来评估过程能力。
这些图形能够帮助你评估数据的分布和检验过程是否受控。
你也可以估计包括规范公差与正常过程变差之间比率的能力指数。
能力指数或统计指数都是评估过程能力的一种方法,因为它们都没有单位,所以,可以用能力统计表来比较不同过程的能力。
选择能力命令MINITAB提供了一组不同的能力分析命令,你可以根据数据的性质和分布从中选择命令,你可以对以下情况进行能力分析:——正态或Weibull概率模式(对于测量数据)——不同子组之间可能有很强变差的正态数据——二项式或Poisson概率模式(对于计数数据或属性数据)当进行能力分析时,选择正确的公式是基本要求,例如,MINITAB提供基于正态或Weibull分布模型上的能力分析工具,使用正态概率模型的命令提供了更完全的统计设置,但是,适用的数据必须近似于正态分布.例如,利用正态概率模型,能力分析(正态)可以估计预期零件的缺陷PPM 数。
这些统计分析建立在两个假设的基础上,1、数据来自于一个稳定的过程,2、数据服从近似的正态分布,类似地,能力分析(Weibull)计算零件的缺陷的PPM 值利用的是Weibull分布。
在这两个例子中,统计分析正确性依赖于假设分布模型的正确性。
如果数据是歪斜非常严重,那么用正态分布分析将得出与实际的缺陷率相差很大的结果。
在这种情况下,把这个数据转化比正态分布更适当的模型,或为数据选择不同的概率模式.用M INITAB,你可以使用Box-Cox能力转化或Weibull概率模型,非正态数据比较了这两种方法.如果怀疑过程中子组之间有很强的变差来源,可以使用能力分析(组间/组内)或SIXpack能力分析(组间/组内)。
04过程能力分析

在M 时,
LSL USL ,所以:
C PL C PU
分析(2)
我们应当把注意力放在这两个较小的一 个,因为这个地方出现的不合格品多。
实际过程能力指数: C pk min C PL , C PU
潜在过程能力指数: Cp USL LSL T 6 6
过程能力不足
M=μ LSL 99.73% 0.5 σ=0.075
USL
PC=6σ
0.9
CP=1
LSL
过程能力恰好
M=μ σ=0.067
USL
99.73% 0.5
PC=6σ
0.9
过程能力满足要求
M=μ LSL 99.73% 0.5 PC=6σ σ=0.075
USL
0.9
各种分布情况下的Cp值
过程能力指数的计算公式
要求 Cp 过程能力
USL LSL 6
T 6
例
子
在用钢材弯曲成钢夹的产品中,其间隙 的上、下规范限分别为(单位:cm): USL=0.9 LSL=0.5 如过程中钢夹间隙大小x值服从正态分布
N(0.7,0.075 ) 即该过程中心恰与 。
2
规范中心重合,μ=M=0.7,标准差 σ=0.075。
什么是过程能力
过程能力(Process capability)以往 也称为工序能力。 过程能力是指过程加工质量方面的能力, 而不是加工数量方面的能力。它是衡量 过程加工内在一致性的,是稳态下的波 动范围。 过程能力决定于质量因素,即:人、机、 料、法、环,过程能力与公差无关。
为什么要分析过程能力
生产或批量很小难以计算;不能重复的过程,如有的服务项 目服务,就很难计算)。
过程能力分析报告 图表
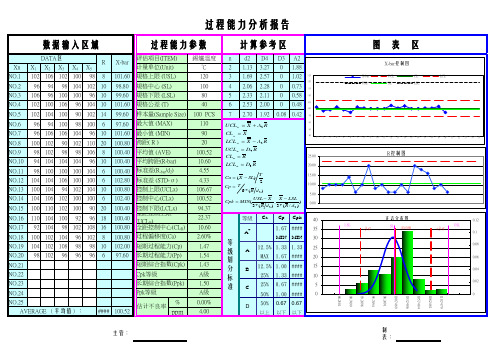
25% 1.33 #### 10
准
C 25% 0.67 ####
5
50% 1.00 #### 0
D 50% 0.67 0.67 以上 以下 以下
0
LSL
-3σ
5 正态分布图 10
SL 平均值
110.7479 108.2481 105.7484 103.2486 100.7489 98.2491 95.7494 93.2496 90.7499 88.2501
100.52
评估項目(ITEM) 计量单位(Unit) 規格上限 (USL) 規格中心 (SL) 規格下限 (LSL) 規格公差 (T) 样本量(Sample Size) 最大值 (MAX) 最小值 (MIN) 跨距( R ) 平均值 (AVE) 平均跨距(R-bar) 标准差(R-bar/d2) 标准差 (STD-σ) 控制上限(UCLx) 控制中心(CLx) 控制下限(LCLx) 全距控制上限 (全UC距L控R) 制中心(CLR) 过程偏移度(Ca) 短期过程能力(Cp) 长期过程能力(Pp) 短期綜合指数(Cpk) Cpk等級 长期綜合指数(Ppk) Ppk等級 估计不良率 %
X-bar控制图
3 1.69 2.57 0 1.02 125
120
4 2.06 2.28 0 0.73 115
5 2.33 2.11 0 0.58 110
6 2.53 2.00 0 0.48 105
100
7 2.70 1.92 0.08 0.42 95
X-bar
UCL
CL
LCL
USL
SL
LSL
UCLX X A2 R
USL X X LSL
Cpk MIN(
,
第六章-控制图、过程能力和直方图

图别
中心线 (C L)
上控制界限(UCL)
下控制界限(LCL)
-R
R
+ A2 D4
- A2 D3
x -R
R
+m 3A2 D4
-m 3A2 D3
x -R
x RS
+2.659 3.267
-2.659 不考虑
x
R
x
x
x
=
x
=
R
R
P
-
n -
(1- )
Pn
-
Pn
-
3
u
-
3
n
u
-
+
u
-
3
n
u -
c
-
3
c —
c
-
3
c +
控制系数选用表
n
2
3
4
5
6
7
8
910Biblioteka A21.8801.023
0.729
0.577
0.483
0.419
0.373
0.337
0.308
D4
3.267
2.575
2.282
2.115
2.004
1.924
单值-移动极差控制图
x - R S
简便省事,并能及时判断工序是否处于稳定状态。缺点是不易发现工序分布中心的变化。
因各种原因(时间、费用等)每次只能得到一个数据或希望尽快发现并消除异常原因。
计 数 值 控 制 图
不合格品数控制图
Pn
较常用,计算简单,操作工人易于理解。
样本容量相等。
不合格品率控制图
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0.01
0.01
0.01
(0.06)
(0.08)
0.01
0.01
0.23
0.12
(0.10)
0.12
(0.04)
(0.10)
(0.20)
0.12
0.12
(0.10)
0.23
(0.20)
0.12
0.12
0.01
(0.10)
(0.10)
0.12
(0.20)
(0.13)
(0.10)
0.12
0.01
0.12
能力指数 下限 (稳C定PL过) 程 能 稳力 定指 过数 程 能力指数
能 标力 准比 偏率 差 (n-1) 标准偏差 变异 (n-
0 0
0.2562
2.0590
2.0427
2.2442 2.1435 2.0427 1.9779 0.1215 0.1210 0.0148
极差 频数
0.7000 0.6000 0.5000 0.4000 0.3000
过程能力分析均值极差(X-R)控制图
双边控制限型
供方信息
供应商 xxx
零件信息 模具信息
零件号 图纸编号 模具编号 描述
尺寸信息
尺寸规格 0.000 下公差限 -0.800
xxx xxx xxx 长度
上公差 规格中线
0.800 下公差 0.000 上公差限
部门 零件名称/描述 工程更改水平 模腔数
0.800 0.800
10 0
统计特性 描述
样 工本 程容 规量 范 下限 规 工格 程中 规线 范 上限
总和 读数均值
均值(X-图)
日期
2013/11/22
数据值
125 -0.8000 0.0000 0.8000 4.7000 0.0376
均值
0.25
0.20
最大值
0.3360
0.15
0.10
0.05
最小值
-0.2040
0.14
0.03
0.08
-0.07
0.10
0.01
-0.05
0.05
-0.07
0.01-0.05源自0.110.060.02
0.12
0.06
0.10
0.12
极差 备注:
0.2160 0.2160 0.2160 0.4360 0.3240 0.3240 0.2160 0.3240 0.2160 0.2160 0.3240 0.2160 0.2160 0.3240 0.2260 0.1080 0.2160 0.2160 0.4660 0.3240 0.2160 0.3080 0.1080 0.2160 0.2160
0.12
0.12
4
(0.10)
(0.20)
0.12
0.23
0.01
0.01
0.01
0.01
0.01
0.01
(0.10)
0.01
(0.10)
0.01
0.08
0.01
0.01
0.01
0.34
0.12
(0.10)
0.23
0.01
0.01
0.12
5
均值
0.06
-0.10
0.06
0.11
0.06
-0.01
0.01
0.12
0.12
0.04
0.12
0.12
(0.20)
0.12
(0.10)
0.01
(0.10)
0.23
0.23
0.12
0.23
0.12
0.12
0.12
2
3
0.01
0.01
(0.10)
(0.10)
0.23
0.01
0.01
0.01
0.01
0.01
0.12
0.23
0.01
0.12
0.13
(0.10)
0.01
极差(R-图)
Data Values
UCLx
LCLx
Average X
变异 (n) 性能指数 性能比率 性能指数
50
45
40
35
0.0146 2.1955 0.4555 2.0923
正态分布
正态分布曲线 44
35
30
25
21 20
15
0.2000
10 8
0.1000
5
2
0 0
0.0000
1
2
3
4
5
6
7
8
9
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
12
3
0
0
0
数据区间
R Value
UCLr
LCLr
Average R
控制图 表现:
数据无 明显异
过程能力分析:
过程能力特足!!
n
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
1
0.12
0.01
0.01
0.34
0.01
0.01
0.01
0.34
0.12
0.01
(0.20)
0.01
(0.10)
(0.20)
0.01
(0.10)
(0.10)
0.01
0.12
0.01
0.01
0.23
0.01
0.23
0.01
0.12
(0.20)
0.12
0.12
0.12
0.12
(0.10)
0.23
0.00
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
-0.05
-0.10 -0.15 -0.20
低于下控 制线点数 (X) 高于上控 制线点数 (X)
极差均值 R
D2 值 (n=4)
能力指数 上限 (CPU)
Data Values
UCLx
LCLx
Average X
控制限
UCLx UCLr
xxx xxx xxx 1*1 单位
0.224 0.585
mm
AVERx AVERr
0.038 0.256
LCLx LCLr
数据重要
过程信息栏
趋势
X图
递增趋势
点数最大长度 递增链数
3 9
点数最大长度 -0.149 超递出减控趋制势 递减链数
3 9
0.000 线点数
0
R图 2 9 3
