资料分析最全公式440
资料分析计算公式整理
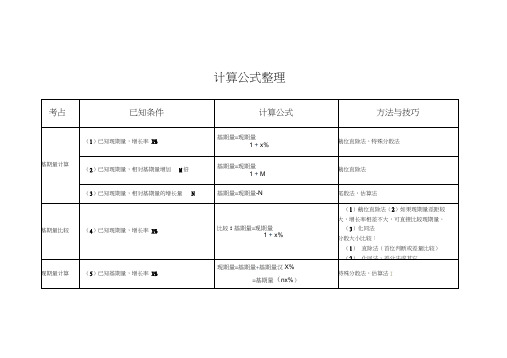
(2) 公式可变换为:
X%
增长量=现期量汉——甘出
1+x%, 其中
X%为增函数,所以现期量大,增长率
1+x%
大的情况下,增长量一定大。
增长率计算
(13)已知基期量与增长量
丄出【/皆增长量
增长率_ ”里 基期量
(1) 截位直除法
(2) 插值法
(14)已知现期量与基期量
增长率 现期量-基期量
基期量
现期量=基期量+基期量xM
=基期量x(1+M)
估算法
(7)已知基期量,增长量N
现期量=基期量+N
尾数法,估算法
4■苗上昌H苗
(8)已知基期量与现期量
增长量=现期量-基期量
尾数法
(9)已知基期量与增长率x%
增长量=基期量汉X%
特殊分数法
(10)已知现期量与增长率X%
增长量=现期量沢X%
1+x%
1
(1)特殊分数法,当X%可以被视为-时,n
1+x%
(1)截位直除法(2)如果现期量差距较 大,增长率相差不大,可直接比较现期量。
(3)化同法
分数大小比较:
(1) 直除法(首位判断或差量比较)
(2) 化冋法,差分法或其它
现期量计算
(5)已知基期量,增长率X%
现期量=基期量+基期量汉X%
=基期量(nx%)
特殊分数法,估算法I
(6)已知基期量,相对基期量增加M倍
截位直除法
(15)如果基期量为A,经N期变为B,平均 增长率为X%
x% =N_-1
\A
代入法或公式法
(16)两期混合增长率:如果第二期与第二期
资料分析公式汇总
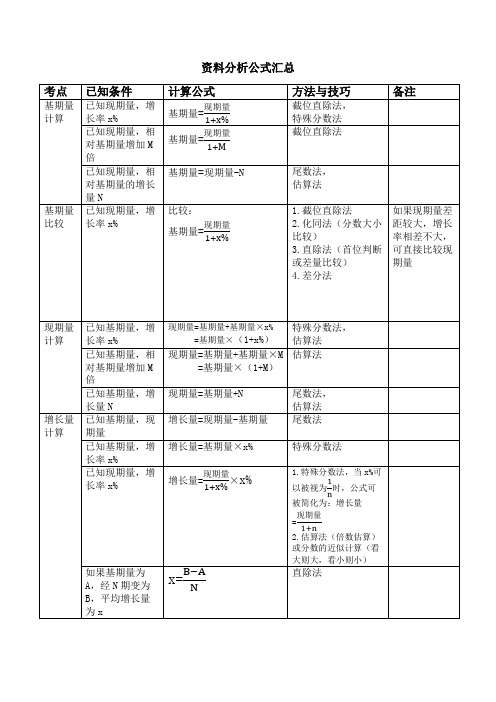
资料分析公式汇总速算技巧一、估算法精度要求不高的情况下,进行粗略估值的速算方式。
选项相差较大,或者在被比较的数字相差必须比较大,差距的大小将直接决定对“估算”时对精度的要求。
二、直除法在比较或者计算较复杂的分数时,通过“直接相除”的方式得到商的首位(首一位、首两位、首三位),从而得出正确答案的速算方式。
常用形式: 1.比较型:比较分数大小时,若其量级相当,首位最大∕小数为最大∕小数2.计算型:计算分数大小时,选项首位不同,通过计算首位便可得出答案。
难易梯度:1.基础直除法:①可通过直接观察判断首位的情形;②需要通过手动计算判断首位的情形。
2.多位直除法:通过计算分数的“首两位”或“首三位”判断答案情形。
三、插值法1.“比较型”插值法如果A与B的比较,若可以找到一个数C,使得A﹥C,而B﹤C,既可以判定A﹥B;若可以找到一个数C,使得A﹤C,而B﹥C,既可以判定A﹤B;2.“计算型”插值法若A﹤C﹤B,则如果f﹥C,则可以得到f=B;如果f﹤C,则可以得到f=A;若A﹥C﹥B,则如果f﹥C,则可以得到f=A;如果f﹤C,则可以得到f=B。
四、放缩法当计算精度要求不高时,可以将中间结果进行大胆的“放”(扩大)或者“缩”(缩小),从而迅速得到精度足够的结果。
常用形式:1. A﹥B,C﹥D,则有A+C﹥B+D;A-D﹥B-C;2. A﹥B﹥0,C﹥D﹥0,则有A×C﹥B×D;A÷D﹥B÷C五、割补法在计算一组数据的平均值或总和值时,首先选取一个中间值,根据中间值将这组数据“割”(减去)或“补”(追上),进而求取平均值或总和值。
常用形式:1.根据该组数据,粗略估算一个中间值;2.将该组值分别减去中间值得到一组数值;3.将得到的新数值相加得到和值,用和值除以该组数值的项数得到商值,将商值加上中间值,即为该组数值的精确平均值;4.用中间值乘以数据项数再加上最后的和值即为总和值。
资料分析计算公式整理

资料分析计算公式整理在进行资料分析时,掌握一些关键的计算公式是至关重要的。
这些公式能够帮助我们快速、准确地从大量的数据中提取有价值的信息,做出合理的判断和决策。
下面,我将为大家整理一些常见且实用的资料分析计算公式。
一、增长率相关公式1、增长率=(现期量基期量)÷基期量× 100%这是最基本的增长率计算公式。
例如,某公司去年的销售额为 100 万元,今年为 120 万元,那么今年的销售额增长率为(120 100)÷ 100 × 100% = 20%。
2、间隔增长率= r1 + r2 + r1×r2当涉及到间隔年份的增长率计算时,就需要用到这个公式。
假设第一年的增长率为 r1,第二年的增长率为 r2,那么从第一年到第二年的间隔增长率就是 r1 + r2 + r1×r2。
3、年均增长率=\(\sqrtn{\frac{现期量}{基期量}} 1 \)(n 为年份差)如果要计算一段时间内的平均增长率,就用这个公式。
比如,某地区 2010 年的 GDP 为 100 亿元,2020 年为 200 亿元,年份差为 10 年,那么年均增长率=\(\sqrt10{\frac{200}{100}} 1 \)。
1、比重=部分量÷整体量× 100%比如,某班级共有 50 名学生,其中男生 25 人,那么男生在班级中的比重就是 25÷50× 100% = 50%。
2、整体量=部分量÷比重已知部分量和比重,求整体量时使用。
假设某企业某产品的销售额占总销售额的 30%,该产品销售额为 100 万元,那么企业总销售额=100÷30% 。
3、部分量=整体量×比重当已知整体量和比重,求部分量时运用。
比如一个城市总人口为100 万人,其中老年人占比 20%,那么老年人的数量= 100×20% = 20 万人。
资料分析常用公式

资料分析常用公式1. 平均数公式平均数(Mean)是表示一组数据集中趋势的量数,计算公式为:$$\text{平均数} = \frac{\sum_{i=1}^{n} x_i}{n}$$其中,$ x_i $ 表示第 $ i $ 个数据,$ n $ 表示数据总数。
平均数适用于描述一组数据的总体水平,常用于市场调研、人口统计等领域。
2. 中位数公式中位数(Median)是将一组数据按大小顺序排列后位于中间位置的数,计算公式为:$$\text{中位数} =\begin{cases}\frac{x_{\frac{n+1}{2}} + x_{\frac{n}{2}}}{2} & \text{当 } n \text{ 为偶数时} \\x_{\frac{n+1}{2}} & \text{当 } n \text{ 为奇数时}\end{cases}$$其中,$ x_i $ 表示第 $ i $ 个数据,$ n $ 表示数据总数。
中位数适用于描述一组数据的中间水平,常用于描述收入、房价等分布不均的数据。
3. 标准差公式标准差(Standard Deviation)是衡量一组数据离散程度的量数,计算公式为:$$\sigma = \sqrt{\frac{\sum_{i=1}^{n} (x_i \mu)^2}{n}}$$其中,$ x_i $ 表示第 $ i $ 个数据,$ \mu $ 表示平均数,$ n $ 表示数据总数。
标准差适用于描述一组数据的波动程度,常用于质量控制、风险评估等领域。
4. 相关系数公式相关系数(Correlation Coefficient)用于衡量两个变量之间的线性关系程度,计算公式为:$$r = \frac{\sum_{i=1}^{n} (x_i \bar{x})(y_i\bar{y})}{\sqrt{\sum_{i=1}^{n} (x_i \bar{x})^2}\sqrt{\sum_{i=1}^{n} (y_i \bar{y})^2}}$$其中,$ x_i $ 和 $ y_i $ 分别表示两个变量中的第 $ i $ 个数据,$ \bar{x} $ 和 $ \bar{y} $ 分别表示两个变量的平均数,$ n $ 表示数据总数。
资料分析公式大全

一、与增长有关的基本公式
1、增长量= 今年的量- 去年的量
2、
3、
4、增长率=去年的量×增长率
5、
6、
7、今年的量=去年的量×(1+增长率)
、
、
二、与隔年增长有关的基本公式(ql表示今年的增长率,q2表示去年的增长率) 1、
2、
3、隔年的增长率=(1+ql)×(1+q2)- 1
4、
三、与比重有关的公式(ql表示部分的增长率,q2表示整体的增长率)
1、
2、部分的量=比重×整体的量
3、
比重的差(百分点)=今年的比重
4、
5、比重的递推
已知则,
已则
四、与平均量有关的公式(q1表示总数的增长率,q2表示份数的增长) 1、
平均量的增长量=今年的平均量)
2、
3、
五、与倍数有关的公式
1、
2、
3、"是"几倍-1="多"几倍=增长率
六、与指数有关的公式
1、(指数-100)%=增长率
2、
七、与拉动增长、贡献率有关的公式1、
2、
3、
八、与去年的和或差有关的公式。
公务员考试资料分析必背公式

公务员考试资料分析必背公式1、现期与基期(1)现期量=基期量×(1+r)(2)基期量=现期量1+r,当|r|<5%时,基期量≈现期量—现期量×r(3)基期量的比较:当1+r未出现成倍变化而现期量有明显倍数关系时,则着重比较现期量。
2、增长量与增长率(1)增长率(r)=现期量−基期量基期量= 现期量基期量—1 = 增长量基期量=增长量现期量−增长量(2)增长率的比较:增长率(r) =现期量−基期量基期量= 现期量基期量—1,因此增长率大小只需比较现期量基期量即可。
(3)增长量=现期量—基期量=基期量×r=现期量×r1+r ,当r≈1n时,增长量≈现期量x1n+1(4)年均增长量=(末期值-初期值)÷n(5)增长量的比较:大大则大,一大一小百化分。
3、特殊增长率(1)间隔增长率:间隔增长率r=r1+r2+r1xr2,当r1xr2<0.01时可忽略,r≈r1+r2。
(2)年均增长率:末期值=初期值(1+r)n,估算技巧,(1+r)n≈1+n·r,当|r|≤5%时,误差较小。
(3)混合增速:混合增速介于部分增长率之间,更加靠近于基数较大的所对应的增长率。
4、比重相关:(1)现期比重:比重=部分÷整体(2)基期比重:BA x1+a1+b,其中部分量为B,部分对应的同比增速为b,整体量为A,整体对应的同比增速为a。
(3)两期比重:现期比重与基期比重的差值为BA x b−a1+b,结论:①b-a的正负决定升降;②上升或下降的具体的数值应该小于|b-a|。
5、平均数与倍数(1)平均数=总数÷总份数(2)倍数,B是A的多少倍,计算公式为:B÷A;如果是多几倍则是B—1;A,其中b代表总数的增长率,a代表总份数的增长率。
(3)平均数的增长率:b−a1+a如人均收入=总收入÷总人数,在计算人均收入的增长率时,b即对应总收入的增长率,a对应总人数的增长率。
公务员考试资料分析公式大全

公务员考试资料分析公式大全①基期量: 对比参照时期的具体数值②现期量: 相对于基期量③增长量: 现期量相对于基期量的变化量④平均增长量: 一段时间内平均每期的变化量⑤增长率: 现期量相对于基期量的变化指标如果基期量就是A,经过n个周期变为B(末期量),年均增长率为r,则可得出:注意: 利用上述公式算出的年均增长率略大于实际值, 且当|x|>10%时, 利用上述公式计算存在一定的误差。
已知第二期与第三期的增长率, 求第三期相对于第一期的增长率。
已知部分的增长率, 求整体的增长率。
如果A的增长率就是a,B的增长率就是b,“A+B”的增长率就是r,其中r 介于a、b之间,且r 数值偏向于基数较大一方的增长率(若A>B,则r 偏向于a;若A<B,则r 偏向于b)。
同比增长: 与历史同期相比的增长情况。
环比增长: 与相邻上一个统计周期相比的增长情况。
百分数:也叫百分率或者百分比,例如10%,12%。
百分点:以百分数形式表示相对指标的变化幅度,增长率之间作比较时可直接相加减。
现期平均数基期平均数:A 为现期总量,a 为对应增长率;B 为现期份数,b 为对应增长率。
平均数的增长率部分在整体中所占的百分比, 用个百分数或者“几成”表示“一成”代表的就是10%,“二成”代表的就是20%,以此类推。
A 就是B 的多少倍,A÷B;A比B多多少倍,(A-B)÷B=A/B-1。
翻几番变为原来数值的倍。
例如, 如果翻一番, 就是原来的 2 倍;翻两番就是原来的 4 倍;翻三番就就是原来的8 倍描述某种事物相对变化的指标值。
( 假设基数为100,其她值与基期相比得到的数值) 资料分析就是行测考试中非常重要的一大模块,对于这一模块而言,难度适中,但计算量偏大,许多小伙伴会花费大量的时间。
做题的速度与准确率就是建立在领略题意并熟悉统计术语的基础上,因此,公考通() 就资料分析中容易混淆且尤为重要的统计术语作简要的辨析。
资料分析速算必背公式

资料分析速算必背公式资料分析速算必背公式主要包括以下11个:1.平均数(arithmetic mean):用于表示一组数据的总体特征,表示为x=X1+X2……Xn/n。
2.方差(variance):用于表示一组数据的离散程度,表示为s²=1/n-1Σ(Xi-x)²。
3.标准差(standard deviation):用于表示一组数据的离散程度,表示为s=√s2。
4.四分位数(quartile value):将原始数据从低到高排序,然后将所有数据划分为4等分,将相应等分数据的中位数称为“四分位数”,表示为Q1、Q2、Q3。
5.百分位数(percentile value):将原始数据从低到高排序,然后将所有数据划分为100等分,将相应等分数据的中位数称为“百分位数”,表示为P1、P2、P3 (99)6.众数(mode):即原始数据中出现次数最多的数据为众数,如果有多个众数,则将其依次列出。
7.几何平均数(geometric mean):将所有原始数据乘积开方得到几何平均数,表示为XG=(X1xX2……Xn)^1/n。
8.几何标准差(geometric standard deviation):用于表示一组数据的离散程度,表示为Sg=(X1X2⋯Xn)^1/n / X的开平方。
9.协方差(covariance):用于衡量两组数据之间的关联性,表示为Cov(X,Y)=1/n-1Σ[(X-x)(Y-y)]。
10.相关系数(correlation coefficient):用于衡量两组数据之间的关联性,表示为r=Cov(X,Y)/sxsz。
11.线性回归(linear regression):是一种用来寻找两变量之间关系的方法,模型表达式为Y=aX+b,其中a为斜率,b为截距。
资料分析计算公式整理

资料分析计算公式整理在进行资料分析时,掌握一些关键的计算公式是至关重要的。
这些公式能够帮助我们快速、准确地从大量的数据中提取有价值的信息,并得出有效的结论。
接下来,让我们一起对常见的资料分析计算公式进行梳理。
一、增长率相关公式增长率是资料分析中常见的一个指标,用于衡量数据的增长情况。
1、增长率=(现期量基期量)÷基期量 × 100%例如,某公司去年的销售额为 100 万元,今年的销售额为 120 万元,那么今年销售额的增长率为:(120 100)÷ 100 × 100% = 20%2、间隔增长率如果已知第二期相对于第一期的增长率为 r1,第三期相对于第二期的增长率为 r2,那么第三期相对于第一期的间隔增长率为:R = r1 +r2 + r1×r23、年均增长率假设初期值为A,末期值为B,经过n 年,年均增长率为r,则有:B = A ×(1 + r)^n二、比重相关公式比重用于反映部分在整体中所占的比例。
1、比重=部分值÷整体值 × 100%比如,某班级总人数为 50 人,其中男生有 25 人,那么男生在班级中的比重为:25÷50×100% = 50%2、整体值=部分值÷比重若已知部分值为 30,比重为 60%,则整体值为:30÷60% = 503、部分值=整体值×比重假如整体值为 80,比重为 25%,则部分值为:80×25% = 20三、平均数相关公式平均数是表示一组数据集中趋势的量数。
1、平均数=总数÷个数例如,一组数据 10、20、30、40、50,总数为 150,个数为 5,则平均数为:150÷5 = 302、总数=平均数×个数若平均数为 40,个数为 8,则总数为:40×8 = 320四、倍数相关公式倍数用于比较两个量之间的关系。
资料分析计算公式整理
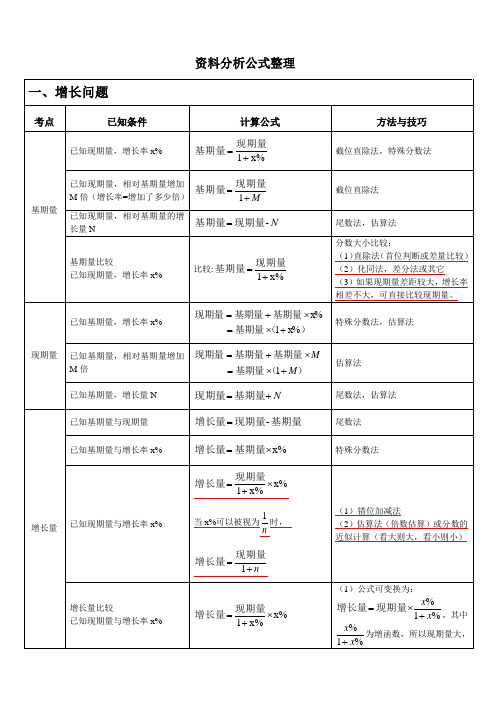
资料分析公式整理一、增长问题考点已知条件计算公式方法与技巧基期量已知现期量,增长率x%x%1+=现期量基期量截位直除法,特殊分数法已知现期量,相对基期量增加M倍(增长率=增加了多少倍)M+=1现期量基期量截位直除法已知现期量,相对基期量的增长量NN-现期量基期量=尾数法,估算法基期量比较已知现期量,增长率x%比较:x%1+=现期量基期量分数大小比较:(1)直除法(首位判断或差量比较)(2)化同法,差分法或其它(3)如果现期量差距较大,增长率相差不大,可直接比较现期量。
现期量已知基期量,增长率x%)(基期量基期量基期量现期量x%1x%+⨯=⨯+=特殊分数法,估算法已知基期量,相对基期量增加M倍)(基期量基期量基期量现期量MM+⨯=⨯+=1估算法已知基期量,增长量N N+=基期量现期量尾数法,估算法增长量已知基期量与现期量基期量现期量增长量-=尾数法已知基期量与增长率x% x%⨯=基期量增长量特殊分数法已知现期量与增长率x%x%x%1⨯+=现期量增长量当x%可以被视为n1时,n+=1现期量增长量(1)错位加减法(2)估算法(倍数估算)或分数的近似计算(看大则大,看小则小)增长量比较已知现期量与增长率x%x%x%1⨯+=现期量增长量(1)公式可变换为:%1%xx+⨯=现期量增长量,其中%1%xx+为增函数,所以现期量大,增长率大的情况下,增长量一定大。
“比”谁,谁就是分母。
甲比乙多1/5,乙比甲少多少?(设甲6乙5,则乙比甲少1/6)增长率增速增幅已知基期量与增长量基期量增长量增长率=基期量基期量现期量增长率-=(1)截位直除法(2)插值法已知现期量与基期量1-=基期量现期量增长率截位直除法增长率比较已知现期量与增长量比较基期量现期量增长率=相当于分数大小比较,同上述做法发展速度已知现期量与基期量增长率基期量现期量发展速度+==1(1)截位直除法(2)插值法增长贡献率已知部分增长量与整体增长量整体增长量部分增长量增长贡献率=(1)截位直除法(2)插值法拉动增长(22)如果B是A的一部分,B拉动A增长x% 整体基期量部分增长量=%x(1)截位直除法(2)插值法隔年增长隔年基期量已知现期量A,同比增长x%,增速增加了n个百分点n)-%%)(11(A=隔年基期量xx++题干有时直接给出上年增长率%)%)(11(A=隔年基期量yx++隔年增长率已知现期量A,同比增长x%,增速增加了n个百分点,求A对于相隔一期的增长率(两期混合增长率)1-n-x%1(x%1))(隔年增长率++=%%xx%x%x1-%x1(%x1%x2121213++=++==))(隔年增长率连续增长,隔年增长率大于增长率之和:%%xx%x%x%x21213++=连续下降,隔年增长率小于增长率之和:%%xx%x-%x%x21213+-=年均增长求平均增长率时特别注意问题的表述方式,例如:1、"从2004 年到2007 年的平均增长率"一般表示不包括2004 年的增长率; N=32、"2004 、2005 、2006 、2007 年的平均增长率"一般表示包括2004 年的增长率。
(完整版)资料分析公式汇总
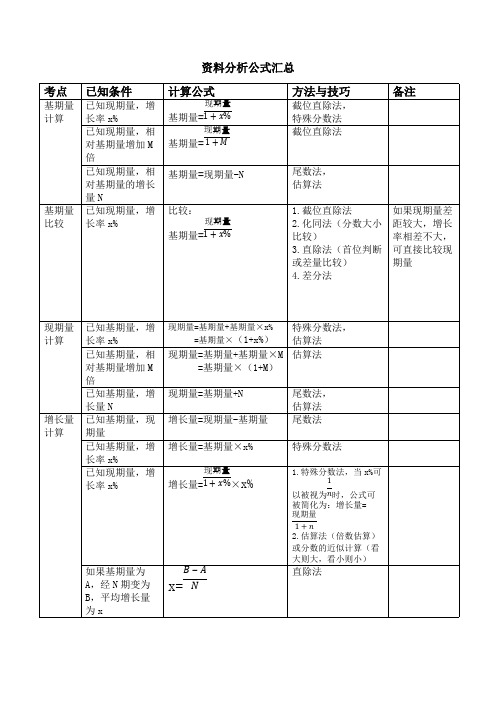
资料分析公式汇总考点已知条件计算公式方法与技巧备注已知现期量,增长率x%基期量=现期量1+x%截位直除法,特殊分数法已知现期量,相对基期量增加M 倍基期量=现期量1+M截位直除法基期量计算已知现期量,相对基期量的增长量N基期量=现期量-N尾数法,估算法基期量比较已知现期量,增长率x%比较:基期量=现期量1+x%1.截位直除法2.化同法(分数大小比较)3.直除法(首位判断或差量比较)4.差分法如果现期量差距较大,增长率相差不大,可直接比较现期量已知基期量,增长率x%现期量=基期量+基期量×x%=基期量×(1+x%)特殊分数法,估算法已知基期量,相对基期量增加M 倍现期量=基期量+基期量×M =基期量×(1+M )估算法现期量计算已知基期量,增长量N现期量=基期量+N 尾数法,估算法已知基期量,现期量增长量=现期量-基期量尾数法已知基期量,增长率x%增长量=基期量×x%特殊分数法已知现期量,增长率x%增长量=×x%现期量1+x% 1.特殊分数法,当x%可以被视为时,公式可1n 被简化为:增长量=现期量1+n2.估算法(倍数估算)或分数的近似计算(看大则大,看小则小)增长量计算如果基期量为A ,经N 期变为B ,平均增长量为xx=B ‒A N直除法增长量比较已知现期量,增长率x%增长量=×x%现期量1+x%1.特殊分数法,当x%可以被视为时,公式可1n被简化为:增长量=现期量1+n2.公式可变换为:增长量=现期量×,其中为x%1+x%x%1+x%增函数,所以现期量大,增长率大的情况下,增长量一定大已知基期量,增长量增长率=增长量基期量截位直除法,插值法已知现期量,基期量增长率=现期量‒基期量基期量截位直除法求平均增长率:如果基期量为A,第n+1期(或经n期)变为B,平均增长率为x%x%=-1nBA代入法,公式法B=A(1+X%)n当x%较小时可简化为B=A(1+nx%)求两期混合增长率:如果第一期和第二期增长率分别为r1和r2,那么第三期相对第一期增长率为r3r3= r1+r2+r1r2简单记忆口诀:连续增长,最终增长大于增长率之和;连续下降,最终下降小于增长率之和(正负号带进公式计算)求总体增长率:整体分为A,B两个部分,分别增长a%与b%,整体增长率x%x%=A×a%+B×b%A+B x%=a%+B(b%-a%)A+B已知总体增长率和其中一个部分的增长率,求另一部分的增长率增长率计算求混合增长率:整体为A,增长率为a%,分为两个部分B,C,增长率为b%和c%混合增长率a%介于b%和c%之间混合增长率大小居中增长率比较已知现期量与增长量比较增长率=代替增现期量基期量长率进行大小比较相当于分数大小比较发展速度已知现期量与基期量发展速度==1+增长率现期量基期量截位直除法,插值法已知部分增长量与整体增长量增长贡献量=部分增长量整体增长量截位直除法,插值法增长贡献率贡献率贡献率%=贡献量(产出量,所得量)投入量(消耗量,占用量)贡献率是指有效或有用成果数量与资源消耗及占用量之比,即投入量与产出量之比拉动增长求B拉动A增长几个百分点:如果B是A的一部分,B拉动A增长x%x%=B的增长量A的基期量截位直除法,插值法某部分现期量为A,整体现期量为为B现期比重=AB截位直除法,插值法某部分基期量为A,增长率a%,整体基期量为B,增长率b%现期比重=AB×1+a%1+b%一般先计算,然后AB根据a和b的大小判断大小某部分现期量为A,增长率a%,整体现期量为B,增长率b%基期比重=×AB1+b%1+a%一般先计算,然后AB根据a和b的大小判断大小比重计算求基期比重-现期比重:某部分现期量为A增长率a%,整体现期量为B,增长率b%两期比重差值计算:现期比重-基期比重=-×ABAB1+b%1+a%=×(1-)AB1+b%1+a%=×ABa%‒b%1+a%1.先根据a与b的大小判断差值计算结果是正数还是负数;2.答案小于|a-b|3.估算法(近似取整估算)4.直除法某部分现期量为A,整体现期量为B 现期比重=AB相当于分数大小比较,同上述做法比重比较基期比重与现期比重比较:某部分现期量为A,增长率a%,整体现期量为B,增长率b%基期比重=×AB1+b%1+a%直除法,当部分增长率大于整体增长率,则现期比重大于基期比重。
(完整版)资料分析公式汇总

资料分析公式汇总考点已知条件计算公式方法与技巧备注已知现期量,增长率x%基期量=现期量1+x%截位直除法,特殊分数法已知现期量,相对基期量增加M 倍基期量=现期量1+M截位直除法基期量计算已知现期量,相对基期量的增长量N基期量=现期量-N尾数法,估算法基期量比较已知现期量,增长率x%比较:基期量=现期量1+x%1.截位直除法2.化同法(分数大小比较)3.直除法(首位判断或差量比较)4.差分法如果现期量差距较大,增长率相差不大,可直接比较现期量已知基期量,增长率x%现期量=基期量+基期量×x%=基期量×(1+x%)特殊分数法,估算法已知基期量,相对基期量增加M 倍现期量=基期量+基期量×M =基期量×(1+M )估算法现期量计算已知基期量,增长量N现期量=基期量+N 尾数法,估算法已知基期量,现期量增长量=现期量-基期量尾数法已知基期量,增长率x%增长量=基期量×x%特殊分数法已知现期量,增长率x%增长量=×x%现期量1+x% 1.特殊分数法,当x%可以被视为时,公式可1n 被简化为:增长量=现期量1+n2.估算法(倍数估算)或分数的近似计算(看大则大,看小则小)增长量计算如果基期量为A ,经N 期变为B ,平均增长量为xx=B ‒A N直除法增长量比较已知现期量,增长率x%增长量=×x%现期量1+x%1.特殊分数法,当x%可以被视为时,公式可1n被简化为:增长量=现期量1+n2.公式可变换为:增长量=现期量×,其中为x%1+x%x%1+x%增函数,所以现期量大,增长率大的情况下,增长量一定大已知基期量,增长量增长率=增长量基期量截位直除法,插值法已知现期量,基期量增长率=现期量‒基期量基期量截位直除法求平均增长率:如果基期量为A,第n+1期(或经n期)变为B,平均增长率为x%x%=-1nBA代入法,公式法B=A(1+X%)n当x%较小时可简化为B=A(1+nx%)求两期混合增长率:如果第一期和第二期增长率分别为r1和r2,那么第三期相对第一期增长率为r3r3= r1+r2+r1r2简单记忆口诀:连续增长,最终增长大于增长率之和;连续下降,最终下降小于增长率之和(正负号带进公式计算)求总体增长率:整体分为A,B两个部分,分别增长a%与b%,整体增长率x%x%=A×a%+B×b%A+B x%=a%+B(b%-a%)A+B已知总体增长率和其中一个部分的增长率,求另一部分的增长率增长率计算求混合增长率:整体为A,增长率为a%,分为两个部分B,C,增长率为b%和c%混合增长率a%介于b%和c%之间混合增长率大小居中增长率比较已知现期量与增长量比较增长率=代替增现期量基期量长率进行大小比较相当于分数大小比较发展速度已知现期量与基期量发展速度==1+增长率现期量基期量截位直除法,插值法已知部分增长量与整体增长量增长贡献量=部分增长量整体增长量截位直除法,插值法增长贡献率贡献率贡献率%=贡献量(产出量,所得量)投入量(消耗量,占用量)贡献率是指有效或有用成果数量与资源消耗及占用量之比,即投入量与产出量之比拉动增长求B拉动A增长几个百分点:如果B是A的一部分,B拉动A增长x%x%=B的增长量A的基期量截位直除法,插值法某部分现期量为A,整体现期量为为B现期比重=AB截位直除法,插值法某部分基期量为A,增长率a%,整体基期量为B,增长率b%现期比重=AB×1+a%1+b%一般先计算,然后AB根据a和b的大小判断大小某部分现期量为A,增长率a%,整体现期量为B,增长率b%基期比重=×AB1+b%1+a%一般先计算,然后AB根据a和b的大小判断大小比重计算求基期比重-现期比重:某部分现期量为A增长率a%,整体现期量为B,增长率b%两期比重差值计算:现期比重-基期比重=-×ABAB1+b%1+a%=×(1-)AB1+b%1+a%=×ABa%‒b%1+a%1.先根据a与b的大小判断差值计算结果是正数还是负数;2.答案小于|a-b|3.估算法(近似取整估算)4.直除法某部分现期量为A,整体现期量为B 现期比重=AB相当于分数大小比较,同上述做法比重比较基期比重与现期比重比较:某部分现期量为A,增长率a%,整体现期量为B,增长率b%基期比重=×AB1+b%1+a%直除法,当部分增长率大于整体增长率,则现期比重大于基期比重。
数学运算、资料分析必背公式大全

数学运算、资料分析必背公式大全如果连最基本的公式都不记得的话,先不说做题速度了,绝大多数的数学运算与资料分析题你肯定都无从下手。
而行测领域中的数学运算与资料分析,其实也都涵盖了大量的公式需要你去掌握,希望所有同学能够认真梳理,并结合做过的例题发散思考。
数学运算篇以下公式源自【爆发篇--数学运算怎能轻言放弃?】行程问题路程=速度×时间1、平均速度平均速度=总路程÷总时间等时间平均速度=(V1+V2)/2等距离平均速度=2V1V2/(V1+V2)(实际上,更好的解题思路是特值法)2、相遇和追及路程和=速度和×相遇时间直线上,两人相向而行时,第n次相遇时,路程和=(2n-1)个全程环形上,两人背向而行,第n次相遇是,路程和=n个周长路程差=速度差×追及时间直线上,只会追上一次。
路程差的产生:1)两人同时但不同点出发:快的在后,慢的在前。
2)两人同点但不同时出发:慢的先出发,快的后出发环形上,可以追上n次,第n次追上,路程差=n个周长3、两岸相遇单岸:3S1+S2=2S(S1、S2分别为第1次和第2次相遇时相遇地点距离某边的距离,S是全程)两岸:3S1-S2=S(S1、S2分别为第1次和第2次相遇时相遇地点距离不同两边的距离,S是全程)4、流水行船顺水速度=船速+水速逆水速度=船速-水速顺水速度+逆水速度=2船速顺水速度-逆水速度=2水速5、火车过桥路程=桥长+车长两车错身而过:路程和=车身长之和两车追及:路程差=车身长之和变型问题—“人和队伍”问题:人追队头,路程差=队伍长度;人从队头出发和队尾相遇,路程和=队伍长6、时钟问题时针速度=0.5°/分钟;分针速度=6°/分钟重合:分针要追的度数=5.5°t垂直:分针多走的度数=5.5°t7、发车问题发车间隔=t分钟(每t分钟发一趟车),两车相隔的距离=车速×发车间隔t。
资料分析常用公式

资料分析常用公式1. 平均数公式平均数(Mean)是表示一组数据集中趋势的量数,计算公式为:$$\text{平均数} = \frac{\sum_{i=1}^{n} x_i}{n}$$其中,$ x_i $ 表示第 $ i $ 个数据,$ n $ 表示数据的总数。
平均数适用于描述数据的中心位置,常用于市场调查、产品评价等领域。
2. 中位数公式中位数(Median)是将一组数据从小到大(或从大到小)排列,位于中间位置的数值。
计算公式为:$$\text{中位数} = \begin{cases}x_{\frac{n+1}{2}} & \text{当 } n \text{ 为奇数时} \\\frac{x_{\frac{n}{2}} + x_{\frac{n}{2}+1}}{2} & \text{当 } n \text{ 为偶数时}\end{cases}$$中位数适用于描述数据的中心位置,特别适用于数据分布不均匀或存在异常值的情况。
3. 标准差公式标准差(Standard Deviation)是衡量一组数据离散程度的量数,计算公式为:$$\sigma = \sqrt{\frac{\sum_{i=1}^{n} (x_i \mu)^2}{n}}$$其中,$ \sigma $ 表示标准差,$ x_i $ 表示第 $ i $ 个数据,$ \mu $ 表示平均数,$ n $ 表示数据的总数。
标准差越大,表示数据的离散程度越大,反之越小。
4. 相关系数公式相关系数(Correlation Coefficient)用于衡量两个变量之间的线性关系程度,计算公式为:$$r = \frac{n(\sum xy) (\sum x)(\sum y)}{\sqrt{[n\sum x^2 (\sum x)^2][n\sum y^2 (\sum y)^2]}}$$其中,$ r $ 表示相关系数,$ x $ 和 $ y $ 分别表示两个变量,$ n $ 表示数据的总数。
资料分析公式汇总
,其中
为
增函数,所以现期量 大,增长率大的情况 下,增长量一定大
增长率 计算
已知基期量,增 长量 已知现期量,基 期量 求平均增长率: 如果基期量为 A,第 n+1 期 (或经 n 期)变 为 B,平均增长率 为 x% 求两期混合增长 率:如果第一期 和第二期增长率
分别为 r1 和 r2,
那么第三期相对 第一期增长率为
基期比重= ×
指数=
截位直除法, 插值法 截位直除法, 插值法
截位直除法, 插值法
截位直除法, 插值法
一般先计算 ,然后 根据 a 和 b 的大小判 断大小
一般先计算 ,然后 根据 a 和 b 的大小判 断大小 1.先根据 a 与 b 的大 小判断差值计算结果 是正数还是负数; 2.答案小于|a-b| 3.估算法(近似取整 估算) 4.直除法 相当于分数大小比 较,同上述做法
某部分现期量为 A,整体现期量 为B 基期比重与现期 比重比较:某部 分现期量为 A, 增长率 a%,整体 现期量为 B,增 长率 b%
发展速度=
=1+增长率
增长贡献量= 贡献率%
=
x%=
现期比重= 现期比重 =
基期比重= ×
两期比重差值计算: 现期比重-基期比重
=-×
= ×(1- ) =×
现期比重=
逆差额=进口额-出口额
基期倍数= ×
A 翻 n 番=A×2n
x%=
100%
x%=
1
x%= r 出- r 死
1000%
人次:次数,可重复计算 人数:数量,不可累计计算
翻番即数量加 倍,翻一番为 原来的 2 倍。 翻 n 番为原来 的 2n 倍
和某一相同时 期(比如去年 同一时期)相 比较的增长情 况 指与之紧紧相 连的上一个统 计周期先比较 的增长情况
(完整word版)资料分析计算公式整理(word文档良心出品)

去年量计算
(1)已知今年量,增长率x%
截位直除法,特殊分数法
(2)已知今年量,相对去年量增加M倍
截位直除法
(3)已知今年量,相对去年量的增长量N
尾数法,估算法
去年量比较
(4)已知今年量,增长率x%
比较:
(1)截位直除法(2)如果今年量差距较大,增长率相差不大,可直接比较今年量。
(3)化同法
(17)合成增长率:整体分为A、B两个部分,分别增长a%与b%,整体增长率r%
(18)混合增长率:整体为A,增长率为rA,分为两个部分B和C,增长率为rB和rC
则rA介于rB和rC之间
混合增长率大小居中
增长率比较
(19)已知今年量与增长量
比较 代替增长率进行大小比较
相当于分数大小比较,同上述做法
发展速度
(20)已知今年量与去年量
(1)截位直除法
(2)插值法
增长贡献率
(21)已知部分增长量与整体增长量
(1)截位直除法
(2)插值法
拉动增长
(22)如果B是A的一部分,B拉动A增长x%
(1)截位直除法
(2ቤተ መጻሕፍቲ ባይዱ插值法
比重计算
(23)某部分今年量为A,整体今年量为B
(1)截位直除法
(2)插值法
(24)某部分去年量为A,增长率a%,整体去年量为B,增长率b%
(3)估算法(近似取整估算)
比重比较
(27)某部分今年量为A,整体今年量为B
相当于分数大小比较,同上述做法
(28)去年比重与今年比重比较:某部分今年量为A,增长率a%,整体今年量为B,增长率b%
当部分增长率大于整体增长率,则今年比重大于去年比重。(方法为“看”增长率)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
资料分析主要测查报考者对各种形式的文字、图表等资料的综合理解与分析加工的能力,针对一段资料一般有1~5个问题,报考者需要根据资料所提供的信息进行分析、比较、推测和计算,从四个备选答案中选出符合题意的答案。
1、统计术语◆现期与基期资料题目中,作为对比参照的时期称为基期,而相对于基期的为现期。
描述基期的具体数值我们称之为基期量,描述现期的具体数值我们称之为现期量。
◆同比与环比同比:与历史同期相比较如:今年五月与去年五月相比较;今年第一季度与去年第一季度相比较;今年上半年与去年上半年相比较。
环比:环比实际上即指“与紧紧相邻的统计周期相比较”,包括日环比、周环比、月环比、年环比等。
【例1】2009年全年民营工业实现增加值8288.8亿元,增长18.9%,增幅同比提高4.2个百分点。
【例2】2010年上半年,全国原油产量为9848万吨,同比增长5.3%,上年同期为下降1%。
◆增长率增长率指的是现期与基期的差值与基期之间的比较。
增长率=(现期量-基期量)÷基期量【特别提示】增速、增幅:一般情况下,均与增长率相同。
(但在特殊语境下,增幅是指具体数值的增加,例如:某企业9月份的产值和上月相比,有了200万元的增幅,这里增幅就是指具体数值的增加。
)【判别特征】:增长率:(现在)……比(过去)……增长(下降)……%式子1:给基期值,现期值,求增长率?增长率=现期值基期值基期值;式子2:给基期值,增长率,求现期值?现期值=基期值×(1+增长率);式子3:给现期值,增长率,求基期值?基期值=现期值增长率。
【例1】1959年与1958年比较,支援农村生产支出和农林水利气象等部门的事业费?A. 提高了151.8%B. 提高了51.8%C. 提高了251.8%D. 提高了105%◆百分数与百分点增长率之间的计算只能用百分点,不能用百分数。
【例1】与上年同期相比,2010年6月汽车零售同比增幅()A.回落42.3个百分点B.加快42.3个百分点C.回落42.3%D.加快42.3%◆减少率(减少幅度、减少速度)减少率=减少量÷基期量×100%,“减少率”本质是一种未带负号的“增长率”2006—2011年我国违法用地案件查处情况(一)【例2】与2006年相比,2011年全国收缴土地面积约减少了:A.52%B.110%C.67%D.205%◆发展速度(理解)发展速度是反映某种社会现象发展程度的相对指标,它是现期发展水平与基期发展水平之比。
计算公式为:发展速度=末期量÷基期量=增长率+100%。
◆拉动增长率(理解)“拉动增长……百分点”这个概念是部分量的增长对总量增长的一个贡献。
即:拉动增长率=部分增长量÷总体基期量◆成数与翻番成数:几成相当于十分之几。
【例】某单位有300名员工,其中有60人是研究生学历,则研究生学历的员工占总人数的 2 成。
(60÷300=2/10)翻番:翻一番为原来的2倍;翻两番为原来的4倍;依此类推,翻n番为原来的2n倍。
◆增长量它说明社会经济现象在一定时期内增长(或减少)的绝对量。
【判别特征】:增长量:(现在)……比(过去)……增长(下降)(具体值)【基本应用】:式子1:给基期值,现期值,求增长量?增长量=现期值-基期值;式子2:给基期值,增长率,求增长量?增长量=基期值×增长率式子3:给现期值,增长率,求增长量?增长量=现期值×增长率增长率2000~2008年XX省进出口总额年份进出口(亿美元)进出口(亿元)总量出口进口总量出口进口2000 212.23 129.08 83.16 1756.87 1068.55 688.32 2008 848.21 569.92 278.29 5890.90 3958.14 1932.76【例1】以2000年为基准,该省2008年的出口总额约增加()。
A.1244亿元B.2000亿元C.2890亿元D.4134亿元俄罗斯是世界最大的管道天然气出口国,占管道天然气总出口量的27.8%,2009年出口量为1764.8亿立方米,较2008年增长14.3%。
【例2】2009年俄罗斯管道天然气出口较上年增长了多少亿立方米?()【例3】如果增长趋势与上年保持一致,预计2003年末移动电话用户约为()。
A.21000万户B.23000万户C.25000万户D.29000万户◆平均数平均数是指在一组数据中所有数据之和再除以数据的个数。
即:把n个数的总和除以n,所得的商叫做这n个数的平均数【例1】某地区新千年以来大力发展旅游业,下表显示其2001年以来游客量统计表。
年份 2001 2002 2003 2004 2005 2006游客量 (人次)1871 3500 8155 26260 83507 452608该地区2001年至2006年平均每年游客量约为多少万人次?( )◆平均增长量-=末期值初期值平均增长量间隔年份【例1】我国第二产业就业人员2005年为18084万人,2009年增加到21684万人;则2009年末与2005年末相比,我国第二产业人员年均增加( )。
A. 566.4万人 B. 708万人 C. 720万人 D. 900万人◆五年计划名 称年 段名 称年 段名 称年 段十五时期 2001-2005 十一五时期 2006-2010 十二五时期【例2】我国“十一五”期间平均每年增加人口A. 660.75万人B. 644万人C. 657.4万人D. 528.6万人◆平均增长速度平均增长速度则是反映现象逐年递增的平均速度。
平均发展速度(水平法)的计算公式如下:末期值=初期值×(1+年均增长率)n末期值=初期值×(1+年均增长率)n在实际应用时多次幂的计算相对复杂,所以当增长率较小的时候我们可以采用如下公式:a(1+x)n≈a(1+nx)进行近似计算。
◆顺差、逆差顺差:在一个时期内,一个国家(或地区)的出口商品额大于进口商品额,叫做对外贸易顺差(又称净出口额、出超)。
逆差:在一个时期内,一个国家(或地区)的出口商品额小于进口商品额,叫做对外贸易逆差(又称净进口额、入超)。
【例】2010年,我国机电产品出口9334.3亿美元,同比增加30.9%; 高新技术产品出口4924.1亿美元,同比增长30.7%。
船舶、汽车零部件出口保持较快增长,其中船舶出口同比增长的44.5%,汽车零部件出口同比增长44.1% .2010年,机电产品进口额达到6603.1亿美元,同比增长34.4%,高新技术产品进口额达到4126.1亿美元,同比增长33.2%下列关于2010年我国进出口贸易的表述正确的是:A.高新技术产品逆差约为800亿美元B.……◆比重比重即部分在整体中所占的比例。
【判别特征】:比重:(个体)……占(整体)……的(比例)% 式子1:给整体,比重,求个体?=个体整体比重式子2:给个体,比重,求整体?=个体整体比重式子3:给个体,整体,求比重?=个体比重整体2011年发现违法用地行为7.0万件,涉及土地5.0万公顷(耕地1.8万公顷),同比分别上升5.8%、11.0%(耕地下降2.4),立案查处违法用地案件4.2万件,涉及土地4.4万公顷(耕地1.5万公顷),同比分别上升2.5%、11.4%(耕地下降5.7万公顷)。
【例1】2011年,发现违法但未立案的违法用地行为占发现违法用地行为总数的比重约为多少?2003年至2011年,我国第一产业年均增长4.6%,第二产业年均增长11.9%,第三产业年均增长11.1%,均保持较快发展态势。
2010年,我国制造业产出占世界的比重为19.8%,超过美国成为全球制造业第一大国。
【例2】如果2010年我国制造业生产总值为135000亿元,那么2010年世界制造业生产总值约为()万亿元。
◆指数(理解)指数:用于衡量某种要素相对变化....的指标量。
一般假定基期为100,其他量和基期相比得出的数值即为指数,即相应两期实际值的比=相应两期指数的比。
年份国民生产总值国内生产总值第一产业第二产业第三产业人均国内生产总值1993 108.7 108.7 102.0 115.8 104.9 106.81994 98.4 98.4 98.2 97.5 100.4 96.91995 107.6 107.6 97.8 113.3 109.5 106.2◆三大产业第一产业:农、林、牧、渔业(不含农、林、牧、渔服务业)。
第二产业:采矿业(不含开采辅助活动)、制造业(不含金属制品、机械和设备修理业)、电力、热力、燃气及水生产和供应业、建筑业。
第三产业:服务业,是指除第一产业、第二产业以外的其他行业。
◆国内生产总值GDP是英文(Gross Domestic Product)的缩写,也即国内生产总值。
它是指一个国家(或地区)所有常住单位在一定时期内生产的最终产品和服务价值的总和,常被公认为衡量国家经济状况的最佳指标,国内生产总值由第一产业、第二产业、第三产业增加值构成,一个国家的国内生产总值就是三大产业的增加值之和。
【例1】经初步核算,2009年上半年我国国内生产总值同比增长7.1%,比一季度加快1.0个百分点。
其中,第一产业增加值12025亿元,增长3.8%,第二产业增加值70070亿元,增长6.6%,第三产业增加值57767亿元,增长8.3%。
则2009年上半年,我国国内生产总值为( )A.139862亿元B.147953亿元C.148634亿元D.151429亿元【知识点汇总】四个知识点【判别特征】:比重:(个体)……占(整体)……的(比例)%式子1:给整体,比重,求个体?=个体整体比重式子2:给个体,比重,求整体?=个体整体比重式子3:给个体,整体,求比重?=个体比重整体【判别特征】:增长率:(现在)……比(过去)……增长(下降)……%式子1:给基期值,现期值,求增长率?增长率=现期值基期值基期值;式子2:给基期值,增长率,求现期值?现期值=基期值×(1+增长率);第10页式子3:给现期值,增长率,求基期值?基期值=现期值增长率。
【判别特征】:增长量:(现在)……比(过去)……增长(下降)(具体值) 式子1:给基期值,现期值,求增长量?增长量=现期值-基期值; 式子2:给基期值,增长率,求增长量?增长量=基期值×增长率 式子3:给现期值,增长率,求增长量?增长量=现期值×增长率 增长率【判别特征】:“平均……”式子1:平均数?把n 个数的总和除以n式子2:平均增长量?-=末期值初期值平均增长量年份间隔数式子3:平均增长速度?末期值=初期值×(1+年均增长率)n。
