物理化学第四章课后答案完整版
物理化学第四版课后答案
第一章气体的pVT性质物质的体膨胀系数与等温压缩率的定义如下试推出理想气体的,与压力、温度的关系。
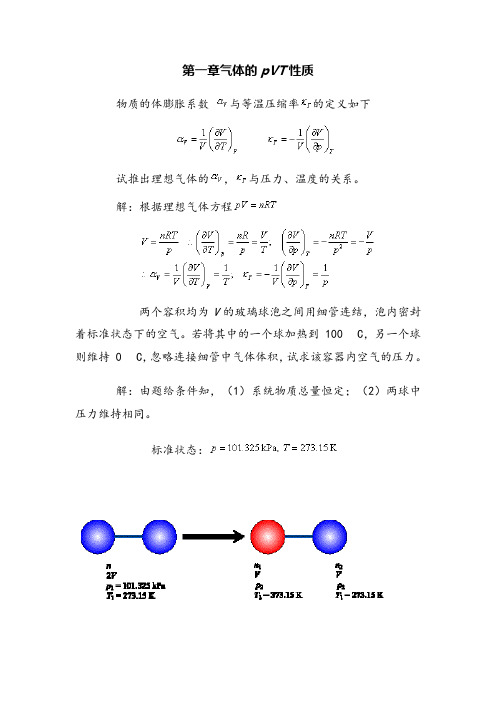
解:根据理想气体方程两个容积均为V的玻璃球泡之间用细管连结,泡内密封着标准状态下的空气。
若将其中的一个球加热到 100 C,另一个球则维持 0 C,忽略连接细管中气体体积,试求该容器内空气的压力。
解:由题给条件知,(1)系统物质总量恒定;(2)两球中压力维持相同。
标准状态:因此,如图所示,一带隔板的容器内,两侧分别有同温同压的氢气与氮气,二者均可视为理想气体。
(1)保持容器内温度恒定时抽去隔板,且隔板本身的体积可忽略不计,试求两种气体混合后的压力。
(2)隔板抽取前后,H2及N2的摩尔体积是否相同(3)隔板抽取后,混合气体中H2及N2的分压立之比以及它们的分体积各为若干解:(1)等温混合后即在上述条件下混合,系统的压力认为。
(2)混合气体中某组分的摩尔体积怎样定义(3)根据分体积的定义对于分压室温下一高压釜内有常压的空气,为进行实验时确保安全,采用同样温度的纯氮进行置换,步骤如下:向釜内通氮气直到4倍于空气的压力,尔后将釜内混合气体排出直至恢复常压。
重复三次。
求釜内最后排气至恢复常压时其中气体含氧的摩尔分数。
解:分析:每次通氮气后至排气恢复至常压p,混合气体的摩尔分数不变。
设第一次充氮气前,系统中氧的摩尔分数为,充氮气后,系统中氧的摩尔分数为,则,。
重复上面的过程,第n次充氮气后,系统的摩尔分数为,因此。
今有0 C, kPa的N2气体,分别用理想气体状态方程及van der Waals方程计算其摩尔体积。
实验值为。
解:用理想气体状态方程计算用van der Waals计算,查表得知,对于N2气(附录七),用MatLab fzero函数求得该方程的解为也可以用直接迭代法,,取初值,迭代十次结果25 C时饱和了水蒸气的湿乙炔气体(即该混合气体中水蒸气分压力为同温度下水的饱和蒸气压)总压力为 kPa,于恒定总压下冷却到10 C,使部分水蒸气凝结为水。
物化教材习题解答(人卫版)第4章习题

第四章(相平衡)习题解答1.指出平衡体系的组分数、自由度(1)NH4Cl(s)部分解离为NH3(g)、HCl(g)K=S–R–R’=3–1–1 = 1f = K–φ +2 = 1–2 + 2 = 1(2)上述体系加少量NH3(g)K=S–R–R’=3–1–0 = 2f = K–φ +2 = 2–2 + 2 = 2(3)NH4HS(s)与任意量NH3(g)、H2S(g)平衡K=S–R–R’=3–1–0 = 2f = K–φ +2 = 2–2 + 2 = 2(4)C(s)、CO(g)、CO2(g)、O2(g)在100︒C平衡独立化学反应数为2: C(s)+O2(g)→CO2(g)2CO(g)+O2(g)→2CO2(g)K=S–R–R’=4–2–0 = 2f = K–φ +2 = 2–2 + 1 = 12. 本体系K=3,当f=0时,φ最大,即f=K-φmax+2=5-φmax=0,(1) 指定T,减少一个变量,f=(5-φmax)-1=0 φmax=4如冰,水和苯含苯甲酸的一对共轭溶液,气相(2) 指定T和水在苯甲酸中的浓度,减少二个变量,f=(5-φmax)-2=0 φmax=3如水和苯含苯甲酸的一对共轭溶液,气相(3) 指定T,p和水在苯甲酸中的浓度,减少三个变量,f=(5-φmax)-3=0 φmax=2如水和苯含苯甲酸的一对共轭溶液4.两相平衡线三相点AB:s正交↔g E:s正交↔ s斜方↔lBC:s斜方↔g B:s正交↔ s斜方↔gCD:l↔g C:s斜方↔l ↔gEB:s正交↔ s斜方G:s正交↔l ↔g(亚稳态)EC:s斜方↔lEC:s正交↔lX→Y变化:正交硫→转晶→斜方硫→熔化→5. 按Trouton 规则,11-v m ol K J 88TH -⋅⋅=∆∆H V =88⨯(273.2+61.5)=29454 J ⋅mol -1⎪⎪⎭⎫⎝⎛-∆-=12v 12T 1T 1R H p p ln ⎪⎭⎫ ⎝⎛+-+-=5.612.2731402.2731R 29454325.101p ln 2 p 2=48.99 kPa 6. ⎪⎪⎭⎫⎝⎛-∆-=12v 12T 1T 1RH p p ln ⎪⎪⎭⎫⎝⎛--=2.3731T 1R 40670325.10199.151ln2 T 2=385.1K=111.9︒C7. ⎪⎪⎭⎫ ⎝⎛-∆-=12v 12T 1T 1RH p p ln⎪⎭⎫⎝⎛+-+∆-=2.27323012.273901R H 3.101267.0ln v∆H V = 64454 J ⋅mol –1⎪⎪⎭⎫ ⎝⎛+--=2.2732301T 1R 644543.10133.1ln2 T 2=392.7K = 119.5︒C8.229.37T13115p ln +-=∆H 升华=-13115R=109044 J ⋅mol -1液←→气平衡,lnp ~1/T 的回归方程为90.26T8521p ln +-=∆H 汽化=-8521R=70848 J ⋅mol -1∆H 熔化=∆H 升华-∆H 汽化=38196 J ⋅mol -1(2) 三相点p ,T 是气液平衡线和气固平衡线的交点,联立两回归方程,解得 T=444.8 K=171.6 ︒C p=2298 Pa(3) T=500K 代入气液平衡回归方程,得沸点压力 p=19083 Pa9. 由0︒C 和10︒C 的蒸汽压求水的汽化热: ⎪⎪⎭⎫⎝⎛-∆-=12v 12T 1T 1R H p p ln⎪⎭⎫ ⎝⎛-∆-=27312831R H 6106.0228.1lnv ∆H v =44880 J ⋅mol -1求出升华热:∆H 升华= ∆H 熔化+∆H 汽化=333.5⨯18+44880=50883 J ⋅mol -1由0︒C 数据求出口处(-25︒C )的蒸气压:⎪⎪⎭⎫⎝⎛-∆-=1212T 1T 1R H p p ln升华 ⎪⎭⎫⎝⎛--=27312481R 508836106.0p ln2 p 2=0.637 kPa计算20︒C 时的蒸汽压(用10︒C 数据,也可用0︒C 数据):⎪⎪⎭⎫⎝⎛-∆-=12v 12T 1T 1RH p p ln⎪⎭⎫⎝⎛--=28312931R 44880228.1p ln2 p 2=2.31 kPa%==饱和蒸汽压实际蒸汽压相对湿度=72.231.20637.010. 1.54p 65.0p x p y *AA *A A ==总 p*A =37.45 kPap 总= p*A x A + p*B x B = 37.45⨯0.65 + p*B ⨯0.35 = 54.1p*B = 85.02 kPa11.2665.078/7092/3092/30M /70M /30M /30x ===苯甲苯甲苯甲苯++甲苯甲苯甲苯x p p ==4.89⨯0.2665=1.303 kPa苯苯苯x p p ==15.76⨯(1-0.2665)=11.56 kPap 总= p 甲苯+p 苯=12.86 kPa12.(1) 作相图(2) 物系组成为x=0.6,由相图,114︒C 时,气相x g =0.92,液相x l =0.53杠杆规则:22.06.092.053.06.0n n lg =--=(3) x=0.6时,沸点为110︒C ,提高到114︒C ,馏出物(气相)组成为0.92 (4) 完全蒸馏(精馏),馏出物为100%的HNO 3,残留液为0.38的恒沸物。
物理化学答案——第四章_化学平衡习题解答[1]
![物理化学答案——第四章_化学平衡习题解答[1]](https://img.taocdn.com/s3/m/995f0e3383c4bb4cf7ecd1f7.png)
第四章 化学平衡一、基本公式和内容提要 1. 化学反应的方向和限度(1)反应系统的吉布斯自由能和反应进度反应进行过程中,A 和B 均各以纯态存在而没有相互混合,则在反应进度为ξ时反应体系的总吉布斯自由能G *为:G * = n A μA * + n B μB * = (1-ξ)μA * +ξμB * = μA * +ξ(μB * -μA *)对于封闭体系在定温定压下在反应实际进行过程中,A 和B 是不可能以纯态存在的。
它们是混合在一起的,因此还存在混合吉布斯自由能△mix G 。
△mix G = RT (n A lnX A + n B lnX B ) = RT [(1-ξ)ln(1-ξ) + ξlnξ](2)化学反应标准平衡常数理想气体的化学反应()()()()aA g bB g gG g hH g −−→++←−− bB a A hH gG P P P P P P P P )/()/()/()/(θθθθ= e )--(1θθθθμμμμB A H G b a h g RT-+= 常数 = K θK θ称为标准平衡常数。
(3)化学反应的等温方程式(a )对任意反应达平衡时:△r G m θ = -RTlnK θ△r G m θ是指产物和反应物均处于标准态时,产物的吉布斯自由能和反 应物的吉布斯自由能总和之差,称为反应的“标准吉布斯自由能变化”。
(b )反应在定温定压条件下△r G m = △r G m θ+ RT ln Q p上式称为范特霍夫(Vait Hoff) 等温方程。
(c )依据吉布斯自由能函数可判断反应进行的方向,在温度、压力一定的条件下:RT ln Q a < RTlnK θ Q a <K θ △r G m <0 反应正向自发进行 若 RT ln Q a >RTlnK θ Q a >K θ △r G m >0 反应逆向自发进行若 RT ln Q a = RTlnK θ Q a = K θ △r G m =0 反应达平衡 2. 反应的标准吉布斯自由能变化 (1)化学反应的△r G m 与△r G m θ(a )在一定温度和压力为p θ下,任何物质的标准态化学势μi θ都有确定值,所以任何化学反应的△r G m θ都是常数;(b )△r G m 不是常数,在一定T ,p 下,它与各物质的活度(分压、浓度)等有关,即与Q a 有关;(c )在定温定压条件下0W '=时,△r G m 的正负可以指示化学反应自发进行的方向,在定温下△r G m θ的正负通常不能指示反应进行的方向,根据公式△r G m = △r G m θ+ RT ln Q p ,但当△r G m θ的数值很大时,也可用其值估计反应的方向。
物理化学第四版课后答案

第一章气体的pVT性质1.1物质的体膨胀系数与等温压缩率的定义如下试推出理想气体的,与压力、温度的关系。
解:根据理想气体方程1.5两个容积均为V的玻璃球泡之间用细管连结,泡内密封着标准状态下的空气。
若将其中的一个球加热到100 C,另一个球则维持0 C,忽略连接细管中气体体积,试求该容器内空气的压力。
解:由题给条件知,(1)系统物质总量恒定;(2)两球中压力维持相同。
标准状态:因此,1.9 如图所示,一带隔板的容器内,两侧分别有同温同压的氢气与氮气,二者均可视为理想气体。
(1)保持容器内温度恒定时抽去隔板,且隔板本身的体积可忽略不计,试求两种气体混合后的压力。
(2)隔板抽取前后,H2及N2的摩尔体积是否相同?(3)隔板抽取后,混合气体中H2及N2的分压立之比以及它们的分体积各为若干?解:(1)等温混合后即在上述条件下混合,系统的压力认为。
(2)混合气体中某组分的摩尔体积怎样定义?(3)根据分体积的定义对于分压1.11 室温下一高压釜内有常压的空气,为进行实验时确保安全,采用同样温度的纯氮进行置换,步骤如下:向釜内通氮气直到4倍于空气的压力,尔后将釜内混合气体排出直至恢复常压。
重复三次。
求釜内最后排气至恢复常压时其中气体含氧的摩尔分数。
解:分析:每次通氮气后至排气恢复至常压p,混合气体的摩尔分数不变。
设第一次充氮气前,系统中氧的摩尔分数为,充氮气后,系统中氧的摩尔分数为,则,。
重复上面的过程,第n次充氮气后,系统的摩尔分数为,因此。
1.13 今有0 C,40.530 kPa的N2气体,分别用理想气体状态方程及van der Waals 方程计算其摩尔体积。
实验值为。
解:用理想气体状态方程计算用van der Waals计算,查表得知,对于N2气(附录七),用MatLab fzero函数求得该方程的解为也可以用直接迭代法,,取初值,迭代十次结果1.16 25 C时饱和了水蒸气的湿乙炔气体(即该混合气体中水蒸气分压力为同温度下水的饱和蒸气压)总压力为138.7 kPa,于恒定总压下冷却到10 C,使部分水蒸气凝结为水。
物理化学第四版答案

物理化学第四版习题及答案【篇一:物理化学第四章课后答案傅献彩第五版】lass=txt>第七章电化学7.1 用铂电极电解能析出多少质量的解:电极反应为溶液。
通过的电流为20 a,经过15 min后,问:(1)在阴极上?(2) 在的27 ?c,100 kpa下的?电极反应的反应进度为因此:7.2 在电路中串联着两个电量计,一为氢电量 1 h后,在氢电量计中收集到的;在银电量计中沉积电流为多少。
对银电量计对氢电量计37.3用银电极电解并知阴极区溶液中溶液。
通电一定时间后,测知在阴极上析出的总量减少了。
求溶液中的和的,。
的解:解该类问题主要依据电极区的物料守恒(溶液是电中性的)。
显然阴极区溶液中总量的改变等于阴极析出银的量与从阳极迁移来的银的量之差:7.4 用银电极电解水溶液。
电解前每反应生成,反应可表示的银与溶液中的为总反应为,并测知阳极区溶液重和。
量的改变为,通电其中含解:量不变,该量 1)与阳极溶解的生成,(2)从阴极迁移到阳极7.5用铜电极电解水溶液。
电解前每溶液中含。
4通电一定时间后,测得银电量计中析出中含。
试计算溶液中的量的改变,并测知阳极区溶液重和。
,其解:同7.4。
电解前后从铜电极溶解的的量为从阳极区迁移出去的的量为因此,7.6 在一个细管中,于的的溶液的上面放入的电流直上而下通过该管,界以后,界面在管内向下移动的距离相当于溶液中的面不断向下度25?c下,。
解:此为用界面移动法测量离子迁移数7.7 已知25 ?c时溶液的电导率为。
一电导池中充5以此溶液,在25 ?c时测得其电阻为的液的电导率;(3)溶液,测得电阻为。
在同一电导池中装入同样体积的质量浓度为。
计算(1)电导池系数;(2)溶溶液的摩尔电导率。
解:(1)电导池系数为(2)溶液的电导率(3)溶液的摩尔电导率7.8 已知25 ?c时此溶液,在25 ?c,溶液,测出其电阻分别为稀释时,,,和溶液的电导率为。
一电导池中充以和的。
试用外推法求无限作图如下【篇三:第五版物理化学第四章习题答案】t>4.1 有溶剂a与溶质b形成一定组成的溶液。
物理化学第四章习题解答

物理化学第四章习题解答思考题3.注:题目为反应对该反应物分别是一级、二级2A——>P+...、三级3A——>P+...。
而A+B——>P+...这个反应若为如书P141所示的二级反应,则对反应物A和B都分别是一级的。
所以本题应该套用简单n级反应的公式进行计算。
设反应物A的初始浓度为a,t时刻生成物P的浓度为某,则对于简单的n级反应我们有:n=1时lnn>1时ak1ta某111ktn1n1n1na(an某)代入n=2得某k2ta(a-2某)代入n=3得1112k3t26a3某a将某=0.5a和某=0.75a分别代入n=1对应的反应速率方程,可得t12ln2ln4t34t12:t341:2k1k1将某=0.25a和某=0.375a分别代入n=1对应的反应速率方程,可得t1213t34t12:t341:32ak22ak215tt12:t341:5342a2k32a2k3.将某=1/6a和某=1/4a分别代入n=1对应的反应速率方程,可得t124.根据阿伦尼乌斯公式的微分形式,我们有dlnk1lnk2Ea1Ea2EadlnkdTRT2dTRT2dlnk1k2Ea1Ea2dTRT2根据平行反应反应速率与生成物浓度之间的关系,我们有dln某1某2Ea1Ea20dTRT2即随着温度增加ln某1某2增大,所以温度升高时更利于反应1的进行。
习题解答d[A]=―k1[A]―k4[A]dtd[B]=k1[A]―k2[B]+k3[C]dtd[C]=k2[B]―k3[C]dtd[D]=k4[A]dtd[A](2)=―k1[A]+k2[B]dtd[B]=k1[A]―k2[B]―k3[B][C]dtd[C]=―k3[B][C]dtd[D]=k3[B][C]dtd[A](3)=―k1[A]+k2[B]2dtd[B]=2(k1[A]―k2[B])2dtd[A](4)=―2k1[A]2+2k2[B]dtd[B]=k1[A]2―k2[B]―k3[B]dtd[C]=k3[B]dt1、解:(1)2、解(1)以lnc对t作图得一直线,说明该反应是一级反应。
物理化学(天津大学第四版)课后答案 第四章 多组分系统热力学

第四章多组分系统热力学4.1有溶剂A 与溶质B 形成一定组成的溶液。
此溶液中B 的浓度为cB ,质量摩尔浓度为bB ,此溶液的密度为。
以MA ,MB 分别代表溶剂和溶质的摩尔质量,若溶液的组成用B 的摩尔分数xB 表示时,试导出xB 与cB ,xB 与bB 之间的关系。
解:根据各组成表示的定义4.2D-果糖溶于水(A )中形成的某溶液,质量分数,此溶液在20°C 时的密度。
求:此溶液中D-果糖的(1)摩尔分数;(2)浓度;(3)质量摩尔浓度。
解:质量分数的定义为4.3在25°C ,1kg 水(A )中溶有醋酸(B ),当醋酸的质量摩w ww .k h d a w .c o m 课后答案网尔浓度bB 介于和之间时,溶液的总体积。
求:(1)把水(A )和醋酸(B )的偏摩尔体积分别表示成bB 的函数关系。
(2)时水和醋酸的偏摩尔体积。
解:根据定义当时4.460°C 时甲醇的饱和蒸气压是84.4kPa ,乙醇的饱和蒸气压是47.0kPa 。
二者可形成理想液态混合物。
若混合物的组成为二者的质量分数各50%,求60°C 时此混合物的平衡蒸气组成,以摩尔分数表示。
解:质量分数与摩尔分数的关系为w w w .k h d a w .c o m 课后答案网求得甲醇的摩尔分数为根据Raoult 定律4.580°C 是纯苯的蒸气压为100kPa ,纯甲苯的蒸气压为38.7kPa 。
两液体可形成理想液态混合物。
若有苯-甲苯的气-液平衡混合物,80°C 时气相中苯的摩尔分数,求液相的组成。
解:根据Raoult 定律4.6在18°C ,气体压力101.352kPa 下,1dm3的水中能溶解O20.045g ,能溶解N20.02g 。
现将1dm3被202.65kPa 空气所饱和了的水溶液加热至沸腾,赶出所溶解的O2和N2,并干燥之,求此干燥气体在101.325kPa ,18°C 下的体积及其组成。
北京大学《物理化学》课后章节练习题第4章习题及答案

第四章 习题1. 1000K 、101.325kPa 时,反应)()(2)(2223g O g SO g SO +⇔的K c =3.54mol ·m -3。
(1)求此反应的K p 和K x 。
(2)求反应)(21)()(223g O g SO g SO +⇔的K p 和K x 2. 已知457K 、总压为101.325kPa 时,NO 2有5%分解,求此反应的。
θp K )()(2)(222g O g NO g NO +⇔3. PCl 5的分解作用为 )()()(235g Cl g PCl g PCl +⇔在523.2K 、101.325kPa 下反应到达平衡后,测得平衡混合物的密度为2.695kg ·m -3,试计算(1)PCl (g )的离解度。
(2)该反应的。
θp K (3)该反应的。
θm r G Δ4. 温度为T 在体积为V 的容器中,充入1mol H 2,3mol I 2,设平衡后有x mol HI生成。
若再加入2 mol H 2,则平衡后HI 的物质的量为2x mol ,试计算K p 的值。
5. 在298.15K 时,有0.01kg 的N 2O 4(g ),压力为202.65kPa ,现把它完全转变成NO 2(g ),压力为30.40kPa ,求过程中的G r Δ。
已知N 2O 4(g )和NO 2(g )的分别为98.29kJ ·mol θmf G Δ-1和51.84kJ ·mol -1。
6. 反应的。
若参加反应的气体是由10%CH )()(2)(42g CH g H s C =+1.19290)1000(−=Δmol J K G m r θ4,80%H 2及10%N 2所组成的,试问在T =1000K 及p =101.325kPa 时能否有甲烷生成。
7. 银可能受到H 2S (g )的腐蚀而发生下面的反应:)()()(2222g H s S Ag s Ag S H +⇔+ 已知 该反应1.24.7−−=Δmol kJ G m r θ今在298K 和标准压力p θ下,将银放在等体积的氢和H 2S 组成的混合气体中(1)试问能否发生腐蚀而生成硫化银。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章多组分系统热力学4.1有溶剂A与溶质B形成一定组成的溶液。
此溶液中B的浓度为c B,质量摩尔浓度为b B,此溶液的密度为。
以M A,M B分别代表溶剂和溶质的摩尔质量,若溶液的组成用B的摩尔分数x B表示时,试导出x B与c B,x B与b B之间的关系。
解:根据各组成表示的定义4.2D-果糖溶于水(A)中形成的某溶液,质量分数,此溶液在20℃时的密度。
求:此溶液中D-果糖的(1)摩尔分数;(2)浓度;(3)质量摩尔浓度。
解:质量分数的定义为4.3 在25℃,1 kg 水(A )中溶有醋酸(B ),当醋酸的质量摩尔浓度b B 介于和之间时,溶液的总体积求:(1) 把水(A )和醋酸(B )的偏摩尔体积分别表示成b B 的函数关系。
(2)时水和醋酸的偏摩尔体积。
解:根据定义当时4.460℃时甲醇的饱和蒸气压是84.4 kPa ,乙醇的饱和蒸气压是47.0 kPa 。
二者可形成理想液态混合物。
若混合物的组成为二者的质量分数各50 %,求60℃时此混合物的平衡蒸气组成,以摩尔分数表示。
解:甲醇的摩尔分数为58980049465004232500423250....x B =+=4.580℃时纯苯的蒸气压为100 kPa,纯甲苯的蒸气压为38.7 kPa。
两液体可形成理想液态混合物。
若有苯-甲苯的气-液平衡混合物,80℃时气相中苯的摩尔分数,求液相的组成。
解:4.6在18℃,气体压力101.352 kPa下,1 dm3的水中能溶解O2 0.045 g,能溶解N2 0.02 g。
现将 1 dm3被202.65 kPa空气所饱和了的水溶液加热至沸腾,赶出所溶解的O2和N2,并干燥之,求此干燥气体在101.325 kPa,18℃下的体积及其组成。
设空气为理想气体混合物。
其组成体积分数为:,解:显然问题的关键是求出O2和N2的亨利常数。
4.7 20℃下HCl 溶于苯中达平衡,气相中HCl 的分压为101.325 kPa 时,溶液中HCl 的摩尔分数为0.0425。
已知20℃时苯的饱和蒸气压为10.0 kPa ,若20℃时HCl 和苯蒸气总压为101.325 kPa ,求100 g 苯中溶解多少克HCl 。
解:设HCl 在苯中的溶解符合亨利定律HCl HCl ,x HCl x k p = Pa .Pa .x p k HCl HCl HCl,x 610×3842=04250101325== HCl,x HCl ,x *HCl ,x *HCl HCl ,x *HCl k x k p x k x p x k x p p p p +1+=+苯苯苯苯苯苯苯苯总)-=()-(=+=96010×38421000010×384210132566...k p k p x HCl,x *HCl ,x =--=--=苯总苯 960=536+7810078100=..mx 苯 m = 1.867g4.8H 2, N 2与100 g 水在40℃ 时处于平衡,平衡总压为105.4 kPa 。
平衡气体经干燥后的组成分数。
假设可以认为溶液的水蒸气压等于纯水的蒸气压,即40 ℃时的7.33 kPa 。
已知40℃时H 2, N 2在水中的亨利系数分别为7.61 GPa 及10.5 GPa ,求40℃时水中溶解H 2, N 2在的质量。
4.9试用吉布斯-杜赫姆方程证明在稀溶液中若溶质服从亨利定律,则溶剂必服从拉乌尔定律。
证明:设溶质和溶剂分别用B ,A 表示。
根据吉布斯-杜赫姆方程( T and p 恒定)溶质B 的化学势表达式为若溶质服从亨利定律,则即溶剂A 服从拉乌尔定律。
4.10 A ,B 两液体能形成理想液态混合物。
已知在温度t 时纯A 的饱和蒸气压,纯B 的饱和蒸气压。
(1) 在温度t 下,于气缸中将组成为的A, B 混合气体恒温缓慢压缩,求凝结出第一滴微小液滴时系统的总压及该液滴的组成(以摩尔分数表示)为多少?(2) 若将A, B 两液体混合,并使此混合物在100 kPa ,温度t 下开始沸腾,求该液态混合物的组成及沸腾时饱和蒸气的组成(摩尔分数)。
解: 由于形成理想液态混合物,每个组分均符合拉乌尔定律;B*B A *A B A x p x p p p p +=+=总3330=6670=2=40×60120×4016040==.x .x ..x x ..y y x p x p y p x p y p x p y p p y p p B A A A B A B *B A*A BB*B AA*A B BA A=-====总总总总kPa .x p x p p p p B *B A *A B A 666=+=+=总 (2)混合物在100 kPa ,温度t 下开始沸腾,要求4.11 25℃下,由各为0.5 mol 的A 和B 混合形成理想液态混合物,试求混合过程的。
解:kJkJ S T H G K J K J x n x n R S H V mix mix mix B B A A mix mix mix 72.1)76.515.298(76.5)5.0ln 5.0314.82()ln ln (011-=⨯-=∆-∆=∆⋅=⋅⨯⨯⨯-=+-=∆=∆=∆-- 4.12 苯与甲苯的混合液可视为理想液态混合物。
今有一混合物组成为,。
求25℃, 100 kPa 下1 mol 该混合物的标准熵、标准生成焓与标准生成吉布斯函数。
所需25℃的热力学数据如表所示。
物质C 6H 6(l) 48.66 123.0 172.8 C 6H 5CH 3(l)12114.15 219.58解:根据生成焓的的定义,混合物的为4.13 液体B 与液体C 可形成理想液态混合物。
在常压及25℃下,向总量n = 10 mol ,组成x C = 0.4的B, C 液态混合物中加入14 mol 的纯液体C ,形成新的混合物。
求过程的△G , △S 。
解:n C =( 14+10×0.4) mol = 18 moln B = ( 10×0.6) mol = 6 moln 总 = 24 mol 250=246=750=2418=.x .x B C 11112111112•7716==••2556=••9555=606+4043148=••2112=2506+750183148=---------=---mol KJ .S ΔT G ΔK mol J .S ΔS ΔS ΔK mol J .).ln .ln (.S ΔK mol J .).ln .ln (.S Δmix mix mix mix4.14 液体B 和液体C 可形成理想液态混合物。
在25℃下,向无限大量组成x C = 0.4的混合物中加入5 mol 的纯液体C 。
(1) 求过程的△G , △S 。
(2) 求原混合物中组分B 和组分C 的△G B , △G C 。
4.15在25℃向1 kg溶剂A(H2O)和0.4 mol溶质B形成的稀溶液中又加入1 kg的纯溶剂,若溶液可视为理想稀溶液,求过程的△G。
4.16(1)25℃时将0.568 g碘溶于50 cm3 CCl4中,所形成的溶液与500 cm3水一起摇动,平衡后测得水层中含有0.233 mmol的碘。
计算点在两溶剂中的分配系数K,。
设碘在两种溶剂中均以分子形式存在。
(2)若25℃在水中的浓度是1.33 mmo l·dm-3,求碘在中的浓度。
解:(1)的分子量为,因此4.1725℃时0.1 mol NH3溶于1 dm3三氯甲烷中,此溶液NH3的蒸气分压为4.433 kPa,同温度时0.1 mol NH3溶于1 dm3水中,NH3的蒸气分压为0.887 kPa。
求NH3在水与三氯甲烷中的分配系数。
4.1820℃某有机酸在水和乙醚中的分配系数为0.4。
今有该有机酸5 g溶于100 cm3水中形成的溶液。
(1)若用40 cm3乙醚一次萃取(所用乙醚已事先被水饱和,因此萃取时不会有水溶于乙醚),求水中还剩下多少有机酸?(2)将40 cm3乙醚分为两份,每次用20 cm3乙醚萃取,连续萃取两次,问水中还剩下多少有机酸?解:设有机酸的分子量为M;分配平衡时,水中的有机酸还剩m克根据分配定律用同样体积的乙醚萃取n次,则有(1)用40 cm3乙醚萃取一次(2)每次用20 cm3乙醚萃取,连续萃取两次4.1925 g的CCl4中溶有0.5455 g某溶质,与此溶液成平衡的CCl4的蒸气分压为11.1888 kPa,而在同一温度时纯CCl4的饱和蒸气压为11.4008 kPa。
(1)求此溶质的相对分子量。
(2)根据元素分析结果,溶质中含C为94.34 %,含氢为5.66 %(质量分数),确定溶质的化学式。
解:(1)设该溶液为理想稀溶液,则溶剂服从拉乌尔定律(2)设该物质的化学式为C n H m,则解得,化学式为C14H10。
4.2010 g葡萄糖(C6H12O6)溶于400 g乙醇中,溶液的沸点较纯乙醇的上升0.1428℃。
另外有2 g有机物质溶于100 g乙醇中,此溶液的沸点则上升0.1250℃。
求此有机物质的相对分子质量。
解:10 g葡萄糖(C6H12O)溶于400 g乙醇中2 g有机物质溶于100 g乙醇中4.21在100 g苯中加入13.76 g联苯(C6H5C6H5),所形成溶液的沸点为82.4℃。
已知纯苯的沸点为80.1℃。
求:(1)苯的沸点升高系数;(2)苯的摩尔蒸发焓。
解:4.22已知0℃,101.325 kPa时,O2在水中的溶解度为;N2在水中的溶解度为。
试计算被101.325 kPa,体积分数,的空气所饱和了的水的凝固点较纯水的降低了多少?解:为101.325 kPa的空气所饱和了的水中溶解的O2和N2的物质分别为查表知水的凝固点降低系数为,因此4.23已知樟脑(C10H16O)的凝固点降低系数为。
(1)某一溶质相对分子质量为210,溶于樟脑形成质量分数为5 %的溶液,求凝固点降低多少?(2)另一溶质相对分子质量为9000,溶于樟脑形成质量分数为5 %的溶液,求凝固点降低多少?解:容易导出质量分数和质量摩尔浓度间的关系因此,4.24现有蔗糖(C12H22O11)溶于水形成某一浓度的稀溶液,其凝固点为-0.200℃,计算此溶液在25℃时的蒸气压。
已知水的,纯水在25℃时的蒸气压为。
解:首先计算蔗糖的质量摩尔浓度由上题可知,质量摩尔浓度和摩尔分数有以下关系假设溶剂服从拉乌尔定律,则此溶液在25℃时的蒸气压4.25在25℃时,10 g某溶剂溶于1 dm3溶剂中,测出该溶剂的渗透压为Π=0.4000kPa,确定该溶质的相对分子质量。
解:溶剂的渗透压表示为4.26在20℃下将68.4 g蔗糖(C12H22O11)溶于1 kg的水中。
