热力学统计物理 第三章 课件
合集下载
热力学统计物理-第五版-汪志诚-精ppt课件

描述).
单位:
1 m 3 1 0 3 L 1 0 3 d m 3
3 温度 T : 气体冷热程度的量度(热学描述).
单位:K(开尔文).
2020/4/29
.
20
简单系统:一般仅需二个参量就能确定的系统, 如PVT系统。
单相系:
复相系:
2020/4/29
.
21
§1.2 热平衡定律和温度
一、热力学第零定律 热交换:系统之间传热但不交换粒子
热平衡:两个系统在热交换的条件下达到了一 个共同的平衡态。
经验表明:如果两个系统A和B同时分别与第三个系 统C达到热平衡,则这两个系统A和B也处于热平衡。 称热力学第零定律(热平衡定律)
2020/4/29
.
22
为了描绘一个系统与另外一个系统处于 热平衡 需要一个物理量:温度
(1)日常生活中,常用温度来表示冷热的程度
在一定的宏观条件下,系统演化方向一般具有确 定的规律性。
研究热运动的规律性以及热运动对物质宏观性质 影响的理论统称为热学理论。按研究方法的不同可 分为热力学与统计物理等。其中,热力学是热学的 宏观理论,统计物理是热学的微观理论。
2020/4/29
.
7
2020/4/29
.
8
热力学理论的发展简介 Introduction to Development of
① 热学
② 分子运动论
③ 原子物理学
2020④/4/29量子力学
.
11
The Fundamental Laws of Thermodynamics
2020/4/29.Fra bibliotek12
目 录 Contents
热力学与统计物理学第三讲

2、开系的热力学方程 、 (1)吉布斯函数 )吉布斯函数G 根据吉布斯函数的全微分式子: 根据吉布斯函数的全微分式子: dG = −SdT +VdP ——此式适用于物质的量不发生变化的情况 此式适用于物质的量不发生变化的情况 由于G是广延量,所以对于开系,上式推广为: 由于 是广延量,所以对于开系,上式推广为: 是广延量
δUα,δVα,δnα和δU β,δV β,δnβ
又孤立系统要求: 又孤立系统要求:
δUα +δUβ = 0,δVα +δV β = 0,δnα +δnβ = 0
又QdU = TdS − PdV + µdn dU + PdV − µdn ⇒dS = T
由此可得出:两相的熵分别为: 由此可得出:两相的熵分别为:
由前面讨论可知: 由前面讨论可知:
δ S〈0
2
为系统的平衡的稳定条件
而系统的总的熵函数的变化为: 而系统的总的熵函数的变化为:
~ δ S = δ 2S +δ 2S0 〈0
2
由于媒质比系统大得多,所以有: 由于媒质比系统大得多,所以有: 故此忽略
δ 2S0
δ S0 << δ S
2 2
∂2S δ 2S ∂2S 根据泰勒展开公式得: 根据泰勒展开公式得: δ 2S = [( )(δU)2 + 2 δUδV + ∂V
δ 2S
对于各种可能的虚变动都小于零,应有: 对于各种可能的虚变动都小于零,应有:
1 1 − 2 〈0 ⇒CV 〉0 T CV ——平衡的稳定条件之一 平衡的稳定条件之一
平衡的稳定条件之二: 平衡的稳定条件之二:
∂P ( )T 〈0 ∂V
同理可得。 同理可得。
热力学统计物理第三章1

第三章 单元系相变
§3.1 热动平衡判据
这一节的中心问题是如何判定一个系统是否达到了平衡状态。 这一节的中心问题是如何判定一个系统是否达到了平衡状态。 如何判定一个系统是否达到了平衡状态
一、熵判据
熵增加原理指出, 孤立系统的熵永不减少。 孤立系统中发 熵增加原理指出 , 孤立系统的熵永不减少 。 生的任何实际的宏观过程,包括趋向平衡的过程, 生的任何实际的宏观过程 , 包括趋向平衡的过程 , 都朝着使系 统的熵增加的方向进行。 统的熵增加的方向进行。 不平衡状态 熵
∆S < 0
将S为泰勒展开,准确到二级。有 为泰勒展开,准确到二级。
1 2 ∆ S = δS + δ S 2
根据数学上熟知的结果: 根据数学上熟知的结果:当熵函数的一级变分 δS = 0 ,熵 时 函数有极值;可以由此得到平衡条件。 函数有极值;可以由此得到平衡条件。当熵函数的一级变分 时熵函数有极大值, δS = 0 ,二级变分 δ 2 S < 0时熵函数有极大值,由可以得到 稳定条件。如果熵函数的极大不止一个, 稳定条件。如果熵函数的极大不止一个,则其中最大的极大 相应稳定平衡。 相应稳定平衡。
泰勒展开: 泰勒展开:
f ( x ) = f ( x 0 ) + f ′( x ) x = x0 ( x − x 0 ) +
f ( x , y ) = f ( x0 , y0 ) + ∂f ( x , y ) ∂x
f ′′ ( x ) x = x 0 ( x − x 0 ) 2!
2
+ ⋯⋯
x = x0
∂p 假如子系统的体积由于某种原因发生收缩, 假如子系统的体积由于某种原因发生收缩,根据平衡稳定条件 <0 ∂p ∂V T <0 ∂V T 子系统的压强将略高于媒质的压强,于是子系统膨胀而恢复平衡。 子系统的压强将略高于媒质的压强,于是子系统膨胀而恢复平衡。
§3.1 热动平衡判据
这一节的中心问题是如何判定一个系统是否达到了平衡状态。 这一节的中心问题是如何判定一个系统是否达到了平衡状态。 如何判定一个系统是否达到了平衡状态
一、熵判据
熵增加原理指出, 孤立系统的熵永不减少。 孤立系统中发 熵增加原理指出 , 孤立系统的熵永不减少 。 生的任何实际的宏观过程,包括趋向平衡的过程, 生的任何实际的宏观过程 , 包括趋向平衡的过程 , 都朝着使系 统的熵增加的方向进行。 统的熵增加的方向进行。 不平衡状态 熵
∆S < 0
将S为泰勒展开,准确到二级。有 为泰勒展开,准确到二级。
1 2 ∆ S = δS + δ S 2
根据数学上熟知的结果: 根据数学上熟知的结果:当熵函数的一级变分 δS = 0 ,熵 时 函数有极值;可以由此得到平衡条件。 函数有极值;可以由此得到平衡条件。当熵函数的一级变分 时熵函数有极大值, δS = 0 ,二级变分 δ 2 S < 0时熵函数有极大值,由可以得到 稳定条件。如果熵函数的极大不止一个, 稳定条件。如果熵函数的极大不止一个,则其中最大的极大 相应稳定平衡。 相应稳定平衡。
泰勒展开: 泰勒展开:
f ( x ) = f ( x 0 ) + f ′( x ) x = x0 ( x − x 0 ) +
f ( x , y ) = f ( x0 , y0 ) + ∂f ( x , y ) ∂x
f ′′ ( x ) x = x 0 ( x − x 0 ) 2!
2
+ ⋯⋯
x = x0
∂p 假如子系统的体积由于某种原因发生收缩, 假如子系统的体积由于某种原因发生收缩,根据平衡稳定条件 <0 ∂p ∂V T <0 ∂V T 子系统的压强将略高于媒质的压强,于是子系统膨胀而恢复平衡。 子系统的压强将略高于媒质的压强,于是子系统膨胀而恢复平衡。
热力学统计物理第三章

可能的变动。孤立系统与外界没有热量和功的交换, 若只有体积功,其约束条件是内能和体积不变。
孤立系统处在稳定平衡状态的必要和充分条件是,虚 变动引起的熵变
S 0
将S作泰勒展开,准确到二级,有 S S 1 2S
2
由数学上的极值条件:
当 S 0, 2S 0 时,熵函数有极大值。
可得
S 0 2S 0
( 相变平衡条件)
即整个系统达到平衡时,两相的温度、压强和化 学势分别相等。
分析:若平衡条件未满足,复相系的变化将朝着熵增加 ( S 0 )的方向进行:
(1)若只有热平衡条件未满足,则向 的方向变化:
U
(
1 T
1 T
)
0
如 T T 则 U 0 即能量从高温的相传到低 温的相。
(2)若只有力学平衡条件未满足,则向 的方向变化:
•因为两相的化学势相等,所以两相可以以任意比例共存; •整个系统的吉布斯函数保持不变,系统处在中性平衡。
(3)单元三相平衡共存,必须满足
T T T p p p
(T , p) (T , p) (T , p)
由上面的方程可以唯一地确定温度和压强的一组解
TA和PA ,即单元系的三相平衡共存的三相点。 水的三相点为:TA = 273.16 K, pA = 610.9 Pa .
dH TdS Vdp
若S, p不变,则 dH 0 ,即过程向焓H减少的方向 进行,因此平衡态的焓H最小。
热力学判据 过程遵循规律
U
dU TdS pdV
H
dH TdS Vdp
F
dF SdT pdV
G
dG SdT Vdp
TdS dU pdV S
TdS dH Vdp
孤立系统处在稳定平衡状态的必要和充分条件是,虚 变动引起的熵变
S 0
将S作泰勒展开,准确到二级,有 S S 1 2S
2
由数学上的极值条件:
当 S 0, 2S 0 时,熵函数有极大值。
可得
S 0 2S 0
( 相变平衡条件)
即整个系统达到平衡时,两相的温度、压强和化 学势分别相等。
分析:若平衡条件未满足,复相系的变化将朝着熵增加 ( S 0 )的方向进行:
(1)若只有热平衡条件未满足,则向 的方向变化:
U
(
1 T
1 T
)
0
如 T T 则 U 0 即能量从高温的相传到低 温的相。
(2)若只有力学平衡条件未满足,则向 的方向变化:
•因为两相的化学势相等,所以两相可以以任意比例共存; •整个系统的吉布斯函数保持不变,系统处在中性平衡。
(3)单元三相平衡共存,必须满足
T T T p p p
(T , p) (T , p) (T , p)
由上面的方程可以唯一地确定温度和压强的一组解
TA和PA ,即单元系的三相平衡共存的三相点。 水的三相点为:TA = 273.16 K, pA = 610.9 Pa .
dH TdS Vdp
若S, p不变,则 dH 0 ,即过程向焓H减少的方向 进行,因此平衡态的焓H最小。
热力学判据 过程遵循规律
U
dU TdS pdV
H
dH TdS Vdp
F
dF SdT pdV
G
dG SdT Vdp
TdS dU pdV S
TdS dH Vdp
热力学与统计物理第三章PPT课件

24.07.2020
2
• 熵判据
一个系统在内能和体积都保持不变的情况下, 对于各种可能的变动,以平衡态的熵为最大。
孤立系统处在稳定平衡状态的必要且充分条件为: Δ~S0
泰勒级数展开为: Δ~S δS1δ2S 2
根据数学知识可知,熵S有极大值的条件应为:
δS0
熵函数有极值
δS0 δ2S 0
24.07.2020
CV 0,
p VT
0
稳定性条件
平衡满足稳定性条件时,系统对平衡发生偏离时,系
统将自发产生相应的过程,以恢复系统的平衡。适用于均 匀系统的任何部分。
24.07.2020
10
气体的范德瓦耳斯方程: pVa2 VbRT
p
V 气体的等温曲线
24.07.2020
11
§3.2 开系热力学基本方程
一、单元复相系平衡性质的描述及特点
24.07.2020
T U
p
U
U
S V , n
V S, n
n S,V
14
3、开系的焓
HGT SUpV
d H T d S V d p d n HH(S,p,n)
T H S p, n
V
H p
S,n
4、开系的自由能
H
n S, p
FGpV UTS
d F S d T p d V d n
16
§3.3 单元系的复相平衡 1.由熵判据推导平衡条件
考虑一单元两相系统( 相与 相 )组成一孤立系,则有:
24.07.2020
17
由开系的基本热力学方程知: d U T d Sp d V d n
SUpTV n SUpTV n 由熵的广延性质: SSS
2021年高中物理第三章热力学定律3能量守恒定律课件人教版必修三.pptx

探究一
探究二
随堂检测
要点提示(1)不能,违反了能量守恒定律。 (2)能量守恒定律是各种形式的能相互转化或转移的过程,总能量保 持不变,它包括各个领域,范围广泛。热力学第一定律是物体内能 与其他形式的能之间的相互转化或转移,是能量守恒定律的具体体 现。
探究一
探究二
随堂检测
知识归纳 1.能量的存在形式及相互转化 各种运动形式都有对应的能:机械运动有机械能,分子的热运动有 内能,还有诸如电磁能、化学能、原子能等。 各种形式的能,通过做功可以相互转化,例如:利用电炉取暖或烧水, 电能转化为内能;煤燃烧,化学能转化为内能;列车刹车后,轮子温度 升高,机械能转化为内能。
探究一
探究二
随堂检测
特别提醒(1)能量守恒定律是自然界中普遍适用的规律,凡是遇到涉 及能量的转化和转移问题时可优先考虑使用其解决。 (2)层出不穷的永动机设计方案,由于违背了能量守恒定律,无一例 外地宣布失败,制造永动机的企图是没有任何成功希望的。
探究一
探究二
随堂检测
实例引导
例1 如图所示,密闭绝热容器内有一绝热的具有一
2.第一类永动机不可制成的原因:违背了能量守恒定律。
必备知识
自我检测
1.正误判断 (1)某个物体的能量减少,必然有其他物体的能量增加。( ) (2)石子从空中落下,最后停止在地面上,说明机械能消失了。( ) (3)能量既可以转移又可以转化,故能量的总量是可以变化的。
() (4)违背能量守恒定律的过程是不可能发生的。( ) (5)用太阳灶烧水是太阳能转化为内能。( ) (6)第一类永动机不能制成,是因为它违背了能量守恒定律。( ) 答案(1)√ (2)× (3)× (4)√ (5)√ (6)√
必备知识
高中物理第3章热力学基础章末整合课件粤教选修33粤教高二选修33物理课件

12/13/2021
第十三页,共十七页。
例2 关于热力学第二定律,下列表述正确的是( )
A.不可能使热量从低温物体传递到高温物体 B.不可能从单一热源吸收(xīshōu)热量并把它全部用来做功
C.第二类永动机是不可能制成的
D.热力学第二定律是热力学第一定律的推论
12/13/2021
第十四页,共十七页。
能量守恒定律是自然界普遍适用的规律,不同形式的能可以 (kěyǐ)相互转化,但总能量守恒.
12/13/2021
第七页,共十七页。
(2)应用能量守恒定律解题的方法步骤
①认清有多少种形式的能(例如动能、势能、内能、电能、化
学能、光能等)在相互转化.
②分别写出减少的能量ΔE减和增加的能量ΔE增的表达式. ③根据下列两种思路列出能量守恒方程:ΔE减=ΔE增. A.某种形式的能量减少,一定(yīdìng)存在其他形式的能量增 加,且减少量与增加量一定(yīdìng)相等.
第九页,共十七页。
例1 一定质量的气体,在从一个状态变化到另一个状态的
过程中,吸收热量280 J,并对外做功120 J.试问:
(1)这些气体的内能发生了怎样的变化?
(2)如果(rúguǒ)这些气体又返回原来的状态,并放出了240 J热量,
那么在返回的过程中是气体对外界做功,还是外界对气体做功?做功多 少?
(2)机械能与内能转化的方向性:不可能从单一热源吸收热量,使之
完全变成功,而不产生其他影响.
2.热力学第二定律的微观解释
一切自然过程总是沿着分子热运动的无序性增大的方向进行,即在 任何自然过程中,一个孤立系统的总熵不会减小.
12/13/2021
第十二页,共十七页。
3.热力学第一定律与热力学第二定律的对比 热力学第一定律和热力学第二定律是热力学知识的基础理 论.热力学第一定律指出任何热力学过程中能量守恒,而对过程没有 其他限制(xiànzhì).热力学第二定律指明哪些过程可以发生,哪些不可能
热学第三章ppt大学物理

例4:已知:一气缸如图,A、B内各有1mol理想气 体N2 ,VA=VB,TA=TB。有335J的热量缓慢地 传给气缸,活塞上方的压强始终是1atm。 (忽略导热板的吸热,活塞重量及摩擦)
求:(1)A,B两部分温度的增量及净吸的热量.
(2)若导热隔板换成可自由滑动的绝热隔板,
1atm.
再求第(1)问的各量.
原平衡态
非平衡态
新平衡态
热力学中研究过程时,为了在理论上能利用系 统处于平衡态时的性质,引入准静态过程的概念.
二.准静态过程: 1.准静态过程是由无数个平衡态组成的过程. 2.准静态过程是实际过程的理想化模型. (无限缓慢)有理论意义,也有实际意义. 2
3.准静态过程可以用 P-V图上的一条曲线 (过程曲线)来表示.
间接法 A=-Δ E=CV.m(T1-T2)……(1)
可见,绝热过程靠减少系统的内能来对外做功.
A也可由直接计算法计算:
A
V2 PdV
V1
V2 C
V V1
dV
C V2
V V1
dV
C
1-
V21-
C -
1
P1V1
-
P2V2
- V11-
……(2)
请大家课下证明(1),(2)的结果是一样的。 22
0
e
1
2
d
3
v(10-3m3)
6
§3.3 内能、热量、 热力学第一定律
一.内能
微观上,热力学系统的内能是指其分子无规则运动 的能量(应含分子动能、分子间的势能)的总和.
内能是状态量 对于一定质量的某种气体: 理想气体的内能是
《热力学第三章》PPT课件_OK

活塞有摩擦完全导热且经历准静态等温过程141活塞移动距离laa1020802080突然不是准静态pdvlnln可求s状态参数1活塞移动距离laa1020802080lnln教材313题氧气瓶v004m20迅速放气p取氧气瓶为开口系试用开口系能量方程求tpvmrt开口系能量方程cvoutoutininnetqdumhmhwcvoutoutdumh2v21v1outoutmctmctmh是不是可逆不敢确定气体减少dm本身为正cvoutoutdumhdudmuuhm指瓶中气体状态outdmuhdmmcdtrtdmdmdt绝热钢瓶放气瓶内气体遵循ln1lntkvconstdmdtdmdvdvdtdtdtdvtvconstpvconst小瓶绝热保温箱初为真空由于小瓶漏气某时刻小瓶内温度为t
R s0
T1
pr (T2 ) pr (T1)
R
定义
pr
exp sT0 R
f (T )
相对压力
已知p1,T1,T2 ,查附表2,得pr(T1)和pr(T2),求p2
vr用得较少,自学
2021/8/21
36
§3-5理想混合气体
37
研究对象
无化学反应的理想气体混合物 例:锅炉烟气 CO2, CO, H2O, N2
T
v
cpdT R dp
T
p
2、按真实比热计算
3、按平均比热法计算
2021/8/21
26
1、按定比热计算理想气体热容
分子运动论
Um
i 2
RmT
运动自由度
Cv,m
dU m dT
i 2
Rm
Cp,m
dH m dT
d (Um RmT ) dT
i
2
R s0
T1
pr (T2 ) pr (T1)
R
定义
pr
exp sT0 R
f (T )
相对压力
已知p1,T1,T2 ,查附表2,得pr(T1)和pr(T2),求p2
vr用得较少,自学
2021/8/21
36
§3-5理想混合气体
37
研究对象
无化学反应的理想气体混合物 例:锅炉烟气 CO2, CO, H2O, N2
T
v
cpdT R dp
T
p
2、按真实比热计算
3、按平均比热法计算
2021/8/21
26
1、按定比热计算理想气体热容
分子运动论
Um
i 2
RmT
运动自由度
Cv,m
dU m dT
i 2
Rm
Cp,m
dH m dT
d (Um RmT ) dT
i
2
热力学统计物理第三章3

这时有
dU α = TdS α − pα dV α + µ α dnα
dU β = TdS β − p β dV β + µ β dn β
dU γ = TdS γ + σdA
假定热平衡条件已经满足,温度保持不变, 假定热平衡条件已经满足 , 温度保持不变 , 用自由能 判据推求系统的力学平衡条件和相变条件。 判据推求系统的力学平衡条件和相变条件。 假想在温度和总体积保持不变的条件下, 假想在温度和总体积保持不变的条件下,系统发生一个 虚变动。在这虚变动中,三相的摩尔数,体积和面积分 虚变动。 在这虚变动中,三相的摩尔数, 的变化。 别有 δ n α , δV α ; δn β,δV β ; δA 的变化 。由于在虚变动 中系统的总摩尔数和总体积保持不变, 中系统的总摩尔数和总体积保持不变,应有
Tα = T β = T
pα = p β + 2σ r
µ α T , pα = µ β T , p β
(
)
(
)
分界面为平面)气液两相的平衡条件为: (分界面为平面)气液两相的平衡条件为:
Tα = T β = T
pα = p β = p
µ α (T , p ) = µ β (T , p )
分界面为曲面)气液两相的平衡条件为: (分界面为曲面)气液两相的平衡条件为:
δ nα + δ n β = 0
δV α + δV β = 0
δF = −( pα − p β )δV α + σδA + ( µ α − µ β )δnα = 0
如果假定液滴是球形的,有 如果假定液滴是球形的,
Vα =
4π 3 r 3
A = 4πr 2
热力学统计物理第三章

五十五分。
第九页,编辑于星期二:十一点 五十五分。
第十页,编辑于星期二:十一点 五十五分。
第十一页,编辑于星期二:十一点 五十五分。
第十二页,编辑于星期二:十一点 五十五分。
第十三页,编辑于星期二:十一点 五十五分。
第十四页,编辑于星期二:十一点 五十五分。
第十五页,编辑于星期二:十一点 五十五分。
第十六页,编辑于星期二:十一点 五十五分。
第十七页,编辑于星期二:十一点 五十五分。
第十八页,编辑于星期二:十一点 五十五分。
第十九页,编辑于星期二:十一点 五十五分。
第二十页,编辑于星期二:十一点 五十五分。
第二十一页,编辑于星期二:十一点 五十五分。
第二十二页,编辑于星期二:十一点 五十五分。
第一页,编辑于星期二:十一点 五十五分。
第二页,编辑于星期二:十一点 五十五分。
第三页,编辑于星期二:十一点 五十五分。
第四页,编辑于星期二:十一点 五十五分。
第五页,编辑于星期二:十一点 五十五分。
第六页,编辑于星期二:十一点 五十五分。
第七页,编辑于星期二:十一点 五十五分。
第八页,编辑于星期二:十一点 五十五分。
第九页,编辑于星期二:十一点 五十五分。
第十页,编辑于星期二:十一点 五十五分。
第十一页,编辑于星期二:十一点 五十五分。
第十二页,编辑于星期二:十一点 五十五分。
第十三页,编辑于星期二:十一点 五十五分。
第十四页,编辑于星期二:十一点 五十五分。
第十五页,编辑于星期二:十一点 五十五分。
第十六页,编辑于星期二:十一点 五十五分。
第十七页,编辑于星期二:十一点 五十五分。
第十八页,编辑于星期二:十一点 五十五分。
第十九页,编辑于星期二:十一点 五十五分。
第二十页,编辑于星期二:十一点 五十五分。
第二十一页,编辑于星期二:十一点 五十五分。
第二十二页,编辑于星期二:十一点 五十五分。
第一页,编辑于星期二:十一点 五十五分。
第二页,编辑于星期二:十一点 五十五分。
第三页,编辑于星期二:十一点 五十五分。
第四页,编辑于星期二:十一点 五十五分。
第五页,编辑于星期二:十一点 五十五分。
第六页,编辑于星期二:十一点 五十五分。
第七页,编辑于星期二:十一点 五十五分。
第八页,编辑于星期二:十一点 五十五分。
热力学与统计物理第三章
P.6/55
单元系的相变
等温等容系统处在稳定平衡状态 的必要和充分条件为
G 0
将G作泰勒展开,准确到二级,有
F 0
将F作泰勒展开,准确到二级,有
1 2 G G G 2
由 G 0 和 2 G 0 可以确定平衡 条件和平衡的稳定性条件。
1 2 F F F 2
泰勒展开,准确到二级有:
1 1 p p s U V 0 T T0 T T0 由于U和V 可独立变化,所以上
式成立,必有平衡条件:
1 S S 2 S 2 1 2 S 0 S 0 S 0 2
2013-7-31
T T0 ,
p p0
意义:达到平衡时,子系统与媒质 具有相同的温度和压强。子系统是 任选的,所以达到平衡时整个系统 的温度和压强是均匀的。
P.9/55
s S S0
平衡时有:
1 2 S 2 S0 2
单元系的相变
2、平衡的稳定性条件 平衡的稳定性条件应满足:
2 S0 2 S
2 ①式近似为: s S 0 2
p 0 V T
讨论:系统处于稳定平衡时,由 于扰动偏离时,系统将自动回落 到平衡态。
根据泰勒展开公式: 2S 2 2 S 2 U U
2S 2 U V
2S 2 U V
2S 2 U V 2 V 0 V P.10/55
单元系的相变
2、平衡的稳定性条件 平衡的稳定性条件应满足:
通过导数变换将上式化为平方和:
s 0 T T0 ; p p0 2 s 2S 2S 0 ①
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
故而,由δS=0可以得到平衡条件,由δ2S<0可以得到 平衡的稳定性条件。
熵判据是基本的平衡判据,适用于孤立系统。 自由能判据和吉布斯函数判据 自由能判据:等温等容系统处在稳定平衡状态的必要 和充分条件为 ΔF > 0
将F作泰勒展开,准确到二级,有 1 F F 2 F 2 由δF=0和δ2F>0可以确定平衡条件和平衡的稳定性条件。
在平衡曲线上两相的化学势相等,两相可以以任意比 例共存。两相平衡是一种中性平衡。
当系统缓慢地从外界吸收或放出热量时,物质将由一
相转变到另一相而始终保持在平衡态,称为平衡相变。
单元系三相共存时,三相的温度、压强和化学势都必须相等,即 Tα = Tβ = Tγ = T , p α = p β = p γ = p
δS = 0
因为δUα、δVα、δnα是可以独立改变的,这要求 1 1 p p 0, 0, 0 T T T T T T 即
Tα = Tβ(热平衡条件)
pα = pβ(力学平衡条件)
μα =μβ(相变平衡条件)
上式指出,整个系统达到平衡时,两相的温度、压强和化 学势必须分别相等。
吉布斯函数是一个广延量,当物质的量发生变化时,吉布斯函 数也将发生变化。
对于开系,上式应推广为
dG = -SdT + Vdp +μdn 式中第三项代表由于物质的量改变dn所引起的吉布斯函数 的改变,而
称为化学势。
G n T , p
由于吉布斯函数是广延量,系统的吉布斯函数等于物
H和F分别是以S、p、n和T、V、n为独立变量的特性函数。
定义一个热力学函数 J = F -μn 称为巨热力势。
巨热力势的全微分为
dJ = -SdT - pdV - ndμ J是以T、V、μ为独立变量的特性函数。若已知J(T,V,μ) ,
则其它热力学量有
J J J S , p , n T V V , T , T ,V 由巨热力势定义知,其也可表为
δ2Ŝ ≈δ2S < 0
根据泰勒展开公式 2S 2S 2S 2 2 2 S 2 U 2 U V 2 V 0 U V U V 选T、V为独立变量,通过导数变换可将上式的二次型化 为平方和,而有 CV 1 p 2 2 2 S 2 T V 0 T T V T 如要求δ2S对于各种可能的虚变动都小于零,应有 p CV 0, 0 V T 介质 子系统 此式是平衡的稳定性条件。
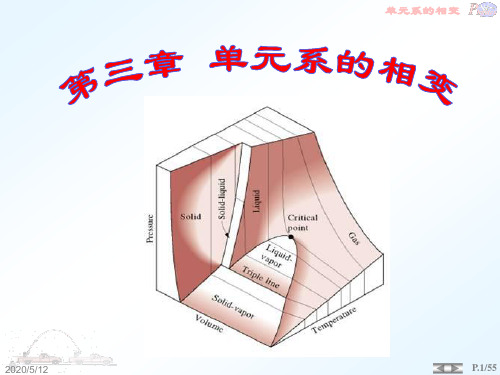
§3.5 临界点和气液两相的转变
实验等温线
Vmg Vm xVml (1 x)Vmg Vml
p
pc以上,气 液不分。
p T
G T 共存线退化为临界点。 c
L
C
pc L
C
Vml Vmg
p
V T 0
L+G G
Tc
气液共存线 随 T 增高变短。
T
Vml Vmc Vmg
Vm
临界点
在等温线上的极大点N,有 p 2 p 0 0, 2 Vm T Vm T 在极小点J,有 p 2 p 0 0, 2 Vm T Vm T 随着温度的升高,极大点与极小点逐渐靠近。达到临界温 度Tc时,两点重合而形成拐点。因此临界点的温度Tc和压 强pc满足
J
A D
0 = Vmdp
p0
p
J
p
R
B
积分等于图中等温线与 p轴之间由p0到p的面积。
K O
p
根据吉布斯函数判据,
在给定T、p下,稳定平衡态 的吉布斯函数最小。因此线
J K O
D N M A B
R
段OKBAMR上各点代表系统
的稳定平衡状态。
p
物质在B点全部处于气态,在A点全部处于液态。 B点和A点的μ值相等,正是在等温线的温度和A、B 两点的压强下气、液两相的相平衡条件。由
当物质熔解、蒸发或升华时,通常比体积增大,且相 变潜热是正的(混乱度增加,因而比熵增加),因此平衡 曲线的斜率dp/dT通常是正的。 在某些情形下,熔解曲线具有负的斜率。例如冰熔解 时比体积变小,因而平衡曲线的斜率dp/dT是负的。
p
C
T
由克拉珀龙方程可以推导蒸气压方程。
与凝聚相(固相或液相)达到平衡的蒸气称为饱和蒸气。
质的量n与摩尔吉布斯函数Gm(T,p)之积
G(T,p,n) = nGm(T,p) 因此
G Gm n T , p
即是说,化学势μ等于摩尔吉布斯函数。 由上面开系吉布斯函数的全微分可知,G是以T、p、n 为独立变量的特性函数。若已知G(T,p,n) ,则 G G G S , , V T p n p ,n T , p T ,n
第三章 单元系的相变
§3.1 热动平衡判据
熵判据
熵增加原理指出,孤立系统的熵永不减少。
熵判据:孤立系统处在稳定平衡状态的必要和充分条 件为 ΔS < 0 将S作泰勒展开,准确到二级,有 1 2 S S S 2 当δS=0时,熵函数有极值;当δS=0,δ2S<0时,熵函数有
极大值。
T = T0, p = p0 此式表明,达到平衡时子系统和介质具有相同的温度和压
强。
由于子系统是整个系统中任意的一个小部分,所以达 到平衡时整个系统的温度和压强是均匀的。
如果熵函数的二级微分是负的,即
δ2Ŝ =δ2S +δ2S0 < 0
则熵函数将具有极大值。
由于介质比子系统大得多(n0>>n),故有|δ2S0|<< |δ2S0|。因此可以忽略δ2S0 ,
μα(T,p) =μβ(T,p) =μγ(T,p)
上式给出三相点的温度与压强。
若已知两相化学势的表达式,由μα(T,p) =μβ(T,p)即可 确定相图的两相平衡曲线。但实际上平衡曲线是由实验直 接测定的。
克拉珀龙方程
设(T,p)和(T+dT,p+dp)是 两相平衡曲线上邻近的两点。
p
两点上,两相的化学势相等,
函数的极值要求
δŜ =δS +δS0 = 0
根据热力学基本方程 U 0 p0 V0 U p V S , S0 T T0
可得
1 1 p p0 ˆ S U V 0 T T0 T T0 因为在虚变动中δU和δV可以独立地改变,δŜ=0 要求
根据吉布斯函数的全微分和内能与吉布斯函数的关系, 易求得开系内能的全微分
dU = TdS - pdV +μdn
此式是开系的热力学基本方程。易知,U是以S、V、n为 独立变量的特性函数。
同理可求得开系的焓和自由能的全微分 dH = TdS + Vdp +μdn dF = -SdT - pdV +μdn
μA=μB
可以看出,这相当于积分
BNDJA
Vmdp 0
或
面积(BND) = 面积( DJA) 此式说明,A、B两点在图中的位置
可以由此式确定,称为麦克斯韦等
面积法则。 根据等面积法则,将范氏气体等温线中的BNDJA段换 为直线BA就与实测等温线相符了。
如前,线段JDN上的状态不满足平衡稳定性的要求,物质不可能 作为均匀系存在而必将发生相变。 线段BN和AJ上的状态满足平衡稳定性的要求。由于其化学势高 于两相平衡的化学势,它们可以作为亚稳态单相存在,分别相应于过 饱和蒸气和过热液体。
吉布斯函数判据:等温等压系统处在稳定平衡状态的 必要和充分条件为
ΔG > 0
将G作泰勒展开,准确到二级,有 1 2 G G G 2 由δG=0和δ2G>0可以确定平衡条件和平衡的稳定性条件。
均匀系统的热动平衡 设子系统发生一虚变动,其内能 和体积变化分别为δU和δV。
子系统 T,p 介质 T0, p0
二氧化碳等温线(安住斯 1869)
范氏气体等温线
a p 2 Vm b RT Vm
麦克斯韦等面积法则
化学势的全微分为 dμ= - SmdT + Vmdp
Vm
O
K G B D G+L N M N A M L R
可知,等温线上压强为
p与p0的两个状态的化学 势之差为
或
Sm dp Sm dT Vm Vm
以L表示1mol物质由α相转变到β相时所吸收的相变潜热, 因为相变时物质的温度不变,得 L = T(Smβ - Smα)
代入上式得
dp L dT T Vm Vm 此式称为克拉珀龙方程。
克拉珀龙方程给出两相平衡曲线的斜率,与实验结果 符合得很好。
如果平衡稳定性条件得到满足,当系统对平衡发生某 种偏离时,系统中将自发产生相应的过程,以恢复平衡。
平衡稳定性条件既适用于均匀系统的任何部分,也适
用于整个均匀系统。
§3.2 开系的热力学基本方程
回顾:单元系、复相系与开系
吉布斯函数的全微分
dG = -SdT + Vdp
适用于物质的量不发生变化的情况。
由于两相平衡时压强与温度间存在一定的关系,饱和
蒸气的压强是温度的函数。
凝聚相的摩尔体积远小于气相的摩尔体积,如果在克 拉珀龙方程中将其Vmα略去,并把气体看作理想气体pVmβ
=RT,则克拉珀龙方程可简化为 1 dp L p dT RT 2 若进一步认为相变潜热与温度无关,则上式积分可得 L ln p A RT 此式是蒸气压方程的近似表达式。
