初中数学经典试题
数学初中经典试题及答案

数学初中经典试题及答案一、选择题1. 下列哪个选项是方程x^2 - 5x + 6 = 0的解?A. x = 2B. x = 3C. x = 1D. x = 4答案:A2. 如果一个三角形的两边长分别为3和4,且这两边夹角的余弦值为1/2,那么第三边的长度是多少?A. √7B. √13C. √15D. √21答案:C3. 一个数的立方根是它自身的数是?A. 0B. 1C. -1D. 以上都是答案:D二、填空题4. 一个圆的直径是10厘米,那么它的半径是______厘米。
答案:55. 一个长方体的长、宽、高分别为2米、3米、4米,那么它的体积是______立方米。
答案:24三、解答题6. 已知一个等差数列的前三项分别为2,5,8,求这个数列的第10项。
答案:第10项为27。
7. 一个矩形的长是宽的两倍,如果长增加4厘米,宽增加1厘米,那么面积增加24平方厘米,求原来矩形的长和宽。
答案:原来矩形的长为8厘米,宽为4厘米。
四、证明题8. 证明:如果一个三角形的两边相等,那么这两边所对的角也相等。
答案:设三角形ABC中,AB=AC,根据等边对等角的性质,可以得出∠B=∠C,从而证明命题成立。
五、应用题9. 一个农场主有一块矩形的土地,长是宽的3倍,如果长增加20米,宽增加10米,那么面积增加600平方米。
求原来矩形土地的长和宽。
答案:原来矩形土地的长为90米,宽为30米。
10. 一个班级有40名学生,其中男生人数是女生人数的1.5倍。
求男生和女生各有多少人。
答案:男生有24人,女生有16人。
初中数学经典试题及答案

初中数学经典试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是偶数?A. 3B. 5C. 8D. 72. 如果一个数的相反数是它本身,那么这个数是:A. 0B. 1C. -1D. 23. 一个数的绝对值是它本身,那么这个数是:A. 正数B. 负数C. 非负数D. 非正数4. 计算下列算式的结果:(2x - 3) + (3x + 4) =A. 5x + 1B. 5x - 1C. 2x + 1D. 2x - 15. 下列哪个选项是方程的解?A. x + 2 = 5,x = 3B. x - 2 = 5,x = 3C. 2x + 3 = 7,x = 2D. 3x - 4 = 5,x = 36. 一个三角形的三个内角之和是:A. 90°B. 180°C. 360°D. 270°7. 一个圆的直径是10厘米,那么它的半径是:A. 5厘米B. 10厘米C. 20厘米D. 15厘米8. 下列哪个选项是不等式的解集?A. x > 5B. x < 5C. x = 5D. x ≠ 59. 一个数的立方是它本身,那么这个数是:A. 0B. 1C. -1D. 以上都是10. 一个数的平方等于它本身,那么这个数是:A. 0B. 1C. -1D. 以上都是二、填空题(每题4分,共20分)11. 一个数的平方根是它本身,那么这个数可以是______。
12. 如果一个数的绝对值是5,那么这个数可以是______。
13. 一个数的倒数是它本身,那么这个数是______。
14. 一个数的相反数是它本身,那么这个数是______。
15. 一个数的立方等于它本身,那么这个数可以是______。
三、解答题(每题5分,共50分)16. 解方程:2x - 5 = 9。
17. 计算:(3x + 2)(2x - 3)。
18. 证明:在一个直角三角形中,斜边的平方等于两直角边的平方和。
初中数学试题库及答案

初中数学试题库及答案一、选择题1. 下列哪个选项是偶数?A. 1B. 2C. 3D. 4答案:D2. 如果一个数的平方等于16,这个数可能是:A. 4B. -4C. 4或-4D. 都不是答案:C3. 一个三角形的内角和等于:A. 180°B. 360°C. 90°D. 120°答案:A二、填空题4. 一个数的绝对值是其本身或其相反数,例如,数______的绝对值是5。
答案:5或-55. 一个圆的周长是其直径的______倍。
答案:π6. 如果一个角是直角的一半,那么这个角是______度。
答案:45三、计算题7. 计算下列表达式的值:(1) (-2) × (-3)(2) √16答案:(1) 6(2) 48. 解方程:(1) 3x + 5 = 14(2) 2y - 1 = 5答案:(1) x = 3(2) y = 3四、解答题9. 一个长方体的长、宽、高分别是8cm、6cm和5cm,求其体积。
答案:长方体的体积为240立方厘米。
10. 若一个直角三角形的两条直角边分别为3cm和4cm,求斜边的长度。
答案:根据勾股定理,斜边的长度为5cm。
五、证明题11. 证明:等腰三角形的两底角相等。
答案:设等腰三角形ABC,其中AB=AC,根据等边对等角原理,∠B=∠C,因此等腰三角形的两底角相等。
六、应用题12. 一个农场有鸡和鸭共150只,鸡的数量是鸭的两倍,问鸡和鸭各有多少只?答案:设鸭的数量为x,则鸡的数量为2x。
根据题意,x + 2x = 150,解得x = 50,所以鸭有50只,鸡有100只。
七、综合题13. 某班有学生50人,其中参加数学竞赛的有20人,参加物理竞赛的有15人,同时参加数学和物理竞赛的有5人。
求只参加数学竞赛的学生人数。
答案:只参加数学竞赛的学生人数为20 - 5 = 15人。
注意:以上试题及答案仅供参考,实际考试内容和形式可能会有所不同。
数学初中经典试题及答案

数学初中经典试题及答案一、选择题(每题3分,共30分)1. 已知一个数的平方等于36,这个数可能是:A. 6B. -6C. 6或-6D. 以上都不是2. 一个三角形的两边长分别为3和5,第三边长为:A. 2B. 4C. 6D. 83. 计算下列表达式的值:\((-3) \times (-2)\)A. 6B. -6C. 3D. -34. 一个圆的半径为5厘米,那么它的面积是:A. 78.5平方厘米B. 25平方厘米C. 78.5平方分米D. 25平方分米5. 以下哪个是等腰三角形?A. 三边长分别为3, 4, 5B. 三边长分别为5, 5, 5C. 三边长分别为2, 3, 4D. 三边长分别为1, 2, 36. 一个数的绝对值是5,这个数可能是:A. 5B. -5C. 5或-5D. 以上都不是7. 计算下列表达式的值:\((-2)^2\)A. 4B. -4C. 2D. -28. 一个直角三角形的两条直角边长分别为6和8,那么斜边长为:A. 10B. 14C. 16D. 209. 一个数的立方等于-64,这个数是:A. 4B. -4C. 2D. -210. 计算下列表达式的值:\((-1)^3\)A. 1B. -1C. 3D. -3二、填空题(每题2分,共20分)1. 一个数的相反数是-7,这个数是________。
2. 一个数的倒数是\(\frac{1}{3}\),这个数是________。
3. 一个数的平方根是4,这个数是________。
4. 一个数的立方根是2,这个数是________。
5. 一个等差数列的首项是2,公差是3,那么第5项是________。
6. 一个等比数列的首项是3,公比是2,那么第3项是________。
7. 一个直角三角形的斜边长是10,一个直角边长是6,那么另一个直角边长是________。
8. 一个圆的直径是10厘米,那么它的周长是________厘米。
9. 一个数的绝对值是8,这个数是________或________。
初中数学试题及答案

初中数学试题及答案一、选择题1. 若 a + b = 5,a - b = 3,则 a 的值为多少?A) 2B) 3C) 4D) 5答案:C) 42. 下列哪个数是无理数?A) 1.5B) 2.0C) √3D) 0.75答案:C) √33. 已知两个正整数的和为100,差为20,这两个整数分别是多少?A) 40、60B) 30、70C) 45、55D) 50、50答案:C) 45、55二、填空题1. √(0.16) 的值是 _______。
答案:0.42. 三个数的平均数是45,其中两个数分别为30和40,第三个数是____________。
答案:603. 单位价格是3.5元/公斤的苹果,小明买了 2.5 公斤,需要支付_______ 元。
答案:8.75三、解答题1. 求解方程 3x + 2 = 14。
解答:将方程两边减去2,得到 3x = 12。
再将方程两边除以3,得到 x = 4。
所以,方程的解为 x = 4。
2. 计算 (2.5 + 7) × 3 - 4.5。
解答:首先,计算括号内的加法运算得到 2.5 + 7 = 9.5。
然后,乘法运算 (9.5) × 3 = 28.5。
最后,减法运算 28.5 - 4.5 = 24。
所以,计算结果为 24。
四、应用题1. 甲乙两人共有的钱数是320元,甲比乙多30元。
他们各自有多少钱?解答:设甲有 x 元,乙有 (x - 30) 元。
根据题意,可以得到方程 x + (x - 30) = 320。
合并同类项,得到 2x - 30 = 320。
将方程两边加上30,得到 2x = 350。
最后,将方程两边除以2,得到 x = 175。
所以,甲有 175 元,乙有 (175 - 30) = 145 元。
2. 小明去超市买了一些水果,苹果每斤4元,梨子每斤3元。
他一共买了6斤水果,总共支付了21元。
苹果和梨子各买了多少斤?解答:设买的苹果重量为 x 公斤,梨子重量为 y 公斤。
初中数学各章试题及答案

初中数学各章试题及答案一、选择题(每题2分,共10分)1. 下列哪个选项是正数?A. -3B. 0C. 5D. -1答案:C2. 以下哪个图形是轴对称图形?A. 平行四边形B. 矩形C. 梯形D. 非等腰三角形答案:B3. 计算 \(3x + 5 = 14\) 的解,正确的是?A. \(x = 3\)B. \(x = 1\)C. \(x = 4\)D. \(x = 2\)答案:A4. 一个圆的半径是5厘米,那么它的面积是多少平方厘米?A. 78.5B. 25πC. 100πD. 50π答案:C5. 以下哪个是二次方程?A. \(x + 2 = 0\)B. \(x^2 + 2x + 1 = 0\)C. \(x^2 - 4x + 4 = 0\)D. \(x^3 - 2x^2 + 3 = 0\)答案:B二、填空题(每题3分,共15分)6. 一个数的相反数是-7,这个数是______。
答案:77. 计算 \((2x - 3) + (x + 4)\) 的结果,合并同类项后得到______。
答案:3x + 18. 一个等腰三角形的底角是45°,那么顶角的度数是______。
答案:90°9. 已知一个长方体的长、宽、高分别是5cm、3cm、2cm,那么它的体积是______立方厘米。
答案:3010. 一个数的平方根是4,那么这个数是______。
答案:16三、解答题(每题10分,共20分)11. 解方程 \(2x - 3 = 7\),并说明解法。
答案:首先移项,得到 \(2x = 7 + 3\),即 \(2x = 10\),然后两边同时除以2,得到 \(x = 5\)。
12. 证明三角形内角和为180°。
答案:设三角形的三个内角分别为A、B、C。
根据三角形的外角定理,一个外角等于两个不相邻内角的和。
因此,角A的外角等于角B加角C。
同理,角B的外角等于角A加角C,角C的外角等于角A加角B。
初中数学试题及答案题库

初中数学试题及答案题库一、选择题1. 下列哪个选项是最小的正整数?A. 0B. 1C. 2D. 3答案:B2. 一个数的平方根是它本身的数有几个?A. 0个B. 1个C. 2个D. 3个答案:C3. 如果一个角的度数是30°,那么它的余角是多少度?A. 30°B. 45°C. 60°D. 90°答案:C二、填空题4. 圆的周长公式是______。
答案:C = 2πr5. 一个数的立方根是它本身,这个数可以是______。
答案:1,-1,06. 一个直角三角形的两条直角边分别为3和4,斜边的长度是______。
答案:5三、计算题7. 计算下列表达式的值:(1) (-3) × (-2)(2) √(16)答案:(1) 6(2) 48. 求下列方程的解:(1) 2x + 5 = 11(2) 3x - 7 = 8x + 2答案:(1) x = 3(2) x = -1四、解答题9. 已知一个长方体的长、宽、高分别为a、b、c,求它的体积。
答案:体积V = a × b × c10. 某工厂生产一批零件,合格率为95%,如果生产了1000个零件,求不合格的零件数。
答案:不合格的零件数= 1000 × (1 - 0.95) = 50五、证明题11. 证明三角形内角和为180°。
答案:根据三角形内角和定理,任意三角形的三个内角之和等于180°。
六、应用题12. 某班级有50名学生,其中30名男生和20名女生。
如果随机抽取一名学生,求抽到男生的概率。
答案:抽到男生的概率 P(男生) = 30/50 = 0.6七、开放性问题13. 请列举5个生活中应用到初中数学知识的例子。
答案:(答案不唯一,以下为示例)(1) 计算购物时的折扣和最终价格。
(2) 确定房间的面积和周长。
(3) 计算平均成绩。
(4) 解决速度、时间和距离的问题。
初中数学经典难题精选

数 学 试 题一、选择题1、若一次函数y=kx+1与两坐标轴围成的三角形面积为3,则k 为( ) A 、16 B 、-16 C 、±16 D 、±132、若11m n -=3,2322m mn nm mn n+---的值是( ) A 、1.5 B 、35 C 、-2 D 、-753、判断下列真命题有( )①任意两个全等三角形可拼成平行四边形;②两条对角线垂直且相等的四边形是正方形;③四边形ABCD ,AB=BC=CD ,∠A=90°,那么它是正方形;④在同一平面内,两条线段不相交就会平行;⑤有一条对角线平分一个内角的平行四边形是菱形 A 、②③ B 、①②④ C 、①⑤ D 、②③④4、如图,矩形ABCD 中,已知AB=5,AD=12,P 是AD 上的动点,PE ⊥AC ,E,PF ⊥BD 于F, 则PE+PF=( )A 、5B 、6013C 、245D 、55125、在直角坐标系中,已知两点A (-8,3)、B (-4,5)以及动点C (0,n )、D(m,0),则当四边形ABCD 的周长最小时,比值为 mn( )A 、-23B 、-32C 、-34D 、34二、填空题 6、当x= 时,||3x x -与3x x-互为倒数。
9、已知x 2-3x+1=0,求(x-1x )2=7、一个人要翻过两座山到另外一个村庄,途中的道路不是上山就是下山,已知他上山的速度为v ,下山的速度为v ′,单程的路程为s .则这个人往返这个村庄的平均速度为 8、将点A (4,0)绕着原点O 顺时针方向旋转30°角到对应点A ',则点A '的坐标是9、菱形ABCD 的一条对角线长为6,边AB 的长是方程(X-3)(X-4)=0的解,则菱形ABCD 的周长为 10、△ABC 中,∠A=90°,AB=AC ,BD 是△ABC 的中线,△CDB 内以CD 为边的等腰直角三角形周长是 11. 如图,边长为6的菱形ABCD 中,∠DAB=60°,AE=AB ,F 是AC•上一动点,EF+BF 的最小值为 12、如图,边长为3的正方形ABCD 顺时针旋转30°,得上图,交DE 于D ’,阴影部分面积是11235 (112)31511211321④③②①10题 11题 12题 13题13、如图,已知四边形ABCD中,AC和BD相交于点O,且∠AOD=90°,若BC=2AD,AB=12,CD=9,四边形ABCD的周长是14、有这样一组数:1,1,2,3,5…,现以这组数据的数作为正方形边长的长度构造如下正方形;再分别从左到右取2个、3个、4个、5个正方形拼成如下矩形记为①、②、③、④.第⑩个矩形周长是15、如图,在直线y=-33x+1与x轴、y轴交于点A、B,以线段AB为直角边在第一象限内作等腰直角△ABC,∠BAC=90°,第二象限内有一点P(a,12),且△ABP的面积与△ABC的面积相等,则a=三、解答题16、如图,已知矩形ABCD,延长CB到E,使CE=CA,连结AE并取中点F,连结AE并取中点F,连结BF、DF,求证BF⊥DF。
初中数学-几何证明经典试题(含答案)

初中几何证明题经典题〔一〕1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO .求证:CD =GF .〔初二〕2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.〔初二〕3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.〔初二〕AP C D BA F G C EBO D D 2 C 2 B 2 A 2 D 1 C 1B 1C BD AA 14、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题〔二〕1、已知:△ABC 中,H 为垂心〔各边高线的交点〕,O为外心,且OM ⊥BC 于M . 〔1〕求证:AH =2OM ;〔2〕假设∠BAC =600,求证:AH =AO .〔初二〕2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q .F3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q .AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.〔初二〕经典题〔三〕1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .〔初二〕3、设P 是正方形ABCD 一边BC 上的任一点,PF⊥AP ,CF 平分∠DCE .4、如图,PC切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .〔初三〕D经典题〔四〕1、已知:△ABC是正三角形,P是三角形内一点,PA=3,PB=4,PC=5.求:∠APB的度数.〔初二〕2、设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.〔初二〕3、设ABCD为圆内接凸四边形,求证:AB·CD+AD·BC=AC·BD.〔初三〕4、平行四边形ABCD中,设E、F分别是BC、AB上的一点,AE与CF相交于P,且AE=CF.求证:∠DPA=∠DPC.〔初二〕经典难题〔五〕1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC , 求证:≤L <2.2ABCD 内的一点,求PA +PB +PC 的最小值. 3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长. 4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =30,∠EBA =200,求∠BED 的度数.APCB ACBPDED CBA ACBPD参考答案经典题〔一〕⊥AB,连接EO。
初中数学试题及答案

初中数学试题及答案一、选择题1. 下列哪个分数是最简分数?A. 2/4B. 3/6C. 5/10D. 3/5答案:D2. 已知一个长方形的长是12厘米,宽是8厘米,那么它的面积是多少平方厘米?A. 20B. 96C. 72D. 144答案:B3. 以下哪个选项是正确的等式?A. 2x + 3 = 5x - 1B. 4a - 6 = 2a + 2C. 3b + 4 = 7b - 2D. 5c - 3 = 2c + 1答案:C4. 一个三角形的三个内角分别是60度、60度和60度,这个三角形是什么类型的三角形?A. 直角三角形B. 等腰三角形C. 等边三角形D. 钝角三角形答案:C5. 一个圆的半径是7厘米,求这个圆的周长(使用π=3.14)。
A. 43.96厘米B. 28.26厘米C. 14.94厘米D. 7.14厘米答案:A二、填空题1. 一个数除以1/3等于乘以_______。
答案:32. 如果a + b = 10,a - b = 2,那么a的值是_______。
答案:63. 在数列3, 6, 12, 24, _______中填入适当的数字,使得数列是等比数列。
答案:484. 一个圆的直径是10厘米,那么它的半径是_______厘米。
答案:55. 一个长方体的长、宽、高分别是5厘米、3厘米和2厘米,求它的体积(单位:立方厘米)。
答案:30三、解答题1. 一辆汽车以每小时60公里的速度行驶,求它行驶4小时后所行驶的距离。
解答:距离 = 速度× 时间距离 = 60公里/小时× 4小时距离 = 240公里2. 一个班级有40名学生,其中25%的学生参加了数学竞赛。
求参加数学竞赛的学生人数。
解答:参加数学竞赛的学生人数 = 总学生人数× 百分比参加数学竞赛的学生人数= 40 × 25%参加数学竞赛的学生人数 = 10人3. 一个水果店有苹果和橘子共180个,苹果的数量是橘子的2倍。
初中数学经典试题100题
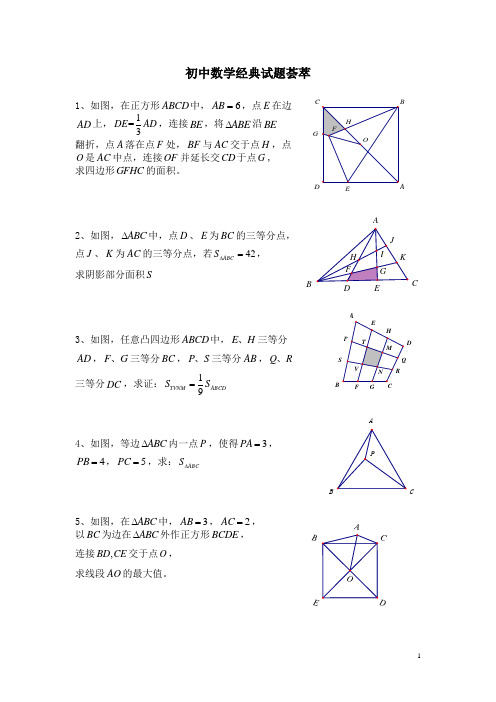
FG BDCBAGECDABCA初中数学经典试题荟萃1、如图,在正方形ABCD 中,6AB =,点E 在边AD 上,1=3DE AD ,连接BE ,将ABE ∆沿BE翻折,点A 落在点F 处,BF 与AC 交于点H ,点 O 是AC 中点,连接OF 并延长交CD 于点G , 求四边形GFHC 的面积。
2、如图,ABC ∆中,点D 、E 为BC 的三等分点, 点J 、K 为AC 的三等分点,若42ABC S ∆=, 求阴影部分面积S3、如图,任意凸四边形ABCD 中,E H 、三等分AD ,F G 、三等分BC ,P S 、三等分AB ,Q R 、 三等分DC ,求证:19TVNMABCD S S =4、如图,等边ABC ∆内一点P ,使得3PA =,4PB =,5PC =,求:ABC S ∆5、如图,在ABC ∆中,3AB =,2AC =, 以BC 为边在ABC ∆外作正方形BCDE , 连接,BD CE 交于点O , 求线段AO 的最大值。
D EFADEFABAB CDBAC6、如图,等边ABC ∆中,120BDC ∠=︒, DC GD =,AG 交CD 延长线于点E 。
求证:AE EG =7、如图,分别以锐角ABC ∆的三边为斜边 向外作等腰Rt DAB ∆、等腰Rt EBC ∆、 等腰Rt FAC ∆。
求证:①AE DF = ②AE DF ⊥8、如图,四边形ABCD 中,E F 、分别 是AB CD 、的中点,P 为对角线AC 延长线上任意一点,PF 交AD 于M ,PE 交BC 于N ,EF 交MN 于K ,求证:K 点平分线段MN9、如图,ABCD 中,E F 、分别是AB BC 、上 的点,DE 交AC 于M ,AF 交BD 于N ,若AF 平分BAC ∠,DE AF ⊥,DE 与AF 交于P ,记BE x OM =,BN y ON =,CF z BF =,试比较x y z 、、的大小关系。
初中数学-几何证明经典试题(含答案)
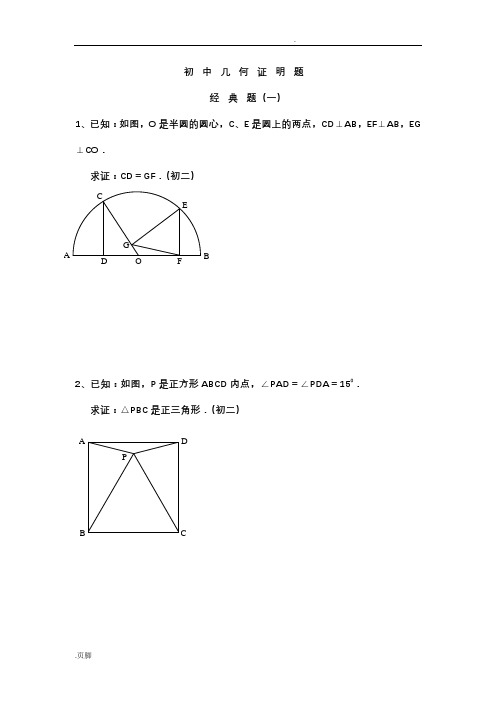
初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO .求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.(初二)AP C DB A F GC EB O D3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)D 2C 2 B 2 A 2D 1 C 1 B 1 C BD A A 14、已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.求证:∠DEN=∠F.经典题(二)1、已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OM⊥BC于M.(1)求证:AH=2OM;(2)若∠BAC=600,求证:AH=AO.(初二)2、设MN是圆O外一直线,过O作OA⊥MN于A,自A引圆的两条直线,交圆于B、C及D、E,直线EB及CD分别交MN于P、Q.F3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.(初二)经典题(三)1、如图,四边形ABCD为正方形,DE∥AC,AE=AC,AE与CD相交于F.2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF⊥AP ,CF 平分∠DCE . 求证:PA =PF .(初二)D4、如图,PC切圆O于C,AC为圆的直径,PEF为圆的割线,AE、AF与直线PO相交于B、D.求证:AB=DC,BC=AD.(初三)经典题(四)1、已知:△ABC是正三角形,P是三角形内一点,PA=3,PB=4,PC=5.求:∠APB的度数.(初二)2、设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.(初二)3、设ABCD为圆内接凸四边形,求证:AB·CD+AD·BC=AC·BD.(初三)4、平行四边形ABCD中,设E、F分别是BC、AB上的一点,AE与CF相交于P,且AE=CF.求证:∠DPA=∠DPC.(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC , 求证:≤L <2.1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.APCBACBP D A CBPD4中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠=200,求∠BED的度数.参考答案经典题(一)1.如下图做GH⊥AB,连接EO。
初中数学题库及答案试题

初中数学题库及答案试题一、选择题(每题2分,共10分)1. 下列哪个选项是正整数?A. -3B. 0C. 5D. 2.5答案:C2. 一个数的相反数是-8,这个数是:A. 8B. -8C. 16D. -16答案:A3. 计算下列哪个表达式的结果为0?A. 3 + 2B. 4 - 4C. 5 × 0D. 6 ÷ 3答案:C4. 一个数的平方是36,这个数是:A. 6B. -6C. 6或-6D. 36答案:C5. 一个三角形的三个内角之和是:A. 90°B. 180°C. 360°D. 720°答案:B二、填空题(每题2分,共10分)1. 一个数的绝对值是5,这个数可以是_______。
答案:±52. 一个数的立方是-27,这个数是_______。
答案:-33. 一个数的倒数是2,这个数是_______。
答案:1/24. 一个数的平方根是4,这个数是_______。
答案:16或-165. 一个数的立方根是3,这个数是_______。
答案:27三、解答题(每题10分,共20分)1. 计算下列表达式的值:(a) 2^3 + 5(b) (-2)^2 - 3答案:(a) 2^3 + 5 = 8 + 5 = 13(b) (-2)^2 - 3 = 4 - 3 = 12. 一个长方形的长是10cm,宽是5cm,求这个长方形的周长和面积。
答案:周长= 2 × (长 + 宽) = 2 × (10cm + 5cm) = 30cm面积 = 长× 宽= 10cm × 5cm = 50cm²四、应用题(每题15分,共30分)1. 一个班级有40名学生,其中20%的学生是优秀学生,求优秀学生的人数。
答案:优秀学生的人数= 40 × 20% = 40 × 0.2 = 8人2. 一个水池装满水需要3小时,放空水需要2小时。
初中数学考试题库及答案

初中数学考试题库及答案一、选择题(每题3分,共30分)1. 下列哪个数是无理数?A. 3.14B. √2C. 0.1010010001…D. 2/3答案:B2. 一个数的相反数是它本身的是:A. 0B. 1C. -1D. 2答案:A3. 一个等腰三角形的两个底角相等,如果一个底角是45°,那么顶角是:A. 90°B. 45°C. 60°D. 30°答案:A4. 一个数的立方等于它本身,这个数是:A. 0B. 1C. -1D. 以上都是答案:D5. 以下哪个选项是二次根式?A. √3B. √(-1)C. √(2/3)D. √(-2)答案:A6. 一个数的绝对值是它本身的数是:A. 正数B. 负数C. 0D. 以上都是答案:A7. 一个数的平方是9,这个数是:A. 3B. -3C. 3或-3D. 以上都不是答案:C8. 以下哪个是一次函数的表达式?A. y = 2x + 1B. y = x^2 + 1C. y = 1/xD. y = x^3答案:A9. 一个数的立方根是它本身的数是:A. 0B. 1C. -1D. 以上都是答案:D10. 以下哪个选项是二次方程的解?A. x = 2B. x = -2C. x = 1/2D. 以上都不是答案:A二、填空题(每题3分,共30分)1. 一个数的平方是16,这个数是______。
答案:±42. 如果一个三角形的两个内角分别是30°和60°,那么第三个内角是______。
答案:90°3. 一个数的绝对值是5,这个数是______。
答案:±54. 一个数的立方等于27,这个数是______。
答案:35. 一个数的平方根是2,这个数是______。
答案:46. 一个数的相反数是-7,这个数是______。
答案:77. 一个等腰三角形的顶角是120°,那么每个底角是______。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学经典题目
1、如图,梯形ABCD 中,AD ∥BC , 点E 在BC 上,AE =BE ,点F 是CD 的中点,且AF ⊥AB ,若AD =2.7,AF =4,AB =6,则CE 的长为
A .2 2
B .23-1
C .2.5
D
.2.3
2.如图,在矩形ABCD 中,BC=8,AB=6,经过点B 和点D 的两个动圆均与AC 相切,且与AB 、BC 、AD 、DC
分别交于点G 、H 、E 、F ,则EF+GH 的最小值是( )
A .6
B .8
C .9.6
D .10
3.如图,在Rt △ABC 中,∠ACB =90°,半径为1的圆A 与边AB 相交于点D ,与边AC 相交于点E ,
连结DE 并延长,与线段BC 的延长线交于点P 。
已知tan ∠BPD=
2
1
,CE=2,则⊿ABC 的周长是
4.如图,直角梯形纸片ABCD ,AD ⊥AB ,AB =8,AD =CD =4,点E 、F 分别在线段AB 、AD 上,将△AEF 沿EF 翻折,点A 的落点记为P .
(1)当AE =5,P 落在线段CD 上时,PD = ;
(2)当P 落在直角梯形ABCD 内部时,PD 的最小值等于 .
A G
B H
C F D
E
A B
C
D E
F
5、如图所示,在ABC ,AB=BC=50,AC=60,点P 在折线AB-BC 方向向点C 运动,是5,点Q 从C 向A 运动,速度为3,当PQC 为等腰三角形时,CQ 的长为
P B A
C
E
Q
6.如图,(1)将抛物线y 1=2x 2向右平移2个单位,得到抛物线y 2的图象,则y 2= ; (2)如图,P 是抛物线y 2对称轴上的一个动点,直线x =t 平行于y 轴,分别与直线y =x 、抛物线y 2交于点A 、B .若△ABP 是以点A 或点B 为直角顶点的等腰直角三角形,求满足条件的t 的值,则t = .
7、四边形ABCD 中,G 、H 分别是AD 、BC 的中点,AB=CD .BA 、CD 的延长线交HG 的延长线于E 、F 。
求证:∠BEH=∠CFH .
8、如图3所示,设BP 、CQ 是∆A B C
的内角平分线,AH 、AK 分别为A 到
BP 、CQ 的垂线。
求证:KH ∥BC
A
B
Q P H
C
K
P
y
x
y x =
2y
O
·
9.如图,直角坐标系中,已知两点(00)(20)O A ,,,,点B 在第一象限且OAB △为正三角形,OAB △的外接圆交y 轴的正半轴于点C ,过点C 的圆的切线交x 轴于点D .
(1)求B C ,两点的坐标; (2)求直线CD 的函数解析式;
(3)设E F ,分别是线段AB AD ,上的两个动点,且EF 平分四边形ABCD 的周长. 试探究:AEF △的最大面积?
10、如图,在平面直角坐标系xOy 中,△ABC 三个顶点的坐标分别为()6,0A -,()6,0B ,
()
0,43C ,延长AC 到点D,使CD=1
2
AC ,过点D 作DE ∥AB 交BC 的延长线于点E.
(1)求D 点的坐标;
(2)作C 点关于直线DE 的对称点F,分别连结DF 、EF ,若过B 点的直线y kx b =+将四边形CDFE 分成周长相等的两个四边形,确定此直线的解析式;
(3)设G 为y 轴上一点,点P 从直线y kx b =+与y 轴的交点出发,先沿y 轴到达G 点,再沿GA 到达A 点,若P 点在y 轴上运动的速度是它在直线GA 上运动速度的2倍,试确定G 点的位置,使P 点按照上述要求到达A 点所用的时间最短。
(要求:简述确定G 点位置的方法)。
