2021年北师大版高中数学选修21期末考试试题及答案(理科)
最新高二数学题库 北师大版高中数学选修21期末考试试题及答案(理科)

高二期末考试数学试题晁群彦一.选择题(每小题5分,满分60分)1.设n m l ,,均为直线,其中n m ,在平面”“”“,n l m l l a ⊥⊥⊥且是则内α的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件2.对于两个命题:①,1sin 1x R x ∀∈-≤≤, ②22,sin cos 1x R x x ∃∈+>,下列判断正确的是( )。
A. ① 假 ② 真B. ① 真 ② 假C. ① ② 都假D. ① ② 都真3.与椭圆1422=+y x 共焦点且过点(2,1)Q 的双曲线方程是( ) A. 1222=-y x B. 1422=-y x C. 1222=-y x D. 13322=-y x 4.已知12,F F 是椭圆的两个焦点,过1F 且与椭圆长轴垂直的弦交椭圆与A ,B 两点, 则2ABF ∆是正三角形,则椭圆的离心率是( )A2 B 12C D 135.过抛物线28y x =的焦点作倾斜角为045直线l ,直线l 与抛物线相交与A ,B 两点,则弦AB 的长是( )A 8B 16C 32D 646.在同一坐标系中,方程)0(0122222>>=+=+b a by ax x b x a 与的曲线大致是( )A .B .C .D .7.已知椭圆12222=+b y a x (b a >>0) 的两个焦点F 1,F 2,点P 在椭圆上,则12PF F ∆的面积 最大值一定是( )A 2a B ab C D 8.已知向量k -+-==2),2,0,1(),0,1,1(与且互相垂直,则实数k 的值是( )A .1B .51C . 53D .579.在正方体1111ABCD A B C D -中,E 是棱11A B 的中点,则1A B与1D E所成角的余弦值为( )A B C D 10.若椭圆x y n m ny mx -=>>=+1)0,0(122与直线交于A ,B 两点,过原点与线段AB 中点的连线的斜率为22,则m n的值是( )2.23.22.292. D C B A11.过抛物线y x 42=的焦点F 作直线交抛物线于()()222111,,,y x P y x P 两点,若621=+y y ,则21P P 的值为 ( )A .5B .6C .8D .1012.以12422y x -=1的焦点为顶点,顶点为焦点的椭圆方程为 ( )A.1121622=+y x B. 1161222=+y x C. 141622=+y x D. 二.填空题(每小题4分)13.已知A 、B 、C 三点不共线,对平面ABC 外一点O ,给出下列表达式:OCOB y OA x OM 31++=其中x ,y 是实数,若点M 与A 、B 、C 四点共面,则x+y=___14.斜率为1的直线经过抛物线y2=4x 的焦点,且与抛物线相交于A,B 两点,则AB等于___15.若命题P :“∀x >0,0222<--x ax ”是真命题 ,则实数a 的取值范围是___.16.已知90AOB ∠=︒,C 为空间中一点,且60AOC BOC ∠=∠=︒,则直线OC 与平面AOB 所成角的正弦值为___.C三.解答题(解答应写出必要的文字说明、证明过程和演算步骤。
【成才之路】2021学年高中数学 第一章综合素养检测 北师大版选修1-1(1)

第一章综合素养检测时刻120分钟,总分值150分。
一、选择题(本大题共10个小题,每题5分,共50分,在每题给出的四个选项中,只有一项为哪一项符合题目要求的)1.设a ∈R ,那么“a >1”是“1a<1”的( ) A .充分没必要要条件B .必要不充分条件C .充要条件D .既不充分也没必要要条件[答案] A[解析] a >1⇒1a <1,1a<1⇒/ a >1,应选A. 2.(2021·辽宁理,5)设a ,b ,c 是非零向量,已知命题p :假设a ·b =0,b ·c =0,那么a ·c =0;命题q :假设a ∥b ,b ∥c ,那么a ∥c ,那么以下命题中真命题是( )A .p 或qB .p 且qC .(¬p )且(¬q )D .p 或(¬q )[答案] A[解析] 取a =c =(1,0),b =(0,1)知,a ·b =0,b ·c =0,但a ·c ≠0,∴命题p 为假命题;∵a ∥b ,b ∥c ,∴∃λ,μ∈R ,使a =λb ,b =μc ,∴a =λμc ,∴a ∥c ,∴命题q 是真命题.∴p 或q 为真命题.3.有以下四个命题①“假设b =3,那么b 2=9”的逆命题;②“全等三角形的面积相等”的否命题;③“假设c ≤1,那么x 2+2x +c =0有实根”;④“假设A ∪B =A ,那么A ⊆B ”的逆否命题.其中真命题的个数是( )A .1B .2C .3D .4[答案] A [解析] “假设b =3,那么b 2=9”的逆命题:“假设b 2=9,那么b =3”,假;“全等三角形的面积相等”的否命题是:“不全等的三角形,面积不相等”,假;若c ≤1,那么方程x 2+2x +c =0中,Δ=4-4c =4(1-c )≥0,故方程有实根;“假设A ∪B =A ,那么A ⊆B ”为假,故其逆否命题为假.4.“假设a ⊥α,那么a 垂直于α内任一条直线”是( )A .全称命题B .特称命题C .不是命题D .假命题[答案] A[解析] 命题中含有全称量词,故为全称命题,且是真命题.5.已知实数a >1,命题p :函数y =log 12(x 2+2x +a )的概念域为R ,命题q :x 2<1是x <a 的充分没必要要条件,那么( )A .p 或q 为真命题B .p 且q 为假命题C .¬p 且q 为真命题D .¬p 或¬q 为真命题 [答案] A[解析] ∵a >1,∴Δ=4-4a <0,∴x 2+2x +a >0恒成立,∴p 为真命题;由x 2<1得-1<x <1,∴-1<x <1时,x <a 成立,但x <a 时,-1<x <1不必然成立,∴q 为真命题,从而A 正确.6.“B =60°”是“△ABC 三个内角A 、B 、C 成等差数列”的( )A .充分而没必要要条件B .充要条件C .必要而不充分条件D .既不充分也没必要要条件[答案] B[解析] 在△ABC 中,假设B =60°,那么A +C =120°,∴2B =A +C ,那么A 、B 、C 成等差数列;假设三个内角A 、B 、C 成等差,那么2B =A +C ,又A +B +C =180°,∴3B =180°,B =60°.7.“a =-1”是方程“a 2x 2+(a +2)y 2+2ax +a =0”表示圆的( )A .充分非必要条件B .必要非充分条件C .充要条件D .既非充分也非必要条件[答案] C[解析] 当a =-1时,方程为x 2+y 2-2x -1=0,即(x -1)2+y 2=2表示圆,若a 2x 2+(a +2)y 2+2ax +a =0表示圆,那么应知足⎩⎪⎨⎪⎧a 2=a +2≠02a 2-4a 3>0,解得a =-1,应选C. 8.假设集合A ={1,m 2},B ={2,4},那么“m =2”是“A ∩B ={4}”的( )A .充分没必要要条件B .必要不充分条件C .充要条件D .既不充分也没必要要条件[答案] A[解析] 由“m =2”可知A ={1,4},B ={2,4},因此能够推得A ∩B ={4},反之,若是“A ∩B ={4}”能够推得m 2=4,解得m =2或-2,不能推得m =2,因此“m =2”是“A ∩B ={4}”的充分没必要要条件.9.以下命题中的真命题是( )A .∃x ∈[0,π2],sin x +cos x ≥2B .∀x ∈⎝ ⎛⎭⎪⎫π2,π,tan x >sin x C .∃x ∈R ,x 2+x =-1D .∀x ∈R ,x 2+2x >4x -3[答案] D[解析] ∵对任意x ∈R ,有sin x +cos x =2sin(x +π4)≤2,∴A 假;∵x ∈(π2,π)时,tan x <0,sin x >0,∴B 假;∵x 2+x +1=(x +12)2+34>0,∴方程x 2+x =-1无解,∴C 假;∵x 2+2x -(4x -3)=x 2-2x +3=(x -1)2+2≥2,∴对任意x ∈R ,x 2+2x -(4x -3)>0恒成立,故D 真.10.以下命题错误的选项是( )A .命题“假设m >0,那么方程x 2+x -m =0有实根”的逆否命题为“假设方程x 2+x -m =0无实根,那么m ≤0”B .关于命题p :“∃x ∈R ,使得x 2+x +1<0”,那么¬p :“∀x ∈R ,均有x 2+x +1≥0”C .假设p 且q 为假命题,那么p 、q 均为假命题D .“x =1”是“x 2-3x +2=0”的充分没必要要条件[答案] C[解析] 若p 且q 为假命题,那么p 、q 均为假命题,或p 、q 一真一假,应选C.二、填空题(本大题共5个小题,每题5分,共25分,将正确答案填在题中横线上)11.命题“∀x ∈[-2,3],-1<x <3”的否定是________.[答案] ∃x ∈[-2,3],x ≤-1或x ≥3[解析] 全称命题的否定是特称命题,将“∀”改成“∃”,将“-1<x <3”改成“x ≤-1或x ≥3”.12.命题“∃x ∈(-1,1),2x +a =0”是真命题,那么a 的取值范围为________.[答案] (-2,2)[解析] 设f (x )=2x +a ,由题意得函数f (x )在(-1,1)内有零点,∴(a +2)(a -2)<0,∴-2<a <2.13.给出命题:“假设函数y =f (x )是幂函数,那么函数y =f (x )的图像只是第四象限”.在它的逆命题、否命题、逆否命题三个命题中,真命题的个数是________.[答案] 1[解析] 因为命题:“假设函数y =f (x )是幂函数,那么函数y =f (x )的图像只是第四象限”是真命题,其逆命题“假设函数y =f (x )的图像只是第四象限,那么函数y =f (x )是幂函数”是假命题,如函数y =x +1.再由互为逆否命题真假性相同知,在它的逆命题、否命题、逆否命题三个命题中,真命题的个数是1.14.在以下所示电路图中,闭合开关A是灯泡B亮的什么条件:(1)如图①所示,开关A闭合是灯泡B亮的______条件;(2)如图②所示,开关A闭合是灯泡B亮的______条件;(3)如图③所示,开关A闭合是灯泡B亮的______条件;(4)如图④所示,开关A闭合是灯泡B亮的______条件.[答案] 充分没必要要必要不充分充要既不充分也没必要要[解析] (1)A闭合,B亮;而B亮时,A不必然闭合,故A是B的充分没必要要条件.(2)A闭合,B不必然亮;而B亮,A必需闭合,故A是B的必要不充分条件.(3)A闭合,B亮;而B亮,A必闭合,因此A是B 的充要条件.(4)A闭合,B不必然亮;而B亮,A不必然闭合,因此A是B的既不充分也没必要要条件.15.给出以下四个命题:①∀x∈R,x2+2x>4x-3均成立;②假设log2x+log x2≥2,故x>1;③命题“假设a>b>0,且c<0,那么ca>cb”的逆否命题是真命题;④“a=1”是“直线x+y=0与直线x-ay=0相互垂直”的充分没必要要条件.其中正确的命题为________(只填正确命题的序号).[答案] ①②③[解析] ①中,x2+2x>4x-3⇔x2-2x+3>0⇔(x-1)2+2>0,故①正确.②中,显然x≠1且x>0,假设0<x<1,那么log2x<0,log x2<0,从而log2x+log x2<0,与已知矛盾,故x>1,故②正确③中,命题“假设a>b>0,且c<0,那么ca>cb”为真命题,故其逆否命题是真命题,∴③正确.④“a=1”是直线x+y=0与直线x-ay=0相互垂直的充要条件,故④不正确.三、解答题(本大题共6小题,共75分,前4题每题12分,20题13分,21题14分) 16.判定以下命题的真假:(1)∀x∈R,2x>0;(2)∀x∈Q,x2-3x-1是有理数;(3)∃x∈N,2x=x2;(4)∃x 、y ∈Z ,x 2+y 2=10.[答案] (1)(2)(3)(4)都是真命题[解析] (1)真命题,对任意的x,2x >0恒成立.(2)真命题,关于任意的有理数x ,x 2-3x -1都是有理数.(3)真命题,x =2,4时,2x =x 2成立.(4)真命题,x =1,y =3时,x 2+y 2=10成立.(1)(2)(3)(4)都是真命题.17.写出命题“假设x 2+7x -8=0,那么x =-8或x =1的逆命题、否命题、逆否命题,并别离判定它们的真假.”[答案] 逆命题:假设x =-8或x =1,那么x 2+7x -8=0.逆命题为真.否命题:假设x 2+7x -8≠0,那么x ≠-8且x ≠1.否命题为真.逆否命题:假设x ≠-8且x ≠1,那么x 2+7x -8≠0.逆否命题为真.18.判定以下命题是全称命题仍是特称命题,并判定其真假.(1)对数函数都是单调函数;(2)至少有一个整数,它既能被11整除,又能被9整除;(3)∀x ∈{x |x >0},x +1x≥2; (4)∃x 0∈Z ,log 2x 0>2.[答案] (1)(3)是全称命题,(2)(4)是特称命题,都是真命题[解析] (1)此题隐含了全称量词“所有的”,其实命题应为“所有的对数函数都是单调函数”,是全称命题,且为真命题.(2)命题中含有存在量词“至少有一个”,因此是特称命题,真命题.(3)命题中含有全称量词“∀”,是全称命题,真命题.(4)命题中含有存在量词“∃”,是特称命题,真命题.19.关于以下命题p ,写出¬p 的命题形式,并判定¬p 命题的真假:(1)p :91∈(A ∩B )(其中全集U =N *,A ={x |x 是质数},B ={x |x 是正奇数});(2)p :有一个素数是偶数;(3)p :任意正整数都是质数或合数;(4)p :一个三角形有且仅有一个外接圆.[答案] (1)(2)(4)¬p 为假命题 (3)¬p 为真命题[解析] (1)¬p :91∉A 或91∉B ;假命题.(2)¬p :所有素数都不是偶数;假命题.(3)¬p :存在一个正整数不是质数且不是合数;真命题.(4)¬p :存在一个三角形至少有两个外接圆或没有外接圆;假命题.20.已知p :|x -3|≤2,q :(x -m +1)(x -m -1)≤0,假设¬p 是¬q 的充分而没必要要条件,求实数m 的取值范围.[答案] [2,4][解析] 由题意p :-2≤x -3≤2,∴1≤x ≤5.∴¬p :x <1或x >5.q :m -1≤x ≤m +1,∴¬q :x <m -1或x >m +1.又∵¬p 是¬q 的充分而没必要要条件,∴⎩⎪⎨⎪⎧ m -1≥1m +1≤5,∴2≤m ≤4. 经查验m =2,m =4适合条件,即实数m 的取值范围为2≤m ≤4.∴m 的取值范围为[2,4].21.(2021·马鞍山二中期中)设命题p :f (x )=2x -m在区间(1,+∞)上是减函数;命题q :x 1,x 2是方程x 2-ax -2=0的两个实根,且不等式m 2+5m -3≥|x 1-x 2|对任意的实数a ∈[-1,1]恒成立,假设(¬p )且q 为真,试求实数m 的取值范围.[答案] m >1[解析] 对命题p :x -m ≠0,又x ∈(1,+∞),故m ≤1,对命题q :|x 1-x 2|=x 1+x 22-4x 1x 2=a 2+8对a ∈[-1,1]有a 2+8≤3, ∴m 2+5m -3≥3⇒m ≥1或m ≤-6. 假设(¬p )且q 为真,那么p 假q 真, ∴⎩⎪⎨⎪⎧ m >1,m ≥1或m ≤-6,∴m >1.。
(完整版)高中数学试题及答案

(完整版)高中数学试题及答案一、选择题1. 下列哪个数是实数?A. 2B. 3C. 4D. 52. 下列哪个图形是圆形?A. 正方形B. 长方形C. 三角形D. 圆形3. 下列哪个式子是等式?A. 2 + 3 = 5B. 2 + 3 = 6C. 2 + 3 = 7D. 2 + 3 = 84. 下列哪个图形是三角形?A. 正方形B. 长方形C. 三角形D. 圆形5. 下列哪个数是整数?B. 3.5C. 4.5D. 5.5二、填空题6. 2 + 3 = ________7. 3 × 4 = ________8. 5 2 = ________9. 6 ÷ 2 = ________10. 7 + 8 = ________三、解答题11. 解方程:2x + 3 = 712. 解方程:3x 2 = 513. 解方程:4x + 5 = 914. 解方程:5x 6 = 815. 解方程:6x + 7 = 10答案:一、选择题1. A2. D3. A4. C5. D二、填空题7. 128. 39. 310. 15三、解答题11. x = 212. x = 313. x = 114. x = 215. x = 1(完整版)高中数学试题及答案一、选择题1. 下列哪个数是实数?A. 2B. 3C. 4D. 52. 下列哪个图形是圆形?A. 正方形B. 长方形C. 三角形D. 圆形3. 下列哪个式子是等式?A. 2 + 3 = 5B. 2 + 3 = 6C. 2 + 3 = 7D. 2 + 3 = 84. 下列哪个图形是三角形?A. 正方形B. 长方形C. 三角形D. 圆形5. 下列哪个数是整数?A. 2.5B. 3.5C. 4.5D. 5.5二、填空题6. 2 + 3 = ________7. 3 × 4 = ________8. 5 2 = ________9. 6 ÷ 2 = ________10. 7 + 8 = ________三、解答题11. 解方程:2x + 3 = 712. 解方程:3x 2 = 513. 解方程:4x + 5 = 914. 解方程:5x 6 = 815. 解方程:6x + 7 = 10答案:一、选择题1. A2. D3. A4. C5. D二、填空题6. 57. 128. 39. 310. 15三、解答题11. x = 212. x = 313. x = 114. x = 215. x = 1四、应用题16. 小明有5个苹果,小红有3个苹果,他们一共有多少个苹果?答案:小明和小红一共有8个苹果。
北师大版高二数学选修21试卷及答案

北师大版高二数学选修21试卷及答案姓名:张平安一 选择题(本题共12个小题,每小题只有一个正确答案,每小题5分,共60分)1.x>2是24x >的 ( )A. 充分不必要条件B. 必要不充分条件C. 既充分又必要条件D. 既不充分又不必要条件2.命题“在ABC 中,若21sin =A ,则A=30º”的否命题是 ( )A.在ABC 中,若21sin =A ,则A≠30ºB. 在ABC 中,若1sin 2A ≠,则A=30ºC.在ABC 中,若1sin 2A ≠,则A≠30ºD .以上均不正确3.已知命题P :若a b ≥,则c>d ,命题Q :若e f ≤,则a b <。
若P 为真且Q的否命题为真,则“c d ≤”是“e f ≤的”( )A .充分条件B .必要条件C .充要条件D .既不充分也不必要条件4、在平行六面体ABCD-A 1B 1C 1D 1中,M 为AC 与BD 的交点,若11A B a =,b D A =11,c A A =1,则下列向量中与M B 1相等的向量是A 、c b a ++-2121B 、c b a ++2121 C 、 c b a +-2121 D 、 c b a +--2121 5、空间直角坐标系中,O 为坐标原点,已知两点A (3,1,0),B (-1,3,0),若点C 满足OC =αOA +βOB ,其中α,β∈R ,α+β=1,则点C 的轨迹为 A 、平面 B 、直线 C 、圆D 、线段6、已知a =(1,2,3),b =(3,0,-1),c =⎪⎭⎫⎝⎛--53,1,51给出下列等式:①∣c b a ++∣=∣c b a --∣ ②c b a ⋅+)( =)(c b a +⋅ ③2)(c b a ++=222c b a ++④c b a ⋅⋅)( =)(c b a ⋅⋅其中正确的个数是 A 、1个 B 、2个 C 、3个 D 、4个7.已知椭圆125222=+y ax )5(>a 的两个焦点为1F 、2F ,且8||21=F F ,弦AB过点1F ,则△2ABF 的周长为( ) (A )10 (B )20 (C )241(D ) 4148.椭圆13610022=+y x 上的点P 到它的左准线的距离是10,那么点P 到它的右焦点的距离是( )(A )15 (B )12 (C )10 (D )89.椭圆192522=+y x 的焦点1F 、2F ,P 为椭圆上的一点,已知21PF PF ⊥,则△21PF F 的面积为( )(A )9 (B )12 (C )10 (D )810.椭圆141622=+y x 上的点到直线022=-+y x 的最大距离是( )(A )3(B )11(C )22(D )1011.过抛物线2y ax =(a>0)的焦点F 作一直线交抛物线于P 、Q 两点,若线段PF 与FQ 的长分别为p 、q ,则11p q+等于( )(A )2a (B )12a (C )4a (D )4a12. 假如椭圆193622=+yx 的弦被点(4,2)平分,则这条弦所在的直线方程是( )(A )02=-y x (B )042=-+y x (C )01232=-+y x (D )082=-+y x 二.填空题(本大题共4个小题,每小题4分,共16分) 13、“末位数字是0或5的整数能被5整除”的 否定形式是 否命题是14.与椭圆22143x y +=具有相同的离心率且过点(2,3方程 。
2021人教版高中数学同步a版选修2-1(理科必考)模块练习题--第1课时椭圆的简单几何性质及其应用

2.2.2 椭圆的简单几何性质第1课时 椭圆的简单几何性质及其应用基础过关练题组一 椭圆的性质及应用1.焦点在x 轴上,右焦点到短轴端点的距离为2,到左顶点的距离为3的椭圆的标准方程是( )A.x 24+y 23=1B.x 24+y 2=1 C.y 24+x 23=1 D.x 2+y24=1 2.过椭圆x 24+y 23=1的焦点的最长弦和最短弦的长分别为()A.8,6B.4,3C.2,√3D.4,2√3 3.(2019陕西宝鸡高二上学期期末)把椭圆x 225+y 216=1的长轴AB 分成8等份,过每个分点作x 轴的垂线分别交椭圆的上半部分于点P 1,P 2,…,P 7,F 是左焦点,则|P 1F|+|P 2F|+…+|P 7F|等于( ) A.21 B.28 C.35 D.424.设AB 是椭圆的长轴,点C 在椭圆上,且∠CBA=π4,若AB=4,BC=√2,则椭圆的两个焦点之间的距离为 .题组二 与椭圆离心率有关的问题5.已知椭圆的两个焦点和短轴的两个端点恰好是一个正方形的四个顶点,则该椭圆的离心率为( ) A.13 B.12C.√33D.√226.已知焦点在y 轴上的椭圆mx 2+y 2=1的离心率为√32,则m 的值为( )A.1B.2C.3D.4 7.已知焦点在x轴上的椭圆方程为x 2a2+y 2=1(a>0),过焦点作垂直于x轴的直线交椭圆于A,B 两点,且|AB|=1,则该椭圆的离心率为( ) A.√32B.12C.√154D.√338.已知椭圆x 2a 2+y 2b2=1(a>b>0)的左焦点为F 1,右顶点为A,点B 在椭圆上,且BF 1⊥x 轴,直线AB 与y 轴交于点P,其中AP ⃗⃗⃗⃗⃗ =2PB ⃗⃗⃗⃗⃗ ,则椭圆的离心率为 .题组三 与椭圆有关的范围问题 9.若点O 和点F分别为椭圆x 24+y 23=1的中心和左焦点,点P 为椭圆上的任意一点,则OP ⃗⃗⃗⃗⃗ ·FP ⃗⃗⃗⃗⃗ 的最大值为( ) A.2 B.3 C.6 D.8 10.已知F 1,F 2是椭圆x 2a 2+y 2b2=1(a>b>0)的两个焦点,若椭圆上存在一点P,使得∠F 1PF 2=60°,则椭圆的离心率e 的取值范围是( ) A.[√22,1) B.(0,√22)C.[12,1) D.[12,√22) 11.已知点P 为椭圆x 2+2y 2=98上的一个动点,点A 的坐标为(0,5),则|PA|的最小值为 .12.已知椭圆C:x 2a 2+y 2b 2=1(a>b>0)的左、右焦点分别为F 1,F 2,离心率e=√22,连接椭圆的四个顶点所得四边形的面积为4√2. (1)求椭圆C 的标准方程;(2)设A,B 是直线l:x=2√2上的不同两点,若AF 1⃗⃗⃗⃗⃗⃗⃗ ·BF 2⃗⃗⃗⃗⃗⃗⃗ =0,求|AB|的最小值.能力提升练一、选择题1.(2019辽宁抚顺六校期末联考,★★☆)已知椭圆x 2+y 2b 2+1=1(b>0)的离心率为√1010,则b 等于( )A.3B.13C.910D.3√10102.(2019山西大同高三开学考试,★★☆)在平面直角坐标系xOy 中,椭圆C 的中心为原点,焦点F 1,F 2在x 轴上,离心率为√22,过F 1的直线l交C 于A,B 两点,且△ABF 2的周长为16,那么椭圆C 的方程为( )A.x 236+y 218=1B.x 216+y 210=1 C.x 24+y 22=1 D.x 216+y 28=1 3.(2020重庆沙坪坝高二期末,★★☆)已知F 是椭圆E:x 2a 2+y 2b2=1(a>b>0)的左焦点,经过原点的直线l 与椭圆E 交于P,Q 两点,若|PF|=2|QF|,且∠PFQ=120°,则椭圆E 的离心率为( ) A.√33 B.12C.13D.√224.(2019黑龙江大庆四中高二上学期期中,★★★)已知点P(x,y)(x≠0,y≠0)是椭圆x 216+y 28=1上的一个动点,F 1,F 2分别为椭圆的左、右焦点,O 是坐标原点,若M 是∠F 1PF 2的平分线上的一点,且F 1M ⃗⃗⃗⃗⃗⃗⃗⃗ ·PM ⃗⃗⃗⃗⃗⃗ =0,则|OM ⃗⃗⃗⃗⃗⃗ |的取值范围为( ) A.[0,3) B.(0,2√2) C.[2√2,3) D.[0,4]二、填空题5.(2019皖西南联盟高二期末联考,★★☆)阿基米德不仅是著名的物理学家,也是著名的数学家,他最早利用“逼近法”得到椭圆的面积除以圆周率等于椭圆的长半轴长与短半轴长的乘积.若椭圆C 的对称轴为坐标轴,焦点在y轴上,且椭圆C的离心率为35,面积为20π,则椭圆C的标准方程为.6.(2019河北石家庄二中高二月考,★★☆)已知椭圆x 2a2+y2b2=1(a>b>0),点P是椭圆上且在第一象限的点,F1,F2分别为椭圆的左、右焦点,O是坐标原点,过F2作∠F1PF2的外角的平分线的垂线,垂足为A,若|OA|=2b,则椭圆的离心率为.三、解答题7.(2019河北张家口高三开学考试,★★☆)设F1,F2分别是椭圆C:x 2a2+y2b2=1(a>b>0)的左、右焦点,M是C上且在第一象限内的一点,且MF2与x轴垂直,直线MF1与C的另一个交点为N.(1)若直线MN的斜率为34,求C的离心率;(2)若直线MN在y轴上的截距为2,且|MN|=5|F1N|,求a,b的值.8.(★★★)如图,F1,F2分别是椭圆C:x 2a2+y2b2=1(a>b>0)的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,AF1=F1F2.(1)求椭圆C的离心率;(2)已知△AF1B的面积为40√3,求a,b的值.答案全解全析 基础过关练1.A 依题意得a=2,a+c=3,故c=1,b=√22-12=√3,故所求椭圆的标准方程是x 24+y 23=1.2.B 过椭圆焦点的最长弦为长轴,其长度为4,最短弦为垂直于长轴的弦.易知c=1,将x=1代入x 24+y 23=1,得124+y 23=1,解得y 2=94,即y=±32,所以最短弦的长为2×32=3.故选B.3.C 设椭圆的右焦点为F',则由椭圆的定义得|P 1F|+|P 1F'|=10,由椭圆的对称性,知|P 1F'|=|P 7F|,∴|P 1F|+|P 7F|=10.同理,|P 2F|+|P 6F|=10,|P 3F|+|P 5F|=10.又|P 4F|=5,∴|P 1F|+|P 2F|+…+|P 7F|=35. 4.答案4√63解析 不妨设椭圆的标准方程为x 2a 2+y 2b 2=1(a>b>0),由题意知2a=4,∴a=2. ∵∠CBA=π4,BC=√2,∴不妨设点C 的坐标为(-1,1). ∵点C 在椭圆上,∴14+1b 2=1,∴b 2=43,∴c 2=a 2-b 2=4-43=83,c=2√63,则椭圆的两个焦点之间的距离为4√63. 5.D 依题意得椭圆的焦距和短轴长相等,故b=c,∴a 2-c 2=c 2,∴e=√22. 6.D 将椭圆的方程化为标准形式为y 2+x 21m=1,由题意得a 2=1,b 2=1m ,∴c 2=a 2-b 2=1-1m ,∴离心率e=ca =√1-1m =√32,∴m=4.7.A 易知椭圆的焦点坐标为(±√a 2-1,0),∵|AB|=1,∴当x=±√a 2-1时,y=±12.不妨设A (√a 2-1,12),则a 2-1a 2+14=1,解得a=2,∴椭圆的离心率为e=√a 2-1a=√32.故选A.8.答案 12解析 如图,易知△ABF 1∽△APO, 则|AP ||AB |=|AO ||AF 1|,即23=aa+c ,所以a=2c,所以e=c a =12.9.C 由题意得F(-1,0),设点P(x 0,y 0),则y 02=3(1-x 024)(-2≤x 0≤2),OP ⃗⃗⃗⃗⃗ ·FP ⃗⃗⃗⃗⃗ =x 0(x 0+1)+y 02=x 02+x 0+y 02=x 02+x 0+3(1-x 024)=14(x 0+2)2+2,当x 0=2时,OP⃗⃗⃗⃗⃗ ·FP ⃗⃗⃗⃗⃗ 取得最大值,最大值为6. 10. C 在△PF 1F 2中,设|PF 1|=m,|PF 2|=n,则m+n=2a,根据余弦定理,得(2c)2=m 2+n 2-2mncos 60°,整理得(m+n)2-3mn=4c 2,所以3mn=4a 2-4c 2, 所以4a 2-4c 2=3mn≤3(m+n 2)2=3a 2(当且仅当m=n 时,等号成立),即a 2≤4c 2,故e 2=c 2a 2≥14,又0<e<1, 所以12≤e<1.11.答案 2解析 设P(x,y),则|PA|=√x 2+(y -5)2=√x 2+y 2-10y +25. 因为点P 为椭圆x 2+2y 2=98上的一点,所以x 2=98-2y 2,-7≤y≤7,则|PA|=√98-2y 2+y 2-10y +25 =√-(y +5)2+148, 因为-7≤y≤7,所以当y=7时,|PA|min =2. 12.解析 (1)由题意得{ e =c a =√22,a 2=b 2+c 2,12×2a ×2b =4√2,解得{a =2,b =√2,c =√2.所以椭圆的标准方程为x 24+y 22=1.(2)由(1)知,F 1(-√2,0),F 2(√2,0),设直线l:x=2√2上的不同两点A,B 的坐标分别为(2√2,y 1),(2√2,y 2),则AF 1⃗⃗⃗⃗⃗⃗⃗ =(-3√2,-y 1),BF 2⃗⃗⃗⃗⃗⃗⃗ =(-√2,-y 2),由AF 1⃗⃗⃗⃗⃗⃗⃗ ·BF 2⃗⃗⃗⃗⃗⃗⃗ =0,得y 1y 2+6=0, 即y 2=-6y 1,不妨设y 1>0,则|AB|=|y 1-y 2|=y 1+6y 1≥2√6,当且仅当y 1=√6,y 2=-√6时等号成立,所以|AB|的最小值是2√6.能力提升练一、选择题1.B 易知b 2+1>1,由题意得(b 2+1)-1b 2+1=b 2b 2+1=110,解得b=13或b=-13(舍去),故选B.2.D 由△ABF 2的周长为16,得|BF 2|+|AF 2|+|BF 1|+|AF 1|=16,根据椭圆的性质,得4a=16,即a=4.又椭圆的离心率为√22,即c a =√22,所以c=2√2,b 2=a 2-c 2=8,则椭圆C 的方程为x 216+y 28=1.3.A 如图,设椭圆的右焦点为F',连接PF',QF',根据椭圆的对称性知,线段FF'与线段PQ 在点O 处互相平分,所以四边形PFQF'为平行四边形,∴|FQ|=|PF'|,∠FPF'=60°.根据椭圆的定义,得|PF|+|PF'|=2a,又|PF|=2|QF|,∴|PF'|=23a,|PF|=43a,而|FF'|=2c.在△F'PF 中,由余弦定理,得(2c)2=(23a)2+(43a)2-2×23a×43a×cos 60°,即c 2a2=13,∴椭圆的离心率e=c a =√33.4.B 如图,延长PF 2,F 1M 交于点N,则△PF 1N 为等腰三角形,M 为F 1N 的中点,|OM ⃗⃗⃗⃗⃗⃗ |=12|F 2N ⃗⃗⃗⃗⃗⃗⃗ |=12(|PN ⃗⃗⃗⃗⃗⃗ |-|PF 2⃗⃗⃗⃗⃗⃗⃗ |)=12·||PF 1⃗⃗⃗⃗⃗⃗⃗ |-|PF 2⃗⃗⃗⃗⃗⃗⃗ ||.由图可知,当P 在短轴端点时,|OM ⃗⃗⃗⃗⃗⃗ |取得最小值,此时|OM⃗⃗⃗⃗⃗⃗ |=0,当P 在长轴端点时,|OM ⃗⃗⃗⃗⃗⃗ |取得最大值,此时|OM ⃗⃗⃗⃗⃗⃗ |=2√2,但点P 不能在坐标轴上,所以|OM⃗⃗⃗⃗⃗⃗ |的取值范围为(0,2√2).二、填空题 5.答案y 225+x 216=1解析 设椭圆C 的标准方程为y 2a 2+x 2b 2=1(a>b>0),则椭圆C 的面积为S=πab=20π,又e=√1-b 2a 2=35,解得a 2=25,b 2=16.所以椭圆C 的标准方程为y 225+x 216=1.6.答案√32解析 如图,延长F 2A 交F 1P 的延长线于点M.由题意可知|PM|=|PF 2|,由椭圆的定义可知|PF 1|+|PF 2|=2a, 则|PF 1|+|PM|=|MF 1|=2a. 易知OA 是△F 1F 2M 的中位线, ∴|OA|=12|MF 1|=a. 又|OA|=2b,∴2b=a,则a 2=4b 2=4(a 2-c 2), 即c 2=34a 2,∴e 2=34,又e∈(0,1),∴e=√32.三、解答题 7.解析 (1)根据c=√a 2-b 2及题设知M (c ,b 2a ),由k MN =k MF 1=34,得b 2a-0c -(-c )=34,即2b 2=3ac.将b 2=a 2-c 2代入,得2c 2+3ac-2a 2=0,即2e 2+3e-2=0,解得e=12或e=-2(舍去).故C 的离心率为12.(2)由题意知,原点O 为F 1F 2的中点,MF 2∥y 轴,设直线MF 1与y 轴的交点为D,则D(0,2)是线段MF 1的中点,故b 2a =4,即b 2=4a.①由|MN|=5|F 1N|,得|DF 1|=2|F 1N|, 则F 1D ⃗⃗⃗⃗⃗⃗⃗ =2NF 1⃗⃗⃗⃗⃗⃗⃗ .设N(x 1,y 1),由题意知y 1<0,则{2(-c -x 1)=c ,-2y 1=2,即{x 1=-32c ,y 1=-1, 代入C 的方程,得9c 24a 2+1b 2=1.② 由①②及a 2=b 2+c 2得9(a 2-4a )4a 2+14a =1,解得a=7,则b=√4a =2√7. 8.解析 (1)∵AF 1=F 1F 2, ∴a=2c,∴e=c a =12.(2)设|BF 2|=m,则|BF 1|=2a-m.∵AF 1=F 1F 2=AF 2,∴△AF 1F 2是等边三角形, ∴∠F 1F 2B=180°-∠F 1F 2A=180°-60°=120°.在△BF 1F 2中,|BF 1|2=|BF 2|2+|F 1F 2|2-2|BF 2||F 1F 2|cos∠F 1F 2B,即(2a-m)2=m 2+a 2-2am×(-12), ∴m=35a. ∵△AF 1B 的面积S=12|BA||F 1A|sin 60° =12×(a +35a)×a×√32=40√3,∴a=10,∴c=5,b=5√3.。
2021学年高中数学第一章统计案例2.2_2.4学案北师大版选修1_2
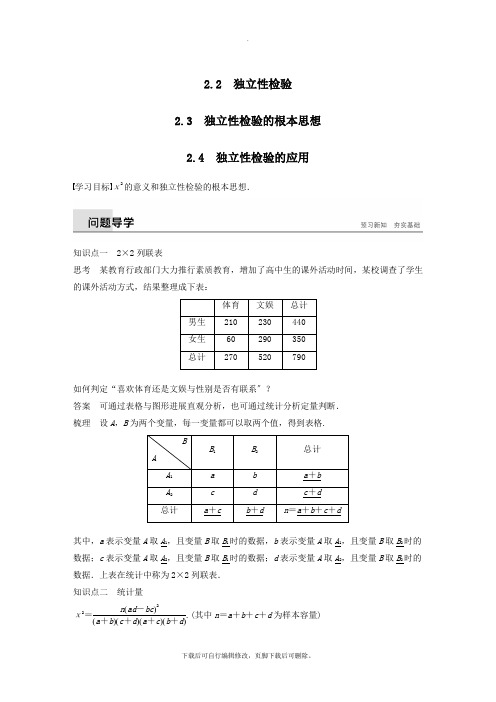
2.2 独立性检验2.3 独立性检验的根本思想2.4 独立性检验的应用学习目标χ2的意义和独立性检验的根本思想.知识点一2×2列联表思考某教育行政部门大力推行素质教育,增加了高中生的课外活动时间,某校调查了学生的课外活动方式,结果整理成下表:体育文娱总计男生210230440女生60290350总计270520790如何判定“喜欢体育还是文娱与性别是否有联系〞?答案可通过表格与图形进展直观分析,也可通过统计分析定量判断.梳理设A,B为两个变量,每一变量都可以取两个值,得到表格.BAB1B2总计A1 a b a+bA2 c d c+d总计a+c b+d n=a+b+c+d其中,a表示变量A取A1,且变量B取B1时的数据,b表示变量A取A1,且变量B取B2时的数据;c表示变量A取A2,且变量B取B1时的数据;d表示变量A取A2,且变量B取B2时的数据.上表在统计中称为2×2列联表.知识点二统计量χ2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d).(其中n=a+b+c+d为样本容量)知识点三独立性检验当χ2≤2.706时,没有充分的证据判定变量A,B有关联;当χ2>2.706时,有90%的把握判定变量A,B有关联;当χ2>3.841时,有95%的把握判定变量A,B有关联;当χ2>6.635时,有99%的把握判定变量A,B有关联.1.列联表中的数据是两个分类变量的频数.( √)2.事件A与B的独立性检验无关,即两个事件互不影响.( ×)3.χ2是判断事件A与B是否相关的统计量.( √)类型一2×2列联表及其应用例1 (1)两个变量X,Y,它们的取值分别为x1,x2和y1,y2,其列联表为:YXy1y2总计x1 a b a+bx2 c d c+d总计a+c b+d a+b+c+d假设两个变量X,Y独立,那么以下结论:①ad≈bc;②aa+b≈cc+d;③c+da+b+c+d≈b+da+b+c+d;④c+aa+b+c+d≈b+da+b+c+d;⑤(a+b+c+d)(ad-bc)(a+b)(b+d)(a+c)(c+d)≈0.共中正确的序号是________.(2)甲、乙两个班级进展一门考试,按照学生考试成绩优秀和不优秀统计成绩后,得到如以下联表:成绩优秀不优秀总计用频率估计的方法可判断成绩与班级________关.(填“有〞或“无〞) 考点 定性分析的两类方法 题点 利用列联表定性分析 答案 (1)①②⑤ (2)无 解析 (1)因为变量X ,Y 独立, 所以aa +b +c +d ≈a +c a +b +c +d ×a +ba +b +c +d,化简得ad ≈bc ,故①⑤正确;②式化简得ad ≈bc ,故②正确. (2)根据2×2列联表得频率表如下:由于1790×12=17180,而19=20180;7390×12=73180,而718=70180; 1790×12=17180,而790=14180; 7390×12=73180,而1945=76180. 这些频率之间相差不大,可以认为成绩是否优秀与班级没有关系.反思与感悟 (1)2×2列联表X ,Y 对应的数据是从总体中抽取样本的统计数据,所以即使X ,Y 独立,ad -bc 一般也不恰好等于零.(2)2×2列联表中,|ad -bc |越小,说明“X ,Y 独立〞正确的可能性越大;|ad -bc |越大,说明“X ,Y 有关联〞(即X ,Y 不独立)正确的可能性越大.跟踪训练1 在列联表中,相差越大,两个变量之间的关系越强的两个比值是( ) A.a a +b 与c c +d B.a c +d 与c a +b C.aa +d 与cb +cD.ab +d 与ca +c考点 定性分析的两类方法 题点 利用列联表定性分析 答案 A 解析aa +b 和cc +d相差越大,说明ad 与bc 相差越大,两个变量之间的关系越强.类型二 利用χ2公式判断两变量的关系例2 为研究时下的“韩剧热〞,对某班45位同学的爸爸、妈妈进展了问卷调查,结果如下表所示.喜欢韩剧 不喜欢韩剧总计 妈妈 31 13 44 爸爸 15 21 36 总计463480试问:是否有99%以上的把握认为“喜欢韩剧和性别有关系〞? 考点 独立性检验及其根本思想 题点 独立性检验的方法 解 由表中的数据,得χ2=80×(31×21-15×13)244×36×46×34≈6.715.因为6.715>6.635,所以有99%以上的把握认为喜欢韩剧和性别有关系. 反思与感悟 解独立性检验问题的根本步骤跟踪训练2 某研究小组调查了在2~3级风时的海上航行中男女乘客的晕船情况,共调查了71人,其中女性34人,男性37人.女性中有10人晕船,另外24人不晕船;男性中有12人晕船,另外25人不晕船.(1)根据以上数据建立2×2列联表; (2)判断晕船是否与性别有关系. 考点 独立性检验及其根本思想 题点 独立性检验的方法 解 (1)2×2列联表如下:晕船情况性别晕船 不晕船 总计 女 10 24 34 男 12 25 37 总计224971(2)χ2=71×(10×25-12×24)222×49×37×34≈0.08.因为0.08<2.706,所以我们没有理由说晕船与性别有关.1.变量X 和Y 的列联表如下,那么( )Y X y 1 y 2 总计x 1 a b a +b x 2c d c +d 总计a +cb +da +b +c +dA.ad -bc 越小,说明X 与Y 的关系越弱 B .ad -bc 越大,说明X 与Y 的关系越强 C .(ad -bc )2越大,说明X 与Y 的关系越强 D .(ad -bc )2越接近于0,说明X 与Y 的关系越强 考点 定性分析的两类方法 题点 利用列联表定性分析 答案 C解析 χ2=n (ad -bc )2(a +b )(c +d )(a +c )(b +d )(其中n =a +b +c +d ),假设(ad -bc )2越大,那么χ2越大,说明X 与Y 的关系越强.2.如果有95%的把握说事件A 与B 有关系,那么具体计算出的数据( ) A .χ2B .χ2C .χ2D .χ2考点 独立性检验及其根本思想 题点 独立性检验的方法 答案 A解析 把χ2的值与临界值比,从而确定A 与B 有关的可信程度. 当χ2>6.635时,有99%的把握认为A 与B 有关系; 当χ2>3.841时,有95%的把握认为A 与B 有关系; 当χ2>2.706时,有90%的握认为A 与B 有关系;当χ2≤2.706时,就没有充分的证据认为A 与B 有关系.应选A.3.在研究吸烟与患肺癌的关系中,通过收集数据、整理分析数据得到“吸烟与患肺癌有关系〞的结论,并且有99%以上的把握认为这个结论是成立的,那么以下说法中正确的选项是( ) A .100个吸烟者中至少有99人患有肺癌B .1个人吸烟,那么这个人有99%的概率患有肺癌C .在100个吸烟者中一定有患有肺癌的人D .在100个吸烟者中可能一个患肺癌的人也没有 考点 独立性检验及其根本思想 题点 独立性检验的思想 答案 D解析 独立性检验的结论是一个数学统计量,它与实际问题中确实定性是存在差异的. 4.为了判断高三学生选修文科是否与性别有关,现随机抽取50名学生,得到如下2×2列联表:根据表中数据,得到χ2=50×(13×20-10×7)223×27×20×30≈4.844,那么认为选修文科与性别有关系出错的可能性约为________. 考点 独立性检验及其根本思想 题点 独立性检验的方法解析 由χ2公式计算得χ2≈4.844>3.841,故认为选修文科与性别有关系出错的可能性约为0.05.5.某省进展高中新课程改革已经四年了,为了解教师对新课程教学模式的使用情况,某一教育机构对某学校的教师关于新课程教学模式的使用情况进展了问卷调查,共调查了50人,其中有老教师20人,青年教师30人.老教师对新课程教学模式赞同的有10人,不赞同的有10人;青年教师对新课程教学模式赞同的有24人,不赞同的有6人. (1)根据以上数据建立一个2×2列联表;(2)判断是否有99%的把握说明对新课程教学模式的赞同情况与教师年龄有关系. 考点 独立性检验及其根本思想 题点 独立性检验的方法 解 (1)2×2列联表如下所示:赞同 不赞同 总计 老教师 10 10 20 青年教师 24 6 30 总计341650(2)假设“对新课程教学模式的赞同情况与教师年龄无关〞. 由公式,得χ2=50×(10×6-24×10)234×16×20×30≈4.963<6.635,所以没有99%的把握认为对新课程教学模式的赞同情况与教师年龄有关.1.独立性检验的思想:先假设两个事件无关,计算统计量χ2的值.假设χ2值较大,那么拒绝假设,认为两个事件有关. 2.独立性检验的步骤 ①画列联表. ②计算χ2.③将得到的χ2值和临界值比拟,下结论.一、选择题1.下面是一个2×2列联表:那么表中a,b的值分别为( )A.94,96 B.52,50C.47,46 D.54,52考点分类变量与列联表题点求列联表中的数据答案 C解析a=68-21=47,b=21+25=46.2.以下关于独立性检验的说法中,错误的选项是( )A.独立性检验依据小概率原理B.独立性检验得到的结论一定正确C.样本不同,独立性检验的结论可能有差异D.独立性检验不是判断两个分类变量是否相关的唯一方法考点独立性检验及其根本思想题点独立性检验的思想答案 B解析独立性检验得到的结论不一定正确,如我们得出有90%的把握认为A与B有关,只是说这种判断的正确性为90%,具体问题中A与B可能有关,也可能无关,应选B.3.下面关于χ2的说法正确的选项是( )A.χ2在任意相互独立的问题中都可以用于检验有关还是无关B.χ2的值越大,两个事件的相关性就越大C.χ2是用来判断两个变量是否相关的统计量,当χ2的值很小时可以判定两个变量不相关D.χ2=n(ad-bc)(a+b)(c+d)(a+c)(b+d)考点独立性检验及其根本思想题点独立检验的思想答案 B解析χ2只适用于2×2列联表问题,且χ2只能推断两个变量相关,但不能判断两个变量不相关.选项D中公式错误,分子上少了平方.应选B.4.利用独立性检验来考察两个分类变量X与Y是否有关系时,通过查阅下表来确定“X与Y有关系〞的可信程度.如果χ2≥5.024,那么就有把握认为“X与Y有关系〞的百分比为( )A.25% B.75%C.2.5% D.97.5%考点独立性检验及其根本思想题点独立性检验的方法答案 D解析由表中数据可知,当χ2≥5.024,P(χ2≥k)=97.5%,应选D.5.在吸烟与患肺病这两个变量的计算中,以下说法中:①假设统计量χ2>6.635,我们有99%的把握说吸烟与患肺病有关,那么某人吸烟,那么他有99%的可能患有肺病;②假设从统计中求出,有99%的把握说吸烟与患肺病有关,那么在100个吸烟者中必有99个人患有肺病;③假设从统计中求出有95%的把握说吸烟与患肺病有关,是指有5%的可能性使得推断错误.正确的个数为( )A.0B.1C.2D.3考点独立性检验及其根本思想题点独立性检验的思想答案 B解析统计量χ2仅仅说明一个统计推断,并不能说明个别案例或某些情况,从而③正确,应选B.6.高二第二学期期中考试,按照甲、乙两个班学生的数学成绩优秀和及格统计人数后,得到如以下联表:那么统计量χ2的值约为( )考点 分类变量与列联表 题点 答案 A解析 根据列联表中的数据,可得统计量 χ2=90×(11×37-34×8)245×45×19×71≈0.600.应选A.7.假设有两个变量x 和y ,它们的值域分别为{x 1,x 2}和{y 1,y 2},其2×2列联表为:对同一样本,以下数据能说明x 与y 有关的可能性最大的一组是( ) A .a =5,b =4,c =3,d =2 B .a =5,b =3,c =4,d =2 C .a =2,b =3,c =4,d =5 D .a =3,b =2,c =4,d =5 考点 分类变量与列联表 题点 求列联表中的数据 答案 D解析 对于同一样本,|ad -bc |越小,说明x 与y 相关性越弱.而|ad -bc |越大,说明x 与y 相关性越强,通过计算知,对于选项A ,B ,C 都有|ad -bc |=|10-12|=2.对于选项D ,有|ad -bc |=|15-8|=7.显然7>2,应选D. 二、填空题8.在一项打鼾与患心脏病的调查中,共调查了1671人,经过计算得χ2=27.63,根据这一数据分析,我们有理由认为打鼾与患心脏病是________.(填“有关的〞或“无关的〞) 考点 独立性检验及其根本思想 题点 独立性检验的方法 答案 有关的解析 χ2=27.63>6.635,有99%以上的把握认为这两个量是有关的.9.下表是某届某校本科志愿报名时,对其中304名学生进入高校时是否知道想学专业的调查表:根据表中数据,那么以下说法正确的选项是________. ①性别与知道想学专业有关; ②性别与知道想学专业无关; ③女生比男生更易知道所学专业. 考点 独立性检验及其根本思想 题点 独立性检验的方法 答案 ②解析 χ2=304×(63×82-42×117)2180×124×105×199≈0.041,因为值非常小,所以性别与知道想学专业无关.10.有两个变量x 与y ,其一组观测值如下面的2×2列联表所示:那么正整数a 的最小值为________时,有90%以上的把握认为“x 与y 之间有关系〞. 考点 独立性检验及其根本思想 题点 独立性检验的方法 答案 1解析 由题意χ2=65[a (30+a )-(20-a )(15-a )]215×50×45×20=13(13a -60)290×60>2.706,易得a =1满足题意. 三、解答题11.某旅行社为调查市民喜欢“人文景观〞景点是否与年龄有关,随机抽取了55名市民,得到数据如下表所示:临界值有:(1)判断是否有99.5%的把握认为喜欢“人文景观〞景点与年龄有关?(2)用分层抽样的方法从喜欢“人文景观〞景点的市民中随机抽取6人作进一步调查,将这6名市民作为一个样本,从中任选2人,求恰有1位大于40岁的市民和1位20岁至40岁的市民的概率.考点 独立性检验思想的应用题点 分类变量与统计、概率的综合性问题解 (1)由公式χ2=n (ad -bc )2(a +b )(c +d )(a +c )(b +d ),得χ2≈11.978>7.879,所以有99.5%以上的把握认为喜欢“人文景观〞景点与年龄有关.(2)由题意知抽取的6人中大于40岁的市民有4个,20岁至40岁的市民有2个,分别记为B 1,B 2,B 3,B 4,C 1,C 2,从中任选2人的根本领件有(B 1,B 2),(B 1,B 3),(B 1,B 4),(B 1,C 1),(B 1,C 2),(B 2,B 3),(B 2,B 4),(B 2,C 1),(B 2,C 2),(B 3,B 4),(B 3,C 1),(B 3,C 2),(B 4,C 1),(B 4,C 2),(C 1,C 2),共15个,其中恰有1位大于40岁的市民和1 位20岁至40岁的市民的事件有(B 1,C 1),(B 1,C 2),(B 2,C 1),(B 2,C 2),(B 3,C 1),(B 3,C 2),(B 4,C 1),(B 4,C 2),共8个,所以恰有1位大于40岁的市民和1位20岁至40岁的市民的概率为815.四、探究与拓展12.某一电视台对年龄高于40岁和不高于40岁的人是否喜欢西班牙队进展调查,对高于40岁的调查了50人,不高于40岁的调查了50人,所得数据制成如以下联表:假设工作人员从所有统计结果中任取一个,取到喜欢西班牙队的人的概率为35,那么有______的把握认为年龄与西班牙队的被喜欢程度有关. 答案 95%解析 设“从所有人中任意抽取一个,取到喜欢西班牙的人〞为事件A ,由得P (A )=q +35100=35, 所以p =25,q =25,a =40,b =60.χ2=100×(25×35-25×15)240×60×50×50=256≈4.167>3.841.故有95%的把握认为年龄与西班牙队的被喜欢程度有关.13.某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在[29.94,30.06)的零件为优质品.从两个分厂生产的零件中各抽出了500件,量其内径尺寸,得结果如下表: 甲厂:乙厂:(1)试分别估计两个分厂生产的零件的优质品率;(2)由以上统计数据填写下面的2×2列联表,并问能否在犯错误的概率不超过0.01的前提下认为“两个分厂生产的零件的质量有差异〞?解 (1)甲厂抽查的产品中有86+182+92=360(件)优质品,从而甲厂生产的零件的优质品率估计为360500=72%;乙厂抽查的产品中有85+159+76=320(件)优质品,从而乙厂生产的零件的优质品率估计为320500=64%.(2)2×2列联表如下:χ2=1000×(360×180-320×140)2500×500×680×320≈7.353>6.635,所以能够在犯错误的概率不超过0.01的前提下认为“两个分厂生产的零件的质量有差异.〞。
高中数学选修2-1试题及答案

数学选修模块测试样题选修2-1 (人教A 版)考试时间:90分钟 试卷满分:100分一、选择题:本大题共14小题,每小题4分,共56分.在每小题给出的四个选项中,只有一项是符合要求的. 1.1x >是2x >的( )A .充分但不必要条件B .必要但不充分条件C .充要条件D .既不充分又不必要条件2.已知命题p q ,,若命题“p ⌝”与命题“p q ∨”都是真命题,则( )A .p 为真命题,q 为假命题B .p 为假命题,q 为真命题C .p ,q 均为真命题D .p ,q 均为假命题3. 设M 是椭圆22194x y +=上的任意一点,若12,F F 是椭圆的两个焦点,则12||||MF MF + 等于( )A . 2B . 3C . 4D . 64.命题0p x x ∀∈≥R :,的否定是( )A .0p x x ⌝∀∈<R :,B .0p x x ⌝∃∈≤R :,C .0p x x ⌝∃∈<R :,D .0p x x ⌝∀∈≤R :,5. 抛物线24y x =的焦点到其准线的距离是( )A . 4B . 3C . 2D . 16. 两个焦点坐标分别是12(5,0)(5,0)F F -,,离心率为45的双曲线方程是( ) A . 22143x y -= B . 22153x y -= C . 221259x y -= D . 221169x y -= 7. 下列各组向量平行的是( )8. 在空间四边形OABC 中,OA AB CB +-等于( )A .OAB .ABC .OCD .AC9. 已知向量(2,3,1)=a ,(1,2,0)=b ,则-a b 等于 ( )A .1B 3C .3D .910. 如图,在三棱锥A BCD -中,DA ,DB ,DC 两两垂直,且DB DC =,E 为BC 中点,则AE BC ⋅ 等于( )A .3B .2C .1D .011. 已知抛物线28y x =上一点A 的横坐标为2,则点A 到抛物线焦点的距离为( ) A .2B .4C .6D .812.设1k >,则关于x ,y 的方程222(1)1k x y k -+=-所表示的曲线是( )A .长轴在x 轴上的椭圆B .长轴在y 轴上的椭圆C .实轴在x 轴上的双曲线D .实轴在y 轴上的双曲线13. 一位运动员投掷铅球的成绩是14m ,当铅球运行的水平距离是6m 时,达到最大高度4m .若铅球运行的路线是抛物线,则铅球出手时距地面的高度是( )A . 1.75mB . 1.85mC . 2.15mD . 2.25m14.正方体1111ABCD A B C D -中,M 为侧面11ABB A 所在平面上的一个动点,且M到平面11ADD A 的距离是M 到直线BC 距离的2倍,则动点M 的轨迹为( )AEDCBA.椭圆B.双曲线C.抛物线D.圆二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.15.命题“若0a >,则1a >”的逆命题是_____________________.16.双曲线22194x y -=的渐近线方程是_____________________. 17.已知点(2,0),(3,0)A B -,动点(,)P x y 满足2AP BP x ⋅=,则动点P 的轨迹方程是 .18. 已知椭圆12222=+b y a x 的左、右焦点分别为21,F F ,点P 为椭圆上一点,且3021=∠F PF , 6012=∠F PF ,则椭圆的离心率e 等于 .三、解答题:本大题共3小题,共28分.解答应写出文字说明,证明过程或演算步骤.19.(本小题满分8分)设直线y x b =+与椭圆2212x y +=相交于A B ,两个不同的点.(1)求实数b 的取值范围; (2)当1b =时,求AB .20.(本小题满分10分)如图,正方体1111ABCD A B C D -的棱长为2,E 为棱1CC 的中点. (1)求1AD 与DB 所成角的大小; (2)求AE 与平面ABCD 所成角的正弦值.ABCA 1B 1C 1DDE21.(本小题满分10分)已知直线y x m =-与抛物线x y 22=相交于),(11y x A ,),(22y x B 两点,O 为坐标原点.(1)当2=m 时,证明:OB OA ⊥;(2)若m y y 221-=,是否存在实数m ,使得1-=⋅?若存在,求出m 的值;若不存在,请说明理由.数学模块测试样题参考答案数学选修2-1(人教A 版)一、选择题(每小题4分,共56分)1. B 2. B 3.D 4.C 5.C 6.D 7. A 8. C 9. B10.D11.B12.D13.A14.A二、填空题(每小题4分,共16分)15.若1a >,则0a > 16.23y x =±17. 26y x =+ 181三、解答题(解答题共28分) 19.(本小题满分8分)解:(1)将y x b =+代入2212x y +=,消去y ,整理得2234220x bx b ++-=.①因为直线y x b =+与椭圆2212x y +=相交于A B ,两个不同的点,所以2221612(22)2480b b b ∆=--=->, 解得b <<所以b 的取值范围为(. (2)设11()A x y ,,22()B x y ,, 当1b =时,方程①为2340x x +=.解得1240,3x x ==-.相应地1211,3y y ==-.所以(AB x ==.20.(本小题满分10分)解:(1) 如图建立空间直角坐标系D xyz -,则(000)D ,,,(200)A ,,,(220)B ,,,1(00D 则(2,2,0)DB =,1(2,0,2)D A =-. 故1111cos ,22DB D A DB D A DB D A⋅〈〉===⋅所以1AD 与DB 所成角的大小为60. (2) 易得(021)E ,,,所以(2,2,1)AE =-.又1(0,0,2)DD =是平面ABCD 的一个法向量,且11121cos ,323AE DD AE DD AE DD ⋅〈〉===⨯⋅. 所以AE 与平面ABCD 所成角的正弦值为13.21.(本小题满分10分)解:(1)当2=m 时,由⎩⎨⎧=-=,,x y x y 222得0462=+-x x ,解得 53,5321-=+=x x , 因此 51,5121-=+=y y .于是 )51)(51()53)(53(2121-++-+=+y y x x 0=, 即0OA OB ⋅=. 所以 OB OA ⊥.(2)假设存在实数m满足题意,由于BA,两点在抛物线上,故希望对大家有所帮助,多谢您的浏览!授课:XXX ⎪⎩⎪⎨⎧==,,22212122x y x y 因此222121)(41m y y x x ==. 所以m m y y x x OB OA 222121-=+=⋅. 由1-=⋅,即122-=-m m ,得1=m .又当1=m 时,经验证直线与抛物线有两个交点,所以存在实数1=m ,使得1-=⋅(注:可编辑下载,若有不当之处,请指正,谢谢!)。
2021人教版高中数学同步a版选修2-1(理科必考)模块练习题--2.1.1 曲线与方程

第二章圆锥曲线与方程2.1 曲线与方程*2.1.1 曲线与方程2.1.2 求曲线的方程基础过关练题组一曲线与方程的概念1.已知曲线C的方程为x3+x+y-1=0,则下列各点中在曲线C上的点是( )A.(0,0)B.(-1,3)C.(1,1)D.(-1,1)2.(2018天津耀华中学高二上学期月考)直线x-y=0与曲线xy=1的交点坐标是( )A.(1,1)B.(-1,-1)C.(1,1),(-1,-1)D.(0,0)3.已知0≤α<2π,点P(cos α,sin α)在曲线(x-2)2+y2=3上,则α的值为( )A.π3 B.5π3C.π3或5π3D.π3或π64.“点M在曲线y2=4x上”是“点M的坐标满足方程y=-2√x”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件题组二 方程的曲线5.方程4x 2-y 2+6x-3y=0表示的图形是( ) A.直线2x-y=0 B.直线2x+y+3=0C.直线2x-y=0和直线2x+y+3=0D.直线2x+y=0和直线2x-y+3=06.下列四个选项中,方程与曲线相符合的是( )7.方程|x|+|y|=1表示的曲线所围成图形的面积为 .题组三 求曲线的方程8.设A 为圆(x-1)2+y 2=1上的动点,PA 是圆的切线,且|PA|=1,则点P 的轨迹方程是( )A.(x-1)2+y 2=2B.(x-1)2+y 2=4C.y 2=2xD.y 2=-2x9.在平面直角坐标系中,O 为坐标原点,点A(1,0),B(2,2).若点C 满足OC ⃗⃗⃗⃗⃗ =OA ⃗⃗⃗⃗⃗ +t(OB ⃗⃗⃗⃗⃗ -OA ⃗⃗⃗⃗⃗ ),其中t∈R ,则点C 的轨迹方程为 .10.(2018湖南岳阳一中高二上学期期末)已知M 为直线l:2x-y+3=0上的一动点,A(4,2)为一定点,点P 在直线AM 上运动,且AP ⃗⃗⃗⃗⃗ =3PM ⃗⃗⃗⃗⃗⃗ ,求动点P 的轨迹方程.11.已知△ABC 中,AB=2,AC=√2BC. (1)求点C 的轨迹方程; (2)求△ABC 的面积的最大值.能力提升练一、选择题1.(2018海南海口一中高二上学期月考,★★☆)方程xy 2+x 2y=1所表示的曲线( )A.关于x 轴对称B.关于y 轴对称C.关于原点中心对称D.关于直线y=x 对称 2.(2020鄂东南九校高二期中联考,★★☆)方程(3x-y+1)(y-√1-x 2)=0表示的曲线为( ) A.一条线段和半个圆 B.一条线段和一个圆 C.一条直线和半个圆 D.两条线段3.(2020北京朝阳高三期末,★★☆)笛卡儿、牛顿都研究过方程(x-1)(x-2)(x-3)=xy,关于这个方程的曲线有下列说法:①该曲线关于y 轴对称;②该曲线关于原点对称;③该曲线不经过第三象限;④该曲线上有且只有三个点的横、纵坐标都是整数.其中正确的是( ) A.②③ B.①④ C.③ D.③④4.(2019江西南昌高三开学摸底考试,★★☆)在平面直角坐标系xOy 中,已知M(-1,2),N(1,0),动点P 满足|PM ⃗⃗⃗⃗⃗⃗ ·ON ⃗⃗⃗⃗⃗⃗ |=|PN ⃗⃗⃗⃗⃗⃗ |,则动点P 的轨迹方程是( )A.y 2=4xB.x 2=4yC.y 2=-4xD.x 2=-4y5.(★★☆)方程x 2+y 2=1(xy<0)表示的曲线形状是( )6.(2018吉林长春五县期末,★★★)已知定点M(-3,0),N(2,0),若动点P满足|PM|=2|PN|,则点P的轨迹所包围的图形的面积等于( )A.100π9 B.142π9C.10π3D.9π二、填空题7.(2020贵州贵阳高二期末,★★☆)以古希腊数学家阿波罗尼斯命名的阿波罗尼斯圆,是指到两定点的距离之比为常数λ(λ>0,λ≠1)的动点M的轨迹.已知A(-2,0),B(2,0),动点M满足|MA||MB|=√2,此时阿波罗尼斯圆的方程为.8.(2020北京房山高二期末,★★☆)已知曲线W的方程为|y|+x2-5x=0.①请写出曲线W的一条对称轴方程: ;②曲线W上的点的横坐标的取值范围是.三、解答题9.(2019贵州铜仁一中高二入学考试,★★☆)已知动点M到点A(-1,0)与点B(2,0)的距离之比为2∶1,记动点M的轨迹为曲线C.(1)求曲线C的方程;(2)过点P(5,-4)作曲线C的切线,求切线方程.10.(2019上海七宝中学高二期末,★★★)在平面直角坐标系xOy中,曲线Γ:x2+y2=1(y≥0).(1)如图1,点B为曲线Γ上的动点,点A(2,0),求线段AB的中点的轨迹方程;(2)如图2,点B为曲线Γ上的动点,点A(2,0),将△OAB绕点A顺时针旋转90°得到△DAC,求线段OC长度的最大值.答案全解全析 基础过关练1.B 点P(x 0,y 0)在曲线f(x,y)=0上⇔f(x 0,y 0)=0.经验证知点(-1,3)在曲线C 上.2.C 由{x -y =0,xy =1,得{x =1,y =1或{x =-1,y =-1.故选C.3.C 将点P 的坐标代入方程(x-2)2+y 2=3,得(cos α-2)2+sin 2α=3,解得cos α=12.又0≤α<2π,所以α=π3或5π3.4.B 设M(x 0,y 0),由点M 的坐标满足方程y=-2√x ,得y 0=-2√x 0,∴y 02=4x 0,∴点M 在曲线y 2=4x 上.反之不成立,故选B.5.C ∵4x 2-y 2+6x-3y=(2x+y)(2x-y)+3(2x-y)=(2x-y)(2x+y+3)=0, ∴原方程表示直线2x-y=0和2x+y+3=0.6.D 对于A,点(0,-1)满足方程,但不在曲线上,排除A;对于B,点(1,-1)满足方程,但不在曲线上,排除B;对于C,由于曲线上第三象限的点的横、纵坐标均小于0,不满足方程,排除C.故选D.7.答案 2解析 方程表示的图形是边长为√2的正方形(如图所示),其面积为(√2)2=2.8.A 设圆(x-1)2+y 2=1的圆心为C,半径为r,则C(1,0),r=1,依题意得|PC|2=r 2+|PA|2,即|PC|2=2,所以点P 的轨迹是以C 为圆心,√2为半径的圆,因此点P 的轨迹方程是(x-1)2+y 2=2. 9.答案 y=2x-2解析 设点C(x,y),则OC ⃗⃗⃗⃗⃗ =(x,y).因为点A(1,0),B(2,2),所以OA ⃗⃗⃗⃗⃗ +t(OB ⃗⃗⃗⃗⃗ -OA ⃗⃗⃗⃗⃗ )=(1+t,2t),所以{x =t +1,y =2t ,消去t,得点C 的轨迹方程为y=2x-2. 10.解析 设M(x 0,y 0),P(x,y), 则AP⃗⃗⃗⃗⃗ =(x-4,y-2),PM ⃗⃗⃗⃗⃗⃗ =(x 0-x,y 0-y), 由题意可得{x -4=3(x 0-x ),y -2=3(y 0-y ),所以{x 0=4x -43,y 0=4y -23.因为点M(x 0,y 0)在直线2x-y+3=0上, 所以2×4x -43-4y -23+3=0,即8x-4y+3=0,所以点P 的轨迹方程为8x-4y+3=0.11.解析 (1)以直线AB 为x 轴,线段AB 的垂直平分线为y 轴建立平面直角坐标系,则A(-1,0),B(1,0).设C(x,y),由AC=√2BC,得(x+1)2+y 2=2[(x-1)2+y 2],即(x-3)2+y 2=8,又在△ABC 中,y≠0,所以点C 的轨迹方程为(x-3)2+y 2=8(y≠0).(2)因为AB=2,所以S △ABC =12×2×|y|=|y|.因为(x-3)2+y 2=8(y≠0), 所以0<|y|≤2√2,所以S △ABC ≤2√2,即△ABC 的面积的最大值为2√2.能力提升练一、选择题1.D 设P(x 0,y 0)是曲线xy 2+x 2y=1上的任意一点,则x 0y 02+x 02y 0=1.设点P 关于直线y=x 的对称点为P',则P'(y 0,x 0),因为y 0x 02+y 02x 0=x 0y 02+x 02y 0=1,所以P'在曲线xy 2+x 2y=1上,故该曲线关于直线y=x 对称.2.A 由方程(3x-y+1)(y-√1-x 2)=0得y=√1-x 2(y≥0)或3x-y+1=0,且满足-1≤x≤1,即x 2+y 2=1(y≥0)或3x-y+1=0(-1≤x≤1),∴方程(3x-y+1)(y-√1-x 2)=0表示一条线段和半个圆.3.C 将x=-x 代入得到(x+1)(x+2)(x+3)=xy,方程改变,故该曲线不关于y 轴对称; 将x=-x,y=-y 代入得到(x+1)(x+2)(x+3)=-xy,方程改变,故该曲线不关于原点对称; 当x<0,y<0时,(x-1)(x-2)(x-3)<0,xy>0,显然方程不成立,∴该曲线不经过第三象限;令x=-1,易得y=24,即(-1,24)在曲线上,同理可得(1,0),(2,0),(3,0)也在曲线上,∴该曲线上有且只有三个点的横、纵坐标都是整数是错误的.4.A 设P(x,y),因为M(-1,2),N(1,0),所以PM ⃗⃗⃗⃗⃗⃗ =(-1-x,2-y),ON ⃗⃗⃗⃗⃗⃗ =(1,0),PN ⃗⃗⃗⃗⃗⃗ =(1-x,-y),因为|PM ⃗⃗⃗⃗⃗⃗ ·ON ⃗⃗⃗⃗⃗⃗ |=|PN⃗⃗⃗⃗⃗⃗ |,所以|1+x|=√(1-x )2+(-y )2, 整理得y 2=4x.5.C 方程x 2+y 2=1(xy<0)表示以原点为圆心,1为半径的圆在第二、四象限的部分,故选C. 6.A 设P(x,y),则由|PM|=2|PN|,得(x+3)2+y 2=4[(x-2)2+y 2],化简,得3x 2+3y 2-22x+7=0, 即(x -113)2+y 2=1009,所以所求图形的面积S=100π9.二、填空题7.答案 x 2+y 2-12x+4=0 解析 设M(x,y),因为|MA ||MB |=√2, 所以√(x+2)2+y 2√(x -2)+y 2=√2,整理得x 2+y 2-12x+4=0.8.答案 ①y=0(或x =52) ②[0,5]解析 ①由W 的方程知,若(x,y)是曲线上的点,则(x,-y)也是曲线上的点,因此直线y=0是曲线W的一条对称轴.同理,点(52-x,y)与(52+x,y)也都是曲线上的点,因此直线x=52也是曲线W的一条对称轴.②由|y|+x2-5x=0得|y|=-x2+5x,因为|y|≥0,所以-x2+5x≥0,解得0≤x≤5.三、解答题9.解析(1)设动点M的坐标为(x,y),则|MA|=√(x+1)2+y2,|MB|=√(x-2)2+y2所以√(x+1)2+y2√(x-2)+y2=2,化简得(x-3)2+y2=4.因此,动点M的轨迹方程为(x-3)2+y2=4.(2)当过点P的直线斜率不存在时,直线方程为x-5=0,圆心C(3,0)到直线x-5=0的距离等于2,此时直线x-5=0与曲线C相切; 当过点P的切线斜率存在时,不妨设斜率为k,则切线方程为y+4=k(x-5),即kx-y-5k-4=0,由圆心到切线的距离等于半径,得√k2+1=2,解得k=-34.所以切线方程为3x+4y+1=0.综上所述,切线方程为x-5=0和3x+4y+1=0.10.解析(1)设点B的坐标为(x0,y0),则y0≥0,设线段AB的中点为M(x,y), 因为点B在曲线Γ上,所以x02+y02=1.①因为M为线段AB的中点,所以{x=x0+22,y=y02,则{x0=2x-2,y0=2y,代入①式得(2x-2)2+4y2=1,化简得(x-1)2+y2=14,其中y≥0.则线段AB的中点的轨迹方程为(x-1)2+y2=14(y≥0).(2)如图所示,将△OAB绕点A顺时针旋转90°得到△DAC,易知点D(2,2),结合图形可知,点C在曲线(x-2)2+(y-2)2=1(x≥2)上运动,则问题转化为求原点O到曲线(x-2)2+(y-2)2=1(x≥2)上一点C的距离的最大值,连接OD并延长交曲线(x-2)2+(y-2)2=1(x≥2)于点C',当点C与C'重合时,|OC|取得最大值,且|OC|max=|OD|+1=2√2+1.。
《创新设计》2021版高考数学(北师大版理科)一轮复习练习:选修4-5 Word版含答案

(建议用时:50分钟)1.(2021·湖南卷)设a >0,b >0,且a +b =1a +1b .证明: (1)a +b ≥2;(2)a 2+a <2与b 2+b <2不行能同时成立.证明 由a +b =1a +1b =a +bab ,a >0,b >0,得ab =1. (1)由基本不等式及ab =1,有a +b ≥2ab =2,即a +b ≥2.(2)假设a 2+a <2与b 2+b <2同时成立,则由a 2+a <2及a >0得0<a <1;同理,0<b <1,从而ab <1,这与ab =1冲突.故a 2+a <2与b 2+b <2不行能同时成立. 2.已知函数f (x )=|x +a |+|x -2|.(1)当a =-3时,求不等式f (x )≥3的解集;(2)若f (x )≤|x -4|的解集包含[1,2],求a 的取值范围.解(1)当a =-3时,f (x )=⎩⎨⎧-2x +5,x ≤2,1,2<x <3,2x -5,x ≥3.当x ≤2时,由f (x )≥3得-2x +5≥3,解得x ≤1; 当2<x <3时,f (x )≥3无解;当x ≥3时,由f (x )≥3得2x -5≥3,解得x ≥4. 所以f (x )≥3的解集为{x |x ≤1,或x ≥4}. (2)f (x )≤|x -4|⇔|x -4|-|x -2|≥|x +a |. 当x ∈[1,2]时,|x -4|-|x -2|≥|x +a |⇔ 4-x -(2-x )≥|x +a |⇔-2-a ≤x ≤2-a . 由条件得-2-a ≤1且2-a ≥2,即-3≤a ≤0. 故满足条件的a 的取值范围是[-3,0].3.已知a ,b ,c 均为正实数,且互不相等,且abc =1,求证:a +b +c <1a +1b +1c . 证明 法一 ∵a ,b ,c 均为正实数,且互不相等,且abc =1,∴a +b +c =1bc +1ca +1ab <1b +1c 2+1c +1a 2+1a +1b 2=1a +1b +1c .∴a +b +c <1a +1b+1c .法二 ∵1a +1b ≥21ab =2c ;1b +1c ≥21bc =2a ;1c +1a ≥21ac =2b .∴以上三式相加,得1a +1b +1c ≥ a +b +c . 又∵a ,b ,c 互不相等,∴1a +1b +1c >a +b +c . 法三 ∵a ,b ,c 是不等正数,且abc =1,∴1a +1b +1c =bc +ca +ab =bc +ca 2+ca +ab 2+ab +bc 2>abc 2+a 2bc +ab 2c =a +b +c .∴a +b +c <1a +1b +1c .4.已知a >0,b >0,a +b =1,求证: (1)1a +1b +1ab ≥8;(2)⎝ ⎛⎭⎪⎫1+1a ⎝ ⎛⎭⎪⎫1+1b ≥9.证明 (1)∵a +b =1,a >0,b >0, ∴1a +1b +1ab =1a +1b +a +b ab =2⎝ ⎛⎭⎪⎫1a +1b=2⎝ ⎛⎭⎪⎫a +b a+a +b b =2⎝ ⎛⎭⎪⎫b a +a b +4≥4 b a ×ab +4=8.∴1a +1b +1ab ≥8(当且仅当a =b =12时等号成立). (2)∵⎝ ⎛⎭⎪⎫1+1a ⎝ ⎛⎭⎪⎫1+1b =1a +1b +1ab +1,由(1)知1a +1b +1ab ≥8.∴⎝ ⎛⎭⎪⎫1+1a ⎝ ⎛⎭⎪⎫1+1b ≥9.5.(2021·全国Ⅰ卷)已知函数f (x )=|x +1|-2|x -a |,a >0. (1)当a =1时,求不等式f (x )>1的解集;(2)若f (x )的图像与x 轴围成的三角形面积大于6,求a 的取值范围. 解 (1)当a =1时,f (x )>1化为|x +1|-2|x -1|-1>0. 当x ≤-1时,不等式化为x -4>0,无解;当-1<x <1时,不等式化为3x -2>0,解得23<x <1; 当x ≥1时,不等式化为-x +2>0,解得1≤x <2.所以f (x )>1的解集为⎩⎨⎧⎭⎬⎫x |23<x <2.(2)由题设可得,f (x )=⎩⎨⎧x -1-2a ,x <-1,3x +1-2a ,-1≤x ≤a ,-x +1+2a ,x >a .所以函数f (x )的图像与x 轴围成的三角形的三个顶点分别为A ⎝ ⎛⎭⎪⎫2a -13,0,B (2a +1,0),C (a ,a +1),△ABC 的面积为23(a +1)2.由题设得23(a +1)2>6, 故a >2.所以a 的取值范围为(2,+∞).6.已知函数f (x )=m -|x -2|,m ∈R ,且f (x +2)≥0的解集为[-1,1]. (1)求m 的值;(2)若a ,b ,c 大于0,且1a +12b +13c =m ,求证:a +2b +3c ≥9. (1)解 ∵f (x +2)=m -|x |, ∴f (x +2)≥0等价于|x |≤m .由|x |≤m 有解,得m ≥0且其解集为{x |-m ≤x ≤m }. 又f (x +2)≥0的解集为[-1,1],故m =1.(2)证明 由(1)知1a +12b +13c =1,且a ,b ,c 大于0, a +2b +3c =(a +2b +3c )⎝ ⎛⎭⎪⎫1a +12b +13c=3+⎝ ⎛⎭⎪⎫2b a +a 2b +⎝ ⎛⎭⎪⎫3c a +a 3c +⎝ ⎛⎭⎪⎫3c 2b +2b 3c≥3+22ab2ab +23c a ·a 3c +23c 2b ·2b 3c =9.当且仅当a =2b =3c =13时,等号成立.因此a +2b +3c ≥9. 7.设函数f (x )=|x -1|+|x -a |. (1)若a =-1,解不等式f (x )≥3; (2)假如∀x ∈R ,f (x )≥2,求a 的取值范围.解(1)当a =-1时,f (x )=|x -1|+|x +1|,f (x )=⎩⎨⎧-2x ,x <-1,2,-1≤x ≤1,2x ,x >1.作出函数f (x )=|x -1|+|x +1|的图像.由图像可知,不等式f (x )≥3的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x ≤-32,或x ≥32. (2)若a =1,f (x )=2|x -1|, 不满足题设条件;若a <1,f (x )=⎩⎨⎧-2x +a +1,x ≤a ,1-a ,a <x <1,2x -(a +1),x ≥1,f (x )的最小值为1-a ;若a >1,f (x )=⎩⎨⎧-2x +a +1,x ≤1,a -1,1<x <a ,2x -(a +1),x ≥a ,f (x )的最小值为a -1.∴对于∀x ∈R ,f (x )≥2,∴当a <1时,1-a ≥2, ∴a ≤-1,当a >1时,a -1≥2,∴a ≥3. ∴a 的取值范围是(-∞,-1]∪[3,+∞).8.设函数f (x )=2|x -1|+x -1,g (x )=16x 2-8x +1.记f (x )≤1的解集为M ,g (x )≤4的解集为N . (1)求M ;(2)当x ∈(M ∩N )时,证明:x 2f (x )+x [f (x )]2≤14. (1)解 f (x )=⎩⎨⎧3x -3,x ∈[1,+∞),1-x ,x ∈(-∞,1)当x ≥1时,由f (x )=3x -3≤1得x ≤43,故1≤x ≤43; 当x <1时,由f (x )=1-x ≤1得x ≥0,故0≤x <1.所以f (x )≤1的解集为M ={x |0≤x ≤43}.(2)证明 由g (x )=16x 2-8x +1≤4得16⎝ ⎛⎭⎪⎫x -142≤4,解得-14≤x ≤34.因此N =⎩⎨⎧⎭⎬⎫x |-14≤x ≤34,故M ∩N =⎩⎨⎧⎭⎬⎫x |0≤x ≤34. 当x ∈M ∩N 时,f (x )=1-x ,于是x 2f (x )+x ·[f (x )]2=xf (x )[x +f (x )]=x ·f (x )=x (1-x )=14-⎝ ⎛⎭⎪⎫x -122≤14.。
高中数学选择性必修二 北京市昌平区新学道临川学校高二上学期期末考试数学(理)试题(含答案)

高二数学理科试卷
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.在等差数列 中,若 , ,则 =()
A. B. C. D.
【答案】C
【解析】
【分析】由等差数列通项公式可求得 ,由 可求得结果.
【详解】设等差数列 的公差为 ,则 , .
【详解】抛物线 ( )的准线为: ,
因为准线经过点 ,可得 ,即 ,
所以抛物线为 ,焦点坐标为 ,
故选:B.
11.椭圆 内有一点 过点 的弦恰好以 为中点,那么这弦所在直线的方程为()
A. B.
C. D.
【答案】B
【解析】
【分析】利用点差法得到直线斜率和中点之间的关系,即可得解.
【详解】设弦的两个端点为 ,
即曲线C右侧部分的点到原点的距离都不超过 ,
再根据对称性可知,曲线C上的所有点到原点的距离都不超过 ,②正确;
对于③,因为在x轴上方,图形面积大于四点(﹣1,0),
(1,0),(1,1),(﹣1,1)围成的矩形面积1×2=2,
在x轴下方,图形面积大于三点(﹣1,0),(1,0),(0,﹣1)围成的等腰直角三角形的面积 ×2×1=1,
故选:C.
2.在等比数列 中, , ,则 与 的等比中项是()
A. B. C. D.
【答案】A
【解析】
【分析】计算出 的值,利用等比中项的定义可求得结果.
【详解】由已知可得 ,由等比中项的性质可得 ,
因此, 与 的等比中项是 .
故选:A.
3.若△ABC中,a=4,A=45°,B=60°,则边b的值为( )
选修2-3 第二章 概率 期末复习卷 2020-2021学年高二下学期数学期末复习(北师大版)

北师大版选修2-3第二章概率期末复习卷一、单选题1.某工厂有A ,B 两套生产线,每周需要维护的概率分别为0.2和0.25,且每周A ,B 两套生产线是否需要进行维护是相互独立的,则至多有一套生产线需要维护的概率为( ) A .0.95 B .0.6C .0.35D .0.152.若随机变量()5,X B p ,()54D X =,则()E X =( )A .15 B .14C .1516D .523.已知某随机变量ξ服从正态分布N (1,32),则P (27ξ-<<)为( )(附:若随机变量ξ服从正态分布N (μ,2σ),则()68.26%P μσξμσ-<<+=,(22)95.44%P μσξμσ-<<+=)A .87.22%B .13.59%C .27.18%D .81.85%4.已知离散型随机变量12,ζζ的分布列为则下列说法一定正确的是( ) A .()()12E E ζζ> B .()()12E E ζζ< C .()()12D D ζζ>D .()()12D D ζζ<5.在5道题中有3道理科试题和2道文科试题.如果不放回地依次抽2道题,则第一次和第二次都抽到理科题的概率是( ) A .25B .12C .35D .3106.已知随机变量()2~1,X N σ,若()00.6P X ≥=,则()2PX >=( )A .0.2B .0.4C .0.6D .0.8个球,所取的3个球中至少有1个红球的概率为( )A .12125B .16 C .98125D .568.随机变量X 的分布列如下表所示,若()1E X =,则()31D X +=( )A .9B .7C .5D .39.甲乙两个两位同学同时看了天气预报,甲说明天下雨的概率是80%,乙说如果明天下雨则后天下雨的概率是40%,如果甲乙说的都是对的,那么明天和后天都会下雨的概率是( ) A .50%B .40%C .32%D .20%10.某工厂的一台流水线生产质量稳定可靠,已知在正常工作状态下生产线上生产的零件内径尺寸Z (单位:m μ)服从正态分布()60,4N .甲、乙两名同学正进行尺寸测量练习.甲、乙对各自抽取的5个零件测量零件内径尺寸(单位:m μ)如下,甲同学测量数据:59,60,62,63,65;乙同学测量数据:52,53,55,57,62.则可以判断( ) A .甲、乙两个同学测量都正确 B .甲、乙两个同学测量都错误 C .甲同学测量正确,乙同学测量错误D .甲同学测量错误,乙同学测量正确11.有6个相同的球,分别标有数字1,2,3,4,5,6,从中有放回的随机取两次,每次取1个球,甲表示事件“第一次取出的球的数字是1”,乙表示事件“第二次取出的球的数字是2”,丙表示事件“两次取出的球的数字之和是8”,丁表示事件“两次取出的球的数字之和是7”,则( ) A .甲与丙相互独立 B .甲与丁相互独立 C .乙与丙相互独立D .丙与丁相互独立12.某中学高一年级和高二年级进行篮球比赛,赛制为3局2胜制,若比赛没有平局,且高二队每局获胜的概率都是112p p ⎛⎫<< ⎪⎝⎭,记比赛的最终局数为随机变量X ,则( )A .2(2)P X p ==B .(3)(1)P X p p ==-C .5()2E X < D .1()4D X >二、填空题13.随机变量X 的分布列如下:其中a ,b ,c 成等差数列,若1()3E X =,则234a b c ++=_________.X 1- 0 1p ab c14.根据天文学有关知识,当且仅当一颗恒星的“赤纬”数值大于58-︒,能在扬州的夜空中看到它.下表列出了10颗恒星的“赤纬”数值:星名天狼星老人星南门二大角星织女一五车二参宿七南河三水委一参宿四赤纬16.7-︒ 52.7-︒ 60.8-︒ 19.2︒ 38.8︒ 46︒ 8.2-︒ 5.2︒ 57.2-︒ 7.4︒现有四名学生从这10颗恒星中各随机选择1颗进行观测,其中有X 人能在扬州的夜空中看到观测目标,则X 的数学期望为___________.15.某班为响应校团委发起的“青年大学习”号召组织了有奖知识竞答活动,第一环节是一道必答题,由甲乙两位同学作答,每人答对的概率均为0.7,两人都答对的概率为0.5,则甲答对的前提下乙也答对的概率是________.(用分数表示)16.用X ,Y ,Z 三个不同的元件连接成如图系统,毎个元件是否正常工作相互独立,已知X ,Y ,Z 正常工作的概率均为13,则系统正常工作的概率为___________.三、解答题17.甲、乙两所学校之间进行排球比赛,采用五局三胜制(先赢3局的学校获胜,比赛结束),约定比赛规则如下:先进行男生排球比赛,共比赛两局,后进行女生排球比赛.按照以往比赛经验,在男生排球此赛中,每局甲校获胜的概率为23,乙校获胜的概率为13,在女生排球比赛中,每局甲校获胜的概率为13,乙校获胜的概率为23.每局比赛结果相互独立.(1)求甲校以3:1获胜的概率;(2)记比赛结束时女生比赛的局数为ξ,求ξ的概率分布.18.为促进物资流通,改善出行条件,驻某县扶贫工作组引入资金新建了一条从该县到市区的快速道路.该县脱贫后,工作组为了解该快速道路的交通通行状况,调查了行经该道路的各种类别的机动车共1000辆,对行车速度进行统计后,得到如图所示的频率分布直方图:(1)试根据频率分布直方图,求样本中的这1000辆机动车的平均车速(同一组中的数据用该组区间的中点值代替);(2)设该公路上机动车的行车速度v 服从正态分布()2,N μσ,其中μ,2σ分别取自该调查样本中机动车的平均车速和车速的方差2s (经计算2210.25s =).(i )请估计该公路上10000辆机动车中车速不低于85千米/时的车辆数(精确到个位): (ii )现从经过该公路的机动车中随机抽取10辆,设车速低于85千米/时的车辆数为X ,求X 的数学期望.附注:若()2~,N ξμσ,则()0.6827P μσξμσ-<≤+=,()220.9545P μσξμσ-<≤+=,()330.9973P μσξμσ-<≤+=.参考数据:229841=.19.2020年是全面建成小康社会之年,是脱贫攻坚收官之年.莲花村是乡扶贫办的科学养鱼示范村,为了调查该村科技扶贫成果,乡扶贫办调查组从该村的养鱼塘内随机捕捞两次,上午进行第一次捕捞,捕捞到60条鱼,共105kg ,称重后计算得出这60条鱼质量(单位kg )的平方和为200.41,下午进行第二次捕捞,捕捞到40条鱼,共66kg .称重后计算得出这40条鱼质量(单位kg )的平方和为117.(1)请根据以上信息,求所捕捞100条鱼质量的平均数z 和方差2s ; (2)根据以往经验,可以认为该鱼塘鱼质量X 服从正态分布()2,N μδ,用z 作为μ的估计值,用2s 作为2δ的估计值.随机从该鱼糖捕捞一条鱼,其质量在[]1.21,3.21的概率是多少?(3)某批发商从该村鱼塘购买了1000条鱼,若从该鱼塘随机捕捞,记ξ为捕捞的鱼的质量在[]1,21,3.21的条数,利用(2)的结果,求ξ的数学期望.附:(1)数据1t ,2t ,…n t 的方差()22221111n n i i i i s t tt nt n n ==⎛⎫=-=- ⎪⎝⎭∑∑, (2)若随机变量X 服从正态分布()2,N μδ,则()0.6827P X μδμδ-≤≤+=;()22P X μδμδ-≤≤+0.9545=;()330.9973P X μδμδ-≤≤+=.20.某学校组织“一带一路”知识竞赛,有A ,B 两类问题,每位参加比赛的同学先在两类问题中选择一类并从中随机抽取一个问题回答,若回答错误则该同学比赛结束:若回答正确则从另一类问题中再随机抽取一个问题回答,无论回答正确与否,该同学比赛结束.A 类问题中的每个问题回答正确得20分,否则得0分:B 类问题中的每个问题回答正确得80分,否则得0分,己知小明能正确回答A 类问题的概率为0.8,能正确回答B 类问题的概率为0.6,且能正确回答问题的概率与回答次序无关.(1)若小明先回答A 类问题,记X 为小明的累计得分,求X 的分布列; (2)为使累计得分的期望最大,小明应选择先回答哪类问题?并说明理由. 21.某种产品的质量以其质量指标值衡量,并依据质量指标值划分等级如表:(1)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品92%”的规定?该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值X 近似地服从正态分布()218,140N ,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?(2)在样本中,按产品等级用分层抽样的方法抽取8件,再从这8件中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率.22.某学校高一年级进行班级之间的中国历史知识竞赛活动,甲、乙两位同学代表各自班级以抢答的形式展开,共五道题,抢到并回答正确者得一分,答错则对方得一分,先得三分者获胜.每一次抢题甲、乙两人抢到每道题的概率都是12,甲、乙正确回答每道题的概率分别为35,45,且两人各道题是否回答正确均相互独立. (1)比赛开始,求甲先得一分的概率; (2)求甲获胜的概率;(3)问:若将题干中的抢答五道题改为抢答三道题,先得两分者获胜,其余条件不变,则对甲更有利还是更不利?请说明理由.参考答案1.A 【分析】由相互独立事件概率计算公式可得结果. 【详解】由题可得至多有一套生产线需要维护的概率0.20.750.80.250.750.80.95P =⨯+⨯+⨯=. 故选:A. 2.D 【分析】根据二项分布的期望与方程的计算公式,由题中条件,列出方程,即可求出结果. 【详解】 因为()5,XB p ,()54D X =,则()()5514D X p p =-=,解得12p =,所以()552E X p ==. 故选:D. 3.D 【分析】由P (27ξ-<<)(2)P =-<<+,结合所给条件,即可得解.【详解】因为p (-2<ξ<4) ()68.26%P =-<<+=μσξμσ, p (-5<ξ<7)= (22)95.44%P μσξμσ-<<+=, 所以p (-2<ξ<7)=68.26%+12(95.44%-68.26%)=81.85%, 故选:D. 4.D 【分析】利用公式计算出两个随机变量的期望和方程后可得正确的选项. 【详解】()()1216512453,344E E ζζ+++++====,故()()12E E ζζ=, ()()2222222121325124592,9 2.544D E ζζ+⨯++++=-==-=,()()12D D ζζ<,故选:D. 5.D 【分析】根据题意,设A 事件为第一次抽到理科试题,B 事件为第二次抽到理科试题,进而()()()3135210P AB P A P B ==⨯=.【详解】设A 事件为第一次抽到理科试题,B 事件为第二次抽到理科试题, 所以第一次和第二次都抽到理科题的概率是()()()3135210P AB P A P B ==⨯=. 故选:D. 6.B 【分析】利用正态密度曲线的对称性可得出()()()2010P X P X P X >=<=-≥,即可得解. 【详解】因为随机变量()2~1,X N σ,则()()()20100.4P X P X P X >=<=-≥=.故选:B. 7.D 【分析】根据题意,该问题符合超几何分布,利用超几何分布概率公式计算所取的3个球中没有1个红球的概率,进而可得答案. 【详解】根据题意,该问题符合超几何分布,其基本事件总数为310C , 其中所取的3个球中没有1个红球的基本事件为36C ,所求概率为36310C 1511C 66-=-=.故选:D. 8.C 【分析】利用离散型随机变量的分布列、数学期望的性质,列出方程组,求出a ,b ,由此能求出方差,再根据方差的性质计算可得. 【详解】解:依题意可得1161110163a b a b ⎧++=⎪⎪⎨⎪-⨯+⨯+⨯=⎪⎩,解得1312a b ⎧=⎪⎪⎨⎪=⎪⎩,所以()22211111151013633329D X ⎛⎫⎛⎫⎛⎫=--⨯+-⨯+-⨯= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭所以()()25313959D X D X +==⨯= 故选:C 9.C 【分析】根据条件概率的概率公式计算可得; 【详解】解:记明天下雨为事件A ,后天下雨为事件B ,依题意可得()80%P A =,()|40%P B A =,所以()()()|80%40%32%P AB P B A P A =⋅=⨯= 故选:C 10.C 【分析】根据3σ原则可确定()54660.9974P Z <<=,可知甲同学测量数据正确,乙同学测量数据中发生了小概率事件,可认为其测量数据错误. 【详解】()60,4ZN ,()330.9974P Z μσμσ∴-<<+=,即()54660.9974P Z <<=;甲同学测量的数据均落在()54,66之间,测量数据正确;乙同学测量的数据中有两个数据落在()54,66之外,即小概率事件发生,知其测量错误. 故选:C. 11.B 【分析】根据独立事件概率关系逐一判断 【详解】11561()()()()6636366P P P P =====甲,乙,丙,丁, ,1()0()()()()()36P P P P P P =≠==甲丙甲丙,甲丁甲丁,1()()()()0()()36P P P P P P =≠=≠乙丙乙丙,丙丁丁丙,故选:B 【点睛】判断事件,A B 是否独立,先计算对应概率,再判断()()()P A P B P AB =是否成立 12.C 【分析】根据实际意义得2X =或3.求得概率后判断AB ,由期望公式计算出期望可判断C ,由均值求出方差可判断D . 【详解】赛制为3局2胜制,比赛没有平局,因此随机变量X 的可能值为2或3,222(2)(1)221P X p p p p ==+-=-+,A 错;222(3)(1)(1)(1)(1)(1)22P X p p p p p p p p p p p p ==-+-+-+--=-+,B 错;222215()2(221)3(22)2222()22E X p p p p p p p =-++-+=-++=--+,因为112p <<,所以5()(2,)2E X ∈,C 正确; 记2222p p t -++=,5(2,)2t ∈,2222()4(221)9(22)1010456E X p p p p p p t =⨯-++⨯-+=-++=-,222251()()()56()24D XE X E X t t t =-=--=--+,因为5(2,)2t ∈,所以1()4D X <,D 错. 故选:C . 【点睛】结论点睛:本题考查随机变量的概率分布列与数学期望、方差等概念.随机变量的期望与方差之间有关系:[]22()()()D X E X E X =-.13.103【分析】利用离散型随机变量的分布列、数学期望的性质、等差数列性质,列出方程组,求出a ,b ,c ,即得解.【详解】 由题意知:1213a b c b a c a c ⎧⎪++=⎪=+⎨⎪⎪-+=⎩, 解得16a =,13b =,12c =, 所以111102342+3+4=6323a b c ++=⨯⨯⨯.故答案为:103【点睛】关键点睛:解答本题的关键是根据已知列出关于,,a b c 的方程组. 14.3.6 【分析】利用二项分布可求数学期望. 【详解】大于58-︒的有9个,小于58-︒的有1个 在扬州能看到的概率为910,9~4,10X B ⎛⎫⎪⎝⎭,()94 3.610E X =⨯=.故答案为:3.6. 15.57【分析】记事件A:甲答对,事件B:乙答对,分别求出()()P A P AB ,,利用条件概率公式直接求解. 【详解】记事件A:甲答对,事件B:乙答对, 则有:()()()0.7,0.5PA PB P AB ===,所以()()()0.550.77P AB P B A P A ===. 故答案为:5716.527【分析】系统正常工作的情况是X 正常工作,同时,Y Z 中至少一个能正常工作,由此利用相互独立事件概率乘法公式和对立事件概率计算公式能求出系统正常工作的概率. 【详解】系统正常工作的情况是X 正常工作,同时,Y Z 中至少一个能正常工作,因为X ,Y ,Z 正常工作的概率均为13, 所以系统正常工作的概率为:2115[1(1)]3327P =--=,故答案为:527. 【点睛】关键点点睛:该题考查的是有关概率的求法,正确解题的关键是用好相互独立事件概率乘法公式和对立事件概率计算公式等基础知识. 17.(1)427;(2)分布列答案见解析. 【分析】(1)根据相互独立事件概率乘法公式计算出所求概率.(2)根据相互独立事件概率乘法公式计算出所求分布列. 【详解】(1)甲校以3:1获胜,则甲校在第四局获胜,前三局胜两局,2122111221484C 3333333818127P ⎛⎫=⋅⋅⋅⋅+⨯⨯=+=⎪⎝⎭. (2)ξ的所有可能取值为1,2,3,()2221122133339P ξ⎛⎫⎛⎫==⨯+⨯= ⎪ ⎪⎝⎭⎝⎭,()2124122211210227333333327P C ξ⎛⎫⎛⎫==+⋅⋅⋅⋅+⨯⨯=⎪ ⎪ ⎪⎝⎭⎝⎭, ()4101131272727P ξ==--=, 故ξ的概率分布为:18.(1)70.5千米/时;(2)(i )1587辆,(ii )()8.4135E X =. 【分析】(1)利用频率直方图,确定各组中点值i a ,由6110()i ii v a f ==∑即可求平均车速.(2)由题设易知(70.5,210.25)vN ,(i )(85)()P v P v μσ≥=≥+,结合所提供的三段区间概率值求概率,进而求10000辆机动车中车速不低于85千米/时的车辆数. (ii )由(i )知车速低于85千米/时的概率,则(10,0.84135),X B 利用二项分布的期望公式即可求期望. 【详解】 (1)由图知:(450.01550.015650.02750.03850.015950.01)1070.5v =⨯+⨯+⨯+⨯+⨯+⨯⨯=千米/时.∴这1000辆机动车的平均车速为70.5千米/时. (2)由(1)及题设知:(70.5,210.25)vN ,则70.5,14.5μσ==,(i )1()(85)()0.158652P v P v P v μσμσμσ--≤≤+≥=≥+==,∴10000辆机动车中车速不低于85千米/时的车辆数100000.158651587⨯≈辆. (ii )由(2)知:车速低于85千米/时的概率为10.158650.84135P =-=,故(10,0.84135),X B∴()100.841358.4135E X =⨯=.19.(1) 1.71z =,20.25s =;(2)0.84;(3)840. 【分析】(1)根据题目中的数据先求出平均数,再结合给出的方差公式()22211n i i s t nt n =⎛⎫=- ⎪⎝⎭∑可求得方差.(2)根据题意可得()~ 1.71,0.25X N ,则()()1.21 3.213P X P X μδμδ≤≤=-≤≤+,根据题目给出的数据,结合正态分布曲线的性质可得答案.(3) 由(2)可得鱼的质量在[]1,21,3.21的概率为0.84,则()~1000,0.84B ξ,由二项分布的数学期望公式可得答案. 【详解】 解:(1)105661.716040z +==+,22200.41117 1.710.25100s +=-=.(2)该鱼塘鱼质量满足()2~,X N μδ,其中 1.71μ=,20.25δ=,即()~ 1.71,0.25X N则()0.682702P X μδ-≤≤=,()0.9973032P X μδ≤≤+=∴()()1.21 3.213P X P X μδμδ≤≤=-≤≤+.()()0.68270.99730030.842P X P X μδμδ+=-≤≤+<≤+==(3)由(2)可得鱼的质量在[]1,21,3.21的概率为0.84. 由题意可知()~1000,0.84B ξ,由二项分布的数学期望公式可得,ξ的数学期望为()10000.84840Eξ=⨯=.20.(1)见解析;(2)B类.【分析】(1)通过题意分析出小明累计得分X的所有可能取值,逐一求概率列分布列即可.(2)与(1)类似,找出先回答B类问题的数学期望,比较两个期望的大小即可.【详解】(1)由题可知,X的所有可能取值为0,20,100.()010.80.2P X==-=;()()200.810.60.32P X==-=;()1000.80.60.48P X==⨯=.所以X的分布列为(2)由(1)知,()00.2200.321000.4854.4E X=⨯+⨯+⨯=.若小明先回答B问题,记Y为小明的累计得分,则Y的所有可能取值为0,80,100.()010.60.4P Y==-=;()()800.610.80.12P Y==-=;()1000.80.60.48P X==⨯=.所以()00.4800.121000.4857.6E Y=⨯+⨯+⨯=.因为54.457.6<,所以小明应选择先回答B类问题.21.(1)不能;17.6;(2)37.【分析】(1)利用直方图求得一、二等品所占比例的和,比较即可判定结论;利用各组的中间值乘以相应频率,求和即得活动前质量指标值的均值的估计值,利用正态分布求得“质量提升月”活动后该企业生产的这种产品的质量指标值的均值,作差即得所求;(2)先求得一、二、三等品的频率分别,得到分层抽样的方法抽取8件,一、二、三等品的件数,再考虑从这8件中随机抽取4件,抽取的4件产品中,一、二、三等品都有的情况,利用先分类后分步的思想,利用组合计数求得相应事件的方法种数,即可得所求概率.【详解】解:(1)根据抽样调查数据可知:一、二等品所占比例的估值0.2000.3000.2600.0900.025=++++0.8750.92=<,故不能认为该企业生产的这种产品符合“一、二等品至少要占全部产品92%”的规定.“质量提升月”活动前该企业生产的这种产品的质量指标值的均值约为:1700.0251800.11900.2⨯+⨯+⨯2000.32100.262200.092300.025200.4+⨯+⨯+⨯+⨯=.“质量提升月”活动后该企业生产的这种产品的质量指标值X近似地服从正态分布()218,140N,则()218E X=.∴“质量提升月”活动后的质量指标值的均值比活动前大约提升了218200.417.6=-=.(2)由频率分布直方图可知:一、二、三等品的频率分别为:0.375,0.5,0.125.故在样本中,按产品等级用分层抽样的方法抽取8件,一、二、三等品的件数分别为:3,4,1.再从这8件中随机抽取4件,抽取的4件产品中,一、二、三等品都有的情况有2种:①一、二、三等品的件数分别为:2,1,1.②一、二、三等品的件数分别为:1,2,1.故所求概率2111213413414837C C C C C CPC+==.22.(1)25;(2)9923125;(3)对甲更有利,理由见解析.【分析】(1)记甲得一分为事件M.M发生有两种可能:抢到题且答对,乙抢到题且答错,从而求得概率.(2)由(1)知,在每道题的抢答中甲、乙得一分的概率分别为25,35,设两人共抢答了X道题比赛结束,且甲获胜.根据比赛规则,X的所有可能取值分别为3,4,5,分别计算出(3)P X=,(4)P X=,(5)P X=,相加即甲获胜的概率.(3)先求得改变规则后甲获胜的概率,然后与(2)中的概率比较即可.【详解】解:(1)每道题的抢答中,记甲得一分为事件M .M 发生有两种可能:抢到题且答对,乙抢到题且答错,∴13112()25255P M =⨯+⨯=, ∴比赛开始,甲率先得一分的概率为25. (2)由(1)知,在每道题的抢答中甲、乙得一分的概率分别为25,35, 设两人共抢答了X 道题比赛结束,且甲获胜. 根据比赛规则,X 的所有可能取值分别为3,4,5,则328(3)5125P X ⎛⎫=== ⎪⎝⎭,3133272(4)C 55625P X ⎛⎫⎛⎫===⎪⎪⎝⎭⎝⎭, 232432432(5)C 553125P X ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭, 则甲获胜的概率992(3)(4)(5)3125P P X P X P X ==+=+==. (3)由(1)(2)知改变规则后甲获胜的概率22112232441100(2)(3)C 5551253125P P X P X ⎛⎫⎛⎫⎛⎫==+==+== ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭, 而110099231253125>, 即1P P >此时甲获胜的概率更大了,对甲更有利. 【点睛】关键点点睛:根据竞赛规则,分别把每种规则下对应的甲得分情况分清楚,然后计算获胜概率即可.。
高中数学理科试题及答案

高中数学理科试题及答案一、选择题(每题4分,共40分)1. 若函数\( f(x) = ax^2 + bx + c \)在\( x = 1 \)处取得极值,则\( a \)的值为:A. 0B. 1C. -1D. 22. 已知圆的方程为\( (x-2)^2 + (y-3)^2 = 9 \),其圆心坐标为:A. (2, 3)B. (-2, 3)C. (2, -3)D. (-2, -3)3. 函数\( y = \log_2(x) \)的图像不经过第几象限:A. 第一象限B. 第二象限C. 第三象限D. 第四象限4. 集合\( A = \{x | x^2 - 1 = 0\} \)和集合\( B = \{x | x^2 - 4x + 3 = 0\} \)的交集为:A. \{1\}B. \{1, 3\}C. \{-1, 1\}D. \{-1, 1, 3\}5. 已知等差数列\( \{a_n\} \)的前三项依次为2,5,8,则该数列的公差为:A. 1B. 2C. 3D. 46. 函数\( y = \frac{1}{x} \)在点\( (1, 1) \)处的切线斜率为:A. 0B. 1C. -1D. 无法确定7. 已知\( \sin \theta = \frac{3}{5} \),\( \theta \)为第一象限角,则\( \cos \theta \)的值为:A. \frac{4}{5}B. -\frac{4}{5}C. \frac{3}{5}D. -\frac{3}{5}8. 直线\( y = 2x + 3 \)与直线\( y = -x + 4 \)的交点坐标为:A. (1, 5)B. (-1, 5)C. (1, -1)D. (-1, -1)9. 已知\( \tan \alpha = 2 \),\( \alpha \)为锐角,则\( \sin \alpha \)的值为:A. \frac{2}{\sqrt{5}}B. \frac{1}{\sqrt{5}}C. \frac{2}{\sqrt{17}}D. \frac{1}{\sqrt{17}}10. 函数\( y = \sqrt{x} \)的定义域为:A. \( (-\infty, 0) \cup (0, +\infty) \)B. \( (0, +\infty) \)C. \( (-\infty, +\infty) \)D. \( (-\infty, 0] \cup [0, +\infty) \)二、填空题(每题4分,共20分)1. 已知等比数列的前三项依次为2,4,8,则该数列的公比为______。
2021人教版高中数学同步a版选修2-1(理科必考)模块练习题--1.4 全称量词与存在量词

1.4 全称量词与存在量词1.4.1 全称量词1.4.2 存在量词基础过关练题组一对全称命题、特称命题的理解1.下列命题中全称命题的个数是( )①任意一个自然数都是正整数;②所有的素数都是奇数;③有的等差数列也是等比数列;④三角形的内角和是180°.A.0B.1C.2D.32.下列命题不是“∃x∈R,x2>3”的另一种表述的是( )A.有一个x∈R,使得x2>3成立B.对有些x∈R,使得x2>3成立C.任选一个x∈R,使得x2>3成立D.至少有一个x∈R,使得x2>3成立3.“a∥α,则a平行于平面α内的任一直线”是( )A.全称命题B.特称命题C.不是命题D.真命题4.命题“有些负数满足不等式(1+x)(1-9x)>0”用“∃”或“∀”可表述为.5.用全称量词或存在量词表示下列语句:①不等式x 2+x+1>0恒成立;②当x 为有理数时,13x 2+12x+1也是有理数;③方程3x-2y=10有整数解.题组二 全称命题、特称命题的真假判定6.下列命题中,既是真命题又是全称命题的是() A.对任意实数a,b,都有a 2+b 2-2a-2b+2<0B.梯形的对角线不相等C.∃x 0∈R ,√x 02=x 0D.对数函数在定义域上是单调函数7.已知a>0,函数f(x)=ax2+bx+c.若x0满足关于x的方程2ax+b=0,则下列命题中为假命题的是( )A.存在x∈R, f(x)≤f(x0)B.存在x∈R, f(x)≥f(x0)C.任意x∈R, f(x)≤f(x0)D.任意x∈R, f(x)≥f(x0)8.下列命题为真命题的是( )A.∀x∈R,cos x<2B.∃x∈Z,log2(3x-1)<0C.∀x>0,3x>3D.∃x∈Q,方程√2x-2=0有解9.命题p:∃x0∈R,x02+2x0+5<0是(填“全称命题”或“特称命题”),它是命题(填“真”或“假”).10.下列命题:①存在x<0,使|x|>x;②对于一切x<0,都有|x|>x;③已知a n=2n,b n=3n,对于任意n∈N*,都有a n≠b n;④已知A={a|a=2n},B={b|b=3n},对于任意n∈N*,都有A∩B=⌀.其中,所有真命题的序号为.题组三根据命题的真假求参数的取值范围=m,则实数m的取值范围是.11.若∃x∈R,x+1x12.已知函数f(x)=x2+mx+1,若命题“∃x>0, f(x)<0”为真,则m的取值范围是.13.(2019湖北武汉部分市级示范性高中高三联考)已知命题p:∀x∈R,ax2+ax+1≥0,命题q:|2a-1|≤3.(1)若命题p是真命题,求实数a的取值范围;(2)若p∨q是真命题,p∧q是假命题,求实数a的取值范围.能力提升练一、选择题1.(2019福建莆田高二期中,★★☆)下列命题中的假命题是( )A.∀x∈R,2x-1>0B.∀x∈N*,(x-1)2>0C.∃x0∈R,ln x0<1D.∃x0∈R,tan x0=22.(★★☆)下列命题中的假命题是( )A.∃x0∈R,3x02-8x0+9=0B.∃x0∈(0,1),lg x0>ln x0C.∀x∈(0,+∞),(12)x>(13)xD.∀x∈R,x2-3x+4>03.(2018宁夏育才中学高二期末,★★☆)若命题“∀x∈R,kx2-kx-1<0”是真命题,则k的取值范围是( )A.-4≤k≤0B.-4≤k<0C.-4<k≤0D.-4<k<04.(★★★)若命题“存在x∈R,使x2+(a-1)x+1<0”是假命题,则实数a的取值范围是( )A.a>3或a<-1B.a≥3或a≤-1C.-1<a<3D.-1≤a≤3二、填空题5.(2019广东潮州高三第二次模拟,★★☆)已知a∈R,命题p:∀x∈[1,2],x2-a≥0,命题q:∃x∈R,x2+2ax+2-a=0,若命题p∧q为真命题,则实数a的取值范围是.6.(★★☆)已知函数f(x)=x2+m,g(x)=(12)x,若对任意x1∈[-1,3],存在x2∈[0,2],使f(x1)≥g(x2),则实数m的取值范围是.7.(2020广东东莞高二期末,★★☆)已知命题“∀x∈[1,3],不等式x2-ax+4≥0”为真命题,则a的取值范围为.三、解答题8.(2019内蒙古赤峰高二期末,★★☆)设命题p:对任意x∈[0,1],不等式2x-2≥m2-3m恒成立,命题q:存在x∈[-1,1],使得不等式x2-x+m-1≤0成立.(1)若p为真命题,求实数m的取值范围;(2)若p∧q为假命题,p∨q为真命题,求实数m的取值范围.9.(★★★)已知a>1且a≠1,命题p:函数f(x)=log(2a-1)x在其定义域2上是减函数;命题q:函数g(x)=√x+|x-a|-2的定义域为R,如果p∨q 为真,试求a的取值范围.10.(★★★)设集合A={(x,y)|(x-4)2+y2=1},B={(x,y)|(x-t)2+(y-at+2)2=1},若命题“∃t0∈R,A∩B≠⌀”是真命题,求实数a的取值范围.答案全解全析基础过关练1.D 命题①②含有全称量词,而命题④可以叙述为“所有的三角形的内角和都是180°”,故有三个全称命题,命题③是特称命题.2.C 选项C 是全称命题,故错误.3.A 该命题是全称命题,且是假命题.4.答案 ∃x 0<0,使得(1+x 0)(1-9x 0)>05.解析 ①对任意实数x,不等式x 2+x+1>0恒成立.②对任意有理数x,13x 2+12x+1是有理数. ③存在一对整数x 0,y 0,使3x 0-2y 0=10成立.6.D A 是全称命题,且a 2+b 2-2a-2b+2=(a-1)2+(b-1)2≥0,故A 是假命题;B 中隐含量词“所有的”,是全称命题,但梯形中只有等腰梯形的对角线相等,故B 是假命题;C 是特称命题;D 是全称命题且是真命题.7.C f(x)=ax 2+bx+c=a (x +b 2a )2+4ac -b 24a (a>0), 由题意知2ax 0+b=0,∴x 0=-b 2a ,当x=x 0时,函数f(x)取得最小值,∴∀x∈R , f(x)≥f(x 0),从而A,B,D 为真命题,C 为假命题.8.A A 中,由于函数y=cos x 的最大值是1,所以A 是真命题;B中,log 2(3x-1)<0⇔0<3x-1<1⇔13<x<23,所以B 是假命题;C 中,当x=1时,31=3,所以C 是假命题;D 中,√2x-2=0⇔x=√2∉Q,所以D 是假命题.故选A.9.答案 特称命题;假解析 命题p:∃x 0∈R ,x 02+2x 0+5<0是特称命题.因为x 02+2x 0+5=(x 0+1)2+4>0恒成立,所以命题p为假命题.10.答案 ①②③解析 命题①②显然为真命题;③由于a n -b n =2n-3n=-n<0,所以∀n∈N *,都有a n <b n ,即a n ≠b n ,故为真命题;④已知A={a|a=2n},B={b|b=3n},如n=1,2,3时,A∩B={6},故为假命题.11.答案 (-∞,-2]∪[2,+∞)解析 依题意得,关于x 的方程x+1x =m 有实数解,设f(x)=x+1x , 由基本不等式,得当x>0时, f(x)≥2,当x<0时, f(x)≤-2,故f(x)的值域为(-∞,-2]∪[2,+∞),故实数m 的取值范围是(-∞,-2]∪[2,+∞).12.答案 (-∞,-2)解析 易知函数f(x)=x 2+mx+1的图象过点(0,1),若命题“∃x>0, f(x)<0”为真,则函数f(x)=x 2+mx+1的图象的对称轴必在y 轴的右侧,且与x 轴有两个交点,所以Δ=m 2-4>0,且-m 2>0,即m<-2,所以m 的取值范围是(-∞,-2).13.解析 (1)命题p 是真命题时,ax 2+ax+1≥0在R 上恒成立,∴①当a=0时,有1≥0恒成立;②当a≠0时,有{a >0,Δ=a 2-4a ≤0,解得0<a≤4,∴a 的取值范围为[0,4].(2)∵p∨q 是真命题,p∧q 是假命题,∴p、q 一真一假,当q 为真时,-1≤a≤2,故①p 真q 假时,有{0≤a ≤4,a <-1或a >2,∴2<a≤4;②p 假q 真时,有{a <0或a >4,-1≤a ≤2,∴-1≤a<0.∴a 的取值范围为[-1,0)∪(2,4].能力提升练一、选择题1.B A.2x-1>0在x∈R 上恒成立,是真命题;B.当x=1时,(x-1)2=0,是假命题;C.当x 0=1时,ln x 0=0<1,是真命题;D.y=tan x 在[0,π2]上的值域为[0,+∞),所以∃x 0∈R ,tan x 0=2是真命题.2.A 选项A 中,Δ=64-4×3×9=-44,则方程3x 2-8x+9=0无实数根,故选A.3.C 当k=0时,有-1<0恒成立;当k≠0时,令y=kx 2-kx-1,∵y<0恒成立,∴抛物线y=kx 2-kx-1开口向下,且与x 轴没有公共点,∴k<0,且Δ=k 2+4k<0,解得-4<k<0.综上所述,k 的取值范围为-4<k≤0.4.D 因为命题是假命题,所以方程x 2+(a-1)x+1=0没有实数根或有两个相等实数根,所以Δ=(a -1)2-4≤0,解得-1≤a≤3.二、填空题5.答案 a≤-2或a=1解析 若命题p:“∀x∈[1,2],x 2-a≥0”为真命题,则1-a≥0,解得a≤1.若命题q:“∃x∈R ,x 2+2ax+2-a=0”为真命题,则Δ=4a 2-4(2-a)≥0,解得a≤-2或a≥1.因为p∧q 是真命题,所以a≤-2或a=1.6.答案 [14,+∞)解析 因为对任意x 1∈[-1,3],f(x 1)∈[m,9+m],所以f(x)的最小值为m.存在x 2∈[0,2],使f(x 1)≥g(x 2)成立,只要满足g(x)在[0,2]上的最小值小于或等于m 即可,而g(x)是单调递减函数,故g(x)的最小值为g(2)=(12)2=14,得m≥14.7.答案 (-∞,4]解析 令f(x)=x 2-ax+4,则其图象的对称轴为直线x=a 2, 要使∀x∈[1,3],不等式x 2-ax+4≥0恒成立,即∀x∈[1,3], f(x)min ≥0.当a 2≤1,即a≤2时, f(x)min =f(1)=12-a+4≥0,解得a≤2; 当1<a 2<3,即2<a<6时, f(x)min =f (a 2)=(a 2)2-a×a 2+4≥0,解得2<a≤4;当a 2≥3,即a≥6时, f(x)min =f(3)=32-3a+4≥0,无解. 综上可得a∈(-∞,4].三、解答题8.解析 对于p,∵2x -2≥m 2-3m 对任意x∈[0,1]恒成立,y=2x-2在[0,1]上的最小值为-2,∴m 2-3m≤-2,解得1≤m≤2.对于q,存在x∈[-1,1],使x 2-x+m-1≤0成立,所以y=x 2-x+m-1在[-1,1]上的最小值小于等于0,即-54+m≤0,∴m≤54. (1)若p 为真命题,则1≤m≤2.(2)若p∧q 为假命题,p ∨q 为真命题,则p,q 一真一假.若p 为真命题,q 为假命题,则{1≤m ≤2,m >54, ∴54<m≤2; 若p 为假命题,q 为真命题,则{m <1或m >2,m ≤54,∴m<1. 综上,m<1或54<m≤2. 9.解析 若p 为真,则0<2a-1<1,得12<a<1.若q 为真,则x+|x-a|-2≥0对任意x∈R 恒成立.记h(x)=x+|x-a|-2,则h(x)={2x -a -2,x ≥a ,a -2,x <a ,所以h(x)的最小值为a-2,即q 为真时,a-2≥0,即a≥2.由p∨q 为真,得12<a<1或a≥2,故a 的取值范围为(12,1)∪[2,+∞). 10.解析 易知A={(x,y)|(x-4)2+y 2=1}表示平面直角坐标系中以M(4,0)为圆心,1为半径的圆,B={(x,y)|(x-t)2+(y-at+2)2=1}表示以N(t,at-2)为圆心,1为半径的圆,且其圆心N 在直线ax-y-2=0上,如图.若命题“∃t0∈R,A∩B≠⌀”是真命题,即两圆有公共点,则圆心M(4,0)到直线ax-y-2=0的距离不大于2,即√a2+1≤2,解得0≤a≤43.所以实数a的取值范围是0≤a≤43.。
高中数学选修本(理科)数学归纳法及其应用举例2

用的方法:乘法公式、因式分解、添拆项、配方等。5)两个步骤、一个结论缺一不可,否则结论不能 成立:。递推基础不可少,归纳假设要用到,结论写明莫忘掉
Image
12/9/2021
第十三页,共十三页。
证明:1、当n=1时,左=12=1,右= 1(11)(21) 1
∴n=1时,等式成立
6
2、假设n=k时,等式成立,即
1 2 2 2 3 2 k 2 k (k 1 )2 ( k 1 )
那么,当n=k+1时
6
左=12+22+…+k2+(k+1)2= k(k1)2 (k1)(k1)2 6
k ( k 1 )2 k ( 1 ) 6 ( k 1 ) 2 ( k 1 )k ( 2 )2 k ( 3 )
数数数数学数学学学(归s(hshùùx归xu归纳ué)é归)归纳纳法纳纳法法及法及其及其其应其应应用应应用(用yìn用g用举yò举ng举)例举例例例例
第二课时
第一页,共十三页。
复习引入:
找准起点 (qǐdiǎn)
奠基要稳
数学归纳法是一种证明与自然数有关的数学命题的重要方法。
其格式主要有两个步骤、一个结论:
第十一页,共十三页。
练习(liànxí)巩固 1.求证:当n∈N*时,
1 1 1 1 1 1 11 1 234 2 n 12 nn 1n 2 2n3n2 n12
4
第十二页,共十三页。
内容(nèiróng)总结
数学归纳法及其应用举例。2、假设n=k时,等式成立,即。那么,当n=k+1时,有。根据①②问可 知,对n∈N*,等式成立.。+k(k+1)=。1)明确(míngquè)首先取值n0并验证命题真假(必不可少)。
(常考题)北师大版高中数学选修1-2第四章《数系的扩充与复数的引入》测试题(含答案解析)(4)

一、选择题1.1z 2z 是复数,则下列结论中正确的是( )A .若22120z z +>,则2212z z >- B .12||z z -=C .22121200z z z z +=⇔==D .2211||||z z =2.复数(),z a bi a b R =+∈,()m z z b =+,n z z =⋅,2p z =,则( )A .m 、n 、p 三数都不能比较大小B .m 、n 、p 三数的大小关系不能确定C .m n p ≤=D .m n p ≥=3.定义运算,,a b ad bc c d=-,则符合条件,10 ,?2z i i i+=-的复数 z 对应的点在( )A .第一象限B .第二象限C .第三象限D .第四象限4.若复数1z ,2z 满足1134z z i +=-,212z i ++=,则12z z -的最小值为( ).A .110B .1110C .2110D .2110-5.若复数2320211z i i i i =++++⋯+,则复数z 对应的点在第( )象限 A .一B .二C .三D .四6.下列关于复数z 的四个命题中,正确的个数是( ) (1)若|1||1|2z z -++=,则复数z 对应的动点的轨迹是椭圆; (2)若|2||2|2z z --+=,则复数z 对应的动点的轨迹是双曲线; (3)若|1||Re 1|z z -=+,则复数z 对应的动点的轨迹是抛物线; (4)若|2|3z -≤,则||z 的取值范围是[1,5] A .4 B .1C .2D .37.若复数1a iz i+=-,且3·0z i >,则实数a 的值等于( ) A .1B .-1C .12 D .12- 8.已知i 为虚数单位,a 为实数,复数(2)(1)z a i i =-+在复平面内对应的点为M ,则“1a =”是“点M 在第四象限”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充要条件 D .既不充分也不必要条件9.已知复数21iz i=+,则共轭复数z =( ) A .1i -+B .1i -C .1i +D .1i --10.若复数()()12i 2i z =-+(其中i 为虚数单位)在复平面中对应的点位于( ) A .第一象限B .第二象限C .第三象限D .第四象限11.已知实数[1,1]a ∈-,实数[1,2]b ∈-,则复数2a biz i+=-在复平面内对应的点位于第一象限的概率为( ) A .524B .14C .724D .1312.设1z ,2z 为复数,则下列命题中一定成立的是( )A .如果22120z z +=,那么120z z == B .如果12=z z ,那么12=±z zC .如果1z a ≤(a 为正实数),那么1a z a -≤≤D .如果1z a =(a 为正实数),那么211z z a ⋅=二、填空题13.已知复数()(()()3422312i iz i i +-=++,那么复数z 的模为______.14.若复数z 满足24z z i +=-(i 为虚数单位),则z 的最小值为__________. 15.若复数z 满足i 12i01z+=,其中i 是虚数单位,则z 的虚部为________16.已知i 是虚数单位,则复数11ii+-的实部为______. 17.已知()21,1xyi x y R i+=∈-,则x y +=__________. 18.若复数是纯虚数(是虚数单位),为实数,则复数的模为__________.19.设复数()21z i =-(i 是虚数单位),则z 的模为__________. 20.复数z 满足()12i z -=,则z 的虚部是__________.三、解答题21.已知复数z 满足|z |2=z 的实部大于0,z 2的虚部为2.(1)求复数z ;(2)设复数z ,z 2,z ﹣z 2之在复平面上对应的点分别为A ,B ,C ,求(OA OB +)⋅OC 的值.22.设z 为关于x 的方程20x mx n ++=(,m n ∈R )的虚根,i 为虚数单位. (1)当1i z =-+时,求m 、n 的值;(2)若1n =,在复平面上,设复数z 所对应的点为P ,复数24i +所对应的点为Q ,试求||PQ 的取值范围.23.设复数n n n z x i y =+⋅,其中n x n y ∈R ,*n ∈N ,i 为虚数单位,1(1)n n z i z +=+⋅,134z i =+,复数n z 在复平面上对应的点为n Z .(1)求复数2z ,3z ,4z 的值;(2)是否存在正整数n 使得n OZ ∥1OZ ?若存在,求出所有满足条件的n ;若不存在,请说明理由;(3)求数列{}n n x y ⋅的前102项之和.24.已知复数()0,z a i a a R =+>∈,i 为虚数单位,且复数2z z+为实数. (1)求复数z ;(2)在复平面内,若复数()2m z +对应的点在第一象限,求实数m 的取值范围.25.已知复数Z 满足23z i z i -=++(其中i 为虚数单位) (1)求z ; (2)若2a iz+为纯虚数,求实数a 的值. 26.已知复数1z 满足()11i 13i z -=+,()2i z a a R =-∈(其中i 是虚数单位),若121z z ->,求a 的取值范围.【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【分析】举反例12z i =+,22z i =-可判断选项A 、B ,举反例11z =,2z i =可判断选项C ,设1z a bi =+,(),a b R ∈,分别计算21||z 、21||z 即可判断选项D ,进而可得正确选项.【详解】对于选项A :取12z i =+,22z i =-,()221232z i i =+=+,()222232z i i =-=-,满足221260z z +=>,但21z 与22z 是两个复数,不能比较大小,故选项A 不正确; 对于选项B :取12z i =+,22z i =-,12||22z z i -==,==B 不正确;对于选项C :取11z =,2z i =,则22120z z +=,但是10z ≠,20z ≠,故选项C 不正确; 对于选项D :设1z a bi =+,(),a b R ∈,则()222212z a bi a b abi =+=-+2221z a b ===+,1z a bi =-,1z =,所以2221z a b =+,所以2211||||z z =,故选项D 正确.故选:D.2.C解析:C 【分析】根据复数的四则运算,结合基本不等式,即可得出结论. 【详解】z a bi =-,()2m a bi a bi b ab =++-=,22()()n a bi a bi a b =+-=+,22p a b =+222a b ab +,当且仅当a b =时,取等号m n p ∴≤=故选:C 【点睛】本题主要考查了复数的四则运算,涉及了基本不等式的应用,属于中档题.3.B解析:B 【解析】 由题意可得:()()(),1210,2z i z i i i i i+=--+=-,即()()()121221222422i i i i i z i i i -----====---,∴1 22iz =-+,则复数z 对应的点的坐标为11,22⎛⎫-⎪⎝⎭在第二象限,故选B. 4.A解析:A 【分析】由复数模的定义求出1z 对应的点在一条直线上,2z 对应的点在圆上,利用圆的性质可求得直线上的点到圆上点的距离的最小值. 【详解】复数1z 对应的点为1(,)Z x y ,因为1134z z i +=-,所以=6870x y +-=,所以点1Z 的轨迹是一条直线.复数2z 对应的点为2(,)Z x y ,因为212z i ++=表示点(),x y 到定点()1,1--的距离为2,所以点2Z 的轨迹表示以()1,1--为圆心、半径为2的圆,12z z -211221010-=-=. 故选:A .本题考查复数的模的运算,考查模的几何意义,利用几何意义把复数问题转化为直线上的点到圆上点的距离的最小值这个几何问题,利用几何性质得出求解方法.5.A解析:A 【分析】根据周期性得到1z i =+,得到答案. 【详解】2320211(11)(11)11z i i i i i i i i i i =++++⋯+=+--+⋯++--++=+,故复数z 对应的点在第一象限. 故选:A. 【点睛】本题考查了复数对应象限,意在考查学生的计算能力和转化能力.6.B解析:B 【分析】(1)根据椭圆的定义来判断;(2)根据双曲线的定义来判断;(3)根据抛物线的定义来判断;(4)利用圆的有关知识点判断. 【详解】(1)|1||1|2z z -++=,表示复平面内到点()()1,0,1,0-距离之和为2的点的轨迹,是由点()()1,0,1,0-构成的线段,故错误;(2)|2||2|2z z --+=,表示复平面内到点()2,0的距离比到点()2,0-的距离大2的点的轨迹,是双曲线的左支,故错误;(3)|1||Re 1|z z -=+,表示复平面内到点()1,0的距离等于到直线1x =-的距离的点的轨迹(点()1,0不在直线1x =-上),所以轨迹是抛物线,故正确;(4)|2|3z -≤,表示点的轨迹是圆心为()2,0,半径为3的圆及其内部(坐标原点在圆内),且z 表示轨迹上的点到原点的距离,所以min 0=,此时z 对应的点为原点,max 325r d =+=+=(d 表示原点到圆心的距离),所以 ||z 的取值范围是[0,5],故错误. 故选B. 【点睛】复数对应的轨迹方程:(1)122z z z z a -+-=,当122a z z >-时,此时z 对应的点的轨迹是椭圆; (2)()1220z z z z a a ---=>,当122a z z <-时,此时z 对应的点的轨迹是双曲线.7.A【分析】由3·0z i >可判定3·z i 为实数,利用复数代数形式的乘除运算化简复数z ,再由实部为0,且虚部不为0列式求解即可. 【详解】()()()()()i 1i 11ii 1i 1i 1i 2a a a a z ++-+++===--+, 所以3·z i =()()()()341i 1i 1i 122a a a a -++--++=,因为3·0z i >,所以3·z i 为实数,102a --= 可得1a =,1a =时3,?10z i =>,符合题意,故选A. 【点睛】复数是高考中的必考知识,主要考查复数的概念及复数的运算.要注意对实部、虚部的理解,掌握纯虚数、共轭复数、复数的模这些重要概念,复数的运算主要考查除法运算,通过分母实数化转化为复数的乘法,运算时特别要注意多项式相乘后的化简,防止简单问题出错,造成不必要的失分.8.A解析:A 【解析】因为(2i)(1+i)=a+2+(a-2)i z a =-,则点M 在第四象限时,满足2>a>-2,因此可知“1a =”是“点M 在第四象限”的充分而不必要条件,选A9.B解析:B 【解析】分析:首先求得复数z ,然后求解其共轭复数即可. 详解:由题意可得:()()()()2121211112i i i iz i i i i -+====+++-, 则其共轭复数1z i =-. 本题选择B 选项.点睛:本题主要考查复数的运算法则,共轭复数的概念等知识,意在考查学生的转化能力和计算求解能力.10.D解析:D 【解析】分析:利用复数的出发计算得到z ,即可得到结论. 详解:()()12i 2i 24243,z i i i =-+=+-+=-故z 在复平面中对应的点位于第四象限. 故选D.点睛:本题考查复数乘法运算及复数的几何意义,是基础题.11.A解析:A 【解析】分析:化简复数z ,得()()225a b a b i z -++=,复数z 在复平面内对应的点位于第一象限,则2020a b a b ->+>,结合[]1,1a ∈-,[]1,2b ∈-,画出可行域,利用几何概型即可求出答案.详解:化简复数z ,得()()225a b a b i z -++=,复数z 在复平面内对应的点位于第一象限,则2020a b a b ->+>,又[] 1,1a ∈-,[]1,2b ∈-,故在平面直角坐标系上画出可行域,如图所示:∴复数z 在复平面内对应的点位于第一象限的概率1515222324P ⨯⨯==⨯. 故选:A.点睛:应用几何概型求概率的方法建立相应的几何概型,将试验构成的总区域和所求事件构成的区域转化为几何图形,并加以度量.(1)一般地,一个连续变量可建立与长度有关的几何概型,只需把这个变量放在数轴上即可;(2)若一个随机事件需要用两个变量来描述,则可用这两个变量的有序实数对来表示它的基本事件,然后利用平面直角坐标系就能顺利地建立与面积有关的几何概型;(3)若一个随机事件需要用三个连续变量来描述,则可用这三个变量组成的有序数组来表示基本事件,利用空间直角坐标系即可建立与体积有关的几何概型.12.D解析:D 【分析】对A,举出反例判断正误; 对B,举出反例判断正误;对C,利用复数的几何意义判断正误; 对D,设出复数即可化简结果,再判断正误即可. 【详解】对于A,如果11z i =-,21z i =+,22120z z +=,所以120z z ==不正确。
(完整版)北师大版高中数学选修2-1期末考试试题及答案(理科),推荐文档

G1,2,0
AP 2,0,2 EF 0,1,0 FG 1,2,1 ………………3 分
………14
设平面 GEF 的法向量 n (x, y, z) ,由法向量的定义得:
我去人也就有人!为UR扼腕入站内信不存在向你偶同意调剖沙 n n
9.在正方体 ABCD A1B1C1D1 中, E 是棱 A1B1 的中点,则 A1B 与 D1E 所成角的余弦值为(
)
5
10
5
10
A. 10 B. 10 C. 5 D. 5
10.若椭圆 mx2 ny 2 1(m 0, n 0)与直线y 1 x 交于 A,B 两点,过原点与线段 AB 中点
n
2
的连线的斜率为 2 ,则 m 的值是(
)
A. 2 2 B. 2 C. 3 D . 2
9
2
2
11.过抛物线 x 2 4 y 的焦点 F 作直线交抛物线于 P1 x1, y1 , P2 x2 , y2 两点,若
y1 y2 6 ,则 P1P2 的值为 ( )
A.5
B.6
DQ 1 (DP DB)
∴
2
,
………………………………13 分
故在线段 PB 上存在一点 Q,使 PC⊥平面 ADQ,且点 Q 为线段 PB 的中点。……15分
解法二:(1)∵EF∥CD∥AB,EG∥PB,根据面面平行的判定定理
∴平面 EFG∥平面 PAB,又 PA 面 PAB,∴AP∥平面 EFG ……………………4 分
(2)∵平面 PDC⊥平面 ABCD,AD⊥DC
∴AD⊥平面 PCD,而 BC∥AD,∴BC⊥面 EFD
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高二期末考试数学试题晁群彦一.选择题(每小题5分,满分60分)1.设n m l ,,均为直线,其中n m ,在平面”“”“,n l m l l a ⊥⊥⊥且是则内α的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件2.对于两个命题:①,1sin 1x R x ∀∈-≤≤, ②22,sin cos 1x R x x ∃∈+>,下列判断正确的是( )。
A. ① 假 ② 真B. ① 真 ② 假C. ① ② 都假D. ① ② 都真3.与椭圆1422=+y x 共焦点且过点(2,1)Q 的双曲线方程是( ) A. 1222=-y x B. 1422=-y x C. 1222=-y x D. 13322=-y x 4.已知12,F F 是椭圆的两个焦点,过1F 且与椭圆长轴垂直的弦交椭圆与A ,B 两点, 则2ABF ∆是正三角形,则椭圆的离心率是( )A2 B 12 C3 D 135.过抛物线28y x =的焦点作倾斜角为045直线l ,直线l 与抛物线相交与A ,B 两点,则弦AB 的长是( )A 8B 16C 32D 646.在同一坐标系中,方程)0(0122222>>=+=+b a by ax x b x a 与的曲线大致是( )A .B .C .D .7.已知椭圆12222=+b y a x (b a >>0) 的两个焦点F 1,F 2,点P 在椭圆上,则12PF F ∆的面积 最大值一定是( )A 2a B ab C 22a a b - D 22b a b -8.已知向量b a b a k b a -+-==2),2,0,1(),0,1,1(与且互相垂直,则实数k 的值是( )A .1B .51C . 53D .579.在正方体1111ABCD A B C D -中,E 是棱11A B 的中点,则1A B与1D E所成角的余弦值为( )A .510B .1010C .55D .10510.若椭圆x y n m ny mx -=>>=+1)0,0(122与直线交于A ,B 两点,过原点与线段AB 中点的连线的斜率为22,则m n的值是( )2.23.22.292. D C B A11.过抛物线y x 42=的焦点F 作直线交抛物线于()()222111,,,y x P y x P 两点,若621=+y y ,则21P P 的值为 ( )A .5B .6C .8D .1012.以12422y x -=1的焦点为顶点,顶点为焦点的椭圆方程为 ( ) A.1121622=+y x B. 1161222=+y x C. 141622=+y x D. 二.填空题(每小题4分)13.已知A 、B 、C 三点不共线,对平面ABC 外一点O ,给出下列表达式:y x 31++=其中x ,y 是实数,若点M 与A 、B 、C 四点共面,则x+y=___14.斜率为1的直线经过抛物线y2=4x 的焦点,且与抛物线相交于A,B 两点,则AB等于___15.若命题P:“∀x >0,0222<--x ax ”是真命题 ,则实数a 的取值范围是___.16.已知90AOB ∠=︒,C 为空间中一点,且60AOC BOC ∠=∠=︒,则直线OC 与平面AE y x D CBAOB 所成角的正弦值为___.三.解答题(解答应写出必要的文字说明、证明过程和演算步骤。
) 17.(本小题满分14)设命题P :2",2"x R x x a ∀∈->,命题Q :2",220"x R x ax a ∃∈++-=; 如果“P 或Q ”为真,“P 且Q ”为假,求a 的取值范围。
18.(15分)如图①在直角梯形ABCP 中,BC ∥AP ,AB ⊥BC ,CD ⊥AP ,AD=DC=PD=2,E ,F ,G 分别是线段PC 、PD ,BC 的中点,现将ΔPDC 折起,使平面PDC ⊥平面ABCD(如图②) (Ⅰ)求证AP ∥平面EFG ;(Ⅱ)求二面角G-EF-D 的大小;(Ⅲ)在线段PB 上确定一点Q ,使PC ⊥平面ADQ ,试给出证明.19.(15分) 如图,金砂公园有一块边长为2的等边△ABC 的边角地,现修成草坪,图中DE 把草坪分成面积相等的两部分,D 在AB 上,E 在AC 上.(Ⅰ)设AD =x ,DE =y ,求y 关于x 的函数关系式;(Ⅱ)如果DE 是灌溉水管,我们希望它最短,则DE 的位置应在哪里?请予以证明.20(本小题满分15分)设21,F F 分别为椭圆)0(1:2222>>=+b a by a x C 的左、右两个焦点.(Ⅰ)若椭圆C 上的点21,)23,1(F F A 到两点的距离之和等于4,求椭圆C 的方程和焦点坐标;(Ⅱ)设点P 是(Ⅰ)中所得椭圆上的动点,的最大值求||),21,0(PQ Q 。
21(本小题满分15分)如图,设抛物线C:y x 42=的焦点为F ,),(00y x P 为抛物线上的任一点(其中0x ≠0), 过P 点的切线交y 轴于Q 点.(Ⅰ)证明:FQ FP =;(Ⅱ)Q 点关于原点O 的对称点为M ,过M 点作平行于PQ 的直线 交抛物线C 于A 、B 两点,若)1(>=λλMB AM ,求λ的值.高二(理科)期末考试数学试题参考答案及评分标准一.选择题:ABCCB D CBDB DD二、填空题:13. 13.8 14.)4,(-∞15详解:由对称性点C 在平面AOB 内的射影D 必在AOB ∠的平分线上作DE OA ⊥于E ,连结CE 则由三垂线定理CE OE ⊥,设1DE =1,2OE OD ⇒==,又60,2COE CE OE OE ∠=⊥⇒=,所以222CD OC OD =-=,因此直线OC 与平面AOB 所成角的正弦值2sin COD ∠=.y ex =三.解答题:17解:命题P :2",2"x R x x a ∀∈->即222(1)1x x x a -=-->恒成立1a ⇔<- …………3分 命题Q :2",220"x R x ax a ∃∈++-= 即方程2220x ax a ++-=有实数根∴2(2)4(2)0a a ∆=--≥ 2a ⇔≤-或1a ≥ .…………6分 ∵“P 或Q ”为真,“P 且Q ”为假,∴P 与Q 一真一假 …………8分 当P 真Q 假时,21a -<<-;当P 假Q 真时,1a ≥ …………10 ∴a 的取值范围是(2,1)[1,)--+∞ ………1418(14分)解法一:(Ⅰ)在图②中 ∵平面PDC ⊥平面ABCD ,AP ⊥CD ∴ PD ⊥CD ,PD ⊥DA ∴PD ⊥平面ABCD如图. 以D 为坐标原点,直线DA 、DC 、DP 分别为yx 、与z 轴建立空间直角坐标系: …………………1分 则()0,0,0D ()0,0,2A ()0,2,2B ()0,2,0C ()2,0,0P()1,1,0E ()1,0,0F ()0,2,1G32()2,0,2-=∴ ()0,1,0-=EF ()1,2,1-=FG ………………3分设平面GEF 的法向量),,(z y x n =,由法向量的定义得: ⎩⎨⎧==⇒⎩⎨⎧=-+=⇒⎩⎨⎧=-•=-•⇒⎪⎩⎪⎨⎧=•=•z x y z y x y EF n 00200)1,2,1()z y,x,(0)0,1,0()z y,x,(00不妨设 z=1, 则………………………………4分 0210212=⨯+⨯+⨯-=⋅ ………………………………5分⊥∴,点P ∉ 平面EFG∴AP ∥平面EFG ………………………………6分(Ⅱ)由(Ⅰ)知平面GEF 的法向量 ,因平面EFD 与坐标平面PDC 重合 则它的一个法向量为=(1,0,0)8分 设二面角D EF G --为θ.则 …………9分由图形观察二面角D EF G --为锐角,故二面角G-EF-D 的大小为45°。
………10分 (Ⅲ)假设在线段PB 上存在一点Q ,使PC ⊥平面ADQ ,∵P 、Q 、D 三点共线,则设t t +-=)1(,又()0,2,2=,()2,0,0=DP ∴)22,2,2(t t t -=,又()2,0,0= …………11分 若PC ⊥平面ADQ ,又)2,2,0(-=则210)22(2220)22,2,2()0,2,-2(0)0,0,2()0,2,-2(00=⇒=--⨯⇒⎩⎨⎧=-•=•⇒⎪⎩⎪⎨⎧=•=•t t t t t t DQ PC DA PC …………15分∴)DB DP DQ +=(21, ………………………………13分故在线段PB 上存在一点Q ,使PC ⊥平面ADQ ,且点Q 为线段PB 的中点。
……15分 解法二:(1)∵EF ∥CD ∥AB ,EG ∥PB ,根据面面平行的判定定理∴平面EFG ∥平面PAB ,又PA ⊂面PAB ,∴AP ∥平面EFG ……………………4分 (2)∵平面PDC ⊥平面ABCD ,AD ⊥DC∴AD ⊥平面PCD ,而BC ∥AD ,∴BC ⊥面EFD过C 作CR ⊥EF 交EF 延长线于R 点连GR ,根据三垂线定理知 ∠GRC 即为二面角的平面角,∵GC=CR ,∴∠GRC=45°, 故二面角G-EF-D 的大小为45°。
…………………8分 (3)Q 点为PB 的中点,取PC 中点M ,则QM ∥BC ,∴QM ⊥PC在等腰Rt △PDC 中,DM ⊥PC ,∴PC ⊥面ADMQ ……………………15分 19(14分)解: (1)在△ADE 中,y 2=x 2+AE2-2x ·AE·cos60°2221cos =⋅==θ)1,0,1(=n )1,0,1(=⇒y 2=x 2+AE2-x ·AE,①又S △ADE = S △ABC = · 2= x ·AE·sin60°⇒x ·AE =2.② ……4分②代入①得y 2=x 2+ -2(y >0), ∴y =6分又x ≤2,若1x <,,矛盾,所以x ≥1∴y = ≤2). ………………………7分(2)如果DE 是水管y = = ………………10分当且仅当x 2=24x ,即x =2时“=”成立, …………………………15分故DE ∥ BC ,且DE =2. ………………………………15分 20解:(Ⅰ)椭圆C 的焦点在x 轴上,由椭圆上的点A 到F 1、F 2两点的距离之和是4,得2a=4,即a=2. …….2分又点.1,31)23(21,)23,1(22222===+c b bA 于是得因此在椭圆上 …….4分所以椭圆C 的方程为).0,1(),0,1(,1342122F F y x -=+焦点 …….6分 (Ⅱ)设134),,(22=+y x y x P 则22344y x -=∴ …….8分 222222141117||()423434PQ x y y y y y y =+-=-+-+=--+ …….10分5)23(312++-=y …….12分又33≤≤-y 5||,23max =-=∴PQ y 时当 …….15分21解:(Ⅰ)证明:由抛物线定义知1||0+=y PF ,2|00x y k x x PQ ='==, 可得PQ 所在直线方程为000()2x y y x x -=-, 22AE x =>22(x 1212∵2004x y =∴得Q 点坐标为(0, 0y -)∴1||0+=y QF ∴ |PF |=|QF |(Ⅱ)设A (x 1, y 1),B (x 2, y 2),又M 点坐标为(0, y 0)∴AB 方程为002y x x y +=…….8分。
