LAB05+队列的操作及应用

合集下载

队列研究的原理和应用

队列研究的原理和应用1. 队列的基本概念队列是一种常见的数据结构，它遵循先进先出（FIFO）的原则。

在队列中，元素按照先后顺序加入队列，而只有最早加入的元素可以被访问和移除。

队列有两个基本操作，即入队（enqueue）和出队（dequeue）。

2. 队列的原理队列可以采用链表或数组来实现。

链表实现的队列使用指针相连的节点来存储元素，每个节点有一个指向下一个节点的指针和一个存储数据的元素。

数组实现的队列则使用连续的存储空间来存储元素，通过两个指针front和rear分别指向队首和队尾。

2.1 队列的入队操作入队操作将元素添加到队尾。

在链表实现中，只需创建一个新节点，并将其插入到队尾节点的后面。

在数组实现中，将元素存储到rear指针所在位置，并将rear指针后移一位。

2.2 队列的出队操作出队操作将队首元素移除。

在链表实现中，只需将队首节点的next指针指向下一个节点，并将原队首节点删除。

在数组实现中，将队首元素移除，并将front指针后移一位。

2.3 队列的空判断和满判断队列是否为空可以通过判断front和rear指针是否相等来进行判断。

如果相等，则队列为空。

队列是否满可以通过判断rear指针的位置是否达到队列的大小来进行判断。

如果rear指针超过了队列的大小，则队列为满。

3. 队列的应用队列在计算机科学和日常生活中有广泛的应用，以下是一些常见的应用场景：3.1 线程池在多线程编程中，线程池用于管理线程的执行顺序。

线程池维护一个固定数量的线程，任务被加入到队列中，每个线程从队列中获取任务并执行。

通过队列来存储任务，可以确保任务按照添加的顺序执行。

3.2 消息队列消息队列用于在分布式系统中传递消息。

生产者将消息发送到消息队列，消费者从消息队列中获取消息并进行处理。

通过消息队列，可以实现不同服务之间的解耦和异步处理。

3.3 操作系统调度在操作系统中，调度算法决定了进程的执行顺序。

队列被用来存储等待执行的进程，根据调度算法的策略，从队列中选择下一个执行的进程。

队列的实现及应用的实验原理是

队列的实现及应用的实验原理1. 实验目的本实验旨在通过分析队列的基本原理和应用，学习队列的实现方法及其在实际问题中的应用。

2. 队列的基本原理队列是一种先进先出（First-In-First-Out，FIFO）的数据结构，可以用线性表来实现。

队列有两个基本操作，即入队和出队。

2.1 入队操作入队操作是将一个元素添加到队列的末尾。

在队列中，新元素永远被追加到尾部。

如果队列已满，则无法执行入队操作。

2.2 出队操作出队操作是将队列首部的元素删除并返回。

在队列中，只有队首的元素才能被删除并返回。

如果队列为空，则无法执行出队操作。

3. 队列的实现方法队列可以通过数组或链表来实现。

下面分别介绍这两种实现方法。

3.1 数组实现数组实现队列时，需要定义两个指针，分别指向队首和队尾。

入队操作将元素添加到队尾，出队操作将队首元素删除并返回。

需要注意的是，当队尾指针到达数组末尾时，需要将队尾指针移到数组的起始位置。

优点•数组实现的队列在空间利用上比较高效。

•入队和出队操作的时间复杂度均为O(1)。

缺点•数组实现的队列在动态调整大小时比较困难。

•如果队列中存在大量删除操作，会导致存储空间的浪费。

3.2 链表实现链表实现队列时，可以使用单向链表或双向链表。

入队操作在链表尾部插入新的节点，出队操作删除链表头部节点。

优点•链表实现的队列在动态调整大小时比较灵活。

•链表实现的队列可以实现任意长度的队列。

缺点•链表实现的队列在空间利用上比较低效。

•入队和出队操作的时间复杂度均为O(1)。

4. 队列的应用队列在实际问题中有广泛的应用，下面介绍几个常见的应用场景。

4.1 任务调度队列可以用来实现任务调度，例如操作系统中的进程调度、网络中的消息调度等。

任务按照加入队列的顺序进行处理，保证了公平性和顺序性。

4.2 网络通信队列可以用来实现网络通信中的消息队列，用于存储待发送的消息和接收到的消息。

发送方将消息加入队列，接收方从队列中读取消息。

LAB05 队列的操作及应用

p = p->nextarc;
>adjveቤተ መጻሕፍቲ ባይዱ].cData);
Visited[p->adjvex]=1; printf(" %c //Visit Function
",ag.vertices[p-
//push stack pStack (LinkNode*)malloc(sizeof(LinkNode)); if(!pStack) return; 立不成功 pStack->parc = p; pStack->next = Stack->next; Stack->next = pStack; //push over } } //pop stack temp = Stack->next; Stack->next = temp->next; p = temp->parc->nextarc; free(temp); //pop over
6．程序的调试与计算结果的分析
得到最佳方案。
k++; if (vx[p].sheep!=vx[q].sheep) k++; if (vx[p].vegetable!=vx[q].vegetable ) k++; if (vx[p].farmer!=vx[q].farmer&&k<=1) { return (1); } else return (0); } void create_graph() { // 创建图 int i, j, f, w, s, v; vnum=0; for (f = 0; f <=1; f++) for (w = 0; w <=1; w++) for (s = 0; s<=1; s++) for (v = 0; v <= 1; v++) if (safe(f, w, s, v)==1) { vx[vnum].farmer=f; vx[vnum].wolf=w; vx[vnum].sheep=s; vx[vnum].vegetable=v; vnum++; } for (i = 0; i < vnum; i++) for (j=0; j<vnum; j++) if (connected(i, j)==1) { matrix[i][j]=1; } else matrix[i][j]=0; return; } void print_path(int u, int v) { // 输出方法 int k=u; while (k!=v) { printf("%d %d %d %d\n", vx[k].farmer,vx[k].wolf,vx[k].sheep, vx[k].vegetable); k=path[k]; } printf("%d %d %d %d\n", vx[k].farmer, vx[k].wolf, vx[k].sheep, vx[k].vegetable); } void dfs_path(int u, int v) { int j; visited[u]=1; for (j = 0; j < vnum; j++) if (matrix[u][j]==1 && visited[j]==0 && visited[v]==0) { path[u]=j; dfs_path(j, v); } }

队列实验报告

队列实验报告队列实验报告引言：队列是一种常见的数据结构，它按照先进先出（FIFO）的原则管理数据。

在计算机科学中，队列被广泛应用于各种算法和数据处理任务中。

本实验旨在通过实际操作和观察，深入了解队列的特性和应用。

实验目的：1. 理解队列的基本概念和特性；2. 学会使用队列进行数据处理；3. 掌握队列在实际问题中的应用。

实验步骤：1. 队列的创建和初始化：首先，我们需要创建一个队列并进行初始化。

队列可以使用数组或链表来实现。

在本实验中，我们选择使用链表实现队列。

通过定义一个队列类，我们可以创建一个空队列，并为其设置头节点和尾节点。

2. 入队操作：入队操作是将元素添加到队列的末尾。

我们可以通过调用队列类的入队方法，在尾节点后插入新的节点。

在插入操作之前，我们需要判断队列是否为空。

如果队列为空，新节点将成为头节点和尾节点；如果队列不为空，新节点将链接到当前尾节点的后面，并成为新的尾节点。

3. 出队操作：出队操作是将队列中的第一个元素移除，并返回该元素的值。

我们可以通过调用队列类的出队方法，将头节点的下一个节点作为新的头节点，并返回旧的头节点的值。

在出队操作之前，我们同样需要判断队列是否为空。

如果队列为空，则无法进行出队操作。

4. 遍历队列：为了观察队列中的元素，我们可以使用遍历操作。

通过遍历队列，我们可以依次访问每个节点，并输出节点的值。

在遍历过程中，我们需要从头节点开始，依次访问每个节点的下一个节点，直到尾节点为止。

实验结果：通过上述实验步骤，我们可以得到以下结果：1. 队列的创建和初始化成功；2. 入队操作能够将元素添加到队列的末尾；3. 出队操作能够将队列中的第一个元素移除，并返回该元素的值；4. 遍历操作能够依次输出队列中的每个元素。

实验应用：队列在实际问题中有着广泛的应用。

以下是一些典型的应用场景：1. 消息队列：在分布式系统中，消息队列被用于异步通信和解耦。

生产者可以将消息发送到队列，而消费者可以从队列中获取消息并进行处理。

队列的建立及应用实验原理

队列的建立及应用实验原理1. 队列的概念队列是一种常见的数据结构，它按照先进先出（FIFO）的原则对元素进行操作。

在队列中，新元素总是从一端（称为队尾）添加，而从另一端（称为队头）删除，类似于现实生活中排队等候的场景。

2. 队列的基本操作队列的基本操作包括入队和出队操作。

其中，入队操作将一个元素插入到队列的队尾，出队操作将队头的元素移除。

队列的典型实现方式有两种：数组和链表。

2.1 数组实现队列1. 初始化一个空队列，包括设置队列的容量和队头、队尾指针。

2. 入队操作：- 判断队列是否已满，如果已满，则无法插入新元素；- 否则，将新元素插入到队尾，并更新队尾指针。

3. 出队操作：- 判断队列是否为空，如果为空，则无法执行出队操作；- 否则，将队头元素移除，并更新队头指针。

2.2 链表实现队列1. 初始化一个空队列，包括设置队头、队尾指针。

2. 入队操作：- 创建一个新的节点，并将新元素赋值给节点的值域；- 将新节点插入到链表的尾部，并更新队尾指针。

3. 出队操作：- 判断队列是否为空，如果为空，则无法执行出队操作；- 否则，移除链表头部的节点，并更新队头指针。

3. 队列的应用实验原理队列的应用非常广泛，在实际编程中常常用到。

以下是一些常见应用实验原理的列举：3.1 队列在多线程编程中的应用•多线程编程中，常常需要使用队列来实现线程间的同步与通信。

一个线程可以将数据放入队列中，另一个线程从队列中取出数据，从而实现线程间的数据传递。

•具体应用场景有消息队列、任务队列等。

3.2 队列在网络编程中的应用•在网络编程中，队列常用来处理客户端请求，将请求加入到队列中并进行排队。

这样可以保证请求按照先后顺序进行处理，避免数据混乱。

•具体应用场景有请求队列、消息队列等。

3.3 队列在操作系统中的应用•在操作系统中，队列被广泛应用于进程调度和页面置换等场景。

操作系统使用队列来管理进程的执行顺序，以及内存中页面的置换算法。

队列的操作实验报告

队列的操作实验报告队列的操作实验报告一、实验目的本次实验旨在通过对队列的操作，加深学生对队列数据结构的理解，掌握队列的基本操作方法。

二、实验原理队列是一种先进先出（First In First Out，FIFO）的线性数据结构。

它可以用数组或链表来实现。

在队列中，新元素插入到队尾，已有元素从队头删除。

因此，队列具有以下几个特点：1. 只允许在一端插入元素，在另一端删除元素。

2. 插入和删除元素时分别称为入队和出队。

3. 入队操作在队尾进行，出队操作在对头进行。

三、实验内容本次实验主要涉及以下几个方面：1. 队列的初始化：初始化一个空的循环队列。

2. 入队操作：将一个元素插入到循环队列中。

3. 出队操作：从循环队列中删除一个元素，并返回该元素值。

4. 判断循环队列是否为空：如果循环对了为空，则返回 true；否则返回 false。

5. 判断循环对了是否已满：如果循环对了已满，则返回 true；否则返回 false。

四、实验步骤1. 队列的初始化首先需要定义一个结构体来表示循环队列，包括以下几个成员变量：```ctypedef struct {int *base; // 队列的基地址int front; // 队头指针int rear; // 队尾指针int size; // 队列长度} Queue;```然后定义一个初始化函数，用来初始化一个空的循环队列：```cvoid initQueue(Queue *queue, int size) {queue->base = (int *) malloc(sizeof(int) * size);queue->front = queue->rear = 0;queue->size = size;}```2. 入队操作入队操作比较简单，只需要将元素插入到队尾即可。

如果队列已满，则无法插入元素。

```cbool enQueue(Queue *queue, int value) {if (isFull(queue)) {return false;}queue->base[queue->rear] = value;queue->rear = (queue->rear + 1) % queue->size;return true;}```3. 出队操作出队操作也比较简单，只需要从队头删除一个元素，并返回该元素值。

lab5_Active_HDL

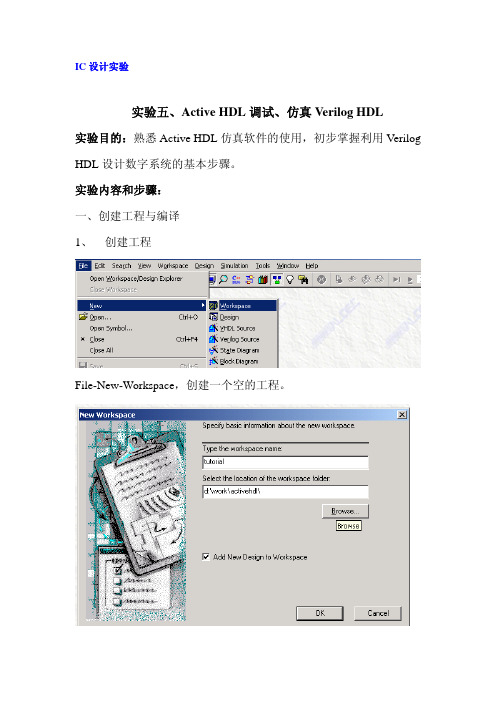
IC设计实验实验五、Active HDL调试、仿真Verilog HDL实验目的：熟悉Active HDL仿真软件的使用，初步掌握利用Verilog HDL设计数字系统的基本步骤。

实验内容和步骤：一、创建工程与编译1、创建工程File-New-Workspace，创建一个空的工程。

将新的工程命名为tutorial，并指定保存路径。

务必保证Add New Design to Workspace设置有效，点OK，启动设计向导New Design Wizard。

2、选中Create an empty design，Next。

3、为设计指定综合、器件类型、编程语言等其它信息，本实验设置如下，Next。

4、打开创建源文件窗口，design name取为tutorial_Verilog，设计路径等接受Active的默认设置。

点下一步，向导最后一步，点完成。

5、现在，你可以看到设计浏览器（Design Browser）里有上面创建的设计tutorial_Verilog了。

在设计浏览器中展开tutorial_Verilog，双击Add New Files,启动向导，点击Verilog Source Code图标，文件名cnt_10b,确定。

（cnt_10b的代码后面给出）。

在HDL Editor输入cnt_10b Verilog代码.6、编译你的源代码，有语法错误即改正之。

右键点击设计浏览器的cnt_10b.v，选Compile，如下图。

编译结果出现在下面的控制台串口，现在你的编译结果应该如下：倘若你没有发现控制台（Console），点击菜单栏的Console图标。

注意现在你的设计浏览器应该包含编译后模块。

二、仿真代码编译完成没有语法错误后，可以利用Active HDL的波形编辑器（Waveform Editor）做功能仿真。

1、设置顶层模块(Top-Level)。

由于上面的例子只有一个module，故已经是Top－Level了。

队列的应用实验报告

一、实验目的1. 理解队列的基本概念和特性，包括先进先出（FIFO）原则。

2. 掌握队列的基本操作，如初始化、入队、出队、判空、判满等。

3. 熟悉队列在实际问题中的应用，如操作系统中的进程调度、任务队列管理等。

4. 通过编程实现队列的应用，验证队列在实际问题中的有效性。

二、实验环境1. 编程语言：Python2. 开发工具：PyCharm3. 操作系统：Windows 10三、实验内容1. 队列的基本操作- 初始化队列：创建一个空队列，并设置队头指针（front）和队尾指针（rear）。

- 入队：将元素添加到队列的队尾。

- 出队：从队列的队头删除元素。

- 判空：判断队列是否为空。

- 判满：判断队列是否已满。

2. 队列的应用- 操作系统中的进程调度：使用队列模拟进程调度，将进程按照到达时间顺序入队，并根据CPU调度的策略进行出队。

- 任务队列管理：使用队列管理任务，将任务按照优先级或到达时间顺序入队，并根据任务处理的需要进行出队。

3. 编程实现- 使用Python实现队列的基本操作。

- 使用队列模拟操作系统中的进程调度。

- 使用队列管理任务队列。

四、实验步骤1. 队列的基本操作```pythonclass Queue:def __init__(self, capacity):self.capacity = capacityself.queue = [None] capacityself.front = 0self.rear = -1self.size = 0def is_empty(self):return self.size == 0def is_full(self):return self.size == self.capacitydef enqueue(self, item):if self.is_full():print("队列已满")returnself.rear = (self.rear + 1) % self.capacity self.queue[self.rear] = itemself.size += 1def dequeue(self):if self.is_empty():print("队列已空")return Noneitem = self.queue[self.front]self.front = (self.front + 1) % self.capacity self.size -= 1return itemdef peek(self):if self.is_empty():print("队列已空")return Nonereturn self.queue[self.front]```2. 操作系统中的进程调度```pythondef process_scheduling(queue):while not queue.is_empty():process = queue.dequeue()print(f"进程 {process} 正在执行")# 模拟进程执行time.sleep(1)```3. 任务队列管理```pythondef task_management(queue):while not queue.is_empty():task = queue.dequeue()print(f"任务 {task} 正在执行")# 模拟任务执行time.sleep(1)```五、实验结果与分析1. 队列的基本操作通过实验，验证了队列的基本操作的正确性，包括入队、出队、判空、判满等。

队列的分类与应用场景

队列的分类与应用场景队列是一种特殊的线性数据结构，按照“先进先出”的原则进行数据操作。

在实际的编程和算法应用中，队列是非常常见且实用的工具。

本文将介绍队列的分类以及其在不同场景下的应用。

一、队列的分类1. 普通队列：普通队列是最基本的队列类型，满足“先进先出”的原则。

在普通队列中，插入数据的操作称为入队（Enqueue），删除数据的操作称为出队（Dequeue）。

2. 双端队列：双端队列是在普通队列的基础上进行了扩展，允许在队列的两端进行插入和删除操作。

双端队列可以在队头和队尾分别进行入队和出队操作，提高了队列的灵活性。

3. 优先队列：优先队列是一种按照优先级进行出队操作的队列，即队列中的元素按照一定的优先级顺序排列。

常见的实现方式有最小堆和最大堆。

二、队列的应用场景1. 网络数据包传输：在计算机网络中，数据包的传输需要按照先来后到的顺序进行，因此可以使用队列进行数据包的缓存和传输控制。

2. 多线程任务管理：在多线程编程中，线程的调度和执行需要按照一定的顺序进行，可以使用队列来管理线程任务的执行顺序，确保任务按顺序执行。

3. 高性能计算：在高性能计算系统中，任务调度和资源分配是非常重要的问题。

使用队列可以方便地管理和调度计算任务，提高整个系统的性能和效率。

4. 操作系统进程调度：操作系统中的进程调度算法通常使用队列来管理待执行的进程。

根据不同的调度策略，可以使用普通队列、优先队列或双端队列来管理进程队列，以实现不同的调度要求。

5. 打印任务管理：在打印任务中，打印机需要按照用户提交的顺序进行打印，可以使用队列来管理打印任务的执行顺序，避免打印任务之间的冲突。

6. 消息队列系统：在分布式系统和微服务架构中，消息队列被广泛应用于实现异步通信和解耦系统的各个组件。

消息队列通过队列的方式进行消息传递，提高系统的可伸缩性和可靠性。

综上所述，队列作为一种常见的数据结构，不仅具有基本的先进先出特性，还可以根据实际需求进行扩展和优化。

队列的操作及应用实验原理

队列的操作及应用实验原理1. 队列的定义队列是一种特殊的线性表，具有先进先出（FIFO）的特性。

在队列中，元素的插入操作称为入队（enqueue），元素的删除操作称为出队（dequeue）。

队列头指针指向队列的第一个元素，而队列尾指针指向队列的最后一个元素。

2. 队列的操作队列主要有以下几种基本操作：2.1 入队（enqueue）入队操作是将元素插入队列的尾部。

当队列为空时，入队操作将头指针和尾指针同时指向该元素。

当队列非空时，入队操作只需将新元素插入到尾指针指向的位置，并更新尾指针。

2.2 出队（dequeue）出队操作是将队列的第一个元素删除，并返回该元素的值。

当队列非空时，出队操作将头指针指向下一个元素，并返回原第一个元素的值。

当队列为空时，出队操作无法执行。

2.3 获取队列长度（size）获取队列的元素个数的操作，即返回队列中元素的个数。

可以通过遍历队列并计数的方式实现。

2.4 判断队列是否为空（isEmpty）判断队列是否为空的操作，即返回队列是否为空的布尔值。

当队列为空时，返回true；否则，返回false。

3. 队列的应用实验原理队列作为一种重要的数据结构，在实际应用中具有广泛的应用。

以下是一些常见的队列应用实验原理的介绍：3.1 网络数据包的传输在网络通信中，数据包的传输常常采用队列的方式。

数据包依次入队，然后按照先进先出的顺序出队进行传输。

这样可以保证数据包的顺序性和一定程度上的公平性。

3.2 打印任务的调度在打印任务的调度中，可以使用队列来管理待打印的任务。

每个打印任务可以看作队列中的一个元素，依次入队。

当打印机可以接受新任务时，从队列中出队一个任务进行打印。

3.3 广度优先搜索算法（BFS）在图论中，广度优先搜索算法是一种重要的算法。

算法中使用队列维护待搜索的节点，并按照每个节点的临接顺序依次出队进行搜索。

3.4 循环队列的应用循环队列是一种特殊的队列，可以避免数据的搬迁操作。

lab贪心算法设计与应用

实验五贪心算法设计与应用一．基本原理的概括贪心法是一种算法设计技术，通常用于求解最优化问题。

通过一系列选择步骤来构造问题的解，每一步都是对当前部分解的一个扩展，直至获得问题的完整解。

所做的每一步选择都必须满足：1）可行的：必须满足问题的约束。

2）局部最优：当前所有可能的选择中最佳的局部选择。

3）不可取消: 选择一旦做出，在后面的步骤中就无法改变了。

要注意的是，贪心法不能保证总能得到最优解（一系列的局部最优选择不能保证最后得到整体最优解）二．该类算法设计与实现的要点贪心算法往往效率高，一般时间复杂性为多项式阶。

贪心算法一般较简单，其关键和难点在于贪心选择策略的确定，以及证明相应的贪心算法确实可求出最优解。

三．实验目的和要求理解贪心算法的基本原理，掌握贪心算法设计的基本方法及其应用；四．实验内容(一)加油问题（Problem Set 1702）：1.问题描述一个旅行家想驾驶汽车从城市A到城市B（设出发时油箱是空的）。

给定两个城市之间的距离dis、汽车油箱的容量c、每升汽油能行驶的距离d、沿途油站数n、油站i离出发点的距离d[i]以及该站每升汽油的价格p[i],i=1,2,…,n。

设d[1]=0<d[2]<…<d[n]。

要花最少的油费从城市A到城市B，在每个加油站应加多少油，最少花费为多少？2.具体要求Input输入的第一行是一个正整数k，表示测试例个数。

接下来几行是k个测试例的数据，每个测试例的数据由三行组成，其中第一行含4个正整数，依次为A和B两个城市之间的距离d1、汽车油箱的容量c（以升为单位）、每升汽油能行驶的距离d2、沿途油站数n (1<=n<=200)；第二行含n个实数d1, d2,…, d n，表示各油站离出发点的距离（d1=0）；第三行含n个实数p1, p2,…, p n，表示各油站每升汽油的价格。

同一行的数之间用一个空格隔开。

Output对于每个测试例输出一行，含一个实数，表示从城市Ａ到城市Ｂ所要花费的最少油费（输出的结果精确到小数点后一位）。

lab05

实验五二叉树的建立和遍历算法【实验目的】1.理解树是一种非线性的数据结构；2.掌握建立一棵给定二叉树的算法；3.熟悉二叉树的四种遍历算法：先序遍历、中序遍历、后序遍历和层次遍历算法；【实验内容】1.阅读exp5.cpp文件，该程序通过调用buildTree（）函数，建立教材中图10-9所示的三棵二叉树。

根据中序遍历算法的基本思想，在该文件中编写中序遍历算法，输出tree1的中序遍历结果。

修改后的程序运行结果如下图所示：图1. 中序遍历结果2.在上题的buildTree（）函数中，添加代码case 3，建立第四棵二叉树，并显示其中序遍历的结果。

该二叉树的树形如图2所示：图2. 第四棵二叉树的树形3.深刻理解第一题中中序遍历算法的设计思想，参考中序遍历的递归算法，实现countNode（）函数，用于统计二叉树t中结点的数目（结点数目保存在变量count中）。

template <typename T>void countNodes(tnode<T> *t, int& count)在main（）函数中调用countNode（）函数，统计并打印输出tree1的结点数。

本程序的运行结果如图3所示。

图3 本程序的运行结果选做题4.在第三题的基础上，设计层次遍历算法函数levelorderOutput（），在main（）函数中调用此函数对tree1进行层次遍历，其运行结果如图4所示。

template <typename T>void levelorderOutput(tnode<T> *t, const string& separator)图4. tree1的层次遍历结果。

队列基本操作实验报告

队列基本操作实验报告一、实验目的本次实验的主要目的是通过编写队列的基本操作，掌握队列数据结构的基本原理及其应用。

二、实验内容1. 队列的定义和基本操作队列是一种先进先出（FIFO）的线性数据结构，它只允许在队尾插入元素，在队头删除元素。

队列的基本操作包括：入队（enqueue）、出队（dequeue）、获取队头元素（getFront）、获取队列长度（getSize）等。

2. 队列的顺序存储结构顺序存储结构是指用数组来存储队列中的元素，其中需要维护两个指针：front指向队头元素，rear指向下一个待插入位置。

当rear等于数组长度时，需要进行循环，即将rear置为0。

3. 队列的链式存储结构链式存储结构是指用链表来存储队列中的元素，其中每个节点包含一个数据域和一个指针域。

head指向链表头节点，tail指向链表尾节点。

4. 实验流程(1) 编写顺序存储结构下的队列基本操作函数。

(2) 编写链式存储结构下的队列基本操作函数。

(3) 分别测试两种存储方式下各个函数是否正确实现。

三、实验步骤1. 顺序存储结构下的队列基本操作函数(1) 定义队列结构体和初始化函数。

typedef struct {int *data;int front, rear;int maxSize;} SeqQueue;SeqQueue* initSeqQueue(int maxSize) {SeqQueue *q = (SeqQueue*)malloc(sizeof(SeqQueue));q->data = (int*)malloc(sizeof(int) * maxSize);q->front = q->rear = 0;q->maxSize = maxSize;return q;}(2) 实现入队操作。

bool enqueue(SeqQueue *q, int x) {if ((q->rear + 1) % q->maxSize == q->front) return false; // 队满q->data[q->rear] = x;q->rear = (q->rear + 1) % q->maxSize; // 循环return true;}(3) 实现出队操作。

队列实验报告

队列实验报告队列实验报告引言：队列（Queue）是一种常见的数据结构，它按照先进先出（FIFO）的原则管理数据。

队列在计算机科学领域被广泛应用，例如操作系统调度、网络通信和图像处理等。

本实验旨在通过设计和实现一个队列，深入了解队列的特性和应用。

实验目的：1. 理解队列的基本概念和操作；2. 掌握队列的实现方法；3. 熟悉队列在实际问题中的应用。

实验过程：1. 队列的定义与特性队列是一种线性数据结构，它只允许在队尾进行插入操作（入队），在队头进行删除操作（出队）。

队列的特性包括先进先出（FIFO）和后进后出（LIFO）。

2. 队列的实现队列可以通过数组或链表来实现。

在本实验中，我们选择使用链表实现队列。

链表由节点组成，每个节点包含一个数据项和指向下一个节点的指针。

3. 队列的操作本次实验中，我们需要实现以下队列操作：- 入队（enqueue）：将元素插入队列的末尾；- 出队（dequeue）：删除队列的第一个元素，并返回该元素的值；- 判空（isEmpty）：判断队列是否为空；- 获取队列长度（size）：返回队列中元素的个数。

4. 队列的应用队列在实际问题中有广泛的应用。

以下是一些典型的应用场景：- 任务调度：操作系统将需要执行的任务按照先后顺序加入队列，并逐个执行；- 网络通信：数据包按照接收顺序加入队列，然后依次发送给目标主机；- 银行排队：顾客按照到达时间加入队列，依次办理业务。

实验结果：经过实验，我们成功实现了队列的基本操作，并验证了其正确性和有效性。

通过编写测试用例，我们对队列的各种操作进行了全面的测试。

结果表明，队列能够按照先进先出的原则管理数据，并且具有良好的性能。

结论：队列是一种重要的数据结构，它在计算机科学中有广泛的应用。

通过本次实验，我们对队列的定义、实现和应用有了更深入的了解。

队列的先进先出特性使其成为解决许多实际问题的有效工具。

在今后的学习和工作中，我们将继续深入研究队列及其相关的数据结构，以提高问题解决的效率和质量。

队列应用实验报告

队列应用实验报告队列应用实验报告引言：队列是一种常见的数据结构，它按照先进先出（FIFO）的原则进行操作。

在计算机科学中，队列被广泛应用于各种领域，如操作系统、网络通信、图形处理等。

本实验旨在通过实际应用，探索队列在实际问题中的应用。

一、队列在操作系统中的应用在操作系统中，队列被用于进程调度。

操作系统通过维护一个就绪队列，按照进程的优先级或到达时间将进程排队。

当一个进程执行完毕或者发生中断时，操作系统从队列中选择下一个要执行的进程。

这种方式确保了每个进程都能按照一定的规则获得CPU的使用权，提高了系统的效率。

二、队列在网络通信中的应用在网络通信中，队列被用于处理数据包。

当数据包到达网络节点时，它们会被放入队列中等待处理。

队列中的数据包按照先后顺序进行处理，保证了数据的有序性。

同时，队列还可以用于解决网络拥塞的问题。

当网络负载过高时，数据包会被放入队列中等待发送，以避免数据的丢失。

三、队列在图形处理中的应用在图形处理中，队列被用于实现图像渲染。

当一个图像需要被渲染时，图像的每个像素点都需要经过一系列的计算和处理。

这些计算和处理的顺序可以通过队列来管理。

每个像素点都被放入队列中，然后按照队列的顺序进行处理。

这种方式可以确保图像的每个像素点都按照正确的顺序进行渲染，保证了图像的质量。

四、队列在实际生活中的应用队列不仅在计算机科学中有广泛的应用，也在我们的日常生活中发挥着重要的作用。

例如，在超市排队结账时，我们都会排队等待。

超市通过维护一个顾客队列，按照先后顺序为每个顾客提供服务。

这种方式保证了每个顾客都能按照一定的规则被服务，提高了服务效率。

结论：队列作为一种常见的数据结构，在各个领域都有重要的应用。

通过本实验，我们对队列的应用有了更深入的了解。

队列的先进先出原则使得它在处理需要按照顺序进行的任务时非常有效。

无论是在操作系统、网络通信还是图形处理中，队列都能发挥重要的作用。

同时，队列在我们的日常生活中也有广泛的应用，帮助我们提高效率和组织秩序。

队列的实现及应用实验原理

队列的实现及应用实验原理1. 队列的定义和基本操作队列是一种先进先出（FIFO）的数据结构，它的插入操作在队列的一端进行，而删除操作则在队列的另一端进行。

队列的基本操作包括初始化、入队、出队和判空等。

•初始化：创建一个空队列。

•入队：将元素插入到队列的末尾。

•出队：删除队列的头部元素，并返回该元素。

•判空：检查队列是否为空。

2. 队列的实现方式队列可以通过数组或链表来实现。

每种实现方式都有其优缺点。

2.1 数组实现队列使用数组实现队列时，需要定义队头和队尾指针，分别指向队列的头部和尾部。

队头指针指向队列中的第一个元素，队尾指针指向队列中的最后一个元素。

2.1.1 初始化使用数组实现队列时，需要初始化队头指针和队尾指针。

队头指针和队尾指针初始值都为-1，表示队列为空。

2.1.2 入队入队操作即向队列中插入元素。

当插入一个新元素时，队尾指针先加1，然后将元素存储在队尾指针所指向的位置。

2.1.3 出队出队操作即删除队列中的一个元素。

当删除一个元素时，队头指针先加1，然后返回队头指针所指向的元素。

2.1.4 判空判空操作用于检查队列是否为空。

当队头指针等于队尾指针时，表示队列为空。

2.2 链表实现队列链表实现队列时，可以使用单链表或双向链表。

在链表实现中，只需保存队列的头部和尾部节点即可。

2.2.1 初始化使用链表实现队列时，需要初始化头部和尾部节点，将它们都指向空节点。

2.2.2 入队入队操作即向队列中插入元素。

当插入一个新元素时，将其作为新的尾部节点，并更新尾部节点指针。

2.2.3 出队出队操作即删除队列中的一个元素。

当删除一个元素时，将头部节点指向下一个节点，并返回被删除的节点。

2.2.4 判空判空操作用于检查队列是否为空。

当头部节点和尾部节点都指向空节点时，表示队列为空。

3. 队列的应用实验原理队列的应用非常广泛，在很多算法和实验中都有着重要的作用。

以下是一些常见的队列应用实验原理：3.1 广度优先搜索（BFS）广度优先搜索是一种图遍历算法，它使用队列来实现。

Lab5-基本-OSPF-配置实验

专业：学号：：专业：学号：：学习目标完成本实验后，您将能够：•根据拓扑图完成网络电缆连接•删除路由器启动配置并将其重新启动到默认状态•在路由器上执行基本配置任务•配置并激活接口•在所有路由器上配置 OSPF 路由•配置 OSPF 路由器 ID•使用 show 命令检验 OSPF 路由•配置静态默认路由•向 OSPF 邻居传播默认路由•配置 OSPF Hello 计时器和 Dead 计时器•在多路访问网络上配置 OSPF•配置 OSPF 优先级•理解 OSPF 选举过程•记录 OSPF 配置场景在本实验练习中有两个独立的场景。

在第一个场景中，您将使用场景 A 中的拓扑图所示的网络学习如何配置 OSPF 路由协议。

该网络中的各个网段使用 VLSM 划分了子网。

OSPF 是一种无类路由协议，可用于在路由更新中提供子网掩码信息。

这将使 VLSM 子网信息可传播到整个网络。

在第二个场景中，您将学习在多路访问网络中配置 OSPF。

您还将学习使用 OSPF 选举过程来确定指定路由器 (DR)、后备指定路由器 (BDR) 和 DRother身份。

场景A：基本OSPF 配置拓扑图：地址表：任务1：准备网络。

步骤1：根据拓扑图所示完成网络电缆连接。

步骤2：清除路由器上现有的配置。

任务2：执行基本路由器配置。

根据下列指导原则在路由器 R1、R2 和 R3 上执行基本配置：1. 配置路由器主机名。

2. 禁用DNS查找。

3. 配置特权执行模式口令。

4. 配置当日消息标语。

5. 为控制台连接配置口令。

6. 为VTY 连接配置口令。

任务3：配置并激活串行地址和以太网地址。

步骤1：在R1、R2 和R3 上配置接口。

使用拓扑图下方的表中的 IP 地址在路由器 R1、R2 和 R3 上配置接口。

步骤2：检验IP 地址和接口。

使用show ip interface brief 命令检验 IP 地址是否正确以及接口是否已激活。

完成后，确保将运行配置保存到路由器的 NVRAM 中。

队列的应用实验原理

队列的应用实验原理简介队列是一种常见的数据结构，具有先进先出（FIFO）的特点，常用于模拟现实生活中的排队过程。

本文将介绍队列的应用实验原理，包括队列的基本概念、实验步骤和实验应用案例。

队列的基本概念队列是由一系列元素组成的集合，按照先进先出的原则进行操作。

队列有两个基本操作：入队（enqueue）和出队（dequeue）。

入队是将元素加入队列的操作，新元素始终加在队列的尾部。

出队是将队列的头部元素移除的操作，即先进队列的元素先出队列。

队列的常见属性包括队列的长度、队列是否为空等。

队列的实验步骤实验准备在进行队列的实验前，需要准备以下设备和材料： - 一台计算机 - 一份编程语言环境（如Python、Java等）实验步骤1.引入队列的数据结构。

2.创建一个队列对象。

3.判断队列是否为空，如果为空，则执行以下步骤。

–加入元素到队列中。

4.执行出队操作，将队列的头部元素移除，并将其打印出来。

5.重复步骤4，直到所有元素都被出队。

6.统计队列的长度，并将结果打印出来。

实验示例下面是一个使用Python语言实现队列的应用实验的示例代码：```python class Queue: def init(self): self.queue = []def enqueue(self, item):self.queue.append(item)def dequeue(self):if self.is_empty():return Nonereturn self.queue.pop(0)def is_empty(self):return len(self.queue) == 0def size(self):return len(self.queue)queue = Queue() for i in range(5): queue.enqueue(i)while not queue.is_empty(): item = queue.dequeue() print(。

2009082224_殷志民_Lab5介绍

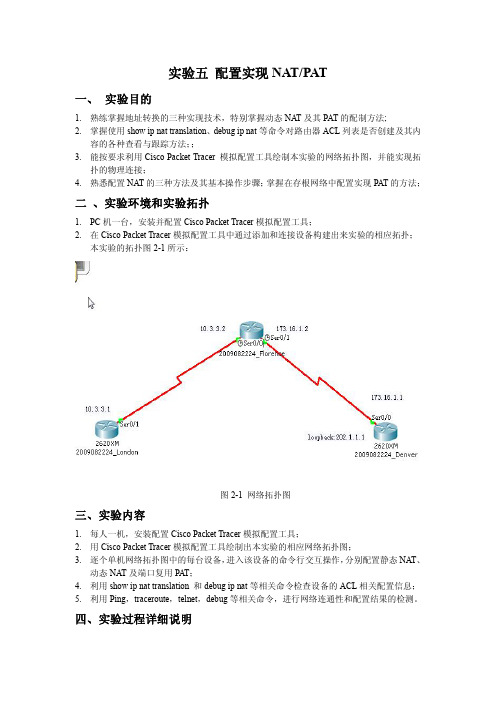
实验五配置实现 NAT/PAT一、实验目的1. 熟练掌握地址转换的三种实现技术，特别掌握动态 NA T及其 PAT的配制方法;2. 掌握使用 show ip nat translation、debug ip nat 等命令对路由器 ACL列表是否创建及其内；容的各种查看与跟踪方法；3. 能按要求利用 Cisco Packet Tracer 模拟配置工具绘制本实验的网络拓扑图，并能实现拓扑的物理连接；4. 熟悉配置NA T的三种方法及其基本操作步骤；掌握在存根网络中配置实现 PA T的方法；二、实验环境和实验拓扑1. PC 机一台，安装并配置 Cisco Packet Tracer 模拟配置工具；2. 在 Cisco Packet Tracer 模拟配置工具中通过添加和连接设备构建出来实验的相应拓扑；本实验的拓扑图 21 所示：图 21 网络拓扑图三、实验内容1. 每人一机，安装配置 Cisco Packet Tracer 模拟配置工具；2. 用 Cisco Packet Tracer 模拟配置工具绘制出本实验的相应网络拓扑图；3. 逐个单机网络拓扑图中的每台设备，进入该设备的命令行交互操作，分别配置静态NA T、动态 NA T及端口复用 PA T；4. 利用 show ip nat translation 和 debug ip nat 等相关命令检查设备的 ACL相关配置信息；5. 利用 Ping，traceroute，telnet，debug等相关命令，进行网络连通性和配置结果的检测。

四、实验过程详细说明1．选择添加3 个 2620XM 路由器设备至逻辑工作空间；（提示：2620XM 路由器需要断电后接插 WIC2T模块才有广域网互联用的高速同步串口）图 41 选择网络设备2．将 Router0 路由器的主机名命名为 2009082224_London；将 Router1 路由器的主机名命名为 2009082224_Florence；将 Router2 路由器的主机名命名为 2009082224_Denver；（提示：注意命名顺序和原设备下标应对应）图 42 Router0 路由器的主机名命名为 2009082224_London图 43Router1 路由器的主机名命名为 2009082224_Florence图 44 Router2 路由器的主机名命名为 2009082224_Denver 3: 配置 2009082224_Florence的 enable口令及 VTY 线路密码；（提示：将enable password设为shzu、将enable secret设为cisco、将VTY线路密码设为cisco）图 45 配置 2009082224_Florence的 enable口令及 VTY 线路密码4: 查看当前 2009082224_Florence路由器的配置文件内容（内存信息）并记录下来。

LabVIEW中队列的使用教学课件

错误输入（无错误）表明节点运行
前发生的错误。该输入提供标准错误输入。
队列输出是对未改动队列的引用。
剩余元素该数组包含从队列中删除的元素。数组中的第一个元素是队
列前部的元素，最后一个元素是队列后部的元素。数据类型可匹配队列的子类型。
错误输出包含错误信息。该输出提
供标准错误输出。
12
2021/10/10
超时？如函数超时并且队列中没有可用空间或出现错误，则值为TRUE。
5
错误输出包含错误信息。
2021/10/10
3 预览队列元素
返回队列前端的元素且不删除该元素。
队列是队列引用。
超时毫秒表明当队列为空时，函数等待队列中可用元素的时间，以毫秒为单位。
超时？的值为TRUE。
错误输入（无错误）表明节点运行前发生的错误。
4
2021/10/10
2 元素入队列
在队列后端添加元素。
队列是队列引用。
元素是添加至队列末尾的元素。数据类型可匹配队列的子类型。
超时毫秒表明队列满时函数等待队列中可用空间的时间，以毫秒为单位。，
超时？输出的值为TRUE。
错误输入（无错误）表明节点运行前发生的错误。
队列输出是对未改动队列的引用。
3
2021/10/10
二队列操作函数细部说明
1 获取队列引用
队列最大值是队列要保持的元素的最大数量。名称包含要获取或创建的队列的名称。元素数据类型是需要队列包含的数据类型。该输入端可连线任意数据类型。如未找到是否创建？指定名称指定的队列不存在时，是否创建新的队列。错误输入（无错误）表明节点运行前发生的错误。队列输出是对已有队列或函数创建的新队列的引用。新建？函数创建新的队列时，值为 TRUE。错误输出包含错误信息。