材料力学第五版部分重点课后题答案
材料力学第五版课后习题答案

7-4[习题7-3] 一拉杆由两段沿n m -面胶合而成。
由于实用的原因,图中的α角限于060~0范围内。
作为“假定计算”,对胶合缝作强度计算时,可以把其上的正应力和切应力分别与相应的许用应力比较。
现设胶合缝的许用切应力][τ为许用拉应力][σ的4/3,且这一拉杆的强度由胶合缝强度控制。
为了使杆能承受最大的荷载F ,试问α角的值应取多大? 解:AFx =σ;0=y σ;0=x τ ατασσσσσα2s i n 2c o s 22x yx yx --++=][22cos 12cos 22σαασα≤+=+=A F A F A F ][22cos 1σα≤+A F ,][cos 2σα≤AFασ2cos ][A F ≤,ασ2max,cos ][AF N = ατασστα2c o s 2s i n 2x yx +-=][3][2sin στατα=≤=F ,σ][5.1A F ≤,σ][5.1max,AF T =由切应力强度条件控制最大荷载。
由图中可以看出,当060=α时,杆能承受最大荷载,该荷载为:A F ][732.1max σ=7-6[习题7-7] 试用应力圆的几何关系求图示悬臂梁距离自由端为m 72.0的截面上,在顶面以下mm 40的一点处的最大及最小主应力,并求最大主应力与x 轴之间的夹角。
解:(1)求计算点的正应力与切应力MPa mm mm mm N bh My I My z 55.1016080401072.01012124363=⨯⨯⋅⨯⨯⨯===σMPa mm mm mm N bI QS z z 88.0801608012160)4080(10104333*-=⨯⨯⨯⨯⨯⨯⨯-==τ (2)写出坐标面应力 X (10.55,-0.88)Y (0,0.88)(3) 作应力圆求最大与最小主应力,并求最大主应力与x 轴的夹角 作应力圆如图所示。
从图中按比例尺量得:MPa 66.101=σ MPa 06.03-=σ 0075.4=α7-7[习题7-8] 各单元体面上的应力如图所示。
材料力学第五版(I)孙训方版课后习题答案

材料力学第五版(I )孙训方版课后习题答案[习题2-2]一打入基地内的木桩如图所示,杆轴单位长度的摩擦力f=kx**2,试做木桩的后力图。
解:由题意可得:33233110,,3/()3/(/)ll N fdx F kl F k F l F x Fx l dx F x l =====⎰⎰1有3[习题2-3] 石砌桥墩的墩身高m l 10=,其横截面面尺寸如图所示。
荷载kN F 1000=,材料的密度3/35.2m kg =ρ,试求墩身底部横截面上的压应力。
解:墩身底面的轴力为:g Al F G F N ρ--=+-=)( 2-3图)(942.31048.935.210)114.323(10002kN -=⨯⨯⨯⨯+⨯--=墩身底面积:)(14.9)114.323(22m A =⨯+⨯=因为墩为轴向压缩构件,所以其底面上的正应力均匀分布。
MPa kPa mkNA N 34.071.33914.9942.31042-≈-=-==σ[习题2-7] 图示圆锥形杆受轴向拉力作用,试求杆的伸长。
2-7图解:取长度为dx 截离体(微元体)。
则微元体的伸长量为:)()(x EA Fdx l d =∆ ,⎰⎰==∆l l x A dxE F dx x EA F l 00)()(lxr r r r =--121,22112112d x l d d r x l r r r +-=+⋅-=, 2211222)(u d x ld d x A ⋅=⎪⎭⎫ ⎝⎛+-=ππ,dx l d d du d x l d d d 2)22(12112-==+- du d d ldx 122-=,)()(22)(221212udu d d l du u d d lx A dx -⋅-=⋅-=ππ 因此,)()(2)()(202100u dud d E Fl x A dx E F dx x EA F l l l l⎰⎰⎰--===∆πlld x l d d d d E Fl u d d E Fl 011221021221)(21)(2⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+--=⎥⎦⎤⎢⎣⎡-=ππ ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+--=21221)(2111221d d l l d d d d E Fl π⎥⎦⎤⎢⎣⎡--=122122)(2d d d d E Fl π214d Ed Fl π=[习题2-10] 受轴向拉力F 作用的箱形薄壁杆如图所示。
材料力学第五版孙训方版课后习题答案

从而得,Ax l2 4.76, Ay l2 2 l1 3 20.23 ( )
(2)
V F Ay F1 l1 +F2 l2 0 Ay 20.33 ( )
[习题 2-17] 简单桁架及其受力如图所示,水平杆 BC 的长度 l 保持不变,斜杆 AB 的长度 可随夹角 的变化而改变。 两杆由同一种材料制造, 且材料的许用拉应力和许用压应力相等。
1000 tan 4.7867339 o 83.7(mm)
(3)求荷载 F 的值 以 C 结点为研究对象,由其平稀衡条件可得:
Y 0 : 2N sin a P 0
P 2 N sin a 2A sin
2 735 0.25 3.14 12 sin 4.787 0 96.239( N )
1 18117 2 1414 256212 1600 ( ) 1.366(mm) 故: A 35000 210000 113 210000 177
[习题 2-13] 图示 A 和 B 两点之间原有水平方向的一根直径 d 1mm 的钢丝, 在钢丝的中点 C 加一竖向荷载 F。 已知钢丝产生的线应变为 0.0035 , 其材料的弹性模量 E 210GPa , 钢丝的自重不计。试求: (1)钢丝横截面上的应力(假设钢丝经过冷拉,在断裂前可认为符合胡克定律) ; (2)钢丝在 C 点下降的距离 ; (3)荷载 F 的值。 解: (1)求钢丝横截面上的应力
N AB cos N BC 0
N BC N AB cos
(2)求工作应力
F cos F cot sin
2-17
AB
BC
孙训方材料力学I第五版课后习题答案完整版

解:(1)求 AB、AC 杆的轴力 以节点 A 为研究对象,其受力图如图所示。 由平衡条件得出:
X 0 : N AC sin 30o N AB sin 45o 0
N AC 2N AB ………………………(a)
Y 0 : N AC cos 30o N AB cos 45o 35 0
C 点的水平位移: CH AH BH l1 tan 45o 0.476(mm)
C 点的铅垂位移: C l1 0.476(mm)
2-12 图示实心圆杆 AB 和 AC 在 A 点以铰相连接,在 A 点作用有铅垂向下的力 F 35kN 。已知 杆 AB 和 AC 的直径分别为 d1 12mm 和 d2 15mm ,钢的弹性模量 E 210GPa 。试求 A 点在铅垂
[习题 2-15]水平刚性杆 AB 由三根 BC,BD 和 ED 支撑,如图,在杆的 A 端承受铅垂荷载 F=20KN, 三根钢杆的横截面积分别为 A1=12 平方毫米,A2=6 平方毫米,A,3=9 平方毫米,杆的弹性模量 E=210Gpa,求:
(1) 端点 A 的水平和铅垂位移。 (2) 应用功能原理求端点 A 的铅垂位移。
d2)
d
2
d 2l
1
1
x
d1 2
0
2Fl
1
E (d1
d
2
)
d
2 d 2l
1
l
d1 2
1 d1 2
2-10 受轴向拉力 F 作用的箱形薄壁杆如图所示。已知该杆材料的弹性常数为 E, ,试求 C 与 D 两点间的距离改变量 。
解:
横截面上的线应变相同
因此
2-11 图示结构中,AB 为水平放置的刚性杆,杆 1,2,3 材料相同,其弹性模量 E 210GPa ,已 知 l 1m , A1 A2 100mm2 , A3 150mm2 , F 20kN 。试求 C 点的水平位移和铅垂位移。
(精品)材料力学第五版(孙训方)课后题答案

材料力学第五版课后答案[习题2-2]一打入基地内的木桩如图所示,杆轴单位长度的摩擦力f=kx**2,试做木桩的后力图。
解:由题意可得:33233110,,3/()3/(/)ll N fdx F kl F kF l F x Fx l dx F x l =====⎰⎰1有3[习题2-3] 石砌桥墩的墩身高m l10=,其横截面面尺寸如图所示。
荷载kN F 1000=,材料的密度3/35.2m kg =ρ,试求墩身底部横截面上的压应力。
解:墩身底面的轴力为:g Al F G F N ρ--=+-=)( 2-3图 )(942.31048.935.210)114.323(10002kN -=⨯⨯⨯⨯+⨯--=墩身底面积:)(14.9)114.323(22m A =⨯+⨯=因为墩为轴向压缩构件,所以其底面上的正应力均匀分布。
MPa kPa m kNA N 34.071.33914.9942.31042-≈-=-==σ[习题2-7] 图示圆锥形杆受轴向拉力作用,试求杆的伸长。
2-7图解:取长度为dx 截离体(微元体)。
则微元体的伸长量为:)()(x EA Fdx l d =∆ ,⎰⎰==∆l l x A dxE F dx x EA F l 00)()(l xr r r r =--121,22112112d x l d d r x l r r r +-=+⋅-=,2211222)(u d x ld d x A ⋅=⎪⎭⎫ ⎝⎛+-=ππ,dx l d d du d x l d d d 2)22(12112-==+-du d d ldx 122-=,)()(22)(221212udu d d l du u d d l x A dx -⋅-=⋅-=ππ 因此,)()(2)()(202100udu d d E Fl x A dx E F dx x EA F l l l l⎰⎰⎰--===∆π lld x l d d d d E Fl u d d E Fl 011221021221)(21)(2⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+--=⎥⎦⎤⎢⎣⎡-=ππ ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+--=21221)(2111221d d l l d d d d E Fl π⎥⎦⎤⎢⎣⎡--=122122)(2d d d d E Fl π214dEd Fl π=[习题2-10] 受轴向拉力F 作用的箱形薄壁杆如图所示。
材料力学第五课后题答案(孙训芳)

材料力学(I)第五版(孙训芳编)甘肃建筑职业技术学院长安大学土木工程材料力学温习材料材料力学第五版课后答案(孙训芳编)4-1试求图示各梁中指定截面上的剪力和弯矩 a (5)=h (4)001100110002222200022132241111223121140,222233RA RB S S q F F a q a q F q a a q aa M q a q a q aF M q a a q a a q a ----==⨯==-⨯==-⨯⨯⨯===⨯-⨯⨯⨯=b (5)=f (4)4-2试写出以下各梁的剪力方程和弯矩方程,并作剪力图和弯矩图 a (5)=a (4)b(5)=b(4)f(5)=f(4)4-3试利用载荷集度,剪力和弯矩间的微分关系做以下各梁的弯矩图和剪力e和f题)(e)(f)(h)4-4试做以下具有中间铰的梁的剪力图和弯矩图。
4-4 (b) 4-5 (b)4-5.依照弯矩、剪力与荷载集度之间的关系指出以下玩具和剪力图的错误的地方,并更正。
4-6.已知简支梁的剪力图如下图,试做梁的弯矩图和荷载图,梁上五集中力偶作用。
4-6(a) 4-7(a)4-7.依照图示梁的弯矩图做出剪力图和荷载图。
4-8用叠加法做梁的弯矩图。
4-8(b) 4-8(c)4-9.选择适合的方式,做弯矩图和剪力图。
4-9(b) 4-9(c)4-104-14.长度l=2m的均匀圆木,欲锯做Fa=的一段,为使锯口处两头面开裂最小,硬是锯口处弯矩为零,现将圆木放在两只锯木架上,一只锯木架放在圆木一段,试求另一只锯木架应放位置。
x=4-184-19M=30KN 4-214-234-254-284-294-334-364-355-25-35-75-155-225-23 选22a工字钢5-246-4 6/((233))A l Fl EA ∆=+6-127-3-55mpa 。
-55mpa7-4[习题7-3] 一拉杆由两段沿n m -面胶合而成。
材料力学第五版课后习题答案

材料力学第五版课后习题答案1. 弹性力学基本概念。
1.1 什么是应力?什么是应变?应力是单位面积上的内力,是描述物体内部受力情况的物理量;而应变则是物体单位长度的形变量,描述了物体在受力作用下的形变情况。
1.2 什么是胡克定律?胡克定律是描述弹性体在弹性变形范围内应力与应变成正比的关系,即应力与应变成线性关系。
1.3 什么是弹性模量?弹性模量是描述物体在受力作用下的变形程度的物理量,通常用E表示,单位是帕斯卡(Pa)。
2. 线弹性力学。
2.1 什么是轴向力?什么是轴向变形?轴向力是指作用在物体轴向的力,轴向变形是指物体在受到轴向力作用下的形变情况。
2.2 什么是泊松比?泊松比是描述物体在轴向受力作用下,横向变形与轴向变形之间的比值,通常用ν表示。
2.3 什么是弯曲应力?什么是弯曲变形?弯曲应力是指物体在受到弯矩作用下的内部应力情况,弯曲变形是指物体在受到弯矩作用下的形变情况。
3. 弹性力学的能量法。
3.1 什么是弹性势能?弹性势能是指物体在受力变形后,能够恢复原状时所具有的能量,通常用U表示。
3.2 什么是弹性线性势能?弹性线性势能是指物体在弹性变形范围内,弹性势能与形变量成线性关系的势能。
3.3 什么是弹性势能密度?弹性势能密度是指单位体积或单位质量物体所具有的弹性势能,通常用u表示。
4. 弹塑性力学。
4.1 什么是屈服点?屈服点是指物体在受力作用下,开始出现塑性变形的临界点。
4.2 什么是屈服应力?屈服应力是指物体在受力作用下开始发生塑性变形时所具有的应力大小。
4.3 什么是塑性势能?塑性势能是指物体在受到超过屈服应力的作用下,发生塑性变形所具有的能量。
5. 薄壁压力容器。
5.1 什么是薄壁压力容器?薄壁压力容器是指壁厚相对于容器直径而言很小的压力容器。
5.2 薄壁压力容器的内、外压力对容器的影响有哪些?内压力会使容器产生膨胀变形,而外压力会使容器产生收缩变形。
5.3 薄壁压力容器的应力分布情况是怎样的?薄壁压力容器内外表面的应力分布情况是不均匀的,通常集中在壁厚的两侧。
材料力学第五版课后习题答案
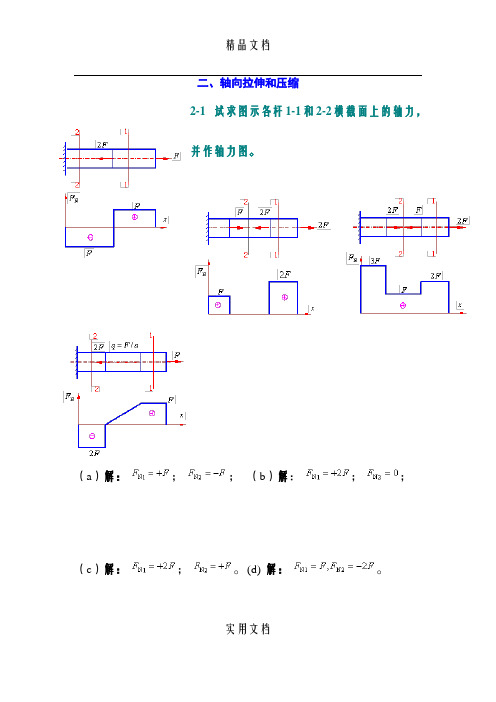
实用文档二、轴向拉伸和压缩2-1 试求图示各杆1-1和2-2横截面上的轴力,并作轴力图。
(a )解:; ; (b )解: ;;(c )解:; 。
(d) 解:。
2-2 试求图示等直杆横截面1-1,2-2和3-3上的轴力,并作轴力图。
若横截面面积,试求各横截面上的应力。
解:实用文档实用文档返回2-3试求图示阶梯状直杆横截面1-1,2-2和3-3上的轴力,并作轴力图。
若横截面面积,,,并求各横截面上的应力。
解:返回2-4 图示一混合屋架结构的计算简图。
屋架的上弦用钢筋混凝土制成。
下面的拉杆和中间竖向撑杆用角钢构成,其截面均为两个75mm实用文档×8mm的等边角钢。
已知屋面承受集度为的竖直均布荷载。
试求拉杆AE和EG横截面上的应力。
解:=1)求内力实用文档取I-I分离体得(拉)取节点E为分离体,故(拉)2)求应力75×8等边角钢的面积A=11.5 cm2(拉)实用文档(拉)实用文档返回2-5(2-6) 图示拉杆承受轴向拉力,杆的横截面面积。
如以表示斜截面与横截面的夹角,试求当,30,45,60,90时各斜截面上的正应力和切应力,并用图表示其方向。
解:实用文档实用文档返回2-6(2-8) 一木桩柱受力如图所示。
柱的横截面为边长200mm的正方形,材料可认为符合胡克定律,其弹性模量E=10 GPa。
如不计柱的自重,试求:(1)作轴力图;(2)各段柱横截面上的应力;(3)各段柱的纵向线应变;(4)柱的总变形。
实用文档解:(压)(压)实用文档返回2-7(2-9) 一根直径、长的圆截面杆,承受轴向拉力,其伸长为。
试求杆横截面上的应力与材料的弹性模量E。
解:2-8(2-11) 受轴向拉力F作用的箱形薄壁杆如图所示。
已知该杆材料的弹性常数为E,,试求C与D 两点间的距离改变量。
解:实用文档横截面上的线应变相同因此实用文档返回2-9(2-12) 图示结构中,AB 为水平放置的刚性杆,杆1,2,3材料相同,其弹性模量E=210GPa,已知,,,。
材料力学第五版课后习题答案详解

Microsoft Corporation材料力学课后答案[键入文档副标题]lenovo[选取日期]第二章轴向拉伸和压缩2-12-22-32-42-52-62-72-82-9下页2-1试求图示各杆1-1和2-2横截面上的轴力,并作轴力图。
(a)解:;;(b)解:;;(c)解:;。
(d)解:。
返回2-2 试求图示等直杆横截面1-1,2-2和3-3上的轴力,并作轴力图。
若横截面面积,试求各横截面上的应力。
解:返回2-3试求图示阶梯状直杆横截面1-1,2-2和3-3上的轴力,并作轴力图。
若横截面面积,,,并求各横截面上的应力。
解:返回2-4 图示一混合屋架结构的计算简图。
屋架的上弦用钢筋混凝土制成。
下面的拉杆和中间竖向撑杆用角钢构成,其截面均为两个75mm×8mm的等边角钢。
已知屋面承受集度为的竖直均布荷载。
试求拉杆AE和EG横截面上的应力。
解:=1)求内力取I-I分离体得(拉)取节点E为分离体,故(拉)2)求应力75×8等边角钢的面积A=11.5 cm2(拉)(拉)2-5(2-6)图示拉杆承受轴向拉力,杆的横截面面积。
如以表示斜截面与横截面的夹角,试求当,30,45,60,90时各斜截面上的正应力和切应力,并用图表示其方向。
解:2-6(2-8) 一木桩柱受力如图所示。
柱的横截面为边长200mm的正方形,材料可认为符合胡克定律,其弹性模量E=10 GPa。
如不计柱的自重,试求:(1)作轴力图;(2)各段柱横截面上的应力;(3)各段柱的纵向线应变;(4)柱的总变形。
解:(压)(压)。
材料力学第五版课后习题答案

材料⼒学第五版课后习题答案⼆、轴向拉伸和压缩2-1试求图⽰各杆1-1和2-2横截⾯上的轴⼒,并作轴⼒图。
(a)解:;;(b)解:;;(c)解:;。
(d)解:。
2-2 试求图⽰等直杆横截⾯1-1,2-2和3-3上的轴⼒,并作轴⼒图。
若横截⾯⾯积,试求各横截⾯上的应⼒。
解:2-3试求图⽰阶梯状直杆横截⾯1-1,2-2和3-3上的轴⼒,并作轴⼒图。
若横截⾯⾯积,,,并求各横截⾯上的应⼒。
解:2-4 图⽰⼀混合屋架结构的计算简图。
屋架的上弦⽤钢筋混凝⼟制成。
下⾯的拉杆和中间竖向撑杆⽤⾓钢构成,其截⾯均为两个75mm×8mm的等边⾓钢。
已知屋⾯承受集度为的竖直均布荷载。
试求拉杆AE和EG横截⾯上的应⼒。
解:=1)求内⼒取I-I分离体得(拉)取节点E为分离体,故(拉)2)求应⼒75×8等边⾓钢的⾯积A=11.5 cm2(拉)(拉)2-5(2-6)图⽰拉杆承受轴向拉⼒,杆的横截⾯⾯积。
如以表⽰斜截⾯与横截⾯的夹⾓,试求当,30,45,60,90时各斜截⾯上的正应⼒和切应⼒,并⽤图表⽰其⽅向。
解:2-6(2-8) ⼀⽊桩柱受⼒如图所⽰。
柱的横截⾯为边长200mm的正⽅形,材料可认为符合胡克定律,其弹性模量E=10 GPa。
如不计柱的⾃重,试求:(1)作轴⼒图;(2)各段柱横截⾯上的应⼒;(3)各段柱的纵向线应变;(4)柱的总变形。
解:(压)(压)2-7(2-9)⼀根直径、长的圆截⾯杆,承受轴向拉⼒,其伸长为。
试求杆横截⾯上的应⼒与材料的弹性模量E。
解:2-8(2-11)受轴向拉⼒F作⽤的箱形薄壁杆如图所⽰。
已知该杆材料的弹性常数为E,,试求C与D两点间的距离改变量。
解:横截⾯上的线应变相同因此2-9(2-12) 图⽰结构中,AB为⽔平放置的刚性杆,杆1,2,3材料相同,其弹性模量E=210GPa,已知,,,。
试求C点的⽔平位移和铅垂位移。
解:(1)受⼒图(a),。
(2)变形协调图(b)因,故=(向下)(向下)为保证,点A移⾄,由图中⼏何关系知;第三章扭转3-1 ⼀传动轴作匀速转动,转速,轴上装有五个轮⼦,主动轮Ⅱ输⼊的功率为60kW,从动轮,Ⅰ,Ⅲ,Ⅳ,Ⅴ依次输出18kW,12kW,22kW和8kW。
材料力学第五版课后习题答案.pdf

5[习题2-2]一打入基地内的木桩如图所示,杆轴单位长度的摩擦力f=kx**2,试做木桩的后力图。
解:由题意可得:33233110,,3/()3/(/)ll N fdx F kl F k F l F x Fx l dx F x l =====⎰⎰1有3[习题2-3] 石砌桥墩的墩身高m l 10=,其横截面面尺寸如图所示。
荷载kN F 1000=,材料的密度3/35.2m kg =ρ,试求墩身底部横截面上的压应力。
解:墩身底面的轴力为:g Al F G F N ρ--=+-=)( 2-3图)(942.31048.935.210)114.323(10002kN -=⨯⨯⨯⨯+⨯--=墩身底面积:)(14.9)114.323(22m A =⨯+⨯=因为墩为轴向压缩构件,所以其底面上的正应力均匀分布。
MPa kPa mkNA N 34.071.33914.9942.31042-≈-=-==σ[习题2-7] 图示圆锥形杆受轴向拉力作用,试求杆的伸长。
2-7图解:取长度为dx 截离体(微元体)。
则微元体的伸长量为:)()(x EA Fdx l d =∆ ,⎰⎰==∆l l x A dxE F dx x EA F l 00)()(l xr r r r =--121,22112112d x l d d r x l r r r +-=+⋅-=,2211222)(u d x ld d x A ⋅=⎪⎭⎫ ⎝⎛+-=ππ,dx l d d du d x l d d d 2)22(12112-==+- du d d l dx 122-=,)()(22)(221212udud d l du u d d lx A dx -⋅-=⋅-=ππ因此,)()(2)()(202100u dud d E Fl x A dx E F dx x EA F l l l l⎰⎰⎰--===∆π lld x l d d d d E Fl u d d E Fl 011221021221)(21)(2⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+--=⎥⎦⎤⎢⎣⎡-=ππ ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+--=21221)(2111221d d l l d d d d E Fl π ⎥⎦⎤⎢⎣⎡--=122122)(2d d d d E Fl π214d Ed Flπ=[习题2-10] 受轴向拉力F 作用的箱形薄壁杆如图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2211222)(udxlddxA?=??????+?=ππ,dxldddudxlddd2)22(12112?==+? duddldx122?=,)()(22)(221212ududdlduuddlxAdx???=??=ππ 因此, )()(2)()(202100ududdEFlxAdxEFdxxEAFllll∫∫∫??===?π lldxlddddEFluddEFl011221021221)(21)(2????????????+??=???????=ππ ?????????????+??=21221)(2111221ddllddddEFlπ ????????=122122)(2ddddEFlπ214dEdFlπ= [习题习题习题习题2-10] 受轴向拉力F作用的箱形薄壁杆如图所示。已知该材料的弹性常数为ν,E,试求C与D两点间的距离改变量CD?。 解:EAFEAFνννεε?=?=?=/' 式中,δδδaaaA4)()(22=??+=,故:δνεEaF4'?= δνεEaFaa4'?==?, δνEFaaa4'?=?=? δνEFaa4'?=,aaaCD12145)()(243232=+=
从W的表达式可知,W是θ角的一元函数。当W的一阶导数等于零时,W取得最小值。 []02sin22cos)cos1(2sinsincos2222=?????????+???=θθθθθθσγθFlddW 022cos22cos32sin2=??+??θθθ 02cos2cos32sin22=???θθθ 12cos3?=θ ,3333.02cos?=θ o47.109)3333.0arccos(2=?=θ,'445474.54oo==θ (5)求两杆横截面面积的比值 θσsin][FAAB=,][cotσθFABC= θθθσθθσcos1cotsin1][cotsin][===FFAABCAB 因为: 12cos3?=θ,311cos22?=?θ,31cos2=θ 31cos=θ,3cos1=θ 所以: 3=BCABAA [习题习题习题习题2-18] 一桁架如图所示。各杆都由两个等边角钢组成。已知材料的许用应力MPa170][=σ,试选择AC和CD的角钢型号。 解:(1)求支座反力 由对称性可知, )(220↑==kNRRBA (2)求AC杆和CD杆的轴力 以A节点为研究对象,由其平 衡条件得: 0=∑Y 2-18 0cos=?αACANR
[习题习题习题习题2-2]一打入基地内的木桩如图所示,杆轴单位长度的摩擦力f=kx**2,试做木桩的后力图。 解:由题意可得: 330233110,,3/()3/(/)llNfdxFklFkFlFxFxldxFxl=====∫∫1有3 [习题习题习题习题2-3] 石砌桥墩的墩身高ml10=,其横截面面尺寸如图所示。荷载kNF1000=,材料的密度3/35.2mkg=ρ,试求墩身底部横截面上的压应力。 解:墩身底面的轴力为: gAlFGFNρ??=+?=)( 2-3图 )(942.31048.935.210)114.323(10002kN?=××××+×??= 墩身底面积:)(14.9)114.323(22mA=×+×= 因为墩为轴向压缩构件,所以其底面上的正应力均匀分布。 MPakPamkNAN34.071.33914.9942.31042?≈?=?==σ [习题习题习题习题2-7] 图示圆锥形杆受轴向拉力作用,试求杆的伸长。 2-7图 解:取长度为dx截离体(微元体)。则微元体的伸长量为: )()(xEAFdxld=? ,∫∫==?llxAdxEFdxxEAFl00)()( lxrrrr=??121,22112112dxlddrxlrrr+?=+??=,
心圆杆AB和AC在A点以铰相连接,在A点作用有铅垂向下的力kNF35=。已知杆AB和AC的直径分别为mmd121=和mmd152=,钢的弹性模量受力图 变形协调图
GPaE210=。试求A点在铅垂方向的位移。 解:(1)求AB、AC杆的轴力 以节点A为研究对象,其受力图如图所示。 由平衡条件得出: 0=∑X:045sin30sin=?oABoACNN ABACNN2=………………………(a) 0=∑Y:03545cos30cos=?+oABoACNN 7023=+ABACNN………………(b) (a) (b)联立解得: kNNNAB117.181==;kNNNAC621.252== (2)由变形能原理求A点的铅垂方向的位移 222211212221EAlNEAlNFA+=? )(122221121EAlNEAlNFA+=? 式中,)(141445sin/10001mmlo==;)(160030sin/8002mmlo== 2211131214.325.0mmA=××=;2221771514.325.0mmA=××= 故:)(366.1)177210000160025621113210000141418117(35000122mmA=××+××=? [习题习题习题习题2-13] 图示A和B两点之间原有水平方向的一根直径mmd1=的钢丝,在钢丝的中点C加一竖向荷载F。已知钢丝产生的线应变为0035.0=ε,其材料的弹性模量GPaE210=, 钢丝的自重不计。试求: (1)钢丝横截面上的应力(假设钢丝经过冷拉,在断裂前可认为符合胡克定律); (2)钢丝在C点下降的距离?; (3)荷载F的值。 解:(1)求钢丝横截面上的应力 )(7350035.0210000MPaE=×==εσ (2)求钢丝在C点下降的距离? )(72100002000735mmElEANll=×=?==?σ。其中,AC和BC各mm5.3。 996512207.05.10031000cos==α
o7867339.4)5.10031000arccos(==α )(7.837867339.4tan1000mmo==? (3)求荷载F的值 以C结点为研究对象,由其平稀衡条件可得: 0=∑Y:0sin2=?PaN ασsin2sin2AaNP== )(239.96787.4sin114.325.0735202N=×××××= [习题习题习题习题2-15]水平刚性杆AB由三根BC,BD和ED支撑,如图,在杆的A端承受铅垂荷载F=20KN,三根钢杆的横截面积分别为A1=12平方毫米,A2=6平方毫米,A,3=9平方毫米,杆的弹性模量E=210Gpa,求: (1) 端点A的水平和铅垂位移。 (2) 应用功能原理求端点A的铅垂位移。 解:(1) 30323311031231111711961222,3/()3/(/)cos450sin4500.450.15060,401,0,60100.153.87210101210401llNNNNNNNfdxFklFkFlFxFxldxFxlFFFFFFFFKNFKNFKNFllEAFllEA?=====?=??+?+=???×+×=?∴=?=?=?××?===××××?==∫∫1有3由胡克定理,796x2y2100.154.762101012104.762320.23AlAll?×=×××?=?=?=?×+?×=↓从而得,,() (2) y1122y+020.33VFAFlFlAε=×??×?×?=?=↓() [习题习题习题习题2-17] 简单桁架及其受力如图所示,水平杆BC的长度l保持不变,斜杆AB的长度可随夹角θ的变化而改变。两杆由同一种材料制造,且材料的许用拉应力和许用压应力的总重量为最小时,试求: (1)两杆的夹角;
(2)两杆横截面面积的比值。 解:(1)求轴力 取节点B为研究对象,由其平衡条件得: ∑=0Y 0sin=?FNABθ θsinFNAB= ∑=0X 0cos=??BCABNNθ θθθθcotcossincosFFNNABBC=?=?= 2-17 (2)求工作应力 θσsinABABABABAFAN== BCBCBCBCAFANθσcot== (3)求杆系的总重量 )(BCBCABABlAlAVW+=?=γγ 。γ是重力密度(简称重度,单位:3/mkN)。 )cos(lAlABCAB+=θγ )cos1(BCABAAl+?=θγ (4)代入题设条件求两杆的夹角 条件①: ][sinσθσ===ABABABABAFAN,θσsin][FAAB= ][cotσθσ===BCBCBCBCAFAN, ][cotσθFABC= 条件⑵:W的总重量为最小。 )cos1(BCABAAlW+?=θγ)cos1(BCABAAl+?=θγ )][cotcos1sin][(σθθθσγFFl+??=)sincoscossin1(][θθθθσγ+=Fl []????????+=θθθσγcossincos12Fl[]????????+=θθσγ2sincos122Fl
