初三数学小测验
初三数学小测试卷答案

一、选择题(每题2分,共20分)1. 如果a > b,那么以下哪个不等式一定成立?A. a + 1 > b + 1B. a - 1 > b - 1C. a / 2 > b / 2D. a 2 > b 2答案:C2. 下列哪个数是负数?A. -5B. 0C. 5D. -5/3答案:A3. 下列哪个数是偶数?A. 7B. 12C. 13D. 20答案:B4. 如果一个数的平方是4,那么这个数可能是:A. 2B. -2C. 4D. 0答案:A、B5. 下列哪个图形是正方形?A. 矩形B. 菱形C. 正方形D. 三角形答案:C6. 如果一个三角形的三边长分别是3、4、5,那么这个三角形是:A. 直角三角形B. 等腰三角形C. 等边三角形D. 不规则三角形答案:A7. 下列哪个函数是反比例函数?A. y = 2x + 3B. y = x^2C. y = 1/xD. y = 3x答案:C8. 下列哪个数是无理数?A. √4B. √9D. √25答案:C9. 下列哪个图形的面积是12平方厘米?A. 正方形B. 长方形C. 三角形D. 圆答案:B10. 下列哪个数是实数?A. √-1B. iC. √2D. π答案:C、D二、填空题(每题2分,共20分)11. 5的倒数是______,0的倒数是______。
答案:1/5,无定义12. 下列数的绝对值分别是:|3| = ______,|-2| = ______。
答案:3,213. 下列方程的解是:2x - 4 = 0,x = ______。
答案:214. 下列方程的解是:x / 3 + 1 = 0,x = ______。
15. 下列方程的解是:2(x + 3) = 8,x = ______。
答案:216. 下列方程的解是:5x - 10 = 0,x = ______。
答案:217. 下列方程的解是:3x + 9 = 0,x = ______。
九年级数学小测

九年级数学小测(6)班级 姓名 得分一、选择题(40分)1、-2015的绝对值是( )A 、2015B 、-2015C 、±2015D 、120152、与无理数31最接近的整数是( )A. 4B. 5C. 6D. 73、下列运算正确的是( )A 、a -2=-a 2B 、a+a 2=a 3C 、 2 + 3 = 5D 、(a 2)3=a 64、一个关于x 的一元一次不等式组的解集在数轴上表示如图,则该不等式组的解集是( )A 、-2<x <1B 、-2<x≤1C 、-2≤x <1D 、-2≤x≤15、现有甲乙两个合唱队队员的平均身高均为170cm ,方差分别为S 甲2、S 乙2,且S 甲2>S 乙2,则两个队的队员的身高较为整齐的是( )A 、甲队B 、乙队C 、两队一样整齐D 、不能确定6、下列命题是真命题的是( )A 、一组对边平行,另一组对边相等的四边形是平行四边形B 、对角线互相垂直的平行四边形是菱形C 、四条边相等的四边形是菱形D 、正方形是轴对称图形,但不是中心对称图形7、岳阳市某校举行运动会,从商场购买一定数量的笔袋和笔记本作为奖品。
若每个笔袋的价格比每个笔记本的价格多3元,且用200元购买笔记本的数量与用350元购买笔袋的数量相同。
设每个笔记本的价格为x 元,则下列所列方程正确的是( )A 、200x = 350x-3B 、200x =350x+3C 、200x+3 =350xD 、200x-3 =350x8、如图,在△ABC 中,AB=BC ,以AB 为直径的⊙O 交AC 于点D ,过点C 作CF ∥AB ,在CF 上取一点E ,使DE=CD ,连接A E ,对于下列结论:①AD=DC ②△CBA ∽△CDE③弧BD=弧AD ④AE 为⊙O 的切线,一定正确的结论全部包含其中的选项是( ) A 、①② B 、①②③ C 、①④ D 、①②④二、填空题(35分)9、单项式-12 x 2y 3的次数是 10、分解因式:x 2-9= 11、据统计,2015年岳阳市参加中考的学生约为49000人,用科学记数法可将49000表示为 12、若关于x 的一元二次方程x 2-3x+m=0有两个相等的实数根,则m=13、在一次文艺演出中,各评委对某节目给出的分数是:9.20,9.25,9.10,9.20,9.15,9.20,9.15,这组数据的众数是 14、一个n 边形的内角和是1800°,则n=15、如图,直线a ∥b ,∠1=50°,∠2=30°,则∠3=FE OD C BA 0-2-11b a 321三、解答题(25分)16、(7分)计算:(-1)4-2tan60°+( 3 - 2 )0+1218、(8分)先化简,再求值:(1- 1x+2 )÷x 2+x x 2+4x+4 ,其中x= 219、(10分)如图,直线y=x+b 与双曲线y=m x 都经过点A (2,3),直线y=x+b 与x 轴、y轴分别交于点B 、C 两点(1)求直线与双曲线的函数关系式; (2)求△AOB 的面积O y x CB A。
初三数学测试题及答案

初三数学测试题及答案一、选择题(每题2分,共10分)1. 下列哪个数是无理数?A. 3.14159B. √2C. 0.33333D. 1/32. 一个二次方程 \( ax^2 + bx + c = 0 \) 的判别式是:A. \( b^2 - 4ac \)B. \( a^2 - 4bc \)C. \( b^2 + 4ac \)D. \( a^2 + 4bc \)3. 如果一个三角形的三边长分别为 3, 4, 5,那么这个三角形是:A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不是三角形4. 下列哪个表达式是正确的?A. \( 2^3 + 2^2 = 2^5 \)B. \( (a+b)^2 = a^2 + b^2 \)C. \( (a-b)^2 = a^2 - 2ab + b^2 \)D. \( (a+b)(a-b) = a^2 - b \)5. 如果一个数的平方根是 2,那么这个数是:A. 4B. -4C. 2D. 8二、填空题(每题2分,共10分)6. 圆的周长公式是 \( C = \pi \times \) ______7. 一个数的立方根是它自己,这个数可以是 ______ 、-1或 0。
8. 如果一个角是直角的一半,那么这个角是 ______ 度。
9. 一个数的绝对值是它自己,这个数是非负数,即 ______ 或正数。
10. 一个二次方程 \( x^2 - 5x + 6 = 0 \) 可以通过因式分解法分解为 \( (x - 2)(x - 3) = 0 \),其根是 ______ 和 ______。
三、解答题(共80分)11. 解一元二次方程 \( x^2 - 7x + 10 = 0 \)。
(10分)12. 证明勾股定理:在一个直角三角形中,直角边的平方和等于斜边的平方。
(15分)13. 计算下列表达式的值:\( \sqrt{81} + \frac{3}{4} -\frac{2}{3} \)。
人教版数学九年级上全册课堂10分钟小测

课堂10分钟小测·21.1 一元二次方程时间:10分钟满分:25分一、选择题(每小题3分,共6分)1.若(a-1)x2+bx+c=0是关于x的一元二次方程,则()A.a≠0 B.a≠1C.a=1 D.a≠-12.一元二次方程2x2-(m+1)x+1=x(x-1)化成一般形式后二次项的系数为1,一次项的系数为-1,则m的值为()A.-1 B.1 C.-2 D.2二、填空题(每小题4分,共12分)3.方程(m+2)x|m|+3mx+1=0是关于x的一元二次方程,则m =_______________.4.若关于x的方程mx2+(m-1)x+5=0有一个解为2,则m的值是______.5.把一元二次方程(x-3)2=5化为一般形式为________________,二次项为________,一次项系数为__________,常数项为________.三、解答题(共7分)6.已知关于x的一元二次方程(2m-1)x2+3mx+5=0有一根是x=-1,求m的值.时间:10分钟 满分:25分一、选择题(每小题3分,共6分)1.用配方法解方程x 2-23x -1=0,正确的配方为( )A.⎝ ⎛⎭⎪⎫x -132=89B.⎝ ⎛⎭⎪⎫x -232=59C.⎝ ⎛⎭⎪⎫x -132+109=0D.⎝ ⎛⎭⎪⎫x -132=1092.一元二次方程x 2+x +14=0的根的情况是( ) A .有两个不等的实数根 B .有两个相等的实数根 C .无实数根 D .无法确定二、填空题(每小题4分,共12分)3.方程x 2-4x -12=0的解x 1=________,x 2=________. 4.x 2+2x -5=0配方后的方程为____________. 5.用公式法解方程4x 2-12x =3,得到x =________. 三、解答题(共7分)6.已知关于x 的一元二次方程x 2-mx -2=0.(1)对于任意实数m ,判断此方程根的情况,并说明理由; (2)当m =2时,求方程的根.时间:10分钟 满分:25分一、选择题(每小题3分,共6分) 1.一元二次方程x 2=3x 的根是( ) A .x =3 B .x =0C .x 1=0,x 2=3D .x 1=0,x 2=-32.方程4(x -3)2+x (x -3)=0的根为( )A .x =3B .x =125C .x 1=-3,x 2=125D .x 1=3,x 2=125 二、填空题(每小题4分,共12分)3.方程x 2-16=0的解是____________.4.如果(m +n )(m +n +5)=0,则m +n =______. 5.方程x (x -1)=x 的解是________. 三、解答题(共7分)6.解下列一元二次方程:(1)2x 2-8x =0; (2)x 2-3x -4=0.课堂10分钟小测·*21.2.3根与系数的关系时间:10分钟满分:25分一、选择题(每小题3分,共6分)1.若x1,x2是一元二次方程x2+4x+3=0的两个根,则x1x2的值是()A.4 B.3 C.-4 D.-32.如果关于x的一元二次方程x2+px+q=0的两根分别为x1=2,x2=1,那么p,q的值分别是()A.-3,2 B.3,-2 C.2,-3 D.2,3二、填空题(每小题4分,共12分)3.已知一元二次方程的两根之和为7,两根之积为12,则这个方程为____________________.4.已知方程x2-3x+m=0的一个根是1,则它的另一个根是______,m的值是______.5.已知x1,x2是方程x2-3x-3=0的两根,不解方程可求得x21+x22=________.三、解答题(共7分)6.已知关于x的一元二次方程x2+(2m-3)x+m2=0的两个不相等的实数根α,β满足1α+1β=1,求m的值.课堂10分钟小测·21.3实际问题与一元二次方程时间:10分钟满分:25分一、选择题(每小题3分,共9分)1.某品牌服装原价173元,连续两次降价x%后售价为127元,下面所列方程中正确的是()A.173(1+x%)2=127 B.173(1-2x%)=127C.173(1-x%)2=127 D.127(1+x%)2=1732.某城市为绿化环境,改善城市容貌,计划经过两年时间,使绿地面积增加44%,这两年平均每年绿地面积的增长率是() A.19% B.20% C.21% D.22%3.一个面积为120 cm2的矩形花圃,它的长比宽多2 m,则花圃的长是()A.10 m B.12 m C.13 m D.14 m二、填空题(每小题4分,共8分)4.已知一种商品的进价为50元,售价为62元,则卖出8件所获得的利润为__________元.5.有一个两位数等于其数字之和的4倍,其十位数字比个位数字小2,则这个两位数是________.三、解答题(共8分)6.某西瓜经营户以2元/千克的进价购进一批小型西瓜,以3元/千克的价格出售,每天可售出200千克.为了促销,该经营户决定降价销售,经调查发现,这种小型西瓜每降价0.1元/千克,每天可多售出40千克,另外,每天的房租等固定成本共24元,该经营户要想每天赢利200元,应将每千克小型西瓜的售价降低多少元?课堂10分钟小测·22.1.1二次函数一、选择题(每小题3分,共6分)1.若y =mx 2+nx -p (其中m ,n ,p 是常数)为二次函数,则( ) A .m ,n ,p 均不为0 B .m ≠0,且n ≠0 C .m ≠0 D .m ≠0,或p ≠02.当ab >0时,y =ax 2与y =ax +b 的图象大致是( )二、填空题(每小题4分,共8分)3.若y =x m -1+2x 是二次函数,则m =________. 4.二次函数y =(k +1)x 2的图象如图J22-1-1,则k 的取值范围为________.图J22-1-1三、解答题(共11分) 5.在如图J22-1-2所示网格内建立恰当直角坐标系后,画出函数y=2x 2和y =-12x 2的图象,并根据图象回答下列问题(设小方格的边长为1):图J22-1-2(1)说出这两个函数图象的开口方向,对称轴和顶点坐标;(2)抛物线y =2x 2,当x ______时,抛物线上的点都在x 轴的上方,它的顶点是图象的最______点;(3)函数y =-12x 2,对于一切x 的值,总有函数y ______0;当x ______时,y 有最______值是______.课堂10分钟小测·22.1.2二次函数图像与性质一、选择题(每小题3分,共6分)1.下列抛物线的顶点坐标为(0,1)的是( ) A .y =x 2+1 B .y =x 2-1 C .y =(x +1)2 D .y =(x -1)22.二次函数y =-x 2+2x 的图象可能是( )二、填空题(每小题4分,共8分)3.抛物线y =x 2+14的开口向________,对称轴是________.4.将二次函数y =2x 2+6x +3化为y =a (x -h )2+k 的形式是________.三、解答题(共11分)5.已知二次函数y =-12x 2+x +4.(1)确定抛物线的开口方向、顶点坐标和对称轴;(2)当x 取何值时,y 随x 的增大而增大?当x 取何值时,y 随x 的增大而减小?课堂10分钟小测·*22.1.3二次函数图像与性质一、选择题(每小题3分,共6分)1.已知二次函数的图象过(1,0),(2,0)和(0,2)三点,则该函数的解析式是( )A .y =2x 2+x +2B .y =x 2+3x +2C .y =x 2-2x +3D .y =x 2-3x +22.若二次函数的图象的顶点坐标为(2,-1),且抛物线过(0,3),则二次函数的解析式是( )A .y =-(x -2)2-1 B .y =-12(x -2)2-1C .y =(x -2)2-1 D .y =12(x -2)2-1二、填空题(每小题4分,共8分) 3.如图J22-1-3,函数y =-(x -h )2+k 的图象,则其解析式为____________.图J22-1-3 4.已知抛物线y =x 2+(m -1)x -14的顶点的横坐标是2,则m 的值是________.三、解答题(共11分)5.已知当x =1时,二次函数有最大值5,且图象过点(0,-3),求此函数关系式.课堂10分钟小测·22.2二次函数与一元二次方程一、选择题(每小题3分,共6分) 1.下表是二次函数y =ax 2+bx +c 的自变量x 的值与函数y 的对应值,判断方程ax 2+bx +c =0(a ≠0,a ,b ,c 为常数)的一个解的范围是(C .6.18<x <6.19D .6.19<x <6.202.二次函数y =2x 2+3x -9的图象与x 轴交点的横坐标是( ) A.32和3 B.32和-3 C .-32和2 D .-32和-2二、填空题(每小题4分,共8分) 3.已知抛物线y =x 2-x -1与x 轴的交点为(m,0),则代数式m 2-m +2 011的值为__________.4.如图J22-2-1是抛物线y =ax 2+bx +c 的图象,则由图象可知,不等式ax 2+bx +c <0的解集是________.图J22-2-1三、解答题(共11分) 5.如图J22-2-2,直线y =x +m 和抛物线y =x 2+bx +c 都经过点A (1,0),B (3,2).(1)求m 的值和抛物线的关系式;(2)求不等式x 2+bx +c >x +m 的解集(直接写出答案).图J22-2-2课堂10分钟小测·22.3实际问题与二次函数时间:10分钟 满分:25分一、选择题(每小题3分,共6分)1.在半径为4 cm 的圆中,挖去一个半径为x cm 的圆,剩下一个圆环的面积为y cm 2,则y 与x 的函数关系为( )A .y =πx 2-4B .y =π(2-x )2C .y =-(x 2+4)D .y =-πx 2+16π 2.已知某种礼炮的升空高度h (m)与飞行时间t (s)的关系式是h =-52t 2+20t +1.若此礼炮在升空到最高处时引爆,则引爆需要的时间为( )A .3 sB .4 sC .5 sD .6 s 二、填空题(每小题4分,共8分)3.出售某种手工艺品,若每个获利x 元,一天可售出(8-x )个,则当x =________元,一天出售该种手工艺品的总利润y 最大.4.如图J22-3-1,某省大学的校门是一抛物线形水泥建筑物,大门的地面宽度为8 m ,两侧距地面4 m 的高处各有一个挂校名横匾用的铁环,两铁环的水平距离为6 m ,则校门的高度为(精确到0.1 m ,水泥建筑物厚度忽略不计)________.图J22-3-1三、解答题(共11分)5.杂技团进行杂技表演,演员从跷跷板右端A 处弹跳到人梯顶端椅子B 处,其身体(看成一个点)的路线是抛物线y =-35x 2+3x +1的一部分,如图J22-3-2.(1)求演员弹跳离地面的最大高度;(2)已知人梯高BC =3.4米,在一次表演中,人梯到起跳点A 的水平距离是4米,问这次表演是否成功?说明理由.图J22-3-2课堂10分钟小测·23.1图像的旋转时间:10分钟满分:25分一、选择题(每小题3分,共6分)1.如图J23-1-1,将△ABC旋转至△CDE,则下列结论中一定成立的是()A.AC=CE B.∠A=∠DEC C.AB=CD D.BC=EC 2.如图J23-1-2,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕点B按顺时针方向转动一个角度到A1BC1的位置,使得点A,B,C1在同一条直线上,那么这个角度等于()A.120°B.90°C.60°D.30°图J23-1-1 图J23-1-2 图J23-1-3 图J23-1-4二、填空题(每小题4分,共8分)3.如图J23-1-3,△ABC绕点C旋转后得到△CDE,则∠A的对应角是__________,∠B=________,AB=________,AC=________.4.如图J23-1-4,AC⊥BE,AC=EC,CB=CF,则△EFC可以看作是△ABC绕点________按________方向旋转了__________度而得到的.三、解答题(共11分)5.如图J23-1-5,△ABC是直角三角形,延长AB到点E,使BE=BC,在BC上取一点F,使BF=AB,连接EF,△ABC旋转后能与△FBE重合,请回答:(1)旋转中心是哪一点?(2)旋转了多少度?(3)AC与EF的关系如何?图J23-1-5课堂10分钟小测·23.2.1中心对称时间:10分钟满分:25分一、选择题(每小题3分,共6分)1.下列图形绕某点旋转180°后,不能与原来图形重合的是()2.如图J23-2-1,△ABC与△A′B′C′关于点O成中心对称,下列结论中不成立的是()A.OC=OC′B.OA=OA′C.BC=B′C′D.∠ABC=∠A′C′B′图J23-2-1 图J23-2-2 图J23-2-3二、填空题(每小题4分,共8分)3.如图J23-2-2,△ABC和△A′B′C′关于点O成中心对称,如果连接线段AA′,BB′,CC′,它们都经过点_____,且AB =________,AC=________,BC=________.4.如图J23-2-3,将等边△ABD沿BD中点旋转180°得到△BDC.现给出下列命题:①四边形ABCD是菱形;②四边形ABCD是中心对称图形;③四边形ABCD是轴对称图形;④AC=BD.其中正确的是________(写上正确的序号).三、解答题(共11分)5.△ABC在平面直角坐标系中的位置如图J23-2-4所示,将△ABC沿y轴翻折得到△A1B1C1,再将△A1B1C1绕点O旋转180°得到△A2B2C2.请依次画出△A1B1C1和△A2B2C2.图J23-2-4课堂10分钟小测·23.2.2关于原点对称的点的坐标时间:10分钟满分:25分一、选择题(每小题3分,共9分)1.若点A(n,2)与点B(-3,m)关于原点对称,则n-m=() A.-1 B.-5C.1 D.52.点P关于原点的对称点为P1(3,4),则点P的坐标为() A.(3,-4) B.(-3,-4)C.(-4,-3) D.(-3,4)3.若点A(2,-2)关于x轴的对称点为B,点B关于原点的对称点为C,则点C的坐标是()A.(2,2) B.(-2,2)C.(-1,-1) D.(-2,-2)二、填空题(每小题4分,共8分)4.点A(-2,1)关于y轴对称的点坐标为________,关于原点对称的点的坐标为________.5.若点A(2,a)关于x轴的对称点是B(b,-3),则ab的值是________.三、解答题(共8分)6.如图J23-2-5,利用关于原点对称的点的坐标的特点,作出与线段AB关于原点对称的图形.图J23-2-5课堂10分钟小测·23.3图像的旋转一、选择题(每小题3分,共9分)1.下列选项中,能通过旋转把图a变换为图b的是()2.图J23-3-1的四个图案中,既可用旋转来分析整个图案的形成过程,又可用轴对称来分析整个图案的形成过程的有()图J23-3-1A.1个B.2个C.3个D.4个3.在下图右侧的四个三角形中,不能由左侧的三角形经过旋转或平移得到的是()二、填空题(每小题4分,共8分)4.正六边形可以看成由基本图形________经过________次旋转而成.5.如图J23-3-2,一串有趣的图案按一定规律排列.请仔细观察,按此规律画出的第10个图案是__________;在前16个图案中“”有______个.图J23-3-2三、解答题(共8分)6.认真观察图J23-3-3中的四个图案,回答下列问题:图J23-3-3(1)请写出这四个图案都具有的两个共同特征:特征1:____________________;特征2:____________________________.(2)请你在图J23-3-4中设计出你心中最美的图案,使它也具备你所写出的上述特征.图J23-3-4课堂10分钟小测·24.1.1圆时间:10分钟满分:25分一、选择题(每小题3分,共9分)1.以已知点O为圆心作圆,可以作()A.1个B.2个C.3个D.无数个2.如图J24-1-1,在⊙O中,弦的条数是()A.2 B.3 C.4 D.以上均不正确图J24-1-1 图J24-1-2 图J24-1-33.如图J24-1-2,在半径为2 cm的⊙O内有长为2 3 cm的弦AB,则∠AOB为()A.60°B.90°C.120°D.150°二、填空题(每小题4分,共8分)4.过圆内的一点(非圆心)有________条弦,有________条直径.5.如图J24-1-3,OE,OF分别为⊙O的弦AB,CD的弦心距,如果OE=OF,那么______(只需写一个正确的结论).三、解答题(共8分)6.如图J24-1-4,已知AB是⊙O的直径,AC为弦,OD∥BC,交AC于点D,OD=5 cm,求BC的长.图J24-1-4课堂10分钟小测·24.1.2垂直于弦的直径,弧、弦、圆心角时间:10分钟满分:25分一、选择题(每小题3分,共6分)1.如图J24-1-5,AB是⊙O的直径,BD=CD,∠BOD=60°,则∠AOC=()A.30°B.45°C.60°D.以上都不正确2.如图J24-1-6,AB,CD是⊙O的直径,AE=BD,若∠AOE=32°,则∠COE的度数是()A.32°B.60°C.68°D.64°图J24-1-5 图J24-1-6 图J24-1-7 图J24-1-8二、填空题(每小题4分,共8分)3.如图J24-1-7,CD⊥AB于点E,若∠B=60°,则∠A=________.4.如图J24-1-8,D,E分别是⊙O的半径OA,OB上的点,CD⊥OA,CE⊥OB,CD=CE,则AC与CB的弧长的大小关系是______________.三、解答题(共11分)5.如图J24-1-9,已知AB=AC,∠APC=60°.(1)求证:△ABC是等边三角形;(2)求∠APB的度数.图J24-1-9时间:10分钟满分:25分一、选择题(每小题3分,共9分)1.已知圆的半径为3,一点到圆心的距离是5,则这点在() A.圆内B.圆上C.圆外D.都有可能答案2.在△ABC中,∠C=90°,AC=BC=4 cm,点D是AB边的中点,以点C为圆心,4 cm长为半径作圆,则点A,B,C,D四点中在圆内的有()A.1个B.2个C.3个D.4个3.⊙O的半径r=5 cm,圆心到直线l的距离OM=4 cm,在直线l上有一点P,且PM=3 cm,则点P()A.在⊙O内B.在⊙O上C.在⊙O外D.可能在⊙O上或在⊙O内二、填空题(每小题4分,共8分)4.锐角三角形的外心在________;直角三角形的外心在________;钝角三角形的外心在________.5.在Rt△ABC中,∠C=90°,AC=5 cm,BC=12 cm,则Rt△ABC 其外接圆半径为________cm.三、解答题(共8分)6.通过文明城市的评选,人们增强了卫生意识,大街随地乱扔生活垃圾的人少了,人们自觉地将生活垃圾倒入垃圾桶中,如图J24-2-1所示,A,B,C为市内的三个住宅小区,环保公司要建一垃圾回收站,为方便起见,要使得回收站建在三个小区都相等的某处,请问如果你是工程师,你将如何选址.图J24-2-1时间:10分钟满分:25分一、选择题(每小题3分,共6分)1.如图J24-2-2,P A切⊙O于点A,PO交⊙O于点B,若P A=6,OP=8,则⊙O的半径是()A.4 B.2 7 C.5 D.102.如图J24-2-3,P A,PB是⊙O的两条切线,切点是A,B.如果OP=4,OA=2,那么∠AOB=()A.90°B.100°C.110°D.120°图J24-2-2 图J24-2-3 图J24-2-4 图J24-2-5二、填空题(每小题4分,共12分)3.已知⊙O的直径为10 cm,圆心O到直线l的距离分别是:①3 cm;②5 cm;③7 cm.那么直线l和⊙O的位置关系是:①________;②________;③________.4.如图J24-2-4,AB是⊙O的直径,点D在AB的延长线上,过点D作⊙O的切线,切点为C,若∠A=25°,则∠D=________.5.如图J24-2-5,⊙O是△ABC的内切圆,与AB,BC,CA分别切于点D,E,F,∠DOE=120°,∠EOF=110°,则∠A=______,∠B =______,∠C=______.三、解答题(共7分)6.如图J24-2-6所示,EB,EC是⊙O的两条切线,B,C是切点,A,D是⊙O上两点,如果∠E=46°,∠DCF=32°,求∠A的度数.图J24-2-6课堂10分钟小测·24.3正多边形和圆时间:10分钟满分:25分一、选择题(每小题3分,共6分)1.一正多边形外角为90°,则它的边心距与半径之比为()A.1∶2 B.1∶ 2C.1∶ 3 D.1∶32.如图J24-3-1,正六边形ABCDEF内接于⊙O,则∠ADB的度数是()图J24-3-1A.60°B.45°C.30°D.22.5°二、填空题(每小题4分,共12分)3.正12边形的每个中心角等于________.4.正六边形的边长为10 cm,它的边心距等于________cm.5.从一个半径为10 cm的圆形纸片上裁出一个最大的正方形,则此正方形的边长为________ cm.三、解答题(共7分)6.如图J24-3-2,要把一个边长为a的正三角形剪成一个最大的正六边形,要剪去怎样的三个三角形?剪成的正六边形的边长是多少?它的面积与原来三角形面积的比是多少?图J24-3-2课堂10分钟小测·24.4.1弧长和扇形面积时间:10分钟 满分:25分一、选择题(每小题3分,共9分)1.在半径为12的⊙O 中,150°的圆心角所对的弧长等于( )A .24π cmB .12π cmC .10π cmD .5π cm2.已知一条弧的半径为9,弧长为8π,那么这条弧所对的圆心角是为( )A .200°B .160°C .120°D .80°3.已知扇形的圆心角为60°,半径为5,则扇形的周长为( ) A.53π B.53π+10 C.56π D.56π+10 二、填空题(每小题4分,共8分)4.如图J24-4-1,已知正方形ABCD 的边长为12 cm ,E 为CD 边上一点,DE =5 cm.以点A 为中心,将△ADE 按顺时针方向旋转得△ABF ,则点E 所经过的路径长为________cm.图J24-4-1 图J24-4-25.如图J24-4-2,在两个同心圆中,两圆半径分别为2,1,∠AOB =120°,则阴影部分面积是____________.三、解答题(共8分)6.如图J24-4-3,在正方形ABCD 中,CD 边的长为1,点E 为AD 的中点,以E 为圆心、1为半径作圆,分别交AB ,CD 于M ,N 两点,与BC 切于点P ,求图中阴影部分的面积.图J24-4-3课堂10分钟小测·24.4.2弧长和扇形面积时间:10分钟满分:25分一、选择题(每小题3分,共6分)1.已知一个扇形的半径为60 cm,圆心角为150°,若用它做成一个圆锥的侧面,则这个圆锥的底面半径为()A.12.5 cm B.25 cm C.50 cm D.75 cm2.如图J24-4-4小红需要用扇形薄纸板制作成底面半径为9厘米,高为12厘米的圆锥形生日帽,则该扇形薄纸板的圆心角为() A.150°B.180°C.216°D.270°图J24-4-4 图J24-4-5 图J24-4-6二、填空题(每小题4分,共12分)3.如图J24-4-5,小刚制作了一个高12 cm,底面直径为10 cm的圆锥,这个圆锥的侧面积是________cm2.4.如图J24-4-6,Rt△ABC分别绕直角边AB,BC旋转一周,旋转后得到的两个圆锥的母线长分别为____________.5.圆锥母线为8 cm,底面半径为5 cm,则其侧面展开图的圆心角大小为______.三、解答题(共7分)6.一个圆锥的高为3 3 cm,侧面展开图为半圆,求:(1)圆锥的母线与底面半径之比;(2)圆锥的全面积.课堂10分钟小测·25.1随机事件与概率一、选择题(每小题2分,共6分)1.下列事件为不可能事件的是()A.若a,b,c都是实数,则a(bc)=(ab)c B.某一天内电话收到的呼叫次数为0C.没有水分,种子发芽D.一个电影院某天的上座率超过50%2.下列事件:①打开电视机,正在播广告;②从只装红球的口袋中,任意摸出一个球恰好是白球;③同性电荷,相互排斥;④抛掷硬币1 000次,第1 000次正面向上.其中为随机事件的是()A.①②B.①④C.②③D.②④3.下列说法错误的是()A.必然发生的事件发生的概率为1B.不可能发生的事件发生的概率为0C.随机事件发生的概率大于0且小于1D.不确定事件发生的概率为0二、填空题(每小题4分,共8分)4.在一个不透明的口袋中,装有5个红球3个白球,它们除颜色外都相同,从中任意摸出一个球,摸到红球的概率为________.5.一只自由飞行的小鸟,将随意地落在如图J25-1-1所示方格地面上(每个小方格都是边长相等的正方形),则小鸟落在阴影方格地面上的概率为________.图J25-1-1三、解答题(第6题6分,第7题5分,共11分)6.指出下列事件中,哪些是必然事件,哪些是不可能事件,哪些是随机事件.①两直线平行,内错角相等;②打靶命中靶心;③掷一次骰子,向上一面是3点;④在装有3个球的布袋里摸出4个球;⑤物体在重力的作用下自由下落.7.一袋中装有除颜色外都相同的红球和黄球共10个,其中红球6个,从袋中任意摸出一球.(1)“摸出的球是白球”是什么事件?它的概率是多少?(2)“摸出的球是黄球”是什么事件?它的概率是多少?课堂10分钟小测·25.2用列举法求概率时间:10分钟 满分:25分一、选择题(每小题2分,共6分)1.从1,2,3,4,5五个数中任意取出1个数,是奇数的概率是( )A.49B.35C.25D.152.有两组扑克牌各三张,牌面数字均为1,2,3,随意从每组牌中各抽一张,数字之和等于4的概率是( )A.29B.13C.49D.59二、填空题(每小题4分,共8分)3.有4条线段,分别为3 cm,4 cm,5 cm,6 cm ,从中任取3条,能构成直角三角形的概率是________.4.小明与父母从广州乘火车回梅州参观某纪念馆,他们买到的火车票是同一批相邻的三个座位,那么小明恰好坐在父母中间的概率是________.三、解答题(共11分)5.从3名男生和2名女生中随机抽取2012年伦敦奧运会志愿者.求下列事件的概率:(1)抽取1名,恰好是女生;(2)抽取2名,恰好是1名男生和1名女生.课堂10分钟小测·25.3用频率估计概率时间:10分钟满分:25分一、选择题(每小题3分,共6分)1.从生产的一批螺钉中抽取1 000个进行质量检查,结果发现有5个是次品,那么从中任取1个是次品概率约为()A.11 000 B.1200 C.12 D.152.在一个不透明的布袋中装有50个黄、白两种颜色的球,除颜色外其他都相同,小红通过多次摸球试验后发现,摸到黄球的频率稳定在0.3左右,则布袋中白球可能有()A.15个B.20个C.30个D.35个二、填空题(每小题4分,共8分)3.若有苹果100万个,小妮从中任意拿出50个,发现有2个被虫子咬了,那么这些苹果大约有________个被虫子咬了.4.为了估计不透明的袋子里装有多少个白球,先从袋中摸出10个球都做上标记,然后放回袋中去,充分摇匀后再摸出10个球,发现其中有一个球有标记,那么你估计袋中大约有________个白球.三、解答题(共11分)5.某位篮球运动员在同样的条件下进行投篮练习,结果如下表:(2)这位运动员投篮一次,进球的概率约是多少?。
初三上册数学小测试卷答案

一、选择题(每题3分,共15分)1. 下列数中,有理数是()A. √2B. √-1C. 3.14D. π答案:C解析:有理数是可以表示为两个整数比的数,3.14可以表示为314/100,是有理数。
2. 若a > b,则下列不等式中正确的是()A. a + 1 > b + 1B. a - 1 < b - 1C. a × 2 > b × 2D. a ÷ 2 < b ÷ 2答案:C解析:根据不等式的性质,当两边同时乘以一个正数时,不等号的方向不变,所以C选项正确。
3. 已知一元二次方程x^2 - 5x + 6 = 0,则x的值为()A. 2B. 3C. 2或3D. 1或4答案:C解析:使用因式分解法解方程,将方程分解为(x - 2)(x - 3) = 0,得到x = 2或x = 3。
4. 若sin A = 1/2,则角A的大小为()A. 30°B. 45°C. 60°D. 90°答案:A解析:sin 30° = 1/2,所以角A的大小为30°。
5. 下列函数中,是反比例函数的是()A. y = x^2B. y = 2xC. y = 1/xD. y = 3x + 2答案:C解析:反比例函数的一般形式是y = k/x(k≠0),所以C选项符合反比例函数的定义。
二、填空题(每题5分,共25分)6. (-2)^3 = _______答案:-8解析:负数的奇数次幂是负数,所以(-2)^3 = -8。
7. 已知等腰三角形底边长为6cm,腰长为8cm,则其高为 _______答案:6√3 cm解析:等腰三角形的高等于底边的一半,所以高为6√3 cm。
8. 在直角三角形中,若直角边分别为3cm和4cm,则斜边长为 _______答案:5cm解析:根据勾股定理,斜边长为√(3^2 + 4^2) = √(9 + 16) = √25 = 5cm。
中考数学小测练习
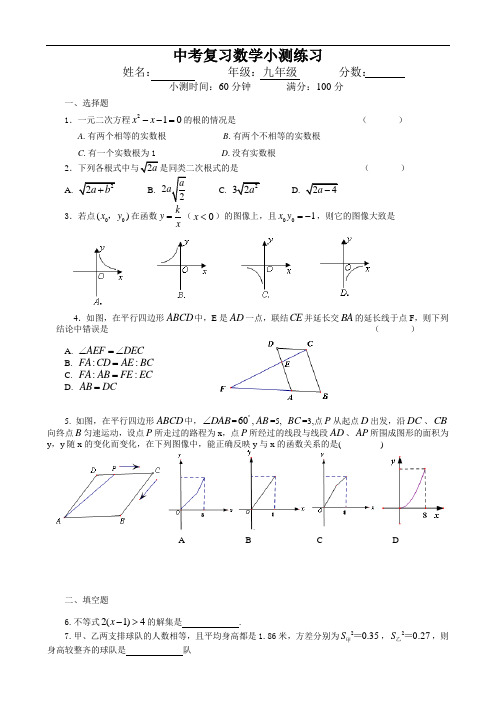
中考复习数学小测练习姓名: 年级:九年级 分数:小测时间:60分钟 满分:100分一、选择题1.一元二次方程210x x --=的根的情况是 ( )A .有两个相等的实数根B .有两个不相等的实数根C .有一个实数根为1D .没有实数根2.下列各根式中与2a 是同类二次根式的是 ( ) A. 22a b + B. 22a aC. 232aD. 24a - 3.若点00()x y ,在函数k y x =(0x <)的图像上,且001x y =-,则它的图像大致是4.如图,在平行四边形ABCD 中,E 是AD 一点,联结CE 并延长交BA 的延长线于点F ,则下列结论中错误是 ( )A. AEF DEC ∠=∠B. ::FA CD AE BC =C. ::FA AB FE EC =D. AB DC =5. 如图,在平行四边形ABCD 中,DAB ∠=60︒,AB =5, BC =3,点P 从起点D 出发,沿DC 、CB向终点B 匀速运动,设点P 所走过的路程为x ,点P 所经过的线段与线段AD 、AP 所围成图形的面积为y ,y 随x 的变化而变化,在下列图像中,能正确反映y 与x 的函数关系的是( )A B C D二、填空题6.不等式2(1)4x ->的解集是 .7.甲、乙两支排球队的人数相等,且平均身高都是1.86米,方差分别为20.35S 甲=,20.27S 乙=,则身高较整齐的球队是 队8.如图,直线//a b ,点B 在直线b 上,且AB BC ⊥,140∠=︒,则2∠= 度.9.如图,用线段AB 表示的高楼与地面垂直,在高楼前D 点测得楼顶A 的仰角为30︒,向高楼前进60米到C 点,又测得楼顶A 的仰角为45︒,且D 、C 、B 三点在同一直线上,则该高楼的高度为 米(结果保留根号).10.如图,点G 是ABC △的重心,CG 的延长线交AB 于D ,5GA =,4GC =,3GB =,将ADG△绕点D 顺时针方向旋转180得到BDE △,则EBC △的面积= .11. 如图,点G 是ABC ∆的重心,AG 的延长线较BC 于点D ,AD =6cm,那么AG = cm三、解答题12、计算:27cos3023+-︒+0()13、解方程:12211x =++-+x x14、如图,⊙O 是△ABC 的外接圆,圆心O 在这个三角形的高AD 上,AB =10,BC =12.求⊙O 的半径.15.如图,EF 是平行四边形ABCD 的对角线BD 的垂直平分线,EF 与边AD 、BC 分别交于点E 、F .(1)求证:四边形BFDE 是菱形;(2)若E 为线段AD 的中点,求证:AB ⊥BD .16.在平面直角坐标系中,抛物线2y x bx c =++经过点(0,2)和点(3,5).(1)求该抛物线的表达式并写出顶点坐标;(2)点P 为抛物线上一动点,如果直径为4的⊙P 与y 轴相切,求点P 的坐标.17、已知:如图,直线PA 交ΘO 与E A 、两点,PA 的垂线CD 切ΘO 与点C ,过点A 作ΘO 的直径AB 。
初三数学专题复习小测验(含答案)

P O ACB初三数学专题小测验1.(3分)如图:若弦BC 经过圆O 的半径OA 的中点P 且PB=3, PC=4,则圆O 的直径为( ) A. 7 B. 8 C. 9 D. 102.(3分)为确保信息安全,信息需要加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密).已知加密规则为:明文a b c ,,对应的密文12439a b c +++,,.例如明文1,2,3对应的密文2,8,18.如果接收方收到密文7,18,15,则解密得到的明文为( )A.4,5,6 B.2,6,7 C.6,7,2 D.7,2,63.(3分)已知第一个三角形的周长为1,它的三条中位线组成第二个三角形,第二个三角形的三条中位线又组成第三个三角形,以此类推,则第2008个三角形的周长为( )A 、200621 B 、200721 C 、200821 D 、2009214. (3分)将4个数a b c d ,,,排成2行、2列,两边各加一条竖直线记成a bc d,定义a bc dad bc =-,上述记号就叫做2阶行列式.若1111x x x x +--+ 6=,则x =__________. 5. (3分)抽取某校学生一个容量为150的样本,测得学生身高后,得到身高频数分布直方图如右,已知该校有学生1500人,则可以估计出该校身高位于160cm 至165cm 之间的学生大约有 人。
6.(3分)三角形纸片ABC 中,55A ∠=︒,75B ∠=︒,将纸片的一角折叠,使点C 落在ABC ∆内(如图),则12∠+∠的度数为_______________。
7.(3分)在数学中,为了简便,记()11231nk k n n ==++++-+∑. 1!1=; 2!21=⨯;3!321=⨯⨯;;()()!12321n n n n =⨯-⨯-⨯⨯⨯⨯.则!2007!20082008120071+-∑∑==k k k k = . 8.(本题满分6分)用换元法解方程:06)1(5)1(2=+---x x x x (cm)504540353025201510509.(本题满分6分)图1是由若干个小圆圈堆成的一个形如正三角形的图案,最上面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了n 层.将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为(1)1232n n n +++++=. 图1 图2 图3 图4如果图1中的圆圈共有12层,(1)我们自上往下,在每个圆圈中都按图3的方式填上一串连续的正整数1234,,,,,则最底层最左边这个圆圈中的数是 ;(2)我们自上往下,在每个圆圈中都按图4的方式填上一串连续的整数23-,22-,21-,,求图4中所有圆圈中各数的绝对值之和.10.(本小题满分8分)如图,ABC △内接于⊙○,点D 在半径OB 的延长线上,30BCD A ∠=∠=°. (1)试判断直线CD 与⊙○的位置关系,并说明理由;(2)若⊙○的半径长为1,求由弧BC 、线段CD 和BD 所围成的 阴影部分面积(结果保留π和根号)11.(本小题8分)电线杆上有一盏路灯O ,电线杆与三个等高的标杆整齐划一地排列在马路一侧的一直线上,AB 、CD 、EF 是三个标杆,相邻的两个标杆之间的距离都是2 m ,已知AB 、CD 在灯光下的影长分别为BM = 1. 6 m ,DN = 0. 6m.(1)请画出路灯O 的位置和标杆EF 在路灯灯光下的影子。
初三质检数学试卷

一、选择题(每题4分,共40分)1. 若a > b,那么下列哪个选项一定成立?A. a + 2 > b + 2B. a - 2 > b - 2C. 2a > 2bD. a^2 > b^22. 下列哪个图形是中心对称图形?A. 等腰三角形B. 等边三角形C. 矩形D. 直角三角形3. 下列哪个数是3的倍数?A. 7 + 8B. 12 + 15C. 9 + 16D. 18 + 214. 若x + y = 5,x - y = 1,则x的值为:A. 3B. 4C. 5D. 65. 在直角坐标系中,点A(2,3)关于x轴的对称点是:A. (2,-3)B. (-2,3)C. (2,-3)D. (-2,-3)6. 下列哪个方程的解是x = 3?A. 2x + 1 = 7B. 3x - 2 = 7C. 4x + 3 = 7D. 5x - 4 = 77. 下列哪个函数的图像是一条直线?A. y = x^2B. y = 2x + 3C. y = x^3D. y = √x8. 若∠A和∠B是补角,且∠A = 60°,则∠B的度数是:A. 30°B. 60°C. 90°D. 120°9. 下列哪个数的平方根是±2?A. 4B. 9C. 16D. 2510. 若一个正方形的边长是a,则它的面积是:A. a^2B. 2aC. a + 1D. a - 1二、填空题(每题4分,共40分)11. 若a + b = 7,ab = 12,则a^2 + b^2的值为______。
12. 在等腰三角形ABC中,AB = AC,∠B = 40°,则∠C的度数是______。
13. 若x = 3,则x^2 - 5x + 6的值为______。
14. 下列哪个数是质数?______。
15. 若∠A和∠B是邻补角,且∠A = 70°,则∠B的度数是______。
初三小测验

比例线段1、 如图,三角形ABC 中,点P 在BC 上,四边形ADPE 为平行四边形,则BD DA∙CE EA=________2、 如图,三角形ABC 中,DEFC 为内接正方形,BC=4cm ,AC=3cm ,则正方形面积为_______3、 已知A 、B 两地的实际距离是250千米,画在比例尺为1:1000000的地图上,量的A 、B图上距离为__________ 4、 如图,在梯形ABCD 中,EF//AD//BC ,若AEEB =23,则FCDC =_________5、 已知线段a 、b 、c ,求作线段x ,使x=acb ,下列做法中正确的是()6、 在三角形ABC 中,点D 、E 分别在边AB 、AC 上,由下列比例式不能得到DE//BC 的是()A.AD=2,DB=4,AE=3,EC=6B.AD=2,AB=6,AE=3,AC=9C.AD=2,DB=4,DE=3,BC=9D.AD=2,AB=6,AE=3,EC=67、 如图,在平行四边形ABCD 中,E 是AB 的中点,G 是AC 上一点,AG :GC=1:5,连EG延长线交AD 于F ,求DFAF 的值DCBA8、如图,在梯形ABCD中,AB//CD,∠B=90°,点M在边AD上,且MN//AB,AB=6,BC=4,CD=3,设DM=X(1)设MN=y,用x的代数式表示y(2)设梯形MNCD的面积为S,用x的代数式表示S(3)若梯形MNCD的面积为S等于梯形ABCD的面积的13,求DM9、如图,Rt三角形ABC中,∠ACB=90°,AB=10,BC=8,点D在BC上运动(不运动至B、C),DE//CA,交AB于E,设BD=x,三角形ADE的面积为y,求y关于x的函数关系式,并写出自变量x的取值范围比例线段二1、已知线段b是线段a、c的比例中项,且a=3,c=4,则b为()A. 2√3B. −2√3C. ∓2√3D.无法确定2、三角形ABC中,直线DE交AB于D,交AC于点E,那么能推出DE//BC的条件是()A. ABAD =32,ECAE=12B. ADDB=23,DEBC=23C. ADDB=23,CEAE=23D.ADAB=43,AEEC=433、如图,三角形ABC中,BEEC =23,G是BD中点,AG延长线交BC于E,求ADDC的值.NC4、如图,已知DE//AC ,DF//BC ,求证:(1)CFAC+EC BC=1;(2)CFAF∙EC BC=1相似三角形(一)1、 如图,在三角形ABC 中,G 是重心,AG 的延长线交BC 于D ,过G 作GF//AB ,交BC于点F ,则S ∆GFD :S ∆ABC =____________2、 如图,∠A=∠CBD ,AB=4,AC=6,BC=5,DB=7.5,则DC=____________3、 如图,在网格交点上找一点C ,使三角形OAB 与A 、B 、C 构成的三角形相似,但不全等,则C 点坐标可以为_____________(只需找一个C 点,网格不能扩大)4、 如图,点D 在三角形ABC 的边AB 上,请你添加一个条件_______,使△ACD ∽△ABC5、如图,AB//DE ,AE//DC ,若S △ABE =18cm 2,S △DEC =12cm 2,则S △ADE =________6、已知等腰梯形的两底分别为4cm 和6cm ,将它的两腰分别延长2cm 后可相交,那么此等腰三角形的腰长是_________cm7、如图,已知PH 是Rt 三角形ABC 斜边AC 上的垂直平分线,垂直为点H ,并交直角边AB 于点P ,D 是PH 上一点,且AD 是AP 与AB 比例中项,求证(1)AP*AB=AH*AC (2)三角形ACD 是等腰直角三角形8、已知,如图,在梯形ABCD 中,AB//CD ,且AB=2CD ,E 、F 分别是AB 和BC 的中点,EF 和BD 相较于点M ,求证:DM=2BM9、如图,等腰梯形ABCD 中,AD//BC ,AD=3,BC=7,∠B=60°,P 为下底BC 上一点(不与B 、C 重合),连接AP ,过点P 作PE 交DC 于E ,使得∠APE=∠B.(1)求证:三角形ABP 相似于三角形PCE ;(2)求AB 的长;(3)在底边BC 上是否存在一点P ,使得DE:EC=5:3?如果存在,求BP 的长,如果不存在,请说明理由.BB相似三角形二1、 如图,DE//FG//BC ,且S ∆ADE =S 梯形DFGE =S 梯形FBCG ,则DE:FG=___________2、 如图,梯形ABCD 中,AD//BC ,AC 、BD 交于点O ,S ∆AOD :S ∆COD =1:9,则S ∆DOC :S ∆BOC =____3、 已知D 是三角形ABC 中的边BC 上的一点,∠BAD=∠C ,那么下列结论中正确的是( )A. AC 2=CD ∙CBB.AB 2=BD ∙CBC. AD 2=CD ∙BDD.BD 2=CD ∙AD4、 如图,DE 是三角形ABC 的中位线,S 1表示三角形ADE 的面积,S 2表示四边形DBCE 的面积,则S 1:S 2为()A. 1:2B. 1:3C. 1:4D. 2:3 5、CB。
初中数学小测试参考答案

1.如图,平行四边形ABCD中,E是BC边上的一点,且AB=AE,若AE平分∠DAB,∠EAC=20°,则∠AED的度数为() A.70°B.75°C.80°D.85°1题图4题图2.菱形ABCD中,边长为10,对角线AC=12.则菱形的面积为.3.观察等式:√3+√32=3√32,2+23=4×23,√5+√54=5√54,….(1)请用含n(n≥3,且n为整数)的式子表示出上述等式的规律____ ____;(2)按上述规律,若√10+ab =10a9,则a+b=;(3)仿照上面内容,当n=11时,计算出结果,验证你在(1)中得到的规律.4.如图,AD是△ABC的角平分线.(1)尺规作图(不写作法,保留作图痕迹):作线段AD的垂直平分线EF,分别交AB、AC于点E、F,连接DE、DF;(2)判断四边形AEDF的形状是_________.(直接写出答案)5.阅读理解:亲爱的同学们,在以后的学习中我们会学习一个定理:直角三角形斜边上的中线等于斜边的一半.即:如图1:在RtΔABC中,∠ACB=90°,若点D是斜边AB的中点,则CD=12AB.(1)牛刀小试:在图1中,若AC=6,BC=8,其他条件不变,则CD=;(2)活学活用:如图2,已知∠ABC=∠ADC=90°,点E、F分别为AC、BD的中点,AC=26,BD=24.求EF的长;(3)问题解决:为了提高全民健身环境,公园管理部门想要建一个形状如图3中的四边形ABCD,其中,∠ABC=90°,∠ADC=60°,AD=CD=6千米,要在公园的B、D之间铺设一条笔直的塑胶跑道,若跑道铺设成本每米200元,当BD最大时,请问管理部门预算160万元够用吗?6.如图,正方形OABC和正方形ODEF有公共顶点O,AO=3,OD=√2,连接AD、CF.(1)如图1,线段AD与线段CF有交点H,求证:AD⊥CF;(2)如图2,点E在CO的延长线上,求CF的长;(3)边EF与AO交于点G,当C,F,E三点共线时,请直接写出S△COG−S△AEG的值.参考答案:1.C【分析】先证明∠B=∠EAD,然后利用SAS证明△ABC≌△EAD,得出∠AED=∠BAC.再证明△ABE为等边三角形,可得∠BAE=60°,求出∠BAC的度数,即可得∠AED的度数.【详解】∵在平行四边形ABCD中,AD∥BC,BC=AD,∴∠EAD=∠AEB,又∵AB=AE,∴∠B=∠AEB,∴∠B=∠EAD,在△ABC和△EAD中,{AB=AE∠ABC=∠EADBC=AD,∴△ABC≌△EAD(SAS),∴∠AED=∠BAC.∵AE平分∠DAB,∴∠BAE=∠DAE,∴∠BAE=∠AEB=∠B,∴△ABE为等边三角形,∴∠BAE=60°,∴∠BAC=∠BAE+∠EAC=80°,∴∠AED=∠BAC=80°;故选C.【点睛】本题考查了平行四边形的性质、全等三角形的判定与性质,等边三角形的判定与性质;熟记平行四边形的性质,证明三角形全等和等边三角形是解决问题的关键.2.96【分析】本题考查菱形的性质,勾股定理.掌握菱形的性质是解题关键.由菱形的性质可知OA=OC=12AC=6,OB=OD=12BD,AC⊥BD,再根据勾股定理可求出BD=16,最后利用菱形的面积公式计算即可.【详解】解:如图,∵四边形ABCD为菱形,∴OA=OC=12AC=6,OB=OD=12BD,AC⊥BD.∵AB=10,∴OB=√AB2−OA2=√102−62=8,∴BD=16,∴S菱形ABCD =12AC⋅BD=12×12×16=96.故答案为:96.3.(1)√n+√nn−1=n√nn−1;(2)√10+9;(3)√11+√1110=11√1110【分析】(1)仿照已知等式得到一般性规律,进而可求出关于n的等式;(2)运用(1)的规律可得√10+√109=10√109,进而求出a、b的值,求解即可;(3)令(1)中的式子中n=11,运用二次根数的加减法法则进行求解即可.【详解】(1)解:∵√3+√32=3√32,2+23=4×23,√5+√54=5√54,….∴√n+√nn−1=n√nn−1,故答案为:√n+√nn−1=n√nn−1;(2)根据题意得√10+√109=10√109,∴a=√10,b=9,∴a+b=√10+9;故答案为:√10+9;(3)当n=11时,√11+√1110=10√1110+√1110=11√1110.【点睛】此题考查了二次根式的加减运算,数字类规律题的理解与运用,正确理解题意掌握二次根式的加减法计算法则是解题的关键.4.(1)见解析;(2)菱形【分析】(1)利用尺规作线段AD的垂直平分线EF即可.(2)根据四边相等的四边形是菱形即可证明.【详解】(1)如图所示:作出直线EF.连接DE、DF.(2)∵AD平分∠BAC,∴∠BAD=∠CAD,∵∠AOE=∠AOF=90°,AO=AO,∴△AOE≌△AOF(ASA),∴AE=AF,∵EF垂直平分线段AD,∴EA=ED,FA=FD,∴EA=ED=DF=AF,∴四边形AEDF是菱形.故答案为:菱形.【点睛】本题考查作图−基本作图,线段的垂直平分线,全等三角形的判定和性质等知识,解题时注意:四条边都相等的四边形是菱形.5.(1)5(2)5(3)不够【分析】(1)由∠ACB=90°,AC=6,BC=8,根据勾股定理求得AB的长为10,再根据“直角三角形上的中线等于斜边的一半”求出CD的长即可;AC=13,而点F是(2)连接BE、DE,因为∠ABC=∠ADC=90°,点E为AC的中点,AC=26,所以BE=DE=12BD的中点,根据等腰三角形的“三线合一”性质得EF⊥BD,则∠BFE=90°,在RtΔBEF中即可根据勾股定理求出EF 的长;(3)连接AC,取AC的中点E,连接BE、DE,先证明ΔADC是等边三角形,根据勾股定理求得DE=3√3千米,再根据直角三角形斜边上的中线等于斜边的一半求出BE的长为3千米,则根据“两点之间,线段最短”可得到不等式BD≤DE+BE,所以当B、E、D在同一直线上时,BD的值最大,此时BD=(3√3+3)千米,再根据跑道铺设成本每米200元计算出跑道铺设的总成本,即可判断出管理部门预算160万元是否够用.【详解】(1)解:如图1,∵∠ACB=90°,AC=6,BC=8,∴AB=√AC2+BC2=√62+82=10,∵点D是斜边AB的中点,∴CD=12AB=12×10=5,故答案为:5.(2)解:如图2,连接BE、DE,∵∠ABC=90°,点E是AC的中点,AC=26,∴BE=12AC=13,∵∠ADC=90°,∴DE=12AC=13,∴BE=DE=13,∵点F是BD的中点,BD=24,∴BF=DF=12BD=12×24=12,EF⊥BD,∴∠BFE=90°,∴EF=√BE2−BF2=√132−122=5,∴EF的长是5.(3)解:如图3,连接AC,取AC的中点E,连接BE、DE,∵AD=CD=6千米,∠ADC=60°,∴ΔADC是等边三角形,∴AC=AD=6千米,∴AE=CE=12AC=12×6=3(千米),∵DE⊥AC,∴∠AED=90°,∴DE=√AD2−AE2=√62−32=3√3(千米),∵∠ABC=90°,∴BE=12AC=3千米,∵BD≤DE+BE,∴BD≤(3√3+3)千米,如图4,当B、E、D在同一直线上时,BD的值最大,此时BD=(3√3+3)千米,∵跑道铺设成本每米200元,∴(3√3+3)×1000×200=(600000√3+600000)元,∴跑道铺设的总成本为(600000√3+600000)元,∵600000√3+600000>1600000,∴管理部门预算160万元不够用.【点睛】此题考查勾股定理的应用、直角三角形斜边上的中线等于斜边的一半、等边三角形的判定与性质、“两点之间,线段最短”等知识与方法,正确地作出辅助线构造直角三角形斜边上的中线是解题的关键.6.(1)见解析(2)CF=√17;(3)S△COG−S△AEG的值为2【分析】(1)证明△DOA≌△FOC,推出∠DAO=∠FCO,利用三角形的外角性质得到∠AHC=90°,即可证明结论成立;(2)连接FD与EO交于点J,利用正方形的性质求得FJ=DJ=JO=1,∠FJC=90°,再利用勾股定理求解即可;(3)证明△DOA≌△FOC,推出S△DAO=S△FCO,得到S△COG−S△AEG的值等于S正方形ODEF,据此即可求解.【详解】(1)证明:∵正方形OABC和正方形ODEF,∴OD=OF,OA=OC,∠DOA=90°+∠FOA=∠FOC,∴△DOA≌△FOC,∴∠DAO=∠FCO,∵∠AIC=90°+∠FCO=∠AHC+∠DAO,∴∠AHC=90°,即AD⊥CF;(2)解:连接FD与EO交于点J,∵正方形ODEF中,OD=√2,⋅√2⋅OD=1,∠FJC=90°,JC=JO+OC=1+3=4,∴FJ=DJ=JO=12∴CF=√FJ2+JC2=√12+42=√17;(3)解:如图,同理OD=OF,OA=OC,∠DOA=90°−∠FOA=∠FOC,∴△DOA≌△FOC,∴S△DAO=S△FCO,∴S△COG−S△AEG=S△FOC+S△FOG−S△AEG=S△FOC−S△AEG+S△FOG=S四边形EDOG +S△FOG=S正方形ODEF=(√2)2=2.【点睛】本题考查了正方形的性质,全等三角形的判定和性质,勾股定理,证明△DOA≌△FOC是解题的关键.。
九年级下数学《数学竞赛---几何》小测验

九年级下数学《数学竞赛---几何》小测验
本文档将为您提供九年级下学期的数学竞赛准备小测验,主题
为几何。
本文档包含800字以上的内容。
第一部分:基础知识
1. 定义:几何是研究空间、形状、大小和相对位置的数学学科。
2. 几何基本概念:
- 点:在几何中,点表示一个位置,没有长度、宽度和高度。
- 直线:无限延伸的线段,由无数个点构成。
- 面:平面是由无限多个点组成的,没有厚度的二维图形。
- 多边形:由线段和端点构成的闭合图形。
- 圆:由一个点向外均匀延伸一定距离形成的闭合图形。
3. 几何中的重要定理:
- 直角三角形定理:直角三角形中,勾股定理成立,即a^2 +
b^2 = c^2。
- 勾股定理:对于任何直角三角形,斜边的平方等于两直角边
平方之和。
- 正弦定理:对于任何三角形,三个边的比例等于其对应角的
正弦比。
- 余弦定理:对于任何三角形,一个边的平方等于其他两个边
的平方和减去这两个边的乘积的两倍的余弦。
第二部分:题练
请解答以下几何题目:
1. 已知直角三角形的两个直角边分别为3cm和4cm,求斜边的长度。
2. 一个正方形的边长为8cm,计算其周长和面积。
3. 已知三角形的三个边长分别为5cm、6cm和8cm,求其面积。
4. 一圆的半径为10cm,请计算其周长和面积。
5. 已知三角形的两个角度分别为60度和70度,求第三个角的度数。
祝你成功完成小测验!。
初中中考复习小测验.docx

初中数学中考复习小测验一、选择题1..如图是一个正六棱柱的主视图和左视图,则图中的6!=()2. 如图所示的二次函数y = ax 2+bx + c 的图象中,刘星同学观察得出了下面四条信息:(1) (2) c>l ; (3) 2a-ZK0; (4) M 济c 〈0。
你认为其中错误的有4.如图6,在等边AABC 中,D 为BC 边上一点,E 为AC 边上一点,且ZADB+ZEDC=nO°,BD=3, CE=2,则AABC 的边长为A. 9B. 12C. 16D. 18 A. 2^3 B. V3 D. 1个3、若样本 Xi+1, x 2+L •-Xn+1的平均数为10,方差为2,则对于样本xi+2, X 2+2, •••, x n +2, 下列结论正确的是() A :平均数为10,方差为2B :平均数为11,方差为3C :平均数为11,方差为2D :平均数为12,方差为4b~ — 4ac > 0 ; 主视图 左视图C. 4个 KIA8. 下列说法错误的是(9.如图,在直角坐标系中,以原点。
为圆心的同心圆的半径由内向外依次为1, 2, 3, 4,…,同心 圆与直线y=x 和y=-x 分别交于Ai, A 2, A 3, A4…,则点A30的坐标是()A. (30, 30)B. (-8扼,8扼)C. ( - 4扼,屿)D. (4扼,-4A /2)10. 如图,将正方形对折后展开(图④是连续两次对折后再展开),再按图示方法折叠,能够得到一 个直角三角形,且它的一条直角边等于斜边的一半.这样的图形有【 5、 如图:ZB=ZC=90° , E 是BC 的中点,DE 平分ZADC,ZCED=35° ,则 ZEAB= 度;6. 若和都有意义,则。
的值是() A.a > 0B.a < 0C. Q = 0D.。
壬 07,7(X 2+4)2的算术平方根是() A 、 (『+4)4 B 、(『+4)2C 、x 2 +4D 、 A . a 2与(一a ) 2相等c.拓'与eu 是互为相反数B .与 D . H 与卜4 B. 互为相反数 互为相反数(D)l 个(B)3 个 (C)2 个(A)4 个二、填空题1.代数式4x2+3mx+9是完全平方式,则血=.2.如图,已知 A^ljO), A2(l,l), A3(—1,1), A4(—1,—1), A5(2,—1),…,则点 A2007 和点 A的坐标分别为 ; 。
九年级数学课前小测1

九年级数学课前小测(1)
2.如图,已知⊙O 是△ABC 的内切圆,且∠ABC =50°,∠ACB =80°, 则∠BOC 是( )
A. 110°
B. 115°
C. 120°
D. 125°
3.如图,将宽为1cm 的纸条沿BC 折叠,使∠CAB =45°,则折叠后重叠部分的面积为( )
A .
2cm 2 B .22cm 2 C .32
cm 2 D . 3cm 2 4.八个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l 将这八个正方形分成面积相等的两部分,则该直线l的解析式为 ( )
A.y=x 53 B.y=x 43 C.y=x 10
9 D.y=x 5.圆锥的侧面积为8π ,母线长为4,则它的底面半径为( )
A.2 B.1 C.3 D.4
6.在函数1
1+=x y 中,自变量x 的取值范围是 . 7.若=-=-+a a a a 42-2016,03222则若 .
8.如图,将矩形纸片ABCD 折叠,使点A 与点C 重合,折痕为EF ,若AB =4,BC =2,那么线段EF 的长为 .
9.如图,在△ABC 中,AB =AC ,以AB 为直径作半圆⊙0,
交BC 于点D ,连接AD ,过点D 作DE ⊥AC ,垂足为点E ,
交AB 的延长线于点F .
(1)求证:EF 是⊙0的切线.
(2)如果⊙0的半径为5,sin ∠ADE =54,求AE 的长。
45°C B A。
暑假新初三小测验 数学

新初三小测验一.填空题1.若22(1)0m n ++-=,则2m n +的值为________2.若一次函数y=(3-k )x-k 的图象经过第二、三、四象限,则k 的取值范围是_________3.当22-+a a 有意义时,a 的取值范围是________4.在实数范围内分解因式:632-x =________二.解答题1.已知31=+x x 不求x 的值,求下列各式的值(1)221x x + (2)441x x+2.如图,AD 是△ABC 的边BC 上的高,由下列条件中的某一个就能推出△ABC 是等腰三角形的是______并证明你的结论。
①∠BAD=∠ACD ;②∠BAD=∠CAD ;③AB+BD=AC+CD ;;④AB-BD=AC-CD答案填空题1.0 分析:m=-2,n=1,所以m+2n=02.k>3 分析:因为一次函数过二三四象限,即030{<-<-k k ,得k>3 3.a>2 分析:要求分式有意义则分母不为0,且二次根式有意义则二次根式里面为非负数,即0202{≥-≠-a a ,得a>2 4.)2)(2(3-+x x 分析:原式=)2(32-x =)2)(2(3-+x x解答题1.因为31=+x x ,则2)1(x x +=9=2221x x ++,所以221x x+=7, 同理,222)1(x x +=49=4421x x ++,所以441x x +=472.应添加的条件是②③④;证明:②当∠BAD=∠CAD 时,∵AD 是∠BAC 的平分线,且AD 是BC 边上的高;则△ABD ≌△ACD ,∴△BAC 是等腰三角形;③延长DB 至E ,使BE=AB ;延长DC 至F ,使CF=AC ;连接AE 、AF ;∵AB+BD=CD+AC ,∴DE=DF ,又AD ⊥BC ;∴△AEF 是等腰三角形;∴∠E=∠F ; ∵AB=BE ,∴∠ABC=2∠E ;同理,得∠ACB=2∠F ;∴∠ABC=∠ACB ,即AB=AC ,△ABC 是等腰三角形;④△ABC 中,AD ⊥BC ,根据勾股定理,得:AB 2-BD 2=AC 2-CD 2,即(AB+BD )(AB-BD )=(AC+CD )(AC-CD );∵AB-BD=AC-CD①,∴AB+BD=AC+CD②;∴①+②得:2AB=2AC ;∴AB=AC ,∴△ABC 是等腰三角形故填②③④.。
九年级数学课前小测8

九年级数学课前小测81、如右图,线段AB 是⊙O 的直径,弦CD 丄AB ,∠CAB =20°,则∠AOD 等于 A .120° B . 140° C .150° D . 160°2、二次函数223y x x =--的最小值为A. 5B. 0C. -3D. -43、如右图,正方形ABCD 和正三角形AEF 都内接于⊙O ,EF 与BC ,CD 分别相交于点G ,H ,则EF GH的值为A.2 B.32C. 3D. 2 4、如右图,AB 是⊙O 的直径,弦CD AB ⊥于点E ,3023CDB CD ∠==o ,, 则阴影部分的面积为 .5、如图,将一个量角器与一张等边三角形(△ABC )纸片放置成轴对称图形,CD ⊥AB ,垂足为D ,半圆(量角器)的圆心与点D 重合,此时,测得顶点C 到量角器最高点的距离CE =2cm ,将量角器沿DC 方向平移1cm ,半圆(量角器)恰与△ABC 的边AC ,BC 相切,如图2,则AB 的长为 cm.6.、如右图,我们把抛物线y =-x (x -3)(0≤x ≤3)记为C 1,它与x 轴交于点O ,A 1;将C 1绕点A 1旋转180°得C 2,交x 轴于另一点A 2;将C 2绕点A 2旋转180°得C 3,交x 轴于另一点A 3;……;如此进行下去,直至得C 2016.①C 1的对称轴方程是 ;②若点P (6047,m )在抛物线C 2016上, 则m = .7.已知二次函数2535652--=x x y 的图象如图,则方程02535652=--x x 的根为 .ABCD OAB CDE O FG H BE DC AO…C 3A 3C 2A 2yxOA 1C 1图1C BAD EED ABC 图28、如图,正方形ABCD 的边长为3cm ,动点P 从B 点出发以3cm /s 的速度沿着边BC ﹣CD ﹣DA 运动,到达A 点停止运动;另一动点Q 同时从B 点出发,以1cm /s 的速度沿着边BA 向A点运动,到达A 点停止运动.设P 点运动时间为x (s ),△BPQ 的面积为y (cm 2),则y 关于x 的函数图象是( )9、如图,点D ,E 分别在△ABC 的AB ,AC 边上,增加下列条件中的一个: ①∠AED =∠B ,②∠ADE =∠C ,③BC DE AB AE =,④ABAE AC AD =,⑤AE AD AC ⋅=2, 使△ADE 与△ACB 一定相似的有A 、①②④B 、②④⑤C 、①②③④D 、①②③⑤10、若二次函数bx x y +=2的图象的对称轴是经过点(2,0)且平行于y 轴的直线, 则关于x 的方程52=+bx x 的解为( ) A. 01=x ,42=x B. 11=x ,52=xC. 11=x ,52-=xD. 11-=x ,52=x。
初三数学水平测试卷

1. 下列各数中,有理数是()A. √2B. √3C. πD. 3/22. 已知x是方程x² - 5x + 6 = 0的解,则x + 2的值为()A. 3B. 4C. 5D. 63. 下列各数中,无理数是()A. √9B. √16C. √25D. √-44. 已知x是方程2x² - 3x - 4 = 0的解,则x² - 2x的值为()A. -4B. -2C. 2D. 45. 若a,b是方程x² - 2ax + b = 0的两根,则a + b的值为()A. 1B. 2C. 3D. 46. 已知x是方程x² + 2x + 1 = 0的解,则x + 1的值为()A. 0B. 1C. 2D. 37. 下列各数中,既是整数又是正数的是()A. -3B. 0C. 2D. -28. 若a,b是方程ax² + bx + c = 0的两根,则a + b的值为()A. aB. bC. cD. ab9. 下列各数中,既是无理数又是负数的是()A. -√2B. -√3C. -√4D. -√910. 已知x是方程x² - 4x + 4 = 0的解,则x - 2的值为()A. 0B. 1C. 2D. 3二、填空题(每题5分,共50分)11. 若a,b是方程x² - 2ax + b = 0的两根,则a + b = __________,ab = __________。
12. 已知x是方程x² - 3x + 2 = 0的解,则x + 1的值为 __________。
13. 若a,b是方程x² - 2ax + b = 0的两根,则a² - b² = __________。
14. 已知x是方程x² + 4x + 4 = 0的解,则x + 2的值为 __________。
15. 若a,b是方程ax² + bx + c = 0的两根,则a + b + c = __________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初三数学小测验(3)2012、10、29
一、选择
( )11
x +在实数范围内有意义,则x 的取值范围是
A . x ≥-1
B . x ≠0
C . x >-1且x ≠0
D . x ≥-1且x ≠0
( )2、下列事件中是必然事件的是
(A )阴天一定下雨 (B )随机掷一枚质地均匀的硬币,正面朝
上
(C )男生的身高比女生高 (D )油滴在水中,油会浮在水面上
( )3、 六张形状、颜色、大小完全相同的纸片上分别写着二次2422a +15b a 2、20.710纸片,上面写着最简二次根式的概率是
A . 16
B .13
C .23
D .12
( )4、如右图,把边长为3的正三角形绕着它的中心旋转
180°后, 则新图形与原图形重叠部分的面积为
A. 33
B. 3
C. 33
D. 93
二、填空
5、已知圆锥的母线长5,底面半径为3,则圆锥的侧面积为
6、已知方程x 2 -2x+k=0有两个相等的实数根,则k=
7、有四条线段,分别为3,4,5,6,从中任取三条,能够成直角
三角形的概率是
8、在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个
圆锥模型,若圆的半径为r,扇形的半径为 R ,扇形的圆心角
等于90°,则r 与R之间的关系是
9、圆弧拱桥的跨度为12m,拱高为4m。
则桥拱所在的圆的直径为。
三、解答题
10、如图8,在平面直角坐标系中,以(1,0)为圆心的⊙P与y 轴相切于原点O,过点A(-1,0)的直线AB与⊙P 相切于点B 。
(1)求AB的长(2)求AB、OA与OB所围成的阴影部分面积(3)求直线AB的解析式;
(4)直线AB上是否存在点M,
使OM+PM的值最小?如果存
B
在,请求出点M的坐标;如果不
存在,请说理。
(-1,0) (1,0)。
