生成三角网格的三种基本方法

GIS名词解释一

GIS名词解释一建立DEM的方法之一【建立不规则三角网方法(TIN)】原理：对有限个离散点,每三个最临近点联结成三角形，每个三角形代表一个局部平面，再根据每个平面方程，计算每个网格点的高程，生成DEM。

TIN定义：将离散分布的实测数据点连成三角网，网中的每个三角形要求尽量接近等边形状，并保证由最近邻的点构成三角形，即三角形的边长之和最小。

【空间插值】常用于将离散点的测量数据转换为连续的数据曲面，它包括内插和外推两种算法。

前者是通过已知点的数据计算同一区域内其他未知点的数据，后者则是通过已知区域的数据，求未知区域的数据。

通常，在以下几种情况下要做空间插值：1、现有数据的分辨率不够，如遥感图象从一种分辨率转换到另一种分辨率。

2、现有数据的结构与所需结构不同，如将栅格数据转换到TIN数据。

3、现有数据没有完全覆盖整个区域，如只有一些离散点数据。

4、需要进行空间插值处理的原始数据包括：航片/卫片、野外测量采样数据、等值线图等。

【空间内插】定义：从已知点或分区的数据推求任意点或分区的数据的方法称为间数据的内插。

有点内插和区域内插两种。

【数字地面（形）模型】定义：描述地球表面形态多种信息空间分布的有序数值阵列，从数学的角度，可以用二维函数系列取值的有序集合来概括地表示数字地面模型的丰富内容和多样形式。

书中定义：用数字化的形式表达的地形信息。

【地理空间的特征实体】概念：地理空间实体特征是指具有形状、属性和时序特征的空间对象或地理实体。

；实体包括点、线、面、曲面和体等类型，它包括两种基本表达形式：矢量表示法、栅格表示法【E-R模型】常用的语义数据模型之一是实体--联系模型。

提供三种重要的语义概念，即实体、联系和属性。

实体: 就是对客观存在起独立作用的客体的抽象，用矩形符号表示；关系: 就是客体间有意义的相互作用或对应关系, 用菱形符号表示；属性: 对实体和联系特征的描述, 每个属性都有一个域，用椭圆表示【数据与信息的关系】数据是信息的一种表现形式，数据通过能书写的信息编码表示信息。

测绘技术中的地形模型生成方法

测绘技术中的地形模型生成方法地形模型是测绘技术中的重要组成部分，它能够提供精确的地理信息，为各个领域的工作提供基础数据支持。

在地理信息系统、城市规划、灾害管理等领域中，地形模型的生成方法起着关键性作用。

本文将探讨测绘技术中的地形模型生成方法，旨在为读者提供一些了解和思考的方向。

一、栅格模型方法：1. 相邻高程法：相邻高程法是地形模型中最简单直接的方法之一。

它基于高程点的邻域关系，将周围的点相连，通过插值算法来估计未知点的高程。

这种方法的优势在于计算简单、可靠，但缺点是不能处理地形变化较大的情况。

2. 内插法：内插法是测绘技术中常用的地形模型生成方法之一。

它通过确定邻近已知高程点的权重，使用合适的插值算法来估计未知点的高程。

常用的内插方法包括反距离加权法、克里金插值法等。

内插法的优势在于可以较好地处理地形变化较为复杂的情况，但在处理地形边界和孤立点时可能会出现插值误差。

3. TIN三角网方法：TIN三角网方法是一种基于三角形连接的地形模型生成方法。

它通过将地形点构建成三角形网络，根据三角形的特征来估计未知点的高程。

这种方法的优势在于可以较好地处理地形的不规则性和边界情况，但生成的地形模型较为稀疏，对于局部细节的表达能力有限。

二、基于激光雷达的方法：随着激光雷达技术的发展，基于激光雷达的地形模型生成方法逐渐成为主流。

激光雷达通过发射激光束并测量其回波时间，可以高精度地获取地面的高程信息。

在地形模型生成中，常用的方法有以下几种：1. 基于点云的方法：点云是激光雷达获取的地面高程数据，通过对点云进行处理和分析，可以生成地形模型。

常见的点云处理方法包括滤波、分类、拟合等。

这种方法的优势在于能够获取较为精细的地形信息，对于地形中的细节和复杂性有很好的表达能力。

2. 基于网格的方法：基于网格的方法是一种将点云数据转换为规则网格的地形模型生成方法。

在网格模型中，每个网格单元都包含一个高程值，通过对点云进行分割和平滑，可以生成规则的网格模型。

图像描述中Delaunay三角形网格的快速生成方法

第３期
图像描述中Ｄｅａｎｙ三角形网格的快速生成方法ｌｕａ
焦卫东，卢朝阳，黄瑾
（安电子科技大学综合业务网理论及关键技术国家重点实验室，西西安西陕７０７）１０１
摘要：针对ＤＴ模型基图像编码方法不能实现实时编码的不足，据图像的多分辨率表示方法，用分根采层搜索的思想，出了一种基于ＭＤ或ＭＶ准则的图像描述中Ｄ网格的快速生成方法，过逐渐精细提Ｔ通
的搜索步长搜索网格节点，少了逐点搜索的次数，而节约了时间，高了运算效率．验表明，基减从提实与于ＭＤ或ＭＶ准则的一般方法相比，方法生成Ｄ网格的速度提高了近一倍，时恢复图像保持了相该Ｔ同近的质量；其他一些方法相比，相同的网格生成时间限制下，复图像的质量明显提高．与在恢
维普报（自然科学版）
Ｊ０ＵＲＮＡＬ０ＦＸＩＡＮＵＮＩ，ＳＴＹＤＩＶＥＲＩ
Ｊｎ．０７ｕ２０
Ｖｏ．４ＮＯ３１３．
第３４卷
ＡｂｔａｔＣｏｉｅｎｇｔａｌｒｆｒａｉｅｃｉｇａｐｉａｉｎｉｈｓｒｃ：ｎｓｄｒｈｅｆｉｕｅｏｅｌｔｏｄｎｐｌｃｔｏｎｔｅＤＴｏｅ－ａｅｍａｅｃｄｎｃｍｅｉｍｍｄｌｂｓｄｉｇｏｉｇｓｈｅ，ａｆｓｔｏｏｇｅｒｔｈｌｕｙＴｒａｇｕａｉｎａｔｍｅｈｄｔｎｅａｅｔｅＤｅａｎａｉｎｌｔｏｍｅｈｆｒｉｇｅｒｐｅｅｔｔｏａｅｎｔＶｒＭＤｓｏｍａｅｒｓｎａｉｎｂｓｄｏｈｅＭｏｃｉｅｉｎｉｏｏｅｙｕｉｇｔｄａｏｕｔｒｓｌｔｏｅｒｈｉｇＩｅｒｈｓｔｅｍｅｈｎｄｓｗｉｈｇａｕｌｒｔｒｏｓｐｒｐｓｄｂｓｎｈｅｉｅｆｍｌｉｅｏｕｉｎｓａｃｎ．ｔｓａｃｅｈｓｏｅｔｒｄａ－ｓｂｌｔｐｌｎｔｎｇｎｒｔｈｅｈｂｕｔｅｓｅｅｇｈｉｅｅａｉｏｆｔｅｍｓｙｗｈｉｈｔｏａｆｓａｃｉｏｎｓｉｒｄｕｅｅｂｎｅＳｉｅｏｎｃｈｅｔｔｌｏｅｒｈｎｇｐｉｔｓｅｃｄｏｎｙｏ，Ｏｔｍｃｎｂａｅｎｄｔｏｐａｉｎｌｅｆｃｅｃｐｏｅａｅｓｖｄａｈｅｃｍｕｔｔｏａｆｉｉｎｙｉｒｖｄ．ＳｉｕａｉｎｒｓｌｈｍｍｌｔｏｅｕｔｓｏｗｓｔａｈｅｐｏｏｅｅｈｄｓｖｓｈｔｔｒｐｓｄｍｔｏａｅａｍｏｔｏｅｈｌｉｅｗｈｉｅｐｎｇｆｎｌｅｏｓｒｃｅｍａｅｑａｉｙｃｍｐｒｄｗｉｈｔｅｇｎｒｌｍｅｈｓｄｌｓｎａｆｔｍｌｋｅｉｉｅｙｒｃｎｔｕｔｄｉｇｕｌｏａｅｔｈｅｅａｔｏｄｂａｅｅｔｏｈＶｒＭＤｒｔｒｏｎｔｅＭｏｃｅｉｎ，ａｈｔｉｔｌｃｎｇｔｍｏｅａｃｒｔｍａｅｒｓｎｔｔｏｎｒｔｅｓｍｅｍｅｈｉｎｄｔａｔｓｉａｅｒｃｕａｅｉｇｅｒｐｅｅａｉｎｕｄｅｈａｓｌｇｎｒｔｉｅｃｍｐｒｄｗｉｈｔｔｅｘｓｉｇｍｅｈｏ．ｅｅａｉｔｍｏａｅｔｈｅｏｈｒｅｉｔｎｔｄｓｏｎＫｅｏｄｙＷｒｓ：Ｄｅａａｒｉｌｕｎｙｔａｎｇｕａｔｏｅｈ；ｕｌｉｒｓｌｉｎｓａｃｎｇ；ｍａｅｅｅａｉｌｉｎｍｓｍｔ— ｅｏｕｔｏｅｒｈｉｉｇｅｒｐｒｓｎｔｔｏｎ

复杂平面区域的三角网格生成算法

ｅｅｎｓｅｒａｂｔｒＤｄｍａｎ．ｌｍｅｔｍｅｈｓｆｒｉａｙ２ｏｉｓｏｒ
Ｋｅｒｓ：ｒｇｌｓｙｗｏｄｔｉｕａｍｅｈ；ｍｅｈｇｎｒｔｏｎａｒｓｅｅａｉｎ；ｍｅｈｒｆｎｍｅｔｅａｍａ－ｐｍｉｅｂｓｃｉｎｓｉｅｎ；ｄｌｔｙｏｔｚｄｉｅｔｏｅｉ
有限元方法计算效率在很大程度上受有限元网格质量的影响。近几十年来，有限元网格生成技术的研究取得了很大进展，并出现了大量网格生成算法。由于三角面片几何相容性好，非结构化三角网格成为一种常用的二维有限元网格，其生成技术分为四叉树、波前法和Ｄｌｎｙｅｕａ等三大类Ⅲ，中，ａ其Ｄｌｎｙｅｕａ方法是迄今为止研究最多、ａ应用最广泛的一类方法。Ｄｌｎｙｅｕａ三角网格中各单元的外接圆内ａ不包含任何节点，具有最小角最大特性，但实际应用中，ｅｕａ方法必须解决边界恢复和内点生Ｄｌｎｙａ
复杂平面区域的三角网格生成算法
陈
（．国防科技大学计算机学院，１湖南长沙
欣熊岳山一，
３１０）２０４
４０７；２浙江师范大学数理与信息工程学院，江金华１０３．浙
摘
要：为生成复杂平面区域的有限元网格，出了基于网格细化的三角网格生成算法。该算法首先采提
ｍｅｔｅｒ－ｅｉｅｎｇｒｕｅｅｔｆｉｔｅｎｔｌｅｈａｎｖｌｓｆｅｅｔｅｏ，ｅａｎｙｏｔｉｄｂｅｔｎｉｅｔｅｓｃｄｉｑ￣ｍｎｂｒｎｎｈｉｉｍｓ，ｏｅｍｅｒｉｍｎｍｔｈｐｐｆｓｉｅｙｅｇｉｉａｈｅｎｈｄＤｌａ－ｐｍｚｉｃｏ，ｓｕｉｅｓｉ

三维地质构造的三角形格架式网格生成方法

ＰｔｌｕＵｎｖｒｉｆｈｎ，Ｄｏｇｉｇ２７６，ＣｉａｅｒｅｍｉｅｓｏＣｉａｏｙｔｎｙｎ５０１ｈｎ）
ＡｂｔａｔＴｅｓｍｕａｉｎｍｅｈｄｏｒｅｄｍｅｓｎｌｙｒｃｒｏｇａｉｎａｄａｃｍｕａｉｎｐｏｅｓｎｅｅｅａｅｔｒｅｄｍｅ — ｓｒｃ：ｈｉｌｔｔｏｆｈｅ — ｉｎｉａｈｄｏａｂｎｍｉｒｔｎｃｕｌｔｏｒｃｓｅｄｔｇｎｒｔｅ — ｉｎｏｔｏｏｏｈｓｏａｅｌｇｃｌｆａｗｏｋｍｅｈＴｈｅｅａｉｎｏｒｅｄｍｅｓｎｌｅｌｇｃｌａｗｏｋｍｅｈｉｂｓｄｏｔｕｔｒｄｌｃｎｉｎｌｏｏｉａｍｅｒｓ．ｇｒｅｇｎｒｔｆｈｅ — ｉｎｉａｏｏｉａｍｅｒｓａｅｎｓｒｃｕｅｍｏｅｏ — ｏｔｏｇｒｆｓｓｒｉｔＩｅｐｎｅｔｉｅｎ，ｔｅｅｉｔｇｍｅｈｇｎｒｔｎｍｅｏｓａｅａａｙｅｎｏａｅ，ａｄｏｈｓａｉｙｔｍｏｔｎｎｒｓｏｓｔｓｄｍａｄｈｘｓｉｓｅｅａｉｔｄｒｎｌｚｄａｄｃｍｐｒｄａｏｈｎｏｈｎｎｔｉｓｓａｓｓｅｆｒｂｔｉｎｕａａｅｒｓｅｅａｉｎｉｒｓｎｅ．ＴｅｃｎｔａｎｄＤｅａｎｙｔｉｎｕａｉｎａｇｒｈｉｕｅｏｓｒｃｅｇｏｏｉａｒｇｌｒｍｗｏｋｍｅｈｇｎｒｔｐｅｅｔｄａｒｆｏｓｈｏｓｒｉｅｌｕａａｇｌｔｌｏｉｍｓｄｔｃｎｔｕｔｈｅｌｇｃｌｒｏｔｓｏｔ

简单的三角形网格生成程序

ee = e*1.e-30
nn = 0
smin = dmax*dmax
do 140 i=1,numnod
cccc do 140 n=nums+1,nume
cccc i = nod2(n)
xx = x(i)
yy = y(i)
s = (xx-xh)**2+(yy-yh)**2
c x,y ............... coordinate arrays of nodal points
c nod1,nod2,nod3 .... nodal No. arrays for each triangle
c node .............. circle boundary nodal No. array
c nums ....... starting edge No. - 1
c numnod ..... number of nodes
c numedge .... number of edges
c mc ......... number of iteration for modifying nodal points
nn = j
write(*,*) 'nn,smin,d =',nn,smin,d
xh = x(nn)
yh = y(nn)
write(*,*) 'xh,yh =',xh,yh
index(nums) = 2
endif
cccc do 1000 n=nums+1,nume
do 1000 n=1,nume
call trinod(nume,nt,x,y,nod1,nod2,nod3)

三角形网格生成算法的研究与应用

三角形网格生成算法的研究与应用一、引言三角网格是计算机图形学领域中最常见的图形表示方式之一。

三角形网格生成算法的出现为图形学在各个领域的应用提供了强有力的支持，如计算机辅助设计、数字娱乐、医学图像处理等等。

然而目前三角形网格的生成算法依然存在许多难点，本文将针对这些难点进行研究和分析，探讨三角形网格生成算法的研究与应用。

二、先进的三角形网格生成算法三角形网格生成算法主要分为离散型和连续型两种。

离散型算法主要是针对离散数据点进行分析和处理，是传统算法的核心。

而连续型算法则主要考虑通过合理的数值方法对连续函数进行求解得到三角形网格。

2.1 离散型算法离散型算法主要方法包括 Delaunay 三角剖分、Voronoi 图、alpha 参数、最小生成树等等。

Delaunay 三角剖分是三角形网格分割中最常见的算法之一。

该算法的核心思想是保持尽量少的单纯形边长相交。

Voronoi 图是一种基于点的分割方法，可以将平面分割成一系列多边形。

Alpha 参数是控制 Delaunay 三角剖分质量的措施之一，通过调整 alpha 参数，可以在不同场景下获得合适的 Delaunay 三角剖分。

最小生成树算法则是对点集进行聚类的一种方法，通常用于优化 Delaunay三角剖分的质量。

2.2 连续型算法连续型算法主要包括渐近线、等值线、样条曲面拟合、卷积核方法等等。

渐近线的求解方法主要是对三角形网格表面进行采样后，通过函数空间中的拟合逼近来求解渐近线。

等值线方法则是在网格表面中寻找等值线，从而实现扫描三角形网格的目的。

样条曲面拟合是利用拟合优化方法，对离散的三角形网格点进行拟合，得到连续的三角形网格。

卷积核方法则通过对三角形表面求导以及在线性空间中构建卷积核，从而求得三角形网格表面的连续性信息。

三、三角形网格生成算法在计算机图形学领域的应用三角形网格生成算法在计算机图形学领域的应用十分广泛，主要包括三维重构、曲面拟合、形状建模、虚拟现实等等。

如何进行三角网的建立与处理

如何进行三角网的建立与处理在计算机科学领域中，三角网是一种用于连接数据点的网格结构。

它由许多三角形组成，每个三角形的三个顶点都是数据点。

三角网的建立和处理是许多计算机图形学和计算机视觉任务中的基础步骤。

本文将探讨如何进行三角网的建立与处理。

一、三角网的建立三角网的建立是通过一系列步骤来生成一个包含数据点的三角网格。

以下是一个简单的流程：1. 数据预处理：首先，需要根据实际应用场景，对数据点进行预处理。

这可能包括数据清洗、数据采样和数据变换等操作，以确保数据的质量和适用性。

2. 确定边界条件：在建立三角网之前，需要确定边界条件。

边界条件可以是已知的数据点或外部提供的信息。

边界条件的选择对于生成合理的三角网格非常重要。

3. 进行三角网格的初始化：在确定边界条件后，可以开始进行三角网格的初始化。

这可以通过将数据点放置在二维平面上，并根据某种规则（如Delaunay三角剖分算法）进行三角剖分来实现。

三角剖分算法是一种常用的方法，它能够确保所有的三角形都是“良好”的，即不会出现重叠或相交的情况。

4. 优化三角网：在初始化完成后，可能需要进行一些优化来改进生成的三角网。

例如，可以使用各种算法来优化三角网的质量和形状，以满足特定的需求。

常用的优化算法包括Laplacian平滑算法和拓扑优化算法等。

二、三角网的处理一旦三角网建立完成，就可以进行各种处理操作。

以下是一些常见的三角网处理技术：1. 网格编辑：三角网的处理通常涉及在网格上进行编辑和修改。

这可以通过添加、删除或移动数据点来实现。

网格编辑技术是计算机图形学和计算机视觉任务中的重要部分，可以用于模型编辑、形变和纹理映射等应用。

2. 网格分析：通过对三角网进行分析，可以获得有关数据点之间关系的更多信息。

例如，可以计算三角形的面积、周长和法向量等属性。

这些信息在许多应用中都是有用的，如物体表面重建、拓扑分析和形状匹配等。

3. 网格变形：通过对三角网进行变形操作，可以实现形状的变化和动画效果。

三角网格的参数化

2) ( 浙江大学计算机科学与技术学院杭州 310027)
3) ( 浙江大学数学系杭州 310027)
摘要参数化变形的大小是衡量参数化好坏的标准基于这个标准, 分别从平面参数域和球面参数域对各种参数化方法的保面积性、保角性和等距性进行深入的讨论, 并从算法的理论基础、运算时间复杂度、适用范围和数值实现方法等方面作了详细的比较和论述最后, 结合作者在本领域的研究工作, 对参数化方法的研究趋势作了一个展望
关键词三角网格; 参数化; 变形; 综述中图法分类号 T P391
Survey on Parameterization of Triangular Meshes
Peng Q unsheng1, 3) H u Guofei1, 2)
1) ( St ate K ey L aboratory of CA D & CG , Zhej i ang U niv ersity , H angz hou 310027) 2) ( Coll ege of Comp ut er S cience , Zhej iang Uni ver si ty, H a ngz hou 310027) 3) ( D epart ment of M athemat ics, Zhej i ang U niv ersity , H angzhou 310027)
7 32
计算机辅助设计与图形学学报
2004 年
实际上, 三角网格参数化可归结为这样一个问
题: 给定一个由空间点集 Pi R 3 组成的二维流形三
角网格 M = { T j } 和一个二维流形参数域 p , 寻求
一个在参数域上的点
P
* i
p 到 Pi M 的一一映

triangle库用法

triangle库用法Triangle是一个Python库，它提供了许多用于处理三角形和计算三角形属性的函数和类。

本文将详细介绍Triangle库的使用方法，以帮助读者更好地了解如何使用这个库来处理三角形。

第一步：安装Triangle库要使用Triangle库，首先需要将其安装在您的Python环境中。

您可以通过以下命令在命令行中安装Triangle库：pip install triangle确保您已经正确安装了Python和pip，以便顺利安装Triangle库。

第二步：导入Triangle库一旦安装了Triangle库，您可以在您的Python程序中导入它，并开始使用它的功能。

要导入Triangle库，只需在程序的开头添加以下代码：pythonimport triangle现在您已经成功导入了Triangle库，并准备开始使用它的功能。

第三步：创建三角形网格Triangle库提供了一个功能强大且简单的三角形网格生成器，可以根据指定的输入数据生成三角形网格。

下面是一个示例代码片段，展示了如何使用Triangle 库生成一个简单的三角形网格：pythonimport trianglevertices = [(0, 0), (1, 0), (0, 1)] # 三角形的顶点坐标tri = triangle.triangulate({'vertices': vertices}, 'p') # 生成三角形网格print(tri['triangles']) # 打印生成的三角形在上面的示例中，我们首先定义了一个包含三角形顶点坐标的列表。

然后，我们使用`triangle.triangulate()`函数生成了一个三角形网格。

最后，我们打印出生成的三角形的列表。

第四步：计算三角形属性Triangle库不仅可以帮助我们生成三角形网格，还可以计算三角形的各种属性，如面积、周长、角度等。

三角形网格的自动生成及其局部加密技术研究

计算区域内尽可能生成正三角形，由节点间距函数控制，最后生成由疏到密的过渡三角形网格。三角形网格生成的步骤如下：（）界离散，定边界网格尺寸。据实际地形图数据，１边确根考察Ｔ程区域，根据经验进行边界离散。程工区域采用较密的网格尺寸，非计算区域可以采用较为稀疏的网格尺寸。这样能节省时间和工作量。（）界空间尺度权函数Ｅ。１得到各初始边界的空间尺度权函数。如边界ＡＡ点和Ｂ点空间２边由（）例Ｂ，
收稿日期：０１０ — ７修回日期：０１０ — ９２１－５２；２１— ６２
作者简介：阳豪（９６）女，戴１８一，湖南省人，硕士研究生，主要从事河口、海岸水动力及泥沙研究。
ＢｏｒｐｙＤＩａｇｈｏ１８一，ｍａ，ｓｒｔｄｎ．ｉｇａｈ：Ａｎ —ａ（９６）ｆｌｍａｔｕｅｔＹｅｅｅｓ
２１０２年２月
戴阳豪，等
三角形网格的自动生成及其局部加密技术研究
７９
（）４网格生成。第（）中离散后的边界开始，从２步在边界中找出长度最大的边Ａ从此处开始生成三角Ｂ，
形。生成三角形的步骤是先由ＡＢ与现有的前沿点Ｅ生成三角形，断三角形是否接近于正三角形，判是否满
第３卷第１３期
２２年２月０１

delaunay三角形的构建原则

Delaunay三角形是计算机图形学中常用的一种离散化方法，它可以将给定的点云数据进行三角形拓扑结构的构建。

在实际的工程应用中，Delaunay三角形被广泛应用于地理信息系统、有限元分析、计算机辅助设计等领域。

本文将从Delaunay三角形的构建原则出发，介绍其基本概念和构建方法。

一、三角形的构建原则1. 最小外接圆原则Delaunay三角形的构建原则之一是最小外接圆原则。

对于给定的点集，Delaunay三角形的构建要求任意三角形的外接圆不含有点集中的其他点。

这意味着在构建三角形的过程中，需要选择使得外接圆半径最大的三角形进行构建。

2. 空圆圆心不含点原则另一个构建Delaunay三角形的原则是空圆圆心不含点原则。

这个原则要求任意三角形的外接圆圆心不包含在其他三角形内部，并且不含有点集中的其他点。

这样可以保证构建出的三角形网格具有良好的性质，避免出现过分倾斜的三角形或者重叠的三角形。

3. 最优性原则除了上述两点，Delaunay三角形的构建还需满足最优性原则。

即在满足上述两个原则的情况下，构建出的三角形网格应当具有最优的性质，比如最大化最小角度，最小化最大边长等。

这样才能得到质量良好的三角形网格，适用于各种工程领域的实际应用。

二、构建方法在实际应用中，有多种方法可以用来构建Delaunay三角形。

其中比较常见的方法包括：1. 递归分治法递归分治法是一种经典的构建Delaunay三角形的方法。

它采用的是分而治之的思想，通过递归地将点集进行分割，并最终合并成一个完整的Delaunay三角形网格。

这种方法的优点是对于大规模的点集速度较快，缺点是实现较为复杂。

2. 增量法增量法是另一种常用的构建Delaunay三角形的方法。

它是一种逐点插入的方法，通过不断地插入新的点，来逐步构建出完整的Delaunay 三角形网格。

这种方法的优点是实现相对简单，缺点是对于大规模的点集计算量较大。

3. 最优三角形化算法最优三角形化算法是一种将最优性原则运用到Delaunay三角形构建中的方法。

三种经典网格细分算法的研究与分析

三种经典网格细分算法的研究与分析作者：王世江来源：《中小企业管理与科技》2009年第12期摘要：曲面造型方法由于其局部性好、计算量小、算法简中、响应速度高等优点已经广泛应用于计算机图形学、CAGD、计算机动画以及虚拟现实领域。

网格细分是一种离散造型方法.可以从数字化仪等设备直接获得数据。

介绍了近年来提出的一些细分算法对其中几种比较经典的算法进行了简中的分类和比较，论述了各自的适用范围。

关键词：细分逼近插值中图法分类号：TP391文献标识码：A0引言细分思想的产生可以追溯到二十世纪40年代末50年代初，当时G.de Rham使用“砍角算法”描述光滑曲线的生成。

细分曲线中常用的许多算法均是砍角算法。

1974年，Chaikin在研究曲线的快速绘制时把离散细分的概念引入到图形学界：1978年Catmnll和Clark…以及Doo和Sabinl21分别发表了一篇在图形学领域具有里程碑意义的论文，也就是图形学界推崇的Catmul—Clark算法和Doo—Sabin算法，标志着网格细分方法研究的真正开始：1987年，Loop 在他的硕士论文中提出了Loop细分策略，细分造型方法的实质是通过对初始控制点或者初始网格进行一系列的细化过程，细化的极限生成所需要的曲线或者曲面。

细分造型方法与传统样条、代数方法、变分造型等方法相比，在执行效率、任意拓扑结构、细分曲面特征以及复杂几何形状等方面都有其独特的优势。

1网格细分算法的分类及比较1.1概念与术语定义1对于四边形网格M中的任一顶点v，如果v为内部顶点且价不等于4或v为边界顶点且价不等于3或2，则称v为奇异顶点。

非奇异顶点称为正则顶点。

定义2权图(Masks)表示旧控制点计算新控制点规则的映射，其中新控制点在映射中用黑点表示，在每个旧控制点旁边的数字代表细分系数。

定义3奇点(0da Vertices)是在每一级细分中，按照某种细分规则所有新生成的点.在三角网格中，奇点也就是边点，实际上是将每条边的中点作为一个新点重新计算新的位置所得到的点.定义4偶点是在每一级细分中，所有从上一级控制点继承得到的点.定义5某项点的价(Valence)是指与该项点通过公共边相连的顶点个数.定义6在一个网格中，如果的一条边只属于一个面，称这条边为边界边(boundary edge)：如果一个顶点属于边界边则称此顶点为边界顶点(或边界点，boundary vertex)：至少包含一个边界顶点的面称为边界面(boundary face)。

三角网格

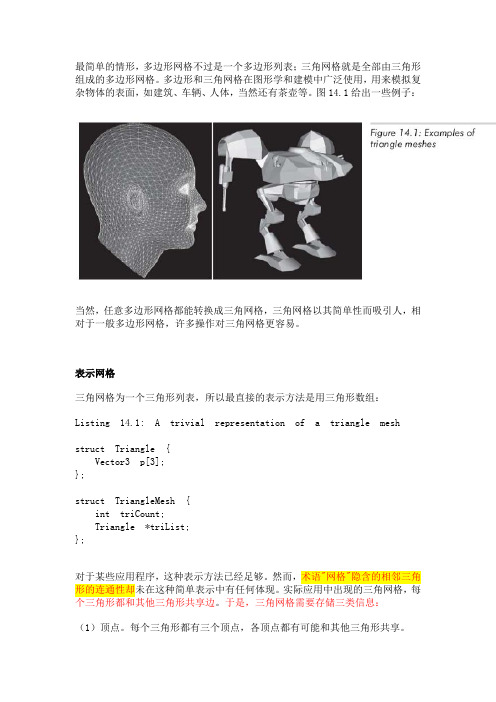
最简单的情形，多边形网格不过是一个多边形列表；三角网格就是全部由三角形组成的多边形网格。

多边形和三角网格在图形学和建模中广泛使用，用来模拟复杂物体的表面，如建筑、车辆、人体，当然还有茶壶等。

图14.1给出一些例子：当然，任意多边形网格都能转换成三角网格，三角网格以其简单性而吸引人，相对于一般多边形网格，许多操作对三角网格更容易。

表示网格三角网格为一个三角形列表，所以最直接的表示方法是用三角形数组：Listing 14.1: A trivial representation of a triangle meshstruct Triangle {Vector3 p[3];};struct TriangleMesh {int triCount;Triangle *triList;};对于某些应用程序，这种表示方法已经足够。

然而，术语"网格"隐含的相邻三角形的连通性却未在这种简单表示中有任何体现。

实际应用中出现的三角网格，每个三角形都和其他三角形共享边。

于是，三角网格需要存储三类信息：（1）顶点。

每个三角形都有三个顶点，各顶点都有可能和其他三角形共享。

（2）边。

连接两个顶点的边，每个三角形有三条边。

（3）面。

每个三角形对应一个面，我们可以用顶点或边列表表示面。

索引三角网格在索引三角网格中，我们维护了两个列表：顶点表与三角形表。

每个顶点包含一个3D位置，也可能有如纹理映射坐标、表面法向量、光照值等附加数据。

每个三角形由顶点列表的三个索引组成。

通常，顶点列出的顺序是非常重要的，因为我们必须考虑面的"正面"和"反面"。

从前面看时，我们将用顺时针方向列出顶点。

另外一些信息也存在这一级中，如预先计算的表面法向量，表面属性（纹理映射）等。

程序清单14.2给出了一段高度简化的代码：Listing 14.2: Indexed triangle mesh// struct Vertex is the information we store at the vertex level struct Vertex{// 3D position of the vertexVector3 p;// Other information could include texture mapping coordinates, // a surface normal, lighting values, etc.}// struct Triangle is the information we store at the triangle level struct Triangle{// Indices into the vertex listint vertex[3];// Other information could include a normal, material information , etc.}// struct TriangleMesh stores an indexed triangle meshstruct TriangleMesh{// The verticesint vertexCount;Vertex *vertexList;// The trianglesint triangleCount;Triangle *triangleList;};实践中，三角网格类会有一系列方法，用于存取和维护顶点、三角形列表。

(完整版)有限元网格剖分方法概述

有限元网格剖分方法概述在采用有限元法进行结构分析时，首先必须对结构进行离散，形成有限元网格，并给出与此网格相应的各种信息，如单元信息、节点坐标、材料信息、约束信息和荷载信息等等，是一项十分复杂、艰巨的工作。

如果采用人工方法离散对象和处理计算结果，势必费力、费时且极易出错，尤其当分析模型复杂时，采用人工方法甚至很难进行，这将严重影响高级有限元分析程序的推广和使用。

因此，开展自动离散对象及结果的计算机可视化显示的研究是一项重要而紧迫的任务。

有限元网格生成技术发展到现在, 已经出现了大量的不同实现方法，列举如下：1．映射法映射法是一种半自动网格生成方法，根据映射函数的不同，主要可分为超限映射和等参映射。

因前一种映射在几何逼近精度上比后一种高，故被广泛采用。

映射法的基本思想是：在简单区域内采用某种映射函数构造简单区域的边界点和内点，并按某种规则连接结点构成网格单元。

也就是根据形体边界的参数方程，利用映射函数，把参数空间内单元正方形或单元三角形(对于三维问题是单元立方体或单元四面体)的网格映射到欧氏空间，从而生成实际的网格。

这种方法的主要步骤是，首先人为地把分析域分成一个个简单可映射的子域，每个子域为三角形或四边形，然后根据网格密度的需要，定义每个子域边界上的节点数，再根据这些信息，利用映射函数划分网格。

这种网格控制机理有以下几个缺点：（1）它不是完全面向几何特征的，很难完成自动化，尤其是对于3D区域。

（2）它是通过低维点来生成高维单元。

例如，在2D问题中，先定义映射边界上的点数，然后形成平面单元。

这对于单元的定位，尤其是对于远离映射边界的单元的定位，是十分困难的，使得对局部的控制能力下降。

（3）各映射块之间的网格密度相互影响程度很大。

也就是说，改变某一映射块的网格密度，其它各映射块的网格都要做相应的调整。

其优点是：由于概念明确，方法简单，单元性能较好，对规则均一的区域，适用性很强，因此得到了较大的发展，并在一些商用软件如ANSYS等得到应用。

三角网格等值线的追踪与填充

的边表。
等值线地图的编制，通常是在地理底图上标出制图对象的相对点位（测站）的数值，然后把数值相等的点联成圆滑曲线，勾画出制图对象的空间结构特征。等值线地图还常辅
以分层设色，以提高地图的直观效果。等值线生成方法中，大体上可归纳为三种方案：
表的数值为整数。
入顶点，删除顶点，得到顶点的数目。可以向三角形列表追加三角形，并可以通过下标得到指定的三角形。可以通过边列表得到边界边的数目，通过下标得到边界的指针，可以通过顶点编号得到对应的边指针。可以根据当前三角网建立自身
行追踪并填充。
［关键词］三角网格；等值线；三次样条曲线；二维块体追踪
１．引言
２．等值线的追踪２．１三角网格数据结构
表１三角网表（ＧＴｒｉＭｅｓｈ）
等值线是制图对象某一数量指标值相等的各点连成的平滑曲线，由地图上标出的表示制图对象数量的各点，采用
项点，得到顶点相关属性值和坐标；通过边表可以访问边索引类，可以得到一条边，通过这条边我们可以到相关的两个顶点坐标及属性值，还可以得到由该边组成的三角形数目，还可以得到需要访问的三角形索引表；可以访问三角形列表，可以访问某个三角形的边和顶点的属性值和方法。
值线的生成；
（２）以不规则原始数据为依据，用二阶曲面方程、三阶曲

三种经典网格细分算法的研究与分析

三种经典网格细分算法的研究与分析摘要:曲面造型方法由于其局部性好、计算量小、算法简中、响应速度高等优点.已经广泛应用于计算机图形学、CAGD、计算机动画以及虚拟现实领域。

网格细分是一种离散造型方法.可以从数字化仪等设备直接获得数据。

介绍了近年来提出的一些细分算法.对其中几种比较经典的算法进行了简中的分类和比较，论述了各自的适用范围。

关键词:细分逼近插值中图法分类号:TP391 文献标识码:A0 引言细分思想的产生可以追溯到二十世纪40年代末50年代初，当时G. de Rham使用“砍角算法”描述光滑曲线的生成。

细分曲线中常用的许多算法均是砍角算法。

1974年，Chaikin在研究曲线的快速绘制时把离散细分的概念引入到图形学界:1978年Catmnll和Clark[1]以及Doo和Sabin[2]分别发表了一篇在图形学领域具有里程碑意义的论文，也就是图形学界推崇的Catmul- Clark算法和Doo -Sabin算法，标志着网格细分方法研究的真正开始:1987年，Loop在他的硕士论文中提出了Loop[3]细分策略，细分造型方法的实质是通过对初始控制点或者初始网格进行一系列的细化过程，细化的极限生成所需要的曲线或者曲面。

细分造型方法与传统样条、代数方法、变分造型等方法相比，在执行效率、任意拓扑结构、细分曲面特征以及复杂几何形状等方面都有其独特的优势。

1 网格细分算法的分类及比较1.1 概念与术语定义1 对于四边形网格M中的任一顶点v，如果v为内部顶点且价不等于4或v为边界顶点且价不等于3 或2，则称v为奇异顶点。

非奇异顶点称为正则顶点。

定义2 权图(Masks)表示旧控制点计算新控制点规则的映射，其中新控制点在映射中用黑点表示，在每个旧控制点旁边的数字代表细分系数。

定义3 奇点(Odd Vertices)是在每一级细分中，按照某种细分规则所有新生成的点.在三角网格中，奇点也就是边点，实际上是将每条边的中点作为一个新点重新计算新的位置所得到的点.定义4 偶点是在每一级细分中，所有从上一级控制点继承得到的点.定义5 某顶点的价(Valence)是指与该顶点通过公共边相连的顶点个数.定义6 在一个网格中，如果的一条边只属于一个面，称这条边为边界边(boundary edge):如果一个顶点属于边界边则称此顶点为边界顶点(或边界点，boundary vertex):至少包含一个边界顶点的面称为边界面(boundary face)。

三角网测量技术的原理与方法

三角网测量技术的原理与方法随着科技的不断进步，三角网测量技术在测量领域得到了广泛应用。

它通过建立具有一定高度的三角形网格，以测量和确定地球上各种地物的空间位置和形状，从而为工程建设、地质勘探等领域提供了有力的支持。

本文将介绍三角网测量技术的原理与方法。

一、三角网测量技术的原理三角网测量技术基于三角形的几何性质进行定位与测量。

原理主要包括以下几个方面：1. 三边测量原理：三边测量原理是三角网测量技术的核心。

通过测量三角形三条边的长度，结合三角形的内角和外角，可以计算出各个角的大小和三角形的边长，从而确定其形状和大小。

2. 角度测量原理：角度测量是三角网测量的关键环节。

通过使用全站仪、经纬仪等测量工具，测量三角形的内角和外角，以及各个角之间的关系，可以准确地确定各个角的位置和大小。

3. 控制点布设原理：控制点是三角网测量的重要环节。

在进行三角网测量之前，需要在测区范围内布设一定数量的控制点，以确定整个测量网的坐标体系和基准。

控制点的布设应满足精度要求，并考虑地形、地貌、地物等因素。

二、三角网测量技术的方法三角网测量技术的方法主要包括以下几个步骤：1. 建立控制网：在测量区域内选择一定数量的控制点，并确定其坐标和高程。

控制网应以闭合的三角形为基本单位，通过布设控制点，建立起整个测量区域的坐标体系和基准。

2. 建立三角形网格：在控制点之间建立起一定数量的三角形，形成三角形网格。

建立三角形网格时需要考虑控制点的位置和分布，以及横平竖直都具有一定规律的三角形网络。

3. 进行三边测量：在三角形网格中，通过使用测量仪器和测量工具，测量各个三角形的三条边的长度。

测量时需要保证测量仪器的精确性和准确性，以提高测量结果的可靠性。

4. 进行角度测量：在三角形网格中，使用全站仪、经纬仪等测量工具测量各个三角形的内角和外角。

通过角度测量可以确定各个角的大小和位置，进而计算出三角形的边长、面积和形状。

5. 数据处理与计算：测量完成后，需要对测量得到的数据进行处理和计算。

tin与等高线的生成方法

tin与等高线的生成方法地形图是一种用来描述地球表面地形特征的图形表示方法，它是地理信息系统（GIS）中最基本的图层之一。

在地形图中，TIN（三角网格）和等高线是最常用的两种地形表示方法。

TIN是一种由三角形组成的地形模型，它可以用来表示地形的高度、坡度和方向等信息。

等高线则是一种用等高线连接成的线条，它可以用来表示地形的高度和坡度等信息。

本文将介绍TIN和等高线的生成方法，以及它们各自的优缺点。

一、TIN的生成方法TIN是一种由三角形组成的地形模型，它的生成方法主要有两种：基于点的TIN生成方法和基于面的TIN生成方法。

1. 基于点的TIN生成方法基于点的TIN生成方法是最常用的TIN生成方法之一。

它的基本思想是先将地形数据中所有的点按照一定的规则连接成三角形，然后在三角形之间进行插值，得到每个点的高程值。

具体步骤如下：（1）将地形数据中的所有点按照一定的规则连接成三角形。

常用的连接规则有：最小劣角法、最大空圆法和Delaunay三角剖分法等。

（2）在三角形之间进行插值，得到每个点的高程值。

插值方法有很多种，常用的有：反距离权重法、双线性插值法和克里金插值法等。

（3）根据插值结果，生成TIN模型。

TIN模型可以用来表示地形的高程、坡度和方向等信息。

基于点的TIN生成方法的优点是：生成速度快，计算量小，适用于大规模的地形数据。

缺点是：容易出现插值误差，三角网格边缘处的精度较低。

2. 基于面的TIN生成方法基于面的TIN生成方法是一种比较少用的TIN生成方法，它的基本思想是先将地形数据中的所有点按照一定的规则连接成面，然后对面进行三角剖分，得到TIN模型。

具体步骤如下：（1）将地形数据中的所有点按照一定的规则连接成面。

常用的连接规则有：凸包法和alpha形法等。

（2）对面进行三角剖分，得到TIN模型。

三角剖分方法有很多种，常用的有：Delaunay三角剖分法和Voronoi图法等。

（3）根据三角剖分结果，生成TIN模型。