小学数学小升初行程问题总结与答案详细讲解
小学数学中的行程问题公式及解析

小学数学中的行程问题公式及解析一、基本行程问题行程问题的三个基本量是距离、速度和时间,按所行方向的不同可分为三种:(1)相遇问题:(2)相离问题;(3)追及问题。
行程问题的主要数量关系是:距离=速度x时间。
它大致分为以下三种情况:(1)相向而行:相遇时间=距离÷速度和(2)相背而行:相背距离=速度和*时间。
(3)同向而行:速度慢的在前,快的在后。
追及时间=追及距离÷速度差在环形跑道上,速度快的在前,慢的在后。
追及距离=速度差x时间。
解决行程问题时,要注意充分利用图示把题中的情节形象地表示出来,有助于分析数量关有助于迅速地找到解题思路。
(一)相遇问题行程问题是研究相向运动中的速度、时间和路程三者之间关系的问题,(涉及两个或两个物体运动的问题)指两个运动的物体同时由两地出发相向而行,在途中相遇,这类应用题相遇问题。
数量关系:路程÷速度和=相遇时间路程÷相遇时间=速度和速度和x相遇时间=路程温馨提示:(1)在处理相遇问题时,一定要注意公式的使用时二者发生关系那一时刻所处的状态;(2)在行程问题里所用的时间都是时间段,而不是时间点(非常重要);(3)无论是在哪类行程问题里,只要是相遇,就与速度和有关。
(2)解题秘诀:(3)(1)必须弄清物体运动的具体情况,运动方向(相向),出发地点(两地),出发时间(同时、先后),运动路径(封闭、不封闭),运动结果(相遇)等。
(4)(2)要充分运用图示、列表等方法,正确反映出数量之间的关系,帮助我们理解题意,迅速的找到解题思路。
(二)追及问题追及问题也是行程问题中的一种情况。
这类应用题的特点是:①两个物体同时同一方向运动;②出发的地点不同(或从同一地点不同时出发,向同一方向运动);迫及路程=路程差=两个物体之间相距的路程迫及速度=速度差=快的速度-慢的速度慢的物体追上快的物体的所用的时间为追及时间③慢者在前,快者在后,因而快者离慢者越来越近,最后终于可以追上。
【小升初】小学数学《行程问题专题课程》含答案

17.行程问题知识要点梳理一、基本公式:1.路程=速度×时间2.速度=路程÷时间3.时间=路程÷速度二、问题类型1.相遇问题:①相遇时间=总路程÷速度和②速度和=总路程÷相遇时间③总路程=速度和×相遇时间2.追及问题:①追及时间=路程差÷速度差②速度差=路程差÷追及时间③路程差=速度差×追及时间3.流水行船问题:①顺水速度=船速+水速②逆水速度=船速-水速③船速=(顺水速度+逆水速度)÷2④水速=(顺水速度-逆水速度)÷24.列车过桥问题:(1) 火车过桥(隧道):火车过桥(隧道)时间=(桥长+车长)÷火车速度(2) 火车过树(电线杆、路标):火车过树(电线杆、路标)时间=车长÷火车速度(3) 火车过人:①火车经过迎面行走的人:迎面错过的时间=车长÷(火车速度+人的速度)②火车经过同向行走的人:追及的时间=车长÷(火车速度-人的速度)(4) 火车过火车:①错车问题:错车时间=(快车车长+慢车车长)÷(快车速度+慢车速度)②超出问题:错车时间=(快车车长+慢车车长)÷(快车速度-慢车速度)考点精讲分析典例精讲考点1 一般行程问题【例1】小王骑公共自行车从家去上班,每分钟行350米,用了20分钟,下午下班沿原路回家,每分钟比去时多骑50米,多少分钟到家?【精析】先根据路程=速度×时间,求出家到单位的距离,再求出下班的速度,最后根据时间=路程÷速度即可解答。
【答案】350×20=7000(米)350+50=400 (米/分)7000÷400=17.5(分钟)答:17.5分钟到家。
【归纳总结】本题考查知识点:依据速度,时间以及路程之间的数量关系解决冋题。
考点2 相遇问题【例2】甲乙两车分别从相距480千米的A 、B 两城同时出发,相向而行,已知甲车从A 城到B 城需6小时,乙车从B 城到A 城需12小时。
小学数学30道“行程问题”专题归纳,公式+例题+解析!

小学数学30道“行程问题”专题归纳,公式+例题+解析!“行程问题”作为小学数学常用知识点之一,想必大家并不陌生。
然而面对各种古怪的命题陷阱,不少考生还是心内发苦,看不出解题思路,频频出错。
解答“行程问题”时,究竟该怎么做呢?“行程问题”离不开三个基本要素:路程、速度和时间。
这也是解题的关键所在!今天为大家分享一份行程问题资料,包含公式、例题和解析,有需要的为孩子收藏一下,希望对学习行程问题有帮助~题型公式行程问题核心公式:S=V×T,因此总结如下:当路程一定时,速度和时间成反比当速度一定时,路程和时间成正比当时间一定时,路程和速度成正比从上述总结衍伸出来的很多总结如下:追击问题:路程差÷速度差=时间相遇问题:路程和÷速度和=时间流水问题:顺水速度=船速+水流速度;逆水速度=船速-水流速度水流速度=(顺水速度-逆水速度)÷2船速=(顺水速度-逆水速度)×2两岸问题:S=3A-B,两次相遇相隔距离=2×(A-B)电梯问题:S=(人与电梯的合速度)×时间平均速度:V平=2(V1×V2)÷(V1+V2)5.列车过桥问题①火车过桥(隧道)火车过桥(隧道)时间=(桥长+车长)÷火车速度②火车过树(电线杆、路标)火车过树(电线杆、路标)时间=车长÷火车速度③火车经过迎面行走的人迎面错过的时间=车长÷(火车速度+人的速度)④火车经过同向行走的人追及的时间=车长÷(火车速度-人的速度)⑤火车过火车(错车问题)错车时间=(快车车长+慢车车长)÷(快车速度+慢车速度)⑥火车过火车(超车问题)错车时间=(快车车长+慢车车长)÷(快车速度-慢车速度)考点精讲分析1、邮递员早晨7时出发送一份邮件到对面的山坳里,从邮局开始要走12千米的上坡路,8千米的下坡路。
他上坡时每小时走4千米,下坡时每小时走5千米,到达目的地后停留1小时,又从原路返回,邮递员什么时候可以回到邮局?【解析】核心公式:时间=路程÷速度去时:T=12/4+8/5=4.6小时返回:T’=8/4+12/5=4.4小时T总=4.6+4.4+1=10小时7:00+10:00=17:00整体思考:全程共计:12+8=20千米去时的上坡变成返回时的下坡,去时的下坡变成返回时的上坡因此来回走的时间为:20/4+20/5=9小时所以总的时间为:9+1=10小时7:00+10:00=17:002、小明从甲地到乙地,去时每小时走6千米,回时每小时走9千米,来回共用5小时。
小升初数学复习重点 :17道行程问题题知识点总结

小升初数学复习重点:17道行程问题题知识点总结行程问题是各大杯赛中必考的知识点,也是令无数同学望而生畏的一个难点,建议各位同学在复习行程问题的时候切忌一味钻研偏题怪题,攻克每个行程专题中的最典型题目,将整个行程体系建立起来才是王道,在这里徐老师给大家总结了每个专题中的最典型题目,抛砖引玉,通过一道典型题的学习带大家复习相应模块的核心知识。
一、相遇与追及1、路程和路程差公式【例1】某城市东西路与南北路交会于路口.甲在路口南边560米的点,乙在路口.甲向北,乙向东同时匀速行走.4分钟后二人距的距离相等.再继续行走24分钟后,二人距的距离恰又相等.问:甲、乙二人的速度各是多少?2、多人相遇【例2】有甲、乙、丙3人,甲每分钟走100米,乙每分钟走80米,丙每分钟走75米.现在甲从东村,乙、丙两人从西村同时出发相向而行,在途中甲与乙相遇6分钟后,甲又与丙相遇.那么,东、西两村之间的距离是多少米?3、多次相遇【例3】甲、乙两车分别同时从A、B两地相对开出,第一次在离A地95千米处相遇.相遇后继续前进到达目的地后又立刻返回,第二次在离B地25千米处相遇.求A、B两地间的距离是多少千米?二、典型行程专题1、火车过桥【例4】某列车通过250米长的隧道用25秒,通过210米长的隧道用23秒,若该列车与另一列长150米.时速为72千米的列车相遇,错车而过需要几秒钟?2、流水行船【例5】甲、乙两艘游艇,静水中甲艇每小时行千米,乙艇每小时行千米.现在甲、乙两游艇于同一时刻相向出发,甲艇从下游上行,乙艇从相距27千米的上游下行,两艇于途中相遇后,又经过4小时,甲艇到达乙艇的出发地.水流速度是多少?3、猎狗追兔【例6】猎人带猎狗去捕猎,发现兔子刚跑出40米,猎狗去追兔子。
已知猎狗跑2步的时间兔子跑3步,猎狗跑4步的距离与兔子跑7步的距离相等,求兔子再跑多远,猎狗可以追上它?。
小升初复习:知识点22行程问题
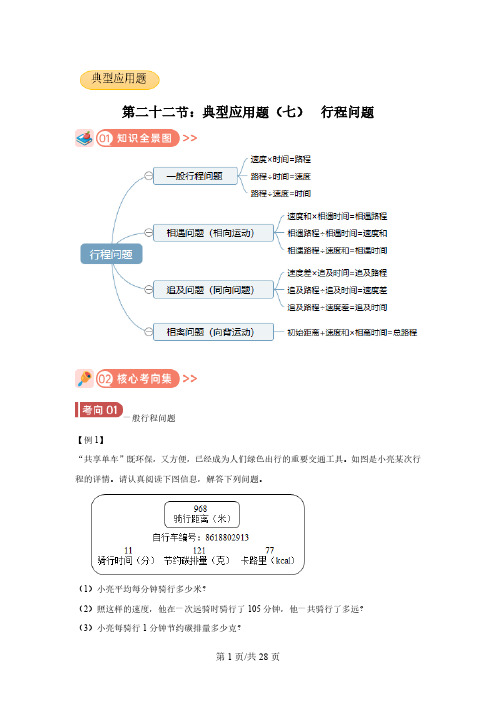
第二十二节:典型应用题(七)行程问题一般行程问题【例1】“共享单车”既环保,又方便,已经成为人们绿色出行的重要交通工具。
如图是小亮某次行程的详情。
请认真阅读下图信息,解答下列问题。
(1)小亮平均每分钟骑行多少米?(2)照这样的速度,他在一次远骑时骑行了105分钟,他一共骑行了多远?(3)小亮每骑行1分钟节约碳排量多少克?思路引导(1)根据路程÷时间=速度,用小亮骑行的路程除以用的时间,求出小亮平均每分钟骑行多少米;(2)他在一次远骑时骑行了105分钟,根据速度×时间=路程,可以求出一共骑行了多少米;(3)已知小亮骑行11分钟节约碳排量121克,那么小亮每骑行1分钟,节约碳排量(121÷11)克。
正确解答:(1)968÷11=88(米)答:小亮平均每分钟骑行88米。
(2)105×88=9240(米)答:他一共骑行了9240米。
(3)121÷11=11(克)答:小亮每骑行1分钟节约碳排量11克。
此题主要考查了行程问题中速度、时间和路程的关系:速度×时间=路程,路程÷时间=速度,路程÷速度=时间。
【变式1】1. 如图是一辆汽车与一列火车的行程图表,根据图示回答问题。
(1)如图是()统计图。
(2)汽车的速度是每分钟()千米。
(3)火车停站时间是()分钟。
(4)火车停站后时速比汽车每分钟快()千米。
(5)汽车比火车早到()分钟。
相遇问题【例2】甲、乙两辆汽车同时从东西两座城市相向开出,甲车每小时行88千米,乙车每小时行80千米。
两车在距中点40千米处相遇。
东西两城相距多少千米?思路引导两车在距中点40千米处相遇,那么甲车比乙车多行了80千米,即两车行的路程相差是80千米,有了路程差与速度差就可以求出相遇的时间,进而根据速度和就可以求出距离。
正确解答:40×2÷(88-80)=80÷8=10(小时)(88+80)×10=168×10=1680(千米)答:东西两城相距1680千米。
小升初数学行程问题精选及详解

试题习题、尽在百度小升初数学行程问题精选及详解1、羊跑5步的时间马跑3步,马跑4步的距离羊跑7步,现在羊已跑出30米,马开始追它.问:羊再跑多远,马可以追上它?解:根据“马跑4步的距离羊跑7步”,可以设马每步长为7x米,则羊每步长为4x米.根据“羊跑5步的时间马跑3步”,可知同一时间马跑3*7x米=21x米,则羊跑5*4x=20米.可以得出马与羊的速度比是21x:20x=21:20根据“现在羊已跑出30米”,可以知道羊与马相差的路程是30米,他们相差的份数是21-20=1,现在求马的21份是多少路程,就是30÷(21-20)×21=630米2、甲乙辆车同时从 a b两地相对开出,几小时后再距中点40千米处相遇?已知,甲车行完全程要8小时,乙车行完全程要10小时,求 a b 两地相距多少千米?答案720千米.由“甲车行完全程要8小时,乙车行完全程要10小时”可知,相遇时甲行了10份,乙行了8份(总路程为18份),两车相差2份.又因为两车在中点40千米处相遇,说明两车的路程差是(40+40)千米.所以算式是(40+40)÷(10-8)×(10+8)=720千米.3、在一个600米的环形跑道上,兄两人同时从同一个起点按顺时针方向跑步,两人每隔12分钟相遇一次,若两个人速度不变,还是在原来出发点同时出发,哥哥改为按逆时针方向跑,则两人每隔4分钟相遇一次,两人跑一圈各要多少分钟?答案为两人跑一圈各要6分钟和12分钟.解:600÷12=50,表示哥哥、弟弟的速度差600÷4=150,表示哥哥、弟弟的速度和(50+150)÷2=100,表示较快的速度,方法是求和差问题中的较大数(150-50)/2=50,表示较慢的速度,方法是求和差问题中的较小数600÷100=6分钟,表示跑的快者用的时间百度文库:精选试题。
小升初--行程问题--专项讲解及试题

行程问题一【知识点导航】行程问题从运动形式上分可以分为五大类:二【典例解析】1. 直线上的相遇与追及只要涉及到速度和、路程和的问题就应该用第一个公式,即使题目的背景是追及;而只要涉及到速度差、路程差的问题就应该用第二个公式,即使题目的背景是相遇。
【例1】甲、乙两辆汽车同时从东西两地相向开出,甲每小时行56千米,乙每小时行48千米,两车在离两地中点32千米处相遇。
问:东西两地间的距离是多少千米?(某重点中学2007年小升初考题)【解析】本题表面上看是一个典型的相遇问题,其实里面暗藏了路程差的关系,就在条件"两车在离两地中点32千米处相遇"这句话中。
【变式】大客车和小轿车同地、同方向开出,大客车每小时行60千米,小轿车每小时行84千米,大客车出发2小时后小轿车才出发,几小时后小轿车追上大客车?【例2】两名游泳运动员在长为30米的游泳池里来回游泳,甲的速度是每秒游1米,乙的速度是每秒游0.6米,他们同时分别从游泳池的两端出发,来回共游了5分钟。
如果不计转向的时间,那么在这段时间内两人共相遇多少次?(某重点中学2006年小升初考题)【解析】相遇次数与两人的路程和有关.如下图所示【变式】甲、乙两车同时从A、B两站相对开出,第一次相遇离A站有90千米,然后各自按原速继续行驶,分别到达对方出发站后立即沿原路返回。
第二次相遇时离A站的距离占AB两站全长的65%。
求AB两站的距离。
2.火车过人、过桥与错车问题在火车问题中,速度和时间并没有什么需要特殊处理的地方,特殊的地方是路程。
因为此时的路程不仅与火车前进的距离有关,还与火车长、隧道长、桥长这些物体长度相关。
就拿火车过桥来说,如果题目考察的是火车过桥的整个过程,那么就应该从"车头上桥"开始到"车尾下桥"结束,对应的路程就等于"车长桥长";如果题目考察的是火车停留在桥上的过程,那就应该从"车尾上桥"到"车头下桥"结束。
小升初数学冲刺-----行程问题(含答案)

小升初数学冲刺-----行程问题1、甲、乙两架飞机同时从一个机场起飞,向同一方向飞行,甲机每小时行300千米,乙机每小时行340千米,飞行4小时后它们相隔多少千米?这时候甲机提高速度用2小时追上乙机,甲机每小时要飞行多少千米?解析:①4小时后相差多少千米:1604)300340(=⨯-(千米).②甲机提高速度后每小时飞行多少千米:4203402160=+÷(千米).2、两地相距900米,甲、乙二人同时、同地向同一方向行走,甲每分钟走80米,乙每分钟走100米,当乙到达目标后,立即返回,与甲相遇,从出发到相遇共经过多少分钟?解析:甲、乙二人开始是同向行走,乙走得快,先到达目标.当乙返回时运动的方向变成了同时相对而行,把相同方向行走时乙用的时间和返回时相对而行的时间相加,就是共同经过的时乙到达目标时所用时间:9100900=÷(分钟),甲9分钟走的路程:720980=⨯(米),甲距目标还有:180720900=-(米),相遇时间:1)80100(180=+÷(分钟),共用时间:1019=+(分钟).3、甲、乙二人分别从东、西两镇同时出发相向而行.出发2小时后,两人相距54千米;出发5小时后,两人还相距27千米.问出发多少小时后两人相遇?解析:根据2小时后相距54千米,5小时后相距27千米,可以求出甲、乙二人3小时行的路程和为)2754(-千米,即可求出两人的速度和:9)25()2754(=-÷-(千米),根据相遇问题的解题规律;相隔距离÷速度和=相遇时间,可以求出行27千米需要:89275=÷+(小时).4、甲乙两座城市相距530千米,货车和客车从两城同时出发,相向而行.货车每小时行50千米,客车每小时行70千米.客车在行驶中因故耽误1小时,然后继续向前行驶与货车相遇.问相遇时客车、货车各行驶多少千米?解析:因为客车在行驶中耽误1小时,而货车没有停止继续前行,也就是说,货车比客车多走1小时.如果从总路程中把货车单独行驶1小时的路程减去,然后根据余下的就是客车和货车共同走过的.再求出货车和客车每小时所走的速度和,就可以求出相遇时间.然后根据路程=速度×时间,可以分别求出客车和货车在相遇时各自行驶的路程.解:相遇时间:4)7050()50530(=+÷-(小时)相遇时客车行驶的路程:280470=⨯(千米)相遇时货车行驶的路程:250)14(50=+⨯(千米).5、两车同时从甲乙两地相对开出,甲车每小时行48千米,乙车每小时行54千米,相遇时两车离中点36千米,甲乙两地相距多少公里?解:甲乙两车的速度比=48:54=8:9那么相遇时甲车行了全程的8/17所以甲乙距离=36/(1/2-8/17)=36/(1/34)=1224千米6、客货两车从甲地到乙地客车出发,30分钟后货车才出发,结果货车比客车早到1小时,如果甲乙两地相距360km,客车速度是货车的3/4.货车和客车行驶的速度分别是多少?解:若同时出发客车比货车晚到1小时30分=1.5小时客车和货车的速度比=3:4时间比=4:3所以客车行驶全程的时间=1.5/(1-3/4)=6小时所以客车速度=360/6=60千米/小时货车速度=60/(3/4)=80千米/小时7、甲乙两车同时从A、B两地相对开出,4小时后相遇,相遇后甲车在开3小时到达B地。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
行程问题经典题型
1、甲、乙两地相距6千米,某人从甲地步行去乙地,前一半时间平均每分钟行80米,后一半时间平均每分钟行70米。
问他走后一半路程用了多少分钟?
2、甲、乙两辆汽车同时从东西两地相向开出,甲每小时行56千米,乙每小时行48千米,两车在离两地中点32千米处相遇。
问:东西两地的距离是多少千米?
3、李华步行以每小时4千米的速度从学校出发到20.4千米外的冬令营报到。
0.5小时后,营地老师闻讯前往迎接,每小时比李华多走1.2千米。
又过了1.5小时,张明从学校骑车去营地报到。
结果3人同时在途中某地相遇。
问:骑车人每小时行驶多少千米?
4 小轿车的速度比面包车速度每小时快6千米,小轿车和面包车同时从学校开出,沿着同一路线行驶,小轿车比面包车早10分钟到达城门,当面包车到达城门时,小轿车已离城门9千米,问学校到城门的距离是多少千米?
5 小张从家到公园,原打算每分种走50米.为了提早10分钟到,他把速度加快,每分钟走75米.问家到公园多远?
6、上午8点8分,小明骑自行车从家里出发,8分钟后,爸爸骑摩托车去追他,在离家4千米的地方追上了他.然后爸爸立即回家,到家后又立刻回头去追小明,再追上小明的时候,离家恰好是8千米,这时是几点几分?
“相遇问题”,常常要考虑两人的速度和.
7、小张从甲地到乙地步行需要36分钟,小王骑自行车从乙地到甲地需要12分钟.他们同时出发,几分钟后两人相遇?
8、小张从甲地到乙地,每小时步行5千米,小王从乙地到甲地,每小时步行4千米.两人同时出发,然后在离甲、乙两地的中点1千米的地方相遇,求甲、乙两地间的距离.
9、一列长100米的火车过一座桥,火车的速度是25米/秒,它过桥一共用了10秒,那么桥的长度是多少?
10、甲骑摩托车,乙骑自行车,同时从相距126千米的A、B两城出发、相向而行。
3小时后,在离两城中点处24千米的地方,甲、乙二人相遇。
求甲、乙二人的速度各是多少?
11、客轮行了全程的3\7时,货轮行全程的多少? 3/7×7/10=3/10 2.甲乙两码头相距多少千米?
12、A、B两城相距240千米,一辆汽车计划用6小时从A城开到B城,汽车行驶了一半路程,因故障在中途停留了30分钟,如果按原计划到达B城,汽车在后半段路程时速度应加快多少?
13、两码头相距231千米,轮船顺水行驶这段路程需要11小时,逆水每小时少行10千米,问行驶这段路程逆水比顺水需要多用几小时?
14、一辆汽车从甲地出发到300千米外的乙地去,在一开始的120千米内平均速度为每小时40千米,要想使这辆车从甲地到乙地的平均速度为每小时50千米,剩下的路程应以什么速度行驶?
15、骑自行车从甲地到乙地,以每小时10千米的速度行驶,下午1时到;以每小时15千米的速度行驶,下午1时到;以每小时15千米的速度行进,上午11时到;如果希望中午12时到,应以怎样的速度行进?
16、一辆公共汽车和一辆小轿车同时从相距299千米的两地相向而行,公共汽车每小时行40千米,小轿车每小时行52千米,问:几小时后两车第一次相距69千米?再过多少时间两车再次相距69千米?
17、一列客车与一列货车同时同地反向而行,货车比客车每小时快6千米,3小时后,两车相距342千米,求两车速度。
18、甲、乙两车同时从A、B两地相向而行,它们相遇时距A、B两地中心处8千米,已知甲车速度是乙车的1.2倍,求A、B两地距离。
19、甲、乙两车同时从A、B两地相向而行,在距B地54千米处相遇,他们各自到达对方车站后立即返回原地,途中又在距A地42千米处相遇,求两次相遇地点的距离。
20、甲、乙、丙三人的步行速度分别为每分钟60米、50米和40米,甲从B 地,乙和丙从A地同时出发相向而行,途中甲遇到乙后15分钟又遇到丙,求A、B两地距离。
答案详情
1、解:(80+70)÷2=75(米) 6000÷75=80(分)
3000÷80=37.5(分) 80-37.5=42.5(分)
2、解:甲乙速度比:56:48=7:6
相遇时甲比乙多行:(7-6)÷(7+6)=1/13
两地距离:2×32÷(1÷13)=832千米。
3、解:老师速度:4+1.2=5.2(千米)
与李相遇时间是老师出发后(20.4-4×0.5)÷(4+5.2)=2(小时)相遇地点距离学校4×(0.5+2)=10(千米)
所以骑车人速度=10÷(2+0.5-2)=20(千米)
4、解:9÷6=1.5(时)
面包车速度是54-6=48(千米/小时).
城门离学校的距离是48×1.5=72(千米).
5、解:追上所需时间=追上距离÷速度差
1小时与40分钟是3∶2.所以两者的速度差之比是2∶3.
马上可看出前一速度差是15.自行车速度是
35- 15=20(千米/小时).
6、解:画一张简单的示意图:
图上可以看出,从爸爸第一次追上到第二次追上,小明走了
8-4=4(千米).
而爸爸骑的距离是4+8=12(千米).
爸爸的速度是小明的12÷4=3(倍).
小明骑8千米,爸爸可以骑行8×3=24(千米).
但事实上,爸爸少用了8分钟,骑行了4+12=16(千米).
少骑行24-16=8(千米).
摩托车的速度是1千米/分,爸爸骑行16千米需要16分钟.
7、解:36÷(3+1)=9(分钟).
8、解:
小张比小王每小时多走(5-4)千米,从出发到相遇所用的时间是
2÷(5-4)=2(小时).
因此,甲、乙两地的距离是(5+4)×2=18(千米).
9、解:25×10=250(米)
那么桥长就是:250-100=150(米)
10、解:甲的速度:(126÷2+24)÷3=29(千米/小时)
乙的速度:(126÷2-24)÷3= 13(千米/小时)
11、解:36÷3/10=120(千米)
12、解:后半段路程长:240÷2=120(千米)
后半段用时为:6÷2-0.5=2.5(小时)
后半段行驶速度应为:120÷2.5=48(千米/时)
原计划速度为:240÷6=40(千米/时)
汽车在后半段加快了:48-40=8(千米/时)。
13、解:顺水速度231÷11=21(千米/时)逆水速度21-10=11(千米/时),
逆水比顺水多需要的时间为:21-11=10(小时)
14、解:300-120=180(千米)300÷50=6(小时)
6-120÷40=3(小时),180÷3=60(千米/小时)
15、解:20÷(15-10)=4(小时)15×4=60(千米)60÷5=12(千米/时)
16、解:299-69=230(千米)230÷(40+52)=2.5(时)
69×2=138(千米)138÷(40+52)=1.5(小时)
17、解:两车速度和为:342÷3=114(千米/小时)
货车速度为(114+6)÷2=60(千米/时)
客车速度为114-60=54(千米/时)
18、解:甲车在相遇时比乙车多走了:8×2=16(千米)
乙所走路程为16÷(1.2-1)=80(千米)
两地距离为(80+8)×2=176(千米)
19、解:第一次相遇时,甲、乙两人走的总路程是A到B距离的3倍
乙所走路程为54×3=162(千米)
这时他们相距A地42千米,也就是说A、B距离为:162-42=120(千米),两次相遇地点距离为120-54-42=24(千米)
20、解答:(60+40)×15=1500(米)
到甲、乙相遇为止,乙、丙走了:1500÷(50-40)=150(分钟)
A、B距离为:(60+50)×150=16500(米)。
