小学数学火柴游戏题

合集下载

小学数学《火柴棍游戏》练习题(含答案)

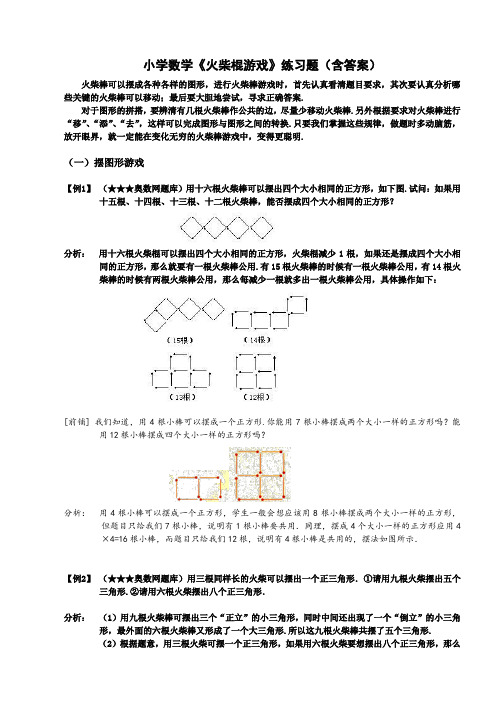
小学数学《火柴棍游戏》练习题（含答案）火柴棒可以摆成各种各样的图形，进行火柴棒游戏时，首先认真看清题目要求，其次要认真分析哪些关键的火柴棒可以移动；最后要大胆地尝试，寻求正确答案.对于图形的拼搭，要辨清有几根火柴棒作公共的边，尽量少移动火柴棒.另外根据要求对火柴棒进行“移”、“添”、“去”，这样可以完成图形与图形之间的转换.只要我们掌握这些规律，做题时多动脑筋，放开眼界，就一定能在变化无穷的火柴棒游戏中，变得更聪明.（一）摆图形游戏【例1】（★★★奥数网题库）用十六根火柴棒可以摆出四个大小相同的正方形，如下图.试问：如果用十五根、十四根、十三根、十二根火柴棒，能否摆成四个大小相同的正方形？分析：用十六根火柴棍可以摆出四个大小相同的正方形，火柴棍减少1根，如果还是摆成四个大小相同的正方形，那么就要有一根火柴棒公用.有15根火柴棒的时候有一根火柴棒公用，有14根火柴棒的时候有两根火柴棒公用，那么每减少一根就多出一根火柴棒公用，具体操作如下：[前铺] 我们知道，用4根小棒可以摆成一个正方形.你能用7根小棒摆成两个大小一样的正方形吗？能用12根小棒摆成四个大小一样的正方形吗？分析：用4根小棒可以摆成一个正方形，学生一般会想应该用8根小棒摆成两个大小一样的正方形，但题目只给我们7根小棒，说明有1根小棒要共用．同理，摆成4个大小一样的正方形应用4×4=16根小棒，而题目只给我们12根，说明有4根小棒是共用的，摆法如图所示．【例2】（★★★奥数网题库）用三根同样长的火柴可以摆出一个正三角形．①请用九根火柴摆出五个三角形.②请用六根火柴摆出八个正三角形．分析：（1）用九根火柴棒可摆出三个“正立”的小三角形，同时中间还出现了一个“倒立”的小三角形，最外面的六根火柴棒又形成了一个大三角形.所以这九根火柴棒共摆了五个三角形.（2）根据题意，用三根火柴可摆一个正三角形，如果用六根火柴要想摆出八个正三角形，那么其中一根火柴应是几个正三角形的边才行．先用三根同样长的火柴摆成一个正三角形，再用剩下的三根同样长的火柴把已摆好的正三角形的三条边交叉等分成3份．用六根同样长的火柴摆出八个正三角形的摆法如图：（1）（2）[拓展] 用三根同样长的火柴可以摆出一个正三角形．请用六根火柴摆出六个正三角形．（二）移动火柴，变换图形游戏【例3】（★★★奥数网题库）下面是一个倒着的缺一条腿的椅子，请你移动两根火柴棒，把它正过来，并看起来没有缺腿，你会吗？分析：把椅子右上的一条腿，移到椅子下面放在前面缺的位置.然后把椅背最下面的一根，移到左上变成椅背，如图所示.[拓展]用14根火柴摆成的房子，见下图.请你移动2根火柴，使房子的方向朝向左.分析：具体操作如右上图：【例4】（★★★奥数网题库）下图是一条“小鱼”.(1)请你移动两根火柴棒使“小鱼”变成头朝上.(2)请你移动三根火柴棒，使“小鱼”变成头朝右.分析：具体操作如下：(1)头向上： (2)头向右：[拓展2] 下图是用小棒摆成的4个小三角形和1个大三角形，请移动4根小棒，使原来大三角形的方向上下颠倒过来．分析：尽量利用原来的小棒所组成的形状，以便减少小棒移动的数量，具体操作如下：【例5】（★★★奥数网题库）下图是用18根小棒摆成的一个六角星，请你想一想，怎样移动其中6根，使它变成6个菱形．分析：我们可以这样来移，保留六角星的6个角，只移动里面的6根小棒，使它们相交于六角星的中心点上，和6个星相对应，就可以摆出6个菱形来，示意如右上图．[拓展] 下图是用六根火柴摆成的一个三角形．请你移动四根火柴，把这个三角形变成六边形．分析：将六根火柴编上号码．[拓展] 如下图用12根火柴摆成的灯，移动三根火柴，变为五个完全一样的三角形.分析：如右上图，把虚线部分移到空缺的地方，便可得到五个完全一样的三角形.【例6】（★★★奥数网题库）下图是由35根火柴组成的，请你移动4根火柴棒，使它变成3个正方形．分析：图中看似有三个比较接近的正方形，这三个正方形都差一根火柴棒就成拼成，但是一共只多出2根火柴棒，只能把外面和中间的正方形拼成，最小的正方形还差一根火柴棒，我们就要利用中间正方形的一根公共火柴棒来拼成，具体操作如右上图：[拓展]在左下图中移动4根火柴棍，使图形成为只有三个正方形的图形.分析：因为只能移动4根火柴，所以图中较长的边(3根或4根火柴的边)都不能动.把图中最里面的4根火柴移补到右上图的相关位置上即可.具体操作如右上图：【例7】（★★★★奥数网题库）用24根火柴摆成（摆时火柴的首尾紧挨）的“回”字形方环，见下图.（1）请移动其中4根火柴，使这两个大小不等的正方形变成两个大小相等的正方形，应该怎么移？（2）求移动后所得图形的周长（已知每根火柴长4厘米）.分析：由题目可见，要用24根火柴摆出两个大小相同的正方形，每个正方形可由12根火柴构成.这样，每个正方形的边长应由三根火柴棍组成，这样的两个正方形可以有下图的四种摆法.考虑到题目要求移四根火柴，若移成图中（1）（2）（4）的形状，移动的火柴都要超过四根，而图（3）则是由上图通过移动四根火柴得到的.图3符合条件：（2）移动后所得图形的周长：方法1：4×16=64（厘米）方法2：4×4×4=64（厘米）方法3：4×（3×4＋4）=64（厘米）方法4：4×3×4＋4×4=64（厘米）[拓展] 下图是用24根火柴棍摆出的两个正方形.(1)请你移动4根，把它变成三个正方形；(2)再移动8根，把(1)中所得图形变成九个完全相同的正方形；(3)在(2)中所得图形上拿走8根火柴，使它变成五个完全相同的正方形.分析：（1）具体操作如下：方法一：方法二：（2）变成一个边长是3根小火柴棒的大正方形，里面就包含了9个小正方形.(3)然后拿走四个角上的8根，就变成了5个小正方形，具体操作如下：（三）去掉火柴，变换图形游戏【例8】（★★★★奥数网题库）下图是用24根火柴棒摆成的，请按下面要求摆成新的图形.(1)拿走4根火柴棒，使它变成6个正方形.(2)拿走6根火柴棒，使它变成3个正方形.(3)拿走8根火柴棒，使它变成2个正方形.分析：（1）取走4根火柴棒后，图形变成图(a)形式.(2)取走6根火柴棒后，图形变成下面图(b)形式.(3)取走8根火柴棒后，图形变成下面图(c)形式.[前铺] 用12根火柴摆成下图，分别取走3根、4根、5根，使它成为3个相同的三角形，应该怎样取?分析：（1）如果取出3根，那么12根火柴还剩9根，用9根火柴摆成3个相同的三角形，9÷3=3，必须是3根火柴摆1个三角形，也就是说，它们是没有公共边的.(如图1) (2)如果取出4根，那么12根火柴还剩8根，用8根火柴摆成3个相同的三角形，8÷3=2……2，必定有1根火柴要充当2个三角形的公共边，也就是说，摆出的3个相同三角形必定有2个三角形连在一起.(如图2)(3)同理取出5根，还剩7根火柴，7--3=2……1，必定有2根火柴要充当三角形的公共边，也就是说摆出的3个相同三角形必定全部连在一起.(如图3)[拓展] 用24根火柴棒组成下面的图形.根据要求拿掉火柴棒变成新的图形.(1)拿掉4根火柴，变成5个正方形；(2)拿掉8根火柴，变成5个正方形；(3)拿掉8根火柴，变成3个正方形；(4)拿掉6根火柴．使它只留下3个四边形；(5)拿掉8根火柴，使它只留下2个正方形.分析：原图用了24根火柴棒拼成了大小不同的14个正方形.要拿掉几根火柴，使正方形的个数变少，实际就要考虑“拆掉”部分正方形.(1)拿掉4根火柴，变成5个正方形； (2)拿掉8根火柴，变成5个正方形；(3)拿掉8根火柴，变成3个正方形；(4)拿掉6根火柴，剩下3个大小各异的四边形；(5)拿掉8根火柴，使它留下一大一小两个正方形.【例9】（★★★奥数网题库）下图是由1 9根火柴棒组成的图形，请拿出其中的5根火柴棒，使剩下的火柴棒组成两个形状、大小完全相同的图形.分析：具体操作如右上图：[巩固] 在左下图中，去掉4根火柴棍，使它变成两个完全相同的图形组合.分析：左上图的面积等于七个边长为1根火柴棍的小正方形的面积之和.要达到规定要求，必须去掉一个小正方形.剩下的部分划分成两个面积等于三个小正方形面积的图形.去掉右上图中虚线所示的火柴棍即可.【例10】（★★★★奥数网题库）在左下图中去掉尽量少的火柴棍，使得图中不存在任何正方形.分析：拿掉的火柴应能尽量多的“破坏”正方形.如右上图拿掉虚线处的4根火柴即可.拿法不唯一.[拓展]用31根火柴棒摆成下图，共有20个正方形．请问：至少需要拿掉多少根火柴棒，才能使图中没有正方形．分析：至少取走6根火柴棒，才能使图中没有正方形.1. 用8根火柴棍摆出八个大小一样的三角形和两个一样大小的正方形.分析：4根火柴可摆出一个正方形，另4根火柴又可摆出一个同样大小的正方形.把这两个正方形如右图所示交叉放在一起，就形成八个相同的三角形.2. (1) 下面是用16根火柴棒摆成的5个正方形.请你移动2根火柴棒，变成4个正方形.(2) 下面是用15根火柴棒摆成的4个正方形.请你移动2根火柴棒，变成6个正方形.分析：具体操作如下：（1）（2）3. (1) 如下面图(1)中所示.请你只移动3根火柴把3个三角形变成5个三角形.（2）下图是用18根火柴棒摆成的图形.请你拿掉4根火柴棒，变成5个三角形.分析：具体操作如下：（1）（2）4. 用10根火柴棒摆成向上飞的蝙蝠图形，如下图所示.试移动三根火柴，使它变成向下飞的蝙蝠图形.分析：要把蝙蝠的头变成朝下的，需要把上面的头拆掉，摆出尾，还要在下面摆出头.由上面的分析，可以移火柴摆成如图所示的样子.(注意：①、②、③所示的火柴，分别移至相应行的虚线位置)5.下图中共有13个三角形，从中拿掉尽量少的火柴棍，使得图中没有三角形.分析：有多种拿法，但至少要拿掉6根火柴.具体操作如右上图：6. 下图是用24根火柴摆成的“◇”形图案.(1)请移动4根火柴，使这两个大小不等的“◇”形变成两个大小相等的“◇”形；(2)如果每根火柴的长是3厘米，那么移动后图形的周长是多少?分析：（1）把外面“◇”形上、下角的各两根火柴移动成如右上图的形状.(2)移动后图形的周长：方法--：3×16=48(厘米)方法二：3×8×2=48(厘米)方法三：3×3×4+3×4=48(厘米)。

小学二年级数学有趣的火柴棒

有趣的火柴棒问题月日姓名【知识要点】用火柴棒摆成有趣的图形，有的是移动规定的根数，使图形的形状，位置发生变化；有的是减少规定的根数，使图形的数量发生变化。

同学们你觉得怎么样？如果用方块或圆圈摆好了一个图形，要求你搬一搬，成为另外的图形，你会吗？小朋友，你注意观察过马路上红绿灯数字的形状吗？我们用火柴棒也能摆出来：这10数字也可以简单地摆出来：移动火柴棒,可以使数字发生变化。

例如：火柴棒不仅可以组成有趣的算式，还可以摆成各种各样的有趣的图形。

【解题策略】例1 移动一根，使下面的算式成立。

例 2 三只盛水的杯子放在左边，三只空杯子放在右边，如下图，请你只搬动一只杯子，使盛水的杯子与空杯子间隔排列。

例3 大伟把10个棋子在桌子摆成了三角形形状（如下图），请你搬动三个棋子，使三角形颠倒一下，你能做到吗？试试看。

【趣题】人带猫，鸡，米过河，船除需要人划外，至少能载猫，鸡，米三者之一，而当人不在场时猫要吃鸡，鸡要吃米，试设计一个安全过河方案并使渡船次数尽量减少。

随堂小测月日姓名家长签名1．请你只移动一根火柴棒，使下列算式成立。

（1）（2）2．下面每一题只能移动1根火柴棒，使等式成立。

（1）（2）3．看下图，请你移动最少的圆，使黑圆、白圆间隔开来。

4．小华用6个圆片摆成了一个三角形，如图，你能不能只搬移两个圆片，使这个三角形颠倒过来。

5．用5根火柴棒拼成了一把小方勺，请你只移动3根火柴棒，使勺把的方向正好与原来相反。

6．用火柴摆成的小船，请至少移动2根火柴棒，使小船的方向正好相反。

7．下图是12根火柴摆成的4个正方形，移动其中3根，使变成3个大小一样的正方形。

课后作业月日姓名家长签名1．下面用火柴棒摆放的两个错误算式，请移动一根火柴棒使算式成立。

（1）（2）2．由9枚硬币组成了一个三角形，要移动3枚硬币，使这个三角形方向相反。

3．下图是9根火柴棒摆成的3个三角形，移动其中的3根，使它变成5个三角形。

☆ 4．你能只移动4根火柴，就把下面的两只杯子的杯口朝上吗？。

火柴棒算式游戏习题附答案-幼小衔接小学生数学思维

1.在下面的阿拉伯数字中，哪些阿拉伯数字可以进行如下的变换？
（1）移除1根火柴能变成另一个阿拉伯数字；
（2）移除2根火柴能变成另一个阿拉伯数字；
（3）移除3根火柴能变成另一个阿拉伯数字；
（4）移动1根火柴能变成另一个阿拉伯数字；
（5）移动2根火柴能变成另一个阿拉伯数字。

2.请小朋友移动一根火柴棒，使下面的等式成立。

3.请小朋友移动1根火柴棒，使下面的等式成立。

1/ 8
4.请小朋友移动1根火柴，使下面的等式成立。

5.使用火柴棒摆出阿拉伯数字0～9和加号、减号、等号3个运算符
号。

6.请小朋友在下面的算式中添加1根火柴，使等式成立。

2/ 8。

趣味数学300题第一章给小学的同学们

趣味数学300题第一章给小学的同学们1 倒转酒杯用4根火柴可以分别摆成两个小酒杯的样子，“杯”中放一枚硬币。

不论哪个酒杯只要移动2根火柴，就可以使“酒杯”倒转过来，并且使硬币在“杯”旁。

你能做到吗？2 十五个正方形11根火柴组成一个图形，有点像“房子”。

请你移动2根火柴，使它变成含有十一个正方形的图形。

要是移动4根火柴，可以变成含有十五个正方形的图形。

该如何做呢？请注意大正方形套着小正方形的情形。

3 八个等式选用加号、减号、乘号、除号和括号当中的某些符号，可以将四个4组成一个等式，运算结果等于1.你看：（4+4）÷（4+4）＝1有趣的是：采用这样的办法，还可以把四个4组成八个等式，结果分别是从2到9八个数。

想想看，这八个等式怎么列？4 五个5等于245 5 5 5 5＝24请你在这个等式中填入减号、乘号、除号和括号，使等式成立。

提示：在运算过程中，会出现小数。

5 放哨有十五名少先队员，在一块方形的玉米地四周放哨。

队长决定，每一条边都应该有五名队员看守。

他注意布置各哨位的人数，果然达到了要求。

请看下图。

后来，又来了两名队员，队长调整了哨位上的人数，每边仍然是五名队员看守。

过不久，抽走了四名队员，队长又调整一次哨位上的人数，每边仍然是五名队员看守。

队长是怎么调整哨位的？6 四个等式围一围请看下图，方框的每一边都是一个等式，只是还没填上数字。

请你将从1到8的八个数字填上去，使四个等式成立。

做数学题，要善于寻找突破口，才能较快地找到正确的答案。

要是不加分析，胡乱填几个数字，再来凑结果，会浪费很多时间。

好好想一想，突破口在哪里呢？7 填数字请将从1到8八个数字填到图里。

有一个要求：每一线段两端的两个数字之差必须大于1.8 消防设备九座仓库，有十三条路连接。

为了防火，打算在这些仓库中放两套消防设备。

一座仓库放了消防设备，凡是与它有路连接的仓库，都可以就近使用。

请你想一想，这两套消防设备应该放在哪里，才能使九座仓库都用得上。

小学一年级移动一根火柴数学题

第7周火柴棒游戏一、知识要点用火柴棒做游戏，小朋友们感兴趣吗？用火柴棒可以拼成许多有趣的图形，做些有趣的游戏，在游戏中还能够长知识、长智慧。

这一周，我们将共同了解火柴棒中的数学，并了解数学的奇妙。

火柴棒游戏中有很多的窍门，今后我们将进一步学习，只要同学们大胆尝试，一定可以从中获得乐趣。

二、精讲精练【例题1】搭一个三角形要3根火柴棒，你能用5根火柴棒搭两个三角形吗？【思路导航】搭一个三角形要3根火柴，如果分开搭两个三角形，需要6根火柴，现在只有5根火柴，少了一根，那么应该把两个三角形合在一起搭，在搭第二个三角形时，利用第一个三角形中的一根火柴，两个三角形其中一边用一根火柴，这样5根就够了。

【温馨提示】用3根火柴棒可搭成一个三角形，用4根火柴棒可搭成一个正方形。

如果要少用一根火柴棒拼三角形或正方形，必须使两个图形共用一条边。

练习1：1.请用4根火柴棒摆一个正方形。

2.你能用7根火柴棒拼成两个相同的正方形吗？3.请添上3根火柴，使下图变成三个正方形。

这里拼成3个正方形一共用了几根火柴？【例题2】你能用9根火柴棒组成四个相同的小三角形吗？【思路导航】搭一个三角形要3根火柴，如果分开搭四个相同的小三角形，一共要12根火柴，现在只有9根，少了3根，那么应将4个三角形摆在一起，有3根火柴棒公用。

【温馨提示】用火柴棒搭图形时，要注意公用边越多，则用的火柴棒越少。

练习2：1.你能用12根火柴棒摆成4个大小一样的正方形吗？2.用16根火柴可以摆成四个正方形，仍用16根火柴要摆成五个同样大小的正方形，该怎样摆？3.请移动3根火柴棒，使下图中的3个三角形变成5个三角形。

【例题3】图中有几个正方形？添上2根火柴，使它变成8个正方形，该怎样添？【思路导航】仔细观察上图，可以数出图中有5个正方形，添上2根火柴，使它变成8个正方形，我们只要添上作为正方形的边的火柴即可。

（7个小正方形，1个大正方形由4个小正方形拼成，共8个正方形。

小学生一年级数学奥数-第十四讲火柴棍游戏（一）

第十四讲火柴棍游戏（一）砖是盖房子用的，但当有一只小狗要咬你时，你会急中生智，拣起一块砖头来打狗。

火柴是点火用的，但当我们把它带到课堂上来时，用火柴棍就可以做有趣的数学游戏，在游戏中就用数学概念，进行数学计算，增强思维的灵敏性。

例1 请你用火柴棍摆图形，并用橡皮泥粘接起来。

（1）用三根火柴棍摆出一个等边三角形。

（2）用四根火柴棍摆出一个正方形。

（3）用四根火柴棍摆出一个菱形。

解：（1）等边三角形的三条边的长度彼此都相等，而火柴棍也都一样长。

所以可以用三根火柴棍摆成一个等边三角形，如图。

（2）正方形的四条边都相等，所以四根同样长的火柴棍可以摆出一个正方形。

但要注意，必须使四个角都摆成直角。

如图。

（3）菱形的四条边也是相等的，所以用四根一样长的火柴棍也能摆出来。

但注意，这时不必使每个角都摆成直角，只要使两组对角分别相等即可。

例2 请用7根火柴棍摆出2个小正方形出来。

解：由例1可知，摆一个正方形需4根火柴棍，所以摆两个独立的正方形需要8根火柴棍。

现在要求用7根火柴棍摆出两个正方形，显然必须有一根火柴棍公用才能办到。

例3 请你用12根火柴棍摆出四个同样大小的小正方形。

解：下图摆一个小正方形需要4根火柴棍，所以摆4个独立的小正方形需4×4=16根火柴棍。

现在要求用12根火柴棍摆出4个小正方形出来，16-12=4（根），所以需要4根火柴棍公用。

例4 下图是用24根火柴棍摆成的回字形图形，如果只允许移动图中的四根火柴棍，使原图形组成三个正方形（大小可以不一样），你能办得到吗？解：可以这样想：①用24根火柴棍摆成三个正方形，每个正方形用24÷3=8根，每边2根。

这是三个独立的、同样大小的正方形。

经尝试，按题目要求，在原图的基础上移动4根组成三个独立的正方形无论如何办不到。

②若是正方形的每边用3根火柴棍，一个正方形用12根，两个正方形共用24根。

但是题目要求用24根摆成三个正方形（大小可以不同），这就要使这两个正方形有“重叠”（使一些火柴棍被公用），（见图（1））从而多产生出一个正方形。

小学一年级奥数题《火柴棒问题大全及答案》题库大全

《火柴棒问题大全及答案》题库大全一、基础篇1. 题目：用4根火柴棒拼出一个正方形。

答案：将4根火柴棒首尾相连，形成一个闭合的四边形，即可得到一个正方形。

2. 题目：用6根火柴棒拼出一个等边三角形。

答案：取3根火柴棒组成一个等边三角形，再用剩余的3根火柴棒分别连接三角形的三个顶点，形成一个更大的等边三角形。

3. 题目：用7根火柴棒拼出一个长方形。

答案：取4根火柴棒组成一个长方形，再用3根火柴棒分别连接长方形的两个对边中点，形成一个更大的长方形。

4. 题目：用8根火柴棒拼出一个正方形和一个等边三角形。

答案：先用4根火柴棒拼出一个正方形，再用剩余的4根火柴棒拼出一个等边三角形。

5. 题目：用10根火柴棒拼出一个梯形。

答案：取6根火柴棒组成一个等边三角形，再用4根火柴棒分别连接三角形的底边两端和顶点，形成一个梯形。

《火柴棒问题大全及答案》题库大全二、进阶篇6. 题目：用5根火柴棒拼出一个星星。

答案：取两根火柴棒交叉放置，形成一个十字形。

然后，将另外三根火柴棒分别放在十字形的三个交叉点上，使它们与十字形的火柴棒相连，形成一个五角星。

答案：取3根火柴棒组成一个等边三角形，再用另外3根火柴棒组成另一个等边三角形，使两个三角形的底边相连。

用剩余的3根火柴棒组成第三个等边三角形，将其底边与前面两个三角形的底边相连。

8. 题目：用12根火柴棒拼出一个六边形。

答案：用6根火柴棒组成一个等边三角形。

接着，将剩余的6根火柴棒分别放在等边三角形的三条边上，使它们与三角形的边平行，形成一个六边形。

9. 题目：用7根火柴棒拼出一个大于号（>）。

答案：取3根火柴棒组成一个等边三角形，然后用4根火柴棒组成一个大于号。

将大于号的尖端与三角形的底边相连，使它们形成一个整体。

10. 题目：用11根火柴棒拼出一个小于号（<）。

答案：先用5根火柴棒组成一个等腰直角三角形，再用6根火柴棒组成一个小于号。

将小于号的尖端与三角形的直角顶点相连，使它们形成一个整体。

小学一年级下奥数专题—移火柴棒

移火柴棒1、下图是用12根小棒组成的4个同样大小的正方形，请你移动3根小棒，使原图形变成3个同样大小的正方形。

想一想，应怎样移？2、下面算式是用火柴棒摆成的，可惜是错的，请你移动其中的一根火柴棒，使等号两边相等。

3、如下图：用12根火柴棒,摆成6个大小一样的三角形，请你拿走3根，还剩下3个大小一样的三角形.答案：拿掉的3根火柴棒如图中的虚线显示。

4、用火柴棒摆成头朝上的龙虾，移动三根火柴，使它头朝下.答案:分析图形，用最少的移动得到新的火柴棒的移动过程如图中虚线显示5、下面的算式是错误的，请你只移动1根火柴棒，把错误的算式变成正确的.6、只移动一根火柴棒，使等号两边相等。

7、只移动一根火柴棒,使下面的等式成立.【练习】1、请给下面的每一个数字只添上1根火柴棒，使它们变成一个新的数字。

2、下面这个算式是错误的，请你移动1根火柴，使下面的等式成立。

【自测题】1、下面有几个火柴棒摆成的错误算式，你能只移动其中的一根火柴棒，使这些算式变成正确的吗？典型例题解析例1：请你在下面的算式中添上一根火柴，使其等式成立。

方法点击：方法可以基本上和上一题基本相同,只有在数字“2”和“5”中寻找解题的方法。

“8”是不可能变的，答案是8。

也就只能是3+5,或2+6。

解：例2: 请你移动下面算式中的两根火柴棒，使其等式成立。

方法点击：解答此题的关键在于：观察式子和几个数字的特点。

要使这个等式能够成立，只能使左边的式子和变大或者右边的和变小。

而数字一般只会变1或2根火柴，变化就是不很大，要找出其中的答案也就不是很难了。

例4：“”移动图中的三根火柴使图形从一个“品”字拼成一个“井”字.方法点击：做这一题时，与前几题有所不同。

我们主要应抓住两个图形的结构特点，尽可能动最少的火柴。

如图可以发现，品字形移去三根火柴后，可以是井字形的一部分。

点评：此题在解答的过程中，尽量寻找移动最少的根数，也就是寻找相似根数最多的根数.例5:,拼出三个角形。

6数学谜题（学生）

火柴游戏大体分为两种：一种是摆图形和变换图形；一种是变换算式。

1. 其中摆图形和图形变换主要根据图形特点以及变换前后图形的关联、差异解题；2. 用火柴棍可以摆出下列数字和符号：3. 这些数字和符号，在去掉或添加或移动火柴棍后有些可以相互变化。

例如：添加1根火柴，可以得到：4. 去掉1根火柴，可以得到：5. 移动1根火柴，可以得到：6. 变换算式类型的火柴棍算式游戏就是利用这些变化，改变算式，使之符合题目要求。

【例1】在科技大会上，三位老科学家相遇，亲热地互相握手，他们一共握了几次手？第六讲数学谜题知识概述例题精讲【拓展】小学毕业时，阿庆、阿立、阿福三人互相赠照片一张，他们一共互赠了多少张照片？【例2】魔术师有一个大盒子，大盒子里装有三个中盒子，每个中盒子里面又装有三个小盒子，魔术师一共有多少个盒子？【拓展】嘉嘉有九本书及四个袋子，用什么方法使每个袋中装书的本数都是单数。

请你试试。

【例3】张杰要在一封信上贴2角钱的邮票，他有一些4分、8分、1角的邮票，可以有几种贴法？【拓展】3块月饼分给4个小朋友吃，每人吃的一样多，请你想一想，应怎么分？【例4】宁宁的妈妈皮包里有4个苹果，其中2个是红苹果，另外2个是黄苹果。

宁宁想从皮包里取出一个红苹果，他必须一次至少取出几个苹果，才能保证一定有红苹果？【拓展】布袋里混有10个白色球和30个红色球。

要想保证一次能拿出两个同色球，至少要拿出几个球？【拓展】妈妈买了30个樱桃和12个小番茄，放在不透光的袋子里。

小明喜欢吃樱桃不喜欢吃小番茄，他一次至少取出几个水果，才能保证其中一定有樱桃？【例5】有一杯牛奶，如果你喝了半杯后，用水加满；再喝去半杯，又用水加满；最后全部喝光，那么你喝了几杯牛奶、几杯水呢？【拓展】20世纪中有一个年份，如果把这个年份写在纸卡上，再倒过来看，仍然是一个年份，但这两个年份相差330年。

你知道这个年份是20世纪的哪一年吗？【例6】⑴佳佳说：“我有一个弟弟和一个姐姐，我是姐姐又是妹妹，我们家有几个男孩，几个女孩”？⑵格拉斯说：“我有两个姐姐和一个弟弟，我是哥哥又是弟弟，我们家有几个男孩？几个女孩？？卡娃说：“我比格拉斯少一个姐姐，多一个哥哥，我是姐姐又是妹妹，我们家有几个男孩？几个女孩？共几个孩子”？【拓展】娴娴家人很多，有祖父母、伯父母、父母、姑姑和姑夫；第二代每家一子一女，第三代的男子都结婚，并有一子，第三代的女孩尚未结婚。

一年级移动火柴棒的题目

一年级移动火柴棒的题目
移动火柴棒是一种经典的数学题目，适合小学一年级的学生练习。

以下是一种常见的移动火柴棒题目：
题目：请将下面的等式中的一根火柴棒移动，使等式成立。

1 +
2 = 3
解答：将等式中的加号（+）的一根火柴棒移动，变成等号（=）：
1 =
2 - 1
这样，等式就成立了。

当然，移动火柴棒的题目有很多变化，可以根据学生的实际情况进行调整和扩展，逐步增加难度。

这类题目可以锻炼学生的逻辑思维能力和数学运算能力，同时也能培养学生的观察力和创造力。

经典数学趣题集锦

经典数学趣题集锦1. 火柴拼字请你用４根火柴拼成一个“田”字。

注意火柴不能折。

2. 井底之蛙井深27米。

一只蜻蛙从某月１号早晨从井底往上爬。

白天能爬３米，夜里又下降２米。

照这样，几号能爬到井上？3. 钓鱼有个人喜欢钓鱼。

一天钓鱼归来，路上有人问他钓了多少条鱼，他答到：“有６条没头的，９条没尾的，８条半截的。

”你知道他钓了多少条鱼吗？4. ａ国与ｂ国从前有两个相邻的ａ国和ｂ国，关系很好，货币可以通用。

后来两国的关系发生了矛盾。

ａ国国王下令：ｂ国的一百元只能购买ａ国八十元货物。

ｂ国的国王也下令：ａ国的一百元只能购买ｂ国八十元的货物。

结果，有个聪明的人利用这个机会发了一笔大财。

他是怎样做的？5. 啤酒与饮料小张请小李到家会餐。

小张知道小李爱动脑筋，于是就给他出了一道题：我今天买啤酒和饮料共花了9.90元，你猜一猜我买了几瓶啤酒、几瓶饮料？猜对了我自罚一杯白酒，猜错了罚你一杯。

小李只用了几分钟时间就算出来了，小张只好自罚一杯。

已知啤酒每瓶1.7元，饮料每瓶0.7元，你能算出小张买了几瓶啤酒、几瓶饮料？☆ 6. 帽子问题 (一)教师把他最得意的三个学生叫到一起，想测测他们的智力。

他先让三个学生前后站成一排，然后拿出三白两黑共五顶帽子，让学生看过后把两顶黑帽子藏起来，把三顶白帽子给他们戴上。

三个学生都看不见自己戴的帽子，但后边的能看见前边的，前边的看不见后边的。

教师让三个学生说出自己戴的帽子的颜色。

经过一段时间的思考后，前边的学生回答说：我戴的是白色的。

他是怎样知道的？☆☆ 7. 帽子问题 (二)本题同上题相似，只是三个学生是相对站立的，彼此互相能看到。

经过一段时间，三个学生异口同声地说自己戴的是白帽子。

他们是怎么猜到？8. 量容积有一个药瓶，上面有刻度，可以从刻度上看出里面的药水的体积。

但是这个刻度并不是从瓶底到瓶顶的，而且瓶子的口处比下面小，怎样能量出瓶子的容积呢？9. 进口货爸爸出远门回来，给小明买了许多好东西，桌子都摆满了：游戏机、变形金钢、牛奶巧克力、洋娃娃、芒果、魔方、太空枪、机器人、小汽车……请你帮小明找一找，哪些是进口货。

小学一年级趣味数学——摆火柴

摆火柴活动目标：1、学会拼摆火柴的游戏，并在日常玩耍中增长见识；2、在游戏中发展学生的观察能力，及动手操作能力；3、培养学生的创造性思维，以及与同伴合作交流意识。

活动准备：一盒火柴、双面胶、白纸板。

教学过程一、导入1.小朋友们，你们都准备好小棒了吗？准备好的请举手。

把准备好的小棒放在铅笔盒的前面。

2.你们猜今天我们用小棒是来做什么的呢？3.今天我们就一起用小棒来摆一摆。

二、摆一摆（一）摆三角形1.请小朋友们先拿出一捆小棒，把其他的放在原来的地方。

2.把拿出的小棒解开，数出3根小棒。

3.数好了吗？现在请小朋友们用数出的3根小棒摆出一个三角形。

4.摆好了吗？谁愿意上来摆一摆？5.大家都和他摆的一样吗？（环视教室中学生摆的）我发现很多同学都是摆对的，真聪明。

6.现在老师拿出2根小棒，摆在原来的三角形边上，你们看，这里有几个三角形？（多请几个，还可以让几个学生来指指这两个三角形）7.现在小朋友们拿出2根小棒，学老师刚才的样子摆一摆。

8.那我们在加2根小棒呢？摆出三个三角形，大家试一试。

9.再往上加2根呢？试一试？请一位同学到上面来摆一摆。

数一数有几个三角形。

10.还有没有同学，和他摆的是不一样的？来上面来看看。

11.大家数一数，我们一共用了小棒？谁来说一说？12.大家来看这幅老师这幅，上面有几个三角形？他一共用几根小棒？谁来说一说？13.同样是九根小棒，为什么这里有四个三角形，这里却只有三个三角形？14.①发现有些小棒是当做2根小棒用的②用一样多的小棒，公用的小棒越多，图形摆得越多（二）摆正方形1.我们再拿出6根新的小棒，一共有16根小棒，你能用他们摆出四个正方形吗？2.谁能用最少小棒，摆出四个一样大的正方形？四人小组合作试一试。

3.（展示结果）①你是用几根小棒摆的？来说一说。

有几个小棒有了两次？②谁有不一样的摆法？……4.（板书）小棒的根数，你们发现了什么？。

火柴棒图形游戏习题附答案-幼小衔接小学生数学思维

1.请小朋友用火柴棒拼出下面的图形。

2.用3根火柴棒可以拼出一个三角形，你能用6根火柴棒拼出两个
三角形吗？如果用5根火柴棒，能拼出两个三角形吗？
3.看看右图中有几个正方形？如果再添两根火柴棒，能否搭出5个
正方形？
4.下面的图是用12根火柴棒拼搭成的田字形，能不能拿走两根火柴
棒，把现在的图形变成两个正方形。

5.右图是用12根火柴棒拼搭成的田字形，能不能移动4根火柴棒，
使右图成为3个正方形。

6.请小朋友用4根火柴拼出1个正方形，用7根火柴棒拼出2个正
方形，用10根火柴拼出3个正方形。

7.请小朋友用16根火柴摆出5个同样大小的正方形。

8.请小朋友用9根火柴摆出4个同样大小的三角形。

小学数学火柴棒游戏

小学数学火柴棒游戏
1、移动一根火柴棒，使得等号成立。
小学数学火柴棒游戏
1、移动一根火柴棒，使得等号成立。
小学数学火柴棒游戏
2、移动一根火柴棒，使得等号成立。
小学数学火柴棒游戏
2、移动一根火柴棒，使得等号成立。
小学数学火柴棒游戏
3、移动一根火柴棒，使得等号成立。
小学数学火柴棒游戏
小学数学火柴棒游戏
6、拿走一根火柴，使得等式成立。
小学数学火柴棒游戏
6、拿走一根火柴，使得等式成立。
小学数学火柴棒游戏
此课件下载可自行编辑修改，供参考！感谢你的支持，我们会努力做得更好！
数字大变身
小学数学火柴棒游戏
游戏规则：四人小组合作一起想答案，哪个四人小组合作最先想出来的就赢。已经获得奖励的四人小组不参加下一题的抢答，在位置上安静的趴下。
违反纪律者要收回奖品！！！
小学数学火柴棒游戏
例：移动一根火柴棒，使得等号成立。
小学数学火柴棒游戏
例：移动一根火柴棒，使得等号成立。
3、移动一根火柴棒，使得等号成立。
小学数学火柴棒游戏
4、移动一根火柴棒，使得等号成立。
小学数学火柴棒游戏
4、移动一根火柴棒，使得等号成立。
小学数学火柴棒游戏
4、移动一根火柴棒，使得等号成立。
小学数学火Байду номын сангаас棒游戏
5、加上一根火柴，使得等式成立。
小学数学火柴棒游戏
5、加上一根火柴，使得等式成立。

小学数学《游戏与对策》练习题

小学数学《游戏与对策》练习题智取火柴棍游戏【例1】桌子上放着55根火柴，甲、乙二人轮流每次取走1～3根．规定谁取走最后一根火柴谁获胜．如果双方采用最佳方法，甲先取，那么谁将获胜？【巩固】将例题中的条件“每次取走1～3根”改为“每次取走1～4根”，其余不变，情形会怎样？【例2】桌子上放着55根火柴，甲、乙二人轮流每次取走1～3根，谁取走最后一根火柴谁输，如果双方采用最佳方法，甲先取，那么谁将获胜？【巩固】桌子上放着60根火柴，甲、乙二人轮流每次取走1～3根。

规定谁取走最后一根火柴谁获胜。

如果双方都采用最佳方法，甲先取，那么谁将获胜？【巩固】在例题中将“每次取走1～3根”改为“每次取走1～6根”，其余不变，情形会怎样？【例3】（1）1998个空格排成一排，第一格中放有一枚棋子，现有两人做游戏，轮流移动棋子，每人每次可前移1格、2格、3格或4格.谁先移到最后一格，谁为胜者.问怎样的移法才能确保获胜？（2）桌面上放着54张扑克牌，两人轮流从中取走1张、2张或3张，取了最后一张者输.问应怎样取，才能确保获胜？想一想：该如何制定“作战”策略呢？【巩固】1111个空格排成一行，最左端空格中放有一枚棋子，甲先乙后轮流向右移动棋子，每次移动1～7个格．规定将棋子移到最后一格者输．甲为了获胜，第一步必须向右移多少格？【例4】甲、乙二人轮流报数，必须报不大于6的自然数，把两人报出的数依次加起来，谁报数后加起来的数是2000，谁就获胜.如果甲要取胜，是先报还是后报？报几？以后怎样报？【巩固】两人从1开始按自然数顺序轮流依次报数，每人每次只能报1～5个数，谁先报到50谁胜。

你选择先报数还是后报数？怎样才能获胜？【巩固】两人轮流报数，但报出的数只能是1至8的自然数，同时把所报数一一累加起来，谁先使这个累加和达到80，谁就获胜.问怎样才能确保获胜？【例5】有1994个球，甲乙两人用这些球进行取球比赛.比赛的规则是：甲乙轮流取球，每人每次取1个，2个或3个，取最后一个球的人为失败者.①甲先取，甲为了取胜，他应采取怎样的策略？②乙先拿了3个球，甲为了必胜，应当采取怎样的策略？【例6】有两堆火柴，一堆35根，另一堆24根．两人轮流在其中任一堆中拿取,取的根数不限,但不能不取.规定取得最后一根者为胜者.如果都采用最佳方法，那么谁将获胜？【巩固】请同学们想一想，如果在上面玩法中，两堆火柴数目一开始就相同，例如两堆都是35根火柴，那么先取者还能获胜吗？【例7】有3堆火柴，分别有1根、2根与3根火柴。

小学数学《数学游戏》练习题(含答案)

小学数学《数学游戏》练习题（含答案）（一）智取火柴【例1】桌上放着100根火柴，甲、乙二人轮流取，每次取1～4根，规定谁取到最后一根谁获胜.假定双方都采用最佳方法，甲先取，谁一定获胜？给出一种获胜方法.分析：乙一定获胜，甲取几根，乙就接着取5减几根火柴.甲取几根，乙取4减几根可以么？不可以，那样的话甲取4根，乙就没法取了.甲取几根，乙取6减几根可以么？不可以，那样的话甲取1根，乙就没法取了.这里我们把（1+4）根火柴看成一组，100共有20组，因为甲先取，所以每一组乙都可以取到最后一根.[前铺]桌子上放着10根火柴，甲、乙二人轮流每次取走1～2根.规定谁取走最后一根火柴谁获胜.如果双方都采用最佳方法，甲先取，那么谁将获胜？分析：如果获胜方在最后取得最后一根火柴，那么在倒数第二次取时，必须留给对方3根，要想留给对方3根，倒数第三次取时，必须留给对方6根.要想留给对方6根，倒数第四次取时必须留给对方9根，而甲每次取完都能留给乙3的倍数根，所以在双方都采用最佳策略的情况下，甲必胜.[拓展一]在例1中将“每次取走1～4根”改为“每次取走1～6根”，其余不变，情形会怎样？分析：由例1的分析知，只要始终留给对方（1+6=）7的倍数根火柴，就一定获胜.因为100÷7＝14……2，所以只要甲第一次取走2根，剩下98根火柴是7的倍数，以后总留给乙7的倍数根火柴，甲必胜.由例题看出，在每次取1～n根火柴，取到最后一根火柴者获胜的规定下，谁能做到总给对方留下（1+n）的倍数根火柴，谁将获胜.[拓展二]将例1中“谁取走最后一根火柴谁获胜”改为“谁取走最后一根火柴谁输”，其余不变，情形又将如何？分析：最后留给对方1根火柴者必胜，按照例1中的逆推的方法分析，只要每次留给对方5的倍数加1根火柴必胜.甲先取，只要第一次取4根，剩下96根（96除以5余1），以后每次都将除以5余1的根数留给乙，甲必胜.由此看出，在每次取1～n根火柴，取到最后一根火柴者为负的规定下，谁能做到总给对方留下（1+n）的倍数加1根火柴，谁将获胜.[小结]我们可以把解决这类问题的一般方法总结为余数问题.，即如果有余数，则先取者胜，且取余数根数；如果没有余数，则后取者胜，每“回合”共取N+1根.【例2】甲、乙两人轮流往一张圆桌面上放同样大小的硬币，规定每人每次只能放一枚，硬币平放且不能有重叠部分，放好的硬币不再移动.谁放了最后一枚，使得对方再也找不到地方放下一枚硬币的时候就赢了.说明放第一枚硬币的甲百战百胜的策略.分析：采用“对称”思想.设想圆桌面只有一枚硬币那么大，当然甲一定获胜.对于一般的较大的圆桌面，由于圆是中心对称的，甲可以先把硬币放在桌面中心，然后，乙在某个位置放一枚硬币，甲就在与之中心对称的位置放一枚硬币.按此方法，只要乙能找到位置放一枚硬币，根据圆的中心对称性，甲定能找到与这一位置中心对称的地方放上一枚硬币.由于圆桌面的面积是有限的，最后，乙找不到放硬币的地方，于是甲获胜.[巩固]今有两堆火柴，一堆35根，另一堆24根.两人轮流在其中任一堆中拿取，取的根数不限，但不能不取.规定取得最后一根者为赢.问：先取者有何策略能获胜？分析：本题虽然也是取火柴问题，但由于火柴的堆数多于一堆，故本题的获胜策略与前面的例题完全不同.先取者在35根一堆火柴中取11根火柴，使得取后剩下两堆的火柴数相同.以后无论对手在某一堆取几根火柴，你只须在另一堆也取同样多根火柴.只要对手有火柴可取，你也有火柴可取，也就是说，最后一根火柴总会被你拿到.这样先取者总可获胜.请同学们想一想，如果在上面玩法中，两堆火柴数目一开始就相同，例如两堆都是35根火柴，那么先取者还能获胜吗？[拓展]有3堆火柴，分别有1根、2根与3根火柴.甲先乙后轮流从任意一堆里取火柴，取的根数不限，规定谁能取到最后一根或最后几根火柴就获胜.如果采用最佳方法，那么谁将获胜？分析：谁在某次取过火柴之后，恰好留下两堆数目相等的火柴，谁就能取胜.甲先取，共有六种取法：从第1堆里取1根，从第2堆里取1根或2根；第3堆里取1根、2根或3根.无论哪种取法，乙采取正确的取法，都可以留下两堆数目相等的火柴（同学们不妨自己试试），所以乙采用最佳方法一定获胜.【例3】有1994个球，甲乙两人用这些球进行取球比赛.比赛的规则是：甲乙轮流取球，每人每次取1个，2个或3个，取最后一个球的人为失败者.（1）甲先取，甲为了取胜，他应采取怎样的策略？（2）乙先拿了3个球，甲为了必胜，应当采取怎样的策略？分析：为了叙述方便，把这1994个球编上号，分别为1～1994号.取球时先取序号小的球，后取序号大的球.还是采用倒推法.甲为了取胜，必须把1994号球留给对方，因此甲在最后一次取球时，必须使他自己取到球中序号最大的一个是1993（也许他取的球不止一个）.为了保证能做到这一点，就必须使乙最后第二次所取的球的序号为1990（=1993-3）～1992（=1993-1）.因此，甲在最后第二次取球时，必须使他自己所取的球中序号最大的一个是1989.为了保证能做到这一点，就必须使乙最后第三次所取球的序号为1986（=1989-3）～1988（=1989-1）.因此，甲在最后第三次取球时，必须使他自己取球中序号最大的一个是1985，….把甲每次所取的球中的最大序号倒着排列起来：1993、1989、1985、….观察这一数列，发现这是一等差数列，公差d=4，且这些数被4除都余1.因此甲第一次取球时应取1号球.然后乙取a个球，因为a+（4-a）=4，所以为了确保甲从一个被4除余1的数到达下一个被4除余1的数，甲就应取4-a个球.这样就能保证甲必胜.由上面的分析知，甲为了获胜，必须取到那些序号为被4除余1的球.现在乙先拿了3个，甲就应拿5-3=2个球，以后乙取a个球，甲就取4-a个球.所以，（1）甲为了获胜，甲应先取1个球，以后乙取a个球，甲就取4-a个球.（2）乙先拿了3个球，甲为了必胜，甲应拿2个球，以后乙取a个球，甲就取4-a个球.【例4】有一种“抢某个数字”的游戏，是两个人从自然数1开始轮流报数，规定每次至少报几个数与至多报几个数(都是自然数)，最后谁报到规定的“某个数字”为胜．如“抢50”游戏，规定每次必须报1．2个自然数，从1开始，谁抢报到50为胜．例如甲先报l，乙就可接着报2或2，3；若乙报2，甲就可接着报3或3，4；若乙报2，3；甲就可接着报4或4，5．依次下去，谁能报到50为胜．如果你是甲，并且先报数，有没有必胜的策略?分析：由于每次必须报1～2个自然数，那么甲先报1次后，就可保证每次与乙刚报的数字数目之和为3．如乙报1个数，甲就接着报2个数；若乙报2个数，甲就接着报1个数．因此，甲若想必胜，报完第一次数剩下的数的个数必须是3个倍数才可以．而50=3×16+2，因此甲有必胜的策略：甲先报1，2，然后，乙若报1个数，甲就报2个数；乙若报2个数，甲就报1个数．[拓展]若是抢别的数字，规定每次必须报别的一定数目的自然数，先报数的人还有没有必胜的策略?分析：借鉴前面经验，若是“抢40”游戏，规定每次必须报1～3个自然数，从1开始轮流往后报数．若甲先乙后，则乙有必胜的策略．因为乙可以保证每次与甲刚报完的数字数目之和为4，而40=4×10刚好是4的倍数．推广开来，若是“抢数字a”游戏，每次必须报1～n个自然数，从1开始轮流往后报数，且甲先乙后，那么会有两种情况：情况1：若a是(1+n)的整数倍，则后报数的乙有必胜的策略；情况2：若a不是(1+n)的整数倍，则先报数的甲有必胜的策略，且甲先报的数字个数必须是数字.除以(1+n)的余数．说明：“抢数字”游戏还有很多与之类似的变形游戏.如果你对“抢数字”游戏的规则与玩法非常熟悉的话，那么类似的变形游戏就会“如鱼得水”.不费功夫了．[小笑话]某天军训中，教练对同学说：“第一排报数！”小明惊讶的看着教练.教练很奇怪的又说了一遍：“第一排报数！”小明还是很无奈很惊讶的看着教练.教练又大声说了一遍：“第一排报数！”于是小明极其不情愿的走到大树前抱着树.（二）其它游戏中的取胜策略【例5】有100个人站成一排，从左到右依次进行1，2报数，凡是报1的人离开队伍，剩下的人继续从左到右进行1，2报数，最后留在队伍中的人获胜，如此下去，要想获胜，应站在队列中的第几个位置？分析：将这100个人从左到右依次编号为1，2，3，…，98，99，100．第一次报完后.剩下的是2的倍数， 2，4，6，8，10，…，96，98，100．第二次报完后，剩下的是4的倍数，4，8，12，16，…，92，96，100．第三次报完后，剩下的是8的倍数，8，16，24，…，80，88，96．第四次报完后，剩下的是16的倍数，16，32，48，64，80，96．第五次报完后，剩下的是32的倍数，32，64，96．第六次报完后，还剩下一人，也就是第64人．所以要想获胜，应站在队伍中的第64个位置.[数学趣题]神父的诡计一艘不大的船只在海上遇到了风暴，摆在船上25位乘客面前的路只有两条：要么全部乘客与船只同归于尽；要么牺牲一部分人的生命，把他们抛进大海，减轻船的载重量，船及其他人还有得救的可能，但是这样做至少得把一半以上的人抛进海里.大家都同意走第二条路，然而谁也不愿意自动跳进海里.乘客里有11个基督徒，其中一个是神父，于是大家就公推神父出个主意.奸诈的神父想了一下，就让大家坐成一个环形，并且从他依序报数，“1，2，3”，规定报到“3”的人就被抛进海里，下一个继续由“1”报起，同时声称这是上帝的旨意，大家的命运都由上帝来安排，不得抗拒.结果有14个人被抛进海里，而剩下的11个人全部都是基督徒.大难不死的其它10个基督徒突然醒悟过来，原来神父是用诡计救了他们.请你想想，这11个人应在什么位置，才可以避免被抛进海里去呢？分析：神父只要让11个基督徒占领1、4、5、8、10、13、14、17、19、22、23这11个位置，就可以保证他们不被抛进海里.【例6】右图是一种“红黑棋”，甲、乙两人玩棋，分别取红、黑两方．规定：下棋时，每人每次只能走任意一枚棋，每枚棋子每次可以走一格或几格．红棋从左向右走，黑棋从右向左走，但不能跳过对方棋子走，也不能重叠在对方有棋子的格中．一直到谁无法走棋时，谁就失败．甲先乙后走棋，问甲有没有必胜的策略？分析：甲若想必胜，那么甲走一次棋后，“乙能走甲就能走”，观察棋盘，第二、三行都有9个空格，第四、五行都有5个空格，而第一行只有1个空格，第六行有3个空格，因此甲第1次只要将第六行也变为1个空格，那么就形成一种对称局面，“乙能走甲就能走”．因此甲有必胜的策略：甲先把第六行的红棋向右走两格，使中间只有一个空格．以后乙走第一行，甲就相应地走第六行；乙走第二行，甲就相应地走第三行；乙走第三行；甲就相应地走第二行；乙走第四行，甲就相应地走第五行，乙走第五行，甲就相应地走第四行；乙走第六行，甲就相应地走第一行．且每次甲与乙走的格数要相同，那么最后肯定是乙无法走棋失败，甲必胜．【例7】把一棋子放在如右图左下角格内，双方轮流移动棋子（只能向右、向上或向右上移），一次可向一个方向移动任意多格.规定不能将棋子直接从左下角移到顶格处，谁把棋子走进顶格，夺取红旗，谁就获胜.问应如何取胜？E DCBA分析：采用倒推法.由于只能向右、向上或向右上移，要把棋子走进顶格，应让对方最后一次把棋子走到最右边一列的格中，为了保证能做到这一点，倒数第二次应让棋子走进右图中的A 格中.（对方从A 格出发，只能向右或向上移至最后一列的格中）所以要获胜，应先占据A 格.同理可知，每次都占据A ～E 这五个格中的某一格的人一定获胜.为保证取胜，应先走.首先把棋子走进E 格，然后，不管对方走至哪一格，（肯定不会走进A ～D 格），先走者可以选择适当的方法一步走进A ～D 格中的某一格.如此继续，直至对方把棋子走进最后一列的某个格中，此时先走者一步即可走进顶格，夺取红旗，从而获胜.黑黑黑黑黑黑红红红红红红【例8】在9×9棋盘的右上角放有一枚棋子，每一步只能向左、向下或向左下对角线走一格.二人交替走，谁先到达左下角，谁为胜者.问必胜的策略是什么？分析：还是采用倒推法分析.要想占领图9—1左下角的O点，就必须先占领图9—1中的A、B、C三点之一.因为：（1）如果你占领了A点，按照游戏规则，对方只能向下走一步，O必然被你占领.（2）如果你占领了C点，按照游戏规则，对方只能向左走一步，O点同样被你占领.（3）如果你占领了B点，按照游戏规则，对方只能向左、向下或向左下对角线走一步.若向左走一步，你可占领A点，可以获胜；若向下走一步，你可占领C点，也可以获胜；若向左下对角线走一步，你可继续向左下对角线走一步而到达O点.下面继续倒推，采用同样的方法分析出：要想占领A点，就必须占领D、E、B三点之一；要想占领B点，就必须占领E、F、G三点之一；要想占领C点，就必须占领B、G、H三点之一.如图9—2所示.依此类推，即可找出应该抢占的所有“制高点”，见图9—3，一旦你占领了一个“制高点”，不管对方怎样走，你都可以去占领下一个“制高点”.所以必胜的策略是：（1）先走，将棋子向左下对角线走一步，到达一个“制高点”.（2）对方每走一步后，你都设法去占领下一个“制高点”（“制高点”如图9—3中的黑点所示），而最终先到达O点.【例9】甲、乙两个人轮流在一个凸七边形中画对角线．规定新画的对角线不能与已经有的相交，画最后一条获胜．如果甲先画，问：谁有必胜的策略?分析：分两种情况讨论：（1）如图a ，甲连1A ，3A ，分出一个三角形和一个六边形．乙只须连15A A ，，将六边形分两个四边形，接下来甲只能在其中一个四边形中画，而乙可在另一个里画，之后甲无法再画，乙胜． (2)如图b ，甲连14A A ，，分出一个四边形和一个五边形．乙只须连15A A ，，则甲只能在余下的两个四边形中的一个里画，而乙就可在另一个里画，仍然是甲先没得画．仍是乙胜．所以，乙有必胜策略．【例10】桌子上有8颗瓜子，甲、乙两人轮流拿瓜子，他们规定，假如甲先拿（当然，乙也可以先拿），甲可拿任意颗瓜子，但不能拿光，接着乙拿，乙可以拿不多于甲所拿瓜子的2倍，又轮到甲拿，甲可以拿不多于乙拿瓜子的2倍，这样交替进行，谁最后把瓜子拿光就算胜利.分析：假如甲先拿，且拿3颗以上，则剩下的瓜子可由乙一次拿走，于是乙胜，甲输；甲为了不让乙胜，显然不能拿多于3颗的瓜子数，而只能拿2或1颗.若甲决定拿2颗，乙就可以拿1（或2、3、4）颗，如乙拿2或3或4都将认输，故乙只能拿1颗.现在桌子上只剩下5颗瓜子，且又轮到甲拿瓜子，因刚才乙只拿了一颗，故甲可拿1或2颗瓜子，如拿2颗，乙就能把剩下的瓜子拿光而获胜.所以甲只能拿1颗，接着拿瓜子的乙也可拿1或2颗，为保证胜利，乙也拿1颗，这样桌子上只剩下3颗瓜子，仍轮到甲拿瓜子，且只能拿1颗或2颗，不管怎样拿，甲都是输定了.若甲决定拿1颗，则乙就拿2颗，此时桌上只剩下5颗且甲拿，情形和以上一样.故无论何种取法甲必输.这个数字游戏和斐波那契数列：1，1，2，3，5，8，13，21，…有关.8为该数列中的一项.事实上是：如果甲、乙两人都清楚这个游戏的“窍门”，那么如瓜子数是该数列的某一项，则先拿者输，如瓜子数不是该数列的某一项，则先拿者赢.1. （例1）桌上放着60根火柴，甲、乙二人轮流取，每次可取1到3根，规定谁取到最后一根谁获胜．假设甲先取，那么谁一定获胜，如何获胜?分析：乙一定获胜.每次可取1～3根，则甲、乙每轮所取的火柴之和总可以凑成4，例如，甲取1根，乙就取3根；甲取2根，乙就取2根；甲取3根，乙就取1根，因为60是4的倍数，无论甲如何取，乙总有相应的取法使得这一轮里火柴共被取走4根，因此，乙必定可以取走最后一根火柴.2. （例2）现有7根火柴，甲乙两人轮流从中取1根、2根或3根，直到取完为止，最后计算各人所得火柴总数，得数为偶数者获胜，问先拿的人是否能取胜?应怎样安排策略?分析：由于7是奇数，所以两人所拿的火柴数必然是一个奇数，一个偶数．而如果火柴总数是偶数的话，分成两个自然数必为同奇或同偶，因此无论如何取，只能是平局，可见如果火柴总数是偶数，比赛就没有意义了，那么我们就对火柴总数为奇数的情况，从少到多开始讨论．（1）如果共有1根火柴，那么先取的人必败，而后取的人必胜．（2）如果共有3根火柴，这时先取的人就占据了有利位置，只要甲直接取2根，乙就只能取1根.那么先取的人必胜，后取的人必败．（3）如果共有5根火柴，由(2)知，甲不能拿2根.因为给乙剩下3根则甲必败．如果甲选择拿1根还剩4根，那么乙有3种选择．①乙拿1根，还剩3根，甲拿3根后总数为1+3=4根，乙只有1根，甲胜；②乙拿2根，还剩2根，甲再拿1根后总数有1+1=2根，乙只能再拿1根，总数为2+1：3根，甲胜；③乙拿3根，还剩1根，甲拿走后总数有1+1=2根，乙有3根，甲胜．（4）如果有7根火柴.甲取走了3根还剩4根，该乙拿．这时的情况与共5根火柴甲取先1根一样，甲有必胜的策略．所以先拿的人有必胜的策略，他要先取走3根火柴．3.（例5）两人轮流报数，但报出的数只能是1至10的自然数.同时把所报数一一累加起来，谁先使这个累加和达到100，谁就获胜.问怎样才能确保获胜？分析：这个问题可以倒着想，要想使总和先达到100，应该最后给对方留下多少个数呢？由于每个人报的数最大是10，最小是1，因此对方最后一次报完数后，总和最大是99，最小是90，所以最后一次应该给对方留下11个数，也就是说要先达到100，就必须先达到89.如何抢到89这个数呢？采用同样的分析方法可知，应先达到78.依此类推，可以得到每次报数应占领的“制高点”是：100，89，78，67，56，45，34，23，12，1.所以获胜的策略是：（1）先报1；（2）每次对方报a（1≤a≤10），你就报11-a.这样，每次你都能占领一个“制高点”，以确保获胜.4.（例6）甲、乙二人轮流报数，报出的数只能是1至7的自然数.同时把所报数一一累加起来，谁先使这个累加和达到80，谁就获胜.问怎样才能确保获胜？分析：采用倒推法．因为每次报1至7的自然数，所以要想报到80，应抢先报到72，给对方留下8个数；同理，要报到72，应抢先报到64；以此类推，每次应抢报的数为80，72，64，56，48，40，32，24，16，8．因此获胜的方法是：（1）让对方先报；（2）对方报a（1≤a≤7），你就报8-a，必胜．B 5.（例8）在下图的A点有一枚棋子，甲先乙后轮流走这枚棋子，每次必须向上或向右走1步或2步(走2步时可以拐弯)，最终将棋子走到B点者获胜．甲有没有必胜的策略?A分析：因为每次走棋子必须向上或向右走，所以不管走什么路径，从A到B的步数是定的，都是10步．而每次必须走1步或2步，因此，甲先走一次后，每次可保证与乙刚走的步数和为3，如乙走1步，甲就走2步；乙走2步，甲就走1步．这样，甲若想必胜，走完第一次后剩下的步数必须是3的倍数，这一点是可以做到的．所以甲有必胜的策略：甲先走1步，然后，若乙走1步，甲就走2步；若乙走2步，甲就走1步．。