数值分析(10)幂法
幂法(指数迭代法)

幂法(指数迭代法) 幂法是通过迭代来计算矩阵的主特征值(按模最⼤的特征值)与其对应特征向量的⽅法,适合于⽤于⼤型稀疏矩阵。
基本定义 设A=(a ij)∈R n×n,其特征值为λi,对应特征向量x i(i=1,...,n),即Ax i=λi x i(i=1,...,n),且{x1,...,x n}线性⽆关。
任取⼀个⾮零向量v0∈R n,且v0≠0,构造⼀个关于矩阵A的乘幂的向量序列:v k=Av k−1=A2v k−2=A3v k−3=...=A k v0 称v k为迭代向量。
设特征值λi的前r个为绝对值最⼤的特征值(ppt中分为λ1强占优和⾮强占优,感觉没必要),即有:|λ1|=|λ2|=...=|λr|>|λr+1|≥...≥|λn| 由于{x1,...,x n} 线性⽆关,所以构成R n的⼀个基,于是v0能被表达为:v0=n∑i=1αi x i(且设α1...αr⾮全零) 由Ax i=λi x i:v k=Av k−1=...=A k v0=n∑i=1A kαi x i=n∑i=1λk iαi x i=λk1(r∑i=1αi x i+εk) 其中:εk=n∑i=r+1(λiλ1)kαix i 因为λ1最⼤,所以有|λiλ1|<1 (i=r+1,...,n),从⽽有:limk→∞(λiλ1)k=0 (i=r+1,...,n) 所以有:limk→∞εk=0limk→∞v k=limk→∞λk1(r∑i=1αi x i+εk)=limk→∞λk1(r∑i=1αi x i) 因为在上式中(r∑i=1αi x i)是固定项,可以看出,迭代到后期,v k+1和v k的各个元素有固定⽐值λ1,即:limk→∞(v k+1)i(v k)i=λ1 这样,收敛到主特征值后,还可另外计算它对应的⼀个特征向量(其实就是构成v0的前r项之和,⽽且只能算⼀个):lim k→∞v kλk1=r∑i=1αi x i 其中收敛速度由⽐值|λr+1λ1|决定,越⼩收敛越快。
数值幂法及反幂法分析方法

xn组成规范化正交组,即(x, x j) ij ),则
1。n
Ax, x x, x
1
对于任意非零向量x Rn
2。1
max
xRn ,x0
Ax, x x, x
.
3。n
min
xRn ,x0
Ax, x x, x
证明:1。设x Rn
由于x1, x2 ,, xn为Rn的一组正交向量,有
X a1x1 a2 x2 an xn
X
2
X
,
X
1 2
a1x1 an xn , a1x1 an xn
a12 a22 ,an2 0.
n
于是
Ax, x x, x
ai 2i
i 1 n
ai 2
i 1
n
n
n ai2
n
i 1 n
ai 2
Ax, x x, xBiblioteka 1 ai 2i1 n
1
ai 2
i 1
i 1
本章主要介绍三种方法:幂法、反幂法、 正交相似变换的方法,来求A的特征值及相应 的特征向量.
w
max
2 1
p p
,
n 1
p p
min,
取2
p n
p,
p
2
p
2
p*时w最小.
这时,2 p* n p* 2 n . 1 p* 1 p* 21 2 n
2.Rayleigh商加速法
计算实对称阵A的主特征值1..
定理2 设A Rnn为实对称阵,1 2 3 n
对应的特征向量满足 xi , x j ij ,应用幂法计算1,
定理3(Gerschgorin’s圆盘定理)
《幂法和反幂法》课件

应用范围比较
总结词
幂法适用于求解特征值和特征向量,而反幂法适用于求解线性方程组和最小二 乘问题。
详细描述
幂法主要用于求解特征值和特征向量,在物理、工程和科学计算等领域有广泛 应用。反幂法适用于求解线性方程组和最小二乘问题,在统计学、机器学习和 数据分析等领域有广泛应用。
优缺点比较
总结词
幂法的优点在于能够求解特征值和特征向量,但缺点是计算复杂度高;反幂法的优点在于计算复杂度低,但缺点 是可能存在数值不稳定性。
幂法的性质
01
02
03
幂法具有高效性
相对于直接计算矩阵的幂 ,幂法可以大大减少计算 量和存储空间。
幂法具有收敛性
在适当的条件下,幂法能 够收敛到正确的矩阵幂的 结果。
幂法具有稳定性
在计算过程中,幂法能够 保持数值的稳定性,避免 误差的累积。
幂法的应用场景
数值分析
用于求解线性方程组、特 征值问题等数值计算问题 。
详细描述
幂法的优点在于能够精确求解特征值和特征向量,适用于需要高精度计算的情况。然而,由于其计算复杂度高, 对于大规模数据集可能效率较低。反幂法的优点在于计算复杂度相对较低,适用于处理大规模数据集。然而,反 幂法可能存在数值不稳定性,对于某些问题可能需要额外的数值稳定化技术。
04
幂法和反幂法的实现
05
幂法和反幂法的应用实 例
幂法在密码学中的应用
加密算法
幂法常被用于构造加密算法,如RSA算法。通过使用幂法,可以 快速地计算大数的幂次,从而实现高效的加密和解密过程。
密钥交换
在Diffie-Hellman密钥交换协议中,幂法被用于生成共享密钥,确 保通信双方安全地交换密钥。
数字签名
初中数学幂的运算方法总结
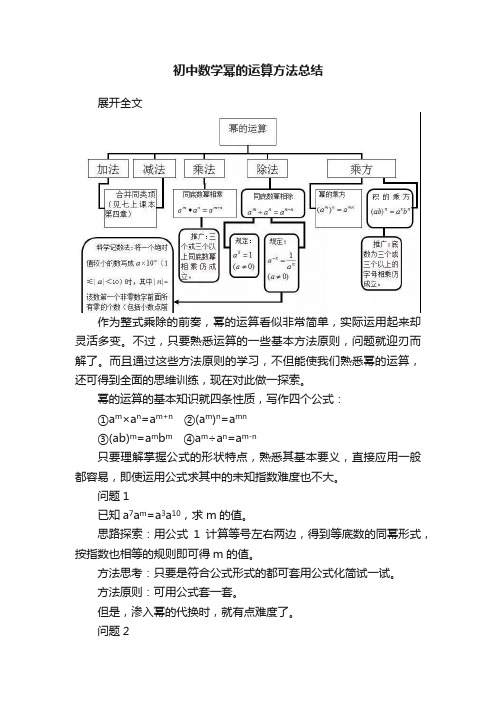
初中数学幂的运算方法总结展开全文作为整式乘除的前奏,幂的运算看似非常简单,实际运用起来却灵活多变。
不过,只要熟悉运算的一些基本方法原则,问题就迎刃而解了。
而且通过这些方法原则的学习,不但能使我们熟悉幂的运算,还可得到全面的思维训练,现在对此做一探索。
幂的运算的基本知识就四条性质,写作四个公式:①a m×a n=a m+n ②(a m)n=a mn③(ab)m=a m b m ④a m÷a n=a m-n只要理解掌握公式的形状特点,熟悉其基本要义,直接应用一般都容易,即使运用公式求其中的未知指数难度也不大。
问题1已知a7a m=a3a10,求m的值。
思路探索:用公式1计算等号左右两边,得到等底数的同幂形式,按指数也相等的规则即可得m的值。
方法思考:只要是符合公式形式的都可套用公式化简试一试。
方法原则:可用公式套一套。
但是,渗入幂的代换时,就有点难度了。
问题2已知x n=2,y n=3,求(x2y)3n的值。
思路探索:(x2y)3n中没有x n和y n,但运用公式3就可将(x2y)3n化成含有x n和y n的运算。
因此可简解为,(x2y)3n =x6n y3n=(x n)6(y n)3=26×33=1728方法思考:已知幂和要求的代数式不一致,设法将代数式变形,变成已知幂的运算的形式即可代入求值。
方法原则:整体不同靠一靠。
然而,遇到求公式右边形式的代数式该怎么办呢?问题3已知a3=2,a m=3,a n=5,求a m+2n+6的值。
思路探索:试逆用公式,变形出与已知同形的幂即可代入了。
简解:a m+2n+6=a m a2n a6=a m(a n)2(a3)2=3×25×4=300方法思考:遇到公式右边的代数式时,通常倒过来逆用公式,把代数式展开,然后代入。
方法原则:逆用公式倒一倒。
当底数是常数时,会有更多的变化,如何思考呢?问题4已知22x+3-22x+1=48,求x的值。
数值分析 -第7讲_幂法和反幂法

则存在酉矩阵U使 定理9( Schur定理) 设A ∈ R n×n, r11 r12 L r1n r22 L r2n ∆ = R, U T AU = O rnn 其中rii (i = 1,2,L, n)为A的特征值.
定理10(实Schur分解) 设A ∈ R n×n, 则存在正交矩阵Q使 R11 R12 L R1m R22 L R2m , QT AQ = O Rmm 其中当Rii (i = 1,2,L, m)为一阶时Rii是A的实特征值,当Rii为 二阶时Rii的两个特征值是A的两个共轭复特征值.
xn xn
α1 x1 α1 x1
数值分析
不同范数选取下的特征值的计算
1. 取范数为2-范数时 取范数为2
T T yk −1uk = yk −1 Ayk −1 ⇒
α1 x1T α1 x1 A = λ1 α1 x1 2 α1 x1 2
对应的迭代公式
∀ u0 ∈ R n T η k −1 = uk −1uk −1 yk −1 = uk −1 η k −1 uk = Ayk −1 T β k = yk −1uk ( k = 1, 2,...)
数值分析
实际使用的迭代公式为: 实际使用的迭代公式为:
uk −1 yk −1 = u k −1 u = Ay k −1 k
于是可得
Auk −1 A2uk −2 A k u0 uk = = = L = k −1 uk −1 Auk −2 A u0
uk Ak u0 yk = = k uk A u0
数值分析
定义3 定义3 设A = (aij ) n×n , 令 n ( )i = ∑ | aij | (2) Di = {z | | z − aii |≤ ri , z ∈ C }, (i = 1,L, n) 1 r , j≠i 称Di为复平面上以aii为圆心以ri为半径的Gerschgorin圆盘.
幂运算总结及方法归纳

幂的运算一、知识网络归纳二、学习重难点学习本章需关注的几个问题:●在运用 a m ? a n a m n( m 、 n 为正整数), a m a n a m n(a 0, m 、 n 为正整数且 m > n ), (a m ) n a mn( m 、 n 为正整数), (ab) n a n b n( n 为正整数), a 01(a 0) ,a n1( a 0 ,n为正整数)时,要特别注意各式子成a n立的条件。
◆上述各式子中的底数字母不不过表示一个数、一个字母,它还可以表示一个单项式,甚至还可以表示一个多项式。
换句话说,将底数看作是一个“整体”即可。
◆注意上述各式的逆向应用。
如计算2004 4 2005,可先逆用同底数幂的乘法法则将42005 写成42004 4 ,再逆用积的乘方法则计算0.25 200442004(0.25 4) 2004120041,由此不难获得结果为1。
◆经过对式子的变形,进一步领悟转变的数学思想方法。
仿佛底数幂的乘法就是将乘法运算转变为指数的加法运算,同底数幂的除法就是将除法运算转变为指数的减法运算,幂的乘方就是将乘方运算转变为指数的乘法运算等。
◆在经历上述各个式子的推导过程中,进一步意会“经过观察、猜想、考据与发现法规、规律” 这一重要的数学研究的方法,学习并领会从特别到一般的归纳推理的数学思想方法。
一、同底数幂的乘法1、同底数幂的乘法同底数幂相乘,底数不变,指数相加.公式表示为:a m a n a m n m、n为正整数2、同底数幂的乘法可推行到三个或三个以上的同底数幂相乘,即a m a n a p a m m p (m、 n、 p为正整数 )注意点:(1)同底数幂的乘法中,第一要找出同样的底数,运算时,底数不变,直接把指数相加,所得的和作为积的指数 .(2)在进行同底数幂的乘法运算时,假如底数不一样,先想法将其转变为同样的底数,再按法规进行计算 .例题:例 1:计算列以下各题(1)a3 a4;( 2) b b2b324;( 3)cc c简单练习:一、选择题1.以下计算正确的选项是 ( )A.a2+a3=a5B.a2·a3=a5m+2m=5m D.a2+a2=2a42.以下计算错误的选项是 ( )A.5 x2- x2=4x2B.am+am=2am m+2m=5m D. x·x2m-1=x 2m3.以下四个算式中①a333②x336325·a=2a+x =x③b·b·b=b④p2+p2+p2=3p2正确的有 ( )个个个个4.以下各题中,计算结果写成底数为10 的幂的形式,此中正确的选项是()A.100 × 102=103× 1010=103C.100 × 103=105×1000=104二、填空题1.a4·a4=_______;a4+a4=_______。
数值分析第三章小结

第三章矩阵特征值与特征向量的计算--------学习小结一、本章学习体会本章我们学习了矩阵特征值与特征向量的计算方法即幂法、反幂法、Jacobi方法和QR方法。
下边介绍一下四种方法各自的特点和适用范围。
幂法:主要用于计算矩阵按模最大的特征值及其相应的特征向量;反幂法:主要用于计算矩阵按模最小的特征值及其相应的特征向量;Jacobi法:用于求实对称矩阵的全部特征值和特征向量的方法;QR法:则适用于计算一般实矩阵的全部特征值,尤其适用于计算中小型实矩阵的全部特征值。
归结起来,这四种方法有一个共同的特点,即都是用了迭代的方法来求矩阵的特征值和特征向量。
还有利用用MATLAB自带的解法求解特征值和特征向量,其自带函数Eig即得到结果是虚数也可以算出,并且结果自动正交化。
二、本章知识梳理在工程技术中,计算矩阵的特征值和特征向量主要使用数值解法。
本章将阐述幂法、反幂法、Jacobi 方法、和QR 方法,并且只限于讨论实矩阵的情况。
3.1 幂法和反幂法(1)幂法幂法主要用于计算矩阵的按模为最大的特征值和相应的特征向量,其思想是迭代。
设n ⨯n 实矩阵A 具有n 个线性无关的特征向量,,...,,321n x x x x 其相应的特征值n λλλ...21,,满足如下不等式 n λλλλ≥≥≥> (321)其中i i i x Ax λ= )。
(n i ,...2,1=现在要求出1λ和相应的特征向量。
任取一n 维非零向量0u ,从0u 出发,按照如下的递推公式 1-=k k Au u ),,(...21=k 因n 维向量组n x x x ,...,21线性无关,故对于向量0u ,必存在唯一的不全为零的数组n ααα,...,21,使得n n x x x u ααα...22110++=n k n k k k k k k x A x A x A u A u A Au u ααα+++=====--......22110221=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛+=+++n kn n k kn k n n k k x x x x x x 12122111222111......λλαλλααλλαλαλα 设01≠α。
数值分析课程设计反幂法

数值分析课程设计反幂法一、教学目标本节课的教学目标是让学生掌握反幂法的原理及其在数值分析中的应用。
知识目标要求学生了解反幂法的定义、性质及其在求解非线性方程中的应用;技能目标要求学生能够运用反幂法求解实际问题,并能够对结果进行分析和评价;情感态度价值观目标则是培养学生的探究精神、合作意识以及对于数学问题的兴趣。
二、教学内容本节课的教学内容主要包括反幂法的原理及其在数值分析中的应用。
首先,介绍反幂法的定义和性质,通过具体的例子让学生理解反幂法的含义和作用。
然后,讲解反幂法在求解非线性方程中的应用,并通过实际问题让学生掌握反幂法的具体操作步骤。
最后,对反幂法的优缺点进行总结,并引导学生思考如何选择合适的数值方法。
三、教学方法为了达到本节课的教学目标,将采用多种教学方法进行教学。
首先,运用讲授法为学生讲解反幂法的原理和性质,让学生掌握基本知识。
其次,通过讨论法让学生探讨反幂法在实际问题中的应用,培养学生的动手能力和解决问题的能力。
此外,还可以采用案例分析法和实验法,让学生在实际操作中感受反幂法的应用,并能够对其进行评价。
四、教学资源为了支持本节课的教学内容和教学方法的实施,将准备以下教学资源。
首先,教材和相关参考书,为学生提供理论知识的学习;其次,多媒体资料,包括PPT、视频等,用于直观展示反幂法的原理和应用;最后,实验设备,如计算机、计算器等,让学生能够在实际操作中掌握反幂法。
通过这些教学资源的使用,丰富学生的学习体验,提高学生的学习效果。
五、教学评估本节课的教学评估将采取多元化方式进行,以确保评估的客观性和公正性,并全面反映学生的学习成果。
评估方式包括平时表现、作业、小测验和期末考试。
平时表现主要评估学生的课堂参与度和提问回答情况;作业则是对学生掌握反幂法知识的检验,要求学生独立完成相关练习题;小测验则是在课程中期进行,用以检查学生对反幂法的理解和应用能力;期末考试则是对学生整个学期学习成果的全面考核,包括理论知识的理解和实际问题的解决。
用幂法求解矩阵特征值和特征向量

x= -0.3930 -0.9774 0.2921 1.0000 第五题 A=[-1 2 1; 2 -4 1; 1 1 -6 ]; v0=[1 1 1]'; tol=1e-4; [lda,x]=mifa(A,v0,tol) lda = -6.4209
第4页
数值分析实验指导
x= -0.0463 -0.3746 000
( 1, 0, 1, 0, 0, 1 )T 105
1 21.30525 6 1.62139 x1 0.8724,0.5401,0.9973,0.5644,0.4972,1.0 T
第1页
数值分析实验指导
2 1 1 2 1 (3) A= 1 2 1 1 2 1 1 2 T 0 104 取 =( 1, 1, 1, 1, 1 ) 参考结果: 3.7321 3 4 2 1 1 3 1 5 (4) A= 3 1 6 2 4 5 2 1 T 2 取 0 =( 1, 1, 1, 1 ) , 10 。
第3页
数值分析实验指导
x= 0.5000 -0.8660 1.0000 -0.8660 0.5000 第四题 A=[2 1 3 4; 1 -3 1 5; 3 1 6 -2; 4 5 -2 -1 ]; v0=[1 1 1 1]'; tol=1e-2; [lda,x]=mifa(A,v0,tol) lda = -8.0136
下面再考虑主特征值 1 的的计算,用 (vk )i 表示 vk 的第 i 个分量,则
( x ) ( k 1 )i (vk 1 )i 1 1 1 i , (vk )i 1 ( x1 )i ( k )i
故
幂的运算总结及方法归纳
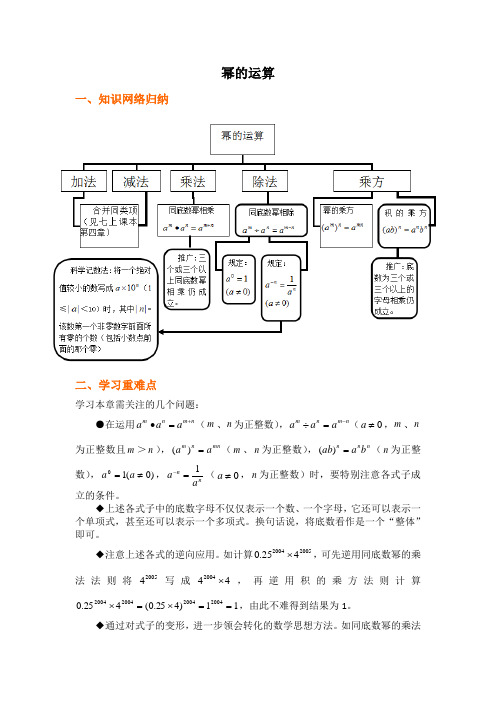
幂的运算一、知识网络归纳二、学习重难点学习本章需关注的几个问题:●在运用n m n m a a a +=•(m 、n 为正整数),n m n m a a a -=÷(0≠a ,m 、n 为正整数且m >n ),mn n m a a =)((m 、n 为正整数),n n n b a ab =)((n 为正整数),)0(10≠=a a ,n n aa 1=-(0≠a ,n 为正整数)时,要特别注意各式子成立的条件。
◆上述各式子中的底数字母不仅仅表示一个数、一个字母,它还可以表示一个单项式,甚至还可以表示一个多项式。
换句话说,将底数看作是一个“整体”即可。
◆注意上述各式的逆向应用。
如计算20052004425.0⨯,可先逆用同底数幂的乘法法则将20054写成442004⨯,再逆用积的乘方法则计算11)425.0(425.02004200420042004==⨯=⨯,由此不难得到结果为1。
◆通过对式子的变形,进一步领会转化的数学思想方法。
如同底数幂的乘法就是将乘法运算转化为指数的加法运算,同底数幂的除法就是将除法运算转化为指数的减法运算,幂的乘方就是将乘方运算转化为指数的乘法运算等。
◆在经历上述各个式子的推导过程中,进一步领悟“通过观察、猜想、验证与发现法则、规律”这一重要的数学研究的方法,学习并体会从特殊到一般的归纳推理的数学思想方法。
一、同底数幂的乘法1、同底数幂的乘法同底数幂相乘,底数不变,指数相加.公式表示为:()m n m n a a a m n +⋅=、为正整数2、同底数幂的乘法可推广到三个或三个以上的同底数幂相乘,即 ()m n p m m p a a a a m n p ++⋅⋅=、、为正整数 注意点:(1) 同底数幂的乘法中,首先要找出相同的底数,运算时,底数不变,直接把指数相加,所得的和作为积的指数.(2) 在进行同底数幂的乘法运算时,如果底数不同,先设法将其转化为相同的底数,再按法则进行计算.例题:例1:计算列下列各题(1) 34a a ⋅; (2) 23b b b ⋅⋅ ; (3) ()()()24c c c -⋅-⋅-简单练习:一、选择题1. 下列计算正确的是( )A.a2+a3=a5B.a2·a3=a5C.3m +2m =5mD.a2+a2=2a4 2. 下列计算错误的是( )A.5x2-x2=4x2B.am +am =2amC.3m +2m =5mD.x·x2m-1= x2m3. 下列四个算式中①a3·a3=2a3 ②x3+x3=x6 ③b3·b·b2=b5 ④p 2+p 2+p 2=3p 2 正确的有( )A.1个B.2个C.3个D.4个4. 下列各题中,计算结果写成底数为10的幂的形式,其中正确的是( )A.100×102=103B.1000×1010=103C.100×103=105D.100×1000=104二、填空题1. a4·a4=_______;a4+a4=_______。
北航数值分析报告第一次大作业(幂法反幂法)

一、问题分析与算法描述1. 问题的提出:〔1〕用幂法、反幂法求矩阵的按摸最大和最小特征值,并求出相应的特征向量。
其中要求:迭代精度达到。
〔2〕用带双步位移的QR法求上述的全部特征值,并求出每一个实特征值相应的特征向量。
2. 算法的描述:(1) 幂法幂法主要用于计算矩阵的按摸为最大的特征值和相应的特征向量。
其迭代格式为:终止迭代的控制选用。
幂法的使用条件为实矩阵A具有n个线性无关的特征向量,其相应的特征值满足不等式或幂法收敛速度与比值或有关,比值越小,收敛速度越快。
(2) 反幂法反幂法用于计算实矩阵A按摸最小的特征值,其迭代格式为:每迭代一次都要求解一次线性方程组。
当k足够大时,,可近似的作为矩阵A的属于的特征向量。
比值越小,收敛的越快。
反幂法要求矩阵A非奇异。
(3) 带双步位移的QR分解法QR方法适用于计算一般实矩阵的全部特征值,尤其适用于计算中小型实矩阵的全部特征值。
本算例中采用带双步位移的QR方法,可加速收敛,其迭代格式为:二、计算结果与分析1. 计算结果:(1) 幂法:初始条件:最大迭代次数L=1000;向量计算结果:第1次迭代结果:最大特征值:0.00000e+000第2次迭代结果:最大特征值:2.48910e+000 相对误差:1.00000e+000 第3次迭代结果:最大特征值:1.67719e+000 相对误差:第4次迭代结果:最大特征值:-2.10960e+000 相对误差:1.79503e+000 第5次迭代结果:最大特征值:-6.13203e-001 相对误差:2.44030e+000 ……第794次迭代结果:最大特征值:-1.97638e+000 相对误差:最大特征值:-1.97638e+000 相对误差:********************最终迭代结果***************特征值:-1.97638e+000 相对误差:迭代次数:795(2) 反幂法:初始条件:最大迭代次数L=1000;向量运行结果:第1次迭代结果:最大特征值:1.07542e+000第2次迭代结果:最大特征值:-3.66550e+000 相对误差:1.29339e+000 第3次迭代结果:最大特征值:1.22709e+001 相对误差:1.29871e+000 第4次迭代结果:最大特征值:-1.03421e+000 相对误差:1.28650e+001 第5次迭代结果:最大特征值:相对误差:……第995次迭代结果:最大特征值:相对误差:第996次迭代结果:最大特征值:相对误差:最大特征值:相对误差:第998次迭代结果:最大特征值:相对误差:第999次迭代结果:最大特征值:相对误差:第1000次迭代结果:最大特征值:相对误差:******************************超过最大设定迭代次数,迭代失败!(3) 带双步位移的QR法:初始条件:最大迭代次数L=1000;向量运行结果:全部特征值:特征向量〔经谱X数归一化〕:实特征值对应特征向量:-0.062705 -0.022368 0.304372 0.064466 0.521833 -0.157024 0.136942 -0.218108 0.250264 -0.043064 -0.228688 -0.184632 -0.072871 0.124721 0.029070 0.102566 -0.136358 0.167727 0.085747 0.546165 实特征值对应特征向量:-0.018001 0.019652 0.273447 0.070528 0.274896 -0.144015 0.048385 0.376439 -0.583051 -0.054008 -0.168682 -0.113430 -0.034709 0.009204 0.472291 0.125664 -0.190617 0.113145 0.046278 0.059871 实特征值对应特征向量:0.106861 0.087709 -0.024967 -0.020897 0.064302 0.034047 0.535143 0.046383 0.028832 0.003479-0.097276 -0.383801 0.089445 -0.039560 -0.036928 -0.021330 0.014811 0.705836 -0.108904 0.082022 实特征值对应特征向量:-0.055201 0.003399 0.242191 0.102847 0.372470 -0.372826 0.113953 0.240659 -0.310401 -0.076590 -0.244632 -0.192549 -0.077259 0.263328 0.201662 0.154166 -0.407814 0.186782 0.094649 0.173302 实特征值对应特征向量:0.427828 -0.546801 0.007822 -0.382580 0.025199 0.012788 0.033241 0.005389 -0.004065 0.043524 -0.032112 -0.044233 0.135395 -0.006564 0.001214 0.020165 0.011678 0.050001 -0.585765 0.013115 实特征值对应特征向量:0.236032 -0.139250 -0.008143 0.638527 -0.009049 -0.002911 -0.001307 0.003054 0.006515 -0.030134 0.012712 0.011368 -0.018792 -0.001753 -0.005749 -0.014290 -0.005292 -0.014591 0.717590 0.001369 实特征值对应特征向量:-0.227404 -0.048154 0.022615 0.297305 0.070372 0.039927 0.078503 0.015822 -0.012182 0.605334 -0.083616 -0.106270 -0.573963 -0.019907 0.003839 0.051362 0.036567 0.115613 0.332707 0.036954 实特征值对应特征向量:-0.027768 -0.051081 -0.159642 -0.054573 -0.084441 0.118378 0.029553 0.211088 0.203867 0.0486272. 结果分析以上三种方法中,幂法计算共进展了795次迭代才达到收敛,计算量较大,收敛性不好;反幂法计算结果未能收敛,通过进一步分析发现,这是因为反幂法迭代程序未考虑按模最小特征值为复数的情况,造成迭代失败。
幂法,反幂法求解矩阵最大最小特征值及其对应的特征向量

幂法,反幂法求解矩阵最大最小特征值及其对应的特征向量数值计算解矩阵的按模最大最小特征值及对应的特征向量一.幂法1. 幂法简介:当矩阵A满足一定条件时,在工程中可用幂法计算其主特征值(按模最大) 及其特征向量。
矩阵A需要满足的条件为:|,|,|,|,...,|,|,0,,为A的特征值(1) 12nix,x,...,x(2) 存在n个线性无关的特征向量,设为 12n1.1计算过程:n(0)(0)对任意向量x,有x,,u,,不全为0,则有 ,iii,1i(k,1)(k)k,1(0),,,xAx...Axnn11k,k,,,Aαuαλu,,iiiii11i,i,,,,, k,1k,1k,1n2,,,,,λu()au?()au11122nn,,,,11,,k,1,,,u111,2||可见,当越小时,收敛越快;且当k充分大时,有,111(k,)k,1(k,),,,xu,x,111(k,1),,,,x1,对应的特征向量即是。
)(k)(kkx,xu,,,111,2 算法实现,(1).输入矩阵A,初始向量x,误差限,最大迭代次数N(k)x(k),(2).k,1,,0;y,(k)max(abs(x),(3).计算x,Ay,,max(x);,,,,(4).若|,|,,输出,y,否则,转(5)(5).若 k,N, 置k,k,1,,,,,转3 ,否则输出失败信息,停机.3 matlab程序代码function [t,y]=lpowerA,x0,eps,N) % t 为所求特征值,y是对应特征向量k=1;, z=0; % z 相当于y=x0./max(abs(x0)); % 规范化初始向量x=A*y; % 迭代格式b=max(x); % b 相当于 ,if abs(z-b)<eps % 判断第一次迭代后是否满足要求t=max(x);return;endwhile abs(z-b)>eps && k<Nk=k+1;z=b;y=x./max(abs(x));x=A*y;b=max(x);end[m,index]=max(abs(x)); % 这两步保证取出来的按模最大特征值t=x(index); % 是原值,而非其绝对值。
北航数值分析第一次大作业(幂法反幂法)

一、问题分析及算法描述1. 问题的提出:(1)用幂法、反幂法求矩阵A =[a ij ]20×20的按摸最大和最小特征值,并求出相应的特征向量。
其中 a ij ={sin (0.5i +0.2j ) i ≠j 1.5cos (i +1.2j ) i =j要求:迭代精度达到10−12。
(2)用带双步位移的QR 法求上述的全部特征值,并求出每一个实特征值相应的特征向量。
2. 算法的描述:(1) 幂法幂法主要用于计算矩阵的按摸为最大的特征值和相应的特征向量。
其迭代格式为:{ 任取非零向量u 0=(h 1(0),⋯,h n (0))T|h r (k−1)|=max 1≤j≤n |h r (k−1)| y ⃑ k−1=u ⃑ k−1|h r (k−1)| u ⃑ k =Ay ⃑ k−1=(h 1(k ),⋯,h n (k ))T βk =sgn (h r (k−1))h r (k ) (k =1,2,⋯) 终止迭代的控制选用≤ε。
幂法的使用条件为n ×n 实矩阵A 具有n 个线性无关的特征向量x 1,x 2,⋯,x n ,其相应的特征值λ1,λ2,⋯,λn 满足不等式|λ1|>|λ2|≥|λ3|≥⋯≥|λn |或λ1=λ2=⋯=λm|λ1|>|λm+1|≥|λm+2|≥⋯≥|λn |幂法收敛速度与比值|λ2λ1|或|λm+1λ1|有关,比值越小,收敛速度越快。
(2) 反幂法反幂法用于计算n ×n 实矩阵A 按摸最小的特征值,其迭代格式为:{任取非零向量u 0∈R nηk−1=√u ⃑ k−1T u ⃑ k−1 y ⃑ k−1=u ⃑ k−1ηk−1⁄ Au ⃑ k =y ⃑ k−1 βk =y ⃑ k−1u ⃑ k (k =1,2,⋯) 每迭代一次都要求解一次线性方程组Au ⃑ k =y ⃑ k−1。
当k 足够大时,λn ≈1βk ,y ⃑ k−1可近似的作为矩阵A 的属于λn 的特征向量。
数值分析课程设计+幂法与反幂法MATLAB

一、问题的描述及算法设计(一)问题的描述本次课程设计我所要做的课题是:对称矩阵的条件数的求解设计 1、求矩阵A 的二条件数问题 A=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----210121012 2、设计内容: 1)采用幂法求出A 的. 2)采用反幂法求出A 的.3)计算A 的条件数 ⅡA Ⅱ2* ⅡA -1Ⅱ2=cond2(A )=/.(精度要求为10-6)3、设计要求 1)求出ⅡA Ⅱ2。
2)并进行一定的理论分析。
(二)算法设计1、幂法算法(1)取初始向量u )0((例如取u )0(=(1,1,…1)T ),置精度要求ε,置k=1. (2)计算v )(k =Au )1(-k ,m k =max(v )(k ), u )(k = v )(k / m k(3)若| m k = m 1-k |<ε,则停止计算(m k 作为绝对值最大特征值1λ,u )(k 作为相应的特征向量)否则置k=k+1,转(2) 2、反幂法算法(1)取初始向量u )0((例如取u )0(=(1,1,…1)T ),置精度要求ε,置k=1. (2)对A 作LU 分解,即A=LU(3)解线性方程组 Ly )(k =u )1(-k ,Uv )(k =y )(k (4)计算m k =max(v )(k ), u )(k = v )(k / m k(5)若|m k =m 1-k |<ε,则停止计算(1/m k 作为绝对值最小特征值n λ,u )(k 作为相应的特征向量);否则置k=k+1,转(3).二、算法的流程图(一)幂法算法的流程图(二)反幂法算法的流程图三、算法的理论依据及其推导(一)幂法算法的理论依据及推导幂法是用来确定矩阵的主特征值的一种迭代方法,也即,绝对值最大的特征值。
稍微修改该方法,也可以用来确定其他特征值。
幂法的一个很有用的特性是它不仅可以生成特征值,而且可以生成相应的特征向量。
实际上,幂法经常用来求通过其他方法确定的特征值的特征向量。
数值分析(10)幂法

n
设矩阵 A (aij ) R
nn
,令
n Z i z : z aii aik k 1 k i
则矩阵 A 的所有特征值包含于
Z
n
i
数值分析
数值分析
数值分析
数值分析
数值分析
数值分析
数值分析
数值分析
数值分析
数值分析
Vk yi( k11) i V yi(kk ) i
因1 x (1) m x ( m )也是矩阵A相应于1的特征向量,故有 X1 Xm
Vk )为相应的特征向量,即对这种情况幂法仍然有效。 y( k
数值分析
数值分析
(2)1 2 , 1 3 , 且矩阵A有n个线性无关的特征向量。
当 k 时, lim Vk X 1 / max X 1
k
数值分析
数值分析
Ak 1V0 AkV0 U k AVk 1 A k 1 max A V0 max Ak 1V0
i k [1 X 1 ( ) i X i ] i 2 1 n k 1 i k 1 max 1 [1 X 1 ( ) i X i ] i 2 1
k
数值分析
数值分析 两种特殊情况
前面假定 1 2 .如果按模最大的特征值有多个,即
1 2 m m 1 n 幂法是否有效?
( )1 是m重根,即1 2 m , 矩阵A仍有n个线性无 1 关的特征向量。此时有 y ( k ) 1k [1 x (1) m x ( m ) X1 Xm Vk
n k 1
n i k 1 max 1 X 1 ( ) i X i i 2 1 Ck max(U k ) n i k 1 max 1 X 1 ( ) i X i i 2 1
幂法 数值分析

(其中,k = 1,2,…,39)。 6. 求出 A 的条件数 cond(A)2 以及 A 的行列式
detA,其中: cond(A)2 = |λ m|/|λ s|; detA = det(LU) = detU。
二、全部源程序:
//1.主程序 #include "stdafx.h" #include "iostream.h" #include "iomanip.h" #include "head.h" #include "math.h"
为:"<<u_min<<endl; cout<<endl;
//求出 A 最大的特征值
//创建初始向量 u0 for ( i = 0; i < n; ++i) u0[i] = 5; u0[0] = 1.0;
//生成矩阵 A 的非零元素 arr_ger( a_U, a_D, a_L, s, r, n, fabs(u_max));
int i, j; //生成上带宽矩阵 a_U 的非 0 元素 for ( i = 0; i < s; ++i ) {
a_U[i] = new double [n-1-i]; } for ( j = 0; j < n-1; ++j ) {
a_U[0][j] = 0.16; } for ( j = 0; j < n-2; ++j ) {
//将带状矩阵 A 压缩为矩阵 C arr_compress( c, a_D, a_U, a_L, s, r, n);
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
当 k 时, lim Vk X 1 / max X 1
k
数值分析
数值分析
Ak 1V0 AkV0 U k AVk 1 A k 1 max A V0 max Ak 1V0
i k [1 X 1 ( ) i X i ] i 2 1 n k 1 i k 1 max 1 [1 X 1 ( ) i X i ] i 2 1
量不为零,这样,以后的计算就满足所设条件。 2)因Vk ) 1k1 x (1) , 计算过程中可能会出现溢出 y ( k 1k 1 X1 ( 1 1)或成为0( 1 1)的情形。解决方法:每次迭 代所求的向量都要归范化。因此,幂法实际使用的 计算公式是
U k AVk 1 Ck max(U k ) V U /C k k k
n k 1
n i k 1 max 1 X 1 ( ) i X i i 2 1 Ck max(U k ) n i k 1 max 1 X 1 ( ) i X i i 2 1
lim Ck 1
数值分析
数值分析
其 第i个 方 程 是 a ii a ij x j ,
j 1 ji
n
因 为 x j 1, ( j 1,2, , n), 得 到 a ii a ij ri 此 式 说 明 必 须 在 以 ii 为 中 心 的 格 希 格 林 圆 内 。 a 盘 定理 4-1 (格希哥林 Gerschgorin 圆盘定理)
数值分析
数值分析
因此,可把Vk ) 作为与i 相应的特征向量的近似。 y( k
X1 X1 y( k 由 Vkk1 1k 11 x (1) , Vk ) 1k1 x (1) y ( 1)
y ( k ) y( k ) Vik i为 Vk 的第i 个分量。
y i Vki(k11) ( i 1, 2, n) 11 (k ) y Vki i
n j 1 ji
设 有Ax x, 将A的 特 征 向 量 规 范 化 使 最 大 元 为 其 x i 1, 则 有 a11 a12 a1n x1 x1 a i 1 a i 2 a in 1 1 a n1 a n 2 a nn x n xn
(4-8 ) 其中 max( U )表示向量 U k k
中绝对值最大的一个分量。
数值分析
数值分析
定理4-2
X1 lim Vk k max( X 1 )
lim C k 1
k
证明 由递推公式(4-8),有 1 1 1 1 1 1 Vk U k AVk 1 A U k 1 A AVk 2 Ck Ck Ck Ck 1 Ck Ck 1
所得向量序列 Vk ) 呈有规律的摆动,则可能为1 2 y(
k
的情况。否则应考虑用别的方法求解。此外,当矩阵 A无n个线性无关的特征量时,幂法收敛很慢,亦应考 虑改用其他方法。 幂法计算简便易行,它是求大型稀疏矩阵按模最 大特征值的常用方法。
数值分析
数值分析
二、幂法的加速
因为幂法的收敛速度是线性的,而且依赖于比值
( ( X i ( x1(i ) , x2i ) , , xni ) ), i 1, 2, n 线性无关。
Vk 1 i 向量 Vk 逼近 A 的优特征值对应的特征向量 , 1 Vk i
任取非零的初始向量V0,构造向量序列Vk AVk 1
数值分析
数值分析
存在不全为零的常数i i 1, 2,, n),(这里假设1 0), ( 使得V0 i X i
i 1 n
Vk AVk 1 AkV0 Ak ( i X i ) i ik X i
i 1 i 1
n
n
由1 0, 1 i ( i 2, 3, , n) 得
i k [1 X 1 ( ) i X i ] i 2 1
n k 1
m 1 k ( X Xm 1) ( n )k n x ( nn) ] ( ) m 1 x m 1 1 1 显然,只要1 , , m 不全为零,当k 充分大时,就有 Xm Vk) 1k (1 x (1) m x ( m ) ) y( k X1 1 2 m
按上面式子计算矩阵A按模最大的特征值 与相应的特征向量的方法称为幂法。 幂法的收
2 敛速度依赖于比值 ,比值越小,收敛越快。 1
数值分析
数值分析
两点说明:
1)如果V0 的选取恰恰使得1 0, 幂法计算仍能 y (0) 进行。因为计算过程中舍入误差的影响,迭代若干
X1 次后,必然会产生一个向量Vk ) , 它在x (1) 方向上的分 y(k
Vk yi( k11) i V yi(kk ) i
因1 x (1) m x ( m )也是矩阵A相应于1的特征向量,故有 X1 Xm
Vk )为相应的特征向量,即对这种情况幂法仍然有效。 y( k
数值分析
数值分析
(2)1 2 , 1 3 , 且矩阵A有n个线性无关的特征向量。
j 1 ji
n
设矩阵 A (aij ) R
nn
,令
n Z i z : z aii aik k 1 k i
则矩阵 A 的所有特征值包含于
Z
n
i
数值分析
数值分析
数值分析
数值分析
数值分析
数值分析
数值分析
数值分析
数值分析
数值分析
k
数值分析
数值分析 两种特殊情况
前面假定 1 2 .如果按模最大的特征值有多个,即
1 2 m m 1 n 幂法是否有效?
( )1 是m重根,即1 2 m , 矩阵A仍有n个线性无 1 关的特征向量。此时有 y ( k ) 1k [1 x (1) m x ( m ) X1 Xm Vk
1 1 2 1 A Vk 2 AkV0 Ck Ck 1 Ck Ck 1 C1
1k [1 X 1 ( i )k i X i ] AkV0 i 2 1 Vk k n k max A V0 i k max 1 [1 X 1 ( ) i X i ] i 2 1
2 1 /
,当比值接近于1时,幂法收敛很慢。幂法
加速有多种,介绍两种。
1. 原点移位法 矩阵A与A pI 的特征值有以下关系:若i 是A的特 征值,则i p就是A pI 的特征值,而且相应的特征
数值分析
数值分析
二、特征值问题的稳定性
数值分析
数值分析
第二节 幂法和反幂法
一、幂法
求矩阵的按模最大的特征值与相应的特征向量。 它是通过迭代产生向量序列,由此计算特征值和特 征向量。
设 n 阶实矩阵 A R
nn
的 n 个特征值为 i (i 1, 2, , n) ,
满足
1 2 n 0 ,所对应的 n 个特征向量
数值分析
故在这种情况下,仍可按幂法产生向量序列。
数值分析
幂法小结 综上可知,当A的特征值分布为 1 2 n
或 1 2 m m 1 n 时,用幂法可以
( Vk 1) AVk(1迭代 Ay k ) 计算出1及相应的特征向量。如果按y k
由上式可知,Vk ) 是个摆动序列,当k 充分大时,有 y( k
k yi(V 2)2 i k 2 k 1 ( k ) 1,2 yi(Vk2)i// Vk( k i) yi 2 yiVk i
3 k n k (3) X y Vk [1 x ( 1) 2 xX 2 ( ) 3 x 3 ( ) n x ( nn) ] X X 1 1
n k 1 n i k i k k 1 [1 X 1 ( ) i X i ] [1 X 1 ( ) i X i ] i 2 1 i 2 1 n n i k i k k 1 max [1 X 1 ( ) i X i ] max [1 X 1 ( ) i X i ] i 2 1 i 2 1 n
数值分析
数值分析
第四章 代数特征值问题
第一节 特征值的估计和数值稳定性 第二节 幂法和反幂法 第三节 求实对称矩阵特征值的雅可比 (Jacobi)方法 第四节 求矩阵全部特征值的QR方法
数值分析
数值分析
第一节 特征值的估计和数值稳定性
一、格希格林圆盘(Gerschgorin)
定义 对n阶矩阵A (aij )nn,令ri aij ,( i 1, 2, , n) 则称Z i z C z aii ri 为格希格林圆盘。
n
由于 Vk 是归一化向量,所以 Ck Ck 1 C1 max A V0
k
U k AVk 1 Ck max(U k ) V 数值分析 C k U k/ k
数值分析
i k [1 X 1 ( ) i X i ] k A V0 i 2 1 Vk k n k max A V0 i k max 1 [1 X 1 ( ) i X i ] i 2 1
数值分析
第四章 代数特征值问题
工程实践中有多种振动问题,如桥梁 或建筑物 的振动,机械机件、飞机机翼的振动,及 一些稳定 性分析和相关分析可转 化为求矩阵特征值与特征向 量的问题。
矩阵A aij
