(含详解)2011-2017新课标高考数学复数分类汇编

合集下载

高考数学专题《复数》习题含答案解析

专题10.2 复数1．（2020·全国高考真题（理））复数113i-的虚部是（）A ．310-B ．110-C ．110D ．310【答案】D 【解析】因为1131313(13)(13)1010i z i i i i +===+--+，所以复数113z i =-的虚部为310.故选：D.2．（2020·全国高考真题（文））（1–i ）4=（）A ．–4B ．4C ．–4i D ．4i【答案】A 【解析】422222(1)[(1)](12)(2)4i i i i i -=-=-+=-=-.故选：A.3．（2021·北京·高考真题）在复平面内，复数z 满足(1)2i z -=，则z =（）A ．1i --B ．1i-+C ．1i-D ．1i+【答案】D 【分析】由题意利用复数的运算法则整理计算即可求得最终结果.【详解】由题意可得：()()()()2121211112i i z i i i i ++====+--+.故选：D.4．（2021·全国·高考真题）已知2i z =-，则()i z z +=（）A ．62i -B ．42i-C ．62i+D ．42i+【答案】C 【分析】练基础利用复数的乘法和共轭复数的定义可求得结果.【详解】因为2z i =-，故2z i =+，故()()()2222=4+42262z z i i i i i i i+=-+--=+故选：C.5．（2021·全国·高考真题（文））已知2(1)32i z i -=+，则z =（）A ．312i--B ．312i-+C ．32i-+D ．32i--【答案】B 【分析】由已知得322iz i+=-，根据复数除法运算法则，即可求解.【详解】2(1)232i z iz i -=-=+，32(32)23312222i i i i z i i i i ++⋅-+====-+--⋅.故选：B.6．（2021·全国·高考真题（理））设()()2346z z z z i ++-=+，则z =（）A ．12i -B ．12i+C ．1i+D ．1i-【答案】C 【分析】设z a bi =+，利用共轭复数的定义以及复数的加减法可得出关于a 、b 的等式，解出这两个未知数的值，即可得出复数z .【详解】设z a bi =+，则z a bi =-，则()()234646z z z z a bi i ++-=+=+，所以，4466a b =⎧⎨=⎩，解得1a b ==，因此，1z i =+.故选：C.7．（2021·全国·高考真题（文））设i 43i z =+，则z =（）A ．–34i -B ．34i-+C ．34i-D ．34i+【答案】C 【分析】由题意结合复数的运算法则即可求得z 的值.【详解】由题意可得：()2434343341i i i i z i i i ++-====--.故选：C.8．（2021·浙江·高考真题）已知a R ∈，()13ai i i +=+，(i 为虚数单位)，则a =（）A ．1-B ．1C ．3-D ．3【答案】C 【分析】首先计算左侧的结果，然后结合复数相等的充分必要条件即可求得实数a 的值.【详解】()213ai i i ai i a a i i +=-=-+=++=，利用复数相等的充分必要条件可得：3,3a a -=∴=-.故选：C.9．（2019·北京高考真题（文））已知复数z =2+i ，则（）ABC ．3D ．5【答案】D 【解析】∵ 故选D.10．（2019·全国高考真题（文））设，则=（）A．2B CD ．1【答案】C 【解析】因为，所以，所以，故选C ．1．（2010·山东高考真题（文））已知，，其中为虚数单位，则=（）A ．-1B ．1C ．2D ．3【答案】B 【解析】z z ⋅=z 2i,z z (2i)(2i)5=+⋅=+-=3i12iz -=+z 312iz i -=+(3)(12)17(12)(12)55i i z i i i --==-+-z ==2a ib i i+=+,a b ∈R i +a b 练提升因为，，所以，则，故选B.2．（全国高考真题（理））复数的共轭复数是( )A ．B ．ｉC ．D ．【答案】A 【解析】，故其共轭复数为.所以选A.3．（2018·全国高考真题（理））设，则（）A ．B ．C ．D【答案】C 【解析】，则，故选c.4．（2009·重庆高考真题（理））已知复数的实部为，虚部为2，则的共轭复数是（）A ．B ．C ．D ．【答案】B 【解析】由题意得：所以，共轭负数为2+i 故选B5．（2017·山东高考真题（理））已知，是虚数单位，若，，22222a i ai i ai b i i i+--==-=+-,a b ∈R 2211b b a a ==⎧⎧⇒⎨⎨-==-⎩⎩+1a b =212ii+-i -35i-35i()()()()2i 12i 5i i12i 12i 5++==-+i -1i2i 1iz -=++||z =0121()()()()1i 1i 1i2i 2i 1i 1i 1i z ---=+=++-+i 2i i =-+=1z =z 1-5iz2i -2i+2i--2i-+R a ∈i z a =4z z ⋅=则（）A ．1或B或C ．D【答案】A 【解析】由得，所以，故选A.6．（2021·广东龙岗·高三期中）已知复数z 满足()2i 34i z +=+（其中i 为虚数单位），则复数z =（）A ．2i -B ．2i-+C ．2i+D ．2i--【答案】C 【分析】根据复数除法运算求出z ，即可得出答案.【详解】()2i 35z +=+= ，()()()52i 52i 2i 2i 2i z -∴===-++-，则2i z =+.故选：C.7．（2021·安徽·合肥一六八中学高一期中）欧拉公式i s co in s i x e x x +=(i 是虚数单位)是由瑞士著名数学家欧拉发现的，它将指数函数的定义域扩大到复数，建立了三角函数和指数函数的关系，它在复变函数论里非常重要，被誉为“数学中的天桥”.根据欧拉公式可知，i 3e π表示的复数位于复平面中的（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】A 【分析】先由欧拉公式计算可得312e π=，然后根据复数的几何意义作出判断即可.【详解】根据题意i s co in s i xe x x +=，故i3is n 1cos 33i 2e πππ=+=，对应点12⎛ ⎝，在第一象限.故选：A .8．【多选题】（2021·全国·模拟预测）已知复数z =（i 为虚数单位），则下列说法正确的是（）A ．复数z 在复平面内对应的点坐标为()sin 3cos3,sin 3cos3+-a =1-,4z a z z =+⋅=234a +=1a =±B ．z 的虚部为C ．2z z ⋅=D ．z ⋅为纯虚数【答案】CD 【分析】根据复数的概念、共轭复数的概念、复数的几何意义以及四则运算法则即可求解.【详解】复数3cos3i sin 3cos3z =++-．因为334ππ<<，所以sin 3cos3304π⎛⎫+=+< ⎪⎝⎭，sin 3cos30->，所以原式()()sin 3cos3i sin 3cos3=-++-，所以选项A 错误；复数z B错误；222z z ⋅=+=，所以选项C 正确；z ⋅=()i 1sin 61sin 62i⋅=++-=，所以选项D 正确.故选：CD.9．【多选题】（2021·河北武强中学高三月考）已知复数cos isin z θθ=+（其中i 为虚数单位），下列说法正确的是（）A ．1z z ⋅=B ．1z z+为实数C ．若83πθ=，则复数z 在复平面上对应的点落在第一象限D ．若(0,)θπ∈，复数z 是纯虚数，则2πθ=【答案】ABD 【分析】对选项A ，根据计算1z z ⋅=即可判断A 正确，对选项B ，根据12cos z zθ+=即可判断B 正确，对选项C ，根据88cosisin 33z ππ=+在复平面对应的点落在第二象限，即可判断C 错误，对选项D ，根据z 是纯虚数得到2πθ=即可判断D 正确.【详解】对选项A ，()()()2222cos isin cos isin cos isin cos sin 1z z θθθθθθθθ⋅=+-=-=+=，故A 正确.对选项B ，因为11cos isin cos isin z z θθθθ+=+++()()cos isin cos isin cos isin cos isin θθθθθθθθ-=+++-cos isin cos isin 2cos θθθθθ=++-=，所以1z z+为实数.故B 正确.对选项C ，因为83πθ=为第二象限角，所以8cos03π<，8sin 03π>，所以88cos isin 33z ππ=+在复平面对应的点落在第二象限.故C 错误.对选项D ，复数z 是纯虚数，则cos 0sin 0θθ=⎧⎨≠⎩，又因为(0,)θπ∈，所以2πθ=，故D 正确.故选：ABD10．（2021·福建·厦门一中模拟预测）在复平面内，复数(,)z a bi a b R =+∈对应向量OZ（O为坐标原点），设||OZ r =，以射线Ox 为始边，OZ 为终边旋转的角为θ，则(cos sin )z r i θθ=+，法国数学家棣莫弗发现了棣莫弗定理：1111(cos sin )z r i θθ=+，2222(cos sin )z r i θθ=+，则12121212[cos()sin()]z z rr i θθθθ=+++，由棣莫弗定理可以推导出复数乘方公式：[(cos sin )](cos sin )n n r i r n i n θθθθ+=+，已知4)z i =，则||z =______；若复数ω满足()*10n n ω-=∈N ，则称复数ω为n 次单位根，若复数ω是6次单位根，且ω∉R ，请写出一个满足条件的ω=______．【答案】16 ()22cossin 1,2,4,566k k i k ππ+= 【分析】2(cos sin )66i i ππ+=+，则4222(cos sin )33z i ππ=+，再由||||z z =求解，由题意知61ω=，设cos sin i ωθθ=+，即可取一个符合题意的θ，即可得解．【详解】解： 2(cos sin )66i i ππ=+，∴4422)2(cos sin )33z i i ππ==+，则4||||216z z ===．由题意知61ω=，设cos sin i ωθθ=+，则6cos 6sin 61i ωθθ=+=，所以sin 60cos 61θθ=⎧⎨=⎩，又ω∉R ，所以sin 0θ≠，故可取3πθ=，则cossin33i ππω=+故答案为：16，cossin33i ππω=+（答案不唯一）．1．（2021·江苏·高考真题）若复数z 满足()1i 3i z +=-，则z 的虚部等于（）A ．4B ．2C ．-2D ．-4【答案】C 【分析】利用复数的运算性质，化简得出12z i =-.【详解】若复数z 满足()1i 3i z +=-，则()()()()3i 1i 3i 12i 1i 1i 1i z ---===-++-，所以z 的虚部等于2-.故选：C.2．（2021·全国·高考真题）复数2i13i--在复平面内对应的点所在的象限为（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】A 【分析】利用复数的除法可化简2i13i--，从而可求对应的点的位置.【详解】()()2i 13i 2i 55i 1i13i 10102-+-++===-，所以该复数对应的点为11,22⎛⎫ ⎪⎝⎭，该点在第一象限，故选：A.3．（2020·全国高考真题（理））若z=1+i ，则|z 2–2z |=（）A ．0B ．1C D ．2练真题【答案】D 【解析】由题意可得：()2212z i i =+=，则()222212z z i i -=-+=-.故2222z z -=-=.故选：D.4．（2020·全国高考真题（文））若312i i z =++，则||=z （）A ．0B ．1CD ．2【答案】C 【解析】因为31+21+21z i i i i i =+=-=+，所以z ==故选：C ．5.（2019·全国高考真题（理））设z =-3+2i ，则在复平面内对应的点位于（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】C 【解析】由得则对应点（-3，-2）位于第三象限．故选C ．6.（2018·江苏高考真题）若复数满足，其中i 是虚数单位，则的实部为________．【答案】2【解析】因为，则，则的实部为.z 32,z i =-+32,z i =--32,z i =--z i 12i z ⋅=+z i 12i z ⋅=+12i2i iz +==-z 2。

高考数学试题分类汇编专题复数理

2011年高考试题数学（理科）复数一、选择题:1. (2011年高考山东卷理科2)复数z=22i i-+(i 为虚数单位)在复平面内对应的点所在象限为（A ）第一象限 (B)第二象限 (C)第三象限 (D)第四象限【答案】D 【解析】因为22(2)34255i i i z i ---===+,故复数z 对应点在第四象限,选D. 2. (2011年高考天津卷理科1)i 是虚数单位，复数131i i--= A ．2i + B ．2i - C ．12i -+ D ．12i --【答案】A.【解析】13(13)(1)4221(1)(1)2i i i i i i i i --+-===---+. 3. (2011年高考安徽卷理科1) (1) 设 i 是虚数单位，复数12ai i+-为纯虚数，则实数a 为（A ）2 (B) -2 (C) 1-2 (D) 12 【命题意图】本题考查了复数的运算和纯虚数的概念，是容易题，是常考题型. 【解析】ai i 1+2-=(1)(2)(2)(2)ai i i i ++-+=2(21)5a a i -++，∵12ai i +-为纯虚数，∴20210a a -=⎧⎨+≠⎩， ∴a =2，故选A.4.(2011年高考浙江卷理科2)把复数z 的共轭复数记作z ，若1z i =+，i 为虚数单位，则(1)z z +=（A ）3i - （B ）3i + （C ）13i +（D ）36.(2011年高考辽宁卷理科1)a 为正实数，i 为虚数单位，2a ii +=，则a=（）（A ）2 （B 答案： B解析：|1|2a iai i +=-==,a>0,故7. (2011年高考全国新课标卷理科1)复数i i212-+的共轭复数是（）A i 53-B i 53C i -D i ;解析：C ，因为i i 212-+=i i i i =--21)21(，所以，共轭复数为i -，选C点评：本题考查复数的概念和运算，先化简后写出共轭复数即可。

2011—2020年新课标全国卷高考数学试卷分类汇编—复数(含答案)

2011—2020年新课标全国卷高考数学试卷分类汇编—复数（含全国Ⅰ卷、Ⅱ卷、Ⅲ卷、新高考Ⅰ卷、新高考Ⅱ卷，共 8 套全国卷）一、选择题1、 (20 20 ·新高考Ⅰ，2 ) （）A ． 1B ．−1C ． iD ．−i2、(20 20 ·全国卷Ⅰ，理 1 ) 若，则（）A ． 0B ． 1C ．D ． 23、(20 20 ·全国卷Ⅰ，文 2 ) 若，则（）A ． 0B ． 1CD ． 24、(20 20 ·全国卷Ⅱ，文 2 ) （ 1–i ） 4 = （）A ．–4B ． 4C ．–4 ID ． 4 i5、 (20 20 ·全国卷Ⅲ，理 2 ) 复数的虚部是（）A ．B ．C ．D ．6、(20 20 ·全国卷Ⅲ，文 2 ) 若，则 z = （）A ． 1– iB ． 1+ iC ．– iD ． i7、(2019·全国卷Ⅰ，理 2 ) 设复数 z 满足， z 在复平面内对应的点为( x ， y ) ，则（）A ．B ．C ．D ．8、(2019·全国卷Ⅰ，文 1 ) 设，则 = （）A ． 2B ．C ．D ． 19、 (2019·全国卷Ⅱ，理 2 ) 设，则在复平面内对应的点位于（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限10、(2019·全国卷Ⅱ，文2 ) 设，则（）A ．B ．C ．D ．11、(2019·全国卷Ⅲ，文理 2 ) 若，则（）A ．B ．C ．D ．12 (2018·新课标Ⅰ，理 1 文 2 ) 设，则（）A. B. C. D.13（ 2018 ·新课标Ⅱ，理 1 ）（）A ．B ．C ．D ．14(2018·新课标Ⅱ，文 1 ) （）A ．B ．C ．D ．15（ 201 8 ·新课标Ⅲ，文理 2 ）（）A ．B ．C ．D ．16（ 2017 ·新课标Ⅰ，理 3 ）设有下面四个命题若复数满足，则；若复数满足，则；若复数满足，则；若复数，则．其中的真命题为（）A ．B ．C ．D ．17、(201 7 ·新课标Ⅰ，文 3 ) 下列各式的运算结果为纯虚数的是（）A ．B ．C ．D ．18、（ 201 7 ·新课标Ⅱ，理 1 ）（）A ．B ．C ．D ．19、（ 201 7 ·新课标Ⅱ，文 2 ）（）A. B. C. D.20、（ 2017·新课标Ⅲ，理 2 ）设复数满足，则（） .A ．B ．C ．D ． 221、 ( 201 7 ·新课标Ⅲ，文 2 ) 复平面内表示复数的点位于（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限22、（ 2016 ·新课标Ⅰ，理 2 ）设，其中是实数，则（）A ．B ．C ．D ．23、(201 6 ·新课标Ⅰ，文 2 ) 设的实部与虚部相等，其中为实数，则（）A ．B ．C ．D ．24、（ 201 6 ·新课标Ⅱ，理 1 ）已知在复平面内对应的点在第四象限，则实数 m 的取值范围是 ( )A ．（ - 3 ， 1 ）B ．（ - 1 ， 3 ）C ．（ 1 ，+∞ ）D ．（ - ∞ ， - 3 ）25、（ 201 6 ·新课标Ⅱ，文 2 ）设复数 z 满足，则= （）A ．B ．C ．D ．。

高中数学—复数的历届高考试题解析.doc

A．1+iB. -1-iC.1-iD. -1+i
【解析】依据虚数运算公式可知可得，选D.
【答案】D
11.（2009江西卷理）若复数为纯虚数，则实数的值为
A． B． C． D．或
答案：A
【解析】由故选A
12.(2009湖北卷理)投掷两颗骰子，得到其向上的点数分别为m和n,则复数（m+ni）(n-mi)为实数的概率为
A.4+8i B.8+2i C.2+4i D.4+i
【答案】C
10.【2010·四川理数】i是虚数单位，计算i＋i2＋i3＝（）
A.－1 B.1 C. D.
【答案】A
【解析】由复数性质知：i2＝－1，故i＋i2＋i3＝i＋(－1)＋(－i)＝－1.
11.【2010·天津文数】i是虚数单位，复数 =（）
【答案】A
【解析】本题主要考查复数代数形式的基本运算，属于容易题。
进行复数的除法的运算需要份子、分母同时乘以分母的共轭复数，同时将i2改为-1.
13.【2010·广东理数】若复数z1=1+i，z2=3-i，则z1·z2=（）
A．4+2i B. 2+i C. 2+2i D.3
【答案】A
【解析】 .
14.【2010·福建文数】是虚数单位, 等于 ( )
答案：D.
解析:设纯虚数 ,代入
由于其为实数，b= -2, 故选D.
19.（2009宁夏海南卷文）复数
（A）（B）（C） (D)
【答案】C
【解析】，故选.C。
20.（2009天津卷理）i是虚数单位， =
（A）1+2i （B）-1-2i （C）1-2i （D）-1+2i

2011-2017年新课标全国卷2理科数学试题分类汇编——2.复数

2011年—2017年新课标全国卷Ⅱ理科数学试题分类汇编2．复数一、选择题（2017·1）31i i+=+（） A ．12i + B ．12i - C ．2i + D ．2i -（2016·1）已知(3)(1)i z m m =++-在复平面内对应的点在第四象限，则实数m 的取值范围是（）A ．（-3，1）B ．（-1，3）C ．（1，+∞）D ．（-∞，-3）（2015·2）若a 为实数且(2+ai )(a -2i ) = -4i ，则a =（）A ．-1B ．0C ．1D ．2（2014·2）设复数1z ，2z 在复平面内的对应点关于虚轴对称，12z i =+，则12z z =（）A ．- 5B ．5C ．- 4 + iD ．- 4 - i（2013·2）设复数z 满足(1i)2i z -=，则z =（）A .1i -+B .1i --C .1i +D .1i -（2012·3）下面是关于复数i z +-=12的四个命题中，真命题为（） P 1: |z |=2，P 2: z 2=2i ， P 3: z 的共轭复数为1+i ， P 4: z 的虚部为-1 . A. P 2，P 3B. P 1，P 2C. P 2，P 4D. P 3，P 4 （2011·1）复数212i i+-的共轭复数是（） A ．35i - B ．35i C ．i - D ．i2011年—2017年新课标全国卷Ⅱ理科数学试题分类汇编2．复数（逐题解析）（2017·1）D 【解析】 ()()()()3134221112i i i i i i i i +-+-===-++-．（2016·1）A 解析：∴30m +>，10m -<，∴31m -<<，故选A ．（2015·2）B 解析：由已知得4a + (a 2 -4)i = -4i ，所以4a = 0，a 2 -4 = -4，解得a = 0，故选B.（2014·2）A 解析：∵12i z =+，复数1z ，2z 在复平面内的对应点关于虚轴对称，∴22z i =-+，∴2212(2)(2)2145z z i i i =+-+=-=--=-.（2013·2）A 解析：由(1-i )·z =2i ，得221=111i i i z i i i (+)=-(-)(+)＝222i -+＝－1＋i .（2012·3）C 解析：经计算2221,||(1)21z i z z i i i==--∴==---+ =，复数z 的共轭复数为1i -+，z 的虚部为1-，综上可知P 2，P 4正确.总是十分注意积累的。

高考数学真题题型分类解析专题专题02 复数

则所求复数对应的点为 ( 6, 8) ，位于第一象限. 故选：A.
一、复数的概念
（）叫虚数单位，满足，当时，． 1 i
i2 = −1 k ∈ Z
i 4k = 1, i 4 k +1 = i, i 4k + 2 = −1, i 4k +3 = −i
（2）形如 a + bi(a, b∈ R) 的数叫复数，记作 a +bi∈C ．
高考数学真题题型分类解析专题 02 复数
命题解读
考向
高考对复数的考查，重点是复数的运共轭复数、复数的除法运算
算、概念、复数的模、复数的几何意义等，难度较低.
复数的乘法运算复数的几何意义
复数的模
考查统计 2022·新高考Ⅰ卷，2 2023·新高考Ⅰ卷，2 2024 新高考Ⅰ卷，2 2022·新高考Ⅱ卷，2 2023 新高考Ⅱ卷，1 2024·新高考Ⅱ卷，1
综上所述，无论方程的判别式b2 −4ac 的符号如何，韦达定理都成立，于是韦达定理能被推广到复数根的
情况，即实系数一元二次方程ax2 +bx + c = 0（ a 、b 、c∈ R 且a ≠ 0 ）的两个根与系数满足关系
， x1
+
x2
=
−
b a
x1 x2
=
c a
4 / 11
一、单选题
1．（2024·安徽芜湖·三模）已知复数
=
(1− i)2
−2i
=
= −1− i .
−2i
故选：D
5．（2024·山东德州·三模）已知复数 z 满足： z − i(2 + z) = 0 ，则 z = （）
．．．． A −1− i B −1+ i C 1+ i D 1− i 【答案】B

近五年(2017-2021)高考数学真题分类汇编03 复数

18．C 【解析】
因为 z
3 i ，所以 z 1 2i
(3 i)(1 2i) (1 2i)(1 2i)
1 7i 55
，所以
z
(1)2 ( 7)2
5
5
2，
故选 C．
19．C 【解析】由 z 3 2i, 得 z 3 2i, 则 z 3 2i, 对应点（-3，-2）位于第三象限．故选 C．
22．D
【解析】 1 i2 i 2 i 2i i2 3 i 故选 D.
23．D
【解析】 i(2 3i) 2i 3i2 3 2i ，故选 D.
24．D
【解析】1 2i (1 2i)2 3 4i 选 D.
1 2i 5
5
25．C
【解析】
z
1 1
i i
2i
1 1
i i
1 1
A． 1 2
B． 2 2
C． 2
D．2
34．（2017·全国（理））设有下面四个命题
p1
：若复数
z
满足
1 z
R
，则
z
R
；
p2 ：若复数 z 满足 z2 R ，则 z R ；
p3 ：若复数 z1, z2 满足 z1z2 R ，则 z1 z2 ；
p4 ：若复数 z R ，则 z R .
其中的真命题为
A．0
B．1
C． 2
14．（2020·全国（文））（1–i）4=（）
A．–4
B．4
C．–4i
D．4i
15．（2019·北京（理））已知复数 z=2+i，则 z z
A． 3
B． 5
C．3
16．（2019·全国（理））若 z(1 i) 2i ，则 z

2011-2019高考数学复数分类汇编

新课标复数分类汇编一、理科【2011新课标】1. 复数212ii+-的共轭复数是（ C ）（A ）35i - （B ）35i （C ）i - （D ）i【2012新课标】3. 下面是关于复数21z i=-+的四个命题，其中的真命题为（ C ） 1:2p z = 22:2p z i = 3:p z 的共轭复数为1i + 4:p z 的虚部为1-()A 23,p p ()B 12,p p ()C ,p p 24 ()D ,p p 34【2013新课标1】若复数z 满足 (3－4i)z ＝|4＋3i |，则z 的虚部为 ( D )A 、－4 （B ）－45 （C ）4 （D ）45【2013新课标2】2. 设复数z 满足(1－i)z ＝2i ，则z ＝( A )． A ．－1＋i B ．－1－I C ．1＋i D ．1－i 【2014新课标1】2.=（ D ）A. 1+iB. 1-iC. -1+iD. -1-i【2014新课标2】2. 设复数1z ，2z 在复平面内的对应点关于虚轴对称，12z i =+，则12z z =（ A ） A. - 5 B. 5 C. -4- i D. -4+【2015新课标1】1. 设复数z 满足1+z1z-=i ，则|z|=（ A ）（A ）1 （B 2（C 3 （D ）2【2015新课标2】2. 若a 为实数且（2+ai ）（a-2i ）=-4i,则a=（ B ）（A ）-1 （B ）0 （C ）1 （D ）2【2016新课标1】2. 设 (1+i)x =1+y i ，其中x ，y 是实数，则i =x y +（ B ）（A ）1 （B 2 （C 3 （D ）2【2016新课标2】1. 已知 z =(m +3)+(m -1)i 在复平面内对应的点在第四象限，则实数m 的取值范围是（ A ）（A ）()31-，（B ）()13-，（C ）()1,∞+（D ）()3∞--，【2016新课标3】2. 若z ＝1＋2i ，则4i zz -1＝( C ) (A )1 (B )－1(C )i(D )－i【2017新课标1】3．设有下面四个命题1p ：若复数z 满足1z∈R ，则z ∈R ；2p ：若复数z 满足2z ∈R ，则z ∈R ；3p ：若复数12,z z 满足12z z ∈R ，则12z z =；4p ：若复数z ∈R ，则z ∈R .其中的真命题为（ B ）A ．13,p pB ．14,p pC ．23,p pD ．24,p p【2017新课标2】1.31ii+=+（ D ） A ．12i + B ．12i - C ．2i + D ．2i -【解析】()()()()3i 1i 3i 2i 1i 1i 1i +-+==-++- 【2017新课标3】2．设复数z 满足(1i)2i z +=，则z =（ C ）A ．12B ．2CD ．2【解析】由题，()()()2i 1i 2i 2i 2i 11i 1i 1i 2z -+====+++-，则z = C 【2018新课标1】1．设1i2i 1i z -=++，则z =（ C ）A ．0B ．12 C ．1D 【2018新课标2】1．12i12i+=-（ D ） A ．43i 55-- B ．43i 55-+ C ．34i 55--D ．34i 55-+【2018新课标3】2．()()1i 2i +-=（ D ）A ．3i --B ．3i -+C ．3i -D ．3i +【2019新课标1】2.设复数z 满足=1i z -，z 在复平面内对应的点为(x ，y )，则（）A. 22+11()x y +=B. 22(1)1x y -+=C. 22(1)1x y +-=D. 22(+1)1y x +=【答案】C【解析】,(1),z x yi z i x y i =+-=+-1,z i -则22(1)1x y +-=．故选C ．【2019新课标2】2. 设i z 23+-=,则在复平面内z 对应的点位于（） A.第一象限 B.第二象限 C.第三象限 D.第四象限【答案】C【解析】i 23z --=，对应的点坐标为），（2-3-,故选C. 【2019新课标3】2．若(1i)2i z +=，则z =（） A ．1i -- B ．1+i -C ．1i -D ．1+i【答案】D【解答】i i z 2)1(=+,i i i i i i i i i z +=-=-+-=+=1)1()1)(1()1(212.JS二、文科【2011新课标】2. 复数512ii=-（ C ） A ．2i - B ．12i - C ．2i -+D ．12i -+ 【2012新课标】2. 复数32iz i-+=+的共轭复数是（ D ）A ．2+iB ．2-iC ．-1+iD ．-1-i【2013新课标1】2. 212i1i +(-)＝( B )． A ． -1-12i B ． -1+12i C ． 1+12i D ． 1-12i 【2013新课标2】2. 21i+＝( C )．A ．．2 C D. 1 【2014新课标1】3. 设i iz ++=11，则=||z （ B ） A.21 B. 22 C. 23 D. 2【2014新课标2】2.131ii+=- （ B ）（A ）12i + （B ）12i -+ （C ）1-2i (D) 1-2i -【2015新课标1】3. 已知复数z 满足（z-1）i=i+1，则z=（ C ）（A ）-2-I （B ）-2+I （C ）2-I （D ）2+i 【2015新课标2】2. 若a 实数，且=+=++a i iai则,312（ D ） A.-4 B. -3 C. 3 D. 4【2016新课标1】2. 设(12i)(i)a ++的实部与虚部相等，其中a 为实数，则a =（ A ）（A ）－3 （B ）－2 （C ）2 （D ）3 【2016新课标2】2. 设复数z 满足i 3i z +=-，则z =（ C ）（A ）12i -+ （B ）12i - （C ）32i + （D ）32i - 【2016新课标3】2. 若43i z =+，则||zz =（ D ）（A ）1（B ）1-（C ）43+i 55 （D ）43i 55-【2017新课标1】3．下列各式的运算结果为纯虚数的是（ C ） A ．i(1+i)2 B ．i 2(1-i) C ．(1+i)2 D ．i(1+i) 【2017新课标2】2.（1+i ）（2+i ）=（ B ） A.1-i B. 1+3i C. 3+i D.3+3i 【解析】原式=2﹣1+3i=1+3i ，故选：B 。

(2010-2019)高考数学真题分类汇编专题02复数文(含解析)

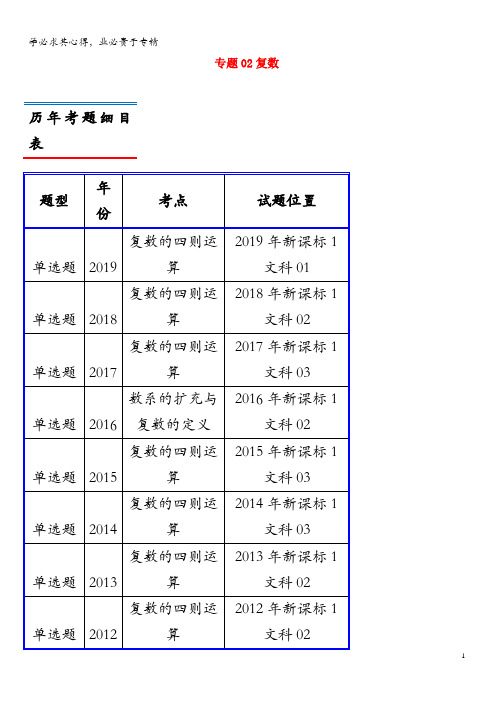
专题02复数历年考题细目表单选题2011复数的四则运算2011年新课标1文科02单选题2010复数的四则运算2010年新课标1文科03历年高考真题汇编1．【2019年新课标1文科01】设z，则|z｜＝（)A．2 B．C．D．1【解答】解：由z，得｜z|＝|｜．故选：C．2．【2018年新课标1文科02】设z2i，则｜z｜＝（）A．0 B．C．1 D．【解答】解：z2i2i＝﹣i+2i＝i，则｜z|＝1．故选：C．3．【2017年新课标1文科03】下列各式的运算结果为纯虚数的是（）A．i（1+i）2B．i2（1﹣i）C．（1+i）2D．i（1+i)【解答】解：A．i（1+i)2＝i•2i＝﹣2，是实数．B．i2（1﹣i）＝﹣1+i，不是纯虚数．C．(1+i）2＝2i为纯虚数．D．i（1+i）＝i﹣1不是纯虚数．故选：C．4．【2016年新课标1文科02】设（1+2i）（a+i）的实部与虚部相等，其中a为实数，则a等于（）A．﹣3 B．﹣2 C．2 D．3【解答】解:（1+2i)（a+i）＝a﹣2+（2a+1)i的实部与虚部相等，可得：a﹣2＝2a+1,解得a＝﹣3．故选：A．5．【2015年新课标1文科03】已知复数z满足(z﹣1)i＝1+i，则z＝（）A．﹣2﹣i B．﹣2+i C．2﹣i D．2+i【解答】解：由（z﹣1）i＝1+i，得z﹣1，∴z＝2﹣i．故选：C．6．【2014年新课标1文科03】设z i，则|z|＝( ）A．B．C．D．2【解答】解：z i i．故|z|．故选：B．7．【2013年新课标1文科02】（)A．﹣1i B．﹣1i C．1i D．1i【解答】解：1i．故选:B．8．【2012年新课标1文科02】复数z的共轭复数是（) A．2+i B．2﹣i C．﹣1+i D．﹣1﹣i【解答】解:复数z1+i．所以复数的共轭复数为：﹣1﹣i．故选：D．9．【2011年新课标1文科02】复数（)A．2﹣i B．1﹣2i C．﹣2+i D．﹣1+2i【解答】解：2+i故选：C．10．【2010年新课标1文科03】已知复数Z，则|z|＝（) A．B．C．1 D．2【解答】解：化简得Z •••,故|z ｜，故选：B ．考题分析与复习建议本专题考查的知识点为：复数的基本概念（复数的实部、虚部、共轭复数、复数的模等),复数相等的充要条件,考查复数的代数形式的四则运算,重点考查复数的除法运算，与向量结合考查复数及其加法、减法的几何意义等，历年考题主要以选择题题型出现，重点考查的知识点为复数的基本概念(复数的实部、虚部、共轭复数、复数的模等),复数相等的充要条件，考查复数的代数形式的四则运算,重点考查复数的除法运算等，预测明年本考点题目会比较稳定,备考方向以知识点复数的基本概念(复数的实部、虚部、共轭复数、复数的模等)，复数相等的充要条件，考查复数的代数形式的四则运算为重点较佳。

高考数学试题解析分项版专题14 复数、推理与证明理

高考数学试题解析分项版专题14 复数、推理与证明理一、选择题:1. (2011年高考山东卷理科2)复数z=22ii-+(i 为虚数单位)在复平面内对应的点所在象限为（A ）第一象限 (B)第二象限 (C)第三象限 (D)第四象限4.(2011年高考浙江卷理科2)把复数z 的共轭复数记作z ，若1z i =+，i 为虚数单位，则(1)z z +=（A ）3i - （B ）3i + （C ）13i +（D ）3 【答案】 A【解析】(1)1(1)(1)123z z z zz i i i i i +=+=-++-=-+=- 故选A5．(2011年高考广东卷理科1)设复数z 满足(1+i)z=2，其中i 为虚数单位，则Z=（） A ．1+i B ．1-i C ．2+2i D ．2-2i 【解析】B.由题得i i i z -=-=+=1)1(2212所以选B. 6.(2011年高考辽宁卷理科1)a 为正实数，i 为虚数单位，2a ii+=，则a=（）（A ）2 （B ）3 (C)2 (D)1 答案： B 解析：2|1|12a iai a i+=-=+=,a>0,故a=3. 7. (2011年高考全国新课标卷理科1)复数ii212-+的共轭复数是（） A i 53- B i 53 C i - D i ;解析：C ，因为i i 212-+=i ii i =--21)21(，所以，共轭复数为i -，选C点评：本题考查复数的概念和运算，先化简后写出共轭复数即可。

8.(2011年高考江西卷理科1)若iz i1+2=，则复数z = A. i -2- B. i -2+ C. i 2- D. i 2+ 【答案】D 【解析】因为iz i1+2==()()i i i 1+2-=2-，所以复数z =i 2+,选D. 9. (2011年高考江西卷理科7)观察下列各式：55=3125，65=15625，75=78125，…，则20115的末四位数字为A ．3125B ．5625C ．0625D ．8125 【答案】D【解析】观察发现幂指数是奇数的,结果后三位数字为125,故排除B 、C 选项;而201153125>,故A 也不正确, 所以选D.10．(2011年高考江西卷理科10)如右图，一个直径为l 的小圆沿着直径为2的大圆内壁的逆时针方向滚动，M 和N 是小圆的一条固定直径的两个端点．那么，当小圆这样滚过大圆内壁的一周，点M ，N 在大圆内所绘出的图形大致是12．(2011年高考湖北卷理科1)i 为虚数单位，则20111()1i i+-= A.－i B.－1C.iD.1答案：A解析：因为11i i i +=-,故2011201125051()(),1i i i i i i +==⋅=--所以选A.13．(2011年高考陕西卷理科7)设集合{}22||cos sin |,M y y x x x R ==-∈，1{|||2,N x x i=-<}i x R ∈为虚数单位，则MN 为（A ）(0,1) （B ）(0,1] （C ）[0,1) （D ）[0,1] 【答案】C【解析】：由22|cos sin ||cos 2|[0,1]y x x x =-=∈即M =[0,1] 由1||2x i-<2||1211x i x x +=+<-<<即N =(1,1)-[0,1)M N =故选C14.(2011年高考重庆卷理科1)复数2341i i i i++=-（A ）1122i -- (B) 1122i -+ (C) 1122i - (D) 1122i +解析：选B. ()()()234111111112i i i i i i ii i i i -+++--+-===---+。

高考数学真题分项汇编专题11 复数(理科)(解析版)

十年（2014－2023）年高考真题分项汇编—复数目录题型一：复数的有关概念 ........................................................................... 1 题型二：复数的几何意义 ........................................................................... 4 题型三：复数的四则运算 ........................................................................... 7 题型四：复数的其他问题 . (16)题型一：复数的有关概念一、选择题1．(2023年北京卷·第2题)在复平面内，复数z对应的点的坐标是(−，则z 的共轭复数z =( )A 1+ B．1C．1− D．1−【答案】D解析：z在复平面对应的点是(−，根据复数的几何意义，1z =−+，由共轭复数的定义可知，1z =−．故选：D2．(2023年新课标全国Ⅰ卷·第2题)已知1i22iz −=+，则z z −=( )A ．i −B ．iC ．0D ．1【答案】A 解析：因为()()()()1i 1i 1i 2i 1i 22i 21i 1i 42z −−−−====−++−，所以1i 2z =，即i z z −=−．故选：A ．3．(2023年全国乙卷理科·第1题)设252i1i iz +=++，则z = ( )A ．12i −B ．12i +C ．2i −D ．2i +【答案】B解析：由题意可得()252i 2i 2i 2i2i 112i 1i i 11i i 1z +++−=====−++−+−， .则12i z =+．故选：B ．4．(2021年高考浙江卷·第2题)已知a R ∈，()13ai i i +=+，(i 为虚数单位)，则a = ( )A ．1−B ．1C ．3−D ．3【答案】C解析:()1ai i i a a i +=−=−+，利用复数相等的充分必要条件可得：3,3a a −=∴=−,故选C ． 5．(2020年浙江省高考数学试卷·第2题)已知a ∈R ，若a –1+(a –2)i (i 为虚数单位)是实数，则a = ( )A ．1B ．–1C ．2D ．–2【答案】C解析：因为(1)(2)a a i −+−为实数，所以202a a −=∴=，，故选：C6． (2015高考数学新课标2理科·第2题)若a 为实数且(2)(2)4ai a i i +−=−，则a =( )A ．1−B ．0C ．D ．2【答案】B解析：由已知得24(4)4a a i i +−=−，所以240,44a a =−=−，解得0a =，故选B ． 7．(2015高考数学新课标1理科·第1题)设复数z 满足1+z1i z =−，则z = ( )A ．1BC D ．2【答案】A 解析：由11zi z +=−得，11i z i −+=+=(1)(1)(1)(1)i i i i −+−+−=，故|z|=1，故选A ． 8．(2015高考数学湖北理科·第1题)i 为虚数单位，607i的共轭复数．．．．为 ( )A ．iB ．i −C ．1D ．1−【答案】A 解析：i i i i−=⋅=×31514607,所以607i 的共轭复数．．．．为，选A ．9．(2015高考数学广东理科·第2题)若复数(32)z i i =−(i 是虚数单位)，则z =A ．23i −B ．23i +C ．32i +D ．32i −【答案】A解析：因为(32)23z i i i =−=+，所以23z i =−，故选A ． 10．(2017年高考数学新课标Ⅰ卷理科·第3题)设有下面四个命题:若复数满足,则;:若复数满足,则;:若复数满足,则;:若复数,则．其中的真命题为 ( )A ．B ．C ．D ．【答案】 B【解析】令,则由得,所以,正确; 1p z 1z∈R z ∈R 2p z 2z ∈R z ∈R 3p 12,z z 12z z ∈R 12z z =4p z ∈R z ∈R 13,p p 14,p p 23,p p 24,p p (,)z a bi a b =+∈R 2211a bi z a bi a b −==∈++R 0b =z ∈R 1p当时,因为,而知,不正确;由知不正确;对于,因为实数没有虚部,所以它的共轭复数是它本身,也属于实数,故正确,故选B ．11．(2017年高考数学课标Ⅲ卷理科·第2题)设复数z 满足,则 ( )．A ．BCD ．2【答案】 C【解析】法一：由可得，所以，故选C ．法二：由可得，故选C ．【考点】复数的模12．(2016高考数学课标Ⅰ卷理科·第2题)设(1i)1i x y +=+，其中,x y是实数，则i =x y +( )(D)2【答案】B【解析】由()11i x yi +=+可知：1x xi yi +=+，故1x x y == ，解得：11x y = =．所以，x yi +．故选B ．二、填空题1．(2019·浙江·第11题)复数11iz =+(i 为虚数单位)，则z = ．【解析】解法一：由于11i 1i 11i 1i (1i)(1i)222z−−====−++−，．解法二：11iz ==+ 2．(2019·天津·理·第9题)i 是虚数单位，则5i1i−+的值为．解析：解法1：5i (5i)(1i)46i 23i,1i (1i)(1i)25i23i 1i−−−−===−∴−−+++−解法2：5i5i 1i 1i−−==++3．(2019·江苏·第2题)已知复数()()21a i i ++的实部为0，其中i 为虚数单位，则实数a 的值是______．z i =221z i ==−∈R i ∉R 2p 1212,1z z i z z R ==⋅=−∈3p 4p 4p ()1i 2i z +=z =12()12i z i +=()2111iz i i i i==−=++z ()12i z i +=()1212i z i i z +=⇒+=z ⇒==【答案】2【解析】因为()()21(2)(2)a i i a a i ++=−++的实部为0，2a =.4．(2018年高考数学江苏卷·第2题)若复数z 满足i 12i z ⋅=+，其中i 是虚数单位，则z 的实部为．【答案】2解析：因为i 12i z ⋅=+，则122iz i i+==−，则z 的实部为2． 5．(2018年高考数学上海·第5题)已知复数z 满足(1i)17i z +=−(i 是虚数单位)，则z = ．【答案】5解析：17i17i 17i ,51i 1i 1iz z −−−=∴===+++． 6．(2017年高考数学江苏文理科·第2题)已知复数其中i 是虚数单位,则的模是________．【答案】．解析:,【考点】复数的模7．(2016高考数学天津理科·第9题)已知,,a b R i ∈是虚数单位，若(1)(1)i bi a +−=，则ab的值为_____________．【答案】2解析：()()11i bi a +−=，1b i bi a ++−=，∴1,10b a b +=−=，12b a = = ，2ab=8．(2016高考数学上海理科·第2题)设iiZ 23+=，期中i 为虚数单位，则Im z =______________________．【答案】3−解析：32i23,Im z=3iz i +==−−．9．(2020江苏高考·第2题)已知i 是虚数单位，则复数(1i)(2i)z =+−的实部是_____．【答案】3【解析】复数()()12z i i =+−2223z i i i i ∴=−+−=+,∴复数的实部为3．故答案为：3． 10．(2019·上海·第2题)已知C z ∈且满足i z=−51，求=z ________. 【答案】512626i − 【解析】i z+=51，i i i i i z 261265)5)(5(551−=−+−=+=. 题型二：复数的几何意义一、选择题(1i)(12i),z =++z (1)(12)112z i i i i =++=++=1．(2021年新高考全国Ⅱ卷·第1题)复数2i13i−−在复平面内对应的点所在的象限为 ( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】A 解析:()()2i 13i 2i 55i 1i13i10102−+−++===−，所以该复数对应的点为11,22 ，该点在第一象限，故选A ． 2．(2022高考北京卷·第2题)若复数z 满足i 34i z ⋅=−，则z =( )A ．1B ．5C ．7D ．25【答案】B 解析:由题意有()()()34i i 34i 43i i i i z −−−===−−⋅−，故|5|z =．故选,B ．3．(2019·全国Ⅱ·理·第2题)设32z i =−+，则在复平面内z 对应的点位于( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】C【解析】∵32z i =−+，∴32z i =−−，对应坐标()3,2−−，是第三象限． 4．(2023年新课标全国Ⅱ卷·第1题)在复平面内，()()13i 3i +−对应的点位于( )．A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】A解析：因为()()213i 3i 38i 3i 68i +−=+−=+，则所求复数对应的点为()6,8，位于第一象限．故选：A ．5．(2018年高考数学北京(理)·第2题)在复平面内，复数11i−的共轭复数对应的点位于 ( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】D 解析：11i 11i 1i (1i)(1+i)22z +===+−− ，则11i 22z =− ，其对应的点为11,22−，位于第四象限．6．(2014高考数学重庆理科·第1题)复平面内表示复数)21(i i −的点位于( ) A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】A解析：根据复数的乘法分配律可得，因此该复数在复平面内所对应的坐标为，它在第一象限。

复数高考题分类总汇编

复数高考真题分类汇编题型一复数的概念及分类1．（2015·卷）i 是虚数单位，若复数))(21(i a i +-是纯虚数，则=a ． 2．（2016·卷）复数)3)(21(i i z -+=，i 为虚数单位，则z 的实部是．3．（2016·卷）设iiz 23+=，其中i 为虚数单位，则其虚部为． 4．（2017·卷）已知R a ∈，i 为虚数单位，若i ia +-2为实数，则a 的值为．5．（2017·全国卷）设有下面四个命题：:1p 若复数满足R z∈1，则R z ∈；:2p 若复数满足R z ∈2，则R z ∈；:3p 若复数1z 、2z 满足R z z ∈21，则21z z =； :4p 若复数R z ∈，则R z ∈；其中真命题为（） A ．1p ，3pB ．1p ，4pC ．2p ，3pD ．2p ，4p题型二与共轭复数、复数相等有关的问题1．（2013·卷）复数满足5)2)(3(=--i z （i 为虚数单位），则z 的共轭复数为（）A ．i +2B ．i -2C ．i +5D ．i -52．（2013·卷）设i 是虚数单位，若z i z z 22=+⋅，则=z （）A ．i +1B ．i -1C ．i +-1D ．i --13．（2013·卷）已知复数的共轭复数i z 21+=（i 为虚数单位），则z 在复平面对应的点位于（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限4．（2013·卷）在复平面，复数iiz +=12（i 为虚数单位）的共轭复数对应的点位于（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限5．（2013·卷）如图，在复平面，点A 表示复数，则图中表示的共轭复数的点是_____6．（2013·卷）已知R b a ∈、，i 是虚数单位，若bi i i a =++)1)((，则=+bi a ．7．（2014·卷）原命题为“若21,z z 互为共轭复数，则21z z =”，关于逆命题，否命题，逆否命题真假性的判断依次如下，正确的是（）A ．真假真B ．假假真C ．真真假D ．假假假8．（2014·卷）已知R b a ∈、，i 是虚数单位，若i a -与bi +2互为共轭复数，则=+2)(bi a （）A ．i 45-B ．i 45+C ． i 43-D ．i 43+9．（2014·卷）z 是z 的共轭复数．若2=+z z ，2)(=-i z z ，i 为虚数单位，则=z （）A ．i +1B ．i --1C ．i +-1D ． i -110．（2014·卷）设i 是虚数单位，z 表示复数z 的共轭复数．若i z +=1，则=⋅+z i iz （）A ．2-B ．i 2-C ．2D ．i 211．（2014·全国卷）设iiz +=310，则z 的共轭复数为（） A ．i 31+-B ．i 31--C ．i 31+D ．i 31-12．（2014·卷）复数i i z )23(-=的共轭复数为（）A ．i 32--B ．i 32+-C ．i 32-D ． i 32+13．（2015·卷）若复数)23(i i z -=（i 是虚数单位），则=z （）A ．i 32-B ．i 32+C ．i 23+D ．i 23-14．（2015·卷）i 为虚数单位，607i 的共轭复数为（）A ．iB ．i -C ．1D ．1-15．（2015·全国卷Ⅱ）若a 为实数，且i i a ai 4)2)(2(-=-+，则=a （）A ．1-B ．0C ． 1D ． 216．（2015·卷）若复数满足i iz=-1，其中i 为虚数单位，则=z （） A ．i -1B ．i +1C ．i --1D ．i +-117．（2016·卷）若复数满足i z z 232-=+，其中i 为虚数单位，则=z （）A ．i 21+B ．i 21-C ．i 21+-D ．i 21--18．（2016·卷）已知R b a ∈、，i 是虚数单位，若a bi i =-+)1)(1(，则ba的值为______．19．（2017·卷）已知R a ∈，i 是虚数单位，若i a z 3+=，4=⋅z z ，则=a （）A ．1或1-B ．3或3-C ．3-D ．320．（2017·卷）已知R b a ∈、，i bi a 43)(2+=+（i 是虚数单位），则=+22b a ______，=ab ________．题型三复数的模 1．（2013·卷）复数11-=i z 的模为（） A ．21B ．22 C ．2 D ．22．（2013·卷）设2)2(i z -=（i 为虚数单位），则复数z 的模为______． 3．（2013·卷）设21z z 、是复数，则下列命题中的假命题是（）A ．若021=-z z ，则21z z =B ．若21z z =，则21z z =C ．若21z z =，则2211z z z z ⋅=⋅D ．若21z z =，则2221z z =4．（2013·卷）已知复数iiz 215+=（i 是虚数单位），则=z _____． 5．（2015·全国卷）设复数z 满足i zz=-+11，则=z （）A ．1B ．2C ．3D ．26．（2015·卷）设复数满足i z 432+=（i 是虚数单位），则z 的模为_____． 7．（2015·卷）设复数bi a +（R b a ∈,）的模为3，则=-+))((bi a bi a ____． 8．（2016·全国卷）设yi x i +=+1)1(，其中y x 、是实数，则=+yi x （）A ．1B ．2C ．3D ．29．（2017·卷）已知复数)21)(1(i i z ++=，曲终i 是虚数单位，则z 的模是______． 10．（2017·全国卷Ⅲ）设复数z 满足i z i 2)1(=+，则=z （）A ．21B ．22 C ．2 D ．2题型四复数的四则运算1．（2013·全国卷）设复数满足i z i 2)1(=-，则=z （）A ．i +-1B ．i --1C ．i +1D ．i -12．（2013·卷）已知i 是虚数单位，则=-+-)2)(1(i i （）A ．i +-3B ．i 31+-C ．i 33+-D ．i +-13．（2013·卷）若复数满足i z i 42+=⋅，则在复平面，z 对应的点的坐标是（）A ．)4,2(B ．)4,2(-C ．)2,4(-D ．)2,4(4．（2014·卷）复数=-+2)11(ii ______． 5．（2014·卷）已知复数2)25(i z -=（i 为虚数单位），则z 的实部为____．6．（2014·卷）复数=+-ii122______． 7．（2014·卷）i 是虚数单位，复数=++ii437（）A ．i -1B ．i +-1C ．i 25312517+D ．i 725717+-8．（2014·全国卷）=-+23)1()1(i i （） A ．i +1 B ．i -1 C ．i +-1 D ．i --19．（2014·卷）设复数满足5)2)(2(=--i i z ，则=z （）A ．i 32+B ．i 32-C ．i 23+D ．i 23-10．（2014·卷）i 为虚数单位，则=+-2)11(ii （）A ．1-B ．1C ．i -D ．i11．（2014·卷）满足i ziz =+（i 是虚数单位）的复数=z （） A ．i2121+B ．i 2121-C ．i 2121+-D ．i 2121--12．（2014·卷）已知复数满足25)43(=+z i ，则=z （）A ．i 43+-B ．i 43--C ．i 43+D ．i 43-13．（2015·卷）复数=-)2(i i （）A ．i 21+B ．i 21-C ．i 21+-D ．i 21--14．（2015·卷）若集合{}432,,,i i i i A =（i 是虚数单位），{}1,1-=B ，则=B A （）A ．{}1-B ．{}1C ．{}1,1-D ．Ø15．（2015·卷）已知i zi +=-1)1(2（i 为虚数单位），则复数=z （） A ．i +1 B ．i -1 C ．i +-1 D ．i --116．（2015·卷）设i 是虚数单位，则复数=-ii 23（） A ．i -B ．i 3-C ．iD ．i 317．（2016·全国卷Ⅲ）若i z 21+=，则=-14z z i（） A ．1B ．1-C ．iD ．i -18．（2016·卷）设i 为虚数单位，则6)(i x +的展开式中含4x 的项为（）A ．415x -B ．415xC ．420ix -D ．420ix19．（2017全国卷Ⅱ）=++ii13（） A ．i 21+B ．i 21-C ．i +2D ．i -2题型五复数的几何意义1．（2013·卷）复数)1(i i z +=（i 为虚数单位）在复平面上对应的点位于（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限3．（2013·卷）已知复数的共轭复数i z 21+=（i 为虚数单位），则z 在复平面对应的点位于（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限4．（2013·卷）在复平面，复数iiz +=12（i 为虚数单位）的共轭复数对应的点位于（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限5．（2013·卷）如图，在复平面，点A 表示复数，则图中表示的共轭复数的点是_____5．（2014·全国卷Ⅱ）设复数21,z z 在复平面的对应点关于虚轴对称，i z +=21，则=21z z （）A ．5-B ．5C ．i +-4D ．i --46．（2014·卷）在复平面表示复数)21(i i -的点位于（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限7．（2015·卷）设i 是虚数单位，则复数ii-12在复平面所对应的点位于（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限8．（2016·卷）设R a ∈，若复数))(1(i a i ++在复平面对应的点位于实轴上，则=a ________．9．（2017·卷）若复数))(1(i a i +-在复平面对应的点在第二象限，则实数a 的取值围是（）A ．)1,(-∞B ．)1,(--∞C ．),1(+∞D ．),1(+∞-。

2011年—2017年新课标全国高考卷理科数学分类汇编——11.复数及其运算

11．复数及其运算一、选择题【2017，3】设有下面四个命题1:p 若复数z 满足1z∈R ，则z ∈R ；2:p 若复数z 满足2z ∈R ，则z ∈R ； 3:p 若复数12,z z 满足12z z ∈R ，则12z z =；4:p 若复数z ∈R ，则z ∈R ．其中的真命题为（）A ．13,p pB ．14,p pC ．23,p pD ．24,p p【2016，2】设yi x i +=+1)1(，其中y x ,是实数，则=+yi x （）A ．1B ．2C ．3D ．2【2015，1】设复数z 满足1i 1z z+=-，则||z =（）A ．1BCD ．2【2014，2）】32(1)(1)i i +-=（） A ．1i + B ．1i - C ．1i -+ D ．1i --【2013，2】若复数z 满足(3－4i)z ＝|4＋3i|，则z 的虚部为( )．A ．－4B ．45-C ．4D ．45 【2012，3】下面是关于复数21z i =-+的四个命题： 1p ：||2z =；2p ：22z i =；3p ：z 的共轭复数为1i +；4p ：z 的虚部为1-．其中的真命题为（）A ．2p ，3pB ．1p ，2pC ．2p ，4pD ．3p ，4p 【2011，1】复数212i i+-的共轭复数是（） A ．35i - B ．35i C ．i - D ．i11．复数及其运算（解析版）一、选择题【2017，3】设有下面四个命题1:p 若复数z 满足1z∈R ，则z ∈R ；2:p 若复数z 满足2z ∈R ，则z ∈R ； 3:p 若复数12,z z 满足12z z ∈R ，则12z z =；4:p 若复数z ∈R ，则z ∈R ．其中的真命题为（）A ．13,p pB ．14,p pC ．23,p pD ．24,p p【解析】1:p 设z a bi =+，则2211a bi z a bi a b -==∈++R ，得到0b =，所以z ∈R ．故1P 正确； 2:p 若z =-21，满足2z ∈R ，而z i =，不满足2z ∈R ，故2p 不正确；3:p 若1z 1=，2z 2=，则12z z 2=，满足12z z ∈R ，而它们实部不相等，不是共轭复数，故3p 不正确； 4:p 实数没有虚部，所以它的共轭复数是它本身，也属于实数，故4p 正确；【2016，2】设yi x i +=+1)1(，其中y x ,是实数，则=+yi x （）A ．1B ．2C ．3D ．2【解析】由()11i x yi +=+可知：1x xi yi +=+，故1x x y =⎧⎨=⎩，解得：11x y =⎧⎨=⎩．所以，x yi += 故选B ．【2015，1】设复数z 满足1i 1z z+=-，则||z =（）A ．1BCD ．2 解析：由1i 1z z +=-得1i(1)z z +=-，即1i 1iz -+=+，2(1i)(1i)(1i)i (1i)(1i)2z -+---===+-，||z =1，选A ．【2014，2）】32(1)(1)i i +-=（） A .1i + B .1i - C .1i -+ D .1i -- 【解析】∵32(1)(1)i i +-=2(1)12i i i i +=---，选D. 【2013，2】若复数z 满足(3－4i)z ＝|4＋3i|，则z 的虚部为( )．A ．－4B ．45-C ．4D ．45 解析：∵(3－4i)z ＝|4＋3i|，∴55(34i)34i 34i (34i)(34i)55z +===+--+. 故z 的虚部为45，选D.【2012，3】下面是关于复数21z i=-+的四个命题： 1p ：||2z =；2p ：22z i =；3p ：z 的共轭复数为1i +；4p ：z 的虚部为1-．其中的真命题为（）A ．2p ，3pB ．1p ，2pC ．2p ，4pD ．3p ，4p【解析】因为22(1)11(1)(1)i z i i i i --===---+-+--，所以||z =22(1)2z i i =--=， z 的共轭复数为1i -+，z 的虚部为1-，所以2p ，4p 为真命题，故选择C ．【2011，1】复数212i i+-的共轭复数是（） A ．35i - B ．35i C ．i - D ．i 解析：212i i +-=(2)(12),5i i i ++=共轭复数为C。

2011年高考数学试题分类汇编复数.doc

十二、复数1．（重庆理1）复数2341i i i i ++=-A ．1122i --B ．1122i -+C ．1122i -D ．1122i +【答案】C2．（浙江理）把复数z 的共轭复数记作z ，i 为虚数单位，若1,(1)z i z z =++⋅r则=A ．3-iB ．3+iC ．1+3iD ．3【答案】A3．（天津理1）i 是虚数单位，复数131ii --=A ．2i +B ．2i -C ．12i -+D ．12i --【答案】B4.（四川理2）复数1i i -+=A ．2i -B ．12iC ．0D ．2i【答案】A【解析】12i i i i i -+=--=-5.（山东理2）复数z=22ii -+（i 为虚数单位）在复平面内对应的点所在象限为A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】D6.（全国新课标理1）（1）复数212ii +=-（A ）35i - （B ） 35i （C ）i - （D ）i【答案】C7.（全国大纲理1）复数1z i =+，z 为z 的共轭复数，则1zz z --=A ．2i -B ．i -C ．iD ．2i【答案】B8.（辽宁理1）a 为正实数，i 为虚数单位，2=+i ia ，则=a（A ）2 （B（C（D ）1【答案】B9.（江西理1）若iz i 1+2=，则复数z =A ． i -2-B ． i -2+C ． i 2-D ． i 2+【答案】D10.（湖南理1）若,a b R ∈，i 为虚数单位，且()a i i b i +=+则A ．1a =，1b =B ．1,1a b =-=C ．1,1a b =-=-D ．1,1a b ==-【答案】D11.（湖北理1）i 为虚数单位，则201111i i +⎛⎫ ⎪-⎝⎭= A ．- i B ．-1 C ．iD ．1 【答案】A12.（福建理1）i 是虚数单位，若集合S=}{1.0.1-，则A ．i S ∈B ．2i S ∈C ． 3i S ∈D ．2S i ∈ 【答案】B13.（广东理1）设复数z 满足()12i z +=，其中i 为虚数单位，则z = A ．1i +B ．1i -C ．22i +D ．22i - 【答案】B 14.（北京理2）复数212i i -=+A ．iB ．-iC ．4355i --D ．4355i -+【答案】A 15.（安徽理1）设 i 是虚数单位，复数aii 1+2-为纯虚数，则实数a 为（A ）2 （B ） -2 （C ） 1-2（D ） 12【答案】A 16.（江苏3）设复数ｚ满足i z i 23)1(+-=+（i 是虚数单位），则z 的实部是_________【答案】117.（上海理19）已知复数1z 满足1(2)(1)1z i i -+=-（i 为虚数单位），复数2z 的虚部为2，12z z ⋅是实数，求2z 。

十年真题(2010-2019)高考数学(理)分类汇编专题02 复数(新课标Ⅰ卷)(解析版)

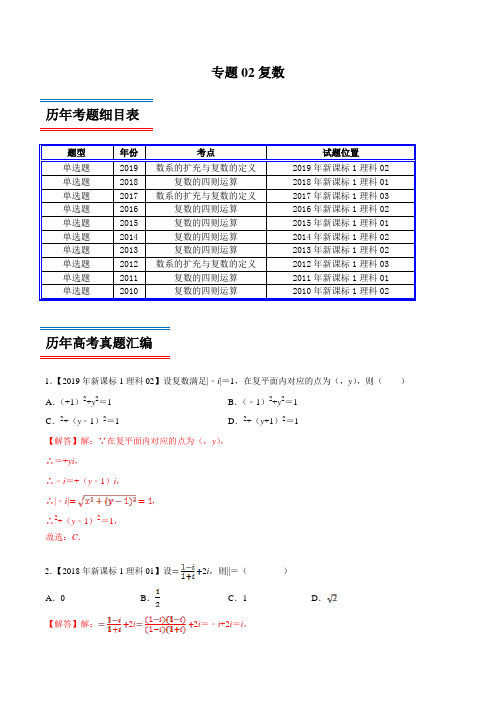
专题02复数历年考题细目表题型年份考点试题位置单选题2019 数系的扩充与复数的定义2019年新课标1理科02 单选题2018 复数的四则运算2018年新课标1理科01 单选题2017 数系的扩充与复数的定义2017年新课标1理科03 单选题2016 复数的四则运算2016年新课标1理科02 单选题2015 复数的四则运算2015年新课标1理科01 单选题2014 复数的四则运算2014年新课标1理科02 单选题2013 复数的四则运算2013年新课标1理科02 单选题2012 数系的扩充与复数的定义2012年新课标1理科03 单选题2011 复数的四则运算2011年新课标1理科01 单选题2010 复数的四则运算2010年新课标1理科02历年高考真题汇编1．【2019年新课标1理科02】设复数满足|﹣i|＝1，在复平面内对应的点为（，y），则（）A．（+1）2+y2＝1 B．（﹣1）2+y2＝1C．2+（y﹣1）2＝1 D．2+（y+1）2＝1【解答】解：∵在复平面内对应的点为（，y），∴＝+yi，∴﹣i＝+（y﹣1）i，∴|﹣i|，∴2+（y﹣1）2＝1，故选：C．2．【2018年新课标1理科01】设2i，则||＝（）A．0 B．C．1 D．【解答】解：2i2i＝﹣i+2i＝i，故选：C．3．【2017年新课标1理科03】设有下面四个命题p1：若复数满足∈R，则∈R；p2：若复数满足2∈R，则∈R；p3：若复数1，2满足12∈R，则1；p4：若复数∈R，则∈R．其中的真命题为（）A．p1，p3B．p1，p4C．p2，p3D．p2，p4【解答】解：若复数满足∈R，则∈R，故命题p1为真命题；p2：复数＝i满足2＝﹣1∈R，则∉R，故命题p2为假命题；p3：若复数1＝i，2＝2i满足12∈R，但1，故命题p3为假命题；p4：若复数∈R，则∈R，故命题p4为真命题．故选：B．4．【2016年新课标1理科02】设（1+i）＝1+yi，其中，y是实数，则|+yi|＝（）A．1 B．C．D．2【解答】解：∵（1+i）＝1+yi，∴+i＝1+yi，即，解得，即|+yi|＝|1+i|，故选：B．5．【2015年新课标1理科01】设复数满足i，则||＝（）A．1 B．C．D．2【解答】解：∵复数满足i，∴1+＝i﹣i，∴（1+i）＝i﹣1，∴i，故选：A．6．【2014年新课标1理科02】（）A．1+i B．1﹣i C．﹣1+i D．﹣1﹣i【解答】解：（1+i）＝﹣1﹣i，故选：D．7．【2013年新课标1理科02】若复数满足（3﹣4i）＝|4+3i|，则的虚部为（）A．﹣4 B．C．4 D．【解答】解：∵复数满足（3﹣4i）＝|4+3i|，∴i，故的虚部等于，故选：D．8．【2012年新课标1理科03】下面是关于复数的四个命题：其中的真命题为（），p1：||＝2，p2：2＝2i，p3：的共轭复数为1+i，p4：的虚部为﹣1．A．p2，p3B．p1，p2C．p2，p4D．p3，p4【解答】解：∵1﹣i，∴，，p3：的共轭复数为﹣1+i，p4：的虚部为﹣1，故选：C．9．【2011年新课标1理科01】复数的共轭复数是（）A．B．C．﹣i D．i【解答】解：复数i，它的共轭复数为：﹣i．故选：C．10．【2010年新课标1理科02】已知复数，是的共轭复数，则（）A．B．C．1 D．2【解答】解：由可得．另解：故选：A．考题分析与复习建议本专题考查的知识点为：复数的基本概念(复数的实部、虚部、共轭复数、复数的模等)，复数相等的充要条件，考查复数的代数形式的四则运算，重点考查复数的除法运算，与向量结合考查复数及其加法、减法的几何意义等，历年考题主要以选择题题型出现，重点考查的知识点为复数的基本概念(复数的实部、虚部、共轭复数、复数的模等)，复数相等的充要条件，考查复数的代数形式的四则运算，重点考查复数的除法运算等，预测明年本考点题目会比较稳定，备考方向以知识点复数的基本概念(复数的实部、虚部、共轭复数、复数的模等)，复数相等的充要条件，考查复数的代数形式的四则运算为重点较佳.最新高考模拟试题1．复数52iz =-在复平面上的对应点位于（） A ．第一象限 B ．第二象限C ．第三象限D ．第四象限【答案】A 【解析】()()()52i 52i 2i 2i 2i z +===+--+，在复平面上的对应点为()2,1，位于第一象限. 故选A.2．设i z a b =+（a ，b ∈R ，i 是虚数单位），且22i z =-，则有（） A ．1a b +=- B ．1a b -=- C ．0a b -= D ．0a b +=【答案】D 【解析】因为2222()()22z a bi a b abi i =+=-+=-，所以220a b -=，22ab =-，解得11a b =⎧⎨=-⎩或11a b =-⎧⎨=⎩，所以0a b +=，故选D.3．若复数1i1ia z +=+为纯虚数，则实数a 的值为( ) A ．1 B ．1-C ．0D ．2【答案】B 【解析】()()()()()11111i 1i 112ai i a a ia z i i +-++-+===++- 故10,10a a +=-≠ ，解1a =- 故选：B4．复数i （1+i ）的虚部为（）A B ．1C ．0D ．1-【答案】B 【解析】∵i （1+i ）=-1+i ，∴i （1+i ）的虚部为1．故选：B ．5．已知复数11z i =-+，复数2z 满足122z z =-，则2z = ( )A ．2B CD ．10【答案】B 【解析】由题得222(1)2(1)11(1)(1)2i i z i i i i -------====+-+-+--，所以2z 故选：B6．已知复数312i z i=+，则复数的实部为（）A ．25-B ．25i -C ．15-D ．15i -【答案】A 【解析】解：∵3(12)2112(12)(12)55i i i z i i i i --===--++-， ∴复数的实部为25-．故选A ． 7．复数122ii-=+（） A ．1i - B ．i -C ．iD ．1i +【答案】B 【解析】12(12)(2)2422(2)(2)5i i i i i i i i i ------===-++-. 故选B8．已知i 为虚数单位,复数满足：()z 12i i +=-，则在复平面上复数对应的点位于（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】D 【解析】因为2(2)(1)131312222i i i i z i i ----====-+，所以复平面上复数对应的点为13(,)22-，位于第四象限，故选D .9．设复数z a i =+，z 是其共轭复数，若3455z i z =+，则实数a =（） A ．4 B ．3C ．2D ．1【答案】C 【解析】解 z a i =+Qz a i ∴=- 343443++2555555z a a i a i i a z ⎛⎫∴=+⇒+=-⇒= ⎪⎝⎭10．已知i 是虚数单位，复数满足2(1)1i i z-=+，则z =（）A B ．2C ．1D 【答案】A 【解析】22(1)(1)22(1)1(1)111(1)(1)i i i i i i z i i i z i i i i ----⋅-=+⇒====--=--+++⋅-，所以1z i =--==，故本题选A.11．复数()()21z i i =+-，其中i 为虚数单位，则的实部是（） A ．-1 B ．1C ．2D ．3【答案】D 【解析】解：∴()()212213z i i i i i =+-=-++=-，∴的实部是3 故选：D ．12．已知复数(1)1z i i -=+，则复数z =（） A ．2i + B ．2i -C ．iD ．i -【答案】C 【解析】由题意，复数(1)1z i i -=+，则()()()()11121112i i i iz i i i i +++====--+，故选C. 13．已知i 为虚数单位，若1(,)1a bi a b R i=+∈-，则b a =（） A ．1 BCD ．2【答案】C 【解析】 i 为虚数单位，若1(,)1a bi a b R i =+∈-，1112i a bi i +==+- 根据复数相等得到1212a b ⎧=⎪⎪⎨⎪=⎪⎩.121()22b a == 故答案为：C.14．已知复数满足2(1i)(3i)z +=+，则||z =（） ABC．D ．8【答案】C 【解析】∵2(1)(3)z i i +=+，∴2(3)86(86)(1)(43)(1)711(1)(1)i i i i z i i i i i i i +++-====+-=-+++-，∴||z ===故选C ．15．已知i 是虚数单位，则复数11i i -+在复平面上所对应的点的坐标为（） A ．()0,1 B ．()1,0-C ．()1,0D ．()0,1-【答案】A 【解析】 ∵()()()()111111i i i i i i i ---==++-，∴该复数在复平面上对应的点的坐标为()0,1. 故选A.16．若复数满足(1i)|1|z +=+，则在复平面内的共轭复数对应的点位于（） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限【答案】A 【解析】由题得22(1)1(1)(1)(1i)i z i i i -===-++-，所以1z i =+，所以在复平面内的共轭复数对应的点为（1,1），在第一象限. 故选：A17．已知复数满足12iz i =+，则的虚部是（） A ．1- B ．i -C ．2D ．2i【答案】A 【解析】因为12iz i =+所以221222i i i z i i i++===-所以虚部为1- 所以选A 18．已知31iz i-=-（其中i 为虚数单位），则z 的虚部为( )A ．i -B ．1-C ．1D ．2【答案】B 【解析】因为3(3)(1)4221(1)(1)2i i i iz i i i i --++====+--+, 所以2z i =-，故z 的虚部为1-，故选B.19．复数2(1)41i z i -+=+的虚部为( )A ．1-B ．3-C ．1D ．2【答案】B 【解析】()()2421(1)44213112i i i i z i i i ---+-====-++ 所以的虚部为3- 故选B 项.20．已知复数()11z ai a R =+∈，212z i =+（i 为虚数单位），若12z z 为纯虚数，则a =（） A ．2- B ．2C ．12-D ．12【答案】C 【解析】∵()12112z ai a R z i =+∈=+，，∴121(1)(12)12212(12)(12)55z ai ai i a a i z i i i ++-+-===+++-， ∵12z z 为纯虚数， ∴12020a a +=⎧⎨-≠⎩，解得12a =-．故选：C ．21．设复数满足2i i z +=，则z =（）A ．1B C ．3 D ．5【答案】B【解析】 2i i z+=Q , 221i z i i+∴==+ 22112i i i=+=-,z ∴== B.22．已知复数1i z i =-，则z +在复平面内对应的点位于（） A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】A【解析】∵ ()()()11111122i i i z i i i i +===-+--+，∴ 11222z i +=+，∴z +在复平面内对应的点的坐标为11,22⎫⎪⎪⎝⎭，位于第一象限．故选：A ．23．复数满足(1)2z i i -=，则复数z =（）A ．1i -B ．12i +C ．1i +D ．1i -- 【答案】D【解析】由题意得：()()()2121111i i i z i i i i +===-+--+ 1z i ∴=-- 本题正确选项：D24．若复数2(1)z m m m i =+++是纯虚数，其中m 是实数，则1z =（） A ．i B ．i - C ．2i D ．2i -【答案】B【解析】复数＝m （m +1）+（m +1）i 是纯虚数，故m （m +1）＝0且（m +1）≠0，解得m ＝0，故＝i ，故111iz i i i ⋅===-⋅i ．故选：B ．25．设i 为虚数单位，则复数22iz i -=+的共扼复数z =（）A ．3455i + B ．3455i -C ．3455i -+ D ．3455i --【答案】A【解析】解：22i(2i)34i 2i (2i)(2i)55z --===-++-Q ，3455z i ∴=+故选：A ．26．已知复数1z 、2z在复平面内对应的点关于虚轴对称，11z =，则12z z =( )A ．2 BCD ．1【答案】D【解析】由题意，复数1z 、2z在复平面内对应的点关于虚轴对称，11z =，则21z =-，所以12212z z ====，故选D.27．已知复数1＝1+2i ，2＝l ﹣i ，则12z z =（）A ．13i 22-- B ．13i 22-+ C ．13i 22- D ．13i 22+【答案】B【解析】∵1212,1z i z i =+=-， ∴1212(12)(1)131(1)(1)22z ii i i z i i i +++===-+--+．故选：B ．28．在复平面内，复数(2i)z -对应的点位于第二象限，则复数可取（）A ．2B ．-1C ．iD ．2i +【答案】B【解析】不妨设(),z a bi a b R =+∈，则()()()()()2222i z i a bi a b b a i -=-+=++-，结合题意可知：20,20a b b a +<->，逐一考查所给的选项：对于选项A ：24,22a b b a +=-=-，不合题意；对于选项B ：22,21a b b a +=--=，符合题意；对于选项C ：21,22a b b a +=-=，不合题意；对于选项D ：25,20a b b a +=-=，不合题意；故选：B .29．已知i 为虚数单位，则复数3(1)iz i i +=-的虚部为（）A ．1B ．2C ．1-D ．2-【答案】C【解析】因为3(3)(1)122(1)2i i i ii i i i i ++++===--，所以的虚部为1-.30．已知复数(i)(1i)z a =+-（i 为虚数单位）在复平面内对应的点在直线2y x =上，则实数a 的值为（）A ．0B ．1-C ．1D ．13-【答案】D【解析】因为(i)(1i)1(1)z a a a i =+-=++-，对应的点为(1,1)a a +-，因为点在直线2y x =上，所以12(1)a a -=+，解得13a =-. 故选D.。

(含详解)2011-2017新课标高考数学复数分类汇编

高考数学专题《复数》习题含答案解析

最新—2017高考全国卷ⅰ文科数学复数及其运算汇编

高考数学试题分类汇编 专题复数 理

2011—2020年新课标全国卷高考数学试卷分类汇编—复数(含答案)

高中数学—复数的历届高考试题解析.doc

2011-2017年新课标全国卷2理科数学试题分类汇编——2.复数

高考数学真题题型分类解析专题专题02 复数

近五年(2017-2021)高考数学真题分类汇编03 复数

2011-2019高考数学复数分类汇编

(2010-2019)高考数学真题分类汇编专题02复数文(含解析)

高考数学试题解析分项版 专题14 复数、推理与证明 理

高考数学真题分项汇编专题11 复数(理科)(解析版)

复数高考题分类总汇编

2011年—2017年新课标全国高考卷理科数学分类汇编——11.复数及其运算

2011年高考数学试题分类汇编 复数.doc

十年真题(2010-2019)高考数学(理)分类汇编专题02 复数(新课标Ⅰ卷)(解析版)

2011-2019高考数学复数分类汇编

高考数学试题分类汇编专题复数理

高考数学试题解析分项版专题14 复数、推理与证明理

2011年高考数学试题分类汇编复数.doc