排序综合

合集下载

综合排序规则

综合排序规则
综合排序规则是一种排序算法，它可以按照各种因素综合进行排序。

在实际应用中，我们经常需要按照多个因素进行排序，比如按照价格、销量、评价等多个维度对商品进行排序。

这时，我们可以使用综合排序规则，将这些因素按照一定的权重进行加权求和，得到一个综合得分，然后根据综合得分进行排序。

综合排序规则的权重分配需要根据实际情况进行调整。

比如，在购物网站中，价格可能是最重要的因素，因此权重应该设置得比较高；而在旅游网站中，评价可能更加重要，因此评价的权重应该设置得比较高。

综合排序规则有多种实现方式，比如TOPSIS算法、熵权法、灰色关联度等。

这些方法各有特点，可以根据具体情况进行选择。

综合排序规则在实际应用中有着广泛的应用，比如在电商、旅游、招聘等领域中都可以使用。

它可以帮助用户快速找到符合自己需求的最佳选项，提高用户体验。

同时，也可以帮助商家和平台优化自己的产品和服务，提升业务效益。

- 1 -。

排名排序标准

排名排序标准是指根据一定的评价指标对事物进行排序的依据和准则。

不同的排名标准适用于不同的场合，其目的是为了客观、公正、准确地反映事物的优劣程度。

以下是几种常见的排名排序标准：
1. 综合排名：根据多个评价指标进行综合评价，以得分高低进行排序。

这种排名标准比较全面，但可能存在权重分配不合理的问题。

2. 单一指标排名：只根据一个或少数几个指标进行排序，如价格、质量、性能等。

这种排名标准比较简单明了，但可能存在忽略其他重要因素的问题。

3. 专家评审排名：由专家根据经验、知识和判断进行排序，具有一定的主观性。

这种排名标准可以避免完全依赖量化指标的片面性，但也可能存在专家主观判断差异的问题。

4. 用户评价排名：基于用户对产品的评价数据进行排序，如评分、评论等。

这种排名标准可以反映用户对产品的真实感受，但也可能存在用户评价不客观、不公正等问题。

在实际应用中，排名排序标准需要根据具体情况进行调整和优化。

例如，在高校排名中，通常会考虑科研实力、师资力量、学科建设等多个指标，同时也会考虑不同指标的权重和加权方法。

在产品评价中，可能会根据用户反馈、评分、评论等多个因素进行排序，同时也会考虑不同因素的权重和加权方法。

此外，排名排序标准还需要考虑公平性和客观性。

排名排序标准应该尽可能客观地反映事物的优劣程度，避免人为因素和主观偏见的影响。

同时，排名排序标准也应该尽可能公平公正，避免不正当手段和利益交换等问题。

总之，排名排序标准需要根据具体情况进行调整和优化，以确保客观、公正、准确地反映事物的优劣程度。

湖北省2024年美术学类、设计学类综合排序成绩一分一段统计表

568 567 566 565 564 563 562 561
分数
560 559 558 557 556 555 554 553 552 551 550 549 548 547 546 545 544 543 542 541
146 82 156 73 154 91 141 114
人数 141 110 143 102 133 94 156 99 144 114 144 105 143 95 137 109 163 101 157 87
累计人数 2208 2241
31 31 43 28 43 30 37 20 41 31 56 26 50 35 59 34 50 46 65 32 67 34 76 40 52 48
人数 69 33
1074 1105 1148 1176 1219 1249 1286 1306 1347 1378 1434 1460 1510 1545 1604 1638 1688 1734 1799 1831 1898 1932 2008 2048 2100 2148 高职高专累计人数 2217 2250
63 高职高专
累计人数 69 74 76 77 84 88 95 100 103 105 111 113 122 125 131 132 144 148 161 169
710 709 708 707 706 705 704 703 702
701 700 699 698 697
分数
696 695 694 693 692 691 690 689 688 687 686 685 684 683
湖北省2024年美术学类、设计学类综合排序成绩一分一段统计表
分数
809 796 792 788 778 775 773 771 770 767 766 763 762 758 756 754 753 752 750 748 745 744 742 741 740 739

综合排序规则

综合排序规则
综合排序是一种常用的排序方法，它通常将多个排序规则进行综合考虑，以得到一种更全面的排序结果。

在实际应用中，综合排序可用于商品、人才、论文等多种领域的排序。

综合排序规则通常包括以下几个方面：
1.权重分配：不同的排序规则在综合排序中往往具有不同的重要性，需要通过权重分配来确定各个排序规则对结果的影响程度。

2.数据标准化：不同的排序规则可能使用不同的数据类型和数据范围，需要通过数据标准化将其转化为统一的指标值，以便综合排序。

3.排序规则的选择：在进行综合排序时，需要选择合适的排序规则来评价对象的优劣。

常用的排序规则包括价格、质量、信誉度、评分等。

4.排序方式的选择：综合排序可以采用不同的排序方式，如升序、降序等。

不同的排序方式在排序结果中呈现的顺序不同，需要根据实际需要进行选择。

5.排序结果的输出：综合排序的最终结果需要进行输出，可以采用图表、列表等形式进行呈现，以便进行进一步的分析和比较。

通过以上综合排序规则的制定和应用，可以得到更加客观、全面、准确的排序结果，为实际应用提供更有价值的参考依据。

- 1 -。

综合排序规则

综合排序规则
综合排序规则是一种常见的排序方式，它能够将多个因素综合考虑后进行排序。

在实际应用中，我们经常需要根据多个条件对数据进行排序，例如商品价格、销量、评价等等。

这时候，就可以使用综合排序规则来进行排序。

综合排序规则通常是根据一定的权重来进行排序。

权重表示了每个因素在综合排序中的重要程度，权重越大的因素在排序中占据的位置就越高。

对于每个数据项，我们可以根据不同的因素给出相应的分数，并根据各个因素的权重进行加权求和。

最终，根据得分高低对数据进行排序，得分高的排在前面。

在使用综合排序规则时，需要注意以下几点：
1. 确定排序因素和权重：在进行综合排序前，需要确定要考虑的排序因素和它们的权重，这将直接影响排序结果。

2. 数据标准化：不同的因素往往具有不同的数量级和单位，因此需要进行数据标准化，将不同的因素转化为相同的数量级和单位。

3. 权重设置：权重的设置需要根据实际情况进行调整，需要根据实际应用场景和目的进行权重的设置。

4. 分值计算：根据每个因素的权重和数据的取值，计算每个数据项的得分。

5. 排序算法：根据得分高低对数据进行排序，可以使用常见的排序算法，如快速排序、归并排序等。

综合排序规则在实际应用中有着广泛的应用，例如电商平台中的
商品排序、搜索引擎中的搜索结果排序等等。

通过合理设置排序因素和权重，可以得到更符合用户需求的排序结果，提高用户体验。

各种排序方法的综合比较

各种排序方法的综合比较在计算机科学中，排序是一种常见的算法操作，它将一组数据按照特定的顺序重新排列。

不同的排序方法具有不同的适用场景和性能特点。

本文将综合比较几种常见的排序方法，包括冒泡排序、选择排序、插入排序、快速排序和归并排序。

一、冒泡排序冒泡排序是一种简单但效率较低的排序方法。

它通过多次遍历数组，每次比较相邻的两个元素，将较大的元素逐渐“冒泡”到数组的末尾。

冒泡排序的时间复杂度为O(n^2)，其中n为待排序元素的数量。

二、选择排序选择排序是一种简单且性能较优的排序方法。

它通过多次遍历数组，在每次遍历中选择最小的元素，并将其与当前位置交换。

选择排序的时间复杂度同样为O(n^2)。

三、插入排序插入排序是一种简单且适用于小规模数据的排序方法。

它通过将待排序元素逐个插入已排序的部分，最终得到完全有序的数组。

插入排序的时间复杂度为O(n^2)，但在实际应用中，它通常比冒泡排序和选择排序更快。

四、快速排序快速排序是一种高效的排序方法，它通过分治法将数组划分为两个子数组，其中一个子数组的所有元素都小于另一个子数组。

然后递归地对两个子数组进行排序，最终将整个数组排序完成。

快速排序的平均时间复杂度为O(nlogn)，但最坏情况下可能达到O(n^2)。

五、归并排序归并排序是一种稳定且高效的排序方法。

它通过将数组分成两个子数组，递归地对两个子数组进行排序，然后合并两个有序的子数组，得到最终排序结果。

归并排序的时间复杂度始终为O(nlogn)，但它需要额外的空间来存储临时数组。

综合比较上述几种排序方法，可以得出以下结论：1. 冒泡排序、选择排序和插入排序都属于简单排序方法，适用于小规模数据的排序。

它们的时间复杂度都为O(n^2)，但插入排序在实际应用中通常更快。

2. 快速排序和归并排序都属于高效排序方法，适用于大规模数据的排序。

它们的时间复杂度都为O(nlogn)，但快速排序的最坏情况下性能较差，而归并排序需要额外的空间。

综合排序热门最新上传

归并排序
采用分治法，将待排序数据分成两部分，分别对这两部分进行排序，然后将这两部分合并成一个有序序列。
排序算法的时间复杂度与空间复杂度
时间复杂度
是指执行排序算法所需的时间，通常用大O表示法来表示。不同的排序算法具有不同的时间复杂度。例如，快速排序的时间复杂度为O(nlogn)，而冒泡排序的时间复杂度为O(n^2)。
空间复杂度
是指执行排序算法所需的额外空间，也通常用大O表示法来表示。一些排序算法需要额外的存储空间来保存排序过程中的数据，例如归并排序。
02
综合排序算法
为什么需要综合排序算法
用户角度
为了方便用户找到感兴趣的内容，需要一种高效的排序方法，将内容按照一定的规则进行排序，并按照用户的偏好进行推荐。
最新上传排序算法的实现细节
1. 为每个文件或内容分配一个唯一的ID。
3. 在需要展示内容时，按照时间戳的顺序从数据库或缓存中取出文件或内容，并按照时间顺序进行排序。
最新上传排序算法的实现相对简单，主要涉及对上传时间和文件或内容的关联。一般来说，实现步骤如下
2. 在上传时，将上传时间戳和文件或内容的ID存储在数据库或缓存中。
常见的排序算法
插入排序
将待排序数据插入到已排序数据中的合适位置，以达到排序的目的。
快速排序
通过选择一个基准元素，将待排序数据分成两部分，其中一部分的所有数据都比另一部分的所有数据要小，然后再按此方法对这两部分数据分别进行快速排序。
选择排序
每次从未排序数据中选择最小（或最大）的一个元素，放到已排序数据的末尾（或开头）。
排序
按照综合得分的高低，将所有内容进行排序，得分高的内容将排在前面。

速卖通搜索排序规则

速卖通搜索排序规则在速卖通上，搜索排序规则对于卖家和买家来说都是非常重要的。

对于卖家来说，搜索排序规则决定了他们的产品在搜索结果中的排名，直接影响到产品的曝光和销量；对于买家来说，搜索排序规则决定了他们看到的产品顺序，直接影响到他们的购物体验和购买决策。

因此，了解速卖通的搜索排序规则对于卖家和买家来说都是非常重要的。

速卖通的搜索排序规则主要包括以下几个方面：1. 综合排序。

综合排序是速卖通搜索结果的默认排序规则，它是根据多个因素综合计算得出的排名。

这些因素包括产品的销量、评价、店铺信誉等。

综合排序的好处是能够全面考量产品的综合表现，但也可能导致一些新产品或者小众产品难以获得曝光。

2. 人气排序。

人气排序是根据产品的点击量和收藏量来进行排序的。

点击量和收藏量是衡量产品受欢迎程度的重要指标，因此人气排序能够很好地体现产品的热度。

但是，人气排序也存在一定的局限性，因为有些卖家可能会通过一些手段来提升产品的点击量和收藏量，从而影响排序结果。

3. 评价排序。

评价排序是根据产品的评价情况来进行排序的。

产品的评价是买家对产品的真实反馈，因此评价排序能够很好地反映产品的质量和性能。

但是，评价排序也存在一定的滞后性，因为产品的评价需要一定的时间积累，新产品可能会受到一定的影响。

4. 价格排序。

价格排序是根据产品的价格来进行排序的。

价格是买家在购买决策中非常重要的因素，因此价格排序能够很好地体现产品的价格竞争力。

但是，价格排序也存在一定的局限性，因为有些卖家可能会通过一些手段来操纵产品的价格，从而影响排序结果。

5. 销量排序。

销量排序是根据产品的销量来进行排序的。

销量是衡量产品市场表现的重要指标，因此销量排序能够很好地反映产品的市场需求。

但是，销量排序也存在一定的滞后性，因为产品的销量需要一定的时间积累，新产品可能会受到一定的影响。

除了以上几种排序规则之外，速卖通还会根据买家的个性化需求和行为来进行个性化排序。

个性化排序会根据买家的搜索历史、点击记录、购买记录等信息来推荐符合其偏好的产品，从而提升购物体验和购买转化率。

C语言排序算法大全综合排序

C语言排序算法大全综合排序利用随机函数产生N个随机整数（20000以上），对这些数进行多种方法进行排序。

基本要求：（1) 至少采用三种方法实现上述问题求解（提示，可采用的方法有插入排序、希尔排序、起泡排序、快速排序、选择排序、堆排序、归并排序）。

并把排序后的结果保存在不同的文件中。

（2) 统计每一种排序方法的性能（以上机运行程序所花费的时间为准进行对比），找出其中两种较快的方法。

问题补充：要纯C语言版，不含C++语言/*================================================================相关知识介绍（所有定义只为帮助理解相关概念，并非严格定义）：1、稳定排序和非稳定排序简单地说就是所有相等的数经过某种排序方法后，仍能保持它们在排序之前的相对次序，我们就说这种排序方法是稳定的。

反之，就是非稳定的。

比如：一组数排序前是a1,a2,a3,a4,a5，其中a2=a4，经过某种排序后为a1,a2,a4,a3,a5，则我们说这种排序是稳定的，因为a2排序前在a4的前面，排序后它还是在a4的前面。

假如变成a1,a4,a2,a3,a5就不是稳定的了。

2、内排序和外排序在排序过程中，所有需要排序的数都在内存，并在内存中调整它们的存储顺序，称为内排序；在排序过程中，只有部分数被调入内存，并借助内存调整数在外存中的存放顺序排序方法称为外排序。

3、算法的时间复杂度和空间复杂度所谓算法的时间复杂度，是指执行算法所需要的计算工作量。

一个算法的空间复杂度，一般是指执行这个算法所需要的内存空间。

==================================================================*/ /*================================================================== 功能：选择排序输入：数组名称（也就是数组首地址）、数组中元素个数==================================================================*/ /*================================================================== 算法思想简单描述：在要排序的一组数中，选出最小的一个数与第一个位置的数交换；然后在剩下的数当中再找最小的与第二个位置的数交换，如此循环到倒数第二个数和最后一个数比较为止。

综合排序算法

综合排序算法
综合排序算法是指一类能够处理多种类型数据，并兼顾多种排序标准的排序方法。

这类算法常用于解决多字段排序的问题，例如在数据库查询或复杂列表排序时，不仅需要根据一个字段排序，还要考虑其他字段的次序规则。

基本思想是先按第一优先级字段排序，遇到相同值时再比较第二优先级字段，以此类推。

常见的实现方式有：
1. 多关键字排序：设置多个排序键，依次对每个键进行排序。

2. 权重排序：给每个字段赋予不同的权重，通过计算加权值进行排序。

3. 复合排序：在编程语言中，利用sort函数提供的自定义比较函数，根据多个字段组合成复合条件进行排序。

综合排序算法可以灵活适应复杂的数据排序需求，提高数据处理的实用性与便利性。

数据结构课程设计(排序)

数据结构课程设计[排序综合]学生姓名：学生学号：院（系）：计算机科学与信息技术学院年级专业：指导教师：付丹丹二〇一一年十二月2- 3 - 3摘要数据结构是由数据元素依据某种逻辑联系组织起来的。

对数据元素间逻辑关系的描述称为数据的逻辑结构；数据必须在计算机内存储，数据的存储结构是数据结构的实现形式，是其在计算机内的表示；此外讨论一个数据结构必须同时讨论在该类数据上执行的运算才有意义。

在许多类型的程序的设计中，数据结构的选择是一个基本的设计考虑因素。

许多大型系统的构造经验表明，系统实现的困难程度和系统构造的质量都严重的依赖于是否选择了最优的数据结构。

许多时候，确定了数据结构后，算法就容易得到了。

有些时候事情也会反过来，我们根据特定算法来选择数据结构与之适应。

不论哪种情况，选择合适的数据结构都是非常重要的。

排序算法是数据结构学科经典的内容，其中内部排序现有的算法有很多种，其中包含冒泡排序，直接插入排序，简单选择排序，希尔排序，快速排序，堆排序等，各有其特点。

对排序算法比较的分析可以遵循若干种不同的准则，通常以排序过程所需要的算法步数作为度量，有时也以排序过程中所作的键比较次数作为度量。

特别是当作一次键比较需要较长时间，例如，当键是较长的字符串时，常以键比较次数作为排序算法计算时间复杂性的度量。

当排序时需要移动记录，且记录都很大时，还应该考虑记录的移动次数。

究竟采用哪种度量方法比较合适要根据具体情况而定。

在下面的讨论中我们主要考虑用比较的次数作为复杂性的度量。

41概要1.1设计目的数据结构与算法课程主要是研究非数值计算的程序设计问题中所出现的计算机操作对象以及它们之间的关系和操作的学科。

数据结构是介于数学、计算机软件和计算机硬件之间的一门计算机专业的核心课程，它是计算机程序设计、数据库、操作系统、编译原理及人工智能等的重要基础，广泛的应用于信息学、系统工程等各种领域。

学习数据结构与算法是为了将实际问题中涉及的对象在计算机中表示出来并对它们进行处理。

各种排序方法的综合比较

各种排序方法的综合比较一、引言排序是计算机科学中非常重要的基本操作之一，它将一组无序的数据按照特定的规则进行排列，使其按照一定的顺序呈现。

在实际应用中，排序算法的选择直接影响到程序的效率和性能。

本文将综合比较几种常见的排序方法，包括插入排序、选择排序、冒泡排序、快速排序和归并排序。

二、插入排序插入排序是一种简单直观的排序方法，它的基本思想是将待排序的数据依次插入到已排序的序列中。

具体实现时，从第二个元素开始，逐个将元素与前面的已排序序列进行比较，并插入到合适的位置。

插入排序的时间复杂度为O(n^2)，空间复杂度为O(1)。

三、选择排序选择排序是一种简单直观的排序方法，它的基本思想是每次从待排序的数据中选择最小（或最大）的元素，放到已排序序列的末尾。

具体实现时，通过不断选择最小元素并交换位置，最终得到一个有序序列。

选择排序的时间复杂度为O(n^2)，空间复杂度为O(1)。

四、冒泡排序冒泡排序是一种简单直观的排序方法，它的基本思想是依次比较相邻的两个元素，如果它们的顺序错误则交换位置，直到整个序列有序为止。

具体实现时，通过多次遍历和比较，每次将最大（或最小）的元素交换到序列的末尾。

冒泡排序的时间复杂度为O(n^2)，空间复杂度为O(1)。

五、快速排序快速排序是一种高效的排序方法，它的基本思想是通过一趟排序将待排序序列分割成独立的两部分，其中一部分的元素都比另一部分小。

具体实现时，选择一个基准元素，通过不断交换比基准元素小的元素和比基准元素大的元素，将序列划分为两个子序列，然后对子序列进行递归排序。

快速排序的时间复杂度为O(nlogn)，空间复杂度为O(logn)。

六、归并排序归并排序是一种稳定的排序方法，它的基本思想是将待排序序列递归地划分为两个子序列，然后对子序列进行排序，并将两个有序的子序列合并为一个有序序列。

具体实现时，通过不断划分和合并，最终得到一个有序序列。

归并排序的时间复杂度为O(nlogn)，空间复杂度为O(n)。

闲鱼的商品排序规则定义

闲鱼的商品排序规则定义闲鱼是中国最大的二手交易平台之一，用户可以在平台上出售和购买二手商品。

为了方便用户浏览和筛选商品，闲鱼采用了一套商品排序规则，根据一定的标准对商品进行排序展示。

以下是闲鱼商品排序规则及其相关参考内容。

1. 综合排序：综合排序是闲鱼上最常见的商品排序方式，它是根据一些算法计算得出的商品综合得分进行的排序。

综合得分考虑了多个因素，包括商品的热度（浏览量、收藏量、购买量等），卖家的信用等级和商品的发布时间等。

综合排序的优势在于能够综合考虑多个因素，为用户展示最有可能符合其需求的商品。

参考内容可以包括商品热度的计算方法、信用等级的评估规则等。

2. 价格排序：价格排序是按照商品的价格从低到高或从高到低的顺序进行排序。

用户可以通过选择价格排序来筛选出自己所需的商品价位范围。

参考内容可以包括价格排序的实现方法、价格区间的划分规则等。

3. 按距离排序：按距离排序是根据用户当前位置与卖家所在位置的距离远近进行排序。

这样用户可以方便地找到离自己最近的商品，减少购买时的运输成本和时间。

参考内容可以包括定位功能的实现原理、距离计算的方法等。

4. 发布时间排序：发布时间排序按照商品的发布时间从最新到最旧进行排序。

这种排序方式适合用户想要了解最新上架的商品或者是抢购限时优惠商品的需求。

参考内容可以包括发布时间的存储和排序算法等。

5. 信用等级排序：信用等级排序是根据卖家的信用等级进行排序。

这种排序方式适合用户对卖家的信用度有较高要求的情况，可以优先选择信用等级较高的卖家发布的商品。

参考内容可以包括信用等级评估标准、评级算法等。

除了以上常见的商品排序规则，闲鱼还可能根据用户的个人偏好和行为习惯进行个性化的排序展示。

闲鱼可能会根据用户的浏览历史、收藏历史、购买历史等数据来推荐相关的商品，并将这些商品展示在首页或搜索结果页面的较为显眼的位置。

这样用户可以更快地找到符合自己兴趣和需求的商品。

参考内容可以包括个性化推荐算法的原理、用户行为数据的收集和处理方法等。

闲鱼的商品排序规则定义

闲鱼的商品排序规则定义闲鱼是一款二手交易平台，用户可以在平台上发布自己的闲置物品进行出售。

为了更好地满足用户的需求，闲鱼采用了一系列的商品排序规则来帮助用户快速找到自己需要的商品。

本文将详细介绍闲鱼的商品排序规则定义。

一、综合排序综合排序是闲鱼默认的商品排序方式，它会根据多个因素进行综合评分，包括商品热度、卖家信用等级、交易成功率等。

这种排序方式可以让用户看到最受欢迎和最可信赖的商品。

二、价格由低到高/由高到低价格由低到高/由高到低是按照商品价格从低到高或从高到低进行排序。

这种方式适合那些注重价格的用户。

三、发布时间由近到远/由远到近发布时间由近到远/由远到近是按照商品发布时间从近到远或从远到近进行排序。

这种方式适合那些想要购买最新或者最早发布的物品的用户。

四、附近优先附近优先是根据用户所在位置和卖家所在位置之间的距离进行排序。

这种方式适合那些想要购买附近物品的用户。

五、好评优先好评优先是根据卖家的好评率进行排序。

这种方式适合那些注重卖家信誉的用户。

六、成交量由高到低成交量由高到低是根据卖家的成交量进行排序。

这种方式适合那些想要购买最受欢迎的商品的用户。

七、关注度由高到低关注度由高到低是根据商品被用户收藏和关注的数量进行排序。

这种方式适合那些想要购买最受欢迎的商品的用户。

八、热度优先热度优先是根据商品被用户浏览和搜索次数进行排序。

这种方式适合那些想要购买最受欢迎的商品的用户。

九、新品优先新品优先是按照商品发布时间从近到远进行排序，只显示最近发布的物品。

这种方式适合那些想要购买最新物品的用户。

十、人气榜单人气榜单是根据商品在闲鱼平台上被浏览和收藏次数进行排名，每天更新一次。

这种方式可以让用户看到最受欢迎和最有价值的物品。

总结：闲鱼的商品排序规则定义包括综合排序、价格由低到高/由高到低、发布时间由近到远/由远到近、附近优先、好评优先、成交量由高到低、关注度由高到低、热度优先、新品优先和人气榜单。

每种排序方式都有其适用的场景和用户群体，用户可以根据自己的需求选择合适的排序方式来查找和购买商品。

分数与小数的比较与排序综合运算培养孩子综合运用分数与小数的比较与排序

分数与小数的比较与排序综合运算培养孩子综合运用分数与小数的比较与排序在数学学习中，分数与小数作为常见的数形式，对孩子的综合运算能力有着重要的培养作用。

掌握分数与小数的比较与排序综合运算，不仅可以提高孩子的算术水平，还能训练他们的思维逻辑，培养他们的综合运用能力。

本文将探讨如何通过分数与小数的比较与排序综合运算来培养孩子的综合运用能力。

一、分数与小数的比较比较是数学中的重要概念，也是日常生活中常常会遇到的问题。

在比较分数与小数时，孩子需要了解比较大小的规则，并能够准确地判断大小关系。

对于分数来说，我们可以将其转化为小数形式进行比较。

例如，比较两个分数大小，我们可以将其转化为小数形式进行比较，然后根据小数的大小关系确定分数的大小。

对于小数来说，我们利用小数点后的数字大小来判断小数的大小关系。

孩子可以通过将小数转化为分数形式，或者将小数进行数轴的绘制，来更好地理解小数的大小关系。

通过比较分数与小数的大小，可以让孩子在实际问题中学会分析、判断，提高他们的问题解决能力和逻辑思维能力。

二、分数与小数的排序排序是数学中的重要概念之一，对于分数与小数来说，同样也需要掌握排序的方法。

孩子在学习中，可以通过多种形式来练习分数与小数的排序。

对于分数来说，孩子可以通过求出不同分数的相等分数形式，然后再进行排序。

例如，将分子分母相同的分数进行比较，可以更直观地判断大小关系，然后再将其排序。

对于小数来说，孩子可以通过转换为分数的形式进行排序。

通过将小数转化为分数后，可以结合比较分数的方法进行排序。

通过练习分数与小数的排序，可以帮助孩子加深对数的概念的理解，提高他们的排序能力和逻辑思维能力。

三、综合运算中的分数与小数的比较与排序在数学综合运算中，分数与小数的比较与排序是常见的题型之一。

孩子通过学习分数与小数的比较与排序，可以更好地理解综合运算，并能够将其应用到实际问题中。

在综合运算中，孩子需要先进行分数与小数的比较，然后根据大小关系来排序。

三年级数学上册综合算式练习数字排序

三年级数学上册综合算式练习数字排序1. 数字排序的重要性在学习数学的过程中，数字排序是一个至关重要的基础概念。

数字排序不仅能帮助我们整理和归类数值，还能培养我们的逻辑思维和分析能力。

在三年级数学上册中，综合算式练习部分也包括了数字排序的内容。

本文将详细介绍该章节的内容，并提供一些实用的练习方法。

2. 数字排序的定义在数学中，数字排序是按照一定规则将一列数字从小到大或从大到小排列的过程。

这个过程涉及对数字的比较和整理，帮助我们直观地了解数字的大小关系。

数字排序的常见形式包括数列排序、数字排列、大小关系比较等。

3. 数列排序的基本方法数列排序是最基本也是最常见的数字排序形式。

在三年级数学上册的综合算式练习中，我们需要通过观察一列数字并按照一定规则对其进行排序。

以下是几种常见的数列排序方法：3.1 从小到大排序在按照从小到大排序的规则下，我们将数列中的数字从左到右逐个比较，在需要交换位置的情况下，将较大的数字向右移动，较小的数字向左移动，直到完成整个数列的排序。

3.2 从大到小排序与从小到大排序相反，从大到小排序是按照从右到左逐个比较数列中的数字，并将较大的数字向左移动，较小的数字向右移动，直到整个数列完成排序。

4. 实用的数字排序练习方法为了帮助同学们更好地理解和掌握数字排序的方法，我们可以采用一些实用的练习方法来提高技能和速度。

4.1 制作排序卡片可以通过制作一组排序卡片来进行练习。

将数字写在卡片上，然后按照不同的排序规则进行整理。

每次练习可以增加卡片的数量，逐渐提高难度，以达到熟练掌握数字排序的目的。

4.2 制作排序游戏可以制作一些趣味性的数字排序游戏来帮助同学们提高数字排序能力。

例如，将一组乱序的数字给予学生，并要求他们在规定时间内按照规则进行排序。

这样的练习既能增加学生们的兴趣，又能培养他们的快速排序能力。

5. 小结通过三年级数学上册的综合算式练习部分，我们了解到数字排序在数学学习中的重要性。

教师职评排序综合评分细则

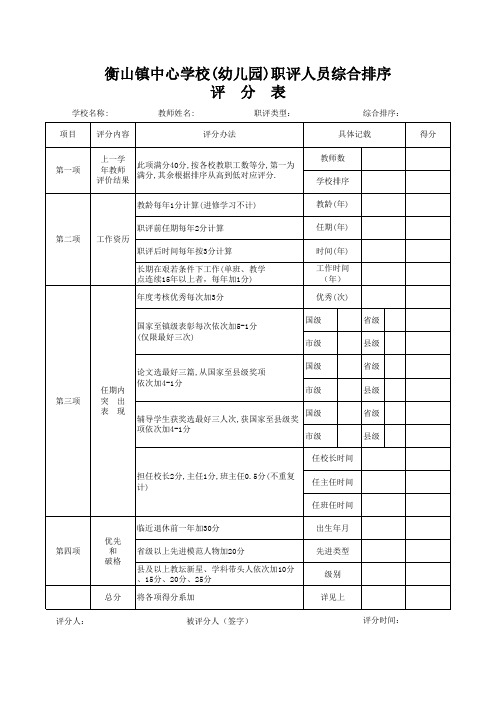
国家至镇级表彰每次表现
论文选最好三篇,从国家至县级奖项依次加4-1分
辅导学生获奖选最好三人次,获国家至县级奖项依次加4-1分
总分评分人：
第一项
上一学此项满分40分,按各校教职工数等分,第一为年教师满分,其余根据排序从高到低对应评分. 评价结果教龄每年1分计算(进修学习不计) 职评前任期每年2分计算
第二项
工作资历职评后时间每年按3分计算长期在艰若条件下工作(单班、教学点连续15年以上者，每年加1分) 年度考核优秀每次加3分
衡山镇中心学校(幼儿园)职评人员综合排序评分表
学校名称: 项目评分内容教师姓名: 评分办法职评类型：综合排序：具体记载教师数学校排序教龄(年) 任期(年) 时间(年) 工作时间（年）优秀(次) 国级市级国级市级国级市级任校长时间担任校长2分,主任1分,班主任0.5分(不重复计) 任主任时间任班任时间临近退休前一年加30分第四项优先和破格省级以上先进模范人物加20分县及以上教坛新星、学科带头人依次加10分、15分、20分、25分将各项得分系加被评分人（签字）出生年月先进类型级别详见上评分时间：省级县级省级县级省级县级得分

综合素质评价的排序

综合素质评价的排序一、引言综合素质评价是一种对个体全面发展进行评估的方法，它涵盖了知识、能力、态度和价值观等方面。

在当今社会，综合素质评价越来越受到重视，它不仅能够帮助我们了解个体的综合能力，还能为个体的成长和发展提供指导。

本文将就综合素质评价的排序进行探讨。

二、综合素质评价的意义综合素质评价的排序对于个体的发展具有重要的意义。

首先，它能够帮助个体了解自己的优势和不足，从而有针对性地进行学习和提升。

其次，综合素质评价的排序能够帮助个体进行职业规划和选择，找到适合自己的发展方向。

最后，它还能够为个体的职业发展提供参考，帮助个体在职场中取得更好的成就。

三、综合素质评价的排序方法综合素质评价的排序方法多种多样，可以从不同的角度进行评估。

以下是几种常见的排序方法：1.基于能力的排序能力是综合素质评价的重要指标之一，它包括专业能力、创新能力、沟通能力等。

基于能力的排序方法可以根据个体在不同能力方面的表现进行评价，从而确定个体的能力水平。

2.基于品德的排序品德是个体的道德修养和行为准则，也是综合素质评价的重要内容之一。

基于品德的排序方法可以从个体的诚信、责任、公正等方面进行评估，从而确定个体的品德水平。

3.基于知识的排序知识是个体的学习和掌握的内容，也是综合素质评价的重要指标之一。

基于知识的排序方法可以从个体在不同学科方面的表现进行评价，从而确定个体的知识水平。

四、综合素质评价的重要性综合素质评价对于个体的发展具有重要的意义。

首先，它能够帮助个体了解自己的优势和不足，从而有针对性地进行学习和提升。

其次，综合素质评价能够帮助个体进行职业规划和选择，找到适合自己的发展方向。

最后，它还能够为个体的职业发展提供参考，帮助个体在职场中取得更好的成就。

五、结论综合素质评价的排序对于个体的发展具有重要的意义，它能够帮助个体了解自己的优势和不足，从而有针对性地进行学习和提升。

同时，综合素质评价还能够帮助个体进行职业规划和选择，找到适合自己的发展方向。

资历章排序方法

资历章排序方法
资历章是一种表彰个人在特定领域中所取得成就的荣誉，通常分为不同的等级或级别。

对于资历章的排序方法，在不同的组织或领域中可能会有所不同，但以下是一些常见的排序方法：
1. 时间排序：按照获得资历章的时间先后顺序进行排序，最新获得的资历章排在前面。

2. 级别排序：按照资历章的级别进行排序，级别高的资历章排在前面。

3. 成就排序：按照获得资历章的成就进行排序，成就高的资历章排在前面。

4. 综合排序：将时间、级别和成就综合考虑进行排序，评估各个方面的重要性，然后按照综合得分进行排序。

在实际应用中，排序方法应该根据实际情况进行选择。

例如，对于某些领域的资历章，时间排序可能更为重要，因为获得资历章的时间越久远，代表着个人在该领域的经验和长期投入；而对于某些需要强调成就的资历章，则成就排序可能更为合适。

此外，综合排序方法可以更全面地考虑各个方面的因素，但是需要对每个因素进行权衡，以确
保排序结果合理和公正。

无论采用哪种排序方法，都应该在颁发资历章时明确规定，并在资历章展示和记录中进行标注。

这样既可以展示个人的荣誉，又可以让人们更全面地了解个人在该领域的表现和经历。