第一章质点运动学汇总
质点运动学的总结和归纳

质点运动学的总结和归纳质点运动学是物理学中研究质点在空间中运动规律和性质的学科。
通过对质点在直线运动和曲线运动中的速度、加速度等物理量进行分析,可以揭示质点运动的规律和特性。
本文将对质点运动学的相关概念、公式和应用进行总结和归纳,以帮助读者更好地理解质点运动学的基本原理。
一、质点运动学的基本概念质点是指物体在运动过程中无视其自身大小和形状,只考虑其位置坐标和质量的理想化模型。
在质点运动学中,我们假设质点可以沿直线或曲线轨迹运动,通过对质点位置、速度和加速度等物理量的描述,来分析质点的运动规律。
二、质点直线运动质点在直线上的运动可以以时间为自变量,通过位移、速度和加速度等物理量来进行描述。
其中,位移表示质点从初始位置到最终位置的位移量,速度是质点在单位时间内位移的变化率,而加速度则是速度在单位时间内的变化率。
质点直线运动的关键公式有以下几个:1. 位移公式:s = s0 + vt,其中s表示位移,s0表示初始位置,v表示速度,t表示时间;2. 平均速度公式:v = Δs/Δt,其中Δs表示位移变化量,Δt表示时间变化量;3. 瞬时速度公式:v = ds/dt,其中ds表示极小位移,dt表示极小时间间隔;4. 加速度公式:a = Δv/Δt = dv/dt,其中Δv表示速度变化量,dv表示极小速度变化量。
三、质点曲线运动质点在曲线上的运动相对复杂,需要通过坐标系和向量运算进行描述。
常见的曲线运动包括匀速圆周运动和抛体运动。
1. 匀速圆周运动:质点在同心圆轨道上以恒定的速度做圆周运动。
此时,我们需要通过极坐标系来描述质点的位置,以及角速度、角加速度等物理量。
2. 抛体运动:质点在重力作用下以抛体轨迹运动,实际上是由于自由落体运动和水平匀速运动的合成。
此时,我们需要通过平面直角坐标系来描述质点的运动,并使用矢量分解和运动学公式进行计算。
四、应用举例质点运动学在日常生活和科学研究中有着广泛的应用。
以下是几个常见的应用举例:1. 射击运动:通过研究质点在飞行过程中的速度和角度等参数,可以计算出射击运动的弹道和飞行轨迹,实现精确的打靶。
第1章 质点运动学
100t
4
t3
0
3
x x0
t
t0 vx (t)dt 0
t
(100t
4
t3 )dt
50t 2
1
t4
0
3
3
第一章 质点运动学
1-5 曲线运动
一、匀速圆周运动
1、匀速圆周运动的加速度
A v B
vA B vB
设质△|量=圆点 t|时vvv周处|存'刻。的在在,质半圆。v质点径周根点从为上据在PR点的加Q,运P处速处圆动,度,心到速的速为Q度定度O点为义,为有vv可v在,速;' 得t其度时在瞬中增刻t+时|,v
解:由
a
ann a
v2 R
n
dv dt
v
ds dt
20
0.6t 2 (m
/
s)
当t=1s时
an
v2 r
(20 0.6)2 200
m / s2
1.88m / s2
a
dv dt
1.2t
1.2m / s2
a a2 an2 2.23m / s2
dt
v0 v
0
v
v e(1.0s1 )t 0
由速度的定义: v
dy dt
v e(1.0s1 )t 0
y
t
dy v0 e dt (1.0s1 )t
y 10 1 e( 1.0s1 )t
0
0
由以上结果, t 时, v 0,此时y 10m。
但实际情况是:t 9.2s时, v 0,此时y 10m。
加速度分量
加速度大小 加速度余弦方向
a | a| a2x a2y a2z
第一章 质点运动学 小结

大学物理各章主要知识点总结

2 转动定律
M I 转动定律内容
刚体定轴转动的角加速度与它所受的合外力矩成 正比 ,与刚体的转动惯量成反比 .
其中:M 是定合义外式力矩M , 相 当r 于 平F 动问题中的合外力
I 是转动惯量,相当于平动问题中的质量
是角加速度,相当于平动问题中的加速度
3 转动定律的两种积分
力矩的空间累积效应
. 力的空间累积效应
r2
F
dr
r1
功、动能、动能定理、势能、机械能、
功能原理、机械能守恒定律
1 动力学问题的解题步骤: (1)确定研究对象 (2)确定参考系(默认大地,可不写) (3)建立坐标系 (4)分析物体的运动或者受力情况 (5)列方程
2 主要方程:
动量守恒定律;机械能守恒定律;动量定理; 动能定理;牛顿第二定律
4 温度与平均平动动能的关系: w 3 k T 2
5 分子自由度
单原子分子 i=3 双原子分子 i=5 多原子分子 i=6
6 速率分布律的定义式和物理意义
⑴ 定义式: dN f (v)dv N
⑵ 物理意义:表示速率在v附近,“dv速率区间” 内的分子数占总分子数的百分比为d N 。
N
7 速率分布函数的定义式和物理意义
n 是分子数密度 注意摩尔质量的单位,以及气体摩尔质量的数值
2 理想气体的内能公式
★ 一定量理想气体的内能为
Ei RT M i RT
2
Mmol 2
说明:内能只与温度有关
★ 若温度改变,内能改变量为
EiRT M iRT
2
Mmol 2
说明:内能变化只与温度变化有关
3 理想气体压强公式
p 2 nw 3
DdSQ0
大学物理——第1章-质点运动学

21
★ 角速度 ω 大小: ω = lim 单位:rad/s ★ 角加速度 β
v
θ dθ = t →0 t dt
v
ω dω d2θ 大小: β = lim = = 2 t →0 t dt dt
单位:rad/s2
22
★ 线量与角量的关系
dS = R dθ
16
取CF的长度等于CD
v v v v vτ vn v v v = lim + lim 加速度: a = lim = aτ + an t →0 t →0 t →0 t t t
v v 当 t →0 时,B点无限接近A点,vA与 vB v v 的夹角 θ 趋近于零,vτ 的极限方向与 vA v 相同,是A点处圆周的切线方向;vn的极 v 限方向垂直于 vA ,沿圆轨道的半径,指向
y
v v v r = r′ + R
v v v dr dr ′ dR 求导: = + dt dt dt
o
y′ M v u v v r′ r v o′ R
x′
z′
x
z v称为质点M的绝对速度, v称为质点M的相对速度, υ υ′
v 称为牵连速度. u
27
v v υ =υ′ +u
v
in 例1-6 一人向东前进,其速率为 υ1 = 50m/ m ,觉得风从 正南方吹来;假若他把速率增大为υ2 = 75m/ m , in
t
9
初始条件:t = 0 , x = 5m 【不定积分方法】
速度表达式是: v = 4+ 2t
x = ∫ vdt = ∫ (4 + 2t)dt = 4t + t 2 + C
大学物理第一章质点运动学

∫ d x = ∫ (2t −t )dt
2 0 0
t
质点的运动方程
13 x = t − t (m) ) 3
2
(3) 质点在前三秒内经历的路程
s = ∫ vdt = ∫ 2t − t 2 dt
0 0
3
3
令 v =2t-t 2 =0 ,得 t =2
8 s = ∫ (2t − t )dt + ∫ (t − 2t)dt = m 0 2 3
初始条件为x 初始条件为 0=0, v0=0 质点在第一秒末的速度;(2)运动方程;(3)质点在前三秒内 运动方程; 质点在前三秒内 运动方程 求 (1) 质点在第一秒末的速度 运动的路程。 运动的路程。 解 (1) 求质点在任意时刻的速度 dv dv a= = 2 − 2t 由 dt dv = (2 − 2t) dt 分离变量 两边积分
y
P点在 系和 '系的空间坐标 、 点在K系和 系的空间坐标、 点在 系和K 时间坐标的对应关系为: 时间坐标的对应关系为:
y'
r v
P
}
r r
o z
r r′
o' x x'
r R
z'
伽利略坐标变换式
2. 速度变换 r r vK、vK′ 分别表示质点在两个坐标系中的速度 r r r d r ′ d(r − vt) r r r vK′ = = = vK − v dr′ r dt t r 即 vK′ = vK − v r r r vK = vK′ + v 伽利略速度变换
dv = g − Bv dt 分离变量并两边积分
t dv ∫0 g - Bv = ∫0 dt v
g v = (1− e−Bt ) B
大学物理 第1-3章 经典力学部分归纳总结

运用
分
和
dv dv dx dv a= = ⋅ =v dt dx dt dx
3
知识点回顾
第二章 质点动力学
2、牛顿三定律? 、牛顿三定律?
r ∑Fi = ma
i →
—— 为什么动? 为什么动? 力?
功是能量交换或转换的一种度量
v v 2、变力作功 、 元功: 元功: dW = F ⋅ dr = Fds cosθ b b v v b W = ∫ F cosθ ds = ∫ F ⋅ dr = ∫ (Fxdx + Fy dy + Fz dz)
a( L) a( L) a( L)
3、功率 、
v v dW F ⋅ dr v v P= = = F ⋅ v = Fv cosθ dt dt
隔离木块a在水平方向绳子张力t和木块b施于的摩擦力?根据牛顿第二定律列出木块a的运动方程?同样隔离木块b分析它在水平方向受力情况列出它的运动方程为17一个质量为m的梯形物体块置于水平面上另一质量为m的小物块自斜面顶端由静止开始下滑接触面间的摩擦系数均忽略不计图中hh均为已知试求m与m分离时m相对水平面的速度及此时m相对于m的速度
15
•解:以地面为参考系。隔离木块A,在水平方向 解 以地面为参考系。隔离木块 , 绳子张力T 和木块B施于的摩擦力 绳子张力 和木块 施于的摩擦力
v t2 v v v v v 动量定理: 动量定理: I = ∫ ∑ F dt = ∑ p2 − ∑ p1 = ∑ mv2 − ∑ mv1
t1
v v v v 角动量定理: 角动量定理: M ⋅ dt = dL = d ( r × mv )
第一章运动学

第一章 运动学第1节 质点运动的基本概念一.质点运动的基本概念1.位置、位移和路程:位置指运动质点在某一时刻的处所,在直角坐标系中,可用质点在坐标轴上的投影坐标(x,y,z )来表示。
在定量计算时,为了使位置的确定与位移的计算一致,人们还引入位置矢量(简称位矢)的概念,如图所示,在直角坐标系中,位矢r 定义为自坐标原点到质点位置P(x,y,z)所引的有向线段,故有222z y x r ++=,r 的方向为自原点O 点指向质点P 。
位移指质点在运动过程中,某一段时间t ∆内的位置变化,即位矢的增量t t t r r s _)(∆+=,它的方向为自始位置指向末位置。
在直角坐标系中,在计算位移时,通常先求得x 轴、y 轴、z 轴三个方向上位移的三个分量后,再按矢量合成法则求合位移。
路程指质点在时间内通过的实际轨迹的长度,它是标量,只有在单方向的直线运动中,路程才等于位移的大小。
2.平均速度和平均速率:平均速度是质点在一段时间内通过的位移和所用时间之比:t s v ∆=平,平均速度是矢量,方向与位移s 的方向相同。
平均速率是质点在一段时间内通过的路程与所用时间的比值,是标量。
3.瞬时速度和瞬时速率:瞬时速度是质点在某一时刻或经过某一位置是的速度,它定义为在时的平均速度的极限,简称为速度,即ts v t ∆=→∆0lim 。
瞬时速度是矢量,它的方向就是平均速度极限的方向。
瞬时速度的大小叫瞬时速率,简称速率。
4.加速度:加速度是描述物体运动速度变化快慢的物理量,等于速度对时间的变化率,即t v a ∆∆=,这样求得的加速度实际上是物体运动的平均加速度,瞬时加速度应为tv a t ∆∆=→∆0lim。
加速度是矢量。
5.匀变速直线运动:质点运动轨迹是一条直线的运动称为直线运动,而加速度又恒定不变的直线运动称为匀变速直线运动,若a 的方向与v 的方向一致称为加速运动,否则称为减速运动。
匀变速直线的运动规律为: 20021at t v s s ++= )(20202s s a v v t -=-二、解题指导:例1:如图所示,物体A 置于水平面上,A 前固定一滑轮B ,高台上有一定滑轮D ,一根轻绳一端固定在C两段绳子的夹角为ɑ时,A 的运动速度。
第一章 质点运动学小结

一、重要概念:
1.位矢、位移、速度、加速度等都是矢量。
2.上述物理量的大小、方向、分量表达式等。 3.切向加速度、法向加速度等概念,角量与线量
的关系。
4.矢量“增量的大小”与该矢量“大小的增量”。
1
二、基本规律 1.运动描述的相对性。 2.运动叠加性原理。 3.伽利略坐标变换。
三、重要公式
ds v et dt
5.速率:
dx dy dz v i j k dt dt dt
v v x i v y j vz k
ds v dt
3
dr v v dt
2 2 2 v v v x v y vz
6.加速度:
2 v dv d r a lim 2 dt dt t 0 t
dv dv d v dv x y z a i j k dt dt dt dt
2 2 2 2
d r d x d y d z a 2 2 i 2 j 2 k dt dt dt dt
4
7.加速度的大小
a a a a a
2 x 2 y 2
vy vz vx cos , cos , cos v v v ay az ax cos , cos , cos a a a
6
9.切向加速度和法向加速度
v dv a e en a e an en dt
2
dv a , dt
2 z 2 2
dv x dv y dvz dt dt dt
2 2 2 2 2
d x d y d z 2 2 2 dt dt dt
大学物理1复习资料(含公式,练习题)

第一章 质点运动学重点:求导法和积分法,圆周运动切向加速度和法向加速度。
主要公式:1.质点运动方程(位矢方程):k t z j t y i t x t r)()()()(++=参数方程:。
t t z z t y y t x x 得轨迹方程消去→⎪⎩⎪⎨⎧===)()()(2.速度3.4.5.线速度与角速度关系6.切向加速度法向加速度 总加速度第二章 质点动力学重点:动量定理、变力做功、动能定理、三大守恒律。
主要公式:1.牛顿第一定律:当0=合外F时,恒矢量=v。
2.牛顿第二定律3.4.5.6 动能定理7.机械能守恒定律:当只有保守内力做功时,0=∆E8. 力矩:F r M⨯=大小:θsin Fr M=方向:右手螺旋,沿F r⨯的方向。
9.角动量:P r L⨯=大小:θsin mvr L =方向:右手螺旋,沿P r⨯的方向。
※ 质点间发生碰撞:完全弹性碰撞:动量守恒,机械能守恒。
完全非弹性碰撞:动量守恒,机械能不守恒,且具有共同末速度。
一般的非弹性碰撞:动量守恒,机械能不守恒。
※行星运动:向心力的力矩为0,角动量守恒。
第三章 刚体重点: 刚体的定轴转动定律、刚体的角动量守恒定律。
主要公式: 1. 转动惯量:⎰=rdm r J2,转动惯性大小的量度。
2. 平行轴定理:2md J Jc +=质点:θsin mvr L =刚体:ωJ L =4.转动定律:βJ M=5.角动量守恒定律:当合外力矩2211:,0,0ωωJ J L M ==∆=即时6. 刚体转动的机械能守恒定律: 转动动能:221ωJ E k =势能:c P mgh E = (c h 为质心的高度。
)※ 质点与刚体间发生碰撞:完全弹性碰撞:角动量守恒,机械能守恒。
完全非弹性碰撞:角动量守恒,机械能不守恒,且具有共同末速度。
一般的非弹性碰撞:角动量守恒,机械能不守恒。
说明:期中考试前的三章力学部分内容,请大家复习期中试卷,这里不再举例题。
大学物理知识点总结

大学物理知识点总结 -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIANBr ∆A rB ryr ∆第一章质点运动学主要内容一. 描述运动的物理量 1. 位矢、位移和路程由坐标原点到质点所在位置的矢量r 称为位矢 位矢r xi yj =+,大小 2r r x y ==+运动方程 ()r r t =运动方程的分量形式()()x x t y y t =⎧⎪⎨=⎪⎩位移是描述质点的位置变化的物理量△t 时间内由起点指向终点的矢量B A r r r xi yj =-=∆+∆△,2r x =∆+△路程是△t 时间内质点运动轨迹长度s ∆是标量。
明确r ∆、r ∆、s ∆的含义(∆≠∆≠∆r r s )2. 速度(描述物体运动快慢和方向的物理量)平均速度xyr x y i j ij t t t瞬时速度(速度) t 0r drv limt dt∆→∆==∆(速度方向是曲线切线方向) j v i v j dt dy i dt dx dt r d v y x +=+==,2222yx v v dt dy dt dx dt r d v +=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛== ds dr dt dt= 速度的大小称速率。
3. 加速度(是描述速度变化快慢的物理量)平均加速度va t ∆=∆ 瞬时加速度(加速度) 220limt d d r a t dt dt υυ→∆===∆△ a 方向指向曲线凹向j dty d i dt x d j dt dv i dt dv dt v d a y x2222+=+== 2222222222⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+=dt y d dt x d dtdv dt dv a a a y x y x二.抛体运动运动方程矢量式为 2012r v t gt =+分量式为 020cos ()1sin ()2αα==-⎧⎪⎨⎪⎩水平分运动为匀速直线运动竖直分运动为匀变速直线运动x v t y v t gt 三.圆周运动(包括一般曲线运动) 1.线量:线位移s 、线速度dsv dt= 切向加速度t dva dt=(速率随时间变化率) 法向加速度2n v a R=(速度方向随时间变化率)。
第一章- 质点运动学
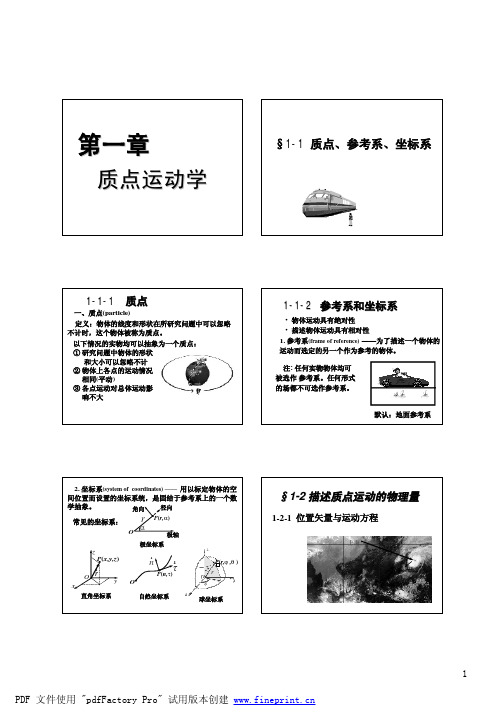
间位置而设置的坐标系统,是固结于参考系上的一个数
学抽象。 常见的坐标系:
角向
r
Oα
径向
•P(r,α)
极轴
z
P•(x,y,z)
r
Or
y
x
极坐标系
r n
τr
P(n,τ)
O
•P(r,ϕ ,θ ) r
直角坐标系
自然坐标系
球坐标系
§1-2 描述质点运动的物理量
1-2-1 位置矢量与运动方程
上海
热带风暴
1 PDF 文件使用 "pdfFactory Pro" 试用版本创建
设质点: t+
t ∆t
时位时移刻刻::: AB∆,, rvrvrBvA
z
A v
∆rv
B
rA
v rB
O
y
x
平均速度: vr = ∆rv ∆t
单位:m⋅s-1
平均速度的方向与∆t时间内位移的方向一致
2 PDF 文件使用 "pdfFactory Pro" 试用版本创建
2. 瞬时速度(速度) 精细地描述质 z
avt
=
dv dt
evt
=
d2s dt 2
evt
v 讨论 det
dt
∆evt
=
v et
(t
+
∆t)
-
v et
(t
)
当: ∆t → 0 , ∆θ → 0
有 ∆et = et ⋅ ∆θ = ∆θ
方向 ∆evt ⊥ evt
v d et dt
= lim ∆evt ∆t→0 ∆t
= lim ∆θ ∆t→0 ∆t
第一章 质点运动学

六. 单位 本课程采用国际单位制( ), ),其中 本课程采用国际单位制(SI),其中 长度单位 时间单位 速度单位 加速度单位 米(符号 m) ) 秒(符号 s) ) 米每秒( 米每秒(符号 m/s ) 米每二次方秒( 米每二次方秒(符号 m/s2 )
例题1-4 已知质点作匀加速直线运动,加速度 已知质点作匀加速直线运动, 例题 求这质点的运动方程。 为 a ,求这质点的运动方程。 dv = a 常量),积分得 ),积分得 解 由定义 (常量), dt
∆r = r1 − r
即等于质点位矢在∆t O 即等于质点位矢在∆ 时间内的增量。 时间内的增量。且有
r
r ∆t 时间内位移 1
t +∆t 时刻位矢 ∆
x
∆r = x1i + y1 j − xi − yj = ( x1 − x )i + ( y1 − y ) j
时间内质点通过的路程 为标量 路程∆ 为标量, ∆t 时间内质点通过的路程∆s为标量,仅当 ∆t→0时,位移的大小 时 lim ∆r = ∆s
d 2 x dv x ax = 2 = = −ω 2 R cos ω t dt dt d 2 y dv y ay = 2 = = −ω 2 R sin ω t dt dt
由此得加速度的大小
v a = ω R cos ωt + sin ωt = ω R = R
2 2 2 2
2
如果把加速度写成矢量式, 如果把加速度写成矢量式,则有
本课程中只讨论平面内的运动问题, 本课程中只讨论平面内的运动问题,常用坐标 系有平面直角坐标系 极坐标系和自然坐标系。 平面直角坐标系、 系有平面直角坐标系、极坐标系和自然坐标系。
二. 质点 一般情况下, 一般情况下,运动物体的形状和大小都可能变化
运动学-质点运动知识点汇总

m1、m2 组成一个系统
dW f 1 dr1 f 2 dr2
f1 f 2
dW f 2 (dr2 dr1) f 2 d(r2 r1)
dr1 r21
m1
f1
r1
r2
m2 f2
r 2 r1 r 21
o
dW f 2 dr21
➢ 系统内的质点间没有相对位移时,一对内力所作的功等于零;
➢ 系统内质点间有相对位移,则一对内力作的功之和等于第一个物
角量
角位置、角速度、角加速度
线量
位矢、速度、加速度
s R
v lim s lim R R d R
t0 t t0 t
dt
an
v2 R
(R)2
R
R 2
at
dv dt
R
d
dt
R
P(t t)
P(t) o
x
思考题
1. 质点作匀变速圆周运动,则
切向加速度的大小和方向都在变化 法向加速度的大小和方向都在变化 切向加速度的方向变化,大小不变 切向加速度的方向不变,大小变化
Li
mi ri 2
mi
ri
2
i
i
i
L J
二、刚体定轴转动的角动量定理
M J J d d (J) dL
dt dt dt
O ri
vi
mi
Mdt dL
t2 t1
Mdt
L2
L1
刚体定轴转动的角动量定理
t2 t1
Mdt
L2
L1
J2
J1
三、刚体定轴转动的角动量守恒定律
t2 t1
Mdt
刚体的转动惯性,其大小反映了改变刚体转动状态的难易
大物知识点梳理完整版

大物知识点整理第一章︰质点运动学1质点运动的描述位置矢量︰从所指定的坐标原点指向质点所在位置的有向线段。
运动方程︰速度︰表示物体运动的快慢。
瞬时速率等于瞬时速度的大小 2圆周运动角加速度α=Δω / Δt 角速度ω=Φ/t=2π/T=2πf 线速度V=s/t=2πR/T , ω×r=V切向加速度沿切向方向法向加速度 指向圆心加速度例题1 已知质点的运动方程x =2t,y =2-t^2,则t=1时质点的位置矢量是( )加速度是( ),第一秒到第二秒质点的位移是( ),平均速度是( )。
(详细答案在力学小测中) 注意:速度≠速率平时作业:P36 1.6 1.11 1.13 1.16 (1.19建议看一下)第二章:牛顿定律1、牛顿第一定律: 1任何物体都具有一种保持其原有运动状态不变的性质。
2力是改变物体运动状态的原因。
2、牛顿第二定律 :F=ma3、牛顿第三定律:作用力与反作用力总是同时存在,同时消失,分别作用在两个不同的物体上,性质相同。
4、非惯性系和惯性力非惯性系:相对于惯性系做加速运动的参考系。
惯性力:大小等于物体质量与非惯性系加速度的乘积,方向与非惯性加速度的方向相反,即F=-ma 例题:P51 2.1 静摩擦力不能直接运算。
2.2 对力的考察比较全面,类似题目P64 2.1 2.2 2.62.3运用了微积分,这种题目在考试中会重点考察,在以后章节中都会用到,类似P66 2.13该章节对惯性力涉及较少,相关题目有P57 2.8 P65 2.7(该题书中的答案是错的,请注意,到时我会把正确答案给你们。
)P67 2.17.第三章 动量守恒定律与能量守恒定律1动量P=mv2冲量 其方向是动量增量的方向。
⎰=-2112 t t dt F I P P=Fdt=dP3动量守恒定律P=C (常量)条件:系统所受合外力为零。
若系统所受合外力不为零,但沿某一方向合力为零时,则系统沿该方向动量守恒。
大学物理第一章 质点运动学

a 常量,v v0 at,
•匀变速直线运动:
1 2 x x0 v0t at 2 2 2 v v0 2a( x x0 )
注意:以上各式仅适用于匀加速情形。
t t
要求 v( y ),可由
dv dv dy dv a v dt dy dt dy
有
积分得
v
dv kv v dy
2
dv kdy v
y dv v ky v0 v k 0 dy ln v0 ky, v v0e
1-3 曲线运动
一.运动的分解
如图,A、B为在同一高度的两个小球。在同一 时刻,使A球自由落体,B球沿水平方向射出,虽然 两球的轨道不同,但是两球总是在同一时刻落地。 说明,B球的运动可分解为在水平方向作匀速直线运 动,在竖直方向作自由落体运动。
其大小注意a aa a2 x 2 y2 z
dv dv a a dt dt
•描述质点运动的状态参量的特性 状态参量包括
r , v, a
应注意它们的
(1)矢量性。注意矢量和标量的区别。
(2)瞬时性。注意瞬时量和过程量的区别。 (3)相对性。对不同参照系有不同的描述。
1 gx y xtg 2 2 2 v0 cos 19.6 2 50tg 50tg 19.6(1 tg ) 2 cos
两边一起定积分得
dv dv adt kv dt kdt 2 v
2
v
v0
t dv k dt 2 0 v
v0 v(t ) kv0t 1
(完整版)大学物理知识点(全)
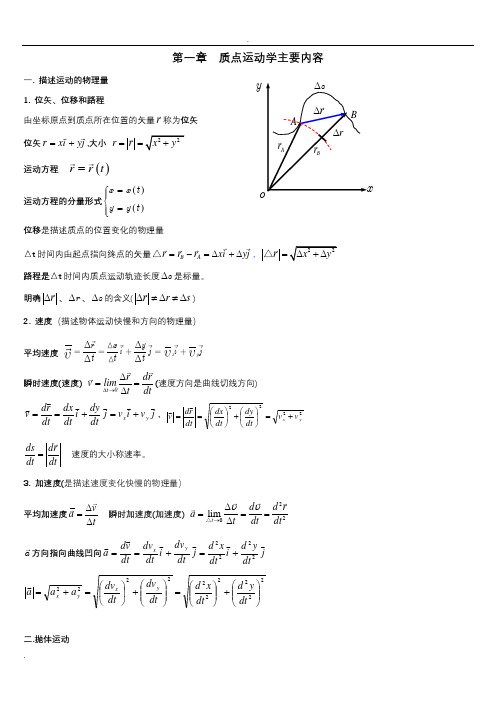
Br ∆ A rB ryr ∆第一章 质点运动学主要内容一. 描述运动的物理量 1. 位矢、位移和路程由坐标原点到质点所在位置的矢量r 称为位矢 位矢r xi yj =+,大小 2r r x y ==+运动方程()r r t =运动方程的分量形式()()x x t y y t =⎧⎪⎨=⎪⎩位移是描述质点的位置变化的物理量△t 时间内由起点指向终点的矢量B A r r r xi yj =-=∆+∆△,2r x =∆+△路程是△t 时间内质点运动轨迹长度s ∆是标量。
明确r ∆、r ∆、s ∆的含义(∆≠∆≠∆r r s ) 2. 速度(描述物体运动快慢和方向的物理量)平均速度xyr x y i j ij t t t瞬时速度(速度) t 0r drv limt dt∆→∆==∆(速度方向是曲线切线方向) j v i v j dt dy i dt dx dt r d v y x +=+==,2222yx v v dt dy dt dx dt r d v +=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛== ds dr dt dt= 速度的大小称速率。
3. 加速度(是描述速度变化快慢的物理量)平均加速度va t ∆=∆ 瞬时加速度(加速度) 220limt d d r a t dt dt υυ→∆===∆△ a 方向指向曲线凹向j dty d i dt x d j dt dv i dt dv dt v d a y x2222+=+== 2222222222⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+=dt y d dt x d dtdv dt dv a a a y x y x二.抛体运动运动方程矢量式为 2012r v t gt =+分量式为 020cos ()1sin ()2αα==-⎧⎪⎨⎪⎩水平分运动为匀速直线运动竖直分运动为匀变速直线运动x v t y v t gt 三.圆周运动(包括一般曲线运动) 1.线量:线位移s 、线速度dsv dt= 切向加速度t dva dt=(速率随时间变化率) 法向加速度2n v a R=(速度方向随时间变化率)。
力学舒幼生第一章质点运动学

P
yj
r(t tx)i
O
x
加速度 a d d v td d2r 2 td dxv i td dyv tjr
15
例 空心入篮
抛射角 12
xvct o2s1 2g2tsin1
yvst in21 2g2tco1s
y0
t 2vsin2 g cos1
第一章 质点运动学
0
1.1 空间和时间
时间和空间的测量
绝对时空观 绝对空间,就其本性来说,与任何外在的情况无关,
始终保持着相似和不变。 绝对的、纯粹的数学的时间,就其本性来说,均匀地
流逝而与任何外在的情况无关。 牛顿——《自然哲学的数学原理》
时间和空间的测量与物体的存在和运动没有任何关系
参考系
参考物:选取的一个有固定大小和形状的物体。 相对参考物,可以确定其它物体的位置。
9
vv0a0(tt0)1 2b(tt0)2
再求 t 时刻的位置
微分关系式 dxvdt
两边积分 tt0 d x tt0 v dtt0[v t0 a 0 (t t0 ) 1 2 b (t t0 )2 ]d
x x 0 v 0 (t t0 ) 1 2 a 0 (t t0 )2 1 6 b (t t0 )3
a心 d d vtvddtR ddtR 2 a切dd/vt/Rd dt R
与速度垂直,改变速度方向
与速度平行,改变速度大小
18
无限小角位移矢量
ddk
r(tt)
d r(t)
⊙k
初、末态矢量与转动正方向满足右手螺旋法则
无限小角位移与有限角位移的区别?
19
有限角位移不是矢量
不满足矢量加法的交换律
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
大学物理学 College Physics
第一章 质点运动学 Chap.1 Kinematics
第一章 质点运动学
本章要点
➢ 矢量及其运算 ➢ 位矢、位移、速度、加速度的定义 ➢ 曲线运动的自然坐标系描述 ➢ 运动学的两类问题
矢量:由大小(模)和其方向(单位矢量)构成:
A A A0
A0 =
A A
模
单位矢量
第一节 矢量( Vector )
二、矢量的加法与减法
矢量加法(Vector Addition): 矢量加法遵循平行四边形法则(或三角形法则)
AB C
B
C
A
第一节 矢量( Vector )
矢量加法的三角形法则,多矢量加法:
动了宇宙学的基础”。
物理学 (Physics)
物质结构
物质相互作用 物质运动规律
物理学是研究物质世界最基本形态的科学 物理学研究的范围 —— 物质世界的层次和数量级
微观粒子 Microscopic
介观物质 mesoscopic
宏观物质 macroscopic
宇观物质 cosmological
空间尺度: 质子 10-15 m 时间尺度: 基本粒子寿命 10-25 s
1) A B -B A
2) 如果: A B 则 A B 0 反之亦成立。
3)两个矢量垂直时,矢积的模最大,方向 按右手螺旋法则。
第一节 矢量( Vector )
四、矢量在直角坐标系中的表示
一个矢量可以分解为两个或多个矢量之和。
例如: A B C D E F 等等分法,但有意义的
是在特定的坐标系里分解。最常见的是直角坐标系。
2013年诺贝尔物理学奖
Francois Englert (比利时) Peter W. Higgs (英国)
两位科学家描述了粒子物理学的标准模型,其预测的基本 粒子——希格斯玻色子,被欧洲核子研究中心运行的大型强子 子对撞机通过实验发现。
2012年诺贝尔物理学奖
• David J. Wineland (美国) • Serge Haroche (法国)
“突破性的试验方法使得测量和操纵单个量子
系统成Байду номын сангаас可能”
物质和反物质不对称问题(宇宙形成)
2011年诺贝尔物理学奖
索尔-佩尔马特
布莱恩-施密特
亚当-里斯
我们宇宙在“大爆炸”中诞生,但会往何处去呢?获得 2011年诺贝尔物理学奖的美、澳三位天体物理学家,通 过对超新星的观测而给出了答案:宇宙膨胀不断加速, 而且逐渐变冷。这个发现,被瑞典皇家科学院称为“震
Y
A
Ay
O
Ax
Ax Acos Ay Asin
X
第一节 矢量( Vector ) Y
Ay
O
Ax
X
A A Ax2 Ay2
tan-1 Ay
Ax
因此,平面上的一个矢量,可以用其两个坐标 分量确定;也可以由其大小和方向确定。
第一节 矢量( Vector )
矢量在空间直角坐标系中的分解
Z
Az P
大学物理学 College Physics
陈 曙 韩永胜 杜锦丽 何正大 蒋岩玲 李亚玲 马 军 杨宏新 杨闽南
2014年诺贝尔物理学奖
赤崎勇
天野浩 中村修二
三位获奖者在发现新型高效、环境友好型光源,即蓝色发光二极 管(LED)方面做出巨大贡献。在蓝光LED的帮助下,白光可以 以新的方式被创造出来。使用LED灯,我们可以拥有更加持久和 更加高效的灯光代替原来的光源。
O Ax
X
OP Ax Ay Az Axi Ay j Az k
量,其大小是第一个矢量的大小乘以第二个矢量在第
一个矢量上的投影。 是指这两个矢量的夹角。
第一节 矢量( Vector )
1) A B B A
2) 如果: A B 则 A B 0 反之亦成立。
3)两个矢量平行、反平行时, 标积最大、最小。
第一节 矢量( Vector )
矢量的矢积或叉乘(Vector product)
三、矢量的乘法
矢量和标量乘: 结果是一个矢量。(大小、方向?)
矢量和矢量乘:
点乘:结果是一个标量。(大小?) 叉乘:结果是一个矢量。(大小、方向?)
第一节 矢量( Vector )
矢量的点乘(Scalar Product):
B
A B AB cos
B cosθ
A
A B AB cos 表示:两个矢量的标积是一个标
同学们可以简单地计 算一下,本课程平均 每次课的教材阅读量
在20页左右!
“干中学”
• I hear, I forget. • I see, I remember. • I do, I understand.
“Learning by doing.” ----MIT
学习方法
听课、阅读、思考、 讨论、练习、总结。
A B C A B C AB sin
两个矢量的矢积是一个矢量,其大小是第一个矢量的
大小与第二个矢量的大小以及两矢量夹角的正弦值,
这三者的乘积,方向按右手螺旋法则确定。
C矢量与 A、B矢量构成的
C
平面永远垂直!它的意义
是A、B 矢量构成的平行四
边形的有向面积。
B
A
第一节 矢量( Vector )
C
B A
显然,矢量加法服从:
交换律 A B B A
结合律 (A B) C A (B C)
第一节 矢量( Vector )
矢量减法(Vector Subtraction):
解决了矢量加法,也就解决了矢量的减法。
A - B A (-B) D
B
A
-B
D A-B
B D A-B
A
第一节 矢量( Vector )
类星体 10 26 m 宇宙寿命 1018 s
现代物理 学的研究对 象,已包括 人类“感知” 的整个空间 尺度范围内 的物体。
观测世界的手段
大量应用初等数学和高等数学, 用数学语言说明物理问题
本课程特点: 进度快,系统性强,数学应用多,信息量大。
理论课时相 对较少
一般均从基 本物理原理 出发展开演 绎、讨论
第一节 矢量( Vector )
一、矢量的定义和表示方法
矢量:既有大小又有方向的量,如速度、力、位移等 标量:仅有大小而与空间方向无关的量,由单一的数和单
位描写,如质量、密度等
矢量的表示: A, A,
矢量相等:A=B
A
B
第一节 矢量( Vector )
负矢量:方向相反,大小相等
A
B
B -A
第一节 矢量( Vector )
