α粒子散射实验 实验报告
教具粒子散射实验报告

一、实验背景粒子散射实验是原子物理学中的一个重要实验,由英国物理学家卢瑟福及其助手在1909年完成。
该实验旨在探究原子内部结构,特别是原子核的存在和性质。
通过观察α粒子与金属箔的相互作用,实验揭示了原子核的存在,推翻了汤姆孙的“布丁模型”,并奠定了现代原子核理论的基础。
二、实验目的1. 观察α粒子散射现象,验证原子核的存在。
2. 理解原子核的大小、质量和电荷分布。
3. 掌握粒子散射实验的基本原理和操作方法。
三、实验原理α粒子是带正电的粒子,其质量远大于电子。
在实验中,α粒子被加速后射向金属箔,与箔中的原子核发生相互作用。
根据经典电磁理论,α粒子与原子核的相互作用可以看作是带电粒子之间的库仑力作用。
当α粒子与原子核发生碰撞时,其运动方向会发生改变,即发生散射。
根据散射角度和散射概率,可以推算出原子核的大小、质量和电荷分布。
实验中常用的散射公式为:\[ \theta = \frac{2Z^2e^4}{4\pi^2\epsilon_0^2m_αv^2a^2} \]其中,θ为散射角度,Z为原子核的电荷数,e为电子电荷,ε0为真空介电常数,mα为α粒子的质量,v为α粒子的速度,a为原子核的半径。
四、实验器材1. α粒子源:用于产生α粒子。
2. 金属箔:用于观察α粒子的散射现象。
3. 粒子探测器:用于记录α粒子的散射角度和数量。
4. 计算机软件:用于数据处理和分析。
五、实验步骤1. 将α粒子源放置在实验装置中,调整实验参数。
2. 将金属箔放置在α粒子源前方,调整金属箔的位置和角度。
3. 启动实验,观察α粒子的散射现象,记录散射角度和数量。
4. 重复实验,改变金属箔的位置和角度,观察散射现象的变化。
5. 使用计算机软件对实验数据进行处理和分析。
六、实验结果与分析1. α粒子散射现象:实验观察到,绝大多数α粒子穿过金属箔后仍沿原来的方向前进,但有少数α粒子发生了较大的偏转,甚至有极少数α粒子被反弹回来。
这表明金属箔中存在一个带正电的核,α粒子与核发生相互作用后发生散射。
卢瑟福散射实验报告

陈杨PB05210097 物理二班实验题目:卢瑟福散射实验实验目的:1.通过卢瑟福核式模型,说明α粒子散射实验,验证卢瑟福散射理论;2.并学习应用散射实验研究物质结构的方法。
实验原理:现从卢瑟福核式模型出发,先求α粒子散射中的偏转角公式,再求α粒子散射公式。
1.α粒子散射理论(1)库仑散射偏转角公式设原子核的质量为M,具有正电荷+Ze,并处于点O,而质量为m,能量为E,电荷为2e的α粒子以速度ν入射,在原子核的质量比α粒子的质量大得多的情况下,可以认为前者不会被推动,α粒子则受库仑力的作用而改变了运动的方向,偏转θ角,如图所示。
图中ν是α粒子原来的速度,b是原子核离α粒子原运动径的延长线的垂直距离,即入射粒子与原子核无作用时的最小直线距离,称为瞄准距离。
图α粒子在原子核的库仑场中路径的偏转当α粒子进入原子核库仑场时,一部分动能将改变为库仑势能。
设α粒子最初的的动能和角动量分别为E和L,由能量和动量守恒定律可知:⎪⎪⎭⎫⎝⎛++⋅=••222202241ϕπεr r m r Ze E (1)L b m mr ==••νϕ2 (2)由(1)式和(2)式可以证明α粒子的路线是双曲线,偏转角θ与瞄准距离b 有如下关系:202242Ze Ebctgπεθ= (3)设E Ze a 0242πε=,则 a bctg22=θ(4)这就是库仑散射偏转角公式。
(2)卢瑟福散射公式在上述库仑散射偏转公式中有一个实验中无法测量的参数b ,因此必须设法寻找一个可测量的量代替参数b 的测量。
事实上,某个α粒子与原子散射的瞄准距离可大,可小,但是大量α粒子散射都具有一定的统计规律。
由散射公式(4)可见,θ与b 有对应关系,b 大,θ就小,如图所示。
那些瞄准距离在b 到db b +之间的α粒子,经散射后必定向θ到θθd -之间的角度散出。
因此,凡通过图中所示以b 为内半径,以db b +为外半径的那个环形ds 的α粒子,必定散射到角θ到θθd -之间的一个空间圆锥体内。
试验11α粒子散射

实验1.1 α粒子散射电子被发现以后,人们普遍认识到电子是一切元素的原子的基本组成部分。
但通常情况下原子是呈电中性的,这表明原子中还有与电子的电荷等量的正电荷,所以,研究原子的结构首先要解决原子中正负电荷怎样分布的问题。
从1901年起,各国科学家提出各种不同的原子模型。
第一个比较有影响的原子模型,是J.J.汤姆逊于1904年提出“电子浸浮于均匀正电球”中的模型。
他设想,原子中正电荷与电子间的作用力以及电子与电子间的斥力的作用下浮游在球内。
这种模型被俗称为“葡萄干布丁模型”。
汤姆逊还认为,不超过某一数目的电子将对称地组成一个稳定的环或球壳;当电子的数目超过一定值时,多余电子组成新的壳层,随着电子的增多将造成结构上的周期性。
因此他设想,元素性质的周期变化或许可用这种电子分布的壳层结构作出解释。
汤姆逊的原子模型很快地被进一步的实验所否定,它不能解释α射线的大角度散射现象。
卢瑟福从1904年到1906年6月,做了许多α射线通过不同厚度的空气、云母片和金属箔(如铝箔)的实验。
英国物理学家W.H.布拉格(Bragg, W.H.1862-1942)在1904-1905年也做了这样的实验。
他们发现, 在此实验中α射线速度减慢,而且径迹偏斜了(即发生散射现象).例如,通过云母的的某些α射线,从它们原来的途径约片斜2°,发生了小角度散射,1906年冬, 卢瑟福还认识到α粒子在某一临界速度以上时能打入原子内部,由它的散射和所引起的原子内电场的反应可以探索原子内部结构.而且他还预见到可能会出现较大角度的散射.1910年12月,卢瑟福对大角度散射过程的受力关系进行计算,得出一个新的原子结构设想。
经过反思索、研究,于1911年4月下旬写出论文为靶的金属箔的原子一次碰撞中改变其方向的,因此原子中有一个体积很小、质量很大的带正电荷的原子核,它对带正电荷的α粒子的很强的排斥力使粒子发生大角度偏转;原子核的体积很小,其直径约为原子直径的万分之一至十万分之一,核外是很大的空的空间,带负电的、质量比核轻得多的电子在这个空间里绕核运动,卢瑟福在论文中提出他的原子有核模型可从几个方面验证,盖革和马斯顿1912年所做的实验证实了原子核的存在。
α粒子散射实验

α粒子散射实验α粒子散射实验α粒子散射实验(a-particle scattering experiment)又称金箔实验、Geiger-Marsden 实验或卢瑟福α粒子散射实验引。
是1909年汉斯·盖革和恩斯特·马斯登在欧内斯特·卢瑟福指导下于英国曼彻斯特大学做的一个著名物理实验。
目录实验用准直的α射线轰击厚度为微米的金箔,发现绝大多数的α粒子都照直穿过薄金箔,偏转很小,但有少数α粒子发生角度比汤姆孙模型所预言的大得多的偏转,大约有1/8000 的α粒子偏转角大于90°,甚至观察到偏转角等于150°的散射,称大角散射,更无法用汤姆孙模型说明。
1911年卢瑟福提出原子的有核模型(又称原子的核式结构模型),与正电荷联系的质量集中在中心形成原子核,电子绕着核在核外运动,由此导出α粒子散射公式,说明了α粒子的大角散射。
卢瑟福的散射公式后来被盖革和马斯登改进了的实验系统地验证。
根据大角散射的数据可得出原子核的半径上限为10-14米,此实验开创了原子结构研究的先河。
这个实验推翻了J.J.汤姆孙在1903年提出的原子的葡萄干圆面包模型,认为原子的正电荷和质量联系在一起均匀连续分布于原子范围,电子镶嵌在其中,可以在其平衡位置作微小振动,为建立现代原子核理论打下了基础。
编辑本段实验目的与过程卢瑟福从1909年起做了著名的α粒子散射实验,实验的目的是想证实汤姆孙原子模型的正确性,实验结果却成了否定汤姆孙原子模型的有力证据。
在此基础上,卢瑟福提出了原子核式结构模型。
为了要考察原子内部的结构,必须寻找一种能射到原子内部的试探粒子,这种粒子就是从天然放射性物质中放射出的α粒子。
卢瑟福和他的助手用α粒子轰击金箔来进行实验,图14-1是这个实验装置的示意图。
在一个铅盒里放有少量的放射性元素钋(Po),它发出的α射线从铅盒的小孔射出,形成一束很细的射线射到金箔上。
当α粒子穿过金箔后,射到荧光屏上产生一个个的闪光点,这些闪光点可用显微镜来观察。
卢瑟福散射_实验报告

一、实验目的1. 验证卢瑟福散射理论,理解原子核式结构模型;2. 掌握实验装置的使用方法,学会数据处理和误差分析;3. 培养科学实验技能和团队协作能力。
二、实验原理卢瑟福散射实验是通过α粒子轰击金箔,观察α粒子在金箔后的散射情况,从而验证原子核式结构模型。
根据卢瑟福散射理论,当α粒子穿过原子时,只有当α粒子与原子核的距离小于某一特定值时,α粒子才会发生散射。
该特定值与原子核的半径有关,即r = (ke^2)/(p^2),其中k为库仑常数,e为电子电荷,p为α粒子的动量。
三、实验仪器与材料1. 实验仪器:卢瑟福散射实验装置、α粒子源、金箔、计数器、显微镜、计算机等;2. 实验材料:金箔、α粒子源、电源、真空泵等。
四、实验步骤1. 安装实验装置,确保所有仪器连接正确;2. 将金箔固定在实验装置上,调整显微镜位置,使其与金箔垂直;3. 打开α粒子源,调整电流,使α粒子流稳定;4. 打开计数器,记录α粒子在金箔后的散射情况;5. 调整显微镜位置,观察不同角度的散射情况,记录散射角度及计数;6. 重复步骤4和5,记录多组数据;7. 关闭α粒子源,关闭电源,整理实验器材。
五、实验数据与处理1. 记录实验数据,包括散射角度、计数等;2. 利用计算机软件处理数据,计算散射角度与计数的关系;3. 对比实验数据与理论计算值,分析误差来源。
六、实验结果与分析1. 实验结果显示,绝大多数α粒子穿过金箔后仍沿原来的方向前进,偏转角度很小;2. 少数α粒子发生了较大的偏转,偏转角度超过90度;3. 极少数α粒子的偏转角度超过180度,甚至被反弹回来。
根据实验结果,可以得出以下结论:1. 原子内部存在一个带正电的核,核的半径远小于原子半径;2. 原子核的质量远大于电子的质量;3. 原子核的正电荷集中在原子内部,电子围绕原子核运动。
七、误差分析1. α粒子源电流不稳定,导致α粒子流不稳定;2. 金箔厚度不均匀,导致α粒子散射角度不准确;3. 实验装置存在一定误差,如显微镜的读数误差等;4. 数据处理过程中存在舍入误差。
α粒子散射实验实验报告

0.436 0.524 0.611 0.698 0.785 0.873
13 1 0 1 0 0
10 3 1 1 1 0
4 4 2 0 0 0
8 2 1 1 0 0
10 5 0 3 0 0
9 3 1 1 0 0
10 3 1 1 0 0
2.曲线拟合
根据表 1,做出探测器探测到的粒子数 N 的平均值与散射角θ的关系; 再按照修正拟合公式(6)式进行曲线拟合,如图 2 所示。 原拟合公式
N P sin ( / 2)
4
(5)
N A
B sin ( / 2) C
4
(6)
图 2 探测到的粒子数平均数 N 与散射角θ的关系
五.结论与思考
1.结论 在一定程度上验证了α例子散射卢瑟福公式的正确性, 即N
1 sin ( / 2) 。
4
2.关于曲线拟合函数的说明
在拟合曲线的过程中,我先将θ以角度制表示,并增加 x 轴偏移量 A 弥补误差使得在θ=0 处取得最大值,得到图 3。红色线表示拟合的曲 线,发现其有一定的周期性,意识到应该使用弧度制。再次拟合得到图 4,发现在θ=0 处曲线无穷大,而理论上不该有这样的奇异性,因此我 更改了原拟合公式式(5) ,补上了常数 C 修正零点处奇异性。
count1 668 806 875 1020 1069 1149 1173 1190 1222 1295 1310 1275 1283 1248 1107 1184 939 811 723 612 514 382 277 250 164 148 85 40 40 31 20
count2 687 790 919 1002 1092 1188 1148 1225 1256 1284 1290 1264 1188 1236 1134 1103 919 882 697 622 501 381 279 225 176 108 82 43 43 29 25
卢瑟福的α粒子散射实验观察和结论

卢瑟福的α粒子散射实验观察和结论卢瑟福的α粒子散射实验观察和结论导言卢瑟福的α粒子散射实验是物理学史上具有里程碑意义的实验之一。
通过此实验,卢瑟福成功地证实了原子结构的基本概念,并揭示了原子核的存在。
本文将探讨卢瑟福的α粒子散射实验的观察结果和结论,并分享我对此实验的观点和理解。
1. 实验背景卢瑟福的α粒子散射实验于1911年进行,当时科学界对原子结构的理解还较为模糊。
卢瑟福希望通过实验来验证当时流行的“杜尔文模型”,即认为原子是由带正电的球体(原子核)和带负电的电子云组成的。
他选择使用α粒子(带有两个负电荷的氦离子)作为入射粒子,通过散射角度的观察来揭示原子的内部结构。
2. 实验过程卢瑟福将一束经过加速的α粒子照射到薄金属箔上,并在周围布置了一个荧光屏。
通过观察荧光屏上出现的散射点和角度,卢瑟福记录下了大量实验数据。
3. 实验观察结果卢瑟福的实验观察结果出人意料,与当时的预期相去甚远:(1) 大多数α粒子出射角度很小,接近与入射方向一致;(2) 一小部分α粒子发生明显的偏转,出射角度远离入射方向;(3) 极少数α粒子甚至发生180度的反向散射,返回入射方向。
4. 实验结论基于上述观察结果,卢瑟福得出了以下结论:(1) 原子具有较大的空隙,大部分α粒子可以直接穿过原子而不发生散射;(2) 原子中存在带正电的原子核,同时带负电的电子云位于其周围;(3) 发生明显偏转的α粒子与正电荷较大的原子核发生了相互作用;(4) 散射角度与入射粒子的能量和散射物质的原子核正电荷有关。
5. 对实验的观点和理解卢瑟福的α粒子散射实验提供了直接证据,证明了历史上首次提出的原子核模型。
此模型认为原子核位于原子的中心,其中带有正电荷,并且占据了大部分原子的质量。
这个实验打破了当时流行的汤姆孙模型,即认为原子是由均匀分布的正负电荷所组成。
对于实验的观察结果,我认为其中最令人震惊的是极少数α粒子的180度反向散射。
这意味着原子核的大小远远小于原子的整体大小,同时具有较大的正电荷。
卢瑟福的a粒子散射实验结论原理计算

卢瑟福的a粒子散射实验结论原理计算卢瑟福的α粒子散射实验是一个具有重要意义的物理实验。
该实验是由新西兰物理学家欧内斯特·卢瑟福于20世纪初进行的,实验中使用了α粒子(即氦离子或称α粒子)射向一个金属薄膜,并对散射角度和散射强度进行了观察和测量。
根据经典的电磁理论,当一个α粒子入射到坚硬物体上时,它会受到库仑力的相互作用。
根据库仑定律,这个作用力具有反比于距离的平方的关系,因此入射到金属薄膜的α粒子将会受到金属原子核的库仑力作用,与之发生散射。
卢瑟福实验的重要结论如下:1.大部分的α粒子直线穿过金属薄膜,只发生微小的散射。
这表明原子的大部分空间是由空隙构成的,因为α粒子直径比原子小得多。
2.少数的α粒子经过散射后,发现其散射角度很大。
这暗示了原子具有一个高度集中的、具有正电荷的中心区域,即原子核。
3.α粒子散射的散射角度与入射粒子的能量有关。
这表明散射的短距离库仑相互作用,与α粒子的能量相关。
根据以上结论,卢瑟福提出了最早的原子核模型,即卢瑟福散射模型。
根据该模型,原子由一个带正电荷的原子核和围绕核的负电荷电子云组成。
原子的大部分体积为空隙,几乎所有的质量都集中在原子核中。
卢瑟福散射实验结论的原理可以通过经典的库仑力和动量守恒定律来解释。
在实验中,当α粒子与金属原子核发生相互作用时,它们之间的库仑力导致了散射。
根据电磁力的方向,α粒子将会受到一个向外的力,从而发生向后的散射。
根据动量守恒定律,散射后的α粒子的动量也会改变,从而使其散射角度发生偏转。
根据电磁力的定性描述和动量守恒定律可以计算散射角度和散射强度。
实际上,卢瑟福通过对散射后α粒子的观察和测量,得出了散射角度与入射粒子能量之间的关系,并从而确定了原子核的存在。
总结起来,卢瑟福的α粒子散射实验结论揭示了原子内部结构的重要特征,尤其是原子核的存在。
这项实验在现代原子物理学的发展中具有深远意义,为原子核物理学的诞生奠定了基础,也为后来的量子力学的发展提供了重要线索。
阿尔法粒子散射实验现象

阿尔法粒子散射实验现象1. 什么是阿尔法粒子散射实验?阿尔法粒子散射实验可是个有趣的故事,想当年,科学家们在做实验的时候,简直像是在上演一场“物理学版的麻将”。
我们知道,阿尔法粒子是原子核中发射出来的一种粒子,听上去有点高大上,但其实就像小球一样,飞来飞去的。
而这个实验的核心,就是要看这些小球碰到其他物体时会发生什么。
说到这里,大家是不是也想象到一个小孩在玩弹珠,碰到墙壁会反弹?就是这个意思!1.1 实验的初衷这个实验的背后有个大名鼎鼎的人物,那就是恩斯特·卢瑟福。
卢瑟福可是物理学界的巨星,他想要搞明白原子的结构,于是就决定用阿尔法粒子去“撞击”一些金属薄膜。
他的想法是,既然粒子那么小,那它们和原子之间的关系就像小朋友在游乐场里玩碰碰车,结果往往出乎意料。
哦,对了,大家想象一下,实验室里一片忙碌,科学家们就像是在调皮捣蛋的小孩,一边忙着调整仪器,一边期待着奇妙的结果。
1.2 结果的惊人反响实验开始了!阿尔法粒子们像箭一样飞向金属薄膜,但谁能想到,大部分粒子居然直接穿了过去,只有少数被偏转或者反弹。
这就好比是我们在走廊里看到一个“大块头”,大多数人都会绕过他,只有少数勇敢者才会试着撞一撞。
这下,卢瑟福大惊失色,原来原子内部是空的,几乎没有什么东西阻挡这些小粒子。
这个发现简直是翻天覆地,让人意识到原子的结构比想象中复杂得多。
2. 阿尔法粒子散射的意义阿尔法粒子散射实验不仅仅是一个有趣的故事,它还揭示了许多深刻的科学道理。
这个实验就像是为原子世界打开了一扇窗,透过这扇窗,我们能看到原子结构的奥秘。
很多人可能会想,“这和我有什么关系呢?”其实,大家要知道,这些小小的粒子在我们生活中无处不在,它们的行为也影响着我们的日常生活,比如电器的工作原理、化学反应等等,都是依赖于这些微观世界的规律。
2.1 科学发展的里程碑阿尔法粒子散射实验不仅仅是一次成功的实验,它还标志着现代物理学的一次飞跃。
可以说,这个实验就像是为未来的科学家们铺了一条光明大道,让他们可以在这条路上继续探索更多未知的领域。
α粒子散射实验 实验报告
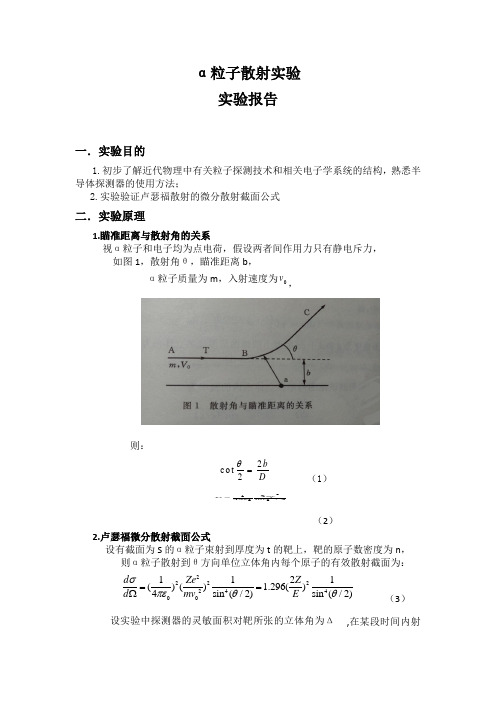
α粒子散射实验实验报告一.实验目的1.初步了解近代物理中有关粒子探测技术和相关电子学系统的结构,熟悉半导体探测器的使用方法;2.实验验证卢瑟福散射的微分散射截面公式二.实验原理1.瞄准距离与散射角的关系视α粒子和电子均为点电荷,假设两者间作用力只有静电斥力,如图1,散射角θ,瞄准距离b ,α粒子质量为m ,入射速度为0v ,则:(1)(2)2.卢瑟福微分散射截面公式设有截面为S 的α粒子束射到厚度为t 的靶上,靶的原子数密度为n ,则α粒子散射到θ方向单位立体角内每个原子的有效散射截面为:2222244001121()() 1.296()4sin (/2)sin (/2)d Ze Z d mv E σπεθθ==Ω (3) 设实验中探测器的灵敏面积对靶所张的立体角为Δ,在某段时间内射2co t2b D θ=00πε到靶上的粒子总数为T ,则观察到的粒子数为:(4)三.实验仪器粒子源 真空室 探测器与计数系统 真空泵 四.实验数据及处理1.原始数据及处理表1 探测到的粒子数count 与散射角的关系Angle/° Angle /rad count1 count2 count3 count4 count5 N=count average count median -10-0.175 668 687 634 683 719 678 683 -9 -0.157 806 790 738 824 776 787 790 -8 -0.140 875 919 924 923 904 909 919 -7 -0.122 1020 1002 960 1032 999 1003 1002 -6 -0.105 1069 1092 1100 1075 1058 1079 1075 -5 -0.087 1149 1188 1201 1115 1149 1160 1149 -4 -0.070 1173 1148 1164 1196 1171 1170 1171 -3 -0.052 1190 1225 1225 1236 1237 1223 1225 -2 -0.035 1222 1256 1288 1283 1225 1255 1256 -1 -0.017 1295 1284 1292 1296 1278 1289 1292 0 0.000 1310 1290 1281 1264 1355 1300 1290 1 0.017 1275 1264 1299 1231 1253 1264 1264 2 0.035 1283 1188 1220 1274 1250 1243 1250 3 0.052 1248 1236 1211 1201 1257 1231 1236 4 0.070 1107 1134 1083 1116 1132 1114 1116 5 0.087 1184 1103 1150 1105 1132 1135 1132 6 0.105 939 919 932 894 934 924 932 7 0.122 811 882 757 853 837 828 837 8 0.140 723 697 729 715 715 716 715 9 0.157 612 622 627 615 610 617 615 10 0.175 514 501 541 517 501 515 514 11 0.192 382 381 412 381 405 392 382 12 0.209 277 279 310 335 294 299 294 13 0.227 250 225 227 228 163 219 227 14 0.244 164 176 160 168 179 169 168 15 0.262 148 108 127 116 135 127 127 16 0.279 85 82 65 72 78 76 78 17 0.297 40 43 33 34 45 39 40 18 0.314 40 43 33 34 45 39 40 19 0.332 31 29 28 29 22 28 29 200.349 20 25 20 14 24 21 2001()()4sin (/2)Ze nt N Tmv πεθ∆Ω=25 0.436 13 10 4 8 10 9 10 30 0.524 1 3 4 2 5 3 3 35 0.611 0 1 2 1 0 1 1 40 0.698 1 1 0 1 3 1 1 45 0.785 0 1 0 0 0 0 0 50 0.873 0 0 0 0 0 0 02.曲线拟合根据表1,做出探测器探测到的粒子数N 的平均值与散射角θ的关系; 再按照修正拟合公式(6)式进行曲线拟合,如图2所示。
卢瑟福的α粒子散射实验结论

卢瑟福的α粒子散射实验结论1. 实验背景说起卢瑟福,那可真是个了不起的科学家,咱们今天要聊的就是他那经典的α粒子散射实验。
大约在1911年,这位大名鼎鼎的物理学家在研究原子结构时,做了个大胆的实验。
想象一下,那个时候,科学界对原子内部的构造可谓是一头雾水,搞得像是在摸黑走路。
卢瑟福和他的团队决定用α粒子,也就是一种带正电的粒子,来探探原子里到底藏了些什么东西。
真是敢为人先啊!实验的过程其实挺简单的。
他们把α粒子从放射性元素发射出来,然后让这些粒子撞击一层极薄的金箔。
金箔薄得就像是纸一样,几乎可以用手指捅破。
接着,卢瑟福用荧光屏观察这些α粒子是怎么散射的。
这里面可有不少戏剧性的时刻,就像一场精彩的表演。
2. 实验结果2.1 意外的发现好吧,结果真是让人瞠目结舌!大部分的α粒子都是笔直穿过金箔的,仿佛金箔根本就不存在。
但有一小部分的粒子却偏偏改变了方向,有的甚至反弹回来,简直像是看见了鬼。
卢瑟福当时一定觉得,哎呀,怎么回事呢?难道原子内部隐藏着什么秘密?这可真是让人百思不得其解。
2.2 原子模型的重构经过一番深入思考,卢瑟福得出一个惊人的结论:原子并不是一团糟的“梅花”,而是有着明确结构的。
他提出,原子里有一个非常小且密集的“原子核”,而α粒子反弹就是因为碰到了这个“核”。
这个核是正电的,周围则是负电的电子在转啊转,真是一个小宇宙!这不禁让人想起一句话:外表光鲜,内里却是别有洞天。
3. 实验的意义3.1 对科学界的影响卢瑟福的发现简直就是科学界的一场地震,彻底颠覆了之前的“汤姆逊的葡萄干布丁模型”。
他这一理论,不但让大家看到了原子的真实结构,还为后来的科学研究铺平了道路。
原子核的概念后来成了核物理学的基石,简直是功德无量。
3.2 对日常生活的启示你可能会问,这跟我们日常生活有什么关系呢?其实,卢瑟福的实验提醒我们,很多时候,表象并不代表真相。
就像我们看到的一个人,可能外表光鲜亮丽,内心却藏着故事。
所以,别轻易下结论,要多观察,多思考!另外,卢瑟福的好奇心也是我们每个人都应该学习的。
α粒子散射-物理试验

实验1.1 α粒子散射电子被发现以后,人们普遍认识到电子是一切元素的原子的基本组成部分。
但通常情况下原子是呈电中性的,这表明原子中还有与电子的电荷等量的正电荷,所以,研究原子的结构首先要解决原子中正负电荷怎样分布的问题。
从1901年起,各国科学家提出各种不同的原子模型。
第一个比较有影响的原子模型,是J.J.汤姆逊于1904年提出“电子浸浮于均匀正电球”中的模型。
他设想,原子中正电荷与电子间的作用力以及电子与电子间的斥力的作用下浮游在球内。
这种模型被俗称为“葡萄干布丁模型”。
汤姆逊还认为,不超过某一数目的电子将对称地组成一个稳定的环或球壳;当电子的数目超过一定值时,多余电子组成新的壳层,随着电子的增多将造成结构上的周期性。
因此他设想,元素性质的周期变化或许可用这种电子分布的壳层结构作出解释。
汤姆逊的原子模型很快地被进一步的实验所否定,它不能解释α射线的大角度散射现象。
卢瑟福从1904年到1906年6月,做了许多α射线通过不同厚度的空气、云母片和金属箔(如铝箔)的实验。
英国物理学家W.H.布拉格(Bragg, W.H.1862-1942)在1904-1905年也做了这样的实验。
他们发现, 在此实验中α射线速度减慢,而且径迹偏斜了(即发生散射现象).例如,通过云母的的某些α射线,从它们原来的途径约片斜2°,发生了小角度散射,1906年冬, 卢瑟福还认识到α粒子在某一临界速度以上时能打入原子内部,由它的散射和所引起的原子内电场的反应可以探索原子内部结构.而且他还预见到可能会出现较大角度的散射.1910年12月,卢瑟福对大角度散射过程的受力关系进行计算,得出一个新的原子结构设想。
经过反思索、研究,于1911年4月下旬写出论文为靶的金属箔的原子一次碰撞中改变其方向的,因此原子中有一个体积很小、质量很大的带正电荷的原子核,它对带正电荷的α粒子的很强的排斥力使粒子发生大角度偏转;原子核的体积很小,其直径约为原子直径的万分之一至十万分之一,核外是很大的空的空间,带负电的、质量比核轻得多的电子在这个空间里绕核运动,卢瑟福在论文中提出他的原子有核模型可从几个方面验证,盖革和马斯顿1912年所做的实验证实了原子核的存在。
卢瑟福的a粒子散射实验现象及结论

卢瑟福的a粒子散射实验现象及结论一、实验介绍二、实验现象1. α粒子的发射与散射2. α粒子的反跳现象三、实验结论1. 原子具有空心结构2. 原子核具有正电荷3. 原子核与电子的比例关系四、实验意义及影响一、实验介绍卢瑟福的a粒子散射实验是物理学中非常重要的一个经典实验,它是对原子结构和性质进行研究的基础。
该实验于1910年由英国物理学家欧内斯特·卢瑟福(Ernest Rutherford)领导完成,是一项利用α粒子对原子核进行探测的实验。
二、实验现象1. α粒子的发射与散射在卢瑟福的a粒子散射实验中,首先将α放射源放置在一个铅盒中,使其向外发出α粒子。
然后将α粒子引入真空玻璃管中,通过调节电压和电流来使α粒子加速,并通过一个小孔射向金箔靶。
在金箔靶后面设立一个荧光屏,用来观察α粒子的散射情况。
实验结果表明,大多数α粒子直线穿过金箔靶,只有极少数α粒子被散射。
这说明原子具有空心结构,其中正电荷集中在原子核内。
2. α粒子的反跳现象在实验中,还观察到了α粒子的反跳现象。
即有些α粒子经过金箔靶后会发生反弹,回到射线源处。
这说明原子核具有正电荷,并且与电子相比非常小。
三、实验结论1. 原子具有空心结构卢瑟福的a粒子散射实验表明,大多数α粒子直线穿过金箔靶,只有极少数α粒子被散射。
这说明原子具有空心结构,其中正电荷集中在原子核内。
2. 原子核具有正电荷实验还观察到了α粒子的反跳现象。
即有些α粒子经过金箔靶后会发生反弹,回到射线源处。
这说明原子核具有正电荷,并且与电子相比非常小。
3. 原子核与电子的比例关系通过对实验数据的分析,卢瑟福得出了一个重要的结论:原子核的质量与电子的质量相比非常大,而原子核的直径只有原子直径的万分之一。
这说明原子核与电子的比例关系是非常不同的。
四、实验意义及影响卢瑟福的a粒子散射实验是对原子结构和性质进行研究的基础。
它揭示了原子具有空心结构,其中正电荷集中在原子核内;同时也证明了原子核具有正电荷,并且与电子相比非常小。
根据α粒子散射实验的现象

放射性物质在自然界中广泛存在, 如铀矿、钍矿等,同时也用于医
学、工业和科学研究等领域。
α粒子的产生
放射性物质通过衰变过程释放出α粒子,衰变过程中原子核释放出一个或多个α粒子。
α粒子是由两个中子和两个质子结合在一起形成的氦原子核,具有较大的质量和电荷。
α粒子的速度相对较慢,通常在空气中只能飞行几厘米至几十厘米,但在某些情况下 可以穿透较薄的物质。
实验结果分析
散射结果的统计
01
02
03
Hale Waihona Puke 散射角度分布观察到α粒子散射的角度 分布,角度越大,散射越 强。
散射次数统计
对多次散射的次数进行统 计,发现散射次数与散射 角度有一定的关联。
散射能量分布
分析散射过程中能量的分 布情况,有助于了解散射 机制。
散射结果的解释
波动性解释
根据德布罗意波理论,粒 子具有波动性,散射是波 的干涉现象。
原子结构的研究对生物学领域产生 了影响,例如在分子生物学和遗传 学方面的研究。
感谢观看
THANKS
散射角度的分布
大部分α粒子穿过金箔后仍沿原来的方向前进
这是因为金箔中的原子核密度较高,大部分α粒子在穿过金箔时只受到微弱的库仑力作用, 因此运动方向基本不变。
小部分α粒子会发生较大的偏转
这是由于金箔中的原子核密度较高,部分α粒子在穿过金箔时会受到较强的库仑力作用,导 致其运动方向发生较大的偏转。
极少数α粒子被反弹回来
根据α粒子散射实验 的现象
• α粒子的发射源 • α粒子的散射过程 • 实验结果分析 • α粒子散射实验的意义
目录
01
α粒子的发射源
放射性物质
放射性物质是一种能够自发地放 出射线的天然或人工元素,常见 的放射性物质包括铀、钚、铯等。
α粒子散射实验

用于放大荧光屏上的轨迹,以便 更准确地观察和分析。
实验操作步骤
01
02
03
04
步骤1
将金箔放置在实验装置中适当 的位置。
步骤2
启动α粒子源,使粒子通过金 箔。
步骤3
使用显微镜观察荧光屏上散射 后的α粒子轨迹。
步骤4
记录并分析观察到的轨迹数据 ,得出结论。
03 α粒子的散射现象
散射分布
散射分布描述了α粒子在穿过物 质时在不同方向上的散射情况。
实验结果表明,绝大多数α粒子穿过金 箔后仍沿原来的方向前进,说明原子 内部绝大部分空间是空的,原子核所 占的空间非常小。
极少数α粒子发生了较大的偏转,并有 极少数α粒子的偏转超过90°,甚至几乎 达到180°而被反弹回来,说明原子核带 正电荷且质量很大。
对后续研究的影响
α粒子散射实验为卢瑟福提出 原子核式结构模型奠定了基础。
对物质波的发现
实验中观察到的α粒子散 射轨迹呈现波动性,为德 布罗意物质波理论的提出 提供了实验依据。
02 实验装置与操作流程
金箔
厚度
金箔的厚度通常在 0.05mm左右,以确保足 够的强度和稳定性。
纯度
为了确保实验结果的准确 性,金箔的纯度要求极高, 通常为99.9%或更高。
制备
金箔通常是通过将纯金压 延成薄片,然后切割成适 当的大小制备而成。
α粒子的性质
01
α粒子是氦原子核,带2个正电荷, 质量约为质子的4倍。
02
α粒子具有强电场和相对较大的质 量,因此具有较大的穿透能力和散 射概率。
实验目的与意义
01
02
03
验证原子核式结构
通过观察α粒子散射实验, 可以验证卢瑟福提出的原 子核式结构是否正确。
α粒子散射实验的研究

α粒子散射实验的研究(光电信息科学与工程学院朵海蛟20120511203)摘要:通过对α粒子散射实验[1]的背景、实验过程和卢瑟福提出原子核式结构模型过程的分析,总结出卢瑟福作为物理学家具有敢于挑战权威、善于怀疑、勇于创新、严谨与自信的治学精神和实事求是的科学态度,以期对我们的科学研究工作有所借鉴。
关键词:α粒子散射;卢瑟福;核式结构模型;散射实验0 α粒子散射实验的研究背景α粒子散射实验(a-particle scattering experiment)又称金箔实验、Geiger-Marsden实验或卢瑟福α粒子散射实验引。
是1909年汉斯·盖革和恩斯特·马斯登在欧内斯特·卢瑟福指导下于英国曼彻斯特大学做的一个著名物理实验[2]。
发生极少数α粒子的大角度偏转现象是出乎意料的。
根据汤姆孙模型的计算,α粒子穿过金箔后偏离原来方向的角度是很小的,因为电子的质量不到α粒子的1/7400,α粒子碰到它,就像飞行着的子弹碰到一粒尘埃一样,运动方向不会发生明显的改变。
正电荷又是均匀分布的,α粒子穿过原子时,它受到原子内部两侧正电荷的斥力大部分相互抵消,α粒子偏转的力就不会很大。
然而事实却出现了极少数α粒子大角度偏转的现象。
卢瑟福后来回忆说:“这是我一生中从未有的最难以置信的事,它好比你对一张纸发射出一发炮弹,结果被反弹回来而打到自己身上……”卢瑟福对实验的结果进行了分析,认为只有原子的几乎全部质量和正电荷都集中在原子中心的一个很小的区域,才有可能出现α粒子的大角度散射。
由此,卢瑟福在1911年提出了原子的核式结构模型,认为在原子的中心有一个很小的核,叫做原子核(nucleus),原子的全部正电荷和几乎全部质量都集中在原子核里,带负电的电子在核外空间里绕着核旋转。
1 实验目的卢瑟福从1909年起做了著名的α粒子散射实验,实验的目的是想证实汤姆孙原子模型的正确性,实验结果却成了否定汤姆孙原子模型的有力证据。
卢瑟福α粒子散射试验的结果

四.原子核的电荷与尺度
根据卢瑟福的原子核式模型和α粒子散射的 实验数据,可以推算出各种元素原子核的 电荷数,还可以估计出原子核的大小。
2.在用α粒子轰击金箔的实验中,卢瑟福观察到的 α粒子的运动情况是(B )
A、全部α粒子穿过金属箔后仍按原来的方向前 进
B、绝大多数α粒子穿过金属箔后仍按原来的方 向前进,少数发生较大偏转,极少数甚至被弹回
C、少数α粒子穿过金属箔后仍按原来的方向前 进,绝大多数发生较大偏转,甚至被弹回
D、全部α粒子都发生很大偏转
❖ 科学成就
1、他关于放射性的研究确立了放 射性是发自原子内部的变化。为开 辟原子物理学做了开创性的工作。
2、1909年起,卢瑟福根据a粒子
散射试验现象提出原子核式结构模 型。把原子结构的研究引上了正确 的轨道,被誉为原子物理学之父。
3、1919年,卢瑟福做了用α粒 子轰击氮核的实验,从而发现了质 子。
(1)原子的半径约为10-10m、原子核半径 约是10-15m,原子核的体积只占原子的体 积的万亿分之一。
(2)原子核所带正电荷数与核外电子数以 及该元素在周期表内的原子序数相等。
四.原子核的电荷与尺度
根据卢瑟福的原子结构模型,原子内部是十分 “空旷”的,举一个简单的例子:露珠和体育场
原子
体育场
原子核
不超过零点几度,发生大角度偏转的几率几乎是零.
实验结果却是有八千分之一的粒子发生了大 角度偏转 !!!
实验结果与之前预测完全不一致, 所以原子结构模型必须重新构思!
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
α粒子散射实验
实验报告
一.实验目的
1.初步了解近代物理中有关粒子探测技术和相关电子学系统的结构,熟悉半
导体探测器的使用方法;
2.实验验证卢瑟福散射的微分散射截面公式
二.实验原理
1.瞄准距离与散射角的关系
视α粒子和电子均为点电荷,假设两者间作用力只有静电斥力,
如图1,散射角θ,瞄准距离b ,
α粒子质量为m ,入射速度为0v ,
则:
(1)
(2)
2.卢瑟福微分散射截面公式
设有截面为S 的α粒子束射到厚度为t 的靶上,靶的原子数密度为n ,
则α粒子散射到θ方向单位立体角内每个原子的有效散射截面为:
2222244
001121
()() 1.296()4sin (/2)sin (/2)d Ze Z d mv E σπεθθ==Ω (3) 设实验中探测器的灵敏面积对靶所张的立体角为Δ
,在某段时间内射
2co t
2b D θ=0
0πε
到靶上的粒子总数为T ,则观察到的粒子数为:
(4)
三.实验仪器
粒子源 真空室 探测器与计数系统 真空泵 四.实验数据及处理
1.原始数据及处理
表1 探测到的粒子数count 与散射角的关系
Angle/° Angle /rad count1 count2 count3 count4 count5 N=count average count median -10
-0.175 668 687 634 683 719 678 683 -9 -0.157 806 790 738 824 776 787 790 -8 -0.140 875 919 924 923 904 909 919 -7 -0.122 1020 1002 960 1032 999 1003 1002 -6 -0.105 1069 1092 1100 1075 1058 1079 1075 -5 -0.087 1149 1188 1201 1115 1149 1160 1149 -4 -0.070 1173 1148 1164 1196 1171 1170 1171 -3 -0.052 1190 1225 1225 1236 1237 1223 1225 -2 -0.035 1222 1256 1288 1283 1225 1255 1256 -1 -0.017 1295 1284 1292 1296 1278 1289 1292 0 0.000 1310 1290 1281 1264 1355 1300 1290 1 0.017 1275 1264 1299 1231 1253 1264 1264 2 0.035 1283 1188 1220 1274 1250 1243 1250 3 0.052 1248 1236 1211 1201 1257 1231 1236 4 0.070 1107 1134 1083 1116 1132 1114 1116 5 0.087 1184 1103 1150 1105 1132 1135 1132 6 0.105 939 919 932 894 934 924 932 7 0.122 811 882 757 853 837 828 837 8 0.140 723 697 729 715 715 716 715 9 0.157 612 622 627 615 610 617 615 10 0.175 514 501 541 517 501 515 514 11 0.192 382 381 412 381 405 392 382 12 0.209 277 279 310 335 294 299 294 13 0.227 250 225 227 228 163 219 227 14 0.244 164 176 160 168 179 169 168 15 0.262 148 108 127 116 135 127 127 16 0.279 85 82 65 72 78 76 78 17 0.297 40 43 33 34 45 39 40 18 0.314 40 43 33 34 45 39 40 19 0.332 31 29 28 29 22 28 29 20
0.349 20 25 20 14 24 21 20
01(
)(
)4sin (/2)
Ze nt N T
mv πεθ∆Ω
=
25 0.436 13 10 4 8 10 9 10 30 0.524 1 3 4 2 5 3 3 35 0.611 0 1 2 1 0 1 1 40 0.698 1 1 0 1 3 1 1 45 0.785 0 1 0 0 0 0 0 50 0.873 0 0 0 0 0 0 0
2.曲线拟合
根据表1,做出探测器探测到的粒子数N 的平均值与散射角θ的关系; 再按照修正拟合公式(6)式进行曲线拟合,如图2所示。
原拟合公式 (5)
4sin (/2)B
N A C θ=+
+ (6)
图2 探测到的粒子数平均数N 与散射角θ的关系
五.结论与思考
1.结论
在一定程度上验证了α例子散射卢瑟福公式的正确性,即4
1
sin (/2)N θ∝。
-200
0200400600800
100012001400N
θ/rad
4
sin (/2)
P N θ=
2.
A 4
-200
02004006008001000
12001400个数N
N
3.Rutherford的假设
若要从实验结果严格得出卢瑟福公式(3)式,实验条件应满足一下假设:
①α粒子与靶核只发生单次散射;
②靶核静止;
③Α粒子与靶核间只有库仑力的作用,忽略靶核外电子的作用
在实验中,若金箔厚度很小,那么靶核互相遮蔽性不大,则可满足①。
而靶核质量远大于电子质量,所以可忽略电子对α粒子轨迹的影响,且当电子撞击到原子核时,也可认为核静止,则②③可满足。
在散射角很小的区域,θ趋近于0,瞄准距离很大,这时核外电子作用应不该忽略。
实际上,根据对曲线的拟合可知,三个假设都只是理想化的。
