连续梁支座的计算方法
连续梁支座数量的计算方法

连续梁支座数量的计算方法一、什么是连续梁。
1.1连续梁啊,简单来说呢,就是梁的一种类型。
它可不是孤零零的一段梁,而是好几段梁连在一起的。
就像咱们排队手拉手一样,一段接着一段,形成一个连续的结构。
这种梁在建筑工程里可太常见了,不管是桥梁啊,还是一些大型建筑的框架结构里,都有它的身影。
1.2连续梁的特点就是它的受力比较均匀。
和那种单独的梁比起来,连续梁能够把力分散开,就像大家一起分担重物一样,每个部分都承担一部分力,这样整个结构就更稳定、更安全。
二、支座在连续梁中的重要性。
2.1支座呢,就像是连续梁的“脚”。
没有支座,连续梁就没地儿站,那整个结构就没法存在了。
支座的作用可大了,它能够支撑连续梁的重量,还能约束梁的位移。
这就好比咱们人站在地上,脚不仅要支撑身体的重量,还得让咱们稳稳地站着,不能随便滑动或者晃动。
2.2不同类型的支座对连续梁的影响也不一样。
有的支座可以让梁在某个方向上自由转动,有的支座则限制梁的转动。
这就像不同的鞋子对脚的约束不一样,有的鞋子宽松,脚能灵活转动,有的鞋子紧一些,脚的转动就受到限制。
3.1首先呢,咱们得看连续梁的跨数。
这跨数就好比是梁中间断开的次数加上1。
比如说,有两段梁中间断开一次,那这个连续梁就是两跨。
一般来说,连续梁的支座数量比跨数多1。
这就像一条绳子上打几个结,结的数量比断开的次数多1一样。
如果是三跨的连续梁,那支座数量就是4个。
这是最基本的计算方法,就像1+1 = 2那么简单。
3.2但是呢,有时候情况会复杂一些。
如果连续梁的端部有特殊的约束条件,比如说一端是固定在墙上的,这种情况就得特殊对待了。
固定的那一端也算是一个支座,而且这个支座的约束能力比普通支座要强。
这就好比一个人被绑在柱子上,他的活动受到的限制就比站在平地上大得多。
在计算支座数量的时候,可不能把这种特殊的端部约束给忽略了,不然计算出来的结果就不对了,那可就是“差之毫厘,谬以千里”了。
四、实际应用中的注意事项。
40+64+40m连续梁边墩支座预偏量计算
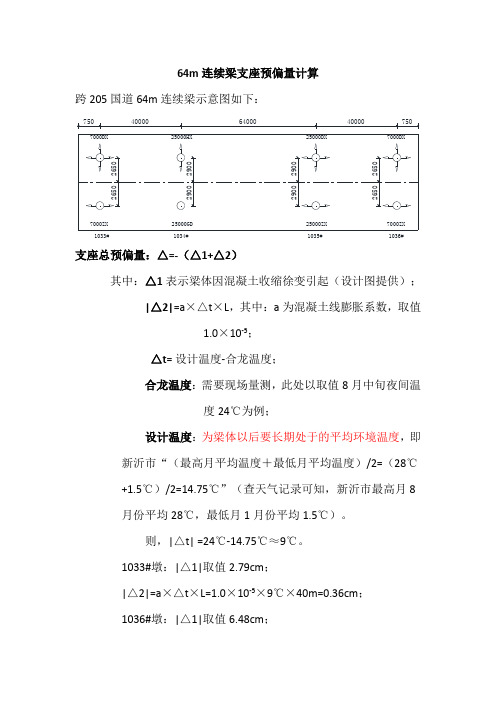
64m 连续梁支座预偏量计算
跨205国道64m 连续梁示意图如下:
支座总预偏量:△=-(△1+△2)
其中:△1表示梁体因混凝土收缩徐变引起(设计图提供); |△2|=a ×△t ×L ,其中:a 为混凝土线膨胀系数,取值
1.0×10-5;
△t = 设计温度-合龙温度;
合龙温度:需要现场量测,此处以取值8月中旬夜间温
度24℃为例;
设计温度:为梁体以后要长期处于的平均环境温度,即新沂市“(最高月平均温度+最低月平均温度)/2=(28℃+1.5℃)/2=14.75℃”(查天气记录可知,新沂市最高月8月份平均28℃,最低月1月份平均1.5℃)。
则,|△t| =24℃-14.75℃≈9℃。
1033#墩:|△1|取值2.79cm ;
|△2|=a ×△t ×L=1.0×10-5×9℃×40m=0.36cm ; 1036#墩:|△1|取值6.48cm ;
750
750
40000
64000
400001033#
1034#
1035#
1036#
|△2|=a×△t×L=1.0×10-5×9℃×104m=0.94cm。
分析:由于以后梁体长期处于的平均环境温度(即设计温度14.75℃)低于合龙时环境温度24℃,所以梁体以后要收缩,因此△2和△1引起的梁体效果要叠加。
即:1033#:△=-(2.79+0.36)=-3.15cm;
1086#:△=6.48+0.94=7.42cm。
2019年6月24日。
连续梁悬浇施工临时固结(支座)设计计算及应用优化

连续梁悬浇施工临时固结(支座)设计计算及应用优化目前铁路及公路桥梁设计时,连续梁凭其自身的诸多优点应用已非常普遍,受现场地形、环境等因素的限制,部分连续梁只能采用采用悬浇法施工。
连续梁在T构悬浇过程中,因施工等诸多因素会产生不平衡弯矩,为了确保施工安全,需要在墩顶设置墩梁临时固结(支座)或墩旁设置临时支墩。
本文结合现场工程实例,介绍了某铁路客运专线跨高速公路连续箱梁,采用悬浇法施工时,墩顶墩梁临时固结的设计计算思路及现场做法;并就根据现场实际情况,如何选取和优化临时固结结构形式做了简单的说明。
标签:连续箱梁;临时固结(支座);设计;计算;应用优化一、工程簡介本工程为××铁路客运专线××铁路特大桥跨××高速公路双线连续梁。
设计目标时速200km/h,结构形式为60m+100m+60m预应力连续箱梁,总长221.5m。
采用挂篮悬臂浇筑法施工。
按施工顺序共划分为51个梁段,各节段长度及混凝土体积见下表(图)。
0#块梁高为7.5m,边跨现浇段及跨中梁高均为4.5m。
连续梁节段参数表二、现场采用的临时固结措施现场墩顶墩梁临时固结采用HRB335Ф32钢筋和C50混凝土设置,每墩采用308根Ф32钢筋,每根长337.2cm,混凝土截面尺寸采用0.6m*2.3m,每墩4个,具体布置形式见下图。
在临时固结混凝土与墩顶及梁底接触面上铺设塑料膜或油毡作为隔离层,便于临时固结拆除。
若条件许可,可以在临时固结顶、底面处,或中间设置厚5~10cm的硫磺砂浆,预埋电阻丝以便于拆除。
三、设计计算说明设计给定的不平衡弯矩为68000KN·m,相应支反力为60000KN。
首先根据现场实际情况计算不同工况下的不平衡弯矩,及相应支反力,验算设计给定值是否满足要求。
若墩顶临时固结采用HRB335Ф32钢筋和C50混凝土,每墩临时固结需要的钢筋数量、长度,混凝土截面尺寸等参数,通过选取的最大不平衡弯矩和反力确定,最后考虑一定的安全系数后,根据现场实际情况,最终确定临时固结措施的各项参数。
先简支后连续梁支座计算

先简支后连续梁支座计算简支和连续梁是常见的桥梁结构形式,而支座则是桥梁结构中的重要组成部分。
在桥梁设计中,支座的设计和计算是十分关键的。
本文将重点介绍以先简支后连续梁支座计算的相关内容。
简支和连续梁支座的设计和计算是有所区别的。
简支梁支座计算主要考虑梁端的转动和水平力,而连续梁支座计算则需要考虑梁端的转动、水平力和垂直力。
两者的设计和计算方法有一定的差异,需要根据具体的桥梁结构形式进行选择。
对于先简支后连续梁结构,首先需要确定简支段和连续段的边界位置。
在边界位置处,支座需要能够满足简支段和连续段之间的转动和水平力的传递。
通常情况下,简支段的支座设计可以采用简单支座,而连续段的支座设计则需要考虑连续梁的特点。
在简支段的支座计算中,主要考虑的是梁端的转动和水平力。
转动可以通过简支段的支座进行传递,而水平力则需要通过支座的摩擦力来平衡。
支座的摩擦力大小与梁端水平力的大小有关,需要根据具体情况进行计算。
在连续段的支座计算中,除了考虑梁端的转动和水平力外,还需要考虑垂直力。
由于连续梁在连续段上存在弯矩和剪力,梁端会受到垂直方向上的力的作用。
支座需要能够承受这些垂直力,并将其传递到桥墩或基础上。
在进行支座计算时,需要考虑支座的承载能力和稳定性。
支座的承载能力需要满足桥梁的荷载要求,同时还需要考虑支座的材料和结构的强度。
支座的稳定性则需要满足桥梁结构的位移和变形要求,避免桥梁的不稳定和破坏。
在具体的支座计算中,可以采用一些经验公式和计算方法。
例如,可以根据支座的类型和桥梁的参数来选择合适的公式。
同时,还需要结合实际工程经验和设计规范进行综合考虑,以确保支座的设计和计算的准确性和可靠性。
先简支后连续梁支座计算是桥梁设计中的重要内容。
通过合理的支座设计和计算,可以确保桥梁结构的安全和稳定。
在实际工程中,需要根据具体情况和设计要求进行选择和应用,以满足桥梁结构的需求。
同时,还需要注意支座的施工和维护,以确保桥梁的长期使用和运营。
连续板支座弯矩

连续板支座弯矩
连续板支座是一种用于支撑连续梁的结构,它通常由若干个单独的板式支座组成。
在连续梁施工过程中,这些支座会承担来自梁体荷载的弯矩、剪力和轴力等作用力。
对于连续板支座的弯矩计算,需要考虑支座的几何形状、材料特性以及荷载情况等因素。
以下是一些常见的计算方法:
1. 简单支承模型:在简单支承模型中,连续板支座简化为一个单独的支座,承载相应的荷载和弯矩。
弯矩的计算可以根据梁体的挠度和弹性模量等参数进行估算。
2. 解析计算模型:解析计算模型通常基于工程力学原理,考虑连续板支座的具体几何形状和材料特性。
例如,可以利用弹性力学原理和边界条件等方法,推导出支座的弯矩和剪力方程式。
3. 有限元分析模型:有限元分析是一种数值计算方法,可用于模拟连续板支座在荷载作用下的行为。
该方法通常需要将支座的几何形状和材料特性划分为若干个小元素,进而采用离散化方法进行计算,并输出支座内部的各种力学参数,包括弯矩、剪力和轴力等。
需要注意的是,在实际工程当中,连续板支座的弯矩计算往往不是一个简单的问题。
它涉及到众多因素的相互作用,例如各种荷载和边界条件,以及支座本身的刚度和材料特性等。
因此,需要通过科学的计算方法和工程实践经验进行建模和计算。
三等跨连续梁支座反力计算

三等跨连续梁支座反力计算
在工程建设中,连续梁是常用的结构形式,它由多个跨度组成,在跨度过大时常常采用三等跨连续梁的结构形式。
在梁体支撑方面,支座是连接梁体和支撑结构的重要构件之一,支座的反力计算是保证梁体正常工作的重要环节。
下面将从三等跨连续梁支座反力计算的步骤来进行一一阐述。
一、梁体受力分析
首先,需要进行梁体受力分析,计算每个跨度的受力情况,在这个过程中需要考虑梁的自重、荷载、风荷载等等多种外因素对梁的影响。
二、支座位移计算
通过第一步的梁体受力分析之后,可以对支座进行位移计算,在计算之前,需要对三等跨连续梁的结构形式进行了解,通常情况下,三等跨连续梁的中间跨度大梁会采用两端跨度小梁的支座设置方法,中间跨度小梁采用三个支座分别设置。
计算时需要考虑不同跨度的支座位移及其所产生的影响。
三、计算支座反力
通过前两部分的计算,即可开始计算支座反力。
在计算支座反力的过程中需要考虑梁体自身重量、梁体受到的荷载、支座的长板、短板分别所承受的压力、支座位移对支座反力的影响、梁体弯矩对支座反力的影响等等因素。
四、检查计算结果
完成支座反力计算之后,需要对结果进行检查,包括检查计算结果是否合理、是否满足规范要求等等,以确保计算结果的准确性和合理性。
综上所述,三等跨连续梁支座反力计算是建设工程中十分关键的环节,需要认真细致的进行。
只有在正确计算的基础上,才能够确保梁体和支撑结构正常工作,同时也能够为工程建设提供更好的保障。
多跨连续梁支座反力计算

多跨连续梁支座反力计算多跨连续梁是由多个跨度连续组成的梁,支座反力的计算对于梁的设计和实施至关重要。
在计算多跨连续梁支座反力时,需要考虑多个因素,包括梁的几何形状、材料性质、荷载等。
本文将详细介绍多跨连续梁支座反力的计算方法。
首先,需要了解梁的基本形状和几何参数。
多跨连续梁通常由简支梁和跨中固定支座组成,支座类型可以是弹性支座、沉降式支座等。
每个跨度内的几何参数包括梁的长度、高度、宽度等。
其次,需要分析梁材料的性质。
常用的材料包括混凝土、钢等。
根据梁的材料和几何形状,可以计算梁的截面面积、惯性矩等相关参数。
接下来,需要考虑梁所受的荷载。
常见的荷载包括静荷载、动荷载等。
静荷载包括自重、活载等,动荷载包括风荷载、地震荷载等。
根据设计规范和实际情况,可以确定梁所受的各种荷载。
在计算支座反力之前,需要根据梁的几何形状、材料性质和所受荷载等参数,确定梁内的弯矩和剪力分布。
常见的计算方法有弯矩分布法、框架法等。
根据这些分布,可以计算每个支座的反力。
以下是多跨连续梁支座反力计算的具体步骤:1.确定每个跨度内的几何形状和材料性质。
包括梁的长度、高度、宽度等几何参数,以及梁的材料类型和截面形状。
2.确定梁所受的荷载。
包括静荷载和动荷载等各种荷载情况。
3.根据荷载情况,计算每个跨度内的弯矩和剪力分布。
可以使用弯矩分布法或框架法等方法进行计算。
4.根据弯矩和剪力分布,确定每个支座的反力。
根据受力平衡原理,可以得到支座反力的计算公式。
5.进行支座反力的计算。
根据得到的公式和参数,计算每个支座的反力。
6.进行支座反力的校核。
根据设计规范,对计算得到的支座反力进行校核,确保满足设计要求。
需要注意的是,在计算支座反力时,还需要考虑跨度间的相互影响。
即不同支座的反力会相互影响,需要进行综合分析。
连续梁的内力是由整个系统共同承担的,因此支座反力的计算需要综合考虑梁的整体性能。
综上所述,多跨连续梁支座反力的计算是一个复杂的问题,需要考虑多个因素,包括梁的几何形状、材料性质、荷载等。
多跨连续梁支座反力计算

多跨连续梁支座反力计算多跨连续梁是现代桥梁结构中一种非常常见的形式,它在跨度和长度方面都具备了较大的优越性,承载能力和经济性均较为突出。
而在设计这样的结构时,支座反力的计算是一个至关重要的环节,在本文中,我们将给大家详细介绍一下多跨连续梁支座反力计算的各个步骤。
第一步:确定梁的几何形状和建模在计算支座反力之前,需要先了解梁的几何形状,包括梁的跨度、受载长度、断面性质、钢材性质等。
然后,将这些信息用计算机建模的方式呈现出来,便于后续的有限元分析。
第二步:进行静力计算在建立好模型之后,就可以进行静力计算,并根据梁在各种受力情况下的运动状态,得出支座反力。
在静力计算过程中,需要考虑到来自上游和下游的外力以及其他特殊负荷因素。
第三步:加入荷载计算进行完静力计算之后,接下来就需要加入不同种类的荷载进行计算了。
常见的荷载包括车辆荷载、温度荷载、风荷载等。
不同的荷载对支座反力的计算产生不同的影响,因此需要十分仔细地进行计算。
第四步:加入变形计算在梁受到荷载后,一定会发生变形,在支座反力的计算过程中,需要考虑到梁的变形。
变形通过不同的应变附加到梁的截面上,并进行计算,在这个过程中,需要考虑到混凝土的弹性模量、梁材料的弹性和塑性特性、预处理等。
第五步:重复计算前面的计算是建立在假设荷载稳定的情况下进行的。
实际上,荷载的突然变化会引起支座反力发生变化,因此,需要重复进行计算,并根据需要进行调整,保证计算结果的准确性。
以上,就是多跨连续梁支座反力计算的整个过程。
虽然这里仅仅提了一个粗略的概要,但是这一过程的计算是复杂而又十分耗费时间的,需要进行多方面的考虑。
在实际应用中,支座反力的计算是设计师需要反复攻坚克难的难点之一,需要进行多次的验证和检验,以保证梁的安全性和稳定性。
先简支后连续梁的支座数量计算

先简支后连续梁的支座数量计算梁是工程中常见的结构元素,用于支撑和传递荷载。
在设计梁的过程中,支座的数量是一个重要的考虑因素。
根据梁的类型和使用条件的不同,支座的数量可以有多种选择。
在设计梁的过程中,先简支后连续梁是一种常见的结构形式。
这种梁的特点是在一定跨度范围内,先将梁两端设置为简支,即支座数量为2,然后再在中间部分设置为连续梁。
这种结构形式在一定程度上能够兼顾梁的刚度和变形的要求,同时简化了支座的数量。
在确定先简支后连续梁的支座数量时,需要考虑以下几个因素:1. 梁的跨度:梁的跨度是指梁在水平方向上的长度。
一般来说,梁的跨度越大,所承受的荷载和变形也会越大。
因此,对于较大跨度的梁,需要增加支座的数量来提高梁的刚度和稳定性。
2. 荷载条件:梁所承受的荷载也是决定支座数量的一个重要因素。
根据设计要求和荷载计算,可以确定梁在不同位置的受力情况,从而决定支座的数量和位置。
例如,在梁的支点处承受的荷载较大时,可以增加支座的数量来分担荷载,提高梁的承载能力。
3. 材料和形状:梁的材料和形状也会对支座数量的确定产生影响。
不同材料和形状的梁在受力和变形方面有所差异,因此需要根据具体情况来确定支座的数量。
例如,对于较大变形的梁,可以增加支座的数量来限制其变形。
总结起来,先简支后连续梁的支座数量计算需要考虑梁的跨度、荷载条件、材料和形状等因素。
通过合理的计算和设计,可以确定适当的支座数量,以满足梁的刚度、稳定性和承载能力的要求。
同时,也需要注意支座的位置和布置,以便实际施工和维护。
在实际工程中,支座数量的计算是结构设计中的一个重要环节。
设计人员需要综合考虑各种因素,根据规范和经验进行计算和判断,以确保梁的安全可靠。
同时,也需要与其他工程部门和施工方进行沟通和协调,确保设计方案的有效实施。
先简支后连续梁的支座数量计算是梁设计中的一个重要问题。
通过合理的计算和设计,可以确定适当的支座数量,以满足梁的使用要求。
同时,也需要考虑实际施工和维护的需求,确保设计方案的可行性和实用性。
连续梁支座纵向预偏量计算
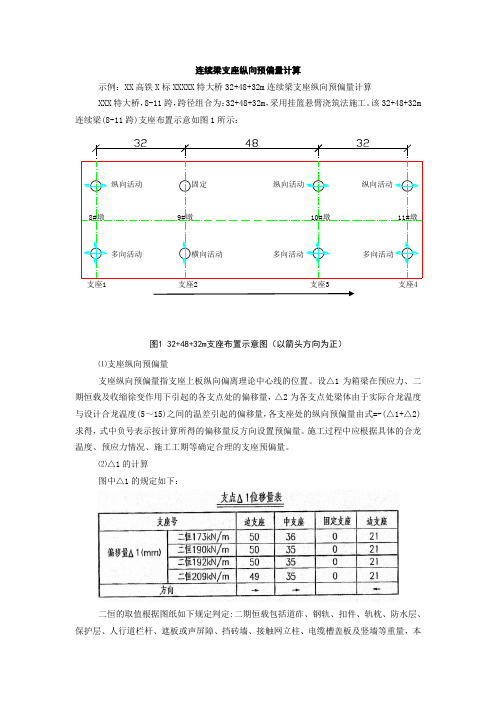
连续梁支座纵向预偏量计算示例:XX 高铁X 标XXXXX 特大桥32+48+32m 连续梁支座纵向预偏量计算XXX 特大桥,8-11跨,跨径组合为:32+48+32m ,采用挂篮悬臂浇筑法施工。
该32+48+32m 连续梁(8-11跨)支座布置示意如图1所示:纵向活动多向活动多向活动多向活动纵向活动纵向活动固定横向活动支座1支座2支座3支座48#墩9#墩10#墩11#墩图1 32+48+32m 支座布置示意图(以箭头方向为正)⑴支座纵向预偏量支座纵向预偏量指支座上板纵向偏离理论中心线的位置。
设△1为箱梁在预应力、二期恒载及收缩徐变作用下引起的各支点处的偏移量,△2为各支点处梁体由于实际合龙温度与设计合龙温度(5~15)之间的温差引起的偏移量,各支座处的纵向预偏量由式=-(△1+△2)求得,式中负号表示按计算所得的偏移量反方向设置预偏量。
施工过程中应根据具体的合龙温度、预应力情况、施工工期等确定合理的支座预偏量。
⑵△1的计算 图中△1的规定如下:二恒的取值根据图纸如下规定判定:二期恒载包括道砟、钢轨、扣件、轨枕、防水层、保护层、人行道栏杆、遮板或声屏障、挡砖墙、接触网立柱、电缆槽盖板及竖墙等重量,本项目梁按直线、曲线无声屏障和直线、曲线有声屏障设计,二期恒载分别取173KN/m和190KN/m和192KN/m和209kN/m,如有变化,应另行计算。
该连续梁属于曲线无声屏障段,故取值为190KN/m。
△1的值即可确定。
⑶△2的计算△2根据下列公式计算得出△2=α×△t×L其中,α—为箱梁混凝土线膨胀系数(10-5/℃),取1×10-5/℃。
△t—实际合拢温度与设计合拢温度的温差;L—计算位置至桥梁固定支座位置的梁体长度;现假定该连续梁设计合拢温度为10℃,实际合拢温度取5℃。
个人总结:△2实际就是热涨泠缩原理的体现,实际合拢温度上升到设计合拢温度就是膨胀,以固定支座为中心两端膨胀,实际合拢温度下降到设计合拢温度就是收缩,以固定支座为中心两端收缩。
最新支座预偏量的计算与设置

连续梁支座预偏量的计算与设置1.工程概况连续梁桥两个主墩(61#、62#)采用GTQZ30000型支座,两个边墩(60#、63#)采用GTQZ6000型支座,固定支座设在61#墩,活动支座的纵向位移量为±100mm。
根据固定支座设置位置相应设置横向位移、纵向位移、多向位移支座,具体如下图:2.支座偏移值计算活动支座位移量指桥梁施工阶段结束后,活动支座的上支座板偏移支座理论中心线的位移,主要分为两部分:因梁体的弹性压缩、混凝土收缩徐变引起的位移量△1 ,由于体系温差引起的位移量△2,故活动支座位移量为△1+△2。
因活动支座的预设偏移量是抵消施工阶段各墩活动支座产生的纵向水平位移量,故支座预设偏移量与支座位移量相反,即支座预设偏移量为△=—(△1+△2)。
2.1. △1的计算△1是因梁体的弹性压缩、混凝土收缩徐变引起各墩活动支座的偏移量。
△1由设计计算出结果,设计图纸中提供相应的偏移值。
2.2. △2的计算一般设计合拢温度取桥位处最低和最高月平均温度平均值,根据现场实际施工状况排出施工进度计划,计算出合拢日期,得出实际计划合拢温度。
△2=a△t*l,其中a为主梁混凝土线膨胀系数,△t为温差,l为计算位置至固定支座位置的梁体长度,△2为梁体的变形。
3.本桥支座偏移值计算3.1.△1的计算设计图纸中提供相应的偏移值,具体如下:以顺桥向方向为正单位:mm3.2.△2的计算该桥位于江西省南昌市范围,气温最高月是7月,平均温度为30.2℃;气温最低月是1月,平均气温为-3℃,则设计合拢温度为16℃。
根据施工现场的施工情况,计划10月8日合拢,合拢温度约13℃。
60#墩支座△2=—a△t*l=1*10-5*(16-13)*40000=—1.2mm62#墩支座△2= a△t*l=1*10-5*(16-13)*72000=2.16mm63#墩支座△2= a△t*l=1*10-5*(16-13)*112000=3.36mm则各墩支座预偏移量为:60#墩支座△= —(△1+△2)= —(15-1.2)=—13.8mm62#墩支座△= —(△1+△2)= —(—30+2.16)=27.84mm63#墩支座△= —(△1+△2)= —(—45+3.36)=41.64mm4.支座偏移值设置4.1.边墩偏移值设置根据上面的计算结果,60#边墩支座偏移值设置,安装支座时将支座上摆横向中心线向59#墩偏移13.8mm。
三跨连续梁支座反力计算

三跨连续梁支座反力计算1. 前言大家好,今天咱们来聊聊一个听起来有点高深,但其实挺有趣的主题——三跨连续梁的支座反力计算。
乍一听可能让人觉得有点晦涩,但没关系,我们一步一步来,轻松愉快地捋顺这个话题。
说实话,工程师的工作就像在解谜游戏中找线索一样,支座反力的计算就像是那关键的一步,没它可真是没法过关呢!2. 三跨连续梁的基础知识2.1 什么是三跨连续梁?首先,咱们得弄明白三跨连续梁到底是个啥。
简单来说,它就是由三段梁组成的结构,中间有支座支撑着,每段梁之间不需要额外的支撑。
就像是个小桥,跨越几道小河,不用任何的支撑柱子,简简单单。
这样的设计不仅美观,还能节省材料,经济实惠,一举两得,简直是建筑界的小能手!2.2 为什么要计算支座反力?那么,支座反力又是什么呢?其实,支座反力就是支撑梁的那些支座上所承受的力量。
想象一下,你在一根细长的木棍上跳舞,当然要考虑到木棍两头的承受力,才能确保你不摔跤!如果不计算支座反力,梁的承载能力可能会超出范围,就像你在木棍上跳舞太久,木棍承受不住直接断掉,那可就得不偿失了,对吧?3. 支座反力的计算步骤3.1 力的平衡好了,现在我们进入正式计算的环节。
首先,你得搞明白一个道理,那就是力的平衡。
就像吃饭时不能只吃肉不吃菜,力量也得均衡分配。
在三跨连续梁上,各个支座承受的力必须得平衡,才能确保整个结构的安全。
一般来说,咱们要考虑梁上的静载荷和活载荷,这些负荷的分布会直接影响到支座的反力。
3.2 运用计算公式接下来就是运用一些计算公式了,别害怕,这里并不会涉及到什么高深的数学。
简单来说,咱们通常用到的是“力的平衡方程”和“力矩平衡方程”。
这就像玩拼图,找对了位置,自然就能拼得美美的。
你可以通过设定一些已知条件,然后求解出各个支座上的反力。
其实就像解方程一样,先找出已知,再逐步推导未知。
4. 小贴士和注意事项4.1 不要忘记边界条件在计算的过程中,有一点千万别忘了,那就是边界条件!就像做饭不能随便加盐,工程计算也有它的规则。
连续梁支座预偏移量的计算与设置

连续梁支座预偏量的计算与设置1.工程概况连续梁桥两个主墩(61#、62#)采用GTQZ30000型支座,两个边墩(60#、63#)采用GTQZ6000型支座,固定支座设在61#墩,活动支座的纵向位移量为±100mm。
根据固定支座设置位置相应设置横向位移、纵向位移、多向位移支座,具体如下图:图一:连续梁支座布置图2.支座偏移值计算活动支座位移量指桥梁施工阶段结束后,活动支座的上支座板偏移支座理论中心线的位移,主要分为两部分:因梁体的弹性压缩、混凝土收缩徐变引起的位移量△1 ,由于体系温差引起的位移量△2,故活动支座位移量为△1+△2。
因活动支座的预设偏移量是抵消施工阶段各墩活动支座产生的纵向水平位移量,故支座预设偏移量与支座位移量相反,即支座预设偏移量为△=—(△1+△2)。
2.1. △1的计算△1是因梁体的弹性压缩、混凝土收缩徐变引起各墩活动支座的偏移量。
△1由设计计算出结果,设计图纸中提供相应的偏移值。
2.2. △2的计算一般设计合拢温度取桥位处最低和最高月平均温度平均值,根据现场实际施工状况排出施工进度计划,计算出合拢日期,得出实际计划合拢温度。
△2=a△t*l,其中a为主梁混凝土线膨胀系数,△t为温差,l为计算位置至固定支座位置的梁体长度,△2为梁体的变形。
3.本桥支座偏移值计算3.1.△1的计算设计图纸中提供相应的偏移值,具体如下:以顺桥向方向为正单位:mm纵向活动支座多向活动支座横向活动支座固定支座12345678支座0支座1支座2支座3正值60#61#62#63#墩号60 61 62 63预偏量-15 0 +30 +453.2.△2的计算该桥位于江西省南昌市范围,气温最高月是7月,平均温度为30.2℃;气温最低月是1月,平均气温为-3℃,则设计合拢温度为16℃。
根据施工现场的施工情况,计划10月8日合拢,合拢温度约13℃。
60#墩支座△2=—a△t*l=1*10-5*(16-13)*40000=—1.2mm62#墩支座△2= a△t*l=1*10-5*(16-13)*72000=2.16mm63#墩支座△2= a△t*l=1*10-5*(16-13)*112000=3.36mm则各墩支座预偏移量为:60#墩支座△= —(△1+△2)= —(15-1.2)=—13.8mm62#墩支座△= —(△1+△2)= —(—30+2.16)=27.84mm63#墩支座△= —(△1+△2)= —(—45+3.36)=41.64mm4.支座偏移值设置4.1.边墩偏移值设置根据上面的计算结果,60#边墩支座偏移值设置,安装支座时将支座上摆横向中心线向59#墩偏移13.8mm。
支座预偏量的计算与设置演示教学

连续梁支座预偏量的计算与设置1.工程概况连续梁桥两个主墩(61#、62#)采用GTQZ30000型支座,两个边墩(60#、63#)采用GTQZ6000型支座,固定支座设在61#墩,活动支座的纵向位移量为±100mm。
根据固定支座设置位置相应设置横向位移、纵向位移、多向位移支座,具体如下图:2.支座偏移值计算活动支座位移量指桥梁施工阶段结束后,活动支座的上支座板偏移支座理论中心线的位移,主要分为两部分:因梁体的弹性压缩、混凝土收缩徐变引起的位移量△1 ,由于体系温差引起的位移量△2,故活动支座位移量为△1+△2。
因活动支座的预设偏移量是抵消施工阶段各墩活动支座产生的纵向水平位移量,故支座预设偏移量与支座位移量相反,即支座预设偏移量为△=—(△1+△2)。
2.1. △1的计算△1是因梁体的弹性压缩、混凝土收缩徐变引起各墩活动支座的偏移量。
△1由设计计算出结果,设计图纸中提供相应的偏移值。
2.2. △2的计算一般设计合拢温度取桥位处最低和最高月平均温度平均值,根据现场实际施工状况排出施工进度计划,计算出合拢日期,得出实际计划合拢温度。
△2=a△t*l,其中a为主梁混凝土线膨胀系数,△t为温差,l为计算位置至固定支座位置的梁体长度,△2为梁体的变形。
3.本桥支座偏移值计算3.1.△1的计算设计图纸中提供相应的偏移值,具体如下:以顺桥向方向为正单位:mm3.2.3.3.3.4.△2的计算该桥位于江西省南昌市范围,气温最高月是7月,平均温度为30.2℃;气温最低月是1月,平均气温为-3℃,则设计合拢温度为16℃。
根据施工现场的施工情况,计划10月8日合拢,合拢温度约13℃。
60#墩支座△2=—a△t*l=1*10-5*(16-13)*40000=—1.2mm62#墩支座△2= a△t*l=1*10-5*(16-13)*72000=2.16mm63#墩支座△2= a△t*l=1*10-5*(16-13)*112000=3.36mm则各墩支座预偏移量为:60#墩支座△= —(△1+△2)= —(15-1.2)=—13.8mm62#墩支座△= —(△1+△2)= —(—30+2.16)=27.84mm63#墩支座△= —(△1+△2)= —(—45+3.36)=41.64mm4.支座偏移值设置4.1.边墩偏移值设置根据上面的计算结果,60#边墩支座偏移值设置,安装支座时将支座上摆横向中心线向59#墩偏移13.8mm。
连续梁支座的计算方法

连续梁支座的计算方法连续梁是一种常见的结构形式,广泛应用于桥梁、大型建筑物、机场跑道等工程中。
作为支撑结构,梁的支座在连续梁设计中起着重要的作用。
在本文中,将介绍连续梁支座的计算方法。
连续梁支座计算方法的主要目标是确定支座的受力、位移和变形,以保证梁在使用阶段的安全和可靠。
首先,我们需要了解梁的受力特点和梁支座的工作原理。
在连续梁中,梁在自重和荷载作用下发生弯曲和剪力,这些力会通过支座传递到地基上。
支座的主要功能是承受和传递这些力,并通过对梁的约束来限制其水平位移。
为了实现这一目标,支座通常由橡胶、钢板等材料组成,具有一定的变形能力。
在进行连续梁支座计算之前,需要进行一些基本的假设和简化。
首先,我们假设梁是一个刚性体,其变形可以忽略不计。
其次,我们假设支座是理想化的约束,可以完全阻止梁的滑动和转动。
最后,我们假设梁的荷载是均匀分布的,并且支座的受力也是均匀分布的。
支座计算的第一步是确定梁的受力情况。
在连续梁中,梁受到的力包括自重力、活荷载和温度效应等。
这些力将导致梁产生弯曲弯矩和剪力。
我们可以通过采用弹性力学理论和静力平衡原理来计算梁的受力分布。
根据受力分布,我们可以进一步计算支座的受力。
支座的主要受力包括垂直反力、水平力和转矩。
这些力需要通过支座的结构来承受和传递到地基上。
我们可以通过应用静力平衡原理和力的平衡条件来计算支座的受力。
同时,支座的位移和变形也是需要考虑的因素。
在连续梁使用阶段,梁的变形会导致对支座的约束产生一定的位移。
这些位移需要通过支座的变形能力来吸收和分散。
支座的变形能力取决于其材料和结构特性。
支座计算的最后一步是确定支座的设计参数。
这些参数包括支座的尺寸、材料和布置等。
支座的尺寸可以根据支座受力和变形情况来确定。
支座的材料需要具有足够的强度和变形能力,以满足其受力和变形要求。
支座的布置需要考虑梁的受力分布和支座的相互作用。
总结起来,连续梁支座的计算方法主要包括受力分析、支座受力计算、支座变形计算和支座设计参数确定。
不等跨连续梁支座弯矩的计算

不等跨连续梁支座弯矩的计算连续梁结构是建筑结构中使用最多的结构,它的出现使建筑物的弯矩受到支座力的影响,从而影响结构的安全性。
然而,当跨度不同的连续梁的支座力没有使用相同的弯矩时,计算连续梁支座弯矩的数学模型是比较复杂的。
在本文中,我们将探讨不等跨连续梁支座弯矩的计算方法。
首先,我们需要明确不等跨连续梁支座弯矩的计算公式。
一般来说,不等跨连续梁支座弯矩的计算公式为:mi = M/I2 + (1I2)Mi,其中i为每个梁段的梁支座处的节点序号,M是梁支座处的正算荷载,I2是梁支座处的支座弯矩系数,ΔMM为各梁支座处的节点荷载减去全梁节点所受荷载的和。
其次,采用数值方法求解不等跨连续梁支座弯矩的具体流程。
这就是一种采用叠加原理分析连续梁支座处的弯矩的简单而有效的方法。
首先,采用传统的梁系数法分析连续梁支座处的弯矩,计算出假设每梁段具有相同支座力的前提下在梁支座处的弯矩,即,假设I2 = 1;然后,计算出各梁支座处的节点荷载减去全梁节点所受荷载的和,即ΔMM;最后,根据计算公式mi = M/I2 + (1I2)Mi计算出实际的梁支座弯矩。
最后,我们还可以使用计算机辅助的方法来求解不等跨连续梁支座弯矩。
计算机辅助的方法或流程包括:(1)已知连续梁支座力及节点荷载,求出梁支座处的梁支座弯矩;(2)根据梁支座弯矩估算梁支座处的支座弯矩系数;(3)将梁支座处的支座弯矩系数代入支座弯矩计算公式,求出实际支座弯矩。
以上就是不等跨连续梁支座弯矩的计算方法。
从上面可以看出,计算不等跨连续梁支座弯矩的方法非常的复杂,但是这种方法可以更准确地计算出连续梁支座弯矩,为设计者提供更加准确的连续梁支座弯矩。
总而言之,不等跨连续梁支座弯矩是一个很复杂的问题,因此必须采用正确的计算方法来确定它的精确值,从而得出合理的结构设计。
在实际的连续梁结构中,必须结合梁系数法和叠加原理,采用传统的数值方法或采用计算机辅助方式,结合不等跨连续梁支座弯矩的计算公式,分步骤地计算梁支座处的弯矩,以保证结构的安全。
连续梁支座弯矩的计算公式

连续梁支座弯矩的计算公式
连续梁支座弯矩的计算公式,是求解连续梁在跨度上的支座弯矩大小所需的公式。
在计算连续梁的支座弯矩时,需要考虑梁的几何形状、荷载情况以及支座的刚度等因素。
一般情况下,计算连续梁支座弯矩的公式可以通过数学方法得出,其中最常用的方法是使用弹性力学理论。
在这个方法中,连续梁支座弯矩的计算公式可以表示为:
M = (w1*l1^2)/2 + w2*l2^2/2 + … + wn*ln^2/2
其中,M为连续梁支座处的弯矩大小,w1、w2…wn分别为梁在不同跨度上的分布荷载大小,l1、l2…ln分别为不同跨度的长度。
除此之外,还有其他一些方法可以用来计算连续梁支座弯矩的大小,例如有限元法、试验法等等。
这些方法都需要结合具体的实际情况进行选择和应用。
需要注意的是,不同的计算方法和公式可能会得出不同的结果,因此在进行计算时需要结合实际情况进行综合考虑,并选择合适的计算方法和公式来得出准确的结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
连续梁支座的计算方法
连续梁支座,即是构成梁的多个支座连接在一起,使其成为一体的结构,在结构分析中,通常将它视为一个完整的梁。
连续梁支座的计算可以采用等效法、计算法和柔性法等多种方法研究。
(1)等效法
等效法是将梁的全部支座进行综合分析,按照一定的综合原理,将多个支座等效为一个梁支座,从而求出等效梁支座的支座力。
该法的优点是简单、快速,但是它不能完全反映支座之间的影响,如载荷分担情况,故不能准确描述连续梁的变形和应力分布。
(2)计算法
计算法是按照梁的刚度矩阵方程计算梁的支座变形,并从而计算支座内的应力和支座力。
这种方法结果准确,但耗时较多。
(3)柔性法
柔性法是用物理分析的方式来计算梁的支座力,即将梁分成多个短梁,从而求出梁的支座力,因而也称为“短梁法”。
这种方法也可以计算出支座力,但其计算时间和复杂性介于两种方法之间,不能完全准确反映支座之间的影响,如载荷分担情况。
因此,在实际计算中,连续梁支座的计算方法可以根据实际情况选用上述三种方法中的一种,以满足工程需要。
- 1 -。
