2020届中考数学复习基础测试卷专练特殊四边形的折叠问题【含答案】

合集下载

专题02特殊平行四边形中的折叠问题教师版

专题02 特殊平行四边形中的折叠问题【典型例题】1．（2020·河北定州初三二模）如图，正方形ABCD 中，AB =6，G 是BC 的中点．将△ABG 沿AG 对折至△AFG ，延长GF 交DC 于点E ，则DE 的长是 ( )A ．1B ．1.5C ．2D ．2.5【解析】连接AE ，∵AB =AD =AF ,∠D =∠AFE =90°，由折叠的性质得：Rt △ABG ≌Rt △AFG ，在△AFE 和△ADE 中，∵AE =AE ，AD =AF ，∠D =∠AFE ，∴Rt △AFE ≌Rt △ADE ，∴EF =DE ，设DE =FE =x ，则CG =3，EC =6−x .在直角△ECG 中，根据勾股定理，得：(6−x )2+9=(x +3)2，解得x =2.则DE =2. 2．（2019·全国初三单元测试）如图，在菱形ABCD 中，AE ⊥BC 于E ，将△ABE 沿AE 所在直线翻折得△AEF ，若AB ＝2，∠B ＝45°，则△AEF 与菱形ABCD 重叠部分（阴影部分）的面积为（）.A ．2B ．C ．D ．【解析】∵在边长为2的菱形ABCD 中，∠B =45°，AE 为BC 边上的高，∴AE ，由折叠的性质可知，△ABF 为等腰直角三角形，∴S △ABF =12AB •AF =2，S △ABE =1，∴CF =BF -BC =-2，∵AB ∥CD ，∴∠GCF =∠B =45°，又由折叠的性质知，∠F =∠B =45°，∴CG =GF =2∴S △CGF =12GC •GF =3-，∴重叠部分的面积为：2-1-（3-）=2，故选D ． 3．（2020·全国）如图，把矩形纸片ABCD 沿EF 折叠后，使得点D 与点B 重合，点C 落在点C ′的位置上．（1）折叠后，DC 的对应线段是，CF 的对应线段是；（2）若∠1=50°，求∠2、∠3的度数；（3）若AB =8，DE =10，求CF 的长度．【答案】（1）由折叠的性质可得：折叠后，DC 的对应线段是BC ′，CF 的对应线段是C ′F ；故答案为：BC ′，C ′F ．（2）由折叠的性质可得：∠2=∠BEF ，∵AD ∥BC ，∴∠1=∠2=50°．∴∠2=∠BEF =50°，∴∠3=180°﹣50°﹣50°=80°；故答案为：50°，80°（3）∵AB =8，DE =10，∴BE =10，∴AE 6，∴AD =BC =6+10=16，∵∠1=∠BEF =50°，∴BF =BE =10， ∴CF =BC ﹣BF =16﹣10=6．故答案为：6【专题训练】一、选择题1．（2020·海南临高）如图，在矩形纸片ABCD 中，AB =3，点E 在边BC 上，将△ABE 沿直线AE 折叠，点B 恰好落在对角线AC 上的点F 处，若∠EAC =∠ECA ，则AC 的长是（）A ．B ．6C ．4D ．5【解析】∵将△ABE沿直线AE折叠，点B恰好落在对角线AC上的点F处，∴AF=AB，∠AFE=∠B=90°，∴EF⊥AC，∵∠EAC=∠ECA，∴AE=CE，∴AF=CF，∴AC=2AB=6，选B．2．（2020·全国）如图，将一张长方形纸片ABCD按图中方式折叠，若AE＝3，AB＝4，BE＝5，则重叠部分的面积为( )A．6B．8C．10D．12【解析】解：∵长方形纸片ABCD按图中那样折叠，∴∠1=∠2，而∠1=∠3，∴∠2=∠3，∴ED=EB=5，∵矩形ABCD中，∠A=90°∴重叠部分△BDE的面积=12DE×AB=12×5×4=10．故选：C.．3．（2020·全国）如图，将矩形纸片ABCD折叠，使点D与点B重合，点C落在C′处，折痕为EF，若AB=1，BC=2，则△ABE和△BC′F的周长之和为（）A．3B．4C．6D．8【解析】解：将矩形纸片ABCD折叠，使点D与点B重合，点C落在C′处，折痕为EF，由折叠特性可得，CD=BC′=AB，∠FC′B=∠EAB=90°，∠EBC′=∠ABC=90°，∵∠ABE+∠EBF=∠C′BF+∠EBF=90°∴∠ABE=∠C′BF在△BAE和△BC′F中，∴△BAE≌△BC′F（ASA），∵△ABE的周长=AB+AE+EB=AB+AE+ED=AB+AD=1+2=3，△ABE和△BC′F的周长=2△ABE的周长=2×3=6．故选C．4．（2020·新疆昌吉初三一模）如图，将边长为8㎝的正方形ABCD折叠，使点D落在BC边的中点E处，点A落在F处，折痕为MN，则线段CN的长是（）A．3cm B．4cm C．5cm D．6cm【解析】设CN=xcm，则DN=（8﹣x）cm，由折叠的性质知EN=DN=（8﹣x）cm，而EC=12BC=4cm，在Rt△ECN中，由勾股定理可知EN2=EC2+CN2，即（8﹣x）2=16+x2，整理得16x=48，所以x=3．故选：A．5．（2019·河北遵化初三一模）如图，菱形纸片ABCD中，∠A=60°，折叠菱形纸片ABCD，使点C落在DP（P为AB中点）所在的直线上，得到经过点D的折痕DE．则∠DEC的大小为（）A．78°B．75°C．60°D．45°【解析】试题分析：连接BD，∵四边形ABCD为菱形，∠A=60°，∴△ABD为等边三角形，∠ADC=120°，∠C=60°．∵P为AB的中点，∴DP为∠ADB的平分线，即∠ADP=∠BDP=30°．∴∠PDC=90°．∴由折叠的性质得到∠CDE=∠PDE=45°．在△DEC中，．故选B．6．（2020·全国）如图，已知四边形ABCD 是边长为6的菱形，且∠BAD =120°，点E ,F 分别在AB ,BC 边上，将菱形沿EF 折叠，点B 正好落在AD 边的点G 处．若EG ⊥AC ，则FG 的长为（）A ．3B ．6C ．D ．【解析】如图，设AC 与EG 交于点O ，FG 交AC 于点H ．∵ 四边形ABCD 是菱形，∠BAD =120°，∴60B D ∠=∠=︒， ∴ABC ACD 、是等边三角形．∴60CAD B ∠=∠=︒．∵EG AC ⊥，∴90GOH ∠=︒．∵60EGF B ∠=∠=︒，∴30OHG ∠=︒，∴18090AGH CAD OHG ∠=︒-∠-∠=︒，∴FG AD ⊥，∴FG 是菱形ABCD 的高，即为等边三角形ABC 的高，∴ =C ．7．（2020·兴仁市真武山街道办事处黔龙学校）如图,把一个矩形纸片ABCD 沿EF 折叠后,点D 、C 分别落在D ′、C ′的位置,若∠EFB =65°,则∠AED ′为（）。

特殊平行四边形的翻折折叠问题(含答案)

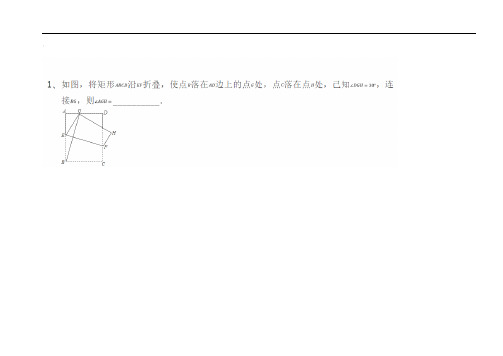
,;【解析】分析：根据翻折的性质可得∠B=∠AB 1E=90°，AB=AB 1，然后求出四边形ABEB 1是正方形，再根据正方形的性质可得BE=AB ，然后根据CE=BC-BE ，代入数据进行计算即可得解．详解：∵沿AE 对折点B 落在边AD 上的点B 1处，∴∠B=∠AB 1E=90°，AB=AB 1，，又∵∠BAD=90°，∴四边形ABEB1是正方形，∴BE=AB=6cm，∴CE=BC-BE=8-6=2cm．故选：D．点睛：本题考查了矩形的性质，正方形的判定与性质，翻折变换的性质，判断出四边形ABEB1是正方形是解题的关键．，。

【>【解析】分析：先判断出△BFC是直角三角形，再利用三角形的外角判断出A正确，进而判断出AE=CE，得出CE 是△ABC的中位线判断出B正确，利用等式的性质判断出D正确．详解：如图，连接CF，∵点D是BC中点，∴BD=CD，由折叠知，∠ACB=∠DFE，CD=DF，∴BD=CD=DF，？∴△BFC是直角三角形，∴∠BFC=90°，∵BD=DF，∴∠B=∠BFD，∴∠EAF=∠B+∠ACB=∠BFD+∠DFE=∠AFE，∴AE=EF，故A正确，由折叠知，EF=CE，∴AE=CE，[∵BD=CD，∴DE是△ABC的中位线，∴AB=2DE，故B正确，∵AE=CE，∴S△ADE=S△CDE，由折叠知，△CDE≌△△FDE，∴S△CDE=S△FDE，∴S△ADE=S△FDE，故D正确，~∴C选项不正确，故选：C．*~*。

中考数学专题复习《四边形的折叠问题》测试卷-附带答案

中考数学专题复习《四边形的折叠问题》测试卷-附带答案学校:___________班级:___________姓名:___________考号:___________一单选题1．如图所示在长方形ABCD 中 610AD AB ==，若将长方形ABCD 沿DE 折叠使点C 落在AB 边上的点F 处则线段CE 的长为（）A ．13B ．1730C ．103D ．102．如图在ABCD 中将ADC △沿AC 折叠后点D 恰好落在DC 延长线上的点E 处．若=60B ∠︒ 1AB = 则ABCD 的周长为( )A ．4B ．43C ．6D ．33．如图在ABC 中已知8AB = 点DE 、分别在边AC AB 、上现将ADE 沿直线DE 折叠使点A 恰好落在点F 处若将线段BC 向左平移刚好可以与线段EF 重合连接CF 若215BC CF += 则2BC CF -的值为（）A ．4B ．5C ．6D ．74．如图矩形ABCD 中 3AB = 4BC = 点E 是BC 边上一点连接AE 把B ∠沿AE折叠使点B 落在点B '处当CEB '为直角三角形时 BE 的长为（）A ．2B ．3C ．2或3D ．3或1.55．如图将长方形纸片ABCD 沿EF 折叠后若170=︒∠ 则2∠的度数为（）A ．110︒B ．115︒C ．120︒D ．125︒6．如图在平面直角坐标中矩形ABCD 的边5,:1:4AD OA OD == 将矩形ABCD 沿直线OE 折叠到如图所示的位置线段1OD 恰好经过点B 点C 落在y 轴的点1C 位置点E 的坐标是（）A ．()1,2B ．1,2C ．)1,2D ．()12 7．如图在平面直角坐标系中已个纸片OACB 顶点10006A B （，），（，）点P 为BC 边上的动点将OBP 沿OP 折叠得到OPD 连接CD AD 、．则下列结论中：①当45BOP ∠=︒时四边形OBPD 为正方形 ①当30BOP ∠=︒时 OAD 的面积为15 ①当P 在运动过程中CD 的最小值为5 ①当OD AD ⊥时 2BP =．其中结论正确的有（）A ．1个B ．2个C ．3个D ．4个 8．如图把一张长方形纸片沿对角线折叠若30EDF ∠= 则长方形纸片的长宽比为( )A ．2：1B 2：1C 31D ．23二填空题9．在平行四边形ABCD 中点E F 在BC 边上把ABE 沿直线AE 折叠 CDF 沿直线DF 折叠使点B C 落在对角线AC 上的点G 处若110AGD ∠=︒ 则B ∠的度数为．10．如图点O 是矩形ABCD 的中心 E 是边AB 上的点沿CE 折叠后点B 恰好与点O 重合若9BC = 则折痕CE 长度为．11．如图将长方形ABCD 沿EF 折叠得到两个全等的小长方形 1210AB BC ==，，点G 在AB 上运动当点 A 关于DG 的对称点A '落在右侧长方形BCEF 内部(含边界)时则AG 的长度 m 的取值范围为．12．如图菱形ABCD 的边5AB = 高4CE = F 是边CD 上一动点将四边形AEFD 沿直线EF 折叠 A 点的对应点为P 当CP 的长度最小时 CF 的长为．13．如图把正方形纸片ABCD 进行如下操作：对折正方形ABCD 得折痕EF 连接CE 将CB 折叠到CE 上点B 对应点H 得折痕CG ．那么AG BG= ．三解答题14．如图1 点E 为矩形ABCD 边BC 上一点且CE CD = 把ABE 沿着AE 折叠点B 的对应点F 恰好落在线段DE 上．(1)求证：≌AFD DCE(2)如图2 延长CF 交AE 于点G 交AB 于点H ．①求证：GE DF GF CD ⋅=⋅①求:GH GA 的值．15．如图沿折痕AE 折叠矩形ABCD 的一边使点D 落在BC 边上一点F 处．若6AB = 且ABF △的面积为24 则：(1)BF 的长为_______________(2)BC 的长为________________(3)求EC 的长．16．如图1 已知长方形纸片ABCD 点E 在边AD 上 F 为AB 上的一个动点 G 为DC 上的一个动点将长方形ABCD 沿直线EF EG 、折叠点A D 、的对应点分别是点A '和点D ．(1)如图2 当点A '落在ED 上时求FEG ∠的度数(2)如图3 若54A ED ''∠=︒ 求FEG ∠的度数(3)如图4 若10A ED ''∠=︒ 求FEG ∠的度数(4)若A ED n ''∠=︒直接写出FEG ∠的度数（用含n 的代数式表示）17．如图在Rt ABC △中 90BAC ∠=︒ 30C ∠=︒ 点D 是ABC 外一点连接AD BD将ABD △沿DB 折叠使点A 落在边BC 上的点1A 处连接1A D 若1A D AC ⊥．(1)求证：四边形1ABA D 是菱形(2)连接1AA DC 若2AB = 求四边形1ADCA 的面积．18．综合探究：如图四边形ABCD 是正方形点M 在边AD 上直线MN AB ∥．将正方形沿MN 折叠点A 落在A '处点B 落在点B '处 MN 与BD 交于点P 连接AP A P ' A P '交CD 与点F ．(1)连接PC 猜想PC 与PA '的数量关系为________ A PC '∠=________°(2)连接B D ' CA ' 两线段交于点O 移动直线MN 若CD 平分PCA '∠ 求证：CP B D '∥(3)移动直线MN 若6=BC 2B C '= 直接写出PAD ∠的度数．参考答案：1．C2．C3．B4．D5．D6．D7．C8．C9．75︒10．11．10103m ≤≤ 12．41314．（1）解：证明：CD CE =CDE ∴为等腰直角三角形45CDE FDA ︒∴∠=∠= ABE 沿AE 折叠得到AEF △ 且四边形ABCD 是矩形 AB AF CD ∴== 90AFE AFD B ∠=∠=∠=︒ 在AFD △与ECD 中AFD ECD CDE FDA AF CE ∠=∠⎧⎪∠=∠⎨⎪=⎩()AAS AFD DCE ∴≌．（2）①证明：AFD DCE ≌△△AD DE ∴= AF DF DC CE ===()11804567.52DCF DFC ∴∠=∠=︒-︒=︒ 45DEC ∠=︒ 180135BED DEC167.52AEF AEB BEF ∴∠=∠=∠=︒ GEF DCF ∴∠=∠ GFE DFC ∠=∠GEF DCF ∴∽GE GF DC DF∴= GE DF GF CD ∴⋅=⋅．①在Rt CED 中 45CDE ∠=︒DE ∴=DF DC CE ==)()2121EF DE DF CD CE ∴=-== 21EF CE ∴ 由①知：67.5BEA DFC ∠=∠=︒18067.5112.5EFC GEC ∴∠=∠=︒-︒=︒ECF GCE ∠=∠CEG CFE ∴△∽△21GE EF GC CE∴==． 15．（1）由矩形的性质可得：90B C ∠=∠=︒ 6AB CD == ABF △的面积为24 ①1242ABF S AB BF =⨯⨯= ①24224286BF AB ⨯⨯=== 故答案为：8（2）在（1）中已得8BF =由矩形的性质可得：90B C ∠=∠=︒ 6AB CD == AD BC = 由折叠的性质可得：AF AD BC == 由勾股定理可得：22228610BC AF BF AB =++= 故答案为：10（3）由（1）（2）可得2CF BC BF =-=根据折叠的性质有：EF DE =设CE x = 则6EF DE x ==-在Rt CEF △中 222CE CF EF +=即()22226x x +=- 解得83x = 即83CE =．16．（1）解：由翻折得：12A EF AEA ''∠=∠ 12D EG DED ''∠=∠ ①180AEA DED ''∠+∠=︒ ①()111809022FEG A EF D EG AEA DED ''''∠=∠+∠=∠+∠=⨯︒=︒（2）解：由 (1) 知12A EF AEA ''∠=∠ 12D EG DED ''∠=∠ ①54A ED ''∠=︒①126AEA DED ''∠+∠=︒①()1632A EF D EG AEA DED ''''∠+∠=⨯∠+∠=︒ ①5463117FEG A ED A EF D EG ''''∠=∠+∠+∠=︒+︒=︒ （3）解：①10A ED ''∠=︒ ①()()11180109522A EF D EG AEA DED ''''∠+∠=∠+∠=︒+︒=︒ ①951085FEG A EF D EG A ED ''''∠=∠+∠-∠=︒-︒=︒ （4）解：如图3 ①A ED n ''∠=︒①()180180AEA DED A ED n ''''∠+∠=︒-∠=-︒ ①2A EF AEA ''∠=∠ 2D EG DED ''∠=∠ ①1802n A EF D EG ︒-︒''∠+∠= ①18018022n n FEG A EF D EG A ED n ︒-︒︒+︒''''∠=∠+∠+∠=+︒= 如图4 ①180AEA DED A ED ''''∠+∠-∠=︒ ''A ED n ∠=︒ ①180AEA DED n ''∠+∠=︒+︒①2A EF AEA ''∠=∠ 2D EG DED ''∠=∠ ①1802n A EF D EG ︒+︒''∠+∠= ①18018022n n FEG A EF D EG A ED n ︒+︒︒-︒''''∠=∠+∠-∠=-︒= 综上 FEG ∠的度数为1802n ︒+︒或 1802n ︒-︒． 17．（1）证明：如图1 连接1AA 设1A D 交AC 于点E由折叠的性质得：1AB A B = 1AD A D =90BAC ∠=︒ 30C ∠=︒903060ABC ∴∠=︒-︒=︒1ABA ∴是等边三角形1AB AA ∴= 160BAA ∠=︒11906030CAA BAC BAA ∴∠=∠-∠=︒-︒=︒1A D AC ⊥190AEA ∴∠=︒1903060AA D ∴∠=︒-︒=︒∴1AA D △是等边三角形1AD AA ∴=11AB A B AD A D ∴===∴四边形1ABA D 是菱形（2）解：如图2由（1）可知四边形1ABA D 是菱形 12A D AB ∴==90BAC ∠=︒ 30ACB ∠=︒24BC AB ∴==22224223AC BC AB ∴--1A D AC ⊥∴四边形1ADCA 的面积=1AA C ADC S S + 111111232232222AC A E AC DE AC A D =⋅+⋅=⋅=⨯= 18．（1）解：①四边形ABCD 是正方形 ①AB BC CD DA === 90BAD ABC BCD CDA ∠∠∠∠====︒ 四边形ABCD 是轴对称图形 BD 所在直线是其一条对称轴①45ADP ∠=︒ PA PC = PAM PCF ∠∠= ①MN AB ∥①90PMD BAD ∠∠==︒①MN AD ⊥18090A DF CDA '∠=︒-∠=︒①将正方形沿MN 折叠点A 落在A '处点B 落在点B '处 ①MN AA '⊥①点A D A '三点共线同理：点B C B '三点共线①将正方形沿MN 折叠点A 落在A '处点B 落在点B '处 ①PA PA '= PA D PAM PCF '∠=∠=∠ 90CB A B A D ABC BAD ''''∠=∠=∠=∠=︒ ①PC PA '=①90A DF '∠=︒ 180A DF PA M DFA PCF PFC A PC ''''∠+∠+∠=∠+∠+∠=︒ PA M PCF '∠=∠ DFA PFC '∠=∠ ①90A D A PC F '∠=︒'∠=故答案为：PC PA '= 90（2）证明：由（1）得PC PA '= 90A PC '∠=︒ ①45PCA PA C ''∠=∠=︒①CD 平分PCA '∠①22.5OCD PCD ∠=∠=︒①90CB A B A D ''''∠=∠=︒ 90A DF '∠=︒ ①四边形A B CD ''是矩形①OA OD OB OC ''===①ODC OCD ∠∠==22.5︒①45A ODC O A OD PC CD ''∠=︒=∠+∠=∠ ①CP B D '∥（3）解：如图在AN 上取一点N 使得AN =①四边形A B CD ''是矩形 ①2,A D B C ''=①将正方形沿MN 折叠点A 落在A '处点B 落在点B '处 ①MN 垂直平分AA ' ①62MA MA +'== 90PMD PMN ∠∠==︒ ①MN AM AN =-=6232662+-=①45PDM ∠=︒ ①904545MPD PDM ∠∠=︒-︒=︒= ①PM DM AD AM ==-62626+-==①在Rt PMN 中6232tan 326PM PNM MN -∠===-①30PNM ∠=︒ ①262N PN PM A === ①PAD APN ∠∠==130152⨯︒=︒．。

2020届中考数学专题复习演练：折叠问题(有答案)

折叠问题一、选择题1.如图，菱形纸片ABCD中，∠A=60°，折叠菱形纸片ABCD，使点C落在DP（P为AB中点）所在的直线上，得到经过点D的折痕DE．则∠DEC的大小为（）A. 78°B. 7 5°C. 60°D. 45°2.如图，在矩形纸片ABCD中，AB＝4，AD＝3，折叠纸片使DA与对角线DB重合，点A落在点A′处，折痕为DE，则A′G的长是A. 1B.C.D. 23.如图，在矩形ABCD中，AB＜AD，E为AD边上一点，且AE= AB，连结BE，将△ABE沿BE翻折，若点A 恰好落在CE上点F处，则∠CBF的余弦值为（）A. B.C.D.4.如图，在矩形纸片ABCD中，AB=6，AD=8，折叠该纸片，使得AB边落在对角线AC上，点B落在点F处，折痕为AE，则线段EF的长为（）A. 3B. 4C. 5D. 65.如图，在Rt△ABC中，∠C=90°，BD平分∠ABC交AC于D，沿DE所在直线折叠，使点B恰好与点A重合，若CD=2，则AB的值为（）A. B.4 C.D. 8二、填空题6.如图，在Rt△ACB中，∠ACB=90°，AB=10，BC=6，点N是线段BC上的一个动点，将△ACN沿AN折叠，使点C落在点C'处，当△NC'B是直角三角形时，CN的长为________．7.如图，在△ABC中，∠C=90°，AC=BC=2 ，D是AB的中点，点E、F分别在AC、BC边上运动（点E不与点A、C重合），且保持AE=CF，连接DE、DF、EF．在此运动变化的过程中，下列结论：①△DFE是等腰直角三角形；②四边形CEDF的周长不变；③点C到线段EF的最大距离为1．其中正确的结论有________．（填写所有正确结论的序号）8.如图，在Rt△ABC中，∠C=90°，BC=2 ，AC=2，点D是BC的中点，点E是边AB上一动点，沿DE所在直线把△BDE翻折到△B′DE的位置，B′D交AB于点F．若△AB′F为直角三角形，则AE的长为________．9.如图，矩形ABCD中，AD=5，AB=6，点E为DC上一个动点，把△ADE沿AE折叠，点F为CD上一个动点，把△BCF沿BF折叠，当点D的对应点和点C的对应点都落在点D′处时，EF的长为________．10.矩形纸片ABCD中，AD=4cm，AB=10cm，按如图方式折叠，使点B与点D重合，折痕为EF，则DE=________ cm．11.如图，在▱ABCD中，AB=，AD=4，将▱ABCD沿AE翻折后，点B恰好与点C重合，则折痕AE的长为________.12.如图，把一个长方形纸片沿EF折叠后，点D，C分别落在D′，C′的位置．若∠EFB＝65°，则∠AED′的度数为________.13.已知等边△ABC中，点D，E分别在边AB，BC上，把△BDE沿直线DE翻折，使点B落在点Bˊ处，DBˊ，EBˊ分别交边AC于点F，G，若∠ADF=80°，则∠EGC的度数为________14.如图，在矩形ABCD中，AB=5，BC=3，点E为射线BC上一动点，将△ABE沿AE折叠，得到△AB′E．若B′恰好落在射线CD上，则BE的长为________．15.如图，在矩形中，将绕点按逆时针方向旋转一定角度后，的对应边交边于点．连接、，若，，，则________（结果保留根号）．三、综合题16.已知将一矩形纸片ABCD折叠，使顶点A与C重合，折痕为EF．（1）求证：CE=CF；（2）若AB =8 cm，BC=16 cm，连接AF，写出求四边形AFCE面积的思路．17.如图，矩形纸片ABCD中，AB=6，BC=8．折叠纸片使点B落在AD上，落点为B′．点B′从点A开始沿AD移动，折痕所在直线l的位置也随之改变，当直线l经过点A时，点B′停止移动，连接BB′．设直线l与AB相交于点E，与CD所在直线相交于点F，点B′的移动距离为x，点F与点C的距离为y．（1）求证：∠BEF=∠AB′B；（2）求y与x的函数关系式，并直接写出x的取值范围．参考答案一、选择题1. B2. C3.B4.A5. C二、填空题6.或7.①③8.3或9. 10.5.811.3 12.50° 13.80° 14.或15 15.三、综合题16.（1）证明：∵矩形纸片ABCD折叠，顶点A与C重合，折痕为EF，∴∠1=∠2，AD∥BC，∴∠1=∠3，∴∠2=∠3，∴CE=CF．（2）解：思路：连接AF① 由矩形纸片ABCD折叠，易证四边形AFCE为平行四边形；② Rt△CED中，设DE为x，则CE为16-x，CD=8，根据勾股定理列方程可求得DE，CE的长；③由CF=CE，可得CF的长；运用平行四边形面积公式计算CF×CD可得四边形AFCE的面积．17.（1）证明：如图，由四边形ABCD是矩形和折叠的性质可知，BE=B′E，∠BEF=∠B′EF，∴在等腰△BEB′中，EF是角平分线，∴EF⊥BB′，∠BOE=90°，∴∠ABB′+∠BEF=90°，∵∠ABB′+∠AB′B=90°，∴∠BEF=∠AB′B；（2）解：①当点F在CD之间时，如图1，作FM⊥AB交AB于点M，∵AB=6，BE=EB′，AB′=x，BM=FC=y，∴在Rt△EAB′中，EB′2=AE2+AB′2，∴（6﹣AE）2=AE2+x2解得AE=，tan∠AB′B==，tan∠BEF==，∵由（1）知∠BEF=∠AB′B，∴=，化简，得y=x2﹣x+3，（0＜x≤8﹣2）②当点F在点C下方时，如图2所示．设直线EF与BC交于点K设∠ABB′=∠BKE=∠CKF=θ，则tanθ==．BK=，CK=BC﹣BK=8﹣．∴CF=CK•tanθ=（8﹣）•tanθ=8tanθ﹣BE=x﹣BE．在Rt△EAB′中，EB′2=AE2+AB′2，∴（6﹣BE）2+x2=BE2解得BE=．∴CF=x﹣BE=x﹣=﹣x2+x﹣3 ∴y=﹣x2+x﹣3（8﹣2＜x≤6）综上所述，y=．。

2020年中考数学总复习训练特殊的四边形矩形菱形含解析

特殊的四边形（矩形、菱形）一、选择题1．如图，点P是矩形ABCD的边AD上的一个动点，矩形的两条边AB、BC的长分别为3和4，那么点P到矩形的两条对角线AC和BD的距离之和是（）A．B．C．D．不确定2．若矩形的一条对角线与一边的夹角是40°，则两条对角线相交所成的锐角是（）A．20° B．40° C．80° D．100°3．如图，矩形ABCD中，AB=8，BC=6，E、F是AC上的三等分点，则S△BEF为（）A．8 B．12 C．16 D．244．把一张长方形的纸片按如图所示的方式折叠，EM、FM为折痕，折叠后的C点落在B′M或B′M的延长线上，那么∠EMF的度数是（）A．85° B．90° C．95° D．100°5．如图，在矩形ABCD中，EF∥AB，GH∥BC，EF、GH的交点P在BD上，图中面积相等的四边形有（）A．3对B．4对C．5对D．6对6．如图，矩形ABCD的周长为68，它被分成7个全等的矩形，则矩形ABCD的面积为（）A．98 B．196 C．280 D．2847．如图，点O是矩形ABCD的中心，E是AB上的点，沿CE折叠后，点B恰好与点O重合，若BC=3，则折痕CE的长为（）A． B．C．D．68．如图所示，把一长方形纸片沿MN折叠后，点D，C分别落在D′，C′的位置．若∠AMD′=36°，则∠NFD′等于（）A．144°B．126°C．108°D．72°9．将矩形纸片ABCD按如图所示的方式折叠，得到菱形AECF．若AB=3，则BC的长为（）A．1 B．2 C．D．10．如图，已知矩形纸片ABCD，点E是AB的中点，点G是BC上的一点，∠BEG＞60°．现沿直线EG将纸片折叠，使点B落在纸片上的点H处，连接AH，则与∠BEG相等的角的个数为（）A．4 B．3 C．2 D．111．如图，在矩形ABCD中，AB=12cm，BC=6cm，点E、F分别在AB、CD上，将矩形ABCD沿EF折叠，使点A、D分别落在矩形ABCD外部的点A′、D′处，则整个阴影部分图形的周长为（）A．18cm B．36cm C．40cm D．72cm12．下列识别图形不正确的是（）A．有一个角是直角的平行四边形是矩形B．有三个角是直角的四边形是矩形C．对角线相等的四边形是矩形D．对角线互相平分且相等的四边形是矩形13．四边形ABCD的对角线相交于点O，下列条件不能判定它是矩形的是（）A．AB=CD，AB∥CD，∠BAD=90°B．AO=CO，BO=DO，AC=BDC．∠BAD=∠ABC=90°，∠BCD+∠ADC=180°D．∠BAD=∠BCD，∠ABC=∠ADC=90°14．直角三角形中，两条直角边边长分别为12和5，则斜边中线的长是（）A．26 B．13 C．30 D．6.515．将一个矩形的纸对折两次，沿图中虚线将一角剪掉再打开后，得到的图形为（）A．B．C．D．16．菱形一条对角线长为8m，周长为20m，则其面积为（）A．40m2B．20m2C．48m2D．24m217．用直尺和圆规作一个菱形，如图，能得到四边形ABCD是菱形的依据是（）A．一组邻边相等的四边形是菱形B．四边相等的四边形是菱形C．对角线互相垂直的平行四边形是菱形D．每条对角线平分一组对角的平行四边形是菱形18．已知DE∥AC、DF∥AB，添加下列条件后，不能判断四边形DEAF为菱形的是（）A．AD平分∠BAC B．AB=AC且BD=CD C．AD为中线D．EF⊥AD二、填空题19．矩形ABCD中，对角线AC=10cm，AB：BC=3：4，则它的周长是cm．20．矩形ABCD的两条对角线相交于点O，如果矩形的周长是34cm，又△AOB的周长比△ABC的周长少7cm，则AB= cm，BC= cm．21．在矩形ABCD中，对角线AC、BD相交于点O，若∠AOB=110°，则∠OAB= 度．22．如图所示，把两个大小完全一样的矩形拼成“L”形图案，则∠FAC= 度，∠FCA= 度．23．如图，在矩形ABCD中，点E是BC上一点，AE=AD，DF⊥AE，垂足为F，线段DF与图中的哪一条线段相等？先将猜想出的结论填写在下面的横线上，然后再加以证明．即DF= ．（写出一条线段即可）24．将矩形ABCD沿AE折叠，得到如图所示图形．若∠CED′=56°，则∠AED的大小是°．25．菱形ABCD的周长为36，其相邻两内角的度数比为1：5，则此菱形的面积为．26．已知菱形的两条对角线长为6cm和8cm，菱形的周长是cm，面积是cm2．27．如图，四边形ABCD中，E，F，G，H分别是边AB，BC，CD，DA的中点．请你添加一个条件，使四边形EFGH为矩形，应添加的条件是．28．已知菱形的两条对角线的长分别是4cm和8cm，则它的边长为cm．29．若四边形ABCD是平行四边形，使四边形ABCD是菱形，请补充条件（写一个即可）．30．已知菱形ABCD的边长为6，∠A=60°，如果点P是菱形内一点，且PB=PD=2，那么AP的长为．31．已知四边形ABCD为菱形，∠BAD=60°，E为AD中点，AB=6cm，P为AC上任一点．求PE+PD的最小值是．32．如图，在菱形ABCD中，对角线AC=6，BD=8，点E、F分别是边AB、BC的中点，点P在AC上运动，在运动过程中，存在PE+PF的最小值，则这个最小值是．33．已知四边形ABCD为平行四边形，要使四边形ABCD为菱形，还应添加条件．34．用两张对边平行的纸条交叉重叠放在一起，则四边形ABCD为；两张纸条互相垂直时，四边形ABCD 为；若两张纸条的宽度相同，则四边形ABCD为．三、解答题35．如图1中的矩形ABCD，沿对角线AC剪开，再把△ABC沿着AD方向平行移动，得到图2．在图2中，△ADC≌△C′BA′，AC∥A′C′，A′B∥DC．除△DAC与△C′BA′外，指出有哪几对全等的三角形（不能添加辅助线和字母）？选择其中一对加以证明．36．如图，在▱ABCD的纸片中，AC⊥AB，AC与BD相交于点O，将△ABC沿对角线AC翻转180°，得到△AB′C．（1）以A，C，D，B′为顶点的四边形是矩形吗（请填“是”、“不是”或“不能确定”）；（2）若四边形ABCD的面积S=12cm2，求翻转后纸片重叠部分的面积，即S△ACE= cm2．37．如图，四边形ABCD中，∠ABC=∠ADC=90°，M、N分别是AC、BD的中点，那么MN⊥BD成立吗？试说明理由．38．如图所示，两个全等菱形的边长为1厘米，一只蚂蚁由A点开始按ABCDEFCGA的顺序沿菱形的边循环运动，行走2020厘米后停下，则这只蚂蚁停在点．39．如图，在平行四边形ABCD中，O是对角线AC的中点，过点O作AC的垂线与边AD、BC分别交于E、F．求证：四边形AFCE是菱形．特殊的四边形（矩形、菱形）参考答案与试题解析一、选择题1．如图，点P是矩形ABCD的边AD上的一个动点，矩形的两条边AB、BC的长分别为3和4，那么点P到矩形的两条对角线AC和BD的距离之和是（）A．B．C．D．不确定【考点】矩形的性质；相似三角形的判定与性质．【专题】压轴题；动点型．【分析】过P点作PE⊥AC，PF⊥BD，由矩形的性质可证△PEA∽△CDA和△PFD∽△BAD，根据和，即和，两式相加得PE+PF=，即为点P到矩形的两条对角线AC和BD的距离之和．【解答】解：法1：过P点作PE⊥AC，PF⊥BD∵矩形ABCD∴AD⊥CD∴△PEA∽△CDA∴∵AC=BD==5∴…①同理：△PFD∽△BAD∴∴…②∴①+②得：∴PE+PF=即点P到矩形的两条对角线AC和BD的距离之和是．法2：连结OP．∵AD=4，CD=3，∴AC==5，又∵矩形的对角线相等且互相平分，∴AO=OD=2.5cm，∴S△APO+S△POD=×2.5•PE+×2.5•PF=×2.5（PE+PF）=×3×4，∴PE+PF=．故选：A．【点评】根据矩形的性质，结合相似三角形求解．2．若矩形的一条对角线与一边的夹角是40°，则两条对角线相交所成的锐角是（）A．20° B．40° C．80° D．100°【考点】矩形的性质．【专题】计算题．【分析】根据矩形的性质，得△BOC是等腰三角形，再由等腰三角形的性质进行答题．【解答】解：图形中∠1=40°，∵矩形的性质对角线相等且互相平分，∴OB=OC，∴△BOC是等腰三角形，∴∠OBC=∠1，则∠AOB=2∠1=80°．故选C．【点评】本题主要考查了矩形的性质，对角线相等且互相平分，矩形被对角线分成四个等腰三角形．3．如图，矩形ABCD中，AB=8，BC=6，E、F是AC上的三等分点，则S△BEF为（）A．8 B．12 C．16 D．24【考点】矩形的性质．【专题】压轴题．【分析】要求S△BEF只要求出底边EF以及EF边上的高就可以，高可以根据△ABC的面积得到，EF=AC，根据勾股定理得到AC，就可以求出EF的长，从而求出△EFG的面积．【解答】解：S△ABC=×8×6=24．又E、F是AC上的三等分点．∴S△BEF=S△ABC=8．故选A．【点评】本题运用了勾股定理，已知直角三角形的两直角边，求斜边上的高，这类题的解决方法是需要熟记的内容．4．把一张长方形的纸片按如图所示的方式折叠，EM、FM为折痕，折叠后的C点落在B′M或B′M的延长线上，那么∠EMF的度数是（）A．85° B．90° C．95° D．100°【考点】翻折变换（折叠问题）．【分析】根据折叠的性质：对应角相等，对应的线段相等，可得．【解答】解：根据图形，可得：∠EMB′=∠EMB，∠FMB′=∠FMC，∵∠FMC+∠FMB′+∠EMB′+∠BME=180°，∴2（∠EMB′+∠FMB′）=180°，∵∠EMB′+∠FMB′=∠FME，∴∠EMF=90°．故选B．【点评】本题通过折叠变换考查学生的逻辑思维能力，解决此类问题，应结合题意，最好实际操作图形的折叠，易于找到图形间的关系．5．如图，在矩形ABCD中，EF∥AB，GH∥BC，EF、GH的交点P在BD上，图中面积相等的四边形有（）A．3对B．4对C．5对D．6对【考点】矩形的性质．【专题】压轴题．【分析】本题考查了矩形的性质，得出△EPD≌△HDP，则S△EPD=S△HDP，通过对各图形的拼凑，得到的结论．【解答】解：在矩形ABCD中，∵EF∥AB，AB∥DC，∴EF∥DC，则EP∥DH；故∠PED=∠DHP；同理∠DPH=∠PDE；又PD=DP；所以△EPD≌△HDP；则S△EPD=S△HDP；同理，S△GBP=S△FPB；则（1）S梯形BPHC=S△BDC﹣S△HDP=S△ABD﹣S△EDP=S梯形ABPE；（2）S□AGPE=S梯形ABPE﹣S△GBP=S梯形BPHC﹣S△FPB=S□FPHC；（3）S梯形FPDC=S□FPHC+S△HDP=S□AGPE+S△EDP=S梯形GPDA；（4）S□AGHD=S□AGPE+S□HDPE=S□PFCH+S□PHDE=S□EFCD；（5）S□ABFE=S□AGPE+S□GBFP=S□PFCH+S□GBFP=S□GBCH故选C．【点评】本题是一道结论开放题，掌握矩形的性质，很容易得到答案．6．如图，矩形ABCD的周长为68，它被分成7个全等的矩形，则矩形ABCD的面积为（）A．98 B．196 C．280 D．284【考点】矩形的性质．【专题】计算题．【分析】等量关系为：5个小矩形的宽等于2个小矩形的长；6个小矩形的宽加一个小矩形的长等于大长方形周长的一半．【解答】解：设小矩形宽为x，长为y．则大矩形长为5x或2y，宽为x+y．依题意有x+y+5x==34；5x=2y．解得：x=4，y=10．则大矩形长为20，宽为14．所以大矩形面积为280．故选C．【点评】本题考查了矩形的面积和一种很重要的思想：方程思想．7．如图，点O是矩形ABCD的中心，E是AB上的点，沿CE折叠后，点B恰好与点O重合，若BC=3，则折痕CE的长为（）A． B．C．D．6【考点】翻折变换（折叠问题）；勾股定理．【分析】先根据图形翻折变换的性质求出AC的长，再由勾股定理及等腰三角形的判定定理即可得出结论．【解答】解：∵△CEO是△CEB翻折而成，∴BC=OC，BE=OE，∠B=∠COE=90°，∴EO⊥AC，∵O是矩形ABCD的中心，∴OE是AC的垂直平分线，AC=2BC=2×3=6，∴AE=CE，在Rt△ABC中，AC2=AB2+BC2，即62=AB2+32，解得AB=3，在Rt△AOE中，设OE=x，则AE=3﹣x，AE2=AO2+OE2，即（3﹣x）2=32+x2，解得x=，∴AE=EC=3﹣=2．故选：A．【点评】本题考查的是翻折变换，熟知折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等的知识是解答此题的关键．8．如图所示，把一长方形纸片沿MN折叠后，点D，C分别落在D′，C′的位置．若∠AMD′=36°，则∠NFD′等于（）A．144°B．126°C．108°D．72°【考点】翻折变换（折叠问题）；矩形的性质．【专题】计算题．【分析】根据∠A MD′=36°和折叠的性质，得∠NMD=∠NMD′=72°；根据平行线的性质，得∠BNM=∠NMD=72°；根据折叠的性质，得∠D′=∠D=90°；根据四边形的内角和定理即可求得∠NFD′的值．【解答】解：∵∠AMD′=36°，∴∠NMD=∠NMD′=72°．∵AD∥BC，∴∠BNM=∠NMD=72°．又∵∠D′=∠D=90°，∴∠NFD′=360°﹣72°×2﹣90°=126°．故选B．【点评】此题综合运用了折叠的性质、平行线的性质、四边形的内角和定理．9．将矩形纸片ABCD按如图所示的方式折叠，得到菱形AECF．若AB=3，则BC的长为（）A．1 B．2 C．D．【考点】菱形的性质；勾股定理．【专题】计算题．【分析】根据题意可知，AC=2BC，∠B=90°，所以根据勾股定理可知AC2=AB2+BC2，即（2BC）2=32+BC2，从而可求得BC的长．【解答】解：∵AC=2BC，∠B=90°，∴AC2=AB2+BC2，∴（2BC）2=32+BC2，∴BC=．故选：D．【点评】此题主要考查学生对菱形的性质及勾股定理的理解及运用．10．如图，已知矩形纸片ABCD，点E是AB的中点，点G是BC上的一点，∠BEG＞60°．现沿直线EG将纸片折叠，使点B落在纸片上的点H处，连接AH，则与∠BEG相等的角的个数为（）A．4 B．3 C．2 D．1【考点】翻折变换（折叠问题）．【分析】连BH，根据折叠的性质得到∠1=∠2，EB=EH，BH⊥EG，则∠EBH=∠EHB，又点E是AB的中点，得EH=EB=EA，于是判断△AHB为直角三角形，且∠3=∠4，根据等角的余角相等得到∠1=∠3，因此有∠1=∠2=∠3=∠4．【解答】解：连BH，如图，∵沿直线EG将纸片折叠，使点B落在纸片上的点H处，∴∠1=∠2，EB=EH，BH⊥EG，而∠1＞60°，∴∠1≠∠AEH，∵EB=EH，∴∠EBH=∠EHB，又∵点E是AB的中点，∴EH=EB=EA，∴△AHB为直角三角形，∠AHB=90°，∠3=∠4，∴∠1=∠3，∴∠1=∠2=∠3=∠4．故选B．【点评】本题考查了折叠的性质：折叠前后的两个图形全等，即对应角相等，对应线段相等．也考查了若三角形一边上的中线等于这边的一半，则此三角形为直角三角形．11．如图，在矩形ABCD中，AB=12cm，BC=6cm，点E、F分别在AB、CD上，将矩形ABCD沿EF折叠，使点A、D分别落在矩形ABCD外部的点A′、D′处，则整个阴影部分图形的周长为（）A．18cm B．36cm C．40cm D．72cm【考点】翻折变换（折叠问题）．【专题】压轴题．【分析】延长A1E交CD于点G，由题意知GE=EH，FH=GF，则阴影部分的周长与原矩形的周长相等．【解答】解：延长A1E交CD于点G，由题意知，GE=EH，FH=GF，四边形EHD1A1≌四边形EGDA，∴AD=A1D1，AE=A1E，DG=D1H，FH=FG，∴阴影部分的周长=矩形的周长=（12+6）×2=36cm．故选：B．【点评】本题利用了翻折的性质：对应图形全等，对应边相等．12．下列识别图形不正确的是（）A．有一个角是直角的平行四边形是矩形B．有三个角是直角的四边形是矩形C．对角线相等的四边形是矩形D．对角线互相平分且相等的四边形是矩形【考点】矩形的判定．【专题】证明题．【分析】矩形的判定定理有：（1）有一个角是直角的平行四边形是矩形．（2）有三个角是直角的四边形是矩形．（3）对角线互相平分且相等的四边形是矩形，据此判定．【解答】解：A、有一个角是直角的平行四边形是矩形，正确；B、有三个角是直角的四边形是矩形，正确；C、对角线相等的四边形不一定是矩形，对角线相等的平行四边形才是矩形，错误；D、对角线互相平分且相等的四边形是矩形，正确．故选C．【点评】本题主要考查的是矩形的判定定理．（1）有一个角是直角的平行四边形是矩形．（2）有三个角是直角的四边形是矩形．（3）对角线互相平分且相等的四边形是矩形，据此判定．13．四边形ABCD的对角线相交于点O，下列条件不能判定它是矩形的是（）A．AB=CD，AB∥CD，∠BAD=90°B．AO=CO，BO=DO，AC=BDC．∠BAD=∠ABC=90°，∠BCD+∠ADC=180°D．∠BAD=∠BCD，∠ABC=∠ADC=90°【考点】矩形的判定．【分析】矩形的判定定理有：（1）有一个角是直角的平行四边形是矩形．（2）有三个角是直角的四边形是矩形．（3）对角线互相平分且相等的四边形是矩形．据此判断．【解答】解：A、一个角为直角的平行四边形为矩形，故A正确．B、矩形的对角线平分且相等，故B正确．C、∠BCD+∠ADC=180°，但∠BCD不一定与∠ADC相等，根据矩形的判定定理，故C不正确．D、因为∠BAD=∠BCD，故AB∥CD，又因为，∠ABC=∠ADC=90°，根据矩形的判定（有一个角是直角的平行四边形是矩形），故D正确．故选C．【点评】本题考查的是矩形的判定定理，但考生应注意的是由矩形的判定引申出来的各图形的判定．难度一般．14．直角三角形中，两条直角边边长分别为12和5，则斜边中线的长是（）A．26 B．13 C．30 D．6.5【考点】勾股定理；直角三角形斜边上的中线．【分析】由勾股定理可以求出斜边，再根据直角三角形中斜边上的中线等于斜边的一半可以求出斜边中线的长．【解答】解：由勾股定理知，斜边c==13，∵直角三角形中斜边上的中线等于斜边的一半知，∴斜边中线的长=×13=6.5．故选D．【点评】本题考查了勾股定理和直角三角形的性质：斜边上的中线等于斜边的一半．15．将一个矩形的纸对折两次，沿图中虚线将一角剪掉再打开后，得到的图形为（）A．B．C．D．【考点】剪纸问题．【分析】根据题意知，对折实际上就是对称，对折两次的话，剪下应有4条边，并且这4条边还相等，从而可以得到剪下的图形展开后一定是菱形．【解答】解：根据题意折叠剪图可得，剪下的四边形四条边相等，根据四边形等的四边形是菱形可得剪下的图形是菱形，故选：A．【点评】此题考查了剪纸问题，关键是掌握菱形的判定方法：四边形等的四边形是菱形．16．菱形一条对角线长为8m，周长为20m，则其面积为（）A．40m2B．20m2C．48m2D．24m2【考点】菱形的性质．【专题】几何图形问题．【分析】菱形对角线互相垂直平分，所以OA2+OB2=AB2，根据已知可得AB=5，BO=4，利用勾股定理求得AO，即可求得AC的长，根据AC、BD即可求菱形ABCD的面积，即可解题．【解答】解：根据题意可得：BD=8m，则BO=DO=4m，∵菱形周长为20m，∴AB=5m，∵菱形对角线互相垂直平分，∴OA2+OB2=AB2，∴AO==3（m），∴AC=6（m），故菱形的面积S=×6×8=24（m2）．故选D．．【点评】本题考查了菱形对角线互相垂直平分的性质，菱形面积的计算，本题中根据勾股定理求AO的值是解题的关键．17．用直尺和圆规作一个菱形，如图，能得到四边形ABCD是菱形的依据是（）A．一组邻边相等的四边形是菱形B．四边相等的四边形是菱形C．对角线互相垂直的平行四边形是菱形D．每条对角线平分一组对角的平行四边形是菱形【考点】菱形的判定；作图—复杂作图．【分析】关键菱形的判定定理（有四边都相等的四边形是菱形）判断即可．【解答】解：由图形作法可知：AD=AB=DC=BC，∴四边形ABCD是菱形，故选：B．【点评】本题主要考查对作图﹣复杂作图，菱形的判定等知识点的理解和掌握，能熟练地运用性质进行推理是解此题的关键．18．已知DE∥AC、DF∥AB，添加下列条件后，不能判断四边形DEAF为菱形的是（）A．AD平分∠BAC B．AB=AC且BD=CD C．AD为中线D．EF⊥AD【考点】菱形的判定．【专题】几何图形问题．【分析】首先根据题意画出图形，然后由DE∥AC、DF∥AB，判定四边形DEAF为平行四边形，再由菱形的判定定理求解即可求得答案；注意掌握排除法在选择题中的应用．【解答】解：如图，∵DE∥AC、DF∥AB，∴四边形DEAF为平行四边形，A、∵AD平分∠BAC，DF∥AB，∴∠BAD=∠CAD，∠BAD=∠ADF，∴∠CAD=∠ADF，∴AF=DF，∴四边形DEAF为菱形；B、∵AB=AC且BD=CD，∴AD平分∠BAC，同理可得：四边形DEAF为菱形；C、∵由AD为中线，得不到AD平分∠BAC，证不出四边形DEAF的邻边相等，∴不能判断四边形DEAF为菱形；D、∵AD⊥EF，∴▱DEAF是菱形．故选C．【点评】此题考查了菱形的判定．此题难度不大，注意掌握数形结合思想的应用．二、填空题19．矩形ABCD中，对角线AC=10cm，AB：BC=3：4，则它的周长是28 cm．【考点】矩形的性质；勾股定理．【专题】计算题．【分析】根据矩形的一组邻边和一条对角线组成一个直角三角形，解题即可．【解答】解：根据矩形的性质得到△ABC是直角三角形，因为对角线AC=10cm，AB：BC=3：4，根据勾股定理得到BC2=AC2﹣（BC）2=100﹣BC2解得BC=8，AB=6，故它的周长=2×8+2×6=28cm．故答案为28．【点评】本题考查对矩形的性质以及勾股定理的运用．20．矩形ABCD的两条对角线相交于点O，如果矩形的周长是34cm，又△AOB的周长比△ABC的周长少7cm，则AB= 10 cm，BC= 7 cm．【考点】矩形的性质；勾股定理．【专题】计算题．【分析】根据矩形的对边相等以及所给的三角形的周长可得到和所求线段相关的两个式子，进而求解．【解答】解：设AB=a，BC=b．∴2OA=2OB=AC=，2a+2b=34，即a+b=17．由题意可知△AOB的周长+7=△ABC的周长．∴AB+OA+OB+7=AB+BC+AC．∴a++7=a+b+．即b=7，a=17﹣7=10．即AB=10，BC=7．故答案为，10，7．【点评】本题综合考查了矩形的性质及勾股定理的运用．21．在矩形ABCD中，对角线AC、BD相交于点O，若∠AOB=110°，则∠OAB= 35 度．【考点】矩形的性质；三角形内角和定理．【专题】计算题．【分析】根据矩形对角线的性质得到△OAB的形状，进而求得底角的度数．【解答】解：∵矩形的对角线相等且互相平分．∴OA=OC．∴△AOB是等腰三角形．∴∠OAB=∠OBA．∵∠OAB+∠OBA+∠AOB=180°．∴2∠OAB+110°=180°．∴∠O AB=35°．故答案为35．【点评】本题考查矩形的性质以及三角形内角和定理．22．如图所示，把两个大小完全一样的矩形拼成“L”形图案，则∠FAC= 90 度，∠FCA= 45 度．【考点】矩形的性质；全等三角形的判定与性质．【专题】计算题．【分析】两个大小完全一样的矩形拼成“L”形图案所构成的△AFG≌△CAB，所以AF=AC，∠FAC=90°，∠FCA=45度．【解答】解：由已知△AFG≌△CAB，∴∠AFG=∠CAB，AF=AC∵∠AFG+∠FAG=90°，∴∠CAB+∠FA G=90°，∴∠FAC=90°．又∵AF=AC，∴∠FCA=（180°﹣90°）×=45°．故答案为：90；45．【点评】根据矩形的性质得到全等三角形，进而求得△AFC是等腰直角三角形．23．如图，在矩形ABCD中，点E是BC上一点，AE=AD，DF⊥AE，垂足为F，线段DF与图中的哪一条线段相等？先将猜想出的结论填写在下面的横线上，然后再加以证明．即DF= BE ．（写出一条线段即可）【考点】矩形的性质；全等三角形的判定与性质．【专题】几何图形问题．【分析】根据矩形的性质得出AD∥BC，推出∠AFD=∠B，推出∠DAF=∠AEB，根据全等三角形的判定推出△AFD≌△EBA即可．【解答】解：DF=BE，理由是：∵四边形ABCD是矩形，DF⊥AE，∴∠B=∠AFD=90°，AD∥BC，∴∠DAF=∠AEB，在△AFD和△EBA中∴△AFD≌△EBA（AAS），∴DF=BE，故答案为：DF=BE．【点评】本题考查了全等三角形的性质和判定，平行线的性质，全等三角形的性质和判定的应用，关键是推出△AFD≌△EBA，注意：矩形的四个角都是直角，矩形的对边平行．24．将矩形ABCD沿AE折叠，得到如图所示图形．若∠CED′=56°，则∠AED的大小是62 °．【考点】翻折变换（折叠问题）．【专题】压轴题；操作型．【分析】易得∠DED′的度数，除以2即为所求角的度数．【解答】解：∵∠CED′=56°，∴∠DED′=180°﹣56°=124°，∵∠AED=∠AED′，∴∠AED=∠DED′=62°．故答案为：62．【点评】考查翻折变换问题；用到的知识点为：翻折前后得到的角相等．25．菱形ABCD的周长为36，其相邻两内角的度数比为1：5，则此菱形的面积为40.5 ．【考点】菱形的性质．【分析】根据相邻两内角的度数比为1：5，可求出一个30°角，根据周长为36，求出菱形的边长，根据直角三角形里30°角的性质求出高，从而求出面积．【解答】解：作AE⊥BC于E点，∵其相邻两内角的度数比为1：5，∴∠B=180°×=30°，∵菱形ABCD的周长为36，∴AB=BC=×36=9．∴AE=×9=．∴菱形的面积为：BC•AE=9×=40.5．故答案为：40.5．【点评】本题考查菱形的性质，菱形的邻角互补，四边相等．26．已知菱形的两条对角线长为6cm和8cm，菱形的周长是20 cm，面积是24 cm2．【考点】菱形的性质；勾股定理．【分析】根据菱形的面积等于两对角线乘积的一半可得到其面积，根据菱形的性质可求得其边长，从而可得到其周长．【解答】解：如图，四边形ABCD是菱形，BD，AC分别是其对角线且BD=6，AC=8，求其面积和周长．∵四边形ABCD是菱形，BD，AC分别是其对角线，∴BD⊥AC，BO=OD=3cm，AO=CO=4cm，∴AB=5cm，∴菱形的周长=5×4=20cm；S菱形=×6×8=24cm2．故本题答案为：20cm；24cm2．【点评】此题主要考查学生对菱形的性质及勾股定理的理解及运用．27．如图，四边形ABCD中，E，F，G，H分别是边AB，BC，CD，DA的中点．请你添加一个条件，使四边形EFGH为矩形，应添加的条件是AC⊥BD ．【考点】中点四边形．【分析】根据三角形的中位线定理，可以证明所得四边形的两组对边分别和两条对角线平行，所得四边形的两组对边分别是两条对角线的一半，再根据平行四边形的判定就可证明该四边形是一个平行四边形；所得四边形要成为矩形，则需有一个角是直角，故对角线应满足互相垂直．【解答】解：如图，∵E，F分别是边AB，BC的中点，∴EF∥AC，EF=AC，同理HG∥AC，HG=AC，∴EF∥HG，EF=HG，∴四边形EFGH是平行四边形；要使四边形EFGH是矩形，则需EF⊥FG，即AC⊥BD；故答案为：AC⊥BD．【点评】此题主要考查了三角形的中位线定理的运用．同时熟记此题中的结论：顺次连接四边形各边中点所得四边形是平行四边形；顺次连接对角线互相垂直的四边形各边中点所得四边形是矩形．28．已知菱形的两条对角线的长分别是4cm和8cm，则它的边长为2cm．【考点】菱形的性质．【专题】计算题．【分析】根据菱形的性质及勾股定理即可求得其边长的值．【解答】解：菱形的两条对角线分别是4cm，8cm，得到两条对角线相交所构成的直角三角形的两直角边是×4=2和×8=4，那么根据勾股定理得到它的斜边即菱形的边长=2cm．故答案为2【点评】本题考查菱形的性质以及勾股定理．29．若四边形ABCD是平行四边形，使四边形ABCD是菱形，请补充条件此题答案不唯一，如AC⊥BD或AB=AD 等（写一个即可）．【考点】菱形的判定．【专题】开放型．【分析】由四边形ABCD是平行四边形，根据菱形的判定定理求解即可求得答案．【解答】解：∵四边形ABCD是平行四边形，∴当AC⊥BD或AB=AD时，四边形ABCD是菱形．故答案为：此题答案不唯一，如AC⊥BD或AB=AD等．【点评】此题考查了菱形的判定．此题难度不大，注意熟记定理是解此题的关键．30．已知菱形ABCD的边长为6，∠A=60°，如果点P是菱形内一点，且PB=PD=2，那么AP的长为或．【考点】菱形的性质．【专题】压轴题；分类讨论．【分析】根据题意得，应分P与A在BD的同侧与异侧两种情况进行讨论．【解答】解：当P与A在BD的异侧时：连接AP交BD于M，∵AD=AB，DP=BP，∴AP⊥BD（到线段两端距离相等的点在垂直平分线上），在直角△ABM中，∠BAM=30°，∴AM=AB•cos30°=3，BM=AB•sin30°=3，∴PM==，∴AP=AM+PM=4；当P与A在BD的同侧时：连接AP并延长AP交BD于点MAP=AM﹣PM=2；当P与M重合时，PD=PB=3，与PB=PD=2矛盾，舍去．AP的长为4或2．故答案为4或2．【点评】本题注意到应分两种情况讨论，并且注意两种情况都存在关系AP⊥BD，这是解决本题的关键．31．已知四边形ABCD为菱形，∠BAD=60°，E为AD中点，AB=6cm，P为AC上任一点．求PE+PD的最小值是3．【考点】轴对称﹣最短路线问题；菱形的性质．【专题】几何图形问题．【分析】根据菱形的性质，可得AC是BD的垂直平分线，可得AC上的点到D、B点的距离相等，连接BE交AC与P，可得答案．【解答】解：∵菱形的性质，∴AC是BD的垂直平分线，AC上的点到B、D的距离相等．连接BE交AC于P点，PD=PB，PE+PD=PE+PB=BE，在Rt△ABE中，由勾股定理得BE==3，故答案为：3．【点评】本题考查了轴对称，对称轴上的点到线段两端点的距离相等是解题关键．32．如图，在菱形ABCD中，对角线AC=6，BD=8，点E、F分别是边AB、BC的中点，点P在AC上运动，在运动过程中，存在PE+PF的最小值，则这个最小值是 5 ．【考点】轴对称﹣最短路线问题；勾股定理；菱形的性质．【专题】计算题．【分析】AC交BD于O，作E关于AC的对称点N，连接NF，交AC于P，则此时EP+FP的值最小，根据菱形的性质推出N是AD中点，P与O重合，推出PE+PF=NF=AB，根据勾股定理求出AB的长即可．【解答】解：AC交BD于O，作E关于AC的对称点N，连接NF，交AC于P，则此时EP+FP的值最小，∴PN=PE，∵四边形ABCD是菱形，∴∠DAB=∠BCD，AD=AB=BC=CD，OA=OC，OB=OD，AD∥BC，∵E为AB的中点，∴N在AD上，且N为AD的中点，∵AD∥CB，∴∠ANP=∠CFP，∠NAP=∠FCP，。

2024年中考数学总复习考点培优训练第七章专项5与特殊四边形有关的折叠问题

(2)若DE＝5，△GDF的周长为20，求四边形BCDE的周长．
(2)解：由折叠的性质得GF＝CF，DG＝DC，
∵△GDF的周长为20，
∴GF＋FD＋GD＝20，
∴CF＋DF＋DC＝20.
∵四边形BFDE是平行四边形，DE＝5，
∴BE＝DF，BF＝DE＝5，
第7题图
∴四边形BCDE的周长为BC＋CD＋DE＋BE＝BF＋
5 )2，
∴点F到AB的距离为1；
第5题解图
专项5 与特殊四边形有关的折叠问题
(2)求CE的长． (2)由(1)知FM＝1，
∴AM＝BM＝2，FN＝ 5－1.
∵∠BFE＝90°，∴∠BFM＋∠EFN＝90°.
∵MN⊥CD，∴∠FNE＝90°，
∴∠EFN＋∠FEN＝90°，∴∠BFM＝∠FEN.
∵∠BMF＝∠FNE＝90°，∴△BMF∽△FNE，
专项5 与特殊四边形有关的折叠问题
5. 如图，在矩形ABCD中，AB＝4，BC＝ 5 ，E为CD边上一点，将
△BCE沿BE折叠，使得点C落到矩形内点F的位置，连接AF，tan ∠BAF
＝
1 2
.
(1)求点F到AB的距离；
解：(1)如解图，过点F作MN∥AD，分别交AB，
CD于点M，N，则MN⊥AB，MN⊥CD. 由折叠的性质，得EC＝EF，BC＝BF＝ 5 ，
第4题图
专项5 与特殊四边形有关的折叠问题
解题关键点观察设问：求DE的长；观察题干：▱ABCD，AB＝6，BC＝8，∠ABC＝120°，△ABE折叠得 △A′BE，点A′落在EC上；关键点：如图，过点C作CH⊥AD交AD的延长线于点H，构造Rt△CDH求得HC的长；连接EC，构造Rt△ECH求得DE的长．

7、2020年重庆中考数学四边形翻折问题七(答案解析)

2020年重庆中考数学复习四边形翻折问题七（含答案）1、如图所示，在菱形ABCD中，BC＝2，∠B＝60°，E为BC的中点，点F在AB边上，连接EF，将△BEF沿EF翻折，使点B落在点B′处，连接AB′，则AB′的最小值是（）A．2﹣B．+1C．2+D．﹣12、如图，矩形ABCD中，AD＝4，AB＝2．点E是AB的中点，点F是BC边上的任意一点（不与B、C重合），△EBF沿EF翻折，点B落在B'处，当DB'的长度最小时，BF的长度为．3、如图，在矩形ABCD中，AB＝4，BC＝3，点E为AD的中点，点F是AB边上任意一点，现将△AEF沿EF翻折，点A的对应点为A′，则当△A′BC面积最小时，折痕EF的长为（）A．B．2C．2D．4、在矩形ABCD中，AB＝3，BC＝2，以点A为旋转中心，逆时针旋转矩形ABCD，旋转角为α（0°＜α＜180°），得到矩形AEFG，点B、点C、点D的对应点分别为点E、点F、点G．如图，设点P为边FG的中点，连接PB，PE，在矩形ABCD旋转过程中，△BEP的面积的最大值为.5、如图，矩形ABCD中，AB＝3，BC＝4，点E是AB边上一点，且AE＝2，点F是边BC上的任意一点，把△BEF沿EF翻折，点B的对应点为G，连接AG，CG，则四边形AGCD的面积的最小值为．6、如图，在矩形ABCD中，AB＝2，BC＝2，将矩形ABCD绕点C顺时针旋转，得到矩形A1B1CD1，点E是A1B1的中点，过B作BF⊥B1C于点F，连接DE，DF，则线段DE长度的最大值是，线段DF长度的最小值是．2020年重庆中考数学复习四边形翻折问题七（答案解析）1、如图所示，在菱形ABCD中，BC＝2，∠B＝60°，E为BC的中点，点F在AB边上，连接EF，将△BEF沿EF翻折，使点B落在点B′处，连接AB′，则AB′的最小值是（）A．2﹣B．+1C．2+D．﹣1解：如图所示，连接AC，AE，∵四边形ABCD是菱形，∴AB＝BC，∵∠B＝60°，∴△ABC是等边三角形，∵BE＝EC，∴AE⊥BC，∵BC＝2，∠BAE＝30°，∴AE＝，BE＝1，∵当A、B′、E共线时，AB′最小（垂线段最短），∴AB′最小值＝AE﹣BE′＝AE﹣BE＝﹣1．故选：D．2、（2019秋•江宁区期中）如图，矩形ABCD中，AD＝4，AB＝2．点E是AB的中点，点F是BC边上的任意一点（不与B、C重合），△EBF沿EF翻折，点B落在B'处，当DB'的长度最小时，BF的长度为．解：如图，连接DE，∵DB′≥DE﹣EB′，DE＝＝＝，EB′＝1，∴DB′≥﹣1，∴当D，B′，E共线时，DB′的值最小，不妨设此时点B′落在DE上的点B″处，设BF′＝F′B″＝x，∵F′D2＝CD2+F′C2＝B″D2+B″F′2，∴22+（4﹣x）2＝（﹣1）2+x2，解得x＝故答案为3、（2018•新华区二模）如图，在矩形ABCD中，AB＝4，BC＝3，点E为AD的中点，点F是AB边上任意一点，现将△AEF沿EF翻折，点A的对应点为A′，则当△A′BC面积最小时，折痕EF的长为（）A．B．2C．2D．解：当△A′BC面积最小时，A′到BC的距离最小，即A′到AD的距离最大，∴当A′到AD的距离＝EA′时，此时A′到AD的距离最大，即EA′⊥AD，∵将△AEF沿EF翻折，点A的对应点为A′，∴AE＝A′E，∠A＝∠EA′F＝∠A′EA＝90°，∴四边形EAF A′是正方形，∴EF＝AE，∵点E为AD的中点，∴AE＝1.5，∴EF＝，∴当△A′BC面积最小时折痕EF的长为，故选：D．4、在矩形ABCD中，AB＝3，BC＝2，以点A为旋转中心，逆时针旋转矩形ABCD，旋转角为α（0°＜α＜180°），得到矩形AEFG，点B、点C、点D的对应点分别为点E、点F、点G．如图，设点P为边FG的中点，连接PB，PE，在矩形ABCD旋转过程中，△BEP的面积的最大值为.解：如图③中，连接P A，作AM⊥PE于M．当AM与AB共线时，△BPE面积最大，由题意：PF＝PG＝，∵AG＝EF＝2，∠G＝∠F＝90°，∴P A＝PE＝，∵S△APE＝S矩形AGFE＝PE•AM，∴AM＝＝＝，则S△BPE＝PE•BM＝××（3+）＝，∴△PBE的面积的最大值为．5、（2019•龙泉驿区模拟）如图，矩形ABCD中，AB＝3，BC＝4，点E是AB边上一点，且AE＝2，点F是边BC上的任意一点，把△BEF沿EF翻折，点B的对应点为G，连接AG，CG，则四边形AGCD的面积的最小值为．解：∵四边形ABCD是矩形，∴CD＝AB＝3，AD＝BC＝4，∠ABC＝∠D＝90°，根据勾股定理得，AC＝5，∵AB＝3，AE＝2，∴点F在BC上的任何位置时，点G始终在AC的下方，设点G到AC的距离为h，∵S四边形AGCD＝S△ACD+S△ACG＝AD×CD+AC×h＝×4×3+×5×h＝h+6，∴要四边形AGCD的面积最小，即：h最小，∵点G是以点E为圆心，BE＝1为半径的圆上在矩形ABCD内部的一部分点，∴EG⊥AC时，h最小，即点E，点G，点H共线．由折叠知∠EGF＝∠ABC＝90°，延长EG交AC于H，则EH⊥AC，在Rt△ABC中，sin∠BAC＝，在Rt△AEH中，AE＝2，sin∠BAC＝，∴EH＝AE＝，∴h＝EH﹣EG＝﹣1＝，∴S四边形AGCD最小＝h+6＝+6＝．6、（2019•武侯区模拟）如图，在矩形ABCD中，AB＝2，BC＝2，将矩形ABCD绕点C顺时针旋转，得到矩形A1B1CD1，点E是A1B1的中点，过B作BF⊥B1C于点F，连接DE，DF，则线段DE长度的最大值是2+，线段DF长度的最小值是﹣．解：如图，取BC的中点O，连接OF，OD，EC．∵四边形ABCD是矩形，∴∠BCD＝90°，AB＝CD＝2，∵OB＝OC＝，∴OD＝＝，∵BF⊥CF，∴∠BFC＝90°，∴OF＝BC＝，∴DF≥OD﹣OF＝﹣，∴DF的最小值为﹣．同法EC＝＝，DE≤CD+CE＝2+，∴DE的最大值为2+，。

8、2020重庆中考数学四边形翻折变换专题三(含答案解析)

四边形翻折变换专题训练三1、如图，点E是矩形纸片ABCD边AB上一点，将△EBC沿EC翻折，点B落在边AD上的点F处，BE：AE＝5：3，若EC＝15cm，则AB＝cm．2、如图，将平行四边形纸片ABCD折叠，使得点D落在AB边上的D'处，折痕为AE．再将△AD'E翻折，点A恰好落在BC的中点A'处，连结AA'，若AD＝2，则线段AA'的长为.3、折叠矩形纸片ABCD时，发现可以进行如下操作：①把△ADE翻折，点A落在DC边上的点F处，折痕为DE，点E在AB边上；②把纸片展开并铺平；③把△CDG翻折，点C落在线段AE上的点H处，折痕为DG，点G在BC边上，若AB＝AD+2，EH＝1，则AD＝．4、（2019•辽阳模拟）在数学拓展课《折叠矩形纸片》上，小林折叠矩形纸片ABCD进行如下操作：①把△ABF翻折，点B落在CD边上的点E处，折痕AF交BC边于点F；②把△ADH翻折，点D落在AE 边长的点G处，折痕AH交CD边于点H．若AD＝6，AB＝10，则的值是（）A．B．C．D．5、如图，在菱形纸片ABCD中，AB＝+1，∠B＝45°，将菱形纸片翻折，使点A落在CD边上的E处，点B落在点F处，折痕为PQ，点P，Q分别在边AD，BC上，若△PDE为直角三角形，则CE的长为．6、（2019•江都区三模）如图1，有一张矩形纸片ABCD，已知AB＝5，AD＝6，现将纸片进行如下操作：首先将纸片沿折痕BF进行折叠，使点A落在BC边上的点E处，点F在AD上（如图2）；然后将纸片沿折痕DH进行第二次折叠，使点C落在第一次的折痕BF上的点G处，点H在BC上（如图3）．则BG的长为．7、（2019•济南）如图，在矩形纸片ABCD中，将AB沿BM翻折，使点A落在BC上的点N处，BM为折痕，连接MN；再将CD沿CE翻折，使点D恰好落在MN上的点F处，CE为折痕，连接EF并延长交BM于点P，若AD＝8，AB＝5，则线段PE的长等于．8、（2016•新县校级模拟）如图，将矩形纸片ABCD沿直线AE折叠，点B恰好落在线段CD的中点F上，点G是线段AF上一动点（不与A，F重合），点G过GH⊥AB，垂足为H，将矩形沿直线GH翻折，点A恰好落在线段BH上点A′处．若AB长为8，则当△A′GE为直角三角形时，AH的长为．9、如图，矩形纸片ABCD中，AB＝6，AD＝10，P是边BC上的动点，现将纸片折叠，使点A与点P重合，折痕与矩形边的交点分别是E，F，要使折痕始终与边AB，AD有交点，则BP的取值范围是（）A．B．2≤BP≤6 C．D．10、（2019秋•江岸区校级月考）如图在矩形ABCD中，AB＝，AD＝3，点P是AD边上的一个动点，连接BP，作点A关于直线BP的对称点A1，连接A1C，设A1C的中点为Q，当点P从点A出发，沿边AD运动到点D时停止运动，点Q的运动路径长为（）A．πB．πC．πD．π四边形翻折变换专题训练三1、如图，点E是矩形纸片ABCD边AB上一点，将△EBC沿EC翻折，点B落在边AD上的点F处，BE：AE＝5：3，若EC＝15cm，则AB＝24cm．解：设AE＝3x，BE＝5x，则CD＝8x，EF＝5x，∵∠A＝90°，∴Rt△AEF中，AF＝4x，∵∠EFC＝∠ABC＝90°＝∠A＝∠D，∴∠AFE+∠DFC＝∠DCF+∠DFC＝90°，∴∠AFE＝∠DCF，∴△AEF∽△DFC，∴＝，即DF＝DC＝6x，∴AD＝10x＝BC，∵∠B＝90°，∴Rt△BCE中，BE2+BC2＝CE2，即（5x）2+（10x）2＝（15）2，解得x＝3，∴AB＝24，故答案为：24．2、如图，将平行四边形纸片ABCD折叠，使得点D落在AB边上的D'处，折痕为AE．再将△AD'E翻折，点A恰好落在BC的中点A'处，连结AA'，若AD＝2，则线段AA'的长为．解：由折叠可得，∠DAE＝∠D'AE，AD＝AD'＝2，∵AB∥CD，∴∠DEA＝∠D'AE，∴∠DAE＝∠DEA，∴AD＝DE＝2，∴AD'＝DE，而AD'∥DE，∴四边形ADED'是平行四边形，∴AD∥D'E，由折叠可得，D'E垂直平分AA'，∴AA'⊥AD，又∵AD∥BC，∴AA'⊥BC，∴△AA'B是直角三角形，∵AD'＝A'D'＝2，∴∠D'AA'＝∠D'A'A，又∵∠D'AA'+∠B＝90°，∠D'A'A+∠D'A'B＝90°，∴∠B＝∠D'A'B，∴D'A'＝D'B＝2，∴AB＝2+2＝4，又∵A'是BC的中点，BC＝AD＝2，∴A'B＝1，∴AA'＝＝＝．故答案为：．3、（2018•杭州）折叠矩形纸片ABCD时，发现可以进行如下操作：①把△ADE翻折，点A落在DC边上的点F处，折痕为DE，点E在AB边上；②把纸片展开并铺平；③把△CDG翻折，点C落在线段AE 上的点H处，折痕为DG，点G在BC边上，若AB＝AD+2，EH＝1，则AD＝3+2．解：设AD＝x，则AB＝x+2，∵把△ADE翻折，点A落在DC边上的点F处，∴DF＝AD，EA＝EF，∠DFE＝∠A＝90°，∴四边形AEFD为正方形，∴AE＝AD＝x，∵把△CDG翻折，点C落在直线AE上的点H处，折痕为DG，点G在BC边上，∴DH＝DC＝x+2，∵HE＝1，当AH＝AE﹣HE＝x﹣1，在Rt△ADH中，∵AD2+AH2＝DH2，∴x2+（x﹣1）2＝（x+2）2，整理得x2﹣6x﹣3＝0，解得x1＝3+2，x2＝3﹣2（舍去），即AD的长为3+2．故答案为：3+2．4、（2019•辽阳模拟）在数学拓展课《折叠矩形纸片》上，小林折叠矩形纸片ABCD进行如下操作：①把△ABF翻折，点B落在CD边上的点E处，折痕AF交BC边于点F；②把△ADH翻折，点D落在AE 边长的点G处，折痕AH交CD边于点H．若AD＝6，AB＝10，则的值是（）A．B．C．D．解：∵四边形ABCD是矩形，∴∠C＝∠D＝90°，AB＝CD＝10，AD＝BC＝6，由翻折可知：AB＝AE＝10，AD＝AG＝6，BF＝EF，DH＝HG，∴EG＝10﹣6＝4，在Rt△ADE中，DE＝＝＝8，∴EC＝10﹣8＝2，设BF＝EF＝x，在Rt△EFC中：x2＝22+（6﹣x）2，∴x＝，设DH＝GH＝y，在Rt△EGH中，y2+42＝（8﹣y）2，∴y＝3，∴EH＝5，∴＝＝，故选：D．5、（2018•鄞州区模拟）如图，在菱形纸片ABCD中，AB＝+1，∠B＝45°，将菱形纸片翻折，使点A落在CD边上的E处，点B落在点F处，折痕为PQ，点P，Q分别在边AD，BC上，若△PDE为直角三角形，则CE的长为或．解：分两种情况：①当∠DEP＝90°时，∠D＝∠B＝45°，故△DEP是等腰直角三角形，设DE＝EP＝AP＝x，则DP＝x，由AD＝AB＝+1，可得x+x＝+1，解得x＝1，即DE＝1，∴CE＝CD﹣DE＝+1﹣1＝；②当∠DPE＝90°时，∠D＝∠B＝45°，故△DEP是等腰直角三角形，∴DP＝PE＝AP＝AD＝（+1），∴Rt△DEP中，DE＝×（+1）＝1+，∴CE＝CD﹣DE＝+1﹣（1+）＝，故答案为：或．6、（2019•江都区三模）如图1，有一张矩形纸片ABCD，已知AB＝5，AD＝6，现将纸片进行如下操作：首先将纸片沿折痕BF进行折叠，使点A落在BC边上的点E处，点F在AD上（如图2）；然后将纸片沿折痕DH进行第二次折叠，使点C落在第一次的折痕BF上的点G处，点H在BC上（如图3）．则BG的长为．解：∵四边形ABCD为矩形，∴AB＝CD＝5，BC＝AD＝6，由折叠可得：AB＝BE，且∠A＝∠ABE＝∠BEF＝90°，∴四边形ABEF为正方形；过点G作MN∥AB，分别交AD、BC于点M、N，如图3所示：∵四边形ABEF是正方形，∴AF＝AB＝5，∵MN∥AB，∴△BNG和△FMG为等腰直角三角形，且MN＝AB＝5，设BN＝x，则GN＝AM＝x，MG＝MN﹣GN＝5﹣x，MD＝AD﹣AM＝6﹣x，又由折叠的性质可知：DG＝DC＝5，在Rt△MDG中，由勾股定理可得MD2+MG2＝GD2，即（6﹣x）2+（5﹣x）2＝52，解得：x＝2，∴GN＝BN＝2，∴BG＝BN＝2．7、（2019•济南）如图，在矩形纸片ABCD中，将AB沿BM翻折，使点A落在BC上的点N处，BM为折痕，连接MN；再将CD沿CE翻折，使点D恰好落在MN上的点F处，CE为折痕，连接EF并延长交BM于点P，若AD＝8，AB＝5，则线段PE的长等于．解：过点P作PG⊥FN，PH⊥BN，垂足为G、H，由折叠得：ABNM是正方形，AB＝BN＝NM＝MA＝5，CD＝CF＝5，∠D＝∠CFE＝90°，ED＝EF，∴NC＝MD＝8﹣5＝3，在Rt△FNC中，FN＝＝4，∴MF＝5﹣4＝1，在Rt△MEF中，设EF＝x，则ME＝3﹣x，由勾股定理得，12+（3﹣x）2＝x2，解得：x＝，∵∠CFN+∠PFG＝90°，∠PFG+∠FPG＝90°，∴△FNC∽△PGF，∴FG：PG：PF＝NC：FN：FC＝3：4：5，设FG＝3m，则PG＝4m，PF＝5m，∴GN＝PH＝BH＝4﹣3m，HN＝5﹣（4﹣3m）＝1+3m＝PG＝4m，解得：m＝1，∴PF＝5m＝5，∴PE＝PF+FE＝5+＝.8、（2016•新县校级模拟）如图，将矩形纸片ABCD沿直线AE折叠，点B恰好落在线段CD的中点F上，点G是线段AF上一动点（不与A，F重合），点G过GH⊥AB，垂足为H，将矩形沿直线GH翻折，点A恰好落在线段BH上点A′处．若AB长为8，则当△A′GE为直角三角形时，AH的长为．解：如图所示，根据翻转的性质可知：△ABE≌△AFE，∴AF＝AB＝8，EF＝BE，∠2＝∠3，DC＝AB＝8，BC＝AD，∵F是DC的中点，∴DF＝CF＝DC＝4，∴BC＝AD＝＝＝4，∵∠D＝90°，AF＝2DF，∴∠1＝30°，∴∠BAF＝60°，∴∠1＝∠2＝30°，设BE＝x，则EF＝x，CE＝4﹣x，在Rt△CEF中，EF2＝CE2+CF2，即，解得：BE＝x＝，∵矩形沿GH翻折，点A落在线段BH上点A′处，∴AG＝A′G，AH＝A′H，∵∠BAF＝60°，∴△AGA′是等边三角形，∴AG＝AA′，在△AGE与△AA′E中，，∴△AGE≌△AA′E，∴GE＝A′E，∴当△A′GE是直角三角形时，只能∠A′EG＝90°，∴△A′EG是等腰直角三角形，设AH＝y，则AA′＝A′G＝2y，A′B＝AB＝AB﹣AA′＝8﹣2y，在等腰直角三角形A′GE中，A′E＝A′G＝y，在直角三角形A′BE中，A′E＝＝，2y2＝（8﹣2y）2+（）2解得：y1＝，y2＝8（不合题意舍去），∴AH＝，9、如图，矩形纸片ABCD中，AB＝6，AD＝10，P是边BC上的动点，现将纸片折叠，使点A与点P重合，折痕与矩形边的交点分别是E，F，要使折痕始终与边AB，AD有交点，则BP的取值范围是（）A．B．2≤BP≤6 C．D．解：当F与D重合时，如图1，由折叠得：AD＝AP＝10，∵四边形ABCD是矩形，∴∠C＝90°，∵AB＝DC＝6，在Rt△PDC中，PC＝＝8，∴BP＝10﹣8＝2；当E与B重合时，如图2，由折叠得：AB＝BP＝6，综上所述，BP的取值范围是：2≤BP≤6；故选：B．10、（2019秋•江岸区校级月考）如图在矩形ABCD中，AB＝，AD＝3，点P是AD边上的一个动点，连接BP，作点A关于直线BP的对称点A1，连接A1C，设A1C的中点为Q，当点P从点A出发，沿边AD运动到点D时停止运动，点Q的运动路径长为（）A．πB．πC．πD．π解：连接BA1，取BC的中点O，连接OQ、BD，如图所示：∵点A关于直线BP的对称点A1，∴AB＝BA1，∵四边形ABCD是矩形，∴∠BAD＝90°，∴tan∠ABD ＝＝＝，∴∠ABD＝60°，∵A1C的中点为Q，BC的中点为O，∴OQ是△CBA1的中位线，∴OQ ＝BA1＝AB ＝，∴点Q的运动轨迹是以O为圆心，OQ为半径的圆弧，圆心角为120°，∴点Q 的运动路径长为：＝π，故选：C．11。

2020年中考数学专题复习学案：折叠类题目中的动点问题(含答案)

专题：折叠类题目中的动点问题折叠问题是中考的热点也是难点问题，通常与动点问题结合起来，这类问题的题设通常是将某个图形按一定的条件折叠，通过分析折叠前后图形的变换，借助轴对称性质、勾股定理、全等三角形性质、相似三角形性质、三角函数等知识进行解答。

此类问题立意新颖，充满着变化，要解决此类问题，除了能根据轴对称图形的性质作出要求的图形外，还要能综合利用相关数学模型及方法来解答。

类型一、求折叠中动点运动距离或线段长度的最值例1. 动手操作：在矩形纸片ABCD中，AB=3，AD=5. 如图例1-1所示，折叠纸片，使点A落在BC边上的A’处，折痕为PQ，当点A’在BC边上移动时，折痕的端点P、Q也随之移动. 若限定点P、Q分别在AB、AD边上移动，则点A’在BC边上可移动的最大距离为 .图例1-1【答案】2.【解析】此题根据题目要求准确判断出点A'的最左端和最右端位置.当点Q与点D重合时，A'的位置处于最左端，当点P与点B重合时，点A'的位置处于最右端. 根据分析结果，作出图形，利用折叠性质分别求出两种情况下的BA'或CA'的长度，二者之差即为所求.①当点Q与点D重合时，A'的位置处于最左端，如图例1-2所示.确定点A'的位置方法：因为在折叠过程中，A'Q=AQ，所以以点Q为圆心，以AQ长为半径画弧，与BC的交点即为点A'. 再作出∠A'QA的角平分线，与AB的交点即为点P.图例1-2 图例1-3由折叠性质可知，AD= A'D=5，在Rt△A'CD中，由勾股定理得，A C==='4②当点P与点B重合时，点A'的位置处于最右端，如图例1-3所示.确定点A'的位置方法：因为在折叠过程中，A'P=AP，所以以点P为圆心，以AP长为半径画弧，与BC的交点即为点A'. 再作出∠A'PA的角平分线，与AD的交点即为点Q.由折叠性质可知，AB= A'B=3，所以四边形AB A'Q为正方形.所以A'C=BC－A'B=5－3=2.综上所述，点A移动的最大距离为4－2=2.故答案为：2.【点睛】此类问题难度较大，主要考察学生的分析能力，作图能力。

初中数学基础测试专项训练：特殊四边形相关的折叠问题(含答案)

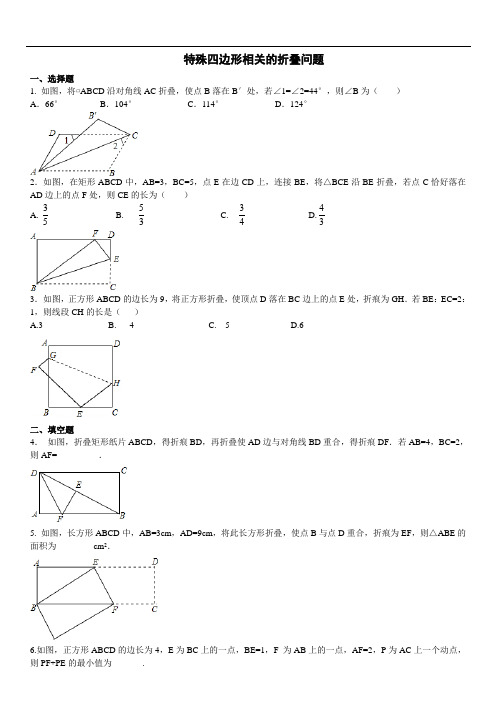
特殊四边形相关的折叠问题一、选择题1. 如图，将▱ABCD 沿对角线AC 折叠，使点B 落在B ′处，若∠1=∠2=44°，则∠B 为（）A ．66°B ．104°C ．114°D ．124°2．如图，在矩形ABCD 中，AB=3，BC=5，点E 在边CD 上，连接BE ，将△BCE 沿BE 折叠，若点C 恰好落在AD 边上的点F 处，则CE 的长为（）A. 53B. 35C. 43D.343．如图，正方形ABCD 的边长为9，将正方形折叠，使顶点D 落在BC 边上的点E 处，折痕为GH ．若BE ：EC=2：1，则线段CH 的长是（）A.3B. 4C. 5D.6二、填空题4．如图，折叠矩形纸片ABCD ，得折痕BD ，再折叠使AD 边与对角线BD 重合，得折痕DF ．若AB=4，BC=2，则AF= _________．5. 如图，长方形ABCD 中，AB=3cm ，AD=9cm ，将此长方形折叠，使点B 与点D 重合，折痕为EF ，则△ABE 的面积为________ cm 2．6.如图，正方形ABCD 的边长为4，E 为BC 上的一点，BE=1，F 为AB 上的一点，AF=2，P 为AC 上一个动点，则PF+PE 的最小值为_______.三、解答题7．在平行四边形ABCD 中，将△BCD 沿BD 翻折，使点C 落在点E 处，BE 和AD 相交于点O.求证：OA=OE8.如图，将□ABCD 沿过点A 的直线l 折叠，使点D 落到AB 边上的点'D 处，折痕l 交CD 边于点E ，连接BE（1）求证：四边形'BCED 是平行四边形（2）若BE 平分∠ABC ，求证：222BE AE AB +=9．如图，AC 为矩形ABCD 的对角线，将边AB 沿AE 折叠，使点B 落在AC 上的点M 处，将边CD 沿CF 折叠，使点D 落在AC 上的点N 处。

2020中考数学压轴专题：图形折叠(含答案)

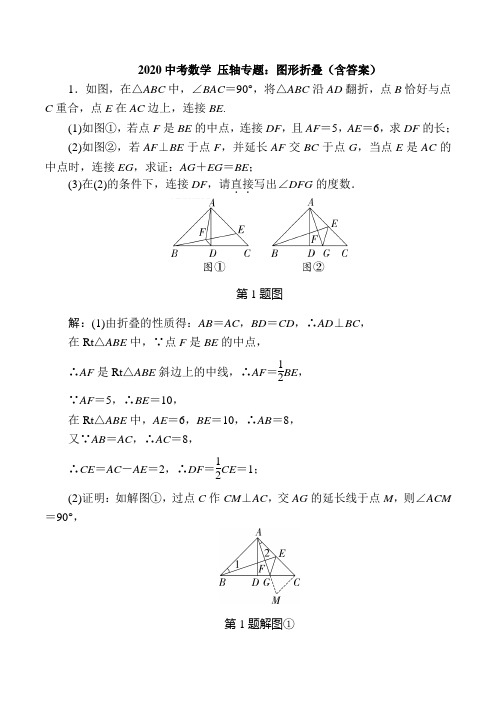
2020中考数学压轴专题：图形折叠（含答案）1．如图，在△ABC 中，∠BAC ＝90°，将△ABC 沿AD 翻折，点B 恰好与点C 重合，点E 在AC 边上，连接BE .(1)如图①，若点F 是BE 的中点，连接DF ，且AF ＝5，AE ＝6，求DF 的长； (2)如图②，若AF ⊥BE 于点F ，并延长AF 交BC 于点G ，当点E 是AC 的中点时，连接EG ，求证：AG ＋EG ＝BE ； (3)在(2)的条件下，连接DF ，请直接．．写出∠DFG 的度数．第1题图解：(1)由折叠的性质得：AB ＝AC ，BD ＝CD ，∴AD ⊥BC ，在Rt △ABE 中，∵点F 是BE 的中点， ∴AF 是Rt △ABE 斜边上的中线，∴AF ＝12BE ， ∵AF ＝5，∴BE ＝10，在Rt △ABE 中，AE ＝6，BE ＝10，∴AB ＝8，又∵AB ＝AC ，∴AC ＝8，∴CE ＝AC －AE ＝2，∴DF ＝12CE ＝1；(2)证明：如解图①，过点C 作CM ⊥AC ，交AG 的延长线于点M ，则∠ACM ＝90°，第1题解图①又∵∠BAC ＝90°，∴∠BAC ＝∠ACM ， ∵AF 是△ABE 的高，∴∠AFB ＝90°，∴∠1＋∠BAF ＝90°， ∵∠BAC ＝90°，∴∠2＋∠BAF ＝90°，∴∠1＝∠2，在△ABE 和△CAM 中， ⎩⎪⎨⎪⎧∠BAE ＝∠ACM AB ＝CA∠1＝∠2， ∴△ABE ≌△CAM (ASA)， ∴AE ＝CM ，BE ＝AM ，又∵点E 是AC 边的中点， ∴CE ＝AE ＝CM ， ∵AB ＝AC ，∠BAC ＝90°， ∴∠ABC ＝∠ACB ＝45°，又∵∠ACM ＝90°， ∴∠MCG ＝∠ACB ＝45°，在△CEG 和△CMG 中， ⎩⎪⎨⎪⎧CE ＝CM ∠ECG ＝∠MCG CG ＝CG， ∴△CEG ≌△CMG (SAS)，∴EG ＝GM ，又∵BE ＝AM ，∴AG ＋EG ＝AG ＋GM ＝AM ＝BE ； (3)∠DFG ＝45°.【解法提示】如解图②，过点D 作DN ⊥DF ，交AG 的延长线于点N ，则∠NDF ＝90°，第1题解图②∵AD ⊥BC ，∴∠ADB ＝90°＝∠NDF ，∴∠ADB ＋∠ADF ＝∠NDF ＋∠ADF ，即∠BDF ＝∠ADN ，∵∠ADB ＝∠AFB ＝90°，∠5＝∠6， ∴∠3＝∠4，在Rt △ABC 中，BD ＝DC ， ∴AD ＝12BC ＝BD ，在△BDF 和△ADN 中，⎩⎪⎨⎪⎧∠BDF ＝∠ADN BD ＝AD ∠3＝∠4，∴△BDF ≌△ADN (ASA)， ∴DF ＝DN ，又∵∠NDF ＝90°，∴∠DFN ＝∠DNF ＝45°，即∠DFG ＝45°.2．如图，在平行四边形ABCD 中，AB ＝9，AD ＝13，tan A ＝125，P 是射线AD 上一点，连接PB ，沿PB 将△APB 折叠，得到△A ′PB .第2题图(1)当∠DP A′＝10°时，∠APB＝________；(2)当P A′⊥BC时，求线段P A的长度；(3)当点A′落在平行四边形ABCD的边所在的直线上时，求线段P A的长度．解：(1)85°或5°或95°；【解法提示】当点P在线段AD上，且∠APB<90°时，点A′在平行四边形ABCD 的内部，∵∠DP A′＝10°，∴∠AP A′＝180°－∠DP A′＝170°，∴∠APB＝12∠AP A′＝85°；如解图①，当点P在线段AD上，且∠APB>90°时，点A′在平行四边形ABCD 的外部，∵∠DP A′＝10°，∴∠AP A′＝180°－∠DP A′＝170°，∴∠APB＝12(360°－∠AP A′)＝95°；如解图②，当点P在AD的延长线上，则∠APB＝12∠DP A′＝5°；第2题解图(2)∵四边形ABCD是平形四边形，∴AD∥BC，若P A′⊥BC，则P A′⊥AD，∴∠APB＝∠A′PB＝45°，如解图③，作BH ⊥AD 于点H ，第2题解图③∵tan A ＝125，∴设AH ＝5x ，BH ＝12x ，在Rt △ABH 中，由勾股定理得AB ＝AH 2＋BH 2＝13x ＝ 9，解得x ＝913， ∴AH ＝4513，BH ＝10813，∵在Rt △BHP 中，∠BPH ＝45°， ∴BH ＝PH ＝10813， ∴AP ＝AH ＋PH ＝15313；(3)①如解图④，当点A ′在AD 上时，第2题解图④∵AB ＝A ′B ， ∴∠1＝∠2，∴BP ⊥AD ，且A ′P ＝AP ，∵tan A ＝125， ∴AP ＝513·AB ＝4513；②如解图⑤，当点A ′在BC 上时，第2题解图⑤由折叠可知，A ′B ＝AB ，AP ＝A ′P ，∠3＝∠4，又∵AD ∥BC ， ∴∠5＝∠4， ∴∠3＝∠5， ∴AB ＝P A ，∴四边形ABA ′P 为菱形， ∴AP ＝9；③如解图⑥，当点A ′在AB 的延长线上时，∠ABP ＝ 12∠ABA ′＝90°， ∴AP ＝135×AB ＝1175.第2题解图⑥综上，线段P A 的长度为4513或9或1175.3．如图，已知一个直角三角形纸片ACB ，其中∠ACB ＝90°，AC ＝4，BC ＝3，E 、F 分别是AC 、AB 边上的点，连接EF .(1)如图①，若将纸片ACB 的一角沿EF 折叠，折叠后点A 落在AB 边上的点D 处，且使S 四边形ECBF ＝3S △EDF ，求AE 的长；(2)如图②，若将纸片ACB 的一角沿EF 折叠，折叠后点A 落在BC 边上的点M 处，且使MF ∥CA .①试判断四边形AEMF 的形状，并证明你的结论； ②求EF 的长；(3)如图③，若FE 的延长线与BC 的延长线交于点N ，CN ＝1，CE ＝47，求AF BF 的值．第3题图解：(1)如解图①，第3题解图①∵折叠后点A 落在AB 边上的点D 处， ∴EF ⊥AB ，△AEF ≌△DEF . ∴S △AEF ＝S △DEF .∵S 四边形ECBF ＝3S △EDF ， ∴S 四边形ECBF ＝3S △AEF . ∵S △ACB ＝S △AEF ＋S 四边形ECBF ， ∴S △ACB ＝S △AEF ＋3S △AEF ＝4S △AEF . ∴ACBAEFS S △△＝14. ∵∠EAF ＝∠BAC ，∠AFE ＝∠ACB ＝90°， ∴△AEF ∽△ABC . ∴ABC AEF S S △△＝(AE AB )2. ∴(AE AB )2＝14.在Rt △ACB 中，∵∠ACB ＝90°，AC ＝4，BC ＝3， ∴AB 2＝AC 2＋BC 2.即AB ＝42＋32＝5. ∴(AE 5)2＝14，∴AE ＝52； (2)①四边形AEMF 是菱形．证明：∵折叠后点A 落在BC 边上的点M 处， ∴∠CAB ＝∠EMF ，AE ＝ME ，又∵MF ∥CA ， ∴∠CEM ＝∠EMF . ∴∠CAB ＝∠CEM . ∴EM ∥AF .∴四边形AEMF 是平形四边形．又∵AE ＝ME ，∴四边形AEMF 是菱形．②连接AM 、AM 与EF 交于点O ，如解图②，第3题解图②设AE ＝x ，则AE ＝ME ＝x ，EC ＝4－x . ∵∠CEM ＝∠CAB ，∠ECM ＝∠ACB ＝90°， ∴Rt △ECM ∽Rt △ACB . ∴EC AC ＝EM AB ， ∵AB ＝5，∴4－x 4＝x 5，解得x ＝209. ∴AE ＝ME ＝209，EC ＝169. 在Rt △ECM 中， ∵∠ECM ＝90°， ∴CM 2＝EM 2－EC 2. 即CM ＝EM 2－EC 2＝（209）2－（169）2＝43.∵四边形AEMF 是菱形， ∴OE ＝OF ，OA ＝OM ，AM ⊥EF . ∴S 菱形AEMF ＝4S AOE ＝2OE ·AO . 在Rt △AOE 和Rt △ACM 中， ∵tan ∠EAO ＝tan ∠CAM ， ∴OE AO ＝CM AC . ∵CM ＝43，AC ＝4，∴AO ＝3OE ， ∴S 菱形AEMF ＝6OE 2. 又∵S 菱形AEMF ＝AE ·CM ， ∴6OE 2＝209×43.∴OE ＝2109. ∴EF ＝4109.(3)如解图③，过点F 作FH ⊥CB 于点H ，第3题解图③在Rt △NCE 和Rt △NHF 中， ∵tan ∠ENC ＝tan ∠FNH ， ∴EC NC ＝FH NH ， ∵NC ＝1，EC ＝47，∴FH NH ＝47，设FH ＝x ，则NH ＝74x ， ∴CH ＝74x －1. ∵BC ＝3，∴BH ＝BC －CH ＝3－(74x －1)＝4－74x . 在Rt △BHF 和Rt △BCA 中，∵tan∠FBH＝tan∠ABC，∴HFBH＝ACBC，解得x＝85.∴HF＝85.∵∠B＝∠B，∠BHF＝∠BCA＝90°，∴△BHF∽△BCA.∴HFCA＝BFBA，即HF·BA＝CA·BF.∴85×5＝4BF.∴BF＝2.∵AF＝3.∴AFBF＝32.4．如图，四边形ABCD为一个矩形纸片，AB＝3，BC＝2，动点P自D点出发沿DC方向运动至C点后停止．△ADP以直线AP为轴翻折，点D落到点D1的位置．设DP＝x，△AD1P与原纸片重叠部分的面积为y.(1)当x为何值时，直线AD1过点C?(2)当x为何值时，直线AD1过点BC的中点E?(3)求出y与x的函数表达式．第4题图解：(1)由题意得，△ADP≌△AD1P，∴AD1＝AD＝2，PD＝PD1＝x，∠PD1A＝∠PDA＝90°，∵直线AD1过点C，∴PD1⊥AC，在Rt △ABC 中，∵AB ＝3，BC ＝2， ∴AC ＝22＋32＝13， CD 1＝13－2，在Rt △PCD 1中，PC 2＝PD 21＋CD 21，即(3－x )2＝x 2＋(13－2)2，解得x ＝213－43， ∴当x ＝213－43时，直线AD 1过点C ； (2)如解图①，连接PE ，第4题解图①∵E 为BC 中点， ∴BE ＝CE ＝1，在Rt △ABE 中， AE ＝AB 2＋BE 2＝10，又∵AD 1＝AD ＝2，PD ＝PD 1＝x ， ∴D 1E ＝10－2，PC ＝3－x ，在Rt △PD 1E 和Rt △PCE 中，有x 2＋(10－2)2＝(3－x )2＋12，解得x ＝210－23， ∴当x ＝210－23时，直线AD 1过BC 的中点E ； (3)如解图②，当0＜x ≤2时，点D 1在矩形内部，y ＝x ；图② 图③ 第4题解图如解图③，当2＜x ≤3时，点D 1在矩形外部，PD 1与AB 交于点F ， ∵AB ∥CD ，∴∠1＝∠2，∵∠1＝∠3，∴∠2＝∠3，∴FP ＝F A ，作PG ⊥AB ，垂足为点G ，设FP ＝F A ＝a ，由题意得，AG ＝DP ＝x ，FG ＝x －a ，在Rt △PFG 中，由勾股定理，得 (x －a )2＋22＝a 2，解得a ＝4＋x 22x ，∴y ＝12×2×4＋x 22x ＝x 2＋42x ，综上所述，当0＜x ≤2时，y ＝x ；当2＜x ≤3时，y ＝x 2＋42x .5．阅读下列材料：如图①，在Rt △ABC 中，∠C ＝90°，D 为边AC 上一点，DA ＝DB ，E 为BD 延长线上一点，∠AEB ＝120°.(1)猜想AC 、BE 、AE 的数量关系，并证明．小明的思路是：根据等腰△ADB 的轴对称性，将整个图形沿着AB 边的垂直平分线翻折，得到点C 的对称点F ，如图②，过点A 作AF ⊥BE ，交BE 的延长线于F ，请补充完成此问题；(2)参考小明思考问题的方法，解答下列问题：如图③，在等腰△ABC 中，AB ＝AC ，D 、F 在直线BC 上，DE ＝BF ，连接AD ，过点E 作EG ∥AC 交FH 的延长线于点G ，∠DFG ＋∠D ＝∠BAC .①探究∠BAD 与∠CHG 的数量关系；②请在图中找出一条和线段AD 相等的线段，并证明．第5题图解：猜想：AC ＝BE ＋12AE . 理由如下：如题图②， ∵DA ＝DB ， ∴∠DAB ＝∠DBA ， ∵AF ⊥BF ， ∴∠F ＝∠C ＝90°，在△ABF 和△BAC 中， ⎩⎪⎨⎪⎧∠F ＝∠C ＝90°∠ABF ＝∠BAC AB ＝BA， ∴△ABF ≌△BAC (AAS)， ∴AC ＝BF ，∵∠AEB ＝120°＝∠F ＋∠F AE ， ∴∠F AE ＝30°， ∴EF ＝12AE ，∴AC ＝BF ＝BE ＋EF ＝BE ＋12AE ，∴AC ＝BE＋12AE ；问题：(1)如题图③中，∵∠ACF ＝∠D ＋∠CAD ，∠D ＋∠DFG ＝∠BAC ，∴∠CHG ＝∠CFH ＋∠FCH ＝∠CFH ＋∠D ＋∠CAD ＝∠BAC ＋∠CAD ＝∠BAD ，∴∠CHG ＝∠BAD ； (2)结论：AD ＝FG . 理由如下：如解图③中，反向延长BD 到R ，使得BR ＝CD ，连接AR ，作AJ ∥CD 交EG 的延长线于点J ，连接FJ ，第5题解图③∵AJ ∥CE ，AC ∥JE ，∴四边形ACEJ 是平行四边形， ∴AJ ＝CE ，AC ＝JE ， ∵AB ＝AC ，∴JE ＝AB ，∠ABC ＝∠ACB ， ∴∠ABR ＝∠ACD ，在△ABR 和△ACD 中， ⎩⎪⎨⎪⎧AB ＝AC ∠ABR ＝∠ACD BR ＝CD， ∴△ABR ≌△ACD (SAS)， ∴AR ＝AD ，∵BR ＝CD ，BF ＝DE ， ∴FR ＝CE ＝AJ ，EF ＝BD ，又∵AJ ∥RF ，∴四边形ARFJ 是平行四边形， ∴JF ＝AR ＝AD ，在△ABD 和△JEF 中，⎩⎪⎨⎪⎧AB ＝JE AD ＝JF BD ＝EF ，∴△ABD ≌△JEF (SSS)， ∴∠EJF ＝∠BAD ，又∵∠JGH ＝∠GHC ， ∵∠BAD ＝∠CHG ＝∠FGJ ， ∴∠EJF ＝∠FGJ ， ∴FG ＝FJ ， ∴AD ＝FG .6．如图，长方形纸片ABCD 中，AB ＝8，将纸片折叠，使顶点B 落在边AD 上的E 点处，折痕的一端G 点在边BC 上．(1)如图①，当折痕的另一端F 在AB 边上且AE ＝4时，求AF 的长； (2)如图②，当折痕的另一端F 在AD 边上且BG ＝10时， ①求证：EF ＝EG ； ②求AF 的长；(3)如图③，当折痕的另一端F 在AD 边上，B 点的对应点E 在长方形内部，E 到AD 的距离为2，且BG ＝10时，求AF 的长．第6题图(1)解：∵纸片折叠后顶点B 落在边AD 上的E 点处， ∴BF ＝EF ，∵AB ＝8，∴EF ＝8－AF ，在Rt △AEF 中，AE 2＋AF 2＝EF 2，即42＋AF 2＝(8－AF )2，解得AF ＝3；(2)①证明：∵纸片折叠后顶点B 落在边AD 上的E 点处，∴∠BGF ＝∠EGF ， ∵长方形纸片ABCD 的边AD ∥BC ，∴∠BGF ＝∠EFG ，∴∠EGF ＝∠EFG ，∴EF ＝EG ； ②解：∵纸片折叠后顶点B 落在边AD 上的E 点处， ∴EG ＝BG ＝10，HE ＝AB ＝8，FH ＝AF ， ∴EF ＝EG ＝10，在Rt △EFH 中，由勾股定理得FH ＝EF 2－HE 2＝102－82＝6，∴AF ＝FH ＝6；(3)解：如解图，设EH 与AD 相交于点K ，过点E 作MN ∥CD 分别交AD 、BC 于点M 、N ，第6题解图∵E 到AD 的距离为2， ∴EM ＝2，EN ＝8－2＝6，在Rt △ENG 中，GN ＝EG 2－EN 2＝102－62＝8， ∵∠GEN ＋∠KEM ＝180°－∠GEH ＝180°－90°＝90°， ∠GEN ＋∠NGE ＝180°－90°＝90°， ∴∠KEM ＝∠NGE ，又∵∠ENG ＝∠KME ＝90°，∴△GEN ∽△EKM ， ∴EK GE ＝KM EN ＝EM GN ，即EK 10＝KM 6＝28，解得EK ＝52，KM ＝32， ∴KH ＝EH －EK ＝8－52＝112，∵∠FKH＝∠EKM，∠H＝∠EMK＝90°，∴△FKH∽△EKM，∴FHEM＝KHKM，即FH2＝11232，解得FH＝223，∴AF＝FH＝223.7．在等腰Rt△ABC中，∠BAC＝90°，AB＝AC，D是斜边BC的中点，连接AD.(1)如图①，E是AC的中点，连接DE，将△CDE沿CD翻折到△CDE′，连接AE′，当AD＝2时，求AE′的值；(2)如图②，在AC上取一点E，使得CE＝13AC，连接DE，将△CDE沿CD 翻折到△CDE′，且AE′交BC于点F，求证：DF＝CF.第7题图(1)解：∵∠BAC＝90°，AB＝AC，D是斜边BC的中点，∴∠ADC＝90°，∠ACD＝45°，在Rt△ADC中，AC＝ADsin 45°＝2，∵E是AC的中点，∴CE＝12AC＝1，∵将△CDE沿CD翻折到△CDE′，∴CE ′＝CE ＝1，∠ACE ′＝90°，由勾股定理得：AE ′＝CE ′＋AC 2＝5；(2)证明：如解图，过B 作AE ′的垂线交AD 于点G ，交AC 于点H ，第7题解图∵∠ABH ＋∠BAF ＝90°，∠CAF ＋∠BAF ＝90°， ∴∠ABH ＝∠CAF ，又∵AB ＝AC ，∠BAH ＝∠ACE ′＝90°， ∴△ABH ≌△CAE ′， ∴AH ＝CE ′＝CE ， ∵CE ＝13AC ， ∴AH ＝HE ＝CE ， ∵D 是BC 中点， ∴DE ∥BH ， ∴G 是AD 中点，在△ABG 和△CAF 中 ⎩⎪⎨⎪⎧∠BAD ＝∠ACD ＝45°AB ＝AC∠ABH ＝∠CAF， ∴△ABG ≌△CAF (ASA)，∴AG ＝CF ， ∵AG ＝12AD ，∴CF ＝12AD ＝12CD ，∴DF ＝CF . 8．【问题情境】在数学综合与实践课上，老师让同学们以“正方形的折叠为主题开展活动”，如图①，四边形ABCD是正方形，AB＝5，点E是CD边上的一动点，连接AE.【操作发现】(1)将△ADE沿AE折叠得△AD′E，如图②，当点D′到BC的距离等于1时，求点E到BC的距离．【继续探究】(2)在(1)的条件下，创新小组在图②中，连接BE，如图③，发现∠AEB＝2∠EBC，请你证明这个结论．【深入探究】(3)创新小组将图②沿MN向下折叠，使点A与点E，连接DD′并延长交BC 于点F，如图④，求四边形MNFD的面积．第8题图解：(1)如解图①，过点D′作XY∥BC，与AB、CD分别交于点X、Y，∵四边形ABCD是正方形，第8题解图①∴∠B＝∠C＝90°，AB∥CD，∴四边形BCYX 是矩形， ∵点D ′到BC 的距离为1， ∴BX ＝CY ＝1，∴AX ＝AB －BX ＝5－1＝4，由折叠知：AD ′＝AD ＝5，在Rt △AXD ′中，由勾股定理得XD ′＝52－42＝3， ∴D ′Y ＝XY －XD ′＝5－3＝2，由题易证△AXD ′∽△D ′YE ， ∴AXD ′Y＝XD ′YE ， ∴42＝3YE ， ∴YE ＝32，∴CE ＝YE ＋YC ＝32＋1＝52， ∴点E 到BC 的距离等于52； (2)证明：由(1)知，CE ＝52， ∴DE ＝DC －CE ＝5－52＝52， ∴DE ＝CE ，又∵AD ＝BC ，∠C ＝∠ADE ， ∴△ADE ≌△BCE ， ∴AE ＝BE ，如解图②，过点E 作EZ ⊥AB 于点Z ，第8题解图②∴EZ 平分∠AEB ， ∴∠AEB ＝2∠BEZ ， ∵EZ ⊥AB ，BC ⊥AB ， ∴EZ ∥BC . ∴∠BEZ ＝∠EBC ， ∴∠AEB ＝2∠EBC ；(3)∵点A 、点E 关于MN 对称， ∴MN 垂直平分AE ，同理：AE 垂直平分DD ′， ∴MN ∥DF ，又∵MD ∥NF ，∴四边形MNFD 是平行四边形，如解图③，设AE 与MN ，DD ′分别相交于点G 、H ，第8题解图③在Rt △ADE 中，由勾股定理得 AE ＝AD 2＋DE 2 ＝52＋（52）2＝552，∴GE ＝12AE ＝12×552＝554. 在Rt △ADE 中，DH ·AE ＝AD ·DE ，∴DH ＝AD ·DEAE ＝5×52552＝5，在Rt △DEH 中，由勾股定理得 EH ＝DE 2－DH 2＝（52）2－（5）2＝52，∴GH ＝GE －EH ＝554－52＝354，∵△ADE ≌△DCF ，∴AE ＝DF ，∴DF ＝552， ∴S 四边形MNFD ＝DF ·GH ＝552×354＝758. 9．【问题情境】(1)数学课上，老师出了一道题，如图①，Rt △ABC 中，∠C ＝90°，AC ＝12AB ，求证：∠B ＝30°，请你完成证明过程；【继续探究】(2)如图②，四边形ABCD 是一张边长为2的正方形纸片，E 、F 分别为AB 、CD 的中点，沿过点D 的折痕将纸片翻折，使点A 落在EF 上的点A ′处，折痕交AE 于点G ，请运用(1)中的结论求∠ADG 的度数和AG 的长；【拓展应用】(3)若矩形纸片ABCD 按如图③所示的方式折叠，B 、D 两点恰好重合于一点O (如图④)，当AB ＝6时，求EF 的长．第9题图(1)证明：Rt △ABC 中，∠C ＝90°，AC ＝12AB ， ∵sin B ＝AC AB ＝12， ∴∠B ＝30°；(2)解：∵正方形边长为2，E 、F 分别为AB 、CD 的中点， ∴EA ＝FD ＝12×CD ＝1，∵沿过点D 的折痕将纸片翻折，使点A 落在EF 上的点A ′处， ∴A ′D ＝AD ＝2， ∴FD A ′D ＝12， ∴∠F A ′D ＝30°，可得∠FDA ′＝90°－30°＝60°，由折叠性质可得∠ADG ＝∠A ′DG ，AG ＝A ′G ， ∴∠ADG ＝∠ADA ′2＝90°－60°2＝15°， ∵A ′D ＝2，FD ＝1，∴A′F＝A′D2－FD2＝3，∴EA′＝EF－A′F＝2－3，∵∠EA′G＋∠DA′F＝180°－∠GA′D＝90°，∴∠EA′G＝90°－∠DA′F＝90°－30°＝60°，∴∠EGA′＝90°－∠EA′G＝90°－60°＝30°，则AG＝AG′＝2EA′＝2(2－3)；(3)解：∵折叠后B、D两点恰好重合于一点O，∴AO＝AD＝CB＝CO，∴DA＝AC 2，∵∠D＝90°，∴∠DCA＝30°，∵AB＝CD＝6，在Rt△ACD中，ADDC＝tan30°，则AD＝DC·tan30°＝6×33＝23，∵∠DAF＝∠F AO＝12∠DAO＝90°－∠DCA2＝30°，∴DFAD＝tan30°＝33，∴DF＝33AD＝2，∴DF＝FO＝2，同理EO＝2，∴EF＝EO＋FO＝4.10．如图，在矩形ABCD纸片中，AB＝10 cm，BC＝12 cm.点P在BC边上，将△P AB沿AP折叠得△P AE，连接CE，DE.(1)当点E落在AD边上时，CE＝________；(2)当△CDE分别满足下列条件时，求PB的长．①DE＝CD；②DE＝CE.第10题图解：(1)226 cm ；【解法提示】如解图①，∵将△P AB 沿AP 折叠，得△P AE ，E 落在AD 边上， ∴四边形ABPE 是正方形， ∴PB ＝PE ＝AB ＝10 cm ， ∴PC ＝2 cm ，∴CE ＝PE 2＋PC 2＝226 cm.第10题解图①(2)①如解图②，过E 作MN ⊥AD 于M ，交BC 于N ，则MN ⊥BC ，第10题解图②∵DE ＝CD ，AE ＝AB ＝CD ＝DE ， ∴AE ＝10 cm ，∴AM ＝12AD ＝BN ＝6 cm ，∴ME ＝AE 2－AM 2＝8 cm ， ∴EN ＝MN －ME ＝2 cm ，易知△AME ∽△ENP ， ∴AM AE ＝EN PE ， ∴610＝2PE ， ∴PE ＝103 cm ， ∴PB ＝PE ＝103 cm ；②如解图③，过E 作MN ⊥AD 于M ，交BC 于N ，过E 作EQ ⊥CD 于Q ，第10题解图③∵DE ＝CE ，∴DQ ＝12CD ＝5 cm ，∴ME ＝5 cm ， ∴EN ＝MN －ME ＝5 cm ， ∴AM ＝AE 2－ME 2＝5 3 cm ， ∴BN ＝5 3 cm ，同理得AM AE ＝EN PE ， ∴5310＝5PE ， ∴PE ＝1033 cm ，103∴PB＝PE＝3cm.。

中考数学专题复习《特殊平行四边形中的折叠问题》测试卷-附带答案

中考数学专题复习《特殊平行四边形中的折叠问题》测试卷-附带答案学校:___________班级:___________姓名:___________考号:___________一单选题1．如图在矩形纸片ABCD 中将BCD △沿BD 折叠 C 点落在C '处则图中共有全等三角形（）A ．2对B ．3对C ．4对D ．5对2．如图对折矩形纸片ABCD 使AB 与DC 重合得到折痕EF 将纸片展平再一次折叠使点D 落到EF 上点G 处并使折痕经过点A 展平纸片后DAG ∠的大小为（）A ．40︒B ．60︒C ．55︒D ．75︒3．如图在矩形ABCD 中 5AB = 8BC = 点E 和F 是边BC 上的两点连结AE DF 、将ABE 和CDF 沿AE DF 、折叠后点B 和点C 重合于点M 则EF 的长是（）A ．2.5B ．3C ．1.5D ．44．如图在矩形纸片ABCD 中已知8AD = 折叠纸片使AB 边与对角线AC 重合点B 落在点F 处折痕为AE 且3EF = 则ABE 的面积为（）A ．10B ．9C ．8D ．75．如图在矩形OABC 中 9OA = 15AB = E 是BC 上一点沿AE 折叠使点B 恰好落在x 轴的点D 处．E 点坐标是（）A ．()5,15B ．()3,15C ．()15,2D ．()15,4 6．如图在矩形ABCD 中点E 是边CD 的中点将ADE 沿AE 折叠后得到AFE △ 且点F 在矩形ABCD 的内部将AF 延长后交边BC 于点G 且45CG GB = 则AB AD 的值为（）A ．43B ．56C ．1D ．77．如图把矩形纸片ABCD 沿对角线BD 折叠设重叠部分为EBD △ 则下列结论不一定成立的是（）A ．AB CD = B ．BAE DCE ≌△△C ．EB ED = D ．30ABE ∠=︒ 8．如图在一张菱形纸片ABCD 中 2AB = 30B ∠=︒ 点E 在BC 边上（不与B C 重合）将ABE 沿直线AE 折叠得到AFE △ 连接BF EF DF 有以下四个结论：AE EF =① 105BFD ∠=︒② ③当AE BC ⊥时 FD AC = ④当FE 平分AFB ∠时则23FD = 其中正确的结论个数是（）A ．1B ．2C ．3D ．4二填空题9．如图正方形纸片ABCD 的边长为12 E 是边CD 上一点连接AE 折叠该纸片使点A 落在AE 上的点G 并使折痕经过点B 得到折痕BF 点F 在AD 上．若5DE = 则GE 的长为．10．将一张长方形纸片ABCD 按如图所示方式折叠 AE AF 为折痕点B D 折叠后的对应点分别为B' 'D 若''4B AD ∠=︒ 则EAF ∠的度数为．11．如图在长方形ABCD 中 3AD = 2AB = 点F 是AB 上一点 1AF = 点E 是BC 上一动点连接EF 将BEF △沿EF 折叠记点B 的对应点为点B ' 连接DB ' 则FB DB '+'的最小值是．12．如图在矩形ABCD 中 5AB = 8AD = 边AD 上有一动点P 连结BP 把ABP沿BP 折叠当点A 的对应点A '刚好落在BC 的垂直平分线上时点A '到AD 的距离为．13．如图所示在完全重合放置的两张矩形纸片ABCD 中 8AB = 16BC = 将上面的矩形纸片折叠使点C 与点A 重合折痕为EF 点D 的对应点为点G 连接DG 则图中阴影部分的面积为．三解答题14．如图正方形纸片ABCD 的边长12AB = E 是DC 上一点 5CE = 折叠正方形纸片使点B 和点E 重合折痕为FG 试求FG 的长．15．如图把一张长方形纸片ABCD 折叠起来使其对角顶点A 与C 重合 D 与G 重合若长方形的长BC 为8 宽AB 为4(1)求DE 的长(2)求阴影部分的面积．16．如图1 将矩形纸片()ABCD AD AB >折叠使点C 刚好落在线段AD 上且折痕分别与边BC AD 相交设折叠后点C D 的对应点分别为点G H 折痕分别与边BC AD 相交于点E F ．（1）求证：四边形CEGF 是菱形（2）如图2 若3AB = 9BC = 当点G 与点A 重合时求折痕EF 的长.17．如图在四边形纸片ABCD 中 AD BC ∥ AD CD > 将纸片沿过点D 的直线折叠使点C 落在AD 上的点C '处折痕DE 交BC 于点E 连接C E '．(1)请确定四边形CDC E '的形状并说明理由(2)若30BCD ∠=︒ 2CE = 过点C '作C F BC '⊥于F 连接CC '交DE 于点M 连接FM ： ①四边形CDC E '的面积为①2FM = ．18．已知矩形ABCD 中 4AB = 6AD = 点P 是边AD 的中点．(1)如图1 连接BP 并延长与CD 的延长线交干点F 问：线段CF 上是否存在点Q 使得PFQ △是以PF 为腰的等腰三角形若存在请直接写出DQ 的长若不存在请说明理由．(2)①如图2 把矩形ABCD 沿直线MN 折叠使点B 落在点D 上直线MN 与AD BD BC 、、的交点分别为M H N 求折痕MN 的长．①如图3：在①的条件下以点A 为原点分别以矩形ABCD 的两条边AD AB 、所在的直线为x 轴和y 轴建立平面直角坐标系若点R 在x 轴上在平面内是否存在点S 使以R M N S 为顶点的四边形是菱形？若存在请求出点S 的坐标若不存在请说明理由．(3)如图4：若点E 为CD 边上的一个动点连结PE 以PE 为边向下方作等边PEG △ 连结AG 则AG 的最小值是______．（请直接写出答案）参考答案：1．C2．B3．B4．B5．D6．A7．D8．B9．491310．43︒111012．213．72514．解：如图过点F 作FM BC ⊥ 垂足为M 连接BE ．①四边形ABCD 为正方形①AB BC CD AD === 90A ABC C D ∠=∠=∠=∠=︒①90A ABC BMF ===︒∠∠∠①四边形ABMF 为矩形①12MF AB BC ===①将正方形纸片ABCD 折叠使点B 落在边CD 上的点E 折痕为FG ①90C FMG ∠=∠=︒ BE FG ⊥①90BNG C ∠=∠=︒①90MGF CBE BEC CBE ∠+∠=∠+∠=︒ ①MGF CEB ∠=∠在FMG 和BCE 中 MGF CEB FMG C FM BC ∠=∠⎧⎪∠=∠⎨⎪=⎩①()AAS FMG BCE ≌①MG CE =．又①5CE =①5MG =．在Rt MFG 中根据勾股定理得13FG == 即FG 的长是13．15．（1）设DE EG x == 则8AE x =- 在Rt AEG △中 222AG EG AE +=所以()22168x x +=-解得：3x =即3DE =（2）过点G 作GM AD ⊥于M 则1122AG GE AE GM ⨯=⨯4AG AB == 5AE = 3GE = 所以1143522GM ⨯⨯=⨯⨯所以125GM = 所以11825CED S GM DE =⨯=△． 16．解：（1）证明：①四边形ABCD 是矩形 ①AD ①BC①①GFE =①FEC①图形翻折后点G 与点C 重合 EF 为折线 ①①GEF =①FEC FG =FC EG =EC ①①GFE =①FEG①GF =GE①GE =EC =CF =FG①四边形CEGF 为菱形（2）当G 与A 重合时由折叠的性质得AE =CE ①①B =90° AB =3 BC =9 BE =9-CE ①Rt ①ABE 中 AE 2=AB 2+BE 2即CE 2=32+(9-CE )2解得 CE =5．AC 222239310AB BC ++=由（1）知四边形CEGF 为菱形 ①12CEGF S EF AC CE AB =⨯=⨯菱形 ①10310EF == 17．（1）解：四边形CDC E '是菱形理由如下：根据折叠的性质可得：CD C D C DE CDE '∠=∠ CE C E '= ①AD BC ∥①C DE CED '∠=∠①CDE CED ∠=∠①CD CE =①CD C D C E CE ''===①四边形CDC E '为菱形（2）①①四边形CDC E '是菱形 ①2C E CE '== C E CD '∥ CM C M '= ①30C EF DCB '∠=∠=︒ ①C F BE '⊥ ①112C F C E ''== EF F '=①四边形CDC E '的面积212CE C F '=⨯=⨯= 故答案为：2①①EF = 2CE =①2CF =①(2222218C C C F CF ''=+=+=+①C F BC CM C M ''⊥=， ①12FM C C '=①22124FM C C '==故答案为：2 18．（1）解：存在理由如下：四边形ABCD 是矩形 90A ADC ∴∠=∠=︒ AB CD = 90FDP ∴∠=︒点P 是边AD 的中点 AP DP ∴=又APB DPF ∠=∠ ()ASA ABP DFP ∴△≌△ PF PB ∴= AB DF = 4,6AB AD ==4DF AB ∴== 132AP PD AD === 90A ∠=︒在Rt ABP 中：2222345PB AB AP +=+=5PF ∴=PFQ △为等腰三角形以PF 为腰的等腰三角形分为两种情形： ①当PF PQ =时此时点Q 与点C 重合故4DQ DC == ①当FP FQ =时如图：5PF = 5FQ = FD =4541DQ FQ FD =-=-=综合①① DQ 的长为：4或1（2）解：①如图：连接BM DN根据题意可知：MN 垂直平分BD ,MN BD BH DH ∴⊥= ,NB ND MB MD == 四边形ABCD 是矩形AD BN ∴MDH HBN ∴∠=∠ 又MHD NHB ∠=∠MHD NHB ∴△≌△MH HN ∴= MD NB =∴四边形MBND 是菱形设AM b = 则6MD MB b ==-在Rt AMB △中222BM AM AB =+即：222(6)4b b -=+ 解得：53b = 5513,6333AM BM ∴==-= 在Rt △ABD 中BD 12BH BD ∴=MH BD ⊥∴在Rt MHB △中MH ==2MN MH ∴== ①建立平面直角坐标系如图：由①知：53AM = 133BN MD MB ===4AB = MN = ①5130433M N ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭，，， R M N S 为顶点的四边形是菱形点R 在x 轴上当MR 为对角线时 MR NS ⊥,M R 都在x 轴上 ∴,N S 关于x 轴对称 1343S ⎛⎫∴ ⎪⎝⎭，当MN 为对角线时 MN RS ⊥ 由（2）知四边形MBND 是菱形则S 与点B 重合 ∴此时(0,4)S -当MS 为对角线时则MR SN ∥ MR SN =MN = 13(,4)3N -①1343S ⎛⎫- ⎪ ⎪⎝⎭综上可知存在点S 使得以R M N S 为顶点的四边形是菱形点S 坐标为：134134⎫--⎪⎪⎝⎭ 134134⎫+-⎪⎪⎝⎭ 13,43⎛⎫⎪⎝⎭ (0,4)- （3）解：如图：分别以PD PC 为边向下方作等边,PDF PCH △△ 过点F 作FI AD ⊥垂足为I 连接AF HF P 为AD 中点 ∴132AP PD AD ===PDF △为等边三角形1322PI PD ∴== 60DPF ∠=︒ PD PF =PA PF = 60DPF ∠=︒30PAF PFA ∴∠=∠=︒120APF ∴∠=︒92AI AP PI ∴=+=点E 为CD 边上的一个动点以PE 为边向下方作等边PEG △ 当点E 与点D 重合时点G 与点F 重合当点E 与点C 重合时点G 与点H 重合 ∴点G 在线段FH 上运动当AG HF ⊥时 AG 最小 PEG △为等边三角形60EPG ∴∠=︒ PE PG =60 FPG FPE FPE EPD∴∠+∠=∠+∠=︒FPG DPE∴∠=∠∴FPG DPE△≌△PDE PFG∴∠=∠90PDE∠=︒∴90PFG∠=︒PF FH∴⊥当AG HF⊥时AG PF120,30APF PAF∠=︒∠=︒18012060PAG∴∠=︒-︒=︒603030 FAG PAG PAF∠=∠-∠=︒-︒=︒IAF GAF∴∠=∠FI AD⊥90AIF∴=︒在AFI和AFI中AIF AGFAF AFFAG FAI∠=∠⎧⎪=⎨⎪∠=∠⎩∴()ASAAFI AFI≌AG AI∴=∴当AG HF⊥时92AG AI==故答案为：92．。

数学《特殊平行四边形中的折叠问题》专题训练含答案

2020-2021学年中考数学培优训练（二）《特殊平行四边形中的折叠问题》专题训练班级姓名座号成绩1．如图，折叠菱形纸片ABCD ，使点C 落在DP(P 为AB 的中点)所在的直线上，得到经过点D 的折痕DE.若∠A ＝60°，则∠DEC 的度数为2．如图，在边长为2的菱形ABCD 中，∠B ＝45°，AE 为BC 边上的高，将△ABE 沿AE 所在直线翻折得△AB′E ，AB′与CD 边交于点F ，则B′F的长度为3．如图，把正方形纸片ABCD 沿对边中点所在直线对折后展开，折痕为MN ，再过点B 折叠纸片，使点A 落在MN 上的点F 处，折痕为BE ，若AB ＝4，则NF 的长为4．如图，矩形OABC 中，OA 在x 轴上，OC 在y 轴上，且2OA =，4=AB ，把ABC ∆沿着AC 对折得到'AB C ∆，'AB 交y 轴于点D ，则'B 点的坐标为5. 如图，正方形纸片ABCD 的边长为3cm ，点E ，F 分别在边BC ，CD上，将AB，AD分别沿AE，AF折叠，点B，D恰好都落在点G处，已知BE＝1cm，求EF的长.6. 在矩形ABCD中，将点A翻折到对角线BD上的点M处，折痕BE交AD于点E.将点C翻折到对角线BD上的点N处，折痕DF交BC于点F.(1)求证：四边形BFDE为平行四边形；(2)若四边形BFDE为菱形，且AB＝2，求BC的长．7.如图①，在矩形ABCD中，AB＞BC，将它沿EF折叠(点E、F分别在边AB、CD上)，使点B落在AD 边上的点M处，点C落在点N处，MN与CD相交于点P，连接EP.(1)如图②，若AB＝8，AD＝4，当M点与D点重合，求BE；(2)如图③，当M为AD的中点，求证：EP＝AE＋DP.答案：6.解：(1)易证△ABE ≌△CDF(ASA)，∴AE ＝CF.∵四边形ABCD 是矩形， ∴AD ＝BC ，AD ∥BC.∴DE ＝BF ，DE ∥BF.∴四边形BFDE 为平行四边形(2)∵四边形BFDE 为菱形，∴BE ＝ED ，∠EBD ＝∠FBD ＝∠ABE. ∵四边形ABCD 是矩形，∴AD ＝BC ，∠ABC ＝90°，∴∠ABE ＝30°.∵∠A ＝90°，AB ＝2，设AE ＝x ，BE ＝2x.根据勾股定理得AB ＝3x.∴x ＝233.即AE ＝233，BE ＝433. ∴BC ＝AD ＝AE ＋ED ＝AE ＋BE ＝233＋433＝2 37. 解：(1)设BE ＝x ，由折叠得DE ＝BE ＝x ，AE ＝8－x.∵四边形ABCD 是矩形，∴∠A ＝90°，由勾股定理，得x 2＝(8－x)2＋42，解得x ＝5，即BE ＝5(2) 取EP 的中点Q ，连接MQ ，∵M 为AD 的中点，∴AE ＋DP ＝2MQ ，由折叠得，∠EMP ＝∠B ＝90°，∴EP ＝2MQ ，∴EP ＝AE ＋DP。

中考数学专题复习《四边形的折叠问题的分类讨论、存在性问题》测试卷(带答案)

中考数学专题复习《四边形的折叠问题的分类讨论存在性问题》测试卷（带答案)学校:___________班级:___________姓名:___________考号:___________一单选题1．图1是一张菱形纸片ABCD 点,E F 是边,AB CD 上的点．将该菱形纸片沿EF 折叠得到图2 BC 的对应边B C ''恰好落在直线AD 上．已知60,6B AB ∠=︒= 则四边形AEFC '的周长为（）A ．24B ．21C ．15D ．122．如图在菱形ABCD 中 60A ∠=︒ 点E F 分别在,AB AD 上沿EF 折叠菱形使点A 落在BC 边上的点G 处且EG BD ⊥于点M GF 交BD 于点N 若27AB =2 1.4 3 1.7）则GN 长是（）A ．7B ．172C ．17D ．183．将矩形纸片ABCD 按如图所示的方式折叠恰好得到菱形AECF 若6AD 则菱形AECF 的面积为（）A ．3B ．43C ．4D ．84．如图四边形ABCD 为一矩形纸带点E F 分别在边AB CD 上将纸带沿EF 折叠点A D 的对应点分别为A ' D 若236∠=︒ 则1∠的度数为（）A ．74︒B ．54︒C ．78︒D ．72︒5．矩形纸片ABCD 中 E 为BC 的中点连接AE 将ABE 沿AE 折叠得到AFE △ 连接CF ．若4AB = 6BC = 则CF 的长是（）A ．3B ．175C ．72D ．1856．如图把矩形纸片ABCD 沿对角线BD 折叠设重叠部分为EBD △ 则下列说法错误的是（）A ．AB CD = B ．BAE DCE ∠=∠C ．EB ED = D ．ADB ADC ∠=∠ 7．如图把长方形ABCD 沿EF 按图那样折叠后 A B 分别落在G H 点处若140∠︒＝则AEF ∠的大小是（）A ．120︒B ．115︒C ．110︒D ．105︒8．如图将长方形ABCD 沿着对角线BD 折叠使点C 落在C '处 BC '交AD 于点E ．若6AB = 8AD = 那么点E 到BD 的距离为（）A ．154B ．754C ．165D ．325二填空题9．如图在ABCD 中 43AB = 12AD = 30C ∠=︒ 点M N 分别在边BC AD 上沿MN 折叠平行四边形使点C 与点A 重合则线段BM 的长度为．10．如图将ABCD 沿对角线AC 折叠使点B 落在B '处 1242∠=∠=︒ 则B ∠= ．11．将矩形ABCD 纸片按图所示方式折叠 M N 、分别为AB CD 、的中点点B 的对应点B '恰好落在MN 上．若10,AB AB BC =< 则DN 的长为折痕AE 长为．12．把一张长方形的纸片沿对角线BD 折叠若AFD △的周长为12 则长方形ABCD 的周长是．13．如图在矩形ABCD 中 3AB = BC m = 点E 在边BC 上且32BE EC =::．连接AE 将ABE 沿AE 折叠若点B 的对应点B '落在矩形ABCD 的CD 边上则m 的值为．三解答题14．如图一张矩形纸片ABCD 10cm AB = 8cmAD =将纸片折叠使点B 落在CD 边上的点E 处折痕为AF ．(1)求线段DE 的长(2)求折痕AF 的长．15．如图已知矩形ABCD 中 E 是边AD 上一点将BDE △沿BE 折叠得到BFE △ 连接DF ．(1)如图1 BF 落在直线BA 上时求证DFA BEA ∽(2)如图2 当2AD AB= BF 与边AD 相交时在BE 上取一点G 使,BAG DAF AG ∠=∠与BF 交于点H ．①求AF AG的值 ①当E 是AD 的中点时若15FD FH ⋅= 求AG 的长．16．如图1 有一块长方形纸板ABCD 它的边6AB = 8BC =．点E F 分别为AD CD 上的点把长方形沿EF 折叠使得点D 落到D 满足EF AC ∥．设DF x =．(1)当x 为多少时点D '落在AC 上(2)当x 为多少时点D '落在BC 上(3)设D EF '和ABC 存在重叠部分重叠部分的面积记为S 当点D '落于ABC 内部时求S 关于x 的函数解析式并写出x 的取值范围．17．如图已知正方形ABCD 边长为10cm 点M 从C 到D 以1cm/s 的速度运动将正方形ABCD 折叠使顶点A 与点M 重合折痕交AD 于E 交BC 于F 边AB 折叠后与BC 边交于点G ．设点M 的运动时间为t (010)t << 单位：s ．(1)求证：DEM CMG ∽(2)当5s t =时求DEM 的周长(3)当510t <<时求CMG 的周长．18．如图正方形纸片ABCD的边长为8 E是AB边上的动点．折叠纸片使点D与点E重合折痕为FG DC的对应边EC'交BC于点H．(1)如图1 当点E是AB的中点时则AF的长______．(2)如图2 设AE的长为x四边形CDFG面积为S．①求DF的长度（用含x的代数式表示）①求S关于x的函数关系式并求S的最小值．(3)如图3 过点D作EC'的垂线垂足为M DM交FG于点N．①求BHE的周长．∠的值．①当BHE与MNE的周长之差为2时请直接写出sin EHB参考答案：1．C2．D3．B4．D5．D6．D7．C8．A9．8310．117︒/117度11． 512．241314．1）解：①10cm AE AB == 222AD DE AE += ①264100DE +=①6cm DE =（2）解：设cm BF x = 则8CF BC BF x =-=- ①1064cm EC DC DE =-=-= 且222EF EC CF =+ ①()2222168EF EC CF x =+=+- ①EF BF x ==①()22168x x =+-解得5cm x =①222AF AB BF =+①AF =．15．（1）证明：如图1 延长BE 交DF 于点G根据折叠性质得到,BF BD EF ED == ①直线BE 是DF 的垂直平分线 ①90DGE ∠=︒①四边形ABCD 是矩形①90DAF BAE ∠=∠=︒①DEG BEA ∠=∠①ADF ABE =∠∠①DFA BEA ∽．（2）解：①延长BE 交DF 于点T根据折叠性质得到,BF BD EF ED == ①直线BE 是DF 的垂直平分线 ①90DTB ∠=︒ DT TF =①四边形ABCD 是矩形①90DAB ∠=︒①DET AEB ∠=∠①ADF ABE =∠∠①BAG DAF ∠=∠①DFA BGA ∽ ①AF AD AG AB = ①2AD AB =①2AF AG①根据解析①可知：直线BE 是DF 的垂直平分线 ①90DTB ∠=︒ DT TF =①四边形ABCD 是矩形①90DAB ∠=︒①90DAG BAG ∠+∠=︒①BAG DAF ∠=∠①90DAG DAF ∠+∠=︒①90GAF ∠=︒①点E 为AD 的中点①DE EA = ①12FE DE EA AD === ①EDF EFD ∠=∠ EFA EAF ∠=∠ ①DFE EFA EAF EDF ∠+∠=∠+∠ ①180DFE EFA EAF EDF ∠+∠+∠+∠=︒ ①90DFE EFA EAF EDF ∠+∠=∠+∠=︒ ①90AFD ∠=︒①90GTF AFT GAF ∠=∠=∠=︒ ①四边形AGTF 是矩形①AG FT DT == 90AGT ∠=︒ AF TG = AG FT ∥ ①90AGB ∠=︒①BAG DAF ∠=∠ 90AGB AFD ∠=∠=︒ ①DFA BGA ∽ ①AF AD DF AG AB BG== 设AG FT DT x === 则2DF x =①AD AB =①2AF x AD BG Bx A ===①AF BG =①12AF BG GT BT ====根据勾股定理得：AB =①AD =①根据勾股定理得：3BD x ==①AG FT ∥ BG GT =①1BG BH GT HF ==①113222BH FH BF BD x ==== ①15FD FH ⋅= ①32152x x ⋅= 解得5,5x x ==- 故5AG =16．（1）解：①长方形纸板ABCD 6AB = 8BC =①6CD = 8AD = 90ADC BCD B ∠=∠=∠=︒如图1 连接DD ' 交EF 于O由翻折的性质可知 DD EF '⊥ 12DO D O DD ''==①EF AC ∥①DD AC '⊥由勾股定理得 2210AC AB BC =+ ①1122ACD S CD AD AC DD '=⋅=⋅ 即11681022DD '⨯⨯=⨯⋅ 解得 245DD '= ①125DO D O '==①DFO ACD ∠=∠ DOF ADC ∠=∠①DFO ACD ∽ ①DF DO AC AD = 即125108x = 解得 3x =①当3x =时点D '落在AC 上（2）解：如图2AI同理（1）DD EF '⊥ 12DO D O DD ''== DD AC '⊥ ①90CDD CD D CD D BCA '''∠+∠=︒=∠+∠ 即CDD BCA '∠=∠ ①90DCD B '∠=∠=︒①DCD CBA '∽ ①DD CD AC BC '= 即6108DD '= 解得 152DD '=①154DO = 同理（1）DFO ACD ∽ ①DF DO AC AD = 即154108x = 解得 7516x =①当7516x =时点D '落在BC 上（3）解：如图3 记DD '交AC 于H D E '交AC 于M D F '交AC 于NAI由（1）可知245DH = 同理（1）DFO ACD ∽ ①DF DO AC AD = 即108x DO =解得 45DO D O x '==①85DD x '= 82455D H DD DH x ''=-=- ①EF AC ∥①DEF DAC ∽ ①DE DF AD DC= 即86DE x = 解得 43DE x = ①2142233D EF DEFS S x x x '==⋅⋅= ①MN AC ∥①D MN D EF ''∽ ①2D EF S D H S D O '⎛⎫= ⎝''⎪⎭ 即22824552435x S x x ⎛⎫- ⎪= ⎪ ⎪⎝⎭ 整理得 ()2833S x =- ①当点D '落于ABC 内部时 S 关于x 的函数解析式为()2833S x =- 75316x <<． 17．（1）根据折叠的性质知：90EMG A ∠=∠=︒①90DME CMG ∠+∠=︒①90DME DEM ∠+∠=︒ ①DEM CMG ∠=∠①90D C ∠=∠=︒①DEM CMG ∽（2）根据折叠的性质知:EM EA =当5t =时 5DM CM == ①DEM 的周长为：15cm DM DE EM DM DE EA DM DA ++=++=+= （3）依题意得：10CM t DM t ==-，设EM EA x == 则]10DE x =- 在Rt DEM 中 222EM DE DM =+ 即()()2221010x x t =-+- 解得：210,20t x t =-+ ①21020t DE x t =-=- DEM CMG ∽ME GM DE CM ∴= 即 10x GM t t=- 解得： 22002020t t GM t-+=- 同理可得： 2002020t CG t-=- CMG ∴的周长为：2200202002020cm 2020t t t CM CG MG t t t--+++=++=--． 18．（1）解：四边形ABCD 是正方形90A ∴∠=︒ 8AB AD ==当E 为AB 的中点时 142AE AB == 设AF x =则8EF FD AD AF x ==-=-在Rt AEF 中 222AE AF EF += 则()22248x x +=-解得：3x =3AF ∴=故答案为：3（2）①如图过点G 作GK AD ⊥ 则四边形CGKD 是矩形连接ED 交FG 于点PE D 关于FG 对称ED FG ∴⊥90FPD FKG ∴∠=∠=︒ADE DFP FGK DFP ∴∠+∠=∠+∠90=︒ADE KGF ∠=∠由正方形性质可知KG CD AD ==ADE KGF ∴≌设AE x = 则FK x = 8DF FE AF ==-()2228x AF AF ∴+=-21416AF x ∴=-∴218416DF AF x =-=+ ①由矩形的性质可得21416CG KD FD FK x x ==-=+- ∴四边形CDFG 面积为()22111844421616S CG FD x x x ⎛⎫=+⨯=+-++ ⎪⎝⎭ 214322x x =-+ ()214242x =-+ ()214242S x ∴=-+ 最小值为24 （3）①如图由（2）可得AE x = 21416AF x =- 21416EF x =+ 则8BE x =-在正方形ABCD 中由于对折可知 90ADC FEH ∠=∠=︒①1290∠∠=︒＋又①90A B ∠=∠=︒①1390∠∠=︒＋①23∠∠=①AEF BHE ∽ ①AF AE EF BE BH EH== ①8BE AB AE x =-=-()281618416x x AE BE x BH AF x x -⋅===+- ()222184641618416x x BE EF x EH AF x x ⎛⎫-⋅+ ⎪⋅+⎝⎭===+- ①BHE 的周长216648168x x BH EH x x BE +++-=+==＋＋即：BHE 的周长为16①连接EN由折叠可知 DFN EFN ∠=∠ =EF FD EF EC '⊥ DM EC '⊥EF DM ∴∥MNG EFN ∴∠=∠ FEN ENM ∠=∠ DFN MNG ∴∠=∠①FND MNG ∠=∠DFN DNF ∴∠=∠DF DN ∴=EF ND ∴=∴四边形EFDN 是平行四边形 EN FD ∴∥ EN FD =EF FD =∴四边形EFDN 是菱形EF EN ∴=EN AD ∴∥FEN AFE ∴∠=∠AEF BHE ∽∴EHB NEM ∠=∠DM EH ⊥90NME B ∴∠=∠=︒EMN HBE ∴∽ BHE 的周长为16当BHE 与MNE 的周长之差为2时则MNE 的周长为14或18 147168EN EH ∴==或189168EN EH == EF EN =78EF EH ∴=或98AEF BHE ∽EF AF EH BE∴= BHE AEF ∠=∠ 78AF BE ∴=或98 8BE x =- 21416AF x =- 21471688x x -∴=-或21491688x x -=- 解得16x = 28x =或18x = 210x = 08x ≤≤6x ∴=∴6AE =2197441644AF x ∴=-=-= 21925441644EF x ∴=+=+= 774sin sin 25254AF EHB AEF EF ∴∠=∠===．。

2020中考数学图形折叠与拼接问题（含答案）

2020中考数学图形折叠与拼接问题（含答案）2020中考数学⼏何培优之图形折叠与拼接问题（含答案）【例1】如图，矩形ABCD 中，AB ＝8，BC ＝4，将矩形沿AC 折叠，点D 落在D '处，则重叠部分△AFC 的⾯积为＿＿＿＿＿.例1题图例2题图【例2】如图，直线26y x =-+ 与x 轴，y 轴分别交于P ，Q 两点，把△POQ 沿PQ 翻折，点O 落在R 处，则点R 的坐标是（）A .2412(,)55B .（2,1）C .（6,3）D .（7，3.5）【例3】如图，将边长为12cm 的正⽅形ABCD 折叠，使得A 点落在CD 边上点E 处，然后压平折痕FG ，若FG ＝13cm ，求CE 长.【例4】将⼀矩形纸⽚OABC 放在平⾯直⾓坐标系中，(00)O ，，(60)A ，，(03)C ，．动点Q 从点O 出发以每秒1个单位长的速度沿OC 向终点C 运动，运动23秒时，动点P 从点A 出发以相等的速度沿AO 向终点O 运动．当其中⼀点到达终点时，另⼀点也停⽌运动．设点P 的运动时间A（1）⽤含t 的代数式表⽰OP OQ ，；（2）当1t 时，如图1，将OPQ △沿PQ 翻折，点O 恰好落在CB 边上的点D 处，求点D 的坐标；（3）连结AC ，将OPQ △沿PQ 翻折，得到EPQ △，如图2．问：PQ 与AC 能否平⾏？PE 与AC 能否垂直？若能，求出相应的t 值；若不能，说明理由．【例5】⽤10个边长分别为3，5，6，11，17，19，22，23，24，25的正⽅形，可以拼接⼀个长⽅形.（1）求这个长⽅形的长和宽；（2）请画出拼接图.【例6】将正⽅形纸⽚ABCD 折叠，使顶点A 与CD 边上的点M 重合，折痕交AD 于E ，交BC 于F ，边AB 折叠后与BC 交于点G.（1）如果M 为CD 边的中点，求证：DE ：DM ：EM ＝3：4：5；（2）如果M 为CD 边上的任意⼀点，设AB ＝2a ，问△CMG 的周长是否有与点M 的位置关系？若有关，请把△CMG 的周长⽤含CM 的长x 的代数式表⽰；若⽆关，请说明理由．图1能⼒训练1、如图，在矩形ABCD中，AB＝6cm，BC＝8cm，若将矩形折叠，使B点与D点重合，则折痕EF的长为＿＿＿cm.2、如图，矩形ABCD中，AB＝12，AD＝10，将此矩形折叠使B点落在AD边上的中点E处，则折痕FG的长为_________.第1题图第2题图第3题图3、如图是⽤12个全等的等腰梯形镶嵌成的图形，这个等腰梯形的上底与下底长的⽐是_____.4、如图，EF为正⽅形纸ABCD的对折线，将∠A沿DK折叠，使它的顶点A落在EF上的G 点，则∠DKG＝_______度.5、如图，已知等边△ABC中，点D，E分别在边AB，BC上，把△BDE沿直线DE翻折，使80，则∠EGC的度数点B落在点B′处，DB′，EB′分别交边AC于点F，G，若∠ADF＝0为________.第4题图第5题图第6题图6、将⼀张长为70cm的长⽅形纸⽚ABCD沿对称轴EF折叠成如图的形状，若折叠后，AB与CD间的距离为60cm，则原纸⽚的宽AB是______cm.7、如图，在矩形纸⽚ABCD 中，已知AD ＝8，折叠纸⽚使AB 边与对⾓线AC 重合，点B 落在F 处，折痕为AE ，且EF ＝3，则AB 的长为( )A .3B .4C .5D .68、如图，在△ABC 中，∠C ＝900，BC ＝6，D ，E 分别在AB ，AC 上，将△ABC 沿DE 折叠，使点A 落在点A ′处，若A ′为CE 的中点，则折痕DE 的长为 ( )A .B 、2C 、3D 、4第7题图第8题图第9题图9、如图，有⼀块菱形的草地，要在其上⾯修筑两条笔直的道路，道路把这块草地分成⾯积相等的四部分，如果道路的宽度可以忽略不计，请你设计三种不同的⽅案. 10、如图，折叠矩形纸⽚ABCD ，先折出折痕(对⾓线)BD ，再折叠使AD 边与对⾓线BD 重合，得折线DG ，若AB ＝2，BC ＝1，求AG.11、如图，折叠矩形ABCD 的⼀边AD ，使点D 落在BC 边上的点F处，已知折痕3.4EC AE FC == ，求矩形ABCD 的周长.EA12、如图1，⼀张矩形纸⽚ABCD，其中AD＝8cm，AB＝6cm，先沿对⾓线BD对折，点C落在点C′处的位置，BC′交AD于点(1) 求证：AG＝G(2) 如图2，再折叠⼀次，使点D与点A重合，得折痕EN，EN交AD于点M，求EM的长.B级1、如图，⼀张宽为3，长为4的矩形纸⽚ABCD，先沿对⾓线BD对折，点C落在C′的位置，BC′交AD于G，再折叠⼀次使D点与A点重合，得折痕EN，EN交AD于点M，则ME 的长为__________.2、如图，矩形纸⽚ABCD中，AB＝3cm，BC＝4cm，现将A，C重合，使纸⽚折叠压平，设折痕为EF，则重叠部分△AFE的⾯积为_________.第1题图第2题图第3题图3、如图，矩形ABCD沿直线BD折叠，使点C落在C′处，BC′交AD于点E，若AD＝8，AB＝4，则DE的长为________.4、如图，把矩形纸⽚OABC放⼊平⾯直⾓坐标系中，使OA，OC分别落在x轴上，y轴上，连结AC，将矩形纸⽚OABC沿AC 折叠，使点B落在点D的位置，若B(1，2)，则点D的横坐标是______.5、如图，在平⾯直⾓坐标系中，已知直线334y x=-+与x轴，y轴分别交于A，B两点，第4题图第5题图第6题图6、如图，矩形纸⽚ABCD，AB＝5cm，BC＝10cm，CD上有⼀点E，ED＝2cm，AD上有⼀点P，PD＝3cm，过P作PF⊥AD 交BC于F，将纸⽚折叠，使P点与E点重合，折痕与PF交于Q点，则PQ的长是_____cm.7、在三⾓形纸⽚ABC中，已知∠ABC＝900，AB＝6，BC＝8，过点A作直线l平⾏于BC，折叠三⾓形纸⽚ABC，使直⾓顶点B落在直线上的T处，折痕为MN，当点T在直线l上移动时，折痕的端点M，N也随之移动，若限定端点M，N分别在AB，BC边上移动，则线段AT 长度的最⼤值与最⼩值之和为__________(计算结果不取近似值)8、如图，矩形纸⽚ABCD中，AB＝8，将纸⽚折叠，使顶点B落在边AD上的E点处，BG＝10.（1）当折痕的另⼀端F在AB边上时，如图．求△EFG的⾯积；（2）当折痕的另⼀端F在AD边上时，如图．证明四边形BGEF为菱形，并求出折痕GF 的长.9、如图，已知三⾓形纸⽚ABC的⾯积为25，BC的长为10，∠B，∠C都为锐⾓，M是AB 边上的⼀动点(M与A，B不重合)，过点M作MN∥BC交AC于点N，设MN＝x.(1）⽤x表⽰△AMN的⾯积；（2）△AMN沿MN折叠，使△AMN紧贴四边形BCNM（边AM、AN落在四边形BCNM 所在的平⾯内），设点A落在平⾯BCNM 内的点A′，△A′MN与四边形BCNM重叠部分的⾯积为y．①⽤含x的代数式表⽰y，并写出x的取值范围．10、如图：⼀正⽅形纸⽚，根据要求进⾏多次分割，把它分割成若⼲个直⾓三⾓形．具体操作过程如下：第⼀次分割：将正⽅形纸⽚分成4个全等的直⾓三⾓形；第⼆次分割：将上次得到的直⾓三⾓形中的⼀个再分成4个全等的直⾓三⾓形；以后按第⼆次分割的⽅法重复进⾏．（1）请你设计出两种符合题意的分割⽅案（分割3次）；（2）设正⽅形的边长为a，请你通过对其中⼀种⽅案的操作和观察，将第⼆、第三次分割后所得的最⼩的直⾓三⾓形的⾯积S 填⼊下表：（3）在条件（2）下，请你猜想：分割所得的最⼩直⾓三⾓形⾯积S 与分割次数n 有什么关系？⽤数学表达式表⽰出来．11、如图1，将边长为4cm 的正⽅形纸⽚ABCD 沿EF 折叠(点E ，F 分别在边AB ，CD 上)，使点B 落在AD 边上的点M 处，点C 落在点N 处，MN 与CD 交于点P ，连结EP .(1)如图②，若M 为AD 边的中点，①△AEM 的周长＝_________cm ；②求证：EP ＝AE ＋DP ；（2）随着落点M 在AD 边上取遍所有的位置（点M 不与A 、D 重合），△PDM 的周长是否发⽣变化？请说明理由.12、如图1，在矩形ABCD 中，AB ＝3，AD ＝1，点P 在线段AB 上运动，设AP ＝x ，现将纸⽚折叠，使点D 与点P 重合，得折痕EF (点E ，F 为折痕与矩形边的交点)，再将纸⽚还原.（1）当0 x 时，折痕EF 的长为________；（2）写出使四边形EPFD 为菱形的x 的取值范围，并求出当x ＝2时菱形的边长；（3）令2EF ＝y ，当点E 在AD 上、点F 在BC 上时，写出y 与x 的函数关系式（写出x的取值范围），当y 取最⼤值时，判断△EAP 与△PBF 是否相似．若相似，求出x 的值；若不相似，请说明理由.参考答案例1 10例2 A 提⽰：作RE ⊥y 轴于E ，RF ⊥x 轴于F ，则Rt △QRE ∽Rt △PRF ，从⽽PFQERF RE PR QR ==，设R (x ，y )，⼜PR ＝OP ＝3，QR ＝OQ ＝6，于是3636--==x y y x ，得x ＝524，y ＝512．例3 7 提⽰：过F 作FM ⊥BC 于M ，证明△FGM ≌△ADE ，则FG ＝AE ＝13，DE ＝5 例4 （1）OP ＝6－t ，OQ ＝t ＋32（2）D (1，3) （3）①PQ 能与AC 平⾏，若PQ ∥AC ，则OC OA OQ OP =，即326+-t t ＝36．得t ＝914，⽽0≤t ≤37，∴t ＝914．②PE 不能与AC 垂直．若PE ⊥AC ，延长QE 交OA 于F ，则OC OQ AC QF =，即33253+=t QF，QF ＝5(t ＋32)．∴EF ＝QF －QE ＝QF －OQ ＝5(t ＋32)－(t ＋32)＝(5－1)t ＋32(5－1)．⼜Rt △EPF ∽Rt △OCA ，∴OA OC EF PE =，即63)32)(15(6=+--t t ，t ≈3.45，⽽0≤t ≤37，∴t 不存在．例5 （1）10个正⽅形的⾯积和：32＋52＋62＋112＋172＋192＋222＋232＋242＋252＝3055＝5×13×47．因为所拼成的长⽅形⾯积是3055．长⽅形的宽显然≥25，所以它的宽应当是47，长应当是5×13＝65．（2）注意23+24=47,25+22=47,23+17+25=65,24+19+22=65.由此便可得拼图.（图略）例6 提⽰：（1）证明：设正⽅形边长为a ，DE 为x ，则DM =（2）设DE=y，则DM=2a-x，EM=2a-y，可证明△DEM∽△CMG.△周长△周长==△CMG的周长△周长，在△DEM中，由勾股定理得（2）2=2+（2）2，化简得4ay=x（4a-x）即. ∴△CMG的周长=44（y+2a-x+2a-y）=（4a-x）=4a，为定值.A级1. 2.656 3.1:2 4.75° 5.80° 6.10 提⽰：长⽅形纸⽚折叠时，AB与CD间的距离缩短了10cm。

2020中考数学压轴专题三大几何变换之折叠问题(含答案)

2020中考数学压轴专题三大几何变换之折叠问题（含答案）1. 如图，E，F分别是▱ABCD的边AD，BC上的点，EF＝6，∠DEF＝60°，将四边形EFCD沿EF翻折．得到四边形EFC′D′，ED′交BC于点G，则△GEF的周长为()A. 6B. 12C. 18D. 24第1题图C2. 如图，Rt△ABC中，AB＝9，BC＝6，∠B＝90°，将△ABC折叠，使A点与BC的中点D重合，折痕为PQ，则线段BQ的长度为()A. 53 B.52 C. 4 D. 5第2题图C3. 如图，将边长为4的菱形ABCD纸片折叠，使点A恰好落在对角线的交点O处，若折痕EF＝23，则∠A＝()A. 120°B. 100°C. 60°D. 30°第3题图A【解析】如解图，连接AC，则两条对角线交于点O，∵点A沿EF折叠与点O重合，∴EF垂直平分AO，∵AO⊥BD，AO⊥EF，∴EF∥BD，∴EF是△ABD的中位线，∴EF＝12BD，∴BD＝43，∴BO＝DO＝12BD＝23，∵AB＝4，∴cos∠ABO＝BOAB＝234＝32，∴∠ABO＝30°，∴∠BAO＝60°，∵四边形ABCD是菱形，∴AC平分∠BAD，∴∠A＝120°，故选A.第3题解图4. 如图的实线部分是由Rt △ABC 经过两次折叠得到的，首先将Rt △ABC 沿BD 折叠，使点C 落在斜边上的点C ′处，再沿ED 折叠，使点A 落在DC ′的延长线上的点A ′处，若图中∠C ＝90°，∠A ＝30°，BC ＝5 cm ，则折痕DE 的长为________．第4题图103【解析】∵∠A ＝30°，∠C ＝90°，∴∠ABC ＝180°－∠C －∠A ＝60°，根据折叠的性质可得，∠DBC ′＝∠DBC ＝12∠ABC ＝12×60°＝30°，在Rt △BCD 中，cos ∠DBC ＝BCBD ，∴BD ＝BC cos ∠DBC ＝5cos30°＝1033，∵∠CDB ＝180°－∠C －∠DBC ＝180°－90°－30°＝60°，∴∠BDA ′＝∠CDB ＝60°，∴∠ADA ′＝180°－∠CDB －∠BDA ′＝180°－60°－60°＝60°，∵DE 是折痕，根据折叠的性质可得，∠EDA ′＝12∠ADA ′＝12×60°＝30°，∴∠BDE ＝∠BDA ′＋∠EDA ′＝60°＋30°＝90°，在Rt △BED 中，DE ＝BD ·tan30°＝1033×33＝103.5. 将矩形纸片ABCD 按如图所示的方式折叠，得到菱形AECF .若AB ＝6，则BC 的长为________．第5题图23 【解析】∵四边形AECF 是菱形，AB ＝6，假设BE ＝x ，则AE ＝6－x ，∴CE ＝6－x ，∵四边形AECF 是菱形，∴∠FCO ＝∠ECO ，∵∠ECO ＝∠ECB ，∴∠ECO ＝∠ECB ＝∠FCO ＝30°，2BE ＝CE ，∴CE ＝2x ，∴2x ＝6－x ，解得：x ＝2，∴CE ＝4，利用勾股定理得出：BC 2＋BE 2＝EC 2，BC ＝EC 2－BE 2＝42－22＝2 3.6. 用剪刀将形状如图①所示的矩形纸片ABCD 沿着直线CM 剪成两部分，其中点M 为AD 的中点．用这两部分纸片可以拼成图②所示的Rt △BCE .若Rt △BCE 是等腰直角三角形，设原矩形纸片中的边AB ＝a ，BC ＝b ，且a 、b 满足关系式a ＋b ＝m －1，ab ＝m ＋1，则点D 到CM 的距离为________．第6题图2 【解析】∵Rt △BCE 是等腰直角三角形，M 为AD 的中点，∴b ＝2a .∵a ＋b ＝m －1，∴a ＋2a ＝m －1，∴a ＝m －13，b ＝2（m －1）3，∵ab ＝m ＋1，∴m －13·2（m －1）3＝m ＋1，整理得2m 2－13m －7＝0，解得m ＝－12(舍去)或m ＝7，∴a ＝2，b ＝4，AM ＝MD ＝2，在Rt △MCD 中，CM ＝22＋22＝22，∴点D 到CM 的距离为2×222＝ 2.7. 将一个矩形纸片ABCD 放置到平面直角坐标系中，点A 、B 恰好落在x 轴的正、负半轴上，若将该纸片沿AF 折叠，点B 恰好落在y 轴上的点E 处，设OA ＝1.(1)如图①，若OB ＝1，则点F 的坐标为________； (2)如图②，若OB ＝2，求点F 的坐标； (3)若OB ＝n ，请直接写出点F 的坐标．第7题图解：（1）(1，233)【解法提示】由折叠的性质可知AE ＝AB ＝2, ∠EAF ＝∠BAF ，∵OA ＝1，AE ＝2，∠AOE ＝90°，∴∠AEO ＝30°，∴∠EAO ＝60°，∴∠F AB ＝30°，∴BF ＝AB ·tan ∠F AB ＝233，则点F的坐标为(1，233)．（2）如解图，作FM ⊥y 轴于点M ，∴∠AEF ＝∠ABF ＝90°，FM ⊥y 轴，∴∠AEO ＋∠FEM ＝90°，∠FEM ＋∠EFM ＝90°， ∴∠AEO ＝∠EFM ，∵sin ∠AEO ＝AO AE ＝13，第7题解图∴sin ∠EFM ＝13.设EM ＝x ，则EF ＝3x ，由勾股定理得MF ＝22x ，OE ＝22， ∵OB ＝2， ∴22x ＝2，解得x ＝22， ∴OM ＝OE －EM ＝322，∴点F 的坐标为(2，322)；（3）(n ，n 2＋nn 2＋2n)．【解法提示】如解图，作FM ⊥y 轴于点M ，同理∠AEO ＝∠EFM ，∵sin ∠AEO ＝AO AE ＝1n ＋1，∴sin ∠EFM ＝1n ＋1，设EM ＝x ，则EF ＝(n ＋1)x ，由勾股定理得MF ＝n 2＋2n x ，OE ＝n 2＋2n ， ∵OB ＝n ， ∴n 2＋2n x ＝n .解得x ＝nn 2＋2n ，∴OM ＝OE －EM ＝n 2＋2n －nn 2＋2n ＝n 2＋n n 2＋2n， ∴点F 的坐标为(n ，n 2＋nn 2＋2n)．8. 如图，将一个正方形纸片AOCD 放置在平面直角坐标系中，点A (0，4)，点O (0，0)，点D 在第一象限，点P 为正方形AD 边上的一点(不与点A 、点D 重合)，将正方形纸片折叠，使点O 落在点P 处，点C 落在点G 处，PG 交DC 于点H ，折痕为EF ，连接OP ，OH .设P点的横坐标为m.(1)若∠APO＝60°，求∠OPG的大小；(2)当点P在边AD上移动时，△PDH的周长l是否发生变化？若变化，用含m的式子表示l；若不变化，求出周长l；(3)设四边形EFGP的面积为S，当S取得最小值时，求点P的坐标(直接写出结果即可)．第8题图解：（1）∵折叠正方形纸片，使点O落在点P处，点C落在点G处，∴∠POC＝∠OPG，∵四边形AOCD是正方形，∴AD∥OC，∴∠APO＝∠POC，∴∠APO＝∠OPG，∵∠APO＝60°，∴∠OPG＝60°；（2）△PDH的周长不发生变化，理由：如解图①，过点O作OQ⊥PG，垂足为点Q，则∠DAO＝∠PQO＝90°.第8题解图①由(3)知∠APO＝∠OPG，又∵OP＝OP，∴△AOP≌△QOP，∴AP＝QP，AO＝QO，∵AO＝OC，∴OC＝OQ，∵∠OCD＝∠OQH＝90°，OH＝OH，∴Rt△OCH≌Rt△OQH，∴CH＝QH，∴△PDH 的周长l ＝PD ＋DH ＋PH ＝PD ＋DH ＋PQ ＋QH ＝PD ＋PQ ＋DH ＋QH ＝PD ＋AP ＋DH ＋CH ＝AD ＋CD ＝8，∴△PDH 的周长l 不发生变化，周长l 为定值8；（3）当S 取得最小值时，点P 的坐标为(2，4)．【解法提示】如解图②，过点F 作FM ⊥OA 于点M ，设EF 与OP 交于点N ，第8题解图②由折叠的性质知△EON 与△EPN 关于直线EF 对称， ∴△EON ≌△EPN ，∴ON ＝PN ，EP ＝EO ，EN ⊥PO ，∵∠OAP ＝∠ENO ，∠AOP ＝∠NOE ， ∴△POA ∽△EON ， ∴PO EO ＝P A EN ＝OAON①，设P A ＝x ， ∵点A (0，4)， ∴OA ＝4，∴OP ＝OA 2＋P A 2＝16＋x 2，∴ON ＝12OP ＝1216＋x 2，将OP ，ON 代入①式得，OE ＝PE ＝ 18(16＋x 2)， ∵∠EFM ＋∠OEN ＝90°， ∠AOP ＋∠OEN ＝90°， ∴∠EFM ＝∠AOP ，在△EFM 和△POA 中， ⎩⎪⎨⎪⎧∠EFM ＝∠AOP FM ＝OA ∠OAP ＝∠EMF， ∴△EFM ≌△POA (ASA)， ∴EM ＝P A ＝x ，∴FG ＝CF ＝OM ＝OE －EM ＝ 18(16＋x 2)－x ＝18x 2－x ＋2，∴S＝S梯形EFGP＝S梯形OCFE＝12(FC＋OE)·OC＝12[18x2－x＋2＋18(16＋x2)]×4＝12(x－2)2＋6，∴当x＝2时，S最小，即AP＝2，∴点P的坐标是(2，4)．。

2020重庆中考数学复习四边形翻折变换专题训练十一(含答案解析)

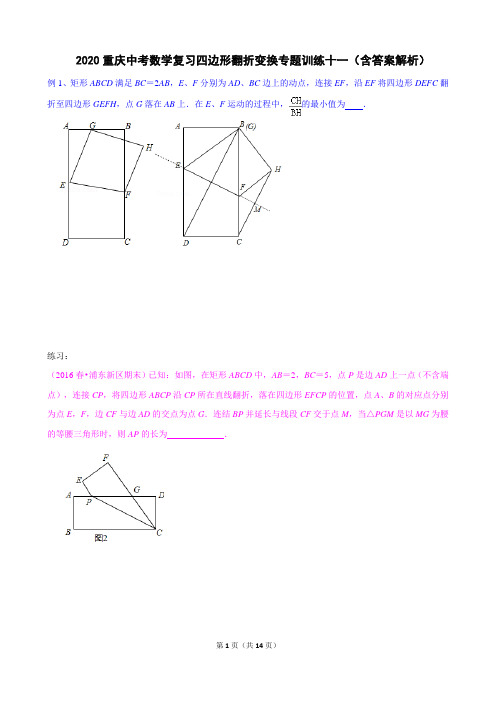
2020重庆中考数学复习四边形翻折变换专题训练十一（含答案解析）例1、矩形ABCD满足BC＝2AB，E、F分别为AD、BC边上的动点，连接EF，沿EF将四边形DEFC翻折至四边形GEFH，点G落在AB上．在E、F运动的过程中，的最小值为．练习：（2016春•浦东新区期末）已知：如图，在矩形ABCD中，AB＝2，BC＝5，点P是边AD上一点（不含端点），连接CP，将四边形ABCP沿CP所在直线翻折，落在四边形EFCP的位置，点A、B的对应点分别为点E，F，边CF与边AD的交点为点G．连结BP并延长与线段CF交于点M，当△PGM是以MG为腰的等腰三角形时，则AP的长为．例2、（2019•桂林）将矩形ABCD按如图所示的方式折叠，BE，EG，FG为折痕，若顶点A，C，D都落在点O处，且点B，O，G在同一条直线上，同时点E，O，F在另一条直线上，则的值为（） A． B． C． D．练习：（2014春•富宁县校级期中）如图所示，将矩形纸片ABCD按如图方式折叠，EF、EC为折痕，折叠后点A 落在边CD的A处，点B落在边A′E的B′处．若A′D＝4，BC＝8，则AE的长是（）A．10 B．11 C．12 D．13例3、（2019•常州一模）如图，正方形ABCD的边长为6，点E，F分别为AB、BC的中点，点H是AD 边上一点，将△DCF沿DF折叠得△DC′F，将△AEH沿EH折叠后点A的对应点A′刚好落在DC′上，则cos∠DA′H＝．例4、如图，在正方形ABCD中，边长为2，点E为边BC的中点，将边AB沿AE折叠到AM，点F为边CD上一点，将边AD沿AF折叠恰能使AD与AM重合．延长AM，交CD于点N，连接EN并延长，交AF的延长线于点G，连接CG，则GN＝．练习：（2016秋•渝中区校级期中）如图，在边长为2的正方形ABCD中，F是DC延长线上一点，且CF＝CD，E是AF中点，将△ABE沿BE翻折至△A'BE处，连接A'D，则A'D的长为．例5、（2010•江东区模拟）如图，在矩形ABCD中，AB＝3，AD＝5，点P在线段BC上运动，现将纸片折叠，使点A与点P重合，得折痕EF（点E、F为折痕与矩形边的交点），设BP＝x，当点E落在AB 上，点F落在AD上时，x的取值范围是（）A．0＜x≤1 B．0＜x≤3 C．1≤x≤3 D．3≤x≤5练习：1、（2014•拱墅区一模）如图，在矩形ABCD中，AB＝2，AD＝5，点P在线段BC上运动，现将纸片折叠，使点A与点P重合，得折痕EF（点E、F为折痕与矩形边的交点），设BP＝x，当点E落在线段AB 上，点F落在线段AD上时，x的取值范围是．2、（2018春•建邺区校级月考）如图，矩形纸片ABCD中，AB＝8，AD＝12，点P是边BC上的动点．现将纸片折叠，使点A与点P重合，折痕与矩形边的交点分别为E，F，要使折痕始终与边AB，AD有交点，则BP的取值范围是．例6、（2019秋•江阴市期中）如图，矩形纸片ABCD中，AB＝10，AD＝5，点E、F分别在线段AB、AD 上，将△AEF沿EF翻折，点A的落点记为P．当P落在矩形ABCD内部时，PD的最小值等于（） A． B． C． D．2练习：1、（2016秋•渝中区校级期中）如图，在矩形ABCD中，AB＝6，AD＝3，点E、F分别在AD、AB线段上，将△AEF沿EF翻折，使得点A落在矩形ABCD内部P点，连接PD，则PD的最小值是．2、（2008•义乌市）如图，直角梯形纸片ABCD，AD⊥AB，AB＝8，AD＝CD＝4，点E、F分别在线段AB、AD上，将△AEF沿EF翻折，点A的落点记为P．当P落在直角梯形ABCD内部时，PD的最小值等于．参考答案例1、矩形ABCD满足BC＝2AB，E、F分别为AD、BC边上的动点，连接EF，沿EF将四边形DEFC翻折至四边形GEFH，点G落在AB上．在E、F运动的过程中，的最小值为．解：如图，当点G与点B重合时，的值最小，设DE＝EB＝a，AB＝CD＝BH＝m，AD＝BC＝2m，在Rt△AEB中，∵AE2+AB2＝EB2，∴（2m﹣a）2+m2＝a2，∴a＝m，∴DE＝EB＝m，∵AD∥BC，∴∠EFB＝∠DEF＝∠FEB，∴BE＝BF＝m，CF＝BC﹣BF＝m，设EF的延长线交CH于M．∵△FMC∽△BAD，∴＝＝，∴CM＝KM＝m，∴CH＝m，∴的最小值＝．练习：（2016春•浦东新区期末）已知：如图，在矩形ABCD中，AB＝2，BC＝5，点P是边AD上一点（不含端点），连接CP，将四边形ABCP沿CP所在直线翻折，落在四边形EFCP的位置，点A、B的对应点分别为点E，F，边CF与边AD的交点为点G．连结BP并延长与线段CF交于点M，当△PGM是以MG为腰的等腰三角形时，则AP的长为．解：设AP＝x，FG＝y，由题意得：CF＝BC＝5，∴CG＝5﹣y，∴PG＝5﹣y，∴DG＝5﹣（5﹣y）﹣x＝y﹣x，∵在RT△DGC中，CD2+DG2＝CG2，∴（y﹣x）2+22＝（5﹣y）2，∴y＝，（0＜x≤3）,∵△PGM是以MG为腰的等腰三角形，∴MG＝MP或MG＝PG，如图1中， ①当MG＝MP时，∵∠MPG＝∠MGP，∵∠APB＝∠MPG，∠MGP＝∠DGC，∴∠APB＝∠DGC，在△APB和△DGC中，，∴△APB≌△DGC，∴AP＝DG，∴y＝2x，∴＝2x，化简整理得：3x2﹣20x+21＝0，解得：x＝，∵x＝＞3不符合题意舍去，∴x＝．②当MG＝PG时，∵∠MPG＝∠PMG，∠MPG＝∠MBC，∴∠MBC＝∠PMC，∴CM＝CB，（即点M与点F重合）．又∵∠BCP＝∠MCP，∴CP⊥BP，∴△ABP，△DPC，△BPC均为直角三角形．∴AP2+AB2+DP2+CD2＝BC2，即x2+22+（5﹣x）2+22＝52，化简整理得：x2﹣5x+4＝0，解得：x＝1或4．∵x＝4＞3不符合题意舍弃，∴x＝1．综上所述：当△PGM是以MG腰2的等腰三角形时，AP＝或1．例2、（2019•桂林）将矩形ABCD按如图所示的方式折叠，BE，EG，FG为折痕，若顶点A，C，D都落在点O处，且点B，O，G在同一条直线上，同时点E，O，F在另一条直线上，则的值为（） A． B． C． D．解：由折叠可得，AE＝OE＝DE，CG＝OG＝DG，∴E，G分别为AD，CD的中点，设CD＝2a，AD＝2b，则AB＝2a＝OB，DG＝OG＝CG＝a，BG＝3a，BC＝AD＝2b，∵∠C＝90°，∴Rt△BCG中，CG2+BC2＝BG2，即a2+（2b）2＝（3a）2，∴b2＝2a2，即b＝a，∴，∴的值为，故选：B．练习：（2014春•富宁县校级期中）如图所示，将矩形纸片ABCD按如图方式折叠，EF、EC为折痕，折叠后点A 落在边CD的A处，点B落在边A′E的B′处．若A′D＝4，BC＝8，则AE的长是（）A．10 B．11 C．12 D．13解：∵矩形ABCD的边BC＝8，∴AD＝BC＝8，由翻折的性质得，AF＝A′F，B′C＝BC，设AF＝x，则DF＝8﹣x，在Rt△A′DF中，由勾股定理得，A′D2+DF2＝A′F2，即42+（8﹣x）2＝x2，解得x＝5，∴DF＝8﹣x＝8﹣5＝3，由翻折得，∠EA′F＝∠A＝90°，∠CB′E＝∠B＝90°，CB′＝BC＝8， ∴∠DA′F+∠CA′B′＝90°，∠A′B′C＝90°，∵∠DA′F+∠A′FD＝90°，∴∠A′FD＝∠CA′B′，又∵∠D＝∠A′B′C＝90°，∴△A′DF∽△CB′A′，∴＝，即＝，解得A′B′＝6，由勾股定理得，A′C＝＝＝10，∴CD＝A′D+A′C＝4+10＝14， ∴AB＝CD＝14，设AE＝y，则BE＝14﹣y，由翻折的性质得，∠AEF＝∠A′EF，∠BEC＝∠B′EC，∴∠AEF+∠BEC＝90°，∵∠AEF+∠AFE＝90°，∴∠AFE＝∠BEC，又∵∠A＝∠B＝90°，∴△AEF∽△BCE，∴＝，即＝，整理得，y2﹣14y+40＝0，解得y1＝4，y2＝10，由图可知，AE大于AB的一半，所以AE＝10．故选：A．例3、（2019•常州一模）如图，正方形ABCD的边长为6，点E，F分别为AB、BC的中点，点H是AD 边上一点，将△DCF沿DF折叠得△DC′F，将△AEH沿EH折叠后点A的对应点A′刚好落在DC′上，则cos∠DA′H＝．解：如图，延长DC'交AB于K，连接FK，分别过H，E作DK的垂线，垂足分别为M，N，∵四边形ABCD为正方形，∴∠A＝∠∠B＝∠C＝90°，AB＝BC＝6，∵E，F分别为AB，BC的中点，∴AE＝BE＝BF＝FC＝×6＝3，由翻折知，△DCF≌△DC'F，△AEH≌△A'EH，∴∠FC'D＝∠C＝90°，∠A＝∠HA'E＝90°，AE＝A'E＝3，C'F＝CF＝BF＝3，DC'＝DC＝6， ∴∠B＝∠FC'K＝90°，又∵KF＝KF，∴Rt△FBK≌Rt△FC'K（HL），∴KB＝KC'，设KB＝KC'＝x，在Rt△ADK中，AD＝6，AK＝6﹣x，DK＝6+x，∵DK2＝AD2+AK2，∴（6+x）2＝62+（6﹣x）2，解得，x＝，∴BK＝C'K＝，∴DK＝DC'+KC'＝6+＝，EK＝BE﹣BK＝，在Rt△KNE与Rt△KAD中，sin∠EKN＝，即，解得，EN＝，∵∠DA'H+∠EA'N＝90°，∠EA'N+∠NEA'＝90°，∴∠HA'D＝∠NEA'，在Rt△EA'N中，cos∠A'EN＝＝＝，即cos∠DA'H＝，故答案为：．例4、如图，在正方形ABCD中，边长为2，点E为边BC的中点，将边AB沿AE折叠到AM，点F为边CD上一点，将边AD沿AF折叠恰能使AD与AM重合．延长AM，交CD于点N，连接EN并延长，交AF的延长线于点G，连接CG，则GN＝．解：延长GE交AB的延长线于点P，过点G作GQ⊥BC交BC的延长线于点Q，如图2所示：由折叠性质得：∠BAE＝∠MAE，∠AEN＝90°，∠EAG＝45°，∴∠AGE＝45°，∴△AEG为等腰直角三角形，∴EG＝AE＝＝＝，∵∠AEB+∠GEQ＝90°，∠AEB+∠BAE＝90°，∴∠GEQ＝∠BAE，在△ABE和△EQG中，，∴△ABE≌△EQG（AAS），∴AB＝EQ，∵点E为边BC的中点，∴EC＝CQ，∵四边形ABCD是正方形，∴CN⊥BC，∴CN∥GQ，∴CN是△EQG的中位线，∴EN＝GN，∴GN＝EG＝，练习：（2016秋•渝中区校级期中）如图，在边长为2的正方形ABCD中，F是DC延长线上一点，且CF＝CD，E是AF中点，将△ABE沿BE翻折至△A'BE处，连接A'D，则A'D的长为．解：如图：以A为原点，AB为x轴，AD为y轴建立平面直角坐标系连接AA'，交BE于M，作A'N⊥AD于N，根据题意得：A（0，0），B（2，0），D（0，3），F（3，2）∵E是AF中点∴E（，1）设BE解析式y＝kx+b∴∴k＝﹣2，b＝4∴BE解析式y＝﹣2x+4，∵将△ABE沿BE翻折至△A'BE，∴BE⊥AA'，AM＝A'M，∴AA'解析式y＝x设M（x，y）∴解得：∵AM＝A'M，∴根据中点坐标公式可得A'（，）∴A'N＝，AN＝∴DN＝AD﹣AN＝，在Rt△A'DN中，A'D＝＝例5、（2010•江东区模拟）如图，在矩形ABCD中，AB＝3，AD＝5，点P在线段BC上运动，现将纸片折叠，使点A与点P重合，得折痕EF（点E、F为折痕与矩形边的交点），设BP＝x，当点E落在AB 上，点F落在AD上时，x的取值范围是（）A．0＜x≤1 B．0＜x≤3 C．1≤x≤3 D．3≤x≤5解：如图；①当F、D重合时，BP的值最小；根据折叠的性质知：AF＝PF＝5；在Rt△PFC中，PF＝5，FC＝3，则PC＝4；∴BP＝x min＝1；②当E、B重合时，BP的值最大；由折叠的性质可得BP＝AB＝3．所以答案应该是1≤x≤3．故选：C．练习：1、（2014•拱墅区一模）如图，在矩形ABCD中，AB＝2，AD＝5，点P在线段BC上运动，现将纸片折叠，使点A与点P重合，得折痕EF（点E、F为折痕与矩形边的交点），设BP＝x，当点E落在线段AB 上，点F落在线段AD上时，x的取值范围是 5﹣≤x≤2．解：如图；①当F、D重合时，BP的值最小；根据折叠的性质知：AF＝PF＝5；在Rt△PFC中，PF＝5，FC＝2，则PC＝；∴BP的最小值为5﹣；②当E、B重合时，BP的值最大；由折叠的性质可得AB＝BP＝2，即BP的最大值为2．所以x的取值范围是5﹣≤x≤2．2、（2018春•建邺区校级月考）如图，矩形纸片ABCD中，AB＝8，AD＝12，点P是边BC上的动点．现将纸片折叠，使点A与点P重合，折痕与矩形边的交点分别为E，F，要使折痕始终与边AB，AD有交点，则BP的取值范围是 12﹣4≤BP≤8．解：①当F、D重合时，BP的值最小，如图1所示：根据折叠的性质知：AF＝PF＝12；在Rt△PFC中，PF＝12，FC＝8，由勾股定理得：PC＝＝4；∴BP＝12﹣4；②当E、B重合时，BP的值最大，如图2所示：根据折叠的性质即可得到AB＝BP＝8，即BP的最大值为8；故答案为：12﹣4≤BP≤8．例6、（2019秋•江阴市期中）如图，矩形纸片ABCD中，AB＝10，AD＝5，点E、F分别在线段AB、AD 上，将△AEF沿EF翻折，点A的落点记为P．当P落在矩形ABCD内部时，PD的最小值等于（） A． B． C． D．2解：如图1：连接ED，过P作PH⊥ED于H，∴在直角三角形HPD中，DP＞DH，∴当点A的对称P落在线段ED上时，此时PD有最小值，即当EP取最大值时，PD有最小值，而E 在线段AB上，∴当E与B重合时，即EP最大，从而此时PD取得最小，（如图2 ）∵AB＝10，AD＝5，∴BD＝＝＝5，∵AB＝PB＝10，∴DP＝BD﹣PB＝5﹣10，故选：C．练习：1、（2016秋•渝中区校级期中）如图，在矩形ABCD中，AB＝6，AD＝3，点E、F分别在AD、AB线段上，将△AEF沿EF翻折，使得点A落在矩形ABCD内部P点，连接PD，则PD的最小值是 3﹣6．解：如图1，设A的对称点为P，连接DF，过P作PG⊥DF于G，在Rt△PDG中，PD＞DG， ∴当点A的对称点P落在DF上时，PD最小，即当FG取最大值时，DG最小，而F在AB上， ∴当F与B重合时，FG最大，GD最小，即PD最小，如图2，点F与B重合，P在BD上，在Rt△ADB中，BD＝＝＝3，由折叠得：AB＝BP＝6，∴PD＝BD﹣BP＝3﹣6，则PD的最小值是3﹣6，故答案为：3﹣6．2、（2008•义乌市）如图，直角梯形纸片ABCD，AD⊥AB，AB＝8，AD＝CD＝4，点E、F分别在线段AB、AD上，将△AEF沿EF翻折，点A的落点记为P．当P落在直角梯形ABCD内部时，PD的最小值等于 4﹣8．解：连接ED，作P1P⊥ED于P，那么在Rt△P1PD中，P1D＞PD，故当点A的对称点P落在线段ED上时，PD有最小值，而E在线段AB上，故当E与B重合时，即EP＝BP，此时PD取最小值此时，AB＝BP＝8，又BD＝＝4， ∴PD＝BD﹣BP＝．。

2020年初二数学专题训练(特殊四边形中的折叠问题)

初二数学专题训练(特殊四边形中的折叠问题)类型一求角度问题1.如图，将矩形ABCD 沿对角线BD 折叠，点C 落在点E 处，BE 交AD 于点F .已知62BDC ∠=︒，则DFE ∠的度数为( )A. 31°B. 28°C. 62°D. 56°2.(2019·扬州)将一张矩形纸片折叠成如图所示的图形，若26ABC ∠=︒，则ACD ∠= .类型二求线段长度问题3.(2019·兰州)的正方形ABCD 的对角线AC 与BD 交于点O ，将正方形ABCD 沿直线DF 折叠，点C 落在对角线BD 上的点E 处.折痕DF 分别交,AC EC 于点,M N ，则OM 的长为( )A. 12B. 2C. 1 1-4. (2019·天津改编)如图，正方形纸片ABCD 的边长为12，E 是边CD 上一点，连接AE .折叠该纸片，使点A 落在AE 上的点G 处，并使折痕经过点B ，得到折痕BF .点F 在AD 上，BF 交AE 于点H .若5DE =，求GE 的长.5.如图，矩形ABCD 沿AE 折叠，使点D 落在BC 边上的点F 处。

若6,10AB BC ==，求EF 的长.类型三求图形的周长问题6.(2019·长春)如图，有一张矩形纸片,8,6ABCD AB AD ==，先将矩形纸片ABCD 折叠，使边AD 落在边AB 上，点D 落在点E 处，折痕为AF .再将AEF ∆沿EF 翻折，AF 与BC 相交于点G ，则GCF ∆的周长为 .7.如图.在四边形ABCD 中，//,,AB CD AB CD BC CD ≠=，AD BD ⊥，E 为AB 的中点.(1)求证:四边形BCDE 是菱形.(2)若6,8AD BD ==，求四边形BCDE 的周长和面积.类型四探究性问题8. (2019·临沂)如图，在正方形ABCD 中，E 是DC 边上一点(与点,D C 不重合)，连接AE ，将ADE ∆沿AE 所在的直线折叠得到AFE ∆.延长EF 交BC 于点G .连接AG .作GH AG ⊥，与AE 的延长线交于点H ，连接CH .显然AE 是DAF ∠的平分线，EA 是DEF ∠的平分线.仔细观察，请逐一找出图中其他的角平分线(仅限于小于180°的角的平分线)，并说明理由.9.(2019·岳阳)操作体验:如图①，在矩形ABCD 中，点,E F 分别在边,AD BC 上，将矩形ABCD 沿直线EF 折叠，使点D 恰好与点B 重合，点C 落在点'C 处.如图②，P 为直线EF 上一动点(不与点,E F 重合)，过点P 分别作直线,BE BF 的垂线，垂足分别为,M N ，以,PM PN 为邻边构造PMQN Y .(1)求证:BE BF =.(2)特例感知:若5,2DE CF ==，当点P 在线段EF 上运动时，求PMQN Y 的周长.(3)类比探究:若,DE a CF b ==.①如图③.当点P 在线段EF 的延长线上运动时.试用含,a b 的代数式表示QM 与QN 之间的数量关系，并证明.②如图④，当点P 在线段FE 的延长线上运动时.试用含,a b 的代数式表示QM 与QN 之间的数量关系(不要求写证明过程).参考答案1. D2. 128︒3. D4. 4913GE =5. 103EF =6. 4+7. (1)点拨：由EDB CBD BD BD EBD CDB ∠=∠⎧⎪=⎨⎪∠=∠⎩可得EBD CBD ∆≅∆，BE BC =，所以CB CD BE DE ===.(2)四边形BCDE 的周长为20，面积为24.8. AG 是BAF ∠的平分线；GA 是BGF ∠的平分线；GH 是EGC ∠的平分线；CH 是BGF ∠ 的平分线.由90AB AF B AFG AG AG =⎧⎪∠=∠=︒⎨⎪=⎩，可得ABG AFG ∆≅∆所以BAG FAG ∠=∠，BGA FGA ∠=∠，所以AG 是BAF ∠的平分线，GA 是BGF ∠的平分线.由90AGE HGE ∠+∠=︒，90AGB HGC ∠+∠=︒，BGA FGA ∠=∠ 可得AGE AGB ∠=∠，所以GH 是EGC ∠的平分线.如图，过点H 作HN BC ⊥，交BC 的延长线于点N .由90B GNH AG GH GAB HGC ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩，可得ABG GNH ∆≅∆，,BG HN GN AB BC ===，所以BG CN =，CN NH =.所以45HCN ECH ∠=∠=︒，CH 是BGF ∠ 的平分线.∠=∠=∠9. (1)点拨：BFE DEF BEFY的周长为(2)PMQN点拨：如图①，延长NP交AD于点G.+=+==PM PN PG PN NG AB(3) ①点拨：如图②，延长PN交AD于点H.-=-=-=== QN QM PM PN PH PN HN AB-=②QM QN。