c语言实现的粒子群算法代码及解释
粒子群算法(PSO)程序(C#语言)

粒子群算法(PSO)程序(C#语言)超简洁的随机粒子群算法,PSO,程序,C,语言, using System; using System.Linq;using System.Collections.Generic;class MyPSO {const int NUM=40;//粒子数const int DIM=30;//维数const double c1=1.8;//参数const double c2=1.8;//参数static double xmin=-100.0;//位置下限static double xmax=100.0;//位置上限static double[] gbestx=new double[DIM];//全局最优位置static double gbestf;//全局最优适应度static Random rand=new Random();//用于生成随机数class particle {//定义一个粒子public double[] x=new double[DIM];//当前位置矢量public double[] bestx=new double[DIM];//历史最优位置public double f;//当前适应度public double bestf;//历史最优适应度}particle[] swarm=new particle[NUM];//定义粒子群double f1(double[] x) {//测试函数:超球函数return x.Sum(a => a*a);}static void Main(string[] args) {for(int i=0; i<DIM; i++)//初始化全局最优gbestx[i]=rand.NextDouble()*(xmax-xmin)+xmin; gbestf=double.MaxValue;for(int i=0; i<NUM; i++) {//初始化粒子群particle p1=new particle();for(int j=0; j<DIM; j++)p1.x[j]=rand.NextDouble()*(xmax-xmin)+xmin;p1.f=f1(p1.x);p1.bestf=double.MaxValue;swarm[i]=p1;}for(int t=0; t<5000; t++) {for(int i=0; i<NUM; i++) {particle p1=swarm[i];for(int j=0; j<DIM; j++)//进化方程p1.x[j]+=c1*rand.NextDouble()*(p1.bestx[j]-p1.x[j]) +c2*rand.NextDouble()*(gbestx[j]-p1.x[j]);p1.f=f1(p1.x);if(p1.f<p1.bestf) {//改变历史最优p1.x.CopyTo(p1.bestx, 0);p1.bestf=p1.f;}if(p1.f<gbestf) {//改变全局最优p1.x.CopyTo(gbestx, 0);for(int j=0; j<DIM; j++)//把当前全局最优的粒子随机放到另一位置p1.x[j]=rand.NextDouble()*(xmax-xmin)+xmin;gbestf=p1.f;}}}Console.WriteLine("{0}", gbestf);}}。
粒子群优化算法 简洁 c语言

粒子群优化算法的C代码如下,运行后为什么提示:d:\program files\microsoft visual studio\vc98\include\eh.h(32) : fatal error C1189: #error : "eh.h is only for C++!"费解了。
由于学matlab,我C语言长时间未碰,有点生疏。
还请各位多多指导,真的谢谢了!#include<iostream>#include<fstream>#include<cmath>#include<ctime>#include<string>#include<iomanip>#include<cstdlib>using namespace std;#include"ran_number.h"const double pi=3.1415926;const int num=60; /*粒子群规模*/const int T=2000; /*最大迭代次数*///**************适应度函数*************//double func(double x){double f=x*sin(10*x*pi)+2.0;f=1.0/f;return f;}//----------------主程序----------------//void main(int argc,char* argv[]){double ran; //随机变量RandomNumber rand;double c1=2.05,c2=2.05; //学习因子double d1=0.2,d2=0.7; //控制因子double ws=0.9,we=0.4; //最大最小惯性权重double x_down=-1.0,x_up=2.0; //粒子空间上下界double w; //惯性权重int m=2;double Vmax; //粒子最大速度double x[num]; //粒子位置(控制参数)double v[num]; //粒子速度double g[num]; //粒子适应度double pbest[num]; //粒子个体最好值double pbest_x[num]; //粒子个体最好位值double gbest; //粒子群体最好值double gbest_x; //粒子群体最好位置Vmax=(x_up-x_down)/8;//--初始化粒子群:位置、速度、个体最优值for(int i=0;i<num;i++){pbest[i]=0.0;ran=rand.fRandom();x[i]=x_down+(x_up-x_down)*ran;v[i]=Vmax*(2*ran-1); //初始化粒子速度pbest[i]=func(x[i]);pbest_x[i]=x[i];}gbest=pbest[0];gbest_x=x[0];//--------------第一次迭代得到的群体最优----------//for(i=0;i<num;i++) // for 粒子数循环{if(pbest[i]<gbest){gbest=pbest[i];gbest_x=pbest_x[i];}}//---------------共T次迭代过程---------------//while(m<=T) //迭代次数循环{w=(ws-we-d1)*exp(1/(1+d2*(m-1)/t)); //惯性权重for(i=0;i<num;i++) //粒子数循环{g[i]=0.0;ran=rand.fRandom();v[i]=w*v[i]+c1*ran*(pbest_x[i]-x[i])+c2*ran*(gbest_x-x[i]);x[i]+=v[i];if(x[i]<x_down){x[i]=x_down;} //保证粒子位置不能超越下界if(x[i]>x_up){x[i]=x_up;} //保证粒子位置不能超出上界g[i]=func(x[i]);if(pbest[i]>g[i]){pbest[i]=g[i];pbest_x[i]=x[i];}if(pbest[i]<gbest){gbest=pbest[i];gbest_x=pbest_x[i];}printf("第%d次迭代的群体最优值及最优位置为%lf %lf ",m,gbest,gbest_x); //输出第m次迭代的群体最优值及最优位置} //结束for循环m=m+1;} //结束while循环printf("全局最优解及全局最优位置为%lf %lf ",gbest,gbest_x);下面为改正点:注意: vc在处理.c 文件是按C 语言编译的,所以假如有以下文件: 1.c#include <fstream>int main(int argc, char* argv[]){return 0;}那么编译时就会出错:fatal error C1189: #error : "eh.h is only for C++!"这是因为fstream标准库要求用到eh.h文件,而Exception Handling的实现需要c++支持。
用c语言或matlab语言求解墨西哥草帽函数最小值的粒子群算法程序

用c语言或matlab语言求解墨西哥草帽函数最小值的粒子
群算法程序
本程序使用粒子群算法来求解墨西哥草帽函数的最小值。
墨西哥草帽函数是一个常用的测试函数,其数学表达式为:
f(x,y) = -sin(sqrt(x^2 + y^2)) / (0.01(x^2 + y^2) + 1) 本程序使用随机生成的初始粒子群,通过不断迭代更新粒子的位置和速度,找到墨西哥草帽函数的全局最小值。
具体实现过程如下:
1. 首先定义墨西哥草帽函数,包括输入参数x和y,输出参数f。
2. 然后定义初始粒子群,包括粒子数目、初始位置和速度等参数。
3. 迭代更新粒子的位置和速度,直到满足停止条件(如迭代次数达到一定值或粒子群的最优解与全局最优解之间的误差达到一定值)。
4. 在迭代过程中,记录每个粒子的最优位置和全局最优位置,并更新粒子群的最优解。
5. 最后输出墨西哥草帽函数的最小值以及对应的最优解。
程序实现可以使用c语言或matlab语言,具体实现方式可以根据个人喜好和实际情况进行选择。
- 1 -。
C++实现粒子群优化算法代码

#include<iostream>#include<cmath>#include<ctime>#include<cstdlib>using namespace std;const int pNum = 10;const int generation = 100;const int dim = 2;const double low = -10;const double high = 10;const double vMax = 10;const double w = 0.5;const double c1 = 2;const double c2 = 2;double p[pNum][dim]; //粒子群体double pv[pNum][dim]; //速度向量double pBest[pNum][dim]; //每个粒子的局部最优向量double pFitness[pNum]; //每个粒子的最优最适值double gFitness; //全局最优适应值double gBest[dim]; //全局最优向量double fitness(double p[]){return p[0] * p[0] + p[1] * p[1]; //根据自己的需要更改函数的适应值}void initialize(){for (int i = 0; i < pNum; i++){for (int j = 0; j < dim; j++){p[i][j] = low + (high - low) * 1.0 * rand() / RAND_MAX;pBest[i][j] = p[1][j];pv[i][j] = -vMax + 2.0 * vMax * rand() / RAND_MAX;}}for (int i = 0; i < pNum; i++)pFitness[i] = fitness(p[i]);gFitness = pFitness[0];for (int i = 0; i < dim; i++){gBest[i] = pBest[0][i];}for (int i = 1; i < pNum; i++){if (gFitness > pFitness[i]){gFitness = pFitness[i];for (int j = 0; j < dim; j++){gBest[j] = pBest[i][j];}}}}void update(){for (int i = 0; i < pNum; i++){for (int j = 0; j < dim; j++){pv[i][j] = w * pv[i][j] + c1 * rand() / RAND_MAX * (pBest[i][j] - p[i][j]) + c2 * rand() / RAND_MAX * (gBest[j] - p[i][j]);if (pv[i][j] < -vMax)pv[i][j] = -vMax;if (pv[i][j] > vMax)pv[i][j] = vMax;p[i][j] = p[i][j] + pv[i][j];if (p[i][j] > high)p[i][j] = high;if (p[i][j] < low)p[i][j] = low;}}}void get_pBest(){for (int i = 0; i < pNum; i++){if (pFitness[i] > fitness(p[i])){pFitness[i] = fitness(p[i]);for (int j = 0; j < dim; j++){pBest[i][j] = p[i][j];}}}}void get_gBest(){for (int i = 0; i < pNum; i++){if (pFitness[i] < gFitness){for (int j = 0; j < dim; j++){gBest[j] = pBest[i][j];}gFitness = pFitness[i];}}}int main(){srand(time(0));initialize();for (int n = 0; n < generation; n++){update();get_pBest();get_gBest();}cout << "gBest is (";for (int i = 0; i < dim - 1; i++)cout << gBest[i] << ",";cout << gBest[dim - 1] << ")" << endl;cout << "the best fitness is " << gFitness << endl;return 0;}。
用c语言或matlab语言求解墨西哥草帽函数最小值的粒子群算法程序

用c语言或matlab语言求解墨西哥草帽函数最小值的粒子群算法程序以下是一种用C语言实现的基本粒子群算法程序,用于求解墨西哥草帽函数的最小值。
#include <stdio.h>#include <stdlib.h>#include <math.h>#define SWARM_SIZE 50 // 粒子群规模#define MAX_ITERATION 1000 // 最大迭代次数#define DIMENSION 2 // 问题维度#define INERTIA_WEIGHT 0.7 // 惯性权重#define COGNITIVE_WEIGHT 1.4 // 认知权重#define SOCIAL_WEIGHT 1.4 // 社会权重#define LOWER_BOUND -10.0 // 自变量下界#define UPPER_BOUND 10.0 // 自变量上界void evaluateFitness(double* positions, double* fitness);double mexicanHatFunction(double* x);double randDouble(double min, double max);int randInt(int min, int max);int maindouble swarm[SWARM_SIZE][DIMENSION]; // 粒子群位置double velocity[SWARM_SIZE][DIMENSION]; // 粒子群速度double bestPosition[DIMENSION]; // 全局最优位置double bestFitness = __DBL_MAX__; // 全局最优适应度double fitness[SWARM_SIZE]; // 粒子适应度//初始化粒子群for (int i = 0; i < SWARM_SIZE; i++)for (int j = 0; j < DIMENSION; j++)swarm[i][j] = randDouble(LOWER_BOUND, UPPER_BOUND);velocity[i][j] = 0.0;}evaluateFitness(swarm[i], &fitness[i]);if (fitness[i] < bestFitness)bestFitness = fitness[i];for (int k = 0; k < DIMENSION; k++)bestPosition[k] = swarm[i][k];}}//迭代求解for (int iter = 0; iter < MAX_ITERATION; iter++)for (int i = 0; i < SWARM_SIZE; i++)for (int j = 0; j < DIMENSION; j++)double r1 = randDouble(0.0, 1.0);double r2 = randDouble(0.0, 1.0);velocity[i][j] = INERTIA_WEIGHT * velocity[i][j] + COGNITIVE_WEIGHT * r1 * (bestPosition[j] - swarm[i][j]) + SOCIAL_WEIGHT * r2 * (bestPosition[j] - swarm[i][j]); swarm[i][j] += velocity[i][j];if (swarm[i][j] < LOWER_BOUND)swarm[i][j] = LOWER_BOUND;else if (swarm[i][j] > UPPER_BOUND)swarm[i][j] = UPPER_BOUND;}evaluateFitness(swarm[i], &fitness[i]);if (fitness[i] < bestFitness)bestFitness = fitness[i];for (int k = 0; k < DIMENSION; k++)bestPosition[k] = swarm[i][k];}}}printf("Best position: ");for (int i = 0; i < DIMENSION; i++)printf("%.4f ", bestPosition[i]);printf("\n");printf("Best fitness: %f\n", bestFitness);return 0;void evaluateFitness(double* positions, double* fitness)*fitness = mexicanHatFunction(positions);double mexicanHatFunction(double* x)double result = 0.0;result = -(pow(x[0], 2) + pow(x[1], 2)) + 2 * exp(-(pow(x[0], 2) + pow(x[1], 2)) / 2);return result;double randDouble(double min, double max)return min + ((double)rand( / RAND_MAX) * (max - min);int randInt(int min, int max)return min + rand( % (max - min + 1);这个程序使用经典的粒子群算法来求解墨西哥草帽函数的最小值。
6种粒子群算法程序

6种粒子群算法程序程序1当c\\ = c i\ = 2 , c n = c22 = 1.5 , w = 1.2 oa)*主函数源程序(main.m)%------ 基本粒子群算法(particle swarm optimization)%------ 名称:基本粒子群算法%------ 初始格式化clear all; %清除所有变量C1C;%清屏format long; %将数据显示为长整形科学计数%……给定初始条条件............N=40; D=10; T=100; cl1=2;%3初始化群体个数%初始化群体维数%初始化群体最迭代次数%学习因子1c21=2;cl2=1.5;c22=1.5;w=L2; eps=10A(-6);%学习因子2%惯性权重%设置精度(在已知最小值的时候用)%……初始化种群个体(限定位置和速度)x=zeros(N,D);v=zeros(N,D); for i=l:Nfor j=l:Dx(lj)=randn; %随机初始化位置v(ij)=randn; %随机初始化速度end end%……显示群位置............... flgure(l)for j=l:Dif(rem(D,2)>0)subplot((D+l)/2,2J)elsesubplot(D/2,2,j)endplot(x(:,j);b*');grid on xlabelC 粒子■) ylabel(*初始位置J tlnfo=strcat(f第*har(j+48)J 维J;tlnfo=strcat(,M \cha r(floor(j/l 0)+48), char(rem(j,l 0)+48),'维');endtitle(tlnfo)end%-一-显示种群速度figure ⑵for j=l:Dif(rem(D^2)>0) subplot((D+l)/2,2J)elsesubplot(D/2,2J)endplot(x(:,j);b*');gricl on xlabelC 粒子') ylabel(,初始速度J tlnfo=strcatf 第,char(j+48),'维');if(j>9)tlnfo=strcat(* 第“har(floor(j/l())+48)9 char(rem(j,l 0)+48),'维);endtitle(tlnfo)endfigure ⑶%第一个图su bp lot( 1,2,1)%……初始化种群个体(在此限定速度和位置) .........xl=x;vl=v;%……初始化个体最优位置和最优值…pl=xl;pbestl=ones(NJ);for i=l:Npbestl (i)=fitness(x 1 (i,: ),D);end%……初始化全局最优位置和最优值 .........gl=l000*ones(l ,D);gbestl=1000;for i=l:Nlf(pbestl(i)<gbest 1)gl=pl(i,:);gbestl=pbestl(i);endendgbl=ones(l,T);%浸入主循环,按照公式依次迭代直到满足精度或者迭代次数…for i=l:Tfor J=1:NIf (fltness(xl(J,:),D)<pbestl(J))pl(J,:)=xl(|,:);pbestl (J)=fitness(x 1Q,: ),D);endlf(pbest 1 (])<gbest 1)gl=pl(j,:); gbestl=pbestl(J);endvl(j,:)=w*vl(J,:)+cll*rand*(pl(J,:)-xl(j,:))+c21*rand*(gl-xl(J,:));xl(J,:)=xl(J,:)+vl(j,:);endgbl(i)=gbestl;endplot(gbl)T empSt r=sprl ntf(• c 1 = %g ,c2=%g\cll,c21);title(TempStr);xiabelC迭代次数);ylabelC适应度值J;%第二个图subplot(l,2,2)%••…初始化种群个体(在此限定速度和位置) .........x2=x;v2=v;%••…初始化种群个体最有位置和最优解 .......p2=x2;pbest2=ones(N,l);for i=l:Npbest2(i)=fltness(x2(i,: ),D);end%••…初始化种全局最有位置和最优解……g2=1000*ones(l ,D);gbest2=1000;for i=X:Nif(pbest2(i)<gbest2)g2=p2(i,:);gbest2=pbest2(i);endendgb2=ones(l,T);%……浸入主循环,按照公式依次迭代直到满足精度或者迭代次数…for i=l:Tfor j=l:Nif (fitness(x2(J,:),D)<pbest2 ⑴)p2(J,:)=x2(j,:); pbest2(j)=fitness(x2(J,:),D);endif(pbest2(J)<gbest2)g2=p2(j,:);gbest2=pbest2(J);endV2(jv)=w*v2(j,:)+cl2*rand*(p2(j,:)-x2(j,:))+c22*rand*(g2-x2(j,:));x2(J,:)=x2(j,:)+v2(j,:);endgb2(i)=gbest2;endplot(gb2)TempStr=sprlntf(t cl= %g ,c2=%g\cl2,c22);title(TempStr);xiabclC迭代次数);ylabelC适应度值J;b)适应度函数%适应度函数(fitness.m)function result=fitness(x,D)sum=0;for i=l:Dsiim=sum+x(i)A2;endresult=sum;程序2当C11 =C2l =2 于C]2 =0,Cj2 = 2,w= 1.2 对比a)%主函数源程序(main.m)% ... 基本粒子群算法(particle swarm optimization)%……名称:基本粒子群算法%……初始格式化clear all; %清除所有变量clc; %清屏format long; %将数据显示为长整形科学计数cl2=0;c22=2;w=1.2; %惯性权重eps=10A(-6); %设置精度(在已知最小值的时候用) %……初始化种群个体(限定位置和速度) .........x=zeros(N,D);v=zeros(N,D);for i=l:Nfor j=l:Dx(lj)=randn; %随机初始化位置v(ij)=randn; %随机初始化速度endend%……显示群位置 ..............figure(l)for j=l:Dif(rem(D,2)>0)subplot((D+1 )/2,2 J)elsesubplot(D/2,2J)endplot(x(:J)/b*t);grid onxlabelC 粒子JylabelC初始位置JtInFo=strcatC 第’,char(j+48),1维f);if(j>9)tlnfo=strcat(f \char(floor(j/10)+48) t char(rem(j,10)+48),'维');endtitle(tlnfo)end%……显示种群速度flgure(2)for j=l:Dif(rem(D,2)>0)subplot((D+l)/2^2J)elsesubplot(D/2,2J)endplot(x(:J)/b*t);grid onxlabelC 粒子JylabelC初始速度Jtlnfo=strcat(v第,char(j+48),'维');if(j>9)tlnfo=strcat(,M t?char(floor(J/10)+48), char(rem(JJ0)+48)/ 维);encltitle(tlnfo)endfigure(3)%第一个图subplot(1^24)%……初始化种群个体(在此限定速度和位置)xl=x;vl=v;%……初始化个体最优位置和最优值…pl=xl;pbestl=ones(N,l);for i=l:Npbestl (i)=fitness(xl(i,:),D);end%……初始化全局最优位置和最优值 .........gl=l000*ones(l Q);gbestl=1000;for i=l:Nif(pbestl(i)<gbestl)gl=pl(i,:); gbestl=pbestl(i); endendgbl=ones(l,T);%••…浸入主循环,按照公式依次迭代直到满足精度或者迭代次数…for i=l:Tfor J=1:Nif (fitness(xl(J^:),D)<pbestl(J))pl(j,:)=xl(j,:);pbest 1 (J)=fitness(x 1 (J),D);endlf(pbestl (J )<gbest 1)gi=pia,:);gbestl=pbestl(j);endvl(J,:)=w*vl(J5:)+cll*ran(l*(pl(J,:)-xl(j,:))+c21*rand*(gl-xl(j,:));xl(j,:)=xl(J,:)+vl(j,:);endgbl(i)=gbestl;endplot(gbl)TempStr=sprlntf(,cl= %g 5c2=%g\cll,c21);title(TempStr);xlabef迭代次数);ylabelC适应度值J;%第二个图subplot( 1,2,2)%••…初始化种群个体(在此限定速度和位置) .........x2=x;v2=v;%-•…初始化种群个体最有位置和最优解 .......p2=x2;pbest2=ones(N,l);for i=l:Npbest2 ⑴=fltness(x2(i,:),D);end%-•…初始化种全局最有位置和最优解……g2=1000*ones(l Q);gbest2=1000;for i=l:Nif(pbest2(i)<gbest2)g2=p2(i,:); gbest2=pbest2(i);endendgb2=ones(l,T);%……浸入主循环,按照公式依次迭代宜到满足精度或者迭代次数…for i=l:Tfor j=l:Nif (fitness(x2(J,:),D)<pbest2(J))p2(j,:)=x2(j,:); pbest2(j)=fitness(x2(J,:),D);endif(pbest2(J)<gbest2)g2=p2(J,:); gbest2=pbest2(j);endv2Q,:)=w*v2(J,:)+cl2*rand*(p2(j,:)-x2(j,:))+c22*rand*(g2-x2(J,:));x2(J,:)=x2(j,:)+v2(j,:);endgb2(i)=gbest2;endplot(gb2)TempStr=sprlntf(,cl= %g ,c2=%f ,cl2,c22);title(TempStr);xlabef迭代次数);ylabelC适应度值J;b)适应度函数%适应度函数(fitness.ni)function result=fitness(x,D)sum=0;for i=l:Dsiim=sum+x(i)A2;end result=sum;程序3当 5 =c 2\ =2,闪=1.2于“2 = 2,C 22 =0,w = 1.2 对比a) %主函数源程序(main.m)% ... 基本粒子群算法(particle swarm optimization )%……名称:基本粒子群算法%……初始格式化clear all;clc;format long; %……给定初始条条件 ........... N=40;D=10;T=100; cl1=2;c21=2;cl2=2;%,初始化群体个数 %初始化群体维数 %初始化群体最迭代次数 %学习因子1 %学习因子2c22=0;w=L2; eps=10A (-6);%惯性权重 %设置精度(在已知最小值的时候用) %……初始化种群个体(限定位置和速度)x=zeros(N,D); v=zeros(N,D);for i=l:Nfor j=l:Dx(ij)=randn; %随机初始化位置 v(ij)=randn; %随机初始化速度 end end%……显示群位置 ..............flgure(l)for J=1:Dif(rem(D,2)>0)subplot((D+l)/2^2J)elsesubplot(D/2,2J)%清除所有变量 %清屏 %将数据显示为长整形科学计数plot(x(:J)/b*,);grid onxlabelC 粒子JylabelC初始位置Jtlnfo=strcat(f第;char(j+48),维J; if(j>9)tlnfo=strcat(,第;char(floor(j/10)+48), char(rem(ja0)+48);维J;encltitle(tlnfo)end%……显示种群速度flgure(2)for j=l:Dif(rem(D^2)>0)su bplot((D+1 )/2,2 J)elsesubplot(D/2,2J)endplot(x(: J;grid onxlabelC 粒子JylabelC初始速度') tInfo=strcatC 第,charQ+48),1维J; if(j>9)tlnfo=strcat(,第;chai*(floor(j/10)+48), char(rem(J40)+48)/ 维);end title(tlnfo)endflgure(3)%第一个图subplot(l929l)%……初始化种群个体(在此限定速度和位置) .........xl=x;vl=v;%……初始化个体最优位置和最优值…pl=xl;pbestl=ones(NJ);for i=l:Nend%……初始化全局最优位置和最优值 .........gl=l000*ones(l ,D);gbestl=1000;for i=l:Nlf(pbestl(i)<gbest 1)gl=pl(i,:);gbestl=pbestl(i);endendgbl=ones(l,T);%浸入主循环,按照公式依次迭代直到满足精度或者迭代次数…for i=l:Tfor J=1:NIf (fltness(xl(J,:),D)<pbestl(J))pl(J,:)=xl(|,:);pbestl (J)=fitness(x 1Q,: ),D);endlf(pbest 1 (])<gbest 1)gl=pl(j,:); gbestl=pbestl(J);endvl(j,:)=w*vl(J,:)+cll*rand*(pl(J,:)-xl(j,:))+c21*rand*(gl-xl(J,:));xl(J,:)=xl(J,:)+vl(j,:);endgbl(i)=gbestl;endplot(gbl)T empSt r=sprl ntf(• c 1 = %g ,c2=%g\cll,c21);title(TempStr);xiabelC迭代次数);ylabelC适应度值J;%第二个图subplot(l,2,2)%••…初始化种群个体(在此限定速度和位置) .........x2=x;v2=v;%••…初始化种群个体最有位置和最优解 .......p2=x2;pbest2=ones(N,l);for i=l:Npbest2(i)=fltness(x2(i,: ),D);end%••…初始化种全局最有位置和最优解……g2=1000*ones(l ,D);gbest2=1000;for i=X:Nif(pbest2(i)<gbest2)g2=p2(i,:);gbest2=pbest2(i);endendgb2=ones(l,T);%……浸入主循环,按照公式依次迭代直到满足精度或者迭代次数…for i=l:Tfor j=l:Nif (fitness(x2(J,:),D)<pbest2 ⑴)p2(J,:)=x2(j,:); pbest2(j)=fitness(x2(J,:),D);endif(pbest2(J)<gbest2)g2=p2(j,:);gbest2=pbest2(J);endv2(J,:)=w*v2(j,:)+cl2*rand*(p2(J,:)-x2(J,:))+c22*rand*(g2-x2(j,:));x2(J,:)=x2(j,:)+v2(j,:);endgb2(i)=gbest2;endplot(gb2)TempStr=sprlntf(f cl= %g ,c2=%g\cl2,c22);title(TempStr);xiabclC迭代次数);ylabelC适应度值J;b)适应度函数%适应度函数(fitness.m)function result=fitness(x,D)sum=0;for i=l:Dsiim=sum+x(i)A2;endresult=sum;程序4对c2, W2分别对其取值Cj =1.1, c2 =2, w, =1.2, w2 =1.5测试函数。
基本粒子群算法

简单的基本粒子群算法#include <stdio.h>#include <stdlib.h>#include <time.h>#include <math.h>#define randf (double)(rand()%10000)/10000 using namespace std;const int dim = 30; // 粒子维数const int num = 100; // 粒子群中粒子的个数. const int c1 = 2; // 学习因子1const int c2 = 2; // 学习因子2const int w = 0.9; // 惯性权重因子double Xmax = 500;double Xmin = -500;double Vmax = 50;double Vmin = -50;double gbest_f; // 全局最优适应值.double gbest[dim]; // 全局最优位置.struct particle // 粒子结构.{double f;double pbest_f;double pbest[dim];double X[dim];double V[dim];} swarm[num]; // 粒子群定义.double fitness(); // 计算粒子适应度.void check(); // 检查粒子的速度和范围是否越界. void initial(); // 粒子群的随机初始化void fly(); // 粒子飞翔.double fitness ( double X[] ){double sum = 0;for ( int i = 0 ; i < dim ; i ++ ){double t = X[i];if ( t < 0 )t *= -1;sum += -1*X[i]*sin(sqrt(t));}return sum;}void check(int index){for ( int i = 0 ; i < dim ; i ++ ){if ( swarm[index].X[i] > Xmax )swarm[index].X[i] = Xmax;if ( swarm[index].X[i] < Xmin )swarm[index].X[i] = Xmin;if ( swarm[index].V[i] > Vmax )swarm[index].V[i] = Vmax;if ( swarm[index].V[i] < Vmin )swarm[index].V[i] = Vmin;}}void initial(){double interval0 = Xmax-Xmin;double interval1 = Vmax-Vmin;for ( int i = 0 ; i < num ; i ++ ){particle * p = &swarm[i];for ( int j = 0 ; j < dim ; j ++ ){p->X[j] = interval0 * randf + Xmin;p->V[j] = interval1 * randf + Vmin;}check(i);p->f = fitness(p->X);p->pbest_f = p->f;for ( int j = 0 ; j < dim ; j ++ )p->pbest[j] = p->X[j];}gbest_f = swarm[0].pbest_f;for ( int j = 0 ; j < dim ; j ++ )gbest[j] = swarm[0].X[j];}void fly (){int i,j;for ( i = 0 ; i < num ; i ++ ){particle * p = &swarm[i];for ( j = 0 ; j < dim ; j ++ ){p->V[j] = w*p->V[j] + c1*randf*( p->pbest[j]- p->X[j]) + c2*randf*(gbest[j]-p->X[j]);p->X[j] = p->V[j] + p->X[j];}check(i);p->f = fitness(p->X);if ( p->f < p->pbest_f ){p->pbest_f = p->f;for ( j = 0 ; j < dim ; j ++ )p->pbest[j] = p->X[j];}if ( p->f < gbest_f ){gbest_f = p->f;for ( j = 0 ; j < dim ; j ++ )gbest[j] = p->X[j];}}}int main() {srand((unsigned)time(NULL));initial();for ( int i = 0 ; i < 50000 ; i ++ )fly();double a = fitness(gbest);printf("%lf",a);return 0;}。
粒子群算法(PSO)源代码

粒子群算法(PSO)源代码%%#################################################################### %%#### Particle swarm optimization%%#### With linkage operator%%#### Deepak devicharan july 2003%%#################################################################### %%## to apply this to different equations do the following%%## generate initial particles in a search space close to actual soln%%## fool around with no of iterations, no of particles, learning rates%%## for a truly generic PSO do the following%%## increase the number of particles , increase the variance%%## i.e let the particles cover a larger area of the search space%%## then fool around as always with the above thins%declare the parameters of the optimizationmax_iterations = 1000;no_of_particles = 50;dimensions = 1;delta_min = -0.003;delta_max = 0.003;c1 = 1.3;c2 = 1.3;%initialise the particles and teir velocity componentsfor count_x = 1:no_of_particlesfor count_y = 1:dimensionsparticle_position(count_x,count_y) = rand*10;particle_velocity(count_x,count_y) = rand;p_best(count_x,count_y) = particle_position(count_x,count_y);endend%initialize the p_best_fitness arrayfor count = 1:no_of_particlesp_best_fitness(count) = -1000;end%particle_position%particle_velocity%main particle swrm routinefor count = 1:max_iterations%find the fitness of each particle%change fitness function as per equation requiresd and dimensionsfor count_x = 1:no_of_particles%x = particle_position(count_x,1);%y = particle_position(count_x,2);%z = particle_position(count_x,3);%soln = x^2 - 3*y*x + z;%x = particle_position(count_x);%soln = x^2-2*x+1;x = particle_position(count_x);soln = x-7;if soln~=0current_fitness(count_x) = 1/abs(soln);elsecurrent_fitness =1000;endend%decide on p_best etc for each particlefor count_x = 1:no_of_particlesif current_fitness(count_x) > p_best_fitness(count_x)p_best_fitness(count_x) = current_fitness(count_x);for count_y = 1:dimensionsp_best(count_x,count_y) = particle_position(count_x,count_y);endendend%decide on the global best among all the particles[g_best_val,g_best_index] = max(current_fitness);%g_best contains the position of teh global bestfor count_y = 1:dimensionsg_best(count_y) = particle_position(g_best_index,count_y);end%update the position and velocity compponentsfor count_x = 1:no_of_particlesfor count_y = 1:dimensionsp_current(count_y) = particle_position(count_x,count_y);endfor count_y = 1:dimensionsparticle_velocity(count_y) = particle_velocity(count_y) + c1*rand*(p_best(count_y)-p_current(count_y)) + c2*rand*(g_best(count_y)-p_current(count_y)); particle_positon(count_x,count_y) = p_current(count_y) +particle_velocity(count_y);endendendg_bestcurrent_fitness(g_best_index)clear all, clc % pso exampleiter = 1000; % number of algorithm iterationsnp = 2; % number of model parametersns = 10; % number of sets of model parametersWmax = 0.9; % maximum inertial weightWmin = 0.4; % minimum inertial weightc1 = 2.0; % parameter in PSO methodologyc2 = 2.0; % parameter in PSO methodologyPmax = [10 10]; % maximum model parameter valuePmin = [-10 -10]; % minimum model parameter valueVmax = [1 1]; % maximum change in model parameterVmin = [-1 -1]; % minimum change in model parametermodelparameters(1:np,1:ns) = 0; % set all model parameter estimates for all model parameter sets to zeromodelparameterchanges(1:np,1:ns) = 0; % set all change in model parameter estimates for all model parameter sets to zerobestmodelparameters(1:np,1:ns) = 0; % set best model parameter estimates for all model parameter sets to zerosetbestcostfunction(1:ns) = 1e6; % set best cost function of each model parameter set to a large numberglobalbestparameters(1:np) = 0; % set best model parameter values for all model parameter sets to zerobestparameters = globalbestparameters'; % best model parameter values for all model parameter sets (to plot)globalbestcostfunction = 1e6; % set best cost function for all model parameter sets to a large numberi = 0; % indicates ith algorithm iterationj = 0; % indicates jth set of model parametersk = 0; % indicates kth model parameterfor k = 1:np % initializationfor j = 1:nsmodelparameters(k,j) = (Pmax(k)-Pmin(k))*rand(1) + Pmin(k); % randomly distribute model parametersmodelparameterchanges(k,j) = (Vmax(k)-Vmin(k))*rand(1) + Vmin(k); % randomly distribute change in model parametersendendfor i = 2:iterfor j = 1:nsx = modelparameters(:,j);% calculate cost functioncostfunction = 105*(x(2)-x(1)^2)^2 + (1-x(1))^2;if costfunction < setbestcostfunction(j) % best cost function for jth set of model parameters bestmodelparameters(:,j) = modelparameters(:,j);setbestcostfunction(j) = costfunction;endif costfunction < globalbestcostfunction % best cost function for all sets of model parameters globalbestparameters = modelparameters(:,j);bestparameters(:,i) = globalbestparameters;globalbestcostfunction(i) = costfunction;elsebestparameters(:,i) = bestparameters(:,i-1);globalbestcostfunction(i) = globalbestcostfunction(i-1);endendW = Wmax - i*(Wmax-Wmin)/iter; % compute inertial weightfor j = 1:ns % update change in model parameters and model parametersfor k = 1:npmodelparameterchanges(k,j) = W*modelparameterchanges(k,j) + c1*rand(1)*(bestmodelparameters(k,j)-modelparameters(k,j))...+ c2*rand(1)*(globalbestparameters(k) - modelparameters(k,j));if modelparameterchanges(k,j) < -Vmax(k), modelparameters(k,j) = modelparameters(k,j) - Vmax(k); endif modelparameterchanges(k,j) > Vmax(k), modelparameters(k,j) = modelparameters(k,j) + Vmax(k); endif modelparameterchanges(k,j) > -Vmax(k) & modelparameterchanges(k,j) < Vmax(k), modelparameters(k,j) = modelparameters(k,j) + modelparameterchanges(k,j); end if modelparameters(k,j) < Pmin(k), modelparameters(k,j) = Pmin(k); endif modelparameters(k,j) > Pmax(k), modelparameters(k,j) = Pmax(k); endendendiendbp = bestparameters; index = linspace(1,iter,iter);figure; semilogy(globalbestcostfunction,'k');set(gca,'FontName','Arial','Fontsize',14); axis tight;xlabel('iteration'); ylabel('cost function');figure; q = plot(index,bp(1,,'k-',index,bp(2,,'k:');set(gca,'FontName','Arial','Fontsize',14); axis tight;legend(q,'x_1','x_2'); xlabel('iteration'); ylabel('parameter')。
c语言实现的粒子群算法代码及解释

//粒子群PSO算法#include<stdio.h>#include<math.h>#include<time.h>#include<stdlib.h>#define PI 3.141592653589 /* */#define P_num 200 //粒子数目#define dim 50#define low -100 //搜索域范围#define high 100#define iter_num 1000#define V_max 20 //速度范围#define c1 2#define c2 2#define w 0.5#define alp 1double particle[P_num][dim]; //个体集合double particle_loc_best[P_num][dim]; //每个个体局部最优向量double particle_loc_fit[P_num]; //个体的局部最优适应度,有局部最优向量计算而来double particle_glo_best[dim]; //全局最优向量double gfit; //全局最优适应度,有全局最优向量计算而来double particle_v[P_num][dim]; //记录每个个体的当前代速度向量double particle_fit[P_num]; //记录每个粒子的当前代适应度double Sphere(double a[]){int i;double sum=0.0;for(i=0; i<dim; i++){sum+=a[i]*a[i];}return sum;}double Rosenbrock(double a[]){int i;double sum=0.0;for(i=0;i<dim-1; i++){sum+= 100*(a[i+1]-a[i]*a[i])*(a[i+1]-a[i]*a[i])+(a[i]-1)*(a[i]-1);return sum;}double Rastrigin(double a[]){int i;double sum=0.0;for(i=0;i<dim;i++){sum+=a[i]*a[i]-10.0*cos(2*PI*a[i])+10.0;}return sum;}double fitness(double a[]) //适应度函数{return Rastrigin(a);}void initial(){int i,j;for(i=0; i<P_num; i++) //随即生成粒子{for(j=0; j<dim; j++){particle[i][j] = low+(high-low)*1.0*rand()/RAND_MAX; //初始化群体particle_loc_best[i][j] = particle[i][j]; //将当前最优结果写入局部最优集合particle_v[i][j] = -V_max+2*V_max*1.0*rand()/RAND_MAX; //速度}}for(i=0; i<P_num; i++) //计算每个粒子的适应度{particle_fit[i] = fitness(particle[i]);particle_loc_fit[i] = particle_fit[i];}gfit = particle_loc_fit[0]; //找出全局最优j=0;for(i=1; i<P_num; i++){if(particle_loc_fit[i]<gfit){gfit = particle_loc_fit[i];j = i;}for(i=0; i<dim; i++) //更新全局最优向量{particle_glo_best[i] = particle_loc_best[j][i];}}void renew_particle(){int i,j;for(i=0; i<P_num; i++) //更新个体位置生成位置{for(j=0; j<dim; j++){particle[i][j] += alp*particle_v[i][j];if(particle[i][j] > high){parti cle[i][j] = high;}if(particle[i][j] < low){particle[i][j] = low;}}}}void renew_var(){int i, j;for(i=0; i<P_num; i++) //计算每个粒子的适应度{particle_fit[i] = fitness(particle[i]);if(particle_fit[i] < particle_loc_fit[i]) //更新个体局部最优值{particle_loc_fit[i] = particle_fit[i];for(j=0; j<dim; j++) // 更新局部最优向量{particle_loc_best[i][j] = particle[i][j];}}}for(i=0,j=-1; i<P_num; i++) //更新全局变量{if(particle_loc_fit[i]<gfit){gfit = particle_loc_fit[i];j = i;}}if(j != -1){for(i=0; i<dim; i++) //更新全局最优向量{particle_glo_best[i] = particle_loc_best[j][i];}}for(i=0; i<P_num; i++) //更新个体速度{for(j=0; j<dim; j++){particle_v[i][j]=w*particle_v[i][j]+c1*1.0*rand()/RAND_MAX*(particle_loc_best[i][j]-particle[i][j])+c2*1.0*rand()/RAND_MAX*(particle_glo_best[j]-particle[i][j]);if(particle_v[i][j] > V_max){particle_v[i][j] = V_max;}if(particle_v[i][j] < -V_max){particle_v[i][j] = -V_max;}}}}int main(){freopen("result.txt","a+",stdout);int i=0;srand((unsigned)time(NULL));initial();while(i < iter_num){renew_particle();renew_var();i++;}printf("粒子个数:%d\n",P_num);printf("维度为:%d\n",dim);printf("最优值为%.10lf\n", gfit);return 0; }。
粒子群算法(C语言版本)

粒子群算法(C语言版本)粒子群算法// PSO.cpp : Defines the entry point for the console application. //#include "stdafx.h"#include"stdio.h"#include"stdlib.h"#include"time.h"#include"math.h"#define rdint(i) (rand()%(int)(i))/*随机数的定义*/#define rdft() (double)((double)rdint(16384)/(16383.0))#define rnd(a,b) (rdint((int)(b)-(int)(a)+1)+(int)(a))#define POPSIZE 20#define DIMENSION1 2 /* 目标函数中所含变量x的个数*/ #define DIMENSION2 6 //约束条件的个数double W=1.0;double C1=1.8;double C2=1.8;double VMAX=3.0;double XMIN=2.0;double XMAX=4.0;double P[DIMENSION1];double PBEST;double H,K;double g[DIMENSION2];//约束条件的值struct indi{double number[DIMENSION1];double best[DIMENSION1];double bestfitness;double fitness;double speed[DIMENSION1];}individual[POPSIZE];void initiate(void);void calculation(int number);void globalbest(int number);void localbest(int number);void judge(int num);void judge(int num){/* 6个约束条件*/g[0]=4*individual[num].number[0]-individual[num].number[1];g[1]=individual[num].number[1]-10*individual[num].number[0];g[2]=-2*K*individual[num].number[1]+3*3.14*pow(individual[num].nu mber[0],3);g[3]=-50*K*individual[num].number[1]+75*3.14*pow(individual[num]. number[0],3); g[4]=-H+3.98*individual[num].number[1];g[5]=3*pow(individual[num].number[1],3)-2000*pow(individual[num].number[0],4); }void initiate(){int i,j;for(i=0;i<popsize;i++)< p="">{do{for(j=0;j<dimension1;j++)< p="">individual[i].number[j]=rdft()*(XMAX-XMIN)+XMIN;judge(i);}while(g[0]<=0 && g[1]<=0 && g[2]<=0 && g[3]<=0 && g[4]<=0 && g[5]<=0);}//如果不在可行域就对这个粒子重新进行初始化for(i=0;i<popsize;i++)< p="">for(j=0;j<dimension1;j++)< p="">individual[i].speed[j]=VMAX*rdft();for(i=0;i<popsize;i++)< p="">for(j=0;j<dimension1;j++)< p="">individual[i].best[j]=individual[i].number[j];for(i=0;i<popsize;i++)< p="">calculation(i);for(i=0;i<popsize;i++)< p="">individual[i].bestfitness=individual[i].fitness;globalbest(0);}void localbest(int number){int i;judge(number);//进行判断,如果不在可行域内就不对粒子的历史最优值进行更新 bool bTrue=g[0]<=0 && g[1]<=0 && g[2]<=0 && g[3]<=0 && g[4]<=0 && g[5]<=0; if(individual[number].bestfitness>individual[number].fitness&& bTrue){for(i=0;i<dimension1;i++)< p="">individual[number].best[i]=individual[number].number[i];individual[number].bestfitness=individual[number].fitness; }}void globalbest(int number){int i,j;double s=0;int flag=0;if(number==0){s=individual[0].fitness;flag=0;for(i=1;i<popsize;i++)< p="">if(individual[i].fitness<s)< p="">{s=individual[i].fitness;flag=i;}for(i=0;i<dimension1;i++)< p="">P[i]=individual[flag].number[i];PBEST=individual[flag].fitness;}else{for(i=0;i<popsize;i++)< p="">{if(individual[i].bestfitness<pbest)< p="">{for(j=0;j<dimension1;j++)< p="">P[j]=individual[i].best[j];PBEST=individual[i].bestfitness;}}}}void calculation(int num){K=(4*individual[num].number[1]-individual[num].number[0])/4*(individual[num].number[1] -individual[num].number[0])+0.615*individual[num].number[0]/individual[num].number [1];H=(2000*pow(individual[num].number[0],5)/pow(individual [num].number[1],3))+1.5*indivi dual[num].number[0] +75*3.14*pow(individual[num].number[0],3)/(4*K);//L=2000*3.14*pow(individual[num].number[0],4)/pow(indi vidual[num].number[1],2)+1.5* 3.14*individual[num].number[1];individual[num].fitness=0.25*3.14*pow(individual[num].nu mber[1],2)*H;}void main(void){int i,j,k,t,total=0;double sum=0;// srand(time(NULL));for(j=0;j<10;j++){initiate();for(i=0;i<5000;i++){W=1.0-i*0.6/4999;if((PBEST-67997.0)<0.1){total++;sum=sum+i;break;}else{for(k=0;k<popsize;k++)< p="">{for(t=0;t<dimension1;t++)< p="">{individual[k].speed[t]=W*individual[k].speed[t]+C1*rdft()*(i ndividual[k].best[t]-individual [k].number[t])+C2*rdft()*(P[t]-individual[k].number[t]);if(individual[k].speed[t]>VMAX)individual[k].speed[t]=VMAX;individual[k].number[t]=individual[k].number[t]+individual[ k].speed[t];if(individual[k].number[t]<xmin)< p="">individual[k].number[t]=2*XMIN-individual[k].number[t];if(individual[k].number[t]>XMAX)individual[k].number[t]=fmod(individual[k].number[t],(XMA X-XMIN))+XMIN;}calculation(k);localbest(k);}globalbest(1);}}// printf("%3d,%f/n",i,PBEST);}printf("T otal number is %d/n",total);printf("Sum is %f/n",sum);printf("Average is %f/n",sum/total); printf("%f/n",PBEST); getchar();}</xmin)<></dimension1;t++)<></popsize;k++)<></dimension1;j++)<></pbest)<></popsize;i++)<></dimension1;i++)<></s)<></popsize;i++)<></dimension1;i++)<></popsize;i++)<></popsize;i++)<></dimension1;j++)<></popsize;i++)<></dimension1;j++)<></popsize;i++)<></dimension1;j++)<></popsize;i++)<>。
粒子群算法原文及解释

粒子群算法原文及解释粒子群优化算法(Particle Swarm Optimization,PSO)是一种模拟鸟群、鱼群等动物社会行为的优化算法。
通过模拟鸟群、鱼群等动物群体中的个体行为,粒子群优化算法能够有效地求解各种优化问题。
本文将从算法原理、算法流程、参数设置、优化问题、实现方式、改进策略、应用领域和性能评价等方面对粒子群优化算法进行详细的介绍。
一、算法原理粒子群优化算法基于群体智能理论,通过模拟鸟群、鱼群等动物群体中的个体行为来寻找最优解。
每个个体被称为一个粒子,它通过跟踪其自身的最优位置和群体的最优位置来更新自己的速度和位置。
粒子的速度和位置更新公式如下:v[i][j] = w * v[i][j] + c1 * rand() * (pbest[i][j] - x[i][j]) + c2 * rand() * (gbest - x[i][j])x[i][j] = x[i][j] + v[i][j]其中,v[i][j]表示粒子i在第j维上的速度,x[i][j]表示粒子i 在第j维上的位置,pbest[i][j]表示粒子i的个体最优位置,gbest 表示全局最优位置,w表示惯性权重,c1和c2表示加速因子,rand()表示随机函数。
二、算法流程粒子群优化算法的基本流程如下:1. 初始化粒子群,随机生成粒子的初始位置和初始速度。
2. 计算每个粒子的适应度值,记录粒子的个体最优位置和全局最优位置。
3. 根据粒子的适应度值更新粒子的速度和位置。
4. 重复步骤2和步骤3,直到满足终止条件(如达到预设的最大迭代次数或全局最优解的变化小于预设阈值)。
三、参数设置粒子群优化算法的参数包括惯性权重w、加速因子c1和c2等。
这些参数对算法的性能和收敛速度有着重要的影响,需要根据具体问题进行调整和优化。
通常需要通过实验来找到合适的参数设置。
四、优化问题粒子群优化算法适用于求解连续的、离散的优化问题。
对于不同的优化问题,需要根据问题的特性和要求来设计合适的粒子和适应度函数。
并行粒子算法代码

并行粒子算法代码对于求解各种物理问题的计算机模拟,粒子算法是一种重要的数值方法。
随着科学计算的不断发展,越来越多的研究者开始尝试使用并行计算来加速粒子算法的计算速度。
并行粒子算法是一种将计算任务分解成多个子任务,并在多个处理器上同时执行的算法。
它可以显著提高计算效率,尤其是对于大规模粒子系统的计算。
下面是一个简单的并行粒子算法代码示例:```c++#include <stdio.h>#include <stdlib.h>#include <math.h>#include <omp.h>#define N 1000#define M 10000struct Particle {double x, y, z;double vx, vy, vz;double ax, ay, az;};void compute_forces(struct Particle *particles) {int i, j;double dx, dy, dz, r;double fx, fy, fz;#pragma omp parallel for private(i,j,dx,dy,dz,r,fx,fy,fz) for (i = 0; i < N; i++) {fx = fy = fz = 0.0;for (j = 0; j < N; j++) {if (i == j) continue; // skip self-interactiondx = particles[j].x - particles[i].x;dy = particles[j].y - particles[i].y;dz = particles[j].z - particles[i].z;r = sqrt(dx*dx + dy*dy + dz*dz);fx += dx / (r*r*r);fy += dy / (r*r*r);fz += dz / (r*r*r);}particles[i].ax = fx;particles[i].ay = fy;particles[i].az = fz;}}void update_particles(struct Particle *particles) {int i;#pragma omp parallel for private(i)for (i = 0; i < N; i++) {particles[i].vx += particles[i].ax * dt; particles[i].vy += particles[i].ay * dt; particles[i].vz += particles[i].az * dt; particles[i].x += particles[i].vx * dt; particles[i].y += particles[i].vy * dt; particles[i].z += particles[i].vz * dt; }}int main(int argc, char **argv) {int i, j, t;double dt = 0.01;struct Particle particles[N];for (i = 0; i < N; i++) {particles[i].x = drand48() * L;particles[i].y = drand48() * L;particles[i].z = drand48() * L;particles[i].vx = 0.0;particles[i].vy = 0.0;particles[i].vz = 0.0;}for (t = 0; t < M; t++) {compute_forces(particles);update_particles(particles);}return 0;}```这个代码使用了OpenMP来实现并行化,其中包括两个函数:compute_forces和update_particles。
粒子群算法(C++版)

//#pragma warning (disable: 4786)//#pragma comment (linker, "/STACK:16777216") //HEAD#include <cstdio>#include <ctime>#include <cstdlib>#include <cstring>#include <queue>#include <string>#include <set>#include <stack>#include <map>#include <cmath>#include <vector>#include <iostream>#include <algorithm>#include <time.h>#include <cstdlib>using namespace std;typedef long long LL;const double MAX_VAL = (double)1e18;const int MAX_GEN = 30;///最大迭代次数const int MAX_SCALE = 3000;///最大种群规模const int MAX_CITY = 20 + 2;///最大城市数const double W_VAL = 0.729;///struct SO{int x, y;SO(){}SO(int x, int y): x(x), y(y){}};struct Point{double x, y;Point(){}Point(int x, int y):x(x), y(y){};void read(){scanf("%lf%lf", &x, &y);}};inline int randomI(int x){ return rand()%x; }inline double randomD(){ return (double)rand()/RAND_MAX; } inline double getDist(Point a, Point b){return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));}struct PSO{double w;int scale;int cityNum;int nowGen;///当前代数int maxGen;///迭代次数int bestNum;int bestGen;///最佳出现代数double dist[MAX_CITY][MAX_CITY];int oPop[MAX_SCALE][MAX_CITY];///粒子群double fitness[MAX_SCALE];///种群适应度,表示种群中各个个体的适应度vector<SO> listV[MAX_SCALE];/// 每科粒子的初始交换序列int Pd[MAX_SCALE][MAX_CITY];///一颗粒子历代中出现最好的解,double vPd[MAX_SCALE];///解的评价值int Pgd[MAX_CITY];/// 整个粒子群经历过的的最好的解,每个粒子都能记住自己搜索到的最好解double vPgd;/// 最好的解的评价值PSO(){}PSO(int s, int c, int mG, double ww, double d[MAX_CITY][MAX_CITY]){scale = s;cityNum = c;maxGen = mG;w = ww;for (int i = 0; i < cityNum; i++)for (int j = 0; j < cityNum; j++)dist[i][j] = d[i][j];}void copyArray(double a[], double b[], int n) {for (int i = 0; i < n; i++) a[i] = b[i];}void copyArray(int a[], int b[], int n){for (int i = 0; i < n; i++) a[i] = b[i];}void init(){nowGen = 0;for (int i = 0; i < scale; i++){for (int j = 0; j < cityNum; ){int x = randomI(cityNum);int r;for (r = 0; r < j; r++){if (x == oPop[i][r]) break;}if (r == j){oPop[i][j] = x;// cout << oPop[i][j] << ' ';j++;}}// cout << endl;}for (int i = 0; i < scale; i++){// cout << i << " :" << endl;int vn = randomI(cityNum) + 1;for (int j = 0; j < vn; j++){int x = randomI(cityNum);int y = randomI(cityNum);while (x == y) y = randomI(cityNum); SO so(x, y);listV[i].push_back(so);// cout << so.x << "*" << so.y << ' '; }// cout <<endl;}getFitness();for (int i = 0; i < scale; i++){vPd[i] = fitness[i];copyArray(Pd[i], oPop[i], cityNum);}bestNum = 0;vPgd = fitness[0];bestGen = 0;for (int i = 0; i < scale; i++) if (vPgd > fitness[i]) {vPgd = fitness[i];bestNum = i;}copyArray(Pgd, oPop[bestNum], cityNum);}double getVal(int x){double ret = 0;for (int i = 0; i < cityNum; i++){int xx = oPop[x][i % cityNum];int yy = oPop[x][(i + 1) % cityNum];ret += dist[xx][yy];}return ret;}void getFitness(){for (int i = 0; i < scale; i++)fitness[i] = getVal(i);}void UpdateVal(){int j = 0;double vj = fitness[0];for (int i = 0; i < scale; i++){if (vPd[i] > fitness[i]){vPd[i] = fitness[i];copyArray(Pd[i], oPop[i], cityNum);///??? }if (vj > fitness[i]){vj = fitness[i];j = i;}}if (vj < vPgd){bestGen = nowGen;///bestNum = j;///vPgd = vj;copyArray(Pgd, oPop[j], cityNum);}}void changeTo(int a[], vector<SO> v)///{int vn = v.size();for (int i = 0; i < vn; i++){int x = v[i].x, y = v[i].y;swap(a[x], a[y]);}}vector<SO> minus(int a[], int b[])///{int c[MAX_CITY], d[MAX_CITY];for (int i = 0; i < cityNum; i++) d[i] = b[i];for (int i = 0; i < cityNum; i++) c[a[i]] = i; vector<SO> v;SO s;for (int i = 0; i < cityNum; i++){{s.x = i, s.y = c[a[i]];swap(d[s.x], d[s.y]);v.push_back(s);}}return v;}void addTo(vector<SO> &v, vector<SO> a, int vn){for (int i = 0; i < vn; i++)v.push_back(a[i]);}/// Vii=wVi+ra(Pid-Xid)+rb(Pgd-Xid)void evolution(){for (int ig = 0; ig < maxGen; ig++){nowGen = ig + 1;///nowGenfor (int is = 0; is < scale; is++){if (is == bestNum) continue;vector<SO> v;int lvn = w * listV[is].size();addTo(v, listV[is], lvn);vector<SO> a = minus(Pd[is], oPop[is]); int an = randomD() * a.size();addTo(v, a, an);vector<SO> b = minus(Pgd, oPop[is]); int bn = randomD() * b.size();addTo(v, b, bn);listV[is] = v;changeTo(oPop[is], listV[is]);// cout << listV[is].size() << endl;}getFitness();UpdateVal();}}void solve(){init();evolution();printf("answer %lf:\n", vPgd);printf("solution \n");for (int i = 0; i < cityNum; i++){if (i) printf(" ");printf("%d\n", Pgd[i]);}cout << bestGen << ' ' << bestNum << endl; puts("");}};int cn;vector<Point> pv;double d[MAX_CITY][MAX_CITY];void pre(vector<Point> pv){int cn = pv.size();for (int i = 0; i < cn; i++)for (int j = i + 1; j < cn; j++){d[i][j] = d[j][i] = getDist(pv[i], pv[j]);}}int main ()srand((unsigned long)time(0)); ///设置时间种子while (cin >> cn){pv.clear();for (int i = 0; i < cn; i++){Point p;p.read();pv.push_back(p);}pre(pv);PSO solver(MAX_SCALE, cn, MAX_GEN, W_VAL, d);cout << "***************************************************" << endl; solver.solve();cout << "***************************************************" << endl; }return 0;}// cout << nowGen << " ------------------------:" << endl;// for (int i = 0; i < scale; i++)// {// cout << vPd[i] << ' ' << fitness[i] << endl;// for (int j = 0; j < cityNum; j++)// cout << Pd[i][j] << ' ';// cout << endl;// }//// for (int i = 0; i < scale; i++)// {// for (int j = 0; j < listV[i].size(); j++)// cout << listV[i][j].x << "*" << listV[i][j].y << ' ';// cout << endl;// }//// cout << vPgd << ' ' << bestGen << ' ' << bestNum << ' ' << nowGen << endl; // for (int i = 0; i < cityNum; i++) cout << Pgd[i] << ' ';// cout << endl;// cout << " ------------------------------------" << endl << endl;/**150 01 02 00 21 110 43 86 78 210 1012 13-10 12 51 10012 12*/(此文档部分内容来源于网络,如有侵权请告知删除,文档可自行编辑修改内容,供参考,感谢您的配合和支持)。
粒子群算法代码实现

粒子群算法代码实现以下是粒子群算法的Python 代码实现,该算法用于解决一个优化问题。
假设我们要最小化函数f(x),其中x 是一个向量。
import random# 优化问题的目标函数def f(x):return x[0]2 + x[1]2# 粒子群算法的实现class ParticleSwarmOptimization:def __init__(self, num_particles, num_dimensions):self.num_particles = num_particlesself.num_dimensions = num_dimensionsself.max_velocity = 2self.inertia_weight = 0.9self.cognitive_weight = 1.5self.social_weight = 1.5self.iterations = 100self.best_position = Noneself.best_fitness = float('inf')self.particles = []for i in range(num_particles):position = [random.uniform(-10, 10) for d inrange(num_dimensions)]velocity = [random.uniform(-self.max_velocity,self.max_velocity) for d in range(num_dimensions)]particle = {'position': position, 'velocity': velocity,'personal_best_position': position, 'personal_best_fitness': float('inf')} self.particles.append(particle)def optimize(self):for iter in range(self.iterations):for particle in self.particles:fitness = f(particle['position'])if fitness < particle['personal_best_fitness']:particle['personal_best_position'] =particle['position']particle['personal_best_fitness'] = fitnessif fitness < self.best_fitness:self.best_position = particle['position']self.best_fitness = fitnessfor particle in self.particles:for d in range(self.num_dimensions):r1 = random.uniform(0, 1)r2 = random.uniform(0, 1)velocity_component_cognitive =self.cognitive_weight * r1 * (particle['personal_best_position'][d] - particle['position'][d])velocity_component_social = self.social_weight * r2 * (self.best_position[d] - particle['position'][d])velocity_component_inertia = self.inertia_weight * particle['velocity'][d]velocity = velocity_component_inertia +velocity_component_cognitive + velocity_component_socialif velocity > self.max_velocity:velocity = self.max_velocityif velocity < -self.max_velocity:velocity = -self.max_velocityparticle['velocity'][d] = velocityfor d in range(self.num_dimensions):particle['position'][d] += particle['velocity'][d]# 测试代码pso = ParticleSwarmOptimization(num_particles=10,num_dimensions=2)pso.optimize()print('Best position:', pso.best_position)print('Best fitness:', pso.best_fitness)以上代码使用了一个简单的函数f(x) = x[0]^2 + x[1]^2 作为目标函数。
c++代码封装粒子群算法

#include <iostream>#include <vector>#include <cmath>#include <random>// 粒子类class Particle {public:std::vector<double> position; // 粒子当前位置std::vector<double> velocity; // 粒子当前速度double fitness; // 适应度std::vector<double> pBestPosition; // 粒子历史最佳位置double pBestFitness; // 粒子历史最佳适应度Particle(int dim) {position.resize(dim);velocity.resize(dim);pBestPosition.resize(dim);fitness = 0.0;pBestFitness = 0.0;}};// 粒子群类class ParticleSwarmOptimization {public:int numParticles; // 粒子数量int maxIterations; // 最大迭代次数double inertiaWeight; // 惯性权重double cognitiveWeight; // 认知权重double socialWeight; // 社会权重std::vector<double> globalBestPosition; // 全局最佳位置double globalBestFitness; // 全局最佳适应度std::vector<Particle> particles; // 粒子群ParticleSwarmOptimization(int numParticles, int maxIterations, double inertiaWeight, double cognitiveWeight, double socialWeight, int dim) { this->numParticles = numParticles;this->maxIterations = maxIterations;this->inertiaWeight = inertiaWeight;this->cognitiveWeight = cognitiveWeight;this->socialWeight = socialWeight;globalBestPosition.resize(dim);globalBestFitness = 0.0;particles.resize(numParticles, Particle(dim));}// 初始化粒子群void initialize() {// TODO: 初始化粒子位置和速度}// 更新粒子位置和速度void update() {// TODO: 更新粒子位置和速度}// 计算适应度double calculateFitness(const std::vector<double>& position) {// TODO: 根据具体问题计算适应度return 0.0;}// 运行粒子群算法void run() {initialize();for (int iter = 0; iter < maxIterations; iter++) {for (int i = 0; i < numParticles; i++) {particles[i].fitness = calculateFitness(particles[i].position);if (particles[i].fitness > particles[i].pBestFitness) {particles[i].pBestFitness = particles[i].fitness;particles[i].pBestPosition = particles[i].position;}if (particles[i].fitness > globalBestFitness) {globalBestFitness = particles[i].fitness;globalBestPosition = particles[i].position;}}update();}}};int main() {// 初始化粒子群算法参数int numParticles = 20;int maxIterations = 100;double inertiaWeight = 0.5;double cognitiveWeight = 2.0;double socialWeight = 2.0;int dim = 2;// 创建粒子群算法对象ParticleSwarmOptimization pso(numParticles, maxIterations, inertiaWeight, cognitiveWeight, socialWeight, dim);// 运行粒子群算法pso.run();return 0;}。
粒子群算法详解-附matlab代码说明
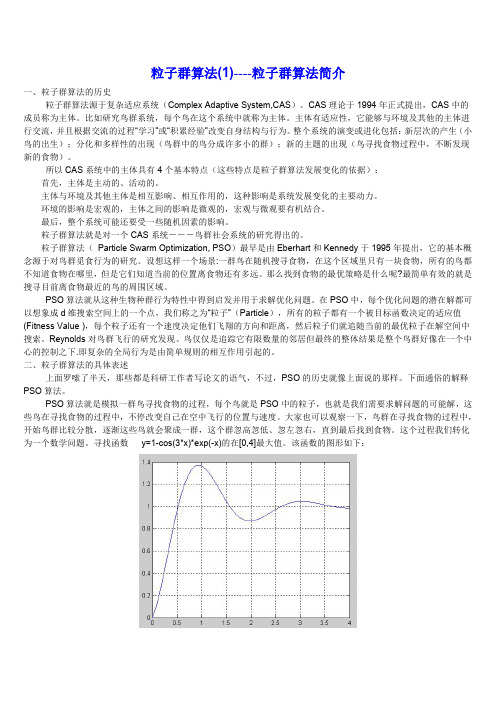
位置更新公式
该算法在文献中讨论了系数 n 取各种不同情况的情况,并且运行来了 20000 次来分析各种系数的结果。
(2)粒子群算法的混合
这个分支主要是将粒子群算法与各种算法相混合,有人将它与模拟退火算法相混合,有些人将它与单纯形方法相
混合。但是最多的是将它与遗传算法的混合。根据遗传算法的三种不同算子可以生成 3 中不同的混合算法。
这两个点就是粒子群算法中的粒子。 该函数的最大值就是鸟群中的食物 计算两个点函数值就是粒子群算法中的适应值,计算用的函数就是粒子群算法中的适应度函数。 更新自己位置的一定公式就是粒子群算法中的位置速度更新公式。 下面演示一下这个算法运行一次的大概过程: 第一次初始化
第一次更新位置
第二次更新位置
第 21 次更新 最后的结果(30 次迭代) 最后所有的点都集中在最大值的地方。
粒子群算法与选择算子的结合,这里相混合的思想是:在原来的粒子群算法中,我们选择粒子群群体的最优值
作为 pg,但是相结合的版本是根据所有粒子的适应度的大小给每个粒子赋予一个被选中的概率,然后依据概率对这些 粒子进行选择,被选中的粒子作为 pg,其它的情况都不变。这样的算法可以在算法运行过程中保持粒子群的多样性, 但是致命的缺点是收敛速度缓慢。
上面罗嗦了半天,那些都是科研工作者写论文的语气,不过,PSO 的历史就像上面说的那样。下面通俗的解释 PSO 算法。
PSO 算法就是模拟一群鸟寻找食物的过程,每个鸟就是 PSO 中的粒子,也就是我们需要求解问题的可能解,这 些鸟在寻找食物的过程中,不停改变自己在空中飞行的位置与速度。大家也可以观察一下,鸟群在寻找食物的过程中, 开始鸟群比较分散,逐渐这些鸟就会聚成一群,这个群忽高忽低、忽左忽右,直到最后找到食物。这个过程我们转化 为一个数学问题。寻找函数 y=1-cos(3*x)*exp(-x)的在[0,4]最大值。该函数的图形如下:
粒子群代码详解

粒子群代码详解粒子群算法是一种常用的优化算法,其核心思想是通过模拟粒子在搜索空间中的运动来寻找最优解。
本篇文章将详细介绍粒子群算法的代码实现细节。
1. 初始化种群首先需要初始化粒子群的状态,也就是将粒子的位置和速度随机初始化。
这可以通过随机数生成器来实现。
同时,需要记录下每个粒子的最佳位置和最佳适应度值。
2. 计算适应度值对于每个粒子,需要计算其当前位置的适应度值。
这通常是通过将位置带入目标函数来计算得到。
如果目标函数的值越小,说明该粒子的位置越优秀。
3. 更新最佳位置对于每个粒子,需要根据当前位置和历史最佳位置来更新自己的最佳位置。
如果当前位置的适应度值比历史最佳位置还要好,那么当前位置就成为该粒子的最佳位置。
4. 更新全局最佳位置对于整个种群,需要记录下当前所有粒子的最佳位置中的最优解,也就是全局最佳位置。
这可以通过迭代所有粒子来实现。
5. 更新速度和位置对于每个粒子,需要根据当前速度和全局最佳位置来更新自己的速度和位置。
这可以通过以下公式来实现:v(t+1) = w * v(t) + c1 * rand() * (pbest - x(t)) + c2 * rand() * (gbest - x(t))x(t+1) = x(t) + v(t+1)其中,v(t)为当前速度,x(t)为当前位置,pbest为该粒子历史最佳位置,gbest为全局最佳位置,w、c1和c2为调节参数,rand()为在[0,1]之间随机生成的数。
6. 判断停止条件可以通过设置最大迭代次数或者最小误差等方式来判断粒子群算法是否应该停止。
通过上述步骤,就可以实现粒子群算法的代码。
当然,不同的问题可能需要针对性地调整参数、适应度函数等细节。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
int i;
double sum=0.0;
for(i=0;i<dim-1; i++)
{
sum+= 100*(a[i+1]-a[i]*a[i])*(a[i+1]-a[i]*a[i])+(a[i]-1)*(a[i]-1);
}
return sum;
}
double Rastrigin(double a[])
{
for(i=0; i<dim; i++) //更新全局最优向量
{
particle_glo_best[i] = particle_loc_best[j][i];
}
}
for(i=0; i<P_num; i++) //更新个体速度
{
for(j=0; j<dim; j++)
{
particle_v[i][j]=w*particle_v[i][j]+
{
particle_v[i][j] = V_max;
}
if(particle_v[i][j] < -V_max)
{
particle_v[i][j] = -V_max;
}
}
}
}
int main()
{
freopen("result.txt","a+",stdout);
int i=0;
srand((unsigned)time(NULL));
initial();
while(i < iter_num)
{
renew_particle();
renew_var();
i++;
}
printf("粒子个数:%d\n",P_num);
printf("维度为:%d\n",dim);
printf("最优值为%.10lf\n", gfit);
return 0;
void initial()
{
int i,j;
for(i=0; i<P_num; i++) //随即生成粒子
{
for(j=0; j<dim; j++)
{
particle[i][j] = low+(high-low)*1.0*rand()/RAND_MAX; //初始化群体
particle_loc_best[i][j] = particle[i][j]; //将当前最优结果写入局部最优集合
#define high 100
#define iter_num 1000
#define V_max 20 //速度范围
#define c1 2
#define c2 2
#define w 0.5
#define alp 1
double particle[P_num][dim]; //个体集合
double particle_loc_best[P_num][dim]; //每个个体局部最优向量
{
particle_fit[i] = fitness(particle[i]);
if(particle_fit[i] < particle_loc_fit[i]) //更新个体局部最优值
{
particle_loc_fit[i] = particle_fit[i];
for(j=0; j<dim; j++) //更新局部最优向量
if(particle[i][j] > high)
{
parti cle[i][j] = high;
}
if(particle[i][j] < low)
{
particle[i][j] = low;
}
}
}
}
void renew_var()
{
int i, j;
for(i=0; i<P_num; i++) //计算每个粒子的适应度
particle_v[i][j] = -V_max+2*V_max*1.0*rand()/RAND_MAX; //速度
}
}
for(i=0; i<P_num; i++) //计算每个粒子的适应度
{
particle_fit[i] = fitness(particle[i]);
particle_loc_fitble particle_loc_fit[P_num]; //个体的局部最优适应度,有局部最优向量计算而来
double particle_glo_best[dim]; //全局最优向量
double gfit; //全局最优适应度,有全局最优向量计算而来
double particle_v[P_num][dim]; //记录每个个体的当前代速度向量
c1*1.0*rand()/RAND_MAX*(particle_loc_best[i][j]-particle[i][j])+
c2*1.0*rand()/RAND_MAX*(particle_glo_best[j]-particle[i][j]);
if(particle_v[i][j] > V_max)
double particle_fit[P_num]; //记录每个粒子的当前代适应度
double Sphere(double a[])
{
int i;
double sum=0.0;
for(i=0; i<dim; i++)
{
sum+=a[i]*a[i];
}
return sum;
}
double Rosenbrock(double a[])
{
particle_glo_best[i] = particle_loc_best[j][i];
}
}
void renew_particle()
{
int i,j;
for(i=0; i<P_num; i++) //更新个体位置生成位置
{
for(j=0; j<dim; j++)
{
particle[i][j] += alp*particle_v[i][j];
}
gfit = particle_loc_fit[0]; //找出全局最优
j=0;
for(i=1; i<P_num; i++)
{
if(particle_loc_fit[i]<gfit)
{
gfit = particle_loc_fit[i];
j = i;
}
}
for(i=0; i<dim; i++) //更新全局最优向量
//粒子群PSO算法
#include<stdio.h>
#include<math.h>
#include<time.h>
#include<stdlib.h>
#definePI 3.141592653589/* */
#define P_num 200 //粒子数目
#define dim 50
#define low -100 //搜索域范围
}
{
int i;
double sum=0.0;
for(i=0;i<dim;i++)
{
sum+=a[i]*a[i]-10.0*cos(2*PI*a[i])+10.0;
}
return sum;
}
double fitness(double a[]) //适应度函数
{
return Rastrigin(a);
}
{
particle_loc_best[i][j] = particle[i][j];
}
}
}
for(i=0,j=-1; i<P_num; i++) //更新全局变量
{
if(particle_loc_fit[i]<gfit)
{
gfit = particle_loc_fit[i];
j = i;
}
}
if(j != -1)
