最基本的粒子群优化算法程序,用Matlab实现

合集下载

matlab 粒子群优化算法

粒子群优化算法（Particle Swarm Optimization，PSO）是一种基于群体智能的优化
算法，它模拟了鸟群或鱼群等生物群体的行为，通过个体之间的协作和信息共享来寻找问题的最优解。

在 MATLAB 中，可以使用 PSO 工具箱来实现粒子群优化算法。

以下是在 MATLAB 中使用 PSO 工具箱实现粒子群优化算法的基本步骤：
步骤1: 定义优化问题
首先，需要定义要优化的目标函数。

目标函数是希望最小化或最大化的目标。

例如，如果希望最小化一个简单的函数，可以这样定义：
步骤2: 设置 PSO 参数
然后，需要设置 PSO 算法的参数，如种群大小、迭代次数、惯性权重等。

这些参
数的选择可能会影响算法的性能，需要根据具体问题进行调整。

步骤3: 运行 PSO 算法
使用particleswarm函数运行 PSO 算法，将目标函数和参数传递给它。

这里@myObjective表示使用myObjective函数作为目标函数，1是变量的维度，[]表
示没有约束条件。

示例：
考虑一个简单的最小化问题，目标函数为 Rosenbrock 函数：
设置 PSO 参数：
运行 PSO 算法：
在这个示例中，rosenbrock函数是一个二维的 Rosenbrock 函数，PSO 算法将寻找使得该函数最小化的变量值。

请注意，实际应用中，需要根据具体问题调整目标函数、约束条件和 PSO 参数。

MATLAB 的文档和示例代码提供了更多关于 PSO 工具箱的详细信息。

粒子群_Matlab程序代码

粒子群优化算法(panicle swarm optimization ，PSO)是kennedy 和Eberhart 在研究鸟类和鱼类的群体行为基础上于1995年提出的一种群智能算法，其思想米源予人工生命和演化计算理论，模仿鸟群飞行觅食行为，通过鸟集体协作使群体达到最优。

1.粒子群算法的原理PSO 中，每个优化问题的解看作搜索空间中的一只鸟(即粒子)，所有的粒子都有一个被优化的函数决定的适应值，并且有一个速度决定它们飞翔的方向和速率，粒子们追随当前的最优粒子在解空间中搜索。

算法首先初始化一群随机粒子，然后通过迭代找到最优解。

在每一次迭代中，粒子通过跟踪两个“极值”即个体极值和全局极值来更新自己的速度与位置。

在D 维目标搜索空间中，由种群数为m 的粒子组成粒子群，其中第f 个粒子在第d 维的位置为Xid ，其飞行速度为Vid ，该粒子当前搜索到的最优位置为Pid(goodvalue)和整个粒子群当前的最优位置Pgd(bestvalue)。

每维的速度与位置更新公式如下112(1)()(1)()(1)id id id id id id v v c rand p x c rand g x ω+=⨯+⨯⨯-+⨯⨯-L 11(2)id id id x x v ++=+LW 为惯性权重，C1和C2为学习因子，rand （）——[0,1]范围内变化的随机数。

2.参数介绍与设置（1）ww 是保持粒子运动惯性的参数，能使种群扩展搜索空间，获得较好的求解效果。

较大的w 有利于群体在更大的范围内进行搜索。

而较小的w 能够保证群体收敛到最优位置，所以w 的选择及在迭代中的变化对搜索能力和跳出局优能力具有重要影响。

一般将w 设定为0.8左右。

（1）加速因子c1和c2c1和c2用于调整粒子自身经验和社会经验在其运动中的作用，表示将每个粒子拉向pbest 和gbest 位置的随机加速项的权重，低的值允许粒子在被拉回前可以在目标区域外徘徊, 而高的值则导致粒子突然冲向或越过目标区域。

(完整word版)基本粒子群算法的原理和matlab程序.doc

基本粒子群算法的原理和matlab 程序作者—— niewei120 （nuaa）一、粒子群算法的基本原理粒子群优化算法源自对鸟群捕食行为的研究，最初由Kennedy 和 Eberhart 提出，是一种通用的启发式搜索技术。

一群鸟在区域中随机搜索食物，所有鸟知道自己当前位置离食物多远，那么搜索的最简单有效的策略就是搜寻目前离食物最近的鸟的周围区域。

PSO 算法利用这种模型得到启示并应用于解决优化问题。

PSO 算法中，每个优化问题的解都是粒子在搜索空间中的位置，所有的粒子都有一个被优化的目标函数所决定的适应值，粒子还有一个速度值决定它们飞翔的方向和距离，然后粒子群就追随当前的最优粒子在解空间中搜索。

PSO 算法首先在给定的解空间中随机初始化粒子群，待优化问题的变量数决定了解空间的维数。

每个粒子有了初始位置与初始速度。

然后通过迭代寻优。

在每一次迭代中，每个粒子通过跟踪两个“极值”来更新自己在解空间中的空间位置与飞翔速度。

第一个极值就是单个粒子本身在迭代过程中找到的最优解粒子，这个粒子叫做个体极值。

另一个极值是种群所有粒子在迭代过程中所找到的最优解粒子，这个粒子是全局极值。

上述的方法叫全局粒子群算法。

如果不用种群所有粒子而只用其中一部分作为该粒子的邻居粒子，那么在所有邻居粒子中的极值就是局部极值，该方法称为局部PSO 算法。

速度、位置的更新方程表示为：每个粒子自身搜索到的历史最优值p i，p i=(p i1 ,p i2 ,....,p iQ )， i=1,2,3,....,n 。

所有粒子搜索到的最优值p g， p g=(p g1 ,p g2,....,p gQ )，注意这里的p g只有一个。

是保持原来速度的系数，所以叫做惯性权重。

是粒子跟踪自己历史最优值的权重系数，它表示粒子自身的认识，所以叫“认知”。

通常设置为 2 。

是粒子跟踪群体最优值的权重系数，它表示粒子对整个群体知识的认识，所以叫做“社会知识”，经常叫做“社会”。

基本粒子群算法MATLAB编程

for i=1:N
v(i,:)=w*v(i,:)+c1*rand*(p(i,:)-x(i,:))+c2*rand*(pg-x(i,:));
x(i,:)=x(i,:)+v(i,:);
if fitness(x(i,:),D)<fitness(p(i,:),D)
p(i,:)=x(i,:);
end
if fitness(p(i,:),D)<fitness(pg,D)
pg=p(i,:);
end
end பைடு நூலகம்
Pbest(t)=fitness(pg,D);
end
%最后给出计算结果
disp('*************************************')
disp('函数的全局最优位置为：')
Solution=pg'
disp('最后得到的优化极值为：')
Result=Pbest(t)
disp('*************************************')
clear all;
%clc;
format long;
%给定初始条件
c1=1.4962;%学习因子1
c2=1.4962;%学习因子2
w=0.7298; %惯性权重
MaxDT=1000;%最大迭代数
D=10;%搜索空间维数
N=40;%初始化群体个体数目
%初始化种群的个体（可以在这里限定位置和速度的范围）
pg=x(1,:);%Pg为全局最优
for i=2:N

粒子群算法matlab程序

粒子群算法matlab程序粒子群算法（PSO）是一种基于群体智能的求解优化问题的算法。

其通过模拟鸟群等大规模群体行为，实现全局搜索和基于群体协作的局部搜索。

在PSO中，通过一组粒子（每个粒子代表一个解）来搜索问题的解空间，在搜索过程中，粒子的位置表示该解在解空间中的位置，速度表示该解在该方向（即属性）上的变化速率，最终达到全局最优解或局部最优解。

PSO算法有着简单易懂、实现简便、计算速度快以及易于与其他算法结合等优点。

下面我将介绍一下如何使用matlab编写简单的粒子群算法程序。

程序主要分为以下步骤：1.初始化在程序开始之前需要对粒子进行初始化操作，其中需要确定粒子群的大小、每个粒子的位置、速度等初始参数。

2.计算适应值计算每个粒子的适应值，即根据当前位置计算该解的适应值。

适应值可以根据实际问题进行定义，如最小化目标函数或最大化收益等。

3.更新粒子速度和位置这一步是PSO算法的核心步骤，通过改变粒子的速度和位置来找到更优的解。

其核心公式为：v(t+1) = w * v(t) + c1 * rand() * (pbest - x(t)) + c2 * rand() * (gbest - x(t)) x(t+1) = x(t) + v(t+1)其中w是惯性权重，c1、c2是学习因子，pbest是该粒子的历史最优解，gbest 是当前全局最优解。

4.更新pbest和gbest在每次更新位置之后需要更新每个粒子自己的历史最优解以及全局最优解。

5.停止条件判断设定停止条件，如最小适应值误差、迭代次数、最大迭代次数等，如果达到了停止条件，则程序结束，输出全局最优解。

下面是一份简单的PSO算法的matlab代码：function [best_fit, best_x] = pso(func, dim, lb, ub, max_iter, swarm_size, w, c1, c2)%初始化粒子v = zeros(swarm_size, dim);x = repmat(lb, swarm_size, 1) + repmat(ub - lb, swarm_size, 1) .* rand(swarm_size, dim);pbest = x;[best_fit, best_idx] = min(func(x));gbest = x(best_idx,:);%开始迭代for iter = 1 : max_iter%更新速度和位置v = w * v + c1 * rand(swarm_size, dim) .* (pbest - x) + c2 * rand(swarm_size, dim) .* repmat(gbest, swarm_size, 1) - x;x = x + v;%边界处理x = max(x, repmat(lb, swarm_size, 1));x = min(x, repmat(ub, swarm_size, 1));%更新pbest和gbestidx = func(x) < func(pbest);pbest(idx,:) = x(idx,:);[min_fit, min_idx] = min(func(pbest));if min_fit < best_fitbest_fit = min_fit;best_x = pbest(min_idx,:);endendend在使用上述代码时，需要定义适应值函数（func）、解空间维度（dim）、每个维度的上界（ub）与下界（lb）、最大迭代次数（max_iter）、粒子群大小（swarm_size）、惯性权重（w）、学习因子（c1、c2）等参数。

粒子群优化算法介绍及matlab程序

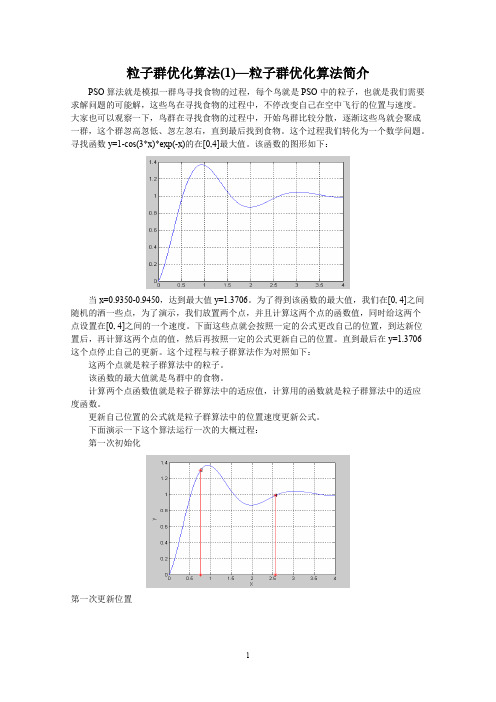
粒子群优化算法(1)—粒子群优化算法简介PSO算法就是模拟一群鸟寻找食物的过程，每个鸟就是PSO中的粒子，也就是我们需要求解问题的可能解，这些鸟在寻找食物的过程中，不停改变自己在空中飞行的位置与速度。

大家也可以观察一下，鸟群在寻找食物的过程中，开始鸟群比较分散，逐渐这些鸟就会聚成一群，这个群忽高忽低、忽左忽右，直到最后找到食物。

这个过程我们转化为一个数学问题。

寻找函数y=1-cos(3*x)*exp(-x)的在[0,4]最大值。

该函数的图形如下：当x=0.9350-0.9450，达到最大值y=1.3706。

为了得到该函数的最大值，我们在[0, 4]之间随机的洒一些点，为了演示，我们放置两个点，并且计算这两个点的函数值，同时给这两个点设置在[0, 4]之间的一个速度。

下面这些点就会按照一定的公式更改自己的位置，到达新位置后，再计算这两个点的值，然后再按照一定的公式更新自己的位置。

直到最后在y=1.3706这个点停止自己的更新。

这个过程与粒子群算法作为对照如下：这两个点就是粒子群算法中的粒子。

该函数的最大值就是鸟群中的食物。

计算两个点函数值就是粒子群算法中的适应值，计算用的函数就是粒子群算法中的适应度函数。

更新自己位置的公式就是粒子群算法中的位置速度更新公式。

下面演示一下这个算法运行一次的大概过程：第一次初始化第一次更新位置第二次更新位置第21次更新最后的结果（30次迭代）最后所有的点都集中在最大值的地方。

粒子群优化算法(2)—标准粒子群优化算法在上一节的叙述中，唯一没有给大家介绍的就是函数的这些随机的点（粒子）是如何运动的，只是说按照一定的公式更新。

这个公式就是粒子群算法中的位置速度更新公式。

下面就介绍这个公式是什么。

在上一节中我们求取函数y=1-cos(3*x)*exp(-x)的在[0, 4]最大值。

并在[0,4]之间放置了两个随机的点，这些点的坐标假设为x1=1.5，x2=2.5；这里的点是一个标量，但是我们经常遇到的问题可能是更一般的情况—x 为一个矢量的情况，比如二维z=2*x1+3*x22的情况。

(完整word版)用MATLAB编写PSO算法及实例

用MATLAB 编写PSO 算法及实例1.1 粒子群算法PSO 从这种模型中得到启示并用于解决优化问题。

PSO 中，每个优化问题的潜在解都是搜索空间中的一只鸟，称之为粒子。

所有的粒子都有一个由被优化的函数决定的适值( fitness value) ，每个粒子还有一个速度决定它们飞翔的方向和距离。

然后粒子们就追随当前的最优粒子在解空间中搜索。

PSO 初始化为一群随机粒子(随机解)，然后通过迭代找到最优解。

在每一次迭代中，粒子通过跟踪两个极值来更新自己；第一个就是粒子本身所找到的最优解，这个解称为个体极值；另一个极值是整个种群目前找到的最优解，这个极值是全局极值。

另外也可以不用整个种群而只是用其中一部分作为粒子的邻居，那么在所有邻居中的极值就是局部极值。

假设在一个维的目标搜索空间中，有个粒子组成一个群落，其中第个粒子表示为一个维的向量，。

第个粒子的“飞行 ”速度也是一个维的向量，记为，。

第个粒子迄今为止搜索到的最优位置称为个体极值，记为，。

整个粒子群迄今为止搜索到的最优位置为全局极值，记为在找到这两个最优值时，粒子根据如下的公式(1.1)和( 1.2)来更新自己的速度和位置：(1.1) (1. 2)其中：和为学习因子，也称加速常数(acceleration constant)，和为[0，1]范围内的均匀随机数。

式(1.1)右边由三部分组成，第一部分为“惯性(inertia)”或“动量(momentum)”部分，反映了粒子的运动“习惯(habit)”，代表粒子有维持自己D N i D ),,,(21iD i i i x x x X N i ,,2,1 i D ),,21i iD i i v v v V ，（ 3,2,1 i i ),,,(21iD i i best p p p p N i ,,2,1 ),,,(21gD g g best p p p g )(2211id gd id id id id x p r c x p r c v w v id id id v x x 1c 2c 1r 2r先前速度的趋势；第二部分为“认知(cognition)”部分，反映了粒子对自身历史经验的记忆(memory)或回忆(remembrance)，代表粒子有向自身历史最佳位置逼近的趋势；第三部分为“社会(social)”部分，反映了粒子间协同合作与知识共享的群体历史经验。

pso算法matlab程序

pso算法matlab程序PSO（粒子群优化）算法是一种启发式优化算法，用于解决各种优化问题。

在Matlab中实现PSO算法可以通过以下步骤进行：1. 初始化粒子群：首先，定义需要优化的目标函数，然后确定粒子群的规模、搜索空间的范围、最大迭代次数等参数。

在Matlab中可以使用数组或矩阵来表示粒子群的位置和速度。

2. 计算适应度：根据目标函数，计算每个粒子的适应度值，以便评估其在搜索空间中的位置的好坏程度。

3. 更新粒子的速度和位置：根据PSO算法的公式，更新每个粒子的速度和位置。

这个过程涉及到调整粒子的速度和位置，使其朝着适应度更高的方向移动。

4. 更新全局最优解：在整个粒子群中找到最优的粒子，即具有最佳适应度值的粒子，然后更新全局最优解。

5. 循环迭代：重复步骤3和步骤4，直到满足停止迭代的条件（如达到最大迭代次数或达到精度要求）。

在Matlab中，可以使用循环结构和数组操作来实现上述步骤。

以下是一个简单的PSO算法的Matlab程序示例：matlab.% 定义目标函数。

function z = objective_function(x)。

z = x(1)^2 + x(2)^2; % 以x1和x2为变量的目标函数示例（可根据实际情况修改）。

% 初始化粒子群。

n = 30; % 粒子数量。

max_iter = 100; % 最大迭代次数。

c1 = 2; % 学习因子。

c2 = 2; % 学习因子。

w = 0.7; %惯性权重。

x = rand(n, 2); % 随机初始化粒子的位置。

v = rand(n, 2); % 随机初始化粒子的速度。

pbest = x; % 个体最佳位置。

pbest_val = zeros(n, 1); % 个体最佳适应度值。

gbest = zeros(1, 2); % 全局最佳位置。

gbest_val = inf; % 全局最佳适应度值。

% 迭代优化。

for iter = 1:max_iter.for i = 1:n.% 计算适应度。

pso算法 matlab程序

pso算法 matlab程序PSO算法，即粒子群优化算法（Particle Swarm Optimization），是一种启发式优化算法，常用于解决搜索和优化问题。

在Matlab中实现PSO算法可以通过以下步骤：步骤1，初始化粒子群。

首先，需要初始化一群粒子，每个粒子都代表了搜索空间中的一个候选解。

每个粒子都有自己的位置和速度。

可以使用随机数函数在搜索空间内随机生成粒子的初始位置和速度。

步骤2，计算适应度。

接下来，需要计算每个粒子的适应度，适应度函数根据具体问题而定。

适应度函数可以是需要最小化或最大化的目标函数。

步骤3，更新粒子的速度和位置。

根据PSO算法的原理，需要根据当前位置和速度以及个体最优位置和全局最优位置来更新粒子的速度和位置。

这个过程可以通过一些数学公式来实现，通常包括学习因子、惯性权重等参数。

步骤4，更新个体和全局最优位置。

在更新粒子的过程中，需要不断更新个体最优位置和全局最优位置。

如果某个粒子找到了比之前更好的位置，就需要更新个体最优位置；如果整个粒子群中出现了更好的位置，就需要更新全局最优位置。

步骤5，重复迭代。

以上步骤需要进行多次迭代，直到满足停止迭代的条件。

通常可以设置迭代次数或者适应度达到某个阈值时停止迭代。

在Matlab中，可以使用循环结构来实现迭代过程，同时根据上述步骤编写相应的代码来实现PSO算法。

常用的Matlab函数和工具包如“fmincon”、“Global Optimization Toolbox”等也可以用来实现PSO算法。

总结来说，实现PSO算法的关键在于理解其基本原理，正确地编写粒子的更新规则和适应度函数，并进行合适的迭代和终止条件设置。

希望这些信息能帮助你在Matlab中实现PSO算法。

粒子群算法matlab(算法已经调试)

程序1当22111==c c ，5.12212==c c ，2.1=w 。

a)%主函数源程序（main.m ）%------基本粒子群算法（particle swarm optimization ）%------名称：基本粒子群算法%------初始格式化clear all ; %清除所有变量clc; %清屏format long ; %将数据显示为长整形科学计数%------给定初始条条件------------------N=40; %³初始化群体个数D=10; %初始化群体维数T=100; %初始化群体最迭代次数c11=2; %学习因子1c21=2; %学习因子2c12=1.5;c22=1.5;w=1.2; %惯性权重eps=10^(-6); %设置精度（在已知最小值的时候用） %------初始化种群个体（限定位置和速度）------------x=zeros(N,D);v=zeros(N,D);for i=1:Nfor j=1:Dx(i,j)=randn; %随机初始化位置v(i,j)=randn; %随机初始化速度endend%------显示群位置----------------------figure(1)for j=1:Dif (rem(D,2)>0)subplot((D+1)/2,2,j)elsesubplot(D/2,2,j)endplot(x(:,j),'b*');grid onxlabel('粒子')ylabel('初始位置')tInfo=strcat('第',char(j+48),'维');if(j>9)tInfo=strcat('第',char(floor(j/10)+48)，char(rem(j,10)+48),'维');endtitle(tInfo)end%------显示种群速度figure(2)for j=1:Dif(rem(D,2)>0)subplot((D+1)/2,2,j)elsesubplot(D/2,2,j)endplot(x(:,j),'b*');grid onxlabel('粒子')ylabel('初始速度')tInfo=strcat('第,char(j+48),'维');if(j>9)tInfo=strcat('第',char(floor(j/10)+48), char(rem(j,10)+48),'维);endtitle(tInfo)endfigure(3)%第一个图subplot(1,2,1)%------初始化种群个体（在此限定速度和位置）------------x1=x;v1=v;%------初始化个体最优位置和最优值---p1=x1;pbest1=ones(N,1);for i=1:Npbest1(i)=fitness(x1(i,:),D);end%------初始化全局最优位置和最优值---------------g1=1000*ones(1,D);gbest1=1000;for i=1:Nif(pbest1(i)<gbest1)g1=p1(i,:);gbest1=pbest1(i);endendgb1=ones(1,T);%-----浸入主循环，按照公式依次迭代直到满足精度或者迭代次数---for i=1:Tfor j=1:Nif (fitness(x1(j,:),D)<pbest1(j))p1(j,:)=x1(j,:);pbest1(j)=fitness(x1(j,:),D);endif(pbest1(j)<gbest1)g1=p1(j,:);gbest1=pbest1(j);endv1(j,:)=w*v1(j,:)+c11*rand*(p1(j,:)-x1(j,:))+c21*rand*(g1-x1(j,:));x1(j,:)=x1(j,:)+v1(j,:);endgb1(i)=gbest1;endplot(gb1)TempStr=sprintf('c1= %g ,c2=%g',c11,c21);title(TempStr);xlabel('迭代次数');ylabel('适应度值');%第二个图subplot(1,2,2)%-----初始化种群个体（在此限定速度和位置）------------x2=x;v2=v;%-----初始化种群个体最有位置和最优解-----------p2=x2;pbest2=ones(N,1);for i=1:Npbest2(i)=fitness(x2(i,:),D);end%-----初始化种全局最有位置和最优解------g2=1000*ones(1,D);gbest2=1000;for i=1:Nif(pbest2(i)<gbest2)g2=p2(i,:);gbest2=pbest2(i);endendgb2=ones(1,T);%------浸入主循环，按照公式依次迭代直到满足精度或者迭代次数---for i=1:Tfor j=1:Nif (fitness(x2(j,:),D)<pbest2(j))p2(j,:)=x2(j,:);pbest2(j)=fitness(x2(j,:),D);endif(pbest2(j)<gbest2)g2=p2(j,:);gbest2=pbest2(j);endv2(j,:)=w*v2(j,:)+c12*rand*(p2(j,:)-x2(j,:))+c22*rand*(g2-x2(j,:)); x2(j,:)=x2(j,:)+v2(j,:);endgb2(i)=gbest2;endplot(gb2)TempStr=sprintf('c1= %g ,c2=%g',c12,c22);title(TempStr);xlabel('迭代次数');ylabel('适应度值');b ）适应度函数%适应度函数（fitness.m ）function result=fitness(x,D)sum=0;for i=1:Dsum=sum+x(i)^2;endresult=sum;程序2当22111==c c 于2.1,2,02212===w c c 对比a)%主函数源程序（main.m ）%------基本粒子群算法（particle swarm optimization ）%------名称：基本粒子群算法%------初始格式化clear all ; %清除所有变量clc; %清屏format long ; %将数据显示为长整形科学计数%------给定初始条条件------------------N=40; %³初始化群体个数D=10; %初始化群体维数T=100; %初始化群体最迭代次数c11=2; %学习因子1c21=2; %学习因子2c12=0;c22=2;w=1.2; %惯性权重eps=10^(-6); %设置精度（在已知最小值的时候用）%------初始化种群个体（限定位置和速度）------------x=zeros(N,D);v=zeros(N,D);for i=1:Nfor j=1:Dx(i,j)=randn; %随机初始化位置v(i,j)=randn; %随机初始化速度endend%------显示群位置----------------------figure(1)for j=1:Dif(rem(D,2)>0)subplot((D+1)/2,2,j)elsesubplot(D/2,2,j)endplot(x(:,j),'b*');grid onxlabel('粒子')ylabel('初始位置')tInfo=strcat('第',char(j+48),'维');if(j>9)tInfo=strcat('第',char(floor(j/10)+48)，char(rem(j,10)+48),'维');endtitle(tInfo)end%------显示种群速度figure(2)for j=1:Dif(rem(D,2)>0)subplot((D+1)/2,2,j)elsesubplot(D/2,2,j)endplot(x(:,j),'b*');grid onxlabel('粒子')ylabel('初始速度')tInfo=strcat('第,char(j+48),'维');if(j>9)tInfo=strcat('第',char(floor(j/10)+48),char(rem(j,10)+48),'维);endtitle(tInfo)endfigure(3)%第一个图subplot(1,2,1)%------初始化种群个体（在此限定速度和位置）------------x1=x;v1=v;%------初始化个体最优位置和最优值---p1=x1;pbest1=ones(N,1);for i=1:Npbest1(i)=fitness(x1(i,:),D);end%------初始化全局最优位置和最优值---------------g1=1000*ones(1,D);gbest1=1000;for i=1:Nif(pbest1(i)<gbest1)g1=p1(i,:);gbest1=pbest1(i);endendgb1=ones(1,T);%-----浸入主循环，按照公式依次迭代直到满足精度或者迭代次数---for i=1:Tfor j=1:Nif (fitness(x1(j,:),D)<pbest1(j))p1(j,:)=x1(j,:);pbest1(j)=fitness(x1(j,:),D);endif(pbest1(j)<gbest1)g1=p1(j,:);gbest1=pbest1(j);endv1(j,:)=w*v1(j,:)+c11*rand*(p1(j,:)-x1(j,:))+c21*rand*(g1-x1(j,:));x1(j,:)=x1(j,:)+v1(j,:);endgb1(i)=gbest1;endplot(gb1)TempStr=sprintf('c1= %g ,c2=%g',c11,c21);title(TempStr);xlabel('迭代次数');ylabel('适应度值');%第二个图subplot(1,2,2)%-----初始化种群个体（在此限定速度和位置）------------x2=x;v2=v;%-----初始化种群个体最有位置和最优解-----------p2=x2;pbest2=ones(N,1);for i=1:Npbest2(i)=fitness(x2(i,:),D);end%-----初始化种全局最有位置和最优解------g2=1000*ones(1,D);gbest2=1000;for i=1:Nif(pbest2(i)<gbest2)g2=p2(i,:);gbest2=pbest2(i);endendgb2=ones(1,T);%------浸入主循环，按照公式依次迭代直到满足精度或者迭代次数---for i=1:Tfor j=1:Nif (fitness(x2(j,:),D)<pbest2(j))p2(j,:)=x2(j,:);pbest2(j)=fitness(x2(j,:),D);endif(pbest2(j)<gbest2)g2=p2(j,:);gbest2=pbest2(j);endv2(j,:)=w*v2(j,:)+c12*rand*(p2(j,:)-x2(j,:))+c22*rand*(g2-x2(j,:));x2(j,:)=x2(j,:)+v2(j,:);endgb2(i)=gbest2;endplot(gb2)TempStr=sprintf('c1= %g ,c2=%g',c12,c22);title(TempStr);xlabel('迭代次数');ylabel('适应度值');b）适应度函数%适应度函数（fitness.m）function result=fitness(x,D)sum=0;for i=1:Dsum=sum+x(i)^2;endresult=sum;程序3当2.1,22111===w c c 于2.1,0,22212===w c c 对比a)%主函数源程序（main.m ）%------基本粒子群算法（particle swarm optimization ） %------名称：基本粒子群算法%------初始格式化clear all ; %清除所有变量clc; %清屏format long ; %将数据显示为长整形科学计数 %------给定初始条条件------------------N=40; %³初始化群体个数D=10; %初始化群体维数T=100; %初始化群体最迭代次数c11=2; %学习因子1c21=2; %学习因子2c12=2;c22=0;w=1.2; %惯性权重eps=10^(-6); %设置精度（在已知最小值的时候用） %------初始化种群个体（限定位置和速度）------------x=zeros(N,D);v=zeros(N,D);for i=1:Nfor j=1:Dx(i,j)=randn; %随机初始化位置v(i,j)=randn; %随机初始化速度endend%------显示群位置----------------------figure(1)for j=1:Dif (rem(D,2)>0)subplot((D+1)/2,2,j)elsesubplot(D/2,2,j)endplot(x(:,j),'b*');grid onxlabel('粒子')ylabel('初始位置')tInfo=strcat('第',char(j+48),'维');if(j>9)tInfo=strcat('第',char(floor(j/10)+48)，char(rem(j,10)+48),'维');endtitle(tInfo)end%------显示种群速度figure(2)for j=1:Dif(rem(D,2)>0)subplot((D+1)/2,2,j)elsesubplot(D/2,2,j)endplot(x(:,j),'b*');grid onxlabel('粒子')ylabel('初始速度')tInfo=strcat('第,char(j+48),'维');if(j>9)tInfo=strcat('第',char(floor(j/10)+48), char(rem(j,10)+48),'维);endtitle(tInfo)endfigure(3)%第一个图subplot(1,2,1)%------初始化种群个体（在此限定速度和位置）------------x1=x;v1=v;%------初始化个体最优位置和最优值---p1=x1;pbest1=ones(N,1);for i=1:Npbest1(i)=fitness(x1(i,:),D);end%------初始化全局最优位置和最优值---------------g1=1000*ones(1,D);gbest1=1000;for i=1:Nif(pbest1(i)<gbest1)g1=p1(i,:);gbest1=pbest1(i);endendgb1=ones(1,T);%-----浸入主循环，按照公式依次迭代直到满足精度或者迭代次数---for i=1:Tfor j=1:Nif (fitness(x1(j,:),D)<pbest1(j))p1(j,:)=x1(j,:);pbest1(j)=fitness(x1(j,:),D);endif(pbest1(j)<gbest1)g1=p1(j,:);gbest1=pbest1(j);endv1(j,:)=w*v1(j,:)+c11*rand*(p1(j,:)-x1(j,:))+c21*rand*(g1-x1(j,:));x1(j,:)=x1(j,:)+v1(j,:);endgb1(i)=gbest1;endplot(gb1)TempStr=sprintf('c1= %g ,c2=%g',c11,c21);title(TempStr);xlabel('迭代次数');ylabel('适应度值');%第二个图subplot(1,2,2)%-----初始化种群个体（在此限定速度和位置）------------x2=x;v2=v;%-----初始化种群个体最有位置和最优解-----------p2=x2;pbest2=ones(N,1);for i=1:Npbest2(i)=fitness(x2(i,:),D);end%-----初始化种全局最有位置和最优解------g2=1000*ones(1,D);gbest2=1000;for i=1:Nif(pbest2(i)<gbest2)g2=p2(i,:);gbest2=pbest2(i);endendgb2=ones(1,T);%------浸入主循环，按照公式依次迭代直到满足精度或者迭代次数---for i=1:Tfor j=1:Nif (fitness(x2(j,:),D)<pbest2(j))p2(j,:)=x2(j,:);pbest2(j)=fitness(x2(j,:),D);endif(pbest2(j)<gbest2)g2=p2(j,:);gbest2=pbest2(j);endv2(j,:)=w*v2(j,:)+c12*rand*(p2(j,:)-x2(j,:))+c22*rand*(g2-x2(j,:)); x2(j,:)=x2(j,:)+v2(j,:);endgb2(i)=gbest2;endplot(gb2)TempStr=sprintf('c1= %g ,c2=%g',c12,c22);title(TempStr);xlabel('迭代次数');ylabel('适应度值');b ）适应度函数%适应度函数（fitness.m ）function result=fitness(x,D)sum=0;for i=1:Dsum=sum+x(i)^2;endresult=sum;程序4对21c c ≠，21w w ≠分别对其取值1.11=c ，22=c ，2.11=w ，5.12=w 测试函数。

pso算法matlab代码

pso算法matlab代码粒子群优化算法（Particle Swarm Optimization，PSO）是一种基于群体智能的优化算法，其基本思想是通过模拟鸟群觅食行为来寻找最优解。

以下是一个简单的 MATLAB 代码示例，用于实现 PSO 算法：matlab复制代码% 定义问题参数n_particles = 100; % 粒子数量n_iterations = 100; % 迭代次数n_dimensions = 2; % 问题的维度lb = [-10-10]; % 问题的下界ub = [1010]; % 问题的上界c1 = 2; % 个体学习因子c2 = 2; % 社会学习因子% 初始化粒子群particles = lb + (ub-lb).*rand(n_particles,n_dimensions);velocities = zeros(n_particles, n_dimensions);p_best = particles;g_best = particles(1, :);g_best_fitness = inf;% 主循环for i = 1:n_iterations% 计算每个粒子的适应度值fitness = evaluate(particles); % 更新个体最优解for j = 1:n_particlesif fitness(j) < p_best(j, :)p_best(j, :) = particles(j, :); endend% 更新全局最优解for j = 1:n_particlesif fitness(j) < g_best_fitness g_best_fitness = fitness(j);g_best = particles(j, :);endend% 更新粒子速度和位置for j = 1:n_particlesr1 = rand(); % 个体学习因子随机数r2 = rand(); % 社会学习因子随机数velocities(j, :) = velocities(j, :) +c1*r1*(p_best(j, :) - particles(j, :)) + c2*r2*(g_best - particles(j, :));particles(j, :) = particles(j, :) + velocities(j, :);% 边界条件处理particles(j, :) = max(particles(j, :) , lb);particles(j, :) = min(particles(j, :) , ub);endend% 输出结果disp('全局最优解：');disp(g_best);disp('全局最优解的适应度值：');disp(g_best_fitness);其中，evaluate函数用于计算每个粒子的适应度值，需要根据具体问题进行定义。

PSOELM(粒子群优化极限学习机)MATLAB程序

clear all;clc;close allclear allclc%load pca1load pca2load pca4load pca3%c =566:984%plot(pca2)%plot(x,P11,x,pca11,'r')%plot(x,EP1,'b',x,EP2,'r',x,EP3,'k',x,EP4,'g') %P11=mapminmax(pca1',0,1);%P22=mapminmax(pca2',0,1);%P33=mapminmax(pca3',0,1);%P44=mapminmax(pca4',0,1);%EP1=EWMA(pca1(566:984)',0.2,18)%EP4=EWMA(pca4(772:984)',0.3,16)%EP2=EWMA(pca2(772:984)',0.3,16)%EP3=EWMA(pca3(691:984)',0.3,16)%plot(x,EP1,'b',x,EP2,'r',x,EP3,'k',x,EP4,'g') %P11=mapminmax(EP1,0,1);%P22=mapminmax(EP2,0,1);%P33=mapminmax(EP3,0,1);%P44=mapminmax(EP4,0,1);EP2=smooth(pca2(772:984))';EP4=smooth(pca4(772:984))';Q=zeros(150,64);%V=zeros(965,20);for j=1:64for i=1:150Q(i,j)=EP2(i+j-1);endendP1=Q;P2=(149:-1:0)';PP=[P1,P2];%..................制作测试集....................% M=zeros(150,64);for j=1:64for i=1:150M(i,j)=EP4(i+j-1);endendT1=M;T2=(149:-1:0)';TT=[T1,T2];clearvars -except PP TTX_data=PP;Y_data=TT;%data=load('Lorenz.txt%% 加载数据%x=xlsread('pso_elmdata.xls');%AllSamIn = x(1:29,1:2)';%AllSamOut = x(1:29,3)';%AllTestIn=x(30:36,1:2)';%AllTestOut=x(30:36,3)'; AllSamIn =PP(:,1:64)'; AllSamOut=PP(:,65)';AllTestIn=TT(:,1:64)';AllTestOut=TT(:,65)';%% 训练样本归一化global minAllSamOut;global maxAllSamOut;[AllSamInn,minAllSamIn,maxAllSamIn,AllSamOutn,minAllSamOut,maxAllSamOut] = premnmx(AllSamIn,AllSamOut);TrainSamIn=AllSamInn;TrainSamOut=AllSamOutn;global Ptrain;Ptrain = TrainSamIn;global Ttrain;Ttrain = TrainSamOut;%% 测试样本归一化global minAllTestOut;global maxAllTestOut;[AllTestInn,minAllTestIn,maxAllTestIn,AllTestOutn,minAllTestOut,maxAllTestOut] = premnmx(AllTestIn,AllTestOut);TestIn=AllTestInn;TestOut=AllTestOutn;global Ptest;Ptest = TestIn;global Ttest;Ttest = TestOut;%% 加载网络的初始变量global indim;indim=64;global hiddennum;hiddennum=65;global outdim;outdim=1;%% 加载PSO模型的相关参数vmax=0.7;minerr=0.0001;wmax=1.2;wmin=0.6;cmax=3;cmin=1;global itmax;itmax=150;c1=2;c2=2;for iter=1:itmaxW(iter)=wmax-((wmax-wmin)/itmax)*iter;end%for iter=1:itmax%c2(iter)=cmax-cmin-((cmax-cmin)/itmax/3)*iter;%end%c1=c2;a=-1;b=1;m=-1;n=1;global N;N=200;global D;D=(indim+1)*hiddennum+(hiddennum+1)*outdim;rand('state',sum(100*clock));X=a+(b-a)*rand(N,D,1);V=m+(n-m)*rand(N,D,1);global fvrec;MinFit=[];BestFit=[];%% PSO优化ELM模型过程1fitness=fitcal(X,indim,hiddennum,outdim,D,Ptrain,Ptest,Ttrain,Ttest,minAllSamOut,maxAllSa mOut);fvrec(:,1,1)=fitness(:,1,1);[C,I]=min(fitness(:,1,1));MinFit=[MinFit C];BestFit=[BestFit C];L(:,1,1)=fitness(:,1,1);B(1,1,1)=C;gbest(1,:,1)=X(I,:,1);for p=1:NG(p,:,1)=gbest(1,:,1);endfor i=1:N;pbest(i,:,1)=X(i,:,1);endV(:,:,2)=W(1)*V(:,:,1)+c1*rand*(pbest(:,:,1)-X(:,:,1))+c2*rand*(G(:,:,1)-X(:,:,1));for ni=1:Nfor di=1:Dif V(ni,di,2) > vmaxV(ni,di,2) = vmax;elseif V(ni,di,2) < -vmaxV(ni,di,2) = -vmax;elseV(ni,di,2) = V(ni,di,2);endendendX(:,:,2)=X(:,:,1)+V(:,:,2);for ni=1:Nfor di=1:Dif X(ni,di,2) > 1X(ni,di,2) = 1;elseif V(ni,di,2) < -1X(ni,di,2) = -1;elseX(ni,di,2) = X(ni,di,2);endendend%% PSO优化ELM模型过程2for j=2:itmaxdisp('Iteration and Current Best Fitness')disp(j-1)disp(B(1,1,j-1))fitness=fitcal(X,indim,hiddennum,outdim,D,Ptrain,Ptest,Ttrain,Ttest,minAllSamOut,maxAllSa mOut);fvrec(:,1,j)=fitness(:,1,j);[C,I]=min(fitness(:,1,j));MinFit=[MinFit C];BestFit=[BestFit min(MinFit)];L(:,1,j)=fitness(:,1,j);B(1,1,j)=C;gbest(1,:,j)=X(I,:,j);[C,I]=min(B(1,1,:));if B(1,1,j)<=Cgbest(1,:,j)=gbest(1,:,j);elsegbest(1,:,j)=gbest(1,:,I);endif C<=minerr, break, endif j>=itmax, break, endfor p=1:NG(p,:,j)=gbest(1,:,j);endfor i=1:N;[C,I]=min(L(i,1,:));if L(i,1,j)<=Cpbest(i,:,j)=X(i,:,j);elsepbest(i,:,j)=X(i,:,I);endendV(:,:,j+1)=W(j)*V(:,:,j)+c1*rand*(pbest(:,:,j)-X(:,:,j))+c2*rand*(G(:,:,j)-X(:,:,j));for ni=1:Nfor di=1:Dif V(ni,di,j+1)>vmaxV(ni,di,j+1)=vmax;elseif V(ni,di,j+1)<-vmaxV(ni,di,j+1)=-vmax;elseV(ni,di,j+1)=V(ni,di,j+1);endendendX(:,:,j+1)=X(:,:,j)+V(:,:,j+1);for ni=1:Nfor di=1:Dif X(ni,di,j+1) > 1X(ni,di,j+1) = 1;elseif V(ni,di,j+1) < -1X(ni,di,j+1) = -1;elseX(ni,di,j+1) = X(ni,di,j+1);endendendenddisp('Iteration and Current Best Fitness')disp(j)disp(B(1,1,j))disp('Global Best Fitness and Occurred Iteration')[C,I] = min(B(1,1,:))for t=1:hiddennumx2iw(t,:)=gbest(1,((t-1)*indim+1):t*indim,j);endfor r=1:outdimx2lw(r,:)=gbest(1,(indim*hiddennum+1):(indim*hiddennum+hiddennum),j);endx2b=gbest(1,((indim+1)*hiddennum+1):D,j);x2b1=x2b(1:hiddennum).';x2b2=x2b(hiddennum+1:hiddennum+outdim).';IWbest1=x2iw;IWbest2=x2lw;IBbest1=x2b1;IBbest2=x2b2;T_sim_test = ELMfun2(IWbest1,IBbest1,Ptrain,Ptest,Ttrain,Ttest,hiddennum,IWbest2,IBbest2); testsamout = postmnmx(T_sim_test,minAllTestOut,maxAllTestOut);realtesterr=mse(testsamout-AllTestOut);err1=norm(testsamout-AllTestOut);disp(['优化模型测试样本的仿真误差:',num2str(err1)])N = length(Ttest);R1 = (N*sum(T_sim_test.*Ttest)-sum(T_sim_test)*sum(Ttest))^2/((N*sum((T_sim_test).^2)-(sum(T_sim_test))^2)*(N*sum((Ttest).^2)-(sum(Ttest))^2));%% 不使用PSO优化ELM算法[IW,B,LW,TF,TYPE] = elmtrain2(Ptrain,Ttrain,65,'sig',0);T_sim_test1 = elmpredict(Ptest,IW,B,LW,TF,TYPE);testsamout2 = postmnmx(T_sim_test1,minAllTestOut,maxAllTestOut);realtesterr2=mse(testsamout2-AllTestOut);err2=norm(testsamout2-AllTestOut);R2 = (N*sum(T_sim_test1.*Ttest)-sum(T_sim_test1)*sum(Ttest))^2/((N*sum((T_sim_test1).^2)-(sum(T_sim_test1))^2)*(N*sum((Ttest).^2)-(sum(Ttest))^2));disp(['原始模型测试样本的仿真误差:',num2str(err2)])RMSE1=sqrt(mse(AllTestOut-testsamout2))%plot(1:150,AllTestOut,'r-*',1:150,testsamout2,'b:o');%% 输出参数图% PSO 优化迭代图%% 输出参数图% PSO 优化迭代图figure(1);P0 = plot(1:itmax,BestFit);grid onxlabel('PSO items');ylabel('MSE rate');%string = {'PSO-ELM模型100次迭代误差变化';['决定系数:R^2=' num2str(R1) ' ' ];['模型仿真均方误差:mse=' num2str(realtesterr) ' ']};%title(string)%bestErr=min(BestFit);%fprintf(['PSO-ELM模型:\n决定系数R^2=',num2str(R1),'\n模型仿真均方误差:mse=',num2str(realtesterr),'\n'])%set(P0,'LineWidth',1.5);% PSO与ELM结果比较图figure(2)plot(1:150,AllTestOut,'r-*',1:150,testsamout,'b:o');legend('真实值','PSO-ELM预测值')RMSE2=sqrt(mse(AllTestOut-testsamout))%,1:151,testsamout2,'y--*')%grid on%legend('真实值','PSO-ELM预测值','单纯ELM预测值')%xlabel('样本编号')%ylabel('样本数据分类号')。

粒子群优化算法matlab程序

粒子群优化算法matlab程序粒子群优化算法（Particle Swarm Optimization，PSO）是一种基于群体智能的优化算法，其原理基于模拟鸟群觅食的行为。

该算法通过不断调整搜索空间中的候选解，来求解优化问题。

相比于其他优化算法，如遗传算法、模拟退火等，粒子群优化算法具有更高的效率和精度。

Matlab是一种强大的数值计算工具，广泛用于科学计算、工程设计、数据分析等领域。

在粒子群优化算法中，Matlab可以用来编写程序进行模拟和优化。

具体而言，可以通过Matlab中的粒子群优化工具箱（Particle Swarm Optimization Toolbox）来实现粒子群优化算法。

编写粒子群优化算法的Matlab程序，需要考虑以下几个方面：1. 问题建模：将优化问题转化为目标函数的最小化或最大化问题，以便于粒子群优化算法进行求解。

2. 参数设置：根据问题的特点，确定粒子群优化算法的参数，如粒子数、惯性权重、加速度常数等。

3. 粒子群初始化：随机生成一组初始粒子，并初始化它们的速度和位置。

4. 粒子群迭代：根据粒子的位置和速度，计算每个粒子的适应度值，并更新粒子的速度和位置。

5. 终止条件：当达到预设的迭代次数或目标函数值满足一定精度要求时，停止粒子群优化算法的迭代。

在Matlab中实现粒子群优化算法，需要掌握Matlab的基本语法和粒子群优化算法的原理。

此外，还可以参考Matlab官方文档和粒子群优化工具箱的文档，来了解如何使用Matlab进行粒子群优化算法的编写和调试。

总之，粒子群优化算法是一种高效、精确的优化算法，在许多领域有着广泛的应用。

通过Matlab编写粒子群优化算法的程序，可以帮助研究者更好地理解和应用这一算法。

粒子群算法matlab代码

一、粒子群主程序psize=20; %粒子个数的设置pd=12; %粒子的维数lz=zeros(psize,pd);for i=1:psize %随机生成粒子群，psize行pd列，pd维。

suiji=rand(1,pd);for j=1:pd/2if suiji(j)<0.5lz(i,j)=fix(unifrnd(0,100))*100;elselz(i,j)=fix(unifrnd(0,100)+1)*100;endendfor j=pd/2+1:1:pdif suiji(j)<0.5lz(i,j)=fix(unifrnd(0,45))/100;elselz(i,j)=fix(unifrnd(0,45)+1)/100;endendlz(i,1:pd/2)=sort(lz(i,1:pd/2));lz(i,pd/2+1:pd)=sort(lz(i,pd/2+1:pd));endlv=lz;goodvalue=lz; %每个粒子自己历史最好值初始化，psize行pd列。

vmax=20; %速度上限c1=2;c2=2; %学习因子w=0.729; %随机因子和惯性因子bestvalue=zeros(1,pd); %全局最好值初始化，1行pd列for j=1:pdbestvalue(1,j)=goodvalue(1,j);endfnew=zeros(1,psize);for j=1:psizefnew(j)=fpso(lz(1,:));endfold=fnew;flagstop=0; %终止标志k=0; %迭代次数记录f0=fpso(bestvalue); %适应值初始化while flagstop==0for i=1:psize %适应值比较，更新各自历史最好值（位置）fnew(i)=fpso(lz(i,:)); %记录每次每个粒子的适应值，便于以后设置终止条件if fnew(i)<fold(i)fold(i)=fnew(i); %fold记录每个粒子的最好历史值goodvalue(i,j)=lz(i,j);endendendfor i=1:psize%每个粒子历史最好值比较，更新全局最好值f1=fold(i);if f1<f0f0=f1;for j=1:pdbestvalue(1,j)=goodvalue(i,j);endendend%*********粒子趋一点终止条件*********%flagstop0=max(abs(fold)); %比较当次的所有粒子的适应值，flagstop1=min(abs(fold)); %若它们之间差别较小，则可以停止。

基于MATLAB的粒子群优化算法程序设计

基于MATLAB的粒子群优化算法程序设计一、概述粒子群优化（Particle Swarm Optimization，PSO）算法是一种基于群体智能的优化搜索技术，它通过模拟鸟群、鱼群等动物群体的社会行为，利用群体中的个体信息共享机制，引导粒子在解空间中搜索最优解。

自1995年由Eberhart博士和Kennedy博士提出以来，PSO 算法因其简单、高效的特点，在函数优化、神经网络训练、模糊系统控制等多个领域得到了广泛的应用。

在MATLAB环境中实现粒子群优化算法，可以充分利用MATLAB强大的数值计算能力和高效的编程环境，实现算法的快速开发和优化。

MATLAB具有简单易用的语法和丰富的函数库，使得开发者能够快速地构建算法模型，进行仿真实验，并对算法性能进行分析和评估。

基于MATLAB的粒子群优化算法程序设计，旨在提供一个完整的算法实现框架，帮助读者理解PSO算法的基本原理和实现细节。

通过该程序设计，读者可以掌握如何在MATLAB中构建粒子群优化算法，如何设置算法参数，如何进行仿真实验，并如何分析和评估算法性能。

该程序设计还可以作为进一步研究和开发粒子群优化算法的基础，为实际应用提供有力的技术支持。

1. 粒子群优化算法（PSO）简介粒子群优化算法（Particle Swarm Optimization, PSO）是一种群体智能优化技术，起源于对鸟群觅食行为的社会心理学模拟。

该算法通过模拟鸟群中的信息共享机制，使得每个个体（粒子）能够在解空间中不断更新自己的位置和速度，从而寻找到问题的最优解。

PSO 算法以其简单、易实现和高效的特点，在函数优化、神经网络训练、模糊系统控制等多个领域得到了广泛应用。

在PSO算法中，每个粒子都代表着问题解空间中的一个候选解，它们根据自己的飞行经验以及群体中最优粒子的飞行经验来调整自己的飞行轨迹。

粒子的位置信息对应着问题的解，而粒子的速度则决定了其搜索解空间的方向和步长。

智能算法之粒子群优化算法-matlab程序-可运行

w = 0.8; % 惯性权重
c1 = 0.5; % 自我学习因子
c2 = 0.5; % 群体学习因子
for i = 1:d
x = limit(i, 1) + (limit(i, 2) - limit(i, 1)) * rand(N, d);%初始种群的位置
plot(x0, f(x0), 'b-', x, f(x), 'ro');title('状态位置变化')
pause(0.1)
iter = iter+1;
end
figure(3);plot(record);title('收敛过程')
x0 = 0 : 0.01 : 20;
d = 1; % 空间维数
ger = 100; % 最大迭代次数
limit = [0, 20]; % 设置位置参数限制
vlimit = [-1, 1]; % 设置速度限制
end
v = v * w + c1 * rand * (xm - x) + c2 * rand * (repmat(ym, N, 1) - x);% 速度更新
%Hale Waihona Puke 边界速度处理 v(v > vlimit(2)) = vlimit(2);
v(v < vlimit(1)) = vlimit(1);
while iter <= ger
fx = f(x) ; % 个体当前适应度
for i = 1:N
if fxm(i) < fx(i)
fxm(i) = fx(i); % 更新个体历史最佳适应度

matlab基本粒子群算法实现（一）

matlab基本粒⼦群算法实现（⼀）算法没有和图像处理直接相关，不过对于图像分类中的模式识别相关算法，也许会⽤到这个优化算法。

不过不管有没有⽤，还是得⼀步⼀步学起来算法步骤：1.⾸先确定粒⼦个数与迭代次数。

2.对每个粒⼦随机初始化位置与速度。

3.采⽤如下公式更新每个粒⼦的位置与速度。

Px=Px+Pv*t;　%位置更新公式　Pv=Pv+(c1*rand*(Gx-Px))+(c2*rand*(PBx-Px)); %速度更新公式main.m[xm,fv]=PSO(@fitness,40,2,2,0.5,100,30)for i=1:30s(i)=0.;endfor i=1:30F=0;for j=1:30F=F+xm(i)^2+xm(i);ends(i)=F;endplot(xm,s,'*')PSO.mfunction [ xm,fv ] = PSO( fitness,N,c1,c2,w,M,D )%PSO Summary of this function goes here% Detailed explanation goes hereformat long;for i=1:Nfor j=1:Dx(i,j)=randn;v(i,j)=rand;endendfor i=1:Np(i)=fitness(x(i,:));y(i,:)=x(i,:);endpg= x(N,:);for i=1:(N-1)if fitness(x(i,:))<fitness(pg)pg=x(i,:);endendfor t=1:Mfor i=1:Nv(i,:)=w*v(i,:)+c1*rand*(y(i,:)-x(i,:))+c2*rand*(pg-x(i,:));x(i,:)=x(i,:)+v(i,:);if fitness(x(i,:))<p(i)p(i)=fitness(x(i,:));y(i,:)=x(i,:);endif p(i)<fitness(pg)pg=y(i,:);endendPbest(t)=fitness(pg);endxm = pg';fv =fitness(pg);end这个就是优化的函数，就是求它的最⼩值，也可能是局部最⼩值，fitness.mfunction F = fitness( x )%F Summary of this function goes here % Detailed explanation goes hereF=0;for i=1:30F=F+x(i)^2+x(i);end。

粒子群优化算法对BP神经网络优化Matlab实现

粒⼦群优化算法对BP神经⽹络优化Matlab实现1、粒⼦群优化算法粒⼦群算法(particle swarm optimization，PSO)由Kennedy和Eberhart在1995年提出，该算法模拟鸟集群飞⾏觅⾷的⾏为，鸟之间通过集体的协作使群体达到最优⽬的，是⼀种基于 Swarm Inteligence的优化⽅法。

同遗传算法类似，也是⼀种基于群体叠代的，但并没有遗传算法⽤的交叉以及变异，⽽是粒⼦在解空间追随最优的粒⼦进⾏搜索。

PSO的优势在于简单容易实现同时⼜有深刻的智能背景，既适合科学研究，⼜特别适合⼯程应⽤，并且没有许多参数需要调整。

粒⼦群优化算法源于1987年Reynolds对鸟群社会系统boids的仿真研究，boids是⼀个CAS。

在boids中，⼀群鸟在空中飞⾏，每个鸟遵守以下三条规则：1）避免与相邻的鸟发⽣碰撞冲突；2）尽量与⾃⼰周围的鸟在速度上保持协调和⼀致；3）尽量试图向⾃⼰所认为的群体中靠近。

仅通过使⽤这三条规则，boids系统就出现⾮常逼真的群体聚集⾏为，鸟成群地在空中飞⾏，当遇到障碍时它们会分开绕⾏⽽过，随后⼜会重新形成群体。

Reynolds仅仅将其作为CAS的⼀个实例作仿真研究，⽽并未将它⽤于优化计算中。

Kennedy和Eberhart在中加⼊了⼀个特定点，定义为⾷物，鸟根据周围鸟的觅⾷⾏为来寻找⾷物。

他们的初衷是希望通过这种模型来模拟鸟群寻找⾷源的现象，然⽽实验结果却揭⽰这个仿真模型中蕴涵着很强的优化能⼒，尤其是在多维空间寻优中。

PSO中，每个优化问题的解都是搜索空间中的⼀只鸟。

称之为“粒⼦(Particle)”。

所有的粒⼦都有⼀个由被优化的函数决定的适应值，每个粒⼦还有⼀个速度决定他们飞翔的⽅向和距离。

然后粒⼦们就追随当前的最优粒⼦在解空间中搜索.PSO 初始化为⼀群随机粒⼦。

然后通过叠代找到最优解。

在每⼀次叠代中，粒⼦通过跟踪两个"极值"来更新⾃⼰。

matlab 群优化算法

matlab 群优化算法群优化算法是一种基于自然界中群体行为的优化算法，其核心思想是通过模拟群体行为来寻找最优解。

在群体中，每个个体都有自己的特点和行为方式，但它们可以通过相互交流和协作来达成共识，从而实现群体智能。

在群优化算法中，个体通常被称为粒子，而群体则被称为粒子群。

本文将介绍几种常见的基于群体行为的优化算法及其在MATLAB中的实现。

1. 粒子群优化算法（Particle Swarm Optimization, PSO）粒子群优化算法是一种基于群体行为的优化算法，其核心思想是通过模拟鸟群觅食行为来寻找最优解。

在PSO中，每个粒子都有自己的位置和速度，它们通过不断地更新自己的位置和速度来寻找最优解。

PSO算法的优点是收敛速度快，但容易陷入局部最优解。

在MATLAB中，可以使用“pso”函数实现PSO算法。

该函数的基本语法如下：[x,fval,exitflag,output] = pso(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon,options)其中，fun是目标函数，nvars是变量数，A、b、Aeq、beq、lb、ub和nonlcon 分别是线性约束、非线性约束和边界条件。

options是一个结构体，可以设置算法的参数和选项。

例如，可以设置种群大小、最大迭代次数、收敛精度等参数。

2. 蚁群优化算法（Ant Colony Optimization, ACO）蚁群优化算法是一种基于蚂蚁觅食行为的优化算法，其核心思想是通过模拟蚂蚁在食物源和巢穴之间的寻找行为来寻找最优解。

在ACO中，每个蚂蚁都有自己的路径和信息素，它们通过不断地更新自己的路径和信息素来寻找最优解。

ACO 算法的优点是全局搜索能力强，但收敛速度较慢。

在MATLAB中，可以使用“aco”函数实现ACO算法。

该函数的基本语法如下：[x,fval,exitflag,output] = aco(fun,nvars,LB,UB,options)其中，fun是目标函数，nvars是变量数，LB和UB分别是变量的下界和上界。