统计学概论练习二(静态分析、动态分析、回归分析、指数分析)
统计学简单题答案整理

统计学简答题2。
统计学研究对象有哪些特点?参考答案:(1)数量性:从数量上认识事物的性质和规律,是统计研究的基本特点;统计研究的不是抽象的数量,而是有特定内容的具体数量。
统计是在质的规定性下研究与所研究现象内容性质密切联系的具体数量。
(2)总体性:统计是以现象总体的数量特征作为自己的研究对象。
统计要对总体中各单位普遍存在的事实进行大量观察和综合分析,得出反映现象总体的数量特征。
(3)变异性:总体各单位的标志特征由于复杂的随机因素而有不同的表现,它是统计研究的前提.⒊什么是标志和指标?两者有何区别与联系?参考答案:指标与标志的区别:(1)指标是说明总体特征的,而标志则是说明总体单位特征的。
(2)标志有不能用数值表示的品质标志与能用数值表示的数量标志,而指标都是用数值表示的,没有不能用数值表示的统计指标。
指标与标志的联系:(1)有许多统计指标的数值是从总体单位的数量标志值汇总而来的,如一个煤炭工业局(公司)的煤炭总产量,是从所属各煤炭工业企业的产量汇总出来的。
(2)指标与标志(数量标志)之间存在着变换关系.由于研究的目的不同,原来的统计总体如果变成总体单位,则相对应的统计指标也就变成数量标志,反之亦然.(比如:如果调查研究各分支煤炭工业企业的产量情况,那么分支企业是总体指标,如果转为研究煤炭工业局的总产量情况,那么各分支公司就成了个体标志)(一)指标与标志之间联系:(1)、标志和指标的关系是个别和整体的关系。
标志反映总体单位的属性和特征,而指标则反映总体的数量特征.许多统计指标是由各单位的数量标志值汇总而来的.(2)、由于总体和单位的概念会随着研究目的不同而变化,在一定条件下,指标和标志之间存在一定的变换关系。
因此指标与标志的概念也是相对而言的.(二)指标和标志的区别:①指标是说明总体数量特征的概念,而标志是说明总体单位特征的概念。
前者范围大些, 后者的范围小些;②指标都是用数值表示的, 而标志有的是用数字表示,有的是用文字表示。
统计学——静态分析方法

第四章 静态分析方法
中位数的概念:中位数是指将总体各单位标 志值按大小排列后,处于中间位置的那个标 志值。 中位数的意义:作为位置平均数其大小不受 极端值的影响(不需要通过全部变量值来计 算),也可以用来说明社会经济现象各单位 标志值的一般水平。
2019/1/24 统计学基础
16
2019/1/24 统计学基础
第四章 静态分析方法
3.平均指标的特点 (1)把数量标志在总体各单位之间的差异抽象 化,它异于各个单位的具体水平,但又反映 了这些单位的一般水平; (2)是同质总体各单位标志值的一般水平的代 表值,反映了总体分布的集中趋势。
17
2019/1/24 统计学基础
第四章 静态分析方法
2、总量指标的作用 (1)认识社会经济现象的起点 (2)是编制计划、实行经济管理的主要依据 (3)是计算相对指标和平均指标的基础
4
2019/1/24
统计学基础
第四章 静态分析方法
二、总量指标的种类 1.按反映现象总体的内容分: (1)单位总量:总体内总体单位的总数 (2)标志总量:总体内各单位某种标志值的总和 注意: 单位总量和标志总量并不是固定不变的; 某一总体中,单位总量只有一个,标志总量 可以有多个。
众数的意义:是总体中最普遍的标志值,也 可以用来说明社会经济现象各单位标志值的 一般水平。作为位置平均数(其大小不需要 通过全部变量值来计算),其大小不受极端 值的影响。
2019/1/24 统计学基础
35
第四章 静态分析方法
众数的确定: 1、根据未分组资料确定众数:观察得出(准确 说,没有众数,从定义易得出结论)。 2、根据已分组资料确定众数 (1)单项数列确定众数:最大次数对应的标志 值。 (2)组距数列确定众数:采用插补法计算。
统计学概论自考试题及答案

统计学概论自考试题及答案一、选择题(每题2分,共20分)1. 下列哪项不是统计学的主要分支?A. 描述统计学B. 推断统计学C. 应用统计学D. 决策统计学答案:D2. 总体是指:A. 研究对象的全体B. 研究对象的一部分样本C. 研究对象的统计量D. 研究对象的测量结果答案:A3. 以下哪个是离散型随机变量的分布列的特点?A. 变量取值是连续的B. 变量取值是离散的C. 变量取值的概率是连续的D. 变量取值的概率是离散的答案:D4. 统计量是对数据集特征的概括,以下哪个不是统计量?A. 平均数B. 中位数C. 众数D. 标准差答案:C5. 在统计学中,以下哪个概念与“平均数”最不相关?A. 均值B. 方差C. 众数D. 极差答案:C6. 下列哪项是统计学中常用的数据收集方法?A. 实验法B. 观察法C. 调查法D. 所有以上选项答案:D7. 以下哪个统计图最适合展示分类变量的分布?A. 直方图B. 饼图C. 散点图D. 箱线图答案:B8. 相关系数的取值范围是:A. -1 到 1B. 0 到 1C. -∞ 到+∞D. 1 到+∞答案:A9. 在进行假设检验时,如果原假设为H0: μ = 50,备择假设为 Ha: μ ≠ 50,那么这是一个:A. 双边检验B. 左尾检验C. 右尾检验D. 单边检验答案:A10. 下列哪项是时间序列分析的主要目的?A. 预测未来趋势B. 描述数据分布C. 检验变量间的关系D. 分类数据类型答案:A二、简答题(每题10分,共30分)1. 简述统计学中的“参数估计”及其重要性。
答案:参数估计是统计学中根据样本数据来推断总体参数的过程。
它的重要性在于,我们通常无法获得总体的全部数据,但通过参数估计,可以对总体的特征有一个合理的推断。
这在科学研究、工业生产、经济分析等领域中都有着广泛的应用。
2. 描述统计学和推断统计学有什么区别?答案:描述统计学主要关注数据的收集、整理和图表展示,以及计算描述性统计量,如均值、中位数、众数、方差等,用以描述和总结数据的特征。
统计学概论练习题及参考答案

2013年《统计学概论》练习题一、单项选择题1.统计学的两大基本内容是( )A .统计资料的收集和分析B .理论统计和运用统计C .统计预测和决策D .描述统计和推断统计 2.下面的变量中哪一个属于分类变量( )A .年龄B .工资C .汽车产量D .付款方式(现金、信用卡、支票) 3.下面哪一个图形最适合描述结构性问题( )A .条形图B .饼图C .直方图D .折线图 4.统计分组后,应使( )A .组内具有同质性,组间具有差异性B .组内具有差异性,组间具有同质性C .组内具有差异性,组间具有差异性D .组内具有同质性,组间具有同质性 5.一组数据中出现频数最多的数值称为( )A .众数B .中位数C .四分位数D .平均数6.根据经验,当算术平均数小于中位数且小于众数时,次数分布为( )A .对称分布B .右偏分布C .左偏分布D .右偏或左偏分布7.对两个总体分布进行变异性比较,当它们的平均数不等,计量单位不同时,需要计算( )比较。
A .标准差系数B .标准差C .平均差D .方差 8.当原假设正确,按检验规则却拒绝了原假设,则犯了( )A .取伪错误B .检验错误C .第Ⅰ类错误D .第Ⅱ类错误9.每一吨铸铁成本c y (万元)和铸件废品率x (%)变动的回归方程为:568c y x =+,这意味着( )A .废品率每增加1%,成本每吨增加64万元B .废品率每增加1%,成本每吨增加8%C .废品率每增加1%,成本每吨增加8万元D .废品率每增加1%,则每吨成本为56万元10.将总体全部单位按照某个标志分组,再从各类型组中随机抽取一定单位组成样本,这种抽样是( )A .随机抽样B .等距抽样C .分层抽样D .整群抽样 11.根据经验,当算术平均数大于中位数且大于众数时,钟形分布为( )A .对称分布B .右偏分布C .左偏分布D .负偏分布 12.正态总体,总体方差σ2未知,小样本(n <30)的情况下,总体均值μ的置信度为1-α的置信区间为( )A .),(22nZ X n Z X σσαα⋅+⋅- B .),(22n SZ X n S Z X ⋅+⋅-αα C .),()1(2)1(2n S t X n S t X n n ⋅+⋅---ααD .),()1(2)1(2n t X n t X n n σσαα⋅+⋅---13.当总体方差未知时,在大样本条件下,估计总体均值使用的分布是( )A .正态分布B .t 分布C .F 分布D .χ2分布 14.当正态总体的方差未知,且为小样本条件下,估计总体均值使用的分布是( )A.正态分布B.t分布C.F分布D.χ2分布15.当备择假设为H1:μ<μ0,此时的假设检验称为()A.双侧检验B.右侧检验C.左侧检验D.显著性检验16.根据你的判断,下面的相关系数取值哪一个是错误的()A.-0.86B.0.78 C.1.25 D.017.说明回归方程拟合优度的统计量主要是()A.相关系数B.回归系数C.判定系数D.估计标准误18.在回归分析中,被预测或被解释的变量称为()A.自变量B.因变量C.随机变量D.非随机变量19.在回归分析中,用来预测或用来解释另一个变量的一个或多个变量称为()A.自变量B.因变量C.随机变量D.非随机变量20.如果相关系数r=0,则表明两个变量之间()A.相关程度很低B.相关程度较高C.不存在线性相关关系D.存在非线性相关关系二、多项选择题1.“统计”一词的基本涵义包括()A.统计学B.统计工作C.统计资料D.统计分析2.以下几项符合统计表编制规则的包括()A.统计表的标题力求简明,内容简明扼要B.统计表栏数较多时,通常要加编号,并可说明其相互关系C.统计表如有相同数字,可以写“同上”,没有数字空格即可D.统计表一般左右两端封闭,表的上下端线划粗线或双线3.非全面调查形式有()A.重点调查B.抽样调查C.典型调查D.普查4.调查问卷可以选择的问句形式包括()A.对选式问句B.多项选择式问句C.顺位式问句D.标度式问句5.下列有关假设检验的说法,正确的是()A.原假设和备择假设相互对立,而且两者只有一个正确B.假设检验的基本思想是小概率原理C.假设检验的首要步骤是建立原假设和备择假设D.根据样本推断总体,有可能犯弃真错误和取伪错误6.下列有关回归分析和相关分析的描述,正确的有()A.回归分析中,X与Y要确定自变量和因变量B.相关分析中,X与Y均为随机变量C.相关分析测定相关程度和方向D.回归分析利用回归模型进行预测和分析7.下列有关一元线性回归模型的描述正确的有()A.可以用最小平方法求解模型的两个参数a和bB.判断系数r2是测定回归直线拟合优度的一个重要指标C.回归系数的符号同相关系数的符号一致D.b>0时,表明X与Y反方向变动8.下列情况中,应采用调和平均数计算的有()A.已知各商品的单价和销售额,求平均价格B.已知各商品的单价和销售量,求平均价格C.已知采购站某月购进农产品的单价及收购量,求平均采购价格D.已知采购站某月购进农产品的单价及收购额,求平均采购价格9.下列分组中属于按品质标志分组的有()。
【DOC】统计学概论练习题.

统计学概论练习题第一章总论思考题1.什么是统计?一般有几种理解?2.统计工作包括哪几个步骤,它们各是什么?3.什么是标志和指标,两者之间有何区别和联系?4.什么是统计指标,它有哪些分类?5.举例说明总体、总体单位、标志、指标、指标体系、变异、变量。
第二章统计调查思考题1.什么是统计调查?2.简述统计调查的主要分类。
3.统计调查方案的主要内容有哪些?4.什么是重点调查?什么是典型调查?第三章统计整理思考题1.什么是统计整理?统计整理有哪几个步骤?2.什么是统计分组?如何进行统计分组?3.举例说明统计表的结构及统计表的分类。
习题1.某班组20名工人的资料如下表所示:某班组工人资料表要求:(1)按性别、文化程度和技术等级分别编制分布数列。
(2)按组距20~30岁,30~40岁,40~50岁,50岁以上分组。
2.某车间50名职工工资资料如下:380 390 400 410 420 460 470 910 600 960560 560 570 570 580 430 480 590 590 590560 550 550 530 520 520 490 600 620 620860 790 780 680 700 720 650 630 640 630830 810 750 680 680 750 650 660 660 880要求:分别按组距50元、100元编制变量数列,并比较哪种分组更为合适。
第四章统计综合指标思考题1什么是总量指标?它有哪些分类?2时期指标与时点指标的区别有哪些?3结构相对数与比较相对数有何不同?4平均指标有几种分类?各是什么?5什么是变异指标?它有几种形式?各是什么?习题1.某公司所属甲、乙两分公司销售额资料如下:金额单位:万元计算上表各空栏数字,并分别说明各是什么类型的指标。
2.某地区2004年计划利税比上年增长20%,实际利税为上年利税的1.6倍,试计算该地区2004年利税计划完成程度。
统计学原理任务四统计分析——静态分析法

4.2
二、相对指标的种类及计算
(一)计划完成相对指标 3.中长期计划完成情况的检查 中长期计划一般指五年计划、十年计划和远景规划等。 其完成情况的检查主要包括两项内容:一是计划完成的 程度,一是在超额完成计划的情况下,提前完成计划的 时间。 (1)水平法 水平法适用于在计划制定中,以计划期最 后一年应达到的能力水平为目标的情况。 用水平法检查中长期计划完成情况时,只要在连续长度 为1年的时间(不论是否在1个日历年度内)内实际达到 水平恰好等于计划规定的最后一年应达到的水平,就算 完成了计划,则余下的时间为提前完成计划的时间。 计划期末年实际达到水 平 计划完成相对指标= 100% 计划期末年规定应达到 水平
4.1
二、总量指标的种类
(一)总量指标按其说明的总体内容不同,可分为总 体单位总量和总体标志总量。 总体单位总量是反映总体内个体单位数量多少的总量 指标,简称为总体总量或单位总量。 总体标志总量是反映总体单位的标志值总和的总量指 标,简称为标志总量。 需要注意的是,一个总量指标究竟属于总体单位总量 还是属于总体标志总量,并不是固定不变的,它会随 着研究目的及研究对象的变换而变换。
4.2
二、相对指标的种类及计算
例4-2 某公司计划规定劳动生产率2000年比1999年提高 8%,实际提高了10%,则该公司劳动生产率计划完成相 对数为: 1+ 10% 计划完成相对数= 100%= 105.8% 1+8% 例4-3 某工业企业某产品上年度实际成本为400元,本 年度计划降低5%,实际降低了6%,则该工业企业产品 单位成本的计划完成相对数为: 1 6% 计划完成相对数= 100 % 98.95% 1 5%
统计学概论课后答案第章统计指数习题解答

统计学概论课后答案第章统计指数习题解答 TTA standardization office【TTA 5AB- TTAK 08- TTA 2C】第八章 对比分析与统计指数思考与练习一、选择题:1.某企业计划要求本月每万元产值能源消耗率指标比去年同期下降5%,实际降低了%,则该项计划的计划完成百分比为( d )。
a. %b. %c. %d. %2.下列指标中属于强度相对指标的是( b )。
a..产值利润率b.基尼系数c. 恩格尔系数d.人均消费支出3.编制综合指数时,应固定的因素是(c )。
a .指数化指标 b.个体指数 c.同度量因素 d.被测定的因素4.指出下列哪一个数量加权算术平均数指数,恒等于综合指数形式的拉氏数量指标指数(c )。
a .1010p q p q k q ∑∑;b.1111p q p q k q ∑∑;c.000p q p q k q ∑∑; d.101p q p q k q ∑∑5.之所以称为同度量因素,是因为:(a )。
a. 它可使得不同度量单位的现象总体转化为数量上可以加总;b. 客观上体现它在实际经济现象或过程中的份额;c. 是我们所要测定的那个因素;d. 它必须固定在相同的时期。
6.编制数量指标综合指数所采用的同度量因素是(a ) a . 质量指标 b .数量指标 c .综合指标 d .相对指标7.空间价格指数一般可以采用( c )指数形式来编制。
a .拉氏指数 b.帕氏指数 c.马埃公式 d.平均指数二、问答题:1.报告期与基期相比,某城市居民消费价格指数为110%,居民可支配收入增加了20%,试问居民的实际收入水平提高了多少?解:(1+20%)/110%-100%=%-100%=%2.某公司报告期能源消耗总额为万元,与去年同期相比,所耗能源的价格平均上升了20%,那么按去年同期的能源价格计算,该公司报告期能源消耗总额应为多少?解:÷(1+20%)=24万元3.编制综合指数时,同度量因素的选择与指数化指标有什么关系同度量因素为什么又称为权数它与平均指数中的权数是否一致解:(略)4.结构影响指数的数值越小,是否说明总体结构的变动程度越小?一般说来,当总体结构发生什么样的变动时,结构影响指数就会大于1。
[财经类试卷]统计分析概论练习试卷2及答案与解析
![[财经类试卷]统计分析概论练习试卷2及答案与解析](https://img.taocdn.com/s3/m/9b0dd009b4daa58da0114a51.png)
统计分析概论练习试卷2及答案与解析一、多项选择题以下每小题至少有两项正确答案,每选对一项得0.5分,全部选对得满分。
多选或错选不得分。
1 统计分析的特点是( )。
(A)以统计数据为依据,利用统计数据说活(B)定量分析与定性分析相结合(C)统计分析方法具有特殊性(D)统计分析的对象具有综合性(E)统计分析的范围具有广泛性2 统计分析中的定性分析是指对客观事物进行逻辑推理式的分析研究,以寻求事物的 ( )。
(A)数量表现(B)数量关系(C)决定事物本质的数量界限(D)本质(E)规律3 统计分析的作用具体表现为( )。
(A)深化统计认识(B)是发挥统计整体功能,提高统计工作地位的重要手段(C)有助于探寻自然发展规律(D)有助于提高统计人员的分析能力(E)是增进社会了解统计的重要窗口4 统计分析中,综合分析的特点是( )。
(A)研究对象的复杂性(B)分析内容的全面性(C)分析方法的综合性(D)针对性强(E)可以提高时效性5 企业对生产经营活动的各方面、各环节、各因素进行全面评价,据以反映工业生产经营活动的基本状况和特点,揭示其发展变化的规律性,是( )。
(A)综合分析(B)专题分析(C)宏观经济分析(D)中观经济分析(E)微观经济分析6 统计分析的第一步就是选题,一个好的选题应符合的要求是( )。
(A)选题要切合实际(B)选题要解放思想(C)选题要新颖独到(D)选题要有针对性(E)选题要切实可行7 分析提纲是进行统计分析前的一种设想,拟定分析提纲包括( )。
(A)分析目的和要求以及从哪些方面进行分析(B)建立分析指标体系(C)分析所需的资料以及资料来源和资料取得的方式(D)分析所用的方法(E)分析结果的表达形式8 有经验的分析人员在利用资料进行分析之前,一般都要对下列( )问题进行判断。
(A)资料的可信程度(B)资料的一致性(C)资料的计量水平(D)资料的全面性和系统性(E)资料的可行性9 统计分析虽然是从数据入手,但在分析过程中,始终是( )两者相结合的。
统计学概论-习题参考答案

2010年《统计学概论》练习题参考答案一、单项选择题1-5:CAACA 6-10: BBCCC 11-15:DACBC16-20:DCDDC21-25: DCDAA 26-30: BBDAC 31-35: CACDD 36-40: ABCBB41-45: AABBB 46-50: CDBDB 51-55:ABBDC 56-60: ACBCC61-64:CAAB二、多项选择题1.ABCE 2.ABC 3.ACD 4.ACD 5.ACE6.ABCE 7.ABCDE 8.ABD 9.BCD 10.AE11.ACD 12.ABCD 13.ABC 14.BCD 15.BCDE16.BCE 17.ABD 18.ACD 19.ADE 20.BCDE21.AD 22.ABC 23.ACD 24.ACDE三、判断题1-10 对错对对对错对对错错11-20 错错错对对对对对对对四、名词解释1.总体与样本-------总体是客观存在的具有相同性质的许多个体的集合,具有同质性、大量性、变异性的特点。
样本是从总体中抽取出来的部分个体的集合,样本是用来推断总体的,样本同样具有同质性、大量性和变异性的特点。
2.标志和指标-------标志是说明总体单位特征的名称,有可以用文字说明的品质标志和用数值表示的数量标志。
指标是说明总体特征的,有总量指标、相对指标、平均指标等区分,所有的指标都是或只能用数字来表示。
3.变量数列-----又称变量分布数列,是总体按数量标志分组所形成数列。
变量数列分为单项数列和组距数列。
4. 复合分组--------对同一总体选择两个或两个以上的标志进行的分组,又分平行分组和交叉分组两种情况。
复合分组便于对总体内部的差别和关系有更深入的分析。
5.中位数、众数----两者都是位置平均数。
中位数是将总体各单位标志值按一定的顺序进行排序后,处于中间位置的那个标志值。
众数则是在分组的情况下,出现次数最多的那个标志值。
自考统计学概论试题及答案

自考统计学概论试题及答案一、选择题(每题2分,共20分)1. 下列哪项不是统计学中常用的数据类型?A. 分类数据B. 顺序数据C. 定量数据D. 时间数据答案:D2. 在统计学中,哪个术语描述了数据的离散程度?A. 方差B. 均值C. 中位数D. 众数答案:A3. 下列哪项不是描述性统计的目的?A. 组织数据B. 描述数据C. 预测未来数据D. 展示数据分布答案:C4. 总体参数和样本统计量的主要区别是什么?A. 总体参数是未知的,样本统计量是已知的B. 总体参数是从样本中计算得出的C. 总体参数描述的是整个总体,样本统计量描述的是样本D. 总体参数通常比样本统计量更准确答案:C5. 一个变量的期望值是指什么?A. 该变量的平均值B. 该变量的中位数C. 该变量的最可能值D. 该变量的标准差答案:A6. 在正态分布中,哪个数值能够将数据分为两个相等的部分?A. 均值B. 中位数C. 众数D. 标准差答案:A7. 以下哪个统计量用于衡量两个变量之间的线性关系?A. 相关系数B. 回归系数C. 方差D. 标准差答案:A8. 一个样本的方差与总体方差相比:A. 总是更大B. 总是更小C. 取决于样本大小D. 无法比较答案:B9. 下列哪项是统计推断的一部分?A. 计算样本均值B. 估计总体参数C. 绘制直方图D. 排序数据答案:B10. 置信区间的宽度主要受哪些因素的影响?A. 样本大小B. 总体方差C. 置信水平D. 所有上述因素答案:D二、简答题(每题10分,共30分)1. 请简述统计学中的中心极限定理,并说明其在实际应用中的重要性。
答案:中心极限定理是统计学中的一个基本定理,它指出,如果从具有任意概率分布的总体中抽取足够大的样本,那么这些样本的均值的分布将趋近于正态分布。
这一定理的重要性在于,它允许研究者即使在总体分布未知的情况下,也能使用正态分布的性质来进行统计推断。
2. 什么是回归分析?它在数据分析中扮演什么角色?答案:回归分析是一种统计方法,用于研究一个或多个自变量(解释变量)和因变量(响应变量)之间的关系。
统计学期末复习题(大题附答案)

• (二)动态趋势分析
– 1、动态数列发展变化的四种趋势 – 2、了解测定长期趋势的方法
七、相关与回归分析
• • • • • • (一)相关与回归分析的主要内容 (二)相关系数的计算及性质 (三)相关分析与回归分析的关系 (四)回归方程的建立 (五)b与r的关系 (六)估计标准误差的计算及与r的关系
八、指数
(一)综合指数的计算 1、数量指标指数的计算 2、质量指标指数的计算 (二)平均数指数的计算 1、算术平均数指数 2、调和平均数指数 (三)指数体系
九 习题
• 1.某班40名学生统计学考试成绩分别为: 57 89 49 84 86 87 75 73 72 68 75 82 97 81 67 81 54 79 87 95 76 71 60 90 65 76 72 70 86 85 89 89 64 57 83 81 78 87 72 61 学校规定,60分以下为不及格,60-70分为及格, 70-80分为中,80-90分为良,90-100分为优 要求:将该班学生分为不及格、及格、中、良、 优五组,编制一张次数分布表; 绘制直方图,并分析本班学生的考试情况。
甲 乙 丙
15 20 30
2100 3000 1500
215 75 50
• 根据上述资料计算并说明哪一年的总平均 成本高。
•7.甲、乙两单位职工资料,试判断哪家单位的平均工资 更具代表性?
甲单位 工资x甲 555 570 595 615
合计
乙单位 人数 f乙 10 24 2 4 40 560 575 597 620
(1)下半年平均人数(首末折半法)
b b1 b2 b3 n 2 b 2 n 1 2850 2750 2680 2800 2780 2850 2840 2 2 2784 6
动态分析方法 习题及答案

第四章动态分析方法习题答案一、名词解释用规范性的语言解释统计学中的名词。
1. 动态数列:是将某种现象的指标数值按时间先后顺序排列而成的统计数列。
2. 平均发展水平:是将不同时期的发展水平加以平均而得到的平均数。
3. 增长量:是说明社会经济现象在一定时期内所增长的绝对数量。
4. 平均发展速度:是各个时期环比发展速度的序时平均数。
5. 长期趋势:是研究某种现象在一个相当长的时期内持续向上或向下发展变动的趋势。
6. 季节变动:是由自然季节变化和社会习俗等因素引起的有规律的周期性波动。
二、判断改错对下列命题进行判断,在正确命题的括号内打“√”;在错误命题的括号内打“×”,并在错误的地方下划一横线,将改正后的内容写入题下空白处。
1. 时期指标与时点指标都是通过连续登记的方式取得统计资料的。
(×)时点指标是通过一次性登记方式取得资料2. 增长量指标反映社会经济现象报告期比基期增长(或减少)的绝对量。
(√)3. 相邻两个时期的累计增长量之差,等于相应时期的逐期增长量。
(√)4. 累计增长量等于相应时期逐期增长量之和。
(√)5. 环比发展速度的连乘积等于定基发展速度,相邻两个时期的定基发展速度之和等于环比发展速度。
(×)之比6. 增长1%的绝对值可以用增长量除以增长速度求得,也可以用基期水平除以100求得。
(×)(增长量除以增长速度)/1007. 利润指标是总量指标,当发生亏损时指标数值相加不仅未增加反而减少,可见时期指标数值大小与时间长短无关。
(×)8. 平均增长量不是序时平均数,而属于静态平均数的范畴,因为它是用简单算术平均法计算求得的。
(×)是,属于动态平均数9. 循环变动是指现象的周期在一年内的变动。
(×)若干年(或一年以上)10. 现象的不规则变动是由各种偶然因素引起的有周期、无规律的变动。
(×)无六、简答题根据题意,用简明扼要的语言回答问题。
静态分析指标 习题及答案

第三章静态分析指标习题答案一、名词解释用规范性的语言解释统计学中的名词。
1. 总量指标:指反映在一定时间、空间条件下某种现象的总体范围、总体规模、总体水平的指标。
2. 强度相对数:指同一时期两个性质不同但有一定联系的总量指标之比。
3. 平均指标:指将同质总体内各单位某一数量标志的差异抽象化,用以反映同类现象在具体条件下的一般水平。
4. 算术平均数:指总体标志总量与总体单位总量之比,它是分析社会经济现象一般水平和典型特征的最基本指标。
5. 调和平均数:指总体各单位标志值倒数的算术平均数的倒数,也称为倒数平均数。
6. 众数:指总体中出现次数最多的标志值,它能直观地说明客观现象分配中的集中趋势。
7. 中位数:指现象总体中各单位标志值按大小顺序排列,居于中间位置的那个标志值。
8. 标准差:指总体各单位标志值与其算术平均数离差平方的平均数的算术平方根。
9. 标志变异指标:指反映总体各单位标志值之间差异大小的综合指标,又称为标志变动度。
二、判断改错对下列命题进行判断,在正确命题的括号内打“√”;在错误命题的括号内打“×”,并在错误的地方下划一横线,将改正后的内容写入题下空白处。
1. 总量指标(或称为绝对指标)随着总体范围的扩大而增加。
(√)2. 总量指标会随着时间范围的扩大而增加。
(×)时期3. 总体单位总量和总体标志总量是不能转化的。
(×)是可以互相转化的4 以国有商业企业为总体,则所有的国有商业企业的总数就是总体单位总量,所有的国有商业企业的职工人数、商品流转额、利税额的合计数就是标志总量。
(√)5. 我国某地区人均粮食产量为480公斤,这一指标是平均指标。
(×)强度相对指标6. 某企业为了节约成本、提高效益,对成本实行定额管理,计划本期成本比上期成本降低5%,实际执行结果是降低了4%,该企业成本计划完成程度为4%/5%=80%。
(×)96%/95%=101.05%7. 某年武汉市地区生产总值为北京市的80%,这一指标属于比较相对指标。
回归分析练习题及参考答案
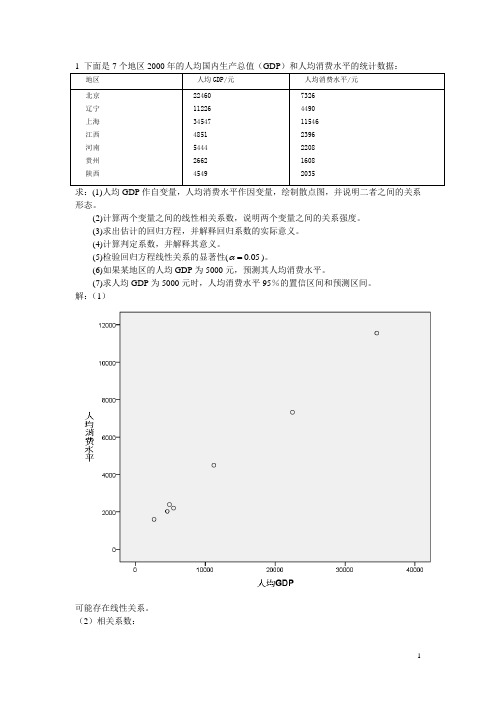
1 下面是7个地区2000年的人均国内生产总值(GDP)和人均消费水平的统计数据:地区人均GDP/元人均消费水平/元北京辽宁上海江西河南贵州陕西 224601122634547485154442662454973264490115462396220816082035求:(1)人均GDP作自变量,人均消费水平作因变量,绘制散点图,并说明二者之间的关系形态。
(2)计算两个变量之间的线性相关系数,说明两个变量之间的关系强度。
(3)求出估计的回归方程,并解释回归系数的实际意义。
(4)计算判定系数,并解释其意义。
(5)检验回归方程线性关系的显著性(0.05α=)。
(6)如果某地区的人均GDP为5000元,预测其人均消费水平。
(7)求人均GDP为5000元时,人均消费水平95%的置信区间和预测区间。
解:(1)可能存在线性关系。
(2)相关系数:(3)回归方程:734.6930.309y x=+回归系数的含义:人均GDP没增加1元,人均消费增加0.309元。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
系数(a)模型非标准化系数标准化系数t 显著性B 标准误Beta1 (常量)734.693 139.540 5.265 0.003人均GDP(元)0.309 0.008 0.998 36.492 0.000 a. 因变量: 人均消费水平(元)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%(4)模型汇总模型R R 方调整 R 方标准估计的误差1 .998a.996 .996 247.303a. 预测变量: (常量), 人均GDP。
人均GDP对人均消费的影响达到99.6%。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
统计学概论练习题及参考答案

2013年《统计学概论》练习题一、单项选择题1.统计学的两大基本内容是( )A .统计资料的收集和分析B .理论统计和运用统计C .统计预测和决策D .描述统计和推断统计 2.下面的变量中哪一个属于分类变量( )A .年龄B .工资C .汽车产量D .付款方式(现金、信用卡、支票) 3.下面哪一个图形最适合描述结构性问题( )A .条形图B .饼图C .直方图D .折线图 4.统计分组后,应使( )A .组内具有同质性,组间具有差异性B .组内具有差异性,组间具有同质性C .组内具有差异性,组间具有差异性D .组内具有同质性,组间具有同质性 5.一组数据中出现频数最多的数值称为( )A .众数B .中位数C .四分位数D .平均数6.根据经验,当算术平均数小于中位数且小于众数时,次数分布为( )A .对称分布B .右偏分布C .左偏分布D .右偏或左偏分布7.对两个总体分布进行变异性比较,当它们的平均数不等,计量单位不同时,需要计算( )比较。
A .标准差系数B .标准差C .平均差D .方差 8.当原假设正确,按检验规则却拒绝了原假设,则犯了( )A .取伪错误B .检验错误C .第Ⅰ类错误D .第Ⅱ类错误9.每一吨铸铁成本c y (万元)和铸件废品率x (%)变动的回归方程为:568c y x =+,这意味着( )A .废品率每增加1%,成本每吨增加64万元B .废品率每增加1%,成本每吨增加8%C .废品率每增加1%,成本每吨增加8万元D .废品率每增加1%,则每吨成本为56万元10.将总体全部单位按照某个标志分组,再从各类型组中随机抽取一定单位组成样本,这种抽样是( )A .随机抽样B .等距抽样C .分层抽样D .整群抽样 11.根据经验,当算术平均数大于中位数且大于众数时,钟形分布为( )A .对称分布B .右偏分布C .左偏分布D .负偏分布 12.正态总体,总体方差σ2未知,小样本(n <30)的情况下,总体均值μ的置信度为1-α的置信区间为( )A .),(22nZ X n Z X σσαα⋅+⋅- B .),(22nS Z X n S Z X ⋅+⋅-ααC .),()1(2)1(2nS t X nS t X n n ⋅+⋅---ααD .),()1(2)1(2nt X nt X n n σσαα⋅+⋅---13.当总体方差未知时,在大样本条件下,估计总体均值使用的分布是( )A .正态分布B .t 分布C .F 分布D .χ2分布 14.当正态总体的方差未知,且为小样本条件下,估计总体均值使用的分布是( )A.正态分布B.t分布C.F分布D.χ2分布15.当备择假设为H1:μ<μ0,此时的假设检验称为()A.双侧检验B.右侧检验C.左侧检验D.显著性检验16.根据你的判断,下面的相关系数取值哪一个是错误的()A.-0.86B.0.78 C.1.25 D.017.说明回归方程拟合优度的统计量主要是()A.相关系数B.回归系数C.判定系数D.估计标准误18.在回归分析中,被预测或被解释的变量称为()A.自变量B.因变量C.随机变量D.非随机变量19.在回归分析中,用来预测或用来解释另一个变量的一个或多个变量称为()A.自变量B.因变量C.随机变量D.非随机变量20.如果相关系数r=0,则表明两个变量之间()A.相关程度很低B.相关程度较高C.不存在线性相关关系D.存在非线性相关关系二、多项选择题1.“统计”一词的基本涵义包括()A.统计学B.统计工作C.统计资料D.统计分析2.以下几项符合统计表编制规则的包括()A.统计表的标题力求简明,内容简明扼要B.统计表栏数较多时,通常要加编号,并可说明其相互关系C.统计表如有相同数字,可以写“同上”,没有数字空格即可D.统计表一般左右两端封闭,表的上下端线划粗线或双线3.非全面调查形式有()A.重点调查B.抽样调查C.典型调查D.普查4.调查问卷可以选择的问句形式包括()A.对选式问句B.多项选择式问句C.顺位式问句D.标度式问句5.下列有关假设检验的说法,正确的是()A.原假设和备择假设相互对立,而且两者只有一个正确B.假设检验的基本思想是小概率原理C.假设检验的首要步骤是建立原假设和备择假设D.根据样本推断总体,有可能犯弃真错误和取伪错误6.下列有关回归分析和相关分析的描述,正确的有()A.回归分析中,X与Y要确定自变量和因变量B.相关分析中,X与Y均为随机变量C.相关分析测定相关程度和方向D.回归分析利用回归模型进行预测和分析7.下列有关一元线性回归模型的描述正确的有()A.可以用最小平方法求解模型的两个参数a和bB.判断系数r2是测定回归直线拟合优度的一个重要指标C.回归系数的符号同相关系数的符号一致D.b>0时,表明X与Y反方向变动8.下列情况中,应采用调和平均数计算的有()A.已知各商品的单价和销售额,求平均价格B.已知各商品的单价和销售量,求平均价格C.已知采购站某月购进农产品的单价及收购量,求平均采购价格D.已知采购站某月购进农产品的单价及收购额,求平均采购价格9.下列分组中属于按品质标志分组的有()。
统计学各章习题及答案

统计学习题目录第一章绪论 _________________________________________________ 2第二章数据的收集与整理 _____________________________________ 4第三章统计表与统计图 _______________________________________ 6第四章数据的描述性分析 _____________________________________ 8第五章参数估计 ____________________________________________ 12第六章假设检验 ____________________________________________ 16第七章方差分析 ____________________________________________ 20第八章非参数检验 __________________________________________ 23第九章相关与回归分析 ______________________________________ 26第十章多元统计分析 ________________________________________ 30第十一章时间序列分析 ______________________________________ 34第十二章指数 ______________________________________________ 37第十三章统计决策 __________________________________________ 41第十四章统计质量管理 ______________________________________ 44第一章绪论习题一、单项选择题1. 推断统计学研究(D)。
A.统计数据收集的方法B.数据加工处理的方法C.统计数据显示的方法D.如何根据样本数据去推断总体数量特征的方法2. 在统计史上被认为有统计学之名而无统计学之实的学派是( D )。
统计学简答题

统计学简答题 Prepared on 22 November 2020第一章:导论1、解释描述统计和推断统计(练习卷答案)(1)描述统计是研究数据收集、处理、汇总、图表描述、概括与分析等统计方法,内容有收集数据、整理数据、展示数据、描述性分析。
(2)推断统计是研究如何利用样本数据来推断总体特征的统计学方法、包含参数估计、假设检验。
2、统计数据可分为哪几种类型不同类型的数据各有什么特点按照所采用的计量尺度不同,可以将统计数据分为分类数据、顺序数据和数值型数据特点:分类数据是只能归于某一类别的非数字型数据,它是对事物进行分类的结果,数据表现为类别,是用文字来表述的。
顺序数据是只能归于某一有序类别的非数字型数据。
顺序数据虽然也是类别,但这些类别是有序的。
数值型数据是按数字尺度测量的观察值,其结果表现为具体的数值。
现实中所处理的大多数是数值型数据。
按照统计数据的收集方法,可以将其分为观测数据和实验数据。
特点:观测数据是通过调查或观测而收集到的数据,这类数据是在没有对事物人为控制条件下得到的,有关社会经济现象的统计数据几乎都是观测数据。
实验数据则是在实验中控制实验对象而收集到的数据。
自然科学领域的大多数数据都为实验数据。
按照被描述的现象与时间关系,可以将其分为截面数据和时间序列数据。
特点:截面数据是在相同或近似相同的时间点上收集的数据,这类数据通常是在不同空间上获得的,用来描述现象在某一时刻的变化情况。
时间序列数据是在不同时间收集到的数据,这列数据是按时间顺序收集得到的,用于所描述现象随时间变化的情况。
3、解释分类数据、顺序数据和数值型数据的含义。
分类数据是只能归于某一类别的非数字型数据,它是对事物进行分类的结果,数据表现为类别,是用文字来表述的。
顺序数据是只能归于某一有序类别的非数字型数据。
顺序数据虽然也是类别,但这些类别是有序的。
数值型数据是按数字尺度测量的观察值,其结果表现为具体的数值。
现实中所处理的大多数是数值型数据。
统计学概论练习二(静态分析、动态分析、回归分析、指数分析)

《统计学概论》练习二一、判断题1、定基发展速度等于相应各个环比发展速度的连乘积,所以定基增长速度也等于相应各个环比增长速度积。
( )2、发展速度是以相对数形式表示的速度分析指标,增长量是以绝对数形式表示的速度分析指标。
( )3、众数是总体中出现次数最多的那个数。
()4、时点指标的数值大小与时点间的间隔长短没有直接联系。
()5、如果把数量指标作为同度量因素,则时期一般固定在基期。
()6、若逐期增长量每年相等,则其各年的环比发展速度是年年下降的。
( )7、已知某市工业总产值2001年至2005年年增长速度分别为4%,5%,9%,11%和6%,则这五年的平均增长速度为6.97%。
()8、计算相关系数的两个变量都是随机变量。
()9、如果某商店商品零售价格增长5%,销售量增加5%,则零售额增长10%。
()10、国民收入中积累额与消费额之比为1:3,这是一个比较相对指标。
()二、单选题1、统计指数划分为个体指数和总指数的依据是 ( )A、反映的对象范围不同B、指标性质不同C、采用的基期不同D、编制指数的方法不同2、间隔相等的时点数列计算序时平均数应采用()A、几何平均法 B、加权算术平均法 C、简单算术平均法 D、首末折半法3、1997年北京市下岗职工已安置了13.7万人,安置率达80.6%,安置率是()。
A、总量指标B、变异指标C、平均指标D、相对指标4、组距、组限、组中值之间关系是()A、组中值=(上限+下限)÷2B、组距=(上限-下限)÷2C、组中值=(上限+下限)×2D、组限=组中值÷25、某厂计划规定单位产品物耗降低3%,实际降低了4.5%,则计划完成程度为()A、98.45%B、150.00%C、66.66%D、101.46%6、已知某企业总产值2001年比1998年增长187.5%,2000年比1998年增长150%,则2001年比2000年增长()A、37.5%B、125%C、115%D、15%7、权数对算术平均数的影响作用,实质上取决于()A、作为权数的各组单位数占总体单位数比重的大小B、各组标志值占总体标志总量比重的大小C、标志值本身的大小D、标志值数量的多少8、总量指标是用()表示的A、绝对数形式B、相对数形式C、平均数形式D、百分比形式9、若物价上涨,商品的需求量相应减少,则物价与商品需求量之间的关系为( )A、不相关B、负相关C、正相关D、复相关10、标志变异指标是反映同质总体的()A、集中程度B、离中程度C、一般水平D、变动程度11、相关关系是指( )A、现象间客观存在的依存关系B、现象间客观存在的数值固定依存关系C、现象间客观存在的数值不固定依存关系D、因果关系12、直接反映总体规模大小的指标是()A、平均指标B、相对指标C、总量指标D、变异指标13、在计算x与y的回归方程式时,如果y=a+bx当b为负数时,则直线是()A、上升趋势B、不升不降C、下降趋势D、上术三种情况都可能出现14、将某企业职工人数中的管理人员与工人人数对比得到的相对指标是( )A、结构相对数B、比较相对数C、比例相对数D、强度相对数15、若某一变量数列中,有变量值为零,则不适宜计算的平均指标有()。
实训 统计实务与原理 第四章 统计静态分析指标2
一、标志变异指标1.一班和二班《统计学》平均考试成绩分别为78.6分和83.3分,成绩的标准差分别为9.5分和11.9分,可以判断()。
A一班的平均成绩有较大的代表性 B二班的平均成绩有较大的代表性C两个班的平均成绩有相同代表性 D无法判断2.比较两个单位的资料,甲的标准差小于乙的标准差,则( )A.两个单位的平均数代表性相同B.甲单位平均数代表性大于乙单位C.乙单位平均数代表性大于甲单位D.不能确定哪个单位的平均数代表性大3.若两组数据的标准差相等而平均数不等,则()。
A.平均数小代表性大B.平均数大代表性大C.代表性也相等D.无法判断4.已知某组数据的平均数是200,离散系数是30%,则该组数据的方差是___ ____。
5.某贸易公司的20个商店本年第一季度按商品销售额分组如下:个商店商品销售额的平均差为_____ ___6.当每天生产线的每小时产量低于平均每小时产量,并大于2个标准差时,该生产线被认为是“失去控制”。
对该生产线来说,昨天平均每小时产量是370件,其标准差每小时为5件。
下表所示的是该天头几个小时的产量,该生产线在时间为时,失去了控制生产线产量表时间(时)8:00 9:00 10:00 11:00 12:00 1:00 2:00产量(件)369 367 365 363 361 359 3577.对成年组和幼儿组共500人身高资料分组,分组资料列表如下:要求:(1)分别计算成年组和幼儿组身高的平均数、标准差和标准差系数。
(2)说明成年组和幼儿组平均身高的代表性哪个大?为什么?8.已知甲班的统计学课程期末考试成绩,见下表:平均考试成绩的代表性高低。
一、基础实训1.时间数列是将总体某一个在不同时间上的指标值,按先后顺序排列而成。
2.时间数列由两个要素构成:一个是指标值所属的;另一个是各时间上的。
3.平均发展速度是的序时平均数,它有和两种计算方法。
4.动态数列的水平指标有、、和等。
5.动态数列的速度指标有、、和等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《统计学概论》练习二
一、判断题
1、定基发展速度等于相应各个环比发展速度的连乘积,所以定基增长速度也等于相应各个环比增长速度积。
( )
2、发展速度是以相对数形式表示的速度分析指标,增长量是以绝对数形式表示的速度分析指标。
( )
3、众数是总体中出现次数最多的那个数。
()
4、时点指标的数值大小与时点间的间隔长短没有直接联系。
()
5、如果把数量指标作为同度量因素,则时期一般固定在基期。
()
6、若逐期增长量每年相等,则其各年的环比发展速度是年年下降的。
( )
7、已知某市工业总产值2001年至2005年年增长速度分别为4%,5%,9%,11%和6%,则这五年的平均增长速度为6.97%。
()
8、计算相关系数的两个变量都是随机变量。
()
9、如果某商店商品零售价格增长5%,销售量增加5%,则零售额增长10%。
()
10、国民收入中积累额与消费额之比为1:3,这是一个比较相对指标。
()
二、单选题
1、统计指数划分为个体指数和总指数的依据是 ( )
A、反映的对象范围不同
B、指标性质不同
C、采用的基期不同
D、编制指数的方法不同
2、间隔相等的时点数列计算序时平均数应采用()
A、几何平均法 B、加权算术平均法 C、简单算术平均法 D、首末折半法
3、1997年北京市下岗职工已安置了13.7万人,安置率达80.6%,安置率是()。
A、总量指标
B、变异指标
C、平均指标
D、相对指标
4、组距、组限、组中值之间关系是()
A、组中值=(上限+下限)÷2
B、组距=(上限-下限)÷2
C、组中值=(上限+下限)×2
D、组限=组中值÷2
5、某厂计划规定单位产品物耗降低3%,实际降低了4.5%,则计划完成程度为()
A、98.45%
B、150.00%
C、66.66%
D、101.46%
6、已知某企业总产值2001年比1998年增长187.5%,2000年比1998年增长150%,则2001
年比2000年增长()
A、37.5%
B、125%
C、115%
D、15%
7、权数对算术平均数的影响作用,实质上取决于()
A、作为权数的各组单位数占总体单位数比重的大小
B、各组标志值占总体标志总量比重的大小
C、标志值本身的大小
D、标志值数量的多少
8、总量指标是用()表示的
A、绝对数形式
B、相对数形式
C、平均数形式
D、百分比形式
9、若物价上涨,商品的需求量相应减少,则物价与商品需求量之间的关系为( )
A、不相关
B、负相关
C、正相关
D、复相关
10、标志变异指标是反映同质总体的()
A、集中程度
B、离中程度
C、一般水平
D、变动程度
11、相关关系是指( )
A、现象间客观存在的依存关系
B、现象间客观存在的数值固定依存关系
C、现象间客观存在的数值不固定依存关系
D、因果关系
12、直接反映总体规模大小的指标是()
A、平均指标
B、相对指标
C、总量指标
D、变异指标
13、在计算x与y的回归方程式时,如果y=a+bx当b为负数时,则直线是()
A、上升趋势
B、不升不降
C、下降趋势
D、上术三种情况都可能出现
14、将某企业职工人数中的管理人员与工人人数对比得到的相对指标是( )
A、结构相对数
B、比较相对数
C、比例相对数
D、强度相对数
15、若某一变量数列中,有变量值为零,则不适宜计算的平均指标有()。
A、算术平均数
B、调和平均数
C、中位数
D、众数
三、简答题
1、简述品质标志与数量标志的区别
2、什么是环比发展速度?什么是定基发展速度?二者有何关系?
3、简述强度相对指标与平均指标的区别?
4、平均指数的基本含义是什么?有哪几种计算形式?
5、什么是时期数列和时点数列?二者相比较有什么特点?
6、从现象总体数量依存关系来看,函数关系和相关关系有何联系和区别?
四、统计业务题
1、某班40名学生统计学考试成绩分别为:
68 89 88 84 86 87 75 73 72 68
75 82 97 58 81 54 79 76 95 76
71 60 90 65 76 72 76 85 89 92
64 57 83 81 78 77 72 61 70 81
要求:(1)根据上面的数据进行适当的分组,编制次数分布表;
(2)如果学校规定:60分以下为不及格,60─70分为及格,70─80分为中, 80─90分为
良,90─100分为优。
要求将该班学生按照不及格、及格、中、良、优,进行分组。
2
要求:计算该集团工人的平均工资。
3、有两个生产小组,都有5 个工人,某天的日产量件数如下:
甲组:8 10 11 13 15
乙组:10 12 14 15 16
要求:计算各组的算术平均数、全距、平均差、标准差和标准差系数,并说明哪个组的平均数
更具有代表性。
4
要求:根据资料: (1)建立学习成绩(y )与学习时间(x )的直线回归方程;
(2)计算学习时数与学习成绩之间的相关系数。
要求:计算三个企业的平均计划完成程度。
7、某商场三种商品的价格及销售量资料如下:
要求:(1)运用拉斯贝尔公式,编制销售量指标指数,并分析销售量的变动对销售额的影响;
(2)运用派许公式,编制价格指标指数,并分析销售价格的变动对销售额的影响。
