子程序的应用(教案)
数控加工与编程车项目五子程序教案

学习情境五学习情境二:不等距槽零件的加工(详案)23一、情境描述给学生发放零件图,并给出零件信息和加工要求。
图5.1 零件图4图5.2 三维图图示零件为不等距槽的一轴类零件,该零件加工表面有外圆柱面、切槽等,要求使用子程序调用的方法进行数控程序的编制,并完成零件的车削加工。
二、制订加工工艺(一)引入新知识1.引入新指令暂停指令---G04格式:G04 X/P___;参数:X、P为暂停时间,X后跟数值单位为s;P后跟数值单位为ms,且后跟数值不能用小数点表示。
应用:车削沟槽或钻孔时,加工到槽底或孔底时刀具做适当时间暂停,使工件回转一周以上,以确保槽底或孔底得到精确的尺寸及光滑的加工表面。
说明:G04在前一程序段的进给速度降到零之后才开始暂停动作;G04为非模态指令,仅在其被规定的程序段中有效;G04可使刀具作短暂停留,以获得圆整而光滑的表面。
2.切槽加工①车削精度不高和宽度较窄的沟槽,可用刀宽等于槽宽的切槽刀,采用直进法一次加工。
②车削精度高的沟槽,可用多次直进法切削,见图5.3所示,并在槽的两侧留一定的精车余量,然后精车至尺寸。
56图5.3 多次直进法切槽3.切断加工切断方法:直进法和左右借刀法,如图5.4所示。
直进法常用于切断铸铁等脆性材料;左右借刀法常用于切断钢等塑性材料。
(a )直进法 (b )左右借刀法图5.4 切断方法(二)零件具体加工工艺制定 1.装夹与定位该零件为轴类零件,其轴心线为工艺基准,用三爪自定心卡盘夹持φ32mm 外圆左 端,使工件伸出卡盘约65mm ,一次装夹完成加工。
2.工步顺序从右端至左端轴向进给切削。
先进行外圆加工,再进行切槽,最后进行切断。
① 装夹工件; ② 车削端面; ③ 加工φ30mm 外圆;; ④ 切槽至φ20mm ; ⑤ 切断。
3.选择刀具根据零件加工要求和加工工艺分析,选用二把刀具:T01 为外圆车刀、T02 为切断刀。
4.确定切削用量车削用量的具体数值应根据机床性能、加工工艺、相关手册并结合实际经验确定:机床转速:外圆加工为800r/min,切槽和切断为400r/min。
江苏中职数控编程技术学案:4.3 子程序(一)

【学习目标】
1.了解子程序的概念及运用。
2.掌握采用子程序的编程方法。
【重点难点】
能熟练运用子程序功能编程
【建议学时】
3
【课前预习】
子程序
1)定义
2)格式
【课堂探究】
课堂步骤
探究内容
探究方式
问题探究
1.子程序的定义
2.子程序的格式
3.子程序的调用
格式一:
格式二:
交流讨论
知识链接
节点坐标的计算
展示结论
提高拓展
提出问题
解决问题
考题回放
锥度计算方法;
总结提高
【课堂检测】
例:在96mm×60mm×15mm的毛坯上加工如图所示六个相同的外形轮廓,试采用子程序编程方式编写
【回扣目标】
1.了解子程序的概念及运用。
2.掌握采用子程序的编程方法。
【课后作业】
Байду номын сангаас整理相关笔记;
“子程序的应用”的教学设计

( ) 问题 情 景 中理 解相 关知识 的 内 涵和 意 要求同学们在计算机上运用仿真软件进行模拟操 二 在
2 . 练习。 学生将 自己所编制的程序运用到计算 行数控加工程序 的编制 , 并对所编制 的程序进行 机上 , 进行仿真训练 , 通过交流 , 充分发表观点 , 教 分析 。 师引导评价 , 帮助学生提炼出核心问题 , 并对子程
工, 证实是完全正确的、 可行的。
3 . 设计意图。在现代教育中, 仿真技术可以对 为复 杂 的 问题就 显得 简单 了 。同学们 通 过 改变 子 信息进 行加工处理 、 显示 、 重放 、 模拟 、 仿真 , 如果 程序名 、 子程序结束符 、 子程序 的格式等 , 很快就
再辅 以动 画技术 ,可 以使 一 些在 普 通条 件 下无 法
Vo .4 1 2
Ge e a . 5 n rl No21
“ 子程序 的应用’ ’ 学设 计 的教
张 守 燕
( 苏省射 阳职业教 育 中心校 , 江 江苏 盐城 2 4 0 ) 2 3 0
摘
要 :以建 构主义学 习理论 为指导设计“ 子程 序的应甩” 的教学方案 , 通过创设 学习情境 。引导学 生在协作 、 探
要性 。产生 对新 学 习任务 的兴趣 ,从 而 主动 地 采 建 构 的平衡 。
集、 分析 、 提炼信息 。在此过程中, 形成对“ 子程 序
的应用” 的初步认识 , 了解相关命令的运用 。
义
( ) 仿 真 、 拟情 境 中学 习 三 在 模
1 . 任务。教师呈现具体的实践操作的任务 , 并
究等主体 活动 中主动建构知识意义, 实现教 学三维 目标 。
关键词 : 子程序的应用” 教 学设 计 “ ;
数控加工子程序的应用

任务二:轮廓零件数控加工
2. 子程序的嵌套
主程序可以调用子程序,同时子程序也可调用另一个子程序,即 子程序的嵌套。
系统不同,其子程序的嵌套级数也不相同。一般情况下,在FANUC 0系统中,子程序可以嵌套4级。
只编写一个轮廓形状的加工程序,然后用主程序来调用子程序。如本 任务所示。
子程序加工相同轮廓
任务二:轮廓零件数控加工
2.实现零件的分层切削
当零件在Z方向上的总铣削深度比较大时,需采用分层切削方
式进行加工。实际编程时先编写该轮廓加工的刀具轨迹子程序, 然后通过子程序调用方式来实现分层切削。
Z向分层切削
➢ 主程序用M02或M30表示主程序结束。 ➢ 子程序则用M99表示子程序结束,并自动返回主程序。
任务二:轮廓零件数控加工
二、子程序的格式与调用
子程序的调用通过辅助功能M98进行,常用程序段格式有以下两种情况: 1)M98 PxxxxLxxxx;
P后面的四位数字表示调用的子程序号,L后面的四位数字表示重复 调用的次数。如果只调用一次,则L及其后面的数字可省略不写。 2)M98Pxxxxxxxx;
任务二:轮廓零件数控加工
二、子程序的格式与调用
1. 子程序的格式
O0100; G54; M03S800; G00 Z100; X20.Y30. Z2. G01 Z-2.0 F100;
…… G00Z100; M99;
任务二:轮廓零件数控加工
二、子程序的格式与调用 1. 子程序的格式
子程序和主程序并无本质区别。子程序和主程序在程序号及程序内 容方面基本相同,但结束标记不同。
子程序的应用(教案)

在完成这个任务时,需要3次使用画Y=SIN(X+C)的正弦函数图像的程序,只是每次C,D的取值不同,因此把画Y=SIN(X+C)图像的一段程序写成子程序,然后在主程序中使用FOR循环语句反复调用它。
具体步骤如下:
1、写出画Y=SIN(X+C)图像的子程序
2、在主程序中实际参数用变量M,N来对应形式参数C,D
此教案中的例1、例2、例3、例4程序分别对应的QBASIC中调试程序TD1.bas,TD2.bas,
TD3.bas, TD4.bas
其中TD1.bas,TD2.bas,TD3.bas, TD4.bas程序均放在文件夹QBASIC中
2004年7月
y=sin(x+c)
pset (x,y),d
for j=1 to 1000
next j
next x
end sub
三、小结:
本节我们通过实际应用来进一步理解子程序的有关概念,同时也是加强我们的分析问题、解决问题的能力,并不断地提高我们的编程水平。
四、作业(略)
注:以上程序均在QBASIC程序环境下调试通过
3、根据C,D的3次取值不同,在主程序中用FOR循环语句调用子程序3次
4、因C,D的值已知,故用READ语句读入初值,即READ M,N,具体的值由DATA语句提供
具体程序如下:
主程序:
declare sub chuxiang(c!,d!)
forI=1 to 3
read m,n
call chuxiang(m,n)
具体程序如下:
主程序:
Declare sub huayuan( )
Declare sub huashanjiaoxing( )
《子程序应用》教案、教学设计自己的
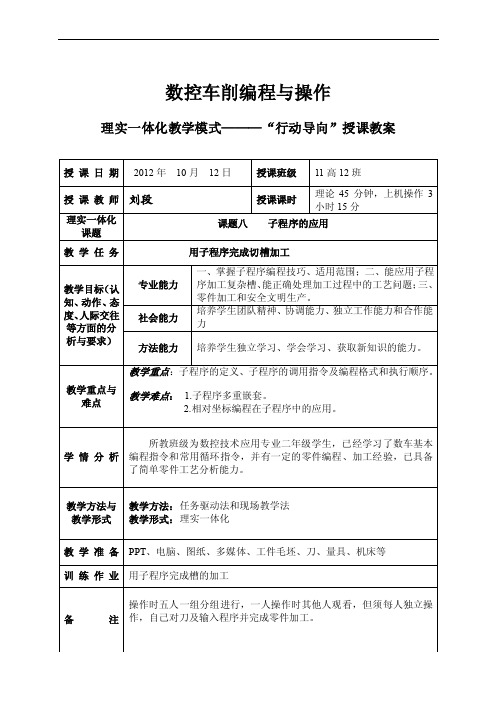
数控车削编程与操作理实一体化教学模式———“行动导向”授课教案授课日期2012年10月12日授课班级11高12班授课教师刘段授课课时理论45分钟,上机操作3小时15分理实一体化课题课题八子程序的应用教学任务用子程序完成切槽加工教学目标(认知、动作、态度、人际交往等方面的分析与要求)专业能力一、掌握子程序编程技巧、适用范围;二、能应用子程序加工复杂槽、能正确处理加工过程中的工艺问题;三、零件加工和安全文明生产。
社会能力培养学生团队精神、协调能力、独立工作能力和合作能力方法能力培养学生独立学习、学会学习、获取新知识的能力。
教学重点与难点教学重点:子程序的定义、子程序的调用指令及编程格式和执行顺序。
教学难点: 1.子程序多重嵌套。
2.相对坐标编程在子程序中的应用。
学情分析所教班级为数控技术应用专业二年级学生,已经学习了数车基本编程指令和常用循环指令,并有一定的零件编程、加工经验,已具备了简单零件工艺分析能力。
教学方法与教学形式教学方法:任务驱动法和现场教学法教学形式:理实一体化教学准备PPT、电脑、图纸、多媒体、工件毛坯、刀、量具、机床等训练作业用子程序完成槽的加工备注操作时五人一组分组进行,一人操作时其他人观看,但须每人独立操作,自己对刀及输入程序并完成零件加工。
模块一数控车床的编程与操作数车基本模块FANUC系统数控车床编程及操作课题八子程序应用◎项目说明:◎通过子程序指令的分析与编程方法的讲解,使学生掌握槽的加工与编程方法,为螺纹加工及综合复杂零件的加工做好准备。
◎能力点◎子程序指令的正确应用能力;◎准确控制切槽宽度保证零件加工精度并具备分析切槽质量的能力◎加工各种槽的能力。
◎知识点◎子程序的编程方法◎本课设计思想项目教学过程是以行动为导向的教学过程——“行动即学习”:“为了行动而学习”和“通过行动来学习”本课的任务是让学生掌握运用子程序进行编程加工,这是一个目的和任务很明确且实践性很强的教学项目,为完成这一项目,采用“行为导向”理实一体化形式进行教学。
数控车床编程与操作--子程序的调用(说课)

G0 Z-23;B G0 U12;
M98 P0002; W-2;
G0 Z-33;C G1 U-12;
M98 P0002; G0 U12;
G0 X100 Z100;M99;
M30;
h
21
组 合子件程的序数的控调车 削用
说课稿
教学过程
1 理论学习 2 仿真训练 3 机床操作
提出问题
任务描述
任务分析
小组协作、讨论交流 完成另两槽
1 理论学习 2 仿真训练 3 机床操作
h
说课稿
17
组 合子件程的序数的控调车 削用
教学过程
1 理论学习 2 仿真训练 3 机床操作
提出问题
任务描述
引入新课
创设问题情境,观看加工视频 外加工件图
是否能简化? 用什么简化? 怎么来简化?
说课稿
任务分析
h
18
组 合子件程的序数的控调车 削用
说课稿
教学过程
1 任务驱动法 2 个性与协作法 3 理实一体法
理论实践一体化教学法:
实践前学习理论, 理论中仿真实践, 实践中运用理论; 实践后总结理论。
说课稿
h
13
组 合子件程的序数的控调车 削用
1 学情分析 2 学法指导
学法分析
说课稿
h
14
组 合子件程的序数的控调车 削用
学法分析
说课稿
1 学情分析 2 学法指导
愿意学 想学好的
能编制基础程序
但学生对本节课的一些内容、新的编程方法和 操作方法仍比较陌生。学生的抽象思维能力,探 究能力有待培养和提高。
h
15
组 合子件程的序数的控调车 削用
1 学情分析 2 学法指导
《子程序应用》说课稿

《子程序应用》说课稿尊敬的各位评委、各位同仁,大家好:切换幻灯片我叫刘段,来自湖南省,我今天说课的题目是《子程序应用》。
切换幻灯片本次说课内容,我将从教材、重点难点、教法学法、教学过程、教学反思五个方面来向大家讲述子程序应用的教学设计。
切换幻灯片《数控车削编程与操作训练》是由高等教育出版社出版的,本书结合了职业教育的特点,注重理论联系实践,易教易学,是我校数控技术专业学生的专用教材,子程序是本书重要内容之一,无论是数车、数铣、加工中心编程都会运用到子程序,因此,学生在编程过程中如能根据零件结构灵活运用子程序,可大大的提高编程效率。
切换幻灯片本次授课对象为我校11级数控技术应用专业的学生,全部为男生。
学生思维活跃,动手能力强,勇于创新,乐于创新,学生对数控编程与操作有着较大的学习兴趣,大部分同学有较强的求知欲。
他们已经完成了数车基本指令和一些常用循环指令的学习,并且有了一定的零件编程基础和零件加工经验切换幻灯片根据教学效果所须达到的目标要求,我确定了以培养学生的职业能力为主的行动导向教学目标。
切换幻灯片首先是专业能力目标:让学生掌握子程序编程技巧、适用范围;培养和提高学生的工艺分析能力以及零件加工能力。
方法能力目标:主要是指在整个教学过程中培养学生的分析能力,创新能力,解决问题的能力。
数控车(机工版)教案:课题十八 子程序.doc

课题十八子程序教学引入言把程序中某些固定顺序和重复出现的程序单独抽出来,按一定格式编成一个程序供调用,这个程序就是常说的子程序,这样可以简化主程序的编制。
子程序可以被主程序调用,同时子程序也可以调用另一个子程序。
这样可以简化程序的编制和节省CNC系统的内存空间。
教学目的:熟练掌握调用子程序的格式及参数的含义。
实训重难点熟练掌握调用子程序的格式及参数的含义。
实训教学方法:现场讲解、示范、让学生分组轮流操作。
任务驱动法。
实习前准备1.实习设备:(广数,华中)、工具:(卡盘扳手、刀架扳手、量具)、刀具:(外圆车刀,切断刀,螺纹刀)、材料:(塑料棒、45#钢)等准备情况。
2.集中学生,清点人数,检查着装状态、精神面貌等。
3.总结前一天实习情况,布置今天实习内容。
4.强调实习过程安全文明、遵章守纪。
实训教学内容:子程序M98、M99子程序必须有一程序号码,且以M99作为子程序的结束指令。
主过程调用子程序的指令格式如下:M98 P___L___;其中P为被调用的子程序号L为重复调用的次数例如:M98 P1234L4主程序调用同一子程序执行加工,最多可执行999次,且子程序亦可再调子程序加工实例用另一子程序执行加工,最多可调用4层子程序(不同的系统其执行的次数及层次可能不同)。
例:以HNC-21T系统子程序指令,加工图2-11工件上的四个槽。
分别编制主程序和子程序如下:主程序%123;M3 S600 G95 T0101;G00 X82.0 Z0;M98 P1234 L4;(调用于程序1234执行四次,切削四个凹槽) X150.0 Z200.0;M30;子程序%1234;W-20.0;G01 X74.0 F0.08;G00 X82.0;M99;M99指令也可用于主程序最后程序段,此时程序执行指针会跳回主程序的第一程序段继续执行此程序,所以此程序将一直重复执行,除非按下RESET键才能中断执行。
子程序的嵌套子程序调用下一级子程序称为嵌套。
《子程序应用》说课稿

《子程序应用》说课稿在学法上,学生以小组讨论的形式对我所给出的资讯进行分析、讨论、并得出结论,学生在电脑仿真软件里验证结论,模拟加工,然后在去真实的机床上实际加工零件,把理论知识逐步应用到实际操作中。
主要学法有讨论法,练习法,实践法。
切换幻灯片根据对教学目标、重难点确实定,我的《子程序应用》的教学过程主要是按照这六个环节进行的:资讯、方案、决策、实施、检查、评估。
切换幻灯片在第一个资讯环节里,我给学生一个加工零件图切换幻灯片和两个用子程序编写的加工程序。
切换幻灯片让学生根据我所给的零件图和程序,再结合教科书,找到新知识,完成我所给的资讯表。
切换幻灯片学生完成表格之后,我给学生布置了一个任务:就是让学生采用子程序编程,完成零件图中槽的加工。
资讯环节的设计是为了让学生更好地了解子程序定义及格式。
主动去思考,自主去学习,培养了学生的学习能力和知识迁移能力。
〔此环节用时10分钟〕切换幻灯片在第二个方案环节里,学生就要思考完成工作任务需要用到哪些工具,由学生自己列出清单:学生根本上都知道要用到零件图,刀具,机床,工件毛坯,量具等这些工具。
切换幻灯片在整个方案环节当中,学生讨论分析出零件图的加工工艺路线,以及如何用子程序编写出一个合理的程序。
切换幻灯片这些图片就是各小组在讨论时的情景。
那么,此环节的设计是为了让学生通过归纳整理,来更好的掌握子程序编程技巧和它的适用范围。
也培养了学生的团结协作能力。
〔此环节用时15分钟〕切换幻灯片第三个决策环节里。
每一小组学生在课堂上通过组内讨论,就必须以书面的形式确定好零件的加工工艺路线以及采用子程序正确编写的程序。
此环节的设计是为了让学生通过对理论知识的分析,加强学生对指令的理解和培养学生的工艺分析能力。
〔此环节用时15分钟〕切换幻灯片第四环节为实施。
这个环节是本次课最重要的局部,实施包括模拟加工和实际加工。
切换幻灯片学生首先在数控仿真软件上自主编程和仿真验证程序,模拟加工出零件,教师作巡回指导。
数控铣工教案——项目五平面加工(中职教育).docx

项目五平面加工[学习目标]掌握子程序编程方法及其在平面加工中的应用。
[知识点]1、子程序指令;2、了程序的编制与应用。
[项目内容]1、零件图形:图5-1方形凸台零件2、编程要求:毛坏尺寸60X60 X30 ,材料45号钢,刀具每次吃刀量不超过2mm,铳削如图所示的外轮廓。
[学习内容]一、子程序的概念某些被加工的零件中,常常会出现几何形状完全相同的加工轨迹,则在程序编制屮将有固定顺序和重复模式的程序段单独抽出来,编成一个程序供调用,该程序就被称为子程序。
二、子程序的应用1、在零件加工中,若路径有规律的变化,则编程时只编写其中一部分加工程序,然后用主程序调用。
2、实现零件的分层切削:有时零件在某个方向总切削深度较大,要进行分层切削,则编写该轮廓加工的刀具轨迹子程序,通过调用该子程序来实现分层切削。
三、程序的指令格式M98 P_ 单次调用指令,P后跟被调用的子程序名。
M98 P_ L _重复调用子程序指令,L后跟重复调用的次数。
子程序可以被主程序调用,同时子程序也可以调用另一个子程序,称为子程序的嵌套,。
其调用方式如图5-2所示。
四、程序结构异同相同:都是完整的程序,包括程序号、程序段、程序结束指令。
不同:程序结束指令不同:主程序用M02或M30指令;子程序用M99指令。
五、-子程序结构应用关钥1、 找出重复程序段规律,确定子程序。
2、 将耍变化的部分写在主程序,不变的部分作子程序。
3、 主一子程序接口:保证主程序调用和子程序返回正确的接口。
如:从某点进入了程序,返冋时也固定在该点。
例1:铳削一工件上表面(120mmX80mm),切削深度为1mm,刀具①12。
00001N10G80 G90 G17 G40; N20 G43 GOO Z50. H01;N30 M03 S800;N40 G54 GOO X0 Y0;N50X-70. Y-50.; N60 Z10;N70 G01 Z-l. F200; N80 M98 P0002 L7;N90 G90 GOO Z200.;N100 X0 Y0;N110 M05;N120 M02;00002G91 G01 Y6. F200;120图5 3矩形平面零件 图5-4走刀路线图X140.;Y6.;X-140.;M99例2:铳削图5-5的工件外轮廓,深度方向分层铳削,每次吃刀量为2mm, 编写外形轮廓加工程序。
子程序教案

N20 G00 X42 Z5; N30 Z-8;
G01 U-12 F20;
W-2;
W-2;
G01 U-12 F20;
G00 U12;
N40 G01 U-12 F20;
N50 G00 U12; 把相同部位移出
N60 W-2; N70 G01 U-12 F20; N80 G00 U12; N90 Z-23; N100 G01 U-12 F20; N110 G00 U12;
4、实例讲解 (2)子程序的调用: M98 PXXXX XXXX(子程序调入) XXXX—调用次数(1—9999次); XXXX—子程序名;
实例
(1)程序:
O0088(O0088); N10 M03 S800 T0101; N20 G00 X42 Z5; N30 Z-8; N40 G01 U-12 F20; N50 G00 U12;
N120 W-2; 把相同部位移出
N130 G01 U-12 F20; N140 G00 U12; N150 Z-33 N160 G01 U-12 F20; N170 G00 U12;
N180 W-2; 把相同部位移出
N190 G01 U-12 F20; N200 G00 U12;
O0089(O0089); N10 G01 U-12 F20; N20 G00 U12; N30 W-2; N40 G01 U-12 F20; N50 G00 U12; N60 M99;
O0089(O0089); N10 G01 U-12 F20; N20 G00 U12; N30 W-2; N40 G01 U-12 F20; N50 G00 U12; N60 M99;
仿真结果:
三、小结:
严格要求同学们细心编程和提高安全操作意识
6 数控车削子程序应用

《数控加工编程与操作》课程教案首页教学内容: 备注子程序应用在程序中存在某一固定顺序且重复出现时,可以将其作为子程序,事先存到存储器中,而不必重复编写,以简化程序。
1.子程序的概念在程序中把某些固定顺序或重复出现的程序单独抽出来,编成一个程序供主程序调用,这类程序叫子程序。
子程序可以被主程序调用,同时子程序也可以调用另一个子程序。
具体可调用的次数,不同的系统其调用次数是不同的,可查系统说明。
子程序调用执行情况如图3-40所示。
2.子程序的调用与返回指令 (1)子程序的调用M98格式:M98 P L ; 图2-51 子程序调用 式中 P:子程序号;L :重复调用子程序的次数,若为1次,可省略。
此指令用于主程序中调用子程序。
如M98P0020L3表示调用O0020子程序3次。
在FANUC 0i Mate 系统中,调用子程序的指令格式如下:如果省略了重复次数, 则认为重复次数为1次。
例如 M98 P30001,表示程序号为0001的子程序连续调用3次。
(2)子程序的返回 格式:M99;M99作为子程序的最后一条程序段,表示子程序结束,并返回主程序中相对应的M98指令下一条程序继续执行。
例1 如图2-52所示。
已知:长棒料毛坯直径Ø32mm ,加工图示零件。
加工工艺过程:车端面→车Ø30外圆→车4槽→切断。
外圆车刀T0101,切槽刀T0303,宽度为2 mm 。
难点M98 重复调用次数 被调用的子程序号 P图2-52 子程序应用举例编程如下:O20017;N10 G21G97 G99 G40;→初始化程序N20 M03 S600 T0101;→主轴正转,600rpm,换1号刀N30 M08;→开切削液N40 G00 X35.0 Z0;→定位在端面位置N50 G01 X-1.0 F0.2;→车端面N60 G00 Z2.0;→轴向退刀N70 G00 X30.0;→进刀至Ø30位置处N80 G01 Z-55.0 F0.2;→车Ø30外圆N90 X35.0;→径向退刀N100 G00 X100.0 Z80.0;→快退至起点N110 M03 S400 T0303;→主轴正转,400rpm,换3号刀N120 X35.0 Z0 ;→进刀N130 M98 P0500 L2;→调用子程序O0500,调用2次N140 G00 W-12.0;→快移至切断位置N150 G01 X-1.0 F0.15;→切断N160 G04 X0.5;→暂停0.5秒N170 G00 X100.0 Z80.0 M09;→快退至起点,关切削液N180 M05;→主轴停转N190 M30;→程序结束O0500 →子程序O0500N200 G00 W-12.0;→快移至切槽位置N210 G01 U-15.0 F0.15;→切槽N220 G04 X0.5;→暂停0.5秒N230 G00 U15.0;→快移径向退刀N240 W-8.0;→快移至切槽位置N250 G01 U-15.0 F0.15;→切槽N260 G04 X0.5;→暂停0.5秒N270 G00 U15.0;→快移径向退刀N280 M99;→子程序结束,返回主程序例2在Ø32mm棒料上一次装夹车削三个工件,如图2-53所示。
子程序应用

思考: 该槽位置有何规律? 有何编程简便方法?
主程序 指令1 指令2 … 调用子程序指令 指令N … …
子程序 指令1 指令2 …
返回主程序
一、子程序的定义
某些被加工的零件中,常常会出现几何形状完全相同的加工 轨迹,在编制加工程序时,有一些固定顺序和重复模式的 程序段,通常在几个程序中都会使用它。这个典型的加工 程序段可以做成固定程序,并单独加以命名,这组程序就 称为子程序。
主程序
O0001; … … M98 P1000;
子程序1
O1000; … … M98 P2000;
子程序2
O2000; … … …
…
… M30
…
… M99;
…
… M99;
注:子程序嵌套不是无穷次的,具体次数由数控系统决定。
例题:如图所示零件,毛坯φ32×100,一号刀为外圆 车刀,二号刀为切断刀(B=2),编写其加工程序。
子程序调用字 子程序号 子程序重复调用次数,L省略时为调用一次;
或 M98 Pxxx xxxx ;
如:M98 P1001 L3 ; M98 P51002;
注:KND系统用第二种
五、子程序嵌套
为进一步简化程序,可以让子程序调用另一个子程序,称为子程序的嵌套。 上一级子程序与下一级子程序的关系,与主程序与第一层子程序的关系相 同。
二、子程序的作用
减少不必要的重复编程,从而达到简化编程的目的。
三、子程序的编程格式
格式与主程序相同,Oxxxx为程序号,结尾用M99.
O0011 … M99 子程序号 程序内容 返回主程序
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
湖南省桃江县第一中学田岱
教学目的:1、激发学生对编程的学习兴趣,并掌握使用QBASIC进行程序设计的基础方法。
2、让学生进一步理解并掌握子程序有关基础知识,并能解决实际问题,不断提高自己的编程水平。
教学重点:算法分析
教学难点:通过对子程序知识的学习来解决实际问题,并能正确编写程序。
具体步骤如下:
1、编写出求一个三角形面积的子程序
2、用FOR循环语句调用子程序4次
3、在主程序中的实际参数用变量X,Y,Z,M来分别对应形式参数A,B,C,S。其中M为每次通过S求得的不同三角形面积的值。
4、又因三角形的边长已知,故用READ语句读入初始数据,即READ X,Y,Z
具体的值由语句DATA提供。
line (120,160)-(320,480)
line (320,480)-(20,80)
end sub
子程序三:
sub huabanyuan
screen 12
circle (120,240),60,4,-1.57,4.71
end sub
例2:求3!+5!+8!的和。
算法分析:
这是一道求阶乘的算术题,虽然我们可以将求3!、5!、8!以子程序的形式编写出来,但这并不是我们所认为的最佳方法,而且比较呆板。既然都是求阶乘,它们有一个通项式即N!。我们只需编写一个求N!的子程序即可。这不仅减少我们的编程量,也大大地提高了编程效率。这里又由于不是求某个阶乘,而是求阶乘的和,涉及到数据的传递,因此子程序宜采用有参子程序来编写。本题中N的取值分别为3,5,8,故需要调用该子程序3次,即用FOR循环语句调用3次子程序。具体步骤如下:
3、调用子程序的命令格式是什么?
无参子程序格式:CALL子程序名
有参子程序格式:CALL子程序名(实际参数)
二、应用举例(程序流程图由学生自己画出)
例1:要求在屏幕上显示如下菜单:
1、画圆
2、画三角形
3、画半圆
4、结束
并要求编写出具有实现上述功能的程序。
算法分析:
在设计这个程序时,需要编写画圆、三角形、半圆图像的3段程序,如果都写在同一模块中,程序会很长,结构不清晰,读起来也很费力。所以我们把它写成3个子程序,它们的功能分别是画圆、三角形、半圆的图像,这样,一个复杂的任务分解为几个简单的子程序,使得复杂的问题简单化。由于没有数据需要传递,故该程序为无参子程序。具体步骤如下:
Print tab(3);”3.huabanyuan”
Print tab(3);”4.end”
Do
Input“please select(1__4)”;n
Loop until n<=4 and n>=1
If n=1 then call huayuan
If n=2 then call huashanjiaoxing
y=sin(x+c)
pset (x,y),d
for j=1 to 1000
next j
next x
end sub
三、小结:
本节我们通过实际应用来进一步理解子程序的有关概念,同时也是加强我们的分析问题、解决问题的能力,并不断地提高我们的编程水平。
四、作业(略)
注:以上程序均在QBASIC程序环境下调试通过
If n=3 then call huabanyuan
Wend
End
三个子程序如下:
子程序一:
sub huayuan
screen 12
circle (160,200),50,4
end sub
子程序二:
sub huashanjiaoxing
screen 12
line (20,80)-(120,160)
3、根据C,D的3次取值不同,在主程序中用FOR循环语句调用子程序3次
4、因C,D的值已知,故用READ语句读入初值,即READ M,N,具体的值由DATA语句提供
具体程序如下:
主程序:
declare sub chuxiang(c!,d!)
forI=1 to 3
read m,n
call chuxiang(m,n)
end
子程序如下:
sub sear(a,b,c,s)
p=(a+b+c)/2
s=sqr(p*(p-a)*(p-b)*(p-c))
end sub
例4:编出子程序CHUXING(C,D),它的功能是画出Y=SIN(X+C)的不同颜色的正弦函数图像,其中C为初相,D为颜色号。写出主程序,在主程序中C,D取3组值,即3次调用子程序个数字送入变量N
3、进行判断:
如果N=1,则调用画圆的子程序
如果N=2,则调用画三角形的子程序
如果N=3,则调用画半圆的子程序
4、重复执行步骤1至3,直到N=4程序结束
5、因为步骤1至3重复执行几次不能确定,是以条件N=4是否成立来决定的,所以这里使用的是:条件循环语句WHILE——WEND
算法分析:
在完成这个任务时,需要3次使用画Y=SIN(X+C)的正弦函数图像的程序,只是每次C,D的取值不同,因此把画Y=SIN(X+C)图像的一段程序写成子程序,然后在主程序中使用FOR循环语句反复调用它。
具体步骤如下:
1、写出画Y=SIN(X+C)图像的子程序
2、在主程序中实际参数用变量M,N来对应形式参数C,D
教学媒体:CAI课件
教学工具:计算机
教学过程:
一、复习提问
1、建立子程序的命令格式?(分无参子程序和有参子程序)
无参子程序格式:有参子程序格式:
SUB子程序名SUB子程序名(形式参数)
语句组语句组
END SUB END SUB
2、对于有参子程序中的形式参数与主程序中对应的实际参数的值是如何传递的?
主程序在调用子程序时,实际参数将其初值传递给与之对应的形式参数,如果形式参数的值发生了变化,那么与之对应的实际参数的值也发生变化。即形式参数的终值返还给与之对应的实际参数。也就是说形式参数与实际参数之间的值是相互传递的。(注:教材没有要求区分按值传递和地址传递)
cls
sum=0:sm=0
forI=1 to 3
input“n=”;n
call jc(n,sm)
sum=sum+sm
nextI
print“sum=”;sum
end
子程序如下:
sub jc(m,s)
t=1
for j=1 to m
t=t*j
next j
print m;”!=”;t
s=t
end sub
例3:求多边形面积。如图所示:
具体程序如下:
主程序:
Declare sub huayuan( )
Declare sub huashanjiaoxing( )
Declare sub huabanyuan( )
Cls
N=1
While n<>4
Print tab(3);”1.huayuan”
Print tab(3);”2.huashanjiaoxing”
具体程序如下:
主程序:
declare sub sear(a!,b!,c!,s!)
cls
sum=0:m=0
forI=1 to 4
read x,y,z
call sear(x,y,z,m)
sum=sum+m
nextI
print sum
data 6.2,5.1,7.4,4.9,3,6.1
data 7.9,5.1,8.1,7.4,6.1,8.1
5.1 3 4.9
6.2 7.4 6.1
8.1
8.1 7.9
算法分析:
本题解题方法与例2差不多(请大家分析)。
因该多边形是由4个三角形组成,要得到多边形面积就只需要求出每一个三角形面积即可。而求三角形面积的公式是一样的(均按海伦公式),故我们只要编写出求一个三角形面积的子程序即可。然后用FOR循环语句来反复调用该子程序4次。这里因涉及到数据的传递,需要采用有参子程序。
此教案中的例1、例2、例3、例4程序分别对应的QBASIC中调试程序TD1.bas,TD2.bas,
TD3.bas, TD4.bas
其中TD1.bas,TD2.bas,TD3.bas, TD4.bas程序均放在文件夹QBASIC中
2004年7月
nextI
data 0,15,1.5708,12,-1.0472,14
end
子程序如下:
sub chuxiang(c,d)
screen 12
window (-4,-10)-(10,10)
line (0,10)-(0,-10),2
line (-4,0)-(10,0),2
for x= -10 to 10 step 0.01
1、编写出一个求N!的子程序
2、在主程序中实际参数用变量N,SM来对应子程序中的形式参数变量M,S,其中SM是通过S求得的N不同取值的阶乘的积。并且用FOR循环语句反复调用子程序3次。
3、用键盘输入语句INPUT给变量N赋初值,也就是给形式参数M赋初值。
具体程序如下:
主程序:
declare sub jc(m!,s!)
