第三章 资产组合理论
合集下载
投资学第三章 资产组合理论 练习题
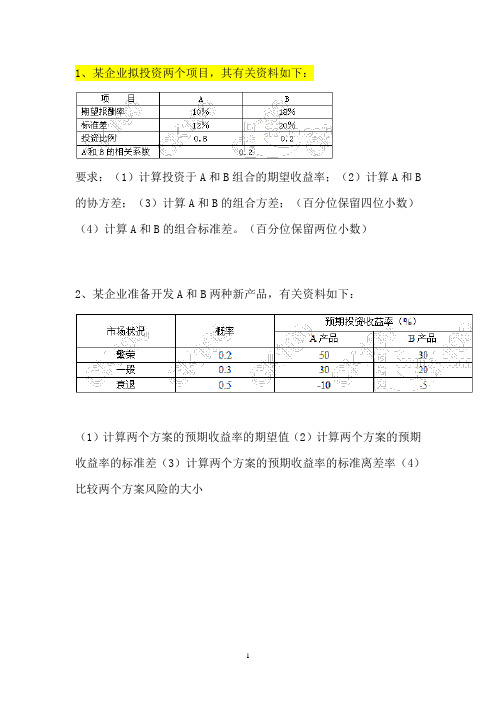
1、某企业拟投资两个项目，其有关资料如下：
要求：（1）计算投资于A和B组合的期望收益率；（2）计算A和B 的协方差；（3）计算A和B的组合方差；（百分位保留四位小数）（4）计算A和B的组合标准差。
（百分位保留两位小数）
2、某企业准备开发A和B两种新产品，有关资料如下：
（1）计算两个方案的预期收益率的期望值（2）计算两个方案的预期收益率的标准差（3）计算两个方案的预期收益率的标准离差率（4）比较两个方案风险的大小
3、某企业准备投资开发一种新产品甲，现有ABC三个方案可供选择，经预测ABC三个方案的预期收益及概率如下表示：
要求：（1）计算三个方案预期收益的期望值；（2）计算三个方案预期收益率的标准离差；（3）如果企业管理层是风险回避者，企业应试选择哪个方案
4、已知：A、B两种证券构成证券投资组织。
A证券的预期收益率10%，方差是0.0144，投资比重为80%；B证券的预期收益率为18%，方差是0.04，投资比重为20%；A证券收益率与B证券收益率的协方差是0.0048。
要求：（1）计算下列指标：①该证券投资组织的预期收益率；②A证券的标准差；③B证券的标准差；④A证券与B证券的相关系数；⑤该证券投资组合的标准差。
（2）当A证券与B证券的相关系数为0.5时，投资组合的标准差为12.11%，结合（1）的计算结果回答以下问题：①相关系数的大小对投资组织收益率有没有影响？②相关系数的大小对投资组合风险有什么样的影响？。
投资学 第三章 资产组合选择理论 均值方差方法
对外经济贸易大学金融学院 《投资学》
12
规则5 由两个资产构成的组合的回报率是构 成资产组合的每个资产的回报率的加权平 均值，资产组合的构成比例为权重。
E(rp ) w 1E(r1 ) w 2E(r2 ) E(rp ) w i E(ri ) i
1
n
2018-3-25
对外经济贸易大学金融学院 《投资学》
2018-3-25 对外经济贸易大学金融学院 《投资学》 16
贝斯特凯迪公司的股票价值对糖的价格很敏感。多年以来， 加勒比海糖产量下降时，糖的价格便猛涨，而贝斯特凯迪 公司便会遭到巨大的损失。下表为公司的股票价值变化情 况：
糖生产的正常年份 股市的牛市 概率 收益率% 股市的熊市 异常年份 糖的生产 危机
对外经济贸易大学金融学院 《投资学》 26
无差异曲线
无差异曲线为水平线，表示风险中性者，对投资风险的大小毫不 在意，他们只关心期望收益率的大小。 无差异曲线为垂直线，表示投资者只关心风险，风险越小越好， 对期望收益率毫不在意，是完全保守的投资者。 对风险厌恶者而言，风险越大，对风险的补偿要求越高，因此， 无差异曲线表现为一条向右凸的曲线。曲线越陡，投资者对风险 增加要求的收益补偿越高，投资者对风险的厌恶程度越强烈;曲线 越平坦，投资者的风险厌恶程度越弱。
s
2018-3-25
对外经济贸易大学金融学院 《投资学》
9
规则3 协方差是两个随机变量相互关系的一 种统计测度，即它测度两个随机变量，如 证券A和B的收益率之间的互动性。
AB cov(rA , rB ) E (rA E (rA ))( rB E (rB ))
2018-3-25
投资组合理论的基本思想：通过分散化的投 资来对冲掉一部分风险。 ——“Don’t put all eggs into one basket”
第三章-资产组合理论和资本资产定价模型
❖ 证券市场线(SML)： Sharpe, Mossin，Lintner,
在以β系数为横轴、期望收益率为纵轴的坐标中 CAPM方程表示的线性关系线即为SML
❖ 命题：若市场投资组合是有效的，则任一资产i的期 望收益满足
ri rf im 2 m （ rm-rf） =rf （ i rm-rf）
❖ 新华公司股票的β系数为1.2，无风险收益率为5％，市场上所有股票的平 均收益率为9％，则该公司股票的必要收益率应为（ ）。 (A) 9％ (B) 9.8％ (C) 10.5% (D) 11.2％
❖ （2）投资者要求收益最大化并且厌恶风险， 即投资者是理性的。
❖ （3）投资者的投资为单一投资期，多期投资 是单期投资的不断重复。
二、组合的可行集和有效集
❖ 可行集：资产组合的机会集合，即资产可构造出的
所有组合的期望收益和方差。
❖ 有效组合：给定风险水平下的具有最高收益的组合 或者给定收益水平下具有最小风险的组合。每一个 组合代表一个点。
其它所有的可能情况都在这两个边界之
中。
❖ 如某投资组合由收益呈完全负相关的两只股票构成，则（ ） 。 (A) 该组合不能抵销任何非系统风险 (B) 该组合的风险收益为零 (C) 该组合的非系统性风险能完全抵销 (D) 该组合的投资收益为50％
❖ 正确答案：c
❖ 解析：把投资收益呈负相关的证券放在一起组合。一种股票的 收益上升而另一种股票的收益下降的两种股票，称为负相关股 票。投资于两只呈完全负相关的股票，该组合投资的非系统性 风险能完全抵销。
三、资产组合选择的两个阶段
❖ 资产选择决策阶段：在众多的风险证券中选 择适当的风险资产构成资产组合。
❖ 资产配置决策阶段：考虑资金在无风险资产 和风险资产组合之间的分配。
投资学之资产组合理论(PPT 40页)
第三章 资产组合理论
第一节 风险与风险偏好
一、风险概述
(一)金融风险的内涵 金融市场是一个若干状态变量构成的复杂多变性 随机系统，这种金融系统中状态变量的事前不确 定性就是风险。 从整个金融经济学框架看，其核心在于如何分 散风险以及如何确定风险的合理价格。 对于投资学而言，其核心在于如何对资产定价 以及对不同风险资产进行优化配置。
i
其中，n代表证券组合中所包含资产类别的数
量； ri 代表第 i 种资产的期望收益率；wi 代
表第 i 种资产的投资比重。
(二)资产组合的方差计算
1、直接法 n 2 pi [ri E(r)]2 i 1
2、间接法
2 p
wA2
2 A
wB2
2 B
2wAwB A,B
资产 A、B 以及三种组合的收益率
n
2 pi [ri E(r)]2 i 1
标准差（standard deviation）：方差的平方根。
n
[ pi (ri r )2 ]1/2 i 1
二、风险资产之间的关联性——协方差和 相关系数
协方差（covariance）和相关系数分别从绝对和 相对角度来测算两个随机变量之间相互关系。 风险资产之间的协方差：
n
E[U ( X )] PiU ( Xi ) i 1
不同风险态度示意图
u(E(x)) E(u(x)) u(E(x)) E(u(x)) u(E(x)) E(u(x))
U (b) U (a)
ab
U (b)
U (b)
U (a)
U (a)
ab
ab
投资者风险类型及行为特征
（1）风险厌恶型（Risk Averse）：不喜欢风险， 承担风险必须相应的风险补偿。相对期望受益， 则选择风险较小的资产；或相同的风险，选择 收益最大资产。
第一节 风险与风险偏好
一、风险概述
(一)金融风险的内涵 金融市场是一个若干状态变量构成的复杂多变性 随机系统，这种金融系统中状态变量的事前不确 定性就是风险。 从整个金融经济学框架看，其核心在于如何分 散风险以及如何确定风险的合理价格。 对于投资学而言，其核心在于如何对资产定价 以及对不同风险资产进行优化配置。
i
其中，n代表证券组合中所包含资产类别的数
量； ri 代表第 i 种资产的期望收益率；wi 代
表第 i 种资产的投资比重。
(二)资产组合的方差计算
1、直接法 n 2 pi [ri E(r)]2 i 1
2、间接法
2 p
wA2
2 A
wB2
2 B
2wAwB A,B
资产 A、B 以及三种组合的收益率
n
2 pi [ri E(r)]2 i 1
标准差（standard deviation）：方差的平方根。
n
[ pi (ri r )2 ]1/2 i 1
二、风险资产之间的关联性——协方差和 相关系数
协方差（covariance）和相关系数分别从绝对和 相对角度来测算两个随机变量之间相互关系。 风险资产之间的协方差：
n
E[U ( X )] PiU ( Xi ) i 1
不同风险态度示意图
u(E(x)) E(u(x)) u(E(x)) E(u(x)) u(E(x)) E(u(x))
U (b) U (a)
ab
U (b)
U (b)
U (a)
U (a)
ab
ab
投资者风险类型及行为特征
（1）风险厌恶型（Risk Averse）：不喜欢风险， 承担风险必须相应的风险补偿。相对期望受益， 则选择风险较小的资产；或相同的风险，选择 收益最大资产。
第三章资产组合理论
的风险，还要考虑资产收益率相互之间的关系。
例：某投资公司已将50%的资金投资于A公司的股票，剩下50%的投资，投资经理决定在A 公司、B公司股票和无风险资产（收益率为3%）之间选择其一，哪一种选择更有利？A、 B公司的收益分布如下表所示。
原料生产的正常年份 股市的牛市 概率 A公司 B公司 无风险资产 收益率（%） 收益率（%） 收益率（%） 0.5 20 2 3 股市的熊市 0.3 10 -10 3 0.2 -20 40 3 原料生产危机年份
资产1所占 资产2所占 比重（W1） 比重（W2） ρ=+1 ρ=0 ρ=-1
r
σ
r
σ
r
σ
1.00 0.65 0.50 0.25 0.00
0.00 0.35 0.50 0.75 1.00
5.00 5.75 6.50 7.25 8.00
4.00 5.50 7.00 8.50 10.0
5.00 5.75 6.50 7.25 8.00
在马克维茨的投资组合理论中，投资组合的风险用投资组合的方差来衡量。 由两种资产组成的投资组合的方差为:
2 2 2 2 2 Var A B A W W WAWBCOVAB B A A BB 2
式（3.8）
包含n种资产的投资组合的方差为：
2 Var RP P
14
3.3 资产组合的收益和风险
经计算，三种选择方案投资组合的预期收益率和风险如下表示：
资产组合 全部投资于A公司股票 A、B公司股票各投资50% 预期收益率（%） 9 7.5 方差 0.0229 0.002425
A公司股票与无风险资产各投资50%
6
0.005725
以上的例子说明，尽管B公司股票本身波动性很大，但根据均值—方差决 策准则，由A、B股票构成的资产组合显然比A与无风险资产构成的组合具有优 势，原因是显而易见的，A公司与B公司的收益率是呈反方向波动的。因此，度 量资产组合的风险必须要考虑到各资产收益间的关系。
3章资产组合理
n
p i i
i 1
i 是在第 i 个资产上的 个资产的期望收益率， 投资额占总投资额的比重。
E (r )是组合中第i E (rp )为投资组合的期望收益率，
i
• 3.3.2 风险的度量
– 风险的度量方法
• 概率（probability）
– 度量风险事件发生或者造成损失的可能性。
• 期望值（expected value）
– 在不确定条件下，所有可能结果的加权平均值
• 方差（variance）
– 每一种结果的取值与期望值之差平方的加权平均数
• 标准差（standard deviation），
– 方差的平方根
• 离散系数（deviation coefficient）
– 标准差与期望值的比值，衡量的是单位期望值的风险
• 偏度(Skewness)亦称偏态、偏态系数
信用风险
又称违约风险，是企业在债务到期时无意愿或 者无力还本付息而产生的风险。
流动性风险
流动性风险有两层含义：一个是资产变现的速 度；二是资产在变现过程中价值的减少程度。 市场流动性 融资流动性
经营风险
由于企业经营方面的问题造成盈利水平的不确定性而 给投资者带来的风险。
政治及政策风险
两种以上证券的组合不是落在线段 上。所有的组合可能落在一个平面 中。
• 3.4.1 风险资产与无风险资产的投资组合
– 从风险收益的角度，将所有金融资产分为：
• 风险资产 • 无风险资产 – 包含一种风险资产与一个无风险资产的投资组合的期望 收益为：
E (rp ) E (r ) (1 )rf
• 2.投资学中单个资产的风险度量 – 风险的度量的含义
• 估计实际收益率与预期收益率之间可能的偏离程 度。
p i i
i 1
i 是在第 i 个资产上的 个资产的期望收益率， 投资额占总投资额的比重。
E (r )是组合中第i E (rp )为投资组合的期望收益率，
i
• 3.3.2 风险的度量
– 风险的度量方法
• 概率（probability）
– 度量风险事件发生或者造成损失的可能性。
• 期望值（expected value）
– 在不确定条件下，所有可能结果的加权平均值
• 方差（variance）
– 每一种结果的取值与期望值之差平方的加权平均数
• 标准差（standard deviation），
– 方差的平方根
• 离散系数（deviation coefficient）
– 标准差与期望值的比值，衡量的是单位期望值的风险
• 偏度(Skewness)亦称偏态、偏态系数
信用风险
又称违约风险，是企业在债务到期时无意愿或 者无力还本付息而产生的风险。
流动性风险
流动性风险有两层含义：一个是资产变现的速 度；二是资产在变现过程中价值的减少程度。 市场流动性 融资流动性
经营风险
由于企业经营方面的问题造成盈利水平的不确定性而 给投资者带来的风险。
政治及政策风险
两种以上证券的组合不是落在线段 上。所有的组合可能落在一个平面 中。
• 3.4.1 风险资产与无风险资产的投资组合
– 从风险收益的角度，将所有金融资产分为：
• 风险资产 • 无风险资产 – 包含一种风险资产与一个无风险资产的投资组合的期望 收益为：
E (rp ) E (r ) (1 )rf
• 2.投资学中单个资产的风险度量 – 风险的度量的含义
• 估计实际收益率与预期收益率之间可能的偏离程 度。
资产组合理论
者在单一期间内以均值和方差标准来评价资产 和资产组合。该前提隐含证券收益率的正态分布 假设，正态分布的特性在于随机变量的变化规律 通过两个参数就可以完全确定，即期望值和方差 。
✓无交易成本，而且证券可以无限细分（即 证券可以 按任一单位进行交易）
✓资金全部用于 ，但不允许卖空；
✓证券间的相关系数都不是-1，不存在无风 险证券，而且至少有两个证券的预期收益 是不同的。
4、 者更偏好位于左上方的无差异曲线。 无差异曲线族：如果将满意程度一样的点连接
成线，则会形成无穷多条无差异曲线。
者更偏好位于左上方的无差异曲线。
5、不同的 者有不同类型的无差异曲线。
– – 风险厌恶型无差异曲线： – 由于一般 者都属于尽量回避风险者，因此我们主
要讨论风险厌恶型无差异曲线。
风险厌恶型无差异曲线
产2的标准差；w1为资产1在组合中的比重，(为：
(wrp1)= w1 +r1(1-w1) r2 （5.2）
当w1＝1时，则有σp=σ1，rp=r1
当w1＝0时，即有σp=σ2，rp=r2
因此，该可行集为连接（ 点的直线。如图。
，r1σ1）和（
，rσ2 2）两
E(rp)
（r1-,σ1）
（r2-,σ2） σp
则2.有如：果两种资产完全负相关，即ρ12 =-1，
= p (w1)
w1212
(1
w1)2
2 2
2w1 (1
w1)1
2
w11 (1 w1) 2
和：(wr1p )=w1 +r1(1-w1) r2 当w1=σ2/(σ1+σ2)时，σp=0
当w1≥σ2/(σ1+σ2)时， σp(w1)=w1σ1-(1-w1)σ2,则可得到：W1=f(σp)
✓无交易成本，而且证券可以无限细分（即 证券可以 按任一单位进行交易）
✓资金全部用于 ，但不允许卖空；
✓证券间的相关系数都不是-1，不存在无风 险证券，而且至少有两个证券的预期收益 是不同的。
4、 者更偏好位于左上方的无差异曲线。 无差异曲线族：如果将满意程度一样的点连接
成线，则会形成无穷多条无差异曲线。
者更偏好位于左上方的无差异曲线。
5、不同的 者有不同类型的无差异曲线。
– – 风险厌恶型无差异曲线： – 由于一般 者都属于尽量回避风险者，因此我们主
要讨论风险厌恶型无差异曲线。
风险厌恶型无差异曲线
产2的标准差；w1为资产1在组合中的比重，(为：
(wrp1)= w1 +r1(1-w1) r2 （5.2）
当w1＝1时，则有σp=σ1，rp=r1
当w1＝0时，即有σp=σ2，rp=r2
因此，该可行集为连接（ 点的直线。如图。
，r1σ1）和（
，rσ2 2）两
E(rp)
（r1-,σ1）
（r2-,σ2） σp
则2.有如：果两种资产完全负相关，即ρ12 =-1，
= p (w1)
w1212
(1
w1)2
2 2
2w1 (1
w1)1
2
w11 (1 w1) 2
和：(wr1p )=w1 +r1(1-w1) r2 当w1=σ2/(σ1+σ2)时，σp=0
当w1≥σ2/(σ1+σ2)时， σp(w1)=w1σ1-(1-w1)σ2,则可得到：W1=f(σp)
第3章资产组合理论与因素模型
E(Ri ) Rj
E
(R
j
)
i1
i1 j1 i j
N
NN
Wi2 E Ri E(Ri )2
WiWj E Ri E(Ri ) R j E(R j )
i1
i1 j1
i j
N
NN
Wi
2
2 i
WiW j ij
i 1
i1 j1
NN
i j
上式也可化为
2 p
WiW j ij
i1 j 1
第3章 资产组合理论与因素模型
3.1 现代资产组合理论的基本思想 3.2 资产组合的收益与风险 3.3 最佳资产组合的确定 3.4 因素模型
1
证券投资理论与实务（第二版）
2020/9/2
3.1.1 马克维茨资产组合分析
资产组合分析的起点：单个证券的信息。 一方面是来自于单个证券过去的历史表现；一方面
4
证券投资理论与实务（第二版）
2020/9/2
3.1.2 投资者的期望效用
马克维茨在资产组合可行集的基础上，设立了区别
有效资产组合与无效资产组合的准则。有效集具备
的条件：第一，必须是可行的；第二，如果存在比
该组合更大期望收益的组合，那么更大期望收益的
组合的方差也应更高；第三，如果存在比该组合更
低方差的组合，那么更低方差组合的期望收益也应
2 p
Rp
R2
R2
1
R1
2
2 p
两证券完全负相关时
Rp
R2
R1
1
R2
2
2 p
Rp
R2
R1
1
R2
2
2 p
11
《证券投资分析》第三章：资产组合理论
• 利率风险
是指市场利率变动引起证券投资收益变动的可能性
• 购买力风险 购买力风险是由于通货膨胀、货币贬值给投资者带 来实际收益水平下降的风险。
2 非系统性风险
• 是指只对某个行业或个别公司的证券产生影响的风 险，它通常是由某以特殊因素引起，与整个证券市 场的价格不存在系统的全面的联系，而只对个别或 少数证券的收益产生影响。包括信用风险和经营风 险 • 信用风险（违约风险）是指证券发行人在证券到期 时无法还本付息而使投资者遭受损失的风险。 • 经营风险是指由于公司经营状况变化引起盈利水平 改变，从而引起投资者预期收益下降的可能。
2
式中， i表示投资组合中收益率方差的平均，故
n 2 lim p lim ( n
i2
n
)0
这表明，当资本市场上证券种类足够多时，等比例投资n种证券的组合 风险趋于零。
讨论2：一般情况下，当 ，i≠j, i、j=1,2,…,n时， 若仍等比例投资n种证券，则有
1 n 2 n 1 n n i / n j ij / n(n 1) n i 1 n i 1i j 1
0
持有期收益率： 持有期回收率：
D ( P P0 ) 1 100 % P0
DP 1 100 % P0
例1
1．每年的股票收益率（r）
r D1 P1 P0 100 % P0
例如，1997年的股票收益率为：
0.05 21.00 20.00 r1997 100 % 5.25% 20.00
无差异曲线
R
I1 I 2
I3
•1
•2
•3
•4
无差异曲线的特点：
投资者对位于同一条无差异曲线上所有 的证券具有相同的偏好。
投资学3 资产组合理论
E（R）（％）
6 5 4 3 2 1 0 0 1 2 3 4
5
6
7
Var（Rp）（％）
证券组合的分散效应
Rj 与 • （2） 当两种证券的收益率 ' 正相关， jj 1 ，则
k 2 k k
Rj'
之间完全
Var ( R) W j 2 ( R j ) W jW ' j ( R j ) ( R j ' )
100
75 50 25 0
0
25 50 75 100
5.62
2．63 0．46 3．34 6．33
4.60
5.58 6.55 7.52 8.50
Wa（%） 100 75 50 25 0
图5 - 1 1 9 8 7 0.46, 6.55
Wb（%） 0 25 50 75 100
Ｖar（Ｒ）p E（Rp） （ %） （ %） 5.62 2．63 0．46 3．34 6．33 4.60 5.58 6.55 7.52 8.50
i 1
n
• 式中，Xi是第i个证券在证券组合中所占的比重， Ri 是第i个证券的预期收益率，i=1,‥,n。
15
一、证券收益率和风险的测度
• （四）N个证券组合收益率和风险的测度
– 2、N个证券组合风险的测度
n n
X
i 1 j 1
i
X j ij
• 式 中 Xi 是 第 i 个 证 券 在 证 券 组 合 中 所 占 比 重 ,σ i 是第 i 个证券标准差 ,σ ij 是第 i 和 j 种 证券的协方差,i,j=1,‥,n • 随着组合中证券数目的增加，在决定组合方 差时，协方差的作用越来越大，而方差的作 用越来越小。
资产组合理论
预期收益率
第i项资产的
投资组合权数
3、证券组合风险的计算
收益率的协方差(Covariance)： 衡量组合中一种资产相对于其它资产的风险，
记作Cov(RA, RB)或σAB
协方差>0，该资产与其它资产的收益率正相关 协方差<0，该资产与其它资产的收益率负相关
AB pi RAi ERA RBi ERB
能得到的所有证券组合的集合。 （三）有效组合的决定
有效边界上的所有组合都是有 效组合。
ρAB取不同值时投资组合的机会集
收益 E(Rp)
20
ρ= -1ρ= 0ρ= -0.51410 B
A
ρ= 0.5 ρ= 1
10
15
风险 σp
1
（三）多种资产组合的有效集
三种资产组合的收益-风险的1,000对 可能组合之模拟
标准差 σ
15% 10%
相关系数 ρAB +0.5
组合 wA wB E(RP) σP
1 0.0 1.0 10.0% 10.0%
2 0.2 0.8 12.0% 9.8%
3 0.4 0.6 14.0% 10.4%
4
5
0.6 0.8
0.4 0.2
16.0% 18.0%
11.5% 13.1%
6 1.0 0.0 20.0% 15.0%
（二）单项资产的收益和风险
1、单项资产的收益 单项资产的预期收益率 (expected return)
n
ER 或 R Ri pi i 1
2、单项资产的风险 单项资产收益率的方差(variance)/标准差 (standard deviation)
n
2或Var(R) pi Ri ER2 i 1
第i项资产的
投资组合权数
3、证券组合风险的计算
收益率的协方差(Covariance)： 衡量组合中一种资产相对于其它资产的风险，
记作Cov(RA, RB)或σAB
协方差>0，该资产与其它资产的收益率正相关 协方差<0，该资产与其它资产的收益率负相关
AB pi RAi ERA RBi ERB
能得到的所有证券组合的集合。 （三）有效组合的决定
有效边界上的所有组合都是有 效组合。
ρAB取不同值时投资组合的机会集
收益 E(Rp)
20
ρ= -1ρ= 0ρ= -0.51410 B
A
ρ= 0.5 ρ= 1
10
15
风险 σp
1
（三）多种资产组合的有效集
三种资产组合的收益-风险的1,000对 可能组合之模拟
标准差 σ
15% 10%
相关系数 ρAB +0.5
组合 wA wB E(RP) σP
1 0.0 1.0 10.0% 10.0%
2 0.2 0.8 12.0% 9.8%
3 0.4 0.6 14.0% 10.4%
4
5
0.6 0.8
0.4 0.2
16.0% 18.0%
11.5% 13.1%
6 1.0 0.0 20.0% 15.0%
（二）单项资产的收益和风险
1、单项资产的收益 单项资产的预期收益率 (expected return)
n
ER 或 R Ri pi i 1
2、单项资产的风险 单项资产收益率的方差(variance)/标准差 (standard deviation)
n
2或Var(R) pi Ri ER2 i 1
第3章资产组合理论2资料
1 0
0 1
r =(11, 2, 3)T , c 2
L
w1
3
wj1 j r1
j 1
w1
0
L
w2
3
w j 2 j
j 1
r2
w2 2
0
L
w3
3
w j 3 j
10/21/2019
投资学第4章
10/21/2019
投资学第4章
命题3.3：一种无风险资产与一个风险组合构成 的新组合的结合线为一条直线
10/21/2019
投资学第4章
组合的标准差为
一种风险资产与无风险资产构 成的组合，其标准差是风险资 产的权重与标准差的乘积。
p w11
(2)
由（1）和（2）可得
10/21/2019
投资学第4章
10/21/2019
L
w1
n
w j1 j r1 0
j 1
L
w2
n
w j 2 j r2 0
j 1
L
wn
n
w j nj rn 0
j 1
n
j 1
r3
w2 3
0
3
wiri w1 2w2 3w3 2
i1
3
10/21/2019 i1
wi
w1 w2
w3 1 投资学第4章
0 1/3
w1 1/ 3 w2 1/ 3 w3 1/ 3 由此得到组合的方差为： 2 1
第3章 资产组合理论
分别表示投资者对风险持回避态度、喜好态度和 中性态度
投资者风险态度的测定举例
假设有两种彩票A和B，彩票A到期可得100元； 彩票B到期可得500元或付出100元，可能性分别 为1/3和2/3 彩票A和B期望收益相同，都是100元 决策：买A或B？
2019/11/22
A、买A的： U(100) > 1/3U(500)+2/3U(-100) => 风险厌恶
Expected return：预期将获得的平均收益率。 所有可能收益率值的概率加权平均
反映了投资者对未来收益水平的一个总体预期
2019/11/22
期望收益率的计算公式
2019/11/22
结论
收益率的概率分布是计算期望收益的基础 反映收益率概率分布特征的两个统计变量
E(r)：未来收益率的中心趋势（期望值并非收益率
通过简单的数学推导来证明：随组合中证券数量的增加， 组合风险将逐步降低
为简化推导做如下假设：构造一个等权重的组合，组合 中有n种证券，求组合的方差？（思考）
结论：随组合中证券种类的增加，单个证券方差对组合 风险的影响越来越小，而证券间协方差对组合风险的影 响越来越大 这与我们定性分析中得出的结论是一致的
相关系数可判断两资产收益变动关联程度大小
ij
ij i j
2019/11/22
方差-协方差矩阵与组合风险
组合的方差等于方差-协方差矩阵中各项的和 假设组合中有N种证券，每种证券的方差、协方
差已知，则组合的方差-协方差矩阵形式如下：
V
N行N列
2019/11/22
（三）资产组合风险分散化原理
概率分布的唯一代表值，但其被认为是最好的，代表 性最强）
投资者风险态度的测定举例
假设有两种彩票A和B，彩票A到期可得100元； 彩票B到期可得500元或付出100元，可能性分别 为1/3和2/3 彩票A和B期望收益相同，都是100元 决策：买A或B？
2019/11/22
A、买A的： U(100) > 1/3U(500)+2/3U(-100) => 风险厌恶
Expected return：预期将获得的平均收益率。 所有可能收益率值的概率加权平均
反映了投资者对未来收益水平的一个总体预期
2019/11/22
期望收益率的计算公式
2019/11/22
结论
收益率的概率分布是计算期望收益的基础 反映收益率概率分布特征的两个统计变量
E(r)：未来收益率的中心趋势（期望值并非收益率
通过简单的数学推导来证明：随组合中证券数量的增加， 组合风险将逐步降低
为简化推导做如下假设：构造一个等权重的组合，组合 中有n种证券，求组合的方差？（思考）
结论：随组合中证券种类的增加，单个证券方差对组合 风险的影响越来越小，而证券间协方差对组合风险的影 响越来越大 这与我们定性分析中得出的结论是一致的
相关系数可判断两资产收益变动关联程度大小
ij
ij i j
2019/11/22
方差-协方差矩阵与组合风险
组合的方差等于方差-协方差矩阵中各项的和 假设组合中有N种证券，每种证券的方差、协方
差已知，则组合的方差-协方差矩阵形式如下：
V
N行N列
2019/11/22
（三）资产组合风险分散化原理
概率分布的唯一代表值，但其被认为是最好的，代表 性最强）
3资产组合理论
负相关：ij 0 then wiwj 0
【例】如果 i 1,2 12 1, i , wi 1/ 2
则
2 p
12 12 12 12
4444
0
1、资产组合中的风险分散
投资组合方差的一般公式：
nn
2 p
wi w jCov ri , rj
【应用】市场指数基金
25
二、关于资产组合风险问题的讨论
不相关风险的分散：i j 0
如果 i , wi 1/ n
n
则
2 p
wi2
2 i
2
/n
2
i 1
且 lim 2 / n 0 n
【例】股票数量对收益波动性的影响
相关风险的对冲
正相关：ij 0 then wiwj 0
rp
rF
rT rF
T
p
15
加入风险资产后的有效投资组合
r
T：最优风险组合点
风险
rF
资产
有效
前沿
0
16
4.1 两种风险资产最优组合的计算 r
w1 w2 1
rP w1r1 w2r2
2 P
w1212
w22
2 2
2w1w212
max
{w1,w2 }
sP
rP rF
包括两种风险资产的投资组合的风险－收益关系
rp wDrD wErE
2 p
wD2
2 D
wE2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第三章资产组合理论
一、单选题
1. 在经典的投资组合理论中，用收益率的（）来度量风险。
A.期望值
B.中间值
C.标准差
D.平均值
2. 根据下表，在下列收益情况下，资产组合的预期收益是多少？（）
3. 资本配置线由直线变成曲线，是什么原因造成的？（）
A. 风险回报率上升
B. 借款利率高于贷款利率
C. 投资者风险承受力下降
D. 无风险资产的比例上升
4. 你管理的股票基金的预期风险溢价为10%，标准差为14%，短期国库券利率为6%。
你的委托人决定将60 000元投资于你的股票基金，将40 000元投资于货币市场的短期国库券基金，股票基金的风险回报率是多少？（）
A. 0.71
B. 1.00
C. 1.19
D. 1.91
5. 能够通过分散投资的方法去除的风险是（）
A.系统风险
B.非系统风险
C.不可分散风险
D.市场风险
二、多选题
1. 在收益-标准差坐标系中，下列哪些是正确的？(纵坐标轴代表收益，横坐标轴代表标
准差)。
（）
A. 投资者个人的无差异曲线可能相交
B. 无差异曲线的斜率是负的
C. 在一系列的无差异曲线中，最高的一条代表的效用最大
D. 两个投资者的无差异曲线可能相交
E. 以上说法均不正确
2．下列有关资本配置线的说法哪些是正确的？（）
A. 资本配置线显示了风险收益的综合情况
B. 资本配置线的斜率等于风险资产组合增加的每单位标准差所引起的期望收益的增加
C. 资本配置线的斜率也称作酬报-波动性比率
D. 资本配置线也称作风险资产有效边界
E. 以上说法均不正确
3．国库券一般被看作无风险证券，是因为（）。
A. 短期的特性使得它们的价值对于利率波动不敏感
B. 通货膨胀在到期前的不确定是可以忽略的
C. 它们的到期期限与广大投资者的希望持有期相同
D. 国库券估值准确
E. 有黄金做本位
4. 关于投资组合分散化，下列说法正确的有（）
A. 正确的分散化投资可以降低和消除系统性风险
B. 当投资组合中包含了15-20种以上的证劵以后，进一步分散化投资对降低风险所产生
的效果已经开始不明显了
C. 因为分散化投资降低投资组合的整体风险，必然也会减少投资组合的收益率
D. 一般来说，当更多的股票加入到资产组合当中时，投资组合的整体风险降低的速度会
越来越慢
E. 分散化事实是低收益换取低风险
5. 下面哪些是系统风险的来源？（）
A. 经济周期
B. 利率
C. 人事变动
D. 通货膨胀率
E. 汇率
三、计算题
假设你管理一种预期回报率为18%和标准差为28%的风险资产组合，短期国债利率为8%。
1. 你的委托人决定将其资产组合的70%投入到你的基金中，另外30%投入到货币市场的短期
国库券基金中，则该资产组合的预期收益率与标准差各是多少？
2. 假设你的风险资产组合包括下面给定比率的几种投资，
股票A：2 5%
股票B：32%
股票C：43%
那么你的委托人包括短期国库券头寸在内的总投资中各部分投资的比例各是多少？
3. 你的风险资产组合的风险回报率是多少？你的委托人的呢？
4. 假如你的委托人决定将占总投资预算为y的投资额投入到你的资产组合中，目标是获得16%的预期收益率。
a. y是多少？
b. 你的委托人在三种股票上和短期国库券基金方面的投资比例各是多少？
c. 你的委托人的资产组合回报率的标准差是多少？
5. 假如你的委托人想把他投资额的y比例投资于你的基金中，以使他的总投资的预期回报最大，同时满足总投资标准差不超过1 8%的条件。
a. 投资比率y是多少？
b. 总投资预期回报率是多少？。