最优化—基于matlab的共轭梯度法
最优化方法-共轭方向和共轭梯度法

由3式可以看出
2020/3/6
16
2.共轭方向-共轭方向法
• 基本定义
利用共轭方向作为搜索方向的无约束极小化算法
• 通用步骤:
(1)任取X 0 ,以及在X 0的下降方向P0 , k 0; (1)求解一维搜索问题
min f ( X k Pk ),为最优步长,是个数值.
(3) X k1 X k k Pk ;
X
T QX
bT
X
c, Q正定,
X 0是初始点,
P0
f
(X0)
X k1 X k k Pk , k 0,1...m 1, k是最优步长,且
Pk1 f ( X k1) ak Pk (这是构造的结果)
其中ak
f
( X k1)T QPk PkT QPk
,
P0
(
X
)T
k 1
Pk
)T
PkT f ( X k1)
f ( X k1) QX k1 b Q( X k k Pk ) b, ( X k 1 X k k Pk )
f ( X k1) (QX k b) kQPk f ( X k ) kQPk
当m 2时 所以,P0,P1, Pm1是线性无关的。
P0T QP1
P0T Q f ( X 1 )
f ( X 1 )T QP0 P0T QP0
P0
P0T Qf ( X 1 ) f ( X 1 )T QP0 0
表明,P0与P1共轭。
2020/3/6
2020/3/6
4
1.共轭方向法的基本原理
• 已知 X1 点是在 X 0 点在直线 l0 上沿 P0 搜索方向的一个极小 点。(l0 与 P0 是平行的)
共轭梯度法和梯度下降法

共轭梯度法和梯度下降法共轭梯度法和梯度下降法是两种常用的优化算法,它们在解决最优化问题时具有重要的作用。
本文将分别介绍共轭梯度法和梯度下降法的原理、优势和应用领域,并对它们进行比较和总结。
一、共轭梯度法共轭梯度法是一种迭代算法,用于求解线性最小二乘问题或者解线性方程组。
它的核心思想是通过迭代求解一系列的共轭方向,从而不断逼近最优解。
共轭梯度法的优势在于它能够充分利用问题的特殊结构,避免不必要的计算。
相比于梯度下降法,共轭梯度法通常收敛更快,并且对于大规模问题的求解效果更好。
共轭梯度法主要应用于求解线性方程组、最小二乘问题以及特定的优化问题,如信号处理、图像处理和机器学习等领域。
二、梯度下降法梯度下降法是一种基于梯度的迭代优化算法,用于求解无约束最优化问题。
它的核心思想是沿着负梯度方向不断迭代,直至达到最优解或者满足停止条件。
梯度下降法的优势在于它的简单性和易于实现性。
它不需要求解二阶导数,只需要计算一阶导数,因此对于大规模问题的求解也比较高效。
梯度下降法广泛应用于机器学习中的参数优化问题,如线性回归、逻辑回归和神经网络等。
此外,它还可以用于函数拟合、特征选择和降维等领域。
三、共轭梯度法与梯度下降法的比较共轭梯度法和梯度下降法都是常见的优化算法,它们的选择取决于具体的问题和需求。
1. 收敛速度:共轭梯度法通常比梯度下降法收敛更快。
共轭梯度法在每次迭代时利用了前面所有迭代步骤的信息,可以更快地逼近最优解。
2. 内存消耗:梯度下降法只需要存储当前的梯度信息,而共轭梯度法需要存储一系列的共轭方向。
因此,对于大规模问题,梯度下降法在内存消耗方面更具优势。
3. 线性方程组求解:共轭梯度法是一种求解线性方程组的有效方法,而梯度下降法通常不适用于求解线性方程组。
4. 二次型优化问题:共轭梯度法对于二次型优化问题的求解效果更好。
梯度下降法在处理非二次型问题时可能会出现收敛速度慢、局部最优等问题。
共轭梯度法和梯度下降法是两种常用的优化算法。
matlab梯度算法

matlab梯度算法Matlab梯度算法在数学和计算机科学中,梯度是指一个多元函数在某一点上的变化率或斜率。
梯度算法是一种优化算法,用于找到函数的最小值或最大值。
在Matlab中,有多种方法可以使用梯度算法来优化函数,包括梯度下降和共轭梯度法。
本文将详细介绍Matlab中的梯度算法,并逐步讲解其原理和应用。
I. 梯度下降法梯度下降法是一种基于迭代的优化算法,通过计算函数的梯度来更新参数的值,以逐步接近函数的最小值。
在Matlab中,可以使用"gradientDescent"函数来实现梯度下降法。
1. 实现梯度下降法首先,我们需要定义一个优化目标函数,例如:f(x) = x^2 + 2x + 1。
然后,定义其梯度函数为g(x) = 2x + 2。
接下来,我们可以使用以下代码来计算梯度下降:matlab定义优化目标函数f = (x) x^2 + 2*x + 1;定义梯度函数g = (x) 2*x + 2;初始化参数x0 = 0;设置学习率和迭代次数alpha = 0.01;iterations = 100;梯度下降法for i = 1:iterationsx0 = x0 - alpha * g(x0);end打印最优解disp(['Optimal solution: ', num2str(x0)]);在这个例子中,我们使用了学习率(alpha)为0.01,迭代次数(iterations)为100。
通过不断更新参数x0的值,最终得到了最优解。
2. 梯度下降法的原理梯度下降法的核心思想是利用函数在当前点的梯度信息来更新参数的值,以便能够向着函数的最小值前进。
具体来说,算法的步骤如下:a. 初始化参数的值:选择一个初始参数的值作为起始点。
b. 计算梯度:计算函数在当前点的梯度,即求解函数关于参数的偏导数。
c. 更新参数:根据当前点的梯度和学习率,通过减去梯度的乘积来更新参数的值。
共轭方向与共轭梯度法-最优化方法

f (X1)T P0 0 ,所以 f (X1)T P0 1P1TQ P0 0
P1TQ P0 0
(1)
以上就是搜索方向P1所必须满足的(必要) 条件。这也是使X2是极小点的充分条件。 P1,P2称为关于Q的共轭方向。
讨论表明 对于二维的具有正定矩阵Q的 二次函数f(X),从任一初始点出发,依次沿关 于Q共轭的两个方向进行一维搜索,必可达到 f(X)的无约束精确极小点。
Pk 1
0
且对j 0,1 , k 2, 有
PjT QPk PjT Q f ( X k ) k1Pk1
PjT Qf
(X
k
)
k
PT
1 j
QPk
1
f ( X k )T QPj
f ( X k )T f ( X j1) f ( X j ) j
f ( X k1 ) QX k1 b Q( X k k Pk ) b (2)
f ( X k1 ) f ( X k ) k QPk
所以
f ( X m ) f ( X m1) m1QPm1
f ( X m2 ) m2QPm2 m1QPm1
其中1 是最优步长,1>0 .因为 X * 是无约束极小点。
故 f ( X * ) 0 即 QX * b 0
f (X1) QX1 b
Q( X * 1P1) b (QX * b) 1QP1 1QP1
又因为 X1是f(X)沿P0方向的直线l0上的极小点,故
设 X En ,
,Q为对称正定矩阵,P0,
P1,···,Pm-1是关于Q共轭的m个共轭方向,
Matlab优化算法以及应用案例分析

Matlab优化算法以及应用案例分析引言Matlab是一款功能强大的数学软件,以其丰富的功能和灵活的编程环境而受到广泛的应用。
在数学建模和优化问题中,Matlab优化算法是一个重要的工具。
本文将介绍Matlab优化算法的基本原理和常见应用案例分析。
一、Matlab优化算法的基本原理1.1 最优化问题的定义在开始介绍优化算法之前,我们首先需要了解什么是最优化问题。
最优化问题可以定义为在一定的约束条件下,找到使得目标函数达到最大或者最小的变量取值。
最优化问题可以分为无约束问题和约束问题两种。
1.2 Matlab优化工具箱Matlab提供了丰富的优化工具箱,其中包含了许多优化算法的实现。
这些算法包括无约束优化算法、约束优化算法、全局优化算法等。
这些工具箱提供了简单易用的函数接口和丰富的算法实现,方便用户在优化问题中使用。
1.3 优化算法的分类优化算法可以分为传统优化算法和启发式优化算法两类。
传统优化算法包括梯度下降法、牛顿法、共轭梯度法等,它们利用目标函数的一阶或二阶导数信息进行搜索。
而启发式优化算法则通过模拟生物进化、遗传算法、蚁群算法等方法来进行搜索。
二、Matlab优化算法的应用案例分析2.1 无约束优化问题无约束优化问题是指在没有约束条件的情况下,找到使得目标函数达到最小或最大值的变量取值。
在Matlab中,可以使用fminunc函数来求解无约束优化问题。
下面以一维函数的最小化问题为例进行分析。
首先,我们定义一个一维的目标函数,例如f(x) = 3x^2 - 4x + 2。
然后使用fminunc函数来求解该问题。
代码示例:```matlabfun = @(x)3*x^2 - 4*x + 2;x0 = 0; % 初始点[x, fval] = fminunc(fun, x0);```在上述代码中,fun是目标函数的定义,x0是初始点的取值。
fminunc函数将返回最优解x和目标函数的最小值fval。
共轭梯度法在优化问题中的应用

共轭梯度法在优化问题中的应用共轭梯度法是一种高效的优化算法,在许多优化问题中都得到了广泛的应用。
它是一种迭代方法,用于解决最小化二次函数的优化问题。
在本文中,我将介绍共轭梯度法的原理和算法,并探讨它在优化问题中的应用。
一、共轭梯度法的原理共轭梯度法的核心思想是通过迭代的方式,找到一个与之前迭代步骤方向相互垂直的搜索方向,以加快收敛速度。
在每一次迭代中,共轭梯度法根据当前的搜索方向更新搜索点,直到找到最优解或达到预定的收敛标准。
具体来说,共轭梯度法从一个初始搜索点开始,计算对应的梯度,并沿着负梯度方向进行搜索。
通过一定的方法找到一个与之前搜索方向相互垂直的新搜索方向,并以一定步长更新搜索点。
迭代过程将重复进行,直到满足收敛标准或达到最大迭代次数。
二、共轭梯度法的算法共轭梯度法的算法包括以下几个步骤:1. 初始化搜索点x0和梯度g0,设置迭代次数k=0。
2. 计算当前搜索方向d_k=-g_k(k为当前迭代次数)。
3. 通过一维搜索方法找到最佳步长α_k。
4. 更新搜索点x_k+1 = x_k + α_k * d_k。
5. 计算更新后的梯度g_k+1。
6. 判断是否满足收敛标准,若满足则算法停止,否则转到步骤7。
7. 计算新的搜索方向β_k+1。
8. 将迭代次数k更新为k+1,转到步骤3。
这个算法保证了每一次迭代中的搜索方向都是彼此相互垂直的,从而加快了收敛速度。
三、共轭梯度法的应用共轭梯度法在优化问题中有广泛的应用,特别是在二次规划、线性规划和非线性规划等领域。
在二次规划问题中,共轭梯度法可以高效地求解线性系统Ax=b,其中A是一个对称正定的矩阵。
由于共轭梯度法的特性,它只需要进行n 次迭代,其中n是问题的维度,就能得到精确的解。
这使得共轭梯度法在大规模线性系统求解中具有重要的应用价值。
在线性规划问题中,共轭梯度法可以用于求解带有线性约束的最小二乘问题。
共轭梯度法通过将线性约束转化为一系列的正交子空间,从而在求解最小二乘问题时能够更快地收敛。
最优化梯度法和共轭梯度法

函数的极小点。
以下分析算法的具体步骤。
(1) 任取初始点 x (1),第一个搜索方向取为 d (1) f ( x (1) ) ;
( 2) 设已求得点 x ( k 1) , f ( x ( k 1) ) 0 , g k 1 f ( x ( k 1) ) , 若 令
局部目标函数值下降最快的方向。 最速下降法是线性收敛的算法。
三. 共轭梯度法
1. 共轭方向和共轭方向法
R 定义 设 A 是 n n 的对称正定矩阵,对于 n中的两个非零向量d 1 和 d 2,
若有 d
1T
Ad 2 0 ,则称 d 1和d 2关于A共轭。
设 d 1 , d 2 ,, d k 是 Rn 中一组非零向量,如果 它们两两关于A
以任意的 x (1) R n为初始点,依次沿 d (1) , d ( 2 ) ,, d ( k ) 进行搜索,
得到点 x ( 2) , x ( 3) ,, x ( k 1) , 则 x ( k 1) 是函数 f ( x )在 x (1) Bk 上的
极小点,其中
Bk { x | x i d ( i ) , i R }
i
d ( i ) A g i 1 d
( i )T
T
Ad
(i )
g i 1T A d ( i ) d
( i )T
Ad ( i )
g i 1T A[ ( x ( i 1) x ( i ) ) / i ] d
( i )T
A [ ( x ( i 1) x ( i ) ) / i ]
共轭,即 d i Ad j 0 , i j , i , j 1 , 2 ,, k 。
最优化方法及其matlab程序设计习题答案

证明:根据严格凸函数定义证明。
定义:对任意x ̸= y,及任意实数λ ∈ (0, 1)都有f (λx + (1 − λ)y) ≤ λf (x) + (1 − λ)f (y).
充分条件:∀x, y ∈ ℜn, 有f (x + y) ≤ f (x) + f (y)
对任意x ̸= y,及任意实数λ ∈ (0, 1)都有f (λx+(1−λ)y) ≤ f (λx)+f ((1−λ)y)
8
k= 2 (2)阻尼牛顿法 function He=Hesstwo(x) n=length(x); He=zeros(n,n); He=[8, 0; 0, 2]; ≫ x0=[0,1]’;[x val k]=dampnm(’funtwo1’,’gfuntwo1’,’Hesstwo’,x0) x= 1 2 val = -8 k= 1 第3题. function f=fun(x) f = (x(1) − 2)4 + (x(1) − 2 ∗ x(2))2; function gf=gfun(x) gf = [4 ∗ (x(1) − 2)3 + 2 ∗ (x(1) − 2 ∗ x(2)), −4 ∗ (x(1) − 2 ∗ x(2))]′; ≫clear all; ≫x0=[0 3]’;[v,val,k]=grad(’fun’,’gfun’,x0)
(1
−
λ)y)=
1 2
(λx
+
(1
−
λ)y)T
G(λx
+
(1
−
λ)y)
+
bT
(λx
+
(1
−
λ)y)
λf
(x)
共轭梯度法求解最优化计算Matlab

syms x1 x2;f=4*(x1)^2-4*(x1)*(x2)+3*(x2)^2+x1;%函数表达式%f=8*(x1)^2+4*(x1)*(x2)+5*(x2)^2;X=—10:0.1:10; Y=—10:0。
1:10;[X,Y]=meshgrid(X,Y);Z=4.*X.^2-4.*X。
*Y+3。
*Y.^2+X;mesh(X,Y,Z)contour(X,Y,Z)x0=[10 10]';%初始点v=[x1,x2];mu=0。
01;%最小误差gradf=gradient(f);%函数的梯度H=jacobian(gradf,v);h0=subs(H,[x1;x2],x0);%在点x0处的Hessiang0=subs(gradf,[x1;x2],x0);%在点x0处的梯度值if g0’*g0〈mu%检验是否满足精度条件minf=subs(f,[x1;x2],x0);%函数的最小值return;endd0=-g0;%搜索方向alpha=-(g0’*d0)/(d0'*h0*d0);%步长xk=x0+alpha*d0;%下一点gk=subs(gradf,[x1;x2],xk);%梯度值beta=gk’*gk/(g0'*g0);%求搜索方向时的系数dk=-gk+beta*d0;%下一个方向x0=xk;%更新点g0=gk;%更新所在点的梯度d0=dk;%更新方向while g0’*g0>mualpha=-(g0’*d0)/(d0’*h0*d0);%步长xk=x0+alpha*d0;%下一点gk=subs(gradf,[x1;x2],xk);%梯度值beta=gk’*gk/(g0’*g0);%求搜索方向时的系数dk=—gk+beta*d0;%下一搜索方向x0=xk;%更新点g0=gk;%更新所在点的梯度d0=dk;%更新方向hk=subs(H,[x1;x2],x0);%在点xk处的梯度值h0=hk;%更新矩阵endminf=subs(f,[x1;x2],xk)%函数的最小值xk。
最优化方法3-5共轭梯度法和共轭方向法

算法 3.5.1
设目标函数为 f (x) 1 xTGx bT x c,其中G 正定。 2
给定控制误差 。
Step1. 给定初始点 x0及初始下降方向 p0,令k 0。
Step2. 作精确一维搜索,求步长k
f
( xk
k
pk )
min
0
f
( xk
pk
)
Step3. 令 xk1 xk k pk 。
称 Fletcher-Reeves 公式,简称 FR 公式。
k 1
gkT Gpk1 pkT1Gpk 1
Gpk 1
1
k 1
(gk
g
k 1 ) ,
gkT Gpk1
1
k 1
gkT
(gk
g
k 1)
,
pkT1Gpk 1
1
k 1
(g
k1 k2
pk2 )T
(gk
g
k 1)
1
k 1
g
g T
k 1 k
1
(2)Polak-Ribiere-Polyak 公式
故
k 1
g
T k
(
gk
g
k 1)
gkT1gk 1
此式是 Polak 和 Ribiere 以及 Polyak 分别于 1969
年提出的,故称 Polak-Ribiere-Polyak 公式,简称 PRP
0,i
1,2,L
,k
(ii) xk1是二次函数在k 维超平面Hk 上的极小点。
证明 由引理 3.5.2,只需证明(i),
(最新整理)Matlab最优化方法

minf = c x
s.t .Axb = ( 1)
x0
这 里 A=(a ij)m , nx , =x1 x2 xnT
b=b 1 b 2 b nT, c =c1 c2 cn
2021/7/26
9
例 m i n z = 1 0 x 1 + 9 x 2 s . t . 6 x 1 + 5 x 2 ≤ 6 0 1 0 x 1 + 2 0 x 2 ≥ 1 5 0 x 1 ≤ 8 x 1 , x 2 ≥ 0
解:这是个最优化问题,其目标为经济价值最高,约束 条件为三种资源的数量有限,决策为生产甲、乙产品的 数量。令生产产品甲的数量为x1,生产产品乙的数量为 x2。由题意可以建立如下的线性规划模型。
2021/7/26
6
故目标函数为:
mz ax 7x15x2
约束条件为:
3 x1 2 x2 90
4
7
内容
1、无约束优化基本思想及基本算法。 2、MATLAB优化工具箱简介 3、用MATLAB求解无约束优化问题。
4、实验作业。
2021/7/26
21
无约束最优化问题
求解无约束最优化问题的的基本思想
*无约束最优化问题的基本算法
2021/7/26
返回 22
求解无约束最优化问题的基本思想
标准形式:
m f X in
问题一 : 任务分配问题:某车间有甲、乙两台机床,可用
于加工三种工件。假定这两台车床的可用台时数分别为800和 900,三种工件的数量分别为400、600和500,且已知用三种 不同车床加工单位数量不同工件所需的台时数和加工费用如 下表。问怎样分配车床的加工任务,才能既满足加工工件的 要求,又使加工费用最低?
最优化课程练习-共轭梯度法
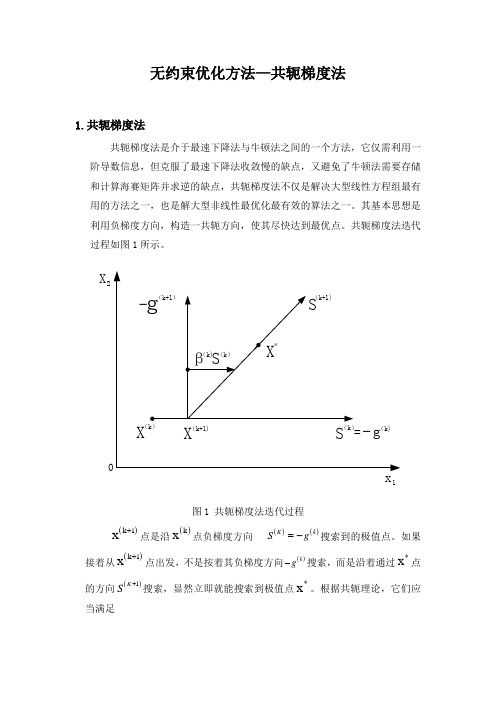
无约束优化方法—共轭梯度法1.共轭梯度法共轭梯度法是介于最速下降法与牛顿法之间的一个方法,它仅需利用一阶导数信息,但克服了最速下降法收敛慢的缺点,又避免了牛顿法需要存储和计算海赛矩阵并求逆的缺点,共轭梯度法不仅是解决大型线性方程组最有用的方法之一,也是解大型非线性最优化最有效的算法之一。
其基本思想是利用负梯度方向,构造一共轭方向,使其尽快达到最优点。
共轭梯度法迭代过程如图1所示。
1X 2图1 共轭梯度法迭代过程()k 1x +点是沿()k x 点负梯度方向()()K k Sg =-搜索到的极值点。
如果接着从()k 1x +点出发,不是按着其负梯度方向()kg -搜索,而是沿着通过*x 点的方向()1K S +搜索,显然立即就能搜索到极值点*x 。
根据共轭理论,它们应当满足()()(1)1k Tk SAS+=即()KS 与()1K S +是互为共轭方向,新构造的共轭方向()1K S +,可由矢量合成,()(1)(1)()()2k k k k SgSβ++=-+()k β值可根据在极值点附近目标函数等值线近似为二次型函数的道理,推到出:()(1)(1)(1)2()()()()2||||3||||k T k k k k T k k gg g g g g β+++==利用两个点的梯度()k g和(1)k g+,就可以构造一个与梯度矢量为共轭的矢量()1K S +,沿着该方向搜索,即可求得极值点。
共轭梯度法程序框图如图2所示。
图2 共轭梯度法程序框图2. 共轭梯度法的应用用共轭梯度法计算22121212()52410f X x x x x x x =+---+ 的最优解,其中:初始点()0[1,1]T X =。
收敛精度ε=0.0001(1).共轭梯度法程序设计#include "stdio.h" #include "math.h"double fun1(double x1,double x2) {double y;y=x1*x1+x2*x2-5*x1*x2-2*x1-4*x2+10; return y; }double fun2(double g[],double d[]) {double buchang;buchang=-(g[0]*d[0]+g[1]*d[1])/(d[0]*(2*d[0]-5*d[1])+d[1]*(-5*d[0]+2*d[1])); return buchang; }main(){ double t, beta,x1=1,x2=1,d[2],g[4], y, m,e=0.0001; int k=1;g[0]=2*x1-5*x2-2; g[1]=2*x2-5*x1-4; m=(sqrt(g[0]*g[0]+g[1]*g[1]));while(m>e&&k<=200) { if (k==1) {d[0]=-g[0]; d[1]=-g[1];beta=0; } else {beta=(g[0]*g[0]+g[1]*g[1])/(g[2]*g[2]+g[3]*g[3]); d[0]=-g[0]+beta*d[0]; d[1]=-g[1]+beta*d[1]; }t=fun2(g,d); x1=x1+d[0]*t; x2=x2+d[1]*t; g[2]=g[0]; g[3]=g[1];g[0]= 2*x1-5*x2-2;g[1]= 2*x2-5*x1-4;m=sqrt(g[0]*g[0]+g[1]*g[1]); k++; }y=fun1(x1,x2);printf("迭代次数为k=%d\n",k);printf("分别输出x1=%f,x2=%f\n",x1,x2); printf("极小值y=%f",y); }(2).程序运行结果(3).结 论用共轭梯度法计算22121212()52410f X x x x x x x =+---+的最优解为*( 1.142857,0.857143)X =-- ,*()12.857143F X = 。
双共轭梯度法matlab_概述及解释说明

双共轭梯度法matlab 概述及解释说明1. 引言1.1 概述引言部分将介绍“双共轭梯度法(Matlab)”,该方法是一种用于解决优化问题的迭代算法,常用于求解大规模线性方程组、最小二乘问题和非线性最优化等。
本文将全面讲解双共轭梯度法的基础知识、算法流程及其在MATLAB中的应用与实现。
1.2 文章结构本文按照以下方式组织:- 第二节将介绍双共轭梯度法的基础知识,包括梯度下降法、共轭梯度法和双共轭梯度法的简介。
- 第三节将详细阐述双共轭梯度法的算法流程及具体步骤解释,包括初始化步骤、迭代更新步骤以及收敛准则和结束条件设定。
- 第四节将以MATLAB为工具,展示双共轭梯度法在实践中的应用与实现举例。
这一部分将给出MATLAB代码编写指导原则,描述一个示例问题,并说明求解过程和结果分析。
- 最后一节是结论与展望,总结了双共轭梯度法的优点和局限性,并提供对未来可能的研究方向的展望和建议。
1.3 目的本文旨在介绍双共轭梯度法的原理、算法流程及其在MATLAB中的实际应用。
读者将通过本文了解如何使用该方法解决优化问题,并深入理解算法背后的理论基础。
同时,本文还将探讨双共轭梯度法存在的局限性,并展望未来可能的研究方向,为相关领域的研究提供参考。
2. 双共轭梯度法基础知识2.1 梯度下降法简介梯度下降法是一种优化算法,用于求解无约束问题的最小值。
其基本思想是通过沿着目标函数的负梯度方向进行迭代更新,以逐步减小目标函数值。
具体而言,对于一个可微分的目标函数f(x),初始值$x_0$被选为起点,然后通过以下公式进行迭代更新:$$x_{k+1} = x_k - \alpha_k \nabla f(x_k)$$其中$\alpha_k$是步长或学习率,$\nabla f(x_k)$表示在点$x_k$处的梯度(即函数$f(x)$在$x_k$处的导数)。
该过程将重复执行直到满足预设的终止条件。
2.2 共轭梯度法简介共轭梯度法是一种高效的迭代方法,用于解决对称正定线性系统的问题。
共轭梯度法

共轭梯度法对于任意形式的目标函数()f X ,在极值点*X 附近展开成泰勒级数,且取前三项,有()()()****2**1()...2TT f X f Xf X X X X X f X X X ⎡⎤⎡⎤⎡⎤⎡⎤≈+∇-+-∇-⎣⎦⎣⎦⎣⎦⎣⎦因在极值点*X 处()*0f X ∇=,而()2**()f X H X ∇=为()f X 在*X 的二阶偏导数矩阵,即Hessian 矩阵,故()****1().().2T f X f X X X H X X X ⎡⎤⎡⎤≈+--⎣⎦⎣⎦ 对于二次函数来说,若令()()()2*2*2*221122,,f X f X f X a b c x x x x ∂∂∂===∂∂∂∂则()**1(),a b H X f X d b c ⎡⎤==⎢⎥⎣⎦而—常数 则,得到()()()()()()()()()()()()()()11221212121122*1**112*2**12**112**1222****11122-1()+--2---1=+--2--1-2---2x x a b f X d x x x x b c x x a x x b x x d x x x x b x x c x x d a x x b x x x x c x x ⎡⎤⎡⎤⎢⎥⎡⎤≈⎢⎥⎣⎦⎢⎥⎣⎦⎣⎦⎡⎤+⎢⎥⎡⎤⎣⎦⎢⎥+⎣⎦⎡⎤=+++⎢⎥⎣⎦由上式可知,当12*1**2x x X X x x ⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦时,得到目标函数的极小值()*1()f X f X d ==,当22(),,...f X d d =时,则有等值线族。
令2()f X d =,代入上式,则有()()()()112222****2111221()-2---2f X d d a x x b x x x x c x x ⎡⎤=≈+++⎢⎥⎣⎦所以目标函数()f X 在*X 点附近的等值线方程为()()()()112222****1122-2---0a x x b x x x x c x x d +++=式中,122()d d d =-=常数。
matlab共轭梯度法求解方程组

主题:matlab共轭梯度法求解方程组近年来,随着科学技术的不断发展,数学建模和计算机仿真成为科学研究和工程技术领域的重要手段。
在实际应用中,我们常常需要解决线性方程组的求解问题,而共轭梯度法作为一种高效的迭代求解方法,广泛应用于信号处理、图像处理、地球物理勘探和优化问题等领域。
本文将介绍如何利用matlab中的共轭梯度法求解线性方程组的基本原理和实际操作方法。
1. 共轭梯度法的基本原理共轭梯度法是一种迭代法,用于求解对称正定线性方程组Ax=b。
该方法的核心思想是通过一系列的迭代操作,逐步逼近方程组的解,直到满足一定的精度要求。
在每一步迭代中,共轭梯度法利用残差和方向向量的共轭性质,不断寻找最优的步长,从而实现方程组的求解。
2. matlab中共轭梯度法的基本调用方法在matlab中,调用共轭梯度法求解线性方程组非常简单。
需要将方程组的系数矩阵A和右端向量b输入到matlab中,然后利用内置函数conjugateGradient进行求解。
具体的调用方法如下:x = conjugateGradient(A, b, x0, maxIter, tol)其中,A为系数矩阵,b为右端向量,x0为初始解向量,maxIter为最大迭代次数,tol为精度要求。
调用完毕后,matlab将返回方程组的近似解x。
3. 共轭梯度法在实际工程中的应用共轭梯度法作为一种高效的求解方法,在工程技术领域得到了广泛的应用。
以图像处理为例,图像处理中经常需要解决大规模的线性方程组,而共轭梯度法能够高效地求解这类问题,提高了图像处理算法的效率和稳定性。
另外,在地球物理勘探中,共轭梯度法也被广泛应用于三维数据的快速处理和解释。
可以说,共轭梯度法在实际工程中发挥着重要的作用。
4. 共轭梯度法的优缺点分析尽管共轭梯度法具有非常高的效率和稳定性,但是该方法也存在一些缺点。
该方法只适用于对称正定的线性方程组,对于一般的线性方程组并不适用。
共轭梯度法的收敛速度受到方程条件数的影响,对于病态问题,可能收敛速度较慢。
