基于MATLAB曲柄滑块机构运动仿真
基于matlab的曲柄滑块机构设计与运动分析_陈长秀

变,从第 i+1 个功能块开始逐位交换。
(3)变异运算的改进
由于在每个功能块中,“1”的数目即是该题型试题的数目, 因此在变异过程中应保证整个种群所有功能块中“1”的数目不 变。可执行如下过程,首先,由变异概率决定某位取反;然后,检 查、修正字符串中“1”的数目,保证不发生变化。
(4)用全局最优解替换本次迭代的最差解 为保证好的字符串不至于流失,每次遗传操作前记录本次 迭代的最优解,若该解优于全局最优解则替换全局最优解,否 则全局最优解保持不变。此次遗传操作后,用全局最优解换本 代的最差解。
(上接第 29 页)
图 1 所示的偏置曲柄滑块机构。设 l1=50mm,l2=100mm, e=20mm,w1=2rad/s,设 φ1 的初始值为 0 , 则 φ1 变化时,杆 2 的角位移、角速度和角加速度以及滑块 3 的位移、速度和加速
>> plot(t,xc,t,vc,t,ac);
度的变化值可计算求得,曲柄转角 φ1 在 0- 360°之间变化时, 在 matlab 的计算窗口输入算式后,滑块 3 的位移、速度和加速
2012 年 1 月 第 1 期(总第 158 期)
轻工科技
LIGHT INDUSTRY SCIENCE AND TECHNOLOGY
机械与电气
基于 m a tla b 的曲柄滑块机构设计与运动分析
陈长秀
(陕西国防工业职业技术学院,陕西 西安 71 0302)
【摘 要】 建立了曲柄滑块机构的计算模型,并使用 matlab 对曲柄滑块机构进行了运动分析,提高了设计效率和设计精度。
图 1 偏置曲柄滑块机构 建立坐标系如图 1 所示,由曲柄滑快机构的矢量封闭图[1] 可得:
φl1 cosφ1+l2 cosφ2=xc
matlab机电系统仿真大作业
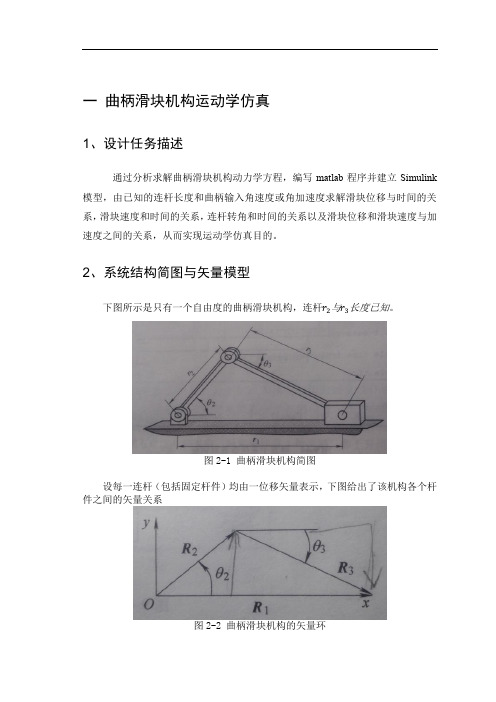
一曲柄滑块机构运动学仿真1、设计任务描述通过分析求解曲柄滑块机构动力学方程,编写matlab程序并建立Simulink 模型,由已知的连杆长度和曲柄输入角速度或角加速度求解滑块位移与时间的关系,滑块速度和时间的关系,连杆转角和时间的关系以及滑块位移和滑块速度与加速度之间的关系,从而实现运动学仿真目的。
2、系统结构简图与矢量模型下图所示是只有一个自由度的曲柄滑块机构,连杆r2与r3长度已知。
图2-1 曲柄滑块机构简图设每一连杆(包括固定杆件)均由一位移矢量表示,下图给出了该机构各个杆件之间的矢量关系图2-2 曲柄滑块机构的矢量环3.匀角速度输入时系统仿真3.1 系统动力学方程系统为匀角速度输入的时候,其输入为ω2=θ2,输出为ω3=θ3,θ3;v 1=r 1,r 1。
(1) 曲柄滑块机构闭环位移矢量方程为:R 2+R 3=R 1(2) 曲柄滑块机构的位置方程{r 2cos θ2+r 3cos θ3=r 1r 2sin θ2+r 3sin θ3=0(3) 曲柄滑块机构的运动学方程通过对位置方程进行求导,可得{−r 2ω2sin θ2−r 3ω3sin θ3=r 1r 2ω2cos θ2+r 3ω3cos θ3=0由于系统的输出是ω3与v 1,为了便于建立A*x=B 形式的矩阵,使x=[ω3v 1],将运动学方程两边进行整理,得到{v 1+r 3ω3sin θ3=−r 2ω2sin θ2−r 3ω3cos θ3=r 2ω2cos θ2将上述方程的v1与w3提取出来,即可建立运动学方程的矩阵形式(r 3sin θ31−r 3cos θ30)(ω3v 1)=(−r 2ω2sin θ2r 2ω2cos θ2) 3.2 M 函数编写与Simulink 仿真模型建立3.2.1 滑块速度与时间的变化情况以及滑块位移与时间的变化情况仿真的基本思路:已知输入w2与θ2,由运动学方程求出w3和v1,再通过积分,即可求出θ3与r1。
曲柄滑块机构的MATLAB优化设计与SolidWorks运动仿真

宝鸡文理学院学报(自然科学版)第39卷,第2期,第6366页,2019年6月Journal of Baoji University of Arts and Sciences(Natural Science)•Vol.39•No.2•pp.63-66•Jun.2019DOI:10.13467/旊i.jbuns.2019.02.002hup:///kcms/detail/61.1290.N.20190612.0952.002.html曲柄滑块机构的MATLAB优化设计与SolidWorks运动仿真"许海强,唐海平灣(宝鸡文理学院机械工程学院,陕西宝鸡721016)摘要:目的得到曲柄滑块机构的最优传力性能,验证其急回特性暎方法以机构运动学参数为设计变量,针对作业任务的要求,通过几何分析导出运动学参数必须满足的约束方程,提出量化机构力学性能的指标,建立机构的优化设计数学模型,给定滑块行程和行程速比系数,用MATLAB优化工具箱求解机构运动学参数的最优尺寸,用SolidWorks建模和运动学仿真暎结果得到了机构运动学参数的最优尺寸和运动学曲线,验证了偏置曲柄滑块机构的急回特性暎结论以MATLAB和SolidWorks 为设计平台进行机构设计与运动分析,具有简单可行和直观高效等优点,可以将其推广到工程实际中暎关键词:曲柄滑块机构;优化设计;M ATL AB;SolidWorks;运动分析中图分类号:TH111文献标志码:A文章编号:1007-1261(2019)02006304 MATLAB optimization design of crank-slider mechanism and SolidWorks motion simulationXU Hai-qiang,TANG Hai-ping灣(Inslilule of Mechanical Engineering•Baoji University of Arts and Sciences•Baoji721016•Shaanxi•China)Abstract:Purposes—To obtain the optimal force transfer performance of the crank-slider mechanism,and to verify its quick-return characteristics.Methods—According to the requirement,of job task,the constraint equation which kinematic parameters shall meet is deduced through geometric analysis with the kinematic parameters of the crank-slider mechanism as design variables,then the mechanic performance indicators of quantitative mechanisms is put forward,and a mathematical model of optimization design is established.When the slider stroke and travel speed ratio coefficient are given, MATLAB optimization toolbox is utilized to solve the optimal size of the kinematic parameters,and SolidWorks is used for modeling and kinematics simulation.Results—The optimal size and kinematic curves of kinematic parameters of the mechanism are obtained,and the quick-return characteristics of offset crank slider mechanism is verified.Conclusions—The mechanism design and motion analysis with MATLAB and SolidWorks as the design platform is simple,feasible,intuitive and efficient,so theycanbeextendedtoengineeringpractice.Key words:crank-slider mechanism;optimization design;MATLAB;SolidWorks;motion analysis曲柄滑块机构是一种平面连杆机构,通过曲柄的回转带动滑块做水平的往复移动,已广泛应用于空气压缩机、往复活塞式发动机等机械系统中暎偏置曲柄滑块机构具有急回特性,在设计机构时,为了保证传动系统的效率,必须对各构件的尺寸参数、位置参数等进行优化设计暎文献[1—收稿日期:2019-01-17,修回日期:2019-03-05,网络出版时间:201906-1209:52:52.作者简介:许海强(1994-),男,陕西宝鸡人,硕士研究生,研究方向:机电一体化技术.Email:xhq9425@ 通讯作者:唐海平C1976-),男,陕西宝鸡人,副教授,博士,硕士生导师,研究方向:材料物理化学.64宝鸡文理学院学报(自然科学版)2019年2]在给定行程速比系数K并且已知曲柄长度a,连杆长度S偏心距e中的任意一个量的情况下,通过解析法推导出其他任意2个未知量暎文献[3—5]通过辅助圆图解法设计了曲柄滑块机构暎但随着MATLAB等计算机优化软件的出现,这2种方法已经不再适用暎作为优化设计领域应用最广的软件之一,MATLAB不仅可以使用优化工具箱中的函数,还能通过算法编程实现相应的最优化设计[]暎偏置曲柄滑块机构的运动学分析是指在不考虑力的前提下,对机构的位移、速度、加速度随时间的变化进行仿真分析暎作为三维设计软件,SolidWorks不但能对机构进行三维建模,还可以使用Motion插件执行复杂机构的运动学和动力学仿真,通过动画、图表、曲线等反映机构的运动特性[]暎本文以曲柄滑块机构在作业任务中满足滑块行程H和行程速比系数K的前提下,以最小传动角Ymin作为目标函数,曲柄长度a,连杆长度b,偏心距e为设计变量暎首先用MATLAB软件进行优化设计,得到机构的最优尺寸参数,再用Solid-Works软件建立偏置曲柄滑块机构的三维模型,最后用Motion插件进行机构运动学仿真,并对仿真结果进行分析暎1优化设计的数学模型优化设计基于数学最优化理论,并使用计算机找到最优解暎在优化实际工程问题时,首先要建立数学模型,即确定设计变量、构造目标函数、选择约束条件;其次根据数学模型选择合适的最优化算法,最后编写程序上机电算择优[]暎1.1确定设计变量优化设计中需要调整和优选的参数称为设计变量。
基于某MATLAB曲柄滑块机构运动仿真报告材料

************************计算机仿真技术matlab报告************************曲柄滑块机构目录一、基于GUI的曲柄滑块机构运动仿真二、基于simulink的曲柄滑块机构运动仿真曲柄滑块机构1.题目描述题目:对如图1所示的曲柄滑块机构的运动过程进行仿真,并用动画的方式显示曲柄滑块机构的运动过程,位移曲线、速度曲线和加速度曲线。
图中,AB长R2,BC长R3mm,A点为坐标原点。
图1 曲柄滑块机构示意图2.实现方法利用GUI界面设计来对曲柄滑块机构的运动过程进行仿真,并用动画的方式显示曲柄滑块机构的运动过程。
3.界面设计1. Gui 设计1)新建GUI:菜单-新建-gui,并保存为test52)界面设计:拖拽左侧图标到绘图区,创建GUI界面拖拽左侧图标值绘图区设置如下的按钮最终的仿真界面如图所示3)代码添加:进入代码界面4.代码编程%模型求解a1=str2double(get(handles.edit1,'String'));a2=str2double(get(handles.edit2,'String'));a3=str2double(get(handles.edit3,'String'));a4=str2double(get(handles.edit4,'String'));a5=str2double(get(handles.edit5,'String'));a=a1*((1-cos(a4*a5))+0.25*(a1/a2)*(1-cos(2*a4*a5))); set(handles.edit6,'String',a);a0=(a4*a1)*(sin(a4*a5)+0.5*(a1/a2)*sin(2*a4*a5));set(handles.edit7,'String',a0);a6=(a4*a4*a1)*(cos(a4*a5)+(a1/a2)*cos(a4*a5));set(handles.edit8,'String',a6);%绘制位移、速度、加速度曲线axes(handles.axes3);r1=str2double(get(handles.edit1,'String'));r2=str2double(get(handles.edit2,'String'));omiga1=str2double(get(handles.edit4,'String'));x11=1:720;for i=1:720x1(i)=i*pi/180;%sin(x2(i)=r1/r2*sin(x1(i));x2(i)=asin(-r1/r2*sin(x1(i)));x22(i)=x2(i)*180/pi;r3(i)=r1*cos(x1(i))+r2*cos(x2(i));B=[-r1*omiga1*sin(x1(i));r1*omiga1*cos(x1(i))]; A=[r2*sin(x2(i)) 1;-r2*cos(x2(i)) 0];X=inv(A)*B;omiga2(i)=X(1,1);v3(i)=X(2,1);endplot(x11/60,0.5*r1*sin(x1));xlabel('ʱ¼äÖá t/sec')ylabel('Á¬¸ËÖÊÐÄÔÚYÖáÉϵÄλÖÃ/mm') figure(2)plot(x11/60,r3);title('λÒÆÏßͼ')grid onhold off;xlabel('ʱ¼ät/sec')ylabel('»¬¿éλÒÆ r3/mm')figure(3)plot(x11/60,omiga2);title('Á¬¸Ë½ÇËÙ¶È')grid onhold off;xlabel('ʱ¼ä t/sec')ylabel('Á¬¸Ë½ÇËÙ¶È omiga2/rad/sec') figure(4)plot(x11/60,v3*pi/180);title('»¬¿éËÙ¶È')grid onhold off;xlabel('ʱ¼ä t/sec')ylabel('»¬¿éËÙ¶È v3/mm/sec')%绘制表格axes(handles.axes3);grid onaxes(handles.axes1);grid on%制作动画axes(handles.axes1);hf=figure('name','Çú±ú»¬¿é»ú¹¹');set(hf,'color','r');hold onaxis([-6,6,-4,4]);grid onaxis('off');xa0=-5;%»îÈû×󶥵ã×ø±êxa1=-2.5;%»îÈûÓÒ¶¥µã×ø±êxb0=-2.5;%Á¬¸Ë×󶥵ã×ø±êxb1=2.2;%Á¬¸ËÓÒ¶¥µã×ø±êx3=3.5;%תÂÖ×ø±êy3=0;%תÂÖ×ø±êx4=xb1;%ÉèÖÃÁ¬¸ËÍ·µÄ³õʼλÖúá×ø±êy4=0;%ÉèÖÃÁ¬¸ËÍ·µÄ³õʼλÖÃ×Ý×ø±êx5=xa1;y5=0;x6=x3;%ÉèÖÃÁ¬Öá³õʼºá×ø±êy6=0;%ÉèÖÃÁ¬Öá³õʼ×Ý×ø±êa=0.7;b=0.7c=0.7a1=line([xa0;xa1],[0;0],'color','b','linestyle','-','linewidth',40); %ÉèÖûîÈûa3=line(x3,y3,'color',[0.5 0.6 0.3],'linestyle','.','markersize',300);%ÉèÖÃתÂÖa2=line([xb0;xb1],[0;0],'color','black','linewidth',10);%ÉèÖÃÁ¬¸Ëa5=line(x5,y5,'color','black','linestyle','.','markersize',40);%ÉèÖÃÁ¬¸Ë»îÈûÁ¬½ÓÍ·a4=line(x4,y4,'color','black','linestyle','.','markersize',50);%ÉèÖÃÁ¬¸ËÁ¬½ÓÍ·a6=line([xb1;x3],[0;0],'color','black','linestyle','-','linewidth',10);a7=line(x3,0,'color','black','linestyle','.','markersize',50);%ÉèÖÃÔ˶¯ÖÐÐÄa8=line([-5.1;-0.2],[0.7;0.7],'color','y','linestyle','-','linewidth',5);%ÉèÖÃÆû¸×±Úa9=line([-5.1;-0.2],[-0.72;-0.72],'color','y','linestyle','-','linewidth',5);%ÉèÖÃÆû¸×±Úa10=line([-5.1;-5.1],[-0.8;0.75],'color','y','linestyle','-','linewidth',5);%ÉèÖÃÆû¸×±Úa11=fill([-5,-5,-5,-5],[0.61,0.61,-0.61,-0.61],[a,b,c]);%ÉèÖÃÆû¸×ÆøÌålen1=4.8;%Á¬¸Ë³¤len2=2.5;%»îÈû³¤r=1.3;%Ô˶¯°ë¾¶dt=0.015*pi;t=0;while 1t=t+dt;if t>2*pit=0;endlena1=sqrt((len1)^2-(r*sin(t))^2);%Á¬¸ËÔÚÔ˶¯¹ý³ÌÖкáÖáÉϵÄÓÐЧ³¤¶Èrr1=r*cos(t);%°ë¾¶ÔÚÔ˶¯¹ý³ÌÖкáÖáÉϵÄÓÐЧ³¤¶È xaa1=x3-sqrt(len1^2-(sin(t)*r)^2)-(r*cos(t));%»îÈûÔÚÔ˶¯¹ý³ÌÖеÄÓÒ¶¥µã×ø±êλÖÃxaa0=xaa1-2.5;%%»îÈûÔÚÔ˶¯¹ý³ÌÖеÄ×󶥵ã×ø±êλÖà x55=x3-cos(t)*r;%Á¬¸ËÔÚÔ˶¯¹ý³ÌÖкá×ø±êλÖÃy55=y3-sin(t)*r;%Á¬¸ËÔÚÔ˶¯¹ý³ÌÖÐ×Ý×ø±êλÖÃset(a4,'xdata',x55,'ydata',y55);%ÉèÖÃÁ¬¸Ë¶¥µãÔ˶¯set(a1,'xdata',[xaa1-2.5;xaa1],'ydata',[0;0]);%ÉèÖûîÈûÔ˶¯set(a2,'xdata',[xaa1;x55],'ydata',[0;y55]);set(a5,'xdata',xaa1);%ÉèÖûîÈûÓëÁ¬¸ËÁ¬½ÓÍ·µÄÔ˶¯set(a6,'xdata',[x55;x3],'ydata',[y55;0]);set(a11,'xdata',[-5,xaa0,xaa0,-5]);%ÉèÖÃÆøÌåµÄÌî³äset(gcf,'doublebuffer','on');%Ïû³ýÕð¶¯drawnow;end5.结果(1)对它的结构参数进行设置,如下图所示点击计算按钮动画,结果如下图所示点击表格对图形进行画表格处理点击绘图,即可得到位移、速度、加速度曲线,如下图所示二、基于simulink 的曲柄滑块机构运动仿真(1)运用矢量求解法求解(2)绘制速度接线图,如下图所示:运动仿真结果如下图:(3)绘制加速度接线图,如下图所示:运行结果如图所示:。
曲柄滑块机构的优化设计及运动仿真学位论文

曲柄滑块机构的优化设计及运动仿真学位论文曲柄滑块机构的优化设计及运动仿真目录目录...............................................................1 摘要............................................................... 第1章绪论........................................................ 选题的目的及意义............................................. 优化设计方法的概述........................................... 国内外的研究现状............................................ 主要研究内容............................................ 第2章曲柄滑块机构的受力分析......................................曲柄滑块机构的分类...........................................曲柄滑块机构的动力学特性.....................................曲柄滑块机构中运动学特性..................................... 第3章偏置式曲柄滑块机构的优化设计................................ 优化软件的介绍.............................................. MATLAB的发展历程和影响...................................MATLAB 在机构设计中的应用................................. 机构优化设计实例分析........................................ 设计目标的建立...........................................根据设计要求,确定约束条件................................利用MATLAB进行优化设计.................................... 编制优化程序.............................................. 程序运行结果及处理........................................ 对优化结果进行验证和分析................................. 第4章偏置曲柄滑块机构的运动学建模与仿真.......................... 偏置曲柄滑块机构运动特性建模................................ 仿真环境简介............................................. 机构的运动学建模........................................ 运动学仿真的实现.......................................... 函数的编制及初始参数的设定............................... 构建Simulink仿真框图.................................... 对仿真结果进行分析...................................... 总结...............................................................〔Toolboxs〕组成虽然该软件的初衷并不是为控制系统设计的,但它提供了强大的矩阵处理和绘图功能,可靠灵活且方便,非常适合现代控制理论的计算机辅助设计。
MATLAB基本杆组-运动学仿真

⎡ ri cos (θ i + π ) ⎤ 2 ⎡ xC ⎤ ⎡ xB ⎤ ⎡ ri cos (θ i + π 2 ) ⎤ ⎢ y ⎥ = ⎢ y ⎥ + ⎢ r sin θ + π 2 ⎥ θi + ⎢ r sin θ + π ⎥ θi ( i )⎦ ⎣ i ( i )⎦ ⎣ C⎦ ⎣ B⎦ ⎣ i
xC = xB − riθi sin (θi ) = xD − rjθ j sin (θ j ) yC = yB + riθi cos (θi ) = yD + rjθ j cos (θ j )
再次对时间t求导数,得到点C的加速度为
xC = xB − riθi sin (θi ) − riθi2 cos (θi ) = xD − rjθ j sin (θ j ) − rjθ j2 cos (θ j ) yC = yB + riθi cos (θi ) − riθi2 sin (θi ) = yD + rjθ j cos (θ j ) − riθ i2 sin (θ j )
( (
) )
§5-1 曲柄的MATLAB运动学仿真模块
xB = ri cos (θi ) + rj cos (θ j ) yB = ri sin (θi ) + rj sin (θ j )
对时间分别求两次导数
xB = − rjθ j sin (θ j ) xB = − rjθ j sin (θ j ) − rjθ j2 cos (θ j )
求导数
−riθi sin (θi ) + rjθ j sin (θ j ) = xD − xB riθi cos (θi ) − rjθ j cos (θ j ) = yD − yB
曲柄滑块机构的运动学仿真

《系统仿真与matlab》综合试题题目:曲柄滑块机构的运动学仿真编号:24难度系数:*****姓名班级学号联系方式成绩第一部分:课题理解1、课题要求:对图示单缸四冲程发动机中常见的曲柄滑块机构进行运动学仿真。
已知连杆长度:m r 1.02=,m r 4.03=,连杆的转速:22θω =,33θω =,设曲柄r 2以匀速旋转,s r / 502=ω。
初始条件:032==θθ。
仿真以2ω为输入,计算3ω和1r,仿真时间0.5s 。
2、个人理解:本实验是对运动进行仿真,根据滑块的运动演示连杆的运动过程。
首先,建立两杆和滑块位置间的数学关系,计算出运动方程;其次,运用matlab 动画功能,对给定的2ω值进行运动仿真;最后,建立友好的界面,方便用户改变2ω,显示3ω和运行动画。
第二部分:试题建模由几何关系可得:两边求导数可得:即得2θ=w2*t; 3θ =arcsin(r2*sin(2θ )/r3);w3=r2/r3*w2*cos(2θ )./cos(3θ );第三部分:程序实现1、程序模块:2、程序流程:特色在于:随动画同时输出的w3值为动画运行到当前位置时的转动角速度。
并可以多次设定w2值,进行波形比较。
2、程序代码:w2 = str2double(get(handles.w2input,'string'));if w2~=0 %判断用户是否输入w2%如果w2被赋值,则进行变量初始化t=0;dt=0.01;r2=0.1;r3=0.4;x0=0.1;y0=0;x1=0.5;y1=0;%在图形显示框axes_d中进行固定图形的绘画axes(handles.axes_d)%画三角支架plot(0,-0.03,'color',[0.5,0.5,0.5],'linestyle','^',...'linewidth',10);hold onplot(0,0,'color',[0.4,0.4,0.4],'linestyle','.',...'markersize',40);%画r3转动轨迹圆m=[0:0.01:2*pi];plot(0.1*cos(m),0.1*sin(m),'color',[0.6,0.8,0.8],'linestyle','.',...'markersize',5);%画水平线plot([-0.2;0.6],[-0.05;-0.05],'color','b','linestyle','--',...'linewidth',1);%画支点等高线plot([-0.2;0.7],[0;0],'color','b','linestyle','--',...'linewidth',1);%设置坐标范围axis([-0.15,0.7,-0.41,0.41]);%不显示坐标轴%axis('off');%创建杆间连接点point=line(x0,y0,'color','k','linestyle','.',...'markersize',30);%创建连接点水平指示线zhishi=line([x0-0.1;x0+0.1],[y0;y0],'color','b','linestyle','--',...'linewidth',2);%创建杆r2body2=line([0;x0],[0;y0],'color',[0.2,0.25,0.25],'linestyle','-',...'linewidth',5);%创建杆r3body3=line([x0;x1],[y0;y1],'color',[0.2,0.25,0.25],'linestyle','-',...'linewidth',5);%创建活塞huosai1=line([x1+0.01;x1+0.15],[y1;y1],'color','b','linestyle','-',...'linewidth',28);%创建活塞连接点huosaidian=line(x1+0.01,y1,'color','k','linestyle','.',...'markersize',40);%创建汽缸qigang1=line([0.651;0.651],[-0.05;0.05],'color',[0.5,0.5,0.5],'linestyle','-',.. .'linewidth',5);qigang2=line([0.3;0.655],[0.056;0.056],'color',[0.5,0.5,0.5],'linestyle','-',...'linewidth',5);qigang3=line([0.3;0.655],[-0.056;-0.056],'color',[0.5,0.5,0.5],'linestyle','-', ...'linewidth',5);set(handles.axes_w3,'XMinorTick','on')%进行动画过程while t<4t=t+dt;a2=w2*t;a3=asin(r2*sin(a2)/r3);w3=r2/r3*w2*cos(a2)./cos(a3);r2=0.1;x0a=r2*cos(a2);y0a=r2*sin(a2);x1a=x0a+r3*cos(a3);y1a=0;x=x0a;y=y0a;%在图形显示框axes_d中进行图形的刷新axes(handles.axes_d)%重绘杆r2set(body2,'xdata',[0;x0a],'ydata',[0;y0a]);%重绘杆r3set(body3,'xdata',[x0a;x1a],'ydata',[y0a;y1a]);%重绘杆活塞set(huosai1,'xdata',[x1a+0.01;x1a+0.15],'ydata',[y1a;y1a]); %重绘活塞连接点set(huosaidian,'xdata',x1a+0.01,'ydata',y1a);%重绘杆连接点set(point,'xdata',x0a,'ydata',y0a);%重绘指示线set(zhishi,'xdata',[x0a-0.1;x0a+0.1],'ydata',[y0a;y0a]);set(handles.axes_d,'XMinorTick','on')%输出实时w3的值set(handles.w3_output,'string',num2str(w3));%在图形显示框axes_w3中绘制w3的实时波形axes(handles.axes_w3)%设置坐标轴axis([0,4,-w2/4-0.1,w2/4+0.1]);hold onplot(t,w3,'color','k','linestyle','.',...'markersize',5);set(handles.axes_w3,'XMinorTick','on')drawnow;endw2=0;end第四部分:GUI界面规划1、控件组成:1.面板(1个):作为背景。
基于MATLAB软件的铰链四杆机构运动分析仿真软件开发

文章编号: 1009-3818(2002)02-0047-03基于MATLAB 软件的铰链四杆机构运动分析仿真软件开发覃虹桥1 魏承辉2 罗佑新2(1华中科技大学材料学院 湖北武汉430074)(2常德师范学院机械工程系 湖南常德415003)摘 要: 建立了铰链四杆机构运动分析的数学模型,以MATLAB 程序设计语言为平台,将参数化设计与交互式相结合,设计了铰链四杆机构仿真软件,该软件具有方便用户的良好界面,并给出界面设计程序,从而使机构分析更加方便、快捷、直观和形象.设计者只需输入参数就可得到仿真结果,再将运行结果与设计要求相比较,对怎样修改设计做出决策.它为四杆机构设计提供了一种实用的软件与方法.关键词: 铰链四杆机构;按钮;界面;仿真中图分类号: TH 311.52;TH 113.2+2 文献标识码: A铰链四杆机构的运动学分析是机构学中典型的机构运动分析之一,如果设计铰链四杆机构时能及时图示其运动轨迹和速度分析,从而将图示结果与设计要求相比较,可以及时修改设计中的偏差.目前,MALTAB 已经不再是/矩阵实验室0,而成为国际上最流行的科学与工程计算的软件工具,以及一种具有广泛应用前景的全新的计算机高级编程语言,它在国内外高校和科研部门正扮演着越来越重要的角色,功能也越来越大,不断适应新的要求提出新的解决办法.可以预见,在科学运算与科学绘图领域,MATLAB 语言将长期保持其独一无二的地位.然而,国内至今尚未见到采用MATLAB 开发的有关机构学的软件,笔者以MATLAB 的科学运算与绘图的强大功能开发了铰链机构运动仿真软件.1 铰链四杆机构运动轨迹仿真软件1.1 程序功能与数学模型1)程序功能 本程序可以进行铰链四杆机构的运动分析及位置求解.用户在铰链四杆机构运动分收稿日期:2002-12-10基金项目:湖南省教育厅科研资助项目(00C289)第一作者:覃虹桥(1959-)男高级工程师研究方向:机械设计制造析仿真软件里输入各种参数,即可自动演示不同的铰链四杆机构(曲柄摇杆机构、双曲柄机构、双摇杆机构)的运动.2)数学模型 已知AB=a ,BC =b ,C D =c ,AD=d .AB 为主动杆,以匀角速度逆时针旋转,AD 为机架,见图1.图1 铰链四杆机构运动简图Fig.1 plame four-linkage motion diagram分析:求B C 的运动轨迹,可找B 、C 两点坐标与转动角度51的关系,然后求51+d 51及B 、C 两点的坐标,即可求出运动轨迹.由图1有矢量方程:AB +BC =AD +DC ,则其分量方程为:a c os 51+b cos 52=d +c cos 53(1)a sin 51+b sin 52=c sin 53(2)将式(1)、(2)联立消去52并整理得:a 2+c 2+d 2-b 22ac +d c os 53a -d cos 51c -cos (51-53)=0(3)再改写为:sin 51sin 53+(cos 51-da)cos 53+a 2+c 2+d 2-b 22ac -d c os 51c=0(4)令r 1=sin 51,r 2=cos 51-d a ,r 2222第14卷第2期常德师范学院学报(自然科学版)Vol.14No.22002年6月Journal of Changde Teachers University(Natural Science Edition)Jun.2002则(4)化为:r 1sin 53+r 2cos 53=r 3(5)由三角恒等式求得:53=2arctg r 1?r 21+r 22-r 23r 2+r 3(6)式(6)两个解对应于机构的两种不同装配形式./+0对应于图1的实线,而/-0对应于图1的虚线.B 点坐标:B x =A x +a cos 51,B y =A y +a sin 51C 点坐示:C x =D x +c cos 53,C y =D y +a sin 53从运动杆的转角53,对时间求导可得DC 的角速度,由式(1)、(2)解出52按速度合成可求得BC 的转动角速度[2].1.2 程序框图以曲柄摇杆机构的运动仿真程度为例,程序框图如下:图2 程序框图Fig.2 Programming frame diagram1.3 程序代码采用MATLAB 开发图形界面,程序如下:%fourlinkages.mh_main=figure(.Units .,.normalized .,.Position .,[.3,.3,.5,.5],,.MenuBar .,.none .,.Name .,.四杆机构仿真.,.Number Title .,,.off .,.Resize .,.off .);h_axis=axes(.Units .,.normalized .,.Position .,[.12,.15,.6,.6],,.Tag .,.axPlot .,.Visible .,.on .,.XLim .,[-50,80<,.YLim .,-60,80]);h_text1=uicontrol (.Style .,.Text .,.Tag .,.myText1.,.Units .,,.normalized .,.Position .,[0.78,0.55,.05,.38],.String .,,.输入已知参数.,,.HorizontalAlignment .,.right .);h_te xt2=uicontrol(.Style .,.Text .,.Tag .,.myText2.,.Units .,,.nor malized .,.Position .,[0.15,0.90,.35,0.05],.String .,,.正在仿真,,OK !.,,.HorizontalAlignment .,.right .);a =20;b =50;c =40;d =50;fai =60;four_linkages0(a,b ,c,fai );%初始化图形h_edit1=uicontrol(.Style .,.Edit .,.Tag .,.myEdit1.,.Units .,,.normalized .,.Position .,[0.86,.85,.10,.1],.String .,.20.,,.HorizontalAlignment .,.right .);h_edit2=uicontrol(.Style .,.Edit .,.Tag .,.myEdit2.,.Units .,,.normalized .,.Position .,[0.86,.75,.10,.1],.String .,.50.,,.HorizontalAlignment .,.right .);h_edit3=uicontrol(.Style .,.Edit .,.Tag .,.myEdit3.,.Units .,,.normalized .,.Position .,[0.86,.65,.10,.1],.String .,.40.,,.HorizontalAlignment .,.right .);h_edit4=uicontrol(.Style .,.Edit .,.Tag .,.myEdit4.,.Units .,,.normalized .,.Position .,[0.86,.55,.10,.1],.String .,.60.,,.HorizontalAlignment .,.right .);h_list=uic ontrol(.Style .,.ListBox .,.Tag .,.myList .,.Units .,,.normalized .,.Position .,[0.78,.35,.20,.15],.String .,.正置|反置.,,.HorizontalAlignment .,.right .,.Value .,1);k=1;h_button1=uicontrol(.Style .,.PushButton .,.Units .,,.normalized .,.Position .,[0.78,.25,.2,.1],.String .,,.运动轨迹仿真.,.CallBack .,,.hd1=findobj(gcf,..Tag ..,..myEdit1..);.,,.a =eval(get(hd1,..String ..));.,,.hd2=findobj(gcf,..Tag ..,..myEdit2..);.,,.b =eval(get(hd2,..String ..));.,,.hd3=findobj(gcf,..Tag ..,..myEdit3..);.,,.c =eval(get(hd3,..String ..));.,,.hd4=findobj(gcf,..Tag ..,..myEdit4..);.,,.d =eval(get(hd4,..String ..));.,,48常德师范学院学报(自然科学版)2002年.kk =get(findobj(gcf,..Ta g ..,..myList ..),..Value ..);.,,.four_linkages(a,b,c,d,kk ).]);%调用回调函数轨迹仿真.h_button2=uicontrol(.Style .,.PushButton .,.Units .,,.normalized .,.Position .,[0.78,.15,.2,.1],.String .,,.角速度分析.,.CallBack .,.four_linkages1(a,b,c,d ,kk ).);h_button3=uicontrol(.Style .,.PushButton .,.Units .,,.normalized .,.Position .,[0.78,.05,.2,.1],,.String .,.退出.,.CallBack .,.four_linkages2.);%调用回调函数退出系统在主程序中有3个回调函数和一个初始化函数,回调函数分别用轨迹仿真、运动分析和退出系统.回调函数程序按前述数学模型编程(程序略);初始化函数用程序运行时初始化界面的图形.运行程序产生以下界面(图3).图3 程序运行界面Fi g.3 Programming Interface在界面中输入已知参数,则可生成相应的图形.当输入a =20,b =50,c =40,d =60,装配形式选取正置时,如果选运动轨迹仿真,则得仿真轨迹(图4);如果装配形式选反置,进行轨迹仿真(图5).(注:图4 运动轨迹仿真(装配形式正置)Fi g.4 Moti on track simulation(positiveset)图5 运动轨迹仿真(装配形式为反置)Fig.5 Motion track simulation (in reverse positive set)在图4、5中为节省篇幅,这两个图形只选了对应图3的图形部分,界面的其它部分未剪取.).而当选取装配形式进行轨迹仿真后,可再选角速度分析,得到连杆与摇杆的角速度图形(略).2 结论1)自动演示不同的四杆机构的运动,模拟仿真运动轨迹与从动件的速度分析,有助于分析机构的速度、加速程度和机构的工作性能;2)采用MATLAB 语言开发机构仿真运动分析软件,开发界面容易,运行程序时无需编辑、连接,给使用者以极大的方便.只要输入数据,即可得到结果.将运行结果与设计要求相比较,从而引导设计者修改设计.参 考 文 献1 薛定宇.科学运算程序MATLAB5.3程序设计与应用[M ].北京:清华大学出版社,2000.2 孟宪源.现代机构手册(上)[M].北京:机械工业出版社,1994.3 王沫然.Si mulink4建模及动态仿真[M].北京:电子工业出版社,2002.THE DEVELOPMENT OF EMULATIONAL SOFTWARE FOR ANALYSIS OF MOTION IN PLANE GEMEL FOUR -LINKAGEBASED ON MATLAB SOFTWAREQING Hong -qiao 1 WEI CH eng -hui 2LU O You -xin 2(1T he material institute,Cen tral China University of Science and T echnology,Wuhan Hubei,430074)(2Department of Mechanical Engineering,Changde Teachers University,Changde Hunan 415003)Abstract A mathematical model of motion analysis was estab -lished in plane four-linkage,and emulational software was deve-loped .The software adop ted Matlab5.3.1as a desi gn language.It combined parametric design with interactive design and had good in -terface for user.Thus,i t was fas ter and more convenient to analyse linkage.The emulational result was obtained as soon as input param -eters was imported and the devisers can make decision-making of modification by the comparing emulational result with design de -mand.It provides an applied software and method for linkage.Key words Gemel Four -Linkage;button;interface;emula -tion(责任编校:谭长贵)49第2期覃虹桥 魏承辉 罗佑新 基于MATLAB 软件的铰链四杆机构运动分析仿真软件开发。
基于MATLABSimulink的5R-P机构运动学数字仿真

基于MATLAB/Simulink 的5R-P 机构运动学数字仿真黄康 许志伟 倪国华(合肥工业大学机械与汽车工程学院,安徽 合肥 230009)摘 要:建立了某5R-P 机构运动学的数学模型,编制了相应的M 函数仿真模块,并利用动态仿真软件MATLAB/Simulink 建立了运动学仿真模型,进行了运动学仿真。
通过整个仿真过程得出:该方法具有运算简单、速度快、方便直观的特点。
与此同时,通过对仿真参数的修改,可进行机构的参数优化。
关键词:运动学 Simulink 仿真研究0 引 言随着仿真技术的发展,对机构进行运动学仿真已变得越来越方便。
机构的运动学分析,主要获得机构中移动构件的位移、速度、加速度或转动构件的角位移、角速度、角加速度。
它是进行机械设计及评价机械运动和动力性能的基础[1]。
对于机构的运动分析,过去一般采用编程的方法进行计算,但是存在程序编写繁琐、可视化差、参数修改麻烦等缺点。
而MATLAB 中的Simulink 模块是一个用来对动态系统进行建模、仿真和分析的软件包,它功能强大,使用方便,已经在学术和工业领域得到广泛的应用[3][4]。
机械式曲柄滑块压力机广泛应用于板料冲压、薄板拉伸等工艺中[6],其增力装置一般采副,因此可简称为5R-P 机构()F [2][5]。
曲柄AB 为原动件,转动副与滑块在同一水平线上,且,各角度如图所示。
将该机构置于直角坐标系中,计算滑块的位置、位移和构件的角位移。
D EF DE l l =XOY DE 由图1可知A 、的位置是给定的,点为研究点。
建立机构的封闭向量方程D FOD CD BC AB OA l l l l l ρϖρρρ=+++ OD OA EF CE BC AB l l l l l l ρρρρρρ+=+++这里取曲柄角位移为0时的位置作为初始位置,根据机构简图的几何关系()()22OD OA AD l l l += (1)()221OAAB OD D B l l l l +−=(2)ODOAl l arctgODA =∠ (3) 构件的初始角DE 1112DC B ODB ∠−∠−=′πθ (4) 其中 DC D B C B D C DB l l l l l DC B 1111112arccos 22211⋅⋅−+=∠ OAOD OAl l l arctgODB −=∠1滑块的初始位置2cos 2θ′⋅⋅+=DE OD c l l x (5) 当曲柄经过时间t 转过角度t ωϕ=()ϕ+∠⋅⋅⋅−+=ODA l l l l l AD AB AD AB BD cos 222 (6)此时构件转过DE BDC ADB ODA ∠−∠−∠−=′′πθ2(7) 其中 BDAD ABBD AD l l l l l ADB ⋅⋅−+=∠2arccos 222,CD BD BC CD BD l l l l l BDC ⋅⋅−+=∠2arccos 222因此,经过时间t ,构件的角位移和滑块的位移DE ⎥⎦⎤⎢⎣⎡−′′⋅⋅+′−′′=⎥⎦⎤⎢⎣⎡c DE ODx l l 22cos 2s θθθθ (8)式(8)分别对时间t 进行一次、二次求导得构件DE 角速度θ&、角加速度θ&&和滑块速度s&、加速度s &&。
matlab曲柄滑块机构课程设计

matlab曲柄滑块机构课程设计一、课程目标知识目标:1. 理解并掌握曲柄滑块机构的基本原理与运动特性;2. 学会使用MATLAB软件进行曲柄滑块机构的运动仿真;3. 掌握运用MATLAB分析曲柄滑块机构的运动数据及性能参数。
技能目标:1. 能够运用所学知识,设计简单的曲柄滑块机构;2. 熟练操作MATLAB软件,进行曲柄滑块机构的运动分析与仿真;3. 能够通过MATLAB处理数据,优化曲柄滑块机构的设计。
情感态度价值观目标:1. 培养学生的团队协作精神,提高沟通与表达能力;2. 激发学生探索科学、技术问题的兴趣,培养创新意识和实践能力;3. 增强学生对机械工程领域的认识和热爱,提高专业认同感。
课程性质:本课程为机械工程专业课程设计,旨在通过实践操作,使学生掌握曲柄滑块机构的设计与分析方法。
学生特点:学生已具备一定的机械原理、力学和MATLAB基础,具有较强的动手能力和学习兴趣。
教学要求:结合实际工程案例,以实践为主,注重培养学生的实际操作能力、分析问题和解决问题的能力。
通过课程学习,使学生能够独立完成曲柄滑块机构的设计与分析任务。
二、教学内容1. 曲柄滑块机构原理及运动特性分析:- 曲柄滑块机构基本组成与工作原理- 曲柄滑块机构的运动学分析- 运动方程的建立及求解2. MATLAB软件在曲柄滑块机构中的应用:- MATLAB软件的基本操作与常用函数- MATLAB曲线拟合、数值计算等功能在曲柄滑块机构分析中的应用- MATLAB/Simulink环境下曲柄滑块机构的运动仿真3. 曲柄滑块机构设计及优化:- 设计原则与步骤- 参数化设计方法- 基于MATLAB的曲柄滑块机构设计优化4. 实践操作与案例分析:- 实际工程案例介绍与分析- 曲柄滑块机构设计及运动分析的实践操作- 数据处理与结果分析教学内容安排与进度:1. 第一周:曲柄滑块机构原理及运动特性分析2. 第二周:MATLAB软件在曲柄滑块机构中的应用3. 第三周:曲柄滑块机构设计及优化4. 第四周:实践操作与案例分析教材章节:1. 《机械原理》中曲柄滑块机构相关章节2. 《MATLAB基础与应用》中相关章节3. 《机械设计》中机构设计及优化相关章节教学内容注重理论与实践相结合,通过系统性的教学,使学生掌握曲柄滑块机构的设计与分析方法,并能够运用MATLAB软件进行实际操作。
matlab曲柄滑块仿真程序代码

Matlab曲柄滑块仿真程序代码随着科学技术的不断发展,计算机仿真在工程设计和研究中扮演着越来越重要的角色。
Matlab作为一种强大的科学计算软件,被广泛应用于工程仿真领域。
曲柄滑块机构是机械工程中常见的一种机构,其运动特性对于设计和分析而言至关重要。
编写Matlab曲柄滑块仿真程序代码,对于工程师和研究人员来说具有重要意义。
本文将对Matlab曲柄滑块仿真程序代码进行详细介绍,包括代码设计思路和程序实现细节等方面。
一、代码设计思路1. 确定曲柄滑块机构的运动方程曲柄滑块机构是由连杆、曲柄和滑块组成的一种机械结构,其运动特性可以通过连杆的运动方程来描述。
通过建立曲柄滑块机构的运动模型,可以确定滑块的位移、速度和加速度等运动特性。
2. 构建Matlab仿真模型基于曲柄滑块机构的运动方程,可以使用Matlab软件进行仿真模拟。
在Matlab中,可以通过编写相应的程序代码,构建曲柄滑块机构的仿真模型,并对其运动特性进行分析和可视化展示。
二、程序实现细节以下是一个简单的Matlab曲柄滑块仿真程序代码示例,代码中包括了曲柄滑块机构的运动方程和仿真模型的构建过程。
```matlab曲柄滑块仿真程序代码示例定义曲柄滑块机构的参数L = 1; 连杆长度r = 0.2; 曲柄半径theta = linspace(0,2*pi,100); 曲柄角度范围omega = 2; 曲柄角速度计算滑块的运动轨迹for i = 1:length(theta)x(i) = r*cos(theta(i)) + sqrt(L^2 - r^2*sin(theta(i))^2);y(i) = r*sin(theta(i)) - sqrt(L^2 - r^2*sin(theta(i))^2);end绘制曲柄滑块机构的运动轨迹figureplot(x,y)xlabel('x')ylabel('y')title('曲柄滑块机构的运动轨迹')计算滑块的速度和加速度vx = diff(x);vy = diff(y);v = sqrt(vx.^2 + vy.^2);a = diff(v);绘制滑块的速度和加速度曲线figuresubplot(2,1,1)plot(v)xlabel('时间')ylabel('速度')title('滑块的速度')subplot(2,1,2)plot(a)xlabel('时间')ylabel('加速度')title('滑块的加速度')```以上代码示例中,首先定义了曲柄滑块机构的参数,包括连杆长度、曲柄半径、曲柄角度范围和曲柄角速度等。
基于Matlab_Simulink平台机构动态仿真的研究

+ F 4, 3
m3 ∞. 口
2.
一
+F 一 m3 m 口
( ( ( 1 ( (
F4 ( 3 3 r 一 3 sn(3 + F, (3 )i 0) 3 r 一 )o ( 3 一 F r3 o (, + F3。 s ( s 一 Ia . cs0) c s0 ) 2 r3 i 0 ) 3s n
下 面 详 细 给 出每 个 步 骤
2 1 力 方 程 .
对 曲柄滑块 中每个连接件应用牛顿定律 , 给出如下的受力 分析 图。
() a连接件2 的受力分析
() b连接件4 的受 力分析
,
() c 连接什3 的受力 分析
图 2 曲柚 滑块 机构 的受 力 图 分析 对 杆 2作受 力 分 析 , 易 写 出它 的运 动方 程 : 容
输入 。
图 1 受外加力矩及力作用力的 曲柄滑块机构 示意图( 曲柄匀速转动)
2 联立 约数 法在 建 立 曲柄 滑块 机构 动态仿真 模 型 中的应 用
机 构 是一 个 约 束 系 统 , 相 对 运 动 的 特 性 由机 构 的几 何关 系 预 先 确 定 。联 立 约 数 法 就 是 对 机 构 中 每 个 连 接 件 应 用 其
.
2
l
)
2
2
i
2
3
2
4
2 2
5
)
2
7
*
司文 荣 , , 苏 张 家 港 市人 。航 天 四院 4 1所 2 0 硕 士 研 究 生 。 男 江 0 0 3级
24
维普资讯
20 年 第 l 06 期 桂 林航天工业高等专科学校 学报 ( 第 4 期 ) J U N LO ULNC L E EO E O P C E H O O Y 司文 荣 曲继和 张 秀玲/ 总 1 O R A FG II O L G FA R S A ET C N L G 文
Matlab在偏置曲柄滑块机构运动分析中的应用

由柄转角奄, I . 图 2 连杆和滑块 的位移 曲线
[i 三+l 。 一。 ] Lc o1 1s [ (o 2 ]on t 缈. I 7 2 2s P s c n  ̄ : ̄ v , , :2 s O ¥  ̄ ! ]
置 曲柄 滑 块 机 构 的滑 块 和连 杆 的运动 特 性进 行
图 1偏置 曲柄滑块机构
以曲柄 固定 铰链 中心 。 为坐 标 原点 ,建立 直 角坐标 系 ,取 封 闭环 OA C B O,矢量 方程 为 :
+, ,= +E ( ) 1
了 分析 ,进而 更加 生动 、清晰 地表 示 出各构 件 的 位移 、速 度和 加速 度 与 曲柄转 角之 间的 关系 , 使
电大 理 工 21 0 2年 6月
SI y f cec n n i eigaR VU td S i e dE gn r t T . l o n a e n
第 2期
总第 2 1 5 期
Mta a lb在偏置 曲柄滑块机构运动分析 中的应用
苗君 明
辽宁装备制造职业技术学院 ( 沈阳 106 ) 11 1
搞
要 偏 置曲柄滑块机构具有急回特性 ,广泛的应 用的机械传动领域 ,以迭到提供 工作效率 的 目
的. 由于滑块 的运动速度 不是 匀速运少振动 冲击奠定理论基础 . 关键词 偏置 曲柄滑块机构 运动分析 MA L B TA
图4 连杆和滑块 的加速度 图
3 结论 通 过构 建 偏 置 曲柄 滑 块机 构 合 理 的 数 学模
型 ,运用 Mal t b语言对 其运 动进 行 分析 ,十 分 a 简 洁地 得 到 了各 个 构件 的运 动 曲线 以及 滑块 的
曲柄滑块机构的优化设计及运动仿真

学士学位论文系别:机电工程系学科专业:机械设计制造及自动化2011年5 月曲柄滑块机构的优化设计及运动仿真系别:机电工程系学科专业:机械设计制造及自动化XX:指导教师:2011年5月曲柄滑块机构的优化设计及运动仿真摘要本论文主要针对目前国外采用图解法对曲柄滑块机构的设计研究,普遍存在着机构的设计效率、设计精度以及设计质量低的诸多不足,从而导致了机构的运动潜能没有得到充分的发挥,还会使得机构的运动性能不良、运动不顺畅,不能实现预期的运动要求。
而运用MATLAB对曲柄滑块机构进行优化设计与运动仿真,可以达到设计的目的。
通过设计的要求,先建立起优化目标的数学模型,然后对设计目标确定约束条件,再运用MATLAB中的优化工具箱编程求解最优方案。
其次根据所求得的优化尺寸,运用仿真工具箱进行运动仿真,最后再对仿真结果运动分析。
为此,利用功能强大的MATLAB软件设计曲柄滑块机构,及其中的Simulink模块,可以方便的实现机构的优化设计和运动仿真,提高了机构的设计效率、设计精度以及降低了开发的成本。
关键词:曲柄滑块机构,优化设计,运动仿真,MATLAB,运动规律OPTIMAL DESIGN OF SLIDER-CRANK MECHANISM AND SIMULATIONABSTRACTIn this paper, using graphic method for the current domestic and international organizations on the design of the slider crank, the prevalence of body design efficiency, design accuracy, and design the disadvantages of low quality, leading to the institution's athletic talent is not given full play, but also will make the poor kinematic performance, movement is not smooth, the movement can not achieve the desired requirements. Crank slider mechanism on the use of MATLAB to optimize the design and motion simulation to achieve the design objectives. Requirements through the design, first built a mathematical model of optimizationobjectives, and then determine the constraints on the design goals, and then use the optimization toolbox in MATLAB programming to solve the optimal solution. Second, the optimization according to the size obtained using the simulation toolbox for simulation, and finally motion analysis. To this end, the use of the powerful MATLAB software slider-crank mechanism, and the Simulink module, you can easily achieve organizational optimization and motion simulation, improved the design efficiency of institutions, design accuracy and reduce the development costs.Key words:Slider-Crank mechanisms; Optimization; Motion Simulation; MATLAB; Law of motion目录目录 (1)摘要...............................................................................................................................第1章绪论.................................................................................................................1.1选题的目的及意义...........................................................................................1.2优化设计方法的概述.......................................................................................1.3 国外的研究现状..............................................................................................1.4 本文主要研究容..............................................................................................第2章曲柄滑块机构的受力分析.............................................................................2.1曲柄滑块机构的分类.......................................................................................2.2曲柄滑块机构的动力学特性...........................................................................2.3曲柄滑块机构中运动学特性...........................................................................第3章偏置式曲柄滑块机构的优化设计.................................................................3.1 优化软件的介绍..............................................................................................3.1.1 MATLAB的发展历程和影响 .......................................................................3.1.2 MATLAB在机构设计中的应用 ...................................................................3.2 机构优化设计实例分析..................................................................................3.2.1 设计目标的建立.........................................................................................3.2.2根据设计要求,确定约束条件..................................................................3.3 利用MATLAB进行优化设计 ........................................................................3.3.1编制优化程序..............................................................................................3.3.2程序运行结果及处理..................................................................................3.3.3 对优化结果进行验证和分析.....................................................................第4章偏置曲柄滑块机构的运动学建模与仿真.....................................................4.1偏置曲柄滑块机构运动特性建模.................................................................4.1.1仿真环境简介............................................................................................4.1.2机构的运动学建模...................................................................................4.2 运动学仿真的实现......................................................................................4.2.1函数的编制及初始参数的设定................................................................4.2.2构建Simulink仿真框图 ............................................................................4.2.3 对仿真结果进行分析...............................................................................总结...............................................................................................................................参考文献....................................................................................................................... 致...................................................................................................................................第一章绪论1.1选题的目的及意义曲柄滑块机构由于可以实现旋转运动与直线运动之间的变换,并可以实现急回运动,所以在机械设备中得到广泛的应用,如冲压机械、惯性筛、自动送料机构、冲床、剪床和往复活塞式发动机等。
曲柄滑块机构的运动学matlab仿真

代码实例[anim_zzy1.m]function f=anim_zzy1(K,ki)% anim_zzy1.m 演示红色小球沿一条封闭螺线运动的实时动画% 仅演示实时动画的调用格式为anim_zzy1(K) % 既演示实时动画又拍摄照片的调用格式为f=anim_zzy1(K,ki)% K 红球运动的循环数(不小于1 )% ki指定拍摄照片的瞬间,取1 到1034 间的任意整数。
% f 存储拍摄的照片数据,可用image(f.cdata) 观察照片。
% 产生封闭的运动轨线t1=(0:1000)/1000*10*pi;x1=cos(t1);y1=sin(t1);z1=-t1;t2=(0:10)/10;x2=x1(end)*(1-t2);y2=y1(end)*(1-t2);z2=z1(end)*ones(size(x2));t3=t2;z3=(1-t3)*z1(end);x3=zeros(size(z3));y3=x3;t4=t2;x4=t4;y4=zeros(size(x4));z4=y4;x=[x1 x2 x3 x4];y=[y1 y2 y3 y4];z=[z1 z2 z3 z4];plot3(x,y,z, 'b' ), axis off % 绘制曲线% 定义" 线" 色、" 点" 型(点)、点的大小(40 )、擦除方式(xor) h=line( 'Color' ,[1 0 0], 'Marker' , '.' , 'MarkerSize' ,40, 'EraseMode' , 'xor' );% 使小球运动n=length(x);i=1;j=1;while 1 % 无穷循环set(h, 'xdata' ,x(i), 'ydata' ,y(i), 'zdata' ,z(i)); % 小球位置drawnow; % 刷新屏幕<21>pause(0.0005) % 控制球速<22>i=i+1;ifnargin==2 &nargout==1 % 仅当输入宗量为2 、输出宗量为1 时,才拍摄照片if (i==ki&j==1);f=getframe(gcf); end % 拍摄i=ki时的照片<25>endif i>ni=1;j=j+1;if j>K; break ; endendend(2)在指令窗中运行以下指令,就可看到实时动画图形。
基于MATLAB的曲柄滑块机构模拟与仿真

2.2设计内容和任务…………………………………………………………..12
2.3实现技术路线……………………………………………………………..12
2.4关键问题和难点分析……………………………………………………..12
2.5设计结果和应用…………………………………………………………….13第三章、程序设计与实现……………………………………………………………14
1.3 用软件进行机构运动学分析的现状和趋势…………………………………9
1.4使用MATLAB/SIMLINK的优势………………………………………………9
1.5 MATLAB/SIMULINK 的特点………………………………………………10
第二章、设计任务分析…………………………………………………………….11
图7曲柄滑块机构运动简图………………………………………………………14
图8Simulink界面展示图…………………………………………………………14
图9曲柄滑块机构运动简图………………………………………………………15
图10new mode…………………………………………………………………15
图11SimMechanics………………………………………………………………15
This design MATLAB GUI design tools and M program combination, the movement of planar four-bar linkage analysis, through the GUI realize interface design, through the M program complete programming and commissioning, and through the interface implementation the slider mechanism analysis and simulation of movement, interface operation mechanism type and judge the pole, the slider shows the driven the instantaneous angular velocity, instantaneous Angle acceleration, extreme position Angle, minimum transmission Angle and anyway, the stroke ratio coefficient.
基于MATLAB的曲柄滑块机构仿真研究

图 3 示波器显示仿真曲线 F ig. 3 The cu rve of si m u lation in the scope
同样可以键入连杆角速度和滑块速度曲线 : p lot( tou, t si m out( : , 2) , tou, t si m out( : , 5) ) 绘制仿真曲线如图 5所示 ( 波动大者为连杆加速度曲线 ) 。 利用仿真得到各变量的响应曲线 , 就可以对机构作出大概的评价。但是为了更加准确评价机构的运 动学特性, 我们常常更加关心各变量的极值大小, 可以使用 MATLAB 的 m ax 命令求出。 在命令行键入: w 2= m ax( si m ou t( : , 2) ) ; a= m ax ( si m out(: , 4) ), v= m ax( si m out( : , 5) ) 即可得到 :
参考文献 : [ 1] 郑文纬 , 吴克坚 . 机械原理 [M ]. 北京 : 高等教育出版社 , 2004 . 33- 103. [ 2] [ 美 ] 约翰 . F. 加得纳 . 机构动态 仿真 2002. [ 3] [ 美 ] Edward B. M ag rab 等 . M ATLA B 原理与工程应用 [ M ]. 高会生 , 等译 . 北京 : 电子工业出版社 , 2002 . 125- 139. [ 4] 张森、 张正亮 . M ATLAB 仿真技术与 实例应用教程 [M ]. 北京 : 机械工业出 版社 , 2004 . [ 5] 张葛祥、 李娜 . M ATLAB 仿真技术与 应用 [M ]. 北京 : 清华大学出版社 , 2003 . 55- 83 . ( 责任编辑 : 李 孟良 ) 使用 M ATLA B 和 SI M UL I NK [M ]. 周进 雄 , 等译 . 西安 : 西 安交通 大学 出版社 ,
基于Matlab的机构动力学仿真分析

1 r2 sinθ2
v3 x
r1ω1 sinθ1
0 - r2 cosθ2 ω2 = r1ω1 cosθ1
(11)
1 r2 sinθ2
a3 x
0 - r2 cosθ2 ε2 =
- r1ε1 sinθ1 - r1ω21 cosθ1 - r2ω22 cosθ2
r1ε1 cosθ1 - r1ω21 sinθ1 - r2ω22 sinθ2
如图 2 所示 。图中函数模块 sxh f1 是根据式 (9) 编
写的 M 函数对机构进行动力分析 ,计算约束反力和
力矩 。函数模块 sxh m1 、sxh m2 ,是根据式 (10) 、
式 (12) 编写的 M 函数对机构进行运动分析 ,计算加
速度 。工作阻力的方向随滑块速度方向变化而变
化 ,通过函数 sxh Fpx 来实现 。在仿真运行之前还 应确定图中 5 个积分器的初始条件。选择从 θ1 = 0 开始 ,则初始位置 θ2 = 0 , x3 = r1 + r2 ;ω1 = 100 radΠ s ,根据式 (10) 可求出速度初值 ω1 = - 20 radΠs , v3 x = 0 。最后设定仿真系统运行 0112 s ,机构运动约 2 个 循环周期 ,执行仿真命令 。仿真运动学结果保存在 矩阵 simout 中 ,动力学结果保存在矩阵 simout1 中 。
4 结语 液压支架设计阶段综合运用 CAE ,借助于三维
造型对液压支架进行有限元分析 ,运动仿真 ,动力学 分析 ,避免运动中的机构干涉现象 ,能够使设计中的 “虚拟样机”检验发挥强大作用 ,确保液压支架安全 可靠 ,结构优化合理 ,探索液压支架设计的新思路 , 提高液压支架设计水平 。
参考文献 : [1 ]赵慧设 ,等 1 基于 Internet 的三维模型协同浏览与批注系统 [J ]1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于MATLAB曲柄滑块机构运动仿真1.题目描述题目:对如图1所示的曲柄滑块机构的运动过程进行仿真,并用动画的方式显示曲柄滑块机构的运动过程,位移曲线、速度曲线和加速度曲线。
图中,AB长R2,BC长R3mm,A点为坐标原点。
图1 曲柄滑块机构示意图2.实现方法利用GUI界面设计来对曲柄滑块机构的运动过程进行仿真,并用动画的方式显示曲柄滑块机构的运动过程。
3.界面设计1. Gui 设计1)新建GUI:菜单-新建-gui,并保存为test52)界面设计:拖拽左侧图标到绘图区,创建GUI界面拖拽左侧图标值绘图区设置如下的按钮最终的仿真界面如图所示3)代码添加:进入代码界面4.代码编程%模型求解a1=str2double(get(handles.edit1,'String'));a2=str2double(get(handles.edit2,'String'));a3=str2double(get(handles.edit3,'String'));a4=str2double(get(handles.edit4,'String'));a5=str2double(get(handles.edit5,'String'));a=a1*((1-cos(a4*a5))+0.25*(a1/a2)*(1-cos(2*a4*a5))); set(handles.edit6,'String',a);a0=(a4*a1)*(sin(a4*a5)+0.5*(a1/a2)*sin(2*a4*a5));set(handles.edit7,'String',a0);a6=(a4*a4*a1)*(cos(a4*a5)+(a1/a2)*cos(a4*a5));set(handles.edit8,'String',a6);%绘制位移、速度、加速度曲线axes(handles.axes3);r1=str2double(get(handles.edit1,'String'));r2=str2double(get(handles.edit2,'String'));omiga1=str2double(get(handles.edit4,'String'));x11=1:720;for i=1:720x1(i)=i*pi/180;%sin(x2(i)=r1/r2*sin(x1(i));x2(i)=asin(-r1/r2*sin(x1(i)));x22(i)=x2(i)*180/pi;r3(i)=r1*cos(x1(i))+r2*cos(x2(i));B=[-r1*omiga1*sin(x1(i));r1*omiga1*cos(x1(i))];A=[r2*sin(x2(i)) 1;-r2*cos(x2(i)) 0];X=inv(A)*B;omiga2(i)=X(1,1);v3(i)=X(2,1);endplot(x11/60,0.5*r1*sin(x1));xlabel('ʱ¼äÖá t/sec')ylabel('Á¬¸ËÖÊÐÄÔÚYÖáÉϵÄλÖÃ/mm')figure(2)plot(x11/60,r3);title('λÒÆÏßͼ')grid onhold off;xlabel('ʱ¼ät/sec')ylabel('»¬¿éλÒÆ r3/mm')figure(3)plot(x11/60,omiga2);title('Á¬¸Ë½ÇËÙ¶È')grid onhold off;xlabel('ʱ¼ä t/sec')ylabel('Á¬¸Ë½ÇËÙ¶È omiga2/rad/sec') figure(4)plot(x11/60,v3*pi/180);title('»¬¿éËÙ¶È')grid onhold off;xlabel('ʱ¼ä t/sec')ylabel('»¬¿éËÙ¶È v3/mm/sec')%绘制表格axes(handles.axes3);grid onaxes(handles.axes1);grid on%制作动画axes(handles.axes1);hf=figure('name','Çú±ú»¬¿é»ú¹¹'); set(hf,'color','r');hold onaxis([-6,6,-4,4]);grid onaxis('off');xa0=-5;%»îÈû×󶥵ã×ø±êxa1=-2.5;%»îÈûÓÒ¶¥µã×ø±êxb0=-2.5;%Á¬¸Ë×󶥵ã×ø±êxb1=2.2;%Á¬¸ËÓÒ¶¥µã×ø±êx3=3.5;%תÂÖ×ø±êy3=0;%תÂÖ×ø±êx4=xb1;%ÉèÖÃÁ¬¸ËÍ·µÄ³õʼλÖúá×ø±êy4=0;%ÉèÖÃÁ¬¸ËÍ·µÄ³õʼλÖÃ×Ý×ø±êx5=xa1;y5=0;x6=x3;%ÉèÖÃÁ¬Öá³õʼºá×ø±êy6=0;%ÉèÖÃÁ¬Öá³õʼ×Ý×ø±êa=0.7;b=0.7c=0.7a1=line([xa0;xa1],[0;0],'color','b','linestyle','-','linewidth',40); %ÉèÖûîÈûa3=line(x3,y3,'color',[0.5 0.60.3],'linestyle','.','markersize',300);%ÉèÖÃתÂÖa2=line([xb0;xb1],[0;0],'color','black','linewidth',10);%ÉèÖÃÁ¬¸Ëa5=line(x5,y5,'color','black','linestyle','.','markersize',40);%ÉèÖÃÁ¬¸Ë»îÈûÁ¬½ÓÍ·a4=line(x4,y4,'color','black','linestyle','.','markersize',50);%ÉèÖÃÁ¬¸ËÁ¬½ÓÍ·a6=line([xb1;x3],[0;0],'color','black','linestyle','-','linewidth',10 );a7=line(x3,0,'color','black','linestyle','.','markersize',50);%ÉèÖÃÔ˶¯ÖÐÐÄa8=line([-5.1;-0.2],[0.7;0.7],'color','y','linestyle','-','linewidth' ,5);%ÉèÖÃÆû¸×±Úa9=line([-5.1;-0.2],[-0.72;-0.72],'color','y','linestyle','-','linewi dth',5);%ÉèÖÃÆû¸×±Úa10=line([-5.1;-5.1],[-0.8;0.75],'color','y','linestyle','-','linewid th',5);%ÉèÖÃÆû¸×±Úa11=fill([-5,-5,-5,-5],[0.61,0.61,-0.61,-0.61],[a,b,c]);%ÉèÖÃÆû¸×ÆøÌålen1=4.8;%Á¬¸Ë³¤len2=2.5;%»îÈû³¤r=1.3;%Ô˶¯°ë¾¶dt=0.015*pi;t=0;while 1t=t+dt;if t>2*pit=0;endlena1=sqrt((len1)^2-(r*sin(t))^2);%Á¬¸ËÔÚÔ˶¯¹ý³ÌÖкáÖáÉϵÄÓÐЧ³¤¶Èrr1=r*cos(t);%°ë¾¶ÔÚÔ˶¯¹ý³ÌÖкáÖáÉϵÄÓÐЧ³¤¶Èxaa1=x3-sqrt(len1^2-(sin(t)*r)^2)-(r*cos(t));%»îÈûÔÚÔ˶¯¹ý³ÌÖеÄÓÒ¶¥µã×ø±êλÖÃxaa0=xaa1-2.5;%%»îÈûÔÚÔ˶¯¹ý³ÌÖеÄ×󶥵ã×ø±êλÖÃx55=x3-cos(t)*r;%Á¬¸ËÔÚÔ˶¯¹ý³ÌÖкá×ø±êλÖÃy55=y3-sin(t)*r;%Á¬¸ËÔÚÔ˶¯¹ý³ÌÖÐ×Ý×ø±êλÖÃset(a4,'xdata',x55,'ydata',y55);%ÉèÖÃÁ¬¸Ë¶¥µãÔ˶¯set(a1,'xdata',[xaa1-2.5;xaa1],'ydata',[0;0]);%ÉèÖûîÈûÔ˶¯set(a2,'xdata',[xaa1;x55],'ydata',[0;y55]);set(a5,'xdata',xaa1);%ÉèÖûîÈûÓëÁ¬¸ËÁ¬½ÓÍ·µÄÔ˶¯set(a6,'xdata',[x55;x3],'ydata',[y55;0]);set(a11,'xdata',[-5,xaa0,xaa0,-5]);%ÉèÖÃÆøÌåµÄÌî³äset(gcf,'doublebuffer','on');%Ïû³ýÕð¶¯drawnow;end5.结果(1)对它的结构参数进行设置,如下图所示。
