第3章角动量与电子自旋之2

合集下载

自旋电子学

自旋电子学
众所周知，电子具有两个重要的内禀属性，即电荷和自旋。现代微电子技术只利用了电子的电荷属性而没有考虑电子的自旋特性。实际上，人们早在20世纪20年代就发现了电子的自旋特性，但直到发现材料的电阻率随着材料磁化状态的变化而呈现显著改变的巨磁电阻效应并用自旋相关散射和双电流模型来解释之后，人们开始认识到电子自旋的应用价值。对电子自旋的研究成为当今研究的一个热点课题，并逐渐形成了一个新的研ห้องสมุดไป่ตู้领域即自旋电子学（spintronics）。自旋电子学中电子的自旋取代电子电荷作为信息储存和传输的载体。电子的自旋态具有较长的驰豫时间，更不容易被杂质或缺陷的散射破坏，而且自旋态也容易通过调节外部的磁场来进行控制。人们正期待着利用电子自旋自由度来设计运行速度更高、能量消耗更低、功能多、高集成的下一代微电子器件。这种器件抛弃了电子的经典特性，转而利用了电子的量子特性，因而原则上将允许电子器件的尺寸进一步大大的减小，从而进入纳米尺度的范围即量级，成为介观物理的重要组成部分之一。
通过对电子电荷和电子自旋性质的研究，最近在电子学和信息技术领域出现了明显的进展。这个进展的重要标志之一就是诞生了自旋电子学。在传统的电子学中，数据处理集成电路所用的是半导体中电子的电荷，但并不是说电子的自旋自由度以前从没有用过，例如传统的数据存储介质，如磁盘，用的就是磁性材料中电子的自旋。 ~2UmX'
尽管对自旋电子学的基本原理和概念的研究非常令人感兴趣，但在人们能够制造出自旋电子学应用器件之前，还有许多障碍需要克服。例如，自旋电子学的一个基本要求是在电子材料中产生和保持大的自旋极化电流到很长的时间。要实现这一点尚需继续努力才能完成。事实上，把足够大的自旋极化电流引入半导体材料也是一个问题。以此类似，对于量子计算，人们要求精密的控制自旋纠缠及利用局域磁场操纵单一自旋。对此，虽然已经提出许多设计方案，但至今尚没有特别好的想法。很清楚的是，对于一个崭新的领域，总是机会与挑战并存。在自旋电子学的应用变成现实之前，确实有大量的基本物理问题需要研究。有关自旋电子学的物理学基础和应用问题的研究现状，有兴趣的读者可以参看最近刚刚发表的一篇极好的评述文章：Zutic′, Fabian, and Das Sarma: Spintronics: Fundamen- tals and applications，Rev. Mod. Phys., 76, 323-410，April 2004。 ;nb>IL

4.3 电子自旋的假设

由于 j l 1 , 2
所以双重原子态分别表示为
n2 L(l1/2)和n2 L(l1/2) （1）
仅当l =0 时，
j s 1 ，双重态只有一个原子态表示。 2
比如nS，nP，nD 态的双重态表示为：
nS n2S1
2
n2P1
nP
2
n2 P3
2
nD
n2 D3
1）g 因子的计算
入射原子的状态通常表示为 n2s1L j，即告诉了我
们该状态的各量子数n,l ,j,s，由方程：记住朗德因子的计算公式
gj
=
1+
J
2
+ S 2 - L2 2J 2
=
3 2
+
1 2
(
S 2 - L2 J2
)
可以求出相应状态的 g 因子
例如
氢原子处于基态时，n

1,
l

0,
j
4.3 电子自旋的假设
前言电子自旋的假设朗德g因子角动量的合成原子态的表示 Stern-Gerlach 实验的理论解释
前言
史特恩-盖拉赫实验中出现偶数分裂的事实启示人们，电子的轨道运动似乎不是全部的运动。换句话说，轨道磁矩应该只是原子总磁矩的一部分，那另一部分的运动是什么呢？
相应的磁矩又是什么呢？
1925年，两位荷兰学生乌仑贝克与古兹米特根据史特恩-盖拉赫实验、碱金属光谱的精细结构等许多实验事实，发展了原子的行星模型，提出电子不仅有轨道运动，还有自旋运动，它具有固有的自旋角动量S。
引入了自旋假设以后，人们成功地解释了碱金属的精细结构，塞曼效应以及史特恩-盖拉赫实验等。

写出全同粒子系统的总轨道角动量lz和l2的二次量子化形式

写出全同粒子系统的总轨道角动量lz和l2的二次量子化形式1. 引言1.1 概述本文旨在探讨全同粒子系统的总轨道角动量lz和l2的二次量子化形式。

在量子力学中，全同粒子系统是一类具有相同物理性质的粒子组成的系统，它们之间没有任何区别。

而总轨道角动量lz和l2则是描述这些粒子在空间中运动时所拥有的角动量。

1.2 文章结构本文按照以下结构进行论述：首先，我们将介绍全同粒子系统总轨道角动量lz 的定义，并给出相关概念和数学表示；其次，我们将阐述lz的本征值及其对应的本征态表示；最后，我们将推导和解释lz的二次量子化表达式。

随后，我们将进行类似的分析并讨论全同粒子系统总轨道角动量l2的二次量子化形式。

1.3 目的本文旨在深入理解全同粒子系统总轨道角动量lz和l2，并通过推导和解释其二次量子化形式，进一步揭示全同粒子系统中这两个重要物理概念的内涵和意义。

这对于更好地理解多粒子体系及其特性、研究复杂体系的性质和行为具有重要的理论与实际意义。

同时，本文还将探讨相关研究的未来发展方向。

以上是“1. 引言”部分内容的详细清晰撰写。

2. 全同粒子系统总轨道角动量lz的二次量子化形式2.1 全同粒子系统总轨道角动量lz的定义在全同粒子系统中，总轨道角动量lz表示所有单个粒子的轨道角动量在z方向上的矢量和。

它是各个粒子的单个轨道角动量lz值之和。

2.2 lz的本征值和本征态表示根据量子力学理论，lz具有离散值，可用来描述全同粒子系统在z方向上的旋转运动。

其本征值为mħ，其中m为整数或半整数，ħ为约化普朗克常数。

对于N个全同粒子构成的系统，其总轨道角动量lz可以通过求解含有N个因素化项的哈密顿算符得到。

由于全同粒子系统需要满足泡利不相容原理，因此泡利原理会导致只有一部分选定组态有效。

2.3 lz的二次量子化表达式推导与解释在二次量子化中，我们使用产生算符a†和湮灭算符a来描述波函数。

这些算符与单个粒子态以及多体态之间的关系如下所示：$$\begin{align*}a^\dagger_i |0⟩ & = \text{产生一个粒子在单粒子态} |i⟩ \\a_i |0⟩ & = 0\end{align*}$$其中，$|0⟩$表示全空模式，没有任何粒子。

电子的角动量与电子的自旋

pl
μs
学习材料
Bl
6
§4.2 电子的角动量与电子的自旋
• 光谱和能级的精细结构应该从原子的运动特征进行解释 • 在球对称的库仑场中，仅仅有电子的轨道运动，不可能产生能级分
裂 • 除了相对论效应外，还应该有其它因素
不同l的能级移动
• 电子应该还有除了轨道运动之外的其它运动特征
• 用其它一个力学量描述这种运动特征
• 尝试引入其它一种角动量
s 1/ 2
2. 自旋角动量的Z重量
1
ps,z 2 ms
1
ms 2
学习材料
ps
3 2
3
2
2
cos1( 1 )
3 54.7
2
3电.s自子旋由em磁pe于s矩自2 旋s(s而1产)生B 电的子轨磁道矩运μp动ll 的dre磁矩μpllBiA2enlm(le1)2emple
3B
l l(l 1)B
4. 自旋磁矩的Z重量
μs
z
Байду номын сангаас
ps
s,z B 2ms B B
ps μs
学习材料
3
Paul Ehrenfest 1880–1933 Austrian physicist
George Eugene Uhlenbeck 1900 – 1988 Netherland physicist
Kramers
Samuel Abraham Goudsmit 1902–1978 Netherland physicist
学习材料
4
z
sz
s
1
2
3
2
s
sz
z s
sz

第三章量子力学中的角动量

39
J 2 j1 , j2 , j , m = j ( j + 1) J z j1 , j2 , j , m = m
2
j1 , j2 , j , m
j1 , j2 , j , m
显然，总角动量量子数 j，它的 z 分量量子数 m 与 j1 , j 2 , m1 , m 2 有关，为了找出它们之间的关系，首先必须将耦合表象和无耦合表象这两个表象联系起来。为此，将耦合表象的基矢
J Z j1 , j2 , j , m =
m1 , m2
∑ (J
1Z
+ J 2 Z ) j1 , m1 , j2 , m2 × j1 , m1 , j2 , m2 j1 , j2 , j , m
于是有
m = m1 + m2
上式可写成
j1 , j2 , j , m = ∑ j1 , m1 , j2 , m − m1
j1 , j 2 , j , m 按无耦合表象的基矢 j1 , m1 , j 2 , m 2 展开，得
j1 , j2 , j , m =
m1 , m2
∑
j1 , m1 , j2 , m2
j1 , m1 , j2 , m2 j1 , j2 , j , m
上式中的系数 j1 , m1 , j 2 , m 2 j1 , j 2 , j , m 称为克莱布希一高登(Clebsch 一 Gordon)系数。以算符式 J z = J1z + J 2 z 分别作用于上式的两端，得
2 2 J , J2 =0
另外显然还存在
2 J Z , J12 = 0, JZ , J2 =0
J 2, JZ =0
这些对易关系表明 J12 , J 22 , J 2 , J Z 这四个算符两两对易，它们具有共同的正交、归一、完备、封闭的本征函数系。记相应于量子数 j1 j 2 , j, m 的本征函数为 j1 , j 2 , j , m 有

量子力学中的角动量与自旋

量子力学中的角动量与自旋量子力学是研究微观领域中粒子行为的理论框架，角动量是其中一个重要的物理量，而自旋则是角动量的一种形式。

在本文中，我将详细介绍量子力学中的角动量与自旋的概念、特性以及在不同领域中的应用。

一、角动量的概念及数学表达在经典物理中，角动量通常被定义为物体围绕某一轴转动的物理量。

然而，在量子力学中，角动量的定义更加复杂。

根据量子力学的原理，角动量是由角动量算符来表示的，而角动量算符有两个重要的分量，即轨道角动量算符和自旋角动量算符。

1. 轨道角动量算符轨道角动量算符由三个独立的分量组成，分别是L_x、L_y和L_z。

它们满足角动量的代数关系，即[L_x, L_y] = iħL_z， [L_y,L_z] = iħL_x，以及[L_z, L_x] = iħL_y。

这些关系体现了角动量算符之间的非对易性质。

2. 自旋角动量算符除轨道角动量外，自旋角动量是粒子的固有属性，用s来表示。

自旋角动量算符由三个分量组成，通常表示为S_x、S_y和S_z。

它们也满足非对易性质的代数关系，即[S_x, S_y] = iħS_z， [S_y,S_z] = iħS_x，以及[S_z, S_x] = iħS_y。

二、角动量与自旋的特性及量子数角动量和自旋都具有一些特殊的性质和量子数，这些性质和量子数决定了它们在量子力学中的角色和行为。

1. 角动量的量子数轨道角动量的量子数由轨道量子数l来表示，它决定了角动量的大小。

轨道量子数l可以取整数或半整数，并满足l = 0,1,2,3,...。

对于给定的轨道量子数l，轨道角动量的大小可以用以下公式表示：L = ħ√(l(l+1))。

2. 自旋的量子数自旋的量子数由自旋量子数s来表示，它决定了自旋角动量的大小。

自旋量子数s通常取半整数值，可以是1/2, 3/2, 5/2等，并满足s = 1/2, 3/2, 5/2,...。

自旋角动量的大小可以用以下公式表示：S = ħ√(s(s+1))。

第三章：碱金属原子和电子自旋

玻尔理论无法解释谱线的这种精细结构。玻尔理论无法解释谱线的这种精细结构。模型的局限性还表现在它缺乏计算原子其它性质的理论方法。例如不能计算出不同谱线的相对强度。换言之，处在n=3态上的电子有多少次直接跳到1态上， n=3态上的电子有多少次直接跳到换言之，处在n=3态上的电子有多少次直接跳到1态上，有多少次先跳到2再到1上发出两种光。对此玻尔理论无能为力。次先跳到2再到1上发出两种光。对此玻尔理论无能为力。其问题出在理论结构本身，它是经典理论与量子条件的结合（其问题出在理论结构本身，它是经典理论与量子条件的结合（所以又称为旧量子论），其量子条件没有理论根据，），其量子条件没有理论根据以又称为旧量子论），其量子条件没有理论根据，缺乏逻辑的统一性。一性。当时的物理学出现了一种比较混乱的情况，当时的物理学出现了一种比较混乱的情况，经典理论与量子理论无法统一。无法统一。就在这个时候，1923年法国物理学家德布罗意根据光的波粒二象就在这个时候，1923年法国物理学家德布罗意根据光的波粒二象年法国物理学家德布罗意性提出物质波假设，认为不仅仅光，其它任何微观客体都有波粒性提出物质波假设，认为不仅仅光，其它任何微观客体都有波粒二象性。二象性。而且这一假设被后来的电子衍射实验所验证。而且这一假设被后来的电子衍射实验所验证。
德布罗意波的理论导致了薛定谔在1925年以波动方程的形式建立德布罗意波的理论导致了薛定谔在1925年以波动方程的形式建立 1925 新的量子理论（标志着量子力学的建立）。新的量子理论（标志着量子力学的建立）。不久薛定谔证明，这两种量子理论是完全等价的，不久薛定谔证明，这两种量子理论是完全等价的，只不过形式不同罢了。同罢了。事实上，玻尔理论中有些观点是不符合量子力学理论的。事实上，玻尔理论中有些观点是不符合量子力学理论的。虽然玻尔理论有一定的局限性，但是，虽然玻尔理论有一定的局限性，但是，我们在以后的讨论中并不打算完全抛弃这个理论模型因为它给出了原子结构一个有用而直观的物理图像，许多原子性因为它给出了原子结构一个有用而直观的物理图像，质特别是原子的磁性实际上都可以根据玻尔轨道概念解释。质特别是原子的磁性实际上都可以根据玻尔轨道概念解释。但我们要对旧量子论作一些修改。但我们要对旧量子论作一些修改。轨道方向）角量子数轨道角动量磁（轨道方向）特殊方向的动量量子数 nф=1,2, h h 旧量子论：旧量子论： ,n pψ = nψ pφ = nφ nψ = nφ , nφ −1,L,0,L,−nφ …,n 2π 2π h l=0,1,2, 量子力学：量子力学：=0,1,2, pl = l(l +1) h m = l,l −1,L,0,L,−l pm = m …,n-1 ,n,n 2π 2π

《工程化学基础》第3章-自用版

晶体粉末狭缝电子束
电子衍射仪
7
表3. 1
粒子电子
粒子的德布罗依波长和半径
半径 /m 10–17 10–10 波动性较明显不明显
质量 /kg 速度 /(m· s–1) 波长 /m 9×10–31
106 108
103 106
7×10–10 7×10–12
4×10–10 4×10–13
氢原子 1.6×10–27
39
3. 2 元素周期律金属材料
学习要求 1. 掌握核外电子排布原则及方法；掌握未成对电子数的确定及未成对电子存在的意义。 2. 了解核外电子排布和元素周期律的关系，明确元素基本性质的周期性变化的规律。 3. 明确耐腐蚀金属、耐高温金属等在周期表中的位臵，了解合金的基本结构类型。 4. 了解合金材料的结构、性能与应用；掌握固溶强化和 d 区碳（氮、硼）化合物熔点、硬度、稳定性变化规律及应用。 5. 了解生命体内元素在周期表中的分布情况，明确微量元素的重要性。
2
目录
3. 1 原子核外电子运动状态 3. 2 元素周期律金属材料 3. 3 化学键分子间力高分子材料
3. 4 晶体缺陷陶瓷和复合材料
3
3. 1 核外电子的运动状态
学习要求 1. 了解量子力学的创立，理解波粒二象性，认识理论的相对性。 2. 了解波函数表达的意义，理解原子轨道、电子云的真实含义。
结果
期待的经典结果
N
S
原子束
史特恩—盖拉赫实验
18
1925年，两位不到25岁的荷兰学生乌仑贝克（G. E. Uhlenbeck）和古兹米特（ S. Goudsmit）大胆地提出了电子自旋假设：自旋磁量子数 ms

粒子物理学中的角动量与自旋

粒子物理学中的角动量与自旋粒子物理学是研究微观世界中构成物质的基本粒子及其相互作用的学科。

在这个领域中，角动量和自旋是两个重要的概念。

本文将介绍粒子物理学中的角动量和自旋的基本概念和性质。

一、角动量的定义与性质在粒子物理学中，角动量是描述粒子自身旋转状态的物理量。

它是经典力学和量子力学中重要的物理量之一。

角动量不仅包含了粒子旋转的快慢，还包含了旋转的方向。

对于经典力学而言，角动量的定义可以表述为J=r×p，其中r是粒子到某一固定点的矢量，p是粒子的线性动量。

角动量的单位是[kg·m^2/s]，它是一种矢量。

在量子力学中，角动量是由角动量算符表示的。

角动量算符可以分为轨道角动量算符L和自旋角动量算符S两部分。

轨道角动量算符描述了粒子围绕某一轴的运动。

自旋角动量算符则描述了粒子自身固有的旋转状态。

具体而言，轨道角动量算符L与位置和动量算符之间的关系可以表示为L=r×p，而自旋角动量算符S则与粒子的内禀自旋有关。

二、自旋与角动量自旋是描述粒子固有性质的物理量。

它与粒子的旋转和内部结构有关，但并不是物体自转的经典概念。

在粒子物理学中，自旋被视为一种内禀角动量，它与粒子的质量和电荷等性质密切相关。

自旋可以是整数或半整数，分别对应于玻色子和费米子。

例如，光子的自旋为1，电子的自旋为1/2。

自旋在粒子物理学中起着重要的作用。

它决定了粒子的性质和行为，例如粒子的稳定性、相互作用方式等。

在量子力学中，自旋角动量算符S与自旋矢量之间的关系可以表示为S=sħ，其中s为自旋量子数，ħ为约化普朗克常数。

三、角动量守恒在粒子物理学中，角动量守恒是一个基本原理。

根据角动量守恒定律，一个封闭系统的总角动量在时间上是守恒的。

这意味着在一个过程中，如果没有外力或外界扰动作用，粒子系统的总角动量将保持不变。

这一原理在粒子物理学中具有广泛的应用。

四、角动量与粒子的识别粒子物理学中，角动量也被用于粒子的识别。

自旋和角动量

a c
b d

a c
b d

a 0 d 0
σX 简化为：
0 b x c 0
由力学量算符厄密性
ˆ
x

ˆ
x

0 c
b0

0 b*
c* 0

0 c
b0
得：b = c* (或c = b*)
σx2,σy2,σZ2 的本征值都是。
即：

2 x

2 y

2 z
1
2. 反对易关系
基于σ的对易关系，可以证明 σ各分量之间满足反对易关系:
左乘σy
ˆ xˆ y ˆ yˆ x 0

ˆ yˆ z ˆ zˆ y 0 ˆ zˆ x ˆ xˆ z 0
2×1 的列矩阵，那末，电子自旋算符的
矩阵表示应该是 2×2 矩阵。
因为Φ1/2 描写的态，SZ有确定值 /2，所以Φ1/2 是 SZ 的本征态，本征
值为 /2，即有：
Sz1 2

2
1 2
矩阵形式

2

a c
b d

1
(r 0
,
t )

2

58 58
96 90
ÅÅ
3s1/2
（三）电子自旋假设
Uhlenbeck 和 Goudsmit 1925年根据上述现象提出了电子自旋假设
（1）每个电子都具有自旋角动量，它在空间任何方向上
的投影只能取两个数值：

S
Sz 2

近代物理量子5-氢原子的量子理论,电子自旋

L l(l 1)
l = 0, 1, 2, 3, …, n-1 称为角量子数(副量子数)。
对同一个 n , 角动量有n个不同的值
定义L为角动量是因为 h 具有角动量的量纲，并不需要有轨道的概念。
当n 1时，l 0，L 0，即电子处于基态时角动量为零。玻尔理论：
L n h n
2
n 1,2,3...
5.求出概率密度分布及其他力学量
一、氢原子的量子力学处理
1.氢原子的定态薛定谔方程
[
22Βιβλιοθήκη U (r )]( r )
E (r )
2m
氢原子中电子的电势能 U e2
4π 0 r
U和方向无关为中心力场U( r )
z
球坐标 x r sin cos
y r sin sin
z r cos
y
x
在球坐标中的薛定谔方程
而且计算得到的两条沉积线之间的距离也与实验符合得很好。
讨论四个量子数 • 电子的状态用量子数 n , l , ml 描述
考虑自旋后还有2种可能相当于还需一个自由度来表征
• 所以电子的状态应用n，l，ml ，ms描述
（1）主量子数 n：n =1，2，3……，可以大体上决
定原子中电子的能量。
1900-1958 1945年诺贝尔物理
学奖获得者
半年后，荷兰物理学家埃斯费斯特的两个学生乌仑贝克和高斯密特在不知上述情形下，也提出了同样的想法，并写了一篇论文，请埃斯费斯特推荐给“自然”杂志。接着又去找洛仑兹，一周后，洛仑兹交给他们一叠稿纸。并告诉他们，如果电子自旋，其表面速度将超过光速，但论文已寄出，他们后悔不已。
1921年史特恩---盖拉赫进行的实验是证明角动量空间量子化的首例实验，是原子物理学最重要的实验之一。

第三章量子力学中的力学量

以上归一化方法称为箱归一化。动量本征函数：
再乘上时间因子：
参见：
P23:2.2-4 式。
自由粒子的波函数，其动量有确定值。
2、角动量算符
3、角动量平方算符
为讨论方便我们要导出上述算符在球坐标下的表示式。同理可得：
同理可得：
同理可得：
把上述表达式分别代入
4、相应的本征方程和本征值（1）角动量的分量
c、分立谱—本征值只能取一系列孤立实数，如粒子在束缚态下的能谱。
重点讨论连续谱和分立谱。通常连续谱记为或，
分立谱记为
。对应的本征函数分别记
为
及。
（2）、力学量算符的本征态及本征值可能不是一一对应，而出现若干个（如个）本征态对应一个本征值，称这种情况为度简并。 §3-2 动量算符和角动量算符 1 动量算符
第三章量子力学中的力学量
经典力学中物质运动的状态总是用坐标、动量、角动量、自旋、动能、势能、转动能等力学量以决定论的方式描述。
量子力学的第一个惊人之举就是引入了波函数这样一个基本概念，以概率的特征全面地描述了微观粒子的运动状态。
但并不能作为量子力学中的力学量。于是，又引入了一个重要的基本概念—算符，用它表示量子力学中的力学量。
算符和波函数作为量子力学的核心概念相辅相承、贯穿始终。
本讲内容是量子力学的重要基础理论之一，也是大家学习的重点。重点掌握以下内容：
一个基本概念：厄米算符（作用及其基本性质）；
两个假设：力学量用线性厄米算符表示，状态用线性厄米算符的本征态表示；
•三个力学量计算值：确定值、可能值、平均值；
四个本征态及本征值：坐标或、动量或、角动量及、能量（哈密顿量）。

电子自旋角动量和自旋磁矩课件

04
自旋电子学应用
自旋电子存储器
总结词
自旋电子存储器是利用电子自旋的特性进行信息存储的设备，具有高存储密度、低能耗和长寿命等优点。
详细描述
自旋电子存储器利用电子自旋的两种状态（向上和向下）来表示二进制信息中的0和1。通过改变电子的自旋方向，可以实现信息的写入和读取。与传统的电荷存储方式相比，自旋电子存储器不需要依赖电荷的移动，因此具有更快的读写速度和更高的稳定性。
在量子力学中的基础性
自旋角动量是量子力学中一个基本且重要的物理量，是理解许多量子现象的关键。
在固体物理中的应用
在固体物理中，电子自旋角动量对理解材料的磁学和电子学性质至关重要。
电子自旋角动量的历史与发展
早期发现
未来展望
自旋角动量的概念最初由乌伦贝克和古德斯密特在1925年提出。
随着技术的进步，对电子自旋角动量的研究和应用将更加深入和广泛。
发展自旋电子学的理论模型
01
建立精确的自旋电子学理论模型
基于量子力学和电磁学的基本原理，建立精确描述自旋电子行为的理论
模型。
02
发展高效的数值模拟方法
开发高效的数值模拟方法，对自旋电子器件进行精细化模拟和优化设计
。
03
探索自旋电子学的物理极限
通过理论分析和数值模拟，探索自旋电子学的物理极限，为新器件和新
发展历程
随着量子力学的发展，人们对自旋角动量的理解不断深入，它在理论物理和实验物理中都得到了广泛应用。
02
自旋磁矩的基本概念
定义与特性
定义
自旋磁矩是粒子自旋角动量与磁场的乘积，是粒子自旋的物理量。
特性
自旋磁矩具有矢量性质，方向与自旋角动量的方向相同，大小与粒子自旋和磁场的强度的乘积成正比。

第一讲电子自旋的实验证明及性质

总磁矩为：
Mz
dM z
Je d r2 sin2
meh
r sin
nlm
2
d
r2 sin2
meh
2
2 r sin
nlm
2
d
meh
2
2 r sin nlm 2 d
• 其中：d rddr，利用波函数 nlm 的归一关系：
nlm 2 d nlm 2 r2 sin d ddr
• 根据轨道磁矩与轨道角动量的关系：
M¶
z
gL
e
2
L$z
• 假设这个关系定性地适用于所有角动量与
磁矩。由于原子核（质子或中子）的质量
远远大于电子的质量，所以核磁矩导致的
贡献要远远小于电子自旋磁矩的贡献。
• 对于氢原子基态而言，l=0，所以原子束分裂是电子自旋磁矩导致的，取值个数为：；所以电子自旋为1/2。
• •
令：属于
1 2
(
S
z)
S
z
为 S2,S
的本征值
z
的共同本征自旋波函数，
ms 1/ 2
S 2, Sz 可互相对易，本征方程为
Sˆz 1
2
(Sz )
h 2
1
2
(Sz ), Sˆz 1 2
(Sz )
h 2
1 2
(Sz )
Sˆ
2
1
2
(Sz
)
3h 4
1
(S
z
),
Sˆ
2
1
(S
z
)
2
2
3h2 4
1 (Sz) 2
• 例如在轨道角动量l的取值中不包含半整数。而角动量A则包含了半整数，因为它代表着角动量的普遍性。

电子自旋角动量

θe -iϕ ⎞ ⎛ a ⎞ sin sinθ ⎛a⎞ ⎟⎜ ⎟ = ±⎜ ⎟ -cos θ ⎠⎝b⎠ -cosθ ⎝b⎠
�
解出 a 和 b 即得相应于本征值 ±1 的本征态 χ ( ± ) ( n ) 为
⎧ θ⎞ ⎛ -iϕ 2 ⎪ ( + ) � ⎜ e cos 2 ⎟ ⎪ χ ( n) = ⎜ ⎟ ⎪ ⎜ e iϕ 2 sin θ ⎟ ⎜ ⎟ ⎪ ⎝ 2⎠ ⎨ ⎛ -iϕ 2 θ ⎞ ⎪ -e sin ⎟ ⎪ ( -) � ⎜ 2 ⎟ ⎪ χ ( n) = ⎜ θ iϕ 2 ⎜ ⎟ ⎪ ⎜ e cos ⎟ ⎝ 2 ⎠ ⎩
Si =
ℏ 2 ℏ σi , 2 (i = x, y, z )
(7.5)
这里已经抽出 Si 的绝对数值，所以 σ i 的本征值只能为 ± 1 ，就是说，
σ i 为自逆矩阵。将 σ i 代入对易规则（7.4）式，就得到决定它们的下
列关系，
⎧ σ i , σ j = 2iε ijk σ k ⎨ 2 σi =σ0 ⎩
t Goudsmit 针对以上难以解释的实验现象，1925 年 Uhlenbeck 和 Goudsmi
提出假设：电子在旋转着，因而表现出称之为自旋的内禀角动量 s , 它
ℏ 2 � � 假定电子存在一个内禀磁矩 μ 并且和自旋角动量 s 之间的关系为（电 �
在任意方向的取值只能有 ± 两个数值。为使这个假设与实验一致，
子电荷为 -e ）
e � � μ= s μc
（7.1）
这表明，电子自旋的廻磁比是轨道廻磁比的两倍。于是，电子便具有
� 了 m,e, s, μ 共四个内禀的物理量。根据实验事实用外加的方式引入电子 �
自旋这一内禀自由度之后，不仅原子的磁性性质，而且原子光谱本身的一些精细结构，以及在外场下的多重分裂现象，也都得到了很好的解释。然而，认为电子自旋角动量来源于电子旋转这一经典图象却立即遭到否定。假设电子半径为 re ，作为定性的估算可以合理地假定

第03章守恒定律及其在力学中的应用3(角动量)

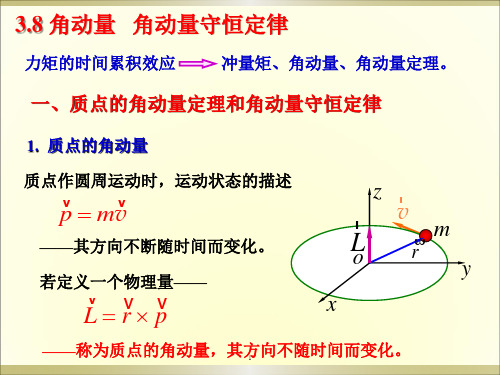
对“m1+m2 + 轻绳 + 滑轮”系统：
条件：M 外 0 所以角动量守恒设两小孩分别以 v1 , v2 速度上升。
外力：m1 g , m2 g , N
N R
0
r L1 m1 Rv1 ∥ ∥ m1 L2 r2 m2 v2 m2 ( R r// ) v2 m2 R v2
i 1
Fi
mi
m1
i 1
第i个质点角动量的时间变化率 dLi mj ri ( Fi f ij ) dt i j ri f ji 质点系角动量的时间变化率 dL fij ) 0 ri Fi (ri rj dt i i j i M 外 M内 M 外 ri Fi M内 ( ri f ij ) 0 i i i j dL M外 M 外 0 时 L Li 常矢量 dt i
M
O
r
r
A

F
大小
M Fr sin Fr
dL 或 M dt
方向：右手螺旋
Mdt dL Mdt冲量矩
质点对某固定点所受的合外力矩等于它对该点角动量的时间变化率

t2
t1
对同一参考点O,质点所受的冲量矩等 Mdt L2 L1 于质点角动量的增量。
O
L
vB

k
L0
B
v0
M A
解: (2) AB, 只有弹力作功,
1 2
机械能守恒
mv0 (m M ) v A
(1) m和M相撞时, 系统的动量守恒

第3章角动量理论

以后会知道该结果可适用于任意矢量算符。矢量图像有利于对角动量的简明理解
三、转动2π的结果
对有：即需转4π才能使态矢复原（复原<S>只需转2π）这种奇特的相位变化是有可观测的物理效应的
四、自旋进动
基于该H的时间演化算符为若将ωt看作Φ，则u(t,0)与转动算符相同。由此容易
即对自旋1/2体系有：类似可得：以上结果表明，转动算符作用于态矢确实使S的期待
值绕z轴转了Φ角即自旋算符期待值具有与经典矢量在转动下的相同变
化行为：
Rkl是对应于给定转动的3×3正交矩阵R的矩阵元由于方法二适用于任何J，故该性质行为不限于自旋
1/2体系。对一般的角动量算符Jk也有:
七、角动量算符的对易关系
对应于有：
得对易关系：综合Jx与Jz及Jy与Jz的关系，可得角动量算符的
基本对易关系：
该式归纳了三维转动的所有基本性质。由于不同Ji不对易，三维的转动群为非Abel群。
§3.2 自旋1/2体系和有限转动
一、自旋1/2体系的转动算符能使角动量对易关系成立的非平庸空间最小维数是2. 电子的自旋算符：
位矢量 nˆ 所表征的轴转dΦ的转动算符：
这里厄米算符Jk为角动量算符。上式可看作量子动力学中角动量算符的定义。该定义比经典的角动量（XxP）定义更普适，适用于自旋等。
五、有限转动
有限大小角度的转动可由无数个无穷小转动组合而成：
六、转动算符的性质假定
D(R)与R具有相同的群性质（合理要求）：
容易验证Sk满足角动量的对易关系，即Sk可看作自旋 1/2体系的Jk，并且其对易关系为实验所证实。
二、转动对自旋角动量的影响
考虑绕Z转Φ，态的变化为：

电子自旋是角动量的讨论

电子自旋是角动量的讨论程剑剑; 郑华【期刊名称】《《大学物理》》【年(卷),期】2019(038)010【总页数】3页(P28-29,46)【关键词】施特恩-盖拉赫实验; 自旋; 矩阵的迹; 对易关系; 算符【作者】程剑剑; 郑华【作者单位】陕西师范大学物理学与信息技术学院陕西西安710119【正文语种】中文【中图分类】O413.1电子自旋从提出之初就直接被归为角动量，并成功解释了当时理论所不能解释的实验现象. 在国内外量子力学教材中介绍电子自旋时，都沿用了自旋属于角动量的结论，自旋算符满足角动量对易关系，然后由对易关系导出自旋的具体矩阵表示——泡利矩阵[1].笔者认为，直接将电子自旋归为角动量更多的是属于物理直觉.为让学生在量子力学的学习过程中更具思辨能力，以一种逻辑的方式引入自旋属于角动量是很有意义的.本文中，笔者将尝试从施特恩-盖拉赫实验测量的结果电子自旋只有两种取值出发，在不引入自旋算符的具体矩阵表示的情况下，利用矩阵求迹，导出自旋算符与轨道角动量算符满足完全相同的对易关系，从而说明自旋与轨道角动量同类，属于角动量.1 自旋的引入1913年，玻尔的量子论提出后，人们对光谱规律的认识有了更深入的了解. 尽管此时从理论上能够解释一些简单的原子光谱规律，但对于复杂光谱，玻尔的理论遇到了一些困难. 实验上，在没有外场的情况下，原有谱线仍存在着细致分裂现象. 1916年，索末菲用玻尔模型解释塞曼效应时，提出了空间量子化的概念.1921年，施特恩和盖拉赫进行了著名的施特恩-盖拉赫实验，让一束银原子通过一处设定的不均匀磁场，并观察它们的偏转轨迹. 实验结果显示，原子的磁矩在磁场中只有两种取向，从而证明了空间是量子化的. 然而，空间量子化的假设仍然不能解释反常塞曼效应.直到1925年，乌伦贝克和古德施密特提出了电子自旋假设，认为电子不仅具有轨道角动量，还应该具有自旋角动量，才彻底将这些问题解决[2]. 此时，电子自旋已经被认为是角动量的一种.2 自旋算符的性质电子自旋是一种纯粹的量子效应，在经典力学中无法找到与之对应的力学量. 施特恩-盖拉赫实验告诉我们, 电子自旋在任意方向上的投影只有两个取值, 且大小相等, 方向相反. 为与量子力学教材一致，引入电子自旋算符(1)现在我们用数学语言来描述施特恩-盖拉赫实验的结果：算符σ在任意方向n的投影本征值只能取±1，其本征态可记为σn|±,n〉=±|±,n〉(2)将σn从左再次作用在式(2)，可以得到(3)(4)因为式(4)对任意方向都成立，所以(5)如果选取n分别指向x、y、z方向，那么(6)同时σn可写为(7)将式(7)展开，可以得到矢量算符σ分量之间满足反对易关系:σxσy+σyσx=0(8)σxσz+σzσx=0(9)σyσz+σzσy=0(10)对式(8)—式(10)式分别取迹可以得到:(11)值得注意的是，我们借用了力学量算符可以用矩阵表示，运用了矩阵的求迹规则，但是没有引入σi(i=x,y,z)的具体矩阵表示.用σy左乘式(8)，取迹有Tr(σyσxσy)+Tr(σyσyσx)=0(12)利用式(6)和矩阵求迹规则可得Tr(σx)=0(13)类似的计算，我们可以从式(9)和式(10)中得到Tr(σy)=Tr(σz)=0(14)式(13)、(14)表明，算符σi(i=x,y,z)可由无迹矩阵表示. 实际上，如果对量子力学的矩阵表示有深刻的认识，上述结论可以直接由算符σ在任意方向上的投影本征值只取±1得到.在量子力学中，力学量在选定表象后总有一个可以与之对应的矩阵. 考虑到电子自旋的实验测量结果在任意方向的投影只有两个取值，因此用2×2的矩阵描述电子自旋是很自然的选择.下面我们将证明σi(i=x,y,z)和单位矩阵I线性独立并能构成2×2矩阵的完备基. 令C0I+C1σx+C2σy+C3σz=0(15)对式(15)取迹并利用式(13)、(14)可得C0=0.将σi(i=x,y,z)分别左乘式(15)，取迹并利用式(6)、(11)、(13)、(14)，可以分别得到C1=0,C2=0,C3=0.这就证明了σx、σy、σz、I是线性独立.对于2×2的矩阵，能够描述的自由度最大为8(=4×2)，理由是2×2的矩阵有4个矩阵元且每个矩阵元可以为复数[3].因此，任意一2×2矩阵都可由线性独立的σx、σy、σz、I展开[4]：M=aσx+bσy+cσz+dI(16)理由是式(16)中展开系数可以是复数，能够描述2个自由度，加上4个展开基. 因此式(16)的左边和右边能够描述的最大自由度是相同的.现选择矩阵M=σxσy，对式(16)取迹并利用式(11)、(13)、(14)可得d=0. 用σx、σy分别左乘式(16)后取迹并利用式(6)、(11)、(13)、(14)可得a=0，b=0. 用σz右乘式(16)可得σxσyσz=c(17)将式(17)从左作用在自身并利用算符σ分量之间的反对易关系式(8)—式(10), 可以得到c2=σxσyσz·σxσyσz=-1(18)因此c=±i. 当取c=i，我们有σxσy=iσz(19)结合式(8)，我们可以得到σx和σy的对易关系[σx,σy]=2σxσy=2iσz(20)利用式(6)、(9)、(10)、(19)，可以很容易得到[σy,σz]=2iσx(21)[σz,σx]=2iσy(22)现将式(20)—式(22)中的σi(i=x,y,z)算符替换成式(1)中相应的自旋算符Si(i=x,y,z)，可以得到[Si,Sj]=iћεijkSk(23)由此可见，电子自旋算符的对易关系式(23)与轨道角动量算符的对易关系完全相同. 这与对电子自旋是角动量的期望一致，故而我们可以将自旋自然的归入角动量.数学上，c=-i也是允许的. 但在这种情况下得到的电子自旋算符的对易关系式与我们的期望不一致. 因此我们将c=-i的情况视为数学上允许，但是却没有被自然选择. 在得到电子自旋算符的对易关系后，如何得到其具体表示，量子力学教材中给出了详细的过程，也有文献给出了不同的导出方法[5]，在此我们就不赘述了.3 结束语区别于历史上和国内外量子力学教材中直接将电子自旋归为角动量，为让学生在量子力学的学习过程中更具思辨能力，本文尝试讨论仅从施特恩-盖拉赫实验测量结果出发，利用力学量可以用矩阵表示及矩阵求迹规则，导出自旋算符与轨道角动量算符满足完全相同的对易关系，从而说明自旋与轨道角动量同类，属于角动量.【相关文献】[1] 曾谨言.量子力学(卷Ⅰ)[M].5版.北京：科学出版社，2013:286-293.[2] 宁长春，汪亚平，等.斯特恩-盖拉赫实验历史概述[J].大学物理，2016，35(3)：43-49.[3] 费恩曼,莱顿.费恩曼物理学讲义[M].上海:上海科学技术出版社,2013:152-156[4] 朗道.理论物理学教程第三卷[M].6版.严肃,译.北京：高等教育出版社,2008:184-190.[5] 胡家骏，李先胤.泡利矩阵的几种导出法 [J].大学物理，1994，13(10)：29-31.。