二元函数偏导数定义公式
一阶偏导和二阶偏导公式

一阶偏导和二阶偏导公式一阶偏导和二阶偏导是微积分中的重要概念,用于描述多变量函数的变化率和曲率。
在实际问题中,一阶偏导和二阶偏导经常被用来求解最优化问题、描述曲线和曲面的性质等。
本文将介绍一阶偏导和二阶偏导的概念及其计算方法,并通过实例加深理解。
一、一阶偏导的概念与计算方法1.概念对于多变量函数,我们可以将其中的一个变量视为常数,而对其他变量求导,这就是偏导数的概念。
一阶偏导数描述了函数在某一点沿着某个坐标轴方向的变化率。
2.计算方法假设有一个二元函数f(x, y),要计算其关于x的偏导数,可以将y 视为常数,然后对x求导。
偏导数的计算方法与普通的导数计算类似,只需将其他变量视为常数。
例如,对于函数f(x, y) = x^2 + y^2,我们要计算其关于x的偏导数。
将y视为常数,对x求导,得到f对x的偏导数为:∂f/∂x = 2x。
二、二阶偏导的概念与计算方法1.概念二阶偏导数是对一阶偏导数再求导,描述了函数在某一点的曲率和变化率的变化率。
2.计算方法对于二元函数f(x, y),我们可以先计算一阶偏导数,再对一阶偏导数进行求导,得到二阶偏导数。
二阶偏导数的计算方法与一阶偏导数类似。
例如,对于函数f(x, y) = x^2 + y^2,我们已经计算了其关于x的一阶偏导数为∂f/∂x = 2x。
再对一阶偏导数∂f/∂x进行求导,得到二阶偏导数∂^2f/∂x^2 = 2。
三、一阶偏导和二阶偏导的应用实例1.最优化问题一阶偏导和二阶偏导在最优化问题中有广泛应用。
通过求解一阶偏导和二阶偏导,可以得到函数的驻点、极值点和拐点等信息,从而帮助我们找到函数的最优解。
例如,对于函数f(x) = x^2 - 2x + 1,我们可以通过求解f的一阶偏导数和二阶偏导数来确定函数的极值点。
首先求解一阶偏导数:f'(x) = 2x - 2,然后求解二阶偏导数:f''(x) = 2。
当二阶偏导数大于0时,函数的极值点为最小值点;当二阶偏导数小于0时,函数的极值点为最大值点。
第二节二元函数的一阶、二阶偏导数

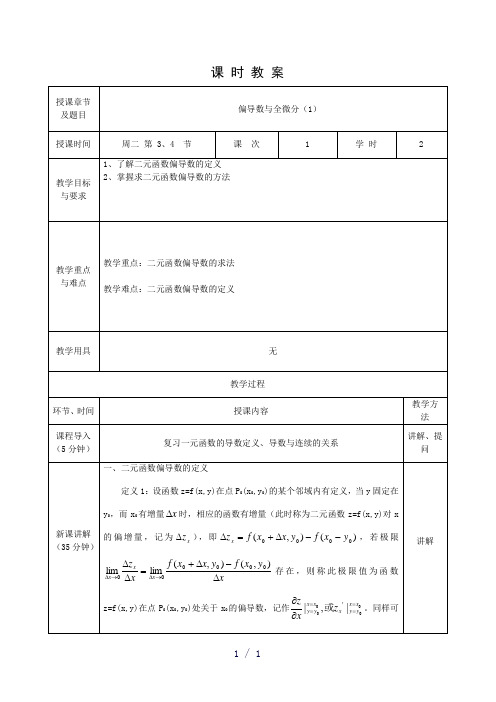
第二节二元函数的一阶、二阶偏导数一、二元函数的一阶偏导数1、在某点处的一阶偏导数——已知二元函数z f(x ,y) 在点(x ,y 0)处及其附近有定义,若一元函数zf(x ,y 0)在点x 0处对x 可导,则称此导数值为二元函数z f(x ,y)在点(x 0,y 0)处对x 的一阶偏导数,记作f x (x 0,y 0) ,或z x |xx 0,或y y 0 f(x 0,y 0)z;,或 |x x xx yy若一元函数zf(x ,y 0 )在点y 0处对y 可导,则称此导数值为二元函数z f (x ,y)在点(x 0,y 0)处对y 的一阶偏导数,记作 f y (x 0,y 0),或z y |xx 0,或f(x 0,y 0),或 y y y 0z x 0。
|x yy y 0 2、可导与连续关系:尽管在某点处两个一阶偏导数都存在,却不能保证在该点处连续。
3、在某区域上的一阶偏导数——若二元函数zf(x ,y)在区域E 上每一点(x ,y)处都有对x ,对y 的一阶偏导数,则对于区域 E 上每一点(x ,y)都有一个对x 的一阶偏导数值和一个对 y 的一阶偏导数值与之对应,于是得到两个新的二元函数,这两个新的二元函数分别称为z f (x ,y)对x ,对y 的一阶偏导函数,简称一阶偏导数,分别记作 f x (x ,y),或z x ,或 f(x ,y) z,或 和f y (x ,y),或z y ,或f(x ,y),或z。
x x yy 二、二阶偏导数1、定义——二元函数 zf(x ,y)一阶偏导数的一阶偏导数称为二元函数z f (x ,y)的二阶偏导数,共有四个,分别记作f xx (x ,y) (f x (x ,y))x ,或z xx ,或 f 2(x ,y)2zx 2 ,或x 22,2f xy (x ,y) (f x (x ,y))y ,或z xy ,或f(x y),或 z y x x y2 ,2f yx(x,y) (f y(x,y))x,或z yx,或f(x y),或zy xx yf yy(x,y) (f y(x,y))y,或z yy,或f2(x,y),或2z。
函数的偏导数word版
新课讲解
(35分钟)
0(x0,y0)处关于y0的导数值。
如果z=f(x,y)在某个邻域内对每一个点x都存在偏导数,则这两个偏导数本身也是关于x,y的二元函数,所以称它们为偏导函数,简称为偏导数。记为zx/,
二、偏导数的求法
从偏导数的定义可以知道,求z对x的偏导数的时候可以把变量y认为是常数,从而可以利用一元函数求导法则和求导公式进行求导;同样,在z对y求偏导数的时候可以把x认为是常数进行求导。
四、高阶导数
二元函数z=f(x,y)的两个偏导数 一般仍然是x,y的二元函数,若这两个函数对x,y的偏导数仍然存在,则称为这些偏导数为z=f(x,y)的二阶偏导数,按照对变量求导次序不同,二阶偏导数有如下几种形式:
在上述公式中要注意 是先对x求偏导数然后再对y求偏导数,而 是先对y求偏导数然后再对x求偏导数。它们正好相反,它们包
讲解、启发、引导
六、学生课堂训练:
具体题目见P1401 (3) (5) 3 (1) (2)
课后小结课后作业
(5分钟)
本次课主要讲解了二元函数的一阶偏导数和二阶偏导数,其中最重要的是这两个偏导数的计算
作业:P1401(2)、(4)、(6) (7) 3 (3)、(4)
教学反思
板书设计
课程导入:
复习一元函数的导数定义、导数与连续的关系
3.
分析:在本题中,实际上考查的是偏导数函数的算法。在本题中,一定要注意对x,y求偏导时我们可以寻找不同的函数类型,从而可以利用一元函数的求导法则来求相应的偏导数。(书写详细的解题过程)
4.
分析:本题实质和上题是类似的,实际上在求偏导数的时候我们可以把相应的某个变量看成是常数就可以了,然后利用一元函数的求导法则即可。(书写详细的解题过程)
二元函数连续偏导数的关系

二元函数连续偏导数的关系设二元函数 z=f(x,y) 为定义在点集 D\subset R^{2} 上的函数。
二元函数连续性的定义:设 p_{0}\in D (它或者是 D 的聚点,或者是 D 的孤立点)。
对于任给的正数 \varepsilon ,总存在相应的正数 \delta ,只要 p\inU(p_{0},\delta)\cap D ,就有 |f(p)-f(p_{0})|<\varepsilon 则称 f 关于集合 D 在点 p_{0} 连续。
简称 f 在点 p_{0} 处连续。
注:二元函数连续性的定义与一元函数连续性的定义有所不同,在一元函数的连续性的定义中,要求函数 f(x) 必须在x_{0} 的某一邻域 U(x_{0}) 上有定义,并且要求的是\forall\varepsilon>0,\exists\delta>0 ,当 |x-x_{0}|<\delta 时, |f(x)-f(x_{0})|<\varepsilon ,则称函数 f(x) 在 x=x_{0} 处连续。
注意到二元函数在定义连续的概念的时候并不是要求函数必须在连续点 x_{0} 的某一邻域U(x_0) 上有定义,只要保证该点是函数的聚点即可,并且对于不是聚点的孤立点仍然可以定义其为连续点(只需要将孤立点带入二元函数连续性的定义加以验证即可发现孤立点也满足该连续性的定义)。
因此在二元函数中,聚点和孤立点是连续点的必要条件,即二元函数的连续点必是该函数的聚点或孤立点中的一种。
二元函数可微的定义:设 p_{0}\in D ,二元函数 z=f(x,y) 在 p_{0} 的某邻域 U(p_{0}) 上有定义,对于 U(p_{0}) 中的点 P(x,y)=(x_0+\triangle x,y_{0}+\triangle y) ,若函数 f 在点 p_{0} 处的全增量 \Delta z 可表示为 \Deltaz=f(x_0+\Delta x,y_{0}+\Delta y)-f(x_{0},y_{0})=A\Delta x+B\Delta y+o(\rho) ,其中 A,B 是仅与点 p_{0} 有关的常数, \rho=\sqrt{\Delta x^{2}+\Delta y^{2}} , o(\rho) 是较 \rho 高阶的无穷小量,则称函数 f 在点 P_{0} 处可微,并称 A\Delta x+B\Delta y 为函数 f 在点 P_{0} 的全微分,记作dz|_{p_{0}}=df(x_{0},y_{0})=A\Delta x+B\Delta y 。
二元函数微分学

二元函数微分学在微积分学中,除了对一元函数的微积分研究,我们也需要了解对于二元函数的微积分,这就是二元函数微分学。
其研究的重点是对于二元函数的导数的概念,以及对其进行求解的方法。
二元函数概念在开始对于二元函数的微积分进行研究之前,我们首先需要了解的是二元函数的概念。
在数学中,二元函数可以表示为$f(x,y)$,其中$x$和$y$都是自变量。
而因变量$f(x,y)$则表示为由$x$和$y$确定的一个实数值,也就是函数值。
对于一个二元函数$f(x,y)$,我们可以通过其中的函数图像来进行具体分析。
函数图像是在$x$和$y$平面上,将函数$f(x,y)$所对应的点$(x,y)$和它的函数值$f(x,y)$之间的关系所形成的图形,常常用于解决问题并进行计算。
二元函数导数概念在了解二元函数之后,我们需要进一步了解二元函数的导数概念。
对于一元函数$f(x)$,其导数表示为$f'(x)$,而对于一个二元函数$f(x,y)$,其导数则表示为$f_x(x,y)$和$f_y(x,y)$,分别表示对于$x$和$y$的偏导数。
二元函数的偏导数概念在微分学中,对于偏导数的概念对于二元函数的研究十分重要。
对于二元函数$f(x,y)$来说,其对于$x$的偏导数可以表示为:$$f_x(x,y)=\lim_{\Delta x \to 0} \frac{f(x+\Delta x,y)-f(x,y)}{\Delta x}$$也可以表示为$\dfrac{\partial f}{\partial x}$。
对于$y$的偏导数同理。
偏导数的求解方法对于二元函数的偏导数,我们可以通过以下方法进行求解,以$f(x,y)=x^2y+2xy^2$为例:1. 对于$x$的偏导数,我们可以将$y$看作常数,将$x$看作变量,通过求解可得$f_x(x,y)=2xy+2y^2$。
2. 对于$y$的偏导数,我们可以将$x$看作常数,将$y$看作变量,通过求解可得$f_y(x,y)=x^2+4xy$。
5.2 二元函数的偏导数与全微分

上页 下页 返回
§5.2 二元函数的偏导数与全微分
(1)几何意义:
偏导数 f x ( x0 , y0 ) 就是曲面被平面 y y0 所 截得的曲线在点 M 0 处的切线 M 0Tx 对 x 轴的斜 率.
偏导数 f y ( x0 , y0 ) 就是曲面被平面 x x0 所截得的曲线在点 M 0 处的切线 M0Ty 对 y 轴的 斜率.
上页 下页 返回
§5.2 二元函数的偏导数与全微分
例1 求 z x 2 3x y y 2 在点(1 , 2)处的偏导数. z z 解法1 2x 3y, 3x 2 y x y z z y (1,2) x (1,2) 解法2
z
y2
x2 6x 4
z 记为 y f , y x x0
y y0 x x0 y y0
, f y ( x0 , y0 ) 或 zy
x x0 y y0
.
上页 下页 返回
§5.2 二元函数的偏导数与全微分
如果函数 z f ( x , y ) 在区域 D 内任一点 ( x , y ) 处对 x的偏导数都存在,那么这个偏导数 就是 x、 y 的函数,它称为函数 z f ( x , y ) 对自 变量 x的偏导函数,简称偏导数. z f 记作 , , zx 或 f x ( x, y ) . x x
同理可以定义函数 z f ( x , y ) 对自变量 y 的偏导 z f 数,记作 , , zy 或 f y ( x, y). y y
上页 下页 返回
§5.2 二元函数的偏导数与全微分
偏导数的概念可以推广到二元以上函数
如函数 u f ( x , y, z ) 在点 ( x , y, z ) 处
偏导数定义

1、偏导数定义由于一元函数微分学知道:若()f x 在点0x 可微,则函数增量()()()00f x x f x A x o x +∆-=∆+∆,其中()'0A f x =。
同样,由上一段已知,若二元函数f 在点()00,x y 可微,则f 在()00,x y 处的全增量可由()()()0000,,z f x x y y f x y A x B y o ρ∆=+∆+∆-=∆+∆+表示。
现在讨论其中A ,B 的值与函数f 的关系。
为此,在z A x B y x y αβ∆=∆+∆+∆+∆中令0y ∆=()0x ∆≠,这时得到z ∆关于x 的偏增量x z ∆,且有x z A x x α∆=∆+∆或x z A xα∆=+∆。
现让0x ∆→,由上式得A 的一个极限表达式()()000000,,lim lim x x x f x x y f x y z A x x ∆→∆→+∆-∆==∆∆。
容易看出,上式右边的极限正是关于x 的一元函数()0,f x y 在0x x =处的导数。
类似地,令()00x y ∆=∆≠,由z A x B y x y αβ∆=∆+∆+∆+∆又可以得到 ()()000000,,lim lim y y y z f x y y f x y B y y∆→∆→∆+∆-==∆∆。
它是关于y 的一元函数()0,f x y 在0y y =处的导数。
二元函数当固定其中一个自变量时,它对另一个自变量的导数称为偏导数,定义如下:设函数()(),,,z f x y x y D =∈。
若()00,x y D ∈,且()0,f x y在0x 的某一邻域内有定义,则当极限()()()00000000,,,lim lim x x x f x y f x x y f x y x x ∆→∆→∆+∆-=∆∆ 存在时,称这个极限为函数f 在()00,x y 关于x 的偏导数,记作()00,x f x y 或()00,x y fx ∂∂。
偏导数知识点公式总结

偏导数知识点公式总结一、偏导数的概念1.1 偏导数的定义偏导数是多元函数对其中一个自变量的导数。
对于一个函数 $f(x_1, x_2, ..., x_n)$,它的偏导数 $\frac{\partial f}{\partial x_i}$ 表示在$x_i$方向上的变化率。
偏导数的定义可以表示为:$$\frac{\partial f}{\partial x_i} = \lim_{\Delta x_i \to 0} \frac{f(x_1, x_2, ..., x_i + \Delta x_i, ..., x_n) - f(x_1, x_2, ..., x_i, ..., x_n)}{\Delta x_i}$$1.2 偏导数的图示解释偏导数可以通过函数曲面的切线来解释。
对于函数 $z = f(x, y)$,在点$(x_0, y_0, z_0)$处的偏导数 $\frac{\partial f}{\partial x}$可以理解为曲面在$x$方向的斜率,即曲面在$x$方向上的变化率。
同样地,$\frac{\partial f}{\partial y}$表示曲面在$y$方向上的变化率。
这样的解释有助于我们更直观地理解偏导数的含义。
二、偏导数的性质2.1 对称性对于二元函数 $f(x, y)$,它的偏导数满足对称性,即$\frac{\partial^2 f}{\partial x \partial y} = \frac{\partial^2 f}{\partial y \partial x}$。
这一性质表明,在计算混合偏导数时,可以不必考虑自变量的顺序。
2.2 连续性在函数的定义域内,若偏导数存在且连续,则函数规定可微。
这一性质是偏导数与函数连续性的关系,对于函数的导数性质有着重要的影响。
2.3 性质总结:和与积对于函数 $u = u(x, y)$ 和 $v = v(x, y)$,它们的偏导数具有和与积的运算法则。
多元函数的偏导数与方向导数计算

多元函数的偏导数与方向导数计算在多元函数中,偏导数与方向导数是常用的求导工具,可以帮助我们研究函数在不同方向上的变化率和导数值。
本文将介绍计算多元函数的偏导数和方向导数的方法和公式,并通过实例进行说明。
一、多元函数的偏导数多元函数是指含有多个自变量的函数,其偏导数表示在各个自变量上的变化率。
1. 一阶偏导数对于二元函数 $z = f(x, y)$,其一阶偏导数表示对每个自变量的偏导数值。
分别记作 $\frac{{\partial z}}{{\partial x}}$ 和 $\frac{{\partial z}}{{\partial y}}$,计算方法如下:$$\frac{{\partial z}}{{\partial x}} = \lim_{{\Delta x \to 0}} \frac{{f(x + \Delta x, y) - f(x, y)}}{{\Delta x}}$$$$\frac{{\partial z}}{{\partial y}} = \lim_{{\Delta y \to 0}} \frac{{f(x, y + \Delta y) - f(x, y)}}{{\Delta y}}$$2. 高阶偏导数如果一阶偏导数存在,我们还可以继续求解二阶、三阶乃至更高阶的偏导数。
对于二阶偏导数,我们可以通过对一阶偏导数再次求导得到,记作 $\frac{{\partial^2 z}}{{\partial x^2}}$、$\frac{{\partial^2 z}}{{\partial x \partial y}}$ 和 $\frac{{\partial^2 z}}{{\partial y^2}}$。
计算方法如下:$$\frac{{\partial^2 z}}{{\partial x^2}} = \frac{{\partial}}{{\partial x}} \left(\frac{{\partial z}}{{\partial x}}\right)$$$$\frac{{\partial^2 z}}{{\partial x \partial y}} =\frac{{\partial}}{{\partial x}} \left(\frac{{\partial z}}{{\partial y}}\right)$$$$\frac{{\partial^2 z}}{{\partial y^2}} = \frac{{\partial}}{{\partial y}} \left(\frac{{\partial z}}{{\partial y}}\right)$$二、多元函数的方向导数方向导数表示函数在某个方向上的变化率,是由函数的梯度(gradient)来表示的。
二元函数的偏导数与全微分

二元函数的偏导数与全微分二元函数是指有两个自变量的函数,例如 $z=f(x,y)$,其中$x$ 和 $y$ 是自变量,$z$ 是因变量。
在微积分中,二元函数的偏导数和全微分是比较重要的概念。
一、偏导数的定义偏导数是指在多元函数中,对某一个变量求导时,把其他变量当作常数来对函数进行求导。
对于二元函数 $z=f(x, y)$,它的偏导数可以用符号 $\frac{\partial z}{\partial x}$ 和 $\frac{\partialz}{\partial y}$ 表示。
其中 $\frac{\partial z}{\partial x}$ 表示当$y$ 固定时,$z$ 对 $x$ 的变化率;$\frac{\partial z}{\partial y}$ 表示当 $x$ 固定时,$z$ 对 $y$ 的变化率。
例如,二元函数 $z=x^2y$,求 $\frac{\partial z}{\partial x}$ 和$\frac{\partial z}{\partial y}$,则有:$$\frac{\partial z}{\partial x}=2xy$$$$\frac{\partial z}{\partial y}=x^2$$二、全微分的定义对于二元函数 $z=f(x,y)$,它的全微分可以表示为:$$dz=\frac{\partial z}{\partial x}dx+\frac{\partial z}{\partialy}dy$$全微分表示 $z$ 在 $(x, y)$ 处的微小变化量,可以理解为$z$ 的无限小增量。
全微分的概念在微积分中有着广泛的应用,如求方程组的解、最大值、最小值等。
例如,对于二元函数 $z=x^2y$,它的全微分可以表示为:$$dz=2xydx+x^2dy$$三、偏导数与全微分的关系对于二元函数$z=f(x,y)$,其偏导数与全微分有着密切的联系。
根据全微分的定义,可以推导出:$$\frac{\partial z}{\partial x}=\lim_{\Delta x \to 0}\frac{f(x+\Delta x,y)-f(x,y)}{\Delta x}$$$$\frac{\partial z}{\partial y}=\lim_{\Delta y \to0}\frac{f(x,y+\Delta y)-f(x,y)}{\Delta y}$$将上述式子代入全微分,可以得到:$$dz=\lim_{\Delta x \to 0}\frac{f(x+\Delta x,y)-f(x,y)}{\Deltax}dx+\lim_{\Delta y \to 0}\frac{f(x,y+\Delta y)-f(x,y)}{\Delta y}dy$$当 $\Delta x$ 和 $\Delta y$ 趋近于 $0$ 时,可以认为二元函数$z=f(x,y)$ 在点 $(x, y)$ 处可微分。
二元函数偏导数定义公式

二元函数偏导数定义公式
二元函数偏导数定义公式指的是,对于一个含有两个自变量的函数f(x,y),其在某一点(x0,y0)处的偏导数定义如下:
对于x的偏导数,可以使用以下公式进行计算:
f/x = lim (f(x0 + h, y0) - f(x0, y0))/h (h趋近于0) 对于y的偏导数,可以使用以下公式进行计算:
f/y = lim (f(x0, y0 + k) - f(x0, y0))/k (k趋近于0) 在这两个公式中,我们可以看到f在(x0,y0)处的偏导数是通过将其中一个自变量固定在某一值上,然后计算f关于另一个自变量的导数得到的。
这个定义公式在微积分中非常重要,因为它能够让我们计算多元函数的导数,而这对于众多科学领域的研究都是至关重要的。
- 1 -。
偏导数与偏微分方程

偏导数与偏微分方程偏导数是微积分中的一种重要的概念,它在数学和物理学中有着广泛的应用。
在这篇文章中,我们将讨论偏导数的定义、性质以及与偏微分方程的关系。
一、偏导数的定义与性质偏导数是多元函数在某一点上对其中一个变量的导数。
对于二元函数f(x, y),它的关于x的偏导数可以表示为∂f/∂x,表示在固定y的情况下,函数f关于x的导数。
同样地,它的关于y的偏导数可以表示为∂f/∂y。
在一般情况下,对于n元函数f(x₁, x₂, ..., xₙ),它的第i个变量的偏导数可以表示为∂f/∂xᵢ。
偏导数有一些重要的性质。
其中最重要的性质是可微性,即如果偏导数存在且连续,那么函数就是可微的。
另外,偏导数满足加法性、乘法性和链式法则。
加法性表示对于两个函数f和g,它们的和的偏导数等于它们的偏导数的和;乘法性表示对于任意常数a,函数af的偏导数等于a乘以f的偏导数;链式法则则是描述复合函数的偏导数的计算规则。
二、偏微分方程的概念与分类偏微分方程是包含多个未知函数的方程,并且这些未知函数的偏导数与它们自身和独立变量的函数关系。
偏微分方程的解是满足方程的函数。
偏微分方程可以分为几类。
常见的分类包括椭圆型、抛物型和双曲型偏微分方程。
椭圆型偏微分方程的特点是随机性,如拉普拉斯方程。
抛物型偏微分方程的特点是时间上的一阶导数,如热方程和扩散方程。
双曲型偏微分方程的特点是空间和时间上的一阶导数,如波动方程。
三、偏微分方程与偏导数的关系偏微分方程与偏导数有着密切的关系。
实际上,偏微分方程可以通过偏导数的概念来表达和求解。
对于偏微分方程中的未知函数,我们可以利用偏导数来表示它们与自变量的关系。
通过对偏微分方程进行适当的变换和求解,我们可以得到这些未知函数的具体形式。
在求解的过程中,我们常常使用一些数学和物理上的技巧来简化问题,如变量分离法、特征线法和变换法等。
最终,通过将偏微分方程转化为一些常微分方程,我们可以得到关于未知函数的一般解或特解。
二元函数求导法则公式

二元函数求导法则公式好的,以下是为您生成的关于“二元函数求导法则公式”的文章:在数学的奇妙世界里,二元函数求导法则公式就像是一把神奇的钥匙,能帮我们打开理解复杂函数关系的大门。
还记得我当初学习二元函数求导法则公式的时候,那可真是一段令人难忘的经历。
当时我和几个同学一起参加数学竞赛的培训,老师在黑板上写下了那些密密麻麻的公式和符号,我的脑袋瞬间就大了一圈。
就拿最简单的偏导数来说吧,对于一个二元函数 z = f(x, y),它关于x 的偏导数记作∂z/∂x ,关于 y 的偏导数记作∂z/∂y。
这就好比我们在一个二维的平面上,沿着 x 轴或者 y 轴的方向去探索函数的变化率。
比如说有个二元函数 f(x, y) = x^2 + 2xy + y^2 ,要求它关于 x 的偏导数,那我们就得把 y 看成一个常数。
这时候,2xy 这一项对 x 求导就变成了 2y ,y^2 就变成 0 了,因为它跟 x 没关系。
最后得出的偏导数就是 2x + 2y 。
再说说全微分,它也是二元函数求导法则中的重要部分。
全微分 dz 可以表示为∂z/∂x dx + ∂z/∂y dy 。
想象一下,我们在这个二维的函数世界里,每一点的微小变化都可以用这个全微分来精确描述。
有一次做练习题,碰到一个挺复杂的二元函数 f(x, y) = sin(x*y) +e^(x + y) ,要求全微分。
我一开始有点懵,心里直犯嘀咕:“这可咋整啊?”但静下心来,按照法则一步一步来,先求出偏导数,再代入全微分的公式,最后居然也做出来了。
那种成就感,简直没法形容!还有复合函数的求导法则,这就更有趣啦。
如果有个二元函数 z =f(u(x, y), v(x, y)) ,那它的求导就得运用链式法则,一层一层地剥开“洋葱皮”。
这就像是解一个复杂的谜题,每一步都需要我们细心思考。
比如说,z = sin(x^2 + y^2) ,我们令 u = x^2 + y^2 ,那么先求出∂u/∂x = 2x ,∂u/∂y = 2y ,然后对 z = sin(u) 求导得到 cos(u) ,最后根据链式法则,∂z/∂x = cos(u) * 2x = 2x cos(x^2 + y^2) ,∂z/∂y = cos(u) * 2y= 2y cos(x^2 + y^2) 。
二元函数的偏导数求解及其相关性分析

二元函数的偏导数求解及其相关性分析二元函数是指具有两个自变量的函数,通常表示为f(x,y),其中x和y分别是自变量,而f(x,y)则是对应的函数值。
对于这种函数,我们可以通过求偏导数来研究其性质和变化规律,这对于很多与数学及物理相关的领域都非常重要。
本文将介绍二元函数的偏导数的基础概念和求解方法,并且分析偏导数与函数相关性的一些特征。
一、偏导数的基础概念偏导数指的是在一个多元函数中,对于一个自变量求导数时,将其他变量视为常数进行求导。
在二元函数中,如果我们想要求f(x,y)关于x的偏导数,可以将其它的自变量y视为常数,从而得到以下求导方式:∂f/∂x = lim Δx → 0 [ f(x+Δx,y) - f(x,y) ] / Δx其中,左边的符号∂表示对于x的偏导数,右边的分数等于根据函数在横坐标方向上的斜率求得。
类似的,我们也可以对于y方向求导,得到:∂f/∂y = lim Δy → 0 [ f(x,y+Δy) - f(x,y) ] / Δy这样,我们就得到了关于x和y的两个偏导数。
二、偏导数的求解方法有些二元函数可能比较简单,求导也比较容易。
但是,有些函数可能很复杂或者不易用解析式表示,这时候就需要一些不同的求导方法。
1. 分步求导法:即将一个多元函数看做由多个一元函数组合而成的,将每个一元函数都求偏导数,最后在将结果组合起来。
2. 隐函数求导法:此方法是用于确定变量之间存在某种特定的关系时。
首先,将这个关系用方程形式,然后用求导法得出对应的偏导数。
3. 参数方程法:当无法使用简单的方程描述函数时,我们可以使用参数方程替代,并且可以将一个变量的变化看做另一个变量的函数关系。
这时可以使用链式法则、乘积法则和商法则等方法求偏导数。
三、偏导数和相关性的分析偏导数可以体现出二元函数某些值或属性的变化趋势,这对于分析函数性质及其相关性是非常有用的。
下面将介绍一些关于偏导数和相关性的分析方法。
1. 偏导数符号的意义:如果偏导数为正值,意味着函数值随着变量的增长而增长;如果偏导数为负值,意味着函数值随着变量的增长而减少;如果偏导数为0,说明函数在这一点斜率为0,表查函数在这一点上取得了局部最大值或局部最小值。
二元函数求偏导数

二元函数求偏导数
二元函数的偏导数是指以一个二维坐标系中的函数,在每个点上关于
每个自变量求取偏导数。
应用梯度法指出,函数f在多元函数上可以表示为一个偏导数向量,其中每个分量指示函数中一个自变量的偏导数。
如果函数f有2个自变量,则该偏导数向量由两个分量组成,表示函数
f对两个变量的偏导数。
偏导数是函数在每个点上的方向导数,它表示
在此点处函数增长的程度以及方向。
因此,可以使用偏导数来求解二
元函数的最值,以及在函数上求最小值水池面积的最优点。
在多元函数求解中,偏导数的定义是用来求取坐标点的导数的一种数
学应用。
若函数为f(x,y),则偏导数就是曲面关于x和y分别积分的两
个函数,分别表示关于x坐标及y坐标的变化率。
它也是函数在每个
点处发展状况的定义,即函数在该点处变化的程度,所以偏导数也揭
示了函数在每个点位置处的方向导数,以此来解答关于函数极值点位
置和大小等问题。
求解二元函数的偏导数,首先需要定义二维坐标系中的函数,然后使
用微积分的定义求取偏导数。
求取偏导的过程主要是通过求函数在某
一点的泰勒级数的偏导数,得出函数在该自变量上的增量比,从而计
算出某一点处函数对自变量的导数。
而求解二元函数偏导数应用的方
法是同时使用两个自变量,求取函数在每个点处关于x和y的偏导数。
文中介绍的二元函数的偏导数的概念在函数的研究中起着重要的作用,它可以帮助我们深入了解函数及其特性,从而得以合理的利用函数的
特性研究问题,有效的解决科学技术的难题。
偏导数解二元二次方程

偏导数解二元二次方程偏导数是微积分中的一个重要概念,它可以用来解决许多实际问题。
本文将以偏导数的概念为基础,探讨如何利用偏导数解二元二次方程。
我们来回顾一下偏导数的定义。
对于一个多元函数,它的偏导数表示在某一点上,沿着某个坐标轴方向的变化率。
对于二元函数f(x,y),它的偏导数可以表示为∂f/∂x和∂f/∂y。
其中,∂f/∂x表示在y固定的情况下,f关于x的变化率;∂f/∂y表示在x固定的情况下,f关于y的变化率。
假设我们有一个二元二次方程:ax^2 + bxy + cy^2 + dx + ey + f = 0,其中a、b、c、d、e、f为常数。
我们的目标是求解这个方程,即找到满足这个方程的x和y的取值。
我们可以利用偏导数的概念来解决这个问题。
首先,对方程两边同时对x求偏导数,得到2ax + by + d = 0。
然后,对方程两边同时对y求偏导数,得到bx + 2cy + e = 0。
这样,我们得到了一个包含两个方程的方程组:2ax + by + d = 0 (1)bx + 2cy + e = 0 (2)接下来,我们可以利用这个方程组来求解x和y的值。
首先,我们可以从方程(2)中解出x,得到x = -(2cy + e)/b。
然后,将这个x 的表达式代入方程(1)中,即可得到关于y的方程。
解这个关于y的方程,我们就可以得到y的值。
举个例子来说明一下。
假设我们有一个二元二次方程:x^2 + 2xy + y^2 - 4x - 2y - 3 = 0。
我们首先求解方程组:2x + 2y - 4 = 0 (3)x + 2y - 2 = 0 (4)从方程(4)中解出x,得到x = 2 - 2y。
然后,将这个x的表达式代入方程(3)中,即可得到关于y的方程:4 - 6y + 2y^2 - 4 + 2y - 3 = 0,化简得2y^2 - 4y - 3 = 0。
解这个关于y的方程,我们可以得到y的值。
再将这个y的值代入x = 2 - 2y的表达式中,就可以得到x的值。
