fisher判别的基本步骤

判别分析(第4节_Fisher判别法)

本章主要内容
第一节第二节第三节第四节第五节
绪论距离判别法贝叶斯判别法 Fisher判别法判别效果检验问题
第三节贝叶斯（BAYES）判别法
■
多元正态总体的贝叶斯判别法
设 Gi ~ N p ( (i ) , i )(i 1,2,, k ) ，并假定错判损失相等，先验概率 q1 , q2 ,, qk ，有时先验概率确定起来不是很明 n qi i 确的，这时可用“样品频率”代替，即可令。 n
第三节贝叶斯（BAYES）判别法
其中 ( h ) , h 意义同前，已知后验概率为
P(Gh | x) qh f h ( x)
q f ( x)
i i i 1
k
由于上式中，分母部分为常数，所以有
P(Gh | x) max qh f h ( x) max
同时
1 1 qh f h ( x) qh (2 ) p / 2 | h |1/ 2 exp ( X ( h ) )h ( X (h) ) 2
* 故问题化简为 Z (Gh | x) max . h
ห้องสมุดไป่ตู้
注意：这里取对数可起到简化算式的作用，同时对数函数是严格单调的，所以取对数不改变原问题的性质。
第三节贝叶斯（BAYES）判别法
◆ 判别准则下面分两种不同的情形考虑。
●
假设协方差阵都相等（ 1 2 k ）
2 2
exp[ y(G x]
i| i 1
k
注意：这意味着 P(Gh | x) max y(Gh | x) max
第三节贝叶斯（BAYES）判别法
证明因为 y(Gh | x) ln[qh f h ] ( x) ，其中 ( x) 是ln[ qh f h ]

4-3_Fisher判别

3
13 44.12 15.02 1.08 15.15 103.12 64.8
3
14 54.17 25.03 2.11 25.15 110.14 63.7
3
15 28.07 2.01 0.07 3.02 81.22 68.3
3
待判 50.22 6.66 1.08 22.54 170.6 65.2
.
待判 34.64 7.33 1.11 7.78 95.16 69.3
在此最大特征值所对应的特征向量这里值得注意的是本书有几处利用极值原理求极值时只给出了不要条件的数学推导而有关充分条件的论证省略了因为在实际问题中往往根据问题本身的性质就能肯定有最大值或最小值如果所求的驻点只有一个这时就不需要根据极值存在的充分条件判定它是极大还是极小而就能肯定这唯一的驻点就是所求的最大值或最小值
从而， uBu 的极大值为。再用 E1 左乘（4.25）式，有
(E1B I)u 0
（ 4.27）
由（4.27）式说明为 E1B 特征值， u 为 E1B 的特征向量。在此
最大特征值所对应的特征向量 u (u1, u2 ,, u p ) 为我们所求结果。
这里值得注意的是，本书有几处利用极值原理求极值时，只
函数后，对于一个新的样品，将它的 p 个指标值代入线性判别函数（4.19）式中求出U (X) 值，然后根据判别一定
的规则，就可以判别新的样品属于哪个总体。
二、Fisher判别函数的构造
1、针对两个总体的情形
假设有两个总体 G1, G2 ，其均值分别为 μ1 和 μ 2 ，协方差矩阵为 Σ1 和 Σ 2 。当 X Gi 时，我们可以求出 uX 的均值和方差，即
令
k
b (uμi uμ)2 i 1

模式识别FISHER线性判别实验

模式识别FISHER线性判别实验
人工知能领域中的模式识别是计算机实现人类识别物体的能力的一种
技术。

它的主要目的是根据给定模式的样本及其特征，自动识别出新的样
本的特征并做出判断。

其中最著名的技术之一就是FISHER线性判别法。

FISHER线性判别法基于正态分布理论，通过计算样本的统计特征来
分类，它是一种基于参数的最优分类算法。

算法的基本思想是通过计算两
个类别的最大类间差异度，以及最小类内差异度，来有效地分类样本。

具
体而言，FISHER线性判别法即求出一个线性超平面，使这个超平面把样
本区分开来，使样本离类中心向量之间的距离最大，同时使类中心向量之
间的距离最小。

FISHER线性判别法的具体实现过程如下：
1.准备好建立模型所需要的所有数据:训练样本集，其样本特征与对
应的类标号。

2.确定每个类的类中心向量c_1，c_2，…，c_m，其中m为类的数目。

3.根据类中心向量求出类间离散度矩阵S_b和类内离散度矩阵S_w。

4.将S_b与S_w相除，得到S_b/S_w，从而求出矩阵的最大特征值
λ_1及最小特征值λ_n。

5.将最大特征值λ_1进行特征值分解，求出其特征向量w，求出判
定函数：
f(x)=w·x+w_0。

6.根据判定函数，将样本进行分类。

Fisher判别函数

Fisher 判别函数的使用具体步骤Fisher 多类判别模型假定事物由p 个变量描述, 即: x=(p x x x ,...,,21)T该种事物有G 个类型, 从每个类型中顺次抽取p n n n ,...,,21个样品, 共计n=∑=Gi i1n个样品。

即从第g 类取了g n 个样品, g=1,2,⋯, G, 第g 类的第i 个样品, 用向量:gi x =(pgi gi gi x x ,...,,x 21)T (1)( 1) 式中, 第一个下标是变量号, 第二个下标是类型号,第三个下标是样品号。

设判别函数为:T x p p v x v x v x v =+++=...y 2211 （2）其中: V=(p v v v ,...,21)T按照组内差异最小, 组间差异最大同时兼顾的原则, 来确定判别函数系数。

（中间推导过程不在这里介绍了）最终就有个判别函数:,y x V Tj j=1,...,2,1s j = 一般只取前M=min(G- 1,p)个, 即:M j x v x v x v y p pj j j j ,...,2,1,...2211=+++= （3）根据上述M 个判别函数, 可对每一个待判样品做出判别。

),...,,(x 020100p x x ｘ=其过程如下:1、把x0 代入式(3) 中每一个判别函数, 得到M 个数,,...,2,1,...y 202101j 0M j x v x v x v p pj j j =+++=记：TM y y y y ),...,,(020100= 2、把每一类的均值代入式（3）得Gg y y y y G g M j x v x v x v y M gggg pg pg g g g g j g ,...,2,1),,...,,(,...2,1,,...,2,1,...212211====+++=3、计算：∑=-=Mj j j g gy y D 1202)(，从这G 个值中选出最小值：)(min 212g Gg h D D ≤≤=。

费歇尔判别法

费歇尔判别法费歇尔判别法（Fisher's Discriminant Analysis）是一种统计学中的方法，用于寻找两个或多个分类变量中最能有效区分它们的线性组合。

这种方法最初是由英国统计学家罗纳德·费歇尔（Ronald A. Fisher）在1936年所提出。

费歇尔判别法的目标是通过将数据投影到低维空间来确定样本类别之间最明显的分离平面。

这个方法假设所有数据员来自正态分布，这使得它的结果具有很高的概率。

此外，这种方法特别适用于小样本数据，在这种情况下，其它多变量方法往往受到数据不足或对角线矩阵估计的影响。

费歇尔判别法通过将多维数据投影到一维空间上，找到最能表示数据差异的线性变量。

具体步骤如下：1. 定义问题在进行费歇尔判别分析之前，首先需要定义问题。

这个问题可以是不同的变量之间的分类问题，或者是同一变量在不同条件下的分类问题。

例如，可以通过费歇尔判别分析找到两个组的区别，这两个组的特征可以用来预测其他类似两个组。

2. 构造分类变量在对数据进行投影之前，需要将分类变量定义为正态分布。

这种变量通常为两个或更多个。

3. 计算均值和方差计算每个分类变量的均值和方差，以用于后面的投影计算。

4. 计算类内离散度矩阵类内离散度矩阵是指每个类别内所有点与该类别均值之间的距离的累加和。

这个矩阵用来衡量类的内部分散程度，通常使用矩阵的矩阵乘法来进行计算。

5. 计算类间离散度矩阵类间离散度矩阵是指不同类别均值之间的距离的累加和。

这个矩阵用来衡量类别之间的分散程度，也通常使用矩阵的矩阵乘法来进行计算。

6. 计算特征值和特征向量计算类内离散度矩阵和类间离散度矩阵的特征值和特— 1 —征向量。

这些值可以使用线性代数中的方法计算。

一般来说，特征向量是正交（perpendicular）的。

7. 选取最大特征值从计算出的特征值中找到最大特征值，找到最大特征值所对应的特征向量。

这个特征向量就是数据的主要方向，也被称为“判别变量”。

判别分析公式Fisher线性判别二次判别

判别分析公式Fisher线性判别二次判别判别分析是一种常用的数据分析方法，用于根据已知的类别信息，将样本数据划分到不同的类别中。

Fisher线性判别和二次判别是两种常见的判别分析方法，在实际应用中具有广泛的应用价值。

一、Fisher线性判别Fisher线性判别是一种基于线性变换的判别分析方法，该方法通过寻找一个合适的投影方向，将样本数据投影到一条直线上，在保持类别间离散度最大和类别内离散度最小的原则下实现判别。

其判别函数的计算公式如下：Fisher(x) = W^T * x其中，Fisher(x)表示Fisher判别函数，W表示投影方向的权重向量，x表示样本数据。

具体来说，Fisher线性判别的步骤如下：1. 计算类别内离散度矩阵Sw和类别间离散度矩阵Sb；2. 计算Fisher准则函数J(W)，即J(W) = W^T * Sb * W / (W^T * Sw * W)；3. 求解Fisher准则函数的最大值对应的投影方向W；4. 将样本数据投影到求得的最优投影方向上。

二、二次判别二次判别是基于高斯分布的判别分析方法，将样本数据当作高斯分布的观测值，通过估计每个类别的均值向量和协方差矩阵，计算样本数据属于每个类别的概率，并根据概率大小进行判别。

二次判别的判别函数的计算公式如下：Quadratic(x) = log(P(Ck)) - 0.5 * (x - μk)^T * Σk^-1 * (x - μk)其中，Quadratic(x)表示二次判别函数，P(Ck)表示类别Ck的先验概率，x表示样本数据，μk表示类别Ck的均值向量，Σk表示类别Ck的协方差矩阵。

具体来说，二次判别的步骤如下：1. 估计每个类别的均值向量μk和协方差矩阵Σk；2. 计算每个类别的先验概率P(Ck)；3. 计算判别函数Quadratic(x)；4. 将样本数据划分到概率最大的类别中。

判别分析公式Fisher线性判别和二次判别是常见的判别分析方法，它们通过对样本数据的投影或概率计算，实现对样本数据的判别。

fisher判别函数

Fisher判别函数，也称为线性判别函数（Linear Discriminant Function），是一种经典的模式识别方法。

它通过将样本投影到一维或低维空间，将不同类别的样本尽可能地区分开来。

一、算法原理：Fisher判别函数基于以下两个假设：1.假设每个类别的样本都服从高斯分布；2.假设不同类别的样本具有相同的协方差矩阵。

Fisher判别函数的目标是找到一个投影方向，使得同一类别的样本在该方向上的投影尽可能紧密，而不同类别的样本在该方向上的投影尽可能分开。

算法步骤如下：(1)计算类内散度矩阵（Within-class Scatter Matrix）Sw，表示每个类别内样本之间的差异。

Sw = Σi=1 to N (Xi - Mi)(Xi - Mi)ᵀ，其中Xi 表示属于类别i 的样本集合，Mi 表示类别i 的样本均值。

(2)计算类间散度矩阵（Between-class Scatter Matrix）Sb，表示不同类别之间样本之间的差异。

Sb = Σi=1 to C Ni(Mi - M)(Mi - M)ᵀ，其中 C 表示类别总数，Ni 表示类别i 中的样本数量，M 表示所有样本的均值。

(3)计算总散度矩阵（Total Scatter Matrix）St，表示所有样本之间的差异。

St =Σi=1 to N (Xi - M)(Xi - M)ᵀ(4)计算投影方向向量w，使得投影后的样本能够最大程度地分开不同类别。

w= arg max(w) (wᵀSb w) / (wᵀSw w)，其中w 表示投影方向向量。

(5)根据选择的投影方向向量w，对样本进行投影。

y = wᵀx，其中y 表示投影后的样本，x 表示原始样本。

(6)通过设置一个阈值或使用其他分类算法（如感知机、支持向量机等），将投影后的样本进行分类。

二、优点和局限性：Fisher判别函数具有以下优点：•考虑了类别内和类别间的差异，能够在低维空间中有效地区分不同类别的样本。

Fisher线性判别分析实验(模式识别与人工智能原理实验1)

F i s h e r线性判别分析实验(模式识别与人工智能原理实验1)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN实验1 Fisher 线性判别分析实验一、摘要Fisher 线性判别分析的基本思想：通过寻找一个投影方向（线性变换，线性组合），将高维问题降低到一维问题来解决，并且要求变换后的一维数据具有如下性质：同类样本尽可能聚集在一起，不同类的样本尽可能地远。

Fisher 线性判别分析，就是通过给定的训练数据，确定投影方向W 和阈值y0，即确定线性判别函数，然后根据这个线性判别函数，对测试数据进行测试，得到测试数据的类别。

二、算法的基本原理及流程图 1 基本原理（1）W 的确定各类样本均值向量mi样本类内离散度矩阵i S 和总类内离散度矩阵w S12w S S S =+样本类间离散度矩阵b S在投影后的一维空间中，各类样本均值T i i m '= W m 。

样本类内离散度和总类内离散度 T T i i w w S ' = W S W S ' = W S W 。

样本类间离散度T b b S ' = W S W 。

Fisher 准则函数满足两个性质：·投影后，各类样本内部尽可能密集，即总类内离散度越小越好。

·投影后，各类样本尽可能离得远，即样本类间离散度越大越好。

根据这个性质确定准则函数，根据使准则函数取得最大值，可求出W ：-1w 12W = S (m - m ) 。

（2）阈值的确定实验中采取的方法：012y = (m ' + m ') / 2。

（3）Fisher 线性判别的决策规则T x S (x m)(x m ), 1,2ii ii X i ∈=--=∑T1212S (m m )(m m )b =--对于某一个未知类别的样本向量x，如果y=W T·x>y0，则x∈w1；否则x∈w2。

R语言中Fisher判别的使用方法

R语⾔中Fisher判别的使⽤⽅法最近编写了Fisher判别的相关代码时，需要与已有软件⽐照结果以确定⾃⼰代码的正确性，于是找到了安装⽅便且免费的R。

这⾥把R中进⾏Fisher判别的⽅法记录下来。

1. 判别分析与Fisher判别不严谨但是通俗的说法，判别分析（Discriminant Analysis）是⼀种多元（多个变量）统计分析⽅法，它根据样本的多个已知变量的值对样本进⾏分类的⽅法。

⼀般来说，判别分析由两个阶段构成——学习（训练）和判别。

在学习阶段，给定⼀批已经被分类好的样本，根据它们的分类情况和样本的多个变量的值来学习（训练）得到⼀种判别⽅法；在判别阶段⽤前⼀阶段得到的判别⽅法对其他样本进⾏判别。

Fisher判别（Fisher Discrimination Method）⼜被称为线性判别（LDA，Linear Discriminative Analysis），是判别分析的⼀种，历史可以追溯到1936年。

它的核⼼思想是将多维数据（多个变量）投影（使⽤线性运算）到⼀维（单⼀变量）上，然后通过给定阈值将样本根据投影后的单⼀变量进⾏分类。

Fisher判别的学习（训练）阶段，就是找到合适的投影⽅式，使得对于已经被分类好的样本，同⼀类的样本被投影后尽量扎堆。

学习阶段的结果是找到⼀系列的系数（Coeffcient），构成形如y=a1 * x1 + a2 * x2 + a3 * x3 + ... + an * xn其中：a1，a2，... an是系数，x1，x2，... ，xn是变量值。

的判别式和阈值。

⽽判别阶段可以根据这个判别式计算出y，并根据阈值将样本进⾏分类。

2. 在R中使⽤Fisher判别R中使⽤Fisher判别说起来很简单，但是我当初也放狗搜索了不短的时间才搞明⽩如何使⽤。

⾸先，它在R⾥不叫Fisher，⽤Fisher搜索多半误⼊歧途。

在R中，它叫LDA（Linear Discriminative Analysis）。

Fisher判别法距离判别法Bayes判别法逐步判别法

设有总体
又D1，D2，┅，Dk是R(p)的一个分划，判别法则为：当样品X落入Di时，则判
i 1,2,3,, k X Di 关键的问题是寻找D1，D2，┅，Dk分划，这个分划应该使平均错判率最小。
【定义】（平均错判损失函数）
用P(j/i)表示将来自总体Gi的样品错判到总体Gj的条件概率。 p( j / i) P( X D j / Gi ) fi ( x)dx i j
P好人 P做好事 / 好人 P好人 P (做好事 / 好人) P (坏人) P (做好事 / 坏人)
P (好人 / 做好事）
0.5 0.9 0.82 0.5 0.9 0.5 0.2
P坏人P做好事 / 坏人 P好人P (做好事 / 好人) P (坏人) P (做好事 / 坏人)
办公室新来了一个雇员小王，小王是好人还是坏人大家都在猜测。按人们主观意识，一个人是好人或坏人的概率均为 0.5。坏人总是要做坏事，好人总是做好事，偶尔也会做一件坏事，一般好人做好事的概率为0.9，坏人做好事的概率为0.2，一天，小王做了一件好事，小王是好人的概率有多大，你现在把小王判为何种人。。
目录上页下页返回结束
7
§4.2
距离判别
2018/10/4
目录上页下页返回结束
8
§4.2
距离判别
2018/10/4
目录上页下页返回结束
9
§4.2
距离判别
2018/10/4
目录上页下页返回结束
10
4.2.2 多总体情况
§4.2
距离判别
1. 协差阵相同。
2018/10/4
目录上页下页返回结束

fisher线性判别

fisher线性判别
fisher 判决⽅式是监督学习，在新样本加⼊之前，已经有了原样本。

原样本是训练集，训练的⽬的是要分类，也就是要找到分类线。

⼀⼑砍成两半！
当样本集确定的时候，分类的关键就在于如何砍下这⼀⼑！
若以⿊⾊的来划分，很明显不合理，以灰⾊的来划分，才是看上去合理的
1.先确定砍的⽅向
关键在于如何找到投影的向量u，与u的长度⽆关。

只看⽅向
找到样本点的中⼼均值m1，m2，以及在向量u上的投影的m1~，m2~。

因为u的⽅向与样本点都有关，所以需要考虑⼀个含有所有样本点的表达式
不妨算出离差阵
算出类内离差矩阵，两个都要求出来，并求和
并且投影的离差阵
根据聚类的理想情况，类内距离⼩，类间距离⼤，所以就⽤类间去处理类内，我们现在的变量是向量u，我们就对u求导，算出max存在的时后u的条件。

为了⽅便化简，引⼊⼀个参数不要以为下⾯除以是向量，（1*2）*（2*2）（2*1）=1 维度变成1，这是⼀个常数。

当求导公式
分⼦为0的时候，推出
所以
⽽且是（1*2）*（2*1）等于1，也是⼀个常数
到此为⽌，u的⽅向已经确定了
2.具体切哪⼀个点。

a，切
切投影均值的终点
2.
切贝叶斯概率的⽐例点
⽅向和具体点均已找到，分析完毕。

实验1 Fisher线性判别实验

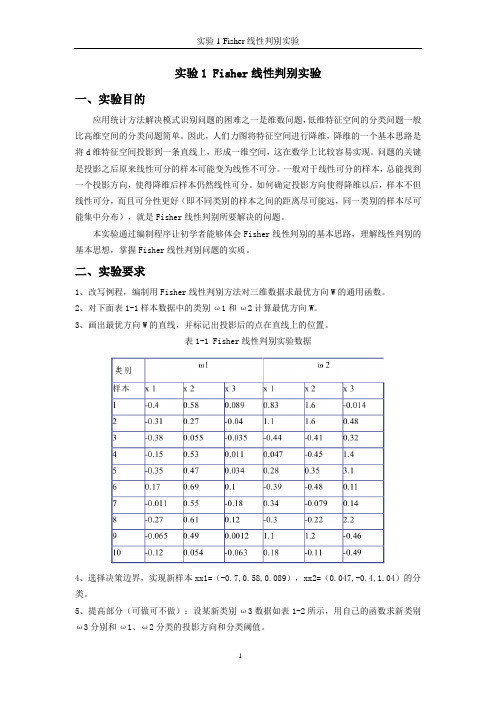
实验1 Fisher线性判别实验一、实验目的应用统计方法解决模式识别问题的困难之一是维数问题，低维特征空间的分类问题一般比高维空间的分类问题简单。

因此，人们力图将特征空间进行降维，降维的一个基本思路是将d维特征空间投影到一条直线上，形成一维空间，这在数学上比较容易实现。

问题的关键是投影之后原来线性可分的样本可能变为线性不可分。

一般对于线性可分的样本，总能找到一个投影方向，使得降维后样本仍然线性可分。

如何确定投影方向使得降维以后，样本不但线性可分，而且可分性更好（即不同类别的样本之间的距离尽可能远，同一类别的样本尽可能集中分布），就是Fisher线性判别所要解决的问题。

本实验通过编制程序让初学者能够体会Fisher线性判别的基本思路，理解线性判别的基本思想，掌握Fisher线性判别问题的实质。

二、实验要求1、改写例程，编制用Fisher线性判别方法对三维数据求最优方向W的通用函数。

2、对下面表1-1样本数据中的类别ω1和ω2计算最优方向W。

3、画出最优方向W的直线，并标记出投影后的点在直线上的位置。

表1-1 Fisher线性判别实验数据4、选择决策边界，实现新样本xx1=（-0.7,0.58,0.089），xx2=（0.047,-0.4,1.04）的分类。

5、提高部分（可做可不做）：设某新类别ω3数据如表1-2所示，用自己的函数求新类别ω3分别和ω1、ω2分类的投影方向和分类阈值。

表1-2 新类别样本数据三、部分参考例程及其说明求取数据分类的Fisher投影方向的程序如下：其中w为投影方向。

clear %Removes all variables from the workspace.clc %Clears the command window and homes the cursor.% w1类训练样本，10组，每组为行向量。

w1=[-0.4,0.58,0.089;-0.31,0.27,-0.04;-0.38,0.055,-0.035;-0.15,0.53,0. 011;-0.35,0.47,0.034;...0.17,0.69,0.1;-0.011,0.55,-0.18;-0.27,0.61,0.12;-0.065,0.49,0.0012;-0 .12,0.054,-0.063];% w2类训练样本，10组，每组为行向量。

Fisher判别

Fisher判别理论，编程步骤和优缺点1.理论判别分析是用于判别个体所属群体的一种统计方法，判别分析的特点是根据已掌握的、历史上每个类别的若干样本的数据信息，总结出客观事物分类的规律性，建立判别公式和判别准则。

然后，当遇到新的样本点时，只要根据总结出来的判别公式和判别准则，就能判别该样本点所属的类别。

判别分析是一种应用性很强的统计数据分析方法。

Fisher判别（1）借助方差分析的思想构造一个线性判别函数：（2）确定判别函数系数时要求使得总体之间区别最大，而使每个总体内部的离差最小。

（3）从几何的角度看，判别函数就是p维向量X在某种方向上的投影。

使得变换后的数据同类别的点“尽可能聚在一起”，不同类别的点“尽可能分离”，以此达到分类的目的。

两类Fisher判别示意图（1）如果有多个类别， Fisher 判别可能需要两个或者更多的判别函数才能完成分类。

（2）一般来说判别函数的个数等于分类的个数减一。

（3）得到判别函数后，计算待判样品的判别函数值，根据判别函数的值计算待判样品到各类的重心的距离，从而完成分类。

2.编程步骤① 把来自两类21/w w 的训练样本集X 分成1w 和2w 两个子集1X 和2X 。

G1 G2X② 由∑∈=i k X x k ii x n M 1，2,1=i ，计算i M 。

③ 由T i X x k i k i M x M x S ik ))((--=∑=计算各类的类内离散度矩阵i S ，2,1=i 。

④ 计算类内总离散度矩阵21S S S w +=。

⑤ 计算w S 的逆矩阵1-w S 。

⑥ 由)(211*M M S w w -=-求解*w 。

3.优点（1）一般对于线性可分的样本，总能找到一个投影方向，使得降维后的样本仍然线性可分，而且可分性更好即不同类别的样本之间的距离竟可能的远，同一类别的尽可能的集中分布。

（2）Fisher 方法可以直接求解法向量。

（3）Fisher 的线性判别不仅适用于确定性的模式分类器的训练，而且对于随机的模机也是适用的，Fisher 还可以推广到多类问题中去。

fisher判别法

1 实验1 Fisher 线性判别实验一、实验目的应用统计方法解决模式识别问题的困难之一是维数问题，在低维空间行得通的方法，在高维空间往往行不通。

因此，降低维数就成为解决实际问题的关键。

Fisher 的方法，实际上涉及维数压缩。

如果要把模式样本在高维的特征向量空间里投影到一条直线上，实际上就是把特征空间压缩到一维，这在数学上容易办到。

问题的关键是投影之后原来线性可分的样本可能变得混杂在一起而无法区分。

在一般情况下，总可以找到某个最好的方向，使样本投影到这个方向的直线上是最容易分得开的。

如何找到最好的直线方向，如何实现向最好方向投影的变换，是Fisher 法要解决的基本问题。

这个投影变换就是我们寻求的解向量*w本实验通过编制程序体会Fisher 线性判别的基本思路，理解线性判别的基本思想，掌握Fisher 线性判别问题的实质。

二、实验原理1．线性投影与Fisher 准则函数各类在d 维特征空间里的样本均值向量：∑∈=i k X x k i i x n M 1，2,1=i (4.5-2)通过变换w 映射到一维特征空间后，各类的平均值为：∑∈=i k Y y k i i y n m 1，2,1=i (4.5-3)映射后，各类样本“类内离散度”定义为：22()k i i k i y Y S y m ∈=-∑，2,1=i (4.5-4)显然，我们希望在映射之后，两类的平均值之间的距离越大越好，而各类的样本类内离散度越小越好。

因此，定义Fisher 准则函数：2122212||()F m m J w s s -=+ (4.5-5) 使F J 最大的解*w 就是最佳解向量，也就是Fisher 的线性判别式。

2．求解*w从)(w J F 的表达式可知，它并非w 的显函数，必须进一步变换。

2 已知：∑∈=i k Y y k ii y n m 1，2,1=i , 依次代入(4.5-1)和(4.5-2)，有： i T X x k i T k X x T i i M w x n w x w n m i k i k ===∑∑∈∈)1(1，2,1=i (4.5-6) 所以：221221221||)(||||||||M M w M w M w m m T T T -=-=- w S w w M M M M w b T T T =--=))((2121 (4.5-7) 其中：T b M M M M S ))((2121--= (4.5-8) b S 是原d 维特征空间里的样本类内离散度矩阵，表示两类均值向量之间的离散度大小，因此，b S 越大越容易区分。

fisher判别式 -回复

fisher判别式-回复【Fisher判别式】一种经典的模式分类方法在机器学习领域，有很多用于模式分类的方法，其中之一就是Fisher判别式。

Fisher判别式是通过线性变换将样本投影到低维空间中，从而实现样本分类的一种方法。

本文将详细介绍Fisher判别式的原理和步骤，并解释该方法在实际应用中的意义。

一、Fisher判别式的原理Fisher判别式的思想是通过找到一个投影方向，使得在该方向上不同类别的样本具有最大的类间距离（即类别间的差异最大），同时最小化类内的方差（即类别内的相似性最小）。

通过这样的投影，我们可以将高维的数据映射到低维的空间中，从而方便进行分类。

具体而言，Fisher判别式考虑了两个指标：类间散度矩阵和类内散度矩阵。

类间散度矩阵衡量的是不同类别之间的差异，而类内散度矩阵则衡量的是同一类别内样本的相似程度。

通过最大化类间散度矩阵与最小化类内散度矩阵的比值，我们可以得到Fisher判别式。

二、Fisher判别式的步骤1. 数据预处理：首先，我们需要收集样本数据，确保该数据集包含了不同的类别。

在收集样本数据后，我们需要对其进行预处理，包括特征选择和数据标准化等操作，以确保数据符合Fisher判别式的前提条件。

2. 计算类内散度矩阵和类间散度矩阵：在第一步的基础上，我们需要计算类内散度矩阵和类间散度矩阵。

类内散度矩阵可以通过计算各类别样本的协方差矩阵并进行加权求和得到，而类间散度矩阵可以通过计算不同类别之间均值差的协方差矩阵得到。

3. 计算投影方向：接下来，我们需要计算投影方向。

这可以通过求解广义特征值问题来实现，其中需要同时考虑类内散度矩阵和类间散度矩阵。

通过求解该特征值问题，我们可以得到投影方向。

4. 数据投影和分类：最后，我们需要将原始数据投影到低维空间中，并进行分类预测。

对于新的样本数据，我们可以使用投影方向将其映射到低维空间，并使用训练得到的分类器对其进行分类。

三、Fisher判别式的应用意义Fisher判别式在实际应用中具有广泛的应用意义。

贝叶斯判别Fisher判别法

Loa n R e cord N umbe r
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
17
Yrs a t Yrs a t Yrs a t Yrs a t
Monthly Monthly H ome Pre se nt Pre vious Pre se nt Pre vious N o. of
第二节贝叶斯判别 Fisher判别法
❖ 贝叶斯判别法是通过计算被判样本x属于k个总体的条件概率
P（n/x),n=1,2…..k. 比较k个概率的大小，将样本判归为来自
出现概率最大的总体（或归属于错判概率最小的总体）的判
别方法。
❖一、最大后验概率准则
设有k个总G体1,G2,G3 Gk 率密度为Gi
q1 q2 qk 1
，样本x来自
qi ,i 1G,且2i 总 k,体
的fi ( x概)
Gi 的先验Gi概率为
满足
P(Gi
x)
qi fi (x)
k
i 1,2 k
．i利1 qi用fi (x贝) 叶斯理论，x属于
的后验概率
x Gl , 若P(Gl
（即当样本x已知时，它属于
x) m1的iaxk 概P(G率i x为) ：
当先验概率相等，
q1
qk
1 k
mi (x) 1 μ(i)Σ μ 1 (i) μ(i)Σ1x 2
完全成为距离判别法。判别准则1：后验概率最大即判断x来自后验概率最大的总体
❖ 例9：下表是某金融机构客户的个人资料，这些资料对一个金融机构来说，对于客户信用度的了解至关重要，因为利用这些资料，可以挖掘出许多的信息，建立客户的信用度评价体系。所选变量为： x1: 月收入 x2：月生活费支出 x3：虚拟变量，住房的所有权，自己的为“1”，租用的“0” x4：目前工作的年限 x5：前一个工作的年限 x6：目前住所的年限 x7：前一个住所的年限 X8: 家庭赡养的人口数 X9：信用程度，“5”的信用度最高，“1”的信用度最低。

Fisher判别

两类Fisher判别示意图
Y
G1
G2
L=b111 x1 l12 x 2 l1m x m y l x l x l x L1 1 L2 2 Lm m L
将原来m个变量综合成L个新变量
Fisher判别法
Fisher判别法(先进行投影)
• 所谓Fisher判别法，就是一种先投影的方法。 • 考虑只有两个（预测）变量的判别分析问题。 • 假定这里只有两类。数据中的每个观测值是二维空间的一个点。见图（下一张幻灯片）。 • 这里只有两种已知类型的训练样本。其中一类有38个点（用“o”表示），另一类有44个点（用“*”表示）。按照原来的变量（横坐标和纵坐标），很难将这两种点分开。 • 于是就寻找一个方向，也就是图上的虚线方向，沿着这个方向朝和这个虚线垂直的一条直线进行投影会使得这两类分得最清楚。可以看出，如果向其他方向投影，判别效果不会比这个好。 • 有了投影之后，再用前面讲到的距离远近的方法来得到判别准则。这种首先进行投影的判别方法就是Fisher判别法。

Fisher判别法

ii)计算判别临界值y0, 然后根据判别准则对新样品判别分类。
假定所建立的判别函数为
组内离差阵总体之间样本离差阵
这说明和C恰好是A、E矩阵的广义特征根
及其对应的特征向量，假设其正根的数目为m。
Fisher判别法（canonical discriminant）
1、两总体Fisher判别法
两类Fisher判别示意图
YG1ຫໍສະໝຸດ G2L=b1X+b2Y
X
假设新建立的判别式为
y c1x1 c2 x2 ....... cp xp
将属于不同两总体的样品观测值带入判别式中去，则得到
将上边两式分别左右相加，再除以相应的样品个数，则有
结果来说没有影响。所以取 1 ，于是方程组变为：
有了判别函数之后，欲建立判别准则还要确定判别临界值，在两总体先验概率相等的假设下，一般取临界值为 y (1) y (2)
的加权平均值即
y0
n1 y (1) n1
n2 y (2) n2
根据 y (1) y (2) 的大小确定判别准则。
两个正态总体等方差情况下的示意图形。
为了使判别函数能够很好的区别来自不同总体的样品，希望判别式能够满足以下的条件：
综合以上两点，就是要求越大越好。
由微积分求极值的必要条件（导数为0）可求出使 I 达到最大的值C1,C2…CP，由此就得到满足要求的判别式。
是常数因子，不依赖于k,它对方程组的解只起到共同扩大
倍的作用，不影响C1,C2…,CP之间的相对比例关系。对判别