圆曲线的施工放样
解析圆曲线坐标及其放样方法

解析圆曲线坐标及其放样方法圆曲线坐标是一种特殊的几何坐标系,它是由一条曲线经过的坐标点组成的。
圆曲线是几何学中的概念,它是一种更贴近自然环境的曲线形状。
其定义是,某一点到曲线所经过的其它点的距离和曲线上某一点到原点O的距离的乘积,此乘积总是常数。
圆曲线坐标的概念是,只要点所形成的距离可以满足圆曲线坐标的定义,它们就是圆曲线坐标。
因此,可以建立一组具有该坐标定义的点,这些点就构成了一条圆曲线。
二、圆曲线坐标的放样方法圆曲线放样方法是将圆曲线上的点按照一定的规律分布以得到一个平面、立体的效果的技术方法。
通常,圆曲线放样方法分为两种:一种是空间放样法,另一种是平面放样法。
空间放样法是将圆曲线上的点放置在一个三维空间中,通过空间放样可以将一条圆曲线变成贴近自然环境的曲线形状。
这种放样方法可以得到更加真实的效果。
平面放样法是把圆曲线上的点放置在一个二维平面上,从而组成一个半圆形。
此外,还可以利用软件进行放样,把圆曲线以图像的形式在屏幕上重现出来,从而得到一个真实的效果。
三、应用圆曲线坐标及其放样方法在工程设计中有着广泛应用。
比如,由于具有平滑曲线的独特特点,它们常常被用来作为管道设计,机械设计和船舶设计等工程设计中的基础几何形状。
此外,它也被用作绘制几何图形的参数化方案,从而能够方便的计算出几何图形的形状参数,进而更加精确地绘制几何图形。
四、总结圆曲线坐标及其放样方法可以帮助我们设计出更加平滑的几何图形,从而更加真实地绘制几何图形。
此外,它还被广泛应用于工程设计中,用于管道设计、机械设计和船舶设计等工程设计中的基础几何形状。
综上所述,圆曲线坐标及其放样方法可被广泛应用到几何图形的设计和工程设计以及其它领域。
道路中线圆曲线放样方案
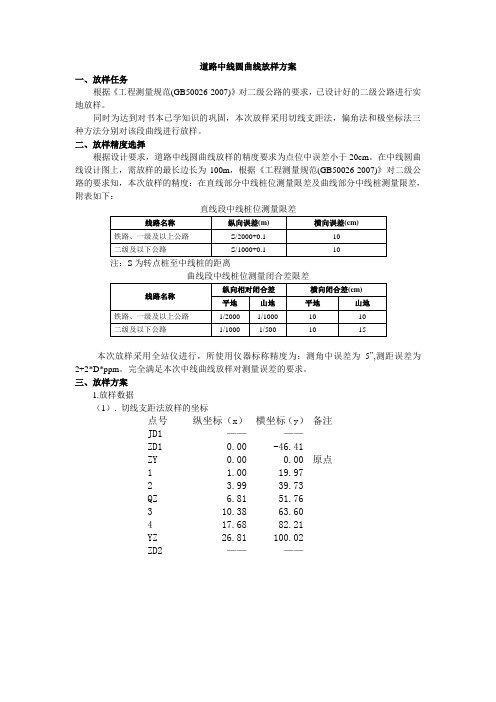
道路中线圆曲线放样方案一、放样任务根据《工程测量规范(GB50026-2007)》对二级公路的要求,已设计好的二级公路进行实地放样。
同时为达到对书本已学知识的巩固,本次放样采用切线支距法,偏角法和极坐标法三种方法分别对该段曲线进行放样。
二、放样精度选择根据设计要求,道路中线圆曲线放样的精度要求为点位中误差小于20cm。
在中线圆曲线设计图上,需放样的最长边长为100m,根据《工程测量规范(GB50026-2007)》对二级公路的要求知,本次放样的精度:在直线部分中线桩位测量限差及曲线部分中线桩测量限差,附表如下:本次放样采用全站仪进行,所使用仪器标称精度为:测角中误差为5”,测距误差为2+2*D*ppm。
完全满足本次中线曲线放样对测量误差的要求。
三、放样方案1.放样数据(1). 切线支距法放样的坐标点号纵坐标(x)横坐标(y)备注JD1 ————ZD1 0.00 -46.41ZY 0.00 0.00 原点1 1.00 19.972 3.99 39.73QZ 6.81 51.763 10.38 63.604 17.68 82.21YZ 26.81 100.02ZD2 ————(2).偏角法放样的角度与距离点号偏角(°′″)距离备注JD1 ————ZD1 ————ZY 00 00 00 0.00 原点1 02 51 52 19.992 05 43 44 39.93QZ 07 29 57 52.213 09 16 14 64.444 12 08 06 84.09YZ 15 00 00 103.55ZD2 ————(3).任意站极坐标法点号角(°′″)距离备注JD1 28 03 45 207.06ZD1 00 00 00 205.31ZY 13 03 51 200.001 18 47 35 200.002 24 31 19 200.00QZ 28 03 45 200.003 31 36 10 200.004 37 19 54 200.00YZ 43 03 58 200.00ZD2 56 07 50 205.312.放样步骤(一)切线支距法放样放样部位:道路中线圆曲线。
第四节圆曲线放样

60 3000 切线长 T 150 * tan 87 .48 m 2
ZY
JD
α
T
E0
L
QZ
YZ
曲线长 L 150 * 60 3000 *
603000 外矢矩 E 150 * (sec 1) 23.64 m 2
切曲差D 2 * 87.48- 158.39 16.57m
•
检查:
QZ
4
26
• ※ 置镜于YZ 点,(如图11-7),测设另一半曲线,偏
角要反拨:逆时针方向转动照准部,使度盘读
数为360°- δi 。
• 检查:弦长丈量是从点到点如 : YZ-1,1-2,2-3„iQZ
QZ 360
4
•
•
在QZ点的总偏角为:
应检核所测设的 QZ 点点位是否闭合 , 如超 限,须及时检查原因,重新测设。
K 180 1= · 2 2R 2 2 1
(11-2)
3 3 1 n n 1
※整弦:里程为 20m 倍数的两相邻曲线点间的弦长 (曲线点间距20m对应的弦长)。
※分弦:有一端里程不为 20m 倍数的两相邻曲线点 间的弦长。
17
•
•
• • •
通常要求曲线点设置在整数(如20m 的倍数)里程上 ,即里程 尾数为00, 20, 40, 60, 80m等点上。
27
二、切线支距法测设圆曲线(稍后)
• (切线支距法适用于地势较 平坦的地区)
1.测设原理:切线支距法即直 角坐标法。 (1)切线坐标系:见图11-8
坐标原点:曲线起点ZY或曲线 终点YZ;
圆曲线放样
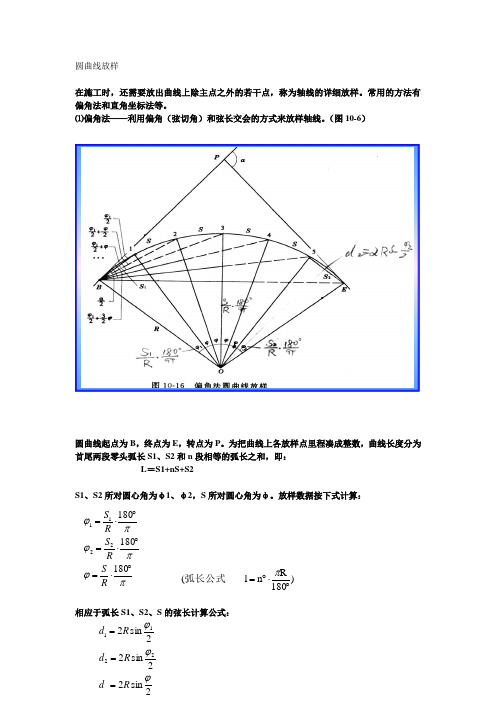
圆曲线放样在施工时,还需要放出曲线上除主点之外的若干点,称为轴线的详细放样。
常用的方法有偏角法和直角坐标法等。
⑴偏角法——利用偏角(弦切角)和弦长交会的方式来放样轴线。
(图10-6)圆曲线起点为B,终点为E,转点为P。
为把曲线上各放样点里程凑成整数,曲线长度分为首尾两段零头弧长S1、S2和n段相等的弧长之和,即:L=S1+nS+S2S1、S2所对圆心角为φ1、φ2,S所对圆心角为φ。
放样数据按下式计算:的弦长计算公式:圆曲线上各点的偏角(弦切角等于弦长所对圆心角的一半)为:放样过程:将仪器安置于圆曲线起点ZY(即B点)上,后视JD(P)点,并将水平度盘置于零,拨角∠PB1,在此方向上量取d1,得1点;然后,再拨角∠PB2,钢尺零点对准1点,以d为半径,摆动钢尺到经纬仪方向线上,得2点;再拨角∠PB3,钢尺零点对准2点,以d为半径,摆动钢尺到经纬仪方向线上,得3点;依此类推…当拨角∠PBE时,视线应当通过圆曲线的终点YZ点。
YZ点至圆曲线上最后一个细部点的距离应为d2。
以此检查放样质量。
⑵直角坐标法——切线支距法,以曲线起点ZY或终点YZ为坐标原点,以切线为x轴,切线的垂线为y轴,如图10-17所示。
根据坐标xi、yi放样曲线上各细部点。
设各细部点之间的弧长为S,所对应的圆心角为φ,则已知R,又给定S值后,即可求出待放样的细部点坐标。
S值一般为10m、20m、30m等整数值。
放样前可按上述公式计算,将计算得结果列表备用。
放样步骤如下:①检核先前放样的三个主点ZY、QZ、YZ的点位有无错误。
②用钢尺沿切线ZY-JD方向放样x1、x2、x3等,并在地面上标定出垂足点m、n、p等。
③在垂足m、n、p等处用经纬仪、直角尺法作切线的垂线,分别在各自的垂线上放样y1、y2、y3等,以桩定细部点1、2、3等。
为了避免支线过长,影响放样精度,可用同法,从YZ-JD切线方向上放样曲线的另一半弧上的细部点。
工程施工圆弧怎么放样

工程施工圆弧怎么放样一、圆弧放样的基本原理在施工中,经常会遇到需要绘制圆弧的情况,如建筑的拱形、桥梁的曲线等。
因此,圆弧放样是施工中常见的基本技术。
圆弧放样的基本原理是通过一定的数学方法,在设计图上确定圆心和半径,然后在实际施工中按照设计图的尺寸和要求进行布置。
在进行圆弧放样时,需要掌握一定的数学知识和测量工具的使用技巧,以保证圆弧的准确性和施工质量。
二、圆弧放样的步骤1. 确定圆弧的圆心在进行圆弧放样时,首先需要确定圆弧的圆心。
通常情况下,圆弧的圆心是根据设计图上的尺寸和要求确定的,可以通过测量或计算的方法找到圆心的位置。
在确定圆心的位置后,需要在设计图上做标记,以便在施工现场进行实际放样。
2. 确定圆弧的半径确定圆心后,接下来需要确定圆弧的半径。
圆弧的半径通常是由设计要求决定的,也可以通过数学计算或测量得出。
在确定了圆弧的半径后,需要使用测量工具在设计图上标注出圆弧的尺寸和半径,以便在施工现场进行放样。
3. 测量并布置圆弧的位置在确定了圆心和半径后,就可以在施工现场进行实际的圆弧放样。
根据设计图上的标注,使用测量工具对施工现场进行测量,并根据圆心和半径进行布置,确保圆弧的尺寸和位置符合设计要求。
4. 进行实际的施工在完成了圆弧的放样后,就可以进行实际的施工了。
根据放样的结果,按照设计图上的要求进行构架、砌砖、浇筑等工作,确保圆弧的几何形状和尺寸符合设计要求。
在施工过程中,需要做好测量和验收工作,及时调整和修正,确保施工质量和安全。
三、圆弧放样的注意事项1. 熟练掌握测量工具的使用技巧在进行圆弧放样时,需要使用各种测量工具,如直尺、量具、量角器等。
因此,施工人员需要熟练掌握这些测量工具的使用技巧,以保证放样的准确性和施工质量。
2. 注意施工现场的环境和现状在进行圆弧放样时,需要考虑施工现场的实际情况和环境,如地形、气候、光线等因素,以保证放样的准确性和施工顺利进行。
3. 按照设计要求进行放样在进行圆弧放样时,需要严格按照设计图上的尺寸和要求进行放样,以保证圆弧的几何形状和尺寸符合设计要求。
圆曲线上构筑物的放样方法

圆曲线上构筑物的放样方法徐海立;李翠萍【摘要】综合运用数学、测量学等知识,介绍施工放样中构筑物位于圆曲线上的放样方法.【期刊名称】《铁道勘察》【年(卷),期】2007(033)003【总页数】3页(P127-129)【关键词】施工放样;圆曲线;控制点【作者】徐海立;李翠萍【作者单位】泰安市建设工程交易中心,山东泰安,271000;泰安市市政工程处,山东泰安,271000【正文语种】中文【中图分类】U2在道桥工程施工过程中,经常会遇到构筑物位于圆曲线上的情况。
如何对构筑物进行施工放样,很少有教科书指导我们怎样做。
这需要我们综合运用数学、测量学等知识来解决这一具体问题。
1 小桥涵位于圆曲线上且与道桥轴线正交如图1所示,某座1-5 m小桥涵,位于圆曲线半径为600 m的道路平曲线上,其中心桩号为K1+100(即E点)。
该小桥放样应以垂直于E点路轴线(即过E点的圆切线)的垂线(即OE,O为圆曲线中心)为桥中线,需要放样桥的纵向中点C、D和两台轴线FG、HI。
图1 圆曲线上放样示例一下面就以该例来讲述一下其具体的放样方法。
首先选择距E点等距离且根据现场实际地形适于放样的两个整桩号点A、B,假如该例中A点桩号为K1+090,B点桩号为K1+110,因为E为AB弧的中点,所以OE⊥AB。
以AB为方向线,将全站仪安置在A点,放样C、F、G点。
根据该例,CD=5 m,则则在此例中,因为圆曲线半径大,所以弧CED与CD、弧AC与AC值接近;若曲线半径小,其值将有差别,因此必须计算。
根据AC长与∠CAB即可放样C点。
放样完C点全站仪不动,根据现场实际地形及C点平面位置,选一适于放样的F′点。
将全站仪对准B点定向后,再对准F′,读取∠F′AB;假若为60°,有又AF=AL/cos∠F′AB=14.999 m据AF长及∠F′AB便可放出F点。
若据此放出的F点不便于施工,可调整∠F′AB值,重新计算AF长度,调至适当位置即可。
公路圆曲线简易放样方法
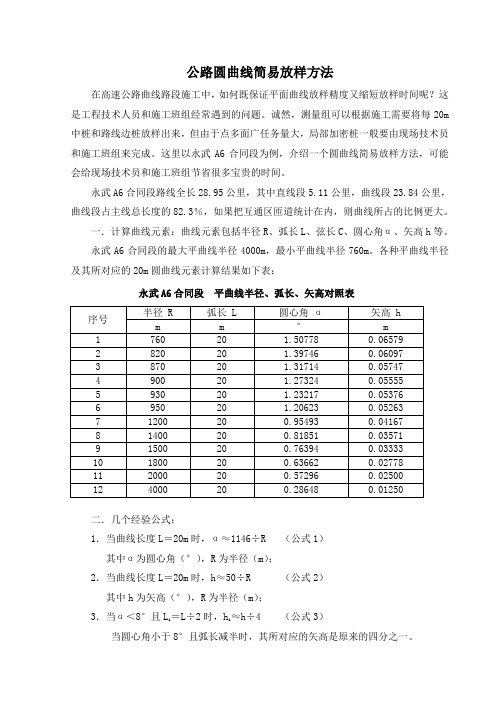
公路圆曲线简易放样方法在高速公路曲线路段施工中,如何既保证平面曲线放样精度又缩短放样时间呢?这是工程技术人员和施工班组经常遇到的问题。
诚然,测量组可以根据施工需要将每20m 中桩和路线边桩放样出来,但由于点多面广任务量大,局部加密桩一般要由现场技术员和施工班组来完成。
这里以永武A6合同段为例,介绍一个圆曲线简易放样方法,可能会给现场技术员和施工班组节省很多宝贵的时间。
永武A6合同段路线全长28.95公里,其中直线段5.11公里,曲线段23.84公里,曲线段占主线总长度的82.3%,如果把互通区匝道统计在内,则曲线所占的比例更大。
一.计算曲线元素:曲线元素包括半径R、弧长L、弦长C、圆心角α、矢高h等。
永武A6合同段的最大平曲线半径4000m,最小平曲线半径760m。
各种平曲线半径及其所对应的20m圆曲线元素计算结果如下表:永武A6合同段平曲线半径、弧长、矢高对照表二.几个经验公式:1.当曲线长度L=20m时,α≈1146÷R (公式1)其中α为圆心角(°),R为半径(m);2.当曲线长度L=20m时,h≈50÷R (公式2)其中h为矢高(°),R为半径(m);3.当α<8°且Li =L÷2时,hi≈h÷4 (公式3)当圆心角小于8°且弧长减半时,其所对应的矢高是原来的四分之一。
三.准备放样工具:钢尺(50m)1把,测量距离用;尼龙线绳50m以上,挂线用;手锤(2~3p)1把,钉子若干,确定点位用。
四.曲线桩加密方法:举一个路基边沟曲线段加密的例子。
为了简便,放样时以设计半径代替边沟曲线半径。
严格来说,由于边沟位于路基的两侧,其曲线半径与路基中线的曲线半径并不相等,但通过计算可知,20m路段两者矢高之差在0~5mm之间,施工中可以忽略不计。
本人多年前在浆砌边沟施工放样时用加密曲线点的方法逐段缩小矢高数值,当加密到曲线的矢高小于10mm时,边沟外观线形圆滑顺畅,令人满意。
圆曲线放样

24
3、将AP1延长一倍到 ,即使AP1=P1P2=C值,与由 量偏距d交会得P2点,且
精选ppt
25
弦线偏距法特点:
方便快捷,但精度较低,放样误差累计快, 因此不宜连续放样多点。在地下工程掘进时, 可以用它指示曲线段的开挖方向。等到巷道 掘进并砌好一定长度后,用导线的方法建立 控制点,然后从控制点出发,按坐标放样放 出曲线上的点。也就是说,本方法仅用来粗 略的指示巷道掘进方向。
E R se 1 c 3 0 s0 e 2 4 c 8 5 1 7 .7(m 7 ) 2 2
D 2 T L 2 6 . 7 8 1 1 . 0 3 2 . 9 3 5 ( m ) 3
精选ppt
10
②计算主点桩里程
JD -)T
ZY +)L
YZ -)L/2
QZ +)D/2 JD
测设分两步进行,先测设圆曲线的三个主点(直圆点 ZY、曲中点QZ和圆直点YZ),再详细测设圆曲线 上按规定桩距各副点(中桩点)。
精选ppt
6
(一)、圆曲线上各点的名称
JD—线路转角点,称为交点 ZY—直线与圆曲线的接点, 称为直圆点 QZ—圆曲线的中点, 称为曲中。 YZ—圆曲线与直线的接点, 称为圆直点。 圆曲线主点—JD、ZY、QZ、YZ 称为圆曲线主点 圆曲线主点测设: 在实地上标定出圆曲线主点的工作。
5.95
1°08′11″
+140 +160
25.95 45.95
4°57′22″ 8°46′33″
QZ K3+181.60
+200
49.14
9°23′06″
+220 +240
YZ K3+249.14
圆曲线的详细测设

2.1圆曲线要素计算在JD1点置经纬仪,以一个测回测定转折角 ,计算路线偏角 。设计圆曲线的半径R=50m,按下列公式计算圆曲线元素(切线长T、曲线长L、外失距E、切曲差D),
(1-0)
(1-1)
(1-2)
D=2T-L(1-3)
用安置于JD1点的经纬仪先后瞄准ZD1,ZD2定出方向,用钢尺在该方向上测设且切线长T,定出圆曲线的起点(直圆点)ZY和圆曲线的终点(圆直点)YZ,打下木桩,重新测设一次,在木桩顶上标出ZY 和YZ的精确位置。
学 号:08300486
专 业 班 级:工程测量与监理384403
指 导 教 师:张晓雅
摘 要
本文阐述了在公路、铁路的路线圆曲线测设中,一般是在测设出曲线各主点后,随之在直圆点或圆直点进行圆曲线详细测设。其中施工测量是整个施工进程和每一施工工序中的首要工作,其内容主要是建立平面控制网和高程系统,测定线路关键点,细部点的测设,中线(线路轴线),对圆曲线进行施工放样测量,并在施工进程中进行相关的测量等,以确保施工质量和施工过程的安全。本文通过仪器安置不同地方进行多种圆曲线测设,提出了偏角法、切线支距法和全站仪法详细测设圆曲线的方法,对圆曲线上各点进行测设。
ZY K4+776.716 K5 123.284
+L/2 164.348 - K5 +17.872
QZ K4+941.064 YZ 105.412
+L/2 164.384
YZ K5+105.412
主点坐标计算:
由上表已知JD2坐标及坐标方位角,可求出ZY点坐标
=9719.009+173.284cos316015、50、、=9844.212
圆弧形建筑定位放线方法

圆形、弧形建筑定位放线方法随着时代的进步,人们审美的提高,方方正正的造型已经不能满足现代建筑的审美需求,进而产生了许多线条复杂、造型别致的优美建筑。
虽然建筑变得越来越漂亮了,但是也给我们施工提出了更高的要求,由其是给施工放线作业带来更多的作业量、计算量,误差、失误也随之增多。
介绍一种采用全站仪和计算机AutoCAD软件直角坐标系辅助法,从而快速准确地完成复杂基础形式下圆形、弧形建筑定位放线,并通过一个在施工程实例加以说明。
该工法具有一定的推广应用价值。
一、工法特点传统圆形放线主要依据解析几何法先进行内业计算后,再用经纬仪与钢卷尺联合放线,当基础形式复杂,基础面起伏不平,将尺子悬空并目估使其水平。
以垂球或测钎对准基础面点或向基础面投点,根据圆形半径确定其距离。
但是存在施工工作繁琐,施工操作麻烦,钢尺水平及垂点误差较大,极易出错。
因此,本工法与常规测量相比较,具体以下特点:1、测量精度高、速度快、内业计算量小根据竖向规划图中圆形平面位置,建立平面施工坐标系,借助计算机Auto CAD 强大的运算功能,可以快速标出圆心位置的坐标点,再采用全站仪对已知坐标点进行放样,快速完成圆心点定位,在圆心点上架好全站仪,利用全站仪自动测距功能,可以快速的确定圆上的任意点,从而降低了圆形放线的难度,提高了放线工作的速度和精准度。
2、受外界施工条件影响少,便于检测和纠正由于能即时得出点位坐标和偏差信息,既降低测量施工的难度和强度,还可以结合放样点坐标进行反验算,随时纠正偏差量。
3、与其他几种方法比较,具有如下优缺点4、适应范围适用于一般圆形、弧形建筑复杂基础形式的定位测量定位的各类建筑物的测量。
二、工艺原理建立施工坐标系1、坐标换算根据建设单位提供的电子版的竖向规划图,把结构施工图按与竖向平面图中相同制图比例进行缩放(AUTOCAD中的快捷键为SC),一般结构施工图纸的制图比例为1:100,竖向规划图中的制图比例为1:1000,然后带基点复制(快捷键为CTRL+SHIFT+C)把结构图复制到竖向规划图中,再执行约束命令中的共线命令,这样就把结构图按照实际坐标放到竖向规划图中,即使施工控制网与测量控制网发生联系时,进行坐标换算,使它们的坐标系统统一。
圆形弧形建筑定位放线完整版

圆形弧形建筑定位放线集团标准化办公室:[VV986T-J682P28-JP266L8-68PNN]复杂基础形式下圆形、弧形建筑定位放线工法1. 前言伴随着我国的经济的不断持续发展;物质世界的不断的丰富的过程中,也是人们不断追求视觉审美的进程,建筑设计发展正是这个过程最有说服力和表现力的产品。
已往四方盒式呆板的建筑,及其灰色外表的装饰是无法表达出建筑的真实美感的。
现代建筑的优美的体量,怡人的空间、线条多样的外形是建筑师们的追求的方向……但这些同时也给施工带来了更大的难度,提出了更高的要求,由其是给施工放线作业带来更多的作业量、计算量,误差、失误也随之增多。
为此,下面叙述一种采用全站仪和计算机AutoCAD软件直角坐标系辅助法,从而快速准确地完成复杂基础形式下圆形、弧形建筑定位放线,并通过一个在施工程实例加以说明。
该工法具有一定的推广应用价值。
2. 工法特点传统圆形放线主要依据解析几何法先进行内业计算后,再用经纬仪与钢卷尺联合放线,当基础形式复杂,基础面起伏不平,将尺子悬空并目估使其水平。
以垂球或测钎对准基础面点或向基础面投点,根据圆形半径确定其距离。
但是存在施工工作繁琐,施工操作麻烦,钢尺水平及垂点误差较大,极易出错。
因此,本工法与常规测量相比较,具体以下特点:(1).测量精度高、速度快、内业计算量小根据竖向规划图中圆形平面位置,建立平面施工坐标系,借助计算机Auto CAD强大的运算功能,可以快速标出圆心位置的坐标点,再采用全站仪对已知坐标点进行放样,快速完成圆心点定位,在圆心点上架好全站仪,利用全站仪自动测距功能,可以快速的确定圆上的任意点,从而降低了圆形放线的难度,提高了放线工作的速度和精准度。
(2). 受外界施工条件影响少,便于检测和纠正由于能即时得出点位坐标和偏差信息,既降低测量施工的难度和强度,还可以结合放样点坐标进行反验算,随时纠正偏差量。
(3).与其他几种方法比较,具有如下优缺点序号方法优点缺点局限性1直接拉线法操作简便,精度不高用于表面平整50m以下2几何作图法施工麻烦,桩点多精度不高受场地的局限3直角坐标法施工操作方便内业计算量大,易出错桩点较多4极坐标法施工操作方便内业计算量大,易出错桩点较多5直角坐标和计算机辅助法施工简便,精度较高内业计算工作量很小不受施工场地限制,自动校正(4)、适应范围适用于一般圆形、弧形建筑复杂基础形式的定位测量定位的各类建筑物的测量。
偏角法圆曲线放样-

铁路隧道施工测量——偏角法圆曲线放样摘要测量方法种类繁多,因为坐标法放样应用范围比较广泛,人们应用的也比较多。
在隧道施工测量放样中,由于大多数情况下并不需要放样具体点位,仅需放样出线路中线,偏角法也被广泛应用。
两者各有长短,只有结合使用,才能发挥出最大的工作效率。
关键词铁路隧道测量圆曲线偏角法测量方法种类繁多,因为坐标法放样应用范围比较广泛,人们应用的也比较多。
在隧道施工测量放样中,由于大多数情况下并不需要放样具体点位,仅需放样出线路中线,偏角法也被广泛应用。
1偏角法原理已知圆曲线上A、B两点位置及AB弧长,也知道BC弧长,放样C点位置。
如图1所示:切线切线图1AB6 1=ZBOD=arcsin通过图1不难得出:科技论文一铁路隧道施工测量在圆曲线半径足够大的情况下,我们用弧长代替弦长,即用弧长AB代替线段AB。
皿一,°.弧长AB贝|3 1=ZBOD=arcsin ------2 R同样地,我们可以推出弧长BC6 2=arcsln -------2 R在实际施工放样中,A、B两点是我们事先埋设的导线控制点(在线路中线上),C点是我们需要样的里程的中点,弧长AB变成了A、B两点的里程差,弧长BC变成了8、C两点的里程差。
经纬仪架设于B点,后视A点,如果曲线是右曲线,照准部顺时针拨6= 6 1+ 6 2+180°,如果曲线是左曲线,照准部逆时针拨6= 6 1+ 6 2+180°,仪器望远镜十字划丝即对准C点方向,C点的里程用钢尺拉即可。
2偏角法误差分析在以上原理论述中提到的用弧长代替弦长、用钢尺拉放样位置里程以及要求A、B两点都在曲线中线上都有可能产生误差,误差有多大呢,我们分析一下。
2.1里程代替距离误差分析在上述中,弧长代替弦长前提是半径足够大的情况下,就一般情况来说,产生的误差有多大呢?福厦铁路客运专线一般的曲线半径为4500米,假设后视距离100米,前视距离50米,用46表示偏角误差。
道路圆曲线施工放样简易法

-108-中国科技信息2006年第2期 CHINA SCIENCE AND TECHNOLOGY INFORMATION Jan.2006工 程 论 坛在道路工程建设中,经常遇有圆曲线施工放样。
常规的放样法有直角坐标法、偏角法和延长弦线法等,这些方法都要利用事先制好的表格查阅有关数据,然后用测量仪器进行放样。
这样,非技术人员难予掌握,而且容易出现差错,特别是在市政道路工程中,常有障碍物阻挡视线,必须将测量仪器移位,换算角度和尺寸,十分不便。
尤其在复曲线的施工放样时,由于不同圆心、不同半径、不同角度交错在一起,更易发生错误。
本人参加多项市政道路工程的圆曲线施工放样,在实践中总结出一种简易的方法,并应用在龙岩市解放路南、中两地段(街心花园至北环路交叉口),取得良好的效果,特别是在北环路交叉口,由四种不同圆心、不同半径和不同角度的复曲线组成,在放样中更显示了简易法优越性,其使用简单,不易差错,误差在允许范围内,值得推广应用。
曲线施工放样可用歌诀表达,即:圆弧曲线难放样,简易方法帮你忙。
连接首尾为旧弦,量出矢高找中点。
首中再连为新弦,新为旧矢半半长。
依次再接新定点,新旧矢比亦半半。
转弯角度小百二,包你成功不变样。
(注:半半为一半之一半,即1/4)。
在工地放样时,实际操作为(如图):1、A、B、E主点为设计已知点。
用钢卷尺量出AB线的中点D,连DE并延长成OX线,DE为矢高a。
2、找出AE1的中点D1,作垂直平分线并延长成OX1线,取D1E1=a1=1/4・a,从而定出E1点,此点为圆曲线的另一点。
3、找出AE1的中点D2,作垂直平分线并延长成OX2线,取D2E2=a2=1/4・a1,从而定出E2点,此点为圆曲线上的又一点。
4、用同样方法可以定出圆曲线上的其余点,将它们用圆滑曲线连成,即为所要放样的圆曲线。
简易法的要点是后一个矢高值为前一个矢高值的1/4,它的理论推导如下(如图所示):点A、E、B为圆曲线上的主点,R为圆曲线的半径,4α为圆曲线的中心角,弧为欲求的圆曲线。
曲线放样PPT课件

x0
5.切垂距 m = x0 Rsinβ0
δ0 b0
y0
7.缓和曲线反偏角
X
b0
=
β 0
δ0
20
第20页/共57页
曲线综合要素计算及主点测设
一、曲线主点
1、ZH(直缓点) 2、HY (缓圆点) 3、QZ (曲中点)
T x0
m
p
ZH
l0
JD
y0
E0
QZ
HY L
β0
YH b0
δ0
HZ
4、YH (圆缓点) 5、HZ (缓直点)
1、仪器设置在JD上,分别以ZD和JD2定向,自交 点起分别沿视线方向量切线长T,即得ZY和YZ点; 2、后视YZ,拨角(180-α)/2,放样
外矢距E,得QZ.
E
JD 1
(180-α)/2
QZ
ZY 1
YZ
1
ZD
ZY
2
YZ 2
JD
注意:主点放样后,要用木桩标定点位,2并注明里程。
图 5 2 主第点10里页/共程5推7页算
设整米加桩。
第29页/共57页
29
正拨与反拨 若切线方向的水平度盘读数为0°00′00″
正拨: 平盘读数 = 偏角值 反拨: 平盘读数=360°- 偏角值。
3
c3
2
正拨
P
P
反拨
c2
δp,3
c1
1 δp,2
δp,1
30
第30页/共57页
二、偏角计算
j
1.圆曲线偏角
i δi,j
R
δi , j
= li , j 2R
5.在始切线上的垂
圆曲线桥墩放样

这个案例还是2010年12月18日网友86550943@发给我的,由于事务繁忙,一直未给予详细解答,在此趁着讲述曲线上构造物坐标计算专题时,一并在此分析解答,还望网友见谅这个迟到的回复。
先看一下相关图纸的截图:这是曲线要素表:这是曲线桥墩中心线与路线中心线的关系图全图与局部放大图:这是图纸上全部的桥墩位置参数图:这里取两处有代表性的位置,这是圆曲线上某段:这是缓和曲线上某段:简支梁墩曲线布置大样图:桥墩及基础尺寸:图纸的附注说明:————————————————————————————————————————————————————————————补充相关尺寸在讲述之前,有必要补充一下以上设计文件中没有给出或者标注不清晰的相关尺寸:1.简支箱梁宽度11.6米;2.直线上,简支箱梁在桥墩上假设时,相邻两箱梁之间留10cm的缝宽,以桥墩中线为界,两侧各5cm;3.两轨道中心线之间的距离为4.4米。
按我的理解,以目前大多数测量工程师的理论和实践基础,本日志所呈现的高铁简支墩梁,在直线上的放样和计算应该没有问题。
因此本文仅针对曲线上的一些情况来阐述。
两个关键点曲线又分圆曲线和缓和曲线两种情况,按照对设计文件的理解,圆曲线和缓和曲线上简支墩梁放样的关键在于两点:1.对外距E的处置,这个涉及到构造物控制线的左、右距离的确定;2.构造物控制线(即桥墩基础的中轴线)相对于路线的夹角,这个涉及到控制线的方位。
第1点,E的数值没有问题,每个桥墩都标注了这个参数,关键是要理解这个E值如何落实到放样计算中,此外,若能自己计算验证出E值的数值则更好。
第2点,控制线的方位,附注说明中说得很清楚,平分偏角的补角,这个在圆曲线上很简单,也就是对应中桩的法线(即正交),而在缓和曲线上就不行了,那到底偏多少呢,这个需要计算确定,而且必须确定好,否则墩梁的施工放样会有问题。
圆曲线上各参数的含义及计算先来简单一点的,理解一下圆曲线上各参数的含义及计算方法。
弧形园路的放线及收边,你知道多少?

弧形园路的放线及收边,你知道多少?建筑设计精选 2022-11-25 17:06Technical post放线/收边技术帖Technology弧形园路的放线及收边弧线形园路是景观中常用的道路形态,下面小编带大家了解一下弧形园路的放线及收边。
如果施工时放线不注意,就会出现(如下图)园路转角走向不畅等情况。
▲转角走向不畅▲园路曲线起伏不过流畅自然注意事项:园路混凝土基础宽度要比面层宽度每边宽2-3cm,每隔6-8 m须设置伸缩缝。
面层铺装前应把混凝土垫层清理干净,在施工过程中如有水泥砂浆掉落面层须及时用干布擦净,地面完工后应及时做好成品保护工作,保证面层不受污染。
▲PVC管放线弧形园路在放线时可以利用柔韧性较强的PVC管弯曲成自然弧形作为园路走向的参考线,具体位置可以结合图纸和现场实际情况进行微调,以保证园路线条流畅(推荐使用∅25mm管径),遇道路交叉口的弧线段,收边材料注意应按照现场弧度进行二次加工。
▲自然式放线,园路走向自然流畅张弛有度▲草坪与园路铺装收边▲灌木与园路的铺装收边弧形园路赏析Appreciation小编来带大家欣赏一下,那些各大示范区景观中,那些弧线形园路。
▲苏州景瑞无双▲重庆金科御临河▲南京银城君颐东方▲长沙龙湖天宸原著▲杭州龙湖旭辉春江悦茗▲大连龙湖星海彼岸▲郑州旭辉正荣首府▲成都龙湖西宸原著▲郑州旭辉正荣首府▲合肥旭辉江山印▲太原万科翡翠公园▲成都龙湖天璞▲福州金辉溪溪里▲河北沧州天成岭秀景观▲天津海河金茂府▲成都保利两河院子弧线园路自然流畅张弛有度,连接着各个区域,不仅满足功能也是一道风景。
在细节方面弧形园路,想要尽善尽美,放线与施工时也要及其注意。
工程测量第6章-工程建筑物的施工放样

b
J
XJ=502.110m
YJ=496.225m
D
XP=450.000m
+244.092
-1
例:右图中J、K为已知导线点,P为 某设计点位。按图中数据计算
XK=746.202m K YK=456.588m
在J点用极坐标法测设P点的放样 数据β、D。 解: JK=XK-XJ=+244.092 JK=YK-YJ=- 39.637 JP=XP-XJ=-52.110 JP=YP-YJ=+63.775 ① D=√(-52.110) +63.775 = 82.357m P -39.637 ② a JK=tg-1 =360- 91325=3504635 YP=560.000m +63.775 a JP=t g -52.110 =180-504453=1291507 b=a JP-α JK=12915 07 -350 46 35 = 138 2832
16
建筑限差
在精度分配处理中,一般先采用“等影响原则”、“忽略不计原则”处理,然后把计算结果与实际作业条件对照。或凭经验作些调整(即不等影响)后再计算。如此反复直到误差分配比较合理为止。
17
精度分配及放样精度要求
设设计允许的总误差为,允许测量工作的误差为1,允许施工产生的误差为2;允许加工制造产生的误差为3。若假定各工种产生的误差相互独立,则可写出: 根据等影响原则,假定1=2=3,则
21
如图所示,为了放样B、C、D等目标点的高程,在O处架设全站仪,后视已知点A(设目标高为l,当目标采用反射片时:l=0),测得O-A的距离S1和垂直角1,从而计算O点全站仪中心的高程为
2009-11-3
21
然后测得O-B的距离S2和垂直角2,从而计算B点的高程为
弧形最简单的放线方法

弧形最简单的放线方法
弧形是一种常见的几何形状,它在建筑、工程、艺术等领域都有着广泛的应用。
在实际操作中,我们经常需要进行弧形的放线工作,而正确的放线方法可以极大地提高工作效率并保证工程质量。
在本文中,我们将介绍弧形最简单的放线方法,希望能对大家有所帮助。
首先,准备工作是非常重要的。
在进行弧形放线之前,需要确保工作场地清洁
整齐,避免杂物干扰工作进程。
同时,需要准备好所需的工具和材料,如放线笔、尺子、绳子等。
这些工具和材料的选择应根据具体的工程要求来确定,确保能够满足实际需要。
接下来,我们来介绍弧形放线的具体步骤。
首先,确定弧形的起点和终点,并
在这两个点上做好标记。
然后,使用放线笔和尺子在起点和终点之间拉直一根绳子,确保绳子的张力均匀,并且与地面平行。
接着,将放线笔固定在绳子的一端,然后将绳子沿着所需的弧形轨迹拉直。
在保持绳子张力的同时,放线笔会在地面上留下一条弧线,这条弧线就是我们所需要的弧形轨迹。
在实际操作中,还需要注意一些细节问题。
首先,要确保绳子的张力均匀,避
免出现松紧不均导致的放线偏差。
其次,要注意放线笔的位置和角度,确保它能够顺利地在地面上留下清晰的弧线。
最后,要及时清理和标注好放线后的弧线轨迹,以便后续的工作。
总的来说,弧形最简单的放线方法并不复杂,关键在于细致的准备工作和严谨
的操作步骤。
只要我们按照正确的方法进行操作,就能够轻松地完成弧形放线工作。
希望本文能够对大家有所帮助,谢谢阅读!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
偏角法在圆曲线施工放样中的应用
随着人们审美观念的改变,人们建造房屋,不局限于四四方方的建筑,把外观设计成各种曲线、流线形,其中最常见的是圆曲线。
圆曲线的施工放样比较复杂,实地放样前需进行一定的内业计算,根据图纸的尺寸及设计要求,确定圆曲线主点的元素,然后,根据工程的特点,从便于施工放样出发,建立不同的坐标方式和计算公式。
现介绍保定高开区某建筑的圆曲线部分的施工放样。
由设计图纸可知,圆曲线的半径R=560m,圆曲线夹角a=28030’,曲线的主点A、B已经在轴线测量时定出,主要是对曲线上加密点的测设,在这里,我主要是采用偏角法测设加密点位。
1、计算测设数据
由已知可计算也圆曲线的切线长T和曲线长L,
T=Rtga/2=304.06m
L=Raл/180=278.546m
△3 c
△2
△1 cφφ
φ
A
根据平面几何原理,偏角(弦切角)等于所夹弧的圆心角的一半,则偏角△与弦长C的计算公式分别为:
△=φ/2
C=2Rsinφ/2
每隔一定的弧长l测设一点,即把圆弧分成n等份,则l=L/n,那么曲线上各点的偏角为第一点偏角的整数倍,即
△1=a/2n=180*l/2ЛR
△2=2△1
△3=3△1
……
△n=n△1=a/2
加密时,把圆曲线分成20等份,即把半圆分成10等份,则分偏角依次为:
a/4=7007’30”
△1=0042’45” △2=1025’30”
△3=2008’15” △4=2051’00”
△5=3033’45” △6=4016’30”
△7=4059’15” △8=5042’00”
△9=6024’45” △10=7007’30”
C=2Rsin△1=13.927m。
2、实测
1)在起点A上安置经纬仪,瞄准转折点定出切线方向,并使水平度盘读数为0000’00”。
2)顺时针方向转动照准部,使度盘的读数为0042’45”,并沿视线方向测设13.927m的水平距离,定出圆曲线上的第一点。
3)继续转动照准部,使水平度盘的读数为1025’30”,从第一点测设13.927m的水平距离与视线方向相交,定出第二点。
依此类推,直至曲线的中点。
4)将经纬仪搬至终点B点,安置仪器,瞄准转折点定出切线方向,并使水平度盘读数为0000’00”。
5)逆时针方向转动照准部,使度盘的读数为0042’45”,并沿视线方向测设13.927m的水平距离,定出圆曲线上的第一点。
3)继续转动照准部,使水平度盘的读数为1025’30”,从第一点测设13.927m的水平距离与视线方向相交,定出第二点。
依此类推,直至曲线的中点。
3、检核
两次测设的曲线中点的点位应重合,若不重合,其闭合差不应超过如下规定:
半径方向(横向)±5cm
切线方向(纵向)±L/2000m=139.27/2000m≈7cm
两者综合产生的误差为:
M= ±52+72 =±8.6cm
若误差超限,应查明原因,并进行调整或重新测设。
