浙江省杭州外国语学校2013-2014学年下学期高二年级期中考试数学试卷(文科)

合集下载

湖北省武汉外国语学校2013-2014学年高二下学期期中考试数学文试题 Word版含答案

武汉外国语学校2013—2014学年度下学期期中考试高二数学（文科）试题考试时间：2014年4月25日上午10:00-12:00 命题人：赵亮满分：150分一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 已知i 是虚数单位，a ∈R ．若复数2i 2ia a +-的虚部为1，则a ＝（）A ．14B ．1C ．2 D．2±2. 函数f (x )＝x 2－2ln x 的单调递减区间是( )A ．(0,1]B ．[1，＋∞)C ．(－∞，－1]∪(0,1]D ．[－1,0)∪(0,1]3. 已知某生产厂家的年利润y (单位：万元)与年产量x (单位：万件)的函数关系式为y ＝－13x 3＋81x －234，则使该生产厂家获取最大年利润的年产量为 ( )A ．13万件B ．11万件C ．9万件D ．7万件4. 已知x >0，由不等式x ＋1x ≥2x ·1x ＝2，x ＋4x 2＝x 2＋x 2＋4x 2≥33x 2·x 2·4x 2＝3，…，我们可以得出推广结论：x ＋ax n ≥n ＋1(n ∈N *)，则a ＝ ( )A ．2nB ．n2C ．3nD ．n n5. 已知x ，y 之间的数据如表所示，则回归直线过点( ) A ．(0,0)B ．(2,1.8)C ．(3,2.5)D ．(4,3.2)6．观察下列各图形：其中两个变量x 、y 具有相关关系的图是 ( ) A ．①②B ．①④C ．③④D ．②③7. 设)(x f 在),0(+∞上是单调递增函数，当*N n ∈时，*)(N n f ∈，且12)]([+=n n f f ，则（）A ．(4)6f =B ．(4)4f =C ．(4)5f =D ．(4)7f = 8. 函数f (x )的定义域为开区间(a ，b )，导函数'()f x 在(a ，b )内的图象如图所示，则函数f (x ) 在开区间(a ，b )内有极小值点 ( )A ．1个B ．2个C ．3个D ．4个9. 已知函数∈-=a x x a x f (sin )(R)，则下列错误．．的是（）A ．若11a -≤≤，则()f x 在R 上单调递减B ．若()f x 在R 上单调递减，则11a -≤≤C ．若1a =，则()f x 在R 上只有1个零点D ．若()f x 在R 上只有1个零点，则1a =10. 已知a 为常数，函数()(ln )f x x x ax =-有两个极值点x x 12、，且x x <12，则（） A ．(),()f x f x >>-12102B. (),()f x f x <<-12102C. (),()f x f x ><-12102 D. (),()f x f x <>-12102二、填空题：本大题共7小题，每小题5分，共35分.把答案填在题中横线上。

浙江省杭州外国语学校2013-2014学年高一物理上学期期中试题新人教版

浙江省杭州外国语学校2013-2014学年（第一学期）高一期中考试物理试卷※试卷共分四个部分，满分100分，考试时间90分钟；所有答案请写在答题卷上。

全卷g=10m/s 2第Ⅰ卷 (选择题，共46分)一、单项选择题(每小题3分，共30分，每小题只有一个选项符合题意，选对的得3分，选错或不答的得0分。

)1．下面关于质点的说法正确的是（）A ．研究汽车通过道路上的斑马线需多少时间可把汽车看作质点B ．蚂蚁很小，可把蚂蚁看成质点C ．研究篮球运动员的技术动作时篮球不能看成为质点D ．研究“天宫一号”和“神舟八号”实现交会对接时“天宫一号”和“神舟八号”可视为质点2．关于速度和加速度，下列运动情况不可能．．．出现的是（） A ．物体的加速度增大时，速度反而减小 B ．物体的加速度为零时，速度反而不为零C ．物体的加速度增大，相等时间内速度的变化量却在减小D ．加速度的方向保持不变，速度方向却发生变化3．一个物体从A 点运动到B 点，下列结论正确的是（）A ．物体的位移的大小总是小于或等于它的路程B ．物体的位移与路程的方向相同，都从A 指向BC ．物体的位移的大小一定等于路程D ．物体的位移是直线，而路程是曲线4．如图为表示三个物体运动位置和时间的函数关系图象，其异同点是( )A ．运动速率相同，3 s 内经过路程相同，起点位置相同B ．运动速率相同，3 s 内经过路程相同，起点位置不同C ．运动速率不同，3 s 内经过路程不同，起点位置相同D ．无共同点5．一物体自t =0时开始做直线运动，其速度—时间图像如图所示。

下列选项正确的是（） A ．在0～6 s 内，物体离出发点最远为30 m B ．在0～6 s 内，物体经过的路程为30 m C ．在0～4s 内，物体的平均速度为7.5 m/sD ．在4～6 s 内，物体的位移不为零6．一个小石子从离地某一高度处由静止自由落下，某摄影爱好者恰好拍到了它下落的一段轨迹AB 。

【原创精品解析纯word版】化学卷·2015届浙江省杭州外国语学校高二第二学期期中考试(2014.05)

浙江省杭州外国语学校2013-2014学年高二第二学期期中考试化学试题考生须知：1．本卷满分100分，考试时间90分钟。

2．请用黑色钢笔在答题卷上相应处写上班级、姓名、座位号、准考证号。

用2B铅笔涂黑相应的准考证号。

所有答题必须涂(选择题)或写(非选择题)在答题纸上。

3．本卷可能用到的相对原子质量：H－1，He— 4，C－12，O－16，Na－23，S－32 【试卷综析】本试卷是高二化学试卷，考查了实验化学和有机化学的知识。

知识考查注重主干知识，兼顾覆盖面。

以基础知识和基本技能为载体，以能力测试为主导，在注重考查学科核心知识，突出考查考纲要求的基本能力。

试题重点考查：化学实验基础、物质分离的方法，注重基本理论与基础知识的考查。

试题涉及的化学题型有：实验仪器的选择、实验操作、物质分离方法、有机化学基础有机方程式书写等；考查学生解决理论知识问题的能力。

难度中等。

第Ⅰ卷（选择题共50分）一、选择题（共25小题，每小题2分，共50分。

每小题只有一个选项是符合题意的。

不选、多选、错选均不得分。

）1．下列基本实验操作与所需关键仪器对应合理的是A．过滤—泥三角B．蒸发—蒸发皿C．蒸馏—分液漏斗D．萃取—玻璃棒【知识点】实验操作与仪器的选择【答案解析】B 解析：过滤操作用漏斗；蒸馏操作用蒸馏烧瓶；萃取用分液漏斗。

故答案选B【思路点拨】常见的实验操作与实验仪器选择的考查是平时同学们知识积累的体现，属于基础知识。

2．下列实验操作中，不能用于物质分离的是【知识点】物质分离实验操作与仪器的选择【答案解析】C 解析：A是过滤，分离不溶于液体的固体混合物；B是蒸馏操作，分离沸点不同的液体混合物；C是一定浓度溶液的配置，不能用于物质分离；D是萃取、分液操作，分离互不相溶的液体混合物；故答案选C【思路点拨】物质分离操作有过滤、蒸馏、分液、分馏等，注意实验仪器的选择，属于基础知识。

3．由草木灰提取钾盐并检验钾元素存在的下列实验操作中，错误的是A．溶解B．过滤C．蒸发D．焰色反应【知识点】实验方案设计与评价【答案解析】D 解析：由草木灰提取钾盐并检验钾元素存在，实验步骤包括溶解、过滤、蒸发结晶，最后用焰色反应证明钾元素的存在，而焰色反应中观察钾元素要透过蓝色钴玻璃观察；故答案选D【思路点拨】常见的物质检验的方法，注意钾元素鉴别的特殊性。

浙江杭州外国语学校2013-2014学年高二第二学期期中地理试卷(带解析)

浙江杭州外国语学校2013-2014学年高二第二学期期中地理试卷（带解析）芬瑟岛，是世界上最大的沙岛，总面积1630平方千米（如下图所示）。

岛上分布的沙漠在世界最古老沙漠中面积最大，现在仍然保留着3万年前的风貌；同时还分布着世界上唯一生长在沙地上的雨林植被。

读下图完成下列各题。

1．关于芬瑟岛上沙漠成因的叙述，正确的是A.是地质变化和海浪堆积作用而形成的B.是全球变暖，降水减少的结果C.因常年受副热带高气压带控制，降水少而形成的D.受热带雨林迁移农业的影响而形成的2．芬瑟岛分布着世界上唯一生长在沙地的雨林植被，其原因可能有①接近热带雨林分布区,雨林植物种子传播到此②沙地土层深厚，利于雨林植物根系向深处延伸③来自海洋的盛行风带来较充沛的降水④沿岸暖流经过，有增温增湿作用A. ①②③B.①②④C.①③④D.②③④【答案】1．A2．C【解析】试题分析：1．芬瑟岛由数百年前大陆南方的山脉受风雨剥蚀开始形成，风把细岩石屑刮到海洋中，又被洋流带向北面，慢慢沉积在海底，冰河时期海面下降，沉积的岩屑露出海面，被风吹成大沙丘，后来海面回升，洋流带来更多的沙子。

结合题文信息，故本题选A。

2．芬瑟岛分布着世界上唯一生长在沙地的雨林植被，其原因可能有近热带雨林分布区, 植物的种子被风和鸟雀带到岛上，雨林植物种子传播到此，沿岸暖流有增温增湿作用这样种子就开始在湿润的沙丘上生长，故本题选C。

考点：不同区域自然环境、人类活动的差异读下图，完成下列各题：2013年中国正式成为北极理事会永久观察员国。

开展对北极地区的考察对促进中国可持续发展具有重要意义。

下图为北极地区冰雪覆盖范围及变化预测示意图。

读图完成下列各题。

3．影响北极地区冰雪覆盖范围变化的主要原因是A．沿岸暖流加强B．全球气候变暖C．极昼天数较多D．太阳辐射增强4．北极地区冰雪覆盖范围的变化会给中国带来的直接影响是A．森林生态系统得以改善B．极端天气事件明显减少C．通往欧洲的北部航线开通D．人口大量向北极地区迁移【答案】3．B4．C【解析】试题分析：3．读图可以看到，北极地区预测冰雪覆盖范围将变小，这一变化的主要原因是全球气候变暖，B对。

浙江省杭州外国语学校2013-2014学年高二物理上学期期中试题新人教版

浙江省杭州外国语学校2013-2014学年（第一学期）高二期中考试理科物理试卷一、单项选择题：本题共7小题，每小题3分，共计21分．每小题只有一个选项符合题意．1．关于电源的电动势，下面叙述不正确．．．的是 A ．同一电源接入不同电路，电动势不会发生变化B ．电动势等于闭合电路中接在电源两极间的电压表测得的电压C ．电源的电动势反映电源把其他形式的能转化为电能的本领大小D ．在外电路接通时，电源的电动势等于内外电路上的电压之和2．如图所示， A 为空心金属球，B 为靠近A 的另一个原来不带电的枕形金属壳。

将另一个带正电的小球C 从A 球开口处放入A 球中央，但不触及A 球。

则B 出现的情况是 A ．靠近A 的一端带正电，远离A 的另一端带负电 B ．靠近A 的一端带负电，远离A 的另一端带正电 C ．靠近A 的一端带负电，远离A 的另一端不带电 D ．靠近A 的一端带正电，远离A 的另一端不带电3．某电场的电场线的分布如图所示。

一个带电粒子由M 点沿图中虚线所示的途径运动通过N 点。

则下列判断正确的是 A ．粒子带负电B ．粒子在M 点的加速度大C ．粒子在N 点的速度大D ．电场力对粒子做负功4．如图所示，电动势为E 、内阻为r 的电池与定值电阻R 0、滑动变阻器R 串联，已知R 0=r ，滑动变阻器的最大阻值是2r ．当滑动变阻器的滑片P 由a 端向b 端滑动时，下列说法中正确的是 A ．滑动变阻器消耗的功率不变 B ．滑动变阻器消耗的功率变大C ．定值电阻R 0上消耗的功率变小D ．滑动变阻器消耗的功率变小5．在如图所示的电路中，E 为电源电动势，r 为电源内阻，R 1和R 3均为定值电阻，R 2为滑动变阻器。

当R 2的滑动触点在a 端时合上开关S ，此时三个电表A 1、A 2和V 的示数分别为I 1、I 2和U 。

现将R 2的滑动触点向b 端移动，则三个电表示数的变化情况是 A ．I 1增大，I 2不变，U 增大 B ．I 1减小，I 2增大，U 减小 C ．I 1增大，I 2减小，U 增大 D ．I 1减小，I 2不变，U 减小6．如图所示，真空中有一个固定的点电荷，电荷量为+Q ．图中的虚线表示该点电荷形成的电场中的四个等势面．有两个一价离子M 、N （不计重力，也不计它们之间的电场力）先后从a 点以相同的速率v 0射入该电场，Ｍ、Ｎ的运动轨迹分别为曲线apb 和aqc ，其中p 、q 分别是它们离固定点电荷最近的位置．①M 一定是正离子，N 一定是负离子．②M 在p 点的速率一定大于N 在q点的速率．③M 在b 点的速率一定大于N 在c 点的速率．④M 从p →b 过程电势能的增量一定小于N 从a →q 电势能的增量．以上说法中正确的是A.只有①③B.只有②④C.只有①④D.只有②③7．如图所示电路，闭合开关时灯不亮，已经确定是灯泡断路或短路引起的，在不能拆开电路的情况下（开关可闭合，可断开），现用一个多用电表的直流电压挡、直流电流挡和欧姆挡分别进行如下操作及对故障作出相应判断（如表所示），以上操作和判断均正确的是A．只有1、2对B．只有3、4对C．只有1、2、4对D．全对二、多项选择题：本题共4小题，每小题4分，共计16分，每小题有多个选项符合题意，全部选对的得4分，选对但不全的得2分，错选或不答的得0分.8．如图所示是一个由电池、电阻R与平行板电容器组成的串联电路，平行板电容器中央有一个液滴处于平衡状态，当增大电容器两板间距离的过程中A．电容器的电容变大 B．电阻R中有从a流向b的电流C．液滴带负电 D．液滴仍然平衡9．有两只电流表A1、A2是由完全相同的小量程电流表G1、G2改装而成，A1的量程为I1=0.6A，A2的量程为I2=3A两表接入电路后均未烧坏，则A．A1、A2表的内阻之比为R1: R2 =1:5B．将A1、A2串联接入电路后，指角偏角之比为5:1C．将A1、A2串联接入电路后，读数之比为5:1D．将A1、A2并联接入电路后，读数之比为1:510．如图水平面的上方有竖直向上的匀强电场，平面上静止着质量为M的绝缘物块，一质量是m的带正电弹性小球，以水平速度v与物块发生碰撞，并以原速率返回，弹回后仅在电场力和重力的作用下沿着虚线运动，则下列说法正确的是A．弹回后球的机械能守恒B．弹回后轨迹是抛物线C．弹回后机械能与电势能的总和守恒D．弹回后动能增加.11．如图所示，在竖直放置的半径为R的光滑半圆弧绝缘细管的圆心O处固定一点电荷，将质量为m，带电量为+q的小球从圆弧管的水平直径端点A由静止释放，小球沿细管滑到最低点B时，对管壁恰好无压力，已知重力加速度为g，则下列说法正确的是A．小球在BB．小球在BC．固定于圆心处的点电荷在AB弧中点处的电场强度大小为3mg/qD．小球不能到达C点（C点和A在一条水平线上）三．实验题：本题共3小题，共计24分．把答案填在相应的横线上．12．某实验小组要描绘一只规格为“2.5 V0.5 A”小电珠的伏安特性曲线，除了提供导线和开关外，还有以下一些器材：A．电源E(电动势为3.0 V，内阻不计)B．电压表V(量程为0～3.0 V，内阻约为2 kΩ)C．电流表A(量程为0～0.6 A，内阻约为1 Ω)D．滑动变阻器R(最大阻值10 Ω，额定电流1 A)(1) 为完成本实验，请用笔画线当导线，将实物图连成完整的电路，要求实验误差尽可能的小．(图中有几根导线已经接好)(2) 下表中的数据是该小组在实验中测得的，请根据表格中的数据在方格纸上作出电珠的13．（1）如下图所示，某同学用多用电表欧姆档测量一个电阻阻值的示数和档位情况，则这个电阻的阻值约为▲ Ω．为了测量得更精确些，该同学进行了第二次测量，请选择下面列出的有关步骤，并按先后顺序写出▲A．将两表笔短接，电阻调零；B．将两表笔分别跟被测电阻两端接触，观察指针位置，记下电阻值；C．将面板上的旋钮旋至×10档；D．将面板上的旋钮旋至×1k档；（2）如果下图是该同学是用直流5mA挡测量电流，则电流为▲ mA。

浙江省杭州外国语学校2023-2024学年高一下学期期中考试数学试卷

浙江省杭州外国语学校2023-2024学年高一下学期期中考试数学试卷学校:___________姓名：___________班级：___________考号：___________一、单选题1．已知,m n 表示两条不同直线，α表示平面，则（） A ．若//,//m n αα，则//m n B ．若//,m m n α^，则n α⊥ C ．若,m m n α⊥⊥，则//n αD ．若,m n αα⊥⊂，则m n ⊥2．如图，在平行六面体（底面为平行四边形的四棱柱）1111ABCD A B C D -中，E 为BC 延长线上一点，3BC CE =u u u r u u u r，则1D E u u u u r =（）A ．11-3AB AD AA +u u u r u u u r u u u rB ．12-3AB AD AA +u u u r u u u r u u u rC ．113AB AD AA ++u u u r u u u r u u u rD ．11-3AB AD AA +u u u r u u u r u u u r3．如图，已知平面α，β，且l αβ=I .设梯形ABCD 中，//AD BC ，且AB α⊂，CD β⊂.则下列结论正确的是（）A ．直线AB 与CD 可能为异面直线 B ．直线AB ，CD ，l 相交于一点C ．AB CD =D ．直线AC 与BD 可能为异面直线4．如图，一个正四棱锥P ABCD -的五个顶点都在球面上，且底面ABCD 经过球心O .若1283-=P ABCD V ，则球O 的表面积是A ．814πB ．36πC ．64πD ．274π5．如图，在正三棱柱111ABC A B C -中，1AB =，若二面角1C C AB --的大小为60︒，则点C 到平面1C AB 的距离为（）A ．1B ．12C ．34D 6．已知正方体1111ABCD A B C D -中，点E 是线段1BB 上靠近1B 的三等分点，点F 是线段11D C 上靠近1D 的三等分点，则平面AEF 截正方体1111ABCD A B C D -形成的截面图形为（） A ．三角形B ．四边形C ．五边形D ．六边形7．北京大兴国际机场的显著特点之一是各种弯曲空间的运用.刻画空间的弯曲性是几何研究的重要内容.用曲率刻画空间弯曲性，规定：多面体顶点的曲率等于2π与多面体在该点的面角之和的差（多面体的面的内角叫做多面体的面角，角度用弧度制），多面体面上非顶点的曲率均为零，多面体的总曲率等于该多面体各顶点的曲率之和，例如：正四面体在每个顶点有3个面角，每个面角是π3，所以正四面体在各顶点的曲率为π2π3π3-⨯=，故其总曲率为4π，则四棱锥的总曲率为（）A ．2πB ．4πC ．5πD ．6π8．已知正方体1111ABCD A B C D -边长为1，点,E O 分别在线段11B D 和BD 上，1114,5EB B D DO BO ==，动点F 在线段1AA 上，且满足1102AF AA λλ⎛⎫=<< ⎪⎝⎭，分别记二面角11,F OB E F OE B ----，1F EB O --的平面角为,,αβγ，则总有（）A ．αβγ>>B ．γβα>>C ．γαβ>>D ．βαγ>>二、多选题9．如图，A B C '''V 为水平放置的ABC V 的直观图，其中2,A B AC B C ''''''===面图形ABC 中有（）A ．AC BC <B ．2AB =C ．AC =D ．ABC S =△10．如图，以等腰直角三角形ABC 的斜边BC 上的高AD 为折痕，翻折ABD △和ACD V ，使得平面ABD ⊥平面ACD .下列结论正确的是（）A ．BD AC ⊥B ．ABC V 是等边三角形 C ．三棱锥D ABC -是正三棱锥D ．平面ACD ⊥平面ABC11．中国古代数学的瑰宝《九章算术》中记载了一种称为“曲池”的几何体，该几何体是上、下底面均为扇环形的柱体（扇环是指圆环被扇形截得的部分）．现有一个如图所示的曲池，1AA 垂直于底面，15AA =，底面扇环所对的圆心角为π2，弧AD 的长度是弧BC 长度的3倍，2CD =，则下列说法正确的是（）A ．弧AD 长度为3π2B ．曲池的体积为10π3C ．曲池的表面积为2014π+D ．三棱锥1A CC D -的体积为512．如图，在直四棱柱1111ABCD A B C D -中，底面ABCD 为菱形，160,2,BAD AB AA P ∠===o 为1CC 的中点，点Q 满足][()10,1,0,1DQ DC DD λμλμ⎡⎤=+∈∈⎣⎦u u u r u u u r u u u u r，则下列结论正确的是（）A ．若13λμ+=，则四面体1A BPQ 的体积为定值 B ．若1A BQ △的外心为O ，则11A B AO ⋅u u u r u u u r为定值2C ．若1AQ =QD ．若1λ=且12μ=，则存在点1E A B ∈，使得AE EQ +三、填空题13．()()1,0,2,1,3,1A B -，点M 在z 轴上且到,A B 两点的距离相等，则M 点的坐标为 .14．如图，在四面体A BCD -中，2,AC BD AC ==与BD 所成的角为45o ，,M N 分别为,AB CD 的中点，则线段MN 的长为 .15．已知()()21,5(0,R)f x ax g x x bx a b =-=+->∈（1）若2a =时，()()f x g x =的两根为12,x x ，则12x x -的最小值为 . （2）若0x >时，()()0f x g x ⋅≥恒成立，则3b a+的最小值为 .16．下列命题正确的是 .（填序号）①若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行； ②垂直于同一条直线的两直线平行；③两个平面互相垂直，过一个平面内任意一点作交线的垂线，必垂直与另一个平面； ④过两个点与已知平面的垂直的平面可能不存在；⑤过两条异面直线外任一点有且只有一条直线与这两条异面直线都垂直； ⑥到一个四面体的四个顶点的距离都相等的平面有7个.四、解答题17．已知空间向量(1,2,1),(2,1,1)a b =-=-r r．(1)计算32a b +r r 和53a b -r r ;(2)求a r 与b r夹角θ的余弦值．18．正方体1111ABCD A B C D -中，M ，N 分别是1BC ，1CD 的中点.(1)求异面直线1CD 与1BC 所成角； (2)求证：//MN 平面ABCD19．已知四棱柱1111ABCD A B C D -如图所示，底面ABCD 为平行四边形，其中点D 在平面1111D C B A 内的投影为点1A ，且1AB AA ==2,120AD ABC ︒∠=．(1)求证：平面1A BD ⊥平面11ADD A ；(2)已知点E 在线段1C D 上（不含端点位置），且平面1A BE 与平面11BCC B的夹角的余弦值为1DE EC 的值．20．已知函数(),(),()f x g x h x 的定义域均为R ，给出下面两个定义：①若存在唯一的x ∈R ，使得(())(())f g x h f x =，则称()g x 与()h x 关于()f x 唯一交换； ②若对任意的x ∈R ，均有(())(())f g x h f x =，则称()g x 与()h x 关于()f x 任意交换． (1)请判断函数()1g x x =+与()1h x x =-关于2()f x x =是唯一交换还是任意交换，并说明理由；(2)设()22()2(0),()1f x a x a g x x bx =+≠=+-，若存在函数()h x ，使得()g x 与()h x 关于()f x 任意交换，求b 的值；(3)在（2）的条件下，若()g x 与()f x 关于e 1()e 1x x w x -=+唯一交换，求a 的值．。

2013-2014学年高一数学上学期期中试题及答案(新人教A版第148套)

浙江省杭州外国语学校2013-2014学年（第一学期）高一期中考试数学试卷一、选择题（本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的，把答案填在答卷．．相应空格中） 1．已知集合|0,1x M x x R x ⎧⎫=≥∈⎨⎬-⎩⎭，{}2|31,N y y x x R ==+∈，则M N ⋂等于( )A ．φB ．{}|1x x ≥C ．{}|1x x >D ．{}|10x x x ≥<或 2．给出下列命题：①第二象限角大于第一象限角；②三角形的内角是第一象限角或第二象限角；③不论用角度制还是用弧度制度量一个角，它们与扇形所在圆的半径的大小无关； ④若sin sin αβ=，则α与β的终边相同； ⑤若cos 0θ<，则θ是第二或第三象限的角．其中正确．．命题的个数是( )A ．1B ．2C ．3D ．43．若()f x =，则()f x 的定义域为 ( )A ．1,02⎛⎫-⎪⎝⎭ B ．1,02⎛⎤- ⎥⎝⎦ C ．1,2⎛⎫-+∞ ⎪⎝⎭D ．()0,+∞ 4．下列函数()y f x =中满足“对任意12,(0,)x x ∈+∞，当12x x <时，都有()12()f x f x <”的是 ( ) A ．1()f x x= B ．()2()1f x x =- C ．2()f x e = D ．()ln(1)f x x =+ 5．454sincos tan 363πππ⎛⎫⋅⋅- ⎪⎝⎭的值是( )A．4-B．4 C．4- D．46．定义在R 上的函数()y f x =是奇函数，且满足(1)(1)f x f x +=-．当[]1,1x ∈-时，3()f x x =，则(2013)f 的值是 ( )A ．1B ．2C ．0D ．1-7．若cos2sinαα+=tanα等于 ( ) A．12B．2 C．12-D．2-8．函数x xx xe eye e--+=-的图象大致为 ( ) 9．已知()y f x=为R上的减函数，则满足1(1)f fx⎛⎫<⎪⎝⎭的实数x的取值范围是 ( ) A．()1,1- B．()0,1 C．()()1,00,1-⋃ D．()(),11,-∞-⋃+∞10．已知函数lg,010()13,105x xf xx x⎧<≤⎪=⎨-+>⎪⎩，若,,a b c互不相等，且()()()f a f b f c==，则abc 的取值范围是 ( ) A．()1,10B．()5,10 C．()10,15D．()15,30二、填空题（本大题共7小题，每小题4分，共28分，把答案填在答卷中相应横线上）11．化简1603[(2)](1)---的值为____▲____.12．函数()f x=的单调增区间为____▲____.13．函数()2()log31xf x=+的值域为____▲____.14．已知cos63πα⎛⎫+=⎪⎝⎭，则5cos6πα⎛⎫-⎪⎝⎭的值为____ ▲____.15．已知函数()ln2f x x x=-+有一个零点所在的区间为(),1k k+ (*k N∈)，则k的值为____▲____.16．已知函数())f x x=，若实数,a b满足(1)()0f a f b-+=，则a b+等于▲ .17．已知不等式2log 0a x x -<，当10,2x ⎛⎫∈ ⎪⎝⎭时恒成立，则实数a 的取值范围是▲ .三、解答题（本大题共4小题，共42分，解答应写出文字说明，证明过程或演算步骤）18．(本小题满分10分）已知集合2{310}M x x x =-≤，{121}N x a x a =+≤≤+．(Ⅰ)若2a =，求M (R N ð)；(Ⅱ)若MN M =，求实数a 的取值范围．19．（本小题满分10分）已知()()sin cos 2ππαπααπ⎛⎫--+=<< ⎪⎝⎭，求下列各式的值： (Ⅰ)sin cos αα-； (Ⅱ) 33sin cos 22ππαα⎛⎫⎛⎫--+⎪ ⎪⎝⎭⎝⎭．20．(本小题满分10分）设a 为实数，函数()2()2f x x x a x a =+--.(Ⅰ)若(0)4f ≥，求a 的取值范围； (Ⅱ)求函数()f x 的最小值.21．(本小题满分12分）已知定义在D 上的函数()f x ，如果满足：对任意D x ∈，存在常数0M >，使得|()|f x M ≤成立，则称()f x 是D 上的有界函数，其中M 称为函数()f x 的上界.下面我们来考虑两个函数：()421xxf x p --=+⋅+， 12()12xxq g x q -⋅=+⋅.（Ⅰ）当1p =时，求函数()f x 在(),0-∞上的值域，并判断函数()f x 在(),0-∞上是否为有界函数，请说明理由；（Ⅱ）若1,22q ⎛∈⎝⎦，函数()g x 在[]0,1上的上界是()H q ，求()H q 的取值范围；（Ⅲ）若函数()f x 在[)0,+∞上是以3为上界的有界函数，求实数p 的取值范围．杭州外国语学校2013-1高一年级期中考试数学答题卷一、选择题：(本大题有10小题，每小题3分，共30分)二、填空题：(本大题有7小题，每小题4分，共28分)11. 3 12.[)2,+∞ 13. ()0,+∞14.1,116⎡⎫⎪⎢⎣⎭三、解答题：(本大题有4小题，共42分，请写出必要的解答过程) 18. (1) 因为a ＝2，所以N ＝{x |3≤x ≤5}，∁R N ＝{x |x ＜3或x ＞5}．又M ＝{x |－2≤x ≤5}，所以M ∩ (∁R N )＝{x |x ＜3或x ＞5}∩{x |－2≤x ≤5}＝{x |－2≤x ＜3}．(2)若M ≠φ，由M N M =，得N ⊆M ，所以⎩⎪⎨⎪⎧a ＋1≥－22a ＋1≤52a ＋1≥a ＋1.解得0≤a ≤2；当N ＝φ，即2a ＋1＜a ＋1时，a ＜0，此时有N ⊆M ，所以a ＜0为所求．综上，实数a 的取值范围是(－∞，2]．____________________________________________________________________________________19.（1）sin cos 3αα+=，所以平方可得：212sin cos 9αα+=，即：7sin cos 18αα=-所以4sin cos 3αα-===（2）原式=3322cossin (sin cos )(sin sin cos cos )αααααααα+=+-+7(1)18=+=_______________________ 姓名_____________ 试场号______________ 考号_______________…………密○………………………………………封○………………………………………○线………………………○20. （1）(0)4f ≥，即：4a a -≥，所以0a <，得到：24a ≤，所以2a ≤-（2）()()22222,()2,x x a x a f x x x a x a⎧+-≥⎪=⎨--<⎪⎩令222212()323,33g x x ax a x a a x a ⎛⎫=-+=-+≥ ⎪⎝⎭；()2222()22,h x x ax a x a a x a =+-=+-<当0a ≥时，2min ()2g g a a ==，2min ()2h h a a =-=-，所以2min 2f a =- 当0a <时，2min 1233g g a a ⎛⎫==⎪⎝⎭，2min ()2h h a a ==，所以2min 23f a =综上：2min22,02,03a a f a a ⎧-≥⎪=⎨<⎪⎩ ____________________________________________________________________________________21. （1）当p=1时，()421xx f x --=++因为)(x f 在(),0-∞上递减，所以()(0)3f x f >=，即)(x f 在(),1-∞的值域为()3,+∞故不存在常数0M >，使|()|f x M ≤成立, 所以函数()f x 在(),1-∞上不是有界函数（2）2()112xg x q =-+⋅，∵ q>0 ，[]1,0∈x ∴ ()g x 在[]0,1上递减，∴)0()()1(g x g g ≤≤ 即121()121q qg x q q--≤≤++∵1(2q ∈，∴112112q q q q --≥-++，∴1()1q g x q -≤+， ∴1()1q H q q-≥+ ，即 1[,)1qq -+∞+ （3）由题意知，3)(≤x f 在[)1,+∞上恒成立.3)(3≤≤-x f ， ∴1142()22()22x x x x p -⋅-≤≤⋅- 在[)0,+∞上恒成立∴ max min 11[42()][22()]22xx x x p -⋅-≤≤⋅-设t x=2，t t t h 14)(--=，tt t p 12)(-=，由x ∈[)0,+∞得 t ≥1，设121t t ≤<，()()2112121241()()0t t t t h t h t t t ---=>, 所以)(t h 在[)1,+∞上递减，)(t h 在[)1,+∞上的最大值为(1)5h =-，又()()012)()(21212121<+-=-t t t t t t t p t p ，所以)(t p 在[)1,+∞上递增， )(t p 在[)1,+∞上的最小值为(1)1p =所以实数p 的取值范围为[]5,1-。

浙江省温州市第二外国语学校2013-2014学年高二上学期期中考试数学(文)试题

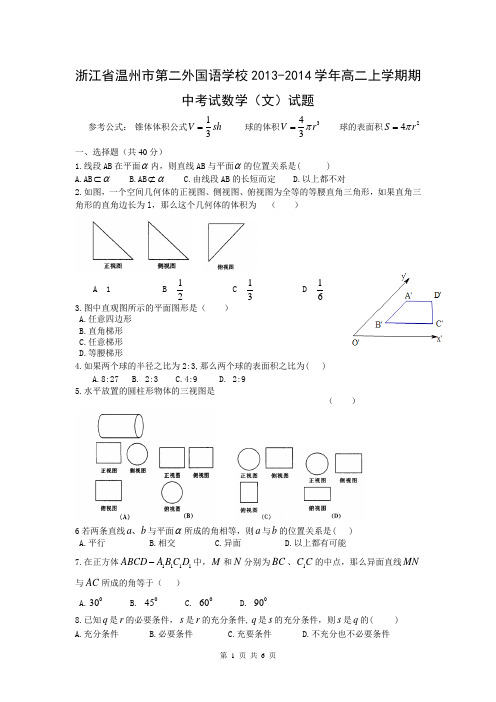
浙江省温州市第二外国语学校2013-2014学年高二上学期期中考试数学（文）试题参考公式：锥体体积公式13V sh = 球的体积343V r π= 球的表面积24S r π= 一、选择题（共40分）1.线段AB 在平面α内，则直线AB 与平面α的位置关系是( ) A.AB α⊂ B.AB α⊄ C.由线段AB 的长短而定 D.以上都不对2.如图，一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形，如果直角三角形的直角边长为l ，那么这个几何体的体积为（）A 1B21C31 D61 3.图中直观图所示的平面图形是（） A.任意四边形 B.直角梯形 C.任意梯形 D.等腰梯形4.如果两个球的半径之比为2:3,那么两个球的表面积之比为( )A.8:27B. 2:3C.4:9D. 2:9 5.水平放置的圆柱形物体的三视图是（）6若两条直线a b 、与平面α所成的角相等，则a 与b 的位置关系是( ) A.平行 B.相交 C.异面 D.以上都有可能7.在正方体1111ABCD A B C D -中，M 和N 分别为BC 、1C C 的中点，那么异面直线MN 与AC 所成的角等于（）A.030B. 045C. 060D. 0908.已知q 是r 的必要条件，s 是r 的充分条件,q 是s 的充分条件，则s 是q 的( ) A.充分条件 B.必要条件 C.充要条件 D.不充分也不必要条件9.空间四边形ABCD 的两条对角线,AC BD 的长分别为4，5，则平行于两条对角线的截面四边形EFGH 在平移过程中，其周长的取值范围是( ) A.(5,10) B.(8,10) C.(3,6) D(6,9)10.在底面是菱形的四棱锥P ABCD -中，点E 在PD 上，且PE ：ED =2：1,在棱PC 上是存在一点F ,使BF ∥平面AEC ,则PF ：FC 的值为( ) A.1：1 B.2：1 C. 3：1 D. 3：2 二、填空题（共20分）11．若命题“p 且q ”为假，且“非p ”为假，则命题q 的真假为_______． 12.有下列四个命题：①“若0=+y x ，则y x ,互为相反数”的逆命题； ②“全等三角形的面积相等”的否命题；③“若1≤q ，则022=++q x x 有实根”的逆命题；④“等边三角形的三个内角相等”的逆否命题；其中真命题的序号是． 13．正方体1111ABCD A B C D -中，则1C A 与平面ABCD 所成角的正弦值为； 14．正方体1111ABCD A B C D -中，二面角1C AB C --的大小为________．15.角“αβ= ”是“tan tan αβ=”成立的条件. 三解答题16.（8分）某几何体的三视图如图所示，求该几何体的体积. 17.（8分）设有两个命题：（1）关于x 的不等式0422>++ax x 对一切R x ∈恒成立；（2）函数()(52)xf x a =-是增函数，若命题有且只有一个是真命题，求实数a 的取值范围。

浙江省杭州外国语学校2013-2014学年下学期高二年级期中考试生物试卷(文科)

浙江省杭州外国语学校2013-2014学年下学期高二年级期中考试生物试卷（文科）注意事项：1、考试时间90分钟，本试卷满分100分。

2、第Ⅰ卷答案请用2B铅笔填涂在答题卡上，第Ⅱ卷请用蓝、黑色钢笔或圆珠笔答题。

在答题卡、答题卷相应处写上考场号、考试序号、班级、姓名。

所有答案均做在答题卡、答题卷的相应位置上，做在试题卷上无效。

第Ⅰ卷（选择题共70分）一、选择题（共50小题，1-30小题每题1分，31-50小题每题2分，共70分。

每小题中只有一个选项是符合题意的。

不选、多选、错选均不得分）1．在临床上已证实，将受SARS病毒感染后治愈患者（甲）的血清，注射到另一SARS患者（乙）体内能够提高治疗效果。

甲血清中具有治疗作用的物质是A．疫苗 B．外毒素 C．抗原 D．抗体2．鸟类体内B淋巴细胞和T淋巴细胞的发育场所依次为A．骨髓胸腺 B．胸腺骨髓 C．腔上囊胸腺 D．胸腺腔上囊3．某生物兴趣小组利用同位素标记法，重复了赫尔希和蔡斯的噬菌体侵染细菌实验的部分实验，预测实验结果是：沉淀物中放射性强。

可是检测实验结果时，却得到了相反的结果，上清液中放射性强。

你认为最可能的原因是A．实验时间过长，细菌解体，子代噬菌体被释放出B．实验时间过短，大量的子代噬菌体没有被释放出C．搅拌力度过大，大量的亲代蛋白质外壳与细菌分离D．搅拌力度过小，大量的亲代蛋白质外壳没有和细菌分离4．切除腺垂体的幼年大白鼠不会出现A．智力下降 B．甲状腺重量下降C．血中促甲状腺激素含量下降 D．血中促甲状腺激素释放激素含量下降5．下列有关植物激素调节的叙述，正确的是A．在植物组织培养中生长素和细胞分裂素可促进愈伤组织的再分化B．无籽番茄的生产过程是：去雄，然后在雌蕊上涂抹一定浓度的脱落酸C．植物激素是由专门器官产生的D．红柿摘下未熟，每篮用木瓜三枚放入，得气即发，并无涩味”这种气体指的是CO26．一个转运RNA的一端3个碱基是CGA，此转运RNA运载的氨基酸是A．酪氨酸（UAC） B．谷氨酸（GAG） C．精氨酸（CGA） D．丙氨酸（GCU）7．下列与多倍体形成原理有关的是A．花药离体培养过程B．纺锤体的形成受到抑制C．个别染色体增加D．非同染色体自由组合8．直接参与人体与外部环境之间的物质交往过程的四大系统为A．呼吸系统消化系统循环系统排泄系统B．神经系统循环系统消化系统内分泌系统C．免疫系统呼吸系统神经系统排泄系统D．排泄系统消化系统免疫系统内分泌系统9．区别细胞是有丝分裂后期还是减数第二次分裂后期的主要依据是A．染色体是奇数还是偶数 B．是否有染色单体C．是否含有同染色体 D．染色体是否联会配对10．让Aa的植株自花授粉，在所结的30粒种子中，表现为A性状的有13粒，表现为a性状的有17粒。

浙江省杭州2023-2024学年高二上学期期中数学试题含解析

杭州2023学年第一学期高二年级期中数学试卷（答案在最后）第Ⅰ卷（选择题）一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.“2m =”是“直线1l：()310m x my -++=与直线2l ：()120mx m y +--=互相垂直”的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】A 【解析】【分析】根据两直线垂直求出参数的值，再根据充分条件、必要条件的定义判断即可.【详解】若直线1l ：()310m x my -++=与直线2l ：()120mx m y +--=互相垂直，则()()310m m m m -+-=，解得0m =或2m =，所以由“2m =”推得出“直线1l ：()310m x my -++=与直线2l ：()120mx m y +--=互相垂直”，即充分性成立；由“直线1l ：()310m x my -++=与直线2l ：()120mx m y +--=互相垂直”推不出“2m =”，即必要性不成立，所以“2m =”是“直线1l ：()310m x my -++=与直线2l ：()120mx m y +--=互相垂直”的充分不必要条件.故选：A2.已知事件,A B 相互独立，()0.5P A =，()0.4P B =，则()P A B +=（）A.0.88 B.0.9C.0.7D.0.72【答案】C 【解析】【分析】根据事件,A B 相互独立得到()()()0.2P AB P A P B ==，结合()()()()P A B P A P B P AB +=+-求出答案.【详解】因为事件,A B 相互独立，故()()()0.50.40.2P AB P A P B ==⨯=，又()0.5P A =，()0.4P B =，所以()()()()0.50.40.20.7P A B P A P B P AB +=+-=+-=.故选：C 3.过点)，且与椭圆2212516y x +=有相同焦点的椭圆的标准方程为（）A.221189x y += B.221189y x += C.221123x y += D.221123y x +=【答案】D 【解析】【分析】设所求椭圆方程为22221y xa b +=()0a b >>，依题意可得22229421a b a b⎧-=⎪⎨+=⎪⎩，解得2a 、2b ，即可求出椭圆方程.【详解】椭圆2212516y x +=的焦点为()0,3或()0,3-，设所求椭圆方程为22221y x a b+=()0a b >>，则22229421a b a b⎧-=⎪⎨+=⎪⎩，解得22123a b ⎧=⎨=⎩，所以椭圆方程为221123y x +=.故选：D4.已知()()()()0,0,2,1,0,1,1,1,0,0,0,0A B C O -，则点O 到平面ABC 的距离是（）A.11B.11C.5D.5【答案】B 【解析】【分析】利用空间向量计算点面距离即可.【详解】由题意可知()()()1,0,3,1,1,2,0,0,2AB AC AO =-=-=-，设面ABC 的一个法向量为(),,n x y z = ，则030200n AB x z x y z n AC ⎧⋅=-=⎧⎪⇒⎨⎨+-=⋅=⎩⎪⎩ ，取13,1z x y =⇒==-，即()3,1,1n =-，所以点O 到平面ABC 的距离是11AO n d n ⋅=== .故选：B5.点(),P x y 在圆222x y +=上运动，则3x y -+的取值范围（）A.[]0,1 B.[]0,4 C.[]1,5 D.[]1,4【答案】C 【解析】(),P x y 到直线30x y -+=的距离d ，求出圆心()0,0O 到直线30x y -+=的距离1d ，从而求出d 的取值范围，即可求出3x y -+的取值范围.【详解】圆222x y +=的圆心为()0,0O ，半径r =因为点(),P x y 在圆222xy +=上运动，又3x y-+=(),P x y 到直线30x y -+=的距离d ，所以3x y -+=，又圆心()0,0O 到直线30x y-+=的距离1322d ==，所以11d rd d r -≤≤+，即22d ≤≤，所以[]31,5x y -+=∈.故选：C6.如图，在边长为3的正方体1111ABCD A B C D -中，3BC EC =，点P 在底面正方形ABCD 上移动（包含边界），且满足11B P D E ⊥，则线段1B P 的长度的最大值为（）A.B.C. D.【答案】B 【解析】【分析】建立合适的空间直角坐标系，求出点P 的轨迹结合函数求最值即可.【详解】依据题意可以建立如图所示的空间直角坐标系，则()()()110,0,3,1,3,0,3,3,3D E B ，设()[](),,0,0,3P x y x y ∈，所以()()113,3,3,1,3,3B P x y D E =---=-，即1133033B P D E x y x y ⋅=+-=⇒=-，所以[]03330,1y y ≤-≤⇒∈，而1B P =，由二次函数的单调性可知22391061810181010t y y y ⎛⎫=-+=-+- ⎪⎝⎭，当1y =时，max 22t =，则1max B P =.故选：B7.已知A ，B 是圆()()()22:330C x m y m -+-=>上两点，且AB =.若存在R a ∈，使得直线1:410l ax y a -++=与2:50l x ay a +-=的交点P 恰为AB 的中点，则实数m 的取值范围为（）A.(0,1⎤-⎦B.(0,2⎤⎦C.(0,1⎤+⎦D.(3⎤+⎦【答案】A 【解析】【分析】根据直线与圆相交的弦长可得AB 中点M 的轨迹为()()2231x m y -+-=，又根据直线1l ，2l 的方程可知12l l ⊥，交点P 的轨迹方程为()()22238x y ++-=，若P 恰为AB 的中点，即圆M 与圆P 有公共点，根据圆与圆的位置关系可得实数m 的取值范围.【详解】圆()()()22:330C x m y m -+-=>，半径为r =，设AB 中点为M ，且直线AB 与圆的相交弦长为AB =即1MC =，所以点M 的轨迹方程为()()()22310x m y m -+-=>，又直线1:410l ax y a -++=过定点()4,1Q -，直线2:50l x ay a +-=过定点()0,5S ，且12l l ⊥，则点P 是两垂线的交点，所以P 在以QS 为直径的圆上，则圆心()2,3-，半径12QS =，所以点P 的轨迹方程为()()22238x y ++-=，由于直线1l 的斜率存在，所以点P 的轨迹要除去点()4,5-，若点P 恰为AB 中点可知圆P 与圆M 有公共点，即11-≤，0m >，即121m -≤+≤+，解得31m -≤≤-，即01m <≤，故选：A.8.已知动点,P Q 分别在正四面体ABCD 的内切球与外接球的球面上，且PQ x AB y AC z AD =++，则2x y z ++的最大值为（）A.1+6B.263C.12+D.83【答案】B 【解析】【分析】计算出正四面体ABCD 的内切球与外接球的半径，求出()2,x y z AT AT ++⋅范围，即可得出2x y z ++的最大值.【详解】由题意，连接,AD EF ，设交点为M ，则点M 是AD 中点设正方体边长为2，由几何知识得，点A 到面BCM 距离即为AM ，设内切球半径为1r ，外接球半径为2r ，三棱锥外接球半径222222232r ++==，而由正三棱锥内切球半径公式，13323r ==，取任意一点P ，使得()22x y z AT xAB y AC z AD xAB y AC z AM ++⋅=++=++，则点T 在面BCM 上，∴()123432333x y z AT PQ r r ++⋅=≤+=+=，点A 到面BCM 距离为=d AM ，则22AT d AM ≥=== ∴()43263232x y z AT x y z AT++⋅++=≤,故选：B.二、多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.9.某学校随机抽取100名学生数学周测成绩的频率分布直方图如图所示,据此估计该校本次数学周测的总体情况(同一组中的数据用该组区间的中点值为代表),下列说法正确的是（）A.众数为60或70B.45%分位数为70C.平均数为73D.中位数为75【答案】BC 【解析】【分析】利用众数的概念直接可判断A ，再根据平均数，中位数及百分位数公式可判断BCD.【详解】A 选项：由频率分布直方图可知众数为6070652+=，A 选项错误；B 选项：由频率分布直方图可得0.005100.04100.45⨯+⨯=，所以45%分位数为70，B 选项正确；C 选项：由频率分布直方图可知平均数为550.00510650.0410750.0310850.0210950.0051073⨯⨯+⨯⨯+⨯⨯+⨯⨯+⨯⨯=，C 选项正确；D 选项：由频率分布直方图可得0.005100.04100.450.5⨯+⨯=<，0.005100.04100.03100.750.5⨯+⨯+⨯=>，所以中位数[)70,80a ∈，所以()0.005100.0410700.030.5a ⨯+⨯+-⨯=，解得71.67a ≈，D 选项错误；故选：BC.10.已知点()0,1P 和直线:210l x y ++=,下列说法不正确的是（）A.经过点P 的直线都可以用方程1y kx =+表示B.直线l 在y 轴上的截距等于1C.点P 关于直线l 的对称点坐标为81,55⎛⎫- ⎪⎝⎭D.直线l 关于点P 对称的直线方程为230x y ++=【答案】ABD 【解析】【分析】当过点P 的直线斜率不存在时，方程为0x =，可判断A 选项，令0x =可判断B 选项，设点P 关于直线l 的对称点为()11,x y ，根据对称的概念列方程，可判断C 选项，设l 上一点()00,x y ，其对称点为(),x y ，根据对称及点()00,x y 在直线l 上，可得直线方程，即可判断D 选项.【详解】A 选项：当过点P 的直线斜率不存在时，方程为0x =，A 选项错误；B 选项：令0x =，得10y +=，即1y =-，所以截距为1-，B 选项错误；C 选项：设点P 关于直线l 的对称点为()11,x y ，所以()111101*********x y y x ++⎧⨯++=⎪⎪⎨-⎪⨯-=--⎪⎩，解得118515x y ⎧=-⎪⎪⎨⎪=⎪⎩，所以点P 关于直线l 的对称点坐标为81,55⎛⎫- ⎪⎝⎭，C 选项正确；设l 上一点()00,x y ，其对称点为(),x y ，则000212x xy y +⎧=⎪⎪⎨+⎪=⎪⎩，即002x x y y =-⎧⎨=-⎩，又点()00,x y 在直线l 上，则()()2210x y ⨯-+-+=，即230x y +-=，D 选项错误；故选：ABD.11.如图,棱长为2的正方体1111ABCD A B C D -中,E 、F 分别为棱111,A D AA 的中点,G 为面对角线1B C 上一个动点,则（）A.三棱锥1A EFG -的体积为定值B.点E 到直线1B CC.线段1B C 上存在点G ,使得FG BD⊥D.线段1B C 上不存在点G ,使平面//EFG 平面1BDC 【答案】ACD【解析】【分析】利用等体积法可判定A ，建立合适的空间直角坐标系利用空间向量计算点线距离，线线与面面位置关系可判定B 、C 、D .【详解】由正方体的结构特征可知1//B C 平面AEF ，故点G 到平面AEF 距离2h AB ==不变，所以11113G A EF A EFG A EF V V S h --==⨯⨯ ，又1122222A EF S =⨯⨯ 是定值，故A正确；如图所示，建立空间直角坐标系，则()()()()111,0,2,0,2,0,2,2,2,0,2,2E C B C ，()()2,0,1,2,2,0F B 所以()()11,2,2,2,0,2EC B C =--=--，故点E 到直线1B C的距离2d ==，故B 错误；设()1101B G B C λλ=<< ，则()()()110,2,12,0,22,2,12FG FB B C λλλλλ=+=+--=--，()2,2,0DB = ，所以4401DB FG λλ⋅=-+=⇒=，即G C 、重合，故C 正确；易知()10,2,2DC = ，设平面1BDC 的一个法向量为(),,n x y z =，则102202200n DB x y y z n DC ⎧⋅=+=⎧⎪⇒⎨⎨+=⋅=⎩⎪⎩ ，取11y x z =-⇒==，即()1,1,1n =- 而()1,0,1EF =- ，则10,2212004n EF n FG λλλ⋅=⋅=--+-=⇒=-<，故不存在G 使得n FG ⊥，故D 正确.故选：ACD12.已知12(,0),(,0)F c F c -分别为椭圆2222:1(0)x y E a b a b+=>>的左、右焦点，下列说法正确的是（）A.若点P 为椭圆上一点,则21||||PF PF -的最大值是2cB.若点T 的坐标为1(,0)2a ,P 是椭圆上一动点,则线段PT 长度的最小值为12aC.过F 2作垂直于x 轴的直线,交椭圆于A ,B 两点,则22c AF a a=-D.若椭圆上恰有6个不同的点P ,使得12PF F △为等腰三角形,则椭圆E 的离心率的取值范围是111,,1322⎛⎫⎛⎫⋃ ⎪ ⎪⎝⎭⎝⎭【答案】ACD 【解析】【分析】A ，结合三角形不等式即可；B ，设出(),P m n ，[],m a a ∈-，则22221m na b+=，表达出22342222221244c a a PT m a b a c c ⎛⎫=-++- ⎪⎝⎭，分3202a a c <<与322a a c≥两种情况，得到不同情况下的线段PT 长度的最小值，B 错误；；C ，x c =代入即可求；D ，选项，先得到上下顶点能够使得12PF F △为等腰三角形，再数形结合得到1F 为圆心，12F F 为半径作圆，只能交椭圆与不同于上下顶点的12,P P 两点，列出不等式组22a c ca c -<⎧⎨≠⎩，求出答案；【详解】对A ，1122||||||PF PF F F -≤，当P 在左顶点时等号成立，则最大值是2c ，A 正确；对B ，设(),P m n ，[],m a a ∈-，则22221m na b+=，22222222222222111244b m c PT m a n m am a b m am a b a a ⎛⎫=-+=-++-=-++ ⎪⎝⎭，2234222221244c a a m a b a c c⎛⎫=-++- ⎪⎝⎭，若b c <，此时222a c <，3202a a c <<，此时当322a m c =时，2PT 取得最小值，最小值为4222144a a b c+-，线段PT ；若b c ≥，此时222a c ≥，322a a c≥，此时当m a =时，2PT 取得最小值，最小值为214a ，线段PT 长度的最小值为12a ，综上：B 错误；对C ，当x c =时，22221c ya b+=，解得2b y a =±，即22222||b a c c AF a a a a-===-，C 正确；对D ，如图，椭圆左右顶点为,A B ，上下顶点为,C D ，显然上下顶点能够使得12PF F △为等腰三角形，要想椭圆上恰有6个不同的点P ，使得12PF F △为等腰三角形，以1F 为圆心，12F F 为半径作圆，只能交椭圆与不同于上下顶点的12,P P 两点，则要满足11F A FQ <，且111FC F P ≠，即22a c c a c-<⎧⎨≠⎩，解得：13c a >，且12c a ≠，故椭圆E 的离心率的取值范围是111,,1322⎛⎫⎛⎫⋃ ⎪ ⎪⎝⎭⎝⎭，D 正确；故选：ACD第Ⅱ卷（非选择题）三、填空题：本题共4小题，每小题5分，共20分.13.在两坐标轴上的截距相等，且与圆22(3)(4)2x y -+-=相切的直线有________条.【答案】4【解析】【分析】分横纵截距为零和横纵截距不为零两种情况讨论即可.【详解】圆()()22342x y -+-=的圆心坐标为()3,4，当横纵截距为零时，直线方程为()0y kx k =≠，=，整理得2724140k k -+=，因为22447141840∆=-⨯⨯=>，所以方程2724140k k -+=有两个解，故当横纵截距为零时存在两条直线与圆相切；当横纵截距不为零时，设直线方程为()0x y a a +=≠，=5a =或9，所以横纵截距不为零时存在两条直线与圆相切，综上可得，存在4条截距相等的直线与圆相切.故答案为：4.14.已知矩形ABCD，1,AB BC ==，沿对角线AC 将ABC 折起，若BD =则二面角B AC D --的余弦值为________．【答案】13【解析】【分析】利用空间向量的数量积与模长计算夹角即可.【详解】如图所示，过B D 、分别作,BE AC DF AC ⊥⊥，垂足分别为E F 、，由矩形ABCD 中，1,AB BC ==，可知12,=60,,122AC BAC BE DF AE CF EF =∠⇒===== ，设二面角B AC D --的平面角为α，则,EB FD α=，2222222BD BE EF FD BD BE EF FD BE EF EF FD BE FD=++⇒=+++⋅+⋅+⋅ ()33312=++1+2cos πcos 4443αα⨯⨯-⇒=.故答案为：1315.已知椭圆2222:1(0)x y C a b a b+=>>的左顶点为A ，上顶点为,B O 为坐标原点，椭圆上的点()(),,,M M N N M x y N x y 分别在第一､二象限内，若OAN 与OBM 的面积相等，且2224M N x x b +=，则C的离心率为__________.【答案】2【解析】【分析】根据题意，由两个三角形面积相等可得N M ay bx =，将点N 的坐标代入椭圆方程，结合条件化简即可得到,a b 关系，再根据离心率公式即可得到结果.【详解】因为OAN 与OBM 的面积相等，且()(),,,M M N N M x y N x y ，则1122N M ay bx =，即N M ay bx =，所以2222N M a y b x =，将(),N N N x y 坐标代入2222:1(0)x y C a b a b +=>>，可得22221N N x y a b+=，化简可得222222N N b x a y a b +=，即222222N M b x b x a b +=，所以()22222NM bxx a b +=，且2224MN x x b +=，所以22224b b a b ⋅=，即224a b =，则离心率为2e ===，故答案为:216.某同学回忆一次大型考试中的一道填空题，题目要求判断一条给定直线与给定圆的位置关系，该同学表示，题中所给直线与圆的方程形式分别为:l y kx b =+，222:C x y r +=，但他忘记了方程中的三个参数的具体值，只记得{},,1,2,3,4k b r ∈，并且他填写的结果为直线与圆相交.若数组(,,)k b r 的每一种赋值的可能性都相等，则该同学该题答对的概率为________.【答案】78##0.875【解析】【分析】利用直线与圆的位置关系结合古典概型分类讨论计算即可.【详解】易知数组(,,)k b r 有3464=种结果，若要直线与圆相交，需圆心()0,0C 到直线l 的距离2221b d r k r =<⇒<+，显然b r ≤时，22211b k r≤<+恒成立，若b r >，①当2,1b r ==，此时1k =不符题意；②当3,1b r ==，此时1,2k =不符题意，当3,2b r ==，此时1k =不符题意；③当4,1b r ==，此时1,2,3k =不符题意，当4,2b r ==，此时1k =不符题意，当4,3b r ==，k 取何值均成立；综上，共有8种情况不符题意，故答对的概率为871648P =-=.故答案为：78四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.17.已知, , a b c 是空间中的三个单位向量,且a b ⊥ ,,,60a c b c == .若2OM a b c =+-，OA a b c =++ ,2OB a b c =++ .（1）求MB;（2）求MB 和OA夹角的余弦值.【答案】（1；（2）15【解析】【分析】利用空间向量的数量积公式计算即可.【小问1详解】由已知可得2MB OB OM a b c =-=-++，所以MB =；【小问2详解】由OA a b c OA =++⇒=，所以MB 和OA夹角的余弦值为222cos ,15MB OA MB OA MB OA⋅==⋅ .18.为调查高一、高二学生心理健康情况,某学校采用分层随机抽样方法从高一、高二学生中分别抽取了60人､40人参加心理健康测试(满分10分).经初步统计,参加测试的高一学生成绩i x ()1,2,3,,60i =⋅⋅⋅的平均分8x =,方差22x s =,高二学生成绩i y (i =1,2,…,40)的统计表如下:成绩y 456789频数12915103（1）计算参加测试的高二学生成绩的平均分y 和方差2y s ；（2）估计该学校高一､高二全体学生的平均分z 和方差2z s .【答案】18.7，1.2；19.7.6，1.92.【解析】【分析】（1）利用统计表计算平均数与方差即可；（2）根据分层抽样的平均数与方差公式计算即可.【小问1详解】由表可知41526971581093712915103y ⨯+⨯+⨯+⨯+⨯+⨯==+++++，()()()()()()222222214725796715771087397 1.240y s ⨯-+⨯-+⨯-+⨯-+⨯-+⨯-==；【小问2详解】由已知及（1）可知6040877.6100100z =⨯+⨯=，()()222226040 1.92100100z x y s s x z s y z ⎡⎤⎡⎤=⨯+-+⨯+-=⎣⎦⎣⎦.19.在信道内传输0，1信号，信号的传输相互独立.发送0时，收到1的概率为12，收到0的概率为12；发送1时，收到0的概率为13，收到1的概率为23.（1）重复发送信号1三次，计算至少收到两次1的概率；（2）依次发送1，1，0，判断以下两个事件：①事件A ：至少收到一个正确信号；②事件B ：至少收到两个0，是否互相独立，并给出证明.【答案】19.2027；20.事件A 与事件B 不互相独立，证明见解析.【解析】【分析】（1）利用事件的相互独立求“至少收到两次1”的概率；（2）利用事件的相互独立性计算()P A ，()P B ，()P AB ，利用独立事件的概率公式验证.【小问1详解】重复发送信号1三次，“至少收到两次1”的可能情况为：(1，1，1)，(1，0，1)，(1，1，0)，(0，1，1)，因为信号的传输相互独立，故“至少收到两次1”的概率为：2222122211222033333333333327⨯⨯+⨯⨯+⨯⨯+⨯⨯=.【小问2详解】事件A 与事件B 不互相独立，证明如下：若依次发送1，1，0，则三次都没收到正确信号的概率为111133218⨯⨯=，故至少收到一个正确信号的概率为()11711818P A =-=；若依次发送1，1，0，“至少收到两个0”的可能情况为：(0，0，0)，(0，0，1)，(0，1，0)，(1，0，0)，根据事件的相互独立性，故()11111112121161332332332332183P B =⨯⨯+⨯⨯+⨯⨯+⨯⨯==，若依次发送1，1，0，“至少收到两个0且至少收到一个正确信号”的可能情况为：(0，0，0)，(0，1，0)，(1，0，0)，根据事件的相互独立性，故()111121211533233233218P AB =⨯⨯+⨯⨯+⨯⨯=，因为()()()P A P B P AB ≠，所以事件A 与事件B 不互相独立.20.已知圆22:46120C x y x y +---=.（1）求过点()75,且与圆C 相切的直线方程;（2）求经过直线70x y +-=与圆C 的交点,且面积最小的圆的方程.【答案】（1）21202470x y +-=或7x =（2）23π【解析】【分析】（1）由已知可得点()75,在圆外，即有两条切线，当切线斜率存在时，设出切线方程，根据点到直线距离公式可得斜率与方程，当切线斜率不存在时，可判断直线与圆相切；（2）由已知可设圆的方程为()22461270x y x y x y λ+---++-=，可得圆的半径1r =，可知当2λ=-时，1r ，此时面积最小为23π.【小问1详解】由22:46120C x y x y +---=得()()22:2325C x y -+-=，圆心()2,3C ，半径=5r ，又()75,到圆心的距离为5=>，所以点()75,在圆外，所以过点()75,的切线共有两条，当切线斜率存在时，设切线方程为()57y k x -=-，即750kx y k --+=，所以圆心C到直线的距离5d =，解得2120k =-，所以直线方程为()215720y x -=--，即21202470x y +-=，当直线斜率不存在时，直线方程为7x =，与圆C 相切，综上所述，切线方程为21202470x y +-=或7x =.【小问2详解】已知可设圆的方程为()22461270x y x y x y λ+---++-=，即()()22461270x y x y λλλ++-+---=，则圆的半径1r =可知当2λ=-时，1r ，此时面积最小为21π23πS r ==.21.如图，三棱台111ABC A B C -中，AB AC ==，112B C BC ==1AA =，点A 在平面111AB C 上的射影在111B A C ∠的平分线上.（1）求证：111AA B C ⊥；（2）若A 到平面111A B C 的距离为4，求直线AC 与平面11AA B B 所成角的正弦值.【答案】（1）证明见解析；（2）35【解析】【分析】（1）利用线面垂直证线线垂直即可；（2）利用棱台的特征补全棱锥，结合等体积法求点面距离，计算即可.【小问1详解】如图所示，补全棱台，延长三条侧棱交于O 点，得到棱锥111O A B C -，由题意可知、、A B C 分别是三条侧棱111OA OB OC 、、的中点，取11B C 的中点D ，连接1A D ，设A 在底面111A B C 的投影为M ，连接AM ，根据题意可知AM ⊥底面111A B C ，且M 在1A D 上，因为11B C ⊂面111A B C ，所以11AM B C ⊥又1111AB AC A B A C =⇒=，所以111A D B C ⊥,而11,A D AM M A D AM ⋂=⊂、平面1AA D ,所以11B C ⊥面1AA D ,因为1AA ⊂面1AA D ，所以111B C AA ⊥；【小问2详解】过O 作ON ⊥底面111A B C ，结合（1）可知N 在1A D 上，且4,8AM ON ==，在111A B C △上，()2211111112225,2225322A B A C B C A D ⎛⎫===⇒=-= ⎪ ⎪⎝⎭，结合题意可知：22111122,2422A M A A AM A N A M DM DN =-===⇒==，则22221166,217OD DN ON OB B D OD =+==+=在11OA B中，22211111111112cos 2A O B O A B OA AA A OB A O B O +-==⇒∠==⋅所以1111sin OA B AOB S ∠=⇒= 设1C 到平面11AA B B 的距离为h ，11A C 与平面11AA B B 的夹角为θ，所以111111111111133O A B C A B C C OA B OA B V ON S V h S --=⋅==⋅ ，解之得：h =，所以11sin 35h A C θ==，因为11//A C AC ，所以直线AC 与平面11AA B B所成角的正弦值为35.22.设圆222150x y x ++-=的圆心为A ，直线l 过点(1,0)B 且与x 轴不重合，l 交圆A 于,C D 两点，过B 作AD 的平行线交AC 于点E.（1）写出点E 的轨迹方程；（2）设点E 的轨迹为曲线1C ，过A 且与l 平行的直线与曲线1C 交于,P Q 两点，求AD PQ ⋅的取值范围.【答案】（1）221(0)43x y y +=≠（2）)⎡⎣【解析】【分析】（1）求得圆A 的圆心和半径，运用直线平行的性质和等腰三角形的性质，可得EB ED =，再由圆的定义和椭圆的定义，可得E 的轨迹为以A ，B 为焦点的椭圆，求得a ，b ，c ，即可得到所求轨迹方程；（2）联立直线与圆，以及直线与椭圆方程，可得跟与系数的关系，结合向量的坐标运算，即可根据数量积的坐标运算得AD PQ ⋅= .【小问1详解】圆A 的标准方程为22(1)16x y ++=，故半径4r =因为||||4AD AC r ===，//EB AC ，故EBC ADC ACD ∠=∠=∠，所以||||EB ED =，故||||||||||EA EB EA ED AD +=+=，因此||||4EA EB +=，由题设得(1,0)A -，(1,0)B ，||2||||AB EA EB =<+，由椭圆定义可得点E 的轨迹方程为：221(0)43x y y +=≠．【小问2详解】设直线CD 的方程为1x ty =+，则直线PQ 的方程为1x ty =-,联立直线CD 与圆的方程2212150x ty x y x =+⎧⎨++-=⎩，消元得()2214120t y ty ++-=，则()2221648164480t t t ∆=++=+>则()2242121t t x t t -±-±==++，联立直线PQ 与圆的方程221143x ty x y =-⎧⎪⎨+=⎪⎩，消元得()2234690t y ty +--=，由于点A 在椭圆内，故该方程一定有两个不相等的实数根，不妨设()()3344,,,P x y Q x y ，则34342269,3434t y y y y t t -+==++，()()()()2222234343422221216944343434t t y y y y y y t t t +-⎛⎫-=+-=-= ⎪++⎝⎭+，()()43434311x x ty ty t y y -=---=-()()43434343,,PQ x x y y ty ty y y =--=-- ，()1,D D AD x y =+ ()()()()()()()()24343434343122D D D D D D AD PQ x ty ty y y y ty ty ty y y y t y y t y y ⋅=+-+-=+-+-=++- ，()22222432121D D t t y y t t t t -±++=+=±+所以2432D D AD PQ t y y t y y ⋅=++-== 令234,4t s s +=≥，则AD PQ ⋅== 令11,04x xs =<≤，则AD PQ ⋅= 由于函数27114y x x =-+的对称轴为1114x =，故27114y x x =-+在10,4x ⎛⎤∈ ⎥⎝⎦单调递减，故当14x =时，27114y x x =-+取最小值2716，故2277114,416y x x ⎡⎫=-+∈⎪⎢⎣⎭，所以)AD PQ ⎡⋅=⎣ 【点睛】圆锥曲线中取值范围问题的五种求解策略：（1）利用圆锥曲线的几何性质或判别式构造不等关系，从而确定参数的取值范围；（2）利用已知参数的范围，求新的参数的范围，解这类问题的核心是建立两个参数之间的等量关系；（3）利用隐含的不等关系建立不等式，从而求出参数的取值范围；（4）利用已知的不等关系建立不等式，从而求出参数的取值范围；（5）利用求函数值域的方法将待求量表示为其他变量的函数，求其值域，从而确定参数的取值范围.。

浙江省杭州外国语学校2013-2014学年下学期高二年级期中考试英语试卷

浙江省杭州外国语学校2013-2014学年下学期高二年级期中考试英语试卷考试须知：1、英语试卷总分值100分，总答题时间100分钟;2、本试卷分―试题卷‖、―答题卷‖，其中―试题卷‖9页，―答题卷‖1页;3、选择题必须使用2B铅笔填涂，修改时用橡皮擦干净；4、非选择题必须使用黑色墨水的钢笔或签字笔，在各题目的答题区域内作答，超出答题区域书写的答案无效；5、保持答题纸面清洁，不要折叠、不要弄皱。

I. Listening comprehension: 10%Part I: Listen to the short conversations and answer the following questions. Each conversation will be read only ONCE. 3%1. Why couldn’t the woman give the man some help?A. She is quite busy right now.B. She doesn’t like grammar at all.C. She is poor in grammar, too.2. What happened to the man?A. He had to do others’ jobs.B. Nobody would like to help him.C. He had to take Jane to hospital.3. How does the woman like eating out?A. She enjoys it.B. She doesn’t care.C. She dislikes it.4. What will the weather probably be like on Thursday?A. Fine.B. Foggy.C. Rainy.5. What is the woman doing?A. Making an apology.B. Asking the way.C. Asking for advice.6. What happened to the man?A. He lost his car.B. He called his girlfriend.C. He left his keys in the car.Part II: Listen to the conversation and answer the following questions. The conversation will be read TWICE. 3%7. What are the speakers talking about?A. Buying a car.B. Choosing a gift.C. Using a computer.8. What’s the relationship between the speakers?A. Husband and wife.B. Professor and student.C. Salesman and customer.9. What do we know about the person mentioned by the speakers?A. Maybe he likes something expensive.B. He is surely over sixty years old.C. He must be fond of learning.Part III: Listen to the long passage and fill in the blanks with missing words. The passage will be read TWICE. 4%The Internet is Changing Our MemoryNew research suggests the Internet is changing our memory. Researchers from Colombia University ____10____ people with different questions and found many began to think of computers. Lead researcher Dr. Betsy Sparrow said that when test participants knew the answers would be available on a computer, they did less well on the memory tests. She said we use the Internet as a new ―transactive memory‖. We rely on this to do the remembering for us. It’s similar to our personal data being backed up on a hard disk. The Internet acts as a huge ____11____ device for all the world’s knowledge, that is there when we need it. Dr. Sparrow said computers were not making us less ____12____. ―I don't think Google is making us stupid. We're just changing the way that we're remembering thi ngs,‖ she said.Dr. Sparrow believes we are becoming very good at remembering where we keep information in different folders on our computers. She said: "This suggests that for the things we can find online, we ____13____ to keep it online as far as memory is _____14_____ -- we keep it ____15____ stored." She explained that because we are remembering the ____16____ of the information, rather than the information itself, we are becoming better at organizing huge quantities of data and facts in a more ____17____ way. She also said the way we use technology is changing our need to remember things, saying: ―If you can find stuff online even when you're walking down the street these days, then the skill to have, the thing to remember, is where to go to find the information."II. Multiple choices: 8%18. In the article ―a day to remember‖, what would have most upset the woman on the dayeverything went wrong for her?A. She had not expected her husband to arrive so early.B. Her husband had not told her he was bringing anyone to dinner.C. The meal she had cooked for the three guests had got burnt.D. She had not got enough crockery left to serve the meal with.19. In Lesson 3 of BOB, when the writer says ―He is forever talking about the friendly people, …‖,the author is trying to show his ______.A. disagreementB. satisfactionC. agreementD. misery20. ______ Chinese people had to use coupons(配给券) to buy life necessities, such as food and cloth.A. At a timeB. At one timeC. For one timeD. In time21. According to the article, the ―stay-at-home dad‖ will probably be __________.A. on the riseB. a high-paying jobC. a temporary trendD. a controversial issue22. In Lesson 2 of SC – Giving Until It Hurts, what stands out mo st about those wealthy people’sgenerosity is their __________.A. incentiveB. sentimentC. dedicationD. fulfillment23. The Wilsons live in ____________ A-shaped house near the coast. It is _____________ 18thcentury cottage.A. the; aB. an; theC. /; theD. an; an24. You __________ as well bring an umbrella with you today. It seems as if it’s going to rain.A. couldB. shouldC. needD. might25. Everyone was on time for the meeting -- _________ Chris, who’s usually ten minutes late for everything.A. butB. onlyC. evenD. yet26. According to the school rule, he ______ be punished if he is late for school again.A. canB. willC. mayD. shall27. If little Jimmy ________ my advice and listen to the teacher carefully in class, he __________the exam next month. But I’m afraid he will definitely turn a deaf ear to my words.A. can accept; will passB. should accept; would passC. had accepted; would have passedD. accepted; would have passed28. The old man, ________________ abroad for twenty years, is on the way back to hismotherland.A. to workB. workingC. to have workedD. having worked29. You should try to get a good night’s sleep ____________ much work you have t o do.A. howeverB. no matterC. althoughD. whatever30. I don’t mind picking up your things from the store. ____________, the walk will do me good.A. Sooner or laterB. StillC. In timeD. Besides31. –Let’s go and have a good drink tonight.-- ________ Have you got the first prize in the competition?A. What for?B. Thanks a lot.C. Yes, I’d like to.D. Why not?32. Jerry, you ____________ talk loudly in the library; you ____________ disturb others.A. can’t; won’tB. mustn’t; mayC. shouldn’t; mustD. can’t; shall33. ---The Chinese athletes did extremely well in the London Olympics.--- Yes, they ______ very hard, or they ______ such great achievements.A.must have been trained; couldn’t have gotB.must have t rained; shouldn’t have gotC.must have been trained; must have gotD.should have been trained; couldn’t have gotIII. Cloze: 20%I often read of incidents of misunderstanding or conflict. I’m left __34__. Why do these people create mistrust and problems, especially with those from other __35__?I was growing up in Kuala Lumpur in the early 1960s, __36__ children from different races and religions played and studied __ 37__ in harmony. At that time my family lived a stone’s __38__ from Ismail’s house. And no on e was bothered that Ismail was a Malay Muslim and I was an Indian Hindu---we just __39__ our differences. Perhaps, our elders had not filled our heads with unnecessary advice -- well __40__ or otherwise.We were nine when we became friends. During the school holidays, we'd __41__ the countryside on our bicycles, hoping to __42__ the unexpected. At times Ismail would accompany my family as we made a rare shopping trip to town. We would be glad of his __43__.When I was twelve, my family moved to Johor. Ismai l’s family later returned to their village, and I _44__ touches with him.One spring afternoon in 1983, I stopped a taxi in Kuala Lumpur. I __45__ my destination.The driver acknowledged my __46__ but did not move off. Instead, he looked __47__ at me. ―R addar?" he said, using my childhood nickname. I was astonished at being so __48__ addressed (称呼). Unexpectedly! It was Ismail! Even after two __49__ we still recognized each other. Grasping his shoulder, I felt a true affection, something __50__ to describe.If we can allow our children to be __51__ without prejudice, they'll build friendships with people, regardless of race or religion, who will be __52__ their side through bitter and sweet. On such friendships are societies built and __53__ we can truly be, as William Shakespeare once wrote, ―We happy few, we band of brothers".34.A. interested B. pleased C. puzzled D. excited35.A. parties B. cities C. villages D. races36.A. why B. which C. how D. when37.A. together B. around C. alone D. apart38.A. drop B. throw C. move D. roll39.A. refused B. made C. sought D. accepted40.A. paid B. intentioned C. known D. treated41.A. explore B. search C. discover D. desert42.A. get through B. deal with C. come across D. take away43.A. arrival B. choice C. effort D. company44.A. lost B. gained C. developed D. missed45.A. stated B. ordered C. decided D. chose46.A. attempts B. instructions C. opinions D. arrangements47.A. anxiously B. carelessly C. disappointedly D. fixedly48.A. familiarly B. strangely C. fully D. coldly49.A. departures B. months C. years D. decades50.A. possible B. funny C. hard D. clear51.A. them B. themselves C. us D. ourselves52.A. from B. by C. with D. against53.A. still B. otherwise C. then D. insteadIV. Reading comprehension: 32%ADear Lee,As I told you, I’ll be gone until Wednesday morning. Thank you so much for taking on my ―children‖ while I’m away. Like real children, they can be kind of irritating sometimes, but I’m going to enjoy myself so much more knowing they’re getting some kind human attention. Remember that Regina (the ―queen‖ in Latin, and she acts like one) is teething. If you don’t watch her, she’ll chew anything, including her sister, t he cat. There are plenty of chew toys around the house. Whenever she starts gnawing on anything illegal, just give her one of those. She generally settles right down to a good hour-long chew. Then you’ll see her wandering around whimpering with the remains of the toy in her mouth. She gets really frustrated because what she wants is to bury the thing. She’ll try to dig a hole between the cushions of the couch. Finding that unsatisfactory, she’ll wander some more, discontent, until you solve her problem for her. I usually show her the laundry basket, moving a few clothes so she can bury her toy beneath them. I do sound like a parent, don’t I? You have to understand, my own son is practically grown up.Regina’s food is the Puppy Chow in the utility room, where the other pet food is stored. Give her a bowl once in the morning and once in the evening. No more than that, no matter how much she begs. Beagles(小猎犬)are notorious overeaters, according to her breeder, and I don’t want her to lose her girlish figure. Sh e can share Rex (the King’s) water, but be sure it’s changed daily. She needs to go out several times a day, especially last thing at night and first thing in the morning. Let her stay out for about ten minutes each time, so she can do all her business. She also needs a walk in the afternoon, after which it’s important to romp with her for a while in the yard. The game she loves most is fetch, but be sure to make her drop the ball. She’d rather play tug of war with it. Tell her, ―Sit!‖ Then, when she does, say, ―Drop it!‖ Be sure to tell her ―good girl,‖ and then throw the ball for her. I hope you’ll enjoy these sessions as much as I do.Now, for the other two, Rex and Paws… (letter continues)54.From the context of the note, it is most likely that the name ―Rex‖ is _____.A. SpanishB. EnglishC. FrenchD. Latin55.If the sitter is to follow the owner’s directions in playing fetch with Regina, at what point willhe or she tell Regina ―good girl‖?A. Every time Regina goes after the ball.B. After Regina finds the ball.C. When Regina brings the ball back.D. After Regina drops the ball.56.The tone of this letter is best described as _____.A. chatty and humorousB. logical and preciseC. confident and trustingD. humble and preachy57.The information in the note is sufficient to determine that there are three animals in the firsttwo paragraphs. They are _____.A. two cats and a dogB. three dogsC. a dog, a cat, and an unspecified animalD. a cat, a dog, and a parrotBExpensive perfumes come in tiny bottles, but many hide a whale sized secret.To perfect a particular smell, perfume makers often use an ingredient that comes from sperm whales (抹香鲸), called ambergris. But using ambergris, which helps a perfume last longer, is strongly opposed by many people who think it is wrong to kill whales just so we can smell sweet. Joerg Bohlmann is neither a perfumer nor a whale expert. He's a plant biologist at the University of British Columbia in Canada. But his discovery of a new plant gene might push whales out of the perfume business.The gene comes from fir trees, found throughout North America and commonly used as Christmas trees. The trees produce a chemical that can be used in perfume in place of ambergris—but with a catch.―There's a problem that many people wouldn't consider. In the tree, the chemical is mixed with many others. That makes separation a challenge‖ Bohlmann says. ―It's like trying to isolate sugar from a biscuit.‖This is where science becomes useful. When Bohlmann learned that fir trees produce the ambergris-like chemical, he decided to use his gene know-how to find the instructions for how to make the ambergris substitute.Bohlmann found that gene and took it out of the tree cells. Then he did something that might sound strange to someone who doesn't work in genetics: Bohlmann put the gene from the tree into yeast (酵母) cells.Yeast may sound familiar because it's used to make things like bread, wine and beer. Biologists like to work with yeast because it easily adopts new genes and changes its features and behavior. When Bohlmann put the fir tree gene into the yeast, the yeast started making the same chemical that had been produced by the tree.Perfumers pay big money for ambergris because it is a fixative, which means it holds a smell in place on a person's body.―Cheap perfumes smell good in the first hour or so and then everything is gone,‖ explains Bohlmann. ―But expensive perfumes are much more stable. Their smell lasts much longer, for hours or even a day afte r you apply them.‖The new chemical, made from the tree genes, can be used as a fixative, too. And using yeast to make it is far cheaper than acquiring ambergris.Bohlmann admits he never thought he'd get into the perfume business. But now, he says, producers have been calling to find out how to use his technology in new perfumes.58. It can be inferred from the passage that if a perfume contains ambergris, ________.A. its user probably supports whale huntingB. its smell will last for about an hourC. there will be a whale symbol on the bottleD. it is probably very expensive59. The underlined expression ―with a catch‖ in Paragraph 3 means ________.A. being difficult to holdB. having a hidden problemC. needing further testingD. being too similar60. According to the passage, why are yeast cells often used in genetic research?A. They can take on the characteristics of other genes.B. They can reproduce much faster than other cells.C. They share some of the qualities of plant genes.D. They're much cheaper to use than ambergris.61. What is the best title for the passage?A. The Christmas tree's secret.B. The sweet smell of success.C. Whale free perfume.D. Save the whale.CMOOCs (Massive Open Online Courses) are free, but without tutoring, and are open to anyone, anywhere in the world. The courses are flexible – normally three to five hours of study a week – done at any time, short (5 to 10 weeks) and video-rich. They are also heavily dependent on crowd sourcing: you can discuss a course with fellow students through online forums, discussionboards and peer review. Students don't have to finish the courses, pass assessments or do assignments, but, if they do, they get a certification of participation.The Open University launched FutureLearn, the UK's answer to US platforms such as Coursera, EdX and Udacity, which have been offering MOOCs from top US universities for the past two years. The response has been incredible, with more than three million people registering worldwide. Meanwhile, in 2012, Edinburgh University became the first non-US institution to join Coursera's partnership, comprising 13 universities. ―We already run 50 online master's degrees, so this was a logical expansion,‖ says Professor Jeff Haywood, Edinburgh's vice-principal. ―It's an investment in teaching methods research. How am I going to teach introductory philosophy to 100,000 people? That's what I call educational R&D.‖ He adds ―If you look ahead 10 years, you'd expect all students graduating to have taken some online courses, so you've got to research that. Our MOOCs are no more in competition with our degrees than a lifelong learning course because they don't carry credits.‖Cooperation is key, Haywood stresses. It is far better to offer 20-30 courses in your own areas of expertise (专门技能) and let other institutions do likewise. Professor Mike Sharples, FutureLearn's academic lead, goes further: ―We've tied the elements available before into a package of courses offered by leading universities worldwide on a new software platform, with a new way of promoting it and also a new social-learning teaching method. You won't just receive an exam, but be able to discuss and mark each other's assignments.‖Bath University, one of more than 20 universities working with FutureLearn, launches its first course, Inside Cancer, next January, and regards MOOCs as a way of breaking down age barriers. "There's no reason why someone doing GCSEs should not look at our MOOCs and get quite a way through them, or someone at PhD level and beyond," says Professor Bernie Morley, expert for learning and teaching.62. MOOCs have these features EXCEPT that_______.A. MOOCs are free of charge for anyoneB. MOOCs can be adjusted according to people’s learning paceC. MOOCs provide teachers’ instructions if you have so me difficultyD. MOOCs have a platform for learners to share their learning experience63. The response to FutureLearn has been thought to be unbelievable because ______.A. all the courses on the platform are available to anyone in the worldB. Edinburgh University became the first non-US institution to join itC. the number of people registering in the platform is beyond expectationD. students can get a certification of participation without passing assessments64. What can be inferred from Professor Bernie Morley in the last paragraph?A. People with various learning levels will probably show interest in MOOCs.B. People at PhD level have already known everything about MOOCs.C. Inside Cancer will be the most popular course for someone doing GCSEs.D. MOOCs are not so competitive as lifelong learning courses due to the problems of credits.65. The passage mainly deals with _____.A. the various opinions on FutureLearnB. the advantages of online teachingmethodsC. the popularity of no-credit coursesD. the emergence of a new learningplatformDThe term culture now is more used to describe everything from the fine arts to the outlook of a business group or a sports team. In its original sense, however, culture includes all identifying aspects of a racial group, nation, or empire: its physical environment, history, and traditions, its social rules and economic structure, and its religious beliefs and arts.The central beliefs and customs of a group are handed down from one generation to another. It is for this reason that most people regard culture as learned rather than innate. People acquire a culture because they are not born with one. The process by which a person develops a taste for regional foods, accented speech, or an outlook on the world over time, therefore, is known as enculturation (文化适应).Cultures are often identified by their symbols —images that are familiar and coated with meaning. Totem poles (图腾柱) carved with animals and creative figures suggest aspects of the Native American peoples of the Pacific Northwest but more literally represent specific tribes. In Asia and India, the color of yellow is connected with temples while in ancient China it was a color only the emperor’s family was allowed to wear. Thus, different cultures may respo nd to a symbol quite differently. For example, to some a flag may represent pride, historical accomplishments, or ideals; to others, however, it can mean danger or oppression.To individuals unfamiliar with cultures outside their own, the beliefs, behaviors, and artisticexpression of other groups can seem strange and even threatening. A society that ranks all other cultures against its own standards is considered to be ethnocentric(from the Greek ethnos, meaning ―people,‖ and kentros, meaning ―center‖). A strongly ethnocentric society assumes also that what is different from its own culture is likely to be inferior and, possibly, wrong or evil.All people are ethnocentric to some degree, and some aspects of ethnocentrism, such as national pride, contribute to a well-functioning society. An appreciation for one’s own culture, however, does not prevent acceptance and respect for another culture. History documents the long-term vigor and success of multicultural groups in which people from numerous and various cultural backgrounds live and work together. Extreme ethnocentrism, in contrast, can lead to racism — the belief that it is race and racial origin that account for variations in human character or ability and that one’s own race is superior to all other s.66. What does the word ―innate‖ in Paragraph 2 most probably mean?A. Natural.B. Developed.C. Believable.D. Cultivated.67. Which of the following is true according to the passage?A. Different interpretations of a symbol help to distinguish one culture from another.B. An ethnocentric country opens welcoming arms to cultures different from its own.C. Culture consists of few positive features of a racial group, nation or empire.D. People from various cultural backgrounds often reach an agreement on some image.68. What can be inferred from the passage?A. All aspects of ethnocentrism can produce negative effects on a society.B. Racism is unlikely to bring about serious conflicts among different cultures.C. Respect and acceptance of different cultures are a proper cultural attitude.D. Countries with a strong sense of national pride play a superior role in the world.69. Which might be the best title of the passage?A. Culture, the origin of racial superiorityB. Culture, a faithful mirror of historyC. Culture, the vigour of world developmentD. Culture, a distinctive identity of a nationV. Fill in the blanks with the proper words. The first letter of each word is given. 10%1.Khaled Hosseini, the writer of ―The Kite Runner‖ presente d a realistic p_____________ ofthe conflicts and different social status between the Pashtuns and the Hazaras.2.Many critics have been arguing about the real reason of the missing flight MH370. Some oftheir opinions sound reasonable, while others are simply too f_____________.3.The United Nations warned, global c_____________ of natural resources could almost tripleto 140 billion tones a year by 2050 unless nations take drastic steps (采取严厉措施) to reduce the use of minerals, ores and fossil and plant fuels.4.Many patients o_____________ refuse to get treatment after they are diagnosed with seriousdiseases such as cancer no matter how hard people try to persuade them.5.The tradition of wearing a special white dress only for the wedding ceremony hasp_____________ for about 2 centuries in many western countries.6.It’s common for African-American, Asian-American or Latin-American employees to suetheir bosses on the grounds of racial d_____________ if they are treated unfairly.7.Unlike military strike (军事打击), n_____________ with terrorists has never become anoption for the US government because terrorists always want to achieve their goals by using violence and killing innocent people and they don't deserve it.8.During military training, students were trained to walk, run and sing in unison, vaguely(大致上，近似地) r_____________ life of soldiers.9.Sir Run Run Shaw （邵逸夫）died on January 7th, 2014, but he divided up his property intoseveral p____________ seventeen years ago and gave one to each of his children and his wife.10.To deal with worsening smog, Tianjin will raise pollution discharge（排污）feesd_____________. For example, fees for SO2 emissions（排放）will rise from 1.26 yuan to 6.3 yuan per kilogram.VI. Fill in each blank with a phrase given in the box in its proper from. There are more items than needed. 5%1.To help the readers fully understand the Renaissance and humanism, a photo of Mona Lisa_______________ the article ―Out of the Middle Ages‖ in Teens 33.2.When the last semester of Senior high school_____________, Sr. 3 students will be busyhaving their pictures taken with their teachers, their goodbye wishes written and their used textbooks sent away.3.After I came back, being an exchange student, from Germany for a year, I corresponded withmy host family ______________, however, about 2 years later, we lost track of each other.4.Since the mid-term examination was around the corner, most students _______________ athome with their heads in books during the weekends, occasionally looking at their classmates’ fun-filled uploads.5.The collapse of the ―fast-food‖ apartment building forced its former residents_______________ hotel rooms, their relatives’ and rented apartments temporarily.6.During Qingming Festival, the heavy traffic ___________________ dangerous drivingconditions which resulted in several accidents on my way to Shaoxing.7. A passenger ship carrying 459 people, mostly high school students, sank off South Korea'ssouthern coast on April 16th, leaving almost two hundred missing and more than 100 people dead according to the report on April 22nd. It is believed that most of the passengers must _________________ in the process of sinking.8. A Claude Monet’s first-ever exhibition in China is being held in Shanghai currently. Manyart lovers living in places far from Shanghai _________________ see the exhibits even if they know the operation involves considerable planning.9.For the Pakistani girl Malala, admission into a school is a big event for her,_________________ girls in patriarchal societies in her country are sometimes deprived of the rights to go to school.10.When it comes to dealing with garbage, Chinese really need to learn from Swedes, who__________________ providing heat and electricity to millions of homes by burning waste.VII. Writing: 15%Write an English composition in 120-150 words according to the instructions given below in Chinese.有的校园活动让你兴奋不已，有的校园活动让你感到枯燥乏味。

浙江省杭州市外国语学校2023-2024学年高二下学期期中考试语文试题(含解析)

杭州市外国语学校2023-2024学年高二下学期期中考试语文试卷一、现代文阅读（28分）（一）课外现代文阅读Ⅰ（本题共4小题，13分）阅读文段，完成下面小题。

孤独者①任何一部新的小说文本的产生，都必须面对此前文学史中的全部文本，尤其是经典文本。

换言之，任何一个小说家，毫无选择地必须面对“互文”的天罗地网，然而小说家对待这一沉重现实的态度，却是可以选择的。

中国现当代小说以开天辟地的姿态开始书写自己的历史。

自新文学革命以来，中国小说的主流，显然并没有选择《红楼梦》所选择的、积极而充分地建构与中国古代文学以及文化传统的互文关系。

也就是说，从新文学发端的中国现当代小说创作，目光始终是关注着当下与未来，有意识回望传统文化的小说家，自然是孤独的。

②在极端的民族危机和文化危机的状态下，中国的现代小说以一种新的姿态开始自己的书写，我们的现代文学就这样以断裂性的“革命”肇始了。

我们的文学价值评判体系都是重新厘定的，而且对于固有的文学标准具有颠覆和否定性质。

自然我们也不可能希求现代小说创作中会出现积极建构与古代主流文学表意符号系统互文指涉的作品，我曾指出的中国源远流长的“互文”手段——用典，在现当代小说中，几乎失去了合法性。

胡适在《文学改良刍议》中郑重其事地列出禁条：“六曰，不用典。

”五四时期似乎还对此问题有所争论，胡适还要适当地作以说明。

但在此后越来越被现实和创新挟裹的现当代小说创作中，这个问题已经没有讨论的必要了。

大规模的“引经据典”在相当长的历史时期内都会被视为“陈腐酸朽”，轻易不会有现当代小说家去冒这个大不韪。

当然，我们不能简单粗暴地把这一断裂认定为中国现当代小说犯下了某种“错误”。

某种意义上，我们甚至可以理解成是“革命”的代价，是先行者探路时付出的“牺牲”。

③如果说，我们此刻对这“代价”与“牺牲”会有些叹惋或遗憾，那也是站在近百年的现当代小说发展的基础上，相对从容地评判其成败得失时产生的。

进一步说，这些“叹惋”与“遗憾”，某种程度上，也是我们在新的历史产化环境下，勾勒出某种中国小说叙事可能的“愿景”刺激下产生的。

【原创·精品解析系列】数学文卷·2015届浙江省杭州外国语学校高二第二学期期中考试(2014.05)

浙江省杭州外国语学校2013-2014学年高二第二学期期中考试数学文试题【试卷综析】这套试卷主要考查基础，考查数学能力，注重双基，突出能力考查试卷的较多试题来自课本，源于平时的练习，以基本概念、基本原理和公式的应用为切入点，考查了学生对基础知识的掌握程度，同时还有提升，对理解和应用能力、运算能力、空间想象能力及对解决综合问题的能力进行了考查。

重视数学基本方法运用，淡化特殊技巧试题回避过难、过繁的题目，解题思路不依靠特殊技巧，只要掌握基本方法，就能找到解题思路以促进数学教学质量的提高为原则，在训练命题中立意明确，迎合了高考命题的要求，把水平测试和能力测试融为一体，命题科学，区分度强，达到了考查目的，是一份较好的试题。

注意事项：1、考试时间100分钟，本试卷满分100分；2、本场考试不准使用计算器等计算工具；3、请用蓝、黑色钢笔或圆珠笔答题，在答题卷相应处写上班级、姓名、考号，所有答案均做在答卷的相应位置上，做在试题卷上无效.一、选择题（共10小题，只有一个选项为真，每小题4分，共40分）1、若复数1z i =+，则(1)z z +⋅= ( )．A ．13i +B ．33i +C ．3i -D ．3【知识点】复数代数形式的乘除运算．【答案解析】A 解析：解：因为1z i =+，所以(1)z z +⋅=(2+i)(1+i)= 13i +【思路点拨】把复数z 代入后前一部分采用复数的除法运算，然后在把实部和实部相加，虚部和虚部相加．2、在100件产品中有6件次品,现从中任取3件产品,至少有1件次品的不同取法的种数是( ）A ．12694C C B.C 16C 299 C.C 3100－C 394 D.A 3100－A 394 【知识点】计数原理的应用．【答案解析】C 解析：解：在100件产品中有6件次品，现从中任取3件产品，共有C 1003种结果，至少有1件次品的对立事件是没有次品，没有次品的事件有C 943， ∴至少有1件次品的不同取法有C 1003-C 943，故选C ．【思路点拨】在100件产品中有6件次品，现从中任取3件产品，至少有1件次品的对立事件是没有次品，没有次品的事件有C 943，得到至少有1件次品的不同取法用所有减去不合题意的．【典型总结】本题考查分步计数原理，是一个基础题，解题时可以从正面来考虑，至少有一件次品包括有一件次品，有两件次品，有三件次品，分别写出结果再相加．3、8名学生和2位老师站成一排合影，2位老师不相邻的排法种数为 ( )．A ．8289A AB ．8289AC C ．8287A AD ．8287A C【知识点】排列、组合及简单计数问题．【答案解析】A 解析：解：用插空法解决的排列组合问题，将所有学生先排列，有A 88种排法，然后将两位老师插入9个空中，共有A 92种排法，∴一共有A 88A 92种排法．故选A ．【思路点拨】要求两个教师不相邻，用插空法来解决问题，将所有学生先排列，有A 88种排法，再将两位老师插入9个空中，共有A 92种排法，根据分步计数原理得到结果．【典型总结】本题考查排列组合的实际应用，考查分步计数原理，是一个典型的排列组合问题，对于不相邻的问题，一般采用插空法来解．4、用数学归纳法证明不等式11111271()24264n n N *-++++>∈成立，其n 的初始值至少应为 ( ) A ．7 B ．8 C ．9D ．10 【知识点】用数学归纳法证明不等式． 112n -++＝112n -++＝12 3 43 4 5 6 74 5 6 7 8 9 10……则第________行的各数之和等于2 0132 ( )．A ．2 014B ．2 013C ．1 007D ．1 008【知识点】数列的求和；等差数列．【答案解析】C 解析：解：观察下列数的规律图：12 3 43 4 5 6 74 5 6 7 8 9 10…知：第1行各数之和是2211211==⨯-（），第2行各数之和是222343221++==⨯-（），第3行各数之和是22345675231++++==⨯-（），第4行各数之和是22456789107241++++++==⨯-（），∴第n 行各数之和是221n -（），由22201321n =-（），解得n=1007．故选C ．【思路点拨】第1行各数之和是2211⨯-（），第2行各数之和是2221⨯-（），第3行各数之和是2231⨯-（），第4行各数之和是2241⨯-（），故第n 行各数之和是221n -（），由此能求出结果．【典型总结】本题考查数列的前n 项和公式的求法和应用，是基础题．解题时要认真审题，仔细解答，注意等价转化思想的合理运用．6、设,,a b c 均为正实数，则三个数111,,a b c b c a+++ ( )． A ．都大于2 B ．都小于2C ．至少有一个不大于2D ．至少有一个不小于2【知识点】不等式比较大小．反证法思想. 基本不等式；进行简单的合情推理．要求两类选修课中各至少选一门，则不同的选法共有 ( )．A ．30种B ．35种C ．42种D ．48种【知识点】分类计数原理、组合知识，以及分类讨论的数学思想．【答案解析】A 解析：解：可分以下2种情况：①A 类选修课选1门，B 类选修课选2门，有1234C C 种不同的选法；②A 类选修课选2门，B 类选修课选1门，有2134C C 种不同的选法．∴根据分类计数原理知不同的选法共有12213434C C C C +=18+12=30种．故选A ．【思路点拨】两类课程中各至少选一门，包含两种情况：A 类选修课选1门，B 类选修课选2门；A 类选修课选2门，B 类选修课选1门，写出组合数，根据分类计数原理得到结果．8、点P 是曲线2ln y x x =-上任意一点，则点P 到直线2y x =+的最小距离为 ( )．A. 2B. C ． D ．2【思路点拨】求出平行于直线y=x+2且与曲线y=x -lnx 相切的切点坐标，再利用点到直线的距离公式可得结论．9、()f x 是定义在(0,)+∞上的非负、可导函数，且满足()()0xf x f x '+≤，对任意正数,a b ，若a b <，则必有 ( )．A ．)()(b bf a af ≤B ．)()(b bf a af ≥C ．)()(b bf a af <D ． )()(b bf a af >【知识点】函数的单调性与导数的关系．【答案解析】B 解析：解：设g （x ）=xf （x ），x ∈（0，+∞），则g′（x ）=xf′（x ）+f （x ）≤0，∴g （x ）在区间x ∈（0，+∞）单调递减．∵a ＜b ，∴g （a ）≥g（b ），即af （a ）≥bf（b ）．故选B ．【思路点拨】构造函数g （x ）=xf （x ），x ∈（0，+∞），通过求导利用已知条件即可得出．10、已知函数()ln x f x e a x =+的定义域是D ，关于函数()f x 给出下列命题： ①对于任意(0,)a ∈+∞，函数()f x 是D 上的减函数；②对于任意(,0)a ∈-∞，函数()f x 存在最小值；③存在(0,)a ∈+∞，使得对于任意的x D ∈，都有()0f x >成立；④存在(,0)a ∈-∞，使得函数()f x 有两个零点．其中正确命题的序号是 ( )．A ．①②B ．②③C ．②④D ．③④【知识点】函数的单调性与导数的关系；命题的真假判断与应用．【思路点拨】先求导数，若为减函数则导数恒小于零；在开区间上，若有最小值则有唯一的极小值，若有零点则对应方程有根．二、填空题（本大题共5小题，每题4分，共20分）11、已知a R ∈，复数112a i i -+-是纯虚数，则a = ________.【知识点】复数的基本概念．【答案解析】－1 解析12i -=()()()111111222a i i a a i i i +-+-+=+-+是纯虚数，所以12a +=0且102a -≠，解得a=－1. 【思路点拨】将复数z 化为z=a+bi 然后利用复数的概念即可得解．12、函数x x x x f ln )(2-+=的单调递增区间为【知识点】分式不等式的解法；利用导数研究函数的单调性．【答案解析】），（∞+21 解析：解：因为x x x x f ln )(2-+=，定义域为0+∞（，）所以1()21f x x x '=+-，欲求函数的单调递增区间，则()0f x '>，即1210x x+->，综上12100x x x ⎧+->⎪⎨⎪>⎩解得函数的单调递增区间为），（∞+21. 【思路点拨】先利用题目给的条件求x 的范围，再在这个大范围内求导，再利用导数判断单调性，求单调区间13、8名世界网球顶级选手在上海大师赛上分成两组，每组各4人，分别进行单循环赛，每组决出前两名，再由每组的第一名与另一组的第二名进行淘汰赛，获胜者角逐冠、亚军，败者角逐第3、4名，大师赛共有________场比赛．【知识点】排列组合．【答案解析】16 解析：解：循环赛：8人平均分成两组，每组4人，比赛场数为：3+2+1=6（场），6×2=12（场）；淘汰赛：还剩下4名，再由每组的第一名，另一组的第二名进行淘汰赛要进行2场，再选出冠军亚军和3、4名要各进行1场；所以共需12+2+1+1=16（场）．【思路点拨】先计算出循环赛的场数，8人平均分成两组，每组4人，比赛场数为：每一组，3+2+1=6（场），所以两组共6×2=12（场）；再计算淘汰赛，循环赛之后剩下4人进行淘汰赛，选出前两名要进行2场，再角逐冠、亚军需1场，败者角逐第3、4名还要1场；最后将所有场数加起来就是所有场数．14、若21()ln(2)2f x x b x =-++在(－1，＋∞)上是减函数，则b 的取值范围是________．【知识点】函数的单调性与导数间的关系；二次函数的值域. 【答案解析】1b ≤- 解析：解：因为21()ln(2)2f x x b x =-++在(－1，＋∞)上是减函数，所以()0f x '<在(－1，＋∞)上恒成立，即22022b x x b x x x --+-+=<++在(－1，＋∞)上恒成立，所以22b x x <+在(－1，＋∞)上恒成立，令2()2g x x x =+ ∈(－1，＋∞)，故1b ≤-.【思路点拨】由函数21()ln(2)2f x x b x =-++在(－1，＋∞)上是减函数，转化为()0f x '<在(－1，＋∞)上恒成立的问题.进而求2()2g x x x =+的值域即可.15、某外商计划在4个候选城市中投资3个不同的项目，且在同一个城市投资的项目不超过2个，则该外商不同的投资方案有________种．【知识点】排列、组合及简单计数问题【答案解析】60 解析：解：分两种情况①在一个城市投资两个项目，在另一城市投资1个项目，将项目分成2个与1个，有3种；在4个城市当中，选择两个城市作为投资对象，有4×3=12种，这种情况有：3×12=36种 ②有三个城市各获得一个投资的项目，选择没有获得投资项目的城市，4种；安排项目与城市对应，有3×2×1=6种这种情况有，4×6=24种综合两种情况，有36+24=60种方案设置投资项目【思路点拨】分两种情况：在一个城市投资两个项目，在另一城市投资1个项目；有三个城市各获得一个投资的项目，从而可得结论．三、解答题（本题有4小题，请写出必要的解答过程，每题10分，共40分）16.已知函数ln ()x f x x=. （Ⅰ）求()f x 在点(1,0)处的切线方程；（Ⅱ）求函数()f x 在[1,]t 上的最大值.【知识点】利用导数求闭区间上函数的最值; 利用导数研究曲线上某点切线方程【答案解析】（Ⅰ）1-=x y （Ⅱ）当],1(e t ∈时，)(x f 最大值是t t t f ln )(=当),(+∞∈e t 时，)(x f 的最大值为e e f 1)(= 解析：解：（Ⅰ）⇒='=⇒-='1)1(ln 1)(2f k xx x f 切线方程为1-=x y （2）由)(x f '知)(x f 在[]e ,1上递增，在[)+∞,e 上递减，故当],1(e t ∈时，)(x f 最大值是tt t f ln )(=当),(+∞∈e t 时，)(x f 的最大值为e f 1)(=17.对于数列n a ：11)12(,1+++==n n c n ca a a (N n ∈,实常数)0≠c （Ⅰ）求432,,a a a ，并猜想n a （Ⅱ）证明你的猜想。

浙江省杭州第二中学2023-2024学年高二下学期期中考试数学试题(解析版)

2023学年第一学期杭州二中高二期中考试数学1. 两条平行直线1l ：注意事项：1．本试卷满分150分，考试用时120分钟.2．答题前，考生务必用黑色字迹钢笔或签字笔将自己的姓名、考生号、考场号和座位号填写答题卡上.用2B 铅笔将试卷类型（B ）填涂在答题卡相应位置上.将条形码横贴在答题卡右上角“条形码粘贴处”.3．作答选择题时，选出每小题答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上.4．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液.不按以上要求作答的答案无效.5．考生必须保持答题卡的整洁.考试结束后，将试卷和答题卡一并交回.一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的，多选、错选或不选都给不分.3450x y +−=与2l：6850x y +−=之间的距离是（） A. 0 B.12C. 1D.32【答案】B 【解析】【分析】利用平行线间距离公式进行求解即可. 【详解】345068100x y x y +−=⇒+−=，12，故选：B2. 已知圆()()()2122292:x m y m m C −+−=−与圆22288340:x y x C y m +−−+−=，则“4m = ”是“圆1C 与圆2C 外切”的（） A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D. 既不充分也不必要条件【答案】C【解析】【分析】利用两圆相切圆心距与两半径之和相等，分别证明充分性和必要性是否成立即可得出答案. 【详解】根据题意将圆2C 化成标准方程为()()22442x y m −+−=−；易知20m −>，所以可得圆心()12,2C m m，半径为1r =，圆心()24,4C，半径为2r =可得122C C =−，两半径之和12r r += 若4m=，圆心距12C C =，两半径之和12r r +，此时1212C C r r =+=，所以圆1C 与圆2C 外切，即充分性成立；若圆1C 与圆2C外切，则2−=4m =或2m =（舍），所以必要性成立；即“4m =”是“圆1C 与圆2C 外切”的充分必要条件. 故选：C3. 已知直线y kx m =+（m 为常数）与圆224x y +=交于点M N ，，当k 变化时，若||MN 的最小值为2，则m =A. 1±B. C. D. 2±【答案】C 【解析】【分析】先求得圆心到直线距离，即可表示出弦长，根据弦长最小值得出m 【详解】由题可得圆心为()0,0，半径为2，则圆心到直线的距离d =，则弦长为||MN =，则当0k =时，MN 取得最小值为2=，解得m =. 故选：C.4. 直线20x y ++=分别与x 轴，y 轴交于A ，B 两点，点P 在圆()2222x y −+=上，则ABP 面积的取值范围是A. []26，B. []48，C. D.【答案】A 【解析】【详解】分析：先求出A ，B 两点坐标得到AB ，再计算圆心到直线距离，得到点P 到直线距离范围，由面积公式计算即可详解：直线x y 20++=分别与x 轴，y 轴交于A ，B 两点 ()()A 2,0,B 0,2∴−−,则AB = 点P 在圆22x 22y −+=（）上∴圆心为（2，0），则圆心到直线距离1d =故点P 到直线x y 20++=的距离2d 的范围为则[]2212,62ABPS AB d ==∈故答案选A.点睛：本题主要考查直线与圆，考查了点到直线的距离公式，三角形的面积公式，属于中档题．5. 已知正方形ABCD 的边长为2，点M 在以C 为圆心，1为半径的圆上，则2MB MD +的最小值为（）A.B.C.D.【答案】D 【解析】【分析】建立直角坐标系，取点1(0,)2E ，探讨满足条件||2||M D M E ′′=的点M ′的轨迹，再结合已知，求出两条线段长度和的最小值作答.【详解】依题意，以点C 为原点，直线,CB CD 分别为,x y 轴建立平面直角坐标系，则(2,0),(0,2)B D ，如图，取点1(0,)2E ，设(,)M x y ′，当||2||M D M E ′′=化简整理得221x y +=，即点M ′的轨迹是以C 为圆心，1为半径的圆，而点M 在以C 为圆心，1为半径的圆上，因此||2||MD ME =，显然点B 在圆C ：221x y +=外，则22||2||2(||||)2||MB MD MB ME MB ME BE +=+=+≥，当且仅当M 为线段BE 与圆C 的交点时取等号，而||BE ，所以2MB MD +的最小值为2||BE =故选：D【点睛】关键点睛：建立坐标系，取点1(0,)2E 并求出满足条件||2||M D M E ′′=的点M ′的轨迹是解题的关键.6. 设椭圆()222210x y a b a b+=>>的左焦点为F ，O 为坐标原点，过F 且斜率为1的直线交椭圆于A ，B两点（A 在x 轴上方）.A 关于x 轴的对称点为D ，连接DB 并延长交x 轴于点E ，若DOF S ，DEF S △，DOE S △成等比数列，则椭圆的离心率e 的值为（）A.B.C.D.【答案】D 【解析】【分析】根据DOF S ，DEF S △，DOE S △成等比数列，得到2EF OF OE =⋅，设直线AB 的方程为：()()()112211,,,,,,y x c A x x c B x x c D x x c =+++−−，与椭圆方程联立，再设直线BD 的方程为：()122221x x c y x cx x x x ++−−=−−，令0y =结合韦达定理，得到点E 的坐标，代入2EF OF OE =⋅求解.【详解】解：如图所示：设,,DOF DEF DOE 分别以OF ，EF ，OE 为底，高为h ，则111,,222DOFDEF DOE S OF h S EF h S OE h === ，因为DOF S ，DEF S △，DOE S △成等比数列，所以2DEFDOF DEF S S S =⋅ ，即2EF OF OE =⋅，设直线AB 的方程为：()()()112211,,,,,,y x c A x x c B x x c D x x c =+++−−，联立22221x y a b y x c += =+，消去y 得()2222222220a b x a cx a c a b +++−=，由韦达定理得：2121222222222,2x x x x a ca c ab a b a b−+=−=++⋅，直线BD 的方程为：()1222212x x cy x c x x x x ++−−=−−，令0y =得，()12121222E x x c x x x x x c⋅++=++，则()22121212222222222222222222E x x c x x a x c a c a b a c a b a b a b x x c c c a ⋅−⋅++===−++−++−++，则2EF OF OE =⋅，即为222a a c c c c ⋅−，则()22222c a ac =−，即422430a c a c −+=，即42310e e −+=，解得2e =e =，故选：D7. 已知椭圆()222210x y a b a b+=>>的左、右焦点分别为1F 、2F ，经过1F 的直线交椭圆于A ，B ，2ABF △的内切圆的圆心为I ，若23450++=IB IA IF ，则该椭圆的离心率是（）A.B.23C.D.12【答案】A 【解析】【分析】对23450++= IB IA IF 变形得到2351882IB IF IA +=−，进而得到以22::3:4:5AF BF AB =，结合椭圆定义可求出2AF a =，245,33BF a AB a ==，1AF a =，由余弦定理求解,a c 关系式，求出离心率.【详解】因为23450++= IB IA IF ，所以2351882IB IF IA +=−，如图，在2BF 上取一点M ，使得2:5:3BM MF =，连接IM ，则12IM IA =−，则点I 为AM 上靠近点M 的三等分点，所以22::3:4:5IAF IBF IBA S S S = ，所以22::3:4:5AF BF AB =设23AF x =，则24,5BF x AB x ==，由椭圆定义可知：224AF BF AB a ++=，即124x a =，所以3ax =，所以2AF a =，245,33BF a AB a ==，1AF a = 故点A 与上顶点重合，在2ABF △中，由余弦定理得：222222222222516399cos 52523a a a AB F A F B BAF AB F A a +−+−∠===⋅×，在12AF F △中，2222243cos 25a a c BAF a +−∠==，解得：c a =故选：A【点睛】对于求解圆锥曲线离心率问题，要结合题目中的条件，直接求出离心率或求出,,a b c 的齐次方程，解出离心率，本题的难点在于如何将23450++=IB IA IF 进行转化，需要作出辅助线，结合内心的性质得到三角形2ABF 三边关系，求出离心率.8. 在平面直角坐标系xOy 中，若抛物线C :y 2=2px (0p >)的焦点为F ，直线x =3与抛物线C 交于A ，B 两点，｜AF |=4，圆E 为FAB 的外接圆，直线OM 与圆E 切于点M ，点N 在圆E 上，则OM ON ⋅的取值范围是（）A. 63,925−B. []3,21−C. 63,2125D. []3,27【答案】B 【解析】【分析】由已知及抛物线的定义，可求p ，进而得抛物线的方程，可求A ，B ，F 的坐标，直线AF 的方程，可得圆的半径，求得圆心，设N 的坐标，求得M 的坐标，结合向量数量积的坐标表示，以及辅助角公式和正弦函数的值域，可得所求范围．【详解】解：由题意，设(A ，所以||342pAF =+=，解得2p =，所以抛物线的方程为24y x =，(3,A ，(3,B −，(1,0)F ，所以直线AF 的方程为1)yx =−，设圆心坐标为0(x ，0)，所以2200(1)(3)12x x −=−+，解得05x =，即(5,0)E ，∴圆的方程为22(5)16x y −+=，不妨设0M y >，设直线OM 的方程为y kx =，则0k >，4=，解得43k =，由2243(5)16y x x y= −+=，解得912,55M，设(4cos 5,4sin )N θθ+，所以364812cos sin 9(3cos 4sin )9555OM ON θθθθ⋅=++=++ ，因为[]3cos 4sin5sin()5,5θθθϕ+=+∈−，所以OM ON ⋅∈[]3,21−．故选：B ．【点睛】关键点点睛：本题解题的关键点是：首先求出圆的方程为22(5)16x y −+=，然后利用直线OM 与圆E 切于点M ，求出M 点的坐标，引入圆的参数方程表示N 点坐标，再根据向量数量积的坐标表示及辅助角公式，可得所求范围．.二、选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.9. 已知直线1l ：230ax y a ++=和直线2l ：()3170x a y a +−+−=，下列说法正确的是（） A. 当25a =时，12l l ⊥ B. 当2a =−时，12l l ∥C. 直线1l 过定点()3,0-，直线2l 过定点()1,1−D. 当1l ，2l 【答案】AD 【解析】【分析】A 选项：把a 的值分别代入两直线，根据直线垂直时，斜率相乘为1−，直接判断即可； B 选项，把a 的值分别代入两直线，根据直线平行时，斜率相等判断即可； C 选项，把直线的方程变形，根据直线过定点的定义判断即可；D 选项，由直线平行时，斜率相等，可求得a 得值，排除重合情况，再利用平行直线的距离公式直接求解即可.【详解】对于A ，当25a =时，那么直线1l 为262055x y ++=，直线2l 为3237055x y −+−=，此时两直线的斜率分别为115k =−和25k =，所以有121k k ⋅=-，所以12l l ⊥，故A 选项正确；对于B ，当2a =−时，那么直线1l 为30x y −+=，直线2l 为30x y −+=，此时两直线重合，故B 选项错误；对于C ，由直线1l ：230ax y a ++=，整理可得： ()320a x y ++=，故直线1l 过定点()3,0-，直线2l ：()3170x a y a +−+−=，整理可得：()1370a y x y −+−+=，故直线2l 过定点()2,1−，故C 选项错误；对于D ，当1l ，2l 平行时，两直线的斜率相等，即213a a −−=−，解得：3a =或2a =−，当2a =−时，两直线重合，舍去；当3a =时，直线1l 为3290x y ++=，2l 为3240x y ++=，此时两直线的距离d，故D 选项正确. 故选：AD .10. 已知椭圆2222:1(0)x y C a b a b+=>>的左，右两焦点分别是12,F F ，其中12||2F F c =.直线()():R l y k x c k =+∈与椭圆交于,A B 两点，则下列说法中正确的有（）A. 2ABF △的周长为4aB. 若AB 的中点为M ，则22OMb k k a⋅=C. 若2124AF AF c ⋅=，则椭圆的离心率的取值范围是 D. 若1k =时，则2ABF △【答案】ACD 【解析】【分析】根据椭圆定义可知2ABF △的周长为4a ，可判断A 正确；联立直线和椭圆方程求出点M 的坐标，表示出斜率公式即可得22OMb k k a⋅=−，可得B 正确；由2124AF AF c ⋅= 易知A 点在以()0,0为圆心，半径为的圆上，即可得圆222115x y c +=与椭圆22221x y a b+=有交点，需满足b a ≤≤，可得离心率e ∈，可知C 正确；将1k =代入联立的方程可得2ABF △的面积12S c x x =−，可得D 正确.【详解】由12||2F F c =可知，()()12,0,,0F c F c −；显然直线()():R l y k x c k =+∈过点()1,0F c −，如下图所示：由椭圆定义可知2ABF △的周长为2212214AB AF BF AF AF BF BF a ++=+++=，所以A 正确；设()()1122,,,A x y B x y ，中点()0,Mx y ；将直线和椭圆方程联立()22221x y a b y k x c += =+ ，消去y 整理可得()2222222222220b a k x a k cx a k c a b +++−=；由韦达定理可得22122222a k c x x b a k +=−+，所以221202222x x a k cx b a k+==−+，代入直线方程解得20222b cky b a k =+，即222222222,a k c b ck M b a k b a k − ++；所以2222222222222200OMb ckb ck b b a k k a kc a k c a k b a k −+==−=−−−+，可得2222OMk b k a k b k a⋅−==⋅−，所以B 错误；根据B 选项，由2124AF AF c ⋅=可得()()2222111111,4,c x y c x y x c y c −⋅=+−−=−−−，可得222115x y c +=，即A 点在以()0,0圆上；又A 点在椭圆上，即可得圆222115x y c +=与椭圆22221x y a b+=有交点，根据对称性可知b a ≤≤，即22256c a c ≤≤，所以可得离心率e ∈，即C 正确；若1k =时，由选项B 可知联立直线和椭圆方程可得()2222222220b axa cx a c ab +++−=；所以可得22222121222222,a c a c a b x x x x b a b a−+=−=++；所以12x x −==易知2ABF △面积12112212121122S F F y F F y c y y c x x =+=−==− 即可得2ABF△，故D 正确. 故选：ACD【点睛】方法点睛：在求解圆锥曲线与直线的位置关系时，特别是在研究跟焦点三角形有关的问题时，经常将直线和圆锥曲线联立并利用韦达定理求解，注意变量间的相互转化即可.11. 已知斜率为k 的直线交抛物线()220y px p =>于()11,A x y 、()22,B x y 两点，下列说法正确的是（） A. 12x x 为定值B. 线段AB 的中点在一条定直线上的的C.11OA OBk k +为定值（OA k 、OB k 分别为直线OA 、OB 的斜率） D. AF BF为定值（F 为抛物线的焦点）【答案】BC 【解析】【分析】分析可知，0k ≠，设直线AB 的方程为y kx m =+，将直线AB 的方程与抛物线的方程联立，利用韦达定理可判断A 选项；求出线段AB 中点的纵坐标，可判断B 选项；利用斜率公式结合韦达定理可判断C 选项；利用抛物线的焦半径公式可判断D 选项.【详解】若0k =，则直线AB 与抛物线()220y px p =>只有一个交点，不合乎题意，则0k ≠，设直线AB 的方程为y kx m =+，联立22y kx m y px=+ = 可得()222220k x km p x m +−+=， ()2222224480km p k m p kmp ∆=−−=−>，对于A 选项，2122m x x k =不一定是定值，A 错；对于B 选项，设线段AB 的中点为()00,P x y ，则12022x x p kmx k+−==， 00p km p y kx m m k k−++为定值，故线段AB 的中点在定直线py k =上，B 对；对于C 选项，()121212122222111222OA OB p kmm k x x m x x y y k k k y y p p p k−+++++=+====为定值，C 对；对于D 选项，21222222222p km p p x x AF k p p BF x x −+−+==++不一定为定值，D 错.故选：BC.12. 已知圆22:(2)1M x y +−=，点P 为x 轴上一个动点，过点P 作圆M 的两条切线，切点分别为A ，B ，直线AB 与MP 交于点C ，则下列结论正确的是（）A. 四边形PAMB周长的最小值为2 B. ||AB 的最大值为2C. 若(1,0)P ，则三角形PAB 的面积为85D.若Q ，则||CQ 的最大值为94【答案】CD 【解析】【分析】首先设||MP t =，对于选项A ，根据题意，表达四边形PAMB 周长关于t 的函数，由t 的取值范围求函数的最小值可判断A 错误；对于选项B ，根据等面积法，求出||AB 关于t 的函数关系，由t 的取值范围求函数的最大值可判断B 错误；对于选项C ，根据题意，计算PAB 底和高，求出面积判断C 正确；对于选项D ，设动点(,0)P m AB 的方程与直线PM 的方程，二者联立消去m 得到二者交点C 的轨迹是圆，||CQ 的最大值为圆心1O 与Q 距离加半径，可判断D 正确．【详解】对于选项A ，设||MP t =，则||||BP AP ==则四边形PAMB周长为2+，则当t 最小时周长最小，又t 最小值为2，所以四边形PABM周长最小为2+，故A 错误；对于选项B ，12||||2MAP PAMBS S MP AB ==△四边形，即1121||22t AB ××=，所以||AB =，因为2t，所以)||AB ∈，故B 错误；对于选项C ，因为(1,0)P，所以||MP =t =，所以||AB ，1||||2AC AB ==，||2AP =，||PC ，所以三角形PAB 的面积为18||||25AB PC =，故C 正确；的对于选项D ，设(,0)P m ，()11,A x y ,则切线PA 的方程为()()11221x x y y +−−=，又因为直线PA 过点(,0)P m ，代入可得()()112021x m y +−−=化简得11230mx y −+= 设()22,B x y ,同理可得22230mx y −+=，因此点,A B 都过直线230mx y −+=，即直线AB 的方程为230mx y −+=， MP 的方程为22y x m=−+，二者联立得，22230y x mmx y =−+−+=①②，由①式解出22x m y =−，代入②式并化简得227302x y y +−+=，配方得2271()416x y +−=，2y ≠，所以点C 的轨迹是以(70,4)为圆心，14为半径的圆，设其圆心为1O ，所以||CQ的最大值为1119||2444O Q R ++=+=，故D 正确．故选：CD.【点睛】本题综合性较强，难度较大，具备运动变化的观点和函数思想是解题的关键，对于AB 选项，设变量||MP t =，用t 分别表达周长函数和距离函数求最值，对于D 选项，设出动点(),0P m ，分别表达直线AB 和MP 的方程，联立消去m ，得到动点C 的轨迹，进一步求解答案.三、填空题：本题共4小题，每小题5分，共20分.13. 已知实数0,0a b ><的取值范围是______.【答案】[)2,1−− 【解析】【分析】根据题意，设直线l ：0ax by +=的几何意义为，点(1,到直线l 的距离，即可求出取值范围.【详解】根据题意，设直线l ：0ax by +=，设点(1,A那么点(1,A 到直线l的距离为：d因为0,0a b ><，所以d =l 的斜率0ak b=−>，当直线l的斜率不存在时，1d ==，所以1d >，当OA l ⊥时，max 2d OA ===，所以12d <≤，即12<≤，=21−≤<−，故答案为：[)2,1−−.14. 形如()0b y ax b x=+≠的函数图象均为双曲线，则双曲线4135y x x =−的一个焦点坐标为______.【答案】或【解析】【分析】先确定双曲线的渐近线、对称轴方程，确定焦点位置及实半轴a ，最后由渐近线与对称轴夹角正切值确定b ，利用双曲线性质求出焦点. 【详解】由4135−x y =x 知，其两条渐近线分别为403x x =,y =，所以双曲线4135−x y =x 的两条对称轴为403xx =,y =的夹角平分线，令43x y =的倾斜角为0,2πθ ∈，则4tan 3θ=，且一条对称轴倾斜角为42πθ+，而22tan42tan 31tan 2θθθ==−，则22tan 3tan 2022θθ+−=，解得tan 22θ=−（舍去），1tan 22θ=，所以11+tan 1+22tan ==31421tan 122π +=−−θθθ，即一条对称轴为3y x =，故另一条对称轴为13y x =−，显然13y x =−与4135−x y =x有交点, 即为双曲线的顶点，则双曲线的实半轴长a = 而渐近线0x =与对称轴13y x =−夹角的正切值为3，3b a =，又因为=a，所以33b =a = 由2222641553+=c =a +b =，设焦点为13 − m,m ，则221433 +−=m m ，所以m =, .故答案为：或.15. 在椭圆2213x y +=上有点31,22P ，斜率为1的直线l 与椭圆交于不同的A ，B 两点（且不同于P ），若三角形ABO 的外接圆恰过点P ，则外接圆的圆心坐标为______. 【答案】71,88 −【解析】【分析】根据题意得到():0AB y x b b =+≠，联立直线AB 与椭圆方程，利用韦达定理求得12x x +，12x x ，12y y +，12y y ；法一：先利用点斜式求得,OP AB 的中垂线方程，联立两者方程即可求得圆心C ，再由半径相等得到2222AC BC OC +=，利用两点距离公式，代入上述式子得到关于b 的方程，解之即可；法二：根据题意得到圆的方程，联立直线AB 与圆的方程，利用韦达定理求得12x x +，12x x ，进而得到,D E 关于b 的表达式，又由点P 在圆上得到关于b 的方程，解之即可.【详解】依题意，设()11,A x y ，()22,B x y ，直线():0AB y x b b =+≠，联立2213y x bx y =++=，消去y ，得246330x bx b ++−=，所以1232x x b +=−，()212314b x x −=，则121212y y x b b b x ++=+=+，()()2121234b y y x b b x =+−=+， .法一：因为31,22P ，所以10123302OP k −==−，OP 的中点坐标为3,414 ，OP 中垂线的斜率为3−，所以OP 中垂线方程为113:344l y x −=−−，即532y x =−+，因为AB 的斜率为1，AB 的中点坐标为1212,22x x y y ++ ，即31,44b b− ，所以AB 中垂线的斜率为1−，则AB 中垂线方程213:44l y b x b−=−+，即12y x b =−−，联立53212y x y x b=−+ =−− ，解得54354b x b y + = + =− ，则圆心坐标535,44b b C ++ − ，因为22222AC BC OC AC +==，所以222222112253515355354424444b b b b b b x y x y +++++++=−+++−++，整理得()()22221212121253522044b b x x x x y y y y ++ +−+++++=，因为1232x x b +=−，()212314b x x −=，1212y y b +=，21234b y y −=，所以()22222112123624x x x x b x x +=+−+=，()2222211212624y b y y y y y −+=+−+=，则2203563614242532244b b b b b b ++  −++=  − + +−× ，整理得22530b b ++=，解得32b =−，1b =-，当1b =-时，直线:1AB y x =−，显然直线AB 过P 点，舍去，当32b =−时，()2299361633361633044b b ∆=−−=×−×−>，直线3:2AB y x =−，满足题意，又535,44b b C ++ −，所以此时圆心坐标71,88C − . 法二：因为圆过原点()0,0O ，所以设圆的方程为220x y Dx Ey +++=()220D E +>，联立220y x b x y Dx Ey =++++=，消去y ，得()22220x b D E x b Eb +++++=，所以1222b D E x x +++=−，2122b Ebx x =+，又1232x x b +=−，()212314b x x −=，所以3222b D E b ++−=−，()223142b b Eb −+=，所以1322D b b=+，1322E b b =−，因为P 点在圆上，所以913104422D E +++=，即530D E ++=，所以13135302222b b b b +++−=，整理得22530b b ++=，解得32b =−，1b =-，当1b =-时，直线:1AB y x =−，显然直线AB 过P 点，舍去，当32b =−时，1332722234D =×−+×−=− ，1332122234E =×−−×−= ，对于方程2246330x bx b ++−=，有()2299361633361633044b b ∆=−−=×−×−>，对于方程()22220x b D E x b Eb +++++=，即29152028x x −+=，有2915Δ42028 =−−××>，满足题意，又因为外接圆的圆心坐标为,22D E −− ，所以圆心为71,88− . 故答案为：71,88 −.【点睛】方法点睛：直线与圆锥曲线位置关系的题目，往往需要联立两者方程，利用韦达定理解决相应关系，其中的计算量往往较大，需要反复练习，做到胸有成竹.16. 已知直线l 过抛物线C ：24y x =的焦点F ，与抛物线交于A 、B 两点，线段AB 的中点为M ，过M作MN 垂直于抛物线的准线，垂足为N ，则2324NF AB +的最小值是______.【答案】【解析】【分析】设直线:1AB x my =+，()11,A x y ，()22,B x y ，联立抛物线方程得到关于y 的一元二次方程，得到韦达定理式，求出,M N 坐标，利用弦长公式和两点距离公式得到AB 和NF 的表达式，再利用基本不等式即可得到答案.【详解】显然当直线AB 斜率为0时，不合题意；故设直线:1AB x my =+，()11,A x y ，()22,B x y ，联立抛物线方程有2440y my −−=，则216160m ∆=+>，124y y m +=，124y y =−，则1222My y y m +==，111x my =+，221x my =+，则()21221224221222M m y y x x m x m ++++====+，则()221,2M m m +，准线方程为=1x −，()1,0F ，则()1,2N m −，()22||41AB y m =−=+，()()()22222||1124441||[4,)NF m m m AB =++−=+=+=∈+∞，所以232||32||||4||4NF AB AB AB +=+==，当且仅当32||||4AB AB =，即()2||41AB m =+=时等号成立，此时m .故答案为：【点睛】关键点点睛：本题的关键是采取设线法联立抛物线方程得到韦达定理式，再利用中点公式得到,M N 点坐标，最后利用弦长公式和两点距离公式得到相关表达式，最后利用基本不等式即可得到答案.四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.17. 已知点()1,0A −和点B 关于直线l ：10x y +−=对称．（1）若直线1l 过点B ，且使得点A 到直线1l 的距离最大，求直线1l 的方程；（2）若直线2l 过点A 且与直线l 交于点C ，ABC 的面积为2，求直线2l 的方程．【答案】（1）30x y +−=（2）0y =或=1x − 【解析】【分析】根据对称先求出B 点坐标（1）过点B 到点A 距离最大的直线与直线AB 垂直，从而求出直线方程；（2）画出图像，可求出点C 到直线AB 的距离，又点C 在直线l 上，可设出C 点的坐标，利用点到直线的距离公式求出C ，又直线过点A ，利用两点A 、C 即可求出直线2l 的方程. 【详解】解：设点(),B m n则1102211m nn m −+ +−== + ，解得：12m n = = ，所以点()1,0A −关于直线l ：10x y +−=对称的点的坐标为()1,2B（1）若直线1l 过点B ，且使得点A 到直线1l 的距离最大，则直线1l 与过点AB 的直线垂直，所以1k =−，则直线1l 为：()21y x −=−−，即30x y +−=. （2）由条件可知：AB =，ABC 的面积为2，则ABC的高为h =又点C 在直线l 上，直线l 与直线AB 垂直，所以点C 到直线AB. 直线AB 方程为1y x =+，设(),C a b，即1b a =−或3b a =+又1b a =−，解得：10a b == 或12a b =− =则直线2l 为：0y =或=1x −【点睛】本题考查求点关于直线的对称点，考查直线与直线相交的综合应用..方法点睛：（1）设出交点坐标（2）两点的中点在直线上，两点连线与原直线垂直，列方程组；（3）解出点坐标.18. 已知圆221:(1)5C x y +−=，圆222:420C x y x y +−+=.（1）求圆1C 与圆2C 的公共弦长；（2）求过两圆的交点且圆心在直线241x y +=上的圆的方程.【答案】（1）（2）22317222x y −++=【解析】【分析】（1）将两圆方程作差可求出公共弦的方程，然后求出圆心1C 到公共弦的距离，再利用弦心距，半径和弦的关系可求得答案，（2）解法一：设过两圆的交点的圆为()()222242240,1x y x y x y y λλ+−+++−−≠−，求出圆心坐标代入241x y +=中可求出λ，从而可求出圆的方程，解法二：将公共弦方程代入圆方程中求出两圆的交点坐标，设所求圆的圆心坐标为(),a b ，然后列方程组可求出,a b ，再求出圆的半径，从而可求出圆的方程.【小问1详解】将两圆的方程作差即可得出两圆的公共弦所在的直线方程，即()()222242240x y x y x y y +−+−+−−=，化简得10x y −−=，所以圆1C 的圆心()0,1到直线10x y −−=的距离为d ，则22215232AB r d =−=−=，解得AB =所以公共弦长为【小问2详解】解法一：设过两圆的交点的圆为()()222242240,1x y x y x y y λλ+−+++−−≠−，则2242240,1111x y x y λλλλλλ−+−+−=≠−+++；由圆心21,11λλλ− −++ 在直线241x y +=上，则()414111λλλ−−=++，解得13λ=，所求圆的方程为22310x y x y +−+−=，即22317222x y −++=. 解法二：由（1）得1y x =−，代入圆222:420C x y x y +−+=，化简可得22410x x −−=，解得x =；当x =时，y =x =时，y =；设所求圆的圆心坐标为(),a b ，则2222241a b a b a b −+=++ += ，解得3212a b ==−；所以222317222r =+−−= ；所以过两圆的交点且圆心在直线241x y +=上的圆的方程为22317222x y −++=19. 已知双曲线2222:1(0,0)x y E a b a b−=>>的焦距为10，且经过点M ．A ，B 为双曲线E 的左、右顶点，P 为直线2x =上的动点，连接P A ，PB 交双曲线E 于点C ，D （不同于A ，B ）．（1）求双曲线E 的标准方程．（2）直线CD 是否过定点？若过定点，求出定点坐标；若不过定点，请说明理由．【答案】（1）221169x y −= （2）直线CD 过定点，定点坐标为(8,0)．【解析】【分析】（1）方法一：将M 代入方程，结合222+=a b c 求得,a b 得双曲线方程；方法二：根据双曲线定义求得a 得双曲线方程.（2）方法一：设CD 的方程为x my t =+，与双曲线联立，由A 点与C 点写出AC 方程，求出p y ，由B 点与D 点写出BD 方程，求出p y ，利用两个p y 相等建立关系式，代入韦达定理可求得t 为定值.方法二：设CD 的方程为,(2,)x my t P n =+，与双曲线联立，由P 点与A 点写出AC 方程，由P 点与B 点写出BD 方程，将()()1122,,,C x y D x y 代入以上两方程，两式相比消去n 建立关系式，代入韦达定理可求得t 为定值. 【小问1详解】法一．由222225,64271,a b ab += −=解得2216,9a b ==，∴双曲线E 的标准方程为221169x y −=．法二．左右焦点为()()125,0,5,0F F −，125,28c a MF MF ∴==−=，22294,a b c a ∴===−，∴双曲线E 的标准方程为221169x y −=．【小问2详解】直线CD 不可能水平，故设CD 方程为()()1122,,,,x my t C x y D x y =+，联立221169x my t x y =+−= 消去x 得()()2222916189144=0,9160m y mty t m −++−−≠， 12218916mt y y m −∴+=−，21229144916t y y m −=−，12y y −，AC 的方程为11(4)4y yx x ++，令2x =，得1164p y y x =+，的BD 的方程为22(4)4y yx x −−，令2x =，得2224p y y x −=−，1221112212623124044y y x y y x y y x x −∴=⇔−++=+− ()()21112231240my t y y my t y y ⇔+−+++=()()1212431240my y t y t y ⇔+−++= ()()()()12121242480my y t y y t y y ⇔+−++−−=()22249144(24)180916916m t t mt m m −−⇔−±=−−3(8)(0m t t ⇔−±−=(8)30t m ⇔−±=，解得8t =3m =±，即8t =或4t =（舍去）或4t =−（舍去）， ∴CD 的方程为8x my =+，∴直线CD 过定点，定点坐标为(8,0)．方法二．直线CD 不可能水平，设CD 的方程为()()1122,,,,,(2,)x my t C x y D x y P n =+，联立22,1,169x my t x y =+ −=，消去x 得()2229161891440m y mty t −++−=， 2121222189144,916916mt t y y y y m m −−∴+==−−， AC 的方程为(4)6nyx =+，BD 的方程为(4)2ny x −−， ,C D 分别在AC 和BD 上，()()11224,462n ny x y x ∴=+=−−，两式相除消去n 得()211211223462444x y y y x x x y −−−=⇔+=+−，又22111169x y −=，()()211194416x x y ∴+−=．将()2112344x y x y −−+=代入上式，得()()1212274416x x y y −−−=⇔()()1212274416my t my t y y −+−+−=()()221212271627(4)27(4)0m y y t m y y t ⇔++−++−=⇔()22222914418271627(4)27(4)0916916t mtm t m t m m −−++−+−=−−．整理得212320t t +=−，解得8t =或4t =（舍去）． ∴CD 方程为8x my =+，∴直线CD 过定点，定点坐标为(8,0)．【点睛】圆锥曲线中直线过定点问题通法，先设出直线方程y kx m =+，通过韦达定理和已知条件若能求出m 为定值可得直线恒过定点，若得到k 和m 的一次函数关系式，代入直线方程即可得到直线恒过定点.20. 已知双曲线22:154x y Γ−=的左右焦点分别为1F ，2F ，P 是直线8:9l y x =−上不同于原点O 的一个动点，斜率为1k 的直线1PF 与双曲线Γ交于A ，B 两点，斜率为2k 的直线2PF 与双曲线Γ交于C ，D 两点．（1）求1211k k +的值；（2）若直线OA ，OB ，OC ，OD 的斜率分别为OA k ，OB k ，,OC k ，OD k ，问是否存在点P ，满足0OA OB OC OD k k k k +++=，若存在，求出P 点坐标；若不存在，说明理由．【答案】（1）94−；（2）存在98(,)55P −或98(,)55P −满足题意．【解析】【分析】（1）设出(9,8)P λλ−，然后计算1211k k +即可得；（2）假设存在，设设00(9,8)P x x −，写出直线AB 方程，设1122(,),(,)A x y B x y ，直线方程代入双曲线方程整理后应用韦达定理得1212,x x x x +，代入到式子OA OB k k +中，同理设3344(,),(,)C x y D x y ，直线CD方程代入双曲线方程，应用韦达定理，代入计算OC OD k k +，然后由条件0OA OB OC OD k k k k +++=求得0x 得定点坐标．的【小问1详解】由已知1(3,0)F −，2(3,0)F ，设(9,8)P λλ−，(0)λ≠， ∴1839k λλ=−−，2893k λλ−=−，121139939884k k λλλλ−−−+=+=−−；【小问2详解】设00(9,8)P x x −，（00x ≠），∴010893x k x −=+，∴直线AB 的方程是008(3)93x yx x −++，设11(,)A x y ，22(,)B x y ，008(3)93x yx x −++代入双曲线方程得2220203204(69)20(93)x x x x x −++=+，即222200000(549)480(112527045)0x x x x x x x ++−−++=， 2012200480549x x x x x +=++，20012200112527045549x x x x x x ++=−++， 00121212012012883()33(2)[2]9393OA OB x x y y x x k k x x x x x x x x ++=+=−++=−+++2000200008832(2(2)93932561x x x x x x x =−+=−−++++ 2000220000082(31)16(31)9325612561x x x x x x x x −+−+=⋅=+++++，同理CD 的方程为008(3)93x yx x −−−，设33(,)C x y ，44(,)D x y ，仿上，直线方程代入双曲线方程整理得：222200000(549)4801125270450x x x x x x x −++−+−=，234200480549x x x x x +=−−+，20034200112527045549x x x x x x −+−=−+， ∴2303400423403400083()83480[2](2)9393112527045OC ODy x x x x x y k k x x x x x x x x −+−⋅+=+=−=−−−−+ 20000220000083216(31)(2)9325613(2561)x x x x x x x x x −−−=−=−−+−+．由0OA OB OC OD k k k k +++=得00022000016(31)16(31)025613(2561)x x x x x x x −+−−+=++−+，整理得200(251)0x x −=，∵00x ≠，∴015x =±， ∴存在98(,)55P −或98(,)55P −满足题意．【点睛】方法点睛：是假设定点存在，题中设00(9,8)P x x −，写出直线方程，设出直线与双曲线的交点坐标如1122(,),(,)x y x y ，直线方程代入双曲线方程整理后应用韦达定理得1212,x x x x +，代入到式子OA OB k k +中，最后利用已知条件求得0x ，若求不出结果说明不存在．本题考查了学生的逻辑能力，运算求解能力，属于困难题．21. 抛物线2:2(0)C x py p =>的焦点为F ，准线为,l A 为C 上的一点，已知以F 为圆心，FA 为半径的圆F 交l 于,B D 两点，（1）若90,BFD ABD ∠=的面积为p 的值及圆F 的方程（2）若直线y kx b =+与抛物线C 交于P ，Q 两点，且OP OQ ⊥，准线l 与y 轴交于点S ，点S 关于直线PQ 的对称点为T ，求||FT 的取值范围.【答案】（1）2p =，圆F 的方程为()2218x y +−=（2）(],4p p 【解析】【分析】（1）由焦半径和圆的半径得到2A py FA FD +===，结合ABD △面积求出2p =，圆F 的方程为()2218x y +−=；（2）表达出0,2p S −关于直线PQ 的对称点的坐标，利用垂直关系列出方程，求出2b p =，从而利用两点间距离公式表达出(],2FT p p ==. 【小问1详解】由对称性可知：90,BFD FS BS DS p ∠=°===，设(),A A A x y，由焦半径可得：2A py FA FD +===，112222ABD A p S BD y p=⋅⋅+=×=解得：2p =圆F 的方程为：()2218x y +−=【小问2详解】由题意得：直线PQ 的斜率一定存在，其中0,2p S−，设0,2p S−关于直线PQ 的对称点为(),T m n ，则12222p n m kp n m k b + =− − =⋅+ ，解得：221212b p m k k b p pn k + =− + +=− + ，联立y kx b =+与22x py =得：2220x pkx pb −−=，设()()1122,,,P x y Q x y ，则12122,2x x pk x x pb +==−，则()()()2212121212y y kx b kx b k x x kb x x b =++=+++，则()()22121212121x x y y k x x kb x x b +=++++ ()222221220pb k pk b b pb b −+++=−+=，解得：0b =（此时O 与P 或Q 重合，舍去）或2b p =，所以FT =(],4p p ==，【点睛】圆锥曲线相关的取值范围问题，一般思路为设出直线方程，与圆锥曲线联立，得到两根之和，两根之积，由题干条件列出方程，求出变量之间的关系，再表达出弦长或面积等，结合基本不等式，导函数，函数单调性等求出最值或取值范围.22. 如图，已知点P 是抛物线24C y x =：上位于第一象限的点，点()20A −，，点,M N 是y 轴上的两个动点(点M 位于x 轴上方)，满足,PM PN AM AN ⊥⊥，线段PN 分别交x 轴正半轴、抛物线C 于点,D Q ，射线MP 交x 轴正半轴于点E ．（1）若四边形ANPM 为矩形，求点P 的坐标；（2）记,DOP DEQ △△的面积分别为12S S ，，求12S S ⋅的最大值．【答案】（1）(2,P（2）192 【解析】【分析】（1）根据矩形性质，可得对角线互相平分，即AP 的中点在y 轴上，然后点P 在抛物线，即可得(2,P ；（2）联立直线PQ 方程与抛物线C ，根据韦达定理求得,P Q 两点的纵坐标关系，再根据,PM PN AM AN ⊥⊥条件判断MOE △与DON △相似，进而求得,D E 两点的坐标关系，再表示并化简12S S ⋅为关于m 的函数，根据,D E 两点的位置关系，以线段DE 为直径的圆K 与抛物线C 有交点得出关于m 的约束，即可确定12S S ⋅中m 取值范围，最后可得12max ()(4192S S g ⋅=−= 【小问1详解】当四边形ANPM 为矩形时，AP 的中点在y 轴上，则有：2P A x x =−=故(2,P -【小问2详解】设点(,0)D m ，直线PQ 方程：x m ty −=，显然有0,0m t >≠联立直线PQ 与抛物线C ，得：24x m ty y x −==消去x 得：2440y ty m −−=则有：4P Q y y m ⋅=− 由AM AN ⊥，得：2||||||4OM ON OA ⋅==又由PM PN ⊥，可得：△MOE ∽△DON 则有：||||||||OM OE OD ON = 从而||||||||4OE OD OM ON ⋅=⋅=，即4E D x x ⋅=所以4E x m=，进而有：4||E D DE x x m m =−=− 结合||,4P Q OD m y y m =⋅=−（注：由E D x x >，得4m m >，故有02m <<）可得：12111(||||)(||||)||||||224P Q P Q S S OD y DE y OD DE y y ⋅=⋅⋅⋅⋅⋅=⋅⋅⋅ 314()444m m m m m m=⋅⋅−⋅=−+ 又由题意知，存在抛物线上的点P 满足条件，即以线段DE 为直径的圆K 与抛物线C 有交点，且易得圆K 方程：24()()0x m x y m−⋅−+=联立抛物线C 与圆K ，得224()()04x m x y my x−⋅−+= = 消去y 得：24(4)40x m x m−+−+= 由0∆≥，结合02m <<，可解得：04m <≤−令3()4g m m m =−+，求导可知()g m在上单调递增又4−≤ 故有：()g m在(0,4−上单调递增因此，12max ()(4192S S g ⋅=−=【点睛】解答直线与抛物线的题目时，时常把两个曲线的方程联立，消去x (或y )建立一元二次方程，然后借助根与系数的关系，并结合题设条件建立有关参变量的等量关系；在求解相关最值问题时，通常是先建立目标函数，然后应用函数的知识来解决问题；。

杭州外国语学校2013-1高二期中数学试卷(文)

杭州外国语学校2013-1高二年级期中考试数学试卷注意事项：1、考试时间100分钟，本试卷满分100分；2、本场考试不准使用计算器等计算工具；3、请用蓝、黑色钢笔或圆珠笔答题，在答题卷相应处写上班级、姓名、学号，所有答案均做在答卷的相应位置上，做在试题卷上无效.一、选择题（本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一个符合题目要求的）1、双曲线2213y x -=的渐近线方程是（） .A y x =± .B 13y x =± .C y = .D3y x =±2. 若命题“p q ∧”为假，且“p ⌝”为假，则（） .A “p q ∨”为假 .B q 假 .C q 真 .D 不能判断q 的真假3.抛物线0212=+x y 的准线方程为（）.A 41=x .B 41-=x .C 81=x .D 81-=x4、命题“存在x Z ∈，使22x x m ++≤0”的否定是（）.A 存在x Z ∈使22x x m ++0> .B 对任意x Z ∈使22x x m ++0>.C 对任意x Z ∈使22x x m ++≤0 .D 不存在x Z ∈使22x x m ++0> 5. 一个三角形在其直观图中对应一个边长为1的正三角形，原三角形的面积为（）.A 46.B 43 .C 23 .D 26 6. 已知c 是椭圆)0(12222>>=+b a b y ax 的半焦距, 则a c b +的取值范围是 ( ).A ),1(∞+ .B ),2(∞+ .C )2,1( .D ]2,1(7. 双曲线22221x y a b -=与椭圆22221x y m b+= (a>0，m>b>0)的离心率互为倒数，那么以a 、b 、m 为边长的三角形一定是( )A ．锐角三角形B ．直角三角形C ．钝角三角形D ．等腰三角形8.如图，1111D C B A ABCD -是正方体， 4111111B A F D E B ==，则1BE 与1DF 所成角的余弦值是（）.A 1715 .B 21 .C 178 .D 239. 若直线//l 平面α，直线m ⊂α，则l 与m 的位置关系是（） .A //l m .B l 与m 异面 C 、l 与m 相交 D 、l 与m 没有公共点10. 已知 A B 、为平面内两定点,过该平面内动点M 作直线AB 的垂线,垂足为N .若2MN AN NB λ=⋅,其中λ为常数,则动点M 的轨迹不可能是（）A ．圆B ．椭圆C ．抛物线D ．双曲线二、填空题（本大题共6小题，每小题4分，共24分）11.已知a R ∈，则“3a >”是“23a a >”的条件.12. 棱长为4的正方体的各顶点都在球面上，则该球的表面积为 13. 已知一个几何体的三视图及其尺寸如图所示（单位cm ），则它的体积为 3cm14.圆0104422=---+y x y x 上的点到直线014=-+y x 的最大距离与最小距离的差是为 .15. 已知双曲线的中心为原点，F (3,0)是焦点，过F 的直线l 与双曲线相交于A ，B 两点，且AB 的中点为N (－12，－15)，则双曲线的方程 .16.若直线mx ＋ny ＝4与圆O ：x 2＋y 2＝4没有交点，则过点P (m ，n )的直线与椭圆x 29＋y 24＝1的交点个数为____________三、解答题（本题有5小题，总共46分，请写出必要的解答过程。

浙江杭州地区(含周边)重点中学2024年高二下学期期中考试数学试卷

2023学年第二学期期中杭州地区（含周边）重点中学高二年级数学学科试题第I 卷一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一考生须知：1.本卷满分150分，考试时间120分钟；2.答题前，在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号并填涂相应数字；3.所有答案必须写在答题卷上，写在试卷上无效4.考试结束后，只需上交答题卷。

项是符合题目要求的。

1.在ABC △中，三个内角A ，B ，C 成等差数列，则()sin A C +=（） A.12D.12.已知()23P B A =，()38P AB =，则()P A =（） A.916 B.316 C.14 D.343.直线3450x y −+=关于x 轴对称的直线的方程为（）A.3450x y +−=B.3450x y ++=C.3450x y −+=D.3450x y −−=4.降雨量是指从天空降落到地面上的雨水，未经蒸发、渗透、流失而在水平面上积聚的水层深度，一般以毫米为单位，它可以直观地表示降雨的多少，目前，测定降雨量常用的仪器有雨量筒和量杯.测量时，将雨量筒中的雨水倒在量杯中，根据杯上的刻度就可知道当天的降雨量.某兴趣小组同学为测量降水量，自制了一种圆台形的雨量器（如图）.某次降水，这种容器收集到的雨水高度为150mm ，则该次降水的降雨量最接近（）A.60mmB.65mmC.70mmD.75mm5.82x 的展开式中的常数项是（） A.7 B.-7 C.28 D.-286.若函数()321132f x x x b =−+有两个零点，则（） A.0b = B.16b = C.16b =− D.0b =或16b = 7.将双曲线22122x y −=绕原点逆时针旋转45°后，能得到反比例函数1y x =的图象（其渐近线分别为x 轴和y 轴），所以我们也称反比例函数1y x =的图象为双曲线.同样“对勾函数”y x =象绕原点旋转得到，则此“对勾函数”所对应的双曲线的实轴长为（）A. B.4 C. D.8.记由0，1，2，3，4五个数字组成的五位数为12345a a a a a .则满足“对任意(),15i i N i ∈≤≤，必存在(),15j i j N j ≠∈≤≤，使i j a a =”的五位数的个数为（）A.120B.160C.164D.172二、多项选择题：本题共3小题，每小题6分，共18分.在每小题给出的四个选项中，有多项符合题目要求.全部选对的得6分，有选错的得0分，部分选对的得部分分.9.下列命题是真命题的是（）A.对向量a ，b ，若0a b ⋅= ，则0a = 或0b =B.对复数1z ，2z ，若120z z ⋅=，则10z =或20z =C.对向量a ，b ，若220a b += ，则0a b ==D.对复数1z ，2z ，若22120z z +=，则120z z == 10.设等比数列{}n a 的公比为q ，其前n 项和为n S ，前n 项积为n T ，若11a >，且202220231a a ⋅>，()()20222023110a a −⋅−<，下列结论正确的是（）A.20232024S S <B.2022202410a a −<C.数列{}n T 无最大值D.2022T 是数列{}n T 中的最大值 11.设抛物线()220y px p =>焦点为F ，()11,A x y ，()22,B x y 是抛物线上两点，下列选项中是“直线AB 经过焦点F ”的必要不充分条件的是（） A.234OA OB p ⋅=− B.212y y p =− C.224p xx = D.112FA FB P+= 第Ⅱ卷三、填空题：本题共3小题，每小题5分，共15分.12.函数()2327ln 2f x x x =−在区间[]1,2上的最大值为____________. 13.在空间直角坐标系中，O 为坐标原点，若()1,0,0OA = ，()0,1,0OB = ，()0,0,2OC = ，则点O 到平面ABC 的距离为____________.14.已知数列{}n a 满足()()*111n n na n a n N +−+=∈，32a =，则1a =____________，2024a =___________.四、解答题：本题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤15.（本题满分13分）如图，在平面四边形ABCD 中，6AB BC ==，BD BC ⊥，AC 为BCD ∠的平分线，且cos ACB ∠. （I ）求线段AC 的长；（Ⅱ）求ACD △的面积.16.（本题满分15分）已知函数()()e x f x ax a R =−∈.（I ）当1a =时，求曲线()y f x =在()()1,1f 处的切线方程；（Ⅱ）若()0f x ≥恒成立，求实数a 的取值范围.17.（本题满分15分）如图，四棱锥A BCDE −中，平面ABC ⊥平面BCDE ，ABC △是边长为2的等边三角形，底面BCDE 是矩形，且BE =. （I ）若点G 是AE 的中点，（i ）求证：AC ∥平面BDG ；（ii ）求直线DG 与平面ABC 所成角的正弦值；（Ⅱ）在线段AB 上是否存在一点F ，使二面角B CE F −−的大小为4π.若存在，求AF AB的值；若不存在，请说明理由.18.（本题满分17分）已知抛物线C ：22x y =，点()00,D x y 为抛物线C 外一点（如图），过点D 作C 的两条切线，切点分别为A ，B .（I ）求证：直线AB 的方程为000x x y y −−=；（Ⅱ）若()00,D x y 在直线12y =−上，以50,2E为圆心的圆与直线AB 相切，且切点为线段AB 的中点，求该圆的方程.19.（本题满分17分）甲口袋中装有2个黑球和1个白球，乙口袋中装有1个黑球和2个白球.设从甲、乙两个口袋中各任取一个球交换放入另一个口袋为一次操作，经过n 次这样的操作，记甲口袋中黑球个数为n X .（I ）写出1X 的分布列并计算()1E X ；（Ⅱ）某人重复进行了100次操作，记1,00,0n n n X a X = =≠ ，(),1100n N n ∈≤≤，求该数列{}n a 的前100项和100S 的最大值；（Ⅲ）定性分析当交换次数趋向于无穷时，()n E X 趋向的值.（简要说明你的理由）。

浙江省杭州外国语学校2014届高三物理上学期期中试题新人教版

浙江省杭州外国语学校2013-2014学年（第一学期）高三期中考试物理试卷注意事项：1、本试卷考试时间100分钟，满分100分。

2、请用蓝、黑色钢笔或圆珠笔答题。

答案均做在答题卷相应的位置上，做在试题卷上无效。

3、全卷g 取10m/s 2，考试中不得使用计算器。

第Ⅰ卷（选择题共48分）一、单项选择题（本大题共10小题，每小题3分，共30分。

每小题只有一个选项符合题意；不选、多选、错选均不给分。

）1．如图，三根长度均为l 的轻绳分别连接于C 、D 两点，A 、B 两端被悬挂在水平天花板上，相距2l 。

现在C 点上悬挂一个质量为m 的重物，为使CD 绳保持水平，在D 点上可施加力的最小值为： A ．mg B ．12 mg C ．33mg D ．14mg 2．如图所示，小车的质量为M ，人的质量为m ，人用恒力F 拉绳，若人与车保持相对静止，且地面为光滑的，又不计滑轮与绳的质量，则车对人的摩擦力可能是：A ．M F m M ⎛⎫ ⎪+⎝⎭，方向向左B ．M F m M ⎛⎫ ⎪+⎝⎭，方向向右 C ．F M m M m ⎪⎭⎫ ⎝⎛+-，方向向右 D ．F M m m M ⎪⎭⎫ ⎝⎛+-，方向向右 3．如图所示，一根细线下端拴一个金属小球P ，细线的上端固定在金属块Q 上，Q 放在带小孔的水平桌面上。

小球在某一水平面内做匀速圆周运动（圆锥摆）。

现使小球改到一个更高一些的水平面上做匀速圆周运动（图上未画出），两次金属块Q 都保持在桌面上静止。

则后一种情况与原来相比较，下面的判断中正确的是： A ．Q 受到桌面的支持力变大B ．Q 受到桌面的静摩擦力不变C ．小球P 运动的角速度变大D ．小球P 运动的周期变大4．如图所示，有一个直角墙，用相同材料做成的三块木板分别倾斜放置于墙上，木板1和木板2的底边位置相同，木板2 和木板3 的顶端位置相同，现给一大小可忽略不计的物块分别从三块木板顶端以相同初速沿木板滑下，则物块从顶端滑至底端过程中，下列说法正确的是：A．沿木板1 滑下时，到底端所需时间最短B．沿木板2 和3滑到底端时动能相同C．沿木板2滑下时，到底端动能最大D．沿木板1滑下时，摩擦力做功最少5．以初速度v0竖直向上抛出一质量为m的小物体。

【原创精品解析纯word版】物理卷·2015届浙江省杭州外国语学校高二第二学期期中考试(2014.05)

浙江省杭州外国语学校2013-2014学年高二第二学期期中考试物理试题【试卷综析】本试题为高二上学期试题，主要考简谐振动、波的图像、光的折射定律、动量定理、动量守恒定律等内容考查知识点的覆盖面广，从题型、分值、知识结构等方面看，能兼顾各层次学生的实际情况。

试卷难度适中，有较好的区分度，即考察了物理的基本知识，也考察分析综合能力，同时与数学知识结合，突出了数学知识在物理上得应用这一能力。

注意事项：本试卷考试时间90分钟，满分100分。

一、单项选择题（本题共8小题，每小题3分，共计24分，每小题只有一．．．个．选项符合题意。

） 1.图（1）是利用砂摆演示简谐运动图象的装置。

当盛砂的漏斗下面的薄木板被水平匀速拉出时，做简谐运动的漏斗漏出的砂在板上形成的曲线显示出砂摆的振动位移随时间变化的关系。

第一次以速度v 1匀速拉动木板，图（2）给出了砂摆振动的图线；第二次仅使砂摆的振幅减半，再以速度v 2匀速拉动木板，图（3）给出了砂摆振动的图线。

由此可知，砂摆两次振动的周期T 1和T 2以及拉动木板的速度v 1和v 2的关系是（）A ．T 1∶T 2=2∶1B ．T 1∶T 2=1∶2C ．v 1∶v 2=1∶2D ．v 1∶v 2=2∶1【知识点】简谐运动的振动图象．【答案解析】D 解析：解：A 、B 、单摆摆动的周期由摆长决定，与振幅无关，故T 1：T 2=1：1，故AB 错误；C 、D 、设板长为d ，图（2）对应速度：v 1=T d 2，图（3）对应的速度：v 2=T d 4，则1221 v v ．故C 错误，D 正确．故选：D ．【思路点拨】砂摆的周期与摆长有关，与振幅无关．板的运动与砂摆的运动具有同时性，根据板上记录的砂摆的振动周期，由时间和位移关系求出拉到木块的速度之比2. 一列简谐横波以1m ／s 的速度沿绳子由A 向B 传播，质点A 、B 间的水平距离x ＝3m ，如图甲所示．若t ＝0时质点A 刚从平衡位置开始向上振动，其振动图象如图乙所示，则B 点的振动图象为下图中的（）[【知识点】横波的图象；简谐运动的振动图象；波长、频率和波速的关系．【答案解析】B 解析：解：A 、C ，由A 振动图象得到T=4s ，则波长λ=vT=4m ，A 点开始振动方向向上．而AB 间距离x=3m=λ43，波从A 传到B 时间为43T =3s ，即B 在A 振动3s 后开始振动．故AC 错误． B 、D ，B 点的起振动方向与A 点相同，均向上．故B 正确，D 错误．故选：B【思路点拨】由振动图象读出周期，求出波长，由AB 距离，结合波形，分析AB 状态关系，由A 的振动图象推断B 图象．3. 如图所示，水下光S 向水面A 点发射一束复色光线，折射光线分成a ，b 两束，则下列说法正确的是( )A ．在水中a 光的速度比b 光的速度小B ．通过同一个单缝发生衍射时，b 光中央条纹比a 光中央条纹宽C ．若a 、b 两种单色光由水中射向空气时，a 光的临界角较小D ．用同一双缝干涉实验装置做实验，a 光的干涉条纹间距大于b 光的干涉条纹间距【知识点】光的折射定律；双缝干涉的条纹间距与波长的关系．【答案解析】D 解析：解：A 、由题，两光束的入射角i 相同，折射角r a ＜r b ，根据折射定律得到，折射率n a ＜n b ．由公式v=nc 分析得知，在水中a 光的速度比b 光的速度大．故A 错误．B 、由于水对b 光的折射率较大，则b 光的波长短，波动性弱，则通过同一个单缝发生衍射时，b 光中央条纹窄．故B 错误．C 、a 光的折射率小，根据临界角公式sinC=n 1，可知，a 光的临界角较大．故C 错误．D 、折射角r a ＜r b ，频率f a ＜f b ，波长λa ＞λb ，根据公式△x=dL λ，则知a 光的干涉条纹间距大于b 光的间距．故D 正确．故选：D 【思路点拨】光源S 向水面A 点发射一束光线，折射光线分成a ，b 两束，两条光路入射角相同，a 光的折射角小于b 光的折射角．根据折射定律分析折射率的大小．由公式v=n c 分析光在水中的速度关系．根据折射率大、频率大，波长短，判断波长关系，即可分析衍射和干涉现象．4.质量为M 的木块放在光滑的水平面上，质量为m 的子弹以水平速度v 0射入木块并留在其中．在此过程中木块所受的冲量应是( )A ．mv 0B ．mv 0－mv 0/(M ＋m)C ．Mmv 0/(M ＋m)D ．Mv 0－mv 0/(M ＋m)【知识点】动量守恒定律；动量定理．【答案解析】C 解析：解：设子弹的方向为正方向；以子弹和木块为系统，由动量守恒可知：mv 0=（m+M ）v 解得：v=m M m v +0；由动量守恒对木块分析，则木块受到的冲量I=Mv=m M Mm v +0，故选：C【思路点拨】先对整体由动量定恒可求得木块的速度；再对木块分析，由动量定理可求得木块受到的冲量．本题考查动量定理及动量守恒定律的应用，要注意正确选择研究对象，并明确子弹打木块为动量守恒的基本模型之一．5．如图所示，A 、B 两物体质量分别为m A 、m B ，且m A ﹥m B ，置于光滑水平面上，相距较远。

浙江省杭州外国语学校2013-2014学年下学期高一年级期中考试英语试卷

浙江省杭州外国语学校2013-2014学年下学期高一年级期中考试英语试卷(考测范围：AEIM Book Level IV Unit 6-12)考试须知：1、英语试卷总分值100分，总答题时间100分钟。

2、本试卷分―试题卷‖和―答题卷‖，其中―试题卷‖10页，―答题卷‖2页。

3、所有客观题请用2B铅笔在―答题卷‖相应的位置上涂黑，其它题答题一律用蓝色、黑色的钢笔、水笔或圆珠笔，否则无效。

I．听力15% （共15题，每小题1分）Part One Listen to ten short dialogues and answer questions 1-10. Each dialogue will be read only once. 10%1. What are the speakers mainly talking about?A. A fireB. A noiseC. A room2. When was the man supposed to board?A. At 540B. At 630C. At 7203. Whose party will the woman go?A. John’sB. Joe’sC. Ann’s4. Who owns the scarf?A. The womanB. The bus driverC. The old lady5. What does the woman suggest the man should do?A. Put on his shoesB. Go to the concertC. Do experiments in the lab6. Why does the man think the team lost the game?A. The goal keeper didn’t play well.B. He got injured during the game.C. He didn’t take part in the game.7. How does the woman feel about the man’s question?A. DisappointedB. PuzzledC. Unhappy8. What does the woman mean?A.She forgot the plate had been broken.B.The man doesn’t have to buy a new plate.C.She can’t help the man look for a new plate.9. What can we learn from the short dialogue?A. Both the man and the woman are Mark Smith’s fans.B. The man is not interested in the news.C. Mark Smith’s biography is interesting to read.10. What makes the man change his mind?A. The demonstration.B. Tina’s being there.C. The light.Part Two Listen to two long dialogues and answer questions 11-15. The dialogues will be read twice. 5%Listen to dialogue 1 and answer questions 11and 12.11. What was the cause of the air crash?A. Bad weatherB. Human error.C. Engine failure.12. What can we learn from the conversation?A. Only the pilots were alive.B. The accident occurred in Argentina.C. The traffic controller wasn’t speaking English.Listen to dialogue 2 and answer questions 13 to 1513. What was the land like when the man’s father bought it?A. It had been opened up.B. There were few animals on it.C. There were many native animals on it.14. How long did it take the land to have a great change?A. 4 yearsB. 10 yearsC. 14 years15. According to the man, what brought about such a great change?A. The damaged environment.B. The people living there.C. The cats and the foxes.II. 单项填空10% （共10小题，每小题1分）从每题所给的A、B、C、D四个选项中，选出可以填入空白处的最佳选项。

浙江省杭州外国语学校2013-2014学年下学期高二年级期中考试语文试卷

浙江省杭州外国语学校2013-2014学年下学期高二年级期中考试语文试卷选择题部分一．选择题（本大题共18题，每小题3分，共54分。

每小题只有1个答案符合题意，多选、少选、错选皆不给分。

）1．下列加点字注音全都相同的一项是（）A．诳．语打夯．粗犷．沆．瀣一气 B．愀．然悄．然蹊跷．人中翘．楚C．搭讪．修缮．膻．味煽．风点火 D．拓．本下榻．鞭挞．纷至沓．2．下列句子有错别字．．．．的一项是（）A．他紧紧地按住我的肩膀，我闻到的是一股烟熏火缭的糊味和脏味，这是从他油腻的制服上发散出的。

B．只是在她猝然去世之后，我才有余暇设想，当我不在家里的那些漫长的时间，她是怎样心神不定坐卧难宁，兼着痛苦、惊恐与一个母亲最低限度的祈求。

C．但我不放心的最是一件：我有一个孽根祸胎，是家里的“混世魔王”，今日因庙里还愿去了，尚未回，晚间你看见便知了。

D．邻里乡亲，早晚在街头巷尾、桥上井边、田塍篱角相见，音容笑貌，闭眼塞耳也彼此了然，横竖呼吸着同一的空气，濡染着同一的风习，千丝万缕沾着边。

3．依次填入下列横线处的词语，最恰当的一项是（）①十五年中，这古园的形体被不能理解它的人______雕琢，幸好有些东西是任谁也不能改变它的。

②但我知道，这并非借题在骂我：因为他所骂的还是康有为。

但是，谈话是总不投机的了，于是不多久，我便一个人______在书房里。

③它是藤上最后的一片叶子。

靠近叶柄的颜色还是深绿的，但是锯齿形的边缘已染上了枯败的黄色，它_____挂在离地面二十英尺的一根藤枝上面。

④况且这通身的_______，竟不像老祖宗的外孙女儿，竟是个嫡亲的孙女，怨不得老祖宗天天口头心头一时不忘。

A．肆意留毅然气派 B．任意剩傲然气势C．肆意剩傲然气派 D．任意留毅然气势4．下列句子成语使用正确的一项是（）A．阳春三月，桃红柳绿，蜂飞蝶舞，春意阑珊．．．．，徜徉于美丽的田野村落，无处不充溢着大自然那盎然的生机和活力。

B．我永远都无法忘记《百年孤独》带给我的美妙的阅读体验，那些翻云覆雨．．．．、时空倒错的想象和叙事。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

浙江省杭州外国语学校2013-2014学年下学期高二年级期中考试数学试卷
（文科）
注意事项：
1、考试时间100分钟，本试卷满分100分；
2、本场考试不准使用计算器等计算工具；
3、请用蓝、黑色钢笔或圆珠笔答题，在答题卷相应处写上班级、姓名、考号，所有答案均做在答卷的相应位置上，做在试题卷上无效.
一、选择题（共10小题，只有一个选项为真，每小题4分，共40分）
1、若复数1z i =+，则(1)z z +⋅= ( )．
A ．13i +
B ．33i +
C ．3i -
D ．3
2、在100件产品中有6件次品,现从中任取3件产品,至少有1件次品的不同取法的种数是( ） A ．12
694C C
B.C 1
6C 299 C.C 3100－C 394
D.A 3
100－A 394
3、8名学生和2位老师站成一排合影，2位老师不相邻的排法种数为 ( )． A ．8289A A B ．8289A C C ．8287A A D ．82
87A C 4、用数学归纳法证明不等式1
11
11271()24
264
n n N *-++++
>∈成立，其n 的初始值至少应为 ( )
A ．7
B ．8
C ．9
D ．10 5、观察下图： 1 2 3 4 3 4 5 6 7 4 5 6 7 8 9 10 ……
则第________行的各数之和等于2 013
2
( )．
A ．2 014
B ．2 013
C ．1 007
D ．1 008
6、设,,a b c 均为正实数，则三个数111
,,a b c b c a
+++ ( )． A ．都大于2
B ．都小于2
C ．至少有一个不大于2
D ．至少有一个不小于2
7、数学教研组开设职业技能类选修课3门，知识类选修课4门，一位同学从中选3门．若要求两类选修课中各至少选一门，则不同的选法共有 ( )． A ．30种 B ．35种 C ．42种 D ．48种
8、点P 是曲线2ln y x x =-上任意一点，则点P 到直线2y x =+的最小距离为 ( )．
．D ．2
9、()f x 是定义在(0,)+∞上的非负、可导函数，且满足()()0xf x f x '+≤，对任意正数,a b ，若a b <，则必有 ( )． A ．)()(b bf a af ≤ B ．)()(b bf a af ≥ C ．)()(b bf a af <
D ． )()(b bf a af >
10、已知函数()ln x f x e a x =+的定义域是D ，关于函数()f x 给出下列命题： ①对于任意(0,)a ∈+∞，函数()f x 是D 上的减函数； ②对于任意(,0)a ∈-∞，函数()f x 存在最小值；
③存在(0,)a ∈+∞，使得对于任意的x D ∈，都有()0f x >成立； ④存在(,0)a ∈-∞，使得函数()f x 有两个零点．
其中正确命题的序号是 ( )． A ．①② B ．②③ C ．②④ D ．③④
二、填空题（本大题共5小题，每题4分，共20分） 11、已知a R ∈，复数
112
a i
i -+-是纯虚数，则a = ________. 12、函数x x x x f ln )(2
-+=的单调递增区间为
13、8名世界网球顶级选手在上海大师赛上分成两组，每组各4人，分别进行单循环赛，每组决出前两名，再由每组的第一名与另一组的第二名进行淘汰赛，获胜者角逐冠、亚军，败者角逐第3、4名，大师赛共有________场比赛．
14、若2
1()l n(2)2
f x x b x =-++在(－1，＋∞)上是减函数，则b 的取值范围是________． 15、某外商计划在4个候选城市中投资3个不同的项目，且在同一个城市投资的项目不超过
2个，则该外商不同的投资方案有________种．
三、解答题（本题有4小题，请写出必要的解答过程，每题10分，共40分） 16.已知函数ln ()x
f x x
=
. （Ⅰ）求()f x 在点(1,0)处的切线方程；（Ⅱ）求函数()f x 在[1,]t 上的最大值.
17.对于数列{}n a ：111)12(,1++++==n n n c n ca a a *(N n ∈,实常数)0≠c （Ⅰ）求432,,a a a ，并猜想n a （Ⅱ）证明你的猜想。

18、给出一个正五棱柱．
（Ⅰ）用3种颜色给其10个顶点染色，要求各侧棱的两个端点不同色，有几种染色方案？（Ⅱ）以其10个顶点为顶点的四面体共有几个？ 19.设函数3()f x x ax b =-+的图像为曲线C
（1）若函数)(x f 不是R 上的单调函数，求实数a 的范围。

（2）若过曲线C 外的点10A （，）作曲线C 的切线恰有两条，
求b a ,的关系式。

（3）若存在00x ∈+∞（，）
，使()000x
f x x e a >⋅+成立，求a 的取值范围。

参考答案：
16解：（1）⇒='=⇒-=
'1)1(ln 1)(2
f k x
x
x f 切线方程为1-=x y （2）由)(x f '知)(x f 在[]e ,1上递增，在[)+∞,e 上递减，
故当],1(e t ∈时，)(x f 最大值是t t t f ln )(=
当),(+∞∈e t 时，)(x f 的最大值为e
e f 1)(=
17解：（1）n n n c n c a c c a c c a c c a )1(15,8,32143432322-+=⇒+=+=+=- （2）证：略
18解：（1）7776235
5
=⋅
（2）180255554
5410=-----C C
19解：（1）题意03)(2=-='a x x f 有两解0>⇒a
（2）设切点为),(00y x ，则切线方程为：))(3(000x x a x y y --=-
切线过（1，0），故)1)(3(000x a x y --=-① ，又b ax x y +-=03
00②，由①②消去0y 得a b x x -=-2
03032
令2332)(x x x g -=，由x x x g 66)(2-='知极值点在0，1，极值为0，－1 故a b =或1-=-a b ，
但A 点不在C 上，故010)1(≠+-⇒≠b a f 综上：b a =
（3）,00>∃x 00
2
0003
0x x e x a a e x b ax x -<⇒+⋅>+-
max )(2
x
e x a -<⇒
x x x e x e x e x -⇒<-='-2202)(是递减的⇒max )(2x e x -不存在，但其上确
界是1)0(-=f ，故所求的a 的范围为：1-<a。