中考综合型问题集二

合集下载

2019中考数学第二部分专题综合强化专题二实际应用型问题针对训练

第二部分专题二类型1 购买、销售、分配类问题1．(2018·常德)某水果店5月份购进甲、乙两种水果共花费1 700元，其中甲种水果8元/千克，乙种水果18元/千克.6月份，这两种水果的进价上调为甲种水果10元/千克，乙种水果20元/千克．(1)若该店6月份购进这两种水果的数量与5月份都相同，将多支付货款300元，求该店5月份购进甲、乙两种水果分别是多少千克．(2)若6月份将这两种水果进货总量减少到120千克，且甲种水果不超过乙种水果的3倍，则6月份该店需要支付这两种水果的货款最少应是多少元？解：(1)设该店5月份购进甲种水果x 千克，购进乙种水果y 千克，根据题意，得⎩⎪⎨⎪⎧8x ＋18y ＝1 700，10x ＋20y ＝1 700＋300，解得⎩⎪⎨⎪⎧x ＝100，y ＝50.答：该店5月份购进甲种水果100千克，购进乙种水果50千克．(2)设购进甲种水果a 千克，需要支付的货款为w 元，则购进乙种水果(120－a )千克，根据题意，得w ＝10a ＋20(120－a )＝－10a ＋2 400. ∵甲种水果不超过乙种水果的3倍， ∴a ≤3(120－a )，解得a ≤90.∵k ＝－10<0，∴w 随a 值的增大而减小，∴当a ＝90时，w 取最小值，最小值为－10×90＋2 400＝1 500. 答：6月份该店需要支付这两种水果的货款最少应是1 500元．2．(2018·泰安)文美书店决定用不多于20 000元购进甲乙两种图书共1 200本进行销售．甲、乙两种图书的进价分别为每本20元、14元，甲种图书每本的售价是乙种图书每本售价的1.4倍．若用1 680元在文美书店可购买甲种图书的本数比用1 400元购买乙种图书的本数少10本．(1)甲、乙两种图书的售价分别为每本多少元？(2)书店为了让利读者，决定甲种图书售价每本降低3元，乙种图书售价每本降低2元，问书店应如何进货才能获得最大利润？(购进的两种图书全部销售完)解：(1)设乙种图书售价每本x 元，则甲种图书售价为每本1.4x 元．由题意，得1 400x －1 6801.4x＝10，解得x ＝20.检验：当x ＝20时，1.4x ≠0，所以x ＝20是原方程的解，且符合题意．所以，甲种图书售价为每本1.4×20＝28(元)．答：甲种图书的售价为每本28元，乙种图书的售价为每本20元． (2)设甲种图书进货a 本，总利润w 元，则w ＝(28－20－3)a ＋(20－14－2)(1 200－a )＝a ＋4 800.又∵20a ＋14×(1 200－a )≤20 000，解得a ≤1 6003，w 随a 的增大而增大，∴当a ＝533时，w 最大，此时，乙种图书进货本数为1 200－533＝667(本)．答：甲种图书进货533本，乙种图书进货667本时能获得最大利润．3．某商场销售A ，B 两种商品，售出1件A 种商品和4件B 种商品所得利润为600元，售出3件A 种商品和5件B 种商品所得利润为1 100元．(1)求每件A 种商品和每件B 种商品售出后所得利润各多少元？(2)若该商场一次购进A ，B 两种商品共34件，全部售完后所得利润不低于4 000元，那么该商场至少需要购进多少件A 种商品？解：(1)设每件A 种商品利润为x 元，每件B 种商品利润为y 元．由题意，得⎩⎪⎨⎪⎧x ＋4y ＝600，3x ＋5y ＝1 100，解得⎩⎪⎨⎪⎧x ＝200，y ＝100，答：每件A 种商品利润为200元，每件B 种商品利润为100元． (2)设购进A 种商品a 件，则购进B 种商品(34－a )件．由题意，得200a ＋100(34－a )≥4 000，解得a ≥6. 答：商场至少需购进6件A 种商品．4．某校周六、周日分别从甲班与乙班各选出20位同学去帮助某果园的果农采摘菠萝，任务都是完成720千克菠萝的采摘、运送、包装三项工作．已知每个同学每小时完成同项工作的工作量一样，且知每人每小时可采摘60千克．(1)周六时甲班将工作做如下分配：6人采摘，8人运送，6人包装，发现刚好各项工作完成的时间相等，那么每人每小时运送、包装各多少千克？(2)得知相关信息后，周日乙班将分配方案调整如下：20人一起完成采摘任务后，然后自由分成两组，第一组运送，第二组包装，发现当第一组完成了任务时，第二组在相等的时间内还有80千克的菠萝还没有包装，于是第一组同学马上帮助第二组同学进行包装直至完成任务，试问自由分成的两组各多少人？解：(1)设采摘了x 小时，根据题意，得 6×60×x ＝720，解得x ＝2，故每人每小时包装：720÷(6×2)＝60(kg)，每人每小时运送720÷(8×2)＝45(kg)．答：每人每小时运送60 kg 、包装45 kg.(2)设负责运送的人数为y 人，则包装人数为(20－y )人，根据题意，得72045y ＝720－80－y，解得y ＝12，检验：当y ＝12时，45y ≠0,20－y ≠0，所以y ＝12是原方程的根，且符合题意，可知自由分成的两组中，第一组12人，第二组为20－12＝8(人)．答：自由分成的第一组12人，第二组8人．类型2 工程、生产、行程类问题1．(2018·昆明盘龙区模拟)一辆汽车计划从A 地出发开往相距180千米的B 地，事发突然，加速为原速的1.5倍，结果比计划提前40分钟到达B 地，求原计划平均每小时行驶多少千米？解：设原计划平均每小时行驶x 千米，则加速后平均每小时行驶1.5x 千米，根据题意，得180x －1801.5x ＝4060，解得x ＝90，经检验，x ＝90是原分式方程的根，且符合题意．答：原计划平均每小时行驶90千米．2．(2018·威海)某自动化车间计划生产480个零件，当生产任务完成一半时，停止生产进行自动化程序软件升级，用时20分钟，恢复生产后工作效率比原来提高了13，结果完成任务时比原计划提前了40分钟，求软件升级后每小时生产多少个零件？解：设升级前每小时生产x 个零件，根据题意，得240x－240＋13x＝4060＋2060. 解得x ＝60.检验，当x ＝60时，(1＋13)x ≠0，所以x ＝60是原方程的解且符合题意．∴60×(1＋13)＝80(个)．答：软件升级后每小时生产80个零件．3．(2018·抚顺)为落实“美丽抚顺”的工作部署，市政府计划对城区道路进行改造，现安排甲、乙两个工程队完成．已知甲队的工作效率是乙队工作效率的32倍，甲队改造360米的道路比乙队改造同样长的道路少用3天．(1)甲、乙两工程队每天能改造道路的长度分别是多少米？(2)若甲队工作一天需付费用7万元，乙队工作一天需付费用5万元，如需改造的道路全长1 200米，改造总费用不超过145万元，至少安排甲队工作多少天？解：(1)设乙工程队每天能改造道路的长度为x 米，则甲工程队每天能改造道路的长度为32x 米，根据题意得360x －36032x ＝3，解得x ＝40，检验：当x ＝40时，32x ≠0，所以x ＝40是原分式方程的解，且符合题意，32x ＝32×40＝60. 答：乙工程队每天能改造道路的长度为40米，甲工程队每天能改造道路的长度为60米． (2)设安排甲队工作m 天，则安排乙队工作1 200－60m40天，根据题意得7m ＋5×1 200－60m40≤145，解得m ≥10.答：至少安排甲队工作10天．4．(2018·官渡区二模)列方程(组)及不等式解应用题某种型号油、电混合动力汽车，从A 地到B 地使用纯燃油行驶的费用为76元；从A 地到B 地使用纯电行驶的费用为26元．已知每行驶1千米用纯燃油行驶的费用比用纯电行驶的费用多0.5元．(1)求用纯电行驶1千米的费用为多少元？(2)若要使从A 地到B 地油电混合行驶所需的油和电总费用不超过39元，则至少用电行驶多少千米？解：(1)设用纯电行驶1千米的费用为x 元，则用纯油行驶1千米的费用为(x ＋0.5)元，根据题意得76x ＋0.5＝26x，解得x ＝0.26，检验，当x ＝0.26时，x ＋0.5≠0，所以x ＝0.26是原分式方程的解．答：用纯电行驶1千米的费用为0.26元． (2)设从A 地到B 地用电行驶y 千米，根据题意得0.26y ＋(0.26＋0.5)(260.26－y )≤39，解得y ≥74. 答：至少用电行驶74千米．类型3 增长率问题1．随着阿里巴巴、淘宝网、京东、小米等互联网巨头的崛起，催生了快递行业的高速发展．据调查，杭州市某家小型快递公司，今年一月份与三月份完成投递的快递总件数分别为10万件和12.1万件．现假定该公司每月投递的快递总件数的增长率相同．(1)求该快递公司投递快递总件数的月平均增长率；(2)如果平均每人每月最多可投递快递0.6万件，那么该公司现有的21名快递投递业务员能否完成今年4月份的快递投递任务？如果不能，请问至少需要增加几名业务员？解：(1)设该快递公司投递快递总件数的月平均增长率为x ，由题意，得 10×(1＋x )2＝12.1，解得x 1＝10%，x 2＝－210%(舍去)．答：该快递公司投递快递总件数的月平均增长率为10%. (2)不能，4月：12.1×1.1＝13.31(万件)，21×0.6＝12.6<13.31，∴该公司现有的21名快递投递业务员不能完成今年4月份的快递投递任务． ∵22<13.310.6<23，∴至少还需增加2名业务员．答：不能，至少需要增加2名业务员．2．受益于国家支持新能源汽车发展和“一带一路”发展战略等多重利好因素，我市某汽车零部件生产企业的利润逐年提高，据统计，2014年利润为2亿元，2016年利润为2.88亿元．(1)求该企业从2014年到2016年利润的年平均增长率；(2)若2017年保持前两年利润的年平均增长率不变，该企业2017年的利润能否超过3.4亿元？解：(1)设该企业从2014年到2016年利润平均增长率为x .根据题意得2(1＋x )2＝2.88，解得x 1＝0.2＝20%，x 2＝－2.2(不合题意，舍去)．答：该企业从2014年到2016年利润平均增长率为20%.(2)如果2017年仍保持相同的年平均增长率，那么2017年该企业年利润为2.88(1＋20%)＝3.456， 3．456>3.4，答：该企业2017年的利润能超过3.4亿元．3．为进一步促进义务教育均衡发展，某市加大了基础教育经费的投入，已知2015年该市投入基础教育经费5 000万元，2017年投入基础教育经费7 200万元．(1)求该市这两年投入基础教育经费的年平均增长率；(2)如果按(1)中基础教育经费投入的年平均增长率计算，该市计划2018年用不超过当年基础教育经费的5%购买电脑和实物投影仪共1 500台，调配给农村学校，若购买一台电脑需3 500元，购买一台实物投影需2 000元，则最多可购买电脑多少台？解：(1)设该市这两年投入基础教育经费的年平均增长率为x ，根据题意得5 000(1＋x )2＝7 200，解得x 1＝0.2＝20%，x 2＝－2.2(舍去)．答：该市这两年投入基础教育经费的年平均增长率为20%. (2)2018年投入基础教育经费为7 200×(1＋20%)＝8 640(万元)，设购买电脑m 台，则购买实物投影仪(1 500－m )台，根据题意得3 500m ＋2 000(1 500－m )≤86 400 000×5%，解得m ≤880.答：2018年最多可购买电脑880台．类型4 方案设计问题与最值问题1．(2018·怀化)某学校积极响应怀化市“三城同创”的号召，绿化校园，计划购进A ，B 两种树苗，共21棵，已知A 种树苗每棵90元，B 种树苗每棵70元．设购买A 种树苗x 棵，购买两种树苗所需费用为y 元．(1)求y 与x 的函数表达式，其中0≤x ≤21；(2)若购买B 种树苗的数量少于A 种树苗的数量，请给出一种费用最省的方案，并求出该方案所需费用．解：(1)根据题意，得y ＝90x ＋70(21－x )＝20x ＋1 470， ∴y 与x 的函数表达式为y ＝20x ＋1 470. (2)∵购买B 种树苗的数量少于A 种树苗的数量， ∴21－x <x ，解得x >10.5.又∵y ＝20x ＋1 470，且x 取整数， ∴当x ＝11时，y 有最小值为1 690，答：使费用最省的方案是购买B 种树苗10棵，A 种树苗11棵，所需费用为1 690元．2．(2018·恩施)某学校为改善办学条件，计划采购A ，B 两种型号的空调，已知采购3台A 型空调和2台B 型空调，需费用39 000元；4台A 型空调比5台B 型空调的费用多6 000元．(1)求A 型空调和B 型空调每台各需多少元；(2)若学校计划采购A ，B 两种型号空调共30台，且A 型空调的台数不少于B 型空调的一半，两种型号空调的采购总费用不超过217 000元，该校共有哪几种采购方案？(3)在(2)的条件下，采用哪一种采购方案可使总费用最低，最低费用是多少元？解：(1)设A 型空调和B 型空调每台各需x 元、y 元，由题意得⎩⎪⎨⎪⎧3x ＋2y ＝39 000，4x －5y ＝6 000，解得⎩⎪⎨⎪⎧x ＝9 000，y ＝6 000，答：A 型空调和B 型空调每台各需9 000元、6 000元． (2)设购买A 型空调a 台，则购买B 型空调(30－a )台， ⎩⎪⎨⎪⎧a ≥12－a ，9 000a ＋－a ，解得10≤a ≤1213，∴a ＝10,11,12，共有三种采购方案，方案一：采购A 型空调10台，B 型空调20台，方案二：采购A 型空调11台，B 型空调19台，方案三：采购A 型空调12台，B 型空调18台． (3)设总费用为w 元，w ＝9 000a ＋6 000(30－a )＝3 000a ＋180 000，∴当a ＝10时，w 取得最小值，此时w ＝210 000，答：采购A 型空调10台，B 型空调20台可使总费用最低，最低费用是210 000元．3．(2018·梧州)我市从2018年1月1日开始，禁止燃油助力车上路，于是电动自行车的市场需求量日渐增多．某商店计划最多投入8万元购进A ，B 两种型号的电动自行车共30辆，其中每辆B 型电动自行车比每辆A 型电动自行车多500元．用5万元购进的A 型电动自行车与用6万元购进的B 型电动自行车数量一样．(1)求A ，B 两种型号电动自行车的进货单价；(2)若A 型电动自行车每辆售价为2 800元，B 型电动自行车每辆售价为3 500元，设该商店计划购进A 型电动自行车m 辆，两种型号的电动自行车全部销售后可获利润y 元．写出y 与m 之间的函数关系式；(3)该商店如何进货才能获得最大利润？此时最大利润是多少元？解：(1)设A ，B 两种型号电动自行车的进货单价分别为x 元、(x ＋500)元．由题意得50 000x ＝60 000x ＋500，解得x ＝2 500，检验：当x ＝2 500时，x (x ＋500)≠0，所以x ＝2 500是分式方程的解，且符合题意，此时x ＋500＝3 000. 答：A ，B 两种型号电动自行车的进货单价分别为2 500元，3 000元． (2)∵购进A 型电动自行车m 辆， ∴购进B 型电动自行车(30－m )辆．根据题意得y ＝(2 800－2 500)m ＋(3 500－3 000)(30－m )＝－200m ＋15 000. (3)根据题意得，2 500m ＋3 000(30－m )≤80 000，解得m ≥20.又∵m ＜30，∴20≤m ＜30，由(2)得y ＝－200m ＋15 000， ∵－200＜0，∴y 随m 的增大而减小，∴当m ＝20时，y 取最大值，最大值为－200×20＋15 000＝11 000(元)．此时30－m ＝10.答：当购进A 种型号电动自行车20辆，B 种型号电动自行车10辆时，能获得最大利润，此时最大利润是11 000元．4．(2018·湘西)某商店销售A 型和B 型两种电脑，其中A 型电脑每台的利润为400元，B 型电脑每台的利润为500元．该商店计划再一次性购进两种型号的电脑共100台，其中B 型电脑的进货量不超过A 型电脑的2倍，设购进A 型电脑x 台，这100台电脑的销售总利润为y 元．(1)求y 关于x 的函数关系式；(2)该商店购进A 型、B 型电脑各多少台，才能使销售总利润最大，最大利润是多少？(3)实际进货时，厂家对A 型电脑出厂价下调a (0<a <200)元，且限定商店最多购进A 型电脑60台，若商店保持同种电脑的售价不变，请你根据以上信息，设计出使这100台电脑销售总利润最大的进货方案．解：(1)根据题意，y ＝400x ＋500(100－x )＝－100x ＋50 000.(2)∵100－x ≤2x ，∴x ≥1003＝3313.∵y ＝－100x ＋50 000中k ＝－100<0， ∴y 随x 的增大而减小．∵x 为正数，∴当x ＝34时，y 取得最大值，最大值为46 600，答：该商店购进A 型电脑34台、B 型电脑66台，才能使销售总利润最大，最大利润是46 600元． (3)据题意得，y ＝(400＋a )x ＋500(100－x )，即y ＝(a －100)x ＋50 000，3313≤x ≤60 ①当0<a <100时，y 随x 的增大而减小， ∴当x ＝34时，y 取最大值，即商店购进34台A 型电脑和66台B 型电脑的销售利润最大． ②当a ＝100时，a －100＝0，y ＝50 000，即商店购进A 型电脑数量满足3313≤x ≤60的整数时，均获得最大利润；③当100<a <200时，a －100>0，y 随x 的增大而增大， ∴当x ＝60时，y 取得最大值．即商店购进60台A 型电脑和40台B 型电脑的销售利润最大．类型5 图象类问题1．(2018·上海)一辆汽车在某次行驶过程中，油箱中的剩余油量y (升)与行驶路程x (千米)之间是一次函数关系，其部分图象如图所示．(1)求y 关于x 的函数关系式；(不需要写定义域)(2)已知当油箱中的剩余油量为8升时，该汽车会开始提示加油，在此次行驶过程中，行驶了500千米时，司机发现离前方最近的加油站有30千米的路程，在开往该加油站的途中，汽车开始提示加油，这时离加油站的路程是多少千米？解：(1)设该一次函数的解析式为y ＝kx ＋b ，将(150,45)，(0,60)代入y ＝kx ＋b 中，⎩⎪⎨⎪⎧150k ＋b ＝45，b ＝60，解得⎩⎪⎨⎪⎧k ＝－110，b ＝60，∴该一次函数的解析式为y ＝－110x ＋60.(2)当y ＝－110x ＋60＝8时，解得x ＝520.即行驶520千米时，油箱中的剩余油量为8升． 530－520＝10千米，油箱中的剩余油量为8升时，距离加油站10千米．∴在开往该加油站的途中，汽车开始提示加油，这时离加油站的路程是10千米．2．(2018·衡阳)一名在校大学生利用“互联网＋”自主创业，销售一种产品，这种产品的成本价10元/件，已知销售价不低于成本价，且物价部门规定这种产品的销售价不高于16元/件，市场调查发现，该产品每天的销售量y (件)与销售价x (元/件)之间的函数关系如图所示．(1)求y 与x 之间的函数关系式，并写出自变量x 的取值范围；(2)求每天的销售利润W (元)与销售价x (元/件)之间的函数关系式，并求出每件销售价为多少元时，每天的销售利润最大？最大利润是多少？解：(1)设y 与x 的函数解析式为y ＝kx ＋b ，将(10,30)，(16,24)代入，得⎩⎪⎨⎪⎧10k ＋b ＝30，16k ＋b ＝24，解得⎩⎪⎨⎪⎧k ＝－1，b ＝40，所以y 与x 的函数解析式为y ＝－x ＋40(10≤x ≤16)． (2)根据题意知，W ＝(x －10)y ＝(x －10)(－x ＋40) ＝－x 2＋50x －400 ＝－(x －25)2＋225，∵a ＝－1<0，∴当x <25时，W 随x 的增大而增大．∵10≤x ≤16，∴当x ＝16时，W 取得最大值，最大值为144，答：每件销售价为16元时，每天的销售利润最大，最大利润是144元．3．为更新果树品种，某果园计划新购进A ，B 两个品种的果树苗栽植培育，若计划购进这两种果树苗共45棵，其中A 种树苗的单价为7元/棵，购买B 种树苗所需费用y (元)与购买数量x (棵)之间存在如图所示的函数关系．(1)求y 与x 的函数关系式；(2)若在购买计划中，B 种树苗的数量不超过35棵，但不少于A 种树苗的数量，请设计购买方案，使总费用最低，并求出最低费用．解：(1)设y 与x 的函数关系式为y ＝kx ＋b ，当0≤x ＜20时，把(0,0)，(20,160)代入y ＝kx ＋b 中，得⎩⎪⎨⎪⎧0＝b ，160＝20k ＋b ，解得⎩⎪⎨⎪⎧k ＝8，b ＝0.此时y 与x 的函数关系式为y ＝8x ；当x ≥20时，把(20,160)，(40,288)代入y ＝kx ＋b 中，得⎩⎪⎨⎪⎧20k ＋b ＝160，40k ＋b ＝288，解得⎩⎪⎨⎪⎧k ＝6.4，b ＝32，此时y 与x 的函数关系式为y ＝6.4x ＋32. 综上可知：y 与x 的函数关系式为y ＝⎩⎪⎨⎪⎧8xx ＜，6.4x ＋x(2)∵B 种树苗的数量不超过35棵，但不少于A 种树苗的数量，∴⎩⎪⎨⎪⎧x ≤35，x ≤45－x ，∴22.5≤x ≤35，设总费用为W 元，则W ＝6.4x ＋32＋7(45－x )＝－0.6x ＋347， ∵k ＝－0.6，∴W 随x 的增大而减小，∴当x ＝35时，W 总费用最低，W 最低＝－0.6×35＋347＝326(元)．答：当B 种树苗为35棵树，总费用最低为326元．4．春节期间，小丽一家乘坐高铁前往某市旅游，计划第二天租用新能源汽车自驾出游．租车公司：按日收取固定租金80元，另外再按租车时间计费．共享汽车：无固定租金，直接以租车时间(时)计费．如图是两种租车方式所需费用y 1(元)，y 2(元)与租车时间x (时)之间的函数图象，根据以上信息，回答下列问题：(1)分别求出y 1，y 2与x 的函数表达式； (2)请你帮助小丽一家选择合算的租车方案．解：(1)由题意，设y 1＝kx ＋80，将(2,110)代入，得110＝2k ＋80，解得k ＝15，则y 1与x 的函数表达式为y 1＝15x ＋80；设y 2＝mx ，将(5,150)代入，得150＝5m ，解得m ＝30，则y 2与x 的函数表达式为y 2＝30x .(2)由y 1＝y 2得，15x ＋80＝30x ，解得x ＝163；由y 1<y 2得，15x ＋80<30x ，解得x >163；由y 1>y 2得，15x ＋80>30x ，解得x <163.故当租车时间为163小时时，两种选择一样；当租车时间大于163小时时，选择租车公司合算；当租车时间小于163小时时，选择共享汽车合算．。

中考数学难点：多种函数“混合”综合型问题

中考数学难点：多种函数“混合”综合型问题
一次函数、反比例函数以及二次函数是初中数学需要掌握的函数知识内容，也是中考必考的热门知识板块。

纵观近几年全国各地中考试题，我们发现二次函数基本上与一次函数结合的综合问题较多；二次函数与反比例函数基本不会涉及；一次函数与反比例函数的综合问题时一个“冷门”中考考点。

经典例题1：
解题反思：
此题考查了反比例函数与一次函数的交点，涉及的知识有：一次函数与坐标系的交点，待定系数法确定反比例函数解析式，坐标与图形性质以及反比例函数的性质，熟练掌握函数的性质是解本题的关键．
经典例题2：
解题反思：
本题考查了二次函数的性质，反比例函数图象上点的坐标特征，熟练掌握反比例函数图象上点的坐标特征是解题的关键．
经典例题3：
解题反思：
本题主要考查了运用待定系数法求反比例函数及一次函数的解析式、求反比例函数及一次函数图象的交点、三角形的中线平分三角形的面积、相似三角形的判定与性质、三角形外角的性质、直角三角形两锐角互余等知识，在解决问题的过程中，用到了分类讨论、数形结合、割补法等重要的数学思想方法，应熟练掌握．
经典例题4：
解题反思：
此题考查了待定系数法求二次函数、一次函数的解析式，二次函数的性质以及三角形面积、线段长度问题．此题难度适中，解题的关键是运用方程思想与数形结合思想．
经典例题5：
解题反思：
（1）此题主要考查了二次函数综合题，考查了分析推理能力，考查了分类讨论思想的应用，考查了数形结合思想的应用，考查了从已知函数图象中获取信息，并能利用获取的信息解答相应的问题的能力．
（2）此题还考查了函数解析式的求法，以及二次函数的最值的求法，要熟练掌握．（3）此题还考查了三角形的面积的求法，要熟练掌握．。

(河南省)聚焦中考数学复习课件：专题9-综合型问题(含答案)

则D的 y＝172a，
坐标是(172a，172a)，OA 的垂直平分线的解析式是 x＝32a，则 C 的坐标是(32a，32a)，则 k＝
94a2.∵以 CD 为边的正方形的面积为27，∴2(172a－32a)2＝27，则 a2＝2(2015·钦州)如图，在平面直角坐标系中，以点 B(0，8)为端点的射线 BG∥x 轴，点 A 是射线 BG 上一个动点(点 A 与点 B 不重合)，在射线 AG 上取 AD＝OB，作线段 AD 的垂直平分线，垂足为 E，且与 x 轴交于点 F，过点 A 作 AC⊥OA，交直线 EF 于点 C，连接 OC，CD.设点 A 的横坐标为 t.
点拨：作∠DAE＝∠BAD 交 BC 于 E，作 DF⊥AE 交 AE 于 F，作 AG⊥BC 交 BC 于 G.∵∠C＋∠BAD＝∠DAC，∴∠CAE＝∠ACB，∴AE＝EC，∵tan∠BAD＝47，∴设 DF＝ 4x，则 AF＝7x，在 Rt△ADF 中，AD2＝DF2＋AF2，即( 65)2＝(4x)2＋(7x)2，解得 x1＝－1(不合题意，舍去)，x2＝1，∴DF＝4，AF＝7，设 EF＝y，则 CE＝7＋y，则 DE＝6－y，在 Rt△ DEF 中，DE2＝DF2＋EF2，即(6－y)2＝42＋y2，解得 y＝53，∴DE＝6－y＝133，AE＝236，∴设 DG＝z，则 EG＝133－z，则( 65)2－z2＝(236)2－(133－z)2，解得 z＝1，∴CG＝12，在 Rt△ADG 中，AG＝ AD2－DG2＝8，在 Rt△ACG 中，AC＝ AG2＋CG2＝4 13.故答案为：4 13
5．(2015·乌鲁木齐)如图，在直角坐标系 xOy 中，点 A，B 分别在 x 轴和 y 轴，OOAB＝ 34.∠AOB 的角平分线与 OA 的垂直平分线交于点 C，与 AB 交于点 D，反比例函数 y＝kx的图象过点 C.当以 CD 为边的正方形的面积为27时，k 的值是( D )

6月最新整理全国各地中考数学模拟试题分类汇编 2--55动态综合型问题.doc

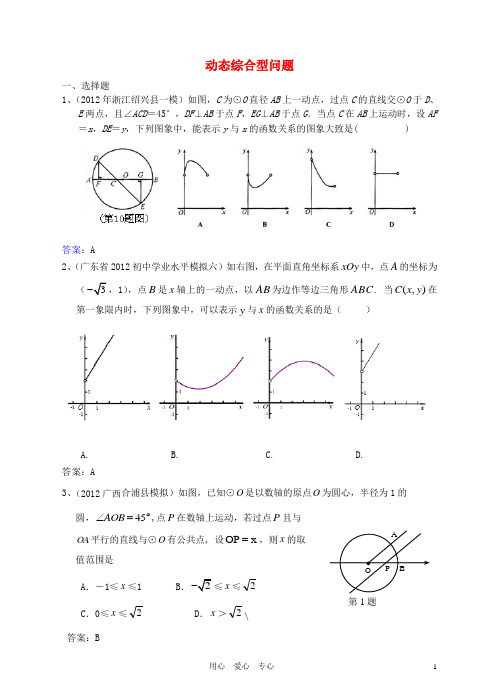
动态综合型问题一、选择题 1、（2012年浙江绍兴县一模）如图，C 为⊙O 直径AB 上一动点，过点C 的直线交⊙O 于D 、E 两点，且∠ACD ＝45°，DF ⊥AB 于点F ，EG ⊥AB 于点G ．当点C 在AB 上运动时，设AF ＝x ，DE ＝y ，下列图象中，能表示y 与x 的函数关系的图象大致是( ) 答案：A2、（广东省2012初中学业水平模拟六）如右图，在平面直角坐标系xOy 中，点A 的坐标为（3-，1），点B 是x 轴上的一动点，以AB 为边作等边三角形ABC . 当),(y x C 在第一象限内时，下列图象中，可以表示y 与x 的函数关系的是（）A. B. C. D. 答案：A3、（2012广西合浦县模拟）如图，已知⊙O 是以数轴的原点O 为圆心，半径为1的圆，45AOB ∠=︒,点P 在数轴上运动，若过点P 且与 OA 平行的直线与⊙O 有公共点, 设x OP =，则x 的取值范围是A ．－1≤x ≤1B ．2-≤x ≤2C ．0≤x ≤2D ．x ＞2\答案：BP AOB第1题11题图A B CNO M P xy 4、（2012四川乐山市市中区毕业会考）一船向东航行，上午8时到达B 处，看到有一灯塔在它的南偏东60°，距离为72海里的A 处，上午10时到达C 处，看到灯塔在它的正南方向，则这艘船航行的速度为（A ）18海里/小时（B ）318海里/小时（C ）36海里/小时（D ）336海里/小时答案：B5、(2012年河北一模) 如图，已知A 、B 是反比例函数ky x（k ＞0，x ＜0）图象上的两点，BC ∥x 轴，交y 轴于点C . 动点P 从坐标原点O 出发，沿O →A →B →C （图中“→”所示路线）匀速运动，终点为C . 过P 作PM ⊥x 轴，PN ⊥y 轴，垂足分别为M 、N .设四边形OMPN 的面积为S ，P 点运动时间为t ，则S 关于t 的函数图象大致为（）A ．B ．OtSOtSOtSOtSC ．D ．答案：A6、（2012年周口二模）如图，点A 的坐标为（－1，0），点B 在直线y =x 上运动，当线段AB 最短时，点B 的坐标为（） A 、（0，0） B 、（，－） C 、（－，－） D 、（－，－）答案：C7、（2012南京江宁区九年级调研卷）如图，把Rt △ABC 放在直角坐标系内，其中∠CAB =90°，BC =5，点A 、B 的坐标分别为（1，0）、（4，0），将△ABC 沿x 轴向右平移，当点C 落在直线y =2x －6上时，线段BC 扫过的面积为（ ▲ ）A ．4B ．8C ．82D ．16答案：D8、（2012江苏江阴青阳九年级下期中检测，8,3分）如图，一只青蛙在圆周上标有数字的五个点上跳，若它停在奇数点上，则下次沿顺时针方向跳两个点；若停在偶数点上，则下次沿逆时针方向跳一个点．若青蛙从5这点开始跳，则经过2012次后它停在哪个数对应的点上 A ．1 B ．2 C ．3 D ．5 （）答案：D9、. 如图所示，半径为1的圆和边长为3的正方形在同一水平线上，圆沿该水平线从左向右匀速穿过正方形，设穿过时间为t ，正方形除去圆部分的面积为S （阴影部分），则S 与t 的大致图象为（）答案：A10、（2012北京市东城区）如图，在正方形ABCD 中，AB =3cm ，动点M 自A 点出发沿AB 方向以每秒1cm 的速度向B 点运动，同时动点N 自A 点出发沿折线AD —DC —CB 以每秒3cm 的速度运动，到达B 点时运动同时停止.设△AMN 的面积为y （cm 2），运动时间为x （秒），则下列图象中能大致反映y 与x 之间的函数关系的是stO A stO BstO Cst O D第12题A B C D 答案：C二、填空题 1、（2012荆门东宝区模拟）如图，动点P 在坐标系中按图中所示箭头方向运动，第1次从原点运动到点(1，1)，第2次接着运动到点(2，0)，第3次接着运动到点(3，2)，…，按这样的运动规律，经过第2011次运动后，动点P 的坐标是．答案：（2011，2）2、（2012鄂州市梁子湖区模拟）如图，Rt ⊿ABC 中，∠C =90°，∠ABC =30°，AB =6．点D 在AB 边上，点E 是BC 边上一点（不与点B 、C 重合），且DA =DE ，则AD 的取值范围．答案：32<≤AD3、(2012年杭州一模)在Rt △ABC 中，∠C =90°，BC =6cm ，CA =8cm ，动点P 从点C 出发，以2cm /秒的速度沿CA ，AB 移动到B ，则点P 出发_________秒时，△BCP 为等腰三角形；答案：3或5.4或6或6.54、（2012江苏江阴华士片九年级下期中检测，17,2分）如图，在锐角△ABC 中，AB =4，∠BAC =45°，∠BAC 的平分线交BC 于点D ，M 、N 分别是AD 和AB 上的动点，则BM +MN 的最小值是．答案：22AB CD NM（第1题）5、（2012荆门东宝区模拟）如图，动点P 在坐标系中按图中所示箭头方向运动，第1次从原点运动到点(1，1)，第2次接着运动到点(2，0)，第3次接着运动到点(3，2)，…，按这样的运动规律，经过第2011次运动后，动点P 的坐标是．答案：（2011，2）6、（.2012江西省新余市一摸）如图，直径AB 为12的半圆，绕A 点逆时针旋转60°，此时点B 到了点B ’，则图中阴影部分的面积是********* .答案：24π7、. （. 2012江西省新余市一摸）如图，△ABC 是一个直角三角形，其中∠C =90゜，∠A =30゜，BC =6；O为AB 上一点，且OB =3, ⊙O 是一个以O 为圆心、OB 为半径的圆；现有另一半径为333-的⊙D 以每秒为1的速度沿B →A →C →B 运动，设时间为t ，当⊙D 与⊙O 外切时，t 的值为 ****** . （本题为多解题，漏写得部分分，错写扣全部分）答案：3612或3312或333+++8、．将点M 向左平移3个单位，再向下平移2个单位得到M ′（—2,—3）,则点M 的坐标是答案：．()1,1-9．在ABC △中，BC 边不动，改变点A 的位置，使得A ∠减少α度，B ∠增加β度，C ∠ 增加γ度，则αβγ，，三者之间的等量关系是答案： γβα+=三、解答题1、（2012年浙江金华模拟）已知：正方形OABC 的边OC 、OA 分别在x 、y 轴的正半轴上，设（第1题） BADO点B （4，4），点P （t ，0）是x 轴上一动点，过点O 作OH ⊥AP 于点H ，直线OH 交直线BC 于点D ，连AD 。

专题6二次根式易错题疑难题综合拓展题及2022中考真题集训(解析版)

专题6 二次根式易错题疑难题综合拓展题及2022中考真题集训类型一易错题：教材易错易混题集训易错点1 考虑问题不全面典例1（2021春•+x 的取值范围是（）A ．x ＞﹣2B ．x ≥3C ．x ≥3且x ≠﹣2D ．x ≥﹣2思路引领：根据二次根式有意义的条件即可求出答案．解：由题意可知：x ―3≥0x +2＞0，解得：x ≥3，故选：B ．总结提升：本题考查二次根式以有意义的条件，解题的关键是正确理解二次根式的条件，本题属于基础题型．变式训练1．（2019•x 应满足的条件是（）A ．x ≠3B ．x ≤―13C ．x ≥―13且x ≠3D ．x ＞―13且x ≠3思路引领：根据二次根式有意义的条件，分式有意义的条件列出不等式，解不等式即可．解：由题意得，1+3x ≥0，x ﹣3≠0，解得，x ≥―13且x ≠3，故选：C ．总结提升：本题考查的是二次根式有意义的条件，分式有意义的条件，掌握二次根式的被开方数是非负数、分式分母不为0是解题的关键．易错点2 (0)a a =³时，忽略a ≥0典例2（2022春•乐陵市期末）先阅读材料，然后回答问题．（1经过思考，小张解决这个问题的过程如下：===在上述化简过程中，第　④　步出现了错误，化简的正确结果为　（2思路引领：（1|a |即可进行判断；（2）把被开方数化成完全平方的形式，然后利用二次根式的性质即可化简求解．解：（1）在化简过程中④故答案是：④―（2）原式====总结提升：本题考查了二次根式的化简求值，正确把被开方数化成完全平方的形式是本题的关键．变式训练1= ．思路引领：根据二次根式的性质和完全平方公式化简即可．===―1，―1．总结提升：本题考查了二次根式的性质和化简，熟练掌握二次根式的性质是解题的关键．2．对于题目：“化简并求值：1a+a =15”，甲、乙两人的解答不同．甲的解答是：1a 1a +1a ―a =2a―a =495，乙的解答是：1a 1a +a ―1a =a =15．阅读后你认为谁的解答是错误的？为什么？思路引领：已知二次根式具有双重非负性，即被开方数为非负数，二次根式的值为非负数，已知a =15，故可得1a ―a ＝5―15＞01a―a ，再对待求式进行化简求值即可解答题目．解：乙错误，理由如下：1a +=1a +=1a +|1a―a |．∵a =15，∴1a―a ＝5―15=245＞0，∴|1a ―a |=1a―a ，1a +1a +1a ―a =2a ―a =495．故乙的解答是错误的．总结提升：本题考查分式的化简求值，正确进行计算是解题关键．易错点3 忽视二次根式的隐含条件典例3阅读下列解答过程，判断是否正确．如果正确，请说明理由；如果不正确，请写出正确的解答过程．已知a ―a （a ﹣1思路引领：先根据二次根式有意义的条件求出a 的取值范围，再进行化简．解：不正确，∵﹣a 3＞0，∴a ＜0，―＝﹣＝（﹣a+1总结提升：本题考查了二次根式有意义的条件，二次根式的化简是解题的关键．变式训练1．（2022秋•长安区期中）求代数式a+a＝﹣2022．下面是小芳和小亮的解题过程，都是把含有字母式子先开方再进行运算的方法，请认真思考、理解解答过程，回答下列问题．小芳：解：原式＝a=a+1﹣a＝1小亮：解：原式＝a=a+a﹣1＝﹣4045（1）的解法是错误的；（2）求代数式a a＝4―思路引领：（1）根据题意得到a﹣1＜0，根据二次根式的性质计算即可；（2）根据二次根式的性质把原式化简，代入计算即可．解：（1）∵a＝﹣2022，∴a﹣1＝﹣2022﹣1＝﹣2023＜0，1﹣a，∴小亮的解法是错误的，故答案为：小亮；（2）∵a＝4∴a﹣3＝4――3＝1―0，3﹣a，则a＝a＝a+2（3﹣a）＝6﹣a，当a＝4―6﹣（4―2+总结提升：=|a|是解题的关键．易错点4 成立的条件是a≥0，b≥0典例4（2022春•⋅x的取值范围是（）A．x≥1B．x≥0C．0≤x≤1D．x为任意实数思路引领：根据二次根式有意义的条件列不等式组求解．解：由题意可得x≥0x―1≥0，解得：x≥1，故选：A．总结提升：a≥0）是解题关键．变式训练1．（2021春•―(x x的取值范围是（）A．x≥﹣1B．x≥﹣2C．x≤﹣1D．﹣2≤x≤﹣1思路引领：根据二次根式化简与有意义的条件，即可求得：x+1≤0x+2≥0，解此不等式组即可求得答案．=―（x+1∴x+1≤0 x+2≥0，解得：﹣2≤x≤﹣1．故选：D．总结提升：此题考查了二次根式化简与有意义的条件．此题比较简单，注意掌握二次根式有意义的条件．易错点5 运用想当然的运算法则典例5（2021秋•÷解：原式=―①=②=(2―③=④（1）老师认为小明的解法有错，请你指出小明从第步开始出错的；（2）请你给出正确的解题过程．思路引领：根据二次根式的运算法则即可求出答案．解：（1）③，故答案为：③．（2）原式＝＝―＝总结提升：本题考查二次根式的运算法则，解题的关键是熟练运用二次根式的运算法则．变式训练1．（2022春•―=4．他的解答过程是否有错误？如果有错误，请写出正确的解答过程．思路引领：根据二次根式的加减法的法则进行分析即可．解：有错误，＝＝总结提升：本题主要考查二次根式的加减法，解答的关键是对二次根式的加减法的法则的掌握．易错点6 误用乘法公式典例6（2022秋•金水区校级期中）计算：下面是李明同学在解答某个题目时的计算过程，请认真阅读并完成相应任务．222+22+2……第一步＝10……第三步任务一：填空：以上步骤中，从第　步开始出现错误，这一步错误的原因是；任务二：请写出正确的计算过程；任务三：除纠正上述错误外，请你根据平时的学习经验，就二次根式运算时还需注意的事项给其他同学提一条建议．思路引领：任务一：利用完全平方公式进行计算即可解答；任务二：先计算二次根式的乘法，再算加减，即可解答；任务三：根据在进行二次根式运算时，结果必须化成最简二次根式，即可解答．解：任务一：填空：以上步骤中，从第一步开始出现错误，这一步错误的原因是完全平方公式运用错误，故答案为：一，完全平方公式运用错误；任务二：222+2﹣[2﹣+2]＝5﹣（6﹣+5）＝5﹣5＝任务三：在进行二次根式运算时，结果必须化成最简二次根式．总结提升：本题考查了二次根式的混合运算，熟练掌握完全平方公式是解题的关键．易错点7 运用运算律出现符号错误典例7（2022秋•迎泽区校级月考）下面是小明同学进行实数运算的过程，认真阅读并完成相应的任务：×+1)︸①×︸②第一步―10+2……第二步―8……第三步任务一：以上化简步骤中第一步中：标①的运算依据是；标②的运算依据是（运算律）．任务二：第步开始出现错误，错误原因是，该式运算后的正确结果是　．思路引领：利用二次根式的性质、二次根式的加减法法则、除法法则计算可得结论．解：任务一、①由②的运算依据是乘法的分配律；故答案为：二次根式的性质．乘法的分配律；任务二、从第二步开始出现错误．×+1)×1―10﹣2―12，故答案为：任务一：二次根式的性质；乘法的分配律．任务二：①12．总结提升：本题考查了二次根式的混合运算，掌握二次根式的性质及运算法则是解决本题的关键．变式训练1．（2022春•12(的过程，请认真阅读并完成相应的任务．―12(―12(2第一步―12×―12×第二步第三步第四步=―第五步任务一：小明同学的解答过程从第步开始出现错误，这一步错误的原因是　．任务二：请你写出正确的计算过程．思路引领：先计算二次根式的乘法，再算加减，即可解答．解：（1）任务一：小明同学的解答过程从第二步开始出现错误，这一步错误的原因是去括号后，括号内第二项没有变号，故答案为：二；去括号后，括号内第二项没有变号；（2―12(―12(2总结提升：本题考查了二次根式的混合运算，准确熟练地进行计算是解题的关键．易错点8 滥用运算律典例8（2021秋•迎泽区校级月考）下面是小倩同学进行实数运算的过程，认真阅读并完成相应的任务：÷1 )第一步1⋯第二步+2第三步+2﹣10…第四步―8…第五步任务一：以上化简步骤中第一步化简的依据是．任务二：第　二　步开始出现错误，该式运算后的正确结果是．思路引领：利用二次根式的性质、二次根式的加减法法则、除法法则计算可得结论．故答案为：二次根式的性质．任务二、从第二步开始出现错误．÷1)÷1）=2+4++52总结提升：本题考查了二次根式的混合运算，掌握二次根式的性质及运算法则是解决本题的关键．类型二疑难题：常考疑难问题突破疑难点1 二次根式非负性的应用1．已知实数a 满足|2019﹣a |+a ，求a ﹣20192的值．思路引领：首先由二次根式有意义的条件来去绝对值，得到a ﹣2019a ，由此得到a ﹣20192＝2019．解：∵a ﹣2019≥0，∴a ＞2019．∴由|2019﹣a |+=a 得到a ﹣2019+a ，整理，得a ﹣2019＝20192．∴a ﹣20192＝2019．总结提升：a ≥0）叫二次根式．性质：二次根式中的被开方数必须是非负数，否则二次根式无意义．疑难点2 整体思想在二次根式中的应用2．（2018春•禹州市期中）已知a =+1，b ―1（a b +b a―1）的值思路引领：先由a 、b 的值计算出ab 、a +b 的值，再代入到原式=•a 2b 2abab a 2得．解：∵a =1，b =―1，∴a +b ＝ab 1）1）＝2，则原式=•a 2b 2ab ab＝总结提升：本题主要考查二次根式的化简求值，解题的关键是熟练掌握二次根式的混合运算顺序和运算法则及完全平方公式．3．（1）已知x =x 2﹣2x +5的值；（2）若a ＝2b ＝2，求a思路引领：（1）先把x 2﹣2x +5化简，再代入求值；（2）先把a―解：（1）由x 2+1，∴x 2﹣2x +5+1）2﹣2+1）+5＝―2+5＝7；（2=a =ab a b，当a ＝2+b ＝2―原式=总结提升：先化简再代入，应该是求值题的一般步骤；不化简，直接代入，虽然能求出结果，但往往导致繁琐的运算．疑难点3 判断求知问题4．（2019春•西湖区校级期中）王老师为了解学生掌握二次根式知识的情况，出了这样一道题：“根据所给”粗心的黎明同学把式子看错了，他根据条件得到2”思路引领：2，继而求出答案．解：45﹣x 2﹣（35﹣x 2）＝10，2，5．总结提升：本题考查二次根式的乘除法运算，难度不大，关键是平方差公式的运用．类型三综合拓展题：思维能力专项特训专题1 二次根式性质的应用1．（2022秋•+|2a ﹣b +1|＝0，则（b ﹣a ）2022＝（）A ．﹣1B ．1C ．52022D ．﹣52022思路引领：因为算术平方根具有非负性，在实数范围内，任意一个数的绝对值都是非负数，若+|2a ﹣b +1|＝0，则a +b +5＝0，2a ﹣b +1＝0，联立组成方程组，解出a 和b 的值即可解答．|2a ﹣b +1|＝0，∴a+b+5=02a―b+1=0，解得a=―2 b=―3，∴（b﹣a）2022＝（﹣3+2）2022＝（﹣1）2022＝1．故选：B．总结提升：本题考查了非负数的性质以及解二元一次方程组，根据几个非负数的和等于0，则每一个算式都等于0列出关于a、b的方程是解题的关键．2．已知x、y为实数，且y=+12，求5x﹣3y的值．思路引领：根据二次根式有意义的条件列出不等式，求出x、y的值，计算即可．解：由题意得，3x﹣4≥0，4﹣3x≥0，解得，x=4 3，∴y=1 2，则5x﹣3y＝5×43―3×12=316．总结提升：本题考查的是二次根式有意义的条件，掌握二次根式中的被开方数是非负数是解题的关键．3．（2022春•大连月考）已知实数a在数轴上的对应点位置如图，则化简|a―1|―（）A．2a﹣3B．﹣1C．1D．3﹣2a思路引领：根据数轴上a点的位置，判断出（a﹣1）和（a﹣2）的符号，再根据非负数的性质进行化简．解：由图知：1＜a＜2，∴a﹣1＞0，a﹣2＜0，原式＝a﹣1﹣[﹣（a﹣2）]＝a﹣1+（a﹣2）＝2a﹣3．故选：A．总结提升：此题主要考查了二次根式的性质与化简，正确得出a﹣1＞0，a﹣2＜0是解题关键．4．当x+6有最小值，最小值为多少？思路引领：≥0，可以得出最小值．0，∴当x =―12时，6有最小值，最小值为6．总结提升：本题考查了算术平方根．解题的关键是掌握算术平方根的非负性．5．（2019秋•渠县校级期中）已知x 、y 、a 满足：+=x 、y 、a 的三条线段组成的三角形的面积．思路引领：直接利用二次根式的性质得出x +y ＝8，进而得出：3x ―y ―a =0x ―2y +a +3=0x +y =8，进而得出答案．解：根据二次根式的意义，得x +y ―8≥08―x ―y ≥0，解得：x +y ＝8，0，根据非负数得：3x ―y ―a =0x ―2y +a +3=0x +y =8，解得：x =3y =5a =4，∴可以组成直角三角形，面积为：12×3×4＝6．总结提升：此题主要考查了二次根式的应用，正确应用二次根式的性质是解题关键．专题2 二次根式大小比较方法1 平方法1．（2022•思路引领：++解：2=202=∴20+故答案为：＜．总结提升：（1）此题主要考查了实数大小比较的方法，要熟练掌握，解答此题的关键是要明确：正实数＞0＞负实数，两个负实数绝对值大的反而小．（2）解答此题的关键是比较出两个数的平方的大小关系．方法2 分子有理化法2．认真阅读下列解答过程：比较2―解：∵2―（2―1，=1，又20即22的大小关系．思路引领：认真阅读题目，然后依据题目所给的方法进行比较即可．―2=21，2＞0，＜1．2．总结提升：1，―2=1是解题的关键．方法3 作商法3．利用作商法比较大小思路引领：根据作商比较法，看最后的比值与1的大小关系，从而可以解答本题．=×=1，总结提升：本题考查分母有理化、实数大小的比较，解题的关键是明确作商法比较大小的方法．方法四定义法4思路引领：根据非负数的性质和有理数大小的比较方法即可得到结论．解：∵5﹣a≥0，∴a≤5，∴a﹣6＜0，00，总结提升：本题考查的是实数的大小比较，要善于借助一个中间数作桥梁是解决问题的关键．专题3 二次根式的运算5．（2019秋•皇姑区校级月考）计算：（1）（2）―÷（3）(1―――1)2．（4―11)―20180――2|．思路引领：（1）直接化简二次根式进而合并即可；（2）直接利用二次根式的混合运算法则进而得出答案；（3）直接利用二次根式的混合运算法则计算进而得出答案；（4）直接利用负整数指数幂的性质以及零指数幂的性质分别化简进而得出答案．解：（1）原式＝+＝（2）原式＝（＝﹣1；（3）原式=+―（12+1﹣=――＝﹣―（4）原式＝3――1﹣2=总结提升：此题主要考查了二次根式的混合运算，正确化简二次根式是解题关键．专题4 二次根式的求值6．（2022秋•宁德期中）已知：x =y =（1）填空：|x ﹣y |＝；（2）求代数式x 2+y 2﹣2xy 的值．思路引领：（1）根据二次根式的减法运算法则计算即可．（2）将代数式转化为（x ﹣y ）2，再分别求出x ﹣y 和xy 的值，进而可得答案．解：（1）|x ﹣y |＝||＝+=故答案为：（2）x 2+y 2﹣5xy ＝（x ﹣y ）2，∵x ﹣y =∴（x ﹣y ）2﹣3xy =2=8．即代数式x 2+y 2﹣2xy 的值为8．总结提升：本题考查二次根式的化简求值，熟练掌握运算法则是解答本题的关键．7．（2020春•川汇区期末）计算题：已知x +1x x ―1x 的值．思路引领：根据平方差公式计算；∵x +1x∴（x +1x）22，∴x 2+2+1x 2=5，∴x 2﹣2+1x 2=5﹣4，∴（x ―1x）2＝1，∴x―1x=±1．总结提升：本题考查的是分式的化简求值、二次根式的乘法，熟记平方差公式、完全平方公式是解题的关键．8．（2017秋•昌江区校级期末）已知正数m、n满足m4n＝3，求值：思路引领：由m4n＝3得出2﹣2﹣3＝0，―13，代入计算即可．解：∵m4n＝3，2+（2﹣23＝0，2﹣2+3＝0，1）+―3）＝0，―1+=3，∴原式=3232012=12015．总结提升：本题主要考查二次根式的混合运算，解题的关键是熟练掌握完全平方公式的运用及二次根式性质．类型四中考真题：精选2022中考真题过关1．（2022•内蒙古）实数a1+|a﹣1|的化简结果是（）A．1B．2C．2a D．1﹣2a思路引领：根据数轴得：0＜a＜1，得到a＞0，a﹣1＜0=|a|和绝对值的性质化简即可．解：根据数轴得：0＜a＜1，∴a＞0，a﹣1＜0，∴原式＝|a|+1+1﹣a＝a+1+1﹣a＝2．故选：B．总结提升：=|a|是解题的关键．2．（2022•安顺）估计（A．4和5之间B．5和6之间C．6和7之间D．7和8之间思路引领：直接利用二次根式的性质结合估算无理数的大小方法得出答案．解：原式＝2∵34，∴5＜2+6，故选：B．总结提升：此题主要考查了二次根式的混合运算，估算无理数的大小，正确估算无理数是解题关键．3．（2022•x的取值范围是（）A．x＞2B．x＜2C．x≤2D．x≥2思路引领：根据二次根式有意义的条件：被开方数是非负数即可得出答案．解：∵3x﹣6≥0，∴x≥2，故选：D．总结提升：本题考查了二次根式有意义的条件，掌握二次根式有意义的条件：被开方数是非负数是解题的关键．4．（2022•广州）代数式1有意义时，x应满足的条件为（）A．x≠﹣1B．x＞﹣1C．x＜﹣1D．x≤﹣1思路引领：直接利用二次根式有意义的条件、分式有意义的条件分析得出答案．解：代数式1有意义时，x+1＞0，解得：x＞﹣1．故选：B．总结提升：此题主要考查了二次根式有意义的条件以及分式有意义的条件，正确掌握相关定义是解题关键．5．（2022•聊城）射击时，子弹射出枪口时的速度可用公式v=a为子弹的加速度，s 为枪筒的长．如果a＝5×105m/s2，s＝0.64m，那么子弹射出枪口时的速度（用科学记数法表示）为（）A．0.4×103m/s B．0.8×103m/s C．4×102m/s D．8×102m/s思路引领：把a＝5×105m/s2，s＝0.64m代入公式v=解：v=8×102（m/s），故选：D．总结提升：此题主要考查了二次根式的性质与化简以及科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．6．（2022•x﹣2在实数范围内有意义，则x的取值范围是（）A．x＞﹣1B．x≥﹣1C．x≥﹣1且x≠0D．x≤﹣1且x≠0思路引领：根据二次根式的被开方数是非负数，a﹣p=1a p（a≠0）即可得出答案．解：∵x+1≥0，x≠0，∴x≥﹣1且x≠0，故选：C．总结提升：本题考查了二次根式有意义的条件，负整数指数幂，掌握二次根式的被开方数是非负数，a﹣p=1a p（a≠0）是解题的关键．7．（2022•荆州）若3―a，小数部分为b，则代数式（2+）•b的值是．思路引领：3―a、b的值，代入所求式子计算即可．解：∵12，∴1＜3―2，∵若3―a，小数部分为b，∴a＝1，b＝31＝2∴（2+）•b＝（2+（2―2，故答案为：2．总结提升：本题考查了估算无理数的大小的应用，解题的关键是求出a、b的值．8．（2022•随州）已知m为正整数，=m有最小值3×7＝21．设n1的整数，则n的最小值为　，最大值为　．思路引领：n最小为31越小，300 n越小，则n=2时，即可求解．∴n最小为3，1的整数，越小，300n越小，则n 越大，2时，300n=4，∴n ＝75，故答案为：3；75．总结提升：本题考查二次根式的乘除法，二次根式的性质与化简，解题的关键是读懂题意，根据关键词“大于”，“整数”进行求解．9．（2022•遂宁）实数a 、b 在数轴上的位置如图所示，化简|a +1|― ．思路引领：根据数轴可得：﹣1＜a ＜0，1＜b ＜2，然后即可得到a +1＞0，b ﹣1＞0，a ﹣b ＜0，从而可以将所求式子化简．解：由数轴可得，﹣1＜a ＜0，1＜b ＜2，∴a +1＞0，b ﹣1＞0，a ﹣b ＜0，∴|a +1|＝a +1﹣（b ﹣1）+（b ﹣a ）＝a +1﹣b +1+b ﹣a＝2，故答案为：2．总结提升：本题考查二次根式的性质与化简、实数与数轴，解答本题的关键是明确题意，利用数形结合的思想解答．10．（2022•内蒙古）已知x ，y 是实数，且满足y+18，则的值是．思路引领：根据负数没有平方根求出x 的值，进而求出y 的值，代入计算即可求出值．解：∵y =18，∴x ﹣2≥0，2﹣x ≥0，∴x ＝2，y =18，则原式==12，故答案为：12总结提升：此题考查了二次根式的化简求值，熟练掌握运算法则是解本题的关键．11．（2022•济宁）已知a ＝2+b ＝2―a 2b +ab 2的值．思路引领：利用因式分解，进行计算即可解答．解：∵a ＝2b ＝2∴a 2b +ab 2＝ab （a +b ）＝（2+（2（2+2―＝（4﹣5）×4＝﹣1×4＝﹣4．总结提升：本题考查了二次根式的混合运算，代数式求值，熟练掌握因式分解是解题的关键．12．（2022•河池）计算：|﹣3﹣1―（π﹣5）0．思路引领：先去绝对值，计算负整数指数幂，零指数幂和二次根式乘法，再合并即可．解：原式＝―13―1=23．总结提升：本题考查实数的混合运算，解题的关键是掌握实数相关运算的法则．13．（2022•泰州）（1×（2）按要求填空：小王计算2x x 24―1x 2的过程如下：解：2x x 24―1x 2=2x (x 2)(x 2)―1x 2⋯⋯第一步=2x (x 2)(x 2)―x 2(x 2)(x 2)⋯⋯第二步=2x x2(x2)(x2)⋯⋯第三步=x2(x2)(x2)⋯⋯第四步=1x2．……第五步小王计算的第一步是（填“整式乘法”或“因式分解”），计算过程的第步出现错误．直接写出正确的计算结果是．思路引领：（1）原式利用二次根式乘法法则计算，合并即可得到结果；（2）观察解题的过程，分析第一步变形的依据，找出出错的步骤，计算出正确的结果即可．解：（1）原式＝＝＝（2）2xx24―1x2=2x(x2)(x2)―1x2=2x(x2)(x2)―x2(x2)(x2)=2x(x2) (x2)(x2)=2x x2 (x2)(x2)=x2(x2)(x2)=1x2，小王计算的第一步是因式分解，计算过程的第三步出现错误．直接写出正确的计算结果是1x2．故答案为：因式分解，三，1x2．总结提升：此题考查了二次根式的混合运算，因式分解﹣运用公式法，以及分式的加减法，熟练掌握运算法则是解本题的关键．。

2017中考英语试题分类汇编(含解析)专题6--阅读理解之综合型问题(2)

2017中考英语试题分类汇编（含解析）专题6 阅读理解之综合型问题(2017?湖北咸宁) CIt was the beginning of a new term. As a new teacher in that school, I didn’t know any of students. A little girl was standing at the gate of the classroom. She looked very shy.I walked up to her and asked why she stood there. But she said nothing. Then a boy shouted,①She didn’t“She is from Grade Four, the worst student in her grade.” I looked at the little girl.seem to be the smart kind. I understood why her teacher asked her to stay in Grade Three. I tookher hand and let her into the classroom.“Sit here. Now you are my student and I’m your teacher,” I said. She still said nothing, but suddenly began to cry.I later learnt that her parents died in a car ②/'?ks?d?nt /. She became sad and didn’tlike talking to others after that.She learned very slowly. I gave her respect and never looked down upon（鄙视）her as Iknow everybody deserves（值得）respect. I helped her after school, and she was makingprogress little by little. ③随着时间流逝，她不像以前那般害羞。

重庆中考专题训练九阅读理解题型问题(二)几何相关

中考专题训练九阅读理解题型问题（二）二、综合型阅读理解例3.对于平面直角坐标系xOy 中的点P 和线段AB ，其中(,0)A t 、(2,0)B t +两点，给出如下定义：若在线段AB 上存在一点Q ，使得P ，Q 两点间的距离不大于1，则称P 为线段AB 的“环绕点”．（1）当3t =-时，①在点1(0,1)M ，2(0,0)M ，3(2,1)M --中，线段AB 的伴随点是；②在直线2y x b =+上存在线段AB “环绕点”M 、N ，且MN =，求b 的取值范围；（2）线段AB 的中点关于点(2,0)的对称点是C ，将射线CO 以点C 为中心，顺时针旋转30︒得到射线l ，若射线l 上存在线段AB 的“环绕点”，直接写出t 的取值范围．例4.“构造图形解题”，它的应用十分广泛，特别是有些技巧性很强的题目，如果不能发现题目中所隐含的几何意义，而用通常的代数方法去思考，经常让我们手足无措，难以下手，这时，如果能转换思维，发现题目中隐含的几何条件，通过构造适合的几何图形，将会得到事半功倍的效果，下面介绍两则实例：实例一：1876年，美国总统伽非尔德利用实例一图证明了勾股定理：由ABC ADE ABE ABCD S S S S ∆∆∆=++四边形得：22111()2222a b ab c +=⨯+，化简得：222a b c +=．实例二：欧几里得的《几何原本》记载，关于x 的方程22x ax b +=的图解法是：画Rt ABC ∆，使90ACB ∠=︒，2a BC =，||ACb =，再在斜边AB 上截取2aBD =，则AD 的长就是该方程的一个正根（如实例二图）．请根据以上阅读材料回答下面的问题：（1）①如果,αβ都为锐角，且11tan ,tan 23αβ==，结合条件作出图1，则由图1可得αβ+= 。

（2）②如果,αβ都为锐角，且3tan 4,tan 5αβ==，则可在图2的正方形网络中，利用已作出的锐角α，画出=MON αβ∠-，由此可得αβ-= 。

2024年中考数学综合与实践：圆、二次函数有关重难点题型

综合与实践、圆、二次函数有关重难点题型题型一综合与实践1.综合与实践问题情境：综合与实践课上，老师让同学们以“等腰直角三角形”为主题开展数学活动，并提出如下问题：如题2-1图，将等腰Rt△ABC的直角边AC与等腰Rt△ADC的斜边AC 重合，∠BAC=∠ADC=90°,试判断线段BC 与CD之间的数量关系，并加以证明.(1)数学思考：请你解答老师提出的问题；(2)猜想证明：如题2-2图，点 E 是线段AD上的一个动点(不与A，D重合)，连接CE，过点 E作EF⊥CE,分别交AB,AC于F,G两点,连接FC,试判断△CEF的形状，并说明理由.2.综合与实践【阅读理解】如题1-1图，在△ABC中，AM是BC边上的高线，由勾股定理得AM²=AB²−BM²,AM²= AC²−CM²,故AB²−BM²=AC²−CM².【知识迁移】如题1-2 图,在矩形ABCD中,当点P在矩形ABCD内任意位置时,连接AP,BP,CP,DP.求证: AP²+ CP²=BP²+DP².【探索发现】如题1-3 图，若点 P在矩形ABCD 的外部时，上述结论是否仍然成立?请加以判断，并说明理由.【尝试应用】如题1-4图，在△ABC中, AB=3,AC=4,Q为平面内一点，且AQ=1,∠BQC=90°,求 BC 的最大值.3.如题1-1图,正方形ABCD的边AB上有一点E,连接DE.(1)若AD=3AE,则sin∠ADE= ;(2)如题1-2图，将边 CB绕点 C顺时针旋转，旋转角为α，使得点 B 的对应点 F 落在DE上(点F不与点D 重合),连接BF,求∠BFE的度数;(3)如题1-3图,在(2)的条件下,若E为AB的中点,DF=n,正方形ABCD的面积为S,求S关于n的函数关系式.4.小颖在学习了摩擦力的相关知识后，准备在水平面上探究滑动摩擦力与压力之间的关系，探究步骤如下：第一步：如题3-1图，在一水平放置的木板上放置一个质量为1kg的木块(压力大小=重力大小)，用弹簧测力计沿水平方向拉动木块，使木块做匀速直线运动(滑动摩擦力的大小可以由弹簧测力计读出)；第二步：在木块上增加质量不同的砝码，使木块做匀速直线运动；当在木块上增加质量不同的砝码后，设弹簧测力计所拉物体的质量为m(kg)，弹簧测力计的示数为F(N)，通过多次测量，得到如下数据：(1)把表中的图的坐标系中，描点，连线，画出弹簧测力计拉力F关于物体质量m的图象；(2)观察所画的图象，猜测F和m之间的函数关系，求出函数表达式；(3)小颖将水平拉动木块实验变成在斜面拉动木块实验，如题3-3图，用弹簧测力计拉着木块分别沿倾斜程度不同的斜面向上做匀速直线运动.经测算，在弹性范围内，沿斜面的拉力 F(N)是高度h(m)的一次函数.当斜面水平放置在地面上时，弹簧测力计的读数为2N，高度h每增加0.1m，弹簧测力计的读数增加0.8N，若弹簧测力计的最大量程是8N，求装置高度h的取值范围.5.综合与实践某数学实验小组在学习了电阻的知识后，计划通过实验探究铂电阻在0∼100°C范围内的温度特性，具体过程如下：【知识背景】电阻温度计是根据导体电阻随温度而变化的规律来测量温度的温度计，铂电阻温度计是最精确的温度计.【实验过程】如题2-1图，将电阻温度计接入电路，开始使导体温度升温，控制温度在( 0°C−100°C范围内，每升温20°C记录一次指示仪表输出的电阻值(单位：Ω)，实验完毕后，关闭所有电源.【收集数据】记录的数据如下表：(1)如题2-2图，建立平面直角坐标系，横轴表示温度( (°C),纵轴表示电阻值(Ω)，描出以上表中的数据为坐标的各点，并进行连线；(2)观察上述各点的分布规律，判断它们是否在同一条直线上，若在同一条直线上，请你建立适当的函数模型，并求出解析式，若不在同一条直线上，请说明理由；(3)当温度为50°C时，求铂电阻的电阻值.题型二圆的综合题1. 如题1图, △ABC内接于⊙O,AB是⊙O 的直径,分别过点 C 作⊙O 的切线，过点 O作AB的垂线，两线相交于点 D.(1)求证: ∠D=2∠A;(2)请用无刻度的直尺和圆规过点O 作AC 的垂线交AC 于点 E(保留作图痕迹，不写作法)；(3)在(2)的条件下,若AB=8,CD=3,求OE的长.2. 如题2图, △ABC内接于⊙O,延长BA至点D,连接DC,使DB=DC,过点A作AE⊥AB交DC于点E,连接B E,BE 与AC相交于点F，且满足∠ADE=2∠EAC.(1)求证:CA=CB;(2)若AD:AB=1:4,求tan∠ABC的值；的值.(3)在(2)的条件下,求AFFC3.如题1-1图, △ABC内接于⊙O,BC是⊙O的直径,CD是∠ACB的平分线,交⊙O 于点D,连接OD,交AB于点E.(1)求证:OD∥AC;,求直线AF与⊙O的位关系.(2)如题1-2图,延长OD至点 F,连接AF,使得AF=BC,且tanB=12在△ABC中,AB=AC,点O是AB边上一动点,以点O为圆心,OB长为半径作圆,交BC于点 D.过点 D作DE⊥AC,垂足为E.(1)如题2-1图,若点O为AB的中点,求证:BD=CD;(2)如题2-2图,当点O为AB 上任意一点时,求证:DE 与⊙O 相切;(3)如题2-3图,若⊙O与AC相切于点F,且⊙O的半径为3,CE=1,求AF的长.如题4图,四边形ABCE内接于⊙O, AB=AC,CE⊥BC,，过点A作BC的平行线交CE的延长线于点 D.(1)求证:AD是⊙O的切线;(2)若DE=2,AE平分∠CAD,求⊙O的半径；(3)新考法探究线段数量关系若( CE=m,DE=n,⊙O的直径为d，探究m，n与d的数量关系，并说明理由.题型三二次函数综合题1. 已知抛物线y₁=ax²−4ax+c经过点(3,−2),与x轴交于点A(x₁,0),B两点.(1)若抛物线过点(−1,2),求抛物线的解析式；(2)若−1<x₁<0,点P(5,n)(n⟩0))在该抛物线上，求a的取值范围；(3)若抛物线y₁向上平移两个单位长度后得到抛物线y₂，抛物y₁与直线y₁=kx+b(k≠0)交于点(x₁,0)(x₁<2),且函数y=y₁+y₁的图象与x轴仅有一个交点.求证：k=2a.2.如题2图，在平面直角坐标系中，抛物线y=−x²+bx+c交x轴于A,B(1,0)两点,交y轴于点C(0,3),连接AC,BC.(1)求抛物线的解析式；(2)N是线段AC上一点，过点N作NN′⊥x轴于点N′,若△ABC的面积被 NN'分为1∶2的两部分，求点N 的坐标；(3)将抛物线向左平移m(m⟩0))个单位长度，与原抛物线的交点为点 D,连接 AD,BD,AC 与 BD 相交于点 E,若△ADE与△BCE的面积差为1，求m的值.3.已知抛物线y=25x2+bx+c的顶点坐标为(−2,185),与x轴交于点A,B(点A在点 B左侧),与y轴交于点C.(1)求b,c的值;(2)点M(-4，2)，N是抛物线上两点，若点N到对称轴的距离等于点M到对称轴距离的2倍，求点 N的坐标；(3)若点 P是第二象限内抛物线上一点，连接PB交AC于点D,求PDBD的最大值.x−3与x轴，y轴交于A，B两点，抛物线y=x²+bx+c经过A，B两点，M是射线4.如题2图,直线y=34BA上一动点，过点 M作MN∥y轴交抛物线于点 N.(1)求抛物线的解析式；(2)当M在线段BA上时,连接AN,BN,若S∆ABN=S∆ABO,求此时点M的坐标；(3)新考法与点的运动结合点M从点 B 出发，沿射线BA方向以每秒5个单位长度的速度匀速运动，设运动的时间为t秒，当t为何值时，MB=MN?请直接写出所有符合条件的t值.5.如题3图，在平面直角坐标系中，已知抛物线y=ax²+bx−2(a≠0)与x轴交于点A(−1,0),B(0)，与y 轴交于点 C，点P为直线BC下方抛物线上一动点.(1)求抛物线的解析式；(2)过点P作PE⊥x轴于点 E，连接OP，是否存在点 P 使得. ∠OPE=∠ABC?若存在，求出点的横坐标；若不存在，请说明理由；(3) 将抛物线沿着x轴翻折，点P 的对应点为P′,连接P'B,求△P′CB面积的最大值及此时点 P的坐标.。

专题十圆的综合问题-2023年中考二轮专题复习(原卷版)(全国适用)

专题十圆的综合问题一、非动态问题例题1如图，在ABC 中，AB AC =，以AB 为直径的O 交BC 于点D ，过点D 作EF AC ⊥于点E ，交AB 的延长线于点F ，连接AD ．(1)求证：EF 是O 的切线．(2)求证：FBD FDA △△∽．(3)若4DF =，2BF =，求O 的半径长．练习题1．在△ABC 中，∠ACB ＝90°，以BC 为直径的⊙O 交AB 于点D ．(1)如图①，以点B 为圆心，BC 为半径作圆弧交AB 于点M ，连结CM ，若∠ABC ＝66°，求∠ACM ；(2)如图②，过点D 作⊙O 的切线DE 交AC 于点E ，求证：AE ＝EC ；(3)如图③，在（1）（2）的条件下，若tanA ＝34，求S △ADE ：S △ACM 的值．2．如图1，在Rt △ABC 中，90C ∠=︒，以BC 为直径的O 交斜边AB 于点M ，若H 是AC 的中点，连接MH ．(1)求证：MH 为O 的切线．(2)若32MH =，34AC BC =，求O 的半径．(3)如图2，在（2）的条件下分别过点A 、B 作O 的切线，两切线交于点D ，AD 与O 相切于点N ，过N 点作NQ BC ⊥，垂足为E ，且交O 于Q 点，求线段AO 、CN 、NQ 的长度．3．如图，点P 在y 轴的正半轴上，P 交x 轴于B 、C 两点，以AC 为直角边作等腰Rt △ACD ，BD 分别交y 轴和P 于E 、F 两点，连接AC 、FC ，AC 与BD 相交于点G ．(1)求证：ACF ADB =∠∠；(2)求证：CF DF =；(3)DBC ∠=______°；(4)若3OB =，6OA =，则△GDC 的面积为______．4．如图，四边形ABCD 内接于半圆O ，BC 是半圆O 的直径，CE 是半圆O 的切线，CE AD ⊥交AD 的延长线于点E ，14DE BC =，OE 与CD 相交于点F ，连接BF 并延长交AE 的延长线于点G ，连接CG ．(1)求证：AD BC ∥．(2)探究OF 与BF 的数量关系．(3)求tan GBC ∠的值．5．【概念提出】圆心到弦的距离叫做该弦的弦心距．【数学理解】如图①，在O 中，AB 是弦，OP AB ⊥，垂足为P ，则OP 的长是弦AB 的弦心距．(1)若O 的半径为5，OP 的长为AB 的长为______．(2)若O 的半径确定，下列关于AB 的长随着OP 的长的变化而变化的结论：①AB 的长随着OP 的长的增大而增大；②AB 的长随着OP 的长的增大而减小；③AB 的长与OP 的长无关．其中所有正确结论的序号是______．(3)【问题解决】若弦心距等于该弦长的一半，则这条弦所对的圆心角的度数为______°．(4)已知如图②给定的线段EF 和O ，点Q 是O 内一定点．过点Q 作弦AB ，满足AB EF =，请问这样的弦可以作______条．6．已知O 为ACD ∆的外接圆，AD CD =．(1)如图1，延长AD 至点B ，使BD AD =，连接CB ．①求证：ABC ∆为直角三角形；②若O 的半径为4，5AD =，求BC 的值；(2)如图2，若90ADC ∠=︒，E 为O 上的一点，且点D ，E 位于AC 两侧，作ADE ∆关于AD 对称的图形ADQ ∆，连接QC ，试猜想QA ，QC ，QD 三者之间的数量关系并给予证明．7．定义：两个角对应互余，且这两个角的夹边对应相等的两个三角形叫做余等三角形．如图1，在△ABC 和△DEF 中，若∠A +∠E ＝∠B +∠D ＝90°，且AB ＝DE ，则△ABC 和△DEF 是余等三角形．(1)图2，等腰直角△ABC ，其中∠ACB ＝90°，AC ＝BC ，点D 是AB 上任意一点（不与点A ，B 重合），则图中△________和△________是余等三角形，并求证：AD 2+BD 2＝2CD 2．(2)图3，四边形ABCD 是⊙O 的内接四边形，⊙O 的半径为5，且AD 2+BC 2＝100，①求证：△ABC 和△ADC 是余等三角形．②图4，连接BD 交AC 于点I ，连接OI ，E 为AI 上一点，连接EO 并延长交BI 于点F ，若∠ADB ＝67.5°，IE ＝IF ，设OI ＝x ，S △y 关于x 的函数关系式．8．如图1，在等腰ABC 中，AB AC ==120BAC ∠=︒，点D 是线段BC 上一点，以DC 为直径作O ，O 经过点A ．(1)求证：AB 是O 的切线；(2)如图2，过点A 作AE BC ⊥垂足为E ，点F 是O 上任意一点，连结EF ．①如图2，当点F 是DC 的中点时，求EF BF的值；②如图3，当点F 是O 上的任意一点时，EF BF 的值是否发生变化？请说明理由．(3)在（2）的基础上，若射线BF 与O 的另一交点G ，连结EG ，当90GEF ∠=︒时，直接写出EF EG -的值．9．【证明体验】（1）如图1，过圆上一点A 作O 切线AD ，AC 是弦（不是直径），若AB 是直径，连接BC ，求证：DAC ABC ∠=∠；（2）如图2，若AB 不是直径，DAC ∠______ABC ∠（填“＞”、“<”或“=”）；（3）如图3，（1）、（2）的结论是否成立，说明理由；【归纳结论】（4）由以上证明可知：切线与弦的夹角等于它所夹的弧对的______；【结论应用】（5）如图4，ABC 内接圆于O ，弦BE AB ⊥，交AC 于F ，过点A 作O 的切线AD ，交EB 的延长线于点D ．若6AD =，2sin 3ACB ∠=，求线段BE 的长．10．定义：有且仅有一组对角相等的凸四边形叫做“准平行四边形”．例如：凸四边形ABCD 中，若∠A=∠C，∠B≠∠D，则称四边形ABCD为准平行四边形(1)如图①，半圆O的直径为BC，OA⊥OB，点E在过点A的切线上，且BE=BA，点D 是AC 上的动点（不在点A、C上），求证：四边形AEBD为准平行四边形．(2)如图②，准平行四边形ABCD内接于⊙O，∠B≠∠D，若⊙O的半径为5，AB=AD，则①准平行四边形ABCD的面积S是线段AC的长x的函数吗？如果是，求出函数解析式；如果不是，请说明理由；②准平行四边形ABCD的面积S有最大值吗？如果有求出最大值，如果没有，说明理由．二、动点问题例题2（2021·浙江温州·三模）如图，在⊙O中，AB是直径，点D在圆内，点C在圆上，CD⊥半径OA于点E，延长AD交⊙O于F点，连结BF．当点M从点C匀速运动到点D 时，点N恰好从点B匀速运动到点A，且M，N同时到达点E．(1)请判断四边形ACBF 的形状，并说明理由．(2)连结AM 并延长交⊙O 于点G ，连结OG ，DN ．记CM ＝x ，AN ＝y ，已知y ＝12．①求出AE 和BF 的长度．②当M 从C 到E 的运动过程中，若直线OG 与四边形BFDN 的某一边所在的直线垂直时，求所有满足条件的x 的值．练习题1．（2021·浙江温州·一模）如图，在矩形ABCD 中，AB ＝8，BC ＝6，E 是线段AB 上的一个动点，经过A ，D ，E 三点的⊙O 交线段AC 于点K ，交线段CD 于点H ，连接DE 交线段AC 于点F ．(1)求证：AE ＝DH ；(2)连接DK ，当DE 平分∠ADK 时，求线段DE 的长；(3)连接HK ，KE ，在点E 的运动过程中，当线段DH ，HK ，KE 中满足某两条线段相等时，求出所有满足条件的AE 的长．2．（2022·河北·石家庄外国语教育集团一模）已知，在半圆O 中，直径AB =6，点C ，D 在半圆AB 上运动，（点C ，D 可以与A ，B 两点重合），弦CD =3．(1)如图1，当∠DAB=∠CBA 时，求证：△CAB ≌△DBA ；(2)如图2，若∠DAB =15°时，求图中阴影部分（弦AD 、直径AB 、弧BD 围成的图形）的面积；(3)如图3，取CD 的中点M ，点C 从点A 开始运动到点D 与点B 重合时结束，在整个运动过程中：①点M 到AB 的距离的最小值是___________；②直接写出点M 的运动路径长___________．3．（2022·湖南长沙·九年级期中）已知O 为ABC ∆的外接圆，AC BC =，点D 是劣弧 AB 上一点（不与点A ，B 重合），连接DA ，DB ，DC ．(1)如图1，若AB 是直径，将ACD ∆绕点C 逆时针旋转得到BCE ∆．若4CD =，求四边形ADBC 的面积；(2)如图2，若AB AC =，半径为2，设线段DC 的长为x ．四边形ADBC 的面积为S ．①求S 与x 的函数关系式；②若点M ，N 分别在线段CA ，CB 上运动（不含端点），经过探究发现，点D 运动到每一个确定的位置．DMN ∆的周长有最小值t ，随着点D 的运动，t 的值会发生变化．求所有t 值中的最大值，并求此时四边形ADBC 的面积S ．4．（2022·广东·深圳中学一模）（1）【基础巩固】如图1，△ABC 内接于⊙O ，若∠C ＝60°，弦AB =r ＝______；（2）【问题探究】如图2，四边形ABCD 内接于⊙O ，若∠ADC ＝60°，AD ＝DC ，点B 为弧AC 上一动点（不与点A ，点C 重合）求证：AB ＋BC ＝BD（3）【解决问题】如图3，一块空地由三条直路（线段AD 、AB 、BC ）和一条道路劣弧 CD围成，已知CM DM =千米，∠DMC ＝60°， CD的半径为1千米，市政府准备将这块空地规划为一个公园，主入口在点M 另外三个入口分别在点C 、D 、P 处，其中点P 在 CD 上，并在公园中修四条慢跑道，即图中的线段DM 、MC 、CP 、PD ，是否存在一种规划方案，使得四条慢跑道总长度（即四边形DMCP 的周长）最大？若存在，求其最大值；若不存在，说明理由．5．（2022·四川·绵阳市桑枣中学一模）在矩形ABCD 中，5AB cm =，BC 10cm =，点P 从点A 出发，沿AB 边向点B 以每秒1cm 的速度移动，同时点Q 从点B 出发沿BC 边向点C 以每秒2cm 的速度移动，P 、Q 两点在分别到达B 、C 两点时就停止移动，设两点移动的时间为t 秒，解答下列问题：(1)如图1，当t 为几秒时，PBQ △的面积等于24cm ？(2)如图2，以Q 为圆心，PQ 为半径作Q ．在运动过程中，是否存在这样的t 值，使Q 正好与四边形DPQC 的一边(或边所在的直线)相切？若存在，求出t 值；若不存在，请说明理由．6．（2022·广东深圳·一模）在O 中，弦CD 平分圆周角ACB ∠，连接AB ，过点D 作DE //AB 交CB 的延长线于点E ．(1)求证：DE 是O 的切线；(2)若1tan3CAB ∠=，且B 是CE 的中点，O ，求DE 的长．(3)P 是弦AB 下方圆上的一个动点，连接AP 和BP ，过点D 作DH BP ⊥于点H ，请探究点P 在运动的过程中，BH AP BP +的比值是否改变，若改变，请说明理由；若不变，请直接写出比值．7．（2021·四川德阳·二模）如图，在△ABC 中，AB ＝AC ，AO ⊥BC 于点O ，OE ⊥AB 于点E ，以点O 为圆心，OE 为半径作半圆，交AO 于点F ．(1)求证：AC 是⊙O 的切线；(2)若点F 是OA 的中点，OE ＝3，求图中阴影部分的面积；(3)在（2）的条件下，点P 是BC 边上的动点，当PE ＋PF 取最小值时，直接写出BP 的长．8．（2022·湖南永州·一模）如图，在ABC ∆中，AB AC =，以AB 为直径的O 交BC 于D ，过D 点作O 的切线DE 交AC 于E ．(1)求证：DE AC ⊥；(2)若10AB =，3cos 5ABC ∠=，求DE 的长；(3)在（2）的条件下,若P 为线段BD 上一动点，过P 点作BC 的垂线交AB 于N ，交CA 的延长线于M ，求证：PN PM +是定值，并求出定值是多少？9．（2022·江苏·南通市海门区东洲国际学校一模）[问题提出](1)如图1，已知线段AB ＝4，点C 是一个动点，且点C 到点B 的距离为2，则线段AC 长度的最大值是________；[问题探究](2)如图2，以正方形ABCD 的边CD 为直径作半圆O ，E 为半圆O 上一动点，若正方形的边长为2，求AE 长度的最大值；[问题解决](3)如图3，某植物园有一块三角形花地ABC，经测量，AC＝BC＝120米，∠ACB ＝30°，BC下方有一块空地（空地足够大），为了增加绿化面积，管理员计划在BC下方找一点P，将该花地扩建为四边形ABPC，扩建后沿AP修一条小路，以便游客观赏．考虑植物园的整体布局，扩建部分 BPC需满足∠BPC＝60°．为容纳更多游客，要求小路AP的长度尽可能长，问修建的观赏小路AP的长度是否存在最大值？若存在，求出AP的最大长度；若不存在，请说明理由．10．（2021·江苏南京·九年级期末）如图，在平行四边形ABCD中，AB=BC＝6，∠B＝45°，点E为CD上一动点，经过A、C、E三点的⊙O交BC于点F．(1)【操作与发现】当E运动到AE CD⊥处，利用直尺与圆规作出点E与F．（保留作图痕迹）(2)在（1）的条件下，证明AF ABAE AD=．(3)【探索与证明】点E运动到任何一个位置时，求证AF AB AE AD=．(4)【延伸与应用】点E在运动的过程中，直接写出EF的最小值______．三、动圆问题例题3（2021·山东威海·一模）如图，在Rt △ABC 中，∠ACB =90°，AB =10，BC =6，点O 在射线AC 上（点O 不与点A 重合），过点O 作OD ⊥AB ，垂足为D ，以点O 为圆心，OD 为半径画半圆O ，分别交射线AC 于E ，F 两点，设OD =x ．(1)如图1，当点O 为AC 边的中点时，则x =；(2)如图2，当点O 与点C 重合时，连接DF ，求弦DF 的长；(3)若半圆O 与BC 无交点，则x 的取值范围是．练习题1．（2022·江苏·常州市武进区前黄实验学校一模）如图，在平面直角坐标系中，矩形ABCD 的边BC 落在x 轴上，点B 的坐标为()1,0-，3AB =，6BC =，边AD 与y 轴交于点E ．(1)直接写出点A 、C 、D 的坐标；(2)在x 轴上取点()3,0F ，直线()0y kx b k =+≠经过点E ，与x 轴交于点M ，连接EF ．①当15MEF ∠=︒时，求直线()0y kx b k =+≠的函数表达式；②当以线段EM 为直径的圆与矩形ABCD 的边所在直线相切时，求点M 的坐标．9．（2021·江苏镇江·一模）如图1，ABC 中，5AB =，AC =7BC =，半径为r 的O 经过点A 且与BC 相切，切点M 在线段BC 上（包含点M 与点B 、C 重合的情况）．(1)半径r 的最小值等于__________．(2)设BM =x ，求半径r 关于x 的函数表达式；(3)当BM =1时，请在图2中作点M 及满足条件的O ．（要求：尺规作图，不写作法，保留作图痕迹，并用2B 铅笔或黑色水笔加黑加粗）10．（2022·浙江温州·一模）如图，在矩形ABCD 中，AB ＝4，BC ＝6，点E ，F 分别在边AD ，CD 上，且∠ABE ＝∠CBF ，延长BE 交CD 的延长线于点G ，H 为BG 中点，连结CH 分别交BF ，AD 于点M ，N ．(1)求证：BF CH ⊥．(2)当FG ＝9时．①求tan FBG ∠的值．②在线段CH 上取点P ，以E 为圆心，EP 为半径作E （如图），当E 与四边形ABMN 某一边所在直线相切时，求所有满足条件的HP 的长．11．（2022·江苏镇江·九年级期末）如图：已知线段5AM =，射线AS 垂直于AM ，点N 在射线AS 上，设AN n =，点P 在经过点N 且平行于AM 的直线上运动，PAM ∠的平分线交直线NP 于点Q ，过点Q 作QB AP ∥，交线段AM 于点B ，连接PB 交AQ 于点C ，以Q 为圆心，QC 为半径作圆．(1)求证：PB 与Q 相切；(2)已知Q 的半径为3，当AM 所求直线与Q 相切时，求n 的值及PA 的长；(3)当2n 时，若Q 与线段AM 只有一个公共点，则Q 的半径的取值范围是______．四、圆的图形变换问题例题4平面上，矩形ABCD 与直径为QP 的半圆K 如图摆放，分别延长DA 和QP 交于点O ，且∠DOQ ＝60°，OQ ＝OD ＝3，OP ＝2，OA ＝AB ＝1．让线段OD 及矩形ABCD 位置固定，将线段OQ 连带着半圆K 一起绕着点O 按逆时针方向形如旋转，设旋转角为α（0°≤α≤60°）．发现（1）当α＝0°，即初始位置时，点P____直线AB 上．（填“在”或“不在”）求当α是多少时，OQ 经过点B ？（2）在OQ 旋转过程中．简要说明α是多少时，点P ，A 间的距离最小？并指出这个最小值：（3）如图，当点P 恰好落在BC 边上时．求α及S 阴影．拓展如图．当线段OQ 与CB 边交于点M ，与BA 边交于点N 时，设BM ＝x （x ＞0），用含x 的代数式表示BN 的长，并求x 的取值范围．探究当半圆K 与矩形ABCD 的边相切时，求sin α的值．练习题1．把一张圆形纸片按如图方式折叠两次后展开，图中的虚线表示折痕，且折痕6AB =，求O 的半径．2．如图，已知AB 为O 的直径，CD 为弦．CD =AB 与CD 交于点E ，将CD沿CD 翻折后，点A 与圆心O 重合，延长BA 至P ，使AP OA =，连接PC ．(1)求O 的半径；(2)求证：PC 是O 的切线；(3)点N 为 ADB 的中点，在PC 延长线上有一动点M ，连接MN 交AB 于点G ．交 BC 于点F的值．（F与B、C不重合）．求NG NF3．如图1，在Rt△ABC中，∠C＝90°，AB＝10，BC＝6，O是AC的中点，以点O为圆心在AC的右侧作半径为3的半圆O，分别交AC于点D、E，交AB于点G、F．(1)思考：连接OF，若OF⊥AC，求AF的长度；(2)探究：如图2，将线段CD连同半圆O绕点C旋转．①在旋转过程中，求点O到AB距离的最小值；②若半圆O与Rt△ABC的直角边相切，设切点为K，连接AK，求AK的长．4．如图，点B在数轴上对应的数是﹣2，以原点O为圆心、OB的长为半径作优弧AB，使C为OB的中点，点D在数轴上对应的数为4．点A点的左上方，且tan∠AOB(1)S扇形AOB＝；(2)点P是优弧AB上任意一点，则∠PDB的最大值为；(3)在（2）的条件下，当∠PDB最大，且∠AOP<180°时，固定△OPD的形状和大小，以原点O为旋转中心，顺时针旋转a（0°≤a≤360°），①连接CP，AD．在旋转过程中，CP与AD有何数量关系，并说明理由；②直接写出在旋转过程中，点C到PD所在直线的距离d的取值范围．5．如图1，在正方形ABCD中，AB＝10，点O，E在边CD上，且CE＝2，DO＝3，以点O为圆心，OE为半径在其左侧作半圆O，分别交AD于点G，交CD的延长线于点F．(1)AG ＝；(2)如图2，将半圆O 绕点E 逆时针旋转α（0°＜α＜180°），点O 的对应点为O ′，点F 的对应点为F ′，设M 为半圆O ′上一点．①当点F ′落在AD 边上时，求点M 与线段BC 之间的最短距离；②当半圆O ′交BC 于P ，R 两点时，若PR 的长为53π，求此时半圆O ′与正方形ABCD 重叠部分的面积；③当半圆O ′与正方形ABCD 的边相切时，设切点为N ，直接写出tan ∠END 的值．6．如图，已知⊙O 的半径为2，AB 为直径，CD 为弦，AB 与CD 交于点M ，将弧CD 沿着CD 翻折后，点A 与圆心O 重合，延长OA 至P ，使AP =OA ，链接PC ．（1）求证：PC 是⊙O 的切线；（2）点G 为弧ADB 的中点，在PC 延长线上有一动点Q ，连接QG 交AB 于点E ，交弧BC 于点F （F 与B 、C 不重合）．问GE ▪GF 是否为定值？如果是，求出该定值；如果不是，请说明理由．7．如图，在ABE △中，BE AE >，延长BE 到点D ，使DE BE =，延长AE 到点C ，使CE AE =．以点E 为圆心，分别以BE 、AE 为半径作大小两个半圆，连结CD ．（1）求证：AB CD =；（2）设小半圆与BD 相交于点M ，24BE AE ==．①当ABE S 取得最大值时，求其最大值以及CD 的长；②当AB 恰好与小半圆相切时，求弧AM 的长．8．在扇形AOB 中，半径6OA =，点P 在OA 上，连结PB ，将OBP 沿PB 折叠得到O BP ' ．（1）如图1，若75O ∠=︒，且BO '与 AB 所在的圆相切于点B ．①求APO ∠'的度数．②求AP 的长．（2）如图2，BO '与 AB 相交于点D ，若点D 为 AB 的中点，且//PD OB ，求 AB 的长．9．如图，矩形ABCD 中，4=AD ，AB m =（4m >），点P 是DC 上一点（不与点D ，C 重合），连接AP ，APQ 与APD △关于AP 对称，PM 是过点A ，P ，Q 的半圆O 的切线，且PM 交射线AB 于点M ．（1）当AP PM =时，半圆O 与AB 所围成的封闭图形的面积为___________；（2）当Q 在矩形ABCD 内部时，①判断PAQ ∠与AMP ∠是否相等，并说明理由；②若3tan 4PAQ ∠=，求AM 的长；（3）当14DP DC =时，若点Q 落在矩形ABCD 的对称轴上，求m 的值及此时半圆O 落在矩形ABCD 内部的弧长．10．如图1，在正方形ABCD 中，10AB =，点O 、E 在边CD 上，且2CE =，3DO =，以点O 为圆心，OE 为半径在其左侧作半圆O ，分别交AD 于点G ，交CD 延长线于点F ．（1）AG =________．（2）如图2，将半圆O 绕点E 逆时针旋转()0180αα︒<<︒，点O 的对应点为O '，点F 对应点为F '，当半圆O '交BC 于P 、R 两点时，若弧PR 的长为5π3，求此时半圆O '与正方形ABCD 重叠部分的面积．（3）当半圆O '与正方形ABCD 相切时，设切点为N ，直接写出tan END ∠的值．11．如图⊙O 中直径AB ＝2，点E 是AB 的中点，点C 是AE 上的一个动点，将CB 沿线段BC 折叠交AB 于点D ．（1）如图1，当∠ABC ＝20°时，求此时 AC 的长．（2）如图2，连结AC ，当点D 与点О重合时，求此时AC 的长．（3）设AC ＝x ，DO ＝y ，请直接写出y 关于x 的函数表达式及自变量x 的取值范围．12．如图，在平行四边形ABCD 中，AB ＝10，AD ＝15，4tan 3A =．点P 为AD 边上任意一点，连接PB ，将PB 绕点P 逆时针旋转90°得到线段PQ ．（1）当∠DPQ ＝10°时，求∠APB 的大小．（2）当tan :tan 3:2ABP A ∠=时，求点Q 与点B 间的距离（结果保留根号）．（3）若点Q 恰好落在平行四边形ABCD 的边所在直线上时，直接写出PB 旋转到PQ 时点B 经过的路径的长（结果保留π）．13．如图1，四边形ABCD 是正方形，且AB ＝8，点O 与B 重合，以O 为圆心，作半径长为5的半圆O ，交BC 于E ，交AB 于F ，交AB 延长线于G 点，M 是半圆O 上任一点；发现：AM 的最大值为，S 阴影＝．如图2，将半圆O 绕点F 逆时针旋转，旋转角为α（0°＜α＜180°）．思考：（1）若点C 落在半圆O 的直径GF 上，求圆心O 到AB 的距离；（2）若α＝90°，求半圆O 落在正方形内部的弧长；探究：在旋转过程中，若半圆O 与正方形的边相切，求点A 到切点的距离．【注：sin37°＝35，sin53°＝45，tan37°＝34】14．如图，在矩形ABCD 中，6AB =，8BC =，O 是AD 的中点，以O 为圆心，在AD 的下方作半径为3的半圆O ，交AD 于点E ，F ．（1）思考：连接BD ，交半圆O 于点G 、H ，求GH 的长；（2）探究：将线段AP 连带半圆O 绕点A 顺时针旋转，得到半圆O '，设其直径为E F ''，旋转角为α（0180α<<︒）；①设F '到直线AD 的距离为m ，当72m >时，求α的取值范围．②若半圆O '与线段AB 相切，或半圆O '与线段BC 相切，设切点为R ，直接写出 F R '的长．（3sin 494︒=，3cos 414︒=，3tan 374︒=，结果保留π）15．如图1，在Rt ABC 中，90C ∠=︒，10AB =，6BC =，O 是AC 的中点，以点O 为圆心在AC 的右侧作半径为3的半圆O ，分别交AC 于点D 、E ，交AB 于点G 、F ．思考：连接OF ，若OF AC ⊥，求AF 的长度；探究：如图2，将线段CD 连同半圆O 绕点C 旋转．（1）在旋转过程中，求点O 到距离的最小值；（2）若半圆O 与Rt ABC 的直角边相切，设切点为K ，连接AK ，求AK 的长．16．如图，在矩形ABCD 中，4=AD ，30BAC ∠=︒，点O 为对角线AC 上的动点（不与A 、C 重合），以点O 为圆心在AC 下方作半径为2的半圆O ，交AC 于点E 、F ．（1）当半圆O 过点A 时，求半圆O 被AB 边所截得的弓形的面积；（2）若M 为 EF的中点，在半圆O 移动的过程中，求BM 的最小值；（3）当半圆O 与矩形ABCD 的边相切时，求AE 的长．17．如图1，扇形OAB 的半径为4，∠AOB ＝90°，P 是半径OB 上一动点，Q 是 AB 上一动点．（1）连接AQ 、BQ 、PQ ，则∠AQB 的度数为；（2）当P 是OB 中点，且PQ ∥OA 时，求 AQ的长；（3）如图2，将扇形OAB 沿PQ 对折，使折叠后的 QB'恰好与半径OA 相切于点C ．若OP ＝3，求点O 到折痕PQ 的距离．18．如图1，在Rt ABC ∆中，90ACB ∠=︒，8AC =，6BC =，以MN 为直径的半圆O 按如图所示位置摆放，点M 与点A 重合，点N 在边AC 的中点处，点N 从现在的位置出发沿AC CB -方向以每秒2个单位长度的速度运动，点M 随之沿AC CB -下滑，并带动半圆O 在平面内滑动，设运动时间为t 秒（0t ≥），点N 运动到点B 处停止，点P 为半圆中点．（1）如图2，当点M 与点A 重合时，连接OP 交边AB 于E ，则EP 为____________；（2）如图3，当半圆的圆心O 落在了Rt ABC ∆的斜边AB 的中线时，求此时的t ，并求出此时CMN ∆的面积；（3）在整个运动的过程中，当半圆与边AB 有两个公共点时，求出t 的取值范围；（4）请直接写出在整个运动过程中点P 的运动路径长．19．如图1，矩形ABCD 中，3AB =，4=AD ，以AD 为直径在矩形ABCD 内作半圆O ．（1）若点M 是半圆O 上一点，则点M 到BC 的最小距离为________；（2）如图2，保持矩形ABCD 固定不动，将半圆O 绕点A 顺时针旋转α()090α︒<<︒度，得到半圆O'，则当半圆O'与BC相切时，求旋转角α的度数；AD'与边BC有交点时，求tanα的取值范围．（3）在旋转过程中，当20．如图，半圆O的直径4AB=，以长为2的弦PQ为直径，向点O方向作半圆M，其中P 点在AQ（弧）上且不与A点重合，但Q点可与B点重合．发现 AP的长与 QB的长之和为定值l，求l；思考点M与AB的最大距离为_______，此时点P，A间的距离为_______；点M与AB的最小距离为________，此时半圆M的弧与AB所围成的封闭图形面积为________．探究当半圆M与AB相切时，求 AP的长．（注：结果保留π，cos35= ，cos55=。

2014中考复习备战策略第二部分专题六_综合型问题

考点知识梳理
中考典例精析
考点训练
应用：如图②，在矩形 ABCD 中， AB＝4， BC＝6，
点 E 在 AD 上，点 F 在 BC 上，AE＝BF，AF 与 BE 交于点 O.
考点知识梳理
中考典例精析
考点训练
(1)求证：△ AOB 和△ AOE 是“友好三角形”； (2)连接 OD，若△AOE 和△DOE 是“友好三角形”，求四边形 CDOF 的面积．
∴S△AOE＝S△FOB，∴S△AOD＝S△ABF. ∴S
四边形
CDOF ＝ S
矩形
1 ABCD － 2S△ABF ＝ 4×6 － 2× 2
×4×3＝12.
考点知识梳理
中考典例精析
考点训练
探究：根据题意，CD 不可能与 AB 垂直， ①当∠ADC 为锐角时，如图所示：
1 1 ∵S△CDE＝ S△ABC＝ S△A′CD＝S△A′CE， 4 2 ∴DE＝A′E.
考点知识梳理
中考典例精析
考点训练
温馨提示解答阅读理解型题的关键在于阅读，核心在于理解，目的在于应用 .解题的策略是：理清阅读材料的脉络，归纳总结重要条件、数学思想方法以及解题的方法技巧，构建相应的数学模型来完成解答 .
考点知识梳理
中考典例精析
考点训练
2．解图表信息题关键是“识图”和“用图”．解题时，要求通过认真阅读、观察和分析图象、图形、表格来获取信息，根据信息中数据或图形的特征，找出数量关系或弄清函数的对应关系，研究图形的性质，进行推理、论证、计算，从而解决实际问题．图表信息问题往往出现在“方程 (组 )、不等式 (组 )、函数、统计与概率”等知识应用题中，审题时注意把握图表中的信息．

中考数学解答题压轴题突破重难点突破八几何综合探究题类型二：操作型探究问题

5．(2022·嘉兴)小东在做九上课本 123 页习题：“1∶ 2 也是一个很有趣的比．已知线段 AB(如图①)，用直尺和圆规作 AB 上的一点 P，使 AP∶ AB＝1∶ 2.”小东的作法是：如图②，以 AB 为斜边作等腰直角三角形 ABC，再以点 A 为圆心，AC 长为半径作弧，交线段 AB 于点 P，点 P 即为所求作的点．小东称点 P 为线段 AB 的“趣点”．
(1)【阅读理解】我国是最早了解勾股定理的国家之一，它被记载于我国古代的数学著作《周髀算经》中．汉代数学家赵爽为了证明勾股定理，创制了一幅如图①所示的“弦图”，后人称之为“赵爽弦图”．根据“赵爽弦图”写出勾股定理和推理过程；
解： a2＋b2＝c2(直角三角形两条直角边的平方和等于斜边的平方)．推理如下： ∵如图①，4 个△ADE 的面积和＋正方形 EFGH 的面积＝正方形 ABCD 的面积，即 4×12ab＋(b－a)2＝c2，整理得 a2＋b2＝c2.
解：∵在正方形 PQMN 中，PN＝PQ＝DE，PN∥BC，∴△APN∽△ABC，AE＝
PN AE AD－DE＝AD－PN，∴BC＝AD，
PN h－PN
ah
ah
∴ a ＝ h ，∴PN＝a＋h，∴正方形 PQMN 的边长为a＋h.
(2)【操作推理】如何画出这个正方形 PQMN 呢？如图②，小杰画出了图①的△ABC，然后又进行以下操作：先在 AB 边上任取一点 P′，画正方形 P′Q′M′N′，使点 Q′，M′在 BC 边上，点 N ′在△ABC 内，然后连接 BN′，并延长交 AC 于点 N，作 NM⊥BC 于点 M， NP⊥NM 交 AB 于点 P，PQ⊥BC 于点 Q，得到四边形 PQMN.证明：图②中的四边形 PQMN 是正方形；【分层分析】先推出四边形 PQMN 是矩形，再根据 P′N′∥PN，M′N′∥ MN，可得P′PNN′＝N′NMM′，结合 M′N′＝P′N′，推得 MN＝PN 进而得证；

九年级中考二轮专题复习：综合性问题

综合性问题一、选择题1. (2014•年山东东营,第10题3分)如图，四边形ABCD为菱形，AB=BD，点B、C、D、G四个点在同一个圆⊙O 上，连接BG并延长交AD于点F，连接DG并延长交AB于点E，BD与CG交于点H，连接FH，下列结论：①AE=DF；②FH∥AB；③△DGH∽△BGE；④当CG为⊙O的直径时，DF=AF．其中正确结论的个数是（）A． 1 B． 2 C． 3 D． 4考点：圆的综合题．分析：①由四边形ABCD是菱形，AB=BD，得出△ABD和△BCD是等边三角形，再由B、C、D、G四个点在同一个圆上，得出∠ADE=∠DBF，由△ADE≌△DBF，得出AE=DF，②利用内错角相等∠FBA=∠HFB，求证FH∥AB，③利用∠DGH=∠EGB和∠EDB=∠FBA，求证△DGH∽△BGE，④利用CG为⊙O的直径及B、C、D、G四个点共圆，求出∠ABF=120°﹣90°=30°，在RT△AFB中求出AF=AB 在RT△DFB中求出FD=BD，再求得DF=AF．解答：解：①∵四边形ABCD是菱形，∴AB=BC=DC=AD，又∵AB=BD，∴△ABD和△BCD是等边三角形，∴∠A=∠ABD=∠DBC=∠BCD=∠CDB=∠BDA=60°，又∵B、C、D、G四个点在同一个圆上，∴∠DCH=∠DBF，∠GDH=∠BCH，∴∠ADE=∠ADB﹣∠GDH=60°﹣∠EDB，∠DCH=∠BCD﹣∠BCH=60°﹣∠BCH，∴∠ADE=∠DCH，∴∠ADE=∠DBF，在△ADE和△DBF中，∴△ADE≌△DBF（ASA）∴AE=DF故①正确，②由①中证得∠ADE=∠DBF，∴∠EDB=∠FBA，∵B、C、D、G四个点在同一个圆上，∠BDC=60°，∠DBC=60°，∴∠BGC=∠BDC=60°，∠DGC=∠DBC=60°，∴∠BGE=180°﹣∠BGC﹣∠DGC=180°﹣60°﹣60°=60°，∴FGD=60°，∴FGH=120°，又∵∠ADB=60°，∴F、G、H、D四个点在同一个圆上，∴∠EDB=∠HFB，∴∠FBA=∠HFB，∴FH∥AB，故②正确，③∵B、C、D、G四个点在同一个圆上，∠DBC=60°，∴∠DGH=∠DBC=60°，∵∠EGB=60°，∴∠DGH=∠EGB，由①中证得∠ADE=∠DBF，∴∠EDB=∠FBA，∴△DGH∽△BGE，故③正确，④如下图∵CG为⊙O的直径，点B、C、D、G四个点在同一个圆⊙O上，∴∠GBC=∠GDC=90°，∴∠ABF=120°﹣90°=30°，∵∠A=60°，∴∠AFB=90°∴AF=AB，又∵∠DBF=60°﹣30°=30°，∠ADB=60°，∴∠DFB=90°，∴FD=BD，∵AB=BD，∴DF=AF，故④正确，故选：D．点评：此题综合考查了圆及菱形的性质，等边三角形的判定与性质，全等三角形的判定和性质，运用四点共圆找出相等的角是解题的关键．解题时注意各知识点的融会贯通．2.（2014•甘肃白银、临夏,第10题3分）如图，边长为1的正方形ABCD中，点E在CB延长线上，连接ED 交AB于点F，AF=x（0.2≤x≤0.8），EC=y．则在下面函数图象中，大致能反映y与x之闻函数关系的是（）A．B．C．D．考点：动点问题的函数图象．。

综合性学习试题

中考综合性学习试题复习指要[考点透视]《语文课程标准》中，综合性学习和识字与写字、阅读、写作、口语交际共同构成了语文课程目标的五个方面的内容，目前已纳入语文教材体系。

综合性学习主要体现为语文知识、语文能力的综合运用，语文课程与其他课程的沟通，书本学习与实践活动的紧密结合。

综合性学习是《语文课程标准》积极提倡的一种新的学习方式。

它注重考查学生的探究精神、创新意识和综合运用能力。

综合性学习题的主要特点是联系学生实际，真实性强，且地方特点明显，乡土气息浓郁，内容涉及学习交流、推广普通话、采访、写公益广告、设计栏目、提建议等，与语言的实际运用相比，内容更加丰富，覆盖面更广，综合性更强。

考试命题上的特点是：①在内容上注重对能反映考生生活的学习资源的开发和利用，有机地扩展考生自我表达的答题空间；②在试题的呈现方式上以独立的综合性学习考试板块出现，题内所需的学科间知识的综合交叉比较充分；③题干的设置文字量较大，富含信息，表述比较亲切，注意拉近与考生的距离，具有一定的审题难度；④在评价上关注考生个性化的理解与表达，考生的语言表述、对跨学科知识的整合以及各种思维能力的综合运用都是重要的采分点。

试题的类型有单一式和综合式两种：单一式：(1)语言创作类：①编拟欣赏广告、宣传语；②对联知识及创作赏析；③心愿表述；④主题访谈；⑤话题辩论；⑥景点介绍。

(2)材料整理类：①语段压缩；②材料的整合与探究。

(3)图表转述类：①表格分析；②图表理解。

(4)活动参与类：①拟活动方案或计划；②设计活动主题或主题语；③提出解决问题的建议。

综合式：多种类型融为一体，在设置的情境或活动中去考查学生的分析综合、比较判断、归纳推理、总结概括、观察理解、联想想像、语言表达等各方面能力。

由于中考过程限于以笔试的形式呈现,因此知识与能力综合型、专题活动型将是主要的考查方式。

[应考策略]要做好综合性学习复习备考，我们必须注意：1.实际操作，贮备技能。

语文综合性学习实践性强,必须调动学生的参与意识.让他们去经历,去探究,有了活动的积累和贮备，就不会担心临场的考试，从一定程度上说，考试是对过去语文活动的回顾及梳理总结。

2011中考数学专题：例+练——第10课时_综合型问题(含答案)

第10课时综合型问题综合型试题是将所学的知识在一定的背景下进行优化组合，找到解决问题的方案，在解决问题的时候所用到的知识不再是单一的知识点，而是相关的知识，可能同时用到方程、函数，也有可能是三角形与多边形，也有可能是相关学科的知识，这类题目对学生综合能力的要求较高，同时这类题目有相对新颖的背静环境，数学综合题是初中数学中覆盖面最广、综合性最强的题型．解数学综合题必须要有科学的分析问题的方法，要善于总结解数学综合题中所隐含的重要的转化思想、数形结合思想、分类讨论的思想、方程的思想等，要结合实际问题加以领会与掌握，这是学习解综合题的关键．类型之一代数类型的综合题代数综合题是指以代数知识为主的或以代数变形技巧为主的一类综合题．主要包括方程、函数、不等式等内容，用到的数学思想方法有化归思想、分类思想、数形结合思想以及代人法、待定系数法等．解代数综合题要注意各知识点之间的联系和数学思想方法、解题技巧的灵活运用，要抓住题意，化整为零，层层深人，各个击破．1.(·安徽省)刚回营地的两个抢险分队又接到救灾命令：一分队立即出发往30千米的A镇；二分队因疲劳可在营地休息a（0≤a≤3）小时再往A镇参加救灾。

一分队出发后得知，唯一通往A镇的道路在离营地10千米处发生塌方，塌方地形复杂，必须由一分队用1小时打通道路，已知一分队的行进速度为5千米/时，二分队的行进速度为（4+a）千米/时。

⑴若二分队在营地不休息，问二分队几小时能赶到A镇？⑵若二分队和一分队同时赶到A镇，二分队应在营地休息几小时？⑶下列图象中，①②分别描述一分队和二分队离A镇的距离y(千米)和时间x(小时)的函数关系，请写出你认为所有可能合理的代号，并说明它们的实际意义。

2．(沈阳市）一辆经营长途运输的货车在高速公路的A处加满油后，以每小时80千米的速度匀速行驶，前往与A处相距636千米的B地，下表记录的是货车一次加满油后油箱内余油量y（升）与行驶时间x（时）之间的关系：（1）请你认真分析上表中所给的数据，用你学过的一次函数、反比例函数和二次函数中的一种来表示y与x之间的变化规律，说明选择这种函数的理由，并求出它的函数表达式；（不要求写出自变量的取值范围）（2）按照（1）中的变化规律，货车从A处出发行驶4.2小时到达C处，求此时油箱内余油多少升？（3）在（2）的前提下，C处前方18千米的D处有一加油站，根据实际经验此货车在行驶中油箱内至少保证有10升油，如果货车的速度和每小时的耗油量不变，那么在D处至少加多少升油，才能使货车到达B地．（货车在D处加油过程中的时间和路程忽略不计）类型之二几何类型的综合题几何综合题考查知识点多、条件隐晦，要求学生有较强的理解能力，分析能力，解决问题的能力，对数学知识、数学方法有较强的驾驭能力，并有较强的创新意识与创新能力．解决几何型综合题的关键是把代数知识与几何图形的性质以及计算与证明有机融合起来，进行分析、推理，从而达到解决问题的目的．3.（龙岩市）如图，在平面直角坐标系xOy中，⊙O交x轴于A、B两点，直线FA⊥x轴于点A，点D在FA上，且DO平行⊙O的弦MB，连DM并延长交x轴于点C.（1）判断直线DC与⊙O的位置关系，并给出证明；（2）设点D的坐标为（-2，4），试求MC的长及直线DC的解析式.4.(益阳) △ABC是一块等边三角形的废铁片，利用其剪裁一个正方形DEFG，使正方形的一条边DE落在BC 上，顶点F、G分别落在AC、AB上.Ⅰ.证明：△BDG≌△CEF；Ⅱ. 探究：怎样在铁片上准确地画出正方形.小聪和小明各给出了一种想法，请你在．．．．．.．．．．．．．．．Ⅱ．a．的解答记分．．．．．．．．．．．．．．．．．．. ．如果两题都解，只以．．．Ⅱ．a．和．Ⅱ．b．的两个问题中选择一个你喜欢的问题解答Ⅱa. 小聪想：要画出正方形DEFG，只要能计算出正方形的边长就能求出BD和CE的长，从而确定D点和E点，再画正方形DEFG就容易了. 设△ABC的边长为2 ，请你帮小聪求出正方形的边长(结果用含根号的式子表示，不要求分母有理化) .Ⅱb. 小明想：不求正方形的边长也能画出正方形. 具体作法是：①在AB边上任取一点G’，如图作正方形G’D’E’F’；②连结BF’并延长交AC于F；③作FE∥F’E’交BC于E，FG∥F′G′交AB于G，GD∥G’D’交BC于D，则四边形DEFG即为所求.你认为小明的作法正确吗？说明理由.类型之三几何与代数相结合的综合题几何与代数相结合的综合题是初中数学中涵盖广、综合性最强的题型.它可以包含初中阶段所学的代数与几何的若干知识点和各种数学思想方法，还能有机结合探索性、开放性等有关问题；它既突出考查了初中数学的主干知识，又突出了与高中衔接的重要内容，如函数、方程、不等式、三角形、四边形、相似形、圆等.它不但考查学生数学基础知识和灵活运用知识的能力还可以考查学生对数学知识迁移整合能力；既考查学生对几何与代数之间的内在联系，多角度、多层面综合运用数学知识、数学思想方法分析问题和解决问题的能力，还考查学生知识网络化、创新意识和实践能力.5.（·恩施自治州）如图1，在同一平面内,将两个全等的等腰直角三角形ABC 和AFG 摆放在一起，A 为公共顶点，∠BAC =∠AGF =90°，它们的斜边长为2，若∆ABC 固定不动，∆AFG 绕点A 旋转，AF 、AG 与边BC 的交点分别为D 、E (点D 不与点B 重合,点E 不与点C 重合),设BE =m ，CD =n.（1）请在图中找出两对相似而不全等的三角形，并选取其中一对进行证明. （2）求m 与n 的函数关系式，直接写出自变量n 的取值范围.（3）以∆ABC 的斜边BC 所在的直线为x 轴，BC 边上的高所在的直线为y 轴，建立平面直角坐标系(如图2).在边BC 上找一点D ，使BD =CE ，求出D 点的坐标，并通过计算验证BD 2+CE 2=DE 2.（4）在旋转过程中,(3)中的等量关系BD 2+CE 2=DE 2是否始终成立,若成立,请证明,若不成立,请说明理由.6.（茂名）如图，在平面直角坐标系中，抛物线y =－32x 2+b x +c ，经过A （0，－4）、B （x 1，0）、 C （x 2，0）三点，且x 2-x 1=5．（1）求b 、c 的值；（2）在抛物线上求一点D ，使得四边形BDCE 是以BC 为对角线的菱形；（3）在抛物线上是否存在一点P ，使得四边形B P O H 是以OB 为对角线的菱形？若存在，求出点P 的坐标，并判断这个菱形是否为正方形？若不存在，请说明理由．7．（嘉兴市）如图，直角坐标系中，已知两点(00)(20)O A ，，，，点B 在第一象限且OAB △为正三角形，OAB △的外接圆交y 轴的正半轴于点C ，过点C 的圆的切线交x 轴于点D ．（1）求B C ，两点的坐标；（2）求直线CD 的函数解析式；（3）设E F ，分别是线段AB AD ，上的两个动点，且EF 平分四边形ABCD 的周长．试探究：AEF △的最大面积？参考答案1.【解析】本题是一道包含着分类思想的应用综合应用题。

历年初中地理中考综合复习题

八年级地理中考综合复习题（一）班级姓名等第一、选择题。

1、我国最东端、最北端所在省区是（）A、黑龙江B、内蒙古、黑龙江C、黑龙江、辽宁D、新疆、黑龙江2、与我国隔海相望的国家是（）A、蒙古B、朝鲜C、越南D、日本3、下列省区与简称、人民政府驻地的连线，正确的是（）A、广西—桂—桂林B、福建—闽—厦门C、青海—甘—兰州D、贵州—黔—贵阳4、下列各组国家中，与我国云南省相邻的一组是（）A、蒙古、俄罗斯B、越南、老挝C、尼泊尔、锡金D、阿富汗、巴基斯坦5、我国下列省级行政区中，有两个简称的是（）A、湖北、湖南B、西藏、台湾C、山西、吉林D、四川、云南6、我国人口最多的少数民族是（）A、维吾尔族B、壮族C、蒙古族D、藏族7、我国季风区与非季风区的地理界线是（）A、大兴安岭—太行山—巫山—雪峰山B、昆仑山—祁连山—横断山C、大兴安岭—阴山—贺兰山—巴颜喀拉山—冈底斯山D、青藏高原的东南边缘—秦岭—淮河8、在渝、鄂两省区交界处的山脉是（）A、太行山B、武夷山C、巫山D、祁连山9、当黑龙江还是冰天雪地时，海南岛已在春耕生产了，这是由于我国（）A、海陆热力性质差异大B、东西距海远近判别大C、地势垂直变化差异大D、南北跨纬度很广10、有关我国冬夏气温的说法，正确的是（）A、夏季气温最低的地方是青藏高原B、冬季气温最高的地方是吐鲁番C、影响我国冬季气温分布的主要因素是冬季风D、漠河镇是我国冬、夏季气温最低的地方11、湖南省所属的温度带和干湿地区是（）A、暖温带、湿润地区B、暖温带、半湿润地区C、亚热带、半湿润地区D、亚热带、湿润地区12、我国降水最多和最少的地区分别是（）A、广州市和托克逊B、海口和呼和浩特C、火烧寮和托克逊D、大连和拉萨13、我国海域辽阔，素有“天然鱼仓”之称并分布有我国最大渔场的海域是（）A、黄海B、东海C、南海D、渤海14、下列说法正确的是（）A、黑龙江北部降水少属于干旱地区B、塔里木盆地气温较高属于热带C、海南省属于热带D、珠江三角洲属于热带15、下列地形区中，位于非季风区的是（）A、东北平原B、四川盆地C、准噶尔盆地D、云贵高原16、我国夏季气温最高的地方是（）A、曾母暗沙B、海南岛C、漠河D、吐鲁番17、我国内流区大致位于（）A、东南部季风区B、西北部非季风区C、南部湿润地区D、北部湿润地区18、关于塔里木盆地的叙述，正确的是（）①暖温带②半干旱地区③干旱地区④草原广阔⑤地表植被以荒漠为主A、①③⑤B、①②④C、①③④D、①②⑤19、黄河水土流失最严重的河段是（）A、上游B、中游C、下游D、中下游20、关于长江的说法，正确的是（）A、长江水能资源主要集中在上中游河段B、“千里长江，险在荆江”，荆江河段水患最频繁C、长江的水能蕴藏量占全国的1/2，被称为“水能宝库”D、长江是我国长度最长、水量最丰富、流域面积最广的河流，但它不是我国第一大河二、填空题21、与我国陆上相邻的东南亚国家是、、缅甸。