WiFiPDR 室内组合定位的无迹卡尔曼滤波算法
卡尔曼滤波算法步骤

卡尔曼滤波算法步骤一、引言卡尔曼滤波算法是一种用于估计系统状态的优化算法,它可以通过利用系统的动态模型和传感器测量数据,实时地进行状态估计,并且具有较高的精度和鲁棒性。
本文将介绍卡尔曼滤波算法的基本步骤,以帮助读者了解和应用该算法。
二、系统模型在开始使用卡尔曼滤波算法之前,我们需要建立系统的动态模型。
系统模型描述了系统状态的变化规律,通常使用状态转移方程来表示。
状态转移方程可以是线性的或非线性的,具体取决于系统的性质。
在建立系统模型时,我们需要考虑系统的物理特性和运动规律,以准确地描述系统的运动过程。
三、观测模型观测模型描述了传感器测量数据与系统状态之间的关系。
通常情况下,传感器的测量数据是不完全的、噪声干扰的,因此我们需要建立观测模型来描述这种关系。
观测模型可以是线性的或非线性的,具体取决于传感器的性质和测量方式。
在建立观测模型时,我们需要考虑传感器的测量误差和噪声特性,以准确地描述传感器的观测过程。
四、预测步骤卡尔曼滤波算法的预测步骤用于预测系统的状态。
预测步骤基于系统的动态模型和当前的状态估计,通过状态转移方程对系统的状态进行预测。
预测步骤的输出是对系统状态的最优预测值和预测误差的协方差矩阵。
预测步骤的目标是尽可能准确地预测系统的状态,以便对系统进行控制或决策。
五、测量更新步骤卡尔曼滤波算法的测量更新步骤用于根据传感器的测量数据来更新对系统状态的估计。
测量更新步骤基于观测模型和预测步骤的输出,通过观测模型将测量数据转换为状态空间中的残差。
然后,通过计算残差的协方差矩阵和系统的预测误差的协方差矩阵的加权平均,得到对系统状态的最优估计值和估计误差的协方差矩阵。
测量更新步骤的目标是通过融合传感器的测量数据和系统的状态估计,得到对系统状态的最优估计。
六、迭代更新卡尔曼滤波算法的预测步骤和测量更新步骤可以交替进行,以实现对系统状态的连续估计。
在每次迭代中,首先进行预测步骤,然后进行测量更新步骤。
通过迭代更新,卡尔曼滤波算法可以逐步优化对系统状态的估计,提高估计的精度和鲁棒性。
卡尔曼滤波算法(含详细推导)

1、kalman滤波问题
E { v ( n ) v ( k )} 1
H 1
Q ( n ), n k 1 0 , n k
......( 3 )
E { v ( n ) v ( k )} 2
H 2
Q ( n ), n k 2 0 , n k
......( 4 )
1、kalman滤波问题
将式(27)代入式(24),便得到kalman增益的计算公式如下:
H 1 G ( n ) F ( n 1 , n ) K ( n , n 1 ) C ( n ) R ( n )......... ...( 28 )
式中R(n)是信息过程的相关矩阵,由式(10)定义。
(3)、Riccati方程
3、kalman滤波算法
由式(28)表示的kalman增益与预测状态误差的相关矩阵K(n,n-1)有关,为了最后 完成kalman自适应滤波算法,还需要再推导K(n,n-1)的递推公式。 考察状态向量的预测误差:
注意到 并利用状态方 E { v ( n )( k )} 0 , k 0 , 1 ,..., n , 1 程(1),易知下式对k=0,1,…,n成立:
3、kalman滤波算法
H E { x ( n 1 ) ( k )} E {[ F ( n 1 , n ) x ( n ) v ( n ) ( k )} 1
(2)、 kalman增益的计算
3、kalman滤波算法
为了完成kalman自适应滤波算法,需要进一步推导kalman增益的实际计 H E { x ( n 1 ) ( k )} 的具体 算公式。由定义式(24)知,只需要推导期望项 计算公式即可。 将新息过程的计算公式(13)代入式(22),不难得出:
卡尔曼滤波算法含详细推导

E{x1 (n)e ( N , N 1)} 0
因此,由式(26)及式(27)易得:
H
3、kalman滤波算法
E{x(n 1) (n)} F (n 1, n) E{[ x(n) e(n, n 1)]e H (n, n 1)}C H (n) F (n 1, n) E{e(n, n 1)e H (n, n 1)}C H (n) F (n 1, n) K (n, n 1)C H (n)........( 27)
卡尔曼滤波算法及 推导
1、kalman滤波问题
考虑一离散时间的动态系统,它由描述状态向量的过程方程 和描述观测向量的观测方程共同表示。 (1)、过程方程
x(n 1) F (n 1, n) x(n) v1 (n).......( 1)
式中,M 1向量x(n)表示系统在离散时间n的状态向量,它是 不可观测的;M M矩阵F(n+1,n)成为状态转移矩阵,描 述动态系统在时间n的状态到n+1的状态之间的转移,应为已 知。而M 1向量 v1 ( n ) 为过程噪声向量,它描述状态转移中 间的加性噪声或误差。
(2)、新息过程的计算
下面分析新息过程的相关矩阵
R(n) E{ (n) H (n)}........ .(10)
在kalman滤波中,并不直接估计观测数据向量的进一步预测 而是先计算状态向量的一步预测 ,
def
(11) x (n) x(n y(1),...y(n 1))........
e(n 1, n) F (n 1, n)[x(n) x1 (n)] G (n)[ y (n) C (n) x1 (n)] v1 (n)
将观测方程(2)代入上式,并代入 e(n,n - 1) x(n) x1 (n) ,则有:
自适应卡尔曼滤波算法

自适应卡尔曼滤波算法
自适应卡尔曼滤波算法是一种基于最小均方差(MSE)
的自适应信号处理算法,它可以有效地实现过滤器的自适应调节,从而提高过滤器的准确性和稳定性。
自适应卡尔曼滤波算法在实际应用中广泛用于信号处理,其中包括无线电定位、航空控制、声纳定位、信号增强等。
特别是在环境条件变化较大的场景中,它可以有效地抑制噪声干扰,提高信号处理的精度。
另外,自适应卡尔曼滤波算法还可以被用于无人机的跟踪和导航,用于数据检测和分析等。
它可以根据实时的环境条件,自动调节滤波器的参数,从而提高无人机的定位和精度。
总之,自适应卡尔曼滤波算法是一种具有高适应性和高精度的信号处理算法,它可以有效地实现过滤器的自适应调节,抗干扰能力强,可以应用于在实际环境中的信号处理和无人机的跟踪和导航等。
无迹卡尔曼滤波算法

无迹卡尔曼滤波算法随着近年来信息科学技术的发展,实时测量和估计技术已成为科研工作者关注的焦点,同时也是众多研究方向的重要组成部分。
卡尔曼滤波(Kalman Filter,KF)作为一种重要的信息滤波算法,已经被广泛地应用于许多领域。
虽然卡尔曼滤波是一种有效的算法,但是它的应用仍受到一些限制,决定其表现的主要原因之一是滤波时的参数是事先设定的,而这些参数经常是不完全正确的,而且随着系统状态变化而发生变化。
为了解决这个问题,研究人员提出了一种名为“无迹卡尔曼滤波(Unscented Kalman Filter,UKF)”的算法,它可以提高滤波的准确性,而且不受参数的设置影响。
本文将介绍无迹卡尔曼滤波算法在现实应用中的重要性,以及它与传统卡尔曼滤波相比的优点,并且介绍无迹卡尔曼滤波算法的基本原理,以及如何在实际应用中使用。
一、无迹卡尔曼滤波算法的重要性无迹卡尔曼滤波(Unscented Kalman Filter,UKF)是一种相对于传统卡尔曼滤波(Kalman Filter,KF)算法研发出来的新算法,它是一种改进型的线性滤波技术,具有更高的准确性和更大的鲁棒性。
UKF的重要性在于它可以用来估计,并实时跟踪nonlinear 系统,这是KF在nonlinear系统上发挥作用时所不能完成的任务。
由于UKF可以更准确的估计nonlinear系统的状态,它被广泛应用于各种领域,例如机器人定位、导航、卫星跟踪等。
二、无迹卡尔曼滤波算法与传统卡尔曼滤波算法相比的优点1、优质的估计性能。
KF和UKF在估计nonlinear系统状态时,根据其测量数据,UKF可以更加精确地求出状态变量,从而获得更准确的估计。
2、不受参数设置影响。
KF在估计nonlinear系统时,其参数受外部因素,如测量噪声、运动误差等影响较大,这些参数的设置会对滤波的效果有重要影响,而UKF不受这些外部参数的影响,在估计系统状态时,其结果更加精确。
卡尔曼滤波计算

卡尔曼滤波计算
摘要:
1.卡尔曼滤波简介
2.卡尔曼滤波的计算方法
3.卡尔曼滤波的应用领域
4.总结
正文:
【卡尔曼滤波简介】
卡尔曼滤波是一种线性高斯状态空间模型,用于估计随时间变化的未知变量。
这种滤波方法通过将观测数据与系统模型结合起来,可以实时地对未知变量进行估计,并随着新的观测数据的到来而不断更新估计结果。
卡尔曼滤波的核心思想是在观测数据的帮助下,通过最小化系统的均方误差来达到提高估计精度的目的。
【卡尔曼滤波的计算方法】
卡尔曼滤波主要包括两个主要步骤:预测和更新。
预测步骤是根据系统模型和先前的估计结果,预测当前时刻的未知变量。
这一步主要是通过先验估计和系统模型来完成的。
先验估计是在没有新观测数据的情况下,对未知变量的估计。
系统模型则描述了未知变量如何随时间变化。
更新步骤是在获得新的观测数据后,对预测结果进行修正。
这一步主要是通过后验估计来完成的。
后验估计是在观测数据的帮助下,对未知变量进行重
新估计。
【卡尔曼滤波的应用领域】
卡尔曼滤波在许多领域都有广泛的应用,包括导航定位、信号处理、机器人控制等。
例如,在导航定位领域,由于测量误差和传感器漂移等因素的影响,定位结果往往存在误差。
通过使用卡尔曼滤波,可以有效地消除这些误差,提高定位的精度和可靠性。
【总结】
卡尔曼滤波是一种有效的估计方法,通过结合观测数据和系统模型,可以实时地对未知变量进行估计。
这种方法在许多领域都有广泛的应用,如导航定位、信号处理和机器人控制等。
基于PDR_WiFi指纹识别_磁场匹配组合的室内行人导航定位_张鹏

收到的 WiFi信号 数;IRP为 数 据 库 中 的 参 考 点 的 集
合。利用加权平均求取 [(ci/C)ri] i=1
(4)
k
式中,ci=1/di;C= ∑ci;ri 为 WiFi信 号 与 待 测 点 i=1
WiFi信号第i接 近 的 参 考 点 坐 标;^r 为 计 算 得 到 的
30
测绘地理信息
2016 年 6 月
FMk = {posk,σposk ,mk }
(2)
式中,posk 和σposk 分 别 为 RPk 点 的 坐 标 及 其 精 度;
mk为 RPk 点上的磁场强度指纹。
1.2 WiFi指 纹 识 别 算 法
图1 PDR、WiFi指纹识别、MM 组合导航算法流程图 Fig.1 Flow Chart of PDR/WiFi/MM Algorithm
此外,也 有 学 者 将 室 内 磁 场 异 常 作 为 一 种 指 纹 来用于定位 。 [5] 磁场匹配定位的优势在于不需 要 任 何发射设备,难 点 在 于 磁 场 指 纹 只 有 三 个 维 度。 为 了提高其维度,通 常 使 用 批 量 匹 配。 批 量 匹 配 的 方 法已经用于室 外 高 精 度 的 重 力[6]、地 磁 以 [7] 及 地 形 匹配导航 。 [8] 但是,消 费 电 子 产 品 中 的 惯 性 传 感 器 误 差 大 ,且 行 人 动 态 复 杂 ,难 以 挖 掘 出 有 效 的 约 束 信 息(除非将 设 备 固 定)。 而 由 于 室 内 环 境 复 杂[9],当 前室内磁场匹配技 术 存 在 较 高 的 误 匹 配 率,导 航 误 差 可 能 达 到 数 十 米 ,极 大 地 影 响 用 户 体 验 。
智能手机 上 WiFi更 新 率 通 常 较 低 (如 三 星 手 机约为 0.3 Hz),因 此 一 旦 WiFi数 据 更 新,便 将 WiFi信号 与 最 邻 近 脚 步 点 的 坐 标 组 合 构 成 一 个 WiFi指纹。第i个参考点(RPi)上的 WiFi指纹为:
卡尔曼滤波算法

卡尔曼滤波器不断的把covariance递归, 从而估算出最优的温度值。其运
行的很快,而且它只保留了上一时刻的covarian2c02e1/3。/28
12
三:卡尔曼滤波引例
2021/3/28
13
四:卡尔曼滤波算法数学推导
引入一个离散控制过程的系统。 该系统可用一个线性随机微分方程来描述:
X(k)=F X(k-1)+B U(k)+W(k) 加上系统的测量值:
五:卡尔曼滤波的典型应用—多传感器数据融合处理
数据融合的模型: (a)集中式融合系统;
(b)无反馈式分布融合系统;
(c)有反馈式分布融合系统; (d)有反馈的全并行系统
(c)有反馈式分布融合系统
融合中心到各传感器有反 馈通道,提高各传感器状态 估计和预测精度。
2021/3/28
27
五:卡尔曼滤波的典型应用—多传感器数据融合处理
• 卡尔曼滤波器源于他的博士论文和1960年 发表的论文《A New Approach to Linear Filtering and Prediction Problems》 (线性滤波与预测问题的新方法)。
卡尔曼将状态变量引入虑波理论,提出了递推滤波算法,建 立了后来被自动控制界称道的“卡尔曼滤波”。
25
五:卡尔曼滤波的典型应用—多传感器数据融合处理
数据融合的模型: (a)集中式融合系统;
(b)无反馈式分布融合系统;
(c)有反馈式分布融合系统; (d)有反馈的全并行系统
(b)无反馈式分布融合系统
各传感器分别滤波,将
各局部状态估计送给 融合中心进行融合,最 后给出融合结果。
2021/3/28
26
四:卡尔曼滤波算法数学推导
基于无迹粒子滤波的WiFi-PDR融合室内定位技术

基于无迹粒子滤波的WiFi-PDR融合室内定位技术
周楚霖;陈敬东;黄凡
【期刊名称】《计算机科学》
【年(卷),期】2022(49)S01
【摘要】为提高室内定位的精度和稳定度,文中提出了一种基于无迹粒子滤波的WiFi-PDR融合的室内定位方法。
为降低室内复杂环境对WiFi定位的影响,采用加权路径损失算法改善WiFi定位;为降低行人航迹推算误差累积效应,通过设定参考值划分行走周期并对加速度数据进行平滑降噪处理,提高了步数计量的精度;在改进WiFi和PDR定位的基础上,提出使用无迹粒子滤波融合定位方法,并对粒子滤波进行抗差自适应优化,提高其鲁棒性。
实验仿真结果表明该方法可以有效提高室内定位的精度和稳定性。
【总页数】6页(P606-611)
【作者】周楚霖;陈敬东;黄凡
【作者单位】武汉数字工程研究所
【正文语种】中文
【中图分类】TP391.9
【相关文献】
1.融合RTS平滑的迭代无迹卡尔曼粒子滤波方法
2.基于卡尔曼滤波的WiFi-PDR 融合室内定位
3.基于无模型无迹粒子滤波的编队卫星相对运动估计
4.融合渐消无
迹粒子滤波与高斯重采样的FastSLAM算法5.一种基于粒子滤波的多源融合室内定位方法
因版权原因,仅展示原文概要,查看原文内容请购买。
WiFi-PDR室内组合定位的无迹卡尔曼滤波算法

WiFi-PDR室内组合定位的无迹卡尔曼滤波算法陈国良;张言哲;汪云甲;孟晓林【摘要】针对当前室内定位的应用需求和亟待解决的关键问题,结合城市室内环境下广泛存在的WiFi无线信号以及智能手机传感器信息,提出了一种WiFi无线信号联合行人航迹推算(PDR)的室内定位方法.该方法采用无迹卡尔曼滤波(UKF)算法对WiFi和PDR定位信息进行融合处理,有效克服了WiFi单点定位精度低和PDR存在累计误差的问题.针对融合算法中WiFi指纹匹配计算量大的问题,用k-means聚类算法对WiFi指纹库进行聚类处理,降低了指纹匹配算法的计算量,提高了算法的实时性.通过在华为P6-U06智能手机平台上实际测试,在时间效率上经过聚类处理后系统定位耗时有很大程度的改善,平均降幅为51%,其中最大降幅达到64%,最小的也达到了36%;在定位精度上,当室内人员为行走状态时WiFi定位平均误差为7.76 m,PDR定位平均误差为4.57 m,UKF滤波融合后平均定位误差下降到1.24 m.【期刊名称】《测绘学报》【年(卷),期】2015(044)012【总页数】8页(P1314-1321)【关键词】室内定位;手机传感器;WiFi;行人航迹推算;k-means;无迹卡尔曼滤波【作者】陈国良;张言哲;汪云甲;孟晓林【作者单位】中国矿业大学环境与测绘学院,江苏徐州221116;中国矿业大学国土环境与灾害监测国家测绘地理信息局重点实验室,江苏徐州221116;中国矿业大学环境与测绘学院,江苏徐州221116;中国矿业大学国土环境与灾害监测国家测绘地理信息局重点实验室,江苏徐州221116;中国矿业大学环境与测绘学院,江苏徐州221116;中国矿业大学国土环境与灾害监测国家测绘地理信息局重点实验室,江苏徐州221116;诺丁汉大学,英国诺丁汉NG7 2TU【正文语种】中文【中图分类】P2281 引言随着基于位置的服务[1](location-based services,LBS)的兴起,人们对室内位置服务的需求日益强烈,如大型商场、地铁、飞机场等。
卡尔曼滤波算法原理和实现

卡尔曼滤波算法原理和实现
卡尔曼滤波算法是一种用于估计系统状态的数学方法,它通过融合来自传感器的测量数据和系统模型的预测值,提供对系统状态的最优估计。
该算法最初由R.E. Kalman在1960年提出,被广泛应用于控制系统、导航系统、机器人技术等领域。
该算法的原理可以简要描述为以下几个步骤:
1. 预测(Predict),利用系统的动态模型,根据先验信息和控制输入,预测系统的状态。
2. 更新(Update),根据传感器提供的测量数据,结合预测的状态值和测量的值,计算出最优的状态估计值。
3. 重复,不断地进行预测和更新,以持续地优化对系统状态的估计。
在实现卡尔曼滤波算法时,需要考虑以下几个关键点:
1. 状态方程和观测方程,需要准确地建立描述系统动态特性的
状态方程和观测方程,这两个方程是卡尔曼滤波算法的基础。
2. 状态估计初始化,需要对系统的初始状态进行估计,并设定状态估计的协方差矩阵。
3. 测量数据处理,需要对传感器提供的测量数据进行预处理,确保其符合卡尔曼滤波算法的要求。
4. 参数调节,卡尔曼滤波算法中有一些参数需要根据具体应用进行调节,如过程噪声协方差矩阵和测量噪声协方差矩阵等。
在实际应用中,卡尔曼滤波算法能够有效地处理传感器数据的噪声和不确定性,提供对系统状态的精准估计,因此被广泛应用于导航、目标跟踪、无人车辆等领域。
总的来说,卡尔曼滤波算法通过不断地预测和更新,结合系统模型和测量数据,提供对系统状态的最优估计。
在实现时需要考虑系统模型的准确性、初始状态的估计、测量数据的处理和参数的调节等因素。
希望这个回答能够帮助你更好地理解卡尔曼滤波算法的原理和实现。
基于粒子滤波融合Wi-Fi和PDR的室内定位研究
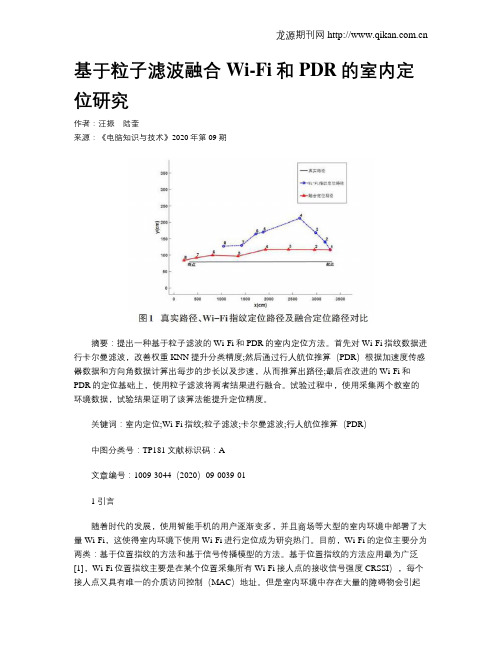
基于粒子滤波融合Wi-Fi和PDR的室内定位研究作者:汪振陆奎来源:《电脑知识与技术》2020年第09期摘要:提出一种基于粒子滤波的Wi-Fi和PDR的室内定位方法。
首先对Wi-Fi指纹数据进行卡尔曼滤波,改善权重KNN提升分类精度;然后通过行人航位推算(PDR)根据加速度传感器数据和方向角数据计算出每步的步长以及步速,从而推算出路径;最后在改进的Wi-Fi和PDR的定位基础上,使用粒子滤波将两者结果进行融合。
试验过程中,使用采集两个教室的环境数据,试验结果证明了该算法能提升定位精度。
关键词:室内定位;Wi-Fi指纹;粒子滤波;卡尔曼滤波;行人航位推算(PDR)中图分类号:TP181文献标识码:A文章编号:1009-3044(2020)09-0039-011 引言随着时代的发展,使用智能手机的用户逐渐变多,并且商场等大型的室内环境中部署了大量Wi-Fi,这使得室内环境下使用Wi-Fi进行定位成为研究热门。
目前,Wi-Fi的定位主要分为两类:基于位置指纹的方法和基于信号传播模型的方法。
基于位置指纹的方法应用最为广泛[1],Wi-Fi位置指纹主要是在某个位置采集所有Wi-Fi接人点的接收信号强度CRSSI),每个接人点又具有唯一的介质访问控制(MAC)地址。
但是室内环境中存在大量的障碍物会引起信号多径衰减问题,也会影响Wi-Fi信号的覆盖范围,从而导致接收信号强度(RSSI)会出现偏差。
这些问题使得在室内环境中基于RSSI的定位精度和穩定性都比较差,无法满足用户在室内的需求。
通过智能设备中的多个传感器采集数据,使用行人航位推算( PDR)[2]方法可以实现连续无缝的定位。
但是PDR也有明显的缺点,即存在误差累积问题,无法长时间的定位。
综上所述,本文提出一种基于粒子滤波[4][5]的Wi-Fi和PDR的室内定位方法。
2 本文算法本文算法首先是对原始的Wi-Fi数据进行卡尔曼滤波[3],设存放原始数据的元胞数组为rawdatacell,Q和R分别为过程噪声协方差和观测噪声协方差,计算卡尔曼增益以及最优估计的协方差,最后滤波后的数据。
无迹卡尔曼滤波中量测方程

无迹卡尔曼滤波中量测方程1 无迹卡尔曼滤波简介对于不确定度较高的系统,如飞行器控制系统、目标跟踪等,需要使用滤波算法将测量数据与模型预测结合起来做出最优估计。
其中较为常用的滤波算法之一便是卡尔曼滤波。
而无迹卡尔曼滤波(Unscented Kalman Filter,UKF)是卡尔曼滤波的一种改进,因为它能在不知道系统的具体动态模型的情况下进行非线性系统的状态估计,所以在实际应用中被广泛使用。
无迹卡尔曼滤波把变量的高斯分布和非高斯分布变换为对称的椭球分布,故称作无迹卡尔曼滤波。
2 量测方程在无迹卡尔曼滤波中,量测方程是通过传感器对系统状态进行测量而得到的方程,也是卡尔曼滤波中的关键一步。
在这里我们先来简单介绍一下量测方程的概念。
1.1 量测方程的定义量测方程是指传感器输出的状态变量方程。
它提供了关于系统状态的信息,这些信息被称为观测量。
量测方程通常由下面这个关系式描述:z = Hx + n其中z是传感器输出的观测量向量,x是系统状态向量,H是一个线性或非线性变换矩阵,称为观测矩阵,描述了传感器和系统状态之间的关系。
n是该观测量的噪声向量,可假设为高斯白噪声。
1.2 量测方程的重要性量测方程在滤波算法中发挥着关键作用。
因为滤波算法的目标在于对系统状态变量做最优估计,而传感器输出的观测量与系统状态变量之间的关系正是量测方程的关注点。
因此,我们需要在估计状态变量时,考虑到量测方程的影响,将其与卡尔曼滤波的预测值进行融合计算。
而这一过程正是卡尔曼滤波算法的核心。
1.3 量测方程的实现在实现无迹卡尔曼滤波时,量测方程的实现通常包括如下几个步骤:1. 在系统状态向量中选择需要测量的变量,组成观测量向量;2. 设计量测方程,将观测量向量与系统状态向量直接关联起来;3. 将系统状态向量通过预测更新为状态预测值;4. 将观测值通过观测方程转化为观测预测值;5. 根据观测预测值和状态预测值估计卡尔曼增益;6. 通过卡尔曼增益融合状态预测值和观测预测值,得到最终状态估计值。
卡尔曼滤波 高效求解算法

卡尔曼滤波高效求解算法卡尔曼滤波是一种用于估计系统状态的数学方法,它通过融合传感器测量值和系统动态模型,可以提供对系统状态的最优估计。
在实际应用中,尤其是在导航、控制系统和信号处理领域,卡尔曼滤波已经被广泛使用。
在这里,我将从几个方面来讨论卡尔曼滤波的高效求解算法。
首先,卡尔曼滤波的高效求解算法包括预测和更新两个主要步骤。
预测步骤利用系统的动态模型来预测下一个状态,并计算相应的协方差矩阵。
更新步骤则利用传感器测量值来校正预测的状态估计,并更新协方差矩阵。
高效的求解算法应当在这两个步骤中尽可能减少计算量和存储需求。
其次,针对卡尔曼滤波的高效求解算法,有一些经典的方法。
比如,针对线性系统,可以使用经典的卡尔曼滤波算法,它的时间复杂度是线性的,适用于实时系统。
对于非线性系统,可以使用扩展卡尔曼滤波(EKF)或者粒子滤波(PF)等方法来近似非线性系统的状态估计,这些方法在处理非线性系统时表现较好。
此外,近年来,基于深度学习的方法也被应用到卡尔曼滤波中,例如使用循环神经网络(RNN)或长短期记忆网络(LSTM)来学习系统的动态模型,从而提高状态估计的准确性和鲁棒性。
这些方法在处理复杂系统和非线性系统时展现出了很好的性能。
最后,除了算法本身的优化,高效求解算法还需要考虑到实际应用中的实时性和计算资源的限制。
因此,针对特定应用场景,可以进一步优化算法的实现,比如利用并行计算、硬件加速等手段来提高算法的求解效率。
综上所述,卡尔曼滤波的高效求解算法需要综合考虑算法的复杂度、适用性和实时性等因素,针对不同的应用场景选择合适的算法,并结合实际情况进行优化,才能达到高效求解的效果。
基于扩展Kalman滤波的室内WiFi-PDR融合定位算法

基于扩展Kalman滤波的室内WiFi-PDR融合定位算法刘庆;关维国;李顺康;王芳【摘要】为解决室内WiFi定位精度较低及行人航位推算(PDR)定位存在累积误差的问题,提出一种基于扩展Kalman滤波(EKF)的WiFi-PDR融合定位算法.WiFi通过改进的WKNN算法实现匹配定位,根据定位点与K近邻点的接收信号强度指示相对偏差进行权值修正,PDR定位采用多重约束条件的步态检测和在线步长估计方法.在此基础上,将EKF作为WiFi和PDR定位的融合滤波器,以降低WiFi定位回跳和PDR累计误差,从而提高定位精度.实验结果表明,在多次行迹转弯条件下,该融合定位算法的定位精度可达1.8m.【期刊名称】《计算机工程》【年(卷),期】2019(045)004【总页数】7页(P66-71,77)【关键词】室内定位;WiFi定位;行人航位推算;扩展Kalman滤波;融合定位【作者】刘庆;关维国;李顺康;王芳【作者单位】辽宁工业大学电子与信息工程学院,辽宁锦州121001;辽宁工业大学电子与信息工程学院,辽宁锦州121001;辽宁工业大学电子与信息工程学院,辽宁锦州121001;国网辽宁省电力有限公司锦州供电公司,辽宁锦州121000【正文语种】中文【中图分类】TP3910 概述随着人们对位置服务需求的提高,室内定位技术成为一个研究热点[1]。
典型的室内定位技术包括WiFi、蓝牙、无线传感器网络、射频识别、超宽带技术等。
WiFi定位的网络覆盖广,可满足多数室内定位需求,但其信号易受环境遮挡,导致定位随机性较大。
行人航位推算(Pedestrian Dead Reckoning,PDR)定位方法利用惯性传感器实现航迹推算定位,其终端支持度高,但存在较大的惯性累积误差。
为解决上述单一定位系统适用性较差且定位精度较低的问题[2],研究人员对有关WiFi-PDR的融合定位进行了探究与分析。
文献[3]使用联邦Kalman滤波融合WiFi和PDR数据,其中,WiFi定位采用支持向量机与回归分析相结合的方法。
基于卡尔曼滤波算法的室内无线定位系统

N k
[2]
2 卡尔曼滤波算法
卡尔曼滤波算法是利用目标的动态信息,在设法 去掉噪声的影响后得到的一个关于目标位置的较准确 的估计。 这个估计可以是对当前位置的估计(滤波), 也 可以是对将来位置的估计(预测), 还可以是对过去位置 的估计(插值或平滑)[4]。 虽然接收信号频率可经调整后 符合环境的变化,但环境干扰同时易导致信号发散或 丢失从而对信号分布产生影响,因此,利用卡尔曼滤 波算法进行滤波处理后可提高接收信号的准确性。该 算法实现方程表达如下。 预测:
Q X ( k +1 / k ) = (1 − K k +1 Bk +1 )Q X ( k +1 / k ) K k +1/ k = Q X ( k +1/ k ) B T k +1 + ( Bk +1Q X ( k +1/ k ) B T k +1 + QL ( k +1) )
(5) (6) (7)
y − y 0 y1 − y 0 = x − x0 x1 − x0
解这个方程,y 的值域为:
(8)
y = y 0 + ( x + x 0)
y1 − y 0 x1 − x0
(9)
这种在一组点(x0,y0)、(x1,y1),…,( xn、yn)中插值的 方式可被定义为点对之间的线性连续插入,可产生一 条实线。在本文研究中,将接收的定位信号经卡尔曼滤 波处理后再用线性插值方法预测已知的多对点对之间 的未知点的信号强度 。这样处理后可得到更准确的 估测位置,如图 2 所示移动曲线会更平缓,说明进一 步提高了室内无线定位系统的稳定性和准确性。
控制的卡尔曼滤波算法。该滤波方法不仅有效地抑制了定位数据信息的误差发散,而且能充分利用线性插值法 对随机误差进行补偿。实验表明它对静止和移动目标都能有效的提高定位精度,能较全面地满足复杂室内空间 定位的需求。 关键词:无线局域网;室内定位;卡尔曼滤波;实时跟踪;线性插值
Wi-Fi与PDR自适应加权的CKF融合定位算法

Wi-Fi与PDR自适应加权的CKF融合定位算法范立;王中元;汪云甲;李孟【期刊名称】《中国科技论文》【年(卷),期】2018(013)008【摘要】针对Wi-Fi定位稳定性差和行人航位推算(pedestrian dead reckoning,PDR)定位产生累积误差的问题,提出并实现了一种通过自适应加权容积卡尔曼滤波算法对Wi-Fi定位和行人航位推算定位进行信息融合的方法.首先采集指纹库,通过智能手机采集Wi-Fi和PDR的数据,采用加权K近邻(weighted-nearest neighbor,WKNN)算法进行Wi-Fi定位以及地图匹配方法辅助PDR定位,然后采用渐消因子自适应地加权两者信息,并使用容积卡尔曼滤波(cubature Kalman filtering,CKF)算法进行滤波计算.实验表明,所提方法能够有效克服Wi-Fi 和PDR两种定位产生的问题,对比经典的扩展卡尔曼滤波(extended kalman filter,EKF)融合算法,能够大幅度提高室内定位的精度,并具有较强的稳定性.【总页数】7页(P950-955,960)【作者】范立;王中元;汪云甲;李孟【作者单位】中国矿业大学国土环境与灾害监测国家测绘局重点实验室 ,江苏徐州221116;中国矿业大学环境与测绘学院 ,江苏徐州221116;中国矿业大学国土环境与灾害监测国家测绘局重点实验室 ,江苏徐州221116;中国矿业大学环境与测绘学院 ,江苏徐州221116;中国矿业大学国土环境与灾害监测国家测绘局重点实验室 ,江苏徐州221116;中国矿业大学环境与测绘学院 ,江苏徐州221116;中国矿业大学国土环境与灾害监测国家测绘局重点实验室 ,江苏徐州221116;中国矿业大学环境与测绘学院 ,江苏徐州221116【正文语种】中文【中图分类】P228【相关文献】1.室内Wi-Fi/PDR自适应鲁棒卡尔曼滤波融合定位方法 [J], 周牧;耿小龙;谢良波;聂伟;田增山2.基于PDR反馈的Wi-Fi室内定位算法研究 [J], 赵建国;王杰贵3.Wi-Fi与PDR自适应加权的CKF融合定位算法 [J], 范立;王中元;汪云甲;李孟;;;;;;;;4.基于改进PDR与指纹库PSO-BP融合室内定位算法 [J], 蔡文炎; 何洋5.基于粒子滤波融合Wi-Fi和PDR的室内定位研究 [J], 汪振;陆奎因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Point,AP)的信号强度。利用 K-means 聚类算法 对所有采样点进行聚类处理生成最终的 WiFi 信号 指纹库;在线定位阶段是将实时测得的 WiFi 信号 采用匹配算法与数据库中的信息比较得到最终的
题,用 K-means 聚类算法对 WiFi 指纹库进行聚类 处理,降低指纹匹配算法的计算量,提高算法的实 时性。最终在智能手机平台进行算法测试,结果表 明该方法的实时性和定位精度满足一般室内人员 定位的应用。
2 WiFi 信号指纹定位
WiFi 信号指纹定位方法分为离线勘测和在线
定位两个阶段。离线勘测阶段是在待定位区域按照
51%,其中最大降幅达到 64%,最小的也达到了 36%;在定位精度上,当室内人员为行走状态时 WiFi 定位
平均误差为 7.76m,PDR 定位平均误差为 4.57m,UKF 滤波融合后平均定位误差下降到 1.24m。
关键词:室内定位;手机传感器;WiFi;PDR;K-means;无迹卡尔曼滤波
中图分类号:P228
文献标识码:A
基金项目:国家高技术研究发展计划项目(863 项目)(2013AA12A201); 国家自然科学基金项目
(41371423); 江苏高校优势学科建设工程(SZBF2011-6-B35)
1引言
随着基于位置的服务(location-based services, LBS[1])的兴起,人们对室内位置服务的需求日益 强烈,如大型商场、地铁、飞机场等。各个领域的 研究者越来越关注基于无线传感器网络(wireless sensing networks,WSN[2])和无线局域网(wireless local area networks,WLAN[3])等面向室内场所环 境的定位技术,研究成果包括红外线[4]、超声波[5]、 射频识别(radio frequency identification, RFID[6])、 蓝牙[7]、超宽带(ultra wide band, UWB[8])、无线 保真(wireless fidelity,WiFi[9])、ZigBee[10]、地磁 定位[11]等典型的室内定位方法,设计出了多个具有 代表性的室内定位系统。由于单一信号无法覆盖全 部室内空间,这就需要多种定位技术的结合使用。 文献[12]将 GPS、RFID、WiFi 和计步器四种定位 技术融合,组成一个定位平台,有效弥补了各种定 位技术的缺点,提高了定位精度和稳定性。文献 [13,14]利用行人航迹推算(PDR)和 UWB 定位互 补技术,采用约束滤波器使得位置估计精度可以达 到亚米级。文献[15]采用 UKF 滤波融合惯导定位 结果和 WiFi 定位结果来对室内车辆进行定位,取 得很好的效果。文献[16,17]开展了多源泛在无线信 号辅助的室内外无缝定位方法研究,提出了一种泛 在无线信号辅助的无缝定位新方法,并对无缝定位 技术的原理、特点和发展趋势进行了讨论。上述这 些定位系统往往需要添加额外的硬件设施,系统实 现复杂,部署成本高,因此,采用各种辅助的方式 来增强系统定位的实时性和适用性,降低部署成本 成为当前室内定位的关键。随着智能手机越来越受 到人们的青睐,它们除了可以提供更好的软件功能 之外,还包含很多先进的硬件设施,如 WiFi 模块, 蓝牙模块和各种惯性传感器等,研究人员可以直接 使用这些硬件设施开发出室内定位系统。文献[18] 将智能手机作为系统平台利用粒子滤波融合手机 惯导信息、WiFi 信息和地图信息在室内环境下得 到一个很好的定位结果。基于移动端惯性传感器的 PDR 算法具有短时间内定位精度高,但定位误差 随时间积累逐渐增大,而利用 WiFi 定位时单点定 位误差大但没有误差积累,因此将这两种定位手段 结合起来,构成 WiFi/PDR 组合定位系统,既能达 到较高的定位精度又能提高定位结果的可靠性。本 文基于智能手机平台实现了一种通过 UKF 滤波算 法融合 WiFi 无线信号和行人航迹推算 PDR 的室内 定位方法。针对融合算法中的 WiFi 计算量大的问
位精度低和 PDR 存在累计误差的问题。针对融合算法中 WiFi 指纹匹配计算量大的问题,用 K-means 聚类
算法对 WiFi 指纹库进行聚类处理,降低指纹匹配算法的计算量提高算法的实时性。通过在华为 P6-U06
智能手机平台上实际测试,在时间效率上经过聚类处理后系统定位耗时有很大程度的改善,平均降幅为
定位结果。 2.1 WiFi 指纹匹配算法
WiFi 指纹匹配算法最常用的是由文献[19]中 采用的信号空间 K 最近邻法(K Nearest Neighbor in Signal Space, k-NNSS)。定位时首先扫描 WiFi 信
号得到扫描信号强度向量 SV=[v1,v2,...,vi,...,vn] 其中 vi(1 £ i £ n) 表示接收到来自第 i 个 WiFi 信号
Unscented Kalman Filter Algorithm for WiFi/PDR Integrated Indoor Positioning
CHEN GuoLiang1,2, ZHANG Yanzhe1,2, WANG Yunjia1,2, MENG Xiaolin3
1.School of Environment Science and Spatial Informatics, China University of Mining and Technology, Xuzhou 221116, China;2.Key Laboratory for Land Environment and Disaster Monitoring of SBSM,China University of Mining and Technology, Xuzhou 221116, China;3. The University of Nottingham, Nottingham, NG7 2TU, UK
发射点的信号强度,然后计算与指纹库中每个采样
点的相似度 Length i 。考虑到定位区域过大时采样 点上不能接收到所有 AP 发射的信号,使得空间距 离相近的采样点搜索到的相同 AP 数目多,空间距 离相距较远的采样点搜索到的相同 AP 数目则少。 因此,相同 AP 的数目在一定程度上可以反映样本
WiFi/PDR 室内组合定位的无迹卡尔曼滤波算法
陈国良 1,2,张言哲 1,2,汪云甲 1,2,孟晓林 3 1.中国矿业大学环境与测绘学院,江苏 徐州 221116;2.中国矿业大学 国土环境与灾害监测国家测绘地 理信息局重点实验室 江苏 徐州 221116;3.诺丁汉大学,英国 诺丁汉 NG7 2TU
一定的间隔距离确定若干采样点,形成一个采样点
集 合 L = {l1,l2,...,lm} 。 每 一 个 L 中 的 元 素 li(1 £ i £ m) 记录两部分数据,一部分是该采样点 的地理坐标 Pi=(xi,yi) ,另一部分是在该采样点收
到 的 WiFi 信 号 强 度 ( RSSI ) 向 量
在线定位阶段搜寻到的 AP 与 WiFi 指纹库中第 i 个
指纹点相同 AP 的数目。图 1 所示为 WiFi 信号示
意图,图中 L1、L2 为指纹点,L1 接收到 AP1、AP2、
Abstract:Indoor positioning still faces lots of fundamental technical problems although it has been widely applied. A novel indoor positioning technology by using the smart phone with the assisting of the widely available and economically signals of WiFi is proposed. It also includes the principles and characteristics in indoor positioning. First, improving the system’s accuracy by fusing the WiFi fingerprinting positioning and PDR (Pedestrian Dead Reckoning) positioning with UKF(Unscented Kalman Filter). Second, improving the real-time performance by clustering the WiFi fingerprinting with k-means clustering algorithm. An investigation test was conducted at the indoor environment to learn about its performance on a HUAWEI P6-U06 smart phone. The result shows that compared to the pattern-matching system without clustering, a average reduction of 51% in the time cost can be obtained without degrading the positioning accuracy. When the state of personnel is walking, the average positioning error of WiFi is 7.76m, the average positioning error of PDR is 4.57m. After UKF fusing, the system’s average positioning error is down to 1.24m. It shows that the algorithm greatly improves the system’s real-time and positioning accuracy. Keywords: Indoor positioning; Smart Phone Sensors ; WiFi; PDR; K-means; UKF Foundation support:The National High-tech Research and Development Program of China (863 Program) (No.2013AA12A201);The National Natural Science Foundation of China (No.41371423);Engineering construction of Jiangsu Universities (No.SZBF2011-6-B35)
