函数的最大值与导数.docx
人教A版选修2《函数的最大值与导数》教案及教学反思

人教A版选修2《函数的最大值与导数》教案及教学反思本文将结合人教A版选修2《函数的最大值与导数》的教学要求和内容,提供一份教案及教学反思,以供初中数学教师借鉴。
一、教学目标1.了解函数的导数概念,掌握求导数的方法;2.理解函数取得最大值的概念,掌握求解函数最大值的方法;3.能够根据实际问题建立函数模型,通过求导数求解问题;4.提高学生对函数概念的理解和应用能力。
二、教学内容本节课的教学内容分为两部分:函数的导数和函数的最大值。
1. 函数的导数1.导数的概念:通过极限的概念,引入导数的概念。
导数是函数在某一点处的变化率。
2.导数的求法:利用导数的定义及基本导数公式,掌握函数求导的方法。
3.导数的应用:通过例子,让学生了解导数在函数图像上的几何意义和在实际问题中的应用。
2. 函数的最大值1.最大值的概念:引入函数最大值的概念,通过例子让学生了解最大值的概念。
2.求解最大值的方法:介绍求解函数最大值的方法,包括边界法、导数法等。
3.最大值在实际问题中的应用:让学生通过例子了解最大值在实际问题中的应用。
三、教学过程1. 函数的导数(1)授课环节1.利用幻灯片,介绍导数的概念和求导数的方法。
2.通过例子,让学生了解导数在函数图像上的几何意义和在实际问题中的应用。
(2)练习环节1.让学生根据函数图像,求解函数在某一点处的导数。
2.给学生练习题,让他们自己计算函数在多个点处的导数。
2. 函数的最大值(1)授课环节1.利用幻灯片,介绍最大值的概念和求解最大值的方法。
2.通过例子,让学生了解最大值在实际问题中的应用。
(2)练习环节1.让学生根据函数图像,确定函数在哪些点处取得最大值。
2.给学生练习题,让他们自己寻找函数的最大值。
3. 课堂小结回顾本节课的教学内容,重点强调函数导数和最大值的概念,以及它们在实际问题中的应用。
四、教学反思1.教学内容紧凑,学生有时无法听出教师的解释。
因此,在解释过程中,需要注意语速和语调的抑扬顿挫,使学生更好地理解。
07函数的最大小值与导数

在闭区间[a,b]上的函数y=f(x)的图象是一 条连续不断的曲线,则它必有最大值和最小值.
f(x1)
f(x3)
y
a
x2
x1
0
x3
g
f(a)
f(x2)
f(b)
g
x4
bx
一般地,求函数y=f(x)在[a,b]上的最大值与最小
值的步骤如下:
①:求y=f(x)在(a,b)内的极值(极大值与极小值);
②:将函数y=f(x)的各极值与端点处的函数值f(a)、 f(b) 比较,其中最大的一个为最大值,最小的一个为最 小值. 求函数的最值时,应注意以下几点:
最大值为 f (4) =76,最小值为 f (1)=-5
小结
1. 求 f ( x)在 [a, b上] 的最大值与最小值的步骤: ①求函数 f ( x)在 (a, b)内的极值;
②求函数 f ( x在) 区间端点 f (a)、f (b)的值;
③将函数 f ( x)在各极值与 f (a)、f (b) 比较,其中最大的一 个是最大值,最小的一个是最小值.
(1)函数的极值是在局部范围内讨论问题,是一个局部概 念,而函数的最值是对整个定义域而言,是在整体范围 内讨论问题,是一个整体性的概念.
(2)闭区间[a,b]上的连续函数一定有最值.开区间(a,b)内 的可导函数不一定有最值,但若有唯一的极值,则此极 值必是函数的最值.
(3)函数在其定义域上的最大值与最小值至多各 有一个,而函数的极值则可能不止一个,也可能没有 极值,并且极大值(极小值)不一定就是最大值(最小 值),但除端点外在区间内部的最大值(或最小值),则 一定是极大值(或极小值).
函数的最大(小)值与导数
复习引入
函数的最大(小)值与导数 课件

f(-2).
而f(2)-f(-2)=16-4a2<0,f(x)max=f(-2)=-8+4a+ 2a2+m,
又∵f(x)≤1在[-2,2]上恒成立,
∴-8+4a+2a2+m≤1,
即m≤9-4a-2a2,在a∈[3,6]上恒成立,
∵9-4a-2a2的最小值为-87,∴m≤-87.
[点评] 1.由于参数的取值范围不同会导致函数在所给区 间上的单调性的变化,从而导致最值的变化,故含参数时, 需注意是否分类讨论.
2.求可导函数y=f(x)在[a,b]上的最大(小)值的步骤: (1)求f(x)在开区间(a,b)内的 极值 ; (2)计算函数f(x)在各 极值点 和 端点 处的函数值f(a),f(b) 比较,其中最大的一个为最大值,最小的一个为最小值.
3.函数f(x)=x4-8x2+2在[-1,3]上的最大值与最小值分 别为________.
[答案] 11 -14
[解析] f ′(x)=4x3-16x=4x(x-2)(x+2). 令f ′(x)=0,解得x1=-2,x2=0,x3=2. 其中x2=0,x3=2在[-1,3]内,计算得 f(0)=2,f(2)=-14,f(-1)=-5,f(3)=11, 故f(x)在[-1,3]上的最大值是11,最小值是-14.
当x变化时,f ′(x),f(x)的变化情况如下表:
x
-1 (-1,0) 0 (0,43)
4 3
(43,2) 2
f ′(x)
+ 0-
0
+
f(x) -2
1
↘ -257
1
故f(x)最大值=1,f(x)最小值=-2.
[点评] 要熟记用导数求最值的一般步骤:一求极值,二 求闭区间端点函数值,三比较找出最值.
导数与函数的最大值与最小值

(2)闭区间[a,b]上的连续函数一定有最值.开区间(a,b)内 的可导函数不一定有最值,但若有唯一的极值,则此极 值必是函数的最值.
2021/6/16
4
(3)函数在其定义域上的最大值与最小值至多各有一个, 而函数的极值则可能不止一个,也可能没有极值,并且 极大值(极小值)不一定就是最大值(最小值),但除端点 外在区间内部的最大值(或最小值),则一定是极大值 (或极小值).
22.0与21/6数/16 学中其它分支的结合与应用.
15
例1: 如图,在二次函数f(x)=
4x-x2的图象与x轴所
y
围成的图形中有一个
内接矩形ABCD,求这
个矩形的最大面积.
解:设B(x,0)(0<x<2), 则
x
A(x, 4x-x2).
从而|AB|= 4x-x2,|BC|=2(2-x).故矩形ABCD的面积
为:S(x)=|AB||BC|=2x3-12x2+16x(0<x<2).
S(x)6x22x 41.6 令 S(x)0,得x12233,x22233.
x1(0,2),所以当 因此当点B为(2 2
x 3 ,02) 时2,3矩3时形,的S(x 最)m 大a面x3积923是.
32
3.
2021/6/16
解:设圆柱的高为h,底半径为r,则表面积S=2πrh+2πr2.
由VS =(πr)r 2h2 ,得rhV r2 V2 r2r,2则2 r V2r2.
令S(r)2rV2 4r0,解得r
4V V 3 23
2
,即h=2r.
3
(完整word版)函数的极值最值与导数
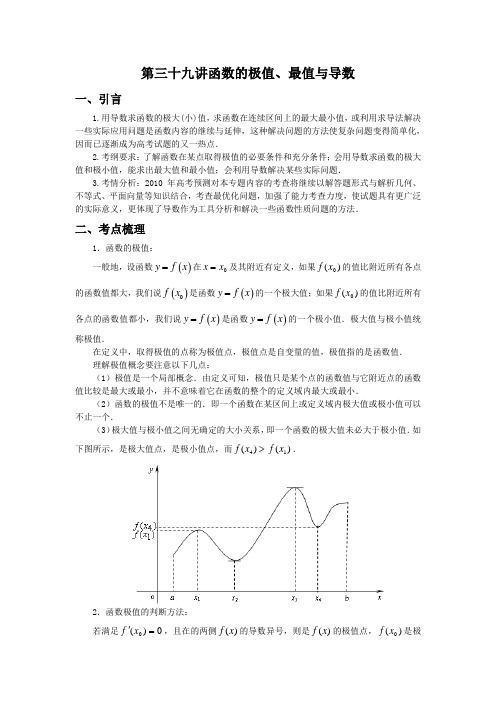
第三十九讲函数的极值、最值与导数一、引言1.用导数求函数的极大(小)值,求函数在连续区间上的最大最小值,或利用求导法解决一些实际应用问题是函数内容的继续与延伸,这种解决问题的方法使复杂问题变得简单化,因而已逐渐成为高考试题的又一热点.2.考纲要求:了解函数在某点取得极值的必要条件和充分条件;会用导数求函数的极大值和极小值,能求出最大值和最小值;会利用导数解决某些实际问题.3.考情分析:2010年高考预测对本专题内容的考查将继续以解答题形式与解析几何、不等式、平面向量等知识结合,考查最优化问题,加强了能力考查力度,使试题具有更广泛的实际意义,更体现了导数作为工具分析和解决一些函数性质问题的方法.二、考点梳理1.函数的极值:一般地,设函数()y f x =在0x x =及其附近有定义,如果)(0x f 的值比附近所有各点的函数值都大,我们说()0f x 是函数()y f x =的一个极大值;如果)(0x f 的值比附近所有各点的函数值都小,我们说()y f x =是函数()y f x =的一个极小值.极大值与极小值统称极值.在定义中,取得极值的点称为极值点,极值点是自变量的值,极值指的是函数值. 理解极值概念要注意以下几点:(1)极值是一个局部概念.由定义可知,极值只是某个点的函数值与它附近点的函数值比较是最大或最小,并不意味着它在函数的整个的定义域内最大或最小.(2)函数的极值不是唯一的.即一个函数在某区间上或定义域内极大值或极小值可以不止一个.(3)极大值与极小值之间无确定的大小关系,即一个函数的极大值未必大于极小值.如下图所示,是极大值点,是极小值点,而4()f x >)(1x f .2.函数极值的判断方法:若满足0)(0='x f ,且在的两侧)(x f 的导数异号,则是)(x f 的极值点,)(0x f 是极值,并且如果)(x f '在两侧满足“左正右负”,则是)(x f 的极大值点,)(0x f 是极大值;如果)(x f '在两侧满足“左负右正”,则是)(x f 的极小值点,)(0x f 是极小值.注意:函数在某点处的导数值等于零,该点不一定是函数的极值点,必须检验函数在该点两侧的符号是否相异,即可导函数有极值是该点处的导数值等于零的充分不必要条件.3.函数的最大值与最小值:在闭区间[],a b 上连续的函数()f x ,在[],a b 是必有最大值与最小值,但在开区间(),a b 上连续的函数不一定有最值.4.极值与最值的区别与联系:①“最值”是整体概念,是比较整个定义域内的函数值得出的,具有绝对性;而“极值”是个局部概念,是比较极值点附近函数值得出的,具有相对性.②从个数上看,一个函数在其定义域上的最值是唯一的;而极值不唯一;③函数在其定义区间上的最大值、最小值最多各有一个,而函数的极值可能不止一个,也可能没有一个;④极值只能在定义域内部取得,而最值可以在区间的端点处取得,有极值的未必有最值,有最值的未必有极值;极值有可能成为最值,最值只要不在端点必定是极值.三、典型例题选讲例1求()31443f x x x =-+的极值,并画出()f x 的草图. 分析:首先求()f x ',再求方程()0f x '=的根,然后检验()f x '在根两边的符号. 解:因为()31443f x x x =-+,所以()'24(2)(2)f x x x x =-=-+. 令()'0f x =解得2x =或2x =-.当变化时,()'fx ,()f x 的变化情况如下表:)因此,当2x =-时,()f x 有极大值,并且极大值为(2)3f -=;当2x =时,()f x 有极小值,并且极小值为4(2)3f =-.函数()31443f x x x =-+的图像如图1所示:归纳小结:(1)本题考查导数的运算及利用导数知识求函数的极值等基本知识和分析问题、解决问题的能力;(2)通过求函数的导数,将函数问题转化为一元二次方程来探究,充分体现了函数与方程相互转化的解题思想与解题策略.(3)求可导函数()f x 的极值的步骤: ①确定函数的定义区间,求导数()f x '; ②求方程()0f x '=的根;③用函数的导数为的点,顺次将函数的定义区间分成若干小开区间,并列成表格.检查()f x '在方程根左右的值的符号,如果左正右负,那么()f x 在这个根处取得极大值;如果左负右正,那么()f x 在这个根处取得极小值;如果左右不改变符号即都为正或都为负,那么()f x 在这个根处无极值.如果函数在某些点处连续但不可导,也需要考虑这些点是否是极值点. 例2(2009安徽)设b a <,函数)()(2b x a x y --=的图像可能是( )解:()(32)y x a x a b '=---,由0y '=得2,3a bx a x +==, ∴当x a =时,取极大值,当23a bx +=时取极小值且极小值为负.故选C . 另解:当x b <时0y <,当x b >时,0y >.选C .归纳小结:(1)本题考查了函数图象与导数极值的基本知识,考查了数形结合思想和分析推理能力.(2)函数的极值是()'0f x =的充分条件,可以利用填表的方式或穿轴法判断是极大值还是极小值.(3)在图形问题中特殊值法是一种常用的方法,要不断练习把握.例3(2008广东)设a ∈R ,若函数3axy e x =+,x ∈R 有大于零的极值点,则( ) A .3a >-B .3a <-C .13a >-D .13a <-解:令'3axy ae =+,则30ax ae +=有大于零的根,所以3axae =-.∴0a <,则13ln x a a ⎛⎫=- ⎪⎝⎭. ∵0x >,∴3ln 0a ⎛⎫-< ⎪⎝⎭,即31a -<,解得3a <-. 故选B .归纳小结:(1)本题考查函数的极值与方程的根的关系,考查了转化思想和分析、计算能力.(2)函数的极值点是方程()'0f x =的根,但要注意方程()'0f x =的根不一定是函数的极值点,如果要判断是否为函数的极值点还需要验证该点两侧导数的符号是否异号.例4已知函数()3239f x x x x a =-+++,(1)求()f x 的单调递减区间;(2)若()f x 在区间[]2,2-上的最大值为,求它在该区间上的最小值.分析:第(1)问属于程序化问题,第(2)问是函数在闭区间的最值问题,只需要求出函数的极值和端点值并进行比较即可解:(1)()2'369f x x x =-++.令()'0f x <,解得1x <-或3x >.所以函数()f x 的单调递减区间为(),1-∞-,()3,+∞. (2)因为()22f a -=+,()222f a =+,()15f a -=-+.所以()2f 和()1f -分别是()f x 在区间[]2,2-上的最大值和最小值,于是有2220a +=,解得2a =-.故()32392f x x x x =-++-,因此()113927f -=+--=-.即函数()f x 在区间[]2,2-上的最小值为.归纳小结:(1)本题考查了利用导数在解决最值问题中的应用问题,考查分析问题、解决问题的能力;(2)求函数()f x 在闭区间[],a b 上的最大值和最小值的步骤: ①求函数()f x 在开区间(),a b 内的极值;②求函数()f x 在区间端点的函数值()f a 和()f b ;③将函数()f x 将各极值与()f a 、()f b 比较,其中最大的一个为最大值,最小的一个为最小值.对于函数()f x 在开区间(),a b 上的最大值和最小值的步骤: ①求函数()f x 在开区间(),a b 内的极值;②将函数()f x 将各极值比较,其中最大的一个为最大值,最小的一个为最小值. 定义在开区间(),a b 上的可导函数,如果只有一个极值点,该极值点必为最值点. 例5(2007全国Ⅰ)设函数32()2338f x x ax bx c =+++在1x =及2x =时取得极值. (1)求,a b 的值;(2)若对于任意的[03]x ∈,,都有2()f x c <成立,求的取值范围.分析:函数()f x 是实数域上的可导函数,因此可先求导确定可能的极值,再通过极值点与导数的关系,建立由极值点1x =,2x =所确定的相等关系式,运用待定系数法求值.解:(1)2()663f x x ax b '=++,因为函数()f x 在1x =及2x =取得极值,则有(1)0f '=,(2)0f '=.即6630241230a b a b ++=⎧⎨++=⎩,.解得3a =-,4b =.(2)由(1)可知,32()29128f x x x x c =-++,2()618126(1)(2)f x x x x x '=-+=--.当(01)x ∈,时,()0f x '>; 当(12)x ∈,时,()0f x '<; 当(23)x ∈,时,()0f x '>.所以,当1x =时,()f x 取得极大值(1)58f c =+,又(0)8f c =,(3)98f c =+. 则当[]03x ∈,时,()f x 的最大值为(3)98f c =+. 因为对于任意的[]03x ∈,,有2()f x c <恒成立,所以298c c +<,解得1c <-或9c >,因此的取值范围为(1)(9)-∞-+∞U ,,. 归纳小结:(1)本题从逆向思维的角度出发,根据题设结构进行逆向联想,合理地实现了问题的转化,使抽象的问题具体化.考查了转化思想及灵活解题的能力;(2)已知函数在点处有极值和函数值()00y f x =,求参数值的问题,是一类常见的关于函数极值的应用问题.解这类问题采用待定系数法,解关于参数的方程组()()000'0f x f x y =⎧⎪⎨=⎪⎩即可;(3)在讨论函数的单调性时,一定要先明确定义域,在定义域范围内研究单调区间.例6已知函数32()f x ax bx cx =++在点处取得极大值,其导函数()y f x '=的图象经过点()1,0,()2,0,如图所示,求:(1)的值;(2),,的值.分析:因为函数()f x 点处取得极大值,因此观察()f x '在,左右两侧的符号就可以判断出极大值点.在根据极值点处导数为和0()5f x =,利用待定系数法求参数,,.解法一:(1)由图象可知,在(),1-∞上()0f x '>,在()1,2上()0f x '<,在(2,)+∞上()0f x '>,故()f x 在(,1)-∞,(2,)+∞上递增,在()1,2上递减.因此()f x 在1x =处取得极大值,所以01x =.(2)2()32f x ax bx c '=++,由(1)0,(2)0,(1)5,f f f ''===得320,1240,5,a b c a b c a b c ++=⎧⎪++=⎨⎪++=⎩解得2,9,12.a b c ==-= 解法二:(1)同解法一.(2)设2()(1)(2)32,f x m x x mx mx m '=--=-+又2()32f x ax bx c '=++,所以3,,232m a b m c m ==-=, ∴323()232m f x x mx mx =-+. 由(1)5f =,得32532m m m -+=,解出6m =,所以2,9,12a b c ==-=.归纳与小结:(1)本题考查了函数()f x 和()'f x 图象之间的联系,同时考查了数形结合思想和识图、用图的能力以及根据导数知识灵活解题的能力;(2)根据函数()f x 的图象中的单调性和极值可以判断出()'f x 在不同区间的符号和极值点;根据函数()'f x 的图象在不同区间的符号及与轴的交点,可以判断出()f x 的单调性和极值点.并能画出草图.例7(2009年湖南)某地建一座桥,两端的桥墩已建好,这两墩相距米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为256万元,距离为米的相邻两墩之间的桥面工程费用为(2x +万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为万元.(1)试写出关于的函数关系式;(2)当640m =米时,需新建多少个桥墩才能使最小?分析:本题是工程费用最优问题,首先应建立关于的函数关系式,再根据解析形式利用导数方法寻找最优解.解:(1)设需要新建个桥墩,(1)1mn x m n x +=-,即=. 所以()25612(2m my f x n n x x x x=+=+(+)(=256(-1)+2562256x m x=+-.(2)由(1)知,2332222561'()(512).22m mf x mx x xx=-+=- 令'()0f x =,得32512x =,所以64x =.当064x <<时()'0f x <,()f x 在区间()0,64内为减函数;当64640x <<时,()'0f x >,()f x 在区间()64,640内为增函数. 所以()f x 在64x =处取得最小值,此时,64011964m n x =-=-=. 故需新建个桥墩才能使最小.归纳小结:(1)本题考查函数建模,函数最值以及导数应用等基本知识,考查建模解模的能力和转化解题能力.(2)利用导数解决实际问题的最优问题的一般步骤:①如果涉及到解析几何问题,要根据实际意义和问题条件,合理建立坐标系; ②分析实际问题中各量之间的关系,列出实际问题的数学模型写出实际问题中变量之间的函数关系()y f x =;③如果()y f x =的形式是高次函数或对数、指数函数或商式形式,则求函数的导数()'f x ,并解方程()'0f x =;④因为只有唯一极值,通过说明该点处两侧的单调性,得到最大者或最小值. (3)在解决实际最优化问题中,要确定函数关系中自变量的定义区间,同时还要注意将不符合实际意义的值舍去.例8(2008四川)已知3x =是函数()()2ln 110f x a x x x =++-的一个极值点.(1)求;(2)求函数()f x 的单调区间;(3)若直线y b =与函数()y f x =的图象有3个交点,求的取值范围.分析:第(1)问实际是解以为未知数的方程()'30f =的根.第(2)问在已知值的基础上解不等式()'0f x >和()'0f x <.第(3)问中图象有3个交点,实际上是平行于轴的动直线y b =在曲线()y f x =的两个极值点之间移动,因此此小题是求函数的极值问题.解:(1)因为()'2101af x x x=+-+, 所以()'361004af =+-=. 因此16a =.(2)由(1)知,()()()216ln 110,1,f x x x x x =++-∈-+∞. ∴()()2'2431x x f x x-+=+.当()()1,13,x ∈-+∞U 时,()'0fx >;当()1,3x ∈时,()'0f x <.所以()f x 的单调增区间是()()1,1,3,-+∞,()f x 的单调减区间是()1,3.(3)由(2)知,()f x 在()1,1-内单调增加,在()1,3内单调减少,在()3,+∞上单调增加,且当1x =或3x =时,()'0fx =.所以()f x 的极大值为()116ln 29f =-,极小值为()332ln 221f =-.所以在()f x 的三个单调区间()()()1,1,1,3,3,-+∞直线y b =与()y f x =的图象各有一个交点,当且仅当()()31f b f <<时成立.因此,的取值范围为()32ln 221,16ln 29--.归纳小结:(1)本题考查了函数的极值与单调性运用等知识,考查了数形结合思想和计算推理能力.(2)一般来说,直线y a =和曲线()y f x =的交点问题可以转化到图象上理解,即直线y a =在曲线的极值点之间移动,但要注意函数值在极值点左右的极限值,否则容易出现错误.例9已知函数3211()32f x x ax bx =++在区间[11)-,,(13],内各有一个极值点. (1)求24a b -的最大值;(2)当248a b -=时,设函数()y f x =在点(1(1))A f ,处的切线为,若在点处穿过函数()y f x =的图象(即动点在点附近沿曲线()y f x =运动,经过点时,从的一侧进入另一侧),求函数()f x 的表达式.解:(1)因为函数3211()32f x x ax bx =++在区间[11)-,,(13],内分别有一个极值点,所以2()f x x ax b '=++在[11)-,,(13],内分别有一个实根,设两实根为12x x ,()12x x <,则21x x -=,且2104x x <-≤.于是04<,20416a b <-≤,且当11x =-,23x =,即2a =-,3b =-时等号成立.故24a b -的最大值是16.(2)由(1)1f a b '=++知()f x 在点(1(1))f ,处的切线的方程是(1)(1)(1)y f f x '-=-,即21(1)32y a b x a =++--,因为切线在点(1())A f x ,处穿过()y f x =的图象, 所以21()()[(1)]32g x f x a b x a =-++--在1x =两边附近的函数值异号,则1x =不是()g x 的极值点.而()g x 321121(1)3232x ax bx a b x a =++-++++, 且22()(1)1(1)(1)g x x ax b a b x ax a x x a '=++-++=+--=-++. 若11a ≠--,则1x =和1x a =--都是()g x 的极值点.所以11a =--,即2a =-,又由248a b -=,得1b =-,故321()3f x x x x =--. 归纳小结:(1)本题考查了函数的极值与切线方程,方程的根,图象与极值点的关系等知识,考查了数形结合思想和运算推理能力.(2)本题解题的关键是:①函数在区间(),a b 上有极值点等价与方程()'0f x =在(),a b 内有根;②函数()f x 在某点处两侧的符号相反,则该点一定不是极值点.四、本专题总结1.导数作为研究函数的一种重要工具,在学习时应引起充分重视,这部分知识点不多,但涉及的题型比较多.(1)理解函数极值与最值的概念,函数极值刻画的是函数的局部性质,而函数的最值刻画的是函数的整体性质;(2)注意比较极值与最值的概念以及它们之间的联系,可导函数在极值点两侧导函数的符号相反,极大值不一定是最大值,极大值可能小于极小值,连续可导函数闭区间上的最值就是端点值与极值中的最大值、最小值;(3)可导函数有极值是该点处的导数值等于零的充分不必要条件; (4)要熟练掌握求解函数极值与最值的方法.2.在复习函数的极值与最值时,要以导数为工具,联系函数的性质,如单调性等.这部分内容在高考中的问题设置多数以综合问题形式出现,因此在解决问题中,要逐步体会数形结合思想、转化与整合思想、函数与方程(不等式)思想、分类讨论思想等,不断提高分析推理、灵活计算、等价变形等数学能力.。
函数的最大值与导数解读课件
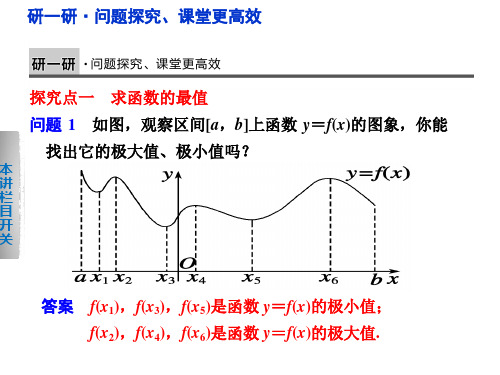
0 0,23π
23π
23π,43π 43π
43π,2π 2π
f′(x) 本
+
0
-
0
+
讲
极大值
极小值
栏 目 开
f(x) 0
↗
π3+
3 2
↘
23π-
3 2
↗
πபைடு நூலகம்
关 ∴当 x=0 时,f(x)有最小值 f(0)=0;
当 x=2π 时,f(x)有最大值 f(2π)=π.
研一研·问题探究、课堂更高效
小结 (1)求函数的最值,显然求极值是关键的一环.但仅仅 是求最值,可用下面简化的方法求得.
x=5 时,函数 f(x)取得最小值 f(5)=-22e5.
研一研·问题探究、课堂更高效
探究点二 含参数的函数的最值问题
例 2 已知 a 是实数,函数 f(x)=x2(x-a).
(1)若 f′(1)=3,求 a 的值及曲线 y=f(x)在点(1,f(1))处
的切线方程.
(2)求 f(x)在区间[0,2]上的最大值.
(1)f(x)=2x3-12x,x∈[-1,3]; (2)f(x)=12x+sin x,x∈[0,2π]. 解 (1)f(x)=2x3-12x,
∴f′(x)=6x2-12=6(x+ 2)(x- 2),
本 讲
令 f′(x)=0,解得 x=- 2或 x= 2.
栏 目
当 x 变化时,f′(x)与 f(x)的变化情况如下表:
0<a≤2 , 2<a<3
综上所述,f(x)max=80-4a
a≤2 a>2 .
小结 由于参数的取值不同会导致函数在所给区间上的单
调性的变化,从而导致最值的变化.所以解决这类问题常需要 分类讨论,并结合不等式的知识进行求解.
§3.3.3 函数的最大(小)值与导数

高二数学选修1-1 §3.3.3 函数的最大(小)值与导数一、学习任务:1.理解函数的最大值和最小值的概念;掌握可导函数在闭区间上所有点(包括端点)处的函数中的最大(或最小)值必有的充分条件;2.掌握用导数求函数的极值及最值的方法和步骤. 二、探究新知: 1.结论一般地,在闭区间[]b a ,上的函数)(x f y =的图像是连续不断的曲线,那么函数)(x f y =在[]b a ,上 .说明: 给定函数的区间必须是 ,在开区间()b a ,内连续的函数)(x f 不一定有最大值与最小值. 函数)(x f 在闭区间[]b a ,上连续,是)(x f 在闭区间[]b a ,上有最大值与最小值的 条件. 2.“最值”与“极值”的区别和联系从个数上看,一个函数在其定义区间上的最大值、最小值 ,而函数的极值 . 3.利用导数求函数的最值步骤由上面函数)(x f 的图象可以看出,只要把连续函数的 与定义区间的 函数值进行比较,就可以得出函数的最值了. 一般地,求函数)(x f 在[]b a ,上的最大值与最小值的步骤如下:自学检查例1 求4+4-31=)(3x x x f 在[]3,0的最大值与最小值.解:例2 求函数5+2-=24x x y 在区间[]2,2-上的最大值与最小值.解: 练习:1.下列说法正确的是( )A.函数的极大值就是函数的最大值B.函数的极小值就是函数的最小值C.函数的最值一定是极值D.在闭区间上的连续函数一定存在最值2.函数)(x f y =在区间],[b a 上的最大值是M ,最小值是m , 若m M =,则)('x f ( ) A.等于0B.大于0C.小于0D.以上都有可能3.函数23421+31+41=x x x y ,在]1,1[-上的最小值为( ) A.0 B.2- C.1- D.1213巩固训练1.下列说法正确的是( )(A )函数的极大值就是函数的最大值 (B )函数的极小值就是函数的最小值 (C )函数的最值一定是极值(D )在闭区间上的连续函数一定存在最值2.函数)(x f y =在区间],[b a 上的最大值是M ,最小值是m ,若m M =,则)('x f ( ) (A )等于0 (B )大于0 (C )小于0 (D )以上都有可能3.函数59323+--=x x x y 在区间]4,4[-上的最大值为( ) (A) 10 (B)-71 (C)-15 (D)-224.函数x e x y -•=在]4,2[∈x 上的最小值为( )(A) 0 (B)e 1 (C)44e (D)22e拓展提升:1.已知函数812)(3+-=x x x f 在区间]3,3[-上的最大值与最小值分别为M 、m,则M-m=2.已知函数a x x x x f +++-=93)(23。
函数的最大(最小)值与导数今天

06 总结与展望
函数极值研究意义
揭示函数性质
通过研究函数的极值,可以深入 了解函数的增减性、凹凸性等基 本性质,为函数分析提供有力工 具。
优化问题求解
在实际问题中,很多优化问题都 可以转化为求函数的极值问题, 如经济学中的成本最小化、收益 最大化等。
辅助定理证明
在数学分析中,一些重要定理的 证明往往涉及到函数极值的研究, 如泰勒公式、拉格朗日中值定理 等。
函数的最大(最小)值与导数
目录
• 引言 • 一元函数极值判定 • 多元函数极值判定 • 驻点与拐点分析 • 应用举例与求解方法 • 总结与展望
01 引言
函数的最大(最小)值定义
函数的最大值
在给定区间上,如果存在一个点 $x_0$,使得对于该区间内的任意 $x$,都有$f(x) leq f(x_0)$,则称 $f(x_0)$为函数在该区间上的最大 值。
二阶导数判定法
寻找驻点
同样先求出一阶导数 $f'(x)$,然后解方程 $f'(x) = 0$ 得到 驻点 $x_0$。
计算二阶导数
求出二阶导数 $f''(x)$,并计算 $f''(x_0)$ 的值。
判断极值类型
若在 $x_0$ 处 $f''(x_0) > 0$,则 $x_0$ 为极小值点;若在 $x_0$ 处 $f''(x_0) < 0$,则 $x_0$ 为极大值点;若 $f''(x_0) = 0$,则需要结合其他方法进一步判 断。
驻点性质
驻点是函数可能取得最大或最小值的点,但并非 所有驻点都是极值点。
驻点与函数单调性
在驻点的左侧和右侧,函数的单调性可能发生改 变。
《高等数学教学资料》05第五节函数极限与最大值最小值.docx

第五节函数的极值与最大值最小值在讨论函数的单调性时,曾遇到这样的情形,两数先是单调增加(或减少),到达某一点后又变为单调减少(或增加),这一类点实际上就是使函数单调性发生变化的分界点.如在上节例3的图3・4・5中,点兀=1和兀=2就是具有这样性质的点,易见,对兀=1的某个邻域内的任一点兀(2 1),恒有f(x) </(I),即曲线在点(1,/(1))处达到“峰顶”:同样,对“2 的某个邻域内的任一点X(XH2),恒有f(x) > /(2),即曲线在点(2,/(2))处达到“谷底”. 具有这种性质的点在实际应用中有着重耍的意义.由此我们引要入函数极值的概念.分布图示★函数极值的定义★函数极值的求法★例1★例2★例3笫二充分条件★例4★例5★例6最大值最小值的求法★例7★例8★例9★例10★例11★例]2内容小结★课堂练习★习题3・5 ★返回内容要点一、函数的极值极值的必要条件第一充分条件与第二充分条件求函数的极值点和极值的步骤(1)确定函数/(兀)的定义域,并求其导数;(2)解方程f\x) = 0求出于(兀)的全部驻点与不可导点;(3)讨论厂(劝在驻点和不可导点左、右两侧邻近符号变化的情况,确定函数的极值点;(4)求出各极值点的函数值,就得到函数/(兀)的全部极值.二、函数的最大值与最小值在实际应用屮,常常会遇到求最大值和最小值的问题.如用料最省、容暈最大、花钱最少、效率最高、利润最大等.此类问题在数学上往往可归结为求某一函数(通常称为目标函数)的最大值或最小值问题.求函数在创上的最大(小)值的步骤如下:(1)计算函数/(兀)在一切可能极值点的函数值,并将它们与相比较,这些值中最大的就是最大值,最小的就是最小值;(2)对于闭区间[d,b]上的连续函数/(兀),如果在这个区间内只有一个可能的极值点,并且函数在该点确有极值,则这点就是函数在所给区I'可上的最大值(或最小值)点.例题选讲求函数的极值例1 (E01)求出函数/(%) = x3 -3x2 -9x4-5的极值.解f(x) =3X2-6X-9=3(X +1)(X一3),令f(x) = 0,得驻点x1=-l,x2=3.列表讨论如下:X(―-1)-1(-1, 3)3(3, 4- °°)•厂⑴+0——0+f(x)f极大值1极小值t所以,极大值/(-!) = 10,极小值/(3) = -22.例2 (E02)求函数的极值.解⑴ 函数f(兀)在(-oo,+oo)内连续,除x = -l外处处可导,且厂(无)=孝二2;3沿+1(2)令f\x) = 0,得驻点x = l;兀=-1为/*(兀)的不可导点;(3)列表讨论如下:(-00,-1)-1(-1, 1)1(1,+呵/'(X)+不存在—0+/⑴f极大值1极小值t⑷ 极大值为/(-1) = 0,极小值为/⑴=-3^4.3例3求函数y(x) = x-jx2/3的单调增减区间和极值.解求导数= 当"1时八0) = 0,而x = 0时/©)不存在,因此,函数只可能在这两点取得极值.列表如下:X(一8,0)0(0,1)1(1, + °°) f\x)+ 不存在—0+fM/极大值0极小值-丄2/由上表可见:函数/(兀)在区间(_oo,0),(l,+oo)单调增加,在区间(0,1)单调减少.在点x =()处有极大值,在点兀=1处有极小值/(I) = 如图.例4 (E03)求出函数/(x) = x3 + 3x2一24兀- 20的极值.解f(x) = 3x2 +6x-24 = 3(x + 4)(兀—2),令f\x) = 0,得驻点册=-4,勺=2.又/'(x) = 6x + 6, ・・・/"(-4) = —18vO,故极大值于(一4) = 60, /*(2) = 18>0,故极小值/(2) = -4&注意:1./"(必)=0吋,/(X)在点勺处不一定収极值,仍用第一充分条件进行判断.2.函数的不可导点,也可能是函数的极值点.例5 (E04)求函数f(x) =(X2 -厅+ I的极值.解由/,(X)=6X(X2-I)2=0,得驻点可=一1,七=0*3=1. f\x) = 6(x2 -l)(5x2 -1).因f\x) = 6 > 0,故/(x)在x = 0处収得极小值,极小值为/(0) = 0.因厂(-1)=厂⑴=0,故用定理3无法判别.考察一阶导数f\x)在驻点册=-1及勺=1左右邻近的符号:当兀取-1左侧邻近的值时,f(x) < 0;当兀取-1右侧邻近的值吋,f(x) < 0;因厂(兀)的符号没有改变,故/(兀)在x = -l处没有极值.同理,/(兀)在x = l 处也没有极值.如图所示.例6求出函数/W=1-(X-2)2/3的极值.2 --解f'M = -一(兀-2) '("2). x = 2是函数的不可导点.当xv2时,f(x) > 0;当x>2时,.厂(兀)v0. /. /(2) = 1为/(兀)的极大值.例7 (E05)求y = 2疋+ 3兀$ _ 12x + 14的在[-3,4]上的最大值与最小值.解*«*= 6(x + 2)(兀一1),解方程f\x) = 0,得x, =-2,X2 =1.计算/(-3) = 23; /(—2) = 34; /⑴二7; /⑷二142;比较得最大值/⑷=142,最小值/(I) = 7.例8求函数)usin2x-x在-彳冷上的最大值及最小值.解函数y = sin2x- x在-巴工上连f\x) = / = 2cos2x-1, 2 2令)/ = (),得/ = 土牛.故皿¥上最大值为务最小值为号例9 (E06)设工厂4到铁路线的垂直距离为20km,垂足为3.铁路线上距离B为100km 处有一原料供应站C,如图3-5-4.现在要在铁路BC屮间某处D修建一个原料屮转车站,再由车站D 向工厂修一条公路.如果已知每km 的铁路运费与公路运费之比为3:5,那么,D 应 选在何处,才能使原料供应站C 运货到工厂A 所需运费最省?解 BD = x (km), CD = 100 — x (km), AD = ^202 + x 2 ・铁路每公里运费眈公路每公里5R,记那里目标函数(总运费)y 的函数关系式: y = 5kAD + 3k-CD 即y = 5k ・ 7400 +x 2 + 3k(l 00-x) (0<x<100).问题归结为:x 収何值时目标函数y 最小./ \ I求导得y f = k 1 =一3,令y" = 0得x = 15(km).、V400 + x~ ) 由于 y(0) = 400£, y(15) = 380£, y(100) = 100@£. 从而当BD = 15 (kmJB'J-,总运费最省.例10(E07)某房地产公司有50套公寓要出租,当租金定为每月180元时,公寓会全部 租111去.当租金每月增加10元时,就有一套公寓租不出去,而租出去的房子每月需花费20 元的整修维护费.试问房租定为多少可获得最大收入?解 设房租为每月兀元,租出去的房子有50-(犬二型]套,每月总收入为10V =70 一一,解 R\x ) = 0,得兀=350 (唯一驻点). 故每月每套租金为350元时收入最高.最大收入为/?(350) = 10890(元).求函数的最大值最小值例11敌人乘汽车从河的北岸A 处以1米/分钟的速度向正北逃窜,同时我军摩托车从 河的南岸B 处向正东追击,速度为2千米/分钟,问我军摩托车何吋射击最好(相距最近射击 最好)?解(1)建立敌我相距函数关系 设t 为我军从B 处发起追击至射击的事件(分).敌我相距函数5(/)5(f) = J(0.5 + r)2+(4-2r)2⑵求5 = 5(r)的最小值点5/-7.5 7(0.5 + z)2+(4-2r)2令= o,得唯一驻点( = 1.5.故得我军从B 处发起追击后1.5分钟设计最好. 实际问题求最值应注意:(1) 建立目标函数; (2) 求最值;若目标函数只有唯一驻点,则该点的函数值即为所求的最人(或最小)值.R(x) = U - 20) 50- x-180、10 )X = (x-20) 68——,I 10丿 + (“20)卜茁2 2例12求内接于椭圆与+务=1而面积最大的矩形的各边之长. a~ b~ 解 设M(x,y)为椭圆上第一象限内任意一点,则 以点M 为一顶点的内接矩形的面积为S(x) = 2x- 2y = — x^a 1 -x 2,0 <x<a,a且 S(0) = S(d) = 0.Qyla 2-x 2是S(x)的最人值,最大值仏=乎诗卜倍!=切课堂练习1. 下列命题正确吗?若兀()为/(X )的极小值点,则必存在旳的某邻域,在此邻域内,/(兀)在兀()的左侧下降,而 在兀()的右侧上升.2. 若/(d)是/(兀)在[d,切上的最大值或最小值,且广⑺)存在,是否一定有f(a) = 0?4b a 2 -2x 2 万需2“由 S3 = o,求得驻点尤0 =为唯一的极值可疑点.依题意,S(x)存在最大值,故对应的y 值为即当矩形的边长分别为血a, Qb 时面积最大.。
函数的最大值最小值与导数

2V 令 s( R) 2 +4π R=0 R
解得,R=
3
V V h= = = 2 V 2 R 3 ( )
即 h=2R
3
4V
2
=2
3
V
V 2
,从而
因为S(R)只有一个极值,所以它是最小值 答:当罐的高与底直径相等时,所用材料最省
例5已知某商品生产成本C与产量q的函数关系式为C=100+4q, 价格p与产量q的函数关系式为 q为何值时,利润L最大?
(3)函数在其定义区间上的最大值、最小 值最多各有一个,而函数的极值可能不止 一个,也可能没有一个。 (4)最值可以在端点处取得,而函数的极 值不可能在端点处取得。
三、求最值的步骤: (1)求f (x)在区间(a,b)内极值(极大值 或极小值) (2)将y=f (x)的各极值与f (a)、f (b) 比较,其中最大的一个为最大值,最小 的一个最小值
2
x f’(x)
(-4,-3) +
-3 0
(-3,3) -
3 0
(3,4) +
4
f(x)
44
3
54
-54
-44
f ( x) x 27x在[4,4]上的最大值为 54, 最小值为 54
五、反馈练习
2、求函数f(x)=3x-x3在区间
[2,3] 内的最大
2
值和最小值
f ' ( x ) 3 3 x , 令f ' ( x ) 3 3 x 0
2
解得x1 1(舍) x2 1(舍)所以f ' ( x) 在x [2,3]单调递减。所以 f max f (2) 2, f min f (3) 18
§133函数的极值与最大(小)值与导数.docx

篠龜:§73夕爲毅的极值鸟眾丈(^)值鸟导嘏教学目标:1.使学生理解函数的最大值和最小值的概念,掌握可导函数在闭区间[a,b]上所有点(包括端点a,b)处的函数中的最大(或最小)值必有的充分条件;2.使学生掌握用导数求函数的极值及最值的方法和步骤・教学重点:利用导数求函数的最大值和最小值的方法.教学难点:函数的最大值、最小值与函数的极大值和极小值的区别与联系。
教学过程:一、创设情景♦函数极值与导数如图为表示高台跳水运动员的高度力随时间f变化的函数/2(r) = -4.9r2+6.5r + 10的图象,我们发现, F = Q 时,高台跳水运动员距水而高度最大.那么,函数加r)在此点的导数是多少呢?此点附近的图像有什么特点?相应地,导数的符号有什么变化规律?【探究】如图,放大2d附近函数⑴的图像,可以看出当t<a时,函数加r)单调递增,/zV)>0; 当Qd时,函数M)单调递减,/2匕)<0;这就说明,在UQ附近,函数值先增后减,这样,当/在Q的附近从小到大经过a时,丹⑴先正后负,且丹⑴连续变化,于是有丹(0) = 0。
【思考】对于一般的函数y = /(X),是否也有这样的性质呢?【想一想】如图,函数y = f(x)在a,b处的函数值与这两个点附近的函数值有什么关系?y = f(x)在这两个点处的导数值是多少?在这两个点附近,y = /(x)的导数的符号有什么规律?【探究】由函数图象可知,函数y = f(x)在点x = 的函数值.f(a)比它在点兀附近其他点的函数值都小,f\a) = 0;而且在点x = «附近左侧,/*(x)<0,在点X = 6Z附近右侧,广(兀)>0。
函数y = /(x)在点x = h 的函数值/(b)比它在点x = b附近其他点的函数值都大,广(b) = 0;而且在点x = b附近左侧,广(兀)>0,在点x = b附近右侧,广⑴<0。
函数的最大值与导数

研一研·问题探究、课堂更高效
探究点二 含参数的函数的最值问题 例 2 已知 a 是实数,函数 f(x)=x2(x-a). (1)若 f′(1)=3,求 a 的值及曲线 y=f(x)在点(1,f(1))处 的切线方程. (2)求 f(x)在区间[0,2]上的最大值.
本 讲 栏 目 开 关
1 令 g(x)=ln x-x,则 g′(x)= -1. x 当 0<x<1 时,g′(x)>0;当 x≥1 时,g′(x)≤0,x=1 是
g(x)的最大值点,∴g(x)≤g(1)=-1.
综上可知,a 的取值范围是-1,+∞.
x-x≤a.
研一研·问题探究、课堂更高效
解析
f′(x)=3x2-3=3(x+1)(x-1),当 x∈(-1,1)时,
f′(x)<0,所以 f(x)在(-1,1)上是单调递减函数,无最大值 和最小值,故选 D.
练一练·当堂检测、目标达成落实处
π y=x-sin x,x∈ ,π的最大值是 2
3.函数
( C )
A.π-1
8-4a 综上所述,f(x)max= 0
本 讲 栏 目 开 关
a≤2 . a>2
小结
由于参数的取值不同会导致函数在所给区间上的单
调性的变化, 从而导致最值的变化.所以解决这类问题常需要 分类讨论,并结合不等式的知识进行求解.
研一研·问题探究、课堂更高效
跟踪训练 2 已知函数 f(x)=ax3-6ax2+b,x∈[-1,2]的最 大值为 3,最小值为-29,求 a,b 的值.
解 (1)f′(x)=3x2-2ax.
本 讲 栏 目 开 关
高二数学人选修课件时函数的最大值与导数

XX
THANKS
感谢观看
REPORTING
利用导数解决实际应用问题的典型例题
01 02 03
例题1
某工厂生产A、B两种配套产品,其中每天生产x吨A产品 ,需生产x+2吨B产品。已知生产A产品的成本与产量的平 方成正比。经测算,生产1吨A产品需要4万元,而B产品 的成本为每吨8万元。问该工厂应如何安排生产,才能使 每天的平均成本最低?
例题2
解题思路:对于综合运用导数和函数 知识解题的题目,需要灵活运用导数 和函数的性质、定理和公式进行求解 。首先根据题意求出函数的表达式或 解析式,然后求出函数的导数并令其 为0求出驻点或不可导点。接着利用 导数的正负判断函数的单调性并确定 单调区间。最后根据驻点或不可导点 左右两侧的函数值变化情况确定极值 点和极值,并进行验证和解释。
综合运用导数和函数知识解题的典型例题
例题1:已知函数$f(x) = x^3 + ax^2 + bx + c$在$x = - frac{2}{3}$ 和$x = 1$时都取得极值,求$a,b$的 值及函数$f(x)$的单调区间和极值。
例题2:已知函数$f(x) = ln x - ax + (1 - a) / x - 1$ (a ∈ R),当a = 1 / 3时,求函数f(x)的单调区间和极值。
XX
高二数学人选修课件
时函数的最大值与导
数
汇报人:XX
20XX-01-17
REPORTING
• 引言 • 函数的基本性质与图像 • 导数的概念与计算 • 利用导数求函数的最大值 • 导数与函数图像的关系 • 典型例题分析与解答
目录
XX
PART 01
引言
函数的最大值与导数

当 x 变化时,f′(x),f(x)的变化情况如下表:
x f′(x) f(x) 0 0
2 0, π 3
2 π 3 0 极大值 π 3 + 3 2
2 4 π, π 3 3
4 π 3 0 极小值 2 3 π- 3 2
4 π,2π 3
2π
+ ↗
- ↘
∴当 x∈(0,1)时,f′(x)>0;当 x∈(1,2)时,f′(x)<0; 当 x∈(2,3)时,f′(x)>0.
∴当 x=1 时,f(x)取极大值 f(1)=5+8c.
又 f(3)=9+8c>f(1), ∴x∈[0,3]时,f(x)的最大值为 f(3)=9+8c.
∵对任意的 x∈[0,3],有 f(x)<c2 恒成立,
又 f(-4)=k-76,f(3)=k-27, f(-1)=k+5,f(4)=k-20.
由 f(x)max=k+5=10,得 k=5, ∴f(x)min=k-76=-71.
1.求函数在闭区间上的最值,只需比较极值和端点处的函数 值即可;函数在一个开区间内只有一个极值,这个极值就 是最值. 2.含参数的函数最值,可分类讨论求解. 3.“恒成立”问题可转化为函数最值问题.
因为 f(-1)=10,f(3)=18,f( 2)=-8 2,
f(- 2)=8 2;
所以当 x= 2时,f(x)取得最小值-8 2; 当 x=3 时,f(x)取得最大值 18. 1 (2)f′(x)= +cos x,令 f′(x)=0,又 x∈[0,2π], 2 2 4 解得 x= π 或 x= π. 3 3
8-4a 综上所述,f(x)max= 0
a≤2 . a>2
小结
由于参数的取值不同会导致函数在所给区间上的单
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1课时 课型:新授课 主备人:武果果
一、学习目标
1•借助函数图像,直观的理解函数的最大值和最小值概念; 2. 弄清函数最大值、最小值与极大值、极小值的区别与联系,理解和熟悉函数于(兀)必有最大 值和最小值的充分条件; 3. 会利用导数求连续函数/(兀)在闭区间["]上的最大值和最小值。
二、
考情分析 1. 考纲要求:会求闭区间上函数的最大值与最小值; 2•考情分析:运用导数研究函数的最值; 3•备考要求:注重导数在研究函数极值与最值中的工具性作用。
三、
课前自主学习
1•导入学习
复习:(1)极大(小)值概念: ____________________________________________________
(2)求函数极值的方法: ________________________________________________
实例导入:预习课本心完成下面问题:
⑴你能找出函数 尸/(兀)在区间上的极大值、极小值、最大值、最小值吗?
(2)函数y = /(x)在开区间仏b)上的极大值、极小值、最大值、最小值存在吗?
⑶若函数)/(x)在区间[d,b ]上不连续还存在极大值、极小值、最大值、最小值吗? 新知:函数y = 在闭区间[⑦切上的最值:
一般地,如果在区间[⑦切上函数y = /(x)的图像是一条 ________ 的曲线,那么它必有最 大值和最小值.
例1・求函数/*(%) = 6 + 12x-x 3在【-亍3]上的最大值与最小值。
选2・2 § 13.3函数的最大(小)值与导数
解-7/(X)=6+12X-A3・••广(0 =
由厂(兀) = 0,解得兀=
当X变化时,f(x)与#(尢)的变化情况如下表:
X1
_32
3
f'(x)+
/(X)单调\
・•・函数心在[-事3]上的最大值是____ ;最小值是_______
结论:求函数y = /(x)在[d,b]上的最值的步骤:
⑴.求函数y = /(%)在(d,b)内的_______ ;
⑵.将函数〉,= /&)的 _____ 与____________ 比较,其中最大的一个是最大值,最小的一个
是________ O
2. 自我检测
练习(1)•已知a为实数,/(x) = (x2-4)(x-a),若广(-1) = 0,求/⑴在
[-2, 2]上的最大值和最小值.
7i n
(2).求函数/(x) =-2cosx-x在区间[-亍,-]上的最大值与最小值。
2. 已知函数f{x ) = ax 3-6ax 2
+b 在[-1,2]上有最大值3,最小值-29,求d,b 的值. 3 (选)设函数/(兀)=饥2+2T 兀+( — 1(兀丘/?,/>()).
⑴求/(兀)的最小值〃(/);⑵若/i (r ) < -2t + m 对于re (0,2)恒成立,求实数m 的取值范围.
五、学习目标检测
1.已知函数/(x ) = 2x 3-6x 2+m (m 为常数)在[-2,2]有最大值3,那么此函数在[-2,2]上的最 小值是()
A. -37
B. -29
C. -5
D.以上都不对
3 (选)已知函数fM = x 2
-2ax + a 在区间(-~1)上有最小值,则函数&(兀)=如在区间(1,+呵上
X 一定( )
A.有最小值
B.有最大值
C.是减函数
D.是增函数 4 (选)函数/(兀)=疋-扌兀2 _2兀+ 5 ,对任意的xe [-1,2]都有/(%) > m ,则实数m 的取值范围
是 ____________ .
5 (选)y = -x 2-2x + 3在区间[d,2]上的最大值为口,贝恂二 __________ ・
6 (选)已知函数f (x ) = x\nx ・
⑴求/(X )的最小值;(2)若对所有兀都有求实数d 的取值范圉.
7 (选)已知函数f(x) = x 3
-3ax-a 在(0,1)内有最小值. 2.函数7 =二在区间[0, 2]上的最大值是(
⑴求Q的取值范围;⑵函数/(x)在(0,1)内能否有最大值?若能,求出a的取值范围,若没有,
说明理由.
3 •问题反馈
四、课堂合作学习
1. 已知函数/(x) = 2x3-6x2+6/在[-2,2]上有最小值-37,求a的值并求/G)在[-2,2] ±的最大
值.。
