四年级数学竞赛奥数讲义-例题
四年级奥数讲义

四年级奥数讲义本页仅作为文档封面,使用时可以删除This document is for reference only-rar21year.March第一讲和倍问题知识点:已知两个量的和与这两个量的倍数关系,要我们求这两个量分别是几。
和÷(倍数+1)= 较小数;较小数 × 倍数= 较大数;和-较小数= 较大数例1:甲、乙两个仓库共存货物960吨,已知甲仓库所存货物是乙仓库的2倍,问甲、乙两个仓库各存货物多少吨?例2:果园里有梨树,苹果树和桃树共1800棵,其中梨树的棵数是苹果树的2倍,桃树的棵数是苹果树的2倍,问三种树各多少棵例3:学校里的足球只数是排球的3倍,篮球的只数是排球的5倍,足球和篮球共72只,问三种球各多少只?例4:三块钢板共重207千克,第一块的重量是第二块的3倍,第二块的重量是第三块的2倍,第三块钢板重多少千克?例5:某小学购进红粉笔和白粉笔共244盒,购进的白粉笔比红粉笔的7倍少12盒,问购进红粉笔、白粉笔各多少盒?例6:两箱茶叶共重88千克,如果从甲箱取15千克放入乙箱,那么乙箱的重量是甲箱的3倍,问两箱原有茶叶各多少千克?例7:甲水池有水1500升,乙水池有水1200升,每分钟从甲水池流入乙水池25升水,问多少分钟后乙水池的水是甲水池的2倍?自我检测:填空。
小红和妈妈的年龄加在一起是40岁,妈妈的年龄是小红年龄的4倍。
妈妈岁,小红岁。
生产队养公鸡、母鸡共404只,其中公鸡是母鸡的3倍。
公鸡有只,母鸡有只。
小明买语文本和数学本共25本,其中语文本比数学本的2倍多4本,语文练习本买了本,数学练习本买了本。
师傅和徒弟一共生产零件190个,师傅生产的个数比徒弟的3倍少10个。
徒弟生产零件个,师傅生产零件个。
A、B两人同时从学校出发相背而行,2小时共行48千米,A的速度是B的2倍,求A的速度是,B的速度是。
一块长方形木板,长是宽的2倍,周长是54厘米。
这块长方形木板的长是厘米,宽是厘米,面积是平方厘米。
四年级数学竞赛奥数讲义例题

×计算:66666×133332求算式{200982009920096999888666⨯÷L L L 123123个个个的计算结果的各位数字之和。
计算:{{222010120108888111-L L 个个计算:22222×99999+33333×33334计算1009100910099999991999⨯+L L L 123123123个个个结果末尾有多少个零?【你还记得吗】 (★★★) 计算:2010××计算:333××测试题1.计算222222×999999A .B .C .D . 2.计算6666×13332A .B .C .D .3.计算:3001300229931111222233334÷L L L 1231424314243个个个A .3013333L 14243个3B .2003333L 14243个3C .3003333L 14243个3D .3063333L 14243个34.计算100×100-99×99+98×98-97×97+…+2×2-1×1A .4950B .5050C .5150D .5250第一讲:多位数计算(★★★)(★★★★)(★★★★)(★★★★)(★★★)(★★★★)(★★★★★)(★★★★)5.计算99999×26+33333×24A.3996366 B.6933669 C.3399966 D.36699666.计算:899×899+1799A.819000 B.810000 C.900000 D.9810007.计算111111×777777+444444×5555558.计算2009×-2007×A.2 B.4016 C.4017 D.0第二讲:容斥原理上(★★)网校老师共50人报名参加了羽毛球或乒乓球的训练,其中参加羽毛球训练的有30人,参加乒乓球训练的有35人,请问:两个项目都参加的有多少人?(★★★)一个班30人,完成作业的情况有三种:一种是完成语文作业没完成数学作业;一种是完成数学作业没完成语文作业;一种是语文、数学作业都完成了。
四年级下册数学试题-奥数讲义-第07讲-逻辑推理初步-(含答案)人教版

第八讲逻辑推理初步【例1】在三只盒子里,一只装有两个黑球,一只装有两个白球,还有一只装有黑球和白球各一个.现在三只盒子上的标签全贴错了.你能否仅从一只盒子里拿出一个球来,就确定这三只盒子里各装的是什么球?分析与解:可以枚举,一一尝试.当从贴有“一黑一白”的盒子中取出一个球,如果是白球,那么这只盒子一定装有两个白球,于是贴有“两个黑球”的盒子一定装有一个白球和一个黑球,最后贴有“两个白球”的盒子一定装有两个黑球.对应的,如果从贴有“一黑一白”的盒子中取出一个球,如果是黑球,那么这只盒子一定装有两个黑球,剩下的两只盒子可以同上分析出.所以,只要从贴有“一黑一白”的盒子中取球即可。
【例2】甲、乙、丙、丁4位同学的运动衫上印有不同的号码.赵说:“甲是2号,乙是3号.”钱说:“丙是4号,乙是2号.”孙说:“丁是2号,丙是3号.”李说:“丁是l 号,乙是3号.”又知道赵、钱、孙、李每人都只说对了一半.那么丙的号码是几号?分析与解:如下表,先假设赵的前半句话正确,判断一次;再假设赵的后半句正确,再判断一次.即甲是1号,乙是3号,丙是4号,丁是2号.所以丙的号码是4号。
拓展训练要点总结课堂精讲有三个人拿着一块金属,第一个人说:“这不是铁,这是锡。
”第二个人说:“不对,是铁不是锡。
”第三人说:“这不是铁也不是铜。
”三人各执一词,最后他们去问一位物理老师。
老师听了以后说:“你们之中,有一个人的两个判断都不对,有一个人的两个判断一对一错,有一个人的两个判断都对。
”三个人想了一会儿,终于明白这是一块什么金属。
现在你知道了吗?答案:这是一块铁。
由第一个人与第二个人的谈话可知,这两个人的观点正好完全相反,因此,这两个人中一定有一个人的结论完全正确,一个人的结论完全错误,而第三个人的结论一对一错。
由此可得出此结论。
【例3】某参观团根据下列条件从A,B,C,D,E这5个地方中选定参观地点:①若去A地,则也必须去B地;②B,C两地中至多去一地;③D,E两地中至少去一地;④C,D两地都去或者都不去;⑤若去E地,一定要去A,D两地.那么参观团所去的地点是哪些?分析与解:假设参观团去了A地,由①知一定去了B地,由②知没去C地,由④知没去D地,由③知去了E地,由⑤知去了4、D两地,矛盾.所以开始的假设不正确,那么参观团没有去A地,由①知也没去B地,由②知去了C地,由④知去了D地,因为A、D两地没有都去,所以由⑤知没去E地.即参观团去了C、D两地。
(四年级奥数讲义)第9讲_鸡兔同笼问题(带答案)

第9讲鸡兔同笼问题◆认识鸡兔同笼问题。
◆用假设法解鸡兔同笼问题。
我国古代数学名著《孙子算经》中有这样的一道应用题:今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各有几何?意思是说:鸡和兔同关在一个笼子里,已知鸡与兔共有35只,鸡脚与兔脚共有94只,问鸡、兔各有多少只?这就是著名的鸡兔同笼问题。
怎样解决这个问题呢?我们通常把题中相当于“鸡”和“兔”的两种量,全部假设看作“鸡”或“兔”,然后找出与实际数量的差,由此求出“鸡”或“兔”,这种解决问题的方法就是假设法。
用假设法解题,首先要根据题意去正确地判断应该怎么假设,一般可假设要求的两个或几个未知量相等,或者假设要求的两个未知量是同一种量;其次要能根据所做的假设,注意到数量关系发生了什么变化,怎样从所给的条件与变化了的数量关系的比较重做出适当的调整,从而找到正确的答案。
【例题1】鸡兔同笼,共100个头,320只脚,鸡兔各多少只?答案:60,40思路点拨:【拓展1】(2009年北京“高思”数学思维能力检测试题)在马达加斯的大草原上,环尾狐猴和斑马进行投篮比赛,每只环尾狐投进一球记2分,每只斑马投进一只球记3分,共投进了100个球,共得了220分,那么斑马一共投进了多少个球? 答案:20思路点拨:【例题2】现在有大小油桶50个,每个大桶可装油4千克,每个小桶可装油2千克,大桶比小桶共多装油20千克,问大、小油桶各多少个? 答案:20,30思路点拨:【拓展2】现有大小塑料袋60个,每个大袋可装苹果5千克,每个小袋可装苹果3千克,小袋比大袋少装苹果60千克。
问大小塑料袋各有多少个? 答案:30,30思路点拨:【例题3】(“希望杯”全国数学大赛试题)小猴和小熊轮流共同完成一批玩具的组装,小猴每天可以完成20件,小熊每天只能完成12件。
它们用8天的时间共组装了112件玩具。
小猴工作了多少天? 答案:2思路点拨:【拓展3】松鼠妈妈采松球,晴天每天可以采20个,雨天每天只能采12个,它一连几天才了112个松球,平均每天14个。
四年级数学竞赛奥数讲义例题图文百度文库

四年级数学竞赛奥数讲义例题图文百度文库一、拓展提优试题1.21个篮子,每个篮子中有48个鸡蛋,现在将这些鸡蛋装到一些盒子中,每个盒子装28个鸡蛋,可以装盒.2.甲、乙、丙、丁四人参加了一次考试,甲、乙的成绩比丙、丁的成绩和高17分,甲比乙低4分,丙比丁高5分.四人中最高分比最低分高分.3.一辆公共汽车有78个座位,空车出发,第一站上一位乘客,第二站上二位乘客,第三站上三位乘客,依次下去,多少站以后,车上坐满乘客?4.如图,小明从A走到B再到C再到D,走了38米,小马从B到C再到D再到A,走了31米,此问长方形ABCD的周长多少米?5.六个人传球,每两人之间至多传一次,那么这六个人最多共进行15次传球.6.豆豆全家有4口人.今年豆豆哥哥比豆豆大3岁,豆豆妈妈比豆豆爸爸小2岁.5年前,全家年龄为59岁,5年后,全家年龄和为97岁,豆豆妈妈今年岁.7.过元旦时,班委会用730元为全班同学每人买了一份价值17元的纪念品,剩余16元,那么,这个班共有学生名.8.如图是长方形,将它分成7部分,至少要画条直线.9.在一个停车场,共有24辆车,其中汽车是4个轮子,摩托车是3个轮子,这些车共有86个轮子,那么三轮摩托车有辆.10.四年级的两个班共有学生72人,其中有女生35人,四(1)班有学生36人,四(2)班有男生19人,则四(1)班有女生人.11.如果,那么=.12.有白棋子和黑棋子共2014个,按照如图的规律从左到右排成一行,其中黑棋子的个数是.○●○●●○●●●○●○●●○●●●○●○●●○…13.(15分)水果店用三种水果搭配果篮,每个果篮里有2个哈密瓜,4个火龙果,10个猕猴桃,店里现有的火龙果的数量比哈密瓜的3倍多10个,猕猴桃的数量是火龙果的2倍,当用完所有的哈密瓜后,还剩130个火龙果.问:(1)水果店原有多少个火龙果?(2)用完所有的哈密瓜后,还剩多少个猕猴桃?14.如图,一个大正方形被分成四个相同的小长方形和一个小正方形,若一个小长方形的周长是28,则大正方形的面积是.15.商店里有甲、乙、丙三筐苹果,丙筐内苹果的个数是甲筐内苹果的个数的2倍,若从乙筐内拿出12个苹果放入甲筐,则此时甲筐内比丙筐内少24个苹果,乙筐内比丙筐内多6个苹果,则乙筐内原有苹果个.16.一个质数的2倍和另一个质数的5倍的和是36,求这两个质数的乘积是多少?17.甲、乙二人从同一天开始工作,公司规定:甲每工作3天后休息1天,乙每工作7天后连续休息3天,则在开始的前1000天中,甲、乙同一天休息的日子有天..18.(8分)如图所示,东东用35米长的栅栏在墙边围出一块梯形的地用来养猪,那么,这块养猪场的面积是平方米.19.洋洋从家出发去学校,若每分钟走60米,则它6:53到达学校,若每分钟走75米,则她6:45到达学校,洋洋从家里出发的时刻是.20.一个正方形的面积与一个长方形的面积相等,若长方形的长是1024,宽是1,则正方形的周长是.21.学校有足球和篮球共20个,恰好可供96名同学同时活动,足球每6人玩一个,篮球每3人玩一个,其中足球有个.22.是三位数,若a是奇数,且是3的倍数,则最小是.23.三个连续自然数的乘积是120,它们的和是.24.已知x,y是大于0的自然数,且x+y=150,若x是3的倍数,y是5的倍数,则(x,y)的不同取值有对.25.如图,把一个边长是5cm的正方形纸片沿虚线分成5个长方形,然后按照箭头标记的方向移动其中的4个长方形,则所得图形的周长是cm.26.观察7=5×1+2,12=5×2+2,17=5×3+2,这里7,12和17被叫做“3个相邻的被5除余2的数”,若有3个相邻的被5除余2的数的和等于336,则其中最小的数是.27.甲乙两所学校共有学生864人.新学期开学前,由甲校调入乙校32人,这时甲校还比乙校多48人.原来甲校有个学生.28.如果今天是星期五,那么从今天算起,57天后的第一天是星期.29.4名工人3小时可以生产零件108个,现在要在8小时内生产504个零件,需增加工人名.30.将1~11填入下图的各个圆圈内,使每条线段上三个圆圈内的数的和都等于18.31.(8分)如图,已知正方形的面积是100m2,图中灰色部分的面积是m2.32.小胖用两个秒表测一列火车的车速.他发现这列火车通过一座660米的大桥需要40秒,以同样的速度从他身边开过需要10秒,请你根据小胖提供的数据算出火车的车身长是米.33.学校组织春游,租船让学生划.每条船坐3人,有16人没有船坐;如果每条船坐5人,则有一条船上差4人.学校共有学生人.34.A说:“我10岁,比B小2岁,比C大1岁.”B说:“我不是年龄最小的,C和我差3岁,C是13岁.”C说:“我比A年龄小,A是11岁,B比A 大3岁.”以上每人所说的三句话中都有一句是错误的,请确定其中A的年龄是岁.35.(7分)有一行数:1,1,2,3,5,8,13,21,…,从第三个数开始,每个数都是前两个数的和,问在前2007个数中,有是偶数.36.(7分)用1,2,3,4,5,6,7,8这八个数字组成两个不同的四位数(每个数字只用一次)使他们的差最小,那么这个差是.37.定义运算:A△B=2A+B,已知(3△2)△x=20,x=.38.一个两位数除723,余数是30,满足条件的两位数共有个,分别是.39.一捆电线,第一次用去全长的一半多3米,第二次用去余下的一半少10米,第三次用去15米,最后还剩7米.这捆电线原来有多少米?40.甲,乙二人先后从一个包裹中轮流取糖果,甲先取1块,乙接着取2块,然后甲再取4块,乙接着取8块,…,如此继续.当包裹中的糖果少于应取的块数时,则取走包裹中所有糖果,若甲共取了90块糖果,则最初包裹中有块糖果.【参考答案】一、拓展提优试题1.【分析】根据乘法的意义,可用21乘48计算出鸡蛋的总个数,然后再根据除法的意义,用总的鸡蛋个数除以28进行计算即可得到需要的盒子数.解:21×48÷28=1008÷28=36(盒)答:可以装36盒.故答案为:36.【点评】此题主要考查的是乘法意义和除法意义的应用.2.解:设乙得了x分,则甲得了x﹣4分,丙得了y分,则丁得了y﹣5分,所以(x+x﹣4)﹣(y+y﹣5)=17,整理,可得:2x﹣2y+1=17,所以2x﹣2y=16,所以x﹣y=8,所以乙比丙得分高;因为x﹣y=8,所以(x﹣4)﹣(y﹣5)=9,所以甲比丁得分高,所以乙得分最高,丁得分最低,所以四人中最高分比最低分高:x﹣(y﹣5)=x﹣y+5=8+5=13(分)答:四人中最高分比最低分高13分.故答案为:13.3.解:设第n站以后车上坐满了乘客,可得:[1+1+(n﹣1)×1]×n÷2=78[2+n﹣1]×n÷2=78,[1+n]×n÷2=78,(1+n)×n=156,由于12×13=156,即n=12.答:12站以后,车上坐满乘客.4.解:长方形长比宽多:38﹣31=7(米),长方形宽:(38﹣7×2)÷3,=24÷3,=8(米),长:8+7=15(米),(15+8)×2,=23×2,=46(米),答:长方形ABCD的周长46米.5.解:一个图形中,如果有K个奇点,那么这个图形会用笔画出来.为了让这个图形用一笔画出来,则要使它只存在2个奇点.上面的图形共有6个奇点,6×5÷2=15条线.最少可以去掉2条线(剩下13条线),使6个奇点变成2个奇点,就可以用一笔画出来了.所以6人两两传球,但每两人之间最多只能传一次,最多就能传13次.故答案为:13.6.解:10×4﹣(97﹣59)=40﹣38=2(岁)所以豆豆是3年前出生的,即今年豆豆应该是3岁,今年豆豆的哥哥的年龄为:3+3=6(岁),今年全家的年龄和为:97﹣5×4=77(岁),今年爸爸妈妈的年龄和为:77﹣3﹣6=68(岁),豆豆的妈妈今年的年龄为:(68﹣2)÷2=33(岁).答:豆豆妈妈今年33岁.故答案为:33.7.【分析】根据题意,由减法的意义,用730元减去16元,求出全班同学每人买一份纪念品的总钱数,再根据数量=总价÷单价,代入数据解答即可.解:(730﹣16)÷17=714÷17=42(名);答:这个班共有学生42名.故答案为:42.【点评】解答此题的关键是求出全班同学每人买一份纪念品的总钱数,再根据单价、数量和总价之间的关系进行解答.8.【分析】两条直线把正方形分成4部分,第三条直线与前两条直线相交多出3部分,共分成7部分;第四条直线与前3条直线相交,又多出4部分.共11部分,第五条直线与前4条直线相交,又多出5部分,如下图所示.解:1+1+2+3=7答:在一个长方形上画上3条直线,最多能把长方形分成7部分.故答案为:3.【点评】此题考查了图形的拆拼.使直线间相互交叉,交点越多,则分割的空间越多.每多第几条直线,就加几个部分.9.解:假设24辆全是4个轮子的汽车,则三轮车有:(24×4﹣86)÷(4﹣3),=10÷1,=10(辆),答:三轮车有10辆.故答案为:10.10.【分析】先用两个班的总人数减去四(1)班的人数,求出四(2)班的人数,再用四(2)班的人数减去四(2)班男生的人数,求出四(2)班女生的人数,再用女生的总人数35人,减去四(2)班的女生人数,就是四(1)班的女生人数.解:35﹣(72﹣36﹣19)=35﹣17=18(人)答:四(1)班有女生 18人.故答案为:18.【点评】解决本题注意理解题意,把总人数按照两种方法进行分类:总人数=四(1)班人数+四(2)班人数=男生人数+女生人数.11.解:因为,所以(b+10a)×65=4800+10a+b,即10a+b=75,因此b=5,a=7.即=75.故答案为:75.12.【分析】根据每9个棋子是一个循环,用2014除以9,用得到的商乘以一个循环中黑棋子的个数,再根据余数的情况判断最后需加上几个黑棋子即可.解:2014÷9=223…7,循环了223次后,还剩7个,里面有4个黑棋子,223×6+4=1338+4=1342(个)答:其中黑棋子的个数是1342个.故答案为:1342.【点评】答此类问题的关键是找出每几个数或每几个图形是一个循环.13.【分析】(1)所有的果篮用掉2个哈密瓜,4个火龙果,8个猕猴桃.当哈密瓜全部用完时,用掉火龙果的数量是哈密瓜的2倍,依题意,可画出线段图帮助理解:剩下的130个对应着箭头部分,然后列式解答;(2)先求出水果店原有的猕猴桃,即370×2=740(个);再求用完所有的哈密瓜后,还剩下的猕猴桃数即可.解:(1)(130﹣10)÷2=120÷2=60(个)60×6+10=360+10=370(个)答:水果店原有370个火龙果.(2)370×2=740(个)740﹣60×10=740﹣600=140(个)答:还剩140个猕猴桃.【点评】此题属于比较难的题目,解答的关键在于画出线段图来理解,找出数量关系式,列式解答.14.【分析】一个小长方形的周长是28,也就是小长方形的长和宽的和是28÷2=14,也就是大正方形的边长,然后根据正方形的面积公式,解决问题.解:28÷2=1414×14=196答:大正方形的面积是196.故答案为:196.【点评】根据长方形的长和宽与正方形边长之间的关系,先求出小长方形的长和宽的和,即求出了大正方形的边长.15.【分析】根据题意“若从乙筐内拿出12个苹果放入甲筐,则此时甲筐内比丙筐内少24个苹果,乙筐内比丙筐内多6个苹果”则原来甲筐比丙筐少(12+24)=36个苹果,结合原来丙筐内苹果的个数是甲筐内苹果的个数的2倍,可以求出原来甲筐和丙筐苹果的数量,同时知道原来乙筐比丙筐多(6+12)个苹果,进而求出原来乙筐苹果的个数.解:根据题意可知,原来甲筐比丙筐少(12+24)=36个苹果,且原来丙筐是甲筐个数的2倍,则原来甲筐有:36÷(2﹣1)=36个,原来丙筐有:36×2=72个,原来乙筐有:72+(6+12)=90(个)答:乙筐内原有苹果 90个.故答案为:90.【点评】此题考查了差倍问题,根据题意得出:原来甲筐比丙筐少(12+24)=36个苹果,原来乙筐比丙筐多(6+12)个苹果,是解答此题的关键.16.【分析】一个质数的2倍一定是偶数,一个质数的5倍一定是5的倍数,而36要拆成两个数的和,要么都是偶数,要么都是奇数,本题中2的倍数一定是偶数,所以只能拆成两个偶数,故此5的倍数只能是个位上带0的数,当是10时,36﹣10=26,26÷2=13当是20时,4×5=20,4不是质数当是30时,5×6=30,6不是质数,据此解答.解:根据分析可得:符合题意的5的倍数只能是10,20,305×2=10,5×4=20,5×6=30,4和6不是质数,所以只能是2,36﹣10=26.答:这两个质数的乘积是26.【点评】本题考查了质数的定义及其奇数与偶数的性质.17.【分析】甲的休息天数为4的倍数,即4,8,12,…1000;乙的休息日为:8,9,10,18,19,20,…,那么甲只要在4的倍数天休息就行了,每三个数中有一个数是4的倍数,那么也就是说,乙每工作10天才会有1天与喜羊羊的重合,那么以10为周期,共有1000÷10=100个周期,每一周期有一天重合,那么100周期共有100天重合解:甲的休息天数为4的倍数,即4,8,12,…1000;乙的休息日为:8,9,10,18,19,20,…,那么乙只要在4的倍数天休息就行了,每三个数中有一个数是4的倍数,那么也就是说,乙每工作10天才会有1天与喜羊羊的重合,那么以10为周期,共有1000÷10=100个周期每一周期有一天重合,那么100周期共有100天重合.故答案为:100.【点评】本题主要考查了公约数与公倍数问题.关键是乙每工作10天才会有1天与甲的重合.18.解:(35﹣7)×7÷2=28×7÷2=98(平方米)答:这块养猪场的面积是 98平方米.故答案为:98.19.【分析】6时53分﹣6时45分=8分钟,设从家到学校若每分钟走60米,x分钟到学校,则若每分钟走75米,x﹣8分钟到学校,因为从家到学校的距离一定,根据“速度×时间=路程”列方程解答即可.解:设从家到学校若每分钟走60米,x分钟到学校,6时53分﹣6时45分=8分钟60x=(x﹣8)×7560x=75x﹣60015x=600x=40;6时53分﹣40分=6时13分;答:洋洋从家里出发的时刻是6:13.故答案为:6:13.【点评】此题考查列方程解应用题,本题关键是根据题意找出基本数量关系,设未知数为x,由此列方程解决问题.20.【分析】若长方形的长是1024,宽是1,根据长方形的面积=长×宽,可求出长方形的面积,再根据正方形的面积公式可求出正方形的边长,然后再根据正方形的周长=边长×4可求出它的周长.解:1024×1=10241024=2×2×2×2×2×2×2×2×2×2=32×32,所以正方形的边长是32.32×4=128答:正方形的周长是128.【点评】本题主要考查了学生对长方形面积和正方形面积与周长公式的掌握.21.解:假设全是足球,96÷6=16(个),4×6=24(人),篮球:24÷(6﹣3),=24÷3,=8(个);足球:20﹣8=12(个);答:其中足球有12个.故答案为:12.22.【分析】要使最小,那么百位数字最小是1,那么十位数字是0,这个数就为,然后根据能被3整除的数的特征确定c的最小值即可.解:要使最小,那么百位数字最小是1,那么十位数字是0,这个数就为,又因为是3的倍数,所以可得:1+0+c的和是3的倍数,所以,c最小是2,则,最小是102.故答案为:102.【点评】本题考查了能被3整除的数的特征的灵活应用,关键是确定百位和十位的数字.23.【分析】首先把120分解质因数,把质因数分作三组,使各组数字相乘后的结果是三个连续的自然数,即可得解.解:120=2×2×2×3×5=(2×2)×(2×3)×5,2×2=4,2×3=6,5,即,三个连续自然数的乘积是120,这三个数是4、5、6,所以,和是:4+5+6=15.故答案为:15.【点评】本题考查了灵活应用合数分解质因数来解决较复杂问题.24.【分析】首先根据5的整除特性可知尾数是0或者5,那么150和5的倍数差依然是尾数是0或者5的数字枚举即可.解:根据5的整除特性可知尾数是0或者5.那么150减去这个数字尾数还是0或者5.可以找到尾数是0或者5的数字是3的倍数.30,60,90,120,15,45,75,105,135共9个数字满足条件.对应的数字就有9对.故答案为:9.【点评】本题是考察数的整除特性,关键在于找到尾数是0或5的数字是3的倍数,枚举即可解决问题.25.【分析】本题考察图形边长的平移.解:画出移动后的图,所得图形的周长是5×2+(5+1×2+2×2+3×2+4×2+5)=10+30=40cm.【点评】本题主要抓住平移后的图形每条边边长为多少即可求解.26.【分析】本题主要考察等差数列中最小的项.解:因为这三个数都是被5除余2,所以这三个相邻的数是个等差数列,中间数是336÷3=112,所以最小的是112﹣5=107.【点评】本题主要找到每相邻两个数相差5就能解答.27.解:甲校比乙校多的人数:32×2+48=112人,甲校的人数:(864+112)÷2,=976÷2,=488(人).答:原来甲校有488人.故答案为:488.28.【分析】今天算起,57天后的第一天也就是经过了57天,用57除以7,求出经过了多少周,还余几天,然后根据余数推算.解:57÷7,=57÷7,=8(周)…1(天);余数是1,星期五再过1天是星期六.故答案为:六.【点评】解决这类问题先求出经过的天数,再求经过的天数里有几周还余几天,再根据余数推算.29.解:504÷8÷(108÷3÷4)﹣4,=504÷8÷9﹣4,=63÷9﹣4,=7﹣4,=3(名),答:需增加3名,故应填:3.30.解:设中间的圆圈中的数是A;根据题意可得:1+2+3+4+5+6+7+8+9+10+11+A+A+A+A=18×5,66+4A=90,4A=24,A=6;那么每条线段剩下的两个数的和是:18﹣6=12;又因为,1+11=12,2+10=12,3+9=12,4+8=12,5+7=12;分别放到每条线段剩下的两个圆圈中;由以上可得:.31.解:根据分析可得,100÷2=50(平方米)答:图中灰色部分的面积是 50m2.故答案为:50.32.解:根据分析可得,660÷(40﹣10),=660÷30,=22(米);22×10=220(米);答:火车的车身长是 220米.故答案为:220.33.解:船:(16+4)÷(5﹣3),=20÷2,=10(条);学生:3×10+16=46(人);答:学校共有学生46人.故答案为:46.34.解:根据题干分析,将讨论分析的过程利用表格的形式进行统计如下:×√以得出:B是11+2=13岁,C是11﹣1=10岁;即A11岁、B13岁、C10岁;将这个结论代入上表中,可以得出B说的C是13岁时错误的,其他两句正好符合题意是正确的,由此可得,此假设成立;答:由上述推理可以得出A是11岁.故答案为:11.35.【分析】因为前两个数相加得偶数,即奇数+奇数=偶数;同理,第四个数是:奇数+偶数=奇数,以此类推,总是奇数、奇数、偶数、奇数、奇数、偶数…;每三个数一个循环周期,然后确定2007个数里面有几个循环周期,再结合余数,即可得出偶数的个数.解:2007÷3=669,又因为,每一个循环周期中有2个奇数,1个偶数,所以前2007个数中偶数的个数是:1×669=669;答:前2007个数中,有699是偶数.故答案为:699.36.【分析】设这两个数为a,b.,且a<b.千位最小差只能是1.为了让差尽量小,只能使a其它位数最大,b的其它位数最小.所以要尽量使a的百位大于b的百位,a的十位大于b的十位,a的个位大于b的个位.因此分别是8和1,7和2,6和3,剩下的4,5分给千位.据此解答.解:设这两个数为a,b.,且a<b.千位最小差只能是1.根据以上分析,应为:5123﹣4876=247故答案为:247.37.解:(3△2)△x=20,(2×3+2)△x=20,8△x=20,2×8+x=20,16+x=20,x=20﹣16,x=4;故答案为:4.38.解:723﹣30=693,693=3×3×7×11,所以一个两位数除723,除数大于30的两位数因数有:11×3=33,11×7=77,3×3×7=63,11×3×3=99,共4个;故答案为:33、63、77、99.39.解:[(15+7﹣10)×2+3]×2=[12×2+3]×2=[24+3]×2=27×2=54(米)答:这捆电线原来长54米.40.【分析】通过题意,甲取1块,乙取2块,甲取4块,乙取8块, (1)20,2=21,4=22,8=23…,可以看出,甲取的块数是20+22+24+26+28+…,相应的乙取得块数是21+23+25+27+29+…,我们看一看90是甲取了几次,乙相应的取了多少次,把两者总数加起来,即可得解.解:甲取的糖果数是20+22+24+…+22n=90,因为1+4+16+64+5=90,所以甲共取了5次,4次完整的,最后的5块是包裹中的糖果少于应取的块数,说明乙取了4次完整的数,即乙取了21+23+25+27=2+8+32+128=170(块),90+170=260(块),答:最初包裹中有 260块糖果.故答案为:260.【点评】判断出甲乙取得次数是解决此题的关键.。
四年级数学奥数讲义+练习-第1讲 找规律(一)(全国通用版,含答案)

奥数已经成为现在孩子学习的加强工具。
一种思维方式的训练,一种让孩子学以致用,举一反三的法宝,一种可以扩宽孩子思维的奥秘兵器。
老师经常对学生们说,养成好的学习品质,拥有好的学习方法比学习知识自己重要得多,它是学好知识的前提。
学习奥数更是如此。
奥数题对学生们的要求是非常严格的,你既要注意到思维有广度有深度,在做题时还要加倍小心。
有些题往往是一字之差,谬之千里。
习惯的养成不是一朝一夕之功。
要养成好的学习习惯,首先,需要学生对这个问题有个正确的认识,有些家长往往错误地认为。
只要是标题问题理解了,出点小错不妨。
这样做的结果,往往助长了学生粗心大意之习气。
而在奥数题中,一点小错,往往是致命的。
学生做题出错了,我们应把它做为一个好的教育学生的契机,引导学生找出错误原因并不停积累,是知识方面的,要牢记。
是习惯方面的,要改正。
相信久而久之,好的习惯必能养成。
第1讲找规律(一)一、知识要点观察是解决问题的根据。
通过观察,得以揭示出事物的发展和变化规律,在一般情况下,我们可以从以下几个方面来找规律:1.根据每组相邻两个数之间的关系,找出规律,推断出所要填的数;2.根据相隔的每两个数的关系,找出规律,推断出所要填的数;3.要善于从整体上把握数据之间的联系,从而很快找出规律;4.数之间的联系往往可以从不同的角度来理解,只要言之有理,所得出的规律都可以认为是正确的。
二、精讲精练【例题1】先找出下列数排列的规律,并根据规律在括号里填上适当的数。
1,4,7,10,(),16,19【思路导航】在这列数中,相邻的两个数的差都是3,即每一个数加上3都等于后面的数。
根据这一规律,括号里应填的数为:10+3=13或16-3=13。
像上面按照一定的顺序排列的一串数叫做数列。
练习1:先找出下列各列数的排列规律,然后在括号里填上适当的数。
(1)2,6,10,14,(),22,26(2)3,6,9,12,(),18,21(3)33,28,23,(),13,(),3(4)55,49,43,(),31,(),19(5)3,6,12,(),48,(),192(6)2,6,18,(),162,()(7)128,64,32,(),8,(),2(8)19,3,17,3,15,3,(),(),11,3..【答案】(1)18(2)15(3)18,8(4)37,25(5)24,96(6)54,486(7)16,4(8)13,3【例题2】先找出下列数排列的规律,然后在括号里填上适当的数。
四年级下册数学试题-奥数专题讲练:1 乘法原理 竞赛篇(解析版)全国通用
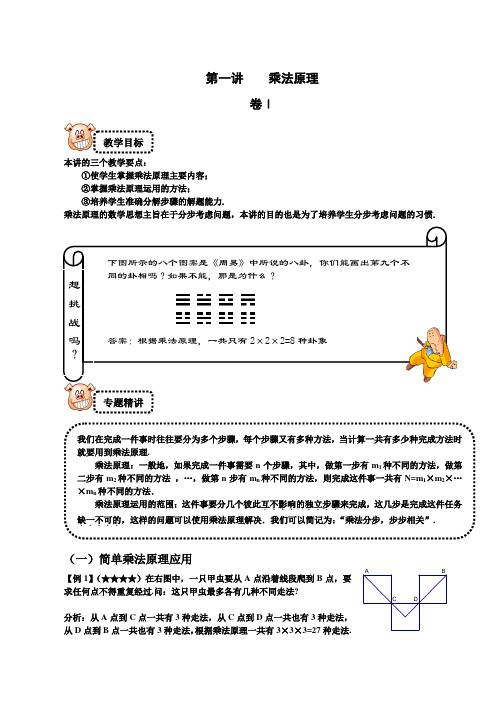
第一讲 乘法原理卷Ⅰ 本讲的三个教学要点:①使学生掌握乘法原理主要内容;②掌握乘法原理运用的方法;③培养学生准确分解步骤的解题能力.乘法原理的数学思想主旨在于分步考虑问题,本讲的目的也是为了培养学生分步考虑问题的习惯.(一)简单乘法原理应用【例1】(★★★★)在右图中,一只甲虫要从A 点沿着线段爬到B 点,要求任何点不得重复经过.问:这只甲虫最多各有几种不同走法?分析:从A 点到C 点一共有3种走法,从C 点到D 点一共也有3种走法,从D 点到B 点一共也有3种走法,根据乘法原理一共有3×3×3=27种走法.我们在完成一件事时往往要分为多个步骤,每个步骤又有多种方法,当计算一共有多少种完成方法时就要用到乘法原理. 乘法原理:一般地,如果完成一件事需要n 个步骤,其中,做第一步有m 1种不同的方法,做第二步有m 2种不同的方法 ,…,做第n 步有m n 种不同的方法,则完成这件事一共有N=m 1×m 2×…×m n 种不同的方法. 乘法原理运用的范围:这件事要分几个彼此互不影响....的独立步骤....来完成,这几步是完成这件任务缺一不可的.....,这样的问题可以使用乘法原理解决.我们可以简记为:“乘法分步,步步相关”. 专题精讲 教学目标 想 挑战 吗?下图所示的八个图案是《周易》中所说的八卦,你们能画出第九个不同的卦相吗?如果不能,那是为什么? 答案:根据乘法原理,一共只有2×2×2=8种卦象 DC B A[拓展] (★★★)在右图中,一只甲虫要从A 点沿着线段爬到B 点,要求任何点不得重复经过.问:这只甲虫最多各有几种不同走法?分析:解这道题时千万不要受原来那道题的影响,A 到C 的地走法不是3条而是4条所以这只甲虫最多有4×4=16种走法.【例2】(★★★★)有三组:(1)1,2,3;(2)0.5,1.5,2.5,3.5;(3)4,5,6.如果从每组数中各取出一个数相乘,那么所有不同取法的三个数乘积的总和是多少?分析:将式子(1+2+3)×(0.5+1.5+2.5+3.5)×(4+5+6)用乘法分配律展开所得的3×4×3=36个加项即为36种不同取法的三个数的乘式,所以(1+2+3)×(0.5+1.5+2.5+3.5)×(4+5+6)的值即为不同取法的三个数乘积的总和为720.【例3】(★★★★)从1到2004这2004个正整数中,共有 个数与四位数8866相加时,至少发生一次进位.分析:考虑不进位的情况. 9999-8866=1133.千位百位各有0,1两种选法,十位、个位各有0,1,2,3四种选法,因为0000不是正整数,所以不进位的数有 2×2×4×4-1=63(个).至少发生一次进位的数有 2004-63=1941(个).[前铺]10到99这90个数中,与66相加不产生进位的数有多少个?分析:十位、个位上不产生进位,要求十位上、个位上的数字不超过3,这样十位的数可以取值1、2、3上,个位上的数可以取值0、1、2、3,所以与66相加不产生进位的数有3×4=12个.(二)较复杂的乘法原理应用【例4】(★★★★)如图,一张地图上有五个国家A ,B ,C ,D ,E ,现在要求用四种不同的颜色区分不同国家,要求相邻的国家不能使用同一种颜色,不同的国家可以使用同—种颜色,那么这幅地图有多少着色方法?分析:第一步,给A 国上色,可以任选颜色,有四种选择;第二步,给B 国上色,B 国不能使用A 国的颜色,有三种选择;第三步,给C 国上色,C 国与B ,A 两国相邻,所以不能使用A ,B 国的颜色,只有两种选择;第四步,给D 国上色,D 国与B ,C 两国相邻,因此也只有两种选择;第五步,给E 国上色,E 国与C ,D 两国相邻,有两种选择.共有4×3×2×2×2=96种着色方法. C B A ED C B A[拓展1] 如图,有一张地图上有五个国家,现在要用四种颜色对这一幅地图进行染色,使相邻的国家所染的颜色不同,不相邻的国家的颜色可以相同.那么一共可以有多少种染色方法?分析:这一道题实际上就是例题,因为两幅图各个字母所代表的国家的相邻国家是相同的,如果将本题中的地图边界进行直角化就会转化为原题,所以对这幅地图染色同样一共有4×3×2×2×2=96种方法.讨论:如果染色步骤为C-A-B-D-E,那么应该该如何解答?答案:也是4×3×2×2×2=96种方法.如果染色步骤为C-A-D-B-E那么应该如何解答?答案:染色的前两步一共有4×3种方法,但染第三步时需要分类讨论,如果D与A颜色相同,那么B有2种染法,E也有2种方法,如果D与A染不同的颜色,那么D有2种染法那么B只有一种染法,E有2种染法,所以一共应该有4×3×(1×2×2+2×1×2)=96种方法,(教师应该向学生说明第三个步骤用到了分类讨论和加法原理,加法原理在下一讲中将会讲授),染色步骤选择的经验方法:每一步骤所染的区块应该尽量和之前所染的区块相邻.[拓展2]如图:将一张纸作如下操作,一、用横线将纸划为相等的两块,二、用竖线将下边的区块划为相等的两块,三、用横线将最右下方的区块分为相等的两块,四、用竖线将最右下方的区块划为相等的两块……,如此进行8步操作,问:如果用四种颜色对这一图形进行染色,要求相邻区块颜色不同,应该有多少种不同的染色方法?分析:对这张纸的操作一共进行了8次,每次操作都增加了一个区块,所以8次操作后一共有9个区块,我们对这张纸,进行染色就需要9个步骤,从最大的区块从大到小开始染色,每个步骤地染色方法有:4、3、2、2、2……,所以一共有:4×3×2×2×2×2×2×2×2=1536.【例5】(★★★)右图中共有16个方格,要把A、B、C、D四个不同的棋子放在方格里,并使每行每列只能出现一个棋子.问:共有多少种不同的放法?分析:由于四个棋子要一个一个地放入方格内,故可看成是分四步完成这件事.第一步放棋子A,A可以放在16个方格中的任意一个中,故有16种不同的放法;第二步放棋子B,由于A已放定,那么放A的那一行和一列中的其他方格内也不能放B,故还剩下9个方格可以放B,B有9种放法;第三步放C,再去掉B所在的行和列的方格,还剩下四个方格可以放C,C有4种放法;最后一步放D,再去掉C所在的行和列的方格,只剩下一个方格可以放D,D有1种放法.由乘法原理,共有16×9×4×1=576种不同的放法.[前铺]:国际象棋棋盘是8×8的方格网,下棋的双方各有16个棋子位于16个区格中,国际象棋中的“车”同中国象棋中的“车”一样都可以将位于同一条横行或竖行的对方棋子吃掉,如果棋局进行到某一时刻,下棋的双方都只剩下一个“车”,那么这两个“车”位置有多少种情况?分析:对于如果只有一只“车”的情况,它可以有64种摆放位置,如果在棋盘中再加入一个“车”,那么它不能在原来那个“车”的同行或同列出现,他只能出现在其他七行七列,所以它只有7×7=49中摆放,所以这两个“车”的摆放位置有64×49=3136种方法.【例6】(★★★★)有10粒糖,每天至少吃一粒,吃完为止,共有多少种不同的吃法?分析:可以将10粒糖如下图所示排成一排,这样每两颗之间共有9个空,从头开始吃,若相邻两块糖是分在两天吃的,就在其间画一条竖线隔开表示之前的糖和之后的糖不是在同一天吃掉的,不同的竖线插入方式代表不同的吃法,所以只需要求出有多少种竖线插入式.○○|○|○○○|○○○|○由于每个空都有画线与不画线两种可能(相当于每吃完一粒考虑今天还吃不吃),根据乘法原理,则不同的吃法共有29=512(种).[拓展]有10粒糖,分三天吃完,每天至少吃一粒,共有多少种不同的吃法?分析:如图:○○|○○○○|○○○○,将10粒糖如下图所示排成一排,这样每两颗之间共有9个空,从头开始吃,若相邻两块糖是分在两天吃的,就在其间画一条竖线隔开表示之前的糖和之后的糖不是在同一天吃掉的,九个空中画两条竖线,一共有9×8÷2=36种方法.(注意这里用到了组和的方法)卷Ⅱ(三)乘法原理在排列组合中的应用【例7】(★★★★)书架上有4本不同的漫画书,5本不同的童话书,3本不同的故事书,全部竖起排成一排,如果同类型的书不要分开,一共有多少种排法?如果只要求童话书和漫画书不要分开有多少种排法?分析:(1)每种书内部任意排序,分别有4×3×2×1,5×4×3×2×1,3×2×1种排法,然后再排三种类型的顺序,有3×2×1种排法,整个过程分4步完成.4×3×2×1×5×4×3×2×1×3×2×1×3×2×1=103680(种)一共有103680种不同排法.(2)方法一:首先将漫画书和童话书全排列,分别有4×3×2×1=24、5×4×3×2×1=120种排法,然后将漫画书和童话书捆绑看成一摞,再和3本故事书一起全排列,一共有5×4×3×2×1=120种排法,所以一共有24×120×120=345600种排法.方法二:首先将三种书都全排列,分别有24、120、6种排法,然后将排好了顺序的漫画书和童话书,整摞得先后插到故事书中,插漫画书时有4个地方可以插,插童话书时就有5个地方可插,所以一共有24×120×6×5×4=345600种排法.[前铺]小明有6本不同的课外书,把他们按顺序放在书架上有多少种排法?如果借出去两本剩下的情况有多少种?分析:(1)6本书的全排列:6!=720种,6本书中取4本排列:6×5×4×3=360种.【例8】(★★★★)用0,1,2,3,4这5个数字,组成各位数字互不相同的四位数,例如1023,2341等,求全体这样的四位数之和.分析:先求出5个数字共能组成多少个符合条件的数,分为4步,第一步确定千位数一共有4种选择,然后确定百位,有4种选择,确定十位数有3种选择,确定个位数有2种选择.一共有4×4×3×2=96种选择. 这96种选择中,千位数字出现1、2、3、4的次数都是24次,百位、十位、个位出现的次数为18次(0出现24次).所以全体这样的四位数和为(1+2+3+4) ×24×1000+(1+2+3+4) ×18×(100+10+1)=259980[前铺] 用1,2,3,4这4个数字,组成各位数字互不相同的三位数,例如123,231等,求全体这样的三位数之和.分析:先求出这4个数字共能组成多少个各位数字互不相同的三位数,分为4步,第一步确定百位数一共有4种选择,确定十位,有3种选择,确定个位数有2种选择,所以一共有24个符合条件的数,其中百位数字是1的有3×2×1=6个,同理、百位数字是2、3、4的也有6个,所以各个数百位数字之和为 6×(1+2+3+4)=60,同理各个数十位数字之和为60,各个数个位数字之和为60,所以,这些数的总和为:60×100+60×10+60×1=6660.【例9】(★★★★★)四对夫妇围一圆桌吃饭,要求每对夫妇两人都要相邻,那么一共有多少安排座位的方法?(如果某种排法可以通过旋转得到另一种排法,那么这两种排法算作同一种.)分析:方法一:事实上如果没有括号中的条件,那么所得的答案是原题答案的八分之一,因为符合原题的所有不同排法都通过旋转可以得到8种各不相同的安排方法.所以我们可以先求出改掉括号中条件的题目答案, 对于改编后的题,显然所有的安排方法分为两大类,如右图所示,每个椭圆中是一对,对于其中的一类,例如右图,第一步,确定1号位的人选:8种,那么2号位只能是他(她)的妻子(丈夫);第二步确定3号位的人选:6种,那么4号位只能是坐3号位的妻子或丈夫……,如此,对于右图可以有8×6×4×2=384种排法,同理左图也有384种排法,一共是768种排法.那么对于有括号中条件的题目一共有768÷8=96种排法.方法二:由于括号中的条件让我们很为难,对于一种新的排法,我们还要将它旋转,看它是否和之前的排法是否相同,当然我们也可以将所有排法都转到一个特殊的角度,以判断这些排法是否有相同的,所以我们可以定义一个特殊角度:先将四对夫妇编号,然后规定对于每一种排法1号夫妇面南坐是它的特殊角度,那么如果两中排法都转到特殊角度后,还不完全一样,那么这两种排法就无论如何也不能通过旋转得到相同的排法,所以我们只要求出特殊角度下的不同排法数,第一步先将4对夫妻的整体位置安排好,当然1号夫妻已经排好了,安排另3对夫妻一共有3×2×1=6种排法,如图所示:432143211234123412344321对于以上每一种排法,夫妻之间都可以交换位置,所以一共有6×2×2×2×2=96种排法.[拓展]3个3口之家在一起举行家庭宴会,围一桌吃饭,要求一家人不可以被拆开,那么一共有多少种排法?(如果某种排法可以通过旋转得到另一种排法,那么这两种排法算作同一种.)分析:使用原题的方法二更方便:共(2×1)×(3×2×1)×(3×2×1)×(3×2×1)=432种7812345687654321【例10】(★★★★)从10名男乒乓球运动员,10名女乒乓球运动员中选派运动员组成代表队去参加男女混合双打比赛,要求选派6人(男女各3),组成3个搭配,那么一共有多少种选派方法?分析:方法一:首先从10名男选手中选出3人(组合),一共有10×9×8÷(3×2×1)=120种,然后从10名女乒乓球运动员挑3人与之对应(排列),一共有10×9×8=720种,所以一共有120×720=86400种.方法二:先将6人挑出来一共是14400种,然后对这六人搭配,一共3×2×1=6种,所以一共有86400种.[前铺]从10名男乒乓球运动员,10名女乒乓球运动员中选派6名运动员组成代表队去参加比赛,要求男女运动员各3名,那么一共有多少种选派方法?分析:第一步:在男运动员中先选一名有10种方法.第二步:在剩下的男生中再选一名有9种方法,第三步:在剩下的男生中再选一名有8种方法,男生中选三人一共有10×9×8=720种方法,需要注意的是,每一种方法,例如,甲乙丙三人的组合,被统计了3×2×1=6次,分别是甲乙丙、甲丙乙,乙丙甲、乙甲丙、丙甲乙、丙乙甲,所以实际有720÷6=120种方法,同理在女生中选取三人一共有120种.所以一共有120×120=14400种选派方法.【例11】(★★★★)用1,2,3,4,5这5个数字组成四位数,至多允许有一个数字重复两次,例如1234和2454是满足条件的,而1212,3335和4444就是不满足条件的,那么满足条件的四位数共有多少个?分析:至多允许有一个数字重复两次的四位数即是由至少3个不同数字组成的四位数.这5个数字组成的四位数共有5×5×5×5=625个,其中由一个数字组成的有5个,包含指定两个数字四位数有2×2×2×2-2=14个,共有5×4÷(2×1)=10种指定方法,所以一共有140个四位数包含两个数字.剩下的四位数都满足条件一共有共有625-5-140=480个.(其中涉及到一点加法原理和排除法)【例12】(★★★★★仁华试题)一台晚会上有6个演唱节目和4个舞蹈节目.问:(1)如果4个舞蹈节目要排在一起,有多少种不同的安排顺序?(2)如果要求每两个舞蹈节目之间至少安排一个演唱节目,一共有多少种不同的安排顺序?分析:(1)将4个舞蹈节目视为1个节目,七个节目一起排列一共有7×6×5×4×3×2×1=5040个,但舞蹈节目还有4×3×2×1=24种排列.所以一共有5040×24=120960种.(2)优先安排将6个演唱节目顺序,一共有6×5×4×3×2×1=720种方法,然后将安排4个舞蹈节目顺序一共有4×3×2×1=24种排列,最后将舞蹈节目按顺序安插到6个演唱节目前后不同位置,包括首尾一共有6+1=7个位置可供4个舞蹈节目安插,共有7×6×5×4÷(4×3×2×1)=35个安插方式,所以一共有720×24×35=60480种排列方式.专题展望本讲介绍了对于分步解决问题所用到的乘法原理,下一讲加法原理中我们将重点介绍对于同一步骤不同类方法的计数原理.练习一1.(★★例10)10个人围成一圈,从中选出三个人,其中恰有两人相邻,共有多少种不同选法?分析:两人相邻的情况有10种,第三个人不能与他们相邻,所以对于每一种来说,只剩6个人可选,10×6=60(种)共有60种不同的选法.2.(★★例3)在21世纪中,有些年的年份数是由4个不相同的数字组成的,这样的年份共有个.分析:符合要求的年份形如20xy,其中x有8种不同选法,y有7种不同选法,所以有56个四位数满足题目要求.3.(★★★)世界杯小组赛一般由4个球队进行单循环赛,如何安排这四个球队先后比赛次序,有几种方法?分析:小组赛一共要赛4×3÷2=6场,排列这六场赛事一共有6×5×4×3×2×1=720种.4.(★★★★例11)用1,2,3,4这4个数字,组成各位数字互不相同的二位数,例如13,24等,求全体这样的二位数之和.分析:先求出2个数字共能组成多少个符合条件的数,分为2步,第一步确定十位数有4种选择,确定个位数有3种选择.一共有4×3=12种选择.这12种选择中,十位或个位出现1、2、3、4的次数都是3次,所以全体这样的二位数和为(1+2+3+4) ×3×(10+1)=330.5.(★★★)从一个班级10名优秀学生中选出5人组成班委,5人中再选出班长,一共有多少种方法?分析:第一步,先把班长选出来,一共有10种选法,第二步,在其余9人中选出4人一共有9×8×7×6÷(4×3×2×1)=126种选法.所以一共有10×126=1260种选法.数学知识二进制记数法的光辉第一次是闪现在中国的一部古书《周易》中.传说在远古时代,伏羲为天下王,他向外探求大自然的奥秘,向内省视自己的内心,终于推演出了太极八卦图.太极八卦图中心是由两条黑白相间、首尾相顾的鱼形成的一个圆圈,四周还围着结构奇特的八组图符,每组都含有三个或断或连的线段.这八组图符便是著名的八卦图,古人曾解释说:“太极生两仪,两仪生四象,四象生八卦.”再进一步,若把八卦两两组合,就会生成六十四卦.据学者考察,德国数学家莱布尼兹(1616-1703)看到“伏羲六十四卦方位图”后,从中领悟出了阴爻“--”代表“0”,阳爻“—”代表“1”,从而完善、撰写了《二进制数字算术》一书,他意味深长地说,自己不过是重新发现了中国古代数学中的秘密而已.古老的太极八卦图竟与现代数学上的二进制有着如此神秘的联系.。
四年级数学奥数培优讲义-专题03公顷与平方千米的换算和应用(含解析)

专题03公顷与平方千米的换算和应用1.一块占地20公顷的果园中,种了25000棵果树,平均每棵树占地________平方米.2.5平方千米=_____公顷=_____平方米。
3.9公顷=( )平方米 180000平方米=( )公顷3平方千米=()公顷=()平方米4.学校有一块边长是10米的方形草坪,( )块这样的草坪面积为1公顷。
5.在下面的( )里填上合适的数.2公顷=()平方米 60平方千米=()公顷600000平方米=()公顷6.一个长方形果园,长是100米,宽是50米,( )个这样的果园的占地面积是1公顷,( )个这样的果园的占地面积是1平方千米.7.9公顷=()平方米 3200平方厘米=()平方分米16000000平方米=()公顷=()平方千米8.在( )里填上“>”“<”或“=”。
7千克( )693克 1000克()2千克6时15分( )325分 8600米()8千米60米306平方分米( )3平方米60平方分米 1.5小时()1小时50分500公顷()5平方千米 425平方米()42平方千米9.2022年冬奥会张家口奥林匹克体育中心占地面积约50公顷,( )个这样的体育中心占地面积约1平方千米。
10.幸福小区占地呈长方形,长800米,宽500米,它的占地面积是( )平方米,合( )公顷。
11.________平方千米=5000公顷 8000000平方米=________平方千米=________公顷12.15000000平方米=( )公顷=()平方千米;我国青海省的面积是722000()(填上适当的面积单位)。
13.一个正方形棉花地的周长是1200米,这块棉花地的面积是( )公顷。
14.10公顷=________平方米 8200公顷=________平方千米14平方千米=________公顷 3500000平方米=________公顷15.30公顷=()平方米;()平方千米=60000公顷。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计算:999999999×111111111计算:66666×133332求算式{200982009920096999888666⨯÷L L L 123123个个个的计算结果的各位数字之和。
计算:{{222010120108888111-L L 个个计算:22222×99999+33333×33334第一讲:多位数计算(★★★)(★★★★)(★★★★)(★★★★)(★★★)(★★★★)计算1009100910099999991999⨯+L L L 123123123个个个结果末尾有多少个零?{201032010420102201053335556444222⨯+⨯⨯L L L L 123123123个个个个【你还记得吗】 (★★★)计算:2010×20112011-2011×计算:333×332332333-332×333333332测试题1.计算222222×999999A .222222217880B .222222788888C .222221777778D .222222177788(★★★★★)(★★★★)2.计算6666×13332A .88871112B .88881112C .88872222D .3.计算:3001300229931111222233334 L L L 1231424314243个个个A .3013333L 14243个3B .2003333L 14243个3C .3003333L 14243个3D .3063333L 14243个34.计算100×100-99×99+98×98-97×97+…+2×2-1×1A .4950B .5050C .5150D .52505.计算 99999×26+33333×24A .3996366B .6933669C .3399966D .36699666.计算:899×899+1799A .819000B .810000C .900000D .9810007.计算111111×777777+444444×555555A .333332666667B .333333666667C .333332777777D .3333337777778.计算2009×-2007×A .2B .4016C .4017D .0第二讲:容斥原理上(★★)网校老师共50人报名参加了羽毛球或乒乓球的训练,其中参加羽毛球训练的有30人,参加乒乓球训练的有35人,请问:两个项目都参加的有多少人?(★★★)一个班30人,完成作业的情况有三种:一种是完成语文作业没完成数学作业;一种是完成数学作业没完成语文作业;一种是语文、数学作业都完成了。
已知做完语文作业的有20人;做完数学作业的有23人。
这些人只完成数学作业的有多少人?(★★★)网校老师组织理财培训,报名股票培训的有23人,报名基金培训的有32人,两项都报名的有8人,两项都没有报名的有5人,那么网校老师有多少人?(★★★)网校组织40名老师参加趣味运动会,参加同心协力项目的有26人,参加万众一心项目的有18人,两个项目都没参加的有6人,两个项目都参加的有多少人?(★★★)网校老师60人组织春游。
报名去香山的有37人,报名去鸟巢的有42人,两个地点都没有报名的有8人,那么只报名其中一个地点的有多少人?(★★★)1~100中是2或5的倍数的数有多少个?(★★★)1~100中既不是3的倍数,也不是4的倍数的数有多少个?(★★★★)写有1到100编号的灯100盏,亮着排成一排,第一次把编号是3的倍数的灯拉一次开关,第二次把编号是5的倍数的灯拉一次开关,那么亮着的灯还有多少盏?本讲总结巧用文氏图,找准每一样。
重复就减去,少算要加上。
不重也不漏,计数你最棒!重点例题:例3,例6,例8测试题1.学而思四年级㈠班共40人报名参加了课外兴趣小组,其中学习画画的有35人,学习音乐的有20人,请问:两个项目都参加的有()人?A.10B.15C.40D.552.一个学校四年级选出40人参加竞赛考试,考试情况如下:一些同学语文得了奖牌而数学没得奖牌;一些同学数学得了奖牌而语文没得奖牌;一些同学语文、数学都得了奖牌。
已知语文获得奖牌的有26人,数学获得奖牌的有28人,这些同学只得了一项奖牌的有()人。
A.12B.14C.26D.283.一个饮料公司对所有网校老师进行问卷调查,结果如下:喜欢喝橙汁的老师有52人,喜欢喝桃汁的老师有63人,既喜欢喝橙汁又喜欢喝桃汁的老师有21人,既不喜欢喝橙汁又不喜欢喝桃汁的老师有12人,则网校老师总共有()人。
A.82B.94C.103D.1064.一天有36名同学去商店买笔,有24人买了圆珠笔,20人买了钢笔,两种笔都没买的同学有4人,两种笔都买了的同学有()人。
A.4B.8C.12D.165.在46人参加的采摘活动中,采了草莓的有22人,采了樱桃的有25人,既没采草莓又没采樱桃的有6人,只采了其中一种水果的有( )人。
A.7B.15C.24D.336.1~100中是4或5的倍数的数有()个。
A.20B.30C.40D.507.1~100中既不是2的倍数,也不是7的倍数的数有( )个。
A.33B.43C.53D.638.50名同学面向老师站成一行,老师先让大家从左至右按1,2,3,…,49,50依次报数,再让报数是3的倍数的同学向后转,接着又让报数是4的倍数的同学向后转,现在面向老师的同学还有()名。
A.24B.27C.30D.33第三讲:容斥原理下(★★★)在网校50名老师中,喜欢看电影的有15人,不喜欢唱歌的有25人,既喜欢看电影也喜欢唱歌的有5人。
那么只喜欢唱歌的有多少人?(★★★)在网校40名老师中,每个人都爱喝橙汁、桃汁、苹果汁中的一种或几种。
其中有10人爱喝橙汁,15人不爱喝橙汁却爱喝桃汁。
请问:只爱喝苹果汁的有几人?(★★★)网校老师组织体育比赛,分成轮滑、游泳和羽毛球三个组进行,参加轮滑比赛的有20人,参加游泳比赛的有25人,参加羽毛球比赛的有30人,同时参加了轮滑和游泳比赛的有8人,同时参加了轮滑和羽毛球比赛的有7人,同时参加了游泳和羽毛球比赛的有6人,三种比赛都参加的有4人,问参加体育比赛的共有多少人?(★★★★)网校老师共有90人,其中有32人参加了专业培训,有20人参加了技能培训,40人参加了文化培训,13人既参加了专业又参加了文化培训,8人既参加了技能又参加了专业培训,10人既参加了技能又参加了文化培训,而三个培训都未参加的有25人,那么三个培训都参加的有多少人?(★★★★★)网校共130名老师,其中70人参加了歌唱小组,80人参加了舞蹈小组,60人参加了模特小组,至少参加两个小组的有60人,参加了三个小组的有30人,那么网校老师有多少人没有参加小组?(★★★★)在1至100的自然数中,既不能被2整除,又不能被3整除,还不能被5整除的数有多少个?(★★★★★)2006盏亮着的电灯,各有一个拉线开关控制,按顺序编号为l,2,…,2006。
将编号为2的倍数的灯的拉线各拉一下;再将编号为3的倍数的灯的拉线各拉一下,最后将编号为5的倍数的灯的拉线各拉一下。
拉完后亮着的灯数为多少盏?本讲总结三者文氏图:奇层加,偶层减重点例题:例3,例4,例7测试题1.在网校45名老师中,会打乒乓球的有12人,不会打网球的有18人,既会打乒乓球也会打网球的有7人,那么只会打网球的有()人。
A.15B.20C.25D.302.在网校60名老师中,每个人都喜欢上微博、论坛、空间中的一种或几种。
其中有28人喜欢上微博,12人不喜欢上微博却喜欢上论坛,则只喜欢上空间的有()人。
A.15B.20C.32D.463.网校组织老师参加业余培训活动,有茶艺、美容化妆和理财三个活动,参加茶艺的有22人,参加美容化妆的有28人,参加理财的有35人;同时参加了茶艺和美容化妆培训的有11人,同时参加了茶艺和理财培训的有9人,同时参加了美容化妆和理财培训的有8人,三种培训都参加的有7人,则参加业余培训活动的共有()人。
A.50B.57C.60D.644.网校老师共有120人,其中有44人喜欢看动作电影,有35人喜欢看爱情电影,52人喜欢看喜剧电影,21人既喜欢看动作又喜欢看喜剧电影,17人既喜欢看动作又喜欢看爱情电影,15人既喜欢看爱情又喜欢看喜剧电影,而三种类型电影都不喜欢看的有20人,那么三种类型电影都喜欢看的有()人。
A.20B.21C.22D.235.网校举办了一个晚会,最后统计如下:网校共96名老师,其中21名老师参加了小品表演,36名老师参加了歌舞表演,11名老师参加了魔术杂技类表演,至少参加了两种表演的有14人,参加了三种表演的有4人,那么网校老师有多少人没有参加晚会表演?A.38B.40C.42D.466.在1至100的自然数中,既不能被3整除,又不能被4整除,还不能被7整除的数有()个。
A.42B.43C.44D.587.2011盏亮着的电灯,各有一个拉线开关控制,按顺序编号为l,2,…,2011。
将编号为3的倍数的灯的拉线各拉一下;再将编号为4的倍数的灯的拉线各拉一下,最后将编号为7的倍数的灯的拉线各拉一下。
拉完后亮着的灯数为多少盏?A.529B.862C.1126D.1195第四讲:应用题综合(★★★)解方程:19x-2(2x+3)=10-x(★★★)5年前爸爸的年龄是阳阳的6倍多5岁,现在爸爸的年龄是阳阳年龄的4倍。
那么现在阳阳多少岁?(★★★)网校给老师发洗发水和沐浴露。
且沐浴露的数量是洗发水的2倍。
如果每个老师分2瓶洗发水,就少6瓶洗发水;如果每个老师分3瓶沐浴露,则多18瓶沐浴露。
网校买来的洗发水和沐浴露各多少瓶?海海默写千字文和弟子规,千字文四字一句,弟子规三字一句。
一共默写了296个字。
其中千字文比弟子规句数的2倍少了14句。
那么海海默写了多少句千字文?佳佳、海海、阳阳共有99本课外书。
佳佳的本数除以海海的本数,海海的本数除以阳阳的本数,商都是2,而且余数也都是2。
海海有多少本课外书?一个六位数abcdef ,如果满足4abcdef fabcde ⨯=,则称为“迎春数”(如4×102564=410256,则102564就是“迎春数”)。
请你求出所有“迎春数”的总和是_________。
老师出了200道题让王亮、李涛、张清三人做。
三人每人都做对了120道,且每道题都有人做对。
如果把三人都做对的称为简单题,有两人都做对的称为中等题,只有一人做对的称为难题,那么难题比简单题多_____道。
