河北张家口市正博高级中学复数经典试题(含答案)
高中复数经典练习题(含答案)

高中复数经典练习题(含答案)一、单选题1.如图,在复平面内,复数z 对应的点为P ,则复数i=z ⋅( )A .2i -B .12i -C .1+2i -D .2i --2.已知复数2ii+=a z (a R ∈,i 是虚数单位)的虚部是3-,则复数z 对应的点在复平面的( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限3.设复数z 满足()1i 2i z -=,则z 在复平面内对应的点在第几象限.( ) A .一 B .二C .三D .四4.已知复数113i z =+的实部与复数21i z a =--的虚部相等,则实数a 等于( ) A .-3 B .3 C .-1 D .15.复数 21(1)i 1z a a =+--是实数,则实数a 的值为( ) A .1或-1 B .1 C .-1D .0或-1 6.若0a <,则a 的三角形式为( ) A .()cos0isin0a + B .()cos isin a ππ+ C .()cos isin a ππ-+ D .()cos isin a ππ-- 7.复数(sin 10°+icos 10°)(sin 10°+icos 10°)的三角形式是( )A .sin 30°+icos 30°B .cos 160°+isin 160°C .cos 30°+isin 30°D .sin 160°+icos 160°8.已知 i 是虚数单位,复数4132⎛⎫+ ⎪ ⎪⎝⎭在复平面内对应的点位于( ) A .第一象限 B .第二象限C .第三象限D .第四象限 9.复数z 满足:(2i)5z +=(i 是虚数单位),则复数z 的虚部为( ) A .2-B .2C .i -D .1-10.下列命题正确的是( )①若复数z 满足2z ∈R ,则z R ∈; ②若复数z 满足i R z∈,则z 是纯虚数;③若复数12,z z 满足12=z z ,则12=±z z ; ④若复数12,z z 满足2121z z z =且10z ≠,则12=z z .A .①③B .②④C .①④D .①③11.已知复数324i 1iz +=-,则z =( )AB C .D .12.若复数z 满足()13i 17i -=-z ,则z 在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限13.已知m 为实数,则“1m =”是“复数()211i z m m =-++为纯虚数”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件14.复数1ii+(其中i 为虚数单位)在复平面内所对应的点位于( ) A .第一象限 B .第二象限 C .第三象限D .第四象限15.下列命题正确的是( ) ①若复数z 满足2R z ∈,则R z ∈;②若复数z 满足i R z∈,则z 是纯虚数; ③若复数1z ,2z 满足12=z z ,则12=±z z ;④若复数1z ,2z 满足2121z z z =且10z ≠,则12=z z .A .①③B .②④C .①④D .②③16.2021i 1i-=( )A .11i 22+ B .11i 22-- C .11i 22-+D .11i 22-17.已知复数z 满足()21i 68i z -=+,其中i 为虚数单位,则z =( )A .10B .5 CD.18.已知复数z 满足()43i 5i z +=,则z =( ) A .1BC .15D .519.设复数1i z =-(i 是虚数单位),则复数22z z+=( ) A .1i - B .1i + C .2i + D .2i -20.若复数(32)(1)i ai +-在复平面内对应的点位于第一象限,则实数a 的取值范围为( )A .32,23⎛⎫- ⎪⎝⎭B .3,2⎛⎫-∞- ⎪⎝⎭C .23,32⎛⎫- ⎪⎝⎭D .2,3⎛⎫-∞- ⎪⎝⎭二、填空题21.已知复数z 满足()1i 42i -=+z ,则z =_________.22.设复数i 12z =+(i 是虚数单位),则在复平面内,复数2z 对应的点的坐标为________.23.已知复数z 满足()1i 42i z -=+,则z =_________(用代数式表示). 24.已知复数z 满足211iz -=+,则z 的最小值为___________; 25.复数1i z =+(其中i 为虚数单位)的共轭复数z =______.26.设复数1z ,2z 满足11z =,22z =,121z z -=,则12z z +=________. 27.设i 是虚数单位,若复数z =1+2i ,则复数z 的模为__________. 28.已知复数1i z =+,则2z z+=____________ 29.在复平面内,复数1z 和2z 对应的点分别是(21)A ,和(01)B ,,则12z z =_______. 30.定义12,C z z ∈,221212121(||||)4z z z z z z ⊕=+--,121212i(i )z z z z z z ⊗=⊕+⊕.若134i z =+,21z =+,则12||z z ⊗=___________.31.已知i 是虚数单位,复数z 满足322i z =+,则z =___________.32.已知复数2i -在复平面内对应的点为P ,复数z 满足|i |1z -=,则P 与z 对应的点Z 间的距离的最大值为________.33.已知复数z 满足()()1i 2i z t t +=∈R,若z =,则t 的值为___________. 34.设复数z =-1-i(i 为虚数单位),z 的共轭复数为z ,则2zz-=________.35.复数1077(cos isin )66ππ+表示成代数形式为________. 36.计算cos 40isin 40cos10isin10________.37.已知i 是虚数单位,则202220211()1+⎛⎫+= ⎪-⎝⎭i i i ___________.38.设复数()21(1)i m m -++为纯虚数,则实数m 的值为________.39.若复数z 满足|z -i|=3,则复数z 对应的点Z 的轨迹所围成的图形的面积为________.40.已知2i +是关于x 的方程()20,R x ax b a b ++=∈的根,则b a -=________. 三、解答题41.在①z 为虚数,②z 为纯虚数,这两个条件中任选一个作为(1)中的已知条件.已知复数()22284i z m m m =--+-(1)若___________,求满足条件的实数m ;(2)若复数()21i 8z m -++的模为m 的值42.设()22112i z m m m =+++-,()224254i z m m m =++-+,若12z z <,求实数m 的取值范围.43.若复平面内单位圆上三点所对应的复数123,,z z z ,满足22z 13z z =且23i i 0z z +-=,求复数123,,z z z .44.实数k 为何值时,复数()()223456i z k k k k =--+--是:(1)实数? (2)虚数? (3)纯虚数? (4)0?45.(1)在复数集C 中解下列方程:2490x +=; (2)已知()12i 43i z +=+,求z .【参考答案】一、单选题 1.D 2.D3.B 4.C 5.C 6.C 7.B 8.C 9.D 10.B 11.B 12.D 13.C 14.D 15.B 16.C 17.B 18.A 19.A 20.A 二、填空题21.13i +22.()34-,23.13i +##3i+1 241##1-25.1i -##i+1-262728.29.12i -##2i+1- 30.35 3132.1##1+33.2或2- 34.-1+2i##2i -135.-5i##-5i -3612i 3738.1 39.9π 40.9 三、解答题41.(1)若选择①,则 2.m ≠±;若选择②,则4m =. (2) 1.m =± 【解析】 【分析】(1)根据虚数和纯虚数的概念可求出结果; (2)根据复数的模长公式列式可求出结果. (1)若选择①,因为z 为虚数,则240m -≠,解得 2.m ≠±若选择②,因为z 为纯虚数,则2280m m --=且240m -≠,解得4m =. (2)因为()22284i z m m m =--+-,所以2222(1i)828(4)i (1i)824i,z m m m m m m -++=--+--++=--=,解得 1.m =± 42.{}1 【解析】 【分析】根据12z z <可知1z R ∈,2z R ∈,由实数定义可构造方程组求得m . 【详解】12z z <,1z R ∴∈,2z R ∈,2220540m m m m ⎧+-=∴⎨-+=⎩,解得:1m =;当1m =时,12z =,26z =,满足12z z <,m ∴的取值范围为{}1.43.答案见解析. 【解析】 【分析】根据复数的几何意义,结合复数的运算求得3z 和2z ,再结合复数的乘除运算,即可求得1z . 【详解】因为单位圆上三点所对应的复数为123,,z z z ,故可设z 1=cos α+isin α,z 2=cos β+isin β,z 3=cos γ+isin γ, 则由23i i 0z z +-=,可得cos sin 0sin cos 10βγβγ-=⎧⎨+-=⎩,利用cos 2β+sin 2β=1,解得1cos 2sin γγ⎧=⎪⎪⎨⎪=⎪⎩z 3故当z 3时,z 2=-i(z 3-1),z 1=223z z=1;当z 3时,z 2=-i(z 3-1)z 1=223z z ==1.44.(1)6k =或1k =-; (2)6k ≠且1k ≠-; (3)4k =; (4)1k =-. 【解析】 【分析】(1)解方程2560k k --=即得解; (2)解不等式2560k k --≠即得解;(3)解不等式2560k k --≠,且2340k k --=即得解; (4)解方程2560k k --=,且2340k k --=即得解. (1)解:当2560k k --=,即6k =或1k =-时,z 是实数; (2)解:当2560k k --≠,即6k ≠且1k ≠-时,z 是虚数; (3)解:当2560k k --≠,且2340k k --=,z 是纯虚数,即4k =时为纯虚数; (4)解:当2560k k --=,且2340k k --=,即1k =-时,z 是0.45.(1)3i 2x =±;(2)2i z =+. 【解析】 【分析】(1)利用直接开平方法求解即可,(2)先由已知式子求出复数z ,从而可求出其共轭复数 【详解】(1)∵2490x +=, ∴294x =-,3i 2x =±.(2)()()()()243i 12i 43i 43i 8i 6i 105i2i 12i 12i 12i 55z +-++---=====-+-+, ∴2i z =+.。
河北张家口市正博高级中学高二物理上学期精选试卷检测题

河北张家口市正博高级中学高二物理上学期精选试卷检测题一、第九章静电场及其应用选择题易错题培优(难)1.如图所示,y轴上固定有两个电荷量相等的带正电的点电荷,且关于坐标原点O对称。
某同学利用电场的叠加原理分析在两电荷连线的中垂线(x轴)上必定有两个场强最强的点A、'A,该同学在得到老师的肯定后又在此基础上作了下面的推论,你认为其中正确的是()A.若两个点电荷的位置不变,但电荷量加倍,则x轴上场强最大的点仍然在A、'A两位置B.如图(1),若保持两个点电荷的距离不变、并绕原点O旋转90°后对称的固定在z轴上,则x轴上场强最大的点仍然在A、'A两位置C.如图(2),若在yoz平面内固定一个均匀带正电圆环,圆环的圆心在原点O。
直径与(1)图两点电荷距离相等,则x轴上场强最大的点仍然在A、'A两位置D.如图(3),若在yoz平面内固定一个均匀带正电薄圆板,圆板的圆心在原点O,直径与(1)图两点电荷距离相等,则x轴上场强最大的点仍然在A、'A两位置【答案】ABC【解析】【分析】【详解】A.可以将每个点电荷(2q)看作放在同一位置的两个相同的点电荷(q),既然上下两个点电荷(q)的电场在x轴上场强最大的点仍然在A、A'两位置,两组点电荷叠加起来的合电场在x轴上场强最大的点当然还是在A、A'两位置,选项A正确;B.由对称性可知,保持两个点电荷的距离不变、并绕原点O旋转90°后对称的固定在z轴上,则x轴上场强最大的点仍然在A、'A两位置,选项B正确;C.由AB可知,在yOz平面内将两点电荷绕O点旋转到任意位置,或者将两点电荷电荷量任意增加同等倍数,在x轴上场强最大的点都在A、A'两位置,那么把带电圆环等分成一些小段,则关于O点对称的任意两小段的合电场在x轴上场强最大的点仍然还在A、A'两位置,所有这些小段对称叠加的结果,合电场在x轴上场强最大的点当然还在A、A'两位置,选项C正确;D.如同C选项,将薄圆板相对O点对称的分割成一些小块,除了最外一圈上关于O点对称的小段间距还是和原来一样外,靠内的对称小块间距都小于原来的值,这些对称小块的合电场在x轴上场强最大的点就不再在A、A'两位置,则整个圆板的合电场在x轴上场强最大的点当然也就不再在A、A'两位置,选项D错误。
高中复数经典练习题(含答案)

高中复数经典练习题(含答案)一、单选题1.复数20222i 1iz =+(其中i 为虚数单位),则z 在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限2.已知复数1i z =-,则2i z z -=( )A .2B .3C .D .3.复数(sin 10°+icos 10°)(sin 10°+icos 10°)的三角形式是( ) A .sin 30°+icos 30° B .cos 160°+isin 160° C .cos 30°+isin 30° D .sin 160°+icos 160°4.若复数(32)(1)i ai +-在复平面内对应的点位于第一象限,则实数a 的取值范围为( )A .32,23⎛⎫- ⎪⎝⎭B .3,2⎛⎫-∞- ⎪⎝⎭C .23,32⎛⎫- ⎪⎝⎭D .2,3⎛⎫-∞- ⎪⎝⎭5.在复平面中,复数z 对应的点的坐标为()1,2,则()i z z -的对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限6.已知复数12i1iz -=+(i 是虚数单位),则复数z 在复平面内对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .筹四象限7.3i3i-+=+( ) A .43i 55+ B .43i 55-+C .43i 55D .43i 55--8.设i 为虚数单位,则)10i 的展开式中含2x 的项为( )A .6210C x - B .6210C x C .8210C x -D .8210C x 9.设复数z 满足()1i 2i z -=,则z 在复平面内对应的点在第几象限.( ) A .一 B .二 C .三D .四10.复数z 满足(1i)23i z -=-,则复数z 的共轭复数z 在复平面内对应的点位于( ) A .第一象限B .第二象限C .第三象限D .第四象限11.在复平面内O 为坐标原点,复数()1i 43i z =-+,27i z =+对应的点分别为12,Z Z ,则12Z OZ ∠的大小为( )A .3πB .23π C .34π D .56π12.设i 为虚数单位,()1i 2i z -+=+,则复数z 的虚部是( ) A .12-B .1i 2C .32-D .3i 2-13.复数2i z =-(i 为虚数单位)的虚部为( ) A .2 B .1C .iD .1-14.设复数53i--的实部与虚部分别为a ,b ,则a b -=( ) A .2-B .1-C .1D .215.已知复数()()31i z m m =++-在复平面内对应的点在第四象限,则实数m 的取值范围是( ). A .()3,1- B .()1,3- C .()1,+∞ D .(),3-∞16.设复数z 满足i 1i(i z ⋅=+为虚数单位),则复数z 在复平面内所对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限17.若5i2iz =+,则||z =( )A .2B C .D .318.已知复数z 满足(34i)5(1i)z +⋅=-,则z 的虚部是( ) A .15-B .75-C .1i 5-D .7i 5-19.设a ,b ∈R ,i 为虚数单位,则“ab >0”是“复数a -b i 对应的点位于复平面上第二象限”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分又不必要条件 20.已知i 是虚数单位,复数12iiz -=,则z 的共轭复数z =( ) A .2i -- B .2i -+C .2i -D .2i +二、填空题21.甲、乙、丙、丁四人对复数z 的陈述如下(i 为虚数单位):甲:z z +=;乙:2z z -=;丙:26;:4z z z z z ⋅==丁,在甲、乙、丙、丁四人陈述中,有且只有两个人的陈述正确,则z =___________.22.设(3i)i 6i a a b +=-,其中a ,b 是实数,则i a b +=____________. 23.已知复数ππsin i cos 33z =+,则z =________.24.设复数1z ,2z 满足11z =,22z =,121z z -=,则12z z +=________. 25.设i 是虚数单位,若复数z =1+2i ,则复数z 的模为__________. 26.设12z i =-,则z =___________ .27.若复数()2i m m m -+为纯虚数,则实数m 的值为________.28.若()i 1)(,x y x x y R +=-∈,则2x y +的值为__________. 29.已知复数z 满足()1i 42i z -=+,则z =_________(用代数式表示). 30.已知复数z 满足1z =,则22z i +-的最大值为______. 31.已知i 是虚数单位,复数z 满足322i z =+,则z =___________.32.已知关于x 的方程,()()()221i i 0,,R x x ab a b a b ++++++=∈总有实数解,则a b +的取值范围是__________.33.已知复数cos isin i z θθ=+(为虚数单位),则1z -的最大值为___________ 34.把复数z 的共轭复数记作z ,已知()12i 43i z +=+(其中i 是虚数单位),则z =______.35.i 是虚数单位,则1i1i+-的值为__________.36.已知z =,则22022z z z ++⋅⋅⋅+=___________. 37.若z 1=2-i ,z 2=-12+2i ,则z 1,z 2在复平面上所对应的点为Z 1,Z 2,这两点之间的距离为________. 38.已知i 为虚数单位,复数21iz =-的虚部为___________. 39.若复数()()32i z a a R =-+-∈为实数,则2021i 1ia a -+的值为______.40.若复数2(1i)34iz +=+,则z =__________.三、解答题41.已知z 是虚数,求证:4z z+是实数的充要条件是2z =.42.已知复数(2)(3)(2)i()z m m m m =++++∈R . (1)若z 是纯虚数,求z ; (2)若i1,i(,)1z m a b a b z +=-=+∈+R ,求a ,b 的值. 43.已知复数()()211i z m m =-++,m R ∈.(1)若z 对应复平面上的点在第四象限,求m 的范围; (2)若z 是纯虚数,求m 的值.44.已知复数()224124i z m m m =--+-,其中m R ∈. (1)若z 为纯虚数,求m 的值;(2)若z 在复平面内对应的点关于虚轴对称得到的点在第一象限,求m 的取值范围.45.已知1z ,2z ∈C ,12z =,23z =,124z z +=,求12z z .(提示:()1122cos isin z z z z θθ=+或()1122cos isin z zz z θθ=-,θ是1z ,2z 所表示的向量的夹角.)【参考答案】一、单选题 1.B 2.D 3.B 4.A 5.D 6.C 7.B 8.A 9.B 10.A 11.C 12.C 13.D 14.A15.A16.D17.B18.B19.B20.B二、填空题21.222.23.124252627.128.129.13i+##3i+1 30.13132.[)2,+∞33.234.2i+##i2+ 35.136.03738.139.i-40.825i 6 25 -三、解答题41.证明见解析【解析】【分析】设()i ,,0z x y x y R y =+∈≠,由复数运算化简得2222444i x y z x y z x y x y⎛⎫⎛⎫+=++- ⎪ ⎪++⎝⎭⎝⎭;当2z =时,可得42z x R z +=∈,证得充分性;当4z z+是实数时,可得224x y +=,必要性得证;由此可得结论.【详解】设()i ,,0z x y x y R y =+∈≠, 则2222224444i 44i i i i x y x y z x y x y x y zx y x y x y x y ⎛⎫⎛⎫-+=++=++=++- ⎪ ⎪++++⎝⎭⎝⎭. 当2z =时,224x y +=,则2240y y x y -=+,2242xx x R x y +=∈+, 42z x R z ∴+=∈,即4z z+是实数,充分性成立; 当4z z+是实数时,2240yy x y-=+,又0y ≠,224x y ∴+=,即2z =,必要性成立;4z z ∴+是实数的充要条件是2z =. 42.(1)i z = (2)42,55a b == 【解析】 【分析】(1)由纯虚数的概念求解 (2)根据复数的运算法则化简 (1)因为(2)(3)(2)i z m m m =++++是纯虚数, 所以(2)(3)0,20,m m m ++=⎧⎨+≠⎩解得3m =-.所以i z =-,则i z =. (2)由1m =-,得2i z =+, 代入ii 1z a b z +=++, 得22i (22i)(3i)42i i 3i (3i)(3i)55a b ++-==+=+++-, 即42,55a b ==.43.(1)(),1m ∈-∞- (2)1m = 【解析】 【分析】(1)由题知21010m m ⎧->⎨+<⎩,再解不等式组即可;(2)由题知21010m m ⎧-=⎨+≠⎩,再解方程即可.(1)解:∵z 对应复平面上的点在第四象限,∴21010m m ⎧->⎨+<⎩,解得1m <-.∴(),1m ∈-∞- (2)解:∵z 是纯虚数,∴21010m m ⎧-=⎨+≠⎩,∴1m =44.(1)6 (2)()2,6 【解析】 【分析】(1)由z 为纯虚数,列方程组,求出m ; (2)由题意列不等式组,即可求出m 的范围. (1)因为复数()224124i z m m m =--+-,其中m R ∈,所以22412040m m m ⎧--=⎨-≠⎩,解得:m =6.(2)因为()224124i z m m m =--+-在复平面内对应的点为()22412,4m m m ---, 所以z 在复平面内对应的点关于虚轴对称得到的点()22412,4m m m -++-.由题意得:22412040m m m ⎧-++>⎨->⎩,解得:26m <<.即m 的取值范围为()2,6.45.16或16【解析】 【分析】算出1z ,2z 所表示的向量的夹角的正、余弦即可. 【详解】设复数1z 对应OA ,2z 对应OB ,OA OB OC +=,则22223431cos 223124OAC +-∠==-=-⨯⨯ 所以1cos 4AOB ∠=,所以15sin AOB ∠=所以122115115346z z ⎛⎫== ⎪ ⎪⎝⎭或121156z z =.。
河北张家口市正博高级中学任务型阅读经典试题(含答案)

一、高中英语任务型阅读1.Read the passage carefully. Fill in each blank with a proper sentence given in the box. Each sentence can be used only once. Note that there are two more sentences than you need.Many people know that trash is a big problem on planet Earth. What many people don't know is that trash has become a problem in outer space too. ________Statistically, there are more than 22,000 pieces of junk in space around the earth. And these are just the items that we can see from the surface of the earth by telescopes or radars. ________Objects, like bits of old space rockets or satellites, move around the planet at very high speeds, so fast that even a very small piece can break important satellites or become dangerous to people, particularly astronauts. If the tiniest piece of junk crashed into a spacecraft, it could damage the vehicle. That's because the faster an object moves, the greater the impact if the object collides with something else.To help minimize additional space junk, countries around the world have agreed to limit the time their space tools stay in orbit to 25 years. Each tool must be built to fall safely into the earth's atmosphere, or the mass of gases that surround the earth, after that. ________Many scientists are also proposing different ways to clean up space junk. The Germans have been planning a space mission with robots that would collect pieces of space trash and bring them back to Earth so that they can be safely destroyed."In our opinion the problem is very challenging, and it's quite urgent as well," said Marco Castronuovo, an Italian Space Agency researcher who is working to solve the problem. ________ Many of these objects are tools that help people use their cell phones or computers. "The time to act is now; as we go farther in time we will need to remove more and more fragments," he says.A. One reason that it's urgent is that countries are sending more and more objects into space.B. There are also millions of smaller pieces of junk that we can't see.C. Blowing up older satellites with a missile may create thousands of smaller pieces!D. In the upper parts of the atmosphere, it will burn up.E. When two objects in space collide, the two objects break into many smaller pieces.F. Years of space exploration have left tons of "space junk" in orbit around the planet.【答案】 F;B;D;A【解析】【分析】本文是一篇说明文,介绍太空垃圾越来越严重,急需解决。
河北张家口市正博高级中学高中生物必修一试卷及答案
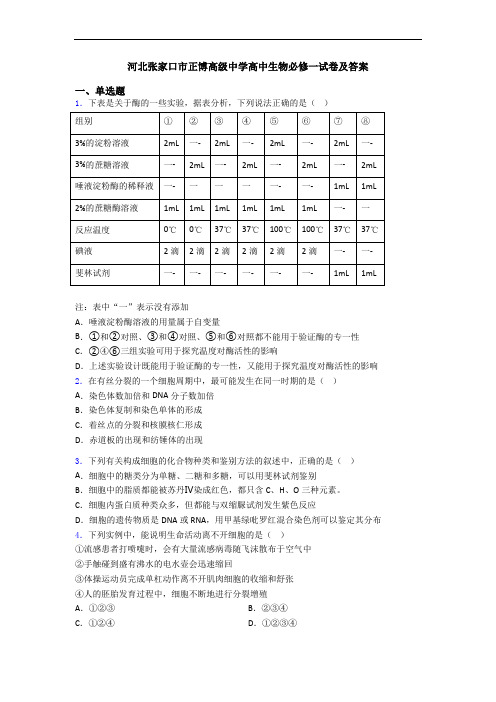
河北张家口市正博高级中学高中生物必修一试卷及答案一、单选题1.下表是关于酶的一些实验,据表分析,下列说法正确的是()注:表中“一”表示没有添加A.唾液淀粉酶溶液的用量属于自变量B.①和②对照、③和④对照、⑤和⑥对照都不能用于验证酶的专一性C.②④⑥三组实验可用于探究温度对酶活性的影响D.上述实验设计既能用于验证酶的专一性,又能用于探究温度对酶活性的影响2.在有丝分裂的一个细胞周期中,最可能发生在同一时期的是()A.染色体数加倍和DNA分子数加倍B.染色体复制和染色单体的形成C.着丝点的分裂和核膜核仁形成D.赤道板的出现和纺锤体的出现3.下列有关构成细胞的化合物种类和鉴别方法的叙述中,正确的是()A.细胞中的糖类分为单糖、二糖和多糖,可以用斐林试剂鉴别B.细胞中的脂质都能被苏丹Ⅳ染成红色,都只含C、H、O三种元素。
C.细胞内蛋白质种类众多,但都能与双缩脲试剂发生紫色反应D.细胞的遗传物质是DNA或RNA,用甲基绿吡罗红混合染色剂可以鉴定其分布4.下列实例中,能说明生命活动离不开细胞的是()①流感患者打喷嚏时,会有大量流感病毒随飞沫散布于空气中②手触碰到盛有沸水的电水壶会迅速缩回③体操运动员完成单杠动作离不开肌肉细胞的收缩和舒张④人的胚胎发育过程中,细胞不断地进行分裂增殖A.①②③B.②③④C.①②④D.①②③④5.糖类和脂质是细胞中两种重要的有机物,相关的叙述错误的是()A.胆固醇可参与构成动物细胞膜B.糖类中的淀粉、纤维素和糖原都完全由葡萄糖缩合而成C.淀粉和脂肪水解的终产物是二氧化碳和水D.质量相同的糖类和脂肪被彻底氧化分解时,糖类耗氧少6.英国医生塞达尼・任格在对离体蛙心进行的实验中发现,用不含钙和钾的生理盐水灌注蛙心,其收缩不能维持;用含有少量钙和钾的生理盐水灌注蛙心时,蛙心可持续跳动数小时。
该实验说明钙盐和钾盐()A.对维持细胞的形态有着重要作用B.是细胞中某些复杂化合物的重要组成部分C.为蛙心的持续跳动提供能量D.对维持生物体的生命活动有重要作用7.古生物学家推测:被原始真核生物吞噬的蓝藻有些未被消化,反而能依靠原始真核生物的“生活废物”制造营养物质,逐渐进化为叶绿体。
高中复数经典练习题(含答案)

高中复数经典练习题(含答案)一、单选题1.已知12z i =-,则(i)z z -的模长为( ) A .4 B .10 C .2 D .10 2.已知复数12z i =-,则z 在复平面内对应的点关于虚轴对称的点是( ) A .(1,2)-B .(1,2)C .(2,1)-D .(1,2)--3.已知复数z 满足()2i 32i +=+z 则||z =( ) A .65 B .13 C .3 D .154.复数 21(1)i 1z a a =+--是实数,则实数a 的值为( ) A .1或-1 B .1 C .-1D .0或-15.在复平面内,复数z 满足()()1i 1i ,z a b a b R +=++∈,且z 所对应的点在第一象限或坐标轴的非负半轴上,则2+a b 的最小值为( ) A .2- B .1-C .1D .26.在复平面中,复数z 对应的点的坐标为()1,2,则()i z z -的对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限7.若复数i (2i)z m m =++在复平面内对应的点在第二象限,则实数m 的取值范围是( ) A .(1,0)-B .(0,1)C .(,0)-∞D .(1,)-+∞8.如图,在复平面内,复数z 对应的点为P ,则复数i=z ⋅( )A .2i -B .12i -C .1+2i -D .2i --9.已知复数()1i z a a =-+(a ∈R ),则1a =是1z =的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件10.若复数2(1i)-的实部为a ,虚部为b ,则a b +=( ) A .3-B .2-C .2D .311.已知复数324i 1iz +=-,则z =( )A B C .D .12.2021i 1i-=( )A .11i 22+ B .11i 22-- C .11i 22-+D .11i 22-13.已知复数z 满足()21i 68i z -=+,其中i 为虚数单位,则z =( )A .10B .5C D .14.若复数z 满足1i 1i 2z +=+,则z 在复平面内所对应的点位于( ) A .第一象限B .第二象限C .第三象限D .第四象限15.已知复数z 满足()43i 5i z +=,则z =( )A .1BC .15D .516.若5i2iz =+,则||z =( ) A.2 B C .D .3 17.复数z 在复平面内对应点的坐标为(-2,4),则1z +=( )A .3B .4C D 18.“1x =”是“22(1)(32)i x x x -+++是纯虚数”的( )A .充要条件B .充分不必要条件C .必要不充分条件D .既不充分也不必要条件19.设a ,b ∈R ,i 为虚数单位,则“ab >0”是“复数a -b i 对应的点位于复平面上第二象限”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分又不必要条件20.已知复数z 满足(12i)43i z -=-(i 为虚数单位),则z =( )A B .5C D .2二、填空题21.已知复数z 为纯虚数且满足1-3z =|z |+3i ,则z =________ 22.已知复数z 满足24(1i)(12i)z --=-,则||z =________. 23.已知复数z 满足211iz -=+,则z 的最小值为___________; 24.18世纪末期,挪威测量学家威塞尔首次利用坐标平面上的点来表示复数,使复数及其运算具有了几何意义,例如,z OZ =,也即复数z 的模的几何意义为z 对应的点Z 到原点的距离,在复数平面内,复数02i1ia z +=+ (i 是虚数单位,)a R ∈是纯虚数,其对应的点为0Z ,Z 为曲线1z =上的动点,则0Z 与Z 之间的最小距离为________________.25.若复数z 满足i 2022i z ⋅=-(i 是虚数单位),则z 的虚部是___________.26.设复数1z ,2z 满足11z =,22z =,121z z -=,则12z z +=________. 27.计算:()()12i 34i 2i-+=+_________.28.化简:i 是虚数单位,复数()2021i 34i z =+=_________. 29.已知复数i 3i z =+(i 为虚数单位),则z =__________.30.已知2i +是关于x 的方程()20,R x ax b a b ++=∈的根,则b a -=________.31.若复数()()32i z a a R =-+-∈为实数,则2021i 1ia a -+的值为______.32.若复数2(1i)34iz +=+,则z =__________.33.复数121i,22i z z =+=-,则12_________.z z -=34.复数1077(cosisin )66ππ+表示成代数形式为________. 35.i 是虚数单位,则1i1i+-的值为__________. 36.方程()()2223256i 0x x x x --+-+=的实数解x =________.37.已知复数z 1=a 2-3-i ,z 2=-2a +a 2i ,若z 1+z 2是纯虚数,则实数a =________.38.若z 1=2-i ,z 2=-12+2i ,则z 1,z 2在复平面上所对应的点为Z 1,Z 2,这两点之间的距离为________. 39.已知复数2i4i ia b +=-,,R a b ∈,则a b +=______. 40.已知复数1i z =+,则2z z+=____________ 三、解答题41.实数x 取什么值时,复平面内表示复数z =x 2+x -6+(x 2-2x -15)i 的点Z :(1)位于第三象限; (2)位于第四象限;(3)位于直线x -y -3=0上.42.(1)若复数22(56)(3)i z m m m m =-++-表示实数,求实数m 的值 ;(2)若复数22(56)(3)i z m m m m =-++-表示纯虚数,求实数m 的值. 43.在复平面内,复数()22234i z a a a a =--+--(其中i 为虚数单位,R a ∈).(1)若复数z 为纯虚数,求a 的值; (2)若复数z >0,求a 的值. 44.根据要求完成下列问题:(1)已知复数1z 在复平面内对应的点在第四象限,1||1z =,且111z z +=,求1z ;(2)已知复数225(15i)3(2i)12im z m =-+-+-为纯虚数,求实数m 的值. 45.判断下列命题的真假. (1)任何复数的模都是非负数; (2)x 轴是复平面的实轴,y 轴是虚轴;(3)若1z =,2z =,3z =42i z =-,则这些复数的对应点共圆; (4)cos isin θθ+,最小值为0.【参考答案】一、单选题 1.B 2.D 3.A 4.C 5.B 6.D 7.A 8.D 9.A10.B11.B12.C13.B14.D15.A16.B17.C18.A19.B20.A二、填空题21.i22.2231##1-24.1 25.2022-2627.43i-##3i4-+ 28.-4+3i##3i-42930.931.i-32.825i 6 25 -3334.-5i##-5i-35.136.237.33839.640.三、解答题41.(1)-3<x <2 (2)2<x <5 (3)x =-2 【解析】 【分析】根据复数的几何意义即可求解. (1)当实数x 满足22602150x x x x ⎧+-<⎨--<⎩,即-3<x <2时,点Z 位于第三象限; (2)当实数x 满足22602150x x x x ⎧+->⎨--<⎩,即2<x <5时,点Z 位于第四象限; (3)当实数x 满足(x 2+x -6)-(x 2-2x -15)-3=0,即3x +6=0,x =-2时,点Z 位于直线x -y -3=0上;综上,(1)()3,2x ∈- ,(2)()2,5x ∈ ,(3)2x =- . 42.(1)0m =或3;(2)2m = 【解析】 【分析】(1)由虚部为0直接求解即可;(2)由实部为0,虚部不为0直接求解即可. 【详解】(1)由复数22(56)(3)i z m m m m =-++-表示实数,可得230m m -=,解得0m =或3;(2)由复数22(56)(3)i z m m m m =-++-表示纯虚数,可得2256030m m m m ⎧-+=⎨-≠⎩,解得2m =. 43.(1)2a = (2)4a = 【解析】 【分析】(1)根据纯虚数的知识列式,从而求得a 的值. (2)根据复数能比较大小列式,从而求得a 的值.(1)由于z 为纯虚数,所以2220340a a a a ⎧--=⎨--≠⎩,可得2a =.(2)由于z 与0可以比较大小,所以z 为实数,且0z >,所以2220340a a a a ⎧-->⎨--=⎩,可得4a =.44.(1)112z = (2)2m =- 【解析】 【分析】(1)设1i z a b =+,由题设可得关于,a b 的方程组,求出其解后可得1z . (2)根据复数的四则运算可求2z ,根据其为纯虚数可求实数m 的值. (1)设1i z a b =+(a b R ∈、),由题意得22121a b a ⎧+=⎨=⎩,解得12a =,b =∵复数1z 在复平面内对应的点在第四象限,∴b =112z =; (2)()()()()2222515i 32i 6253i 12im z m m m m m =-+-+=--+---,依题意得260m m --=,解得3m =或2m =-, 又∵22530m m --≠,∴3m ≠且12m ≠-, ∴2m =-. 45.(1)真命题; (2)真命题; (3)真命题; (4)假命题; 【解析】 【分析】由复数模长公式判断(1),由复平面的定义判断(2),根据复数的模长判断(3),由模长计算公式求解cos isin θθ+,判断(4). (1)真命题,若()i ,z a b a b R =+∈,则0z =≥,故该命题为真命题; (2)真命题,由复平面的定义可知,x 轴是实轴,y 轴是虚轴,故该命题为真命题; (3)真命题,因为3124z z z z ===(4)假命题,cos isin 1θθ+==为定值,所以其最大最小值均为1,故该命题为假命题.。
高中复数经典练习题(含答案)

高中复数经典练习题(含答案)一、单选题 1.复数1ii+(其中i 为虚数单位)在复平面内所对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限 2.设复数z 满足()1i 2i z -=,则z 在复平面内对应的点在第几象限.( )A .一B .二C .三D .四3.若0a <,则a 的三角形式为( )A .()cos0isin0a +B .()cos isin a ππ+C .()cos isin a ππ-+D .()cos isin a ππ-- 4.复数(sin 10°+icos 10°)(sin 10°+icos 10°)的三角形式是( )A .sin 30°+icos 30°B .cos 160°+isin 160°C .cos 30°+isin 30°D .sin 160°+icos 160°5.向量1OZ ,2OZ ,分别对应非零复数z 1,z 2,若1OZ ⊥2OZ ,则12Z Z 是( ) A .负实数 B .纯虚数C .正实数D .虚数a +b i(a ,b ∈R ,a ≠0) 6.设||(12i)34i z -=+,则z 的共轭复数对应的点在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限 7.设复数z 满足i 3i z z --=,则z 的虚部为( ) A .2i -B .2iC .2-D .28.下列命题正确的是( )①若复数z 满足2z ∈R ,则z R ∈; ②若复数z 满足i R z∈,则z 是纯虚数;③若复数12,z z 满足12=z z ,则12=±z z ; ④若复数12,z z 满足2121z z z =且10z ≠,则12=z z .A .①③B .②④C .①④D .①③9.已知复数()1i z a a =-+(a ∈R ),则1a =是1z =的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件 10.已知m 为实数,则“1m =”是“复数()211i z m m =-++为纯虚数”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件11.复数1i1i+-(i 为虚数单位)的共轭复数的虚部等于( ) A .1B .1-C .iD .i -12.已知复数23i z =-,则()1i z +=( ) A .3i - B .3+3i -C .3i +D .3i -+13.如果1i12z =-,那么在复平面内,复数z 所对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限 14.已知i 为虚数单位,则复数1i -+在复平面内对应的点位于( ) A .第一象限 B .第二象限C .第三象限D .第四象限15.已知复数()()31i z m m =++-在复平面内对应的点在第四象限,则实数m 的取值范围是( ). A .()3,1- B .()1,3- C .()1,+∞ D .(),3-∞16.设复数z 满足i 1i(i z ⋅=+为虚数单位),则复数z 在复平面内所对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限17.若复数4i1iz =-,则复数z 的模等于( ) AB .2C .D .418.已知z1,z 2∈C ,|z 1+z 2|=|z 1|=2,|z 2|=2,则|z 1-z 2|等于( ) A .1 B .12 C .2D .19.设a ,b ∈R ,i 为虚数单位,则“ab >0”是“复数a -b i 对应的点位于复平面上第二象限”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分又不必要条件20.复数20222i 1iz =+(其中i 为虚数单位),则z 在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限二、填空题 21.已知23iz-=-i ,则复数z =________. 22.若i(,)i+∈a b a b R 与3+4i 互为共轭复数,则a b -=___________. 23.若i 为虚数单位,复数3i z =+,则表示复数1iz+的点在第_______象限.24.设复数1z ,2z 满足11z =,22z =,121z z -=,则12z z +=________. 25.若()1i 1i z +=-,则z =_______26.已知2i +是关于x 的方程()20,R x ax b a b ++=∈的根,则b a -=________.27.若复数()2i m m m -+为纯虚数,则实数m 的值为________.28.若()i 1)(,x y x x y R +=-∈,则2x y +的值为__________. 29.若复数31i 2iz a -=-为实数,则实数a 的值为_______.30.已知复数z 满足()1i 42i -=+z ,则z =_________.31.设i 为虚数单位,则复数2(1i)1i+-=____.32.设复数z =-1-i(i 为虚数单位),z 的共轭复数为z ,则2zz-=________. 33.复数1515cos77isin ππ+的辐角主值是________.34.已知复数12,z z ,满足121z z ==,且12z z +=,则12z z =________.35.已知i 是虚数单位,则202220211()1+⎛⎫+= ⎪-⎝⎭i i i ___________.36.已知z =,则22022z z z ++⋅⋅⋅+=___________. 37.已知复数z 满足2i z +∈R ,4zz-是纯虚数,则z 的共轭复数z =______. 38.设i 是虚数单位,复数z =,则z =___________. 39.已知复数2i4i ia b +=-,,R a b ∈,则a b +=______. 40.已知复数z 为纯虚数且满足1-3z =|z |+3i ,则z =________ 三、解答题41.已知i 为虚数单位,实数m 分别取什么数值时,复数()22(1)iz m m m =+-+-满足下列条件:(1)纯虚数;(2)复平面内对应的点在直线y x =上.42.设复数z =log 2(m 2-3m -3)+ilog 2(m -2)(m ∈R ),对应的向量为OZ .(1)若OZ 的终点Z 在虚轴上,求实数m 的值及|OZ |; (2)若OZ 的终点Z 在第二象限内,求m 的取值范围.43.已知复数()()211i z a a a R =-++∈.(1)若复数z 是虚数,求实数a 的值; (2)若复数z 是纯虚数,求实数a 的值. 44.已知复数()()()2i 1i 24i z a a a R =--+++∈.(1)若z 在复平面中所对应的点在直线0x y -=上,求a 的值; (2)求2i 7iz --的取值范围.45.已知复数()()211i z m m =-++,m R ∈.(1)若z 对应复平面上的点在第四象限,求m 的范围; (2)若z 是纯虚数,求m 的值.【参考答案】一、单选题 1.D 2.B 3.C 4.B 5.B 6.D 7.C 8.B 9.A 10.C 11.B 12.B14.B15.A16.D17.C18.D19.B20.B二、填空题21.3+2i22.123.四2425.i26.927.128.129.2-30.13i+31.1i-+32.-1+2i##2i-1π33.734.1-23536.037.22i+##2i2+38.39.640.i三、解答题41.(1)2m=-【解析】 【分析】(1)实部为0,虚部不为0即可; (2)实部等于虚部即可得解. (1)由已知22010m m m ⎧+-=⎨-≠⎩解得211m m m =-=⎧⎨≠⎩或 2m =-所以(2)由已知212m m m -=+-21m =1m =±42.(1)m =4,|1OZ =(2)342m ⎛⎫∈ ⎪⎪⎝⎭. 【解析】 【分析】(1)显然是复数z 的实部为0,即可求解; (2)z 的实部为负数,虚部为正数即可. (1)因为OZ 的终点z 在虚轴上,所以复数z 的实部为0, 则有log 2(m 2-3m -3)=0,所以m 2-3m -3=1, 所以m =4或m =-1; 因为20m -> ,所以m =4, 此时z =i ,()0,1OZ =,1OZ = ; (2)因为OZ 的终点Z 在第二象限内,则有()()2222log 330log 2033020m m m m m m ⎧--<⎪⎪->⎨-->⎪⎪->⎩4m << ,所以4m ⎫∈⎪⎪⎝⎭43.(1)1a ≠-; (2)1. 【解析】 【分析】(1)根据虚数的概念求解即可;(2)根据纯虚数的概念由虚部不为0,实部为0建立关系式求解即可. (1)因为()()211i z a a a R =-++∈是虚数,所以10a +≠,解得1a ≠-, (2)因为()()211i z a a a R =-++∈是纯虚数,所以21010a a ⎧-=⎨+≠⎩,解得1a =.44.(1)4a =(2)⎫+∞⎪⎪⎣⎭【解析】 【分析】(1)首先根据复数代数形式的乘法运算化简复数z ,即可得到复数在复平面内所对应的点的坐标,最后代入直线方程,即可求出a ;(2)根据复数代数形式的除法运算化简2i 7iz --,再根据复数模的计算公式及二次函数的性质计算可得; (1)解:因为复数()()()2i 1i 24i z a a a R =--+++∈,所以()222i i i 24i 326i z a a a a a =-+-+++=-++,所以z 在复平面内对应的点为()32,6a a -+,因为在复平面内对应的点在直线0x y -=上,即为()3260a a --+=,解得4a =;(2) 解:由[]()232(6)i i 32(6)i2i 72i 72i 7(6)32i 2i 713i i i i a a z a a a a a a -++-++--=--=--=+----=--所以2i 713i iza a --=--==所以当且仅当110a =2i 7i z --的取值范围是⎫+∞⎪⎪⎣⎭45.(1)(),1m ∈-∞- (2)1m = 【解析】 【分析】(1)由题知21010m m ⎧->⎨+<⎩,再解不等式组即可;(2)由题知21010m m ⎧-=⎨+≠⎩,再解方程即可.(1)解:∵z 对应复平面上的点在第四象限,∴21010m m ⎧->⎨+<⎩,解得1m <-.∴(),1m ∈-∞- (2)解:∵z 是纯虚数,∴21010m m ⎧-=⎨+≠⎩,∴1m =。
高中复数经典练习题(含答案)

高中复数经典练习题(含答案)一、单选题1.复数z 满足(1i)23i z -=-,则复数z 的共轭复数z 在复平面内对应的点位于( ) A .第一象限B .第二象限C .第三象限D .第四象限2.已知复数z 满足()2i 32i +=+z 则||z =( )AB C D 3.设集合A 实数 ,{}B =纯虚数,{}C =复数,若全集SC ,则下列结论正确的是( ) A .AB C =B .A B =C .()S A B ⋂=∅D .SSABC4.已知a R ∈,“实系数一元二次方程2904x ax ++=的两根都是虚数”是“存在复数z 同时满足2z =且1z a +=”的( )条件. A .充分非必要 B .必要非充分 C .充分必要 D .既非充分又非必要 5.复数(sin 10°+icos 10°)(sin 10°+icos 10°)的三角形式是( )A .sin 30°+icos 30°B .cos 160°+isin 160°C .cos 30°+isin 30°D .sin 160°+icos 160° 6.在复平面内,复数z 满足()1i 3i z -=-+,则复数z 对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限7.复数z 满足()12i z =,i 为虚数单位,则复数z 的虚部为( )A .BC .D 8.下列命题:①若i 0a b +=,则0a b ;②i 22i 2x y x y +=+⇔==;③若y R ∈,且()()211i 0y y ---=,则1y =.其中正确命题的个数为( )A .0个B .1个C .2个D .3个9.已知复数13i z a =-,22i z =+(i 为虚数单位),若12z z 是纯虚数,则实数=a ( )A .32-B .32C .6-D .610.已知i 是虚数单位,复数12iiz -=,则z 的共轭复数z =( ) A .2i --B .2i -+C .2i -D .2i +11.设O 为原点,向量OA ,OB 对应的复数分别为2+3i ,-3-2i ,那么向量BA 对应的复数为( )A .-1+iB .1-iC .-5-5iD .5+5i 12.已知复数z 满足(12i)43i z -=-(i 为虚数单位),则z =( )AB .5CD .213.设z 的共轭复数是z ,若4i z z -=,8z z ⋅=,则z =( )A .22i --B .22i +C .22i -+D .22i +或22i -+ 14.若复数z 在复平面内对应的点为(1,1),则其共轭复数z 的虚部是( ) A .i B .i - C .1 D .1- 15.若复数2(1i)-的实部为a ,虚部为b ,则a b +=( )A .3-B .2-C .2D .316.已知复数z 满足()21i 24i z -=-,其中i 为虚数单位,则复数z 的虚部为( ) A .2 B .1C .2-D .i17.若5i2iz =+,则||z =( )A.2 B C .D .318.“1x =”是“22(1)(32)i x x x -+++是纯虚数”的( )A .充要条件B .充分不必要条件C .必要不充分条件D .既不充分也不必要条件 19.已知复数z 满足z +2i -5=7-i ,则|z |=( )A .12B .3C .D .920.已知复数z 满足i 232i z z +=-(i 为虚数单位),则z 在复平面内对应的点位于( ) A .第一象限 B .第二象限C .第三象限D .第四象限二、填空题21.已知复数z 满足294i z z +=+,则z =___________. 22.已知复数z 满足24(1i)(12i)z --=-,则||z =________.23.设复数1z ,2z 是共轭复数,且12229i,-=-+z z ,则1z =___________. 24.设i 为虚数单位,若复数(1i)(i)a -+的实部与虚部相等,其中a 是实数,则|1i |-+=a ________.25.18世纪末期,挪威测量学家威塞尔首次利用坐标平面上的点来表示复数,使复数及其运算具有了几何意义,例如,z OZ =,也即复数z 的模的几何意义为z 对应的点Z 到原点的距离,在复数平面内,复数02i1ia z +=+ (i 是虚数单位,)a R ∈是纯虚数,其对应的点为0Z ,Z 为曲线1z =上的动点,则0Z 与Z 之间的最小距离为________________. 26.复数2ii 1+-的共轭复数是_______. 27.已知复数3i (2i)z =⋅-,则z 的虚部为__________.28.若复数()2(2)9i()z m m m R =++-∈是正实数,则实数m 的值为________.29.在复平面内,复数1z 和2z 对应的点分别是(21)A ,和(01)B ,,则12zz=_______. 30.设复数1z ,2z 满足11z =,22z =,121z z -=,则12z z +=________.31.设i 为虚数单位,则复数2(1i)1i+-=____.32.设z C ∈,且1i 0z z +--=,则i z +的最小值为________. 33.已知复数z =(,a b ∈R 且0,0a b ≠≠)的模等于1,则12b a b++的最小值为______.34.已知复数z 满足()1i 42i -=+z ,则z =_________.35.设复数()21(1)i m m -++为纯虚数,则实数m 的值为________.36.已知m R ∈,复平面内表示复数()3i m m --的点位于第三象限内,则m 的取值范围是____________ 37.i 是虚数单位,则1i1i+-的值为__________. 38.若z 1=2-i ,z 2=-12+2i ,则z 1,z 2在复平面上所对应的点为Z 1,Z 2,这两点之间的距离为________. 39.已知i 是虚数单位,复数12iiz -=,则z 的共轭复数z =___________. 40.若复数2iiz -=-,则z =_______. 三、解答题41.定义运算ab ad bc c d=-,如果()()32i 3i 1x y x y x y++++=-,求实数x ,y 的值.42.已知复数()2i z a =+,i 43w =-其中a 是实数,(1)若在复平面内表示复数z 的点位于第一象限,求a 的范围; (2)若zw是纯虚数,a 是正实数, ①求a ,②求232023z z z z w w w w ⎛⎫⎛⎫⎛⎫+++⋅⋅⋅+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭43.已知向量OZ 与实轴正向的夹角为45,向量OZ 对应的复数z 的模为1,求z .44.已知复数()()2224i z m m m =--+-(其中,m R ∈,i 为虚数单位)在①0z >;②z 为纯虚数;③z 的实部与虚部相等.这三个条件中任选一个,补充在下面问题中,并解答问题. (1)若______,求实数m 的值;(2)若复数2(1i)1z m -++的模为5,求实数m 的值.45.设222215(6)i 4a a z a a a +-=--+-(R a ∈),试判断复数z 能否为纯虚数?并说明理由.【参考答案】一、单选题 1.A 2.A 3.D 4.D 5.B 6.C 7.D 8.B 9.A 10.B 11.D12.A13.D14.D15.B16.B17.B18.A19.C20.A二、填空题21.522.2232425.126.13i-+22 27.-228.329.12i-##2i+1-3031.1i-+32. 33.734.13i+35.10,3 36.() 37.13839.2i-+ 40.12i-三、解答题41.1x =-,2y = 【解析】 【分析】根据题意得到()()()3i 32i x y x x y y +++=++,列出方程组求解即可. 【详解】 由定义运算ab ad bc c d=-,得32i 32i 1x y x y y y+=++-,所以()()()3i 32i x y x x y y +++=++ 因为x ,y 为实数,所以有323x y x yx y+=+⎧⎨+=⎩,解得1x =-,2y =.42.(1)1a > (2)①2; ②1-. 【解析】 【分析】(1)化简复数212i z a a =-+,根据复数z 在第一象限,列出不等式组,即可求解;(2)化简复数()()22464383i25a a a a zω--++-=,由zw是纯虚数,求得2a =,化简得到i zω=,结合虚数单位的性质,即可求解.(1)解:由题意,复数()22i 12i z a a a =+=-+,因为复数z 在第一象限,可得21020a a ⎧->⎨>⎩,解得1a >.(2)解:由题意,复数()()()()()()()()2222222i i 43i i i 43i 43i43i 43i 43i a a a a zω++++++===--+- ()()()2222223464383i 48i 4i 3i 6i 3i 16925a a a a a a a a --++-+++++==--,因为zw 是纯虚数,则2246403830a a a a ⎧--=⎨+-≠⎩,解得2a =或12a =-,又因为a 是正实数,则2a =,当2a =时,复数224648i 3i 3i 16i 12i 3ii 2525za a a a ω--++-+-===, 因为41i i n +=,42i 1n +=-,43i i n +=-,4i 1n =,n N ∈,所2320232334202i i i i i zz z z ωωωω⎛⎫⎛⎫⎛⎫+++⋅⋅⋅+=++++⋅⋅⋅+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭()()()4678202122352023022i i i i i i i i i i i =++++++++⋅⋅⋅+++()00i i 11=+++--=-.43.z =或z = 【解析】 【分析】由题,OZ 与实轴正向的夹角为45,故OZ 可能在第一象限或第四象限,设出Z 的坐标,结合OZ 对应的复数z 的模为1列式,即可求解. 【详解】由题,向量OZ 与实轴正向的夹角为45,故OZ 在第一象限或第四象限,设点Z 的坐标为(,)a b ,则0a >,b a =,又1z =,故可解得a b ==b =,所以z =+或z =. 44.(1)选①, 2m =-; 选②, 1m =-; 选③, 2m =; (2)2m =或4m =-. 【解析】 【分析】(1)选①根据题意知复数为正实数,由实部大于0,虚部等于0列出式子求解,选②根据纯虚数知实部为0,虚部不为0求解,选③由实部虚部相等列方程求解;(2)化简复数,根据复数的模列出方程求解. (1)若选①,因为0z >,则222040m m m ⎧-->⎨-=⎩,解得2m =-;若选②,因为z 为纯虚数,则222040m m m ⎧--=⎨-≠⎩,解得1m =-;若选③,因为z 的实部与虚部相等,则2224m m m --=-,解得2m =. (2)因为()()22222(1i)124i i+1=(1)4i z m m m m m m m -++=--+------,5=, 解得2m =或4m =-.45.不存在a 使复数z 为纯虚数,理由见解析 【解析】 【分析】先假设复数z能为纯虚数,则可得260a a--=且222154a aa+-≠-,然后求解,若a存在,则复数z能为纯虚数,否则不能【详解】假设复数z能为纯虚数,则222260215440a aa aaa⎧--=⎪+-⎪≠⎨-⎪-≠⎪⎩,所以325,3,2,2a aa a a a==-⎧⎨≠-≠≠≠-⎩或且且且,解得a∈∅,所以不存在a使复数z为纯虚数.。
复数经典试题(含答案)doc

一、复数选择题1.已知复数1z i =+,则21z+=( )A .2BC .4D .52.复数21i=+( ) A .1i --B .1i -+C .1i -D .1i +3.在复平面内,复数534ii-(i 为虚数单位)对应的点的坐标为( ) A .()3,4B .()4,3-C .43,55⎛⎫- ⎪⎝⎭D .43,55⎛⎫- ⎪⎝⎭4.若复数z 为纯虚数,且()373z i m i -=+,则实数m 的值为( ) A .97- B .7 C .97D .7-5.已知复数31iz i -=,则z 的虚部为( ) A .1 B .1- C .i D .i - 6.复数z 满足12i z i ⋅=-,z 是z 的共轭复数,则z z ⋅=( )A B C .3D .57.设2iz i+=,则||z =( )A B C .2 D .58.已知复数z 满足22z z =,则复数z 在复平面内对应的点(),x y ( ) A .恒在实轴上 B .恒在虚轴上C .恒在直线y x =上D .恒在直线y x=-上9.若复数()41i 34iz +=+,则z =( )A .45B .35C .25D .510.在复平面内,复数z 对应的点为(,)x y ,若22(2)4x y ++=,则( ) A .22z += B .22z i +=C .24z +=D .24z i +=11.122ii-=+( ) A .1B .-1C .iD .-i12.设21iz i+=-,则z 的虚部为( ) A .12B .12- C .32 D .32-13.设复数z 满足(1)2i z -=,则z =( )A .1 BC D .214.若复数11iz i,i 是虚数单位,则z =( ) A .0 B .12C .1D .215.题目文件丢失!二、多选题16.已知复数Z 在复平面上对应的向量(1,2),OZ =-则( ) A .z =-1+2iB .|z |=5C .12z i =+D .5z z ⋅=17.下面是关于复数21iz =-+的四个命题,其中真命题是( )A .||z =B .22z i =C .z 的共轭复数为1i -+D .z 的虚部为1-18.(多选题)已知集合{},nM m m i n N ==∈,其中i 为虚数单位,则下列元素属于集合M 的是( ) A .()()11i i -+ B .11ii-+ C .11ii+- D .()21i -19.复数z 满足233232iz i i+⋅+=-,则下列说法正确的是( )A .z 的实部为3-B .z 的虚部为2C .32z i =-D .||z =20.若复数z 满足()1z i i +=,则( )A .1z i =-+B .z 的实部为1C .1z i =+D .22z i =21.已知i 为虚数单位,复数322iz i+=-,则以下真命题的是( ) A .z 的共轭复数为4755i - B .z 的虚部为75i C .3z =D .z 在复平面内对应的点在第一象限22.已知复数1z =-+(i 为虚数单位),z 为z 的共轭复数,若复数zw z=,则下列结论正确的有( )A .w 在复平面内对应的点位于第二象限B .1w =C .w 的实部为12-D .w 23.下列结论正确的是( )A .已知相关变量(),x y 满足回归方程ˆ9.49.1yx =+,则该方程相应于点(2,29)的残差为1.1B .在两个变量y 与x 的回归模型中,用相关指数2R 刻画回归的效果,2R 的值越大,模型的拟合效果越好C .若复数1z i =+,则2z =D .若命题p :0x R ∃∈,20010x x -+<,则p ⌝:x R ∀∈,210x x -+≥24.已知1z ,2z 为复数,下列命题不正确的是( ) A .若12z z =,则12=z z B .若12=z z ,则12z z =C .若12z z >则12z z >D .若12z z >,则12z z >25.任何一个复数z a bi =+(其中a 、b R ∈,i 为虚数单位)都可以表示成:()cos sin z r i θθ=+的形式,通常称之为复数z 的三角形式.法国数学家棣莫弗发现:()()()n cos sin co i s s nn nz i n r i r n n N θθθθ+==+⎡⎤⎣∈⎦+,我们称这个结论为棣莫弗定理.根据以上信息,下列说法正确的是( ) A .22z z = B .当1r =,3πθ=时,31z =C .当1r =,3πθ=时,12z =D .当1r =,4πθ=时,若n 为偶数,则复数n z 为纯虚数26.下面四个命题,其中错误的命题是( ) A .0比i -大 B .两个复数当且仅当其和为实数时互为共轭复数C .1x yi i +=+的充要条件为1x y ==D .任何纯虚数的平方都是负实数 27.给出下列命题,其中是真命题的是( ) A .纯虚数z 的共轭复数是z -B .若120z z -=,则21z z =C .若12z z +∈R ,则1z 与2z 互为共轭复数D .若120z z -=,则1z 与2z 互为共轭复数28.(多选)()()321i i +-+表示( ) A .点()3,2与点()1,1之间的距离 B .点()3,2与点()1,1--之间的距离 C .点()2,1到原点的距离D .坐标为()2,1--的向量的模29.已知i 为虚数单位,下列命题中正确的是( ) A .若x ,y ∈C ,则1x yi i +=+的充要条件是1x y == B .2(1)()a i a +∈R 是纯虚数C .若22120z z +=,则120z z == D .当4m =时,复数22lg(27)(56)m m m m i --+++是纯虚数 30.设复数z 满足12z i =--,i 为虚数单位,则下列命题正确的是( )A .|z |=B .复数z 在复平面内对应的点在第四象限C .z 的共轭复数为12i -+D .复数z 在复平面内对应的点在直线2y x =-上【参考答案】***试卷处理标记,请不要删除一、复数选择题 1.B 【分析】先求出,再计算出模. 【详解】 , , . 故选:B. 解析:B 【分析】先求出21z +,再计算出模. 【详解】1z i =+,()()()21221112111i i z i i i -∴+=+=+=-++-,21z∴+==.2.C【分析】根据复数的除法运算法则可得结果. 【详解】.故选:C解析:C【分析】根据复数的除法运算法则可得结果.【详解】2 1i =+2(1)(1)(1)ii i-=+-2(1)12ii-=-.故选:C3.D【分析】运用复数除法的运算法则化简复数的表示,最后选出答案即可. 【详解】因为,所以在复平面内,复数(为虚数单位)对应的点的坐标为.故选:D解析:D【分析】运用复数除法的运算法则化简复数534ii-的表示,最后选出答案即可.【详解】因为55(34)15204334(34)(34)2555i i i iii i i⋅+-===-+--+,所以在复平面内,复数534ii-(i为虚数单位)对应的点的坐标为43,55⎛⎫-⎪⎝⎭.故选:D4.B【分析】先求出,再解不等式组即得解. 【详解】依题意,,因为复数为纯虚数,故选:B 【点睛】易错点睛:复数为纯虚数的充要条件是且,不要只写.本题不能只写出,还要写上.解析:B 【分析】先求出321795858m m z i -+=+,再解不等式组3210790m m -=⎧⎨+≠⎩即得解.【详解】 依题意,()()()()3373321793737375858m i i m i m m z i i i i +++-+===+--+, 因为复数z 为纯虚数, 故3210790m m -=⎧⎨+≠⎩,解得7m =.故选:B 【点睛】易错点睛:复数(,)z a bi a b R =+∈为纯虚数的充要条件是0a =且0b ≠,不要只写0b ≠.本题不能只写出790m +≠,还要写上3210m -=.5.B 【分析】化简复数,可得,结合选项得出答案. 【详解】则,的虚部为 故选:B解析:B 【分析】化简复数z ,可得z ,结合选项得出答案. 【详解】()311==11i iz i i i i i--=-=+- 则1z i =-,z 的虚部为1- 故选:B6.D 【分析】求出复数,然后由乘法法则计算.由题意, . 故选:D .解析:D 【分析】求出复数z ,然后由乘法法则计算z z ⋅. 【详解】 由题意12122i z i i i-==-+=--, 22(2)(2)(2)5z z i i i ⋅=---+=--=.故选:D .7.B 【分析】利用复数的除法运算先求出,再求出模即可. 【详解】 , . 故选:B .解析:B 【分析】利用复数的除法运算先求出z ,再求出模即可. 【详解】()22212i i i z i i i++===-,∴z ==故选:B .8.A 【分析】先由题意得到,然后分别计算和,再根据得到关于,的方程组并求解,从而可得结果. 【详解】由复数在复平面内对应的点为得,则,, 根据得,得,.所以复数在复平面内对应的点恒在实轴上, 故【分析】先由题意得到z x yi =+,然后分别计算2z 和2z ,再根据22z z =得到关于x ,y 的方程组并求解,从而可得结果. 【详解】由复数z 在复平面内对应的点为(),x y 得z x yi =+,则2222z x y xyi =-+,222z x y =+,根据22z z =得222220x y x y xy ⎧-=+⎨=⎩,得0y =,x ∈R .所以复数z 在复平面内对应的点(),x y 恒在实轴上, 故选:A .9.A 【分析】首先化简复数,再计算求模. 【详解】 , . 故选:A解析:A 【分析】首先化简复数z ,再计算求模. 【详解】()()()2242112434343434i i i z i i i i⎡⎤++⎣⎦====-++++ ()()()()43443412163434252525i i i i i --=-=-=-++-,45z ∴==.故选:A10.B 【分析】利用复数模的计算公式即可判断出结论. 【详解】因为复数对应的点为,所以 ,满足则 故选:B解析:B 【分析】利用复数模的计算公式即可判断出结论. 【详解】因为复数z 对应的点为(,)x y ,所以z x yi =+x ,y 满足22(2)4x y ++=则22z i +=故选:B11.D 【分析】利用复数的除法求解. 【详解】 . 故选:D解析:D 【分析】利用复数的除法求解. 【详解】()()()()12212222i i i i i i i ---==-++-. 故选:D12.C 【分析】根据复数的除法运算,先化简复数,即可得出结果. 【详解】 因为, 所以其虚部为. 故选:C.解析:C 【分析】根据复数的除法运算,先化简复数,即可得出结果. 【详解】 因为()()()()21223113111222i i i i z i i i i ++++-====+--+,所以其虚部为32. 故选:C.13.B 【分析】由复数除法求得,再由模的运算求得模. 【详解】 由题意,∴. 故选:B .解析:B 【分析】由复数除法求得z ,再由模的运算求得模. 【详解】由题意22(1)11(1)(1)i z i i i i +===+--+,∴z == 故选:B .14.C 【分析】由复数除法求出,再由模计算. 【详解】 由已知, 所以. 故选:C .解析:C 【分析】由复数除法求出z ,再由模计算. 【详解】由已知21(1)21(1)(1)2i i iz i i i i ---====-++-, 所以1z i =-=. 故选:C .15.无二、多选题 16.AD【分析】因为复数Z 在复平面上对应的向量,得到复数,再逐项判断.【详解】因为复数Z 在复平面上对应的向量,所以,,|z|=,,故选:AD解析:AD【分析】因为复数Z 在复平面上对应的向量(1,2)OZ =-,得到复数12z i =-+,再逐项判断.【详解】因为复数Z 在复平面上对应的向量(1,2)OZ =-,所以12z i =-+,12z i =--,|z 5z z ⋅=,故选:AD17.ABCD【分析】先根据复数的除法运算计算出,再依次判断各选项.【详解】,,故A 正确;,故B 正确;的共轭复数为,故C 正确;的虚部为,故D 正确; 故选:ABCD.【点睛】本题考查复数的除法解析:ABCD【分析】先根据复数的除法运算计算出z ,再依次判断各选项.【详解】()()()2121111i z i i i i --===---+-+--,z ∴==,故A 正确;()2212z i i =--=,故B 正确;z 的共轭复数为1i -+,故C 正确;z 的虚部为1-,故D 正确;故选:ABCD.【点睛】本题考查复数的除法运算,以及对复数概念的理解,属于基础题.18.BC【分析】根据集合求出集合内部的元素,再对四个选项依次化简即可得出选项.根据题意,中,时,;时,;时,;时,,.选项A 中,;选项B 中,;选项C 中,;选项D 中,.解析:BC【分析】根据集合求出集合内部的元素,再对四个选项依次化简即可得出选项.【详解】 根据题意,{},n M m m i n N ==∈中, ()4n k k N =∈时,1n i =;()41n k k N =+∈时,n i i =;()42n k k N =+∈时,1n i =-;()43n k k N =+∈时,n i i =-,{}1,1,,M i i ∴=--.选项A 中,()()112i i M -+=∉;选项B 中,()()()211111i i i i i i M --==-+-∈+; 选项C 中,()()()211111i i i i i i M ++==-+∈-; 选项D 中,()212i i M -=-∉.故选:BC.【点睛】此题考查复数的基本运算,涉及复数的乘方和乘法除法运算,准确计算才能得解. 19.AD【分析】由已知可求出,进而可求出实部、虚部、共轭复数、复数的模,进而可选出正确答案.解:由知,,即,所以的实部为,A 正确;的虚部为-2,B 错误;,C 错误;,D 正确;故选:A解析:AD【分析】由已知可求出32z i =--,进而可求出实部、虚部、共轭复数、复数的模,进而可选出正确答案.【详解】 解:由233232i z i i +⋅+=-知,232332i z i i +⋅=--,即()()()2233232232313i i i z i i ---=-=+ 39263213i i --==--,所以z 的实部为3-,A 正确;z 的虚部为-2,B 错误;32z i =-+,C 错误;||z ==D 正确; 故选:AD.【点睛】 本题考查了复数的除法运算,考查了复数的概念,考查了共轭复数的求解,考查了复数模的求解,属于基础题.20.BC【分析】先利用复数的运算求出复数z ,然后逐个分析判断即可【详解】解:由,得,所以z 的实部为1,,,故选:BC【点睛】此题考查复数的运算,考查复数的模,考查复数的有关概念,考查共轭 解析:BC【分析】先利用复数的运算求出复数z ,然后逐个分析判断即可【详解】解:由()1z i i +=,得2(1)2(1)11(1)(1)2i i z i i i i --====-++-, 所以z 的实部为1,1z i =+,22z i =-,故选:BC【点睛】此题考查复数的运算,考查复数的模,考查复数的有关概念,考查共轭复数,属于基础题21.AD【分析】先利用复数的除法、乘法计算出,再逐项判断后可得正确的选项.【详解】,故,故A 正确.的虚部为,故B 错,,故C 错,在复平面内对应的点为,故D 正确.故选:AD.【点睛】本题考解析:AD【分析】先利用复数的除法、乘法计算出z ,再逐项判断后可得正确的选项.【详解】()()32232474725555i i i i i z i ++++====+-,故4755i z =-,故A 正确.z 的虚部为75,故B 错,355z ==≠,故C 错, z 在复平面内对应的点为47,55⎛⎫ ⎪⎝⎭,故D 正确. 故选:AD.【点睛】本题考查复数的概念、复数的运算以及复数的几何意义,注意复数(),z a bi a b R =+∈的虚部为b ,不是bi ,另外复数的除法运算是分子分母同乘以分母的共轭复数.22.ABC【分析】对选项求出,再判断得解;对选项,求出再判断得解;对选项复数的实部为,判断得解;对选项,的虚部为,判断得解.【详解】对选项由题得.所以复数对应的点为,在第二象限,所以选项正确解析:ABC【分析】对选项,A 求出1=2w -+,再判断得解;对选项B ,求出1w =再判断得解;对选项,C 复数w 的实部为12-,判断得解;对选项D ,w 判断得解. 【详解】对选项,A 由题得1,z =-221=422w -+∴===-+.所以复数w 对应的点为1(2-,在第二象限,所以选项A 正确;对选项B ,因为1w ==,所以选项B 正确; 对选项,C 复数w 的实部为12-,所以选项C 正确;对选项D ,w 的虚部为2,所以选项D 错误. 故选:ABC【点睛】 本题主要考查复数的运算和共轭复数,考查复数的模的计算,考查复数的几何意义,考查复数的实部和虚部的概念,意在考查学生对这些知识的理解掌握水平.23.ABD【分析】根据残差的计算方法判断A ,根据相关指数的性质判断B ,根据复数的模长公式判断C ,根据否定的定义判断D.【详解】当时,,则该方程相应于点(2,29)的残差为,则A 正确;在两个变量解析:ABD【分析】根据残差的计算方法判断A ,根据相关指数的性质判断B ,根据复数的模长公式判断C ,根据否定的定义判断D.【详解】当2x =时,ˆ9.429.127.9y=⨯+=,则该方程相应于点(2,29)的残差为2927.9 1.1-=,则A 正确;在两个变量y 与x 的回归模型中,2R 的值越大,模型的拟合效果越好,则B 正确;1z i =-,z ==C 错误;由否定的定义可知,D 正确;故选:ABD【点睛】本题主要考查了残差的计算,求复数的模,特称命题的否定,属于中档题.24.BCD【分析】根据两个复数之间不能比较大小,得到C 、D 两项是错误的,根据复数的定义和复数模的概念,可以断定A 项正确,B 项错误,从而得到答案.【详解】因为两个复数之间只有等与不等,不能比较大小解析:BCD【分析】根据两个复数之间不能比较大小,得到C 、D 两项是错误的,根据复数的定义和复数模的概念,可以断定A 项正确,B 项错误,从而得到答案.【详解】因为两个复数之间只有等与不等,不能比较大小,所以C 、D 两项都不正确;当两个复数的模相等时,复数不一定相等, 比如11i i -=+,但是11i i -≠+,所以B 项是错误的;因为当两个复数相等时,模一定相等,所以A 项正确;故选:BCD.【点睛】该题考查的是有关复数的问题,涉及到的知识点有两个复数之间的关系,复数模的概念,属于基础题目.25.AC【分析】利用复数的三角形式与模长公式可判断A 选项的正误;利用复数的棣莫弗定理可判断B 选项的正误;计算出复数,可判断C 选项的正误;计算出,可判断D 选项的正误.【详解】对于A 选项,,则,可得解析:AC【分析】利用复数的三角形式与模长公式可判断A 选项的正误;利用复数的棣莫弗定理可判断B 选项的正误;计算出复数z ,可判断C 选项的正误;计算出4z ,可判断D 选项的正误.【详解】对于A 选项,()cos sin z r i θθ=+,则()22cos2sin 2z r i θθ=+,可得()222cos 2sin 2z r i r θθ=+=,()222cos sin z r i r θθ=+=,A 选项正确;对于B 选项,当1r =,3πθ=时,()33cos sin cos3sin3cos sin 1z i i i θθθθππ=+=+=+=-,B 选项错误;对于C 选项,当1r =,3πθ=时,1cos sin 332z i ππ=+=+,则12z =,C 选项正确;对于D 选项,()cos sin cos sin cos sin 44n n n n z i n i n i ππθθθθ=+=+=+, 取4n =,则n 为偶数,则4cos sin 1z i ππ=+=-不是纯虚数,D 选项错误.故选:AC.【点睛】本题考查复数的乘方运算,考查了复数的模长、共轭复数的运算,考查计算能力,属于中等题.26.ABC【分析】根据虚数不能比大小可判断A 选项的正误;利用特殊值法可判断B 选项的正误;利用特殊值法可判断C 选项的正误;利用复数的运算可判断D 选项的正误.【详解】对于A 选项,由于虚数不能比大小,解析:ABC【分析】根据虚数不能比大小可判断A 选项的正误;利用特殊值法可判断B 选项的正误;利用特殊值法可判断C 选项的正误;利用复数的运算可判断D 选项的正误.【详解】对于A 选项,由于虚数不能比大小,A 选项错误;对于B 选项,()()123i i ++-=,但1i +与2i -不互为共轭复数,B 选项错误; 对于C 选项,由于1x yi i +=+,且x 、y 不一定是实数,若取x i =,y i =-,则1x yi i +=+,C 选项错误;对于D 选项,任取纯虚数()0,ai a a R ≠∈,则()220ai a =-<,D 选项正确. 故选:ABC.【点睛】本题考查复数相关命题真假的判断,涉及共轭复数的概念、复数相等以及复数的计算,属于基础题.27.AD【分析】A .根据共轭复数的定义判断.B.若,则,与关系分实数和虚数判断.C.若,分可能均为实数和与的虚部互为相反数分析判断.D.根据,得到,再用共轭复数的定义判断.【详解】A .根据共轭解析:AD【分析】A .根据共轭复数的定义判断.B.若120z z -=,则12z z =,1z 与2z 关系分实数和虚数判断.C.若12z z +∈R ,分12,z z 可能均为实数和1z 与2z 的虚部互为相反数分析判断.D. 根据120z z -=,得到12z z =,再用共轭复数的定义判断.【详解】A .根据共轭复数的定义,显然是真命题;B .若120z z -=,则12z z =,当12,z z 均为实数时,则有21z z =,当1z ,2z 是虚数时,21≠z z ,所以B 是假命题;C .若12z z +∈R ,则12,z z 可能均为实数,但不一定相等,或1z 与2z 的虚部互为相反数,但实部不一定相等,所以C 是假命题;D. 若120z z -=,则12z z =,所以1z 与2z 互为共轭复数,故D 是真命题.故选:AD【点睛】本题主要考查了复数及共轭复数的概念,还考查了理解辨析的能力,属于基础题. 28.ACD【分析】由复数的模的意义可判断选项A,B ;整理原式等于,也等于,即可判断选项C,D【详解】由复数的几何意义,知复数,分别对应复平面内的点与点,所以表示点与点之间的距离,故A 说法正确,B解析:ACD【分析】由复数的模的意义可判断选项A,B ;整理原式等于2i +,也等于2i --,即可判断选项C,D【详解】由复数的几何意义,知复数32i +,1i +分别对应复平面内的点()3,2与点()1,1,所以()()321i i +-+表示点()3,2与点()1,1之间的距离,故A 说法正确,B 说法错误;()()3212i i i +-+=+,2i +可表示点()2,1到原点的距离,故C 说法正确;()()()()3211322i i i i i +-+=+-+=--,2i --可表示表示点()2,1--到原点的距离,即坐标为()2,1--的向量的模,故D 说法正确,【点睛】本题考查复数的几何意义,考查复数的模29.BD【分析】选项A :取,满足方程,所以错误;选项B :,恒成立,所以正确;选项C :取,,,所以错误;选项D :代入,验证结果是纯虚数,所以正确.【详解】取,,则,但不满足,故A 错误;,恒成解析:BD【分析】选项A :取x i =,y i =-满足方程,所以错误;选项B :a ∀∈R ,210a +>恒成立,所以正确;选项C :取1z i =,21z =,22120z z +=,所以错误;选项D :4m =代入 22lg(27)(56)m m m m i --+++,验证结果是纯虚数,所以正确.【详解】取x i =,y i =-,则1x yi i +=+,但不满足1x y ==,故A 错误;a ∀∈R ,210a +>恒成立,所以2(1a i +)是纯虚数,故B 正确;取1z i =,21z =,则22120z z +=,但120z z ==不成立,故C 错误; 4m =时,复数2212756=42g m m m m i i --+++()()是纯虚数,故D 正确.故选:BD .【点睛】本题考查复数有关概念的辨析,特别要注意复数的实部和虚部都是实数,解题时要合理取特殊值,属于中档题.30.AC【分析】根据复数的模、复数对应点的坐标、共轭复数等知识,选出正确选项.【详解】,A 正确;复数z 在复平面内对应的点的坐标为,在第三象限,B 不正确;z 的共轭复数为,C 正确;复数z 在复平面内对【分析】根据复数的模、复数对应点的坐标、共轭复数等知识,选出正确选项.【详解】||z ==A 正确;复数z 在复平面内对应的点的坐标为(1,2)--,在第三象限,B 不正确;z 的共轭复数为12i -+,C 正确;复数z 在复平面内对应的点(1,2)--不在直线2y x =-上,D 不正确.故选:AC【点睛】本小题主要考查复数的有关知识,属于基础题.。
河北省张家口市正博高级中学2019-2020学年高三英语模拟试题含解析

河北省张家口市正博高级中学2019-2020学年高三英语模拟试题含解析一、选择题1. Upon arriving home, Lily found that her husband _____ a beautiful candlelight dinner.A. had preparedB. is preparingC. has preparedD. would prepare参考答案:A【详解】考查时态。
句意:一到家Lily就发现她的丈夫已经准备好了一桌美丽的烛光晚宴。
根据题干可知Lily回家时发现使用了一般过去时(found),她的丈夫准备好一桌美丽的烛光晚宴应发生在Lily到家之前。
故应用过去完成时(had done)。
故答案选A。
2. All the people who were in the room when the watch was stolen must ______ being searched.A. refer toB. submit toC. objectto D. take to参考答案:B略3. Unlike watching TV, reading is a highly active process _________ it requires attention as well as memory and imagination.A. untilB. althoughC. unlessD. for参考答案:D考查连词。
句意:阅读不同于看电视,它是一个(思维)高度活跃的过程,因为它不仅需要专注还需要记忆和想象。
由此可知前后是因果关系,因此用for。
4. Though it’s a challenging job, he did it it took me.A. one-third a timeB. one-third timeC. the one-third timeD. one-third the time参考答案:D5. _____ on a clear day, far from the city crowds, the mountains gave him a sense of peace.A. If walkingB. While walkingC. WalkingD. When he was walking参考答案:D6. People all think it strange that the boy should tell what’s written on the paper in another room without looking at it. It really ________ explanation.A. preventsB. challengesC. interruptsD. confuses参考答案:B7. -What about inviting Tracy to host the party?-Good idea! She is very quick in mind. Oh, _______, here she comes.A. don’t pull my legB. a little bird told meC. speak of the devilD. it’s a piece of cake参考答案:C【详解】考查习惯表达辨析。
河北省张家口市正博高级中学2021-2022学年高三英语期末试题含解析

河北省张家口市正博高级中学2021-2022学年高三英语期末试题含解析一、选择题1. This house is big enough for us two __, but we'll have to move if we have a baby.A. for a momentB. in a momentC. for the momentD. on the moment参考答案:D2. The most exciting moment during the Spring Festival is _____ the family enjoy the big dinner together.A. whatB. whyC. whichD. when参考答案:D本题考察名从。
横线前有be 动词,说明主句不完整少表语,从句主谓宾结构齐全,不缺少成分,但需要补充句子含义,句义和时间相关,因此选择D 选项。
【翻译】春节最让人兴奋的时刻就是家人团聚分享大餐的时间。
3. Scientists will find alternative energy to run our cars and homes before oil is_______.A. died outB. run overC. used upD. broken up参考答案:C略4. I’ve always _____ Bill for his courage and determination.A. looked up toB. lived up toC. faced up toD. added up to参考答案:A5. It was between 1830 and 1835 ______ the modern newspaper was born.A howB thatC whichD because参考答案:B略6. ____________ to go out alone, the retired minister had to go for a walk with several policemen following him.A.Warning notB. Warned notC. Not warningD. Not warned参考答案:B7. ------You’ve left the light on.------Oh, so I have. _____________to turn it off.A. I’ll goB. I’ve goneC. I goD. I’m going参考答案:A8. It is said that the old coins ______ under the earth for about 100years by the time they were discovered.A. had buriedB. had been buriedC.buried D. were buried参考答案:B9. Shooting, as __________ means of survival originally, developed into _____ sport only in the late 19th century.A. a; aB. the; theC. a; theD. the; a参考答案:A10. I felt so bad all day yesterday that I decided this morning I couldn’t face ________ day like that.A. otherB. anotherC. the otherD. others参考答案:B解析:本题考查与other 相关的单词的区别,由题意知:我昨天一整天感到很糟糕,以至于我今天早晨决定我不会面对那样的一天。
河北张家口市正博高级中学期末精选单元综合测试(Word版 含答案)

河北张家口市正博高级中学期末精选单元综合测试(Word 版 含答案)一、第一章 运动的描述易错题培优(难)1.雨滴从高空由静止开始下落,由于空气阻力作用,其加速度逐渐减小,直到变为零(整个过程其加速度方向不变),在此过程中雨滴的运动情况是( ) A .速度一直保持不变B .速度不断增大,加速度为零时,速度最大C .速度不断减小,加速度为零时,速度最小D .速度的变化率越来越小 【答案】BD 【解析】 【分析】根据加速度的方向与速度方向的关系,判断雨滴的速度是增大还是减小,速度的变化率等于加速度,结合加速度的变化判断速度的变化率变化. 【详解】A 、B 、C 、雨滴下落过程中,加速度方向与速度方向相同,加速度减小,速度仍然增大,当加速度减小为零,雨滴做匀速直线运动,此时速度达到最大,故A 错误,B 正确,C 错误.D 、速度的变化率等于加速度,加速度减小,则速度的变化率减小,故D 正确. 故选BD. 【点睛】解决本题的关键知道当加速度方向与速度方向相同,雨滴做加速运动,当加速度方向与雨滴方向相反,雨滴做减速运动.2.一个质点做变速直线运动的v-t 图像如图所示,下列说法中正确的是A .第1 s 内与第5 s 内的速度方向相反B .第1 s 内的加速度大于第5 s 内的加速度C .OA 、AB 、BC 段的加速度大小关系是BC OA AB a a a >>D .OA 段的加速度与速度方向相同,BC 段的加速度与速度方向相反 【答案】CD 【解析】 【分析】 【详解】A .第1s 内与第5s 内的速度均为正值,方向相同,故A 错误;B .第1 s 内、第5 s 内的加速度分别为:2214m/s 2m/s 2a == 22504m/s 4m/s 1a -==- 1a 、5a 的符号相反,表示它们的方向相反,第1s 内的加速度小于于第5 s 内的加速度,故B 错误;C .由于AB 段的加速度为零,故三段的加速度的大小关系为:BC OA AB a a a >>故C 正确;D .OA 段的加速度与速度方向均为正值,方向相同;BC 段的加速度为负值,速度为正值,两者方向相反,故D 正确; 故选CD 。
高考数学压轴专题张家口备战高考《复数》知识点总复习含解析

新数学《复数》试卷含答案一、选择题1.已知复数i z x y =+(x ,y ∈R),且2z +=1y x -的最大值为( ) ABC.2+D.2【答案】C【解析】【分析】根据模长公式,求出复数z 对应点的轨迹为圆,1y x -表示(,)x y 与(0,1)连线的斜率,其最值为过(0,1)点与圆相切的切线斜率,即可求解.【详解】∵复数i z x y =+(x ,y ∈R),且2z +==()2223x y ++=. 设圆的切线l :1y kx =+=化为2420k k --=,解得2k =∴1y x-的最大值为2 故选:C.【点睛】 本题考查复数的几何意义、轨迹方程、斜率的几何意义,考查数形结合思想,属于中档题.2.在复平面内,若复数z 满足|z +1|=|1+i z |,则z 在复平面内对应点的轨迹是( ) A .直线B .圆C .椭圆D .抛物线【答案】A【解析】【分析】设()z x yi x y R =+∈、,代入11z iz +=+,求模后整理得z 在复平面内对应点的轨迹是直线.【详解】设()z x yi x y R =+∈、,1x yi ++=,()11iz i x yi +=++=y x =-,所以复数z x yi =+对应点的轨迹为直线,故选A.【点睛】本题考查复数的代数表示法及其几何意义,考查复数模的求法,动点的轨迹问题,是基础题.3.已知复数z 的模为2,则z i -的最大值为:( )A .1B .2CD .3 【答案】D【解析】 因为z i -213z i ≤+-=+= ,所以最大值为3,选D. 4.若z C ∈且342z i ++≤,则1z i --的最大和最小值分别为,M m ,则M m -的值等于( )A .3B .4C .5D .9 【答案】B【解析】【分析】根据复数差的模的几何意义可得复数z 在复平面上对应的点的轨迹,再次利用复数差的模的几何意义得到,M m ,从而可得M m -的值.【详解】因为342z i ++≤,故复数z 在复平面上对应的点P 到134z i =--对应的点A 的距离小于或等于2, 所以P 在以()3,4C --为圆心,半径为2的圆面内或圆上,又1z i --表示P 到复数21z i =+对应的点B 的距离,故该距离的最大值为222AB +==,最小值为22AB -=,故4M m -=.故选:B.【点睛】本题考查复数中12z z -的几何意义,该几何意义为复平面上12,z z 对应的两点之间的距离,注意12z z +也有明确的几何意义(可把12z z +化成()12z z --),本题属于中档题.5.已知i 是虚数单位,则131i i+=+( )A .2i -B .2i +C .2i -+D .2i --【答案】B【解析】【分析】 利用复数的除法运算计算复数的值即可.【详解】由复数的运算法则有:13(13)(1)422(1)(11)2i i i i i i i i ++-+===++-+. 故选B .【点睛】对于复数的乘法,类似于多项式的四则运算,可将含有虚数单位i 的看作一类同类项,不含i 的看作另一类同类项,分别合并即可;对于复数的除法,关键是分子分母同乘以分母的共轭复数,解题中要注意把i 的幂写成最简形式.6.在复平面内,已知复数z 对应的点与复数2i --对应的点关于实轴对称,则z i =( ) A .12i -B .12i +C .12i -+D .12i -- 【答案】B【解析】【分析】由已知求得z ,代入z i,再由复数代数形式的乘除运算化简得答案. 【详解】由题意,2z i =-+, 则22(2)()12z i i i i i i i-+-+-===+-. 故选:B .【点睛】 本题考查复数代数形式的乘除运算,考查复数的基本概念,是基础题.7.已知i 为虚数单位,,a b ∈R ,复数12i i a bi i+-=+-,则a bi -=( )A .1255i - B .1255i + C .2155i - D .21i 55+ 【答案】B【解析】【分析】 由复数的除法运算,可得(1)(2)12(2)(2)55i i i i i i a b i=+++-=--+,即可求解a b i -,得到答案.【详解】 由题意,复数12i i a bi i+-=+-,得(1)(2)1312(2)(2)555i i a b i=i i i i i i ++++-=-=--+, 所以1255a b i=i -+,故选B . 【点睛】 本题主要考查了复数的运算,其中解答中熟记复数的基本运算法则,准确化简是解答的关键,着重考查了推理与运算能力,属于基础题.8.已知复数z 满足(1)43z i i +=-,其中i 是虚数单位,则复数z 在复平面中对应的点到原点的距离为( )AB.2 C .52 D .54【答案】B【解析】【分析】利用复数的除法运算化简z, 复数z 在复平面中对应的点到原点的距离为||,z 利用模长公式即得解.【详解】由题意知复数z 在复平面中对应的点到原点的距离为||,z43(43)(1)1717,12222||i i i i z i i z ----====-+∴== 故选:B【点睛】本题考查了复数的除法运算,模长公式和几何意义,考查了学生概念理解,数学运算,数形结合的能力,属于基础题.9.设复数21i x i =-(i 是虚数单位),则112233202020202020202020202020C x C x C x C x +++⋅⋅⋅+=( )A .1i +B .i -C .iD .0【答案】D【解析】【分析】 先化简1x +,再根据所求式子为2020(1)1x +-,从而求得结果.【详解】 解:复数2(1i x i i=-是虚数单位), 而1122332020202020202020202020202020(1)1C x C x C x C x x +++⋯+=+-, 而2121(1)111(1)(1)i i i i x i i i i i -++++====--+-, 故11223320202020202020202020202020202020(1)11110C x C x C x C x x i +++⋯+=+-=-=-=, 故选:D .【点睛】本题主要考查复数的乘除法运算、二项式定理的应用,属于中档题.10.若复数z 满足2(12)1i z z +=+,则其共轭复数z 为( )A .1188i +B .1188i -+C .1188i --D .1188i - 【答案】B【解析】【分析】 计算得到18i z --=,再计算共轭复数得到答案. 【详解】 21111(12)1,,44888i i z z z z i i --+=+∴===-+-Q . 故选:B .【点睛】本题考查了复数的化简,共轭复数,意在考查学生的计算能力.11.设3i z i +=,i 是虚数单位,则z 的虚部为( ) A .1B .-1C .3D .-3【答案】D【解析】因为z=3i i+13i =-∴z 的虚部为-3,选D.12.复数z 满足(2)1i z i -=+,那么||z =( )A .5B .15C .25D 【答案】D【解析】【分析】 化简得到1355z i =+,再计算复数模得到答案. 【详解】(2)1i z i -=+,∴1(1)(2)13255i i i i z i ++++===-,∴1355z i =+,∴||z =. 故选:D .【点睛】 本题考查了复数的运算,复数模,意在考查学生的计算能力.13.若复数1a i z i +=-,且3·0z i >,则实数a 的值等于( ) A .1B .-1C .12D .12- 【答案】A【解析】【分析】由3·0z i >可判定3·z i 为实数,利用复数代数形式的乘除运算化简复数z ,再由实部为0,且虚部不为0列式求解即可.【详解】 ()()()()()i 1i 11i i 1i 1i 1i 2a a a a z ++-+++===--+Q , 所以3·z i =()()()()341i 1i 1i 122a a a a -++--++=,因为3·0z i >,所以3·z i 为实数,102a --= 可得1a =,1a =时3,?10z i =>,符合题意,故选A. 【点睛】复数是高考中的必考知识,主要考查复数的概念及复数的运算.要注意对实部、虚部的理解,掌握纯虚数、共轭复数、复数的模这些重要概念,复数的运算主要考查除法运算,通过分母实数化转化为复数的乘法,运算时特别要注意多项式相乘后的化简,防止简单问题出错,造成不必要的失分.14.如果复数z 满足336z i z i ++-=,那么1z i ++的最小值是( )A .1B C .2 D 【答案】A【解析】 分析:先根据已知336z i z i ++-=找到复数z 对应的点Z 的轨迹,再利用数形结合求 1z i ++的最小值.详解:设复数z 对应的点Z(x,y),6=,它表示点Z 到A (0,-3)和B (0,3)的距离和为6,所以点Z 的轨迹为线段AB,因为1z i ++Z 到点C (-1,-1)的距离,所以当点Z 在点D(0,-1)时,它和点C (-1,-1)的距离最小,且这个最小距离为1. 故答案为:A点睛:(1)本题主要考查复数的几何意义,意在考查学生对这些知识的掌握水平和数形结合的思想方法.(2)z a bi ++表示复数z 对应的点到(-a,-b )的距离,类似这样的结论还有一些,大家要结合直角坐标理解它的几何意义,并做到能利用它解题.15.设复数z a bi =+(i 为虚数单位,,a b ∈R ),若,a b 满足关系式2a b t =-,且z 在复平面上的轨迹经过三个象限,则t 的取值范围是( )A .[0,1]B .[1,1]-C .(0,1)(1,)⋃+∞D .(1,)-+∞【答案】C【解析】【分析】首先根据复数的几何意义得到z 的轨迹方程2x y t =-,再根据指数函数的图象,得到关于t 的不等式,求解.【详解】由复数的几何意义可知,设复数对应的复平面内的点为(),x y ,2a x a y b t=⎧⎨==-⎩ ,即2x y t =- , 因为z 在复平面上的轨迹经过三个象限,则当0x =时,11t -< 且10t -≠ ,解得0t >且1t ≠ ,即t 的取值范围是()()0,11,+∞U .故选:C【点睛】本题考查复数的几何意义,以及轨迹方程,函数图象,重点考查数形结合分析问题的能力,属于基础题型.16.复数52i -的共轭复数是( ) A .2i + B .2i -C .2i -+D .2i -- 【答案】C【解析】【分析】 先化简复数代数形式,再根据共轭复数概念求解.【详解】 因为522i i =---,所以复数52i -的共轭复数是2i -+,选C. 【点睛】本题考查复数运算以及共轭复数概念,考查基本求解能力.17.已知下列三个命题:①若复数z 1,z 2的模相等,则z 1,z 2是共轭复数;②z 1,z 2都是复数,若z 1+z 2是虚数,则z 1不是z 2的共轭复数;③复数z 是实数的充要条件是z z =.则其中正确命题的个数为( )A .0个B .1个C .2个D .3个【答案】C【解析】【分析】运用复数的模、共轭复数、虚数等知识对命题进行判断.【详解】对于①中复数1z 和2z 的模相等,例如1=1+z i ,2z ,则1z 和2z 是共轭复数是错误的;对于②1z 和2z 都是复数,若12+z z 是虚数,则其实部互为相反数,则1z 不是2z 的共轭复数,所以②是正确的;对于③复数z 是实数,令z a =,则z a =所以z z =,反之当z z =时,亦有复数z 是实数,故复数z 是实数的充要条件是z z =是正确的.综上正确命题的个数是2个.故选C【点睛】本题考查了复数的基本概念,判断命题是否正确需要熟练掌握基础知识,并能运用举例的方法进行判断,本题较为基础.18.已知复数z 满足()11z i i +=-,则z = ( )A .iB .1C .i -D .1-【答案】B【解析】 ()()1i 1i z +=-,则()()()21i 1i 2i 1i 1i 1i 2z ---====-++-i ,1z ∴=,故选B.19.已知方程()()2440x i x ai a R ++++=∈有实根b ,且z a bi =+,则复数z 等于( )A .22i -B .22i +C .22i -+D .22i --【答案】A【解析】【详解】由b 是方程()()2440x i x ai a R ++++=∈的根可得()2440b i b ai ++++=, 整理可得:()()2440b a i b b ++++=, 所以20440b a b b +=⎧⎨++=⎩,解得22a b =⎧⎨=-⎩,所以22z i =-,故选A . 20.已知i 是虚数单位,则2331i i i -⎛⎫-= ⎪+⎝⎭( ) A .32i --B .33i --C .24i -+D .22i -- 【答案】B【解析】【分析】根据虚数单位i 的性质以及复数的基本运算法则,直接计算化简.【详解】()()()22231i 3i 3i i i 12i i 33i 1i 2轾--骣-÷犏ç-=+=-+=--÷ç÷犏ç桫+臌 故选B.【点睛】本题考查复数代数形式的混合运算.除法中关键是分子分母同乘以分母的共轭复数,实现分母实数化.。
河北省张家口市复数练习题(有答案) 百度文库

一、复数选择题1.复数()1z i i =⋅+在复平面上对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限2.i =( )A .i -B .iC i -D i3.已知复数()2m m m i z i --=为纯虚数,则实数m =( )A .-1B .0C .1D .0或1 4.212ii +=-( )A .1B .−1C .i -D .i5.已知i 为虚数单位,若复数()12iz a R a i +=∈+为纯虚数,则z a +=( )A B .3 C .5 D .6.满足313i z i ⋅=-的复数z 的共扼复数是( )A .3i -B .3i --C .3i +D .3i -+7.若(1)2z i i -=,则在复平面内z 对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限8.已知复数z 的共轭复数212iz i -=+,i 是虚数单位,则复数z 的虚部是( )A .1B .-1C .iD .i -9.已知复数1z i =+,z 为z 的共轭复数,则()1z z ⋅+=( )A B .2 C .10 D10.复数112z i =+,21z i =+(i 为虚数单位),则12z z ⋅虚部等于( ). A .1- B .3 C .3i D .i -11.3( )A .i -B .iC .iD .i -12.复数12z i =-(其中i 为虚数单位),则3z i +=( )A .5BC .2D 13.若复数()()1i 3i a +-(i 为虚数单位)的实部和虚部互为相反数,则实数a =( )A .1-B .12-C .13D .114.已知i 是虚数单位,设11i z i ,则复数2z +对应的点位于复平面( ) A .第一象限 B .第二象限C .第三象限D .第四象限 15.设复数满足(12)i z i +=,则||z =( )A .15BCD .5二、多选题16.已知复数202011i z i+=-(i 为虚数单位),则下列说法错误的是( )A .z 的实部为2B .z 的虚部为1C .z i =D .||z =17.已知复数z 满足220z z +=,则z 可能为( ).A .0B .2-C .2iD .2i+1-18.下面是关于复数21i z =-+的四个命题,其中真命题是( )A .||z =B .22z i =C .z 的共轭复数为1i -+D .z 的虚部为1-19.已知复数12z =-+(其中i 为虚数单位,,则以下结论正确的是( ). A .20zB .2z z =C .31z =D .1z = 20.下面是关于复数21i z =-+(i 为虚数单位)的命题,其中真命题为( ) A .||2z =B .22z i =C .z 的共轭复数为1i +D .z 的虚部为1- 21.复数z 满足233232i z i i+⋅+=-,则下列说法正确的是( )A .z 的实部为3-B .z 的虚部为2C .32z i =-D .||z =22.下列说法正确的是( )A .若2z =,则4z z ⋅=B .若复数1z ,2z 满足1212z z z z +=-,则120z z =C .若复数z 的平方是纯虚数,则复数z 的实部和虛部相等D .“1a ≠”是“复数()()()211z a a i a R =-+-∈是虚数”的必要不充分条件23.已知复数1z =-+(i 为虚数单位),z 为z 的共轭复数,若复数z w z=,则下列结论正确的有( ) A .w 在复平面内对应的点位于第二象限 B .1w =C .w 的实部为12-D .w 的虚部为2i 24.下列结论正确的是( )A .已知相关变量(),x y 满足回归方程ˆ9.49.1yx =+,则该方程相应于点(2,29)的残差为1.1B .在两个变量y 与x 的回归模型中,用相关指数2R 刻画回归的效果,2R 的值越大,模型的拟合效果越好C .若复数1z i =+,则2z =D .若命题p :0x R ∃∈,20010x x -+<,则p ⌝:x R ∀∈,210x x -+≥25.已知复数122,2z i z i =-=则( )A .2z 是纯虚数B .12z z -对应的点位于第二象限C .123z z +=D .12z z =26.已知复数z 满足(2i)i z -=(i 为虚数单位),复数z 的共轭复数为z ,则( )A .3||5z =B .12i 5z +=-C .复数z 的实部为1-D .复数z 对应复平面上的点在第二象限 27.(多选)()()321i i +-+表示( )A .点()3,2与点()1,1之间的距离B .点()3,2与点()1,1--之间的距离C .点()2,1到原点的距离D .坐标为()2,1--的向量的模28.对任意1z ,2z ,z C ∈,下列结论成立的是( )A .当m ,*n N ∈时,有m n m n z z z +=B .当1z ,2zC ∈时,若22120z z +=,则10z =且20z = C .互为共轭复数的两个复数的模相等,且22||||z z z z ==⋅D .12z z =的充要条件是12=z z29.设复数z 满足12z i =--,i 为虚数单位,则下列命题正确的是( )A .|z |=B .复数z 在复平面内对应的点在第四象限C .z 的共轭复数为12i -+D .复数z 在复平面内对应的点在直线2y x =-上30.已知复数i z a b =+(a ,b ∈R ,i 为虚数单位),且1a b +=,下列命题正确的是( ) A .z 不可能为纯虚数B .若z 的共轭复数为z ,且z z =,则z 是实数C .若||z z =,则z 是实数D .||z 可以等于12【参考答案】***试卷处理标记,请不要删除一、复数选择题1.B【分析】先利用复数的乘法化简复数z ,再利用复数的几何意义求解.【详解】因为复数,所以在复数z 复平面上对应的点位于第二象限故选:B解析:B【分析】先利用复数的乘法化简复数z ,再利用复数的几何意义求解.【详解】因为复数()11z i i i =⋅+=-+,所以在复数z 复平面上对应的点位于第二象限故选:B2.B【分析】由复数除法运算直接计算即可.【详解】.故选:B.解析:B【分析】由复数除法运算直接计算即可.【详解】()21i i i+==-. 故选:B. 3.C【分析】结合复数除法运算化简复数,再由纯虚数定义求解即可【详解】解析:因为为纯虚数,所以,解得,故选:C.解析:C【分析】结合复数除法运算化简复数z ,再由纯虚数定义求解即可【详解】解析:因为()()22m m m iz m m mi i --==--为纯虚数,所以200m m m ⎧-=⎨≠⎩,解得1m =,故选:C.4.D【分析】利用复数的除法运算即可求解.【详解】,故选:D解析:D【分析】利用复数的除法运算即可求解.【详解】()()()()2221222255121212145i i i i i i i i i i i +++++====--+-, 故选:D5.A【分析】根据复数运算,化简后由纯虚数的概念可求得,.进而求得复数,再根据模的定义即可求得【详解】由复数为纯虚数,则,解得则 ,所以,所以故选:A解析:A【分析】根据复数运算,化简后由纯虚数的概念可求得a ,.进而求得复数z ,再根据模的定义即可求得z a +【详解】()()()()()()2221222121122111i a i a a i a i i a z a i a i a i a a a +-++--++====+++-+++ 由复数()12i z a R a i +=∈+为纯虚数,则222012101a a a a +⎧=⎪⎪+⎨-⎪≠⎪+⎩,解得2a =- 则z i =- ,所以2z a i +=--,所以z a +=故选:A6.A【分析】根据,利用复数的除法运算化简复数,再利用共扼复数的概念求解.【详解】因为,所以,复数的共扼复数是,故选:A解析:A【分析】根据313i z i ⋅=-,利用复数的除法运算化简复数,再利用共扼复数的概念求解.【详解】因为313i z i ⋅=-, 所以()13133i z i i i i-==-=+-, 复数z 的共扼复数是3z i =-,故选:A7.B【分析】先求解出复数,然后根据复数的几何意义判断.【详解】因为,所以,故对应的点位于复平面内第二象限.故选:B.【点睛】本题考查复数的除法运算及复数的几何意义,属于基础题. 化简计解析:B【分析】先求解出复数z ,然后根据复数的几何意义判断.【详解】因为(1)2z i i -=,所以()212112i i i z i i +===-+-, 故z 对应的点位于复平面内第二象限.故选:B.【点睛】 本题考查复数的除法运算及复数的几何意义,属于基础题. 化简计算复数的除法时,注意分子分母同乘以分母的共轭复数.8.A【分析】先化简,由此求得,进而求得的虚部.【详解】,所以,则的虚部为.故选:A解析:A【分析】 先化简z ,由此求得z ,进而求得z 的虚部.【详解】()()()()212251212125i i i i z i i i i ----====-++-, 所以z i ,则z 的虚部为1.故选:A9.D【分析】求出共轭复数,利用复数的乘法运算以及复数的求模公式可得答案.【详解】因为,所以,,所以,故选:D.解析:D【分析】求出共轭复数,利用复数的乘法运算以及复数的求模公式可得答案.【详解】因为1z i =+, 所以1z i =-,12z i +=+,所以()()()1123z z i i i ⋅+=-⋅+=-==故选:D.10.B【分析】化简,利用定义可得的虚部.【详解】则的虚部等于故选:B解析:B【分析】化简12z z ⋅,利用定义可得12z z ⋅的虚部.【详解】()()1212113z z i i i ⋅=+⋅+=-+则12z z ⋅的虚部等于3故选:B11.B【分析】首先,再利用复数的除法运算,计算结果.【详解】复数.故选:B解析:B【分析】首先3i i =-,再利用复数的除法运算,计算结果.【详解】3133i i i +====. 故选:B 12.B【分析】首先求出,再根据复数的模的公式计算可得;【详解】解:因为,所以所以.解析:B【分析】首先求出3z i +,再根据复数的模的公式计算可得;【详解】解:因为12z i =-,所以31231z i i i i +=-+=+所以3z i +==故选:B . 13.B【分析】利用复数代数形式的乘法运算化简,再由实部加虚部为0求解.【详解】解:,所以复数的实部为,虚部为,因为实部和虚部互为相反数,所以,解得 故选:B解析:B【分析】利用复数代数形式的乘法运算化简,再由实部加虚部为0求解.【详解】解:()()()()21i 3i 33331a i ai ai a a i +-=-+-=++-,所以复数()()1i 3i a +-的实部为3a +,虚部为31a -,因为实部和虚部互为相反数,所以3310a a ++-=,解得12a =- 故选:B14.A【分析】由复数的除法求出,然后得出,由复数的几何意义得结果.【详解】由已知,,对应点为,在第一象限,故选:A.解析:A【分析】由复数的除法求出z i =-,然后得出2z +,由复数的几何意义得结果.【详解】 由已知(1)(1)(1)(1)i i z i i i --==-+-, 222z i i +=-+=+,对应点为(2,1),在第一象限,15.B【分析】利用复数除法运算求得,再求得. 【详解】依题意,所以.故选:B解析:B【分析】利用复数除法运算求得z,再求得z.【详解】依题意()()()12221 121212555i ii iz ii i i-+====+ ++-,所以z==故选:B二、多选题16.AC【分析】根据复数的运算及复数的概念即可求解. 【详解】因为复数,所以z的虚部为1,,故AC错误,BD正确.故选:AC解析:AC【分析】根据复数的运算及复数的概念即可求解.【详解】因为复数2020450511()22(1)1 1112i i iz ii i i+++=====+ ---,所以z的虚部为1,||z=故AC错误,BD正确.故选:AC17.AC【分析】令,代入原式,解出的值,结合选项得出答案.【详解】令,代入,得,解得,或,或,所以,或,或.故选:AC【点睛】本题考查复数的运算,考查学生计算能力,属于基础题.解析:AC【分析】令()i ,z a b a b R =+∈,代入原式,解出,a b 的值,结合选项得出答案.【详解】令()i ,z a b a b R =+∈,代入220z z +=,得222i 0a b ab -+=,解得00a b =⎧⎨=⎩,或02a b =⎧⎨=⎩,或02a b =⎧⎨=-⎩, 所以0z =,或2i z =,或2i z =-.故选:AC【点睛】本题考查复数的运算,考查学生计算能力,属于基础题.18.ABCD【分析】先根据复数的除法运算计算出,再依次判断各选项.【详解】,,故A 正确;,故B 正确;的共轭复数为,故C 正确;的虚部为,故D 正确; 故选:ABCD.【点睛】本题考查复数的除法解析:ABCD【分析】先根据复数的除法运算计算出z ,再依次判断各选项.【详解】()()()2121111i z i i i i --===---+-+--,z ∴==,故A 正确;()2212z i i =--=,故B 正确;z 的共轭复数为1i -+,故C 正确;z 的虚部为1-,故D 正确;故选:ABCD.【点睛】本题考查复数的除法运算,以及对复数概念的理解,属于基础题.19.BCD【分析】计算出,即可进行判断.【详解】,,故B 正确,由于复数不能比较大小,故A 错误;,故C 正确;,故D 正确.故选:BCD.【点睛】本题考查复数的相关计算,属于基础题. 解析:BCD【分析】 计算出23,,,z z z z ,即可进行判断.【详解】122z =-+, 221313i i=2222z z ,故B 正确,由于复数不能比较大小,故A 错误; 33131313i i i 1222222z ,故C 正确; 2213122z,故D 正确.故选:BCD.【点睛】 本题考查复数的相关计算,属于基础题.20.BD【分析】把分子分母同时乘以,整理为复数的一般形式,由复数的基本知识进行判断即可.【详解】解:,,A 错误;,B 正确;z 的共轭复数为,C 错误;z 的虚部为,D 正确.故选:BD.【点解析:BD【分析】 把21iz =-+分子分母同时乘以1i --,整理为复数的一般形式,由复数的基本知识进行判断即可.【详解】 解:22(1)11(1)(1)i z i i i i --===---+-+--,||z ∴=A 错误;22i z =,B 正确;z 的共轭复数为1i -+,C 错误;z 的虚部为1-,D 正确.故选:BD.【点睛】本题主要考查复数除法的基本运算、复数的基本概念,属于基础题.21.AD【分析】由已知可求出,进而可求出实部、虚部、共轭复数、复数的模,进而可选出正确答案.【详解】解:由知,,即,所以的实部为,A 正确;的虚部为-2,B 错误;,C 错误;,D 正确;故选:A解析:AD【分析】由已知可求出32z i =--,进而可求出实部、虚部、共轭复数、复数的模,进而可选出正确答案.【详解】 解:由233232i z i i +⋅+=-知,232332i z i i +⋅=--,即()()()2233232232313i i i z i i ---=-=+ 39263213i i --==--,所以z 的实部为3-,A 正确;z 的虚部为-2,B 错误;32z i =-+,C 错误;||z ==D 正确; 故选:AD.【点睛】 本题考查了复数的除法运算,考查了复数的概念,考查了共轭复数的求解,考查了复数模的求解,属于基础题.22.AD【分析】由求得判断A ;设出,,证明在满足时,不一定有判断B ;举例说明C 错误;由充分必要条件的判定说明D 正确.【详解】若,则,故A 正确;设,由,可得则,而不一定为0,故B 错误; 当时解析:AD【分析】由z 求得z z ⋅判断A ;设出1z ,2z ,证明在满足1212z z z z +=-时,不一定有120z z =判断B ;举例说明C 错误;由充分必要条件的判定说明D 正确.【详解】 若2z =,则24z z z ⋅==,故A 正确;设()11111,z a bi a b R =+∈,()22222,z a b i a b R =+∈由1212z z z z +=-,可得()()()()222222121212121212z z a a b b z z a a b b +=+++=-=-+-则12120a a b b +=,而()()121122121212121212122z z a bi a b i a a bb a b i b a i a a a b i b a i =++=-++=++不一定为0,故B 错误;当1z i =-时22z i =-为纯虚数,其实部和虚部不相等,故C 错误;若复数()()()211z a a i a R =-+-∈是虚数,则210a -≠,即1a ≠± 所以“1a ≠”是“复数()()()211z a a i a R =-+-∈是虚数”的必要不充分条件,故D 正确; 故选:AD【点睛】本题考查的是复数的相关知识,考查了学生对基础知识的掌握情况,属于中档题.23.ABC【分析】对选项求出,再判断得解;对选项,求出再判断得解;对选项复数的实部为,判断得解;对选项,的虚部为,判断得解.【详解】对选项由题得.所以复数对应的点为,在第二象限,所以选项正确解析:ABC【分析】对选项,A 求出1=2w -+,再判断得解;对选项B ,求出1w =再判断得解;对选项,C 复数w 的实部为12-,判断得解;对选项D ,w 的虚部为2,判断得解. 【详解】对选项,A 由题得1,z =-221=422w -+∴===-+.所以复数w 对应的点为1(,22-,在第二象限,所以选项A 正确;对选项B ,因为1w ==,所以选项B 正确; 对选项,C 复数w 的实部为12-,所以选项C 正确;对选项D ,w 的虚部为2,所以选项D 错误. 故选:ABC【点睛】 本题主要考查复数的运算和共轭复数,考查复数的模的计算,考查复数的几何意义,考查复数的实部和虚部的概念,意在考查学生对这些知识的理解掌握水平.24.ABD根据残差的计算方法判断A ,根据相关指数的性质判断B ,根据复数的模长公式判断C ,根据否定的定义判断D.【详解】当时,,则该方程相应于点(2,29)的残差为,则A 正确;在两个变量解析:ABD【分析】根据残差的计算方法判断A ,根据相关指数的性质判断B ,根据复数的模长公式判断C ,根据否定的定义判断D.【详解】当2x =时,ˆ9.429.127.9y=⨯+=,则该方程相应于点(2,29)的残差为2927.9 1.1-=,则A 正确;在两个变量y 与x 的回归模型中,2R 的值越大,模型的拟合效果越好,则B 正确;1z i =-,z ==C 错误;由否定的定义可知,D 正确;故选:ABD【点睛】本题主要考查了残差的计算,求复数的模,特称命题的否定,属于中档题. 25.AD【分析】利用复数的概念及几何有意义判断A 、B 选项是否正确,利用利用复数的四则运算法则计算及,并计算出模长,判断C 、D 是否正确.【详解】利用复数的相关概念可判断A 正确;对于B 选项,对应的解析:AD【分析】利用复数的概念及几何有意义判断A 、B 选项是否正确,利用利用复数的四则运算法则计算12z z +及12z z ,并计算出模长,判断C 、D 是否正确.【详解】利用复数的相关概念可判断A 正确;对于B 选项,1223z z i -=-对应的点位于第四象限,故B 错;对于C 选项,122+=+z z i ,则12z z +==,故C 错;对于D 选项,()122224z z i i i ⋅=-⋅=+,则12z z ==D 正确. 故选:AD本题考查复数的相关概念及复数的计算,较简单.26.BD【分析】因为复数满足,利用复数的除法运算化简为,再逐项验证判断.【详解】因为复数满足,所以所以,故A 错误;,故B 正确;复数的实部为 ,故C 错误;复数对应复平面上的点在第二象限解析:BD【分析】因为复数z 满足(2i)i z -=,利用复数的除法运算化简为1255z i =-+,再逐项验证判断. 【详解】因为复数z 满足(2i)i z -=, 所以()(2)1222(2)55i i i z i i i i +===-+--+所以5z ==,故A 错误; 1255z i =--,故B 正确; 复数z 的实部为15- ,故C 错误; 复数z 对应复平面上的点12,55⎛⎫- ⎪⎝⎭在第二象限,故D 正确. 故选:BD【点睛】本题主要考查复数的概念,代数运算以及几何意义,还考查分析运算求解的能力,属于基础题. 27.ACD【分析】由复数的模的意义可判断选项A,B ;整理原式等于,也等于,即可判断选项C,D【详解】由复数的几何意义,知复数,分别对应复平面内的点与点,所以表示点与点之间的距离,故A 说法正确,B解析:ACD【分析】由复数的模的意义可判断选项A,B ;整理原式等于2i +,也等于2i --,即可判断选项C,D【详解】由复数的几何意义,知复数32i +,1i +分别对应复平面内的点()3,2与点()1,1,所以()()321i i +-+表示点()3,2与点()1,1之间的距离,故A 说法正确,B 说法错误;()()3212i i i +-+=+,2i +可表示点()2,1到原点的距离,故C 说法正确;()()()()3211322i i i i i +-+=+-+=--,2i --可表示表示点()2,1--到原点的距离,即坐标为()2,1--的向量的模,故D 说法正确,故选:ACD【点睛】本题考查复数的几何意义,考查复数的模28.AC【分析】根据复数乘法的运算律和复数的模及共轭复数的概念可判断出答案A 和C 正确;C 中可取,进行判断;D 中的必要不充分条件是.【详解】解:由复数乘法的运算律知,A 正确;取,;,满足,但且不解析:AC【分析】根据复数乘法的运算律和复数的模及共轭复数的概念可判断出答案A 和C 正确;C 中可取11z =,2z i =进行判断;D 中12z z =的必要不充分条件是12=z z .【详解】解:由复数乘法的运算律知,A 正确;取11z =,;2z i =,满足22120z z +=,但10z =且20z =不成立,B 错误; 由复数的模及共轭复数的概念知结论成立,C 正确;由12z z =能推出12=z z ,但12||||z z =推不出12z z =,因此12z z =的必要不充分条件是12=z z ,D 错误. 故选:AC【点睛】本题主要考查复数乘法的运算律和复数的基本知识以及共轭复数的概念,属于基础题.29.AC【分析】根据复数的模、复数对应点的坐标、共轭复数等知识,选出正确选项.【详解】,A 正确;复数z 在复平面内对应的点的坐标为,在第三象限,B 不正确;z 的共轭复数为,C 正确;复数z 在复平面内对解析:AC【分析】根据复数的模、复数对应点的坐标、共轭复数等知识,选出正确选项.【详解】||z ==A 正确;复数z 在复平面内对应的点的坐标为(1,2)--,在第三象限,B 不正确;z 的共轭复数为12i -+,C 正确;复数z 在复平面内对应的点(1,2)--不在直线2y x =-上,D 不正确.故选:AC【点睛】本小题主要考查复数的有关知识,属于基础题.30.BC【分析】根据纯虚数、共轭复数、复数的模、复数为实数等知识,选出正确选项.【详解】当时,,此时为纯虚数,A 错误;若z 的共轭复数为,且,则,因此,B 正确;由是实数,且知,z 是实数,C 正确;由解析:BC【分析】根据纯虚数、共轭复数、复数的模、复数为实数等知识,选出正确选项.【详解】当0a =时,1b =,此时z i 为纯虚数,A 错误;若z 的共轭复数为z ,且z z =,则a bi a bi +=-,因此0b =,B 正确;由||z 是实数,且||z z =知,z 是实数,C 正确;由1||2z =得2214a b +=,又1a b +=,因此28830a a -+=,64483320∆=-⨯⨯=-<,无解,即||z 不可以等于12,D 错误. 故选:BC【点睛】本小题主要考查复数的有关知识,属于基础题.。
河北张家口市正博高级中学高中英语完形填空经典试题(含答案)

一、高中英语完形填空1.阅读下面短文,从短文后各题所给的A、B、C和D四个选项中,选出可以填入空白处的最佳选项。
Several years ago I started riding a bike. At first, I thought it was only a 1 ride. But as I built up strength, my friends encouraged me to try some longer 2 . The first one to come along was a 150-mile journey, an event held every year that 3 money to fight cancer.When I signed my name, the 4 seemed great — to support a worthy cause while going for the 5 — and I trained with great excitement. But as the time for the ride approached, my 6 gained ground over my endurance(耐力). I didn't really want to 7 all those miles for two days straight.The ride began on a Sunday morning in the Georgia countryside, 8 for the first few hours I felt wonderful. This was just the 9 I had imagined, and my spirits were 10 . But by the end of the day, I felt tired. I was sure I'd have to 11 .As I topped the hill, the nice sunset 12 me going for a few minutes more. Then in the distance, I 13 a lone rider riding very slowly. I 14 that the person looked different in some way, but I couldn't tell why. I managed to 15 . There she was, riding slowly but steadily, with a 16 smile on her face — and she had only one leg.My focus 17 at that moment. I'd been doubting my body for a whole day. But now I knew — it wasn't the body, but the 18 that would help me reach my goal.It rained all the second day. I 19 saw the one-legged biker again, but I pushed on without complaining. And at the end of the day, still feeling 20 , I completed the 150th mile.1. A. free B. short C. hard D. boring2. A. trips B. fights C. swims D. jumps3. A. gives B. borrows C. counts D. raises4. A. dream B. life C. idea D. advice5. A. record B. distance C. job D. fame6. A. self-doubt B. self-respect C. self-control D. self-love7. A. hike B. walk C. bike D. drive8. A. but B. so C. and D. or9. A. adventure B. experience C. excitement D. struggle10. A. low B. proud C. brave D. high11. A. carry on B. give up C. break out D. hold back12. A. kept B. protected C. stopped D. found13. A. called B. interviewed C. saw D. missed14. A. approved B. hoped C. remembered D. noticed15. A. look back B. pay back C. cheer up D. catch up16. A. determined B. forced C. strange D. shy17. A. strengthened B. changed C. built D. fixed18. A. person B. will C. bicycle D. cause19. A. never B. often C. even D. still20. A. tired B. comfortable C. strong D. injured【答案】(1)B;(2)A;(3)D;(4)C;(5)B;(6)A;(7)C;(8)C;(9)B;(10)D;(11)B;(12)A;(13)C;(14)D;(15)D;(16)A;(17)B;(18)B;(19)A;(20)C;【解析】【分析】本文是一篇记叙文,在一段150英里的骑行旅程中,作者受到一个只有一条腿的骑行者的鼓舞,认识到帮助自己实现目标的不是身体,而是意志,最终完成了这段骑行旅程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、复数选择题1.复数11z i=-,则z 的共轭复数为( ) A .1i -B .1i +C .1122i +D .1122i - 2.已知复数1=-i z i ,其中i 为虚数单位,则||z =( )A .12B .2CD .23.若复数1z i i ⋅=-+,则复数z 的虚部为( )A .-1B .1C .-iD .i4.))5511--+=( )A .1B .-1C .2D .-2 5.复数12i z i=+(i 为虚数单位)在复平面内对应的点位于( ) A .第一象限B .第二象限C .第三象限D .第四象限 6.已知复数1z i =+,z 为z 的共轭复数,则()1z z ⋅+=( )A B .2 C .10 D7.复数()()212z i i =-+,则z 的共轭复数z =( )A .43i +B .34i -C .34i +D .43i -8.已知i 为虚数单位,则43i i =-( ) A .2655i + B .2655i - C .2655i -+ D .2655i -- 9.复数21i i +的虚部为( ) A .1- B .1 C .i D .i -10.若i 为虚数单位,,a b ∈R ,且2a i b i i +=+,则复数a bi -的模等于( )A B C D11.已知i 是虚数单位,设11i z i ,则复数2z +对应的点位于复平面( ) A .第一象限 B .第二象限C .第三象限D .第四象限 12.设复数z 满足(1)2i z -=,则z =( )A .1BCD .213.若复数11i z i ,i 是虚数单位,则z =( ) A .0 B .12C .1D .2 14.设复数满足(12)i z i +=,则||z =( )A .15BCD .515.题目文件丢失!二、多选题16.i 是虚数单位,下列说法中正确的有( )A .若复数z 满足0z z ⋅=,则0z =B .若复数1z ,2z 满足1212z z z z +=-,则120z z =C .若复数()z a ai a R =+∈,则z 可能是纯虚数D .若复数z 满足234z i =+,则z 对应的点在第一象限或第三象限17.已知复数z 满足220z z +=,则z 可能为( ).A .0B .2-C .2iD .2i+1-18.下列四个命题中,真命题为( )A .若复数z 满足z R ∈,则z R ∈B .若复数z 满足1R z ∈,则z R ∈C .若复数z 满足2z ∈R ,则z R ∈D .若复数1z ,2z 满足12z z R ⋅∈,则12z z =19.已知复数122z =-+(其中i 为虚数单位,,则以下结论正确的是( ). A .20zB .2z z =C .31z =D .1z = 20.已知复数z 满足2724z i =--,在复平面内,复数z 对应的点可能在( )A .第一象限B .第二象限C .第三象限D .第四象限21.若复数z 满足()1z i i +=,则( ) A .1z i =-+B .z 的实部为1C .1z i =+D .22z i =22.已知复数122,2z i z i =-=则( )A .2z 是纯虚数B .12z z -对应的点位于第二象限C .123z z +=D .12z z =23.任何一个复数z a bi =+(其中a 、b R ∈,i 为虚数单位)都可以表示成:()cos sin z r i θθ=+的形式,通常称之为复数z 的三角形式.法国数学家棣莫弗发现:()()()n cos sin co i s s nn n z i n r i r n n N θθθθ+==+⎡⎤⎣∈⎦+,我们称这个结论为棣莫弗定理.根据以上信息,下列说法正确的是( )A .22z z =B .当1r =,3πθ=时,31z =C .当1r =,3πθ=时,122z =-D .当1r =,4πθ=时,若n 为偶数,则复数n z 为纯虚数24.已知复数z 满足(2i)i z -=(i 为虚数单位),复数z 的共轭复数为z ,则( )A .3||5z = B .12i 5z +=- C .复数z 的实部为1- D .复数z 对应复平面上的点在第二象限25.已知i 为虚数单位,下列说法正确的是( )A .若,x y R ∈,且1x yi i +=+,则1x y ==B .任意两个虚数都不能比较大小C .若复数1z ,2z 满足22120z z +=,则120z z == D .i -的平方等于126.以下命题正确的是( )A .0a =是z a bi =+为纯虚数的必要不充分条件B .满足210x +=的x 有且仅有iC .“在区间(),a b 内()0f x '>”是“()f x 在区间(),a b 内单调递增”的充分不必要条件D .已知()f x =()1878f x x '= 27.复数21i z i +=-,i 是虚数单位,则下列结论正确的是( )A .|z |=B .z 的共轭复数为3122i +C .z 的实部与虚部之和为2D .z 在复平面内的对应点位于第一象限28.设()()2225322z t t t t i =+-+++,t ∈R ,i 为虚数单位,则以下结论正确的是( )A .z 对应的点在第一象限B .z 一定不为纯虚数C .z 一定不为实数D .z 对应的点在实轴的下方 29.已知复数z ,下列结论正确的是( )A .“0z z +=”是“z 为纯虚数”的充分不必要条件B .“0z z +=”是“z 为纯虚数”的必要不充分条件C .“z z =”是“z 为实数”的充要条件D .“z z ⋅∈R ”是“z 为实数”的充分不必要条件30.设复数z 满足12z i =--,i 为虚数单位,则下列命题正确的是( )A .|z |=B .复数z 在复平面内对应的点在第四象限C .z 的共轭复数为12i -+D .复数z 在复平面内对应的点在直线2y x =-上【参考答案】***试卷处理标记,请不要删除一、复数选择题1.D【分析】先由复数的除法化简该复数,再由共轭复数的概念,即可得出结果.【详解】因为,所以其共轭复数为.故选:D.解析:D【分析】先由复数的除法化简该复数,再由共轭复数的概念,即可得出结果.【详解】 因为()()11111111222i i z i i i i ++====+--+, 所以其共轭复数为1122i -. 故选:D.2.B【分析】先利用复数的除法运算将化简,再利用模长公式即可求解.【详解】由于,则.故选:B解析:B【分析】先利用复数的除法运算将1=-i z i 化简,再利用模长公式即可求解. 【详解】 由于()(1i)(1i)111(1i)222i i i i z i i ++====-+--+,则||2z ===. 故选:B3.B【分析】,然后算出即可.【详解】由题意,则复数的虚部为1故选:B解析:B【分析】1i z i-+=,然后算出即可. 【详解】 由题意()11111i i i i z i i i i -+-+--====+⋅-,则复数z 的虚部为1 故选:B4.D【分析】先求和的平方,再求4次方,最后求5次方,即可得结果.【详解】∵,,∴,,∴,,∴,故选:D.解析:D【分析】先求)1-和)1+的平方,再求4次方,最后求5次方,即可得结果. 【详解】∵)211-=--,)2+1=-,∴)()42117-=--=-+,)()42+17=-=--,∴)()51711-=-+-=--,)()51711+=--+=-,∴))55121-+=--, 故选:D.5.A【分析】对复数进行分母实数化,根据复数的几何意义可得结果.【详解】由,知在复平面内对应的点位于第一象限,故选:A.【点睛】本题主要考查了复数除法的运算以及复数的几何意义,属于基础题 解析:A【分析】对复数z 进行分母实数化,根据复数的几何意义可得结果.【详解】 由()()()122112121255i i i z i i i i -===+++-, 知在复平面内对应的点21,55⎛⎫⎪⎝⎭位于第一象限, 故选:A.【点睛】本题主要考查了复数除法的运算以及复数的几何意义,属于基础题.6.D【分析】求出共轭复数,利用复数的乘法运算以及复数的求模公式可得答案.【详解】因为,所以,,所以,故选:D.【分析】求出共轭复数,利用复数的乘法运算以及复数的求模公式可得答案.【详解】因为1z i =+, 所以1z i =-,12z i +=+,所以()()()1123z z i i i ⋅+=-⋅+=-==故选:D.7.D【分析】由复数的四则运算求出,即可写出其共轭复数.【详解】∴,故选:D解析:D【分析】 由复数的四则运算求出z ,即可写出其共轭复数z .【详解】2(2)(12)24243z i i i i i i =-+=-+-=+∴43z i =-,故选:D8.C【分析】对的分子分母同乘以,再化简整理即可求解.【详解】,故选:C解析:C 【分析】对43i i-的分子分母同乘以3i +,再化简整理即可求解. 【详解】 ()()()434412263331055i i i i i i i i +-+===-+--+, 故选:C9.B将分母乘以其共轭复数进行分母实数化,化成的代数形式即得结果.【详解】,故虚部为1.故选:B.解析:B【分析】将分母乘以其共轭复数进行分母实数化,化成(),a bi a b R +∈的代数形式即得结果.【详解】22(1)11(1)(1)i i i i i i i -==+++-,故虚部为1. 故选:B.10.C【分析】首先根据复数相等得到,,再求的模即可.【详解】因为,所以,.所以.故选:C解析:C【分析】首先根据复数相等得到1a =-,2b =,再求a bi -的模即可.【详解】因为()21a i b i i bi +=+=-+,所以1a =-,2b =.所以12a bi i -=--==故选:C 11.A【分析】由复数的除法求出,然后得出,由复数的几何意义得结果.【详解】由已知,,对应点为,在第一象限,故选:A.解析:A 【分析】由复数的除法求出z i =-,然后得出2z +,由复数的几何意义得结果.由已知(1)(1)(1)(1)i i z i i i --==-+-, 222z i i +=-+=+,对应点为(2,1),在第一象限,故选:A.12.B【分析】由复数除法求得,再由模的运算求得模.【详解】由题意,∴.故选:B .解析:B【分析】由复数除法求得z ,再由模的运算求得模.【详解】由题意22(1)11(1)(1)i z i i i i +===+--+,∴z == 故选:B .13.C【分析】由复数除法求出,再由模计算.【详解】由已知,所以.故选:C .解析:C【分析】由复数除法求出z ,再由模计算.【详解】 由已知21(1)21(1)(1)2i i i z i i i i ---====-++-, 所以1z i =-=.故选:C .14.B【分析】利用复数除法运算求得,再求得.依题意,所以.故选:B解析:B【分析】利用复数除法运算求得z ,再求得z .【详解】 依题意()()()12221121212555i i i i z i i i i -+====+++-,所以z == 故选:B15.无二、多选题16.AD【分析】A 选项,设出复数,根据共轭复数的相关计算,即可求出结果;B 选项,举出反例,根据复数模的计算公式,即可判断出结果;C 选项,根据纯虚数的定义,可判断出结果;D 选项,设出复数,根据题解析:AD【分析】A 选项,设出复数,根据共轭复数的相关计算,即可求出结果;B 选项,举出反例,根据复数模的计算公式,即可判断出结果;C 选项,根据纯虚数的定义,可判断出结果;D 选项,设出复数,根据题中条件,求出复数,由几何意义,即可判断出结果.【详解】A 选项,设(),z a bi a b R =+∈,则其共轭复数为(),z a bi a b R =-∈, 则220z z a b ⋅=+=,所以0a b ,即0z =;A 正确;B 选项,若11z =,2z i =,满足1212z z z z +=-,但12z z i =不为0;B 错;C 选项,若复数()z a ai a R =+∈表示纯虚数,需要实部为0,即0a =,但此时复数0z =表示实数,故C 错;D 选项,设(),z a bi a b R =+∈,则()2222234z a bi a abi b i =+=+-=+, 所以22324a b ab ⎧-=⎨=⎩,解得21a b =⎧⎨=⎩或21a b =-⎧⎨=-⎩,则2z i =+或2z i =--, 所以其对应的点分别为()2,1或()2,1--,所以对应点的在第一象限或第三象限;D 正确. 故选:AD.17.AC【分析】令,代入原式,解出的值,结合选项得出答案.【详解】令,代入,得,解得,或,或,所以,或,或.故选:AC【点睛】本题考查复数的运算,考查学生计算能力,属于基础题.解析:AC【分析】令()i ,z a b a b R =+∈,代入原式,解出,a b 的值,结合选项得出答案.【详解】令()i ,z a b a b R =+∈,代入220z z +=,得222i 0a b ab -+=,解得00a b =⎧⎨=⎩,或02a b =⎧⎨=⎩,或02a b =⎧⎨=-⎩, 所以0z =,或2i z =,或2i z =-.故选:AC【点睛】本题考查复数的运算,考查学生计算能力,属于基础题.18.AB【分析】利用特值法依次判断选项即可得到答案.【详解】对选项A ,若复数满足,设,其中,则,则选项A 正确;对选项B ,若复数满足,设,其中,且,则,则选项B 正确;对选项C ,若复数满足,设解析:AB【分析】利用特值法依次判断选项即可得到答案.【详解】对选项A ,若复数z 满足z R ∈,设z a =,其中a R ∈,则z R ∈,则选项A 正确; 对选项B ,若复数z 满足1R z ∈,设1a z =,其中a R ∈,且0a ≠, 则1z R a=∈,则选项B 正确; 对选项C ,若复数z 满足2z ∈R ,设z i ,则21z R =-∈,但z i R =∉,则选项C 错误;对选项D ,若复数1z ,2z 满足12z z R ⋅∈,设1z i =,2z i =,则121z z ⋅=-∈R , 而21z i z =-≠,则选项D 错误;故答案选:AB【点睛】本题主要考查复数的运算,同时考查复数的定义和共轭复数,特值法为解决本题的关键,属于简单题.19.BCD【分析】计算出,即可进行判断.【详解】,,故B 正确,由于复数不能比较大小,故A 错误;,故C 正确;,故D 正确.故选:BCD.【点睛】本题考查复数的相关计算,属于基础题.解析:BCD【分析】 计算出23,,,z z z z ,即可进行判断.【详解】122z =-+,221313i i=22z z ,故B 正确,由于复数不能比较大小,故A 错误; 33131313i i i 1222z ,故C 正确; 2213122z,故D 正确.故选:BCD.【点睛】 本题考查复数的相关计算,属于基础题.20.BD【分析】先设复数,根据题中条件,由复数的乘法运算,以及复数相等的充要条件求出,即可确定对应的点所在的象限.【详解】设复数,则,所以,则,解得或,因此或,所以对应的点为或,因此复解析:BD【分析】先设复数(),z a bi a b R =+∈,根据题中条件,由复数的乘法运算,以及复数相等的充要条件求出z ,即可确定对应的点所在的象限.【详解】设复数(),z a bi a b R =+∈,则2222724z a abi b i =+-=--,所以2222724z a abi b i =+-=--,则227224a b ab ⎧-=-⎨=-⎩,解得34a b =⎧⎨=-⎩或34a b =-⎧⎨=⎩, 因此34z i =-或34z i =-+,所以对应的点为()3,4-或()3,4-,因此复数z 对应的点可能在第二或第四象限.故选:BD.【点睛】本题主要考查判定复数对应的点所在的象限,熟记复数的运算法则,以及复数相等的条件即可,属于基础题型.21.BC【分析】先利用复数的运算求出复数z ,然后逐个分析判断即可【详解】解:由,得,所以z 的实部为1,,,故选:BC【点睛】此题考查复数的运算,考查复数的模,考查复数的有关概念,考查共轭 解析:BC【分析】先利用复数的运算求出复数z ,然后逐个分析判断即可【详解】解:由()1z i i +=,得2(1)2(1)1(1)(1)2i i z i i i --====-+-, 所以z 的实部为1,1z i =+,22z i =-,故选:BC【点睛】此题考查复数的运算,考查复数的模,考查复数的有关概念,考查共轭复数,属于基础题22.AD【分析】利用复数的概念及几何有意义判断A 、B 选项是否正确,利用利用复数的四则运算法则计算及,并计算出模长,判断C 、D 是否正确.【详解】利用复数的相关概念可判断A 正确;对于B 选项,对应的解析:AD【分析】利用复数的概念及几何有意义判断A 、B 选项是否正确,利用利用复数的四则运算法则计算12z z +及12z z ,并计算出模长,判断C 、D 是否正确.【详解】利用复数的相关概念可判断A 正确;对于B 选项,1223z z i -=-对应的点位于第四象限,故B 错;对于C 选项,122+=+z z i ,则12z z +==,故C 错;对于D 选项,()122224z z i i i ⋅=-⋅=+,则12z z ==D 正确.故选:AD【点睛】本题考查复数的相关概念及复数的计算,较简单.23.AC【分析】利用复数的三角形式与模长公式可判断A 选项的正误;利用复数的棣莫弗定理可判断B 选项的正误;计算出复数,可判断C 选项的正误;计算出,可判断D 选项的正误.【详解】对于A 选项,,则,可得解析:AC【分析】利用复数的三角形式与模长公式可判断A 选项的正误;利用复数的棣莫弗定理可判断B 选项的正误;计算出复数z ,可判断C 选项的正误;计算出4z ,可判断D 选项的正误.【详解】对于A 选项,()cos sin z r i θθ=+,则()22cos2sin 2z r i θθ=+,可得()222cos 2sin 2z r i r θθ=+=,()222cos sin z r i r θθ=+=,A 选项正确; 对于B 选项,当1r =,3πθ=时,()33cos sin cos3sin3cos sin 1z i i i θθθθππ=+=+=+=-,B 选项错误;对于C 选项,当1r =,3πθ=时,1cos sin 3322z i ππ=+=+,则12z =,C 选项正确;对于D 选项,()cos sin cos sin cos sin 44n n n n z i n i n i ππθθθθ=+=+=+, 取4n =,则n 为偶数,则4cos sin 1z i ππ=+=-不是纯虚数,D 选项错误.故选:AC.【点睛】本题考查复数的乘方运算,考查了复数的模长、共轭复数的运算,考查计算能力,属于中等题.24.BD【分析】因为复数满足,利用复数的除法运算化简为,再逐项验证判断.【详解】因为复数满足,所以所以,故A 错误;,故B 正确;复数的实部为 ,故C 错误;复数对应复平面上的点在第二象限解析:BD【分析】因为复数z 满足(2i)i z -=,利用复数的除法运算化简为1255z i =-+,再逐项验证判断. 【详解】因为复数z 满足(2i)i z -=, 所以()(2)1222(2)55i i i z i i i i +===-+--+所以z ==,故A 错误; 1255z i =--,故B 正确; 复数z 的实部为15- ,故C 错误; 复数z 对应复平面上的点12,55⎛⎫- ⎪⎝⎭在第二象限,故D 正确. 故选:BD【点睛】本题主要考查复数的概念,代数运算以及几何意义,还考查分析运算求解的能力,属于基础题. 25.AB【分析】利用复数相等可选A ,利用虚数不能比较大小可选B ,利用特值法可判断C 错误,利用复数的运算性质可判断D 错误.【详解】对于选项A ,∵,且,根据复数相等的性质,则,故正确;对于选项B ,解析:AB【分析】利用复数相等可选A ,利用虚数不能比较大小可选B ,利用特值法可判断C 错误,利用复数的运算性质可判断D 错误.【详解】对于选项A ,∵,x y R ∈,且1x yi i +=+,根据复数相等的性质,则1x y ==,故正对于选项B ,∵虚数不能比较大小,故正确;对于选项C ,∵若复数1=z i ,2=1z 满足22120z z +=,则120z z ≠≠,故不正确; 对于选项D ,∵复数()2=1i --,故不正确;故选:AB .【点睛】本题考查复数的相关概念,涉及复数的概念、复数相等、复数计算等知识,属于基础题. 26.AC【分析】利用纯虚数的概念以及必要不充分条件的定义可判断A 选项的正误;解方程可判断B 选项的正误;利用导数与函数单调性的关系结合充分不必要条件的定义可判断C 选项的正误;利用基本初等函数的导数公式解析:AC【分析】利用纯虚数的概念以及必要不充分条件的定义可判断A 选项的正误;解方程210x +=可判断B 选项的正误;利用导数与函数单调性的关系结合充分不必要条件的定义可判断C 选项的正误;利用基本初等函数的导数公式可判断D 选项的正误.综合可得出结论.【详解】对于A 选项,若复数z a bi =+为纯虚数,则0a =且0b ≠,所以,0a =是z a bi =+为纯虚数的必要不充分条件,A 选项正确;对于B 选项,解方程210x +=得x i =±,B 选项错误;对于C 选项,当(),x a b ∈时,若()0f x '>,则函数()f x 在区间(),a b 内单调递增, 即“在区间(),a b 内()0f x '>”⇒“()f x 在区间(),a b 内单调递增”.反之,取()3f x x =,()23f x x '=,当()1,1x ∈-时,()0f x '≥,此时,函数()y f x =在区间()1,1-上单调递增,即“在区间(),a b 内()0f x '>”⇐/“()f x 在区间(),a b 内单调递增”.所以,“在区间(),a b 内()0f x '>”是“()f x 在区间(),a b 内单调递增”的充分不必要条件.C 选项正确;对于D 选项,()11172488f x x x ++===,()1878f x x -'∴=,D 选项错误. 故选:AC.【点睛】本题考查命题真假的判断,涉及充分条件与必要条件的判断、实系数方程的根以及导数的计算,考查推理能力与计算能力,属于中等题.【分析】根据复数的四则运算,整理复数,再逐一分析选项,即得.【详解】由题得,复数,可得,则A 不正确;的共轭复数为,则B 不正确;的实部与虚部之和为,则C 正确;在复平面内的对应点为,位于第一解析:CD【分析】根据复数的四则运算,整理复数z ,再逐一分析选项,即得.【详解】 由题得,复数22(2)(1)13131(1)(1)122i i i i z i i i i i ++++====+--+-,可得||z ==,则A 不正确;z 的共轭复数为1322i -,则B 不正确;z 的实部与虚部之和为13222+=,则C 正确;z 在复平面内的对应点为13(,)22,位于第一象限,则D 正确.综上,正确结论是CD.故选:CD【点睛】本题考查复数的定义,共轭复数以及复数的模,考查知识点全面.28.CD【分析】利用配方法得出复数的实部和虚部的取值范围,结合复数的概念和几何意义可判断出各选项的正误,由此可得出结论.【详解】,,所以,复数对应的点可能在第一象限,也可能在第二象限,故A 错误 解析:CD【分析】利用配方法得出复数z 的实部和虚部的取值范围,结合复数的概念和几何意义可判断出各选项的正误,由此可得出结论.【详解】22549492532488t t t ⎛+⎫= ⎪⎝⎭+-->-,()2222110t t t ++=++>, 所以,复数z 对应的点可能在第一象限,也可能在第二象限,故A 错误;当222530220t t t t ⎧+-=⎨++≠⎩,即3t =-或12t =时,z 为纯虚数,故B 错误;因为2220t t ++>恒成立,所以z 一定不为实数,故C 正确;由选项A 的分析知,z 对应的点在实轴的上方,所以z 对应的点在实轴的下方,故D 正确. 故选:CD.【点睛】本题考查复数的几何意义与复数的概念相关命题真假的判断,解题的关键就是求出复数虚部和实部的取值范围,考查计算能力与推理能力,属于中等题.29.BC【分析】设,可得出,利用复数的运算、复数的概念结合充分条件、必要条件的定义进行判断,从而可得出结论.【详解】设,则,则,若,则,,若,则不为纯虚数,所以,“”是“为纯虚数”必要不充分解析:BC【分析】设(),z a bi a b R =+∈,可得出z a bi =-,利用复数的运算、复数的概念结合充分条件、必要条件的定义进行判断,从而可得出结论.【详解】设(),z a bi a b R =+∈,则z a bi =-, 则2z z a +=,若0z z +=,则0a =,b R ∈,若0b =,则z 不为纯虚数, 所以,“0z z +=”是“z 为纯虚数”必要不充分条件; 若z z =,即a bi a bi +=-,可得0b =,则z 为实数,“z z =”是“z 为实数”的充要条件;22z z a b ⋅=+∈R ,z ∴为虚数或实数,“z z ⋅∈R ”是“z 为实数”的必要不充分条件.故选:BC.【点睛】本题考查充分条件、必要条件的判断,同时也考查了共轭复数、复数的基本概念的应用,考查推理能力,属于基础题.30.AC【分析】根据复数的模、复数对应点的坐标、共轭复数等知识,选出正确选项.【详解】,A 正确;复数z 在复平面内对应的点的坐标为,在第三象限,B 不正确;z 的共轭复数为,C 正确;复数z 在复平面内对解析:AC【分析】根据复数的模、复数对应点的坐标、共轭复数等知识,选出正确选项.【详解】||z ==A 正确;复数z 在复平面内对应的点的坐标为(1,2)--,在第三象限,B 不正确;z 的共轭复数为12i -+,C 正确;复数z 在复平面内对应的点(1,2)--不在直线2y x =-上,D 不正确.故选:AC【点睛】本小题主要考查复数的有关知识,属于基础题.。
