樊昌信《通信原理》(第6版)笔记和课后习题(含考研真题)详解(第12~14章)【圣才出品】
通信原理(第六版)习题答案

通信原理(第六版)课后答案通信原理第六版(樊昌信曹丽娜著)国防工业出版社课后答案 第一章绪论1-1设英文字母盘出現的概卒药0.105, I 出璇的槪率为0.a02t 试求迓和JT 的信息昼°解:厶=log 2 — = log1-2皐信息源的符号集由Z2D 和E 组咸,设每一符号■独立出现,其出现槪率分别为1炸 1朋・1.岛3/lGi 5/15.徐亲该信息源符号的平均信息壘。
解=平均信息量 疋=Pgbj 恥Ji-LI . 1 V 1 k 1 3 , 3 5 . 5一才叫厂冠吨迈飞呃乔护喝忆 二2.2咖/棉门设駆个消息乩氐C. D 分别以概率lf4、1他1区 ⑴传送 斑一消息的出现是相 互独立的,试计算其平均信息量.M —个由字母直pep 组咸的字,对于告输的每一字囹用二进制眛冲编码,00代替每01 代清即U 代替匚11代替D ,每个脉冲宽度丸%弘⑴不同的宇毎等可能蜩时.试计算传輸的平均信息速率; ⑵ 若霉个字囹出现的等可能性另别光甩=1/5耳=1曲用尸1地山3/10,试计聲传需的平均信 息Jt 率-解;平均信息量用二—£ FUJI 躍」P 〔Gj-10.002解;(1)因一b字母衬翻个二ffi制圖中「属于四进41符号,故一b字母的持剜间为25, 传達宇母的符吕頑率为=1005&4 = ------------ 7聃2x5xl0-3等概时,平均信息速率尽=弘logs 4 = 200^/B ⑵每个符号平均信息量为H= 一工目leg 2 =-丄bg Q 丄1。
呂 2 丄一丄1笔」 --- l og 了——h 5 5 4 2 4 4 S 10 a10-1985边库f号平均信息速率R t=理斗月=100x1.985 = 198.5&/ff1-5国磅尔斯电码用点和划的序列发遊英文字母,划用持续3单位的电臟沖表示,虽用持续1个劉i的电瞒冲表示且到出现的概率是点t±®的概率的1心⑴求点和划的信息墨(刀求点和划的平均信息量-解:⑴由已知条件划出现的概率是点出现的概率的1/3,即PT3巳且P卄Pi所以卩产14 PTA '划的信息量几=-1唱卜加点的信息量厶二-1隅肓=0⑷気左N 1⑵平均信息量/f = -x0.415 + -x2 = 0.81加/符号皿某离散信I.W出忌尬…唧个不同的符号符号遠率为24D逻其中4个符号出现概率为尸财"⑹"MP 兔)=1他利无)="4具余符号等概出BL⑴求该信息源的平均信息率i⑵求传逆“的信息量◎ 解(1由已知条件得巩心)■户(忑訂■用(衍)■刀(花)■—僖耳源航:用(兀)一迟戸(吗)呱尸3” -“丄叱拮!□1D-2.87了加“符号则信忌源的平均信M連率为尺# = x H =2400 x 2. £75 = d?0O bit / $ ⑵舱1血的传亘量酋:f =『X/?』■ 3(500 y tS90D = 2.434 xlO7^1-7设某信息-源以每秒2000个符号的速率发送消息信息源由ARGDE五个信息符号组成发送盘的慨率为12发送其余符号的概率相同,且设每一符号出现是相互独立的。
樊昌信《通信原理》(第6版)(课后习题 通信网)【圣才出品】
14-1 若一个用户拨打国内长途电话需要用10位数字的信令,试问“拨号脉冲”法和“双音多频”法分别要用多长时间?解:(1)“拨号脉冲”法中,发送每个数字平均需用0.55s时间,若不计算各位数字间的间隔,10位数字的信令至少需要0.55×10=5.5s的时间。
(2)“双音多频”法中,发送每个数字平均需用0.08s时间,若不计算各位数字间的间隔,10位数字的信令至少需要0.08×10=0.8s的时间。
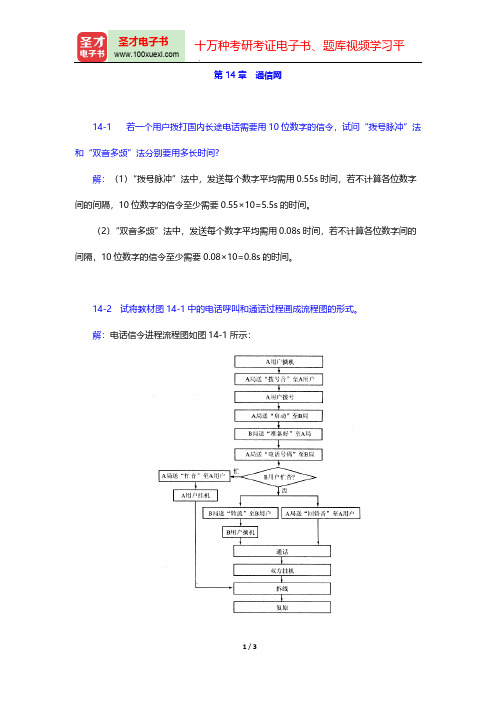
14-2 试将教材图14-1中的电话呼叫和通话过程画成流程图的形式。
解:电话信令进程流程图如图14-1所示:14-3 设一个公共电话网中共有800部用户电话机,平均每部电话机产生的流入话务量等于0.2Erl ,每次呼叫的平均持续时间为200s ,试求出其每小时的平均呼叫次数。
解:根据题意可知,,则每小时的平均呼叫次数为0.2,2000.056A Erl t s h ===次/h 。
023570056A ..t .λ==≈14-4 在题14-3中,若有某个用户通话3min ,试求出在此期间网内平均产生多少次新的呼叫。
解:网内3min 内平均产生新的呼叫次数为次。
3578003601428./.⨯⨯=14-5 试证明纯ALOHA 系统归一化通过量P 的最大值等于1/2e 。
证明:纯ALOHA 系统中,设归一化总业务量为P ,则归一化通过量对P 求偏导令偏导等于0,得 P=1/2故归一化通过量的最大值为 。
14-6 试证明时隙ALOHA 系统归一化通过量P 的最大值等于1/e 。
证明:时隙ALOHA 系统中,设归一化总业务量为P ,则归一化通过量对P 求偏导,得令偏导等于0,得 P=1故归一化通过量的最大值为。
通信原理第六版课后答案樊昌信

通信原理第六版课后答案樊昌信第一章简介1.1 概述通信原理是一门研究信息传递的基本原理和方法的学科。
本章主要介绍了通信系统的基本结构和组成部分,以及通信系统的基本原理、分类和性能指标。
1.2 通信系统的基本结构通信系统由信息源、信源编码器、发送器、信道、接收器、信道解码器和信息目的地组成。
信息源能产生符合人类感知的信息,信源编码器将信息源产生的信息进行源编码,发送器将源编码后的信息通过信道传输给接收器。
1.3 通信系统的基本原理通信系统的基本原理包括信源编码、信道编码、调制和解调、传输和接收等几个方面。
信源编码是将信息源产生的信息进行编码,以提高信息的传输效率和可靠性;信道编码是为了提高通信系统在信道中传输时的抗干扰性和纠错能力;调制和解调是将数字信号转换为模拟信号以及将模拟信号转换为数字信号的过程;传输和接收是指通过信道传输和接收信息的过程。
1.4 通信系统的分类通信系统可以分为有线通信系统和无线通信系统。
有线通信系统主要通过有线媒介传输信息,如光纤通信系统和电力线通信系统等;无线通信系统则主要通过无线电波传输信息,如移动通信系统和卫星通信系统等。
1.5 通信系统的性能指标通信系统的性能指标包括传输速率、频谱利用率、误码率、误差概率、信噪比等。
传输速率是指单位时间内传输的比特数;频谱利用率是指在给定带宽内传输的比特数;误码率是指传输中出现错误比特的比例;误差概率是指在解调和解码过程中出现错误的比例;信噪比是信号功率与噪声功率之比。
第二章信号与系统2.1 信号的定义和分类信号是随时间、空间或其他变量而变化的物理量。
根据信号的分类标准,信号可以分为连续信号和离散信号、周期信号和非周期信号、模拟信号和数字信号等。
2.2 系统的定义和性质系统是对输入信号进行处理并产生输出信号的装置或算法。
系统可以分为线性系统和非线性系统、时不变系统和时变系统、因果系统和非因果系统等。
2.3 信号的时域分析信号的时域分析主要是对信号在时间上的变化进行分析。
樊昌信《通信原理》笔记和课后习题(含考研真题)详解(12-13章)【圣才出品】

第12章正交编码与伪随机序列12.1复习笔记一、正交编码1.正交编码的基本概念(1)正交编码的定义正交编码是指码组两两正交的编码方式。
(2)正交编码的正交性(ρ=0)①互相关系数a.码元为“+1”,“-1”设长为n 的编码中码元取值“+1”和“-1”,则码组x,y 的互相关系数为式中,x,y 表示两个码组,记为b.码元为“0”,“1”设二进制数字码元取值为“0”和“1”,则互相关系数为式中,A 为x 和y 中对应码元相同的个数;D 为x 和y 中对应码元不同的个数。
若码组x 和y 正交,则必有ρ(x,y)=0(11ρ-≤≤+)。
②自相关系数一个长为n的码组x的自相关系数为式中,x的下标按模n运算。
(3)超正交编码(ρ<0)①超正交编码的定义超正交编码是指编码中任两码组间均超正交的编码方式。
②超正交编码的特性任意两个码组间的相关系数ρ<0。
(4)双正交编码(ρ=0或-1)①双正交编码的定义双正交编码是指码组由正交编码和其反码构成的编码方式。
②双正交编码的特性任意两码组间的相关系数ρ为0或-1。
2.阿达玛矩阵(1)阿达玛矩阵的定义阿达玛矩阵是指由元素+1和-1构成,且其各行(或列)互相正交的方阵,记为H矩阵。
(2)阿达玛矩阵的表示阶数为2的幂的高阶H矩阵表示为式中,N=2m;为直积,指将中的每一个元素用矩阵H 2代替;H2为最低阶H 矩阵,下式中+1和-1简写为“+”和“-”,即(3)阿达玛矩阵的正规形式①正规阿达玛矩阵的定义正规阿达玛矩阵是指元素对称且第一行和第一列的元素全为“+”的H矩阵。
②正规阿达玛矩阵的特点正规H矩阵交换任意两行(或列),或改变任一行(或列)中每个元素的符号:a.不会影响矩阵的正交性质;b.交换后的矩阵H不一定正规。
3.沃尔什函数(1)沃尔什函数的定义沃尔什函数用差分方程定义为式中,p=0或1,j=0,1,2,…;指数中的[j/2]表示取j/2的整数部分。
(2)沃尔什函数的特点①函数取值仅为“+1”和“-1”;②任意两个沃尔什函数相乘积分的结果等于0,即满足两两正交;③具有数字信号的特性。
通信原理第六版樊昌信课后答案

通信原理第六版樊昌信课后答案通信原理是电子信息类专业的一门重要课程,它涉及到无线通信、数字通信、模拟通信等多个方面的知识。
樊昌信编著的《通信原理》第六版作为该领域的经典教材,对于学习通信原理的同学来说是一本不可多得的好书。
在学习过程中,课后习题是加深理解和掌握知识的重要途径。
然而,很多同学在学习过程中会遇到课后习题的难题,无法得到及时的解答和指导。
因此,本文将针对《通信原理》第六版樊昌信编著的课后习题进行详细解答,希望能够帮助到正在学习该教材的同学们。
1. 信号与系统。
1.1 什么是信号的功率?如何计算?信号的功率是指单位时间内信号能量的平均值,通常用均方值来表示。
对于连续时间信号,其功率可以通过信号的均方值来计算;对于离散时间信号,其功率可以通过信号的均方值和采样周期来计算。
1.2 什么是信号的谱密度?如何计算?信号的谱密度是指单位频率范围内信号功率的平均密度,通常用功率谱密度函数来表示。
对于连续时间信号,其功率谱密度可以通过信号的傅里叶变换来计算;对于离散时间信号,其功率谱密度可以通过信号的离散傅里叶变换来计算。
2. 模拟调制。
2.1 什么是调制?为什么需要调制?调制是指将低频信号(基带信号)转换成高频信号(载波信号)的过程。
调制的主要作用是使信号能够在信道中传输,同时也可以提高信号的传输效率和抗干扰能力。
2.2 什么是调幅调制(AM)?其调制过程是怎样的?调幅调制是一种将基带信号的幅度变化映射到载波信号幅度上的调制方式。
其调制过程包括将基带信号与载波信号相乘,得到调制信号。
3. 数字调制。
3.1 什么是数字调制?与模拟调制有何区别?数字调制是指将数字信号转换成模拟信号的过程,其主要区别在于数字调制是在数字领域进行的,而模拟调制是在模拟领域进行的。
3.2 什么是调频调制(FM)?其调制过程是怎样的?调频调制是一种将基带信号的频率变化映射到载波信号频率上的调制方式。
其调制过程包括将基带信号与载波信号相加,得到调制信号。
通信原理第六版_思考题答案_樊昌信_曹丽娜_编著

通信原理第六版_思考题答案_樊昌信_曹丽娜_编著第一章绪论1-1 以无线广播和电视为例,说明图1-1模型中信息源,受信者及信道包含的具体内容是什么1-2 数字通信有那些特点答:第一,数字传输抗干扰能力强,尤其在中继时,数字信号可以再生而消除噪声的积累;第二,传输差错可以控制,从而改善了传输质量;第三,便于使用现代数字信号处理技术对数字信息进行处理;第四,数字信息易于做高保密性的加密处理;第五,数字通信可以综合传递各种消息,使通信系统功能增强。
1-3 按消息的物理特征,通信系统如何分类答:根据消息的特征不同,通信系统可以分为:第一:电报通信系统;第二:电话通信系统;第三:数据通信系统;第四:图像通信系统。
1-4 按调制方式,通信系统如何分类答:按调制方式,通信系统可以分为:基带传输和频带传输。
1-5 按传输信号的特征,通信系统如何分类答:按传输信号的特征,通信系统可以分为:模拟通信系统和数字通信系统。
1-6 按传送信号的复用方式,通信系统如何分类答:按传送信号的复用方式,通信系统可以分为:频分复用,时分复用和码分复用。
1-7 通信方式是如何确定的答:通信方式是根据消息的传送方向与时间关系确定的。
1-8 通信系统的主要性能指标是什么答:通信系统的主要性能指标是:传输速率和差错率。
1-9 什么是误码率什么是误信率它们之间的关系如何答:所谓误码率,是指错误接收的码元数在传送总码元数中所占的比例,或者更确切起的说,误码率即是码元在传输系统中被传错的概率。
所谓误信率,又称误比特率,是指错误接收的信息量在传送信息总量中所占的比例,或者更确切地说,它是码元的信息量在传输系统中被丢失的概率。
二者之间的关系:它们都是表示差错率的。
1-10 什么是码元速率什么是信息速率它们之间的关系如何答:码元速率是指每秒钟传送码元的数目,单位为“波特“,常用符号“B”表示。
信息速率是指每秒钟传递的信息量,单位是比特/秒。
二者之间的关系:在二进制下,二者在数值上相等,只是单位不同;在N进制下,设信息速率为Rb(bit/s),码元速率为Rbn(B),则有:RbnN=bitRb?2)/(log s1-11 未来通信技术的发展趋势如何1-12 什么是信源符号的信息量什么是离散信源的信息熵答:信源符号的信息量是它出现的概率P(x)的函数。
《通信原理》_樊昌信_曹丽娜_编著第六版课件_第14章_通信网

11
第14章 通信网
14.2.2电话网中的交换
电路转接方法:用于早期的电话网
双向交换矩阵
用户1 用户2
不适宜用于数字电路 用户3
用户1 用户2 (入线)用用用用用户户户户户46357
16
第14章 通信网
局间信令:
随路信令(CAS) : ➢ 是指信令和用户信息(语音)在同一信道中传输的 信令。 ➢ R2信令是一种基于E-1时分复用系统的随路信令。在 E-1系统中时隙TS16被预留用来传递这种信令。
共路信令(CCS) : ➢ 将呼叫控制信息和其他业务信息通过一个独立的信 令网络传输。 ➢ SS7信令为一种共路信令 。它比R2信令更高效,更 可靠。SS7信令的标准化程度要比R2信令好。
交换设备:按照信令将通信链路传来的信号转接到 另一条链路的设备。
有些通信网中还包含转发设备。
3
第14章 通信网
通信网的分类
按照功能区分
电报网、电话网、电传(Telex)网以及电视网等等。
综合业务数字网(ISDN)
➢ 窄带综合业务数字网(N-IDN)
话务量:
电话网中负担的业务量多少由话务量衡量,它分为
➢ 流入话务量A :其定义是单位时间(1 h)内平均
呼叫次数和每次呼叫平均持续(占用线路)时间
h之积,即
A h (Erl )
式中,h 的单位是h/次,的单位是次/h,故A是无 量纲的。而A的单位则称为爱尔兰。
流入话务量表示每小时中平均线路占用时间。
单向交换矩阵
通信原理(第六版)樊昌信曹丽娜课后答案

通信原理(第六版)课后习题答案第一章绪论1-1没奨文字母总出视笛⅛S率为O 105, X 的槪奉为0.002,试求总和Jr的信息量“解:I S— IQg 2 —= IOg ? —-—- 3.25 bii> S S 2P 5 1 0.105I X = Iog a—= IOg 2——-——=8.97bitT f30 0021∙2某信息源的符号集由査BCD和E组成,设每一符号独立出现其出现概率分别再1招,1/8» l/Et 3/1, 5/16-试求该信息源苻号的平均信息量Il解:平均信息量H = ~∑Fx) IOg 2 Fu i)J-I1 I 1 I i 1 1 I 1 3 I 3 5 I5=_ —log 3—_ —1Og a———log 3—- Io I g a----------------------------------- ——IGg 3-------4 2A8 e28 S 2 8 16 3 16 16 62 16=2.23 WW 号1-3设有四个消息乩B、C、D分别以M率1练1煤1/& 1门传送4消息的Lt®是相互独立Kh试计算其平均信息量*解:平均信息量j v = -∑¾)iog2¾)i-11.方竝/符号14—个由字母点PCD组成的宇,对于传输的毎一字母用二进制脉冲编码,00代替钉1 代替代替CJl代替D行个脉沖宽度为5沁Ii)不同的字母等可能版时.试计算传输的平均信息速率;⑺若环字母出现的等可能性分删为凡=1∕5∕>%Pe咫防剂W试计算传输的平均信息速率II解:(1X≡→ 字母对应两个二≡制脉沖,属于四进》」符号,故一b字母的持貓间为2× ‰τ 传送字母的符号速率为=——J—=IOO^刖2x5xl0^j等概时,平均信息速率& = Iog2 4 = 200⅛∕s(2)每个符号平均信息量为4 1 Il II 13 3H = -ZRTE=--L IOg 2---Iog3 --^IQg ,---Iog2- h 5 5 4 a 44 2 4 10 3IO=1.985 to/W 号平均信息速率肮=R M H =100xl.9S5 = 198 5⅛∕ff1-5国际莫尔斯电码用点和划的序列发送英文字母,划用持续3单位的电流脉冲表示,点用持续1个单位的电流脉沖表示]且划出现的概率是点出现的嘅率的1/3.⑴求点和划的信®⅛(2)求点和划的平均信S⅛≡解⑴由己知条件划出现的概率是点出现的概率的1/3,即P^∖β P2且Λ+⅛L 所以尸尸1砂Pj=3∕4划的信息量Z l= -IOS3- = 2⅛⅛43点的信息量厶=-Iog 2 - = 0-415⅛ii(2)平均信息量^ = ^XO.415+-^-x2 = 0.31驗/符号M某离散信忌獅出忌心…杯个不同的符号.符号逋率为如迥苴中4个符号出现概率为尸(殆=巩再)= IJg Pg = 1∕3>Fg= IM其余符号等概出现。
樊昌信《通信原理》第六版课后答案

第二章2-1 试证明图P2-1中周期性信号可以展开为 (图略)0 4(1) ()cos(21)21 n nstnt n证明:因为()()stst所以0000 22 ()coscoscos 2kkkkkkktktstccckt T101()00stdtc1111 221111224 ()cos()coscossin2kk cstktdtktdtktdt k0,2 4(1)21(21) n knknn所以0 4(1) ()cos(21)21 n nstnt n2-2设一个信号()st 可以表示成 ()2cos(2)sttt试问它是功率信号还是能量信号,并求出其功率谱密度或能量谱密度。
解:功率信号。
222()cos(2)sin(1)sin(1) [] 2(1)(1) jftjjsftedt ff eeff21()limPfs2222222222sin(1)sin(1)sin(1)sin(1)lim2cos2 4(1)(1)(1)(1) ffff ffff由公式2 2 sin lim()t xt x tx 和 sinlim()txtx x有()[(1)][(1)]44 1[(1)(1)] 4Pfff ff或者001()[()()]4Pfffff2-3 设有一信号如下: 2exp()0 ()00tt xt t试问它是功率信号还是能量信号,并求出其功率谱密度或能量谱密度。
解:220()42txtdxedt是能量信号。
2 (12) 0()() 2 212 jft jft Sfxtedtedt jf22224()1214 Gf jff2-4 试问下列函数中哪一些满足功率谱密度的性质: (1)2()cos2ff (2)()afa (3)exp()af解:功率谱密度()Pf 满足条件:()Pfdf(3)满足功率谱密度条件,(1)和(2)不满足。
2-5 试求出()cosstAt解:该信号是功率信号,自相关函数为22 2 21()limcoscos() cos 2T TTRAttT A21(0)2PRA2-6 设信号()st 的傅里叶变换为()sinSfff ()sR解:2 2 222()()sin1,11jf s jf RPfedf fedff2-7 已知一信号()st 的自相关函数为()2ks k Re k 为常数(1)试求其功率谱密度()sPf 和功率P ; (2)试画出()sR ()sPf 的曲线。
樊昌信《通信原理》(第6版)【课后习题+章节题库+模拟试题】(名校考研真题)【圣才出品】

4 / 111
圣才电子书 十万种考研考证电子书、题库视频学习平台
解:由题可知,当 PA=PB=PC=PD=PE= 时,信息量最大。 (1)信源熵为
平均信息速率为 Rb=RB·H(χ)=1000×2.23=2.23×103(bit/s)
C.4800b/s,2400B
D.4800b/s,1600B
【答案】D
【解析】十六进制数字信号的传信率为: R b RB log 2 16 4800b / s ;
传信率不变,则八进制传码率为: R B
Rb log 2 8
4800 3
1600B 。
2.一个事件的发生概率越( ),所含信息越( )。[南邮 2009 研] A.高;高 B.大;大 C.大;丰富 D.小;大 【答案】D
时,信源的熵
H(X)达到最大值为
log 2
1 2
1;当信源
X
不等概率时,信息熵
H1 ( X
)
1。
4.若离散信源输出 16 进制独立等概随机序列,则此信源输出的每个符号所包含的平 均信息量( )。若 16 进制符号不是等概出现,则此信源输出的每个符号所包含的平均信 息量( )。[北科 2010 研]
2.信源编码是降低信号中( )的编码,目的是提高通信系统的( );信道编码是增 加信号中( )的编码,目的是提高通信系统的( )。[南京大学 2010 研]
【答案】信息冗余度;有效性;信息冗余度;可靠性 【解析】信源中存在一些不必要传送的信息,因此信源也就存在进一步压缩其信息速率 的可能性,信源编码是降低信号中的信息冗余度,提高系统的有效性;由于实际信道存在噪 声和干扰的影响,使得信息在传送过程中出现差错,信道编码是依靠增加信息冗余度,提高 系统的可靠性。
通信原理第六版樊昌信课后答案

通信原理第六版樊昌信课后答案通信原理是电子信息类专业的一门重要课程,涉及到了无线通信、有线通信、调制解调、信道编码等多个方面的知识。
樊昌信编著的《通信原理》第六版作为该领域的经典教材,深受广大学生和教师的喜爱。
而课后习题的答案则是学习和教学的重要辅助资料。
本文将针对《通信原理第六版樊昌信》的课后习题答案进行解析和讨论,希望能够对学习者有所帮助。
第一章。
1. 信号的频率是指单位时间内信号波形重复的次数,通常用赫兹(Hz)来表示。
而信号的周期则是指信号波形重复一个完整周期所需要的时间,通常用秒(s)来表示。
信号的频率和周期是互为倒数的关系,即频率 f 和周期 T 满足 f=1/T。
2. 信号的幅度是指信号的振幅大小,通常用伏特(V)来表示。
而信号的相位则是指信号波形在时间轴上的偏移,通常用弧度(rad)来表示。
在正弦信号中,相位的改变会导致信号波形的移动,但不会改变信号的频率和幅度。
3. 信号的能量和功率是描述信号强度的重要指标。
信号的能量指的是信号在一段时间内的总能量,通常用焦耳(J)来表示。
而信号的功率则是指单位时间内信号的平均功率,通常用瓦特(W)来表示。
在通信系统中,能量和功率的概念对于信号的传输和处理至关重要。
第二章。
1. 信道的带宽是指信道能够传输的频率范围,通常用赫兹(Hz)来表示。
而信道的带宽和信号的最高频率之间存在着一定的关系,即带宽应该大于等于信号的最高频率。
在实际的通信系统中,带宽的合理分配和利用对于提高信号传输的效率和质量至关重要。
2. 信道的带宽限制了信号的传输速率,带宽越大,则信号的传输速率也就越高。
而在实际的通信系统中,由于信道带宽是有限的,因此需要对信号进行调制和编码,以适应信道的传输特性。
调制和编码技术的选择对于信号的传输速率和误码率有着重要的影响。
3. 信道的噪声是指信道中存在的各种干扰和噪声,会对信号的传输和接收造成影响。
噪声的来源包括了信道本身的噪声、外部干扰以及其他信号的干扰等。
通信原理第六版_思考题答案解析_樊昌信_曹丽娜_编著

第一章绪论1-1 以无线广播和电视为例,说明图1-1模型中信息源,受信者及信道包含的具体内容是什么?1-2 数字通信有那些特点?答:第一,数字传输抗干扰能力强,尤其在中继时,数字信号可以再生而消除噪声的积累;第二,传输差错可以控制,从而改善了传输质量;第三,便于使用现代数字信号处理技术对数字信息进行处理;第四,数字信息易于做高保密性的加密处理;第五,数字通信可以综合传递各种消息,使通信系统功能增强。
1-3 按消息的物理特征,通信系统如何分类?答:根据消息的特征不同,通信系统可以分为:第一:电报通信系统;第二:电话通信系统;第三:数据通信系统;第四:图像通信系统。
1-4 按调制方式,通信系统如何分类?答:按调制方式,通信系统可以分为:基带传输和频带传输。
1-5 按传输信号的特征,通信系统如何分类?答:按传输信号的特征,通信系统可以分为:模拟通信系统和数字通信系统。
1-6 按传送信号的复用方式,通信系统如何分类?答:按传送信号的复用方式,通信系统可以分为:频分复用,时分复用和码分复用。
1-7 通信方式是如何确定的?答:通信方式是根据消息的传送方向与时间关系确定的。
1-8 通信系统的主要性能指标是什么?答:通信系统的主要性能指标是:传输速率和差错率。
1-9 什么是误码率?什么是误信率?它们之间的关系如何?答:所谓误码率,是指错误接收的码元数在传送总码元数中所占的比例,或者更确切起的说,误码率即是码元在传输系统中被传错的概率。
所谓误信率,又称误比特率,是指错误接收的信息量在传送信息总量中所占的比例,或者更确切地说,它是码元的信息量在传输系统中被丢失的概率。
二者之间的关系:它们都是表示差错率的。
1-10 什么是码元速率?什么是信息速率? 它们之间的关系如何?答:码元速率是指每秒钟传送码元的数目,单位为“波特“,常用符号“B”表示。
信息速率是指每秒钟传递的信息量,单位是比特/秒。
二者之间的关系:在二进制下,二者在数值上相等,只是单位不同;在N进制下,设信息速率为Rb(bit/s),码元速率为Rbn(B),则有:RbnN=bitRb•2)/(log s1-11 未来通信技术的发展趋势如何?1-12 什么是信源符号的信息量?什么是离散信源的信息熵?答:信源符号的信息量是它出现的概率P(x)的函数。
樊昌信《通信原理》(第6版)笔记和课后习题(含考研真题)详解(模拟调制系统)

二、幅度调制(线性调制)原理 1.标准调幅 AM (1)调制 标准调幅就是常规双边带调制,简称调幅(AM)。其原理框图如图 5-2 所示。
⑤要求ωc≥ωH,否则,収生交叠失真。
(2)解调——包络解调,属于非线性解调。
AM 信号在满足
的条件下,其包络不调制信号 m(t)的形状完全一样。
因此,AM 信号一般都用简单的包络检波法来恢复信号。包络检波器通常由半波或者全波整
流器和低通滤波器组成。一个二极管峰值包络检波器如图 5-4 所示。
图 5-4 包络检波器 当 Ao+m(t)≥0 且 fH≤1/(RC)≤fc 时,检波器输出 mo(t)≈Ao+m(t),经隔直电路得到 m(t)。
2.双边带调幅 DSB (1)调制 m(t)为直流为0的基带信号,若m(t)含有直流分量,通过隔直电路去掉,即可得到抑制 载波双边带信号,简称双边带信号(DSB)。其原理框图如图5-5所示。
其时域表达式为:
图 5-5 DSB 调制模型
DSB的频谱不AM的谱相似,只是没有了在
处的δ函数,即
4 / 47
图 5-3 AM 信号的波形和频谱
说明:
①调制使频谱搬秱,但未改发形状。AM 频谱波形关于±ωc 对称,分上、下边带;
②调制使已调信号带宽增加一倍,即 BAM 2 fH ;
③若 m(t)为随机信号,频域使用功率谱描述,结论相同;
④要求 A0+m(t)≥0,否则,“过调幅”,使包络失真,称|m(t)|max/A0 为调幅指数;
通信原理(第六版)樊昌信曹丽娜_第六版--课后思考题及习题答案

第一章绪论1.1以无线广播和电视为例,说明图1-1模型中的信息源,受信者及信道包含的具体内容是什么在无线电广播中,信息源包括的具体内容为从声音转换而成的原始电信号,收信者中包括的具体内容就是从复原的原始电信号转换乘的声音;在电视系统中,信息源的具体内容为从影像转换而成的电信号。
收信者中包括的具体内容就是从复原的原始电信号转换成的影像;二者信道中包括的具体内容分别是载有声音和影像的无线电波1.2何谓数字信号,何谓模拟信号,两者的根本区别是什么数字信号指电信号的参量仅可能取有限个值;模拟信号指电信号的参量可以取连续值。
他们的区别在于电信号参量的取值是连续的还是离散可数的1.3何谓数字通信,数字通信有哪些优缺点传输数字信号的通信系统统称为数字通信系统;优缺点:1.抗干扰能力强;2.传输差错可以控制;3.便于加密处理,信息传输的安全性和保密性越来越重要,数字通信的加密处理比模拟通信容易的多,以话音信号为例,经过数字变换后的信号可用简单的数字逻辑运算进行加密,解密处理;4.便于存储、处理和交换;数字通信的信号形式和计算机所用的信号一致,都是二进制代码,因此便于与计算机联网,也便于用计算机对数字信号进行存储,处理和交换,可使通信网的管理,维护实现自动化,智能化;5.设备便于集成化、微机化。
数字通信采用时分多路复用,不需要体积较大的滤波器。
设备中大部分电路是数字电路,可用大规模和超大规模集成电路实现,因此体积小,功耗低;6.便于构成综合数字网和综合业务数字网。
采用数字传输方式,可以通过程控数字交换设备进行数字交换,以实现传输和交换的综合。
另外,电话业务和各种非话务业务都可以实现数字化,构成综合业务数字网;缺点:占用信道频带较宽。
一路模拟电话的频带为4KHZ带宽,一路数字电话约占64KHZ。
1.4数字通信系统的一般模型中的各组成部分的主要功能是什么数字通行系统的模型见图1-4所示。
其中信源编码与译码功能是提高信息传输的有效性和进行模数转换;信道编码和译码功能是增强数字信号的抗干扰能力;加密与解密的功能是保证传输信息的安全;数字调制和解调功能是把数字基带信号搬移到高频处以便在信道中传输;同步的功能是在首发双方时间上保持一致,保证数字通信系统的有序,准确和可靠的工作。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
樊昌信《通信原理》(第6版)笔记和课后习题(含考研真题)详解
第12章正交编码与伪随机序列
12.1复习笔记
一、正交编码
1.正交编码的基本概念
若M个周期为T模拟信号s1(t),s2(t),...,s M(t)构成一个正交集合,则有:
设长为n的编码中码元只取+1和一1,以及x和y是其中的两个码组
则x,y之间的相关系数为:
若码组x和y正交,则:
相关系数的性质:相关系数ρ的取值范围在±1之间,即有-1≤ρ≤1。
若两个码组间的相关系数ρ<0,则称这两个码组互相超正交;如果一种编码中任意两码组间均超正交,则称这种编码为超正交编码。
2.阿达玛矩阵
哈达玛(Hadamard)矩阵是一种方阵,且仅由元素+1和-1构成。
H矩阵各行(或列)是
相互正交的,所以H矩阵是正交方阵。
若把其中每一行都看作一个码组,则这些码组也是互相正交的,而整个H矩阵就是一种长为n的正交编码,它包含n个码组。
3.沃尔什函数和沃尔什矩阵
沃尔什函数具有完备正交性,可以用来表示任一波形。
若将哈达玛中行的次序按“+1”和“-1”交变次数的多少重新排列,可得到沃尔什(Walsh)矩阵。
二、伪随机序列
伪随机噪声具有类似于随机噪声的某些统计特性,同时又能够重复产生。
1.m序列
m序列是最长线性反馈移位寄存器的简称,它是由带线性反馈的移位寄存器产生的周期最长的序列。
(1)与产生m序列有关的3个方程:
①递推方程:
②特征方程:
③母函数:
用代数方程表示反馈移存器的输出序列{a},且有f(x)g(x)=h(x),式中,h(x)为次数低f(x)次数的多项式。
(2)原本多项式
若一个n次多项式f(x)满足下列条件:
①f(x)为既约的;②f(x)可整除(x m+1),m=2n-1;③f(x)除不尽(x q+1),q<m,q<m;
则称f(x)为本原多项式。
(3)反馈移位寄存器能产生m序列的充要条件:反馈移存器的特征多项式为本原多项式。
一个n级线性反馈移位寄存器之相继状态具有周期性,周期为p<2n-1。
(4)m序列的性质
①均衡性:在m序列的一个周期中“1”和“0’的数目基本相等。
②游程分布:在m序列中,长度为k的游程占游程总数的2-k,1<k≤n-l,在长度为k,1<k≤n-2的游程中,连“1”的游程和连“0”的游程各占一半。
③移位相加特性:一个m序列M p与其经过任意次迟延移位产生的另一不同序列M r 模2相加,得到的仍是M p的某次迟延移位序列M s,即。
④自相关函数:m序列的自相关函数为:
⑤伪噪声特性:由于m序列的均衡性、游程分布、自相关特性和功率谱等与随机序列的性质相似,所以常认为m序列属于伪噪声序列或伪随机序列。
2.M序列
由非线性反馈移存器产生的周期最长的序列简称为M序列。
其最长周期可达2n。
M序列具有和m序列类似的均衡性和游程分布特性,但不具有m序列的移位相加特性及双值自相关特性。
其最主要的优点是数量大,即同样级数π的移存器能够产生的平移不等价M序列,总数比m序列大得多,且随n的增大迅速增加。
三、扩展频率普通信
扩展频谱是指将信号的频谱扩展至占用很宽的频带,简称扩频。
1.扩频技术的分类
(1)直接序列扩频:用一段伪随机序列(又称为伪码)表示一个信息码元,对载波进行调制。
伪码的一个单元称为一个码片。
(2)跳频:使发射机的载波在一个信息码元的时间内,按照预定的规律,离散地快速跳变,从而达到扩频的目的。
载频跳变的规律一般也是由伪码控制的。
(3)线性调频:载频在一个信息码元时间内在一个宽的频段中线性地变化,从而使信号带宽得到扩展。
2.扩频的目的
(1)提高抗窄带干扰的能力,例如敌对电台的有意干扰;(2)防止窃听;(3)提高抗多径传输效应的能力;(4)使多个用户可以共用同一频带;(5)提供测距能力。
四、伪随机序列的其他应用
伪随机序列可用于误码率测量、时延测量、噪声发生器、通信加密、数据序列的扰乱与解扰、扩展频谱通信以及分离多径等方面。
12.2课后习题详解
【12-1】一个3级线性反馈移存器,已知其特征方程为f(x)=1+x 2+x 3,试验证它为本原多项式。
证明
(1)23
1f (x )x x =++的最高次幂为3,且无法继续因式分解,故f(x)是既约的;(2)令3
217m =-=,有7432231111m x x x x x f (x )x x +-==+++++即f(x)能整除1m
x +;
(3)经验证,1q x +(其中q m <)都不能被f(x)整除。
综上,231f (x )x x =++是本原多项式。
【12-2】已知3级线性反馈移存器的原始状态为111,试写出两种m 序列的输出序列。
解:三级线性反馈移存器的生成多项式有两种情况:
(1)本原多项式32
1f (x )x x =++,此时线性反馈移存器如图12.1所示:
图12.1
其工作状态如下:
则原始状态为111时,其输出序列为:11110010。
(2)本原多项式3
1f (x )x x =++,此时线性反馈移存器如图12.2所示:
图12.2
其工作状态如下:
则原始状态为111时,其输出序列为:11110100。
【12-3】一个4级线性反馈移存器的特征方程为f(x)=x 4+x 3+x 2+x+1,试证明由它所产生的序列不是m 序列。
