如何使用MATLAB创建一个最简单地程序
matlab 编写界面例程

matlab 编写界面例程如何使用MATLAB编写界面例程?MATLAB是一种强大的数值计算和数据可视化软件,它提供了许多用于处理和分析数据的功能。
为了更方便地使用这些功能,MATLAB还提供了编写界面例程的能力。
本篇文章将一步一步回答如何使用MATLAB编写界面例程。
第一步:理解界面例程的概念界面例程是一个允许用户以图形化方式与MATLAB功能交互的程序。
它们通常包含一个或多个图形界面元素,如按钮、滑块、文本框等,用于获取用户的输入和展示输出结果。
第二步:选择界面例程的类型在MATLAB中,可以使用不同的工具箱和函数库来创建各种不同类型的界面例程。
例如,可以使用MATLAB App Designer来创建交互式应用程序,使用MATLAB GUIDE来创建经典的GUI界面,或者使用命令行界面来实现简单的交互。
第三步:创建界面和设计布局一旦选择了适当的界面类型,就可以开始创建界面并设计布局。
界面设计可以通过拖放图形界面元素来完成,也可以通过编写代码来实现更高级的定制。
在App Designer中,可以使用可视化编辑器来创建和编辑界面。
在GUIDE中,可以使用可视化布局编辑器来设计布局。
在命令行界面下,可以使用MATLAB命令来创建和修改界面元素。
第四步:添加交互功能界面例程的核心功能是与用户的交互。
为了实现这一点,需要添加交互功能,例如按钮点击、滑块滑动、文本框输入等。
在App Designer中,可以使用交互式编辑器来添加交互功能。
在GUIDE中,可以添加回调函数来处理用户交互事件。
在命令行界面下,可以编写脚本来实现交互功能。
第五步:处理用户输入和计算结果一旦用户与界面进行交互,就需要处理用户的输入,并根据输入计算结果。
这可以通过添加MATLAB代码来实现。
在App Designer和GUIDE中,可以在回调函数中编写代码来处理用户输入和计算结果。
在命令行界面下,可以编写脚本来实现相同的功能。
第六步:展示结果和反馈最后,需要将计算结果展示给用户,并提供任何必要的反馈。
matlab b样条曲面程序

matlab b样条曲面程序在MATLAB中,使用B样条曲面(B-Spline Surface)需要使用`bsxfun`函数或`meshgrid`函数来生成网格,然后通过`bspline_bivariate`或`spmak`函数创建B样条曲面。
以下是一个简单的MATLAB示例,演示如何创建B样条曲面:```matlab%定义B样条曲面的控制点ctrl_points=[000;100;200;300;011;112;211;310;020;12-1;220;320;030;130;230;330];%定义B样条曲面的节点矢量knots_u=[00001111];knots_v=[00001111];%创建B样条曲面spline_surface=spmak({knots_u,knots_v},ctrl_points');%生成网格u=linspace(0,1,100);v=linspace(0,1,100);[u,v]=meshgrid(u,v);%评估B样条曲面evaluated_surface=fnval(spline_surface,{u,v});%绘制B样条曲面surf(evaluated_surface(:,:,1),evaluated_surface(:,:,2),evaluated_surface(:,:,3));xlabel('X轴');ylabel('Y轴');zlabel('Z轴');title('B样条曲面');```请根据你的实际情况修改控制点、节点矢量以及其他参数。
这个示例中,`ctrl_points`定义了B样条曲面的控制点,`knots_u`和`knots_v`定义了曲面的节点矢量。
通过`spmak`函数创建B样条曲面对象,然后使用`fnval`函数在给定的网格上评估曲面,最后使用`surf`函数绘制曲面。
gurobi在matlab上的程序实现

Gurobi是一个用于线性规划,混合整数规划等优化问题的求解器。
以下是一个简单的Gurobi在Matlab上的程序实现示例。
假设我们有一个简单的线性规划问题:matlabfunction main% 创建一个模型model = gurobi.Model('myModel');% 添加变量x = model.addVar(0, Inf, 0, gurobi.BINARY, 'x');y = model.addVar(0, Inf, 0, gurobi.BINARY, 'y');% 添加约束条件model.addConstr(2*x + y <= 4, 'c0');model.addConstr(x + 3*y >= 3, 'c1');% 设定目标函数model.setObjective(3*x + y, gurobi.MAXIMIZE);% 优化求解status = model.optimize();% 显示结果fprintf('Status: %s\n', model.getStatus());fprintf('Obj: %f\n', model.get(gurobi.attr.ObjVal));x.display();y.display();end这个程序的目标函数是最大化3x + y,约束条件是2x + y <= 4和x + 3y >= 3,x和y都是二进制变量。
注意:运行此代码需要安装Gurobi和Matlab的Gurobi接口。
这是一个非常基本的示例,实际使用中可能需要更复杂的模型和算法。
在使用Gurobi时,可以参考Gurobi的官方文档和教程,了解更多关于如何使用Gurobi进行优化的信息。
牛顿插值matlab程序

牛顿插值matlab程序牛顿插值是一种多项式插值方法,其基本思想是利用分差表来构造一个一次到n 次多项式,从而逼近给定的数据点集合。
牛顿插值法有着计算简单,精度高,兼容性好等优点。
在Matlab中,牛顿插值法的实现非常简单。
接下来将介绍如何使用Matlab编写牛顿插值程序。
首先,我们需要明确牛顿插值法的基本思想,这可以用一个公式表示:f(x)≈Nn(x)=y0+C1(x−x0)+C2(x−x0)(x−x1)+⋯+Cn(x−x0)(x−x1)⋯(x−xn−1)其中y0即为给定数据点中的第一个点的纵坐标,x0到xn-1为已知的节点,Ci 表示节点x0到xi的差商,x为我们要求解的插值点。
据此,我们可以编写如下的Matlab代码实现牛顿插值:matlabfunction [result] = newton_interpolation(x, y, z)% x, y为已知的节点,z为插值点n = length(x);diff = zeros(n, n);diff(:, 1) = y';for j = 2:nfor i = j:ndiff(i, j) = (diff(i, j-1) - diff(i-1, j-1)) / (x(i) - x(i-j+1));endendresult = diff(n, n);for k = n-1:-1:1result = diff(k, k) + (z - x(k)) * result;end我们首先定义一个函数newton_interpolation,其输入为已知节点x和纵坐标y,以及插值点z。
接着,我们使用双重循环来计算分差表,并按照公式计算插值多项式的值。
最后,我们得到了插值点z处的函数值。
需要注意的是,在计算分差表时,我们需要根据已知的节点计算出所有的差商,并记录在diff中。
在计算插值点z处的函数值时,我们需要按照公式从n-1到0依次计算出多项式的各项系数。
如何使用MATLAB创建一个最简单的程序

如何使用MATLAB创建一个最简单的程序使用MATLAB创建一个最简单的程序可以按照以下步骤进行:
例如,你可以使用disp函数在命令窗口中打印消息:
```
disp('Hello, World!');
```
或者,你可以使用fprintf函数在命令窗口中输出格式化的文本:```
fprintf('The sum of 2 and 3 is %d\n', 2+3);
```
这里,%d是一个格式化占位符,它将被替换为一个整数值。
4.运行程序。
在MATLAB命令窗口中,输入脚本文件名(不带.m扩展名),并按下回车键即可运行程序。
例如,如果你的脚本文件名为hello_world,你可以在命令窗口中输入:
```
hello_world
```
这将执行你所编写的MATLAB程序,并在命令窗口中显示输出结果。
以上是创建最简单的MATLAB程序的基本步骤。
此外,MATLAB还提供了一系列丰富的功能和工具箱,可以用于进行数值计算、绘图和数据分析等。
你可以在程序中使用这些功能来实现更复杂的任务。
如何使用MATLAB创建一个最简单的程序
如何使用MATLAB创建一个最简单的程序
网上很多有关于MATLAB的介绍,都是在讲MATLAB有这样那样的功能,但就是没有人讲用如何用MATLAB创建一个最简单的程序,毕竟万事开头难,在这里我就讲一讲如何用MATLAB创建一个最简单的程序.
第一步,肯定是打开MATLAB啦
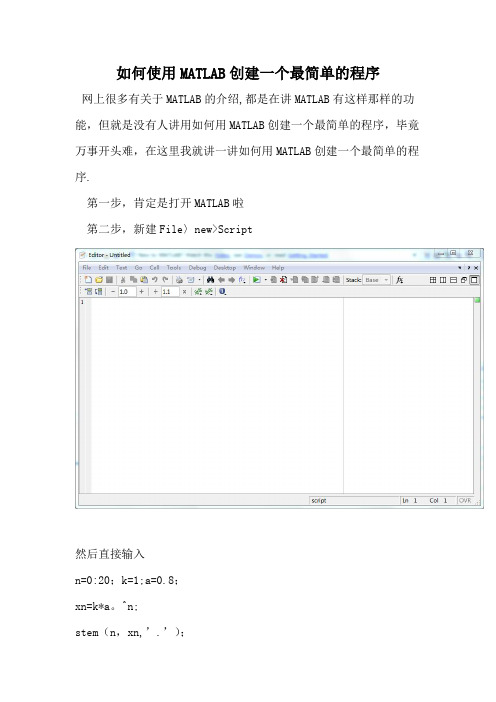
第二步,新建File〉new>Script
然后直接输入
n=0:20;k=1;a=0.8;
xn=k*a。
^n;
stem(n,xn,’.’);
(这个程序是显示指数序列的图形)
第三步,点击run按钮
会让你选择保存路径,这里我直接保存到了桌面,然后可能会跳出下面这个选项框
意思大概是在文件不是保存在默认的文件路径中的,是要添加路径还是更改当前工作路径。
选择change folder更改当前工作路径更简单一点。
然后显示结果了
很简单的,一看就会,希望可以给五星评价哦。
matlab坐标转换程序

MATLAB坐标转换程序简介MATLAB是一种强大的数学计算软件,适用于矩阵计算、数据绘图、算法开发等领域。
在处理与二维或三维坐标相关的问题时,MATLAB提供了一些方便的函数和方法来进行坐标转换。
本文将介绍如何使用MATLAB编写一个简单的坐标转换程序。
背景在许多科学和工程应用中,需要在不同的坐标系之间进行转换。
例如,一个物体在笛卡尔坐标系中的位置可能需要转换为极坐标系中的位置。
MATLAB提供了处理这种坐标转换的函数和方法,使得程序的编写变得简单和方便。
坐标转换为了演示坐标转换程序的编写过程,假设我们要将三维笛卡尔坐标系中的点转换为极坐标系中的点。
具体而言,我们将从用户输入得到三维点的X、Y和Z坐标,然后将其转换为极径、极角和Z坐标,并输出转换后的结果。
下面是MATLAB代码的示例:% 获取用户输入的三维坐标x = input('请输入X坐标:');y = input('请输入Y坐标:');z = input('请输入Z坐标:');% 坐标转换[rho, theta, phi] = cart2sph(x, y, z);% 输出转换结果disp(['转换后的极径:', num2str(rho)]);disp(['转换后的极角:', num2str(theta)]);disp(['转换后的Z坐标:', num2str(phi)]);在这个例子中,input函数用于获取用户输入的三维坐标值。
cart2sph函数用于将笛卡尔坐标转换为极坐标。
转换后的结果存储在rho、theta和phi变量中。
最后,使用disp函数输出转换后的结果。
使用示例让我们通过一个示例来演示如何使用这个坐标转换程序。
假设我们希望将三维坐标(3, 4, 1)转换为极坐标。
我们可以按照以下步骤进行:1.运行MATLAB程序。
2.在提示下输入X坐标: 3。
密码锁编程 matlab程序

密码锁编程 matlab程序密码锁编程 Matlab 程序引言概述:密码锁编程是一种常见的应用程序开发技术,它在现代生活中起到了重要的作用。
本文将介绍如何使用 Matlab 编程语言来开发一个密码锁程序。
通过这个程序,我们可以实现密码的输入、验证和控制等功能,以保护重要信息和财产的安全。
正文内容:1. 密码输入界面1.1 设计用户界面:使用 Matlab 的 GUI 工具箱,创建一个密码输入界面。
1.2 输入密码功能:通过文本框或按钮等控件,允许用户输入密码。
1.3 密码长度限制:设置密码的最小和最大长度,确保密码的安全性。
2. 密码验证功能2.1 密码加密算法:使用 Matlab 提供的加密函数,对用户输入的密码进行加密。
2.2 存储密码:将加密后的密码存储在数据库或文件中,以供后续验证使用。
2.3 密码比对:在用户再次输入密码时,对输入的密码与存储的密码进行比对,判断其是否一致。
3. 锁定与解锁功能3.1 密码错误次数限制:设置密码输入错误的次数限制,达到限制后锁定密码输入。
3.2 锁定时间设置:在密码输入错误次数达到限制后,设置一段时间的锁定时间,以防止暴力破解。
3.3 解锁方式:在锁定时间结束后,允许用户通过输入特定的解锁密码或通过其他验证方式解锁密码。
4. 安全性增强功能4.1 防止密码截获:使用 SSL/TLS 等安全协议,对密码传输过程进行加密,防止密码被截获。
4.2 强制密码更改:定期要求用户更改密码,以增加密码的安全性。
4.3 防止暴力破解:设置密码输入次数限制、锁定时间和复杂度要求,以防止暴力破解密码。
5. 扩展功能5.1 多用户支持:允许多个用户使用密码锁,每个用户拥有独立的密码和权限。
5.2 远程控制:通过网络连接,允许用户远程控制密码锁,进行密码的输入和验证。
5.3 日志记录:记录密码输入、验证和控制的日志,以便后续审计和追踪。
总结:通过本文的介绍,我们了解了如何使用 Matlab 编程语言开发一个密码锁程序。
matlab加工自由曲面程序代码

一、引言Matlab是一种高级技术计算语言和交互环境,被广泛用于工程、科学和数学领域的计算与模拟。
在Matlab中,加工自由曲面是一项常见的任务,例如创建和修改三维曲面模型。
本文将介绍如何使用Matlab 编写程序代码来加工自由曲面,以实现对曲面的精确控制和调整。
二、准备工作在编写程序代码之前,首先需要明确自由曲面的定义和参数化方法。
自由曲面通常由参数方程或控制点构成,对于不同的曲面类型,需要选择合适的参数化方法。
还需要了解Matlab中与曲面加工相关的函数和工具,以便在编写程序时能够调用这些资源。
三、编写程序代码1. 定义自由曲面在Matlab中,可以使用符号变量和代数表达式定义自由曲面的参数方程。
对于二次曲面,可以使用二次多项式表示其参数方程。
具体代码如下:syms u vx = a*u^2 + b*v^2 + c*u*v + d*u + e*v + f;y = g*u^2 + h*v^2 + i*u*v + j*u + k*v + l;z = m*u^2 + n*v^2 + o*u*v + p*u + q*v + r;其中a-r为曲面的系数,u和v为曲面的参数。
2. 控制曲面形状通过调整曲面的参数和系数,可以控制曲面的形状。
可以通过改变系数a-r的值来实现对曲面的放大缩小、旋转、偏移等操作。
具体代码如下:a = 1;b = 1;c = 0;d = 0;e = 0;f = 0;g = 1; h = 1; i = 0; j = 0; k = 0; l = 0;m = 1; n = 1; o = 0; p = 0; q = 0; r = 0;这里以简单的二次曲面为例,通过调整系数的数值来控制曲面的形状。
3. 曲面绘制和可视化在定义和控制曲面之后,可以使用Matlab中的绘图函数将曲面绘制出来。
可以使用surf函数创建曲面图形,并通过设置图形属性来进行可视化调整。
具体代码如下:[u, v] = meshgrid(-2:0.1:2);x = a*u.^2 + b*v.^2 + c*u.*v + d*u + e*v + f;y = g*u.^2 + h*v.^2 + i*u.*v + j*u + k*v + l;z = m*u.^2 + n*v.^2 + o*u.*v + p*u + q*v + r;surf(x, y, z);四、应用实例在实际应用中,自由曲面加工可以用于创建各种复杂的曲面模型。
电力系统短路故障分析的MATLAB辅助程序设计短路计算程序

电力系统短路故障分析的MATLAB辅助程序设计短路计算程序电力系统短路故障分析是电力系统设计和运行过程中非常重要的一环。
短路故障会导致电力系统各个部分的电压、电流和功率的突然变化,对设备的保护和稳定运行产生不利影响甚至引起事故。
因此,进行短路计算和故障分析非常必要。
MATLAB是一种功能强大的数值计算和数据可视化工具,对于电力系统短路计算和故障分析也可以发挥重要的作用。
下面将介绍如何使用MATLAB设计一个简单的电力系统短路计算程序。
首先,我们需要建立一个电力系统的模型。
电力系统可以用图模型表示,其中节点表示发电机、变压器、负荷等设备,边表示导线、变压器等电力连接。
我们可以使用MATLAB中的图模型工具箱创建电力系统模型,并且设置各个节点和边的属性,例如电压、电流、阻抗等。
然后,我们需要编写短路计算程序。
短路计算可以分为对称故障和不对称故障两种情况。
对称故障是指短路故障发生在电力系统的正常运行条件下,例如三相短路。
不对称故障是指短路故障发生在电力系统的不正常运行条件下,例如单相接地短路。
对于对称故障,我们可以使用节点电流法进行计算。
首先,应用基尔霍夫电流定律,根据电压和阻抗计算电流。
然后,根据节点电流方程和电流方程计算电流分布。
最后,根据电流分布计算短路电流和故障点的电压。
对于不对称故障,我们可以使用仿真方法进行计算。
首先,需要设置故障位置和故障类型,例如A相到地短路。
然后,根据故障位置和类型修改节点和边的参数,例如将故障位置的阻抗设置为零。
最后,使用数值方法求解电力系统的动态响应,得到短路电流和故障点的电压。
在MATLAB中,可以使用矩阵运算和数值求解函数实现短路计算。
例如,可以使用矩阵乘法和矩阵求逆函数计算节点电流和电流分布。
可以使用ODE求解器求解动态响应方程。
可以使用MATLAB的绘图函数绘制电力系统的电流分布和故障点的电压。
总结起来,电力系统短路故障分析的MATLAB辅助程序设计涉及建立电力系统模型、编写短路计算程序并使用MATLAB的数值计算和数据可视化工具进行计算和分析。
matlab行最简形代码

matlab行最简形代码1.引言1.1 概述概述部分旨在介绍本篇文章的主题以及要解决的问题。
本文标题为《Matlab行最简形代码》,主要讨论如何在编写Matlab代码时尽可能简洁地表达功能。
对于编程初学者或者需要快速开发的程序员来说,编写简洁的代码非常重要,可以提高代码的可读性和可维护性。
在实际的编程过程中,我们经常会遇到重复的操作,比如循环、条件判断等。
传统的写法往往需要几行甚至更多的代码来完成,这不仅增加了代码的长度,还增加了出错的可能性。
而Matlab行最简形代码则通过巧妙地运用Matlab的特性和语法糖,可以将原本需要多行代码实现的功能简化为一行。
这种简洁的代码不仅方便了程序员的编写,而且提高了代码的效率和可读性。
本文将围绕Matlab行最简形代码的定义展开阐述。
首先,我们将介绍背景信息,包括Matlab的特点和应用领域。
然后,我们将详细阐述什么是Matlab行最简形代码,包括它的特点、优势和适用场景。
同时,我们还将提供一些示例代码,以帮助读者更好地理解和应用这一编程风格。
最后,我们将总结本文的主要观点,并展望未来Matlab行最简形代码的发展前景。
希望通过本文的阐述,读者能够更好地理解和应用这种简洁的编程风格,从而提升自己的编程能力和工作效率。
文章结构部分的内容如下:1.2 文章结构本文主要包含以下几个部分:1. 引言:介绍本文的背景、目的和概述。
2. 正文:包括背景介绍和Matlab行最简形代码的定义两个小节。
2.1 背景介绍:简要介绍Matlab编程语言及其在科学和工程领域的应用,突出Matlab行最简形代码的重要性。
2.2 Matlab行最简形代码的定义:详细解释Matlab行最简形代码的概念,包括代码简洁性、可读性和高效性等方面的内容。
3. 结论:对本文进行总结,并对Matlab行最简形代码的发展前景进行展望。
3.1 总结:总结本文的主要内容,强调Matlab行最简形代码对于提高编程效率和代码质量的重要性。
matlab程序设计教程第三版 实验指导

matlab程序设计教程第三版实验指导MATLAB 是一种非常强大的数学软件工具,可以用于问题建模、算法实现、数据分析和可视化等多个领域。
本实验指导将引导读者从基本的程序设计开始,逐步学习如何使用 MATLAB 进行编程。
在开始编程之前,我们首先要熟悉 MATLAB 的界面。
MATLAB 的界面非常直观和友好,具有丰富的交互功能和图形界面。
我们将逐步介绍 MATLAB 工作环境中的各个组件,并向读者展示如何创建新的脚本文件、运行代码以及调试程序。
接下来,我们将深入研究 MATLAB 编程的核心概念和语法。
我们将介绍如何定义变量、进行数学运算、编写条件语句和循环结构,以及如何使用函数和脚本文件。
我们还将探讨如何创建和操作矩阵、处理字符串和字符数组,并介绍 MATLAB 中常用的文件处理和输入输出操作。
在学习完基本的 MATLAB 编程知识后,我们将进一步学习如何解决实际的问题和应用。
我们将通过一系列的实例,引导读者学习如何构建和调试复杂的算法,如排序、搜索、图形绘制等。
我们还将介绍如何处理和分析实际的数据集,包括数据读取、预处理、统计分析和可视化等。
最后,我们将介绍如何通过 MATLAB 进行更高级的编程和应用开发。
我们将向读者展示如何编写自定义函数和类,以及如何使用MATLAB 的工具箱和库函数进行更加专业和复杂的编程任务。
我们还将了解如何编写 GUI 界面程序,以及如何进行并行计算和部署应用程序。
通过本实验指导的学习,读者将能够掌握 MATLAB 的基本编程技巧和应用技术,并能独立解决实际问题。
无论是从事科学研究、工程设计还是数据分析和可视化,MATLAB 都是一种非常有用和高效的工具。
希望本实验指导能够为读者提供全面、生动和有指导意义的学习内容,帮助读者在 MATLAB 的世界中游刃有余。
第5掌 MATLAB程序设计及应用实例2

matlab用户可以根据需要编辑自己的m文件,
它们可以像库函数一样方便的调用,从而极大地
扩展了matlab 的能力。 对于某一类特殊问题,如创建了许多m函数文件, 则可形成新的工具箱。 用matlab语言创建定义新的matlab函数的功 能,正体现了matlab语言强大的扩展功能。
5.4 选择结构-try语句
语句格式为: try 语句组1 catch 语句组2 end
try语句先试探性执行语句组1,如果语句组1在执行过 程中出现错误,则将错误信息赋给保留的lasterr变量, 并转去执行语句组2。这种试探性执行语句是其他高级 语言所没有的。
例 矩阵乘法运算要求两矩阵的维数相容,否则会出错。先 求两矩阵的乘积,若出错,则自动转去求两矩阵的点乘
函数的递归调用 例:利用递归调用函数文件factor.m: function f=factor(n) if n<=1 f=1; else f=factor(n-1)*n; end 然后在MATLAB命令窗口调用该函数:
f=factor(5)
f=5!
(2)函数文件的调用
函数所传递参数的可调性
条件 语句组
2.双分支if语句
双分支if语句格式为:
if 条件 语句组1 语句组2 end 当条件成立时,执行语句组1,否则执行语句组 2,语句组1或语句组2执行后,再执行if语句的 后继语句。
else
例 计算分段函数值
程序如下: x=input('请输入x的值:'); if x==10 y=cos(x+1)+sqrt(x*x+1); else y=x*sqrt(x+sqrt(x)); end y
matlab中cmake命令

matlab中cmake命令CMake是一款开源的跨平台构建工具,它可以帮助开发人员更轻松地管理和构建其项目。
在Matlab中,CMake命令被用于编译和构建Matlab 代码。
本文将介绍CMake的基础知识以及如何在Matlab中使用CMake 命令来构建项目。
第一步:了解CMake基础知识CMake(Cross-platform Make)是一个跨平台的构建工具,它可以通过一个简单的配置文件来生成项目构建脚本。
CMake支持多种编程语言,包括C/C++、Fortran、Python等,并能够自动生成适用于不同操作系统和编译器的构建脚本。
CMake通过生成Makefiles或者其他本地构建系统来实现项目的编译和构建。
其主要特点包括跨平台、简单易学、高效等。
第二步:安装CMake在使用CMake之前,我们需要先安装CMake工具。
前往官方网站第三步:创建CMakeLists.txt文件在开始使用CMake命令之前,我们需要先创建一个名为CMakeLists.txt 的文件,该文件是CMake的核心配置文件。
在Matlab项目目录中创建一个文本文件,将其命名为"CMakeLists.txt"。
第四步:配置CMakeLists.txt文件在CMakeLists.txt文件中,我们需要指定项目的名称、版本号、编译选项、依赖库等。
以下是一个简单的CMakeLists.txt文件示例:# minimum required version of CMakecmake_minimum_required(VERSION 3.0)# set project name and versionproject(MyProject VERSION 1.0)# set compiler and flagsset(CMAKE_CXX_COMPILER g++)set(CMAKE_CXX_FLAGS "{CMAKE_CXX_FLAGS} -std=c++11 -Wall")# add source filesset(SOURCES main.cpp utils.cpp)# add executableadd_executable(myapp {SOURCES})# link librariestarget_link_libraries(myapp mylib)在以上示例中,我们首先指定了CMake的最低版本号为3.0。
matlab求素数的程序

matlab求素数的程序MATLAB是一款流行的科学计算软件,在其中编写程序来计算素数是一个常见的任务。
本文将介绍如何使用MATLAB编写一个求素数的程序。
1. 理解素数首先,我们需要理解素数的概念。
素数是只能被1和它本身整除的正整数。
比如,2、3、5、7、11等都是素数,而4、6、8、9、10等都不是素数。
2. 编写程序我们将使用MATLAB来编写一个求素数的程序。
请按照以下步骤操作:(1)创建一个新的MATLAB脚本文件。
(2)定义任意一个正整数n,我们将从1开始枚举每一个小于等于n的正整数。
n = 100;(3)使用一个for循环来遍历1到n之间的每个整数。
for i=1:n(4)我们使用一个布尔变量isPrime来记录当前的数字是否为素数,初始值为true。
isPrime = true;(5)接下来,我们将枚举2到i之间的每个正整数,如果其中存在i能被整除的数,那么i不是一个素数。
我们可以使用一个for 循环来枚举2到i-1之间的每个数。
for j=2:i-1if mod(i,j)==0isPrime = false;break;endend(6)如果isPrime为true,那么说明i是一个素数,我们将其输出到命令窗口。
if isPrime == truedisp(i)end(7)我们将for循环嵌套在一个函数中,并将n作为函数的输入参数。
function primes = getPrimes(n)primes = [];for i=1:nisPrime = true;for j=2:i-1if mod(i,j)==0isPrime = false;break;endendif isPrime == trueprimes = [primes i];endend(8)现在我们可以调用该函数并输出结果:primes = getPrimes(100);disp(primes);3. 检验结果最后我们需要检查输出的结果是否正确。
关于小波分析的matlab程序

关于小波分析的matlab程序小波分析是一种在信号处理和数据分析领域中广泛应用的方法。
它可以匡助我们更好地理解信号的时域和频域特性,并提供一种有效的信号处理工具。
在本文中,我将介绍小波分析的基本原理和如何使用MATLAB编写小波分析程序。
一、小波分析的基本原理小波分析是一种基于窗口函数的信号分析方法。
它使用一组称为小波函数的基函数,将信号分解成不同频率和不同时间尺度的成份。
与傅里叶分析相比,小波分析具有更好的时频局部化性质,可以更好地捕捉信号的瞬时特征。
小波函数是一种具有局部化特性的函数,它在时域上具有有限长度,并且在频域上具有有限带宽。
常用的小波函数有Morlet小波、Haar小波、Daubechies小波等。
这些小波函数可以通过数学运算得到,也可以通过MATLAB的小波函数库直接调用。
小波分析的基本步骤如下:1. 选择合适的小波函数作为基函数。
2. 将信号与小波函数进行卷积运算,得到小波系数。
3. 根据小波系数的大小和位置,可以分析信号的时频特性。
4. 根据需要,可以对小波系数进行阈值处理,实现信号的去噪和压缩。
二、MATLAB中的小波分析工具MATLAB提供了丰富的小波分析工具箱,可以方便地进行小波分析的计算和可视化。
下面介绍几个常用的MATLAB函数和工具箱:1. `waveinfo`函数:用于查看和了解MATLAB中可用的小波函数的信息,如小波函数的名称、支持的尺度范围等。
2. `wavedec`函数:用于对信号进行小波分解,得到小波系数。
3. `waverec`函数:用于根据小波系数重构原始信号。
4. `wdenoise`函数:用于对小波系数进行阈值处理,实现信号的去噪。
5. 小波分析工具箱(Wavelet Toolbox):提供了更多的小波分析函数和工具,如小波变换、小波包分析、小波阈值处理等。
可以通过`help wavelet`命令查看工具箱中的函数列表。
三、编写小波分析程序在MATLAB中编写小波分析程序可以按照以下步骤进行:1. 导入信号数据:首先需要导入待分析的信号数据。
实验3MATLAB程序设计

实验3MATLAB程序设计实验目的:学习使用MATLAB进行程序设计,掌握MATLAB中的函数、循环和条件语句的使用。
实验内容:设计一个MATLAB程序,实现以下功能:1.根据给定的身高和体重计算BMI指数;2.根据BMI指数判断体重状况,分为偏瘦、正常、超重和肥胖四种情况;3.将计算得到的BMI指数和体重状况进行输出。
实验步骤:1.首先,创建一个新的MATLAB脚本文件,命名为"BMI.m";2. 定义两个变量,height表示身高(单位:米),weight表示体重(单位:千克);3.根据给定的身高和体重计算BMI指数,使用公式:BMI = weight / (height^2);4. 利用MATLAB中的条件语句,判断BMI指数对应的体重状况,将结果存储在一个字符串变量status中,例如:当BMI < 18.5时,status = '偏瘦';当18.5 <= BMI < 24时,status = '正常';当24 <= BMI < 28时,status = '超重';当BMI >= 28时,status = '肥胖';5. 输出计算得到的BMI指数和体重状况,使用MATLAB中的disp函数,例如:disp(['BMI指数为:', num2str(BMI)]);disp(['体重状况为:', status]);6.保存并运行脚本文件,输入身高和体重,观察输出结果。
实验注意事项:1.身高应为正数,体重应为非负数;2.在计算BMI指数时,注意身高的单位应与体重的单位相匹配;3.判断体重状况时,注意条件语句的范围划分,避免重叠和遗漏;4.观察输出结果,检查是否符合预期。
实验总结:本次实验通过设计一个MATLAB程序,实现了根据身高和体重计算BMI指数并判断体重状况的功能。
niqe matlab 示例程序

niqe matlab 示例程序当涉及到 MATLAB 的示例程序时,有很多不同的方向可以探讨。
首先,我们可以讨论一些基本的示例程序,比如如何在 MATLAB 中创建矩阵、向量或者数组,以及如何对它们进行操作和运算。
另外,我们也可以讨论一些高级的示例程序,比如如何使用 MATLAB 进行数据可视化、图像处理或者机器学习等方面的应用。
举个例子,我们可以创建一个简单的 MATLAB 示例程序来计算两个矩阵的乘积。
首先,我们可以定义两个矩阵 A 和 B,然后使用MATLAB 的矩阵乘法运算符来计算它们的乘积。
下面是一个示例程序:matlab.A = [1, 2, 3; 4, 5, 6; 7, 8, 9];B = [9, 8, 7; 6, 5, 4; 3, 2, 1];C = A B;disp(C);这个示例程序中,我们首先定义了两个 3x3 的矩阵 A 和 B,然后使用矩阵乘法运算符计算它们的乘积,并将结果存储在矩阵C 中。
最后,我们使用 disp 函数来显示结果。
除了这个基本的示例程序之外,我们还可以讨论如何在 MATLAB 中进行数据可视化。
比如,我们可以创建一个简单的示例程序来绘制正弦函数的图像。
下面是一个示例程序:matlab.x = 0:0.1:2pi;y = sin(x);plot(x, y);xlabel('x');ylabel('sin(x)');title('Sine Function');在这个示例程序中,我们首先创建了一个包含从 0 到2π 的等间隔点的向量 x,然后计算了这些点的正弦值并存储在向量 y 中。
接下来,我们使用 plot 函数将 x 和 y 的值绘制成图像,并使用xlabel、ylabel 和 title 函数添加了坐标轴标签和标题。
除了这些示例程序之外,还有很多其他方面的示例程序,比如如何在 MATLAB 中读取和处理数据、如何进行图像处理、如何实现简单的机器学习算法等等。
lmi的matlab程序

lmi的matlab程序LMI的Matlab程序LMI(线性矩阵不等式)是一种常用的工具,用于解决线性系统控制问题。
Matlab是一种流行的数值计算软件,它提供了丰富的工具箱和函数库,可以帮助工程师和科学家解决各种数学和工程问题。
在本文中,我们将探讨如何使用Matlab编写和求解LMI的程序。
让我们简要介绍一下LMI。
LMI是一种特殊的线性不等式,其形式为AX + XB < C,其中A、B和C是已知的矩阵,X是待求解的变量矩阵。
LMI在控制理论和优化领域中有广泛的应用,例如线性系统稳定性分析、鲁棒控制设计和最优控制问题等。
在Matlab中,我们可以使用控制系统工具箱来编写和求解LMI。
首先,我们需要定义已知的矩阵A、B和C。
然后,我们可以使用lmi函数来创建LMI对象。
例如,我们可以使用以下代码创建一个LMI对象:```matlabA = [1 2; 3 4];B = [5 6; 7 8];C = [9 10; 11 12];LMI = lmi(A, B, C);```创建LMI对象后,我们可以使用lmiinfo函数来获取LMI的信息,例如LMI的维度和约束条件的数量。
例如,我们可以使用以下代码获取LMI的信息:```matlabinfo = lmiinfo(LMI);```接下来,我们可以使用lmiterm函数来添加约束条件。
约束条件可以是线性约束、二次约束或多项式约束。
例如,我们可以使用以下代码添加一个线性约束条件:```matlablmiterm([1 1 1 X], A', 1, 's');```在这个约束条件中,[1 1 1 X]表示约束项的位置和变量,A'表示已知矩阵A的转置,1表示约束项的系数,'s'表示约束的类型为小于等于。
添加约束条件后,我们可以使用lmisolve函数来求解LMI。
lmisolve函数将返回LMI的最优解,并将其存储在变量x中。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如何使用MATLAB创建一个最简单的程序
网上很多有关于MATLAB的介绍,都是在讲MATLAB有这样那样的功能,但就是没有人讲用如何用MATLAB创建一个最简单的程序,毕竟万事开头难,在这里我就讲一讲如何用MATLAB创建一个最简单的程序。
第一步,肯定是打开MATLAB啦
第二步,新建File>new>Script
然后直接输入
n=0:20;k=1;a=0.8;
xn=k*a.^n;
stem(n,xn, ’. ’);
( 这个程序是显示指数序列的图形)
第三步,点击run 按钮
会让你选择保存路径,这里我直接保存到了桌面,然后可能会跳出下面这个选项框
意思大概是在文件不是保存在默认的文件路径中的,是要添加路径还是更改当前工作路径。
选择change folder 更改当前工作路径更简单一点。
然后显示结果了
很简单的,一看就会,希望可以给五星评价哦。
