矩量法matlab程序设计实例
MATLAB程序设计及应用实例

c=input('请输入一个字符','s'); if c>='A' & c<='Z'
disp(setstr(abs(c)+1)); elseif c>='a'& c<='z'
disp(setstr(abs(c)-1)); elseif c>='0'& c<='9'
disp(abs(c)-abs('0')); else
disp(c); end
5.1.4 选择结构- switch语句
switch语句
其语句格式为: switch 表达式 case 值1 语句组1 case 值2 语句组2 …… case 值m 语句组m otherwise 语句组m+1 end
5.1.4 选择结构- switch语句
例 某商场对顾客所购买的商品实行打折销售,已知打折标 准,求所售商品的实际销售价格
例 矩阵乘法运算要求两矩阵的维数相容,否则会出错。 先求两矩阵的乘积,若出错,则自动转去求两矩阵的点乘
资料:23矩量法分析屏蔽带状线

作业23 用矩量法分析屏蔽带状线冯容辉一.题目:设有一长直屏蔽带状线,外导体为矩形金属柱面,矩形。
内导体为一宽度等于W的薄条的宽边和窄边分别为a和b,a b带,用矩量法分析该带状线。
屏蔽带状线的结构示意图:图1 屏蔽带状线的结构示意图二.使用MATLAB仿真可得:(1)单位电容、电感与特性阻抗与带状线宽度w的关系图2 单位电容与宽度w的关系图3 单位电感与宽度w的关系图4 单位特性阻抗与宽度w的关系三.源程序:function C=liu19(w,a,b)e0=8.854187818e-12;u0=pi*(4e-7);deltal=0.01;N1=w/deltal;N2=a/deltal;N3=b/deltal;N4=N2;N5=N3;N=N1+N2+N3+N4+N5;for m1=1:N1x1(m1)=-w/2+(m1-1/2)*deltal;y1(m1)=0;endfor m2=1:N2x2(m2)=-a/2+(m2-1/2)*deltal;y2(m2)=b/2;endfor m3=1:N3x3(m3)=a/2;y3(m3)=b/2-(m3-1/2)*deltal;endfor m4=1:N4x4(m4)=a/2-(m4-1/2)*deltal;y4(m4)=-b/2;endfor m5=1:N5x5(m5)=-a/2;y5(m5)=-b/2+(m5-1/2)*deltal;endx=[x1,x2,x3,x4,x5];y=[y1,y2,y3,y4,y5];dx=[deltal*ones(N1+N2,1);zeros(N3,1);deltal*ones(N4,1);zeros(N5,1)]; dy=[zeros(N1+N2,1);deltal*ones(N3,1);zeros(N4,1);deltal*ones(N5,1)]; c1=deltal^2;c2=c1;for m=1:Nfor n=1:Na1=(x(1)-x(n))^2+(y(1)-y(n))^2;b1=-2*(x(1)-x(n))*dx(n)+2*(y(1)-y(n))*dy(n);a2=(x(m)-x(n))^2+(y(m)-y(n))^2;b2=-2*(x(m)-x(n))*dx(n)-2*(y(m)-y(n))*dy(n);c1=deltal^2;c2=c1;p1=b1^2-4*a1*c1;if p1>=0s1(m,n)=(1/2+b1/2/c1)*log(a1+b1*1/2+c1*1/4)-2*1/2+sqrt(p1)/c1*atanh(( c1+b1)/sqrt(p1))-((-1/2+b1/2/c1)*log(a1-b1*1/2+c1*1/4)+2*1/2+sqrt(p1) /c1*atanh((-c1+b1)/sqrt(p1)));elses1(m,n)=(1/2+b1/2/c1)*log(a1+b1*1/2+c1*1/4)-2*1/2+sqrt(-p1)/c1*atan(( c1+b1)/sqrt(-p1))-((-1/2+b1/2/c1)*log(a1-b1*1/2+c1*1/4)+2*1/2+sqrt(-p 1)/c1*atan((-c1+b1)/sqrt(-p1)));endp2=b2^2-4*a2*c2;if p2>=0s2(m,n)=(1/2+b2/2/c2)*log(a2+b2*1/2+c2*1/4)-2*1/2+sqrt(p2)/c2*atanh(( c2+b2)/sqrt(p2))-((-1/2+b2/2/c2)*log(a2-b2*1/2+c2*1/4)+2*1/2+sqrt(p2) /c2*atanh((-c2+b2)/sqrt(p2)));elses2(m,n)=(1/2+b2/2/c2)*log(a2+b2*1/2+c2*1/4)-2*1/2+sqrt(-p2)/c2*atan(( c2+b2)/sqrt(-p2))-((-1/2+b2/2/c2)*log(a2-b2*1/2+c2*1/4)+2*1/2+sqrt(-p2)/c2*atan((-c2+b 2)/sqrt(-p2)));endS(m,n)=deltal*(s1(m,n)-s2(m,n));endendSS=S(2:N,:);SSS=[deltal*ones(1,N);SS];B=4*pi*e0*[ones(N1,1);zeros(N2+N3+N4+N5,1)];A=inv(SSS)*B;C=sum(A(1:N1))*deltal;clear all;clf;clc;d=1.2;e0=8.854*10^(-12);u0=4*pi*10^(-7);a=1;b=0.01;for k=1:6;w(k)=0.1+0.05*k;C(k)=liu19(w(k),a,b);L(k)=u0*e0/C(k);Z(k)=sqrt(L(k)/C(k));sumc=0;for n=1:2:1999CC(n)=4*a*sin(n*pi*w(k)/(2*a))*sinh(n*pi*b/(4*a))/((n*pi)^2*e0*cosh(n *pi*b/(2*a)));sumc=sumc+CC(n);endC1(k)=w(k)/sumc;L1(k)=u0*e0/C1(k);Z1(k)=sqrt(L1(k)/C1(k));%C1(k)=2*pi*e0/log(D(k)/d);%L1(k)=u0*e0/C1(k);%Z1(k)=sqrt(L1(k)/C1(k));%t(k)=C1(k)/C(k)endfigure(1)plot(w,C,'r-')hold onplot(w,C1,'b-')grid onlegend('½âÎö½â','¾ØÁ¿·¨')xlabel('´ø×´Ïß³¤¶Èw')ylabel('µ¥Î»³¤¶ÈµçÈÝ(F/m)')title('µ¥Î»µçÈÝËæ´ø×´Ïß³¤¶ÈwµÄ±ä»¯(a=1,b=0.01)') figure(2)plot(w,L,'r-')hold onplot(w,L1,'b-')grid onlegend('½âÎö½â','¾ØÁ¿·¨')xlabel('´ø×´Ïß³¤¶Èw')ylabel('µ¥Î»³¤¶Èµç¸Ð(H/m)')title('µ¥Î»µç¸ÐËæ´ø×´Ïß³¤¶ÈwµÄ±ä»¯(a=1,b=0.01)') figure(3)plot(w,Z,'r-')hold onplot(w,Z1,'b-')hold onlegend('½âÎö½â','¾ØÁ¿·¨')grid onxlabel('´ø×´Ïß³¤¶Èw')ylabel('ÌØÐÔ×迹(\Omega)')title('µ¥Î»ÌØÐÔ×迹Ëæ´ø×´Ïß³¤¶ÈwµÄ±ä»¯(a=1,b=0.01)')。
基于矩量法二维金属体散射(内含matlab程序)

基于矩量法的二维金属体散射计算1 问题的描述本题是用矩量法计算二维金属圆柱体的散射场,如图所示为一圆柱体和一个椭圆柱的截面,为了计算简单,选入射波为垂直z 轴入射的TM 或TE 平面波i z E i z E x22 矩量法求解过程电场积分方程问题的分析由麦克斯韦方程组H j E ωμ-=⨯∇ (1) J E j H +=⨯∇ωε (2)可得电场积分方程为''20')()(4)(ds K H J KZ E x z ρρρρ--=⎰⎰(3) 表示在圆柱表面的面电流在远处产生的总场。
设入射场为E i z ,散射场为E s z ,由金属表面的边界条件s z i z z E E E +==0 (4)得 ''20')()(4)(dl K H J KZE Cz iz ρρρρ-=⎰ (5) 离散化设入射波为)sin cos (φφy x jk iz eE +-=,将散射体截面C 分为N 份△C n ,用点匹配法对上述积分式子进行离散化, 即基函数可取{上在其它C n f ∆=10)(ρ (6)可得下列离散方程:[P]{J}={b} (7) 其中:dt y y x x K H KZ P m m C mn n))()((42220-+-=⎰∆ (8) )sin cos (i m i m y x ik m eb φφ+-= (9)当m ≠n 时,()))((42220m n m n n mn y y x x K H C KZ P -+-∆=(10) 当m=n 时 解析积分为⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛∆-∆=e C K j C ZK P n n nn 4lg 214γπ (11) 其中γ=,e=方程组的求解可用LU 分解求解方程组,即P=LU ,其中P 为可逆矩阵,L 为上三角矩阵,U 为下三角矩阵,则可利用这两个基本的三角矩阵进行求解J ,求出J 之后,就可求散射场dl e y x J KZF F y x jk z Cs ))sin()cos((),()(ϕϕφ+⎰= (12))4/3(81)(πρπρρ+-=K j e KF (13)与二维场中的散射截面2))sin()cos((2),(4)(dle y x J KZ y x jK Cz φφφσ+⎰=(14)输出结果的验证此散射问题也可用模式展开法进行求解,可用此结果对本问题进行验证。
matlab编程实例100例

1-32是:图形应用篇33-66是:界面设计篇67-84是:图形处理篇85-100是:数值分析篇实例1:三角函数曲线(1)function shili01h0=figure('toolbar','none',...'position',[198 56 350 300],...'name','实例01');h1=axes('parent',h0,...'visible','off');x=-pi:0.05:pi;y=sin(x);plot(x,y);xlabel('自变量X');ylabel('函数值Y');title('SIN( )函数曲线');grid on实例2:三角函数曲线(2)function shili02h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例02');x=-pi:0.05:pi;y=sin(x)+cos(x);plot(x,y,'-*r','linewidth',1);grid onxlabel('自变量X');ylabel('函数值Y');title('三角函数');实例3:图形的叠加function shili03h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例03');x=-pi:0.05:pi;y1=sin(x);y2=cos(x);plot(x,y1,...'-*r',...x,y2,...'--og');grid onxlabel('自变量X');ylabel('函数值Y');title('三角函数');实例4:双y轴图形的绘制function shili04h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例04');x=0:900;a=1000;b=0.005;y1=2*x;y2=cos(b*x);[haxes,hline1,hline2]=plotyy(x,y1,x,y2,'semilogy','plot'); axes(haxes(1))ylabel('semilog plot');axes(haxes(2))ylabel('linear plot');实例5:单个轴窗口显示多个图形function shili05h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例05');t=0:pi/10:2*pi;[x,y]=meshgrid(t);subplot(2,2,1)plot(sin(t),cos(t))axis equalsubplot(2,2,2)z=sin(x)-cos(y);plot(t,z)axis([0 2*pi -2 2])subplot(2,2,3)h=sin(x)+cos(y);plot(t,h)axis([0 2*pi -2 2])subplot(2,2,4)g=(sin(x).^2)-(cos(y).^2);plot(t,g)axis([0 2*pi -1 1])实例6:图形标注function shili06h0=figure('toolbar','none',...'position',[200 150 450 400],...'name','实例06');t=0:pi/10:2*pi;h=plot(t,sin(t));xlabel('t=0到2\pi','fontsize',16);ylabel('sin(t)','fontsize',16);title('\it{从0to2\pi 的正弦曲线}','fontsize',16) x=get(h,'xdata');y=get(h,'ydata');imin=find(min(y)==y);imax=find(max(y)==y);text(x(imin),y(imin),...['\leftarrow最小值=',num2str(y(imin))],...'fontsize',16)text(x(imax),y(imax),...['\leftarrow最大值=',num2str(y(imax))],...'fontsize',16)实例7:条形图形function shili07h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例07');tiao1=[562 548 224 545 41 445 745 512];tiao2=[47 48 57 58 54 52 65 48];t=0:7;bar(t,tiao1)xlabel('X轴');ylabel('TIAO1值');h1=gca;h2=axes('position',get(h1,'position'));plot(t,tiao2,'linewidth',3)set(h2,'yaxislocation','right','color','none','xticklabel',[]) 实例8:区域图形function shili08h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例08');x=91:95;profits1=[88 75 84 93 77];profits2=[51 64 54 56 68];profits3=[42 54 34 25 24];profits4=[26 38 18 15 4];area(x,profits1,'facecolor',[0.5 0.9 0.6],...'edgecolor','b',...'linewidth',3)hold onarea(x,profits2,'facecolor',[0.9 0.85 0.7],...'edgecolor','y',...'linewidth',3)hold onarea(x,profits3,'facecolor',[0.3 0.6 0.7],...'edgecolor','r',...'linewidth',3)hold onarea(x,profits4,'facecolor',[0.6 0.5 0.9],...'edgecolor','m',...'linewidth',3)hold offset(gca,'xtick',[91:95])set(gca,'layer','top')gtext('\leftarrow第一季度销量')gtext('\leftarrow第二季度销量')gtext('\leftarrow第三季度销量')gtext('\leftarrow第四季度销量')xlabel('年','fontsize',16);ylabel('销售量','fontsize',16);实例9:饼图的绘制function shili09h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例09');t=[54 21 35;68 54 35;45 25 12;48 68 45;68 54 69];x=sum(t);h=pie(x);textobjs=findobj(h,'type','text');str1=get(textobjs,{'string'});val1=get(textobjs,{'extent'});oldext=cat(1,val1{:});names={'商品一:';'商品二:';'商品三:'};str2=strcat(names,str1);set(textobjs,{'string'},str2)val2=get(textobjs,{'extent'});newext=cat(1,val2{:});offset=sign(oldext(:,1)).*(newext(:,3)-oldext(:,3))/2; pos=get(textobjs,{'position'});textpos=cat(1,pos{:});textpos(:,1)=textpos(:,1)+offset;set(textobjs,{'position'},num2cell(textpos,[3,2]))实例10:阶梯图function shili10h0=figure('toolbar','none',...'position',[200 150 450 400],...'name','实例10');a=0.01;b=0.5;t=0:10;f=exp(-a*t).*sin(b*t);stairs(t,f)hold onplot(t,f,':*')hold offglabel='函数e^{-(\alpha*t)}sin\beta*t的阶梯图'; gtext(glabel,'fontsize',16)xlabel('t=0:10','fontsize',16)axis([0 10 -1.2 1.2])实例11:枝干图function shili11h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例11');x=0:pi/20:2*pi;y1=sin(x);y2=cos(x);h1=stem(x,y1+y2);hold onh2=plot(x,y1,'^r',x,y2,'*g');hold offh3=[h1(1);h2];legend(h3,'y1+y2','y1=sin(x)','y2=cos(x)') xlabel('自变量X');ylabel('函数值Y');title('正弦函数与余弦函数的线性组合');实例12:罗盘图function shili12h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例12');winddirection=[54 24 65 84256 12 235 62125 324 34 254];windpower=[2 5 5 36 8 12 76 14 10 8];rdirection=winddirection*pi/180;[x,y]=pol2cart(rdirection,windpower); compass(x,y);desc={'风向和风力','气象台','10月1日0:00到','10月1日12:00'};gtext(desc)实例13:轮廓图function shili13h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例13');[th,r]=meshgrid((0:10:360)*pi/180,0:0.05:1); [x,y]=pol2cart(th,r);z=x+i*y;f=(z.^4-1).^(0.25);contour(x,y,abs(f),20)axis equalxlabel('实部','fontsize',16);ylabel('虚部','fontsize',16);h=polar([0 2*pi],[0 1]);delete(h)hold oncontour(x,y,abs(f),20)实例14:交互式图形function shili14h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例14');axis([0 10 0 10]);hold onx=[];y=[];n=0;disp('单击鼠标左键点取需要的点'); disp('单击鼠标右键点取最后一个点'); but=1;while but==1[xi,yi,but]=ginput(1);plot(xi,yi,'bo')n=n+1;disp('单击鼠标左键点取下一个点');x(n,1)=xi;y(n,1)=yi;endt=1:n;ts=1:0.1:n;xs=spline(t,x,ts);ys=spline(t,y,ts);plot(xs,ys,'r-');hold off实例14:交互式图形function shili14h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例14');axis([0 10 0 10]);hold onx=[];y=[];n=0;disp('单击鼠标左键点取需要的点'); disp('单击鼠标右键点取最后一个点'); but=1;while but==1[xi,yi,but]=ginput(1);plot(xi,yi,'bo')n=n+1;disp('单击鼠标左键点取下一个点');x(n,1)=xi;y(n,1)=yi;endt=1:n;ts=1:0.1:n;xs=spline(t,x,ts);ys=spline(t,y,ts);plot(xs,ys,'r-');hold off实例15:变换的傅立叶函数曲线function shili15h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例15');axis equalm=moviein(20,gcf);set(gca,'nextplot','replacechildren') h=uicontrol('style','slider','position',...[100 10 500 20],'min',1,'max',20) for j=1:20plot(fft(eye(j+16)))set(h,'value',j)m(:,j)=getframe(gcf);endclf;axes('position',[0 0 1 1]);movie(m,30)实例16:劳伦兹非线形方程的无序活动function shili15h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例15');axis equalm=moviein(20,gcf);set(gca,'nextplot','replacechildren') h=uicontrol('style','slider','position',...[100 10 500 20],'min',1,'max',20) for j=1:20plot(fft(eye(j+16)))set(h,'value',j)m(:,j)=getframe(gcf);endclf;axes('position',[0 0 1 1]);movie(m,30)实例17:填充图function shili17h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例17');t=(1:2:15)*pi/8;x=sin(t);y=cos(t);fill(x,y,'r')axis square offtext(0,0,'STOP',...'color',[1 1 1],...'fontsize',50,...'horizontalalignment','center') 例18:条形图和阶梯形图function shili18h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例18');subplot(2,2,1)x=-3:0.2:3;y=exp(-x.*x);bar(x,y)title('2-D Bar Chart')subplot(2,2,2)x=-3:0.2:3;y=exp(-x.*x);bar3(x,y,'r')title('3-D Bar Chart')subplot(2,2,3)x=-3:0.2:3;y=exp(-x.*x);stairs(x,y)title('Stair Chart')subplot(2,2,4)x=-3:0.2:3;y=exp(-x.*x);barh(x,y)title('Horizontal Bar Chart')实例19:三维曲线图function shili19h0=figure('toolbar','none',...'position',[200 150 450 400],...'name','实例19');subplot(2,1,1)x=linspace(0,2*pi);y1=sin(x);y2=cos(x);y3=sin(x)+cos(x);z1=zeros(size(x));z2=0.5*z1;z3=z1;plot3(x,y1,z1,x,y2,z2,x,y3,z3)grid onxlabel('X轴');ylabel('Y轴');zlabel('Z轴');title('Figure1:3-D Plot')subplot(2,1,2)x=linspace(0,2*pi);y1=sin(x);y2=cos(x);y3=sin(x)+cos(x);z1=zeros(size(x));z2=0.5*z1;z3=z1;plot3(x,z1,y1,x,z2,y2,x,z3,y3)grid onxlabel('X轴');ylabel('Y轴');zlabel('Z轴');title('Figure2:3-D Plot')实例20:图形的隐藏属性function shili20h0=figure('toolbar','none',...'position',[200 150 450 300],...'name','实例20');subplot(1,2,1)[x,y,z]=sphere(10);mesh(x,y,z)axis offtitle('Figure1:Opaque')hidden onsubplot(1,2,2)[x,y,z]=sphere(10);mesh(x,y,z)axis offtitle('Figure2:Transparent') hidden off实例21PEAKS函数曲线function shili21h0=figure('toolbar','none',...'position',[200 100 450 450],...'name','实例21');[x,y,z]=peaks(30);subplot(2,1,1)x=x(1,:);y=y(:,1);i=find(y>0.8&y<1.2);j=find(x>-0.6&x<0.5);z(i,j)=nan*z(i,j);surfc(x,y,z)xlabel('X轴');ylabel('Y轴');zlabel('Z轴');title('Figure1:surfc函数形成的曲面') subplot(2,1,2)x=x(1,:);y=y(:,1);i=find(y>0.8&y<1.2);j=find(x>-0.6&x<0.5);z(i,j)=nan*z(i,j);surfl(x,y,z)xlabel('X轴');ylabel('Y轴');zlabel('Z轴');title('Figure2:surfl函数形成的曲面')实例22:片状图function shili22h0=figure('toolbar','none',...'position',[200 150 550 350],...'name','实例22');subplot(1,2,1)x=rand(1,20);y=rand(1,20);z=peaks(x,y*pi);t=delaunay(x,y);trimesh(t,x,y,z)hidden offtitle('Figure1:Triangular Surface Plot'); subplot(1,2,2)x=rand(1,20);y=rand(1,20);z=peaks(x,y*pi);t=delaunay(x,y);trisurf(t,x,y,z)title('Figure1:Triangular Surface Plot'); 实例23:视角的调整function shili23h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例23');x=-5:0.5:5;[x,y]=meshgrid(x);r=sqrt(x.^2+y.^2)+eps;z=sin(r)./r;subplot(2,2,1)surf(x,y,z)xlabel('X-axis')ylabel('Y-axis')zlabel('Z-axis')title('Figure1')view(-37.5,30)subplot(2,2,2)surf(x,y,z)xlabel('X-axis')ylabel('Y-axis')zlabel('Z-axis')title('Figure2')view(-37.5+90,30)subplot(2,2,3)surf(x,y,z)xlabel('X-axis')ylabel('Y-axis')zlabel('Z-axis')title('Figure3')view(-37.5,60)subplot(2,2,4)surf(x,y,z)xlabel('X-axis')ylabel('Y-axis')zlabel('Z-axis')title('Figure4')view(180,0)实例24:向量场的绘制function shili24h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例24');subplot(2,2,1)z=peaks;ribbon(z)title('Figure1')subplot(2,2,2)[x,y,z]=peaks(15);[dx,dy]=gradient(z,0.5,0.5); contour(x,y,z,10)hold onquiver(x,y,dx,dy)hold offtitle('Figure2')subplot(2,2,3)[x,y,z]=peaks(15);[nx,ny,nz]=surfnorm(x,y,z);surf(x,y,z)hold onquiver3(x,y,z,nx,ny,nz)hold offtitle('Figure3')subplot(2,2,4)x=rand(3,5);y=rand(3,5);z=rand(3,5);c=rand(3,5);fill3(x,y,z,c)grid ontitle('Figure4')实例25:灯光定位function shili25h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例25');vert=[1 1 1;1 2 1;2 2 1;2 1 1;1 1 2;12 2;2 2 2;2 1 2];fac=[1 2 3 4;2 6 7 3;4 3 7 8;15 8 4;1 2 6 5;5 6 7 8];grid offsphere(36)h=findobj('type','surface');set(h,'facelighting','phong',...'facecolor',...'interp',...'edgecolor',[0.4 0.4 0.4],...'backfacelighting',...'lit')hold onpatch('faces',fac,'vertices',vert,...'facecolor','y');light('position',[1 3 2]);light('position',[-3 -1 3]); material shinyaxis vis3d offhold off实例26:柱状图function shili26h0=figure('toolbar','none',...'position',[200 50 450 450],...'name','实例26');subplot(2,1,1)x=[5 2 18 7 39 8 65 5 54 3 2];bar(x)xlabel('X轴');ylabel('Y轴');title('第一子图');subplot(2,1,2)y=[5 2 18 7 39 8 65 5 54 3 2];barh(y)xlabel('X轴');ylabel('Y轴');title('第二子图');实例27:设置照明方式function shili27h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例27');subplot(2,2,1)sphereshading flatcamlight leftcamlight rightlighting flatcolorbaraxis offtitle('Figure1')subplot(2,2,2)sphereshading flatcamlight leftcamlight rightlighting gouraudcolorbaraxis offtitle('Figure2')subplot(2,2,3)sphereshading interpcamlight rightcamlight leftlighting phongcolorbaraxis offtitle('Figure3')subplot(2,2,4)sphereshading flatcamlight leftcamlight rightlighting nonecolorbaraxis offtitle('Figure4')实例28:羽状图function shili28h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例28');subplot(2,1,1)alpha=90:-10:0;r=ones(size(alpha));m=alpha*pi/180;n=r*10;[u,v]=pol2cart(m,n);feather(u,v)title('羽状图')axis([0 20 0 10])subplot(2,1,2)t=0:0.5:10;x=0.05+i;y=exp(-x*t);feather(y)title('复数矩阵的羽状图')实例29:立体透视(1)function shili29h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例29');[x,y,z]=meshgrid(-2:0.1:2,...-2:0.1:2,...-2:0.1:2);v=x.*exp(-x.^2-y.^2-z.^2);grid onfor i=-2:0.5:2;h1=surf(linspace(-2,2,20),...linspace(-2,2,20),...zeros(20)+i);rotate(h1,[1 -1 1],30)dx=get(h1,'xdata');dy=get(h1,'ydata');dz=get(h1,'zdata');delete(h1)slice(x,y,z,v,[-2 2],2,-2)hold onslice(x,y,z,v,dx,dy,dz)hold offaxis tightview(-5,10)drawnowend实例30:立体透视(2)function shili30h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例30');[x,y,z]=meshgrid(-2:0.1:2,...-2:0.1:2,...-2:0.1:2);v=x.*exp(-x.^2-y.^2-z.^2); [dx,dy,dz]=cylinder;slice(x,y,z,v,[-2 2],2,-2)for i=-2:0.2:2h=surface(dx+i,dy,dz);rotate(h,[1 0 0],90)xp=get(h,'xdata');yp=get(h,'ydata');zp=get(h,'zdata');delete(h)hold onhs=slice(x,y,z,v,xp,yp,zp);axis tightxlim([-3 3])view(-10,35)drawnowdelete(hs)hold offend实例31:表面图形function shili31h0=figure('toolbar','none',...'position',[200 150 550 250],...'name','实例31');subplot(1,2,1)x=rand(100,1)*16-8;y=rand(100,1)*16-8;r=sqrt(x.^2+y.^2)+eps;z=sin(r)./r;xlin=linspace(min(x),max(x),33); ylin=linspace(min(y),max(y),33); [X,Y]=meshgrid(xlin,ylin);Z=griddata(x,y,z,X,Y,'cubic'); mesh(X,Y,Z)axis tighthold onplot3(x,y,z,'.','Markersize',20)subplot(1,2,2)k=5;n=2^k-1;theta=pi*(-n:2:n)/n;phi=(pi/2)*(-n:2:n)'/n;X=cos(phi)*cos(theta);Y=cos(phi)*sin(theta);Z=sin(phi)*ones(size(theta));colormap([0 0 0;1 1 1])C=hadamard(2^k);surf(X,Y,Z,C)axis square实例32:沿曲线移动的小球h0=figure('toolbar','none',...'position',[198 56 408 468],...'name','实例32');h1=axes('parent',h0,...'position',[0.15 0.45 0.7 0.5],...'visible','on');t=0:pi/24:4*pi;y=sin(t);plot(t,y,'b')n=length(t);h=line('color',[0 0.5 0.5],...'linestyle','.',...'markersize',25,...'erasemode','xor');k1=uicontrol('parent',h0,...'style','pushbutton',...'position',[80 100 50 30],...'string','开始',...'callback',[...'i=1;',...'k=1;,',...'m=0;,',...'while 1,',...'if k==0,',...'break,',...'end,',...'if k~=0,',...'set(h,''xdata'',t(i),''ydata'',y(i)),',...'drawnow;,',...'i=i+1;,',...'if i>n,',...'m=m+1;,',...'i=1;,',...'end,',...'end,',...'end']);k2=uicontrol('parent',h0,...'style','pushbutton',...'position',[180 100 50 30],...'string','停止',...'callback',[...'k=0;,',...'set(e1,''string'',m),',...'p=get(h,''xdata'');,',...'q=get(h,''ydata'');,',...'set(e2,''string'',p);,',...'set(e3,''string'',q)']); k3=uicontrol('parent',h0,...'style','pushbutton',...'position',[280 100 50 30],...'string','关闭',...'callback','close');e1=uicontrol('parent',h0,...'style','edit',...'position',[60 30 60 20]);t1=uicontrol('parent',h0,...'style','text',...'string','循环次数',...'position',[60 50 60 20]);e2=uicontrol('parent',h0,...'style','edit',...'position',[180 30 50 20]); t2=uicontrol('parent',h0,...'style','text',...'string','终点的X坐标值',...'position',[155 50 100 20]); e3=uicontrol('parent',h0,...'style','edit',...'position',[300 30 50 20]); t3=uicontrol('parent',h0,...'style','text',...'string','终点的Y坐标值',...'position',[275 50 100 20]);实例33:曲线转换按钮h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例33');x=0:0.5:2*pi;y=sin(x);h=plot(x,y);grid onhuidiao=[...'if i==1,',...'i=0;,',...'y=cos(x);,',...'delete(h),',...'set(hm,''string'',''正弦函数''),',...'h=plot(x,y);,',...'grid on,',...'else if i==0,',...'i=1;,',...'y=sin(x);,',...'set(hm,''string'',''余弦函数''),',...'delete(h),',...'h=plot(x,y);,',...'grid on,',...'end,',...'end'];hm=uicontrol(gcf,'style','pushbutton',...'string','余弦函数',...'callback',huidiao);i=1;set(hm,'position',[250 20 60 20]);set(gca,'position',[0.2 0.2 0.6 0.6])title('按钮的使用')hold on实例34:栅格控制按钮h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例34');x=0:0.5:2*pi;y=sin(x);plot(x,y)huidiao1=[...'set(h_toggle2,''value'',0),',...'grid on,',...];huidiao2=[...'set(h_toggle1,''value'',0),',...'grid off,',...];h_toggle1=uicontrol(gcf,'style','togglebutton',...'string','grid on',...'value',0,...'position',[20 45 50 20],...'callback',huidiao1);h_toggle2=uicontrol(gcf,'style','togglebutton',...'string','grid off',...'value',0,...'position',[20 20 50 20],...'callback',huidiao2);set(gca,'position',[0.2 0.2 0.6 0.6])title('开关按钮的使用')实例35:编辑框的使用h0=figure('toolbar','none',...'position',[200 150 350 250],...'name','实例35');f='Please input the letter';huidiao1=[...'g=upper(f);,',...'set(h2_edit,''string'',g),',...];huidiao2=[...'g=lower(f);,',...'set(h2_edit,''string'',g),',...];h1_edit=uicontrol(gcf,'style','edit',...'position',[100 200 100 50],...'HorizontalAlignment','left',...'string','Please input the letter',...'callback','f=get(h1_edit,''string'');',...'background','w',...'max',5,...'min',1);h2_edit=uicontrol(gcf,'style','edit',...'HorizontalAlignment','left',...'position',[100 100 100 50],...'max',5,...'min',1);h1_button=uicontrol(gcf,'style','pushbutton',...'string','小写变大写',...'position',[100 45 100 20],...'callback',huidiao1);h2_button=uicontrol(gcf,'style','pushbutton',...'string','大写变小写',...'position',[100 20 100 20],...'callback',huidiao2);实例36:弹出式菜单h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例36');x=0:0.5:2*pi;y=sin(x);h=plot(x,y);grid onhm=uicontrol(gcf,'style','popupmenu',...'string',...'sin(x)|cos(x)|sin(x)+cos(x)|exp(-sin(x))',...'position',[250 20 50 20]);set(hm,'value',1)huidiao=[...'v=get(hm,''value'');,',...'switch v,',...'case 1,',...'delete(h),',...'y=sin(x);,',...'h=plot(x,y);,',...'grid on,',...'case 2,',...'delete(h),',...'y=cos(x);,',...'h=plot(x,y);,',...'grid on,',...'case 3,',...'delete(h),',...'y=sin(x)+cos(x);,',...'h=plot(x,y);,',...'grid on,',...'case 4,',...'y=exp(-sin(x));,',...'h=plot(x,y);,',...'grid on,',...'end'];set(hm,'callback',huidiao)set(gca,'position',[0.2 0.2 0.6 0.6])title('弹出式菜单的使用')实例37:滑标的使用h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例37');[x,y]=meshgrid(-8:0.5:8);r=sqrt(x.^2+y.^2)+eps;z=sin(r)./r;h0=mesh(x,y,z);h1=axes('position',...[0.2 0.2 0.5 0.5],...'visible','off');htext=uicontrol(gcf,...'units','points',...'position',[20 30 45 15],...'string','brightness',...'style','text');hslider=uicontrol(gcf,...'units','points',...'position',[10 10 300 15],...'min',-1,...'max',1,...'style','slider',...'callback',...'brighten(get(hslider,''value''))');实例38:多选菜单h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例38');[x,y]=meshgrid(-8:0.5:8);r=sqrt(x.^2+y.^2)+eps;z=sin(r)./r;h0=mesh(x,y,z);hlist=uicontrol(gcf,'style','listbox',...'string','default|spring|summer|autumn|winter',...'max',5,...'min',1,...'position',[20 20 80 100],...'callback',[...'k=get(hlist,''value'');,',...'switch k,',...'case 1,',...'colormap default,',...'case 2,',...'colormap spring,',...'case 3,',...'colormap summer,',...'case 4,',...'colormap autumn,',...'case 5,',...'colormap winter,',...'end']);实例39:菜单控制的使用h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例39');x=0:0.5:2*pi;y=cos(x);h=plot(x,y);grid onset(gcf,'toolbar','none')hm=uimenu('label','example');huidiao1=[...'set(hm_gridon,''checked'',''on''),',...'set(hm_gridoff,''checked'',''off''),',...'grid on'];huidiao2=[...'set(hm_gridoff,''checked'',''on''),',...'set(hm_gridon,''checked'',''off''),',...'grid off'];hm_gridon=uimenu(hm,'label','grid on',...'checked','on',...'callback',huidiao1);hm_gridoff=uimenu(hm,'label','grid off',...'checked','off',...'callback',huidiao2);实例40:UIMENU菜单的应用。
Matlab编程技巧与实例分析

Matlab编程技巧与实例分析引言Matlab是一种强大的数学软件工具,广泛应用于科学、工程、金融等领域。
本文将分享一些Matlab编程的技巧和实例分析,帮助读者更好地使用和理解这个工具。
一、向量化操作在Matlab中,向量化操作是一种重要的编程技巧。
通过将循环操作转换为矢量操作,可以大大提高代码的效率。
例如,假设我们有一个包含10000个元素的向量x,我们想将其中大于0的元素设置为1,小于0的元素设置为-1,可以使用以下代码实现:```Matlabx(x > 0) = 1;x(x < 0) = -1;```通过使用向量化操作,我们避免了使用循环,并且代码更简洁。
二、矩阵运算Matlab中矩阵运算相比其他编程语言更加方便和高效。
例如,矩阵乘法可以使用`*`操作符实现,而不需要使用循环。
另外,Matlab还提供了一些内置的矩阵函数,例如`transpose`(转置矩阵)和`inv`(求逆矩阵)等。
在实例分析中,我们可以考虑一个线性回归的问题。
假设我们有一组数据集X和对应的目标值y,我们想通过线性回归拟合一个模型。
使用Matlab的矩阵运算,可以简洁地表示为:```Matlabtheta = inv(X' * X) * X' * y;```这里,`X'`表示矩阵X的转置,`inv`表示求逆矩阵。
通过这种方式,我们可以快速地得到线性回归的参数。
三、绘图和数据可视化Matlab提供了丰富的绘图和数据可视化功能,可以帮助我们更直观地理解数据和结果。
例如,我们可以使用`plot`函数绘制函数的曲线,使用`scatter`函数绘制散点图,并使用`histogram`函数绘制直方图。
在实例分析中,我们可以考虑一个简单的例子:绘制正弦函数的曲线。
可以使用以下代码实现:```Matlabx = linspace(0, 2*pi, 100);y = sin(x);plot(x, y);```通过这种方式,我们可以看到正弦函数的周期性和变化趋势。
学习matlab程序-简单示例

Matlab 编程示例.程序结构及函数作用在软件Matlab 中实现主成分分析可以采取两种方式实现:一是通过编程来实现;二是直接调用Matlab 种自带程序实现。
下面主要主要介绍利用Matlab 的矩阵计算功能编程实现主成分分析。
1程序结构主函数子函数2函数作用Cwstd.m ——用总和标准化法标准化矩阵Cwfac.m ——计算相关系数矩阵;计算特征值和特征向量;对主成分进行排序;计算各特征值贡献率;挑选主成分(累计贡献率大于85%),输出主成分个数;计算主成分载荷Cwscore.m ——计算各主成分得分、综合得分并排序Cwprint.m ——读入数据文件;调用以上三个函数并输出结果3.源程序3.1 cwstd.m 总和标准化法标准化矩阵%cwstd.m,用总和标准化法标准化矩阵function std=cwstd(vector)cwsum=sum(vector,1); %对列求和[a,b]=size(vector); %矩阵大小,a 为行数,b 为列数for i=1:afor j=1:bCwprint.m Cwstd.m Cwfac.m Cwscore.mstd(i,j)= vector(i,j)/cwsum(j);endend3.2 cwfac.m计算相关系数矩阵%cwfac.mfunction result=cwfac(vector);fprintf('相关系数矩阵:\n')std=CORRCOEF(vector) %计算相关系数矩阵fprintf('特征向量(vec)及特征值(val):\n')[vec,val]=eig(std) %求特征值(val)及特征向量(vec)newval=diag(val) ;[y,i]=sort(newval) ; %对特征根进行排序,y为排序结果,i为索引fprintf('特征根排序:\n')for z=1:length(y)newy(z)=y(length(y)+1-z);endfprintf('%g\n',newy)rate=y/sum(y);fprintf('\n贡献率:\n')newrate=newy/sum(newy)sumrate=0;newi=[];for k=length(y):-1:1sumrate=sumrate+rate(k);newi(length(y)+1-k)=i(k);if sumrate>0.85 break;endend %记下累积贡献率大85%的特征值的序号放入newi中fprintf('主成分数:%g\n\n',length(newi));fprintf('主成分载荷:\n')for p=1:length(newi)for q=1:length(y)result(q,p)=sqrt(newval(newi(p)))*vec(q,newi(p));endend %计算载荷disp(result)3.3 cwscore.m%cwscore.m,计算得分function score=cwscore(vector1,vector2);sco=vector1*vector2;csum=sum(sco,2);[newcsum,i]=sort(-1*csum);[newi,j]=sort(i);fprintf('计算得分:\n')score=[sco,csum,j]%得分矩阵:sco为各主成分得分;csum为综合得分;j为排序结果3.4 cwprint.m%cwprint.mfunction print=cwprint(filename,a,b);%filename为文本文件文件名,a为矩阵行数(样本数),b为矩阵列数(变量指标数)fid=fopen(filename,'r')vector=fscanf(fid,'%g',[a b]);fprintf('标准化结果如下:\n')v1=cwstd(vector)result=cwfac(v1);cwscore(v1,result);4.程序测试例题4.1原始数据中国大陆35个大城市某年的10项社会经济统计指标数据见下表。
matlab编程悬臂梁例题

matlab编程悬臂梁例题
悬臂梁是结构工程中常见的一个问题,可以用来研究梁的挠曲
和应力分布。
在MATLAB中,我们可以通过编程来模拟悬臂梁的行为。
首先,我们需要确定悬臂梁的几何形状、材料特性和受力情况。
然后,我们可以使用有限元分析或者基本的梁理论来建立模型。
在MATLAB中,我们可以使用不同的工具箱或者自己编写代码来
解决悬臂梁的例题。
首先,我们需要建立悬臂梁的几何形状和材料
特性,包括梁的长度、截面形状、材料的弹性模量和截面惯性矩等。
然后,我们可以通过应力分析公式或者有限元分析来计算悬臂梁上
的应力分布。
接着,我们可以编写MATLAB代码来绘制悬臂梁上的应
力分布图,并进一步分析梁的挠曲情况。
另外,我们还可以使用MATLAB的符号计算工具箱来求解悬臂梁
的挠曲方程,并进行参数化分析。
这样可以帮助我们更好地理解悬
臂梁的行为,比如在不同的受力情况下梁的挠曲情况会如何变化。
此外,我们还可以通过MATLAB的优化工具箱来进行悬臂梁的优化设计,比如在保证强度的前提下最小化梁的重量。
总之,MATLAB提供了丰富的工具和功能来解决悬臂梁的例题,
我们可以通过编程来模拟悬臂梁的行为,并进行多方面的分析和优化设计。
希望这些信息能够帮助你更好地理解如何在MATLAB中进行悬臂梁的编程例题。
基于matlab和矩量法的电磁仿真开发

算的函数写成基函数之间的线性组合,接着匹配方程,
再由离散的线性方程组求解出展开系数,便能由此近似
的解出未知函数。
矩量法电磁计算时常用的基函数为 RWG 基函数,
关于 RWG 基函数已有大量文献进行了详细描述,本文
采用的也是此基函数。
3 仿真应用 3.1 散射
图 2 平面波参数输入框
完成入射电磁波的设定后就可以开始计算,依据模 型网格剖分后的网格数据采用矩量法进行阻抗矩阵的 计算,得到网格的电流大小,由此计算出散射场的结果。
Lu Ju-cheng1,Yang Shuo2(1.China Airborne Missile Academy,Henan Luoyang 471009;2.First military representative office of the air force in Luoyang,Henan Luoyang 471009)
图 3 球体
图 4 方体
模型进行网格剖分,网格大小与仿真波长有关,网 格越小越好,但计算机计算能力有限制,应折中考虑。网 格剖分后模型如图 5、图 6 所示。
矩量法[5-9]是将算子方程化为矩阵方程,然后求解该
矩阵方程的方法。
对于实际的电磁散射或辐射问题,数学上可以用一
个一般的算子方程来描述,即:
L*f= g
(1)
一般要获得式(1)的精确解是非常困难的,除非 L 为
非常简单的线性算子。在计算电磁学中它们可以是空间
和时间的函数。
使用矩量法求解问题的一般步骤是,先要将所需计
摘 要:利用数值计算软件 MATLAB 开发基于矩量法的电磁仿真软件,具备建模、仿真设置、电磁散射和辐
射的计算、辐射场的绘制等功能,经验证计算结果较为可靠。
数学建模 第3讲 MATLAB的具体实例

解答
用MATLAB优化工具箱解线性规划
1、模型: min z=cX s.t. AX b 命令:x=linprog(c,A,b)
2、模型:min z=cX s.t. AX b Aeq X beq 命令:x=linprog(c,A,b,Aeq,beq)
AX b 存在,则令A=[ ],b=[ ]. 注意:若没有不等式:
三、模型的建立与分析
1.总体风险用所投资的Si中最大的一个风险来衡量,即max{ qixi|i=1,2,…n}
2.购买 Si 所付交易费是一个分段函数,即 pixi xi>ui 交易费 = piui xi≤ui 而题目所给定的定值 ui(单位:元)相对总投资 M 很小, piui 更小, 可以忽略不计,这样购买 Si 的净收益为(r i-pi)xi
五、 结果分析 1.风险大,收益也大。
2.当投资越分散时,投资者承担的风险越小,这与题意一致。即: 冒险的投资者会出现集中投资的情况,保守的投资者则尽量分散投资。
3.曲线上的任一点都表示该风险水平的最大可能收益和该收益要求的最 小风险。对于不同风险的承受能力,选择该风险水平下的最优投资组合。 4.在a=0.006附近有一个转折点,在这一点左边,风险增加很少时,利润增长 很快。在这一点右边,风险增加很大时,利润增长很缓慢,所以对于风险和 收益没有特殊偏好的投资者来说,应该选择曲线的拐点作为最优投资组合, 大约是a*=0.6%,Q*=20% ,所对应投资方案为: 风险度 收益 x0 x1 x2 x3 x4 0.0060 0.2019 0 0.2400 0.4000 0.1091 0.2212
8 4 x1 8 3 x2 32 x1 24 x2
因检验员错检而造成的损失为:
matlab矩阵位移法求解钢架
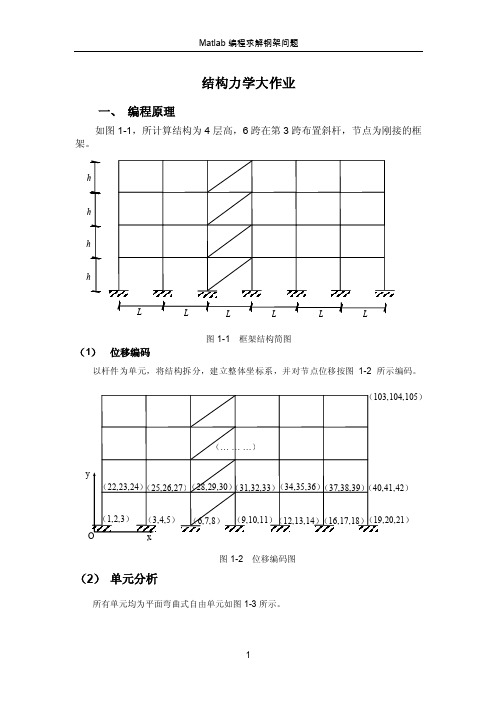
结构力学大作业一、 编程原理如图1-1,所计算结构为4层高,6跨在第3跨布置斜杆,节点为刚接的框架。
图1-1 框架结构简图(1) 位移编码以杆件为单元,将结构拆分,建立整体坐标系,并对节点位移按图1-2所示编码。
图1-2 位移编码图(2) 单元分析所有单元均为平面弯曲式自由单元如图1-3所示。
LLLLLLhhhhLLLLL图1-3 自由式单元干段位移和杆端力杆件的单元刚度矩阵322222223222000012612600646200000012612600626400EAEAllEI EI EI EI l l l l EI EI EI EI l ll l K EA EAl lEI EI EI EI l l l l EI EI EI EI l l l l ⎡⎤-⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥=⎢⎥-⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦其中32112001260640EAlEIEIl l K EI EI l l⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦ 22122001260620EAl EI EI l l K EI EI l l ⎡⎤-⎢⎥⎢⎥⎢⎥-⎢⎥=⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎣⎦21222001260620EA lEI EI K l l EI EI l l⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦ 22322001260640EAl EI EI K l l EI EI l l ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦(3) 建立局部坐标系分别建立如图1-4所示的竖向分体系局部坐标系,水平分体系局部坐标系和斜杆分体系坐标系。
图1-4 分体系局部坐标系的建立(4) 建立分体系刚度分别建立三个分体系的105×105的刚度矩阵,引入循环变量,依次对相应位移刚度赋值。
(5) 坐标转换对竖向坐标系和斜杆体系进行转置,其坐标转换阵为1010100001T ⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦3000001L hd d hT d ⎡⎤⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦其中d =。
matlab程序算例

matlab程序算例Matlab程序算例Matlab是一种广泛应用于科学和工程领域的高级计算机编程语言及环境。
它的简洁、高效和强大的功能使得许多人选择使用Matlab来解决复杂的数学和工程问题。
在本文中,我将以一个具体的Matlab程序算例为例,详细说明每一步是如何完成的。
那么我们首先来看一下这个具体的Matlab程序算例。
假设我们希望计算并绘制一个二维正弦函数,代码如下:matlab设置步长,定义x轴的范围dx = 0.1;x = 0:dx:10;计算对应的y值y = sin(x);绘制图像plot(x, y);在这个例子中,我们通过定义一个步长`dx`和一个x轴的范围`x`来生成一系列的x值。
然后,我们使用`sin()`函数计算对应的y值,并将结果保存在`y`中。
最后,我们使用`plot()`函数绘制x和y的图像。
现在,让我们一步一步来回答这个程序算例中的问题。
第一步:设置步长和定义x轴的范围。
matlabdx = 0.1;x = 0:dx:10;这里我们设置步长`dx`为0.1,表示x轴上两个相邻点之间的间距为0.1。
然后,我们使用冒号运算符`:`创建一个从0到10的向量`x`,其中每个元素之间的间隔为`dx`。
也就是说,`x`中的元素为0, 0.1, 0.2, …, 9.9, 10。
第二步:计算对应的y值。
matlaby = sin(x);这里,我们使用`sin()`函数计算每个x值对应的正弦值,并将结果保存在`y`中。
例如,如果x的第一个元素为0,则使用`sin(0)`计算得到y的第一个元素的值。
第三步:绘制图像。
matlabplot(x, y);最后,我们使用`plot()`函数将x和y的值绘制成图像。
这样就可以观察到x和y之间的关系。
在这个例子中,由于x的范围是从0到10,并且y是对应的正弦值,因此我们将得到一个周期为2π的正弦函数的图像。
以上就是这个Matlab程序算例的每一步的解释。
matlab十个简单案例编写

matlab十个简单案例编写1. 求解线性方程组线性方程组是数学中常见的问题之一,而MATLAB提供了用于求解线性方程组的函数。
例如,我们可以使用"linsolve"函数来求解以下线性方程组:2x + 3y = 74x - 2y = 2代码如下所示:A = [2, 3; 4, -2];B = [7; 2];X = linsolve(A, B);disp(X);解释:上述代码定义了一个2x2的矩阵A和一个2x1的矩阵B,分别表示线性方程组的系数矩阵和常数向量。
然后,使用linsolve函数求解线性方程组,结果存储在X中,并通过disp函数打印出来。
运行代码后,可以得到x=2和y=1的解。
2. 求解非线性方程除了线性方程组外,MATLAB还可以用于求解非线性方程。
例如,我们可以使用"fzero"函数求解以下非线性方程:x^2 + 2x - 3 = 0代码如下所示:fun = @(x) x^2 + 2*x - 3;x0 = 0;x = fzero(fun, x0);disp(x);解释:上述代码定义了一个匿名函数fun,表示非线性方程。
然后,使用fzero函数传入fun和初始值x0来求解非线性方程的根,并通过disp函数打印出来。
运行代码后,可以得到x=1的解。
3. 绘制函数图像MATLAB提供了强大的绘图功能,可以帮助我们可视化函数的形状和特征。
例如,我们可以使用"plot"函数绘制以下函数的图像:y = cos(x)代码如下所示:x = linspace(0, 2*pi, 100);y = cos(x);plot(x, y);解释:上述代码首先使用linspace函数生成一个从0到2π的100个等间距点的向量x,然后计算对应的cos值,并存储在向量y中。
最后,使用plot函数将x和y作为横纵坐标绘制出函数图像。
运行代码后,可以看到cos函数的周期性波动图像。
Matlab实现矩量法计算框形天线的输入阻抗

+
-
2= 3, … 整个积分区间可表示为N 个分区间之和。拐
角点的处理, 这里近似地视其为直线。
(3) 方程的收敛性
随着天线半径 a 增大和选配点增多, 矩阵元素相
关 性变差, 这时求得的结果误差较大。当场点 r 满足 r
< 10a 时, 即近区情况, 可将 exp {- jk (R m n - r) } R m n
…
0 从而: [ In ] = [ Ym n ] [Vm ]
则输入导纳为:
Y in =
I1 V0
输入阻抗为: Z in =
1 Y in
(6)
2 难点的分析与处理
(1) 基函数与权函数的选取 基函数与权函数的选取是非常重要的, 直接关系 到解的正确性。基函数的选取原则应尽可能地与导线 上预期的电流分布相接近, 权函数可选与基函数相同 的函数。本矩量法选取的基函数为脉冲基函数, 权函 数选取的是 ∆(D irac) 函数。由于基函数和权函数选取 的是相同的, 故称为伽略金 (Ga lerk in) 法。
有关积分方程转换成一个矩阵方程来求解的数学运算
过程, 比较复杂, 容量较大, 但结果较为准确[3]。
框形天线的输入阻抗矩量法计算过程目前尚未见
报道, 本文首先采用了矩量法建立了计算框形天线的 电流分布及输入阻抗的数学模型。鉴于M a tlab 对矩阵 运算在运算速度及精确度方面都有其独特的优势, 采 用了M a tlab 计算了框形天线的电流分布及输入阻抗, 得到了输入阻抗的频率特性, 结果与工程结果一致性 较一般常用的方法更好。
参 考 文 献
[ 1 ] 周朝栋, 王元坤, 周良明 1 线天线理论与工程 [M ] 1 西安: 西安电子科技大学出版社, 19881
矩阵位移法matlab编程例题

矩阵位移法matlab编程例题下题是桁架结构:其中,F p =1,试求各杆的轴⼒clear[ length1,theta1,T1 ] = Geometry( 1,0, 1,1) % 由结点坐标求六个单元⼏何信息 [ length2,theta2,T2 ] = Geometry( 0,0, 1,0) [ length3,theta3,T3 ] = Geometry( 0,0, 0,1) [ length4,theta4,T4 ] = Geometry( 0,1, 1,1) [ length5,theta5,T5 ] = Geometry( 1,0, 0,1) [ length6,theta6,T6 ] = Geometry( 0,0, 1,1) g1=[1 2 3 4] % 六个单元定位向量g2=[0 0 1 2] g3=[0 0 0 0] g4=[0 0 3 4] g5=[1 2 0 0] g6=[0 0 3 4]E=1;A=1; % 材料信息 k1=LocalElementStiff(E,A,length1) % 局部单刚 k2=LocalElementStiff(E,A,length2)k3=LocalElementStiff(E,A,length3) k4=LocalElementStiff(E,A,length4) k5=LocalElementStiff(E,A,length5)k6=LocalElementStiff(E,A,length6)K1=T1'*k1*T1 % 整体单刚K2=T2'*k2*T2 K3=T3'*k3*T3(6)3214K4=T4'*k4*T4K5=T5'*k5*T5K6=T6'*k6*T6GK=zeros(4) % 由六个单元和相应定位向量聚集总刚GK=ElementAssemble1(GK,K1,g1)GK=ElementAssemble1(GK,K2,g2)GK=ElementAssemble1(GK,K3,g3)GK=ElementAssemble1(GK,K4,g4)GK=ElementAssemble1(GK,K5,g5)GK=ElementAssemble1(GK,K6,g6)P=[1 0 0 1]' % 荷载信息U=GK\P % 求解⽅程U1=ElementDisp(U,g1) % 定位向量提取六个单元的结点位移U2=ElementDisp(U,g2)U3=ElementDisp(U,g3)U4=ElementDisp(U,g4)U5=ElementDisp(U,g5)U6=ElementDisp(U,g6)f1=k1*T1*U1 % 求局部坐标下的单元杆端内⼒f2=k2*T2*U2f3=k3*T3*U3f4=k4*T4*U4f5=k5*T5*U5f6=k6*T6*U6下题是钢架结构:(4,0,5)(1,2,3)(0,0,0)clear[ length1,theta1,T1 ] = Geometry( 0,0, 0,10) % 由结点坐标求两个单元⼏何信息[ length2,theta2,T2 ] = Geometry( 0,0, 10,0) g1=[1 2 3 0 0 0] % 两个单元定位向量g2=[1 2 3 4 0 5]E=128000;A=2;I=7/640 % 材料信息k1=LocalElementStiff(E,A,I,length1) % 局部单刚k2=LocalElementStiff(E,A,I,length2)K1=T1'*k1*T1K2=T2'*k2*T2GK=zeros(5) % 由两个单元和相应定位向量聚集总刚GK=ElementAssemble1(GK,K1,g1)GK=ElementAssemble1(GK,K2,g2)P=[10 0 0 0 20]' % 荷载信息U=GK\P % 求解⽅程U1=ElementDisp(U,g1) % 定位向量提取两个单元的结点位移U2=ElementDisp(U,g2)f1=k1*T1*U1 % 求局部坐标下的单元杆端内⼒f2=k2*T2*U2故M图:Q图:N图:下题是两个连续梁单元的结构clearlength1 = Geometry( 0,0, 6,0) % 由结点坐标求2个单元⼏何信息length2 = Geometry( 6,0, 12,0) g1=[0 1] % 2个单元定位向量g2=[1 2]E=1,I=1 % 材料信息k1=LocalElementStiff(E,I,length1) % 局部单刚k2=LocalElementStiff(E,I,length2)K1=k1 % 整体单刚K2=k2GK=zeros(2) % 由2个单元和相应定位向量聚集总刚GK=ElementAssemble1(GK,K1,g1)GK=ElementAssemble1(GK,K2,g2)P=[50 0]' % 荷载信息U=GK\P % 求解⽅程U1=ElementDisp(U,g1) % 定位向量提取2个单元的整体坐标结点位移U2=ElementDisp(U,g2) u1=U1 % 局部坐标结点位移u2=U2f1=k1*u1 % 求局部坐标下的单元杆端内⼒f2=k2*u2故M图为:。
Matlab分析矩量法在线天线中的应用

西 安 邮 电 学 院 学 报 JOU RNA L OF XI. AN U NI VERSIT Y O F POST AN D T ELECOM M U N ICAT IO NS
Jan. 2009 Vol1 14 N o1 1
基于 M at lab 分析矩量法在线天线中的应用
T
图1
偶极子天线
2. 2
海伦方程的建立及其矩量法解[ 3- 5 ] 应用矢量位 A 的波动方程结合电场边界条件
由扩展边界条件及电流连续性方程可得双位方 程:
EQ -l
lm
n
N
[ ip # i smI m ( s m ) +
m
1 dI m ( S m ) ip ¨ ] # dS m k2
可解得海伦方程: l ex p(- j kR m n ) i ( z c) dz c+ c 1 cos kz + c 2 sin kz 4P R mn - l =
由上述结果可见 , 双位方程和海伦方程计算结 果与解析解基本一致。说明这两种方法的正确性。 通过取不同 N 值仿真表明, 双位方程的增益相对较 大, 分段数目对电流分布影响不大, 比较稳定, 只是
图4 不同半径天线电流分布比较
由上述 结果 可见, 当半径 比波长 值小于 0. 01
# 52 #
西
安
# 50 #
西
安
邮
电
学
院
学
报
2009 年 1 月
义。 以下采用双 位积分方 程、 海伦 ( H allen) 积分 方 程, 应用矩量法对半波对称振子天线特性分析 , 在此 基础上分析不同长度和不同半径的偶极子天线的特 性。 此处采用迟后位积分公式作为分析工具, 可以用 有限差分逼近导数的方法来处理。 2. 1 双位方程的建立及其矩量法解 总长为 2 l , 半径为 a 的半波偶极子天线如图 1 放置, 在已知外加场 E i 的作用下 , 天线的电流在空 间产生辐射场 E ,则 E = - j XA - ¨5 ( 1 - 6)
矩量法matlab程序设计实例

矩量法matlab程序设计实例第一篇:矩量法matlab程序设计实例矩量法matlab程序设计实例:Hallen方程求对称振子天线一、条件和计算目标已知:对称振子天线长为L,半径为a,且天线长度与波长的关系为L=0.5λ,a<<L,a<<λ,设λ=1,半径a=0.0000001,因此波数为k=2π/λ=2π。
目标: 用Hallen方程算出半波振子、全波振子以及不同L/λ值的对应参数值。
求:(1)电流分布(2)E面方向图(二维),H面方向图(二维),半波振子空间方向性图(三维)二、对称振子放置图l/2电流分布馈电端~l/2yx图1 半波振子的电流分布半波振子天线平行于z轴放置,在x轴和y轴上的分量都为零,坐标选取方式有两种形式,一般选取图1的空间放置方式。
图1给出了天线的电流分布情况,由图可知,当天线很细时,电流分布近似正弦分布。
三、Hallen方程的解题思路z2z1z⎰izzGz,zdz+c1coskz+c2sinkz=()('')'kjωμz0i''Ezsinkz-z'dz()()z⎰对于中心馈电的偶极子,Hallen方程为⎰L2L-2+i(z')G(z,z')dz'+c1coskz+c2sinkz=脉冲函数展开和点选配,得到Visinkz,j2η-LL<z<+22∑In⎰n=1N'+1zn'znG(zm,z')dz'+c1coskzm+c2sinkzm=Visinkzm,j2ηm=1,2,⋅⋅⋅,N 上式可以写成矩阵形式为∑In=2N-1npmn+c1qm+c2sm=tm,m=1,2,⋅⋅⋅,N⎡p12,p13,ΛΛ,p1,N-1,q1,s1⎤⎡I2⎤⎡t1⎤⎢⎥⎢⎥⎢t⎥p,p,ΛΛ,p,qsI22232,N-12,23⎢⎥⎢⎥⎢2⎥⎢ΛΛΛΛΛΛΛΛΛΛΛΛΛ⎥⎢Λ⎥⎢Λ⎥⎢⎥⎢⎥=⎢⎥⎢ΛΛΛΛΛΛΛΛΛΛΛΛΛ⎥⎢IN-1⎥⎢Λ⎥⎢ΛΛΛΛΛΛΛΛΛΛΛΛΛ⎥⎢c⎥⎢t⎥⎢⎥⎢1⎥⎢N-1⎥⎢⎣tN⎥⎦⎣c2⎥⎦⎢⎣pN2,pN3,ΛΛ,pN,N-1,qN,sN⎥⎦⎢四、结果与分析(1)电流分布图2 不同L/λ电流分布图分析:由图2可知半波振子天线L/λ=0.5的电流分布最大,馈点电流最大,时辐射电阻近似等于输入电阻,因为半波振子的输入电流正好是波腹电流。
matlab计算灰度图像的一阶矩,二阶矩,三阶矩实例

matlab计算灰度图像的⼀阶矩,⼆阶矩,三阶矩实例⼀阶矩,定义了每个颜⾊分量的平均强度⼆阶矩,反映待测区域颜⾊⽅差,即不均匀性三阶矩,定义了颜⾊分量的偏斜度,即颜⾊的不对称性close all;clear all;clc;J = imread('lena.jpg');K = imadjust(J,[70/255 160/255],[]);figure;subplot(121),imshow(J);subplot(122),imshow(K);[m,n] = size(J);mm = round(m/2);mn = round(n/2);[p,q] = size(K);pp = round(p/2);qq = round(q/2);J = double(J);K = double(K);colorsum = 0.0;Javg = mean2(J) %求原图像⼀阶矩Kavg = mean2(K) %求增强对⽐度后的图像⼀阶矩Jstd = std(std(J)) %求原图像的⼆阶矩,因为⼀次std函数表⽰按列求标准差,两次std表⽰求整个矩阵的标准差Kstd = std(std(K)) %求增强对⽐度后的图像⼆阶矩for i=1:mmfor j=1:mncolorsum = colorsum+(J(i,j)-Javg)^3;endendJske = (colorsum/(mm*mn))^(1/3) %求原图像的三阶矩colorsum = 0.0;for i=1:ppfor j=1:qqcolorsum = colorsum + (J(i,j)-Kavg)^3;endendKske = (colorsum/(pp*qq))^(1/3) %求增强对⽐度后的图像三阶矩部分函数说明:mean2(A) : 求矩阵A的均值std(x,flag,dim): 求x的标准偏差std(x,0,1) : 0表⽰求标准差时除n-1,1表⽰按列划分std(x,1,2) : 1表⽰求标准差时除n,2表⽰按⾏划分补充知识:图像的重⼼和⼆阶矩图像的重⼼图像实际上就是个矩阵,每个位置的元素就是该处的像素。
用matlab编程实现图像的Hu的七个不变矩特征

% 功能:计算图像的H u的七个不变矩特征% 输入:二值化图像% 输出:inv_m7-七个不变矩%算法描述:%用零阶中心矩对其余各界中心矩进行归一化,得到图像归一化中心矩;%利用2阶和3阶归一化中心距可以导数7个不变矩组;%编写时间:2012.5.31fu nctio n inv_m7 = getf eatur e4(im age)%将图像矩阵的数据类型转换成双精度型image=doub le(im age);%%%=================计算、、=========================%计算图像的零阶几何矩m00=sum(sum(image)); m10=0;m01=0;[r ow,co l]=si ze(im age);fori=1:r ow for j=1:col m10=m10+i*ima ge(i,j); m01=m01+j*ima ge(i,j); en dend%%%=================计算、 ================================u10=m10/m00;u01=m01/m00;%%%=================计算图像的二阶几何矩、三阶几何矩============ m20 =0;m02 = 0;m11 = 0;m30 = 0;m12= 0;m21 =0;m03 = 0;fori=1:r ow for j=1:col m20=m20+i^2*i mage(i,j);m02=m02+j^2*imag e(i,j); m11=m11+i*j*im age(i,j); m30=m30+i^3*image(i,j);m03=m03+j^3*ima ge(i,j); m12=m12+i*j^2*imag e(i,j); m21=m21+i^2*j*image(i,j); endend%%%=================计算图像的二阶中心矩、三阶中心矩============ y00=m00;y10=0;y01=0;y11=m11-u01*m10;y20=m20-u10*m10;y02=m02-u01*m01;y30=m30-3*u10*m20+2*u10^2*m10;y12=m12-2*u01*m11-u10*m02+2*u01^2*m10;y21=m21-2*u10*m11-u01*m20+2*u10^2*m01;y03=m03-3*u01*m02+2*u01^2*m01;%%%=================计算图像的归格化中心矩==================== n20=y20/m00^2;n02=y02/m00^2; n11=y11/m00^2; n30=y30/m00^2.5; n03=y03/m00^2.5; n12=y12/m00^2.5; n21=y21/m00^2.5;%%%=================计算图像的七个不变矩====================== h1 = n20+ n02; h2 = (n20-n02)^2 + 4*(n11)^2;h3 = (n30-3*n12)^2 +(3*n21-n03)^2;h4= (n30+n12)^2 + (n21+n03)^2;h5 = (n30-3*n12)*(n30+n12)*((n30+n12)^2-3*(n21+n03)^2)+(3*n21-n03)*(n21+n03)*(3*(n30+n12)^2-(n21+n03)^2);h6 =(n20-n02)*((n30+n12)^2-(n21+n03)^2)+4*n11*(n30+n12)*(n21+n03);h7 = (3*n21-n03)*(n30+n12)*((n30+n12)^2-3*(n21+n03)^2)+(3*n12-n30)*(n21+n03)*(3*(n30+n12)^2-(n21+n03)^2);inv_m7= [h1 h2 h3 h4 h5h6 h7]; 。
用Matlab改进一次二阶矩法程序

用Matlab编的计算结构可靠指标的改进一次二阶矩法程序(验算点法)题目:编制改进一次二阶矩法计算可靠指标的程序,并给出算例,要求提供源程序选取的算例为:z=g(x,y)=x*y-1140,其中x,y服从正态分布,μx=38,Vx=0.1, μy=38,Vy=0.05本程序采用Matlab编写。
选取β1=3.0,β2=2.5计算结果为:可靠指标β=4.2672,最终验算点为:(22.8430 , 49.9060),在验算点处功能函数值为:1.2354e-004%保存为strRlbt.m,在Matlab命令窗口中输入strRlbt执行即可N = 2;%变量个数miu = [38 54];%均值v = [0.1 0.05];%变异系数sgma = miu .* v;%方差syms x yg = sym('x * y - 1140');%功能函数jacg = jacobian( g ,[x;y]);%计算雅可比矩阵initvalue = [miu;v;sgma];%用作函数参数%选取beta,定义x0=miubeta1 = 3.0;xopt0 = [38 54];alpha0 = zeros(1,2);[ alpha1 , xopt1 , result ] = calforbeta( initvalue , beta1 , alpha0 , xopt0 , jacg , g );if result == 1disp('第一次假定的可靠指标');returnend%再次假定betabeta2 = 2.5;xopt0 = miu - beta2 * alpha1 .* sgma;gvalue = jacgfunc(jacg,xopt1);alpha0 = (sgma .* gvalue) / sqrt(sum((sgma .* gvalue).^2));[ alpha2 , xopt2 , result ] = calforbeta( initvalue , beta2 , alpha0 , xopt0 , jacg , g );if result == 1disp('第二次假定的可靠指标');returnend%beta迭代求解g1 = gfunc(g,xopt1);g2 = gfunc(g,xopt2);eps = 0.1; %精度while abs(g2) > epstemp = beta2;beta2 = beta2 - (beta2 - beta1)/(g2 - g1) * g2;beta1 = temp;[ alpha2 , xopt2 , result ] = calforbeta( initvalue , beta2 , alpha1 , xopt1 , jacg , g );temp = g2;g2 = gfunc(g,xopt2);g1 = temp;if result == 1breakendenddisp('可靠指标为:');disp(beta2);disp('最终验算点为:');disp(xopt2);disp('在验算点处功能函数值为:');disp(g2);function g_out = gfunc( g , x_in )%功能函数值计算x = x_in(1);y = x_in(2);g_out = eval(g);%函数值%将以上内容保存为gfunc.mfunction g_out = jacgfunc( jacg , x_in )%功能函数偏导数计算,即雅可比矩阵计算x = x_in(1);y = x_in(2);for i = 1:2g_out(i) = eval(jacg(i));%1为对x的导数,2为对y的导数end%将以上内容保存为jacgfunc.mfunction [ alpha1 , xopt1 ,result ] = calforbeta( initvalue , beta0 , alpha0 , xopt0 , jacg , g) %对选取的beta进行计算result = 0;N = length(xopt0);alpha = alpha0;xopt = xopt0;%initvalue为初始值miu = initvalue(1,:);%第一行为均值v = initvalue(2,:);%第二行为变异系数sgma = initvalue(3,:);%第三行为方差eps = 0.1;while 1%功能函数达到精度则退出循环,result=1表示计算出可靠指标if abs(gfunc(g,xopt0)) < epsalpha1 = alpha0;xopt1 = xopt0;result = 1;break;end%计算alpha和新的验算点xoptgvalue = jacgfunc(jacg,xopt);sgmaz = sqrt(sum((sgma .* gvalue).^2));alpha0 = sgma .* gvalue / sgmaz;xopt0 = miu - beta0 * alpha0 .* sgma;sum1 = sum((alpha - alpha0).^2);sum2 = sum((xopt - xopt0).^2);alpha = alpha0;xopt = xopt0;%醝和验算点xi达到精度则退出循环if sum1 < 0.001 | sum2 < 0.001alpha1 = alpha0;xopt1 = xopt0;break;endend。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
矩量法m atla b程序设计实例:
Ha llen 方程求对称振子天线
一、条件与计算目标 已知:
对称振子天线长为L,半径为a ,且天线长度与波长得关系为,,设,半径a=0、0000001,因此波数为。
目标:
用H all en 方程算出半波振子、全波振子以及不同值得对应参数值。
求:(1)电流分布
(2)E 面方向图 (二维),H 面方向图(二维),半波振子空间方向性图(三维)
二、对称振子放置图
图1 半波振子得电流
分布
半波振子天线平行于z 轴放置,在x轴与y轴上得分量都为零,坐标选取方式有两种形式,一般选取图1得空间放置方
式。
图1给出了天线得电流分布情况,由图可知,当天线很细时,电流分布近似正弦分布。
三、Ha llen 方程
得解题思路
()()()()2
1
'
'
'
'
12,cos sin sin 'z z
i
z z
z
z i z k
z G z z dz c kz c kz E k z z dz j ωμ'++=-⎰⎰
对于中心馈电得偶极子,Hallen 方程为
()22'1222
('),'cos sin sin ,2L L i
L L V i z G z z dz c kz c kz k z z j η
+
--
++=
<<+⎰
脉冲函数展开与点选配,得到
()1121
,''cos sin sin ,1,2,,2n
n
N
z i
n m m m m z n V I G z z dz c kz c kz k z m N j η
+''=++=
=⋅⋅⋅∑⎰
上式可以写成 矩阵形式为
四、结果与分析 (1)电流分布
图2
不同电流
分布图
分
析:由图
2可知半
波振子
天线=
0、5得
电流分
布最大,
馈点电流最大,时辐射电阻近似等于输入电阻,因为半波振子得输入电流正好就
是波腹电流。
(2)E面方向图(二维)
图5不同得E 面方向图(1)
分析:
(a)θ=0时,辐射场为0。
(b)当(短振子)时,方向
函数与方向图与电流元
得近似相同。
(c)时,最大辐射方向为,主瓣随增大变窄。
后开始出现副瓣。
由图6可以瞧出。
(d)时,随增大,主瓣变窄变小,副瓣逐渐变大;继续增大,主瓣转为副瓣,而原副瓣
变为主瓣。
(如图6所示)
图6不同得E面方向图(2)
H面方向图(二维)
图7未归一化得不同
得H面方向图
图8 归一化得不同得H面方向图空间方向性图(三维)
图9半波振子得空间方向图
图10 半波
振子得空间
剖面图
附程序:
clc;
clear
all
clf;
tic; %计时
lambda=1;
N=31;a=0、0000001;%已知天线与半径
ii=1;
for h=0、2:0、1:0、9
L=h*lambda;
len=L/N;%将线分成奇数段,注意首末两端得电流为0
e0=8、854e-012;u0=4*pi*10^(—7);k=2*pi/lambda;
c=3e+008;w=2*pi*c;%光速,角频率
ata=sqrt(u0/e0);
z(1)=—L/2+len/2;
for n=2:N
z(n)=z(n—1)+len;
end
for m=1:N
forn=1:N
if (m==n)
p(m,n)=log(len/a)/(2*pi)-j*k*len/4/pi;
else
r(m,n)=sqrt((z(m)-z(n))^2+a^2);
p(m,n)=len*exp(—j*k*r(m,n))/(4*pi*r(m,n));
end
end
end
for m=1:N
q(m)=cos(k*z(m));
s(m)=sin(k*z(m));
t(m)=sin(k*abs(z(m)))/(j*2*ata);
end
pp=p(N+1:N^2—N);
pp=reshape(pp,N,N-2);
mat=[pp,q',s'];%构造矩阵
I=mat\t';
II=[0;I(1:N-2);0];%加上两端零电流
Current=abs(II);
x=linspace(-L/2,L/2,N);
figure(1);
string=['b','g','r',’y','c’,'k’,’m','r'];
string1=['ko’,'bo’,’yo’,'co','mo’,’ro’,'go’,'bo'];
plot(x,Current,string(ii),'linewidth',1、3);
xlabel(’L/\lambda’),ylabel(’电流分布’);
grid on
hold on
%legend(’L=0、1\lambda',’L=0、2\lambda',’L=0、3\lambda','L=0、4\lambda',’L=0、5\lambda','L=0、6\lambda’,'L=0、7\lambda’,’L=0、8\lambda','L=0、9\lambda','L=1\lambda')
legend('L=0、1\lambda’,’L=0、3\lambda’,'L=0、5\lambda','L=0、7\l ambda','L=0、9\lambda','L=1、1\lambda’,'L=1、3\lambda',’L=1、5\lambda')
Zmn=1/I((N+1)/2);%%%%%%V=1v
theta=linspace(0,2*pi,360);
for m=1:360
for n=1:N
F1(m,n)=II(n)、*exp(j*k*z(n)*cos(m*pi/180))*len*sin(m *pi/180);
end
end
F2=—sum(F1’);
F=F2/max(F2);%%%归一化
figure(2);
polar(theta,abs(F),string(ii));
title('E面归一化方向图’)
view(90,-90)
%legend(’L=h\lambda’,’L=0、3\lambda’,'L=0、3\lambda’,'L=0、4\lambda',’L=0、5\lambda',’L=0、6\lambda','L=0、7\lambda',’L=0、8\lambda',’L=0、9\lambda','L=1\lambda')
legend('L=0、1\lambda',’L=0、3\lambda',’L=0、5\lambda',’L=0、7\lambda',’L=0、9\lambda',’L=1、1\lambda’,'L=1、3\lambda’,’L=1、5\lambda')
hold on
figure(3)
kk=1;
for phi=0:pi/180:2*pi
forn=1:N
FF(n)=II(n)*len*exp(i*k*len*n*cos(pi/2))*sin(pi/2);
end;
FFF(kk)=sum(FF);
kk=kk+1;
end;
phi=0:pi/180:2*pi;
polar(phi,FFF/max(abs(FFF)),string(ii));title('不同L/\lambd aH-plane pattern,F({\theta},{\phi}),\theta=90');
legend('L=0、1\lambda’,'L=0、3\lambda','L=0、5\lambda','L=0、7\lambda’,'L=0、9\lambda',’L=1、1\lambda’,'L=1、3\lambda','L=1、5\lambda')
holdon
figure(4)
polar(phi,FFF/max((FFF)),string(ii));title('归一化H-plane pattern,F({\theta},{\phi}),\theta=90');
hold on
figure(5)
mm=1;
fortheta=0:0、01*pi:pi;
for n=1:N
E(1,n)=2*pi*c*u0*len/(4*pi*1)*(exp(-i*k*1)*exp(i*k*len*n *cos(theta))*sin(theta));
end
EE=E*II;
G(mm)=(4*pi*1^2)/ata/abs(II((N—1)/2+1))^2/(—real(Zmn))*abs(EE)^2;
mm=mm+1;
end。
