机械原理大作业(平面六杆机构的运动分析)
平面六杆机构的运动分析

平面六杆机构的运动分析(题号3-C)指导老师陈永琴班级041011学号04101042姓名师汉同组人戴峰杨彤王建雄1、题目说明下图为一平面六杆机构。
直各构件的尺寸如下表,又知原动件1以角速度为1rad/s沿逆时针方向回转,要求个从动件的角位移、角速度、及角加速度以及E 点的位移、速度及加速度变化情况。
组号L i L2 L2'L3 L4 L5 1_6 a(X G)L4'(Y G)L73-C600题目要求:三人一组计算出原动件从0到2口变化时(计算点数37)所要求的各运动变量的大小, 并绘出运动曲线图及E点的轨迹曲线。
2、题目分析1) 建立封闭图形:L 2-L 3= L 4 - L iL 2 + L 2' + L 5 - L 6+ L 7= L 4' - L i2)机构运动分析A.角位移分析由图形封闭性得:L ? cos 2 L 3 cos 3 L 4 L i cos 1L 2 sin2L 3 sin3L 1 sin 1L 2 cos 2 L 2' cos 2 a2L 5co s 5 L 6cos6L 4' L 1 cos1 L2 sin 2 L 2'sin 2a2L5sin5L6 sin 6L 7L 1 sin 1B.角速度分析上式对时间求一阶导数,可得速度方程L 2 sin22 L3 sin 3 3 L 1 sin 1 1L 2 cos 22 L3 cos 33 L [ cos 11L 2 sin 2 12 L 2 sin(a 2)2L 5 sin5 5 L6 sin 66L1sin 1 1 L 2 cos 221 L2 cos( 2 )2 L 5 cos 5 5L 6 cos 6 6L 1cos 11化为矩阵形式为:L2sin 2 L 3 sin 3 0 0 2L 2cos 2 L 3 cos 30 0 3 L 2 sin2 L 2' sin a 2 0 L 5 sin 5 L e sin 6 5 L 2 cos2L 2 cos a 2L 5 cos 5L 6 cos 66L 1 sin 1 L 〔 cos iiL 1 sin 1 L i cos iC.角加速度分析:角速度矩阵对时间求一阶导数,可得加速度矩阵为:L 2 sin 2 L asin 30 2L 2 cos 2L 3 cos 30 3L :2 sin 2L 2' sin a 20 L 5 sin 5 L 6 sin 6 5L 2cos 2 L 2' cos a 2L 5 cos 5L 6 cos 66L 2 cos 2 L 3 cos 30 22 L i cos 1L 2 sin 2L 3 sin 30 2 3 2Li sin iL 2 cos 2 L 2' cos a 20 L ; 5 cos 5 L 6 cos 6 2 5 1L i cos iL 2 sin 2 L 2' sin a 2L5sin 5L 6 sin 62 6L i siniD.E 点的运动状态XEXGL6COs6L5COs5v EX Lsin 66 L5 sin 5 5 速度: v EEyL 6cos 6 6L5cos 55位移:y y L 6 sin 6L 5 sin 5调用MATLAB 系统函数fsolve 求解各从动件的角位移分别存 至 th2,th3,th5,th6。
机械原理大作业平面连杆机构报告

平面连杆机构的运动分析(题号:平面六杆机构)一、题目说明图示为一平面六杆机构。
设已知各构件的尺寸如表1所示,又知原动件1以等角速度ω1=1 rad/s沿逆时针方向回转,试求各从动件的角位移、角速度及角加速度以及E点的位移、速度及加速度的变化情况。
已知其尺寸参数如下表所示:二、题目分析1、建立封闭图形:L 1 + L 2= L 3+ L 4组号1ll2l 3 l 4 l 5 l 6 α A B C2-A2-B 2-C26.5 67.5 87.5 52.4 43.0 60l 2=116.6 l 2=111.6l 2=126.6L 1 + L 2= L 5+ L 6+AG2、机构运动分析:a 、角位移分析由图形封闭性得:⎪⎪⎩⎪⎪⎨⎧⋅-⋅+=+-⋅-⋅+⋅⋅-⋅+=+-⋅-⋅+⋅⋅=⋅+⋅+⋅=⋅+⋅55662'2221155662'222113322114332211sin sin )sin(sin sin cos cos )cos(cos cos sin sin sin cos cos cos θθθαπθθθθθαπθθθθθθθθL L y L L L L L x L L L L L L L L L L G G 将上式化简可得:⎪⎪⎩⎪⎪⎨⎧=⋅-⋅+-⋅+⋅-=⋅-⋅+-⋅+⋅⋅-=⋅-⋅⋅-=⋅-⋅G G y L L L L L x L L L L L L L L L L L 66552'233466552'2331133221143322sin sin )sin(sin cos cos )cos(cos sin sin sin cos cos cos θθαθθθθαθθθθθθθθb 、角速度分析上式对时间求一阶导数,可得速度方程:化为矩阵形式为:⎪⎪⎩⎪⎪⎨⎧=⋅⋅-⋅⋅+⋅-⋅+⋅⋅=⋅⋅+⋅⋅-⋅-⋅-⋅⋅-⋅⋅-=⋅⋅-⋅⋅⋅⋅=⋅⋅+⋅⋅-0cos cos )cos(cos 0sin sin )sin(sin cos cos cos sin sin sin 66655522'233366655522'2333111333222111333222ωθωθωαθωθωθωθωαθωθωθωθωθωθωθωθL L L L L L L L L L L L L L⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⋅-⋅⋅=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⋅⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⋅-⋅⋅-⋅⋅⋅-⋅--⋅-⋅-⋅⋅⋅-00cos sin cos cos cos )cos(sin sin sin )sin(00cos cos 00sin sin 1111165326655332'26655332'233223322θθωωωωωθθθαθθθθαθθθθθL L L L L L L L L L L L L Lc 、角加速度分析:矩阵对时间求一阶导数,可得加速度矩阵2233222333'223355665'22335566622332233'22sin sin 0cos cos 00sin()sin sin sin cos()cos cos cos cos cos 00sin sin 00cos(L L L L L L L L L L L L L L L L L θθεθθεθαθθθεθαθθθεθθθθθα-⋅⋅⎡⎤⎡⎤⎢⎥⎢⎥⋅-⋅⎢⎥⎢⎥⋅=⎢⎥⎢⎥-⋅--⋅-⋅⋅⎢⎥⎢⎥⋅-⋅⋅-⋅⎣⎦⎣⎦-⋅⋅-⋅⋅⋅-211221123123355665'2223355666cos sin )cos cos cos 0sin()sin sin sin 0L L L L L L L L L θωθωωθθθωθαθθθω⎡⎤⋅⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⋅⎢⎥⎢⎥⎢⎥⋅+⋅⎢⎥⎢⎥⎢⎥⋅⋅-⋅⎢⎥⎢⎥⎢⎥⋅-⋅⋅-⋅⎢⎥⎣⎦⎣⎦⎣⎦d 、E 点的运动状态位移:⎩⎨⎧⋅-⋅+=⋅-⋅+=55665566sin sin cos cos θθθθL L y y L L x x G EG E速度:⎪⎩⎪⎨⎧⋅⋅-⋅⋅=⋅⋅+⋅⋅-=555666555666cos cos sin sin ωθωθωθωθL L v L L v yx E E 加速度:⎪⎩⎪⎨⎧⋅⋅-⋅⋅+⋅⋅+⋅⋅-=⋅⋅+⋅⋅+⋅⋅-⋅⋅-=5552555666266655525556662666cos sin cos sin sin cos sin cos εθωθεθωθεθωθεθωθL L L L a L L L L a yx E E三、流程图四、源程序#include<stdio.h>#include<stdlib.h>#include<math.h>#define PI 3.1415926#define N 4void Solutionangle(double [18],double ); /*矢量法求角位移*/void Solutionspeed(double [N][N],double [N],double [18],double ); /*角速度求解*/void Solutionacceleration(double [N][N],double [N][N],double [N],double [18]);/*角加速度求解*/void GaussianE(double [N][N],double [N],double [N]);/*高斯消去*/void FoundmatrixA(double [18],double [N][N]); //创建系数矩阵Avoid FoundmatrixB(double [18],double ,double [N]);//创建系数矩阵Bvoid FoundmatrixDA(double [18],double [N][N]);//创建矩阵DAvoid FoundmatrixDB(double [18],double ,double [N]);//创建矩阵DB//定义全局变量double l1=26.5,l2=111.6,l3=67.5,l4=87.5,l5=52.4,l6=43.0;double l2g=65.0,xg=153.5,yg=41.7,inang=60*PI/180,as1=1.0;//主函数void main(){int i,j;FILE *fp;double shuju[36][18];double psvalue[18],a[N][N],da[N][N],b[N],db[N],ang1;//建立文件,并制表头if((fp=fopen("filel","w"))==NULL){printf("Cann't open this file.\n");exit(0);}fprintf(fp,"\n The Kinematic Parameters of Point 5\n"); fprintf(fp," ang2 ang3 ang5 ang6"); fprintf(fp," as2 as3 as5 as6"); fprintf(fp," aas2 aas3 aas5 aas6");fprintf(fp," xe ye vex vey aex aey\n");//计算数据并写入文件for(i=0;i<36;i++){ang1=i*PI/18;Solutionangle(psvalue,ang1);FoundmatrixB(psvalue,ang1,b);FoundmatrixA(psvalue,a);Solutionspeed(a,b,psvalue,ang1);FoundmatrixDA(psvalue,da);FoundmatrixDB(psvalue,ang1,db);Solutionacceleration(a,da,db,psvalue);for(j=0;j<4;j++){shuju[i][j]=psvalue[j]*180/PI;}for(j=4;j<18;j++){shuju[i][j]=psvalue[j];}fprintf(fp,"\n");for(j=0;j<18;j++)fprintf(fp,"%12.3f",shuju[i][j]);}fclose(fp);//输出数据for(i=0;i<36;i++){ang1=i*PI/18;printf("\n输出ang1=%d时的求解\n",i*10);printf("angle angspeed angacceleration E:\n"); for(j=0;j<4;j++)printf("%lf\t",shuju[i][j]);printf("\n");for(j=4;j<8;j++)printf("%lf\t",shuju[i][j]);printf("\n");for(j=8;j<12;j++)printf("%lf\t",shuju[i][j]);printf("\n");for(j=12;j<18;j++)printf("%lf\t",shuju[i][j]);printf("\n");}}/*矢量法求角位移*/void Solutionangle(double value[18],double ang1){double xe,ye,A,B,C,phi,alpha,csn,ang5g,d2,d,ang2,ang3,ang5,ang6; A=2*l1*l3*sin(ang1);B=2*l3*(l1*cos(ang1)-l4);C=l2*l2-l1*l1-l3*l3-l4*l4+2*l1*l4*cos(ang1);ang3=2*atan((A+sqrt(A*A+B*B-C*C))/(B-C));if(ang3<0)//限定ang3大小{ang3=2*atan((A-sqrt(A*A+B*B-C*C))/(B-C));}ang2=asin((l3*sin(ang3)-l1*sin(ang1))/l2);xe=l4+l3*cos(ang3)+l2g*cos(ang2-inang);ye=l3*sin(ang3)+l2g*sin(ang2-inang);phi=atan2((yg-ye),(xg-xe));d2=(yg-ye)*(yg-ye)+(xg-xe)*(xg-xe);d=sqrt(d2);csn=(l5*l5+d2-l6*l6)/(2.0*l5*d);alpha=atan2(sqrt(1.0-csn*csn),csn);ang5g=phi-alpha;ang5=ang5g-PI;ang6=atan2(ye+l5*sin(ang5g)-yg,xe+l5*cos(ang5g)-xg);value[0]=ang2;value[1]=ang3;value[2]=ang5;value[3]=ang6;value[12]=xe;value[13]=ye;//限定角度大小for(int i=0;i<4;i++){while(value[i]>2*PI)value[i]-=2*PI;while(value[i]<0)value[i]+=2*PI;}}/*角速度求解*/void Solutionspeed(double a2[N][N],double b2[N],double value[18],double ang1) {double ang2,ang3;ang2=value[0];ang3=value[1];double p2[N];GaussianE(a2,b2,p2);value[4]=p2[0];value[5]=p2[1];value[6]=p2[2];value[7]=p2[3];value[14]=-l3*value[5]*sin(ang3)-l2g*value[4]*sin(ang2-inang);value[15]=l3*value[5]*cos(ang3)+l2g*value[4]*cos(ang2-inang);}/*角加速度求解*/void Solutionacceleration(double a3[N][N],double da3[N][N],double db3[N],double value[18]){int i,j;double ang2,ang3;ang2=value[0];ang3=value[1];double bk[N]={0};double p3[N];for(i=0;i<N;i++){for(j=0;j<N;j++){bk[i]+=-da3[i][j]*value[4+j];}bk[i]+=db3[i]*as1;}GaussianE(a3,bk,p3);value[8]=p3[0];value[9]=p3[1];value[10]=p3[2];value[11]=p3[3];value[16]=-l3*value[9]*sin(ang3)-l3*value[5]*value[5]*cos(ang3)-l2g*value[8]*si n(ang2-inang)-l2g*value[4]*value[4]*cos(ang2-inang);value[17]=l3*value[9]*cos(ang3)-l3*value[5]*value[5]*sin(ang3)+l2g*value[8]*cos (ang2-inang)-l2g*value[4]*value[4]*sin(ang2-inang);}/*高斯消去法解矩阵方程*/void GaussianE(double a4[N][N],double b4[N],double p4[N]){int i,j,k;double a4g[N][N],b4g[N],t;for(i=0;i<N;i++)for(j=0;j<N;j++)a4g[i][j]=a4[i][j];for(i=0;i<N;i++)b4g[i]=b4[i];//使主对角线上的值尽可能大if(a4g[0][0]<a4g[1][0] && a4g[0][1]>a4g[1][1]){for(j=0;j<N;j++){t=a4g[0][j];a4g[0][j]=a4g[1][j];a4g[1][j]=t;}t=b4g[0];b4g[0]=b4g[1];b4g[1]=t;}if(a4g[2][2]<a4g[3][2] && a4g[2][3]>a4g[3][3]){for(j=0;j<N;j++){t=a4g[2][j];a4g[2][j]=a4g[3][j];a4g[3][j]=t;}t=b4g[2];b4g[2]=b4g[1];b4g[3]=t;}//初等行变换for(j=0;j<N;j++)for(i=0;i<N;i++){if(i!=j){for(k=0;k<N;k++)if(k!=j){a4g[i][k]-=a4g[i][j]/a4g[j][j]*a4g[j][k];} b4g[i]-=b4g[j]*a4g[i][j]/a4g[j][j];a4g[i][j]=0;}}for(i=0;i<N;i++)b4g[i]/=a4g[i][i];p4[0]=b4g[0];p4[1]=b4g[1];p4[2]=b4g[2];p4[3]=b4g[3];}//创建系数矩阵Avoid FoundmatrixA(double value5[18],double a5[N][N]){double ang2,ang3,ang5,ang6;ang2=value5[0];ang3=value5[1];ang5=value5[2];ang6=value5[3]; a5[0][0]=-l2*sin(ang2);a5[0][1]=l3*sin(ang3);a5[1][0]=l2*cos(ang2);a5[1][1]=-l3*cos(ang3);a5[2][0]=-l2*sin(ang2)-l2g*sin(ang2-inang);a5[2][2]=l5*sin(ang5);a5[2][3]=l6*sin(ang6);a5[3][0]=l2*cos(ang2)+l2g*cos(ang2-inang);a5[3][2]=-l5*cos(ang5);a5[3][3]=-l6*cos(ang6);a5[0][2]=a5[0][3]=a5[1][2]=a5[1][3]=a5[2][1]=a5[3][1]=0;}//创建系数矩阵Bvoid FoundmatrixB(double value6[18],double ang1,double b6[N]){b6[0]=b6[2]=l1*sin(ang1)*as1;b6[1]=b6[3]=-l1*cos(ang1)*as1;}//创建矩阵DAvoid FoundmatrixDA(double value7[18],double da7[N][N]){double ang2,ang3,ang5,ang6,as2,as3,as5,as6;ang2=value7[0];ang3=value7[1];ang5=value7[2];ang6=value7[3]; as2=value7[4];as3=value7[5];as5=value7[6];as6=value7[7];da7[0][0]=-l2*as2*cos(ang2);da7[0][1]=l3*as3*cos(ang3);da7[1][0]=-l2*as2*sin(ang2);da7[1][1]=l3*as3*sin(ang3);da7[2][0]=as2*(-l2*cos(ang2)-l2g*cos(ang2-inang));da7[2][2]=as5*l5*cos(ang5);da7[2][3]=as6*l6*cos(ang6);da7[3][0]=as2*(-l2*sin(ang2)-l2g*sin(ang2-inang));da7[3][2]=as5*l5*sin(ang5);da7[3][3]=as6*l6*sin(ang6);da7[0][2]=da7[0][3]=da7[1][2]=da7[1][3]=da7[2][1]=da7[3][1]=0; }//创建矩阵DBvoid FoundmatrixDB(double value8[18],double ang1,double db8[N]){db8[0]=db8[2]=l1*as1*cos(ang1);db8[1]=db8[3]=l1*as1*sin(ang1);}五、计算结果及相关曲线图:A组:数据图像角位移角速度角加速度E点的位移、速度及加速度六、体会及建议:这次的作业给了我们一次锻炼机会,让我们基本掌握了平面六杆机构解析算法的基本原理,从理论到程序实践,每一步都环环相扣,每一个结果都息息相关,最终在我们共同的努力下完成了本次作业。
机械原理课程设计六杆机构运动分析

机械原理课程设计说明书题目六杆机构运动分析学院工程机械学院专业机械设计制造及其自动化班级机制三班设计者秦湖指导老师陈世斌2014年1月15日目录一、题目说明∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ 21、题目要求∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ 32、原理图∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ 33、原始数据∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ 3二、结构分析∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ 4三、运动分析∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ 51、D点运动分析∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ 82、构件3运动分析∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙93、构件4运动分析∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙94、点S4运动分析∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10四、结论∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10五、心得体会∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10六、参考文献∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙11一、题目说明1、题目要求此次机械原理课程设计是连杆机构综合,通过对其分析,选择合适的机构的尺寸大小,并进行下列操作:⑴对机构进行结构分析;⑵绘制滑块D的运动线图(即位移、速度和加速度线图);⑶绘制构件3和4的运动线图(即角位移、角速度和角加速度线图);⑷绘制S4点的运动轨迹。
基于UGCAE的平面六杆机构的运动分析

基于UG/CAE的平面六杆机构的运动分析1、题目说明如上图所示平面六杆机构,试用计算机完成其运动分析。
已知其尺寸参数如下表所示:题目要求:两人一组计算出原动件从0到360时(计算点数37)所要求的各运动变量的大小,并绘出运动曲线图及轨迹曲线。
注:为了使计算的结果更好的拟合运动的实际情况,同时考虑到UG在运动仿真分析计算方面的快速性,我们决定在绘制曲线时将计算点由37点增加到600点。
数据输出到Excel表格时计算点取100点。
建模及其分析方法附后!2、建模及其运动分析软件介绍:UG NX是集CAD\CAE\CAM于一体的三维参数化软件,也是当今世界最先进的设计软件,它广泛应用于航空航天、汽车制造、机械电子等工程领域。
还有在系统创新、工业设计造型、无约束设计、装配设计、钣金设计、工程图设计等方面的功能。
运动仿真是UG/CAE(Computer Aided Engineering)模块中的主要部分,它能对任何二维或三维机构进行复杂的运动学分析、动力分析和设计仿真。
通过UG/Modeling的功能建立一个三维实体模型,利用UG/Motion的功能给三维实体模型的各个部件赋予一定的运动学特性,再在各个部件之间设立一定的连接关系既可建立一个运动仿真模型。
UG/Motion的功能可以对运动机构进行大量的装配分析工作、运动合理性分析工作,诸如干涉检查、轨迹包络等,得到大量运动机构的运动参数。
通过对这个运动仿真模型进行运动学或动力学运动分析就可以验证该运动机构设计的合理性,并且可以利用图形输出各个部件的位移、坐标、加速度、速度和力的变化情况,对运动机构进行优化。
我们通过学习UG,通过建立平面六杆机构模型,通过UG/CAE模块对平面连杆的运动进行分析。
3.六连杆机构的三维造型连杆L1连杆L2连杆L3连杆L5连杆L6六杆机构装配示意图机构装配后运动演示见附件—平面六杆运动演示.avi (本报告相同目录下)3. 运动分析数据计算结果在附件的Excel表格中。
机械原理课程设计--六杆机构运动与动力分析

目录第一部分:六杆机构运动与动力分析一.机构分析分析类题目 3 1分析题目 32.分析内容 3 二.分析过程 4 1机构的结构分析 42.平面连杆机构运动分析和动态静力分析 53机构的运动分析8 4机构的动态静力分析18 三.参考文献21第二部分:齿轮传动设计一、设计题目22二、全部原始数据22三、设计方法及原理221传动的类型及选择22 2变位因数的选择22四、设计及计算过程241.选取两轮齿数242传动比要求24 3变位因数选择244.计算几何尺寸25 五.齿轮参数列表26 六.计算结果分析说明28 七.参考文献28第三部分:体会心得29一.机构分析类题目3(方案三)1.分析题目对如图1所示六杆机构进行运动与动力分析。
各构件长度、构件3、4绕质心的转动惯量如表1所示,构件1的转动惯量忽略不计。
构件1、3、4、5的质量G1、G3、G4、G5,作用在构件5上的阻力P工作、P空程,不均匀系数δ的已知数值如表2所示。
构件3、4的质心位置在杆长中点处。
2.分析内容(1)对机构进行结构分析;(2)绘制滑块F的运动线图(即位移、速度和加速度线图);(3)绘制构件3角速度和角加速度线图(即角位移、角速度和角加速度线图);(4)各运动副中的反力;(5)加在原动件1上的平衡力矩;(6)确定安装在轴A上的飞轮转动惯量。
图1 六杆机构方案号L DF(mm)L CE(mm)L CD(mm)L AB(mm)L AC(mm)n1r/minJ S3kg.m2J S4kg.m23 510 575 170 140 375 80 0.22 0.16方案号G1(kg)G3(kg)G4(kg)G5(kg)P工作(N)P空程(N)δ3 14 75 55 80 1400 140 1/40二.分析过程:通过CAD制图软件制作的六杆机构运动简图:图2 六杆机构CAD所做的图是严格按照题所给数据进行绘制的。
并机构运动简图中活动构件的序号从1开始标注,机架的构件序号为0。
平面六杆机构运动分析
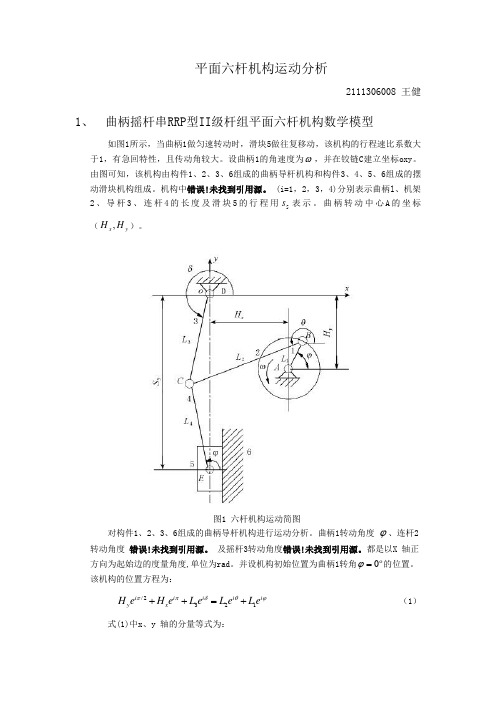
平面六杆机构运动分析2111306008 王健1、 曲柄摇杆串RRP 型II 级杆组平面六杆机构数学模型如图1所示,当曲柄1做匀速转动时,滑块5做往复移动,该机构的行程速比系数大于1,有急回特性,且传动角较大。
设曲柄1的角速度为ω,并在铰链C 建立坐标oxy 。
由图可知,该机构由构件1、2、3、6组成的曲柄导杆机构和构件3、4、5、6组成的摆动滑块机构组成。
机构中错误!未找到引用源。
(i=1,2,3,4)分别表示曲柄l 、机架2、导杆3、连杆4的长度及滑块5的行程用5s 表示。
曲柄转动中心A 的坐标(y x H H ,)。
图1 六杆机构运动简图对构件1、2、3、6组成的曲柄导杆机构进行运动分析。
曲柄1转动角度 ϕ、连杆2转动角度 错误!未找到引用源。
及摇杆3转动角度错误!未找到引用源。
都是以X 轴正方向为起始边的度量角度,单位为rad 。
并设机构初始位置为曲柄1转角0=ϕ的位置。
该机构的位置方程为: ϕθδππi i i i x i y e L e L e L e H e H 1232/+=++ (1) 式(1)中x 、y 轴的分量等式为:{θϕδθϕδcos cos cos cos sin sin 213213L L L H L L L H x y +=+-+=+ (2) 当 错误!未找到引用源。
在 3600-作匀速变化时,就可以求出对应的连杆2的转角 错误!未找到引用源。
以及摇杆3的转角δ的值。
将式消去 错误!未找到引用源。
,得到: ()()22213213cos cos sin sin L L H L L H L x y =--+-+ϕδϕδ (3) 将(3)式分解,并分别定义:()212122231cos )sin (ϕϕL H L H L L A x y ++-+-=)sin (2131ϕL H L B y -=)cos (2131ϕL H L C x +=摇杆3的角位移()]/)tan[(2112121211C A C A B B a --+-+=δ (4) 由(2)式可得连杆 2 的角位移]/)sin sin arcsin[(213L L L H y ϕδθ-+= (5)假设曲柄作匀角速度dt d /φω=是常数,对式2求时间导数,得到连杆2的角速度2ω以及摇杆3角速度3ω,方程式如下:()()][sin cos sin cos sin cos 11233322ϕωϕωωωδδθθL L L L L L =-- (6) 对式(6)求时间导数, 得到连杆 2 的角加速度及摇杆 3 的角加速度2a ,方程式如下: ()()][cos cos cos sin sin sin sin cos sin cos 3232221232322212233322δωθϕωδωθϕωδδθθL L w L L L w L a a L L L L -+-----= (7) 再对构件3、4、5、6 组成的摆动滑块机构进行运动分析。
机械原理大作业(平面六杆机构的运动分析)

a[3][1]=L[3]*cos((*p).theta[2]);
a[3][2]=L[5]*cos((*p).theta[3]);
a[3][3]=-L[6]*cos((*p).theta[4]);
b[0]=L[2]*cos((*p).theta[1])*(*p).w[0]*(*p).w[0]-L[3]*cos((*p).theta[2])*(*p).w[1]*(*p).w[1]+w1*w1*L[1]*cos((*p).theta[0]);
a[2][2]=-L[5]*sin((*p).theta[3]);
a[2][3]=L[6]*sin((*p).theta[4]);
a[3][0]=L[0]*cos((*p).theta[1]-Alpha);
a[3][1]=L[3]*cos((*p).theta[2]);
a[3][2]=L[5]*cos((*p).theta[3]);
#include "conio.h"
#define Alpha (PI/3)
#define PI 3.979
#define Angle (PI/180)
FILE *fp;
struct motion
{
int theta1;
double theta[5]; /*theta1,2,3,5,6*/
double w[4];/*w2,3,5,6*/
for(m=0;m<4;m++)
(*p).theta[m+1]=x[m];
printf("%d %d",n,i);
getchar();
平面机构的运动分析习题和答案Word版
24.在同一构件上.任意两点的绝对加速度间的关系式中不包含哥氏加速度。- - - - ( )
25.当牵连运动为转动.相对运动是移动时.一定会产生哥氏加速度。- - - - - - - - ( )
26.在平面机构中.不与机架直接相连的构件上任一点的绝对速度均不为零。- - - ( )
27.两构件组成一般情况的高副即非纯滚动高副时.其瞬心就在高副接触点处。- - ( )
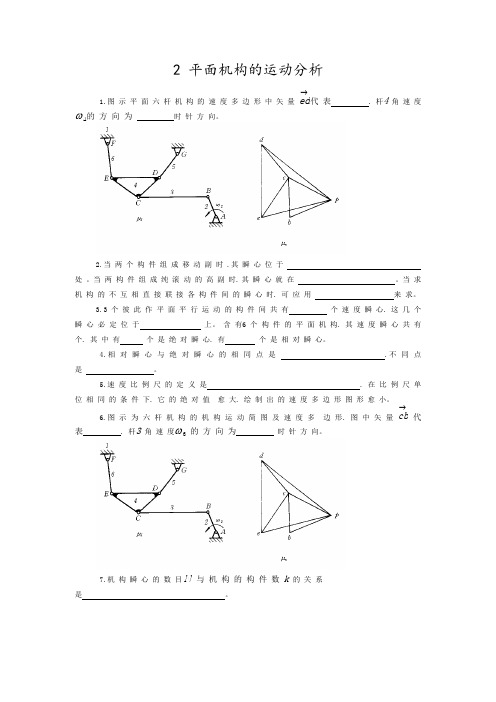
28.给定导杆机构在图示位置的速度多边形。该瞬时 和 的正确组合应是图。
29.给定图示六杆机构的加速度多边形.可得出
(A)矢量 代表 . 是顺时针方向;
(B)矢量 代表 . 是逆时针方向;
(C)矢量 代表 . 是顺时针方向;
(A)绝对速度等于零的重合点;
(B)绝对速度和相对速度都等于零的重合点;
(C)绝对速度不一定等于零但绝对速度相等或相对速度等于零的重合点。
40.下图是四种机构在某一瞬时的位置图。在图示位置哥氏加速度不为零的机构为。
41.利用相对运动图解法求图示机构中滑块2上 点的速度 的解题过程的恰当步骤和利用的矢量方程为:
9.当两构件组成转动副时.其速度瞬心在处;组成移动副时.其速度瞬心在处;组成兼有相对滚动和滑动的平面高副时.其速度瞬心在上。
10..速度瞬心是两刚体上为零的重合点。
11.铰链四杆机构共有个速度瞬心.其中个是绝对瞬心.个是相对瞬心。
12.速度影像的相似原理只能应用于的各点.而不能应用于机构的的各点。
13.作相对运动的3个构件的3个瞬心必。
14.当两构件组成转动副时.其瞬心就是。
15.在摆动导杆机构中.当导杆和滑块的相对运动为动.牵连运动为动时.两构件的重合点之间将有哥氏加速度。哥氏加速度的大小为;方向与的方向一致。
平面六杆机构的运动分析

平面六杆机构的运动分析
1.确定机构的几何特性:首先,需要根据机构的构件和铰链的几何特
性确定机构的几何特性。
这包括确定构件的长度、铰链的位置和角度。
2.建立机构的运动方程:根据机构的几何特性,可以建立机构的运动
方程。
运动方程描述了机构各构件之间的运动关系,可以通过几何关系和
运动链法建立运动方程。
3.解决运动方程:通过求解运动方程,可以得到机构各构件的位置、
速度和加速度。
这可以通过数值方法或解析方法来完成。
4.分析机构的运动特性:根据机构的运动方程和解决的结果,可以分
析机构的运动特性。
这包括机构的平稳性、运动范围、速度和加速度的变
化等。
5.优化机构的设计:根据分析的结果,可以对机构的设计进行优化。
例如,可以调整构件的长度、角度和铰链的位置,以改善机构的运动性能。
总之,平面六杆机构的运动分析是研究和设计机械系统的重要步骤。
通过分析机构的运动特性,可以优化机构的设计,提高机械系统的性能和
效率。
因此,对平面六杆机构的运动分析有着重要的理论和实际意义。
机械原理大作业1(六杆机构)
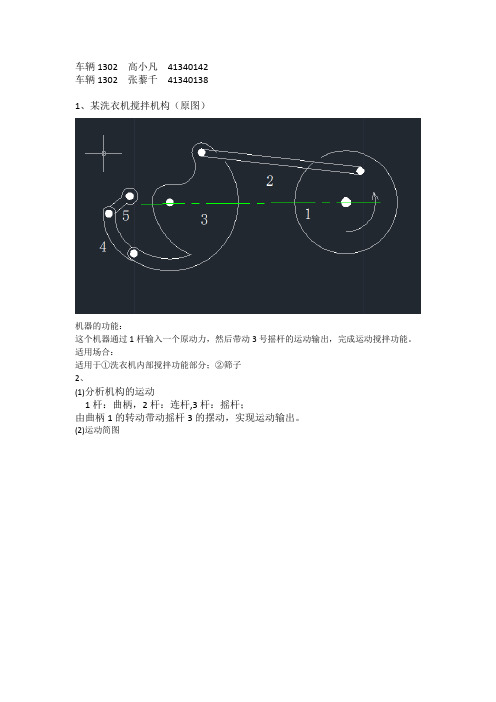
车辆1302 高小凡41340142车辆1302 张藜千413401381、某洗衣机搅拌机构(原图)机器的功能:这个机器通过1杆输入一个原动力,然后带动3号摇杆的运动输出,完成运动搅拌功能。
适用场合:适用于①洗衣机内部搅拌功能部分;②筛子2、(1)分析机构的运动1杆:曲柄,2杆:连杆,3杆:摇杆;由曲柄1的转动带动摇杆3的摆动,实现运动输出。
(2)运动简图(3)如图,该六杆机构只有一个原动件----1杆(4)自由度F=3(n-1)-2P5=3*5-2*7=1上述六杆机构的运动形式可简化为如图四杆机构的运动形式,4,5杆的运动作为摇杆3的输出机构。
3、大致测绘出构件尺寸4、确定机构所含杆组的数目和级别(拆杆组),并判断机构的级别;依次拆下4-5/2-3两个II级杆组及原动件1(II级杆组),所以该机构为II级杆组5、用图解法求出最小传动角值:由下图可知,在极限位置2时,压力角最大为70°,则最小传动角为42°6、分析该机构有无急回特性和死点位置;有急回,无死点;180+1809k 1.11180-1809θθ+===>-7、用瞬心法对机构进行运动分析上图中标出了该机构的简化四杆机构的所有瞬心P 12 P 13 P 16 P 23 P 26 P 36其中,绝对瞬心有:P 16 P 36 P 26 相对瞬心有:P 12P 13 P 23速度分析:若1的角速度为w1,则V(P12)=l1*w1V(P23)= [V(P12)/|P12P13|]*|P13P23 | w3= V(P23)/l3w6= V(P23)/| P23P26 |(1)角速度比mv=w6/w2=l1sinv/l3sinuv=0, mv=0,w6=0,此时构件1、2共线,机构处于极限位置;(2)mv=w6/w2=OP13/CP13 (瞬心P13能够用来确定速度比)上图为该机构(六杆机构)全部瞬心(15个)绝对瞬心:P16, P26,P36,P46,P56相对瞬心:P15,P25,P35,P45P14,P24,P34,P13,P23P12中间密集部分的的放大图如下图:8、用杆组法(或其他解析法)对机构进行运动分析(写出数学模型和程序框图);已知该机构的尺寸为:两个固定铰链点a,d,g的坐标分别为(0,0)(420,0)(-80,-35),曲柄原动件|ab|=100mm,连杆2长为300mm,摇杆3长150mm,杆4长100mm,杆5长50mm.经分析,该机构由一个曲柄原动件和两个RRR二级杆组组成的二级机构用杆组法搭建该机构的步奏如下:1)添加曲柄原动件ab;2)添加RRR二级杆组(2-3),杆组的两个动铰链点分别为已有铰链点b和固定铰链点d; 3)在连杆cd上添加铰链点e;4)添加RRR二级杆组(4-5),杆组的两个动铰链点分别为已有铰链点e和固定铰链点g; 5)该机构搭建完成,利用该程序可自动求出任意给定铰链点或构件的位置、速度、和加速度。
机械原理课程设计基于矢量图解法的平面六杆机构运动分析

机械原理课程设计设计题目:基于矢量图解法的平面六杆机构运动分析姓名:专业班级:学号:指导老师:目录目录 (1)一、设计说明 (2)二、设计内容及数据 (2)1.构件位置的确定及相应尺寸 (3)2.速度分析 (3)3.加速度分析 (5)三、数据汇总 (9)四、参考文献 (10)一、设计说明机构的运动分析,是指原动件的运动规律已知时,求解其余构件的运动规律,确定指定构件上点的位移、轨迹、速度与加速度。
对机构作运动分析的方法很多,本课程设计采用矢量方程图解法。
对机构作运动分析的目的是确定机构的运动空间、检验相关构件的运动规律是否符合设计要求以及为构件的强度设计、运动副的尺寸设计提供计算惯性力与惯性力矩的参数。
矢量方程图解法,也称相对运动图解法,其依据的原理是将动点的运动划分为伴随参考构件的运动以及相对于参考构件的运动。
二、设计内容及数据图(a)为一平面六杆机构,主动件1的杆长r=AB=0.122m,1ϕ==40°,角速度ωL=10rad/s,机架6上的h1=AC=0.280m,=0.164m,比例尺μl=实际尺寸/图上尺寸=2。
试用相对运动图解h2法求移动从动件5的速度V5与加速度a5。
μ=图(a)AUTOCAD绘制图2L1.构件位置的确定及相应尺寸由图(a )得导杆3上B 、C 两点之间的实际长度BC L = 381.6mm ,C 、D 两点之间的实际长度 CD L =167.45mm; B 、C 两点之间的图上长度BC=190.8mm , C 、D 两点之间的图上长度CD=83.7mm 。
2.速度分析列出方程,进行分析,对两个位置点的分析。
(1)根据两构件上重合点之间的速度合成原理,得导杆3上的B 3点与滑块2上的B 2点之间的速度方程为:B3V = B2V + B3B2V1BA : //: ? ?BC BA CBωl ⊥⊥方向大小 (1)式(2)根据两构件上重合点之间的速度合成原理及已知条件,速度分析应由B 点开始,滑块2上的B 2点的速度为:2B V =1B V =1ω1r =10⨯0.122=1.22 m/s其方向垂直于AB ,指向与1ω的转向一致。
机械原理课程设计说明书--平面六杆机构

机械原理课程设计说明书设计题目:平面六杆机构学院:机械工程学院姓名:林立班级:机英101同组人员:刘建业张浩指导老师:王淑芬题目三:平面六杆机构.一. 机构简介1.此平面六杆机构主要由一个四杆机构,和一个曲柄滑块机构构成,其中四杆机构是由1杆,2杆,3杆和机架构成的曲柄摇杆机构,1杆为主动件,转速为90rpm ,匀速转动。
其中滑块机构由3杆,4杆,滑块5和机架构成,以四杆机构的摇杆为主动件2.设计要求:各项原始数据如图所示,要求对机构的指定位置进行运动分析和动态静力分析,计算出从动件的位移,速度(角速度),加速度(角加速度)和主动件的平衡力偶M ,进行机构运动分析,建立数学模型。
之后进行动态静力分析,建立数学模型,必须注意,工作行程和返回行程阻力的大小,方向,主动件处于何位置时有力突变,需要计算两次。
二. 机构运动分析:1.首先分析1杆,2杆,3杆和机架组成的四杆机构,可列复数矢量方程 (1-1) 应用欧拉公式 将实部和虚部分 离得332211cos cos cos θθθl b l l +=+ 332211sin sin sin θθθl a l l +=+把以上两式消元整理得0cos sin 33=++CB A θθ36213621θθθθi i i i l e l l l e e e +=+θθθsin cos i i +=e其中)sin cos (22cos 22sin 21112223212231313131θθθθa b l b a l l l C bl l l B al l l A ++----=-=-=解之可得)/(])([)2/tan(2/12223C B C B A A --+±=θ (1)速度分析将式(1-1)对时间t 求导,可得333222111cos cos cos θθθw l w l w l =+ 333222111sin sin sin θθθw l w l w l =+联解以上两式可求得两个未知角速度,3杆和2杆的角速 度3w 和2w)]-sin()/[l -sin(l )]sin(/[)sin(3223111223321113θθθθθθθθw w l l w w -=--=(2)加速度分析将式(1-1)对时间t 两次求导。
机械原理课程设计 六杆机构分析完整版

机械原理课程设计说明书设计题目:六杆机构运动分析学院:工程机械学院专业:机械设计制造及其自动化班级:25041004设计者:25041004指导老师:张老师日期:2013年01月07日目录1.课程设计题目以及要求————————————————————32.运用辅助软件对结构进行结构分析———————————————43.数据收集以及作图———————————————————————114.总结————————————————————————————17六杆机构运动分析1、分析题目对如图5所示的六杆机构进行运动与动力分析,各构件长度、滑块5的质量G 、构件1转速n1、不均匀系数δ的已知数据如表5所示。
2、分析内容(1)对机构进行结构分析:(2)绘制滑块D 的运动线图(即位移、速度和加速度线图):(3)绘制构件3和4的运动线图(即角位移、角速度和角加速度线图): (4)绘制S4点的运动轨迹。
图5表5方案号L CDmmL ECmmymm L AB mm L CS4 mm n 1r/mi n1 975 360 50 250 400 23.52 975 325 50 225 350 33.53 9003005020030035(一)对机构进行结构分析选取方案三方案号L CDmm L ECmmymmL ABmmL CS4mmn 1r/mi n3 900 300 50 200 300 35对六杆机构进行运动分析:(1)原始数据的输入:(2)基本单元的选取及分析:(3)各点运动参数:(4)长度变化参数(5)各构件角运动参数:(二)滑块D的运动线图(位移-速度-加速度线图):(三)构件3的运动线图(角位移-角速度-角加速度线图):(四)构件4的运动线图(角位移-角速度-角加速度线图):(五)S4点的运动轨迹:(六)数据收集以及作图(1)滑块D 点x 、y 方向的运动参数如表6.1所示表6..1由上表可以得到D 点运动线图如图6.1所示图6.1位置 0123456789101112位 移X 1188.097 1187.376 1058.394 848.5281 680.2758 607.9142 606.0113 651.5314 734.6896 848.5281 980.0058 1105.089 1188.097 Y 0 0 0 0 0 0 0 0 0 0 0 0 0 速 度X 332.4289 -434.0533 7293.698 -1466.08 -831.5157 -222.7902 169.5616 457.6898 699.4701 879.648 933.0263 776.3062 332.4289 Y 0 0 0 0 0 0 0 0 0 0 0 0 0 加 速度X -4255.382 -6281.231 -4679198 2533.081 4920.073 3387.318 2265.425 1834.254 1530.378 911.9092 -264.7796 -2020.469 -4255.382 y 0(2)构件3的运动参数如表6.2所示表6.2位置0 1 2 3 4 5 6 7 8 9 10 11 12角位移φ14.03624 -16.10211 -50.93532 -90 230.9353 196.1021 165.9638 139.1066 114.1333 90 65.86674 40.89339 14.03624角速度ω-3.4496 -3.947138 -4.561904 -4.886933 -4.561904 -3.947138 -3.4496 -3.1416 -2.981412 -2.93216 -2.981412 -3.1416 -3.4496角加速度ɛ-2.789002 -4.130385 -3.972855 -6.092957 3.972855 4.130385 2.789002 1.582846 0.7038764 2.368942 -0.703876 -1.582846 -2.789002由上表得构件3的运动线图如图6.2所示图6.2(3)构件4的运动参数如表6.3所示表6.3位置0 1 2 3 4 5 6 7 8 9 10 11 12 φ-4.63715 5.304571 14.99956 19.471122 14.99956 5.304571 -4.63715 -12.60438 -17.70998 -19.47122 -17.70998 -12.60438 -4.63715 角位移ω 1.119198 1.269533 0.992103 1.253846 -0.9921031 -1.269533 -1.119198 -0.8111576 -0.4265414 -1.775216 0.4265414 0.1811158 1.119198 角速度ɛ 1.768468 0.031558 -4.448388 -8.443604 -4.448388 0.031558 1.768468 2.468482 2.88811092 3.039697 2.881092 2.468482 1.768468 角加速度由表6.3参数可得构件4的运动线图如图6.3所示图6.3(4)S4点x、y方向的运动参数如表6.4所示表6.4位置0 1 2 3 4 5 6 7 8 9 10 11 12位移X 590.0608 586.9459 478.8375 282.8427 100.7192 10.48452 7.975251 65.99134 163.1245 282.8427 408.4406 519.5487 590.0608 Y 48.50713 -55.47002 755.287 -200 -155.287 -55.47002 48.50713 130.9307 182.5194 200 182.5194 130.9307 48.50713速度X 278.1398 -363.6323 -1139.637 -1466.08 -985.5764 -293.2113 223.8507 563.8953 777.3222 879.648 855.1742 670.1007 278.1398 Y -669.3207 -758.4576 -574.98 -8.42273 574.98 758.4576 669.3207 474.9653 243.7962 7.905602 -243.7962 -474.9653 -669.3207加速度X -3592.063 -5316.593 -4799.736 844.3604 4920.073 4351.956 2928.744 1896.326 1108.512 303.9697 -686.6455 -1958.397 -3592.063 y -1118.368 70.54837 2730.937 4776.623 2730.937 70.54837 -1118.368 -1531.544 -1679.939 -1719.512 -1679.939 -1531.544 -1118.368(七)总结:六杆机构的运动分析相比课本上的平面四杆机构来说难度大些,而且是用辅助软件进行运动分析,这看起来似乎难度更大。
机械原理6杆机构设计实例

机械原理6杆机构设计实例机械原理中的六杆机构是一种基本的机械结构,由六个连杆组成,可以实现特定的运动和转换功能。
本文将为您提供一个六杆机构的设计实例,以便更好地理解其工作原理和应用。
1. 设计目标:我们的设计目标是创建一个六杆机构,可以将旋转运动转换为直线运动。
该机构将用于驱动一个线性推进器,以实现物体在直线轴上的移动。
2. 机构设计:为了实现我们的设计目标,我们选择了一种常见的六杆机构类型,即双曲线传动机构。
该机构由两个相交的双曲线连杆和四个普通连杆组成。
其中两个普通连杆连接驱动轴和双曲线连杆,另外两个普通连杆连接双曲线连杆和线性推进器。
3. 工作原理:当驱动轴旋转时,通过连杆的连接,双曲线连杆也开始旋转。
由于双曲线曲面的特性,使得连接在其上的普通连杆产生复杂的运动轨迹。
这种运动轨迹可以被利用,使得线性推进器在直线轴上产生直线运动。
4. 应用:这种六杆机构设计可以广泛应用于需要将旋转运动转换为直线运动的场景中。
例如,在自动化生产线中,可以使用该机构实现工件的装配和定位。
另外,在机床中,该机构也可以用于驱动刀具进行直线切削操作。
5. 设计考虑:在进行六杆机构设计时,需要考虑以下几个因素:- 机构尺寸:根据特定应用的需求,确定机构的尺寸和比例。
- 运动平稳性:为了确保机构运动平稳,需要进行合理的连杆长度和角度的选择。
- 载荷承受能力:根据应用场景中的负载要求,设计机构以承受相应的载荷。
- 动力传递效率:通过减少摩擦和能量损失来提高机构的动力传递效率。
6. 结论:通过设计一个六杆机构,我们成功地实现了将旋转运动转换为直线运动的目标。
该机构可以在自动化生产线和机床等领域中发挥重要作用。
在设计过程中,我们需要考虑机构尺寸、运动平稳性、载荷承受能力和动力传递效率等因素。
这个设计实例展示了六杆机构在实际应用中的重要性和灵活性。
以上就是关于机械原理六杆机构设计的一个实例解释。
通过这个例子,我们可以更好地理解六杆机构的工作原理和应用,以及设计过程中需要考虑的因素。
六杆机构运动分析

机械原理课程设计六杆机构运动分析学院:工程机械专业:机械设计制造及其自动化班级:25041004设计者:王东升于新宇2013年 1月8日一、分析题目如图1所示六杆机构,对其进行运动和动力分析。
已知数据如表1所示。
r1=r3=L2=110mm ,L4=600mm ,L AD=39mm ,n1=40r/min ,L CS4=220mm.图1 六杆机构二、分析内容(1)进行机构的结构分析;如2图所示,建立直角坐标系。
机构中活动构件为1、2、3、4、5,即活动构件数n=5。
A、C、B、D、E处运动副为低副(6个转动副,1个移动副),共7个,即P l=7。
则机构的自由度为:F=3n-2P l=3Χ5-2Χ7=1。
图2(a)图2(b) 图2(c)如图2,拆出基本杆组,(a)为原动件,(b)、(c)为二级杆组,该机构是由机架0、原动件1和2个Ⅱ级杆组组成,故该机构是Ⅱ级机构。
(2)绘制滑块E的运行线图;利用JYCAE软件求解。
1、将题设所给的原始数据(机构的活动构件数、转动副数、移动副数、己知长度值总数和机构的自由度)分别输入JYCAE软件中,如图3:图3—1图3—2图3—3图3—42、机构的运动分析输入完所有的原始数据以后,开始运动分析。
求E点的运动线图,要选取基本单元5,但是利用基本单元5的条件是已知C点的运动状态,所以先利用基本单元1、2求得C点的运动状态,然后求的E点运动线图。
如图4。
图4—1 解得B点运动参数图4—2 解得C点运动参数图4—3 解得E点运动参数共选取3个基本单元,如图4—4,然后运算。
图4—4运算后,E点运动参数如表1,运动线图如图5。
表1 点E的x、y方向的运动参数图5 点E运动线图(3)绘制构件3和4的运动线图;由(2)可知各点运动参数,继续上述程序求解。
如下图:求构件3运动线图是,选取基本单元6中的摆动倒杆(1),如图6—1,运算后,运动参数如表2,运动线图如图6—2。
图6—1表2 构件3的运动参数图6—2求构件4运动线图时,选取基本单元6中的摆动倒杆(1),如图6—3,运算后,运动参数如表3,运动线图如图6—2。
平面六杆机构可视化运动分析

文 章 编 号 :1 0 0 2 — 6 6 7 3( 2 0 1 3 )0 2 — 0 8 5 — 林 权 ,游 张平 ,王 克 刚
( 丽 水 学 院 工 学 院 ,浙 江 丽水 3 2 3 0 0 0 )
摘
要 :运 动分 析是 平 面 六杆 结构研 究 的重要 内容 ,对 于机 构设 计 具 有 重要 指导 意 义 。首 先建 立 并 求解机 构
的矢量 方程 ,从 而得 到 其速 度 、加速 度 和位 移等 的数 学模 型 。在 此基 础 上利 用 Ma l f a b软件 在 数值 计
算 和 图形 绘制 等 方 面 的强 大功 能 ,采 用 模 块化 设 计 ,开发 了一种 界 面友好 的 可视 化人 机 交 互程 序 , 用户 只需 改 变机构 参数 就 可 以方便 的 实现 运动 分析 和 运动 仿 真 .用 户可 以 形 象直观 地 观察 到 关键 点 的运动 轨迹 、速 度 变化及 加 速度 变化规 律 ,为 平 面六杆 机 构 的分 析 计算 提供 了方便 。 同时也提 高 了 设 计效 率 ,对 实 际设 计 具有 一定 的指 导 意 义。 关 键词 :运 动分析 ;Ma t l a b ;六杆机 构 ;仿 真
Abs t r ac t :M ot i on Ana l y s i s i s a l l i mp o r t a nt c o nt e n t o f t h e s t ud y o f p l a na r s i x —s ha nk s t r u c t ur e ,a n d i t i s i m po r t a nt t o s t r u c ur t e de s i g n.F i r s t l y ,
p l a n r a s x— i s h a n k s t r u c t u r e v i s u l a mo i t o n a n l a y s i s p r o g r a m wi t h f r i e n d l y u s e r i n t e r f a c e wa s d e v e l o p e d it w h Ma t l a b , S O ha t t u s e s r o 由
机械原理(2015春)机构组成原理及机构分析
(1)除去虚约束、局部自由度,计算机构的自由度并确定原动件。
(2)拆杆组:从远离原动件的构件开始拆分,按基本杆组的特征, 首先试拆Ⅱ级组,若不可能时再试拆Ⅲ级组。
(3)确定机构的级别。
举例:计算图示机构自由度,并确定机构的级别
构件5为原动件: Ⅱ级机构
机构的自由度: F=3n(2 pl + ph –p’) –F’ =3*5(2*7+00)0=1
构件2为原动件:
Ⅲ级机构
机构组成原理及结构分析
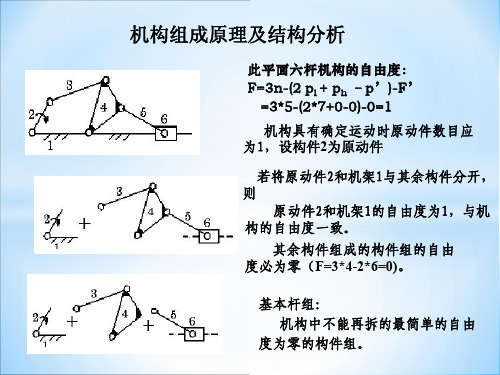
此平面六杆机构的自由度: F=3n-(2 pl + ph –p’)-F’
=3*5-(2*7+0-0)-0=1
机构具有确定运动时原动件数目应 为1,设构件2为原动件
若将原动件2和机架1与其余构件分开, 则
原动件2和机架1的自由度为1,与机 构的自由度一致。
其余构件组成的构件组的自由 度必为零(F=3*42*6=0)。
F = 3n - 2 pl = 0
n
=
2 3
pl
基本杆组的分类: 若n=2, pl=3,含有2个构件3个低副,叫 Ⅱ 级组。
若n=4, pl=6,含有4个构件6个低副,叫 Ⅲ 级组。 ( Ⅲ级组中有一个包含3个低副的构件)
2、平面机构的结构分类
Ⅰ级机构:只有原动件和机架组成的机构。 Ⅱ级机构:由最高级别为Ⅱ级组的基本杆组构成的机构。 Ⅲ级机构:由最高级别为Ⅲ级组的基本杆组构成的机构。 3、平面机构的结构分析
基本杆组: 机构中不能再拆的最简单的自由
度为零的构件组。
1、机构的组成原理
机械原理大作业平面连杆机构的运动分析

机械原理大作业1报告名称平面连杆机构的运动分析学院机电学院专业机械设计制造及其自动化班级 05021001学号 2010301173姓名覃福铁同组人员勾阳采用数据第一组(1-A)平面六杆机构1.题目要求2.题目分析(1)建立封闭图形: L 1 + L 2= L 3+ L 4L 1 + L 2= L 5+ L 6+AG(2) 机构运动分析 a 、角位移分析由图形封闭性得:⎪⎪⎩⎪⎪⎨⎧⋅-⋅+=+-⋅-⋅+⋅⋅-⋅+=+-⋅-⋅+⋅⋅=⋅+⋅+⋅=⋅+⋅55662'2221155662'222113322114332211sin sin )sin(sin sin cos cos )cos(cos cos sin sin sin cos cos cos θθθαπθθθθθαπθθθθθθθθL L y L L L L L x L L L L L L L L L L G G 将上式化简可得:⎪⎪⎩⎪⎪⎨⎧=⋅-⋅+-⋅+⋅-=⋅-⋅+-⋅+⋅⋅-=⋅-⋅⋅-=⋅-⋅G G y L L L L L x L L L L L L L L L L L 66552'233466552'2331133221143322sin sin )sin(sin cos cos )cos(cos sin sin sin cos cos cos θθαθθθθαθθθθθθθθb 、角速度分析上式对时间求一阶导数,可得速度方程:⎪⎪⎩⎪⎪⎨⎧=⋅⋅-⋅⋅+⋅-⋅+⋅⋅=⋅⋅+⋅⋅-⋅-⋅-⋅⋅-⋅⋅-=⋅⋅-⋅⋅⋅⋅=⋅⋅+⋅⋅-0cos cos )cos(cos 0sin sin )sin(sin cos cos cos sin sin sin 66655522'233366655522'2333111333222111333222ωθωθωαθωθωθωθωαθωθωθωθωθωθωθωθL L L L L L L L L L L L L L 化为矩阵形式为:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⋅-⋅⋅=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⋅⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⋅-⋅⋅-⋅⋅⋅-⋅--⋅-⋅-⋅⋅⋅-00cos sin cos cos cos )cos(sin sin sin )sin(00cos cos 00sin sin 1111165326655332'26655332'233223322θθωωωωωθθθαθθθθαθθθθθL L L L L L L L L L L L L L c 、角加速度分析:矩阵对时间求一阶导数,可得加速度矩阵为:2233222333'223355665'22335566622332233'22sin sin 0cos cos 00sin()sin sin sin cos()cos cos cos cos cos 00sin sin 00cos(L L L L L L L L L L L L L L L L L θθεθθεθαθθθεθαθθθεθθθθθα-⋅⋅⎡⎤⎡⎤⎢⎥⎢⎥⋅-⋅⎢⎥⎢⎥⋅=⎢⎥⎢⎥-⋅--⋅-⋅⋅⎢⎥⎢⎥⋅-⋅⋅-⋅⎣⎦⎣⎦-⋅⋅-⋅⋅⋅-211221123123355665'2223355666cos sin )cos cos cos 0sin()sin sin sin 0L L L L L L L L L θωθωωθθθωθαθθθω⎡⎤⋅⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⋅⎢⎥⎢⎥⎢⎥⋅+⋅⎢⎥⎢⎥⎢⎥⋅⋅-⋅⎢⎥⎢⎥⎢⎥⋅-⋅⋅-⋅⎢⎥⎣⎦⎣⎦⎣⎦d 、E 点的运动状态位移:⎩⎨⎧⋅-⋅+=⋅-⋅+=55665566sin sin cos cos θθθθL L y y L L x x G EG E速度:⎪⎩⎪⎨⎧⋅⋅-⋅⋅=⋅⋅+⋅⋅-=555666555666cos cos sin sin ωθωθωθωθL L v L L v yx E E 加速度:⎪⎩⎪⎨⎧⋅⋅-⋅⋅+⋅⋅+⋅⋅-=⋅⋅+⋅⋅+⋅⋅-⋅⋅-=5552555666266655525556662666cos sin cos sin sin cos sin cos εθωθεθωθεθωθεθωθL L L L a L L L L a y x E E3.用solideworks 开发4.装备体动画截图5.计算结果 (1):各杆角位移(2):各杆角速度(3)各杆角加速度(4)E点位移(5)E点速度(6)E点加速度(7)E点轨迹6.本次大作业的心得体会:作为一名机械设计制造专业的学生,学好机械原理是非常重要的,而这次通过做机械原理大作业使我受益匪浅。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
b[0]=L[1]*sin((*p).theta[0])*w1;
b[1]=-L[1]*cos((*p).theta[0])*w1;
b[2]=0.;
b[3]=0.;
if(agaus(a,b,4)!=0)
for(m=0;m<4;m++)
(*p).w[m]=b[m];
平面六杆机构的运动分析
(题号1 -B)
成 绩 ___________________________
指导老师
班 级
学 号
姓 名
1、题目说明
如右图所示平面六杆机构,试用计算机完成其运动分析。
已知其尺寸参数如下表所示:
组号
L1
L2
L2’
L3
L4
L5
L6
α
xG
yG
1-B
24.0
105.6
65.0
67.5
87.5
a[1][2]=0.;
a[1][3]=0.;
a[2][0]=-L[0]*sin((*p).theta[1]-Alpha);
a[2][1]=-L[3]*sin((*p).theta[2]);
a[2][2]=-L[5]*sin((*p).theta[3]);
a[2][3]=L[6]*sin((*p).theta[4]);
a[1][0]=L[2]*cos((]*cos((*p).theta[2]);
a[1][2]=0.;
a[1][3]=0.;
a[2][0]=-L[0]*sin((*p).theta[1]-Alpha);
a[2][1]=-L[3]*sin((*p).theta[2]);
double YG=41.7;
double w1=1.0;
double t=0.1;
double h=0.1;
double eps=0.0000001;
main()
{
int n,i,m;
double x[4]={26.23*Angle,49.75*Angle,87.16*Angle,37.25*Angle};
a[0][0]=-L[2]*sin((*p).theta[1]);
a[0][1]=L[3]*sin((*p).theta[2]);
a[0][2]=0.;
a[0][3]=0.;
a[1][0]=L[2]*cos((*p).theta[1]);
a[1][1]=-L[3]*cos((*p).theta[2]);
a[2][2]=-L[5]*sin((*p).theta[3]);
a[2][3]=L[6]*sin((*p).theta[4]);
a[3][0]=L[0]*cos((*p).theta[1]-Alpha);
a[3][1]=L[3]*cos((*p).theta[2]);
a[3][2]=L[5]*cos((*p).theta[3]);
fp=fopen("num-output.txt","w");
for(n=0,p=mot;n<=36;n++,p++)
{ double a[4][4];
double b[4];
(*p).theta1=n*10;
(*p).theta[0]=n*10*Angle;
i=dnetn(4,eps,t,h,x,k);
34.4
25.0
600
153.5
41.7
题目要求:
三人一组计算出原动件从0到360时(计算点数37)所要求的各运动变量的大小,并绘出运动曲线图及轨迹曲线。
2、题目分析
1)建立封闭图形:
L1+L2=L3+L4
L1+L2=L5+L6+AG
2) 机构运动分析
a、角位移分析
由图形封闭性得:
将上式化简可得:
b、角速度分析
上式对时间求一阶导数,可得速度方程:
化为矩阵形式为:
c、角加速度分析:
矩阵对时间求一阶导数,可得加速度矩阵为:
d、E点的运动状态
位移:
速度:
加速度:
3、流程图
4、源程序
#include <math.h>
#include <stdio.h>
#include "agaus.c"
#include "dnetn.c"
b[1]=L[2]*sin((*p).theta[1])*(*p).w[0]*(*p).w[0]-L[3]*sin((*p).theta[2])*(*p).w[1]*(*p).w[1]+w1*w1*L[1]*sin((*p).theta[0]);
b[2]=L[0]*cos((*p).theta[1]-Alpha)*(*p).w[0]*(*p).w[0]+L[3]*cos((*p).theta[2])*(*p).w[1]*(*p).w[1]+L[5]*cos((*p).theta[3])*(*p).w[2]*(*p).w[2]-L[6]*cos((*p).theta[4])*(*p).w[3]*(*p).w[3];
a[3][0]=L[0]*cos((*p).theta[1]-Alpha);
a[3][1]=L[3]*cos((*p).theta[2]);
a[3][2]=L[5]*cos((*p).theta[3]);
a[3][3]=-L[6]*cos((*p).theta[4]);
b[0]=L[2]*cos((*p).theta[1])*(*p).w[0]*(*p).w[0]-L[3]*cos((*p).theta[2])*(*p).w[1]*(*p).w[1]+w1*w1*L[1]*cos((*p).theta[0]);
double alpha[4];
double XYe[2],Ve[3],ae[3];
};
struct motion mot[37];
struct motion *p;
int k=100;
double L[7]={65.0,24.0,105.6,67.5,87.5,34.4,25.0};
double XG=153.5;
for(m=0;m<4;m++)
(*p).theta[m+1]=x[m];
printf("%d %d",n,i);
getchar();
a[0][0]=-L[2]*sin((*p).theta[1]);
a[0][1]=L[3]*sin((*p).theta[2]);
a[0][2]=0.;
a[0][3]=0.;
#include "conio.h"
#define Alpha (PI/3)
#define PI 3.149
#define Angle (PI/180)
FILE *fp;
struct motion
{
int theta1;
double theta[5]; /*theta1,2,3,5,6*/
double w[4];/*w2,3,5,6*/
