第三部分数值积分代数精度与误差优秀课件
合集下载
《数值计算的误差》课件

了解误差可以帮助我们评估数值计算结果的可靠性和适用性。
常见的误差类型
1 绝对误差
绝对误差是指数值计算结果与真实值之间的 差异的绝对值。
2 相对误差
相对误差是指数值计算结果与真实值之间的 差异与真实值的比值。
3 截断误差
截断误差是由于计算方法中所采用的有限精 度导致的误差。
4 舍入误差
舍入误差是由于将无限精度的数值结果截断 为有限精度导致的误差。
Hale Waihona Puke 误差分析的方法前向误差分析
通过正向推导和逐步改进方法,分析误差在计算过 程中如何积累。
后向误差分析
通过反向推导和逆向改进方法,分析误差在计算过 程中如何传播。
误差的减小技术
1
增加迭代次数
2
通过增加迭代次数来逐渐逼近精确结果,
减小误差的影响。
3
提高精度
使用更高精度的计算方法和数据类型来 减小误差的累积。
优化算法
优化算法可以减小误差的产生,并提高 计算效率。
实际应用中的误差控制
科学计算
在科学研究和工程领域中,准 确的数值计算结果对实际应用 至关重要。
金融领域
在金融市场中,准确计算利息、 风险和收益是关键,误差可能 导致巨大损失或风险。
物理模拟
在物理模拟中,误差的积累可 能导致模拟结果与真实现象之 间存在显著差异。
总结
数值计算的误差是不可避免的,但我们可以通过技术和方法来减小误差的影 响。了解误差类型和分析方法对提高计算结果的准确性和可靠性至关重要。
《数值计算的误差》PPT 课件
欢迎来到《数值计算的误差》的PPT课件。在本课程中,我们将深入探讨数值 计算中常见的误差类型,并学习如何分析和减小这些误差。
常见的误差类型
1 绝对误差
绝对误差是指数值计算结果与真实值之间的 差异的绝对值。
2 相对误差
相对误差是指数值计算结果与真实值之间的 差异与真实值的比值。
3 截断误差
截断误差是由于计算方法中所采用的有限精 度导致的误差。
4 舍入误差
舍入误差是由于将无限精度的数值结果截断 为有限精度导致的误差。
Hale Waihona Puke 误差分析的方法前向误差分析
通过正向推导和逐步改进方法,分析误差在计算过 程中如何积累。
后向误差分析
通过反向推导和逆向改进方法,分析误差在计算过 程中如何传播。
误差的减小技术
1
增加迭代次数
2
通过增加迭代次数来逐渐逼近精确结果,
减小误差的影响。
3
提高精度
使用更高精度的计算方法和数据类型来 减小误差的累积。
优化算法
优化算法可以减小误差的产生,并提高 计算效率。
实际应用中的误差控制
科学计算
在科学研究和工程领域中,准 确的数值计算结果对实际应用 至关重要。
金融领域
在金融市场中,准确计算利息、 风险和收益是关键,误差可能 导致巨大损失或风险。
物理模拟
在物理模拟中,误差的积累可 能导致模拟结果与真实现象之 间存在显著差异。
总结
数值计算的误差是不可避免的,但我们可以通过技术和方法来减小误差的影 响。了解误差类型和分析方法对提高计算结果的准确性和可靠性至关重要。
《数值计算的误差》PPT 课件
欢迎来到《数值计算的误差》的PPT课件。在本课程中,我们将深入探讨数值 计算中常见的误差类型,并学习如何分析和减小这些误差。
数值积分与数值微分ppt课件

a
,
x1
b
2
a
,
x2
b
,h
b
2
a
Cotes系数:
C0( 2 )
1 4
2
1
(t 1)(t 2)dt
0
6
4.5 4
C1(2)
1 2
2
t(t 2)dt
0
4 6
3.5 3
2.5
C2(2)
1 4
2
1
(t 1)tdt
0
6
2 1.5
1
求积公式:
2
Q2( f ) (b a)
n (t j)h
0
0
jn
(k
j)h
h
dt
jk
jk
h (1)nk n
(t j)dt
k!(n k)! 0 0 jn
jk
Ak
ˆ
(b
a
)
C (n) k
C
(n)称
k
为Cotes系
数
(1)nk
n
Ak
(b a)
3
I3(
f
)
b
6
a
(a2
(a
b)2
b2
)
b3
3
a3
R( , x2 ) 0
(3)当 f (x) x3时,I ( f ) b4 a4
4
I3(
f
)
b
《数值积分方法》课件

数值积分的分类
按方法分类
可分为直接法和间接法。直接法如蒙特卡洛方法,间 接法如梯形法则、辛普森法则等。
按精确度分类
可分为低阶和高阶方法。低阶方法如梯形法则,高阶 方法如复合梯形法则、复合辛普森法则等。
按使用范围分类
可分为有限区间上的数值积分和无限区间上的数值积 分。
02
直接法
矩形法
总结词:简单直观
在金融建模中的应用
期权定价模型
数值积分方法可以用于求解期权定价模型,从而为金融衍生品定价提供依据。例如,二叉 树模型和蒙特卡洛模拟等。
利率衍生品定价
在利率衍生品定价中,数值积分方法可以用于求解利率期限结构模型,例如LIBOR市场模 型等。
风险管理
通过数值积分方法,可以对金融风险进行量化评估和管理。例如,计算VaR(风险价值) 和CVaR(条件风险价值)等指标,以评估投资组合的风险暴露程度。
自适应插值控制法
总结词
自适应插值控制法是一种通过插值技术来提 高数值积分精度的控制方法。
详细描述
在数值积分过程中,自适应插值控制法利用 插值技术对积分函数进行逼近,以提高数值 积分的精度。这种方法能够根据积分区间和 积分函数的特性,自动选择合适的插值方法 ,以获得更高的积分精度。同时,自适应插 值控制法还能够有效地处理复杂积分函数和
80%
算法设计与实现
数值积分方法的设计与实现是计 算数学的重要研究内容,推动了 科学计算的发展。
数值积分的概念
定义
数值积分是对函数在某个区间 上的定积分进行数值逼近的方 法。
思想
通过选取适当的积分点和权函 数,将定积分的计算转化为数 值逼近问题。
近似公式
常用的数值积分公式有梯形公 式、辛普森公式、复合梯形公 式、复合辛普森公式等。
精度检验及误差分析PPT课件 (2)

图3-25 圆柱塞规 1-通规 2-止规
一、内孔直径的测量
2.内径百分表 内径百分表(见图3-27)是一种比较测量工具,通过测量工件内孔与标准 环形量规直径尺寸做比较,即可检验工件内孔尺寸和形状误差。测量前先调整 内径百分表的零位, 如图3-27所示,调整时将内径百分表的定心装置和活动量 杆放入标准环形量规孔中,再放入可换量头,然后把内径百分表在孔的轴线平 面内摆动,求出标准环形量规孔直径的真值,即可转动百分表的表圈,使表盘 零位与表示真值的指针对准。调整时要正确地摆动内径百分表。
精度检验及误差分析
—磨床工艺与技能训练
一、内孔直径的测量
1.圆柱塞规 圆柱塞规是检验孔用的一种极限量规,塞规的两端制成圆柱形,如图3-25所 示。塞规的一端为通规,检验孔的最小极限尺寸;另一端为止规,检验孔的最大 极限尺寸。止规通过则工件报废。测量时要擦净工件孔和塞规,使塞规对准孔中 心,轻轻将塞规推入孔中,不能用力摇晃或敲击塞规。应在正常温度下使用塞规。
பைடு நூலகம்
一、内孔直径的测量
图3-27 内径百分表 1-活动测头 2-摆杆 3-可换测头 4-弹簧 5、6-推杆 7-定心装置 8-直管
一、内孔直径的测量
3.内径千分尺 内径千分尺常用于测量ϕ75mm以上的孔。如图3-28所示, 内径千分尺的右 端为球面测量头1;微分筒2借螺母与螺杆相连接;固定套筒3的左端为固定测 量头5;测量不同孔径时,可更换接长杆4。如图3-29所示,测量时将内径千分 尺放在孔中摆动,使上端测量头与工件孔壁有轻微接触感,量出工件内孔的最 大读数值。内径千分尺量取尺寸后,可用外径千分尺校对尺寸,以达到较高的 测量精度。
二、内圆磨削产生废品的原因及预防方法
二、内圆磨削产生废品的原因及预防方法
一、内孔直径的测量
2.内径百分表 内径百分表(见图3-27)是一种比较测量工具,通过测量工件内孔与标准 环形量规直径尺寸做比较,即可检验工件内孔尺寸和形状误差。测量前先调整 内径百分表的零位, 如图3-27所示,调整时将内径百分表的定心装置和活动量 杆放入标准环形量规孔中,再放入可换量头,然后把内径百分表在孔的轴线平 面内摆动,求出标准环形量规孔直径的真值,即可转动百分表的表圈,使表盘 零位与表示真值的指针对准。调整时要正确地摆动内径百分表。
精度检验及误差分析
—磨床工艺与技能训练
一、内孔直径的测量
1.圆柱塞规 圆柱塞规是检验孔用的一种极限量规,塞规的两端制成圆柱形,如图3-25所 示。塞规的一端为通规,检验孔的最小极限尺寸;另一端为止规,检验孔的最大 极限尺寸。止规通过则工件报废。测量时要擦净工件孔和塞规,使塞规对准孔中 心,轻轻将塞规推入孔中,不能用力摇晃或敲击塞规。应在正常温度下使用塞规。
பைடு நூலகம்
一、内孔直径的测量
图3-27 内径百分表 1-活动测头 2-摆杆 3-可换测头 4-弹簧 5、6-推杆 7-定心装置 8-直管
一、内孔直径的测量
3.内径千分尺 内径千分尺常用于测量ϕ75mm以上的孔。如图3-28所示, 内径千分尺的右 端为球面测量头1;微分筒2借螺母与螺杆相连接;固定套筒3的左端为固定测 量头5;测量不同孔径时,可更换接长杆4。如图3-29所示,测量时将内径千分 尺放在孔中摆动,使上端测量头与工件孔壁有轻微接触感,量出工件内孔的最 大读数值。内径千分尺量取尺寸后,可用外径千分尺校对尺寸,以达到较高的 测量精度。
二、内圆磨削产生废品的原因及预防方法
二、内圆磨削产生废品的原因及预防方法
数值分析学习课件

Ak =
∫ ∏
xn x0 i≠k
n 0
=∫
(t − i ) h (b − a )( − 1) n − k ∏ (k − i ) h × h dt = n k !( n − k )! i≠k
( x − xi ) dx ( x k − xi )
令
x =a+th
∫ ∏ (t − i )dt
n 0 i≠k
注:Cotes 系数仅取决于 n 和 k, , 可查表得到。 可查表得到。与 f (x) 及区 均无关。 间[a, b]均无关。 均无关
2
n
机械求积
∫ f ( x ) dx ≈ ∑ A f ( x )
a k =0 k k
注:机械求积是将积分求值问题归结为函数值的计算。 机械求积是将积分求值问题归结为函数值的计算。
1.2 代数精度
如果某个求积公式对于次数不超过m的多项式均能 如果某个求积公式对于次数不超过 的多项式均能 准确成立,但对于m+1次多项式就不准确成立,则 次多项式就不准确成立, 准确成立,但对于 次多项式就不准确成立 称该求积公式具有m次代数精度 次代数精度。 称该求积公式具有 次代数精度。 例如:梯形公式和矩形公式都具有 次代数精度 次代数精度。 例如:梯形公式和矩形公式都具有1次代数精度。 一般,若要使得求积公式具有m次代数精度,只要令 一般, 次代数精度, 2 m 都能准确成立, 它对于 f ( x ) = 1, x, x ,L , x 都能准确成立,即
∫ f ( x ) dx = f (ξ )( b − a )
b a
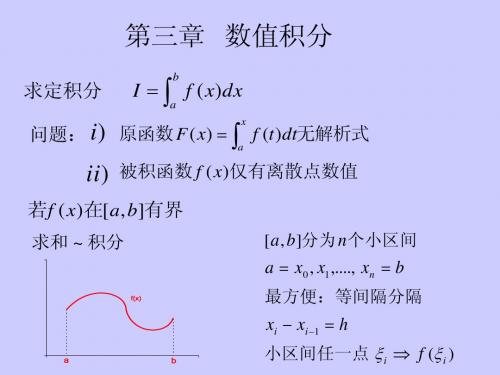
1.1 数值积分的基本思想
思 只要对平均高度 提供一种算法, f (ξ ) 提供一种算法,相应地便获 路 得一种数值求积的方法。 得一种数值求积的方法。
数值积分PPT讲稿

),
0,
只要
~ f ( xk ) fk
(k 0,1,, n)
构造求积公式,原则上是一个确定参数
xk
和 A的k 代数问题.
b
n
f ( x)dx
a
Ak f ( xk ),
k 0
11
例 求a,b,c的值使下列求积公式的代数精度 达到最高。
1
f ( x)dx a f (1) bf (0) cf (1) 1
12
3. 插值型的求积公式
设给定一组节点
a x0 x1 x2 xn b,
x
初等函数表示的原函数; (2)当 f是(x由) 测量或数值计算给出的一张数据表.
这时,牛顿-莱布尼茨公式也不能直接运用. 因此有必要研究积分的数值计算问题. 由积分中值定理知,在积分区间 [a内, b存]在一点ξ,
成立
b
a f (x)dx (b a) f ( ),
3
就是说,底为 b 而a高为 f的(矩)形面积恰等于所求
曲边梯形的面积 I(图4-1).
图4-1
4
问题在于点ξ的具体位置一般是不知道的,因而难以
准确算出 f (的)值. 将 f 称(为) 区间
上[a的, b平]均高度.
这样,只要对平均高度 f提(供) 一种算法,相应地便
获得一种数值求积方法.
用两端点“高度“ f (a与) f的(b算) 术平均作为平均高度
j 0
15
注意到 lk (x j ) kj, 上式右端实际上等于 Ak , 因而
b
Ak a lk (x)dx
成立. 这样,有下面定理.
定理1
求积公式至少有 次代n数精度的
充分必要条件是,它是插值型的.
数值积分ppt
( xi h )和( xi h )之间面积 ()
h 3 '' h 5 IV I ( xi h ) I ( xi h ) 2 ( hf i fi fi E (h )7 3! 5!
h f ( xi ) ( f i 1 2 f i f i 1 ) h f 12
b
a
f ( x ) dx
i 0
n 1
x2 i2
x2 i
f ( x ) dx
h2 n 3
f 0 4 ( f1
f 3 ... f 2 n 1 ) 2( f 2 f 4 ... f 2 n 2 ) f 2 n
其中 f 0 f ( a ), h2 n
(7)
-3E2n
设 I n , I 2 n 分别为梯形积分近似值 则 I 2 n I n 3 E 2 n 3( I I 2 n ) I I2n 1 3 (I 2n I n )
待求的未知量
由I n以及 I 2 n的值可估算数值积分 I 2 n的误差
允许绝对误差 . 相对误差 .
i 1
(4)
梯形积分的截断误差: E ( x ) 2 12 ( b a ) f '' ( x ) (5)
设 n 为[ a , b ]的分割区间数, x En (b a ) 3 12 n
'' 2
(b a ) n (6.1)
f '' ( x n ) 1
a xn b
i 1 n
h1
(b a ) 2 h2 n hn 2
3 hn I n I 2 n 及积分值
数值积分实用PPT课件PPT课件

二simpson积分法抛物线积分法第20页共39页3几何意义第21页共39页4复合抛物线积分法分成n偶数个相等的小区间每个区间的长度第22页共39页计算公式几何意义第23页共39页5定步长抛物线积分抛物线积分较梯形积分更精确
微积分学中,积分计算是利用 Newton – Leibniz
公式:
来计算的。
例,某气体由温度 T1 加热到 T2 时所需热量 Q 可由下式表示:
Q
T1 T2
Cp
.mdT
Cp .m 该气体的摩尔定压热容
不知道该气体的 与CTp的.m函数关系式,而实验测得该气体的
系数据如下表所示。
C p .m
与 T 的关
T/℃
25 100 150 200 250 300 350 400 450 500 600 700 800
32 k0
f
( x ) 12
k1
k0
4
f
( xk1 ) 2
n1
n1
32 f ( x ) 14 f ( x )
k0
k3 4
k 1
k
第27页/共39页
龙贝格算法
第28页/共39页
数值方法中常利用一序列{ F1、F2、…、Fk、…} 去逼近精确值,然后在理论上给出序列F的误差估计。
新思路:
能否在某种理论(截断误差估计)基础上,通过简单方法,在序列
值,而这些值又是成倍增加的,所以计算工作量较大。
第37页/共39页
程序例子:P207
作 业:
将P207的程序改为求解积分
eps=0.000001 结果(0.1115718)
1x
0 4 x2 dx
第38页/共39页
感谢您的观看。
微积分学中,积分计算是利用 Newton – Leibniz
公式:
来计算的。
例,某气体由温度 T1 加热到 T2 时所需热量 Q 可由下式表示:
Q
T1 T2
Cp
.mdT
Cp .m 该气体的摩尔定压热容
不知道该气体的 与CTp的.m函数关系式,而实验测得该气体的
系数据如下表所示。
C p .m
与 T 的关
T/℃
25 100 150 200 250 300 350 400 450 500 600 700 800
32 k0
f
( x ) 12
k1
k0
4
f
( xk1 ) 2
n1
n1
32 f ( x ) 14 f ( x )
k0
k3 4
k 1
k
第27页/共39页
龙贝格算法
第28页/共39页
数值方法中常利用一序列{ F1、F2、…、Fk、…} 去逼近精确值,然后在理论上给出序列F的误差估计。
新思路:
能否在某种理论(截断误差估计)基础上,通过简单方法,在序列
值,而这些值又是成倍增加的,所以计算工作量较大。
第37页/共39页
程序例子:P207
作 业:
将P207的程序改为求解积分
eps=0.000001 结果(0.1115718)
1x
0 4 x2 dx
第38页/共39页
感谢您的观看。
代数精度插值求积及复化公式 ppt课件

k0
称之为n阶牛顿一柯特斯(Newton-Cotes)公式简记为N-C公式,
称
C
( k
n
)
为柯特斯系数。显然,柯特斯系数与被积函数f
(x)
和积
分区间[a, b] 无关,且为多项式积分,其值可以事先求出备用。
表7-1中给了了部分柯特斯系数。
表7-1
柯特斯系数
C k ( n ) A B k ( k 0 , 1 , ,n )
k 0
k 0
因此,式(7-1)可作为一般的求积公式,其特点是将积分问
题归结为函数值的计算,从而避开了使用牛顿一莱布尼慈公式需
要求原函数的困难,适合于函数给出时计算积分,也非常便于设计
算法,便于上机计算。
求积公式(7-1)的截断误差为:
b
n
R (f)R nIInaf(x )d x A kf(x k) Rn也称为积分余项.
则有:
b
n
I f(x)dx a
Akf(xk)In
k0
这种求积系数由式(7-5)所确定的求积公式称为插值型求积公式.
根据插值余项定理,插值型求积公式的求积余项为:
R n I Ina b [f(x ) L n (x )]d xa bf(( n n 1 ) 1 ( ))! k n 0(x x k)d x (-7 6其)中[a,b] 与x有关.
n
A
Bk
1
1/2
11
2
1/6
1 41
3
1/8
1 33 1
4
1/90
7 32 12 32 7
5
1/288 19 75 50 50 75 19
6
1/840 41 216 27 272 27 216 41
称之为n阶牛顿一柯特斯(Newton-Cotes)公式简记为N-C公式,
称
C
( k
n
)
为柯特斯系数。显然,柯特斯系数与被积函数f
(x)
和积
分区间[a, b] 无关,且为多项式积分,其值可以事先求出备用。
表7-1中给了了部分柯特斯系数。
表7-1
柯特斯系数
C k ( n ) A B k ( k 0 , 1 , ,n )
k 0
k 0
因此,式(7-1)可作为一般的求积公式,其特点是将积分问
题归结为函数值的计算,从而避开了使用牛顿一莱布尼慈公式需
要求原函数的困难,适合于函数给出时计算积分,也非常便于设计
算法,便于上机计算。
求积公式(7-1)的截断误差为:
b
n
R (f)R nIInaf(x )d x A kf(x k) Rn也称为积分余项.
则有:
b
n
I f(x)dx a
Akf(xk)In
k0
这种求积系数由式(7-5)所确定的求积公式称为插值型求积公式.
根据插值余项定理,插值型求积公式的求积余项为:
R n I Ina b [f(x ) L n (x )]d xa bf(( n n 1 ) 1 ( ))! k n 0(x x k)d x (-7 6其)中[a,b] 与x有关.
n
A
Bk
1
1/2
11
2
1/6
1 41
3
1/8
1 33 1
4
1/90
7 32 12 32 7
5
1/288 19 75 50 50 75 19
6
1/840 41 216 27 272 27 216 41
《数值分析误差》PPT课件

如果x*为x的近似值, 称e*=x-x*为绝对误差。
绝对误差往往是未知的,而只知道它的一个上
限,此上限|e*|=|x-x*|记为ℇ*, 称为绝对误差
限(accuracy)。
工程上常记为x=x*±ℇ* ,例如
1ex2dx 0.740 3.006 0
相对误差 (relative error)
e r * e x * * x x * x * 或 e r * e x * x x x *
1.3 方法误差 (截断误差 Truncation Error〕
在数学模型〔包括参数值〕确定以后,就常要考虑 选用某种数值方法具体进展计算,许多数值方法都 是近似方法,故求出的结果与准确值之间是有误差 的,该误差称为截断误差或方法误差。例如,函数 f(x)用Taylor多项式
f ( x ) p n ( x ) f ( 0 ) f 1 '( ! 0 ) x f ' 2 '( ! 0 ) x 2 f ( n n ) ! ( 0 ) x n
1. 来源与分类 ( Source & Classification )
• 模型误差 • 参数误差(观测误差) • 方法误差(截断误差) • 舍入误差
1.1 模型误差 (Modeling Error)
用计算机解决实际问题时,首先要建立数学 模型,各种实际问题是十分复杂的,而数学 模型是对被描述的实际问题进展抽象、简化 而得到的,往往忽略了一些次要因素,因而 是近似的,我们把数学模型与实际问题之间 出现的这种误差称为模型误差。如自由落体 公式
|e r *| (x y x )* (x y * * y * ) 0 .0 0 .0 0 0 .0 1 3 1 7% 0
可以看到相对误差比较大.
绝对误差往往是未知的,而只知道它的一个上
限,此上限|e*|=|x-x*|记为ℇ*, 称为绝对误差
限(accuracy)。
工程上常记为x=x*±ℇ* ,例如
1ex2dx 0.740 3.006 0
相对误差 (relative error)
e r * e x * * x x * x * 或 e r * e x * x x x *
1.3 方法误差 (截断误差 Truncation Error〕
在数学模型〔包括参数值〕确定以后,就常要考虑 选用某种数值方法具体进展计算,许多数值方法都 是近似方法,故求出的结果与准确值之间是有误差 的,该误差称为截断误差或方法误差。例如,函数 f(x)用Taylor多项式
f ( x ) p n ( x ) f ( 0 ) f 1 '( ! 0 ) x f ' 2 '( ! 0 ) x 2 f ( n n ) ! ( 0 ) x n
1. 来源与分类 ( Source & Classification )
• 模型误差 • 参数误差(观测误差) • 方法误差(截断误差) • 舍入误差
1.1 模型误差 (Modeling Error)
用计算机解决实际问题时,首先要建立数学 模型,各种实际问题是十分复杂的,而数学 模型是对被描述的实际问题进展抽象、简化 而得到的,往往忽略了一些次要因素,因而 是近似的,我们把数学模型与实际问题之间 出现的这种误差称为模型误差。如自由落体 公式
|e r *| (x y x )* (x y * * y * ) 0 .0 0 .0 0 0 .0 1 3 1 7% 0
可以看到相对误差比较大.
精度检验及误差分析PPT课件

图2-34所示为0~25千分尺的读数。图2-34a所示读数为8.35mm,图2-34b所 示读数为14.68mm,图2-34c所示读数为12.765mm。
图2-35所示为25~50mm千分尺的读数。图2-35a所示读数为26.5mm,图2-35 b示读数为30.01mm,图2-35 c所示读数为34.48mm。
三、径向圆跳动误差的测量
三、径向圆跳动误差的测量
图2-40 钟表式百分表的结构 1-测杆 2-小齿轮 3、6-大齿轮 4-中心齿轮 5-大指针 7-簧片
8-小指针 9-弹簧 10-表盘
三、径向圆跳动误差的测量
图2-41 杠杆式百分表的结构 1-球面测杆 2-扇形齿轮 3-钢丝 4-表盘 5-表壳
6-指针 7-扳手 8-小齿轮 9、10-齿轮
三、径向圆跳动误差的测量
2.分表的使用 图2-42所示为在磨床上测量径向圆跳动误差的方法。测量时先在工作台 上安放一个测量桥板,然后将百分表架放在测量桥板上,使百分表测杆与被 测工件轴线垂直,并使测头位于工件圆周最高点上,转动工件即可测量圆跳 动误差。图2-43所示为圆跳动检查仪的使用,测量时百分表测杆应垂直于测 量表面,并使百分表转动1/4周,调整百分表的零位,转动工件即可测量圆 跳动误差。
精度检验及误差分析
—磨床工艺与技能训练
一、外径的测量
1.用外径千分尺测量外径 外径千分尺是常用的测量工具。它的测量精度为0.01mm。常用的规格有 0 ~25mm、25 ~50mm、50~75mm、75 ~100mm等。 (1)外径千分尺的结构 (2)外径千分尺的刻线原理及读数方法
千分尺的读数分为两步,先读出固定套筒上露出的刻线整数毫米和半毫米数; 然后在微分筒上看哪一格与固定套筒基准线对准,并读出小数部分;最后将整数 和小数部分相加, 即为工件的尺寸。
图2-35所示为25~50mm千分尺的读数。图2-35a所示读数为26.5mm,图2-35 b示读数为30.01mm,图2-35 c所示读数为34.48mm。
三、径向圆跳动误差的测量
三、径向圆跳动误差的测量
图2-40 钟表式百分表的结构 1-测杆 2-小齿轮 3、6-大齿轮 4-中心齿轮 5-大指针 7-簧片
8-小指针 9-弹簧 10-表盘
三、径向圆跳动误差的测量
图2-41 杠杆式百分表的结构 1-球面测杆 2-扇形齿轮 3-钢丝 4-表盘 5-表壳
6-指针 7-扳手 8-小齿轮 9、10-齿轮
三、径向圆跳动误差的测量
2.分表的使用 图2-42所示为在磨床上测量径向圆跳动误差的方法。测量时先在工作台 上安放一个测量桥板,然后将百分表架放在测量桥板上,使百分表测杆与被 测工件轴线垂直,并使测头位于工件圆周最高点上,转动工件即可测量圆跳 动误差。图2-43所示为圆跳动检查仪的使用,测量时百分表测杆应垂直于测 量表面,并使百分表转动1/4周,调整百分表的零位,转动工件即可测量圆 跳动误差。
精度检验及误差分析
—磨床工艺与技能训练
一、外径的测量
1.用外径千分尺测量外径 外径千分尺是常用的测量工具。它的测量精度为0.01mm。常用的规格有 0 ~25mm、25 ~50mm、50~75mm、75 ~100mm等。 (1)外径千分尺的结构 (2)外径千分尺的刻线原理及读数方法
千分尺的读数分为两步,先读出固定套筒上露出的刻线整数毫米和半毫米数; 然后在微分筒上看哪一格与固定套筒基准线对准,并读出小数部分;最后将整数 和小数部分相加, 即为工件的尺寸。
数值积分方法课件

热力学分析
通过数值积分方法,可以对物体的传热过程进行精确 分析。
在金融计算中的应用
01
股票价格预测
数值积分方法可以用于预测股票 价格的变动趋势,为投资决策提 供支持。
02
03
风险管理
精算学
在金融风险管理中,数值积分方 法可以用于评估投资组合的风险 水平。
在精算学中,数值积分方法可以 用于计算生命保险、养老保险等 保险产品的精算现值。
THANKS
感谢观看
按照被积函数的特征分类
可以分为有理函数的积分、无理函数的积分、超越函数的积分等。
02
常见数值积分方法
矩形法
总结词
简单、易理解、精度低
详细描述
矩形法是一种简单的数值积分方法,其基本思想是将积分区间划分为一系列小的矩形,然后用每个小 矩形的面积近似代替该区域的积分。该方法易于理解和实现,但精度较低。
分。
Gauss-Legendre积分法
03
精度高,计算量较大,适用于求解具有特定形状的积
分。
适用范围与场景
梯形法则
适用于简单的一维函数不定积分,如常数函 数、三角函数等。
Simpson法则
适用于具有对称性的积分,如奇函数或偶函数的积 分。
Gauss-Legendre积分法
适用于求解具有特定形状的积分,如圆环域 、球域等。
常见的数值积分公式包括梯形法则、辛普森法则 、高斯积分等。
数值积分的重要性
解决实际问题
数值积分被广泛应用于各种实际问题中,如物理学、工程学、经济学等。
理论计算基础
数值积分也是许多理论计算的基础,如微分方程、偏微分方程的求解等。
数值积分的分类
按照所使用的数值方法分类
通过数值积分方法,可以对物体的传热过程进行精确 分析。
在金融计算中的应用
01
股票价格预测
数值积分方法可以用于预测股票 价格的变动趋势,为投资决策提 供支持。
02
03
风险管理
精算学
在金融风险管理中,数值积分方 法可以用于评估投资组合的风险 水平。
在精算学中,数值积分方法可以 用于计算生命保险、养老保险等 保险产品的精算现值。
THANKS
感谢观看
按照被积函数的特征分类
可以分为有理函数的积分、无理函数的积分、超越函数的积分等。
02
常见数值积分方法
矩形法
总结词
简单、易理解、精度低
详细描述
矩形法是一种简单的数值积分方法,其基本思想是将积分区间划分为一系列小的矩形,然后用每个小 矩形的面积近似代替该区域的积分。该方法易于理解和实现,但精度较低。
分。
Gauss-Legendre积分法
03
精度高,计算量较大,适用于求解具有特定形状的积
分。
适用范围与场景
梯形法则
适用于简单的一维函数不定积分,如常数函 数、三角函数等。
Simpson法则
适用于具有对称性的积分,如奇函数或偶函数的积 分。
Gauss-Legendre积分法
适用于求解具有特定形状的积分,如圆环域 、球域等。
常见的数值积分公式包括梯形法则、辛普森法则 、高斯积分等。
数值积分的重要性
解决实际问题
数值积分被广泛应用于各种实际问题中,如物理学、工程学、经济学等。
理论计算基础
数值积分也是许多理论计算的基础,如微分方程、偏微分方程的求解等。
数值积分的分类
按照所使用的数值方法分类
第三部分数值积分代数精度与误差演示文稿

Rn[ f ] Cnhn3 f (n2) ( )
其中
1 Cn (n 2)!
n t 2 (t 1)
0
(t n)dt
(2)当n为奇数时,如果 f C (n,1)则[a, b]
Rn[ f ] Cnhn2 f (n1) ( )
其中
1
n
Cn (n 1)!
t(t 1)
0
(t n)dt
第十四页,共14页。
S(
f
)
ba 6
f (a) 4 f (a b) 2
f (b)
3次代数精度
第十页,共14页。
Simpson公式 设 f (4)( x) 连续
b
R2[ f ]
f ( x)dx S( f )
a
构造次数不超过3次的多项式 H3( x,) 满足:
H3(a) f (a), H3(b) f (b) H3(c) f (c), H3(c) f (c)
ቤተ መጻሕፍቲ ባይዱ
b
b
b
f ( x)dx
a
a H3( x)dx
a f ( x) H3( x)dx
b f (4)( ) ( x a)( x c)2( x b)dx a 4!
f (4)( ) b ( x a)( x c)2( x b)dx 4! a
b
a
b (
a )4
f
(4) ( )
180 2
时求积公式精确成立,而 f (为x) 时x求m积1 公式不能成
为等式。
第五页,共14页。
梯形公式
1
I1( f ) Ak f ( xk ) A0 f ( x0 ) A1 f ( x1) k0
T ( f ) b a f (a) f (b) 1次代数精度
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
➢求积公式的代数精度
n
定理: 求积公式 In( f ) Ak f(xk)
k0
具有次m代数精度的充要条件是 f ( x为) 代数精度
1 、 x、 x2、 x3 xm
的判别方 法
时求积公式精确成立,而 f ( x为) 时x m求 1积公式不能
成为等式。
梯形公式
1
I1(f) A kf(xk)A 0f(x0)A 1f(x1) k0
梯形公式
b
b f ( )
R1[ f ]
f ( x)dx T ( f )
a
a
( x a)( x b)dx 2!
f ( )
b
( x a)( x b)dx
f ( ) (b a)3
2! a
12
Simpson公式
2
I2 (f)A kf(x k) A 0f(x 0 ) A 1f(x 1 ) A 2f(x 2 ) k 0
0
(tn)dt
(2)当n为奇数时,如果 f C(n1,)[a则,b]
Rn[
f
]
C
hn2
n
f
( n 1)
(
)
其中
1n
Cn(n1)!
t(t1)
0
(tn)dt
n
定理:形如 In( f ) 的Ak求f积(x公k式) 至少 k0
有n次代数精度的充要条件是它是插值型求积公式。
证明: 充分性 设它是插值型求积公式
第三部分数值积分 代数精度与误差
插值型求积公式:
b
b
bn
f ( x)dx
a
a Ln ( x )dx
a
lk ( x) f ( xk )dx
k0
n
b
n
f ( xk ) a lk ( x)dx Ak f ( xk )
k0
k0
其中
Ak
b
a lk ( x)dx
b n1( x)dx
b
R4[ f ]
f ( x)dx C ( f )
a
2(ba)(ba)6f(6)()
945 4
(补充:Newton—Cotes求积公式的误差估计)
(1)当n为偶数时,如果 f C(n,2)则[a,b]
Rn [ f ] C nhn3 f (n 2) ( )
其中
1 Cn(n2)!
nt2(t1)
a
a H 3 ( x )dx
a f ( x ) H 3( x )dx
b f (4) ( ) ( x a)( x c)2 ( x b)dx
a 4!
f (4) ( )
b ( x a)( x c)2 ( x b)dx
4! a
ba(ba)4f(4)()
180 2
Cotes公式 设 f ( 6 ) ( x ) 连续
b
n
a lk ( x)dx A j lk ( x j ) Ak
j0
n
因此求积公式 In ( f ) A是k插f 值( x型k )的。 k0
当 f(x)1,x,x2, ,xn时,
Rn[ f ]
b a
f (
(n1) ( )
n 1)!
n
1
(
x
)dx
0
即它对所有不超过n次的多项式精确成立,故至少有n次 代数精度。
必要性 设求积公式至少有n次代数精度
则对所有不超过n次的多项式求积公式精确成立
取 f ( x ) lk ( x ) k 0,1, 2, , n
2
b
ba
a H3( x)dx 6 H3(a) 4H3(c) H 3(b)
f (x) H3(x)
f (4)( ) ( x a)( x c)2( x b)
4!
b
b
R2[ f ]
f ( x)dx S ( f )
a
S ( f ) a H 3( x )dx
b
b
b
f ( x)dx
S(f)b 6a f(a)4f(a 2b)f(b)
3次代数精度
Simpson公式 设 f ( 4 ) ( x ) 连续
b
R2[ f ]
f ( x)dx S ( f )
a
构造次数不超过3次的多项式 H 3 ( x ) ,满足:
H3(a)f(a),H3(b)f(b) 其中c a b
H3(c)f(c),H3(c)f(c)
a
(x
x
k
)
n
1
(
xk
)
插值型求积公式:
余项
Rn[ f ]
b a
f (
(n
n
1) ( )
1)!
n
1
(
x
)dx
➢求积公式的代数精度
n
定义 如果求积公式 In( f ) Ak f(xk) k0
对一切不高于m次的多项式都恒成立,而对于某个 m+1次多项式不能精确成立,则称该求积公式具有 m次代数精度。
T(f)baf(a)f(b) 1次代数精度
2
梯形公式
b
b f ( )
R1[ f ]
f ( x)dx( x a)( x b)dx 2!
f ( )
b
( x a)( x b)dx
f ( ) (b a)3
2! a
12
积分第一中值定理
如果函数f(x)、g(x)在闭区间[a,b]上可积, 且 g(x)在[a,b]上不变号, 则在积分区间[a,b]上至少存 在一个点ξ, 使下式成立:
