哈工大理论力学课后习题答案第六版
理论力学课后习题答案-第6章--刚体的平面运动分析
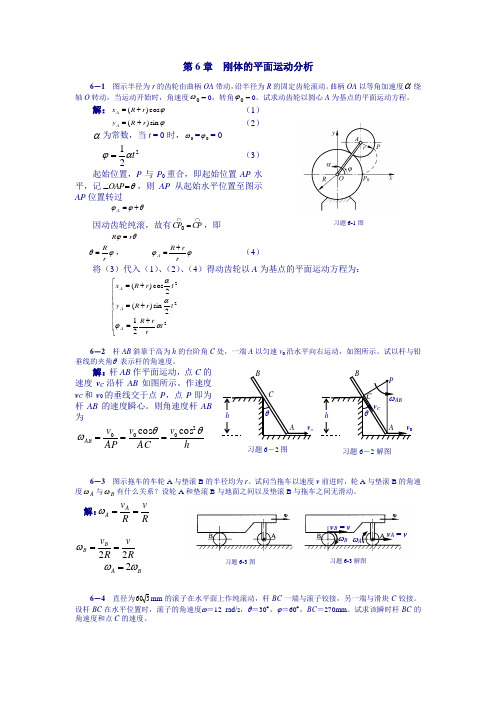
第6章 刚体的平面运动分析6-1 图示半径为r 的齿轮由曲柄OA 带动,沿半径为R 的固定齿轮滚动。
曲柄OA 以等角加速度α绕轴O 转动,当运动开始时,角速度0ω= 0,转角0ϕ= 0。
试求动齿轮以圆心A 为基点的平面运动方程。
解:ϕcos )(r R x A += (1) ϕsin )(r R y A +=(2)α为常数,当t = 0时,0ω=0ϕ= 0 221t αϕ=(3)起始位置,P 与P 0重合,即起始位置AP 水平,记θ=∠OAP ,则AP 从起始水平位置至图示AP 位置转过θϕϕ+=A因动齿轮纯滚,故有⋂⋂=CP CP 0,即 θϕr R = ϕθr R =, ϕϕrr R A += (4)将(3)代入(1)、(2)、(4)得动齿轮以A 为基点的平面运动方程为:⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+=+=222212sin )(2cos )(t r r R t r R y t r R x A A A αϕαα6-2 杆AB 斜靠于高为h 的台阶角C 处,一端A 以匀速v 0沿水平向右运动,如图所示。
试以杆与铅垂线的夹角θ 表示杆的角速度。
解:杆AB 作平面运动,点C 的速度v C 沿杆AB 如图所示。
作速度v C 和v 0的垂线交于点P ,点P 即为杆AB 的速度瞬心。
则角速度杆AB 为6-3 图示拖车的车轮A 与垫滚B 的半径均为r 。
试问当拖车以速度v 前进时,轮A 与垫滚B 的角速度A ω与B ω有什么关系?设轮A 和垫滚B 与地面之间以及垫滚B 与拖车之间无滑动。
解:RvR v A A ==ωR v R v B B 22==ωB A ωω2=6-4 直径为360mm 的滚子在水平面上作纯滚动,杆BC 一端与滚子铰接,另一端与滑块C 铰接。
设杆BC 在水平位置时,滚子的角速度ω=12 rad/s ,θ=30︒,ϕ=60︒,BC =270mm 。
试求该瞬时杆BC 的角速度和点C 的速度。
hv AC v AP v ABθθω2000cos cos ===习题6-1图ABCv 0hθ习题6-2图PωABv CABCv ohθ习题6-2解图习题6-3解图习题6-3图v A = vv B = v ωAωB习题6-6图习题6-6解图解:杆BC 的瞬心在点P ,滚子O 的瞬心在点D BDv B ⋅=ωBPBD BP v B BC ⋅==ωω ︒︒⨯=30sin 27030cos 36012 rad/s 8=PC v BC C ⋅=ωm/s 87.130cos 27.08=︒⨯=6-5 在下列机构中,那些构件做平面运动,画出它们图示位置的速度瞬心。
理论力学课后题参考答案

1.1 沿水平方向前进的枪弹,通过某一距离s 的时间为t 1,而通过下一等距离s 的时间为2t .试证明枪弹的减速度(假定是常数)为由题可知示意图如题1.1.1图: {{SSt t 题1.1.1图设开始计时的时刻速度为0v ,由题可知枪弹作匀减速运动设减速度大小为a .则有:()()⎪⎪⎩⎪⎪⎨⎧+-+=-=221210211021221t t a t t v s at t v s 由以上两式得 11021at t s v +=再由此式得 ()()2121122t t t t t t s a +-=1.26一弹性绳上端固定,下端悬有m 及m '两质点。
设a 为绳的固有长度,b 为加m 后的伸长,c 为加m '后的伸长。
今将m '任其脱离而下坠,试证质点m 在任一瞬时离上端O 的距离为解 以绳顶端为坐标原点.建立如题1.26.1图所示坐标系.题1.26.1图设绳的弹性系数为k ,则有 kb mg = ① 当 m '脱离下坠前,m 与m '系统平衡.当m '脱离下坠前,m 在拉力T 作用下上升,之后作简运.运动微分方程为 ()ym a y k mg &&=-- ② 联立①② 得 b b a g y b g y +=+&& ③ 0=+y bg y &&齐次方程通解 t b g A t b g A Y sin cos 211+= 非齐次方程③的特解 b a Y +=0 所以③的通解b a t bg A t b g A Y +++=sin cos 211代入初始条件:0=t 时,,c b a y ++=得0,21==A c A ;故有 b a t b g c y ++=cos 即为m 在任一时刻离上端O 的距离.'1.39 一质点受一与距离23次方成反比的引力作用在一直线上运动。
试证此质点自无穷远到达a 时的速率和自a 静止出发到达4a 时的速率相同。
理论力学课后的习题及答案解析...doc
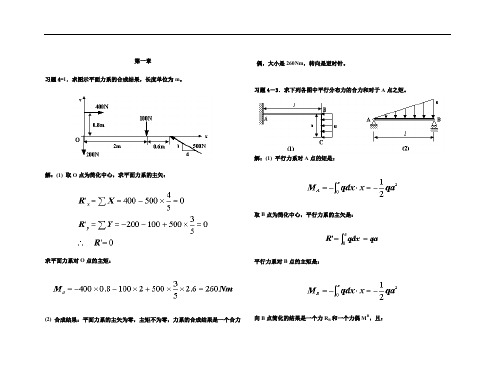
第一章习题4-1.求图示平面力系的合成结果,长度单位为m。
解:(1) 取O点为简化中心,求平面力系的主矢:求平面力系对O点的主矩:(2) 合成结果:平面力系的主矢为零,主矩不为零,力系的合成结果是一个合力偶,大小是260Nm,转向是逆时针。
习题4-3.求下列各图中平行分布力的合力和对于A点之矩。
解:(1) 平行力系对A点的矩是:取B点为简化中心,平行力系的主矢是:平行力系对B点的主矩是:向B点简化的结果是一个力R B和一个力偶M B,且:如图所示;将R B向下平移一段距离d,使满足:最后简化为一个力R,大小等于R B。
其几何意义是:R的大小等于载荷分布的矩形面积,作用点通过矩形的形心。
(2) 取A点为简化中心,平行力系的主矢是:平行力系对A点的主矩是:向A点简化的结果是一个力R A和一个力偶M A,且:如图所示;将R A向右平移一段距离d,使满足:最后简化为一个力R,大小等于R A。
其几何意义是:R的大小等于载荷分布的三角形面积,作用点通过三角形的形心。
习题4-4.求下列各梁和刚架的支座反力,长度单位为m。
解:(1) 研究AB杆,受力分析,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
(2) 研究AB杆,受力分析,将线性分布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
(3) 研究ABC,受力分析,将均布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
习题4-5.重物悬挂如图,已知G=1.8kN,其他重量不计;求铰链A的约束反力和杆BC所受的力。
解:(1) 研究整体,受力分析(BC是二力杆),画受力图:列平衡方程:解方程组:反力的实际方向如图示。
习题4-8.图示钻井架,G=177kN,铅垂荷载P=1350kN,风荷载q=1.5kN/m,水平力F=50kN;求支座A的约束反力和撑杆CD所受的力。
理论力学 第六版部分习题答案 第十章

上式代入式(4)得
FN = 4mB g − mB
10-6 如图 11-10a 所示,质量为 m 的滑块 A,可以在水平光滑槽中运动,具有刚性系 数为 k 的弹簧 1 端与滑块相连接,另 1 端固定。杆 AB 长度为 l,质量忽略不计,A 端与滑 块 A 铰接,B 端装有质量 m1,在铅直平面内可绕点 A 旋转。设在力偶 M 作用下转动角速度 ω 为常数。求滑块 A 的运动微分方程。
F = 1 068 N = 1.068 kN 10-3* 如图 11-3a 所示浮动起重机举起质量 m1=2 000 kg 的重物。设起重机质量 m2=20 000 kg,杆长 OA=8 m;开始时杆与铅直位置成 60°角,水的阻力和杆重均略去不计。当起 重杆 OA 转到与铅直位置成 30°角时,求起重机的位移。
vC = 2vC1 = lω
代入式(1),得
149
p=
lω (5m1 + 4m2 ) (方向如图 11-7b 所示) 2
A
p
vC
C
vC1
ω
O
ωt
C1
B
(a) 图 11-7
(b)
10-5
质量为 m1 的平台 AB,放于水平面上,平台与水平面间的动滑动摩擦因数为 f。
质量为 m2 的小车 D,由绞车拖动,相对于平台的运动规律为 s = 不计绞车的质量,求平台的加速度。
棱柱 B 接触水平面时系统质心坐标
a b ⎤ ⎡ m A (l − ) + m B ⎢l − (a − )⎥ 3 3 ⎦ 3(m A + m B )l − a(m A + 3m B ) + m B b ⎣ ′ = = xC m A + mB 3(m A + m B )
理论力学 第六版部分习题答案 第七章
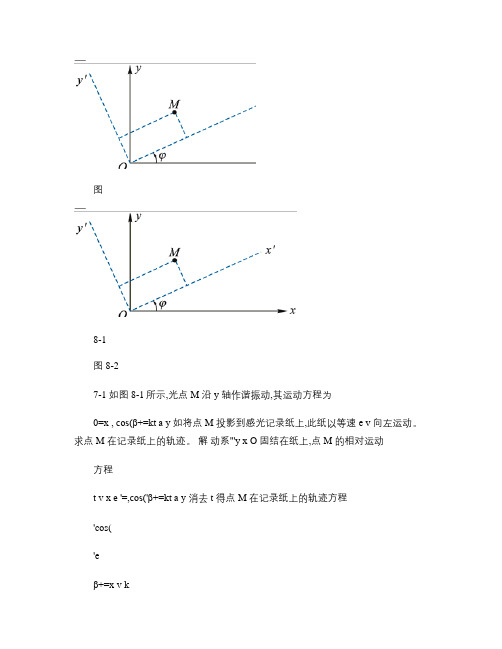
图8-1图8-27-1 如图8-1所示,光点M 沿y 轴作谐振动,其运动方程为0=x , cos(β+=kt a y 如将点M 投影到感光记录纸上,此纸以等速e v 向左运动。
求点M 在记录纸上的轨迹。
解动系'''y x O 固结在纸上,点M 的相对运动方程t v x e '=,cos('β+=kt a y 消去t 得点M 在记录纸上的轨迹方程'cos('eβ+=x v ka y 7-2 如图8-2所示,点M 在平面''y Ox 中运动,运动方程为cos 1(40't x −=,t y sin 40'= 式中t 以s 计,'x 和'y 以mm 计。
平面''y Ox 又绕垂直于该平面的轴O 转动,转动方程为rad t =ϕ,式中角ϕ为动系的'x 轴与定系的x 轴间的交角。
求点M 的相对轨迹和绝对轨迹。
解由点M 的相对运动方程可改写为t yt x sin 40cos 140''=−=⎟⎟⎠⎞⎜⎜⎝⎛−上2式两边平方后相加,得点M 的相对轨迹方程 1600'40'(22=+−y x 由题得点M 的坐标变换关系式ϕϕsin 'cos 'y x x −= ϕϕcos 'sin 'y x y +=将t =ϕ和相对运动方程代入,消去t 得点M 的绝对轨迹方程160040(22=++y x7-3 水流在水轮机工作轮入口处的绝对速度m/s 15a =v ,并与直径成°=60β角,如图8-3a 所示,工作轮的半径m 2=R ,转速r/min 30=n 。
为避免水流与工作轮叶片相冲击,叶片应恰当地安装,以使水流对工作轮的相对速度与叶片相切。
求在工作轮外缘处水流对工作轮的相对速度的大小方向。
′′v(a (b图8-3解水轮机工作轮入口处的1滴水为动点M ,动系固结于工作轮,定系固结于机架/地面(一般定系可不别说明,默认为固结于机架,下同;牵连运动为定轴转动,相对运动与叶片曲面相切,速度分析如图8-3b 所示,设θ为r v 与'x 轴的夹角。
理论力学课后习题及答案解析..

第一章习题4-1.求图示平面力系的合成结果,长度单位为m。
解:(1) 取O点为简化中心,求平面力系的主矢:求平面力系对O点的主矩:(2) 合成结果:平面力系的主矢为零,主矩不为零,力系的合成结果是一个合力偶,大小是260Nm,转向是逆时针。
习题4-3.求下列各图中平行分布力的合力和对于A点之矩。
解:(1) 平行力系对A点的矩是:取B点为简化中心,平行力系的主矢是:平行力系对B点的主矩是:向B点简化的结果是一个力R B和一个力偶M B,且:如图所示;将R B向下平移一段距离d,使满足:最后简化为一个力R,大小等于R B。
其几何意义是:R的大小等于载荷分布的矩形面积,作用点通过矩形的形心。
(2) 取A点为简化中心,平行力系的主矢是:平行力系对A点的主矩是:向A点简化的结果是一个力R A和一个力偶M A,且:如图所示;将R A向右平移一段距离d,使满足:最后简化为一个力R,大小等于R A。
其几何意义是:R的大小等于载荷分布的三角形面积,作用点通过三角形的形心。
习题4-4.求下列各梁和刚架的支座反力,长度单位为m。
解:(1) 研究AB杆,受力分析,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
(2) 研究AB杆,受力分析,将线性分布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
(3) 研究ABC,受力分析,将均布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
习题4-5.重物悬挂如图,已知G=1.8kN,其他重量不计;求铰链A的约束反力和杆BC所受的力。
解:(1) 研究整体,受力分析(BC是二力杆),画受力图:列平衡方程:解方程组:反力的实际方向如图示。
习题4-8.图示钻井架,G=177kN,铅垂荷载P=1350kN,风荷载q=1.5kN/m,水平力F=50kN;求支座A的约束反力和撑杆CD所受的力。
理论力学课后习题及答案解析..

第一章习题4-1.求图示平面力系的合成结果,长度单位为m。
解:(1) 取O点为简化中心,求平面力系的主矢:求平面力系对O点的主矩:(2) 合成结果:平面力系的主矢为零,主矩不为零,力系的合成结果是一个合力偶,大小是260Nm,转向是逆时针。
习题4-3.求下列各图中平行分布力的合力和对于A点之矩。
解:(1) 平行力系对A点的矩是:取B点为简化中心,平行力系的主矢是:平行力系对B点的主矩是:向B点简化的结果是一个力R B和一个力偶M B,且:如图所示;将R B向下平移一段距离d,使满足:最后简化为一个力R,大小等于R B。
其几何意义是:R的大小等于载荷分布的矩形面积,作用点通过矩形的形心。
(2) 取A点为简化中心,平行力系的主矢是:平行力系对A点的主矩是:向A点简化的结果是一个力R A和一个力偶M A,且:如图所示;将R A向右平移一段距离d,使满足:最后简化为一个力R,大小等于R A。
其几何意义是:R的大小等于载荷分布的三角形面积,作用点通过三角形的形心。
习题4-4.求下列各梁和刚架的支座反力,长度单位为m。
解:(1) 研究AB杆,受力分析,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
(2) 研究AB杆,受力分析,将线性分布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
(3) 研究ABC,受力分析,将均布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
习题4-5.重物悬挂如图,已知G=1.8kN,其他重量不计;求铰链A的约束反力和杆BC所受的力。
解:(1) 研究整体,受力分析(BC是二力杆),画受力图:列平衡方程:解方程组:反力的实际方向如图示。
习题4-8.图示钻井架,G=177kN,铅垂荷载P=1350kN,风荷载q=1.5kN/m,水平力F=50kN;求支座A的约束反力和撑杆CD所受的力。
理论力学 第六版部分习题答案 第12章

T=
m 2 2 2 ω l sin θ 6
12-5 自动弹射器如图 13-5a 放置,弹簧在未受力时的长度为 200 mm,恰好等于筒长。 欲使弹簧改变 10 mm,需力 2 N。如弹簧被压缩到 100 mm,然后让质量为 30 g 的小球自弹 射器中射出。求小球离开弹射器筒口时的速度。
Fk 30°
12-9 2 个质量均为 m2 的物体用绳连接,此绳跨过滑轮 O,如图 13-10 所示。在左方 物体上放有 1 带孔的薄圆板,而在右方物体上放有 2 个相同的圆板,圆板的质量均为 m1。 此质点系由静止开始运动,当右方物体和圆板落下距离 x1 时,重物通过 1 固定圆环板,而 其上质量为 2m1 的薄板则被搁住。摩擦和滑轮质量不计。如该重物继续下降了距离 x2 时速 度为零,求 x2 与 x1 的比。 解 第 1 阶段:系统由静止运动 x1 距离。由动能定理
12-6 平面机构由 2 匀质杆 AB,BO 组成,2 杆的质量均为 m,长度均为 l,在铅垂平 面内运动。在杆 AB 上作用 1 不变的力偶矩 M,从图 13-7a 所示位置由静止开始运动。不计 摩擦,求当杆端 A 即将碰到铰支座 O 时杆端 A 的速度。
P
P
θ
B vB
ω AB
vB vC vA
(c)
即
1 (2m1 g + m2 g ) x1 − (m1 g + m2 g ) x1 = (3m1 + 2m2 )v 2 2 1 (1) m1 gx1 = (3m1 + 2m2 )v 2 2 m2 gx2 − (m1 g + m2 g ) x2 = 0 − 1 (m1 + 2m2 )v 2 2
(2)
图 13-10
哈工大理论力学第六版答案
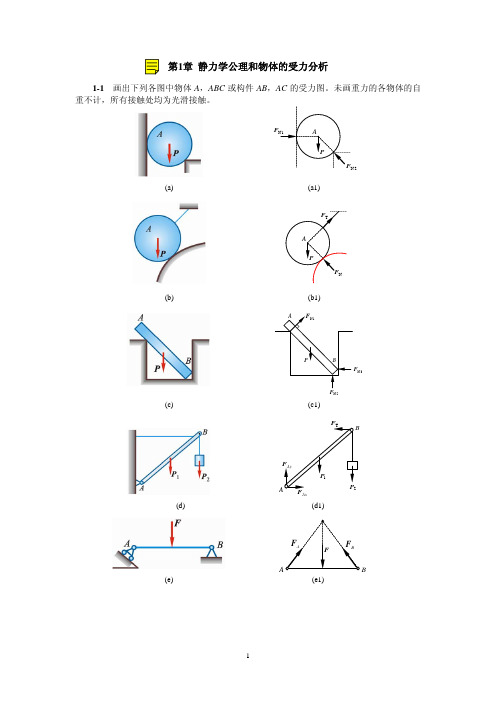
FR = (80 N) 2 + (140 N) 2 = 161 N
2-2 如图 2-2a 所示,固定在墙壁上的圆环受 3 条绳索的拉力作用,力 F1 沿水平方向, 力 F3 沿铅直方向,力 F2 与水平线成 40°角。3 个力的大小分别为 F1=2 000 N,F2=2 500 N, F3=1 500 N。求 3 个力的合力。
F
FA
A
(o)
B
FC
C
(o1)
F
FE
E
FG
G
FB
A FA
(o2)
B ′ FB
D
D
F
F C C (o3)
图 1-2
FD
′ FD
FE FF E (o4)
8
第2章 平面汇交力系与平面力偶系
2-1 铆接薄板在孔心 A,B 和 C 处受 3 个力作用,如图 2-1a 所示。 F1 = 100 N ,沿铅 直方向; F3 = 50 N ,沿水平方向,并通过点 A; F2 = 50 N ,力的作用线也通过点 A,尺 寸如图。求此力系的合力。
∠( FR , Fx ) = arccos(
( 3 915
2
+ 3 107 2
)
N = 4 998 N
∑ Fx 3 915 N ) = arccos( ) = 38°26′ 4 998 N FR
(2)几何法 作力多边形 Oabc,封闭边 Oc 确定了合力 FR 的大小和方向。根据图 2-2c,得
FR = ( F1 + F2 cos 40°) 2 + ( F3 + F2 sin 40°) 2
y
《理论力学》课后习题解答(赫桐生版)
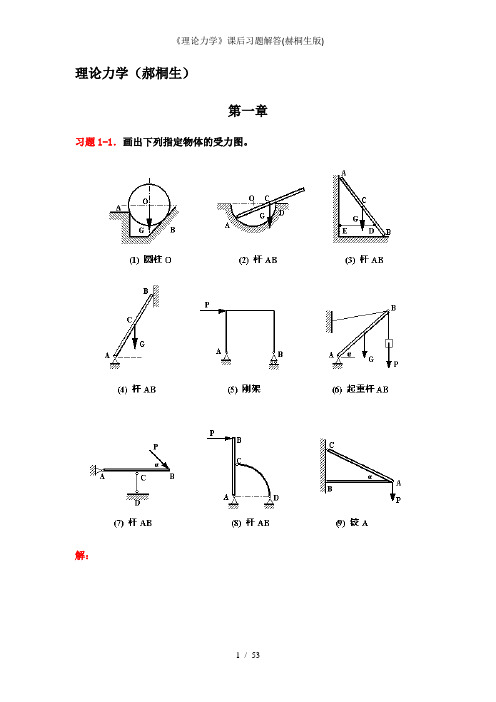
理论力学(郝桐生)第一章习题1-1.画出下列指定物体的受力图。
解:习题1-2.画出下列各物系中指定物体的受力图。
解:习题1-3.画出下列各物系中指定物体的受力图。
解:第二章习题2-1.铆接薄钢板在孔心A、B和C处受三力作用如图,已知P1=100N沿铅垂方向,P2=50N沿AB方向,P3=50N沿水平方向;求该力系的合成结果。
解:属平面汇交力系;合力大小和方向:习题2-2.图示简支梁受集中荷载P=20kN,求图示两种情况下支座A、B的约束反力。
解:(1)研究AB,受力分析:画力三角形:相似关系:几何关系:约束反力:(2) 研究AB,受力分析:画力三角形:相似关系:几何关系:约束反力:习题2-3.电机重P=5kN放在水平梁AB的中央,梁的A端以铰链固定,B端以撑杆BC支持。
求撑杆BC所受的力。
解:(1)研究整体,受力分析:(2) 画力三角形:(3) 求BC受力习题2-4.简易起重机用钢丝绳吊起重量G=2kN的重物,不计杆件自重、磨擦及滑轮大小,A、B、C三处简化为铰链连接;求杆AB和AC所受的力。
解:(1) 研究铰A,受力分析(AC、AB是二力杆,不计滑轮大小):建立直角坐标Axy,列平衡方程:解平衡方程:AB杆受拉,BC杆受压。
(2) 研究铰A,受力分析(AC、AB是二力杆,不计滑轮大小):建立直角坐标Axy,列平衡方程:解平衡方程:AB杆实际受力方向与假设相反,为受压;BC杆受压。
习题2-5.三铰门式刚架受集中荷载P作用,不计架重;求图示两种情况下支座A、B的约束反力。
解:(1) 研究整体,受力分析(AC是二力杆);画力三角形:求约束反力:(2) 研究整体,受力分析(BC是二力杆);画力三角形:几何关系:求约束反力:习题2-6.四根绳索AC、CB、CE、ED连接如图,其中B、D两端固定在支架上,A端系在重物上,人在E点向下施力P,若P=400N,α=4o,求所能吊起的重量G。
解:(1) 研究铰E,受力分析,画力三角形:由图知:(2) 研究铰C,受力分析,画力三角形:由图知:习题2-7.夹具中所用的两种连杆增力机构如图所示,书籍推力P作用于A点,夹紧平衡时杆AB与水平线的夹角为;求对于工件的夹紧力Q和当α=10o时的增力倍数Q/P。
理论力学课后习题答案 第6章 刚体的平面运动分析

理论力学课后习题答案第6章刚体的平面运动分析第6章刚体的平面运动分析6-1 图示半径为r 的齿轮曲柄OA带动,沿半径为R的固定齿轮滚动。
曲柄OA以等角加速度绕轴O转动,当运动开始时,角速度= 0,转角= 0。
试求动齿轮以圆心A为基点的平面运动方程。
00解:sx A(Rr)coA001(Rr)sin 为常数,当t = 0时,== 02起始位置,P与P重合,即起始位置AP 水0平,记,则AP从起始水平位置至图示A CP CP AP位置转过习题6-1图因动齿轮纯滚,故有,即rRR r 0, A rr将代入、、得动齿轮以A为基点的平面运动方程为:y2x1R r2 (R t r)costA 2r A22(Rr)sintA 26-2 杆AB斜靠于高为h的台阶角C处,一端A以匀速v沿水平向右运动,如图所示。
试以杆与铅垂线的夹角表示杆的角速度。
解:杆AB作平面运动,点C的 B B P速度v沿杆AB如图所示。
作速度Cv和v的垂线交于点P,点P即为C C 杆AB的速度瞬心。
则角速度杆cosvcoso0000h 为 A v A v 2ABAPACh习题6-2图习题6-2解图6-3 图示拖车的车轮A与垫滚B的半径均为r。
试问当拖车以速度v前进时,轮A与垫滚B的角速度与有什么关系?设轮A和垫滚B与地面之间以及垫滚B与拖车之间无滑动。
ABvv ARR A解:B2R2R习题v = v Bv = v vv BA B6-3解图习题6-3图AB6036-4 直径为mm 的滚子在水平面上作纯滚动,杆BC一端与滚子铰接,另一端与滑块C铰接。
速度=12 rad/s,=设杆BC在水平位置时,滚子的角,=,BC=270mm。
试求该瞬时杆BC的角速度和点C的速度。
解:杆BC 的瞬P 心在点P,滚子O的瞬心在点D BC v C B vBD C B B B 12603cos30vBD B270sin30O BCBPBP O v 习题6-4图 D 8rad/svPC 习题6-4解图CBC/s 6-5 在下列机构中,那些构件做平面运动,画出它们图示位置的速度瞬心。
哈工大理力习题及习题答案

理论力学(I)第六版哈尔滨工业大学理论力学教研室第二章 平面汇交力系与平面力偶系2-1铆接薄板在孔心A 、B 和C 处受三力作用,如题2-1图(a )所示。
F 1=100N ,沿铅直方向;F 3=50N ,沿水平方向,并通过点A ;F 2=50N ,力的作用线也通过点A ,尺寸如题2-1图(a)所示。
求此力系的合力。
解法一 几何法。
应用力的多边形法,将力F 1、F 2和F 3首尾相接后,再从F 1的起点至F 3的终点连一直线,此封闭边便是三力的合力F R ,如题2-1图(b )所示。
根据预先选好的比例尺,利用直尺和量角器便可确定合力F R 的大小和方向。
解法二 解析法。
合力的矢量表达式为∑∑+=+=j F i F j F i F F y x Ry Rx R即合力R F 在x 轴和y 轴上的投影,分别等于力系各力在同一坐标轴上投影的代数和,所以有:N N F F F F xx x Rx 805080606050022321=⎪⎪⎭⎫ ⎝⎛++⨯+=++= N N F F F F yy y Rx 14008060805010022321=⎪⎪⎭⎫ ⎝⎛++⨯+=++= 所以,合力的大小为:N N F F F Ry Rx R2.161140802222=+=+=合力F R 与x 轴的夹角为:︒===24.602.16180arccos cosR Rx F F acr α 2-3物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在铰车D 上,如题2-3图(a )所示。
转动铰车,物体便能升起。
设滑轮的大小、AB 与CB 杆自重及磨擦略去不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,试求拉杆AB 和支杆CB 处受的力。
解:这是一个平面汇交力系的平衡问题。
选取滑轮B 为研究对象,并作B 点的受力图,如题2-3图(b )所示。
由平衡方程∑∑==0,0y xF F,有:030sin 30cos =︒-︒+-T F F BC BA (1) 030cos 30sin =-︒-︒P T F BC (2)因忽略了滑轮B 的磨擦,所以P=T ,将P 、T 的数值代入(2)式,得KN F BC 64.74=将T 和F BC 的数值代入(1)式,得:kN F BA64.54=所以拉杆AB 和CB 分别受拉力54.64kN 和压力74.64kN 。
