正常色散介质中群速度与相速度的相对关系
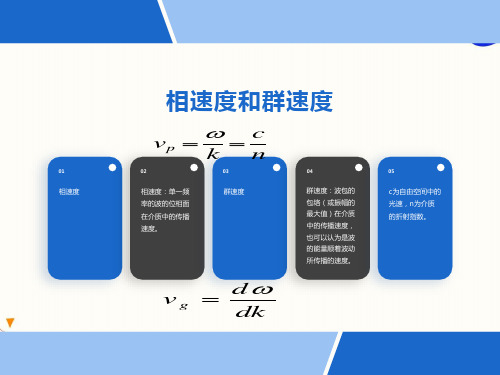
相速度和群速度
群速度色散效应
由(7)式,不同的波长会有不同的群速度,波长越大,群速度越大。 early time late time
群速度色散的计算
单位:
Thank You !
单击此处添加副标题
Add your company slogan
汇报人姓名
群速度与波长的关系
相速度色散和群速度色散
群速度色散
在介质中由于不同频率的光的相速度也不一样,于是波包的形状会发生变化,这就是群速度色散,也称之为群速弥散. 相速度色散是色散的一阶效应,而群速度色散是色散的二阶效应。
相速度色散
由于不同频率的光在同一介质中的折射率是不一样的,于是不同频率的光的相速度也不一样,这就是相速度色散。
相速度和群速度
ቤተ መጻሕፍቲ ባይዱ
图中,波形传播的速度为群速度。 群速度和相速度的示意图 图中,包络面的移动速度为群速度 包络面
群速度的计算
群速度与频率的关系
由(4)式 当 时,有 时,有 正常色散 反常色散
01
因此,一般情况下(正常色散),群速度小于相速度。
分析:
02
当
时,有
03
当
无色散
吸收带
在吸收带附近长波一边的折射率比短波的大. 在吸收带内,n是无法测量的.
微波:波速、相速、群速和能量传输速度的区别与联系

波速、相速、群速、能量传输速度1、定义波速(wave celerity):单位时间内波形传播的距离,以波长与波周期之比表示.V=入/T.相速(phase velocity):相速度,单一频率的正弦电磁波波的等相面(例如波峰面或波谷面)在介质中传播的速度v=c/n,c为自由空间中的光速,n为介质对该频率电磁波的折射指数。
在理想介质中,电磁波的相速仅与介质参数有关.群速(group velocity):(1)、波列作为整体的传播速度(2)波群传播的速度。
波的群速度,简称群速,是指波的包络传播的速度。
实际上就是波实际前进的速度。
群速是一个代表能量的传播速度。
概念引入原因:实用系统的信号总是由许多频率分量组成,在色散介质中,各单色分量将以不同的相速传播,因此要确定信号在色散介质中的传播速度就发生困难,为此引入群速的概念,它描述信号的能量传播速度。
能量传播速度:群速是波群的能量传播速度.2、相互关系(1)相关概念非色散介质:无线电波在介质中传播时,介电常数ε与频率无关,波的传播速度也与频率无关的介质;色散介质:与此相反,如果介电常数ε或传播速度v与频率有关的介质.正常色散:一切无色透明介质在可见光区域均表现为正常色散。
特点:波长变大时,由v=λf,频率不变,则V增大。
而n=c/v,则折射率值n变小,角色散率D变小。
反常色散:在某些波段会出现,波长变大时折射率值增大的现象,这称为反常色散。
反常色散同样是物质的普遍性质。
反常色散与选择吸收密切相关,即在发生物质的选择吸收波段附近出现反常色散。
角色散率:由夫琅和费衍射理论知,产生衍射亮条纹的条件(光栅方程):dsinθ=kλ(k= 1, 2,…, n)光栅方程对λ微分,就可得到光栅的角色散率:ψ=Δθ/Δλ=k/dcos.角色散率是光栅、棱镜等分光元件的重要参数,随着k的增大,色散率也就越大。
它表示单位波长间隔内两单色谱线之间的角间距,当光栅常数d愈小时,角色散愈大;光谱的级次愈高,角色散也愈大。
§1-8 相速、群体及色散特性

二、色 散 特 性
相速与工作频率的关系称为色散特性。显然,我们更感兴趣的是导波模的色散特性。表示色散 特性的常用方法包括如下几种: (1) β = f (ω)或ω = f (β ) ,见图 1-8-1。图中画出了三个导波模 a、b、c 的色散特性。由§ 1-5 的讨论可知,它们都夹在 (β / ω) = n 1 / c和(β / ω) = n 2 / c 的扇形区域 II 内。其中 b、c 的截 止角频率为 ωcb 和ωcc 。模式 a 的截止频率最低(在本例中为 0),称为基模。当 ω → ∞ 时各模式
−2 −1 2
,或光强角谱 A (u ) 下降
。对 s 上述两种不同 E(r)的计算结果见表 1-10-1。 表 1-10-1 光束的角谱及相关参数
E(r) A(u) ud θd
∞
高斯光束 exp(-r2/w2) exp[-(uw/2)2] 2/w 0.32λ/nw
阶跃光束 1, 0≤r<w 0, r>w 2J1(uw)/uw ≈ exp[-0.14(uw)2] 2.7/w 0.43λ/nw
2 2
(
2 1/ 2
(1-5-13)有该分量应为 [k n
2 0
2
(x ) − β 2 ]1/ 2 。二维限制光波导中,当 n = n (r ) 时,由式(1-5-13)
1/ 2
)
;当折射率为对称渐变分布(图 1-2-4)时,由式(1-2-8)、
2 2 v2 2 有该分量应为 k 0 n (r ) − β − 2 r
2
ˆ (r ) 是空间位置的函数。只要与波长相比,n(r)是空间位置的慢变函数,此近似就 k (r ) = n (r )k 0 k
二、用本地平面波概念确定波导模的本征值
相速度和群速度 (Phase velocity and group velocity )

2. 复色波的速度 该式表明:这个二色波是如图所示的、频率为 、 振幅随时间和空间在 0 到 2E0 之间缓慢变化的光波。 这种复色波可以叫做波群或振幅调制波。 x
振动的合成.exe
2. 复色波的速度
对于上述复色波,其传播速度包含两种含义: 等相位面的传播速度,称为相速度; 等振幅面的传播速度,称为群速度。 形象一点说,你拿电钻在一个很坚固的墙上钻洞, 你会觉得电钻的钻头的螺纹在旋转时似乎以高速前 进,但这只是你的错觉,因为你看到的是螺纹的 “相速度”,虽然很快,但是你的电钻却很慢很慢 地向墙内推进,也就是说电钻的总的向前推进的速 度就是“群速度”。
n
折射率随着波长 增加(或光频率的 减少)而减小的色 散叫正常色散。
由 k=2 / ,有dk=-(2 / 2)d ,可将上式变为
d g = d (77)
d(k ) d g +k dk dk
k=2 / dk=-(2 / 2)d
(76)
2)复色波的群速度
由=c/n,有d =- (c/n2)dn,上式还可表示为
dz m g = = dt km k
EE (z, t )cos (t kz)
E (z,t )=2E0 cos (mt km z)
(73)
m t km z =常数
dz m k m 0 dt dz m dt km
1 1 m = (1 2 )= 2 2 1 1 km = (k1 k2 )= k 2 2 dz m
2. 复色波的速度
2,则 若 E01 E02 E0 且 1 2 1、
EE (z, t )cos (t kz) (73)
式中
E (z ,t )=2E0 cos (m t km z) 1 1 m = (1 2 )= 2 2 1 1 km = (k1 k2 )= k 2 2 1 = (1 2 ) 2 1 k = (k1 k2 ) 2
光速的测定光的相速度和群速

随着光速测定技术的不断发展,其应用领域也将 不断拓展,有望在更多领域实现应用。
光速测定在科学研究中的应用前景
01
02
03
验证物理理论
光速的测定结果对于验证 物理理论具有重要意义, 例如验证相对论中的光速 不变原理等。
推动光学研究发展
光速的测定有助于推动光 学研究的发展,例如研究 光的传播特性、光的干涉 和衍射等现象。
群速的测量
脉冲延迟法
利用脉冲光在介质中传播时的延迟现象来测 量群速。通过测量脉冲光在介质中传播的时 间延迟,并根据光速与延迟时间的关系计算 群速。这种方法需要使用脉冲光源和高速探 测器等设备。
频率扫描法
通过改变光的频率并测量其在介质中的传播 速度来得到群速。使用可调谐激光器或光谱 仪等设备,在不同频率下测量光的传播速度, 并根据速度与频率的关系计算群速。
激光干涉法
利用激光的干涉现象来测量光速。将激光分为两路,一路作为参考光路,另一路经过待测距离后返回 与参考光路发生干涉,通过测量干涉条纹的移动来推算光速。
光纤法
利用光纤中光的传输特性来测量光速。将光信号通过光纤传输一段已知距离后,测量其传输时间并计 算光速。这种方法具有高精度和可重复性好的优点。
04 相速度和群速的测量技术
光速的测定光的相速度和群速
目 录
• 引言 • 光速测定的基本原理 • 光速测定的实验方法 • 相速度和群速的测量技术 • 光速测定在现代物理学中的应用 • 总结与展望
01 引言
光的速度概念
相速度
光在介质中传播时,其电磁波的 相位变化的速度,即相速度。相 速度与光的频率和介质的折射率 有关。
群速度
02 光速测定的基本原理
光的波动性质
《相速度和群速度》课件

它并不等于波的能量 或信息传播的速度, 这是群速度的概念。
相速度的物理意义
相速度决定了波在介质中的传 播速度,即波峰和波谷的运动 速度。
它决定了波的相位变化和干涉 、衍射等物理现象的发生。
在某些情况下,相速度可以接 近无穷大,例如在无损介质中 传播的波。
相速度的计算方法
根据波动方程和介质的物理性质,可以求解波的相速度。
影响因素不同
相速度只与介质性质有关,而群速度不仅与介质性质有关,还与频 率有关。
在某些介质中的行为不同
在色散介质中,相速度可以超过光速,而群速度不能超过光速。
相速度与群速度的联系
在某些情况下,两者可能相等
01
在无色散介质中,波的相速度和群速度是相等的。
两者都是描述波动现象的重要参数
02
相速度和群速度分别从不同的角度描述了波动现象,对于理解
展望
未来研究方向
随着科技的发展,相速度和群速 度的研究将更加深入,未来可以 进一步探索其在不同领域的应用
,如量子力学、生物医学等。
技术发展与挑战
随着通信、信号处理等技术的快速 发展,对相速度和群速度的研究将 面临更多挑战,需要不断探索新的 理论和方法。
跨学科合作与交流
相速度和群速度的研究涉及到多个 学科领域,未来需要加强跨学科的 合作与交流,促进相关领域的发展 。
波动现象的本质和传播规律具有重要意义。
两者都是波动方程的解
03
无论是相速度还是群速度,都是波动方程的解,用于描述波动
在介质中的传播行为。
PART 04
相速度和群速度的应用
REPORTING
通信领域的应用
相速度的应用
在通信领域中,相速度控制着信号的相位信息传递。通过调 整相速度,可以实现对信号的相位调制,如调相(PM)和调 频(FM)等,从而实现更高效、更可靠的数据传输。
相速度和群速度方案

(4)
由(4)式 vg vp/(1 / n dn / d)
分析:
当 dn/ d o时,有 vg vp 当 dn/ d o时,有 vg vp 当 dn/ d o时,有 vg vp
无色散 正常色散 反常色散
因此,一般情况下(正常色散),群速度小 于相速度。
吸收带
1.在吸收带附近长波一边的折射率比短波的大. 2.在吸收带内,n是无法测量的.
群速度与波长的关系
vg
( c ) /(1
n
n
dn )
d
dn dn d d d d
2c /
dn 2c 2c 2 d 2 (2c / )2 2c
d 2k d 2
d d
dk d
d [1 d vg
]
2 2c
d [1 (n d c
dn )] d
2 2c2
d [n d
dn ] d
2 [ dn d 2n dn )] 3 d 2n 2c d d2 d 2c2 d2
(10)
GVD
k '' ()
3 2c2
d 2n
d2
单位:s2 m
LOGO
Add your company slogan
人有了知识,就会具备各种分析能力, 明辨是非的能力。 所以我们要勤恳读书,广泛阅读, 古人说“书中自有黄金屋。 ”通过阅读科技书籍,我们能丰富知识, 培养逻辑思维能力; 通过阅读文学作品,我们能提高文学鉴赏水平, 培养文学情趣; 通过阅读报刊,我们能增长见识,扩大自己的知识面。 有许多书籍还能培养我们的道德情操, 给我们巨大的精神力量, 鼓舞我们前进。
色散和群速.ppt

dz vg dt
可见,在损耗媒质中,相速度不再是一个常数,而是与频率相关的 函数。
不同频率的波将以不同的相速度传播,这 种现象称为色散现象. 损耗媒质是一种色散媒质。
vblue vred v green
无色散媒质
vblue vred v green
色散媒质
6.4.2 群速度 下面讨论一种最简单的情况。假设色散媒质中同时存在两 个线极化电磁波,它们的场强方向相同,振幅相同,频率不 同,均沿z轴传播。它们的角频率和相位系数为
d v d v d v d p p p v v v v g p p g d d d v d p
v
g
1
v
p
v
p
dv
p
d
其合成波
其振幅是受调制的,按余弦规律变化的,称为包络 波。如图中的虚线所示。 群速度vg定义:包络波上某一恒定相位点推进的速度。
(3)
No Image
第六章平面电磁波64色散和群速主要内容群速学习目的掌握群速与相速的区别关系641色散可见相速度是一个与频率无关的常数
第六章 平面电磁波
6.4 色散和群速
主要内容
色散 群速
学习目的
掌握群速与相速的区别、关系
6.4.1 色散
在理想介质中,相速度为
可见,相速度是一个与频率无关的常数。 在导电媒质中,相速度为
● ●
z
● ●
群速和相速
即由
No Image
得
设 则
故
t z const
No Image
显然存在以下三种可能的情况: ( 1) ( 2)
群速折射率和相速折射率关系证明

群速折射率和相速折射率关系证明
群速折射率和相速折射率一般指的是一个介质中电磁波同时传播的速率。
它们本质上是介质中声音和电磁两种波的特性,所以它们之间存在着一定的关系。
这里首先来解释群速折射率。
群速折射率代表的是电磁波的聚拢速度,就是电磁波从一种介质被传播到另一种介质时的变化速度。
而相速折射率是磁暴动量与气体中由磁暴而引起的压力变化之间的比率。
它是由磁场引起介质中声音或者电磁波传播的速度,比率越大说明介质中电磁波的传播速度越快。
V=v/n此V表示群速折射率,v表示光速,n表示相速折射率。
也就是说,当电磁波穿过不同的介质时,群速折射率就是电磁波的真实传播速度,而相速折射率是由介质中的因素决定的,即介质中的各种分子,原子,温度,压强等决定着电磁波传播时发生的变化等因素决定。
在一个介质中,只要相速折射率给定,群速折射率就可以由公式给出。
此外,群速折射率和相速折射率之间还有一个有趣的关系,就是相速折射率可以用来描述介质中对电磁波传播折射的程度。
从上面可以看出,群速折射率和相速折射率之间可以有比较大的关系,当介质的相速折射率不同时,电磁波的传播速度也会发生变化,这使得群速折射率和相速折射率之间的关系非常重要。
因此,只要介质的状态引起的相速折射率发生变化,就可以推测出电磁波的传播速度发生变化,并且之间也存在一定的关系。
关于相速度,群速度,信号速度

关于相速度、群速度、信号速度作者:自出洞来读了"对《这是编译还是胡编?--评新浪科技的一则新闻》的说明"一文后,觉得有些内容,特别是文中故儒的附文"误解可能来自一些量子力学课本"的描述,给广大读者造成了混乱。
在此觉得有必要澄清一下概念。
首先声明本人是著名(或曾经很著名)重点大学物理系毕业,如所言有错,欢迎广大新语丝网友批评指正。
关于到底是相速度还是群速度可以超过真空中的光速(以下简称c),正确答案是复杂的,这里涉及到反常色散(和介质的吸收带有关)的问题。
所谓相速度,指的是单一频率的波的传播速度,在正常色散的情况下它不可能超过c。
但是实际存在的波不是单频的,媒质对这个(或这些)波必然是色散的,那么,传播中的波由于各不同频率的成分运动快慢不一致,会出现扩散,但假若(注意这个假设)这个波是由一群频率差别不大的简谐波组成,这时在相当长的传播途程中总的波仍将维持为一个整体,以一个固定的速度运行。
这个特殊的波群称为"波包",这个速度称为群速度。
与相速度不同,群速度的值比波包的中心相速度要小,并且二者的差值同中心相速度随波长而变化的平均率成正比。
群速度是波包的能量传播速度,也是波包所表达信号的传播速度(这是在上述假设的基础上)。
这也是Bohm的《量子理论》中写的(见故儒的附文):In general, the phase velocity has little physical significance; for example, the speed of transmission of a signal through a dielectric is given by the group velocity, as is also the speed of transport of energy.Bohm写得没错,在一般情况下确实如此,他并没有混淆群速度与信号传送速度。
相速度和群速度

2. 复色波的速度 该式表明:这个二色波是如图所示的、频率为 、 振幅随时间和空间在 0 到 2E0 之间缓慢变化的光波。 这种复色波可以叫做波群或振幅调制波。 x
振动的合成.exe
2. 复色波的速度
对于上述复色波,其传播速度包含两种含义: 等相位面的传播速度,称为相速度; 等振幅面的传播速度,称为群速度。 形象一点说,你拿电钻在一个很坚固的墙上钻洞, 你会觉得电钻的钻头的螺纹在旋转时似乎以高速前 进,但这只是你的错觉,因为你看到的是螺纹的 “相速度”,虽然很快,但是你的电钻却很慢很慢 地向墙内推进,也就是说电钻的总的向前推进的速 度就是“群速度”。
1.4 相速度和群速度 (Phase velocity and group velocity )
在前面的讨论中,提到了光波速 这个物理量,下面 讨论它的具体含义。 1. 单色光波的速度 2. 复色波的速度
1. 单色光波的速度
假设单色光波电场的表示式为
E E0 cos[(t (r )] ( 69)
dz m g = = dt km k
EE (z, t )cos (t kz)
E (z,t )=2E0 cos (mt km z)
(73)
m t km z =常数
dz m k m 0 dt dz m dt km
1 1 m = (1 2 )= 2 2 1 1 km = (k1 k2 )= k 2 2 dz m
k c
r r
(71)
2. 复色波的速度 如前所述,实际上的光波都不是严格的单色光波,而 是复色波,它的光电场是所包含各个单色光波电场的 叠加,即
E E0l cos(l t kl z )
相速度与群速度

相速度与群速度振动状态在空间的传播速度称为波速,又称相速度。
如沿x轴正方向传播的平面简谐波,其表达式为式中(ωt-kx)称为波相,当(ωt-kx)一定时,则ξ值一定。
当t增大时,x必须增大,才能保持(ωt-kx)不变。
这意味着用(ωt-kx)描述的振动状态随着时间的推移向x的正方向传播。
相速度即波相传播的速度,等于x对t的变化率,令ωt-kx=常量将上式两边微分,经整理可得(1)u即所求相速度。
这里ω=2πv,,代入则得此即大家熟悉的相速度的公式。
从根本上讲,相速度的大小取决于媒质的性质。
弹性波由弹性媒质的力学性质决定,电磁波由媒质的折射率决定。
实验和理论证明,相速度的大小还与波的频率有关。
光的色散现象就是波速与频率有关的明显例证。
通常把相速度与频率无关的媒质称为无色散媒质;把相速度随频率而变的媒质称为色散媒质。
在无色散媒质中,只要用相速度描述波的传播即可,但是在色散媒质中,要描述任意一种波(如图1所示的非简谐波)的传播只有相速度就不够了,需要引入群速度的概念。
p/dλ≠0,vg≠vp),并且在正常色散区域(dvp/dλ>0,dn/d λ<0),群速度小于相速度(vg<vp);在反常色散区域(dvp/dλ<0,dn/d λ>0),群速度则大于相速度(vg>vp)。
只有在无色散介质或真空中(dvp/dλ=0,dn/d λ=0),群速度才等于相速度(vg=vp)。
根据付里叶分析,任何一个复杂的波,都可以分解成许多不同频率成分的简谐波的叠加。
在色散媒质中,不同频率的简谐波传播速度不同,那么这许多简谐波合成的波是以什么速度传播呢?为了方便,以两个频率相近的等振幅简谐波的合成波的传播为例说明群速度的概念。
设合成波为(2)式(2)中或,或k2,所以变化缓慢,如图中虚线所示的包络线;而表示图中一个个小的波形。
令,,,,则式(2)可改写为在波传播过程中,一个个小的波形在向前传播的同时,整个波形即包络也在向前移动,二者移动速度可如下求得:令=常量等式两边微分,可求得小波形移动的速度为(3)同样可求得包络移动的速度或称波群移动的速度为一般表示为:(4)U g即群速度。
色散关系公式 推导

色散关系公式推导首先,我们需要了解两个概念:相速度和群速度。
相速度是指在介质中传播的波最快的速度,而群速度是指一组波的平均速度。
假设在介质中传播的波的频率为ω,波长为λ,相速度为v,群速度为vg。
根据波动方程可知:v = ω / k其中,k为波数,k = 2π / λ。
因此,v = ωλ / 2π接下来,我们考虑介质中的折射率n与波长λ之间的关系。
根据光的波动理论,折射率与介质中电场的振幅成正比,即n = f(E)其中,E为电场的振幅。
根据经典电动力学理论,电场振幅与光波的振幅成正比,即E = Acos(ωt)其中,A为振幅。
因此,n = f(A)将波长λ表示为n和角频率ω的函数,可得λ = f(n, ω)对λ关于ω求导,得到dλ / dω = (f / ω) / (f / n)根据著名的几何光学理论,n与λ之间的关系可以用折射率的色散函数来表示,即n = f(λ)此时,色散函数的导数为dn / dλ = (f / λ)因此,dλ / dω = 1 / (c * dn / dλ)其中,c为真空中光速。
将折射率的色散函数展开,得到n(λ) = A + B / λ^2 + C / λ^4 + ...其中,A、B、C等为常数。
因此,dn / dλ = -2B / λ^3 - 4C / λ^5 - ...代入色散关系公式中,得到v = c / n = c / [A + B / λ^2 + C / λ^4 + ...] 群速度vg可以通过色散函数的二阶导数求得,即vg = dω / dk = dω / (dλ / dk) = c / [n + λ * dn / d λ] = c / [n + λ * (d^2n / dλ^2)]综上所述,色散关系公式的推导涉及相速度、群速度、折射率的色散函数以及偏微分等知识。
掌握这些关键概念和推导方法,有助于更深入地理解光的传播规律。
相速 群速 色散

E (t ) = 2 E m cos (Δ w t Δ β z ) cos (w 0 t β 0 z )
某一时刻,合成波随z的分布如图所示:
包络波,速度vg
z
载波,速度vp
合成波的振幅随时间按余弦变化,是一调幅波,该包络波的等相位面为:
Δ w t Δ β z = 常数
z = 常数
dV p dβ
∴
= V p+ β
dV p dλ dλ dβ
λ
dλ 2π = 2 β dβ
dV p 2π dV p Vg = V p = Vp λ β dλ dλ
7.5 相速、群速与色散
Vg =
1 βቤተ መጻሕፍቲ ባይዱ
Vp = dV p dw
Vp w dV p 1 V p dw
Vg = V p λ
dV p dλ
定义:包络波上某一恒定相位点传播的速度为群速Vg
dz Δ w = ∴Vg = dt Δ β
当 Δw → 0时
Vg =
dw dβ
只有对窄带信号(Δω<< ω0),且β随w变化很缓慢的情况下,群 速才有意义
7.5 相速、群速与色散
3、群速和相速的关系
Vg = dw d = Vpβ dβ dβ
dw Vp = Vg = β dβ
对于非色散媒质
dV p dw
=0
dV p dw dλ dV p dλ ≠0
Vg = V p
对于色散媒质
若 若
dV p dw dV p dw
> 0或 < 0或
dV p
< 0,则 V g < V P > 0,则 V g > V P
正常色散
非正常色散
电磁波群速度与相速度原理

电子信息工程学院Quency Chen 之宇文皓月创作1.相速度与群速度如果只考虑均匀介质中的小幅度的波,可利用描述介质的方程和麦克斯韦方程得到一常系数方程组,求解可得到解为:)exp(t j r k j ω-⋅ (1)的解其中k 为波矢量,r 为空间位置矢量,ω为角频率。
式(1)中的ω和k 满足:0),(=ωk F (2)的关系,这个关系只与介质的特性有关,称为色散关系。
式(1)描述的电磁波,ω表征波的时间变更,波矢量k 描述波的空间变更。
λπ2=k (3)式(3)中λ为波长,因此波矢量k=1/λ暗示单位距离有多少个波,即波的数量,然后再乘以2π暗示单位距离内波的总相位,若把空间相位变更2π相当于一个全波,则k 暗示单位距离内全波的数目,k 也被称为电磁波的相位常数,因为它暗示传播方向上波行进单位距离时相位变更的大小,注意这里相位单位为弧度制。
将(1)式变形为:)]()(exp[t t j r r jk ∆+-∆+⋅ω (4)若满足0=∆-∆t r k ω (5),则式(4)和式(3)一样,这说明在空间距离延长Δr 的位置处,若在时间上也滞后Δt 则信号相位与r 处t 时刻的相位坚持一致。
这说明r 处的波相位在Δt 时间后传播到r+Δr 处,因此将式(5)变形可得到t rk V ∆∆==Φω(6),暗示波的相速度由角频率和波矢量共同决定。
在真空中电磁波的相速度为c 。
折射指数n 定义为:ωkc V c n =Φ= (7),由于介质中电波相速度既可能小于真空光速,也可能大于真空光速,所以折射指数也可能大于1,也可能小于1。
如果限制ω是实数,若有一解,使得k 和n 也是实数,则代表无衰减的波传播。
若k 和n 为纯虚数,则相应的波是消散波。
波场强度随距离指数地减小。
如果将介质等效为阻抗负载,则实数负载代表介质从输入端口全部吸收能量,然后又从输出端口全部放出能量,类似传输线特性;如果负载为虚数,则代表负载从输入端口全部吸收能量后,又从输入端口全部释放出去,因此电波就不克不及传播,只能到达一定的深度后就反射出去了,类似界面反射。
微波:波速、相速、群速和能量传输速度的区别与联系

波速、相速、群速、能量传输速度1、定义波速〔wave celerity〕:单位时间内波形传播的距离,以波长与波周期之比表示.V=入/T.相速(phase velocity):相速度,单一频率的正弦电磁波波的等相面〔例如波峰面或波谷面〕在介质中传播的速度v=c/n,c为自由空间中的光速,n为介质对该频率电磁波的折射指数。
在理想介质中,电磁波的相速仅与介质参数有关.群速(group velocity):〔1〕、波列作为整体的传播速度〔2〕波群传播的速度。
波的群速度,简称群速,是指波的包络传播的速度。
实际上就是波实际前进的速度。
群速是一个代表能量的传播速度。
概念引入原因:实用系统的信号总是由许多频率分量组成,在色散介质中,各单色分量将以不同的相速传播,因此要确定信号在色散介质中的传播速度就发生困难,为此引入群速的概念,它描述信号的能量传播速度。
能量传播速度:群速是波群的能量传播速度.2、相互关系〔1〕相关概念非色散介质:无线电波在介质中传播时,介电常数ε与频率无关,波的传播速度也与频率无关的介质;色散介质:与此相反,如果介电常数ε或传播速度v与频率有关的介质.正常色散:一切无色透明介质在可见光区域均表现为正常色散。
特点:波长变大时,由v=λf,频率不变,则V增大。
而n=c/v,则折射率值n变小,角色散率D变小。
反常色散:在某些波段会出现,波长变大时折射率值增大的现象,这称为反常色散。
反常色散同样是物质的普遍性质。
反常色散与选择吸收密切相关,即在发生物质的选择吸收波段附近出现反常色散。
角色散率:由夫琅和费衍射理论知,产生衍射亮条纹的条件〔光栅方程〕:dsinθ=kλ〔k= 1, 2,…, n〕光栅方程对λ微分,就可得到光栅的角色散率:ψ=Δθ/Δλ=k/dcos.角色散率是光栅、棱镜等分光元件的重要参数,随着k的增大,色散率也就越大。
它表示单位波长间隔内两单色谱线之间的角间距,当光栅常数d愈小时,角色散愈大;光谱的级次愈高,角色散也愈大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正常色散介质中群速度与相速度的相对关系
光的传播速度在不同介质中会发生改变,这种现象被称为光在介质中的折射,其中光传播的速度,在正常色散介质中群速度与相速度有一定的关系。
在正常色散介质中,介质中的光速度与频率之间呈现线性关系,也就是说在相同介质中,频率越高,光速度也越高。
根据自然的光学原理,光在介质中的传输速度是由群速度和相速度组成的。
群速度和相速度在正常色散介质中是有一定的关系的。
群速度表示的是光信号在介质中整体传播的速度,而相速度则是光的电场和磁场在介质中传播的速度。
在正常的色散介质中,群速度通常要大于相速度,也就是说,在介质中传输光信号的速度整体上要快于电场和磁场的传输速度。
这可以通过正常色散介质中材料的复合折射率来解释。
光的相位速度与群速度之间的差异是由折射率的频率依赖性造成的。
在正常色散材料中,较高频率的光会快速折射并且离开表面,而较低频率的光则会被材料捕获和重新释放,从而形成相对较慢的群速度。
在光纤通讯系统中,光速度和光的传输性能至关重要。
对于正常色散介质,光信号传播的快慢由材料的折射率决定,因此了解群速度和相速度之间的相对关系对于光纤通讯系统的设计和优化非常重要。
总之,在正常色散介质中,群速度和相速度之间存在一定程度的相对关系。
群速度比相速度更高,这是由于复合折射率的频率依赖性造成的。
这种相对关系在光学系统的优化中非常重要,因为光速和光的传输性能通常是光学系统设计和优化的关键因素之一。
