弦振动共振波形及波的传播速度测量
实验一弦振动共振波形及波的传播速度测量

实验一弦振动共振波形及波的传播速度测量【思考题】1、通过实验,说明弦线的共振频率和波速与哪些条件有关?μ值比较,分析其差异及形成原因。
2、试将按公式求得μ值与静态线密度3、试用一种方法求出波束V与张力T的函数关系。
4、如果弦线有弯曲或者粗细不均匀,对共振频率和形成驻波有何影响?实验二复摆振动的研究【思考题】1.什么是回转轴、回转半径、等值摆长?改变悬挂点时,等值摆长将会改变吗?摆动周期会改变吗?2.由T—h 图线定性分析复摆摆动周期与回转轴到重心距离之间的关系。
3.如果所用复摆不是均匀的钢板,重心不在板的几何中心,对实验的结果有无影响?两实验曲线还是否对称?为什么?实验三阻尼振动【思考题】1、何谓半衰期?何谓品质因数?二者有何关系?2、讨论在振动系统的m和k相同的情况下,阻尼的大小对对数衰减δ和品质因数Q的影响。
实验四金属线胀系数的测定【思考题】1. 游标卡尺的使用注意事项是什么?2. 本实验测量公式(4-4)中,各个长度量分别用不同仪器测量,是根据什么原则确定的?哪一个量的测量误差对结果的影响最大?3. 在实验中若仪器的支杆也由于受热而膨胀,则对实验结果将产生怎样的影响?4. 你能否设想出另一种测量微小伸长量的方法,从而测量出材料的线胀系数?实验五落球法测量液体粘滞系数【思考题】1、如何判断小球在作匀速运动?2、如果遇到待测液体的 值较小,而钢珠直径较大,这时为何须用(5-5)式计算?3、用激光光电开关测量小球下落时间的方法测量液体粘滞系数有何优点?实验六气体比热容比的测定【思考题】1、注入气体流量的多少对小球的运动情况有没有影响?2、在实际问题中,物体振动过程并不是十分理想的绝热过程,这时测得的值比实际值大还是小?为什么?实验七准稳态法测导热系数和比热【思考题】1.试述准稳态法测不良导体导热系数的基本思想方法和优点?2.实验过程中,环境温度的变化对实验有无影响?为什么?3. 本实验中,如何判断系统进入了准稳态,即准稳态的条件是什么?实验八超声波声速的测量【思考题】1.用逐差法处理数据的优点是什么?还有没有别的合适的数据处理方法?2.在声速测试实验中为什么要在换能器谐振状态下测试空气中的声速?为什么换能器的发射面和接收面要保持互相平行?3.怎样确定换能系统的谐振频率?实验九光学材料折射率的测定【思考题】1、几种测量物质折射率方法各有什么优点?实验十迈克尔逊干涉仪的调整及使用【思考题】1、简述本实验所用干涉仪的读数方法。
弦振动的实验研究

弦振动的实验研究弦振动的实验研究弦是指⼀段⼜细⼜柔软的弹性长线,⽐如⼆胡、吉它等乐器上所⽤的弦。
⽤薄⽚拨动或者⽤⼸在张紧的弦上拉动就可以使整个弦的振动,再通过⾳箱的共鸣,就会发出悦⽿的声⾳。
对弦乐器性能的研究与改进,离不开对弦振动的研究,对弦振动研究的意义远不只限于此,在⼯程技术上也有着极其重要的意义。
⽐如悬于两根⾼压电杆间的电⼒线、⼤跨度的桥梁等,在⼀定程度上也是⼀根“弦”,它们的振动所带来的后果可不象乐器上的弦的振动那样使我们们感到愉快。
对于弦振动的研究,有助于我们理解这些特殊“弦”的振动特点、机制,从⽽对其加以控制。
同时,弦的振动也提供了⼀个直观的振动与波的模型,对它的分析、研究是处理其它声与振动问题的基础。
欧拉最早提出了弦振动的⼆阶⽅程,⽽后达朗贝尔等⼈通过对弦振动的研究开创了偏微分⽅程论。
本实验意在通过对⼀段两端固定弦振动的研究,了解弦振动的特点和规律。
预备问题1.复习DF4320⽰波器的使⽤。
2.什么是驻波?它是如何形成的?3.什么是弦振动的模式?共振频率与哪些因素有关?4.张⼒对波速有何影响?试⽐较以基频和第⼀谐频共振时弦中的波速。
⼀、实验⽬的:1、了解驻波形成的条件,观察弦振动时形成的驻波;2、学会测量弦线上横波传播速度的⽅法:3、⽤作图法验证弦振动频率与弦长、频率与张⼒的关系。
⼆、实验原理⼀根两端固定并张紧的弦,静⽌时处于⽔平平衡位置,当在弦的垂直⽅向被拉离平衡位置后,弦会有回到平衡位置的趋势,在这种趋势和弦的惯性作⽤下,弦将在平衡位置附近振动。
令弦线长度⽅向为x 轴,弦被拉动的⽅向(与x 轴垂直的⽅向)为y 轴,如图1所⽰。
若设弦的长度为L ,线密度为ρ,弦上的张⼒为T ,对⼀⼩段弦线微元dl 进⾏受⼒分析,运⽤⽜顿第⼆定律定律,可得在y ⽅向的运动微分⽅程()2222tydx dx x y T ??=??ρ(1)若令ρ/2T v =,上式可写为222221tyv x y ??=?? (2)y 图1(2)式反映了弦的位移y 与位置x 、时间t 的关系,其中)/(ρT v =代表了在弦线上横波传播的波速。
弦振动实验报告e

弦振动的研究一、实验目的1、观察固定均匀弦振动共振干预形成驻波时的波形,加深驻波的认识。
2、了解固定弦振动固有频率与弦线的线密ρ、弦长L和弦的张力Τ的关系,并进行测量。
三、波,沿X轴负方向传播的波为反射波,取它们振动位相始终相同的点作坐标原点“O〞,且在X=0处,振动质点向上达最大位移时开始计时,那么它们的波动方程分别为:Y1=Acos2 (ft-x/ )Y2=Acos[2 (ft+x/λ)+ ]式中A为简谐波的振幅,f为频率, 为波长,X为弦线上质点的坐标位置。
两波叠加后的合成波为驻波,其方程为:Y1+Y2=2Acos[2 〔x/ 〕+ /2]Acos2 ft ①由此可见,入射波与反射波合成后,弦上各点都在以同一频率作简谐振动,它们的振幅为|2A cos[2 〔x/ 〕+ /2] |,与时间无关t,只与质点的位置x有关。
由于波节处振幅为零,即:|cos[2 〔x/ 〕+ /2] |=02 〔x/ 〕+ /2=(2k+1) / 2 ( k=0. 2. 3. … )可得波节的位置为:x=k /2 ②而相邻两波节之间的距离为:x k+1-x k =(k+1) /2-k / 2= / 2 ③又因为波腹处的质点振幅为最大,即|cos[2 〔x/ 〕+ /2] | =12 〔x/ 〕+ /2 =k ( k=0. 1. 2. 3. )可得波腹的位置为:x=(2k-1) /4 ④这样相邻的波腹间的距离也是半个波长。
因此,在驻波实验中,只要测得相邻两波节或相邻两波腹间的距离,就能确定该波的波长。
在本实验中,由于固定弦的两端是由劈尖支撑的,故两端点称为波节,所以,只有当弦线的两个固定端之间的距离〔弦长〕等于半波长的整数倍时,才能形成驻波,这就是均匀弦振动产生驻波的条件,其数学表达式为:L=n / 2 ( n=1. 2. 3. … )由此可得沿弦线传播的横波波长为:=2L / n ⑤式中n为弦线上驻波的段数,即半波数。
弦振动规律研究实验指导书

弦振动规律研究实验指导书俸用格一:注意事项二:弦振动规律研究实验基本原理三:弦振动规律研究综合实验仪操作指南四:参考表格海南大学物理实验室一:注意事项1.进入实验室不可移动、摆弄实验台/桌上的所有仪器用具。
以免拉断仪器间的连接电缆/线、改变教师设置好的各种实验参数!2.实验结束后必需经任课教师检查你所使用的实验仪器与用具,器具完好无损方可离开实验室!3.实验过程中不可盲目转动示波器面板各旋钮,连线时务必正确使用探笔以免损坏探笔探针和内部芯线!4.实验过程中不可用手触碰弦线和电磁传感器线圈表面!5.实验过程中千万不可接错驱动传感器和接收传感器!6.实验过程中驱动与接收传感器不可靠得太近,以免相互产生干扰,通过观察示波器中的接收波形可以检验干扰的存在。
当他们靠得太近时,波形会改变。
为了得到较好的测量结果,至少两传感器的距离应大于cm10。
7.悬挂,、更换砝码以及砝码杆水平调节时务必动作轻巧,以免使弦线崩断,造成砝码坠落而发生事故。
二:弦振动规律研究实验基本原理【实验目的】1、巩固示波器的使用方法和操作技巧。
2、了解驻波形成的基本条件与弦振动的基本规律。
3、测量不同弦长和不同张力时弦振动的共振频率。
4、测量弦线的线密度。
5、测量弦振动时波的传播速度。
【实验仪器】301FB 型弦振动研究实验仪与弦振动实验信号源各1台,双踪示波器1台。
【实验原理】正弦波沿着拉紧的弦传播,可用式(1)来描述:)(2cos 1λπxt f y y m -⨯= (1)如果弦的一端被固定,那么当波到达固定端时会反射回来,反射波可表示为:)(2cos 1λπxt f y y m +⨯= (2)在保证这些波的振幅不超过弦所能承受的最大振幅时,两束波叠加后的波方程为: )2cos()/2cos(2t f x y y m ⋅⋅⋅=πλπ (3)等式的特点:当时间固定为0t 时,弦的形状是振幅为)2cos(20t f y m ⋅⋅π的正弦波形。
弦振动实验中驻波波长的测量方法

弦振动实验中驻波波长的测量方法张宇亭;赵斌;王茂香【摘要】弦驻波实验是大学物理实验之一。
相比于早期的音叉,该实验采用了钢质弦线,不仅能观察到弦线上的驻波,而且还能听到弦线振动的声音,便于研究振动与声音的关系,有助于理解弦乐器的工作原理。
文中基于新型弦振动实验仪器,对弦线上的驻波进行了研究,给出了驻波波长的两种测量方法,即驻波公式计算求波长和直接观察驻波求波长的方法,通过大量数据处理与分析,对两种方法进行了对比,为实验仪器的测评和改进提供一定的参考。
%Standing wave experiment is one of experiments of college paring to the tuning fork in the earlier time, metallic string is applied in the new experimental instruments.The standing waves can not only be observed on the string,but also the voice of string vibration can be heard.It will be convenient to study the relationship between vibration and voice,and this will help to understand the mechanics of string instruments.In this paper,we studied the standing waves on the metallic string and gave two meth-ods on the measurement of standing wavelength using the new experimental instrument.One was based on the formula of standing wave and the other was directly observing standing waves to get the wavelength.Through a lot of data processing and analysis,we compared these two methods and gave definite reference for determining and improving the experimental instrument.【期刊名称】《实验科学与技术》【年(卷),期】2016(014)001【总页数】4页(P42-45)【关键词】关;键;词;弦振动;驻波;弦线张力【作者】张宇亭;赵斌;王茂香【作者单位】南京理工大学物理实验中心,南京 210094;南京理工大学物理实验中心,南京 210094;南京理工大学物理实验中心,南京 210094【正文语种】中文【中图分类】O4-34;O321弦振动实验一直是高等学校普通物理实验中的基础实验之一,是帮助学生理解波的形成、传播和干涉的一个重要实验[1-3]。
弦振动实验

弦振动实验实验二弦振动实验在自然现象中,振动现象广泛地存在着,振动在媒质中传播就形成波,波的传播有两种形式:纵波和横波。
驻波是一种波的干涉,比如乐器中的管、弦、膜、板的共振干涉都是驻波振动。
弦振动实验则是研究振动和波的形成、传播和干涉现象的出现,以及驻波的形状,和与有关物理量的关系,并进行测量。
【一】实验目的1.了解均匀弦振动的传播规律,加深振动与波和干涉的概念。
2.观察固定均匀弦振动共振干涉形成驻波时的波形,加深对干涉的特殊形式――驻波的认识。
3.了解固定弦振动固有频率与弦线的线密ρ、弦长L和弦的张力Τ的关系,并进行测量。
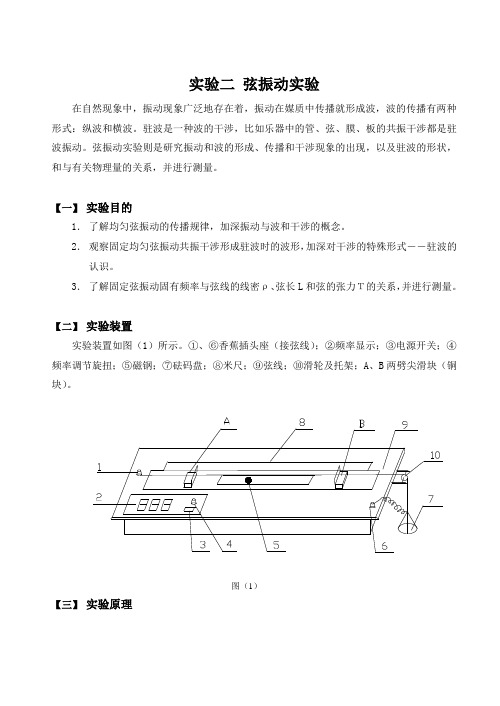
【二】实验装置实验装置如图(1)所示。
①、⑥香蕉插头座(接弦线);②频率显示;③电源开关;④频率调节旋扭;⑤磁钢;⑦砝码盘;⑧米尺;⑨弦线;⑩滑轮及托架;A、B两劈尖滑块(铜块)。
图(1)信号源。
在磁场中,通有电流的弦线就会受到磁场力(称为安培力)的作用,若细铜丝上通有正弦交变电流时,则它在磁场中所受的与电流垂直的安培力,也随着正弦变化,移动两劈尖(铜块)即改变弦长,当固定弦长是半波长倍数时,弦线上便会形成驻波。
移动磁钢的位置,使弦振动调整到最佳状态(弦振动面与磁场方向完全垂直),使弦线形成明显的驻波。
此时我们认为磁钢所在块为了研究问题的方便,认为波动是从A点发出的,沿弦线朝B端方向传播,称为入射波,再由B端反射沿弦线朝A端传播,称为反射波。
入射波与反射波在同一条弦线上沿相反方向传播时将相互波被分成几段形成波节和波腹。
驻波形成如图(2)所示。
设图中的两列波是沿X轴相向方向传播的振幅相等、频率相同振动方向一致的简谐波。
向右传播的用细实线表示,向左传播的用细虚线表示,图它们的合成驻波用粗实线表示。
由图可见,两个波腹间的距离都是等于半个波长,这可从波动方程推导出来。
下面用简谐波表达式对驻波进行定量描述。
设沿X轴正方向传播的波为入射波,沿X轴负方向传播的波为反射波,取它们振动位相始终相同的点作坐标原点“O”,且在X=0处,振动质点向上达最大位移时开始计时,则它们的波动方程分别为:Y1=Acos2 (ft-x/ )Y2=Acos[2 (ft+x/λ)+ ]式中A为简谐波的振幅,f为频率, 为波长,X 为弦线上质点的坐标位置。
大学物理《弦振动》实验报告

大学物理《弦振动》实验报告大学物理《弦振动》实验报告(报告内容:目的、仪器装置、简单原理、数据记录及结果分析等)一.实验目的1.观察弦上形成的驻波2.学习用双踪示波器观察弦振动的波形3.验证弦振动的共振频率与弦长、张力、线密度及波腹数的关系二.实验仪器XY弦音计、双踪示波器、水平尺三实验原理当弦上某一小段受到外力拨动时便向横向移动,这时弦上的张力将使这小段恢复到平衡位置,但是弦上每一小段由于都具有惯性,所以到达平衡位置时并不立即停止运动,而是继续向相反方向运动,然后由于弦的张力和惯性使这一小段又向原来的方向移动,这样循环下去,此小段便作横向振动,这振动又以一定的速度沿整条弦传播而形成横波。
理论和实验证明,波在弦上传播的速度可由下式表示:=ρ1------------------------------------------------------- ①另外一方面,波的传播速度v和波长λ及频率γ之间的关系是:v=λγ-------------------------------------------------------- ②将②代入①中得γ=λ1-------------------------------------------------------③ ρ1又有L=n*λ/2 或λ=2*L/n代入③得γn=2L------------------------------------------------------ ④ ρ1四实验内容和步骤1.研究γ和n的关系①选择5根弦中的一根并将其有黄铜定位柱的一端置于张力杠杆的槽内,另一端固定在张力杠杆水平调节旋钮的螺钉上。
②设置两个弦码间的距离为60.00cm,置驱动线圈距离一个弦码大约5.00cm的位置上,将接受线圈放在两弦码中间。
将弦音计信号发生器和驱动线圈及示波器相连接,将接受线圈和示波器相连接。
③将1kg砝码悬挂于张力杠杆第一个槽内,调节张力杠杆水平调节旋钮是张力杠杆水平(张力杠杆水平是根据悬挂物的质量精确确定,弦的张力的必要条件,如果在张力杠杆的第一个槽内挂质量为m的砝码,则弦的张力T=mg,这里g是重力加速度;若砝码挂在第二个槽,则T=2mg;若砝码挂在第三个槽,则T=3mg…….)④置示波器各个开关及旋钮于适当位置,由信号发生器的信号出发示波器,在示波器上同时显示接收器接受的'信号及驱动信号两个波形,缓慢的增加驱动频率,边听弦音计的声音边观察示波器上探测信号幅度的增大,当接近共振时信号波形振幅突然增大,达到共振时示波器现实的波形是清晰稳定的振幅最大的正弦波,这时应看到弦的震动并听到弦振动引发的声音最大,若看不到弦的振动或者听不到声音,可以稍增大驱动的振幅(调节“输出调节”按钮)或改变接受线圈的位置再试,若波形失真,可稍减少驱动信号的振幅,测定记录n=1时的共振频率,继续增大驱动信号频率,测定并记录n=2,3,4,5时的共振频率,做γn图线,导出γ和n的关系。
实验六弦振动的实验研究
实验六 弦振动的实验研究弦是指一段又细又柔软的弹性长线,比如二胡、吉它等乐器上所用的弦。
用薄片拨动或者用弓在张紧的弦上拉动就可以使整个弦的振动,再通过音箱的共鸣,就会发出悦耳的声音。
对弦乐器性能的研究与改进,离不开对弦振动的研究,对弦振动研究的意义远不只限于此,在工程技术上也有着极其重要的意义。
比如悬于两根高压电杆间的电力线、大跨度的桥梁等,在一定程度上也是一根“弦”,它们的振动所带来的后果可不象乐器上的弦的振动那样使我们们感到愉快。
对于弦振动的研究,有助于我们理解这些特殊“弦”的振动特点、机制,从而对其加以控制。
同时,弦的振动也提供了一个直观的振动与波的模型,对它的分析、研究是处理其它声与振动问题的基础。
欧拉最早提出了弦振动的二阶方程,而后达朗贝尔等人通过对弦振动的研究开创了偏微分方程论。
本实验意在通过对一段两端固定弦振动的研究,了解弦振动的特点和规律。
随着科学技术的发展,实验技术和手段都也在与时俱进,以下我们介绍两种仪器配置有所不同的研究弦振动的方法。
一、预备问题1. 什么是驻波?它是如何形成的?2. 什么是弦振动的模式?共振频率与哪些因素有关?3. 张力对波速有何影响?试比较以基频和第一谐频共振时弦中的波速。
4. 比较两种仪器配置,分析各自的特点。
二、引言一根两端固定并张紧的弦,静止时处于水平平衡位置,当在弦的垂直方向被拉离平衡位置后,弦会有回到平衡位置的趋势,在这种趋势和弦的惯性作用下,弦将在平衡位置附近振动。
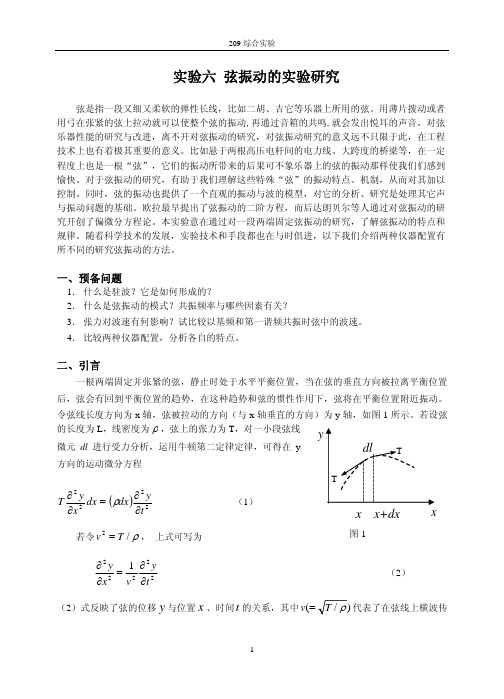
令弦线长度方向为x 轴,弦被拉动的方向(与x 轴垂直的方向)为y 轴,如图1所示。
若设弦的长度为L ,线密度为ρ,弦上的张力为T ,对一小段弦线微元dl 进行受力分析,运用牛顿第二定律定律,可得在y方向的运动微分方程y 图1 ()2222ty dx dx x y T ∂∂=∂∂ρ (1) 若令, 上式可写为 ρ/2T v =222221ty v x y ∂∂=∂∂ (2) (2)式反映了弦的位移与位置y x 、时间t 的关系,其中)/(ρT v =代表了在弦线上横波传播的波速。
弦振动的实验研究

弦振动的实验研究弦是指一段又细又柔软的弹性长线,比如二胡、吉它等乐器上所用的弦。
用薄片拨动或者用弓在张紧的弦上拉动就可以使整个弦的振动,再通过音箱的共鸣,就会发出悦耳的声音。
对弦乐器性能的研究与改进,离不开对弦振动的研究,对弦振动研究的意义远不只限于此,在工程技术上也有着极其重要的意义。
比如悬于两根高压电杆间的电力线、大跨度的桥梁等,在一定程度上也是一根“弦”,它们的振动所带来的后果可不象乐器上的弦的振动那样使我们们感到愉快。
对于弦振动的研究,有助于我们理解这些特殊“弦”的振动特点、机制,从而对其加以控制。
同时,弦的振动也提供了一个直观的振动与波的模型,对它的分析、研究是处理其它声与振动问题的基础。
欧拉最早提出了弦振动的二阶方程,而后达朗贝尔等人通过对弦振动的研究开创了偏微分方程论。
本实验意在通过对一段两端固定弦振动的研究,了解弦振动的特点和规律。
预备问题1. 复习DF4320示波器的使用。
2. 什么是驻波?它是如何形成的?3. 什么是弦振动的模式?共振频率与哪些因素有关?4. 张力对波速有何影响?试比较以基频和第一谐频共振时弦中的波速。
一、 实验目的:1、了解驻波形成的条件,观察弦振动时形成的驻波;2、学会测量弦线上横波传播速度的方法:3、用作图法验证弦振动频率与弦长、频率与张力的关系。
二、实验原理一根两端固定并张紧的弦,静止时处于水平平衡位置,当在弦的垂直方向被拉离平衡位置后,弦会有回到平衡位置的趋势,在这种趋势和弦的惯性作用下,弦将在平衡位置附近振动。
令弦线长度方向为x 轴,弦被拉动的方向(与x 轴垂直的方向)为y 轴,如图1所示。
若设弦的长度为L ,线密度为ρ,弦上的张力为T ,对一小段弦线微元dl 进行受力分析,运用牛顿第二定律定律,可得在y 方向的运动微分方程()2222tydx dx x y T ∂∂=∂∂ρ (1) 若令ρ/2T v =, 上式可写为222221tyv x y ∂∂=∂∂ (2)y 图1(2)式反映了弦的位移y 与位置x 、时间t 的关系,其中)/(ρT v =代表了在弦线上横波传播的波速。
声音的共振与波速的测量实验

声音的共振与波速的测量实验声音是我们生活中非常重要的一种波动形式,而声音的共振以及波速的测量是声学实验中常见的研究内容。
本文将介绍声音的共振现象以及一种实验方法来测量声音的波速。
一、声音的共振现象共振是指当一个物体受到外部周期性作用力时,如果作用力的频率接近物体自身的固有频率,则会引起物体振动幅度的显著增加。
在声学中,声音的共振是声波在特定空间中的放大现象。
我们可以通过以下实验来观察声音的共振现象。
首先,准备一个空的玻璃杯或者瓶子。
然后,用手指轻轻敲击玻璃杯的边缘,会发出清脆的声音。
接下来,加入适量的水,并再次敲击杯子的边缘。
当加入的水量达到一定程度时,我们会观察到声音的明显放大效果,这就是声音的共振现象。
二、测量声音的波速实验方法测量声音的波速是声学实验中的重要内容之一。
下面将介绍一种简单的实验方法来测量声音的波速。
材料:1. 扬声器2. 示波器3. 信号发生器4. 直尺5. 计时器实验步骤:1. 将扬声器固定在水平桌面上,并与示波器相连。
2. 将示波器与信号发生器相连,并调节信号发生器的频率为f。
3. 在示波器上观察到声波在扬声器中的传播情况。
4. 将直尺放置在扬声器前面的一定距离处,并用计时器测量声波从扬声器到直尺的传播时间t。
5. 重复实验多次,并记录下不同频率下的声波传播时间。
实验原理及计算:声音的波速v可以通过以下公式进行计算:v = f * λ其中,f为声波的频率,λ为声波的波长。
根据实验数据,我们可以得到不同频率下声波的传播时间t,然后根据下面的公式计算波长:λ = v * t将计算得到的波长代入公式v = f * λ,即可计算出声音的波速v。
结论:通过以上实验方法,我们可以测量出声音的波速。
声音的共振现象则展示了声音的波动特性以及与物体的相互作用,具有重要的科学意义和实际应用价值。
总结:声音的共振与波速的测量实验是声学研究中常用的实验方法之一。
通过实验可以观察到声音的共振现象以及测量声音的波速。
弦振动实验
实验二弦振动实验在自然现象中,振动现象广泛地存在着,振动在媒质中传播就形成波,波的传播有两种形式:纵波和横波。
驻波是一种波的干涉,比如乐器中的管、弦、膜、板的共振干涉都是驻波振动。
弦振动实验则是研究振动和波的形成、传播和干涉现象的出现,以及驻波的形状,和与有关物理量的关系,并进行测量。
【一】实验目的1.了解均匀弦振动的传播规律,加深振动与波和干涉的概念。
2.观察固定均匀弦振动共振干涉形成驻波时的波形,加深对干涉的特殊形式――驻波的认识。
3.了解固定弦振动固有频率与弦线的线密ρ、弦长L和弦的张力Τ的关系,并进行测量。
【二】实验装置实验装置如图(1)所示。
①、⑥香蕉插头座(接弦线);②频率显示;③电源开关;④频率调节旋扭;⑤磁钢;⑦砝码盘;⑧米尺;⑨弦线;⑩滑轮及托架;A、B两劈尖滑块(铜如图(1)实验时在①和⑥间接上弦线(细铜丝),使弦线绕过定滑轮⑩结上砝码盘并接通正弦信号源。
在磁场中,通有电流的弦线就会受到磁场力(称为安培力)的作用,若细铜丝上通有正弦交变电流时,则它在磁场中所受的与电流垂直的安培力,也随着正弦变化,移负方向传播的波为反射波,取它们振动位相始终相同的点作坐标原点“O”,且在X=0处,振动质点向上达最大位移时开始计时,则它们的波动方程分别为:Y1=Acos2π(ft-x/ λ)Y2=Acos[2π (ft+x/λ)+ π]式中A为简谐波的振幅,f为频率,λ为波长,X为弦线上质点的坐标位置。
两波叠加后的合成波为驻波,其方程为:Y1+Y2=2Acos[2π(x/ λ)+π/2]Acos2πft ……………①由此可见,入射波与反射波合成后,弦上各点都在以同一频率作简谐振动,它们的振幅为|2A cos[2π(x/ λ)+π/2] |,与时间无关t,只与质点的位置x有关。
由于波节处振幅为零,即:|cos[2π(x/ λ)+π/2] |=02π(x/ λ)+π/2=(2k+1) π / 2 ( k=0. 2. 3. … )可得波节的位置为:x=kλ /2 ……………②而相邻两波节之间的距离为:x k+1-x k =(k+1)λ/2-kλ / 2=λ / 2 ……………③又因为波腹处的质点振幅为最大,即|cos[2π(x/ λ)+π/2] | =12π(x/ λ)+π/2 =kπ( k=0. 1. 2. 3. ) 可得波腹的位置为:x=(2k-1)λ/4 ……………④这样相邻的波腹间的距离也是半个波长。
弦振动实验报告

弦振动的研究一、实验目的1、观察固定均匀弦振动共振干涉形成驻波时的波形,加深驻波的认识。
2、了解固定弦振动固有频率与弦线的线密ρ、弦长L和弦的张力Τ的关系,并进行测量。
三、波,沿X轴负方向传播的波为反射波,取它们振动位相始终相同的点作坐标原点“O”,且在X=0处,振动质点向上达最大位移时开始计时,则它们的波动方程分别为:Y1=Acos2 (ft-x/ )Y2=Acos[2 (ft+x/λ)+ ]式中A为简谐波的振幅,f为频率, 为波长,X为弦线上质点的坐标位置。
两波叠加后的合成波为驻波,其方程为:Y1+Y2=2Acos[2 (x/ )+ /2]Acos2 ft ①由此可见,入射波与反射波合成后,弦上各点都在以同一频率作简谐振动,它们的振幅为|2A cos[2 (x/ )+ /2] |,与时间无关t,只与质点的位置x有关。
由于波节处振幅为零,即:|cos[2 (x/ )+ /2] |=02 (x/ )+ /2=(2k+1) / 2 ( k=0. 2. 3. … )可得波节的位置为:x=k /2 ②而相邻两波节之间的距离为:x k+1-x k =(k+1) /2-k / 2= / 2 ③又因为波腹处的质点振幅为最大,即|cos[2 (x/ )+ /2] | =12 (x/ )+ /2 =k ( k=0. 1. 2. 3. )可得波腹的位置为:x=(2k-1) /4 ④这样相邻的波腹间的距离也是半个波长。
因此,在驻波实验中,只要测得相邻两波节或相邻两波腹间的距离,就能确定该波的波长。
在本实验中,由于固定弦的两端是由劈尖支撑的,故两端点称为波节,所以,只有当弦线的两个固定端之间的距离(弦长)等于半波长的整数倍时,才能形成驻波,这就是均匀弦振动产生驻波的条件,其数学表达式为:L=n / 2 ( n=1. 2. 3. … )由此可得沿弦线传播的横波波长为:=2L / n ⑤式中n为弦线上驻波的段数,即半波数。
弦振动实验报告

弦振动实验报告一、实验目的。
本实验旨在通过实际操作,观察和研究弦的振动规律,了解弦的振动特性,加深对波动理论的理解。
二、实验仪器与设备。
1. 弦,使用直径均匀、材质均匀的弦;2. 震动器,产生弦的振动;3. 杆状支架,固定弦;4. 张力器,调整弦的张力;5. 示波器,观察弦的振动波形。
三、实验原理。
当弦被扰动后,会产生横波。
横波是指波动的介质振动方向与波的传播方向垂直的波动。
弦的振动可以用波的传播来描述,其波速与张力、线密度和振动的频率有关。
四、实验步骤。
1. 将弦固定在杆状支架上,并调整张力,使得弦保持水平并且张力均匀;2. 使用震动器产生弦的振动,调整频率和振幅,观察弦的振动情况;3. 将示波器连接到弦上,观察并记录弦的振动波形;4. 改变振动频率和振幅,重复步骤3,记录不同振动条件下的波形。
五、实验数据与分析。
通过实验记录和观察,我们发现了一些规律性的现象。
随着振动频率的增加,弦的振动波形发生了变化,波的振幅和波长也随之改变。
当频率达到一定值时,弦产生了共振现象,振幅达到最大值。
此外,我们还发现了不同频率下的波形特点,比如频率较低时,波形较为平缓,频率较高时,波形则变得更为复杂。
六、实验结论。
通过本次实验,我们深入了解了弦的振动特性,了解了振动频率对弦振动波形的影响,加深了对波动理论的理解。
同时,我们也通过实验数据和观察,验证了波动理论中的一些规律性原理。
七、实验总结。
本次实验不仅让我们通过实际操作加深了对波动理论的理解,也锻炼了我们的观察和记录能力。
在今后的学习和科研中,我们将继续深入学习和探索波动理论,为更深层次的科学研究打下坚实的基础。
八、参考文献。
1. 《大学物理实验》。
2. 《波动理论基础》。
以上为本次实验的报告内容。
(文档结束)。
《弦振动实验报告范文》

《弦振动实验报告范文》弦振动的研究一、实验目的1、观察固定均匀弦振动共振干涉形成驻波时的波形,加深驻波的认识。
2、了解固定弦振动固有频率与弦线的线密ρ、弦长L和弦的张力Τ的关系,并进行测量。
二、实验仪器弦线,电子天平,滑轮及支架,砝码,电振音叉,米尺三、实验原理为了研究问题的方便,认为波动是从A点发出的,沿弦线朝B端方向传播,称为入射波,再由B端反射沿弦线朝A端传播,称为反射波。
入射波与反射波在同一条弦线上沿相反方向传播时将相互干涉,移动劈尖B到适合位置.弦线上的波就形成驻波。
这时,弦线上的波被分成几段形成波节和波腹。
驻波形成如图(2)所示。
设图中的两列波是沿某轴相向方向传播的振幅相等、频率相同振动方向一致的简谐波。
向右传播的用细实线表示,向左传播的用细虚线表示,它们的合成驻波用粗实线表示。
由图可见,两个波腹间的距离都是等于半个波长,这可从波动方程推导出来。
下面用简谐波表达式对驻波进行定量描述。
设沿某轴正方向传播的波为入射波,沿某轴负方向传播的波为反射波,取它们振动位相始终相同的点作坐标原点“O”,且在某=0处,振动质点向上达最大位移时开始计时,则它们的波动方程图(2)分别为:Y1=Aco2(ft-某/)Y2=Aco[2(ft+某/λ)+]式中A为简谐波的振幅,f为频率,为波长,某为弦线上质点的坐标位置。
两波叠加后的合成波为驻波,其方程为:Y1+Y2=2Aco[2(某/)+/2]Aco2ft①由此可见,入射波与反射波合成后,弦上各点都在以同一频率作简谐振动,它们的振幅为|2Aco[2(某/)+/2]|,与时间无关t,只与质点的位置某有关。
由于波节处振幅为零,即:|co[2(某/)+/2]|=02(某/)+/2=(2k+1)/2(k=0.2.3.…)可得波节的位置为:某=k/2②而相邻两波节之间的距离为:某k+1-某k=(k+1)/2-k/2=/2③又因为波腹处的质点振幅为最大,即|co[2(某/)+/2]|=12(某/)+/2=k(k=0.1.2.3.)可得波腹的位置为:某=(2k-1)/4④这样相邻的波腹间的距离也是半个波长。
大学物理《弦振动》实验报告

( 实验报告)姓名:____________________单位:____________________日期:____________________编号:YB-BH-054153大学物理《弦振动》实验报告Experimental report of string vibration in College Physics大学物理《弦振动》实验报告(报告内容:目的、仪器装置、简单原理、数据记录及结果分析等)一.实验目的1.观察弦上形成的驻波2.学习用双踪示波器观察弦振动的波形3.验证弦振动的共振频率与弦长、张力、线密度及波腹数的关系二.实验仪器XY弦音计、双踪示波器、水平尺三实验原理当弦上某一小段受到外力拨动时便向横向移动,这时弦上的张力将使这小段恢复到平衡位置,但是弦上每一小段由于都具有惯性,所以到达平衡位置时并不立即停止运动,而是继续向相反方向运动,然后由于弦的张力和惯性使这一小段又向原来的方向移动,这样循环下去,此小段便作横向振动,这振动又以一定的速度沿整条弦传播而形成横波。
理论和实验证明,波在弦上传播的速度可由下式表示:=ρ1------------------------------------------------------- ①另外一方面,波的传播速度v和波长λ及频率γ之间的关系是:v=λγ-------------------------------------------------------- ②将②代入①中得γ=λ1-------------------------------------------------------③ρ1又有L=n*λ/2 或λ=2*L/n代入③得γn=2L------------------------------------------------------ ④ρ1四实验内容和步骤1.研究γ和n的关系①选择5根弦中的一根并将其有黄铜定位柱的一端置于张力杠杆的槽内,另一端固定在张力杠杆水平调节旋钮的螺钉上。
弦振动共振波形及波的传播速度测量

弦振动共振波形及波的传播速度测量本实验研究波在弦上的传播,驻波形成的条件,及改变弦长、张力、线密度、驱动信号频率等状况下对波形的影响,并可观察共振波形与波速的测量。
301FB 型弦振动实验仪就是在传统的弦振动实验仪、弦音计的基础上改进而成的,能做标准的定性弦振动实验,即通过改变弦线的松紧、长短、粗细去观察相应的弦振动的改变及音调的改变。
还能配合示波器进行定量的实验,测量弦线上横波的传播速度与弦线的线密度等。
【实验目的】1.了解波在弦上的传播及驻波形成的条件。
2.测量不同弦长与不同张力时的共振频率。
3.测量弦线的线密度。
4.测量弦振动时波的传播速度。
【实验原理】正弦波沿着拉紧的弦传播,可用等式(1)来描述。
如果弦的一端被固定,那么当波到达)(2sin 1ft x y y m -=π (1)端点时会反射回来,这反射波可表示为: )(2sin 2t f x y y m ⋅+=λπ (2) 在保证这些波的振幅不超过弦所能承受的最大振幅时,两束波叠加后的波方程为:)(2sin )(2sin 21ft x y ft x y y y y m m ++-=+=λππ (3)利用三角公式可求得:)2cos()/2sin(2ft x y y m πλπ= (4)等式的特点:当时间固定为0t 时,弦的形状就是振幅为)2cos(20ft y m π的正弦波形。
在位置固定为0x 时,弦作简谐振动,振幅为)/2sin(20λπx y m 。
因此,当λλλ45 , 43 , 41 0=x …,振幅达到最大,当λλλ23 , , 210=x …,振幅为零。
这种波形叫驻波。
以上分析就是假定驻波就是由原波与反射波叠加而成的,实际上弦的两端都就是被固定的,在驱动线圈的激励下,弦线受到一个交变磁场力的作用,会产生振动,形成横波。
当波传到一端时都会发生反射,一般来说,不就是所有增加的反射都就是同相的,而且振幅都很小。
当均匀弦线的两个固定端之间的距离等于弦线中横波的半波长的整数倍时,反射波就会同相,产生振幅很大的驻波,弦线会形成稳定的振动。
弦振动的研究及波传播的测量实验报告

弦振动的研究及波传播的测量实验报告摘要:本实验旨在研究弦振动的基本特性以及波的传播规律。
实验采用悬挂一根弦,并通过各种方法探究弦振动的频率、波速以及波长等参数的测量和计算。
实验结果表明,弦的振动频率与弦的长度、张力以及质量有关,波的传播速度与弦的张力和质量线密度有关。
实验结果与理论计算相符,验证了弦振动和波传播的基本理论。
1. 引言弦是在物理学中常用的振动实验对象,其振动现象具有广泛的应用。
例如,音乐中的乐器弦是通过振动产生声音的,而弦仪器如吉他、小提琴等以及弦乐器大提琴等,都是基于弦的振动的原理。
此外,弦振动还与波的传播密切相关,通过实验研究弦振动及波传播的特性,有助于理解并应用相关原理。
2. 实验目的本实验的主要目的有以下几点:1) 研究弦的基本振动特性,探究弦振动频率与弦长度、张力以及质量之间的关系;2) 研究波在弦上的传播规律,测量波的传播速度和波长;3) 验证实验结果与理论计算的一致性,验证弦振动及波传播的基本理论。
3. 实验仪器和材料1) 弦仪,用于产生和控制弦的振动;2) 高斯计时器,用于测量振动的时间间隔;3) 数字示波器,用于观测和记录实验数据;4) 弦片,用于感知弦的振动。
4. 实验方法1) 悬挂弦仪:将弦仪固定在实验桌上,并拉紧弦仪保持水平状态;2) 调整弦的张力:通过调整弦仪下方的锂镁锰三元电池的张力调节旋钮,使弦的张力适中;3) 测试弦振动的频率:通过用手指弹动弦片,在实验桌上保持振动的弦片,并用高斯计时器测量两次连续振动的时间间隔,计算平均振动周期;4) 测试弦的长度:使用尺子或卷尺测量弦的长度;5) 重复步骤3和步骤4,分别改变弦的张力和长度,记录实验数据;6) 测量波的传播速度:将实验所得不同条件下的振动频率及弦长度代入波的传播速度公式进行计算;7) 计算波长:将波速与频率代入波长公式进行计算;8) 比较实验结果与理论计算结果,并进行讨论分析。
5. 实验结果与讨论通过对实验数据的记录和计算,得到了弦的振动频率、波速和波长等参数。
弦驻波观察实验报告

一、实验目的1. 观察在两端被固定的弦线上形成的驻波现象;2. 了解弦线达到共振和形成稳定驻波的条件;3. 测定弦线上横波的传播速度;4. 确定弦线作受迫振动时的共振频率与驻波波长、张力和弦线线密度之间的关系。
二、实验原理1. 横波的波速:横波沿弦线传播时,在维持弦线张力不变的情况下,横波的传播速度v与张力FT及弦线的线密度(单位长度的质量)l之间的关系为:v =√(FT/l)。
2. 驻波的形成:考虑两列振幅、频率相同,有固定相位差,传播方向相反的间谐波u1(x, t) = Acos(kx - ωt)和u2(x, t) = A cos(kx + ωt)。
其中k为波数,ω为角频率,u1与u2之间的相位差为2π,叠加后的合成运动为:u(x, t) =u1(x, t) + u2(x, t) = 2Acos(kx)cos(ωt)。
3. 驻波的特性:由上可知,时间和空间部分是分离的,某个x点振幅不随时间改变,振幅最大的点称为波腹,振幅为零的点为波节。
上述运动状态为驻波。
驻波中振动的相位取决于cos(kx/2)因子的正负,它每经过波节变号一次。
三、实验仪器1. 弦音计装置一套(包括驱动线圈和探测器线圈各一个,1Kg砝码和不同密度的吉他线,信号发生器,数字示波器,千分尺,米尺)。
四、实验步骤1. 将吉他线一端固定在支架上,另一端连接驱动线圈,驱动线圈与信号发生器相连。
2. 将探测器线圈放置在弦线上,用于检测驻波。
3. 调整信号发生器的频率,观察示波器上的波形变化。
4. 改变弦线的张力,重复步骤3,观察驻波的变化。
5. 改变弦线的线密度,重复步骤3,观察驻波的变化。
6. 记录不同条件下驻波的频率、波长、振幅等数据。
五、实验结果与分析1. 驻波的形成:通过实验观察,当驱动线圈振动时,弦线上形成了一系列驻波。
在弦线两端固定的条件下,驻波呈现出波腹和波节的分布。
2. 驻波的频率与波长的关系:根据实验数据,可以得出驻波的频率f与波长λ之间的关系为f = v/λ,其中v为弦线上横波的传播速度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
弦振动共振波形及波的传播速度测量
本实验研究波在弦上的传播,驻波形成的条件,及改变弦长、张力、线密度、驱动信号频率等状况下对波形的影响,并可观察共振波形和波速的测量。
301FB 型弦振动实验仪是在传统的弦振动实验仪、弦音计的基础上改进而成的,能做标准的定性弦振动实验,即通过改变弦线的松紧、长短、粗细去观察相应的弦振动的改变及音调的改变。
还能配合示波器进行定量的实验,测量弦线上横波的传播速度和弦线的线密度等。
【实验目的】
1.了解波在弦上的传播及驻波形成的条件。
2.测量不同弦长和不同张力时的共振频率。
3.测量弦线的线密度。
4.测量弦振动时波的传播速度。
【实验原理】
正弦波沿着拉紧的弦传播,可用等式(1)来描述。
如果弦的一端被固定,那么当波到达
)(2sin 1ft x y y m -=π (1)
端点时会反射回来,这反射波可表示为:
)(2sin 2t f x y y m ⋅+=λπ (2) 在保证这些波的振幅不超过弦所能承受的最大振幅时,两束波叠加后的波方程为:
)(2sin )(2sin 21ft x y ft x y y y y m m ++-=+=λππ (3)
利用三角公式可求得:
)2cos()/2sin(2ft x y y m πλπ= (4)
等式的特点:当时间固定为0t 时,弦的形状是振幅为)2cos(20ft y m π的正弦波形。
在位置固定为0x 时,弦作简谐振动,振幅为)/2sin(20λπx y m 。
因此,当λλλ4
5 , 4
3 , 4
1 0=x …,
振幅达到最大,当λλλ2
3 , , 210=x …,振幅为零。
这种波形叫驻波。
以上分析是假定驻波是由原波和反射波叠加而成的,实际上弦的两端都是被固定的,在
驱动线圈的激励下,弦线受到一个交变磁场力的作用,会产生振动,形成横波。
当波传到一端时都会发生反射,一般来说,不是所有增加的反射都是同相的,而且振幅都很小。
当均匀弦线的两个固定端之间的距离等于弦线中横波的半波长的整数倍时,反射波就会同相,产生振幅很大的驻波,弦线会形成稳定的振动。
当弦线的振动为一个波腹时,该驻波为基波,基波对应的的驻波频率为基频,也称共振频率。
当弦线的振动为两个波腹时,该驻波为二次谐波,对应的的驻波频率为基频的两倍。
一般情况下,基波的振动幅度比谐波的振动幅度大。
另外,从弦线上观察到的频率(即从示波器上观察到的波形)一般是驱动频率的两倍,这是因为驱动的磁场力在一个周期内两次作用于弦线的缘故。
当然,通过仔细的调节,弦线的驻波频率等于驱动频率或者其他倍数也是可能的,这时的振幅会小些。
下面就共振频率与弦长、张力、弦的线密度之间的关系进行分析。
只有当弦线的两个固定端的距离等于弦线中横波对应的半波长的整数倍时,才能形成驻波,即有: 2λ
n
L =
或 n
L
2=
λ 其中L 为弦长,λ为驻波波长,n 为波腹数
另外,根据波动理论,假设弦柔性很好,波在弦上传播速度(V )取决于两个变量:线密度(μ)和弦的拉紧度(T ),其关系式为:
μ
T V = (5)
其中μ 为弦线的线密度,即单位长度的弦线的质量(单位:m kg / ),T 为弦线的张力,单位:N ,或 2
/s m kg ⋅ 再根据λ⋅=f V 这个普遍公式可得:
μλT f V =⋅=
(6) 如果已知µ值时,即可求得频率:
L n T
f 2⋅
=
μ (7)
如果已知f ,则可求得线密度:
222
4f
L T n =μ (8)
【实验仪器】
301FB 型弦振动研究实验仪、301FB 型弦振动实验信号源各一台,双踪示波器一台。
实验仪器结构描述见图1。
1.调节螺杆 2.圆柱螺母 3.驱动传感器 4.钢丝弦线 5.接收传感器 6.支撑板
7.拉力杆 8.悬挂砝码 9.信号源 10.示波器
【实验内容】
一.实验前准备:
1.选择一条弦,将弦的带有铜圈的一端固定在拉力杆的U 型槽中,把另一端固定到调整螺杆上圆柱形螺母上端的小螺钉上。
2.把两块支撑板放在弦下相距为L 的两点上(它们决定振动弦的长度)。
3.挂上砝码(kg 50.0或kg 00.1可选)到实验所需的拉紧度的拉力杆上,然后旋动调节螺杆,使拉力杆水平(这样才能从挂的物块质量精确地确定弦的拉紧度),见图2。
如果悬挂砝码“M ”在拉力杆的挂钩槽1处,弦的拉紧度(张力)等于Mg 1,g 为重力加速度(2
80.9s m g =),如果挂在如图2挂钩槽2处,弦张力为Mg 2,……。
注意:由于砝码的位置不同,弦线的伸长量也有变化,故需重新微调拉力杆的水平。
4.按图1连接好导线。
二.实验内容:
提示:为了避免接收传感器和驱动换能器之间的电磁干扰,在实验过程中要保证两者之间的距离不小于cm 10 。
1.放置两个支承板相距cm 60 ,装上一条弦。
在拉力杠杆上挂上质量为kg 00.1的铜砝码,(仪器随带砝码:g 500一个, g 200一个, g 100二个, g 50一个, 钩码g 50一个,总质量共计kg 00.1),旋动调节螺杆,使拉力杠杆处于水平状态,把驱动线圈放在离支承板大约cm 10~5处,把接收线圈放在弦的中心位置。
把弦的张力T 和线密度μ记录下来。
2.调节信号发生器,产生正弦波,同时把示波器灵敏度调节到:格/5mV k y = 。
3.慢慢提高信号发生器频率,观察示波器接收到的波形振幅的改变。
注意:频率调节过程不能太快,因为弦线形成驻波过程需要一定的能量积累时间,太快则来不及形成驻波。
如果不能观察到波形,则可以适当增大信号源的输出幅度;如果弦线的振幅太大,造成弦线敲击传感器,则应适当减小信号源输出幅度。
一般信号源输出为p p V -3~2 (峰-峰值)时,即可观察到明显的驻波波形,同时观察弦线,可看到有明显的振幅。
当弦振动最大时,示波器接收到的波形振幅最大,弦线达到了共振,这时的驻波频率就是共振频率。
记下示波器上波形的周期,即可得到共振频率f 。
注意:一般弦的振动频率不等于信号源的驱动频率,而是2倍或整数倍的关系。
4.记录下弦线的波腹波节的位置,如果弦线只有一个波腹,这时的共振频率为基频。
且波节就是弦线的两个固定端(两个支承板处)。
5.再增加输出频率,连续找出几个共振频率(3~5个),当驻波的频率较高,弦线上形成几个波腹、波节时,弦线的振幅会较小,肉眼可能不易观察到。
这时先把接收线圈移向右边支承板,再逐步向左移动,同时观察示波器,找出并记下波腹和波节的个数及每个波腹和波节的位置。
一般这些波节应该是均匀分布的。
6.根据所得数据,算出共振波的波长(两个相邻波节的距离等于半波长)。
7.移动支承板,改变弦的长度。
根据以上步骤重复做五次。
记录下不同的弦长和共振频率。
注意,两个支承板的距离不要太小,如果弦长较小、张力较大时,需要较大的驱动信号幅度。
8.放置两个支承板相距cm 60(或自定),并保持不变。
通过改变弦的张力(也称拉紧度),弦的张力由砝码所挂的位置决定(如图2所示,这些位置的张力成1、2、3、4、5的整倍数关系)。
测量并记录下不同拉紧度下的驻波的共振频率(基频)和张力。
观察共振波的波形(幅度和频率)是否与弦的张力有关?
9.使弦处于第三档拉紧度,即物块挂于Mg 3处,放置两个支承板相距cm 60(上述条件也可自选一合适的范围)。
保持上述条件不变,换不同的弦,改变弦的线密度(共有3根线密度不同的弦线),根据步骤⑶、⑷测量一组数据。
观察共振频率是否与弦的线密度有关;共振波的波形是否与弦的线密度有关?
【数据处理】
1.不同弦长时的共振频率: 弦的线密度0μ
作弦长与共振频率的关系图。
2.不同张力时的共振频率:
这里的共振频率应为基频,如果误记为倍频的数值,则将得出错误的结论。
3.求弦线的线密度:
求得f 后,则可求得线密度: 2224f
L T
n =μ
式中L 为弦长,f 为驻波共振频率,n 为波腹数,T 为张力
4.求波的传播速度:
根据 μT V =算出波速,这一波速与λ⨯=f V (f 是共振频率,λ是波长)作比较。
作张力与波速的关系图。
【注意事项】
1.弦上观察到的频率可能不等于驱动频率,一般是驱动频率的2倍,因为驱动器的电磁铁在一周内两次作用于弦。
在理论上,使弦的静止波等于或是驱动频率的整数倍都是可能的。
2.如果驱动与接收传感器靠得太近,将会产生干扰,通过观察示波器中的接收波形可以检验干扰的存在。
当他们靠得太近时,波形会改变。
为了得到较好的测量结果,至少两传感器的距离应大于cm 10 。
3.在最初的波形中,偶然会看到高低频率的波形叠置在一起,这种复合静止波的形成是可能的。
例如,弦振动可以是驱动频率,也可以是它的两倍,因而形成复合波。
4.悬挂和更换砝码时动作应轻巧,以免使弦线崩断,造成砝码坠落而发生事故。
【思考题】
1)通过实验,说明弦线的共振频率和波速与哪些条件有关?
2)试将按公式求得μ值与静态线密度0μ值比较,分析其差异及形成原因。
3)如果弦线有弯曲或者粗细不均匀 ,对共振频率和形成驻波有何影响?。
