2016电工杯A题国家二等奖电力系统短期负荷预测
短期电力负荷预测影响因素分析与研究

短期电力负荷预测影响因素分析与研究短期电力负荷预测是电力系统运行中的关键问题,准确的负荷预测可以帮助电力系统进行有效的调度和运行,从而保障电力系统的安全稳定运行。
影响电力负荷预测的因素多种多样,包括天气、人口变化、经济活动等,本文将对这些影响因素进行分析与研究。
一、天气因素天气是影响电力负荷的重要因素之一。
气温的变化会直接影响到用电需求,一般来说,夏季高温和冬季寒冷会使得电力负荷急剧增加,而春秋季节的气温变化对电力负荷的影响也比较明显。
降雨、下雪等天气情况也会对电力负荷产生一定的影响,比如暴雨导致的停电事件、雪灾导致的电网故障等都会使得电力负荷的预测产生较大的偏差。
在短期电力负荷预测中,对天气因素进行准确的预测和分析是非常关键的。
目前,气象预测技术已经非常发达,可以通过气象资料和气象模型对未来的天气情况进行较为准确的预测,这为短期电力负荷预测提供了重要的依据。
二、人口变化人口变化也是影响电力负荷的重要因素之一。
随着城市化进程的不断加快,人口的集中分布和增长都会对电力系统的负荷产生影响。
比如在工作日的早晚高峰期,由于上下班的人流聚集,导致电力负荷急剧增加;而在节假日或者夜间,人口分布相对分散,电力负荷相对减少。
对人口变化进行准确的预测和分析是短期电力负荷预测的重要内容之一。
通过对城市化进程、人口流动情况等进行深入研究,可以掌握人口分布规律,从而更准确地预测未来的电力负荷。
三、经济活动经济活动也是影响电力负荷的重要因素之一。
一般来说,经济的发展水平越高,工业生产和商业活动越发达,电力负荷就会越大。
经济的发展状况、行业结构的变化等都会对电力负荷产生影响。
四、其他因素除了天气、人口变化、经济活动等因素外,还有一些其他因素也会对电力负荷预测产生影响,比如节假日的安排、特殊事件的发生等。
在研究电力负荷预测的影响因素时,还需要充分考虑这些因素的影响,并进行科学的分析和预测。
在总结各种影响因素的基础上,我们可以利用现代科技手段,比如大数据分析、人工智能等技术,对电力负荷进行更准确的预测。
【文献综述】电力系统短期负荷预测方法及研究

文献综述电气工程与自动化电力系统短期负荷预测方法及研究一、负荷预测的原理电力系统负荷预测是根据现在和过去时刻的用电负荷情况,估计未来时刻用电负荷的大小。
因此它的研究对象是不确定的事件,随机事件。
而电力负荷预测要预知负荷的发展趋势和可能达到的状况,下面介绍一些原理,用于指导负荷预测工作:1)可知性原理:预测对象的发展规律,其未来的发展趋势和状况是可以为人民所知道的,这是人们进行预测活动的基本依据。
2)可能性原理因事物的发展变化是在内因和外因共同作用下进行的,内因的变化和外因作用大小不同,因此事物的发展变化会有很多可能。
3)连续性原理预测对象的发展是一个连续化的过程,其未来的发展是这个过程的连续。
电力系统负荷的发展变化同样存在着惯性,这种惯性正是进行负荷预测的主要依据4)相似性原理在很多情况下,作为预测对象的一个事物,其现在的发展过程和状况可能与过去一定阶段的发展过程和状况相似,因此可根据已知的发展过程及状况来预测所预测对象的未来的发展过程及状况。
5) 系统性原理预测对象的未来发展是系统整体的动态发展,而整个系统的动态发展与它的各个组成部分和影响因素之间的相互作用相互影响密切相关。
只有系统整体最佳预测,才是最高质量的预测,才能为决策者提供最佳预测方案。
二、负荷预测的研究背景众所周知,电力系统的作用就是为各类用户提供可靠且合乎质量要求的电能,以随时满足各类负荷的需求。
而电力系统负荷预测是电力系统调度,用电,计划,规划等管理部门的主要工作之一。
提供负荷预测技术水平,有利于用电管理,有利于合理安排电网运行方式和机组检修计划,有利于节煤,节油和见地发电成本,有利于制定合理的电源建设规划,有利于提供电力系统的经济效益和社会效益。
因此,负荷预测已成为事先电力系统管理现代化的主要内容之一。
电力系统负荷预测按预测时间可以分为长期,中期,短期和超短期。
短期电力负荷预测主要是指预报未来几小时、一天至几天的电力负荷并做出估计,目的是给各个电厂安排日,周发电计划,是电力系统最为关键的一类负荷预测。
电力系统中负荷预测与管理

电力系统中负荷预测与管理在现代社会中,电力已经成为了我们生活和生产不可或缺的能源。
从家庭的照明、电器使用,到工厂的大规模生产设备运转,无一不需要稳定可靠的电力供应。
而电力系统的高效运行,离不开对负荷的准确预测和科学管理。
负荷预测,简单来说,就是对未来一段时间内电力用户的用电需求进行预估。
这可不是一件简单的事情,它需要考虑众多因素。
比如说季节的变化,夏天大家都开空调,冬天要用电取暖,这用电量自然就上去了;还有每天不同的时间段,白天工厂开工、写字楼办公,用电量比较大,晚上居民用电增多,工业用电减少。
另外,社会经济的发展状况也会对负荷产生影响,新的工厂开业、新的商业区建成,都会增加用电需求。
准确的负荷预测对于电力系统的规划和运行具有极其重要的意义。
如果预测过高,就会导致电力设施的过度建设,造成资源的浪费;而预测过低,则可能无法满足用户的需求,出现停电等问题,影响正常的生产生活。
那怎么进行负荷预测呢?目前有多种方法。
一种是基于历史数据的分析。
通过收集过去一段时间内的用电数据,找出其中的规律和趋势,然后利用数学模型来预测未来的负荷。
另一种是考虑各种影响因素,比如天气、节假日、经济形势等,建立综合的预测模型。
在实际操作中,通常会将多种方法结合起来使用,以提高预测的准确性。
比如说,先通过历史数据的分析得出一个初步的预测结果,然后再根据当前的天气情况、节假日安排等因素进行调整。
说完负荷预测,咱们再来说说负荷管理。
负荷管理的目的是在满足用户用电需求的前提下,实现电力系统的经济、安全和稳定运行。
为了实现有效的负荷管理,电力部门通常会采取一些措施。
比如实行分时电价,在用电高峰时段电价较高,低谷时段电价较低,引导用户合理安排用电时间,从而达到削峰填谷的效果,减轻电网的压力。
还有就是推广节能设备和技术,提高能源利用效率,减少不必要的电力消耗。
对于一些大型的用电企业,电力部门还会与其签订合同,约定在用电高峰时适当减少用电量,以保障整个电网的稳定运行。
电力系统负荷预测

04
年负荷预测
根据历史年负荷数据 ,对未来一年的电力 需求进行预测。
负荷预测的步骤
数据收集
收集历史负荷数据、天气数据、节假日信息等。
数据处理
对收集的数据进行清洗、整理,消除异常值和缺失值。
影响因素分析
分析天气、节假日、政策等因素对负荷的影响。
模型选择与建立
选择适合的预测模型,如时间序列分析、神经网络等,建立预测模型 。
电价政策
电价政策也会影响电力负荷,如提高电价可以抑制电力浪费,从而降低电力负 荷。
03
负荷预测的方法
Chapter
时间序列法
时间序列法需要具备连续、准确 的历史负荷数据,数据质量对预 测结果影响较大。
时间序列法简单易行,但受历史 数据影响较大,如历史数据存在 异常或缺失,将影响预测结果的 准确性。
稳定性
评估预测模型在时间序列上的表现是否稳定,通 常通过计算预测误差的方差或标准差来实现。
3
鲁棒性
评估预测模型对于异常数据或噪声数据的抵抗能 力。
模型优化方法
数据预处理
对原始数据进行清洗、去噪、填充缺失 值等处理,以提高预测模型的准确性。
超参数调优
通过调整模型的超参数(如学习率、 迭代次数、隐藏层节点数等),以提
电力系统负荷预测
汇报人: 日期:
目录
• 电力系统负荷预测概述 • 负荷预测的影响因素 • 负荷预测的方法 • 负荷预测的模型构建与优化 • 负荷预测的应用案例 • 负荷预测的未来发展趋势与挑战
01
电力系统负荷预测概述
Chapter
负荷预测的概念
01
负荷预测是指根据历史负荷数据,考虑天气、节假日、政策等因素,对未来电力 需求进行预测。
电力系统负荷预测方法及特点

电力系统负荷预测方法及特点1引言负荷预测是从已知的用电需求出发,考虑政治、经济、气候等相关因素,对未来的用电需求做出的预测。
负荷预测包括两方面的含义:对未来需求量(功率)的预测和未来用电量(能量)的预测。
电力需求量的预测决定发电、输电、配电系统新增容量的大小;电能预测决定发电设备的类型(如调峰机组、基荷机组等)。
负荷预测的目的就是提供负荷发展状况及水平,同时确定各供电区、各规划年供用电量、供用电最大负荷和规划地区总的负荷发展水平,确定各规划年用电负荷构成。
2负荷预测的方法及特点2.1单耗法按照国家安排的产品产量、产值计划和用电单耗确定需电量。
单耗法分”产品单耗法"和“产值单耗法”两种。
采用”单耗法”预测负荷前的关键是确定适当的产品单耗或产值单耗。
从我国的实际情况来看,一般规律是产品单耗逐年上升,产值单耗逐年下降。
单耗法的优点是:方法简单,对短期负荷预测效果较好。
缺点是:需做大量细致的调研工作,比较笼统,很难反映现代经济、政治、气候等条件的影响。
2.2趋势外推法当电力负荷依时间变化呈现某种上升或下降的趋势,并且无明显的季节波动,又能找到一条合适的函数曲线反映这种变化趋势时,就可以用时间t为自变量,时序数值y为因变量,建立趋势模型y=f(t)°当有理由相信这种趋势能够延伸到未来时,赋予变量t所需要的值,可以得到相应时刻的时间序列未来值。
这就是趋势外推法。
应用趋势外推法有两个假设条件:①假设负荷没有跳跃式变化;②假定负荷的发展因素也决定负荷未来的发展,其条件是不变或变化不大。
选择合适的趋势模型是应用趋势外推法的重要环节,图形识别法和差分法是选择趋势模型的两种基本方法。
外推法有线性趋势预测法、对数趋势预测法、二次曲线趋势预测法、指数曲线趋势预测法、生长曲线趋势预测法。
趋势外推法的优点是:只需要历史数据、所需的数据量较少。
缺点是:如果负荷出现变动,会引起较大的误差。
2.3弹性系数法弹性系数是电量平均增长率与国内生产总值之间的比值,根据国内生产总值的增长速度结合弹性系数得到规划期末的总用电量。
电力系统负荷预测方法研究

电力系统负荷预测方法研究随着社会的不断发展,电力已经成为了现代工业、农业、交通等各行各业中不可或缺的基础设施之一。
而负荷预测就是电力系统中至关重要的环节。
一般而言,负荷预测包括长期预测、中期预测和短期预测三个层次。
其中长期预测可以用于电力生产和输电设施的投入规划,中期预测则用于电力系统运行调度和电力市场交易,而短期预测则主要涉及电力系统实时调度和安全运行管理等方面。
本文主要就电力系统负荷预测的方法进行讨论。
一、时间序列预测方法时间序列预测方法是目前电力系统负荷预测主要手段之一。
这种方法最重要的是基于一个假设,即历史负荷记录与未来负荷变化之间存在一定的规律,可以利用这种规律进行负荷预测。
时间序列预测方法通常分为单变量预测和多变量预测两种类型。
1. 单变量预测单变量预测并不涉及负荷变化所可能影响的其他因素,而是仅基于历史负荷数据来预测未来负荷变化。
该方法适用于短期预测,可使用的预测模型包括时间序列分析、单指数平滑法、双指数平滑法和三指数平滑法四种。
时间序列分析是以时间序列为基础的建模方法,它通常分为平稳时间序列和非平稳时间序列两个类别。
对于平稳时间序列,可使用ARMA模型进行建模和预测。
而对于非平稳时间序列,常使用ARIMA模型来进行预测。
单指数平滑法、双指数平滑法和三指数平滑法是基于加权平均值的方法,通过对历史数据进行平滑处理,然后预测未来数据。
其中,单指数平滑可用于短期预测,而双指数平滑和三指数平滑则可用于中期预测。
2. 多变量预测多变量预测是一种更加复杂的预测方法,它考虑了负荷变化可能涉及的其他因素。
这些因素可以是天气、经济、节假日、工业生产等等,不同的因素之间关系非常复杂。
因此,这种方法需要使用更加复杂的模型进行建模和预测,如神经网络、支持向量机、贝叶斯网络、决策树等等。
二、模糊数学预测方法模糊数学预测方法是一种基于模糊逻辑理论的预测方法。
这种方法主要是针对具有不确定性的问题,因此对于电力系统等涉及多种因素的负荷预测而言,能够有效地发挥作用。
短期负荷预测

短期负荷预测引言短期负荷预测是电力系统运行和能源管理中非常重要的一部分。
通过对未来一段时间内的负荷进行准确的预测,可以有效地规划发电计划、购买电力和优化电网运行。
本文将介绍短期负荷预测的背景、方法和应用,并探讨电力行业中使用的一些常见的短期负荷预测技术。
背景随着经济的发展和人们对电力需求的增加,电力系统的负荷变化日益复杂。
准确地预测负荷变化对于电力系统的稳定运行和经济运营至关重要。
短期负荷预测一般指预测未来数小时、数天或数周内的负荷变化。
准确的短期负荷预测可以帮助电力系统实现以下目标:•确定电力需求,以满足各个时段的负荷需求;•优化发电计划和购买电力,以实现运营成本最小化;•预测电力需求的峰值和谷值,以优化电网运行和资源分配。
方法短期负荷预测的方法有多种,下面介绍一些常用的预测方法:统计方法统计方法是最常用的短期负荷预测方法之一。
它基于历史负荷数据进行预测,通过分析负荷的周期性和趋势来预测未来的负荷。
常见的统计方法包括:•移动平均法:根据历史负荷数据的平均值来预测未来的负荷;•季节性分解法:将负荷数据分解为长期趋势、季节性和随机成分,然后对这些分量进行预测;•线性回归法:通过拟合历史负荷数据的线性模型来预测未来的负荷。
机器学习方法机器学习方法是近年来在短期负荷预测中得到广泛应用的方法之一。
机器学习方法通过训练模型来学习输入特征与负荷之间的关系,并用学习到的模型对未来的负荷进行预测。
常见的机器学习方法包括:•支持向量机(SVM):通过构建一个高维特征空间来将样本分为不同类别,并用于负荷预测;•神经网络(NN):使用多层神经元来模拟人脑的学习和决策过程,对负荷进行预测;•随机森林(RF):将多个决策树组合起来,通过投票的方式预测负荷。
基于物理模型的方法基于物理模型的方法是基于电力系统的物理特性和运行原理进行负荷预测的方法。
这种方法需要建立电力系统的数学模型,并使用模型对未来的负荷进行预测。
常见的基于物理模型的方法包括:•方程组方法:根据负荷的物理特性,建立负荷预测模型,并使用模型对未来的负荷进行预测;•优化方法:将短期负荷预测问题转化为优化问题,并使用数学优化方法求解最优解。
2016电工杯数模大赛a题

2016电工杯数模大赛a题
2016年电工杯数学建模大赛A题是一个涉及数学建模和解决实际问题的竞赛题目。
根据我的了解,A题的具体内容可能涉及到某个具体的实际问题,可能涉及到数学模型的建立和求解,也可能需要进行数据分析和结果的解释等方面。
在这个题目中,参赛者可能需要考虑如何利用数学工具和方法对所提出的问题进行建模,可能需要运用概率统计、微积分、线性代数等数学知识,结合实际情况进行分析和求解。
此外,A题可能还需要参赛者具备一定的编程能力,能够利用计算机对模型进行仿真和求解。
在参赛者回答A题时,需要从实际问题出发,分析问题的背景和意义,明确问题的求解目标,提出合理的数学假设和模型假设,选择合适的数学方法进行建模和求解,并对结果进行合理的解释和分析。
同时,还需要考虑模型的合理性和稳定性,以及对结果的敏感性分析等方面。
总的来说,2016年电工杯数学建模大赛A题是一个综合性较强的竞赛题目,需要参赛者具备扎实的数学基础知识、良好的建模能
力和分析能力,以及较强的团队合作能力和创新思维。
希望我的回答能够对你有所帮助。
电力系统短期负荷预测方法综述

(上接 29 页)
[1]叶瑰昀,罗耀华,刘勇, 力系统短期负荷预测中的应用[J].中国电机工
等.基于 ARMA 模型的电力负荷预测方法研究 程学报,2004,24(1):24-29.
求较高,只适用于负荷变化比较均匀的短期预 丰富的经验、知识和高水平的技术,而且经验 的,尤其在环境因素和社会信息等变化较大的
测;没有考虑影响负荷变化的因素,对不确定 可以不断丰富和积累,不受时间和空间的限制 条件下,数据挖掘技术可以在错综复杂的庞大
性因素(如天气、节假日等)等考虑不足 [1]。
而广泛使用,永久保存。专家系统的不足之处 历史数中,剔除错误和无用的数据,挖掘出隐
指预报未来几小时、一天至几天的电力负荷。 据某个单一的指标进行预测,方法虽然简单, 择是短期负荷预测精度关键点,因此,根据各
短期负荷预测作用的大小主要取决于预 但比较笼统,且很难反映当今经济、政治和天 种算法的优点和不足,以及针对不同情况的预
测精度,针对目前的短期预测方法进行了综合 气等条件的影响。2.3 灰色预测法。灰色系统理 测精度的差异,将几种算法有机地结合起来,
于实际应用中难以估计出噪音的统计特性,例 忆、自主学习、知识推理和优化计算的特点,还 予的新内涵,而在实际应用中,应根据当地短
如,量测噪音和系统噪音方差等。2.2 指数平滑 有很强的计算能力、复杂映射能力、容错能力 期负荷的具体特征和各种影响因素进行灵活
法。指数平滑法采用电力系统负荷趋势外推预 及各种智能处理能力。人工神经网络预测方法 地选用预测模型。
节,高层建筑筏形基础的设计需满足冲切验算
和剪切验算等计算要求,并提出当柱荷载较大,
电力系统负荷预测方法

引言
负荷分类
预测内容
基本方法
预测评估
是什么?
所谓的电力负荷预测是指以电力负荷变化以及外界因素变化为基础,以 特定的数学方法或者建立数学模型的方式为手段,通过对电力负荷历史数据 进行分析,对电力系统的需求做出估计以及研究相关因素对电力负荷的影响
负荷预测包括两方面的含义:电力需求量的预测决定发电、输电、配电 系统新增容量的大小;电量需求量预测决定发电设备的类型如调峰机组基荷 类型等
• 变电所负荷、分区负荷及全系统负荷
引言
负荷分类
预测内容
基本方法
预测评估
电力系统负荷的分类(完)
•1.5 按时间分类(有功P)
• 年、月、周、日负荷
• 每年、每月、每周性分类 (有功P)
• 一级负荷 中断供电将造成人身伤亡,或在政治经济上有重大损失的负荷
• 二级负荷 中断供电将影响重要用电单位的正常工作或将在政治经济上有较 大损
引言
负荷分类
预测内容
基本方法
预测评估
电力负荷预测的基本方法
•回归分析法
回归分析法是研究一个变量(被解释变量)关于另一个(些)变量(解释 变量)的具体依赖关系的计算方法和理论。根据负荷过去的历史资料,建立可进行 数学分析的数学模型,回归模型有一元线性回归、多元线性回归、非线性回归等回 归预测模型对未来的负荷进行预测。
引言
负荷分类
预测内容
基本方法
预测评估
电力负荷预测的基本方法
•3 电力系统负荷预测基本方法
用电(产值)单耗法
• 将预测期的产品产量(或产值)乘以用电单耗,可得所需要的用电量。适用于已有 生产或建设计划的中近期负荷预测。 •关键问题:确定适当的产品单耗或产值单耗。 •常用:三次产业产值(或增加值)单耗法+居民生活用电。(应用时应注意各年 度产值应归算至同一年度)。 三次产业需电量预测可根据各地的工业、农业布局、结构产业情况进一步细分, 如按八大类的单耗电量预测;对于用电比重大的二产业,可再细分冶金、石油化 工建材等。 优点是:方法简单,对短期负荷预测效果较好。 缺点是:需做大量细致的调研工作,比较笼统,很难反映现代经济、政治、气候 等条件的影响。
电力系统负荷预测

电力系统负荷预测随着能源需求的不断增长,电力系统负荷预测在能源行业中扮演着至关重要的角色。
准确地预测电力系统负荷可以帮助电力公司合理调度发电设备,提高电能利用率,实现能源资源优化配置。
本文将从负荷预测的意义、方法和挑战三个方面进行论述。
一、负荷预测的意义负荷预测是指通过对历史负荷数据和相关因素的分析,利用数学模型和算法预测未来特定时间段内的负荷水平。
负荷预测对于电力系统的运行与管理至关重要。
首先,它可以帮助电力公司制定合理的发电计划和能源采购策略,以满足用户的用电需求。
其次,负荷预测还可以帮助电力公司优化发电设备的调度,减少能源浪费和排放,提高能源利用率。
因此,准确地进行负荷预测对于节约能源、降低电力成本和保护环境都具有重要意义。
二、负荷预测的方法目前,负荷预测主要通过数学模型和算法来实现。
常用的负荷预测方法包括时间序列分析、回归分析、神经网络和支持向量机等。
时间序列分析是一种基于时间数据的统计分析方法,通过分析历史负荷数据的趋势和周期性,进行负荷预测。
它的优点是简单易行,适用于稳定和具有明显规律的负荷数据。
回归分析是一种建立因变量和自变量之间关系的统计方法,通过分析历史负荷数据与相关因素之间的关系,进行负荷预测。
这些相关因素包括气象因素、经济指标、季节因素等。
回归分析方法的优点是能够考虑多个因素的影响,并进行多变量预测。
神经网络是一种模拟人脑神经元网络的计算模型,通过训练网络模型,可以实现负荷预测。
神经网络方法的优点是具有较强的非线性建模能力,适用于复杂和非线性的负荷数据。
支持向量机是一种基于统计学习理论的预测模型,通过将输入数据映射到高维特征空间来实现负荷预测。
支持向量机方法的优点是能够有效地处理高维数据和小样本数据,并对异常数据具有较强的鲁棒性。
三、负荷预测的挑战负荷预测虽然具有重要意义,但也面临一些挑战。
首先,负荷数据具有不确定性和时变性,加之外部因素的干扰,负荷预测的准确性难以保证。
其次,负荷预测模型的建立需要大量历史数据进行训练,但由于电力系统的复杂性和数据采集的困难,历史负荷数据的获取可能存在一定的难度。
电力负荷预测

一、必要性
实时控制? 运行计划??前提 发展规划??
提高精度
?增强电力系统运行的安 ??改善电力系统运行的经
全性 济性
三、精度
各个电网的负荷特性是不同的
?研究负荷变化模型
关键
? ?
选择算法
?? 使用者的水平
四、影响负荷变化因素
1. 负荷构成
2. 负荷随时间变化规律 3.气象变化的影响
4.负荷随机波动
第六章 电力负荷预测 第一节 预测的种类及程序 一、预测内容 电量预测和电力预测,其中电力预测包括峰值负荷、负荷曲线的预测 二、预测的种类 1.实时负荷预报(在线) 几分钟、1 刻钟、半小时或 1 小时,用于电力市场的实时电力调度与经 济运行,即报价平衡 2、短期预测 日、周、月、年,用于确定电力系统的运行方式 3、中期预测 预测的时间为 3~5 年,用于扩建规划,制订电力系统的长期运行方式 4、长期预测 5~20 年,用于电力系统的远景规划
(1)因子模型
S(t ) ? (B(t) ? W(t)) ?K
K:接近于 1 (2)叠加模型
S(t) ? ? L(t)
S(t) :特别条件负荷分量
? L(t) :特别条件引起的负荷变化值
四、随机负荷分量模型
1.自回归 2.动平均 3.自回归动平均 4.累积式自回归动平均模型
第三节 直观分析预测法
i?1
n
? xi yi
i ?1
?
1 n
n
(
i ?1
xi
)
n
yi )
i ?1
Sxx 、 Syy 及 Sxy 分别称为 x、y 的平方离差及叉乘离差,结合式( 6-22)可
得回归系数为
b ? Sxy S xx
电工杯A题国家二等奖电力系统短期负荷预测
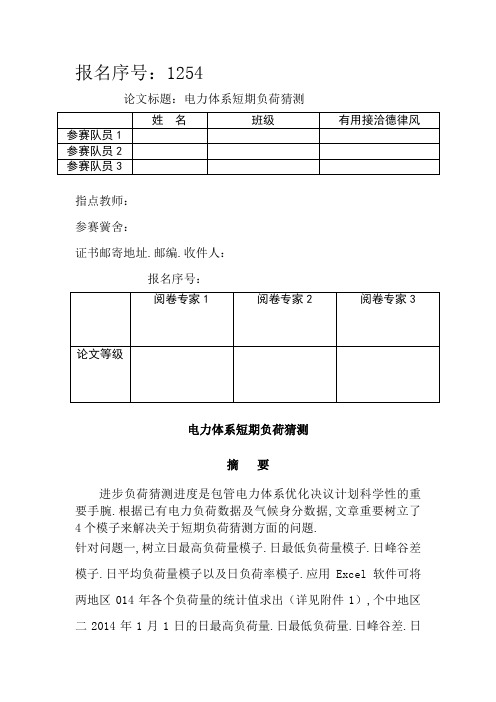
报名序号:1254论文标题:电力体系短期负荷猜测指点教师:参赛黉舍:证书邮寄地址.邮编.收件人:报名序号:电力体系短期负荷猜测摘要进步负荷猜测进度是包管电力体系优化决议计划科学性的重要手腕.根据已有电力负荷数据及气候身分数据,文章重要树立了4个模子来解决关于短期负荷猜测方面的问题.针对问题一,树立日最高负荷量模子.日最低负荷量模子.日峰谷差模子.日平均负荷量模子以及日负荷率模子.应用Excel软件可将两地区014年各个负荷量的统计值求出(详见附件1),个中地区二2014年1月1日的日最高负荷量.日最低负荷量.日峰谷差.日平均负荷量以及日负荷率分离为...和.经由过程不雅察两地2014年负荷数据变更曲线图,斟酌数据的摇动性等身分可得出地区二更精确的猜测成果的结论.针对问题二,构建多元线性回归模子,应用SPSS 软件对日最高负荷.日最低负荷.日平均负荷与各气候身分进行回归剖析.经由过程不雅察尺度化残差图(详见图4),认为没有趋向性,回归模子有用.用同样的办法可得出两地区各个因变量的回归方程(详见表5).对多元线性方程做回归误差剖析,认为将不重要的气候身分剔除可减小误差.应用慢慢回归法可进行更合理的回归剖析,得出优先推举平均温度来进步负荷猜测精度.针对问题三,构建ARIMA 猜测模子,对数据进行预处理,取每年春季的负荷量作为参照数据,清除了季候成分的影响.经由过程自相干方面的剖析,肯定模子为ARIMA (1,1,1),应用SPSS 软件可得出所需的猜测成果.例如地区一在时光点T0000的负荷量猜测模子为10.9280.999t t t x x ε-=+-.模子拟合的可决系数都在以上,解释猜测成果精度比较高.针对问题四,构建基于BP 神经收集算法的多元非线性体系模子,肯定模子为12345(,,,,)y ANN x x x x x =,应用Matlab 编程可练习出响应的神经收集构造,得出猜测成果.经由过程参照数据.模子道理这两个方面,论证了计及气候身分影响的负荷猜测成果的精度得到了改良这一结论.针对问题五,提取两地区日负荷率作为待处理数据,分离对两地区日负荷率进行正态拟合.T 散布拟合.Logistic 拟合,做出拟合曲线并对各个拟合进行拟合曲线广义似然比磨练.得出地区二的数据比地区一的数据更有纪律的结论.症结词:短期负荷猜测;多元线性回归;ARIMA 猜测模子;BP 神经收集;拟合1.问题的重述短期负荷猜测是电力体系运行与剖析的基本,对机组组合.经济调剂.安然校核等具有重要意义.进步负荷猜测精度,是包管电力体系优化决议计划科学性的重要手腕.现代电力体系中,构成电力负荷的用电器种类繁多,空调等受气候前提影响的负荷占比中断增高,气候身分(温度.湿度.降雨量等)对电力体系负荷的影响愈显凸起.斟酌气候身分成为调剂中间进一步改良负荷猜测精度的重要手腕之一.已知地区1.地区2从2009年1月1日至2015年1月10日的电力负荷数据(每15 min一个采样点,每日96点,量纲为MW)以及2012年1月1日至2015年1月17日的气候身分数据(日最高温度.日最低温度.日平均温度.日相对湿度以及日降雨量).具体请求如下:1.请剖析两个地区2014年1月1日一2014年12月31日的负荷数据,统计各地区全年的日最高负荷.日最低负荷.日峰谷差.日负荷率指标的散布情形,并绘制两地区2014年全年的负荷中断曲线;结合上述成果,剖析两地区负荷变更的重要差别;初步预判哪个地区的负荷可以获得更精确的猜测成果,解释你的来由.2.根据2012年1月1日至2014年12月31日的数据,分离对日最高负荷.日最低负荷.日平均负荷与各气候身分的关系进行回归剖析,剖析回归误差;假如要用气候身分来进步负荷猜测精度,在诸气候身分中,你优先推举哪个(或哪几个)?扼要解释来由.3.请根据已知负荷数据,构建猜测办法,对两个地区2015年1月11日至17日共7天的电力负荷进行猜测(距离15min),给出负荷猜测结;在不知道现实负荷数据的前提下,你对猜测成果的精确度有何揣摸,请解释来由.4.假如已获得2015年1月11日至17日的气候身分数据,你可否构建计及气候身分的负荷猜测办法,对两个地区2015年1月11日至17日共7天的电力负荷再次进行猜测(距离15min),给出猜测成果;与原有的猜测成果比拟,你认为计及气候身分影响的负荷猜测成果精度得到改良了吗?有何证据?请解释来由.5.分解上述盘算成果,你若何评价两地区负荷纪律性的好坏?你还有什么证据可以佐证两地区负荷整体纪律性好坏的断定?2.问题的剖析2.1 对于问题一的剖析问题一请求剖析两个地区二014年的负荷量数据的一些统计量,全年的日最高负荷.日最低负荷.日峰谷差.日负荷率指标的散布情形.可以直接树立最大量最小量模子以及一些简略算数模子来解决,应用Excel软件可以很快求出答案.标题还请求绘制出两地区二014年全年的负荷数据变更曲线,可以应用Matlab的画图对象来绘制出想要的成果.最后对所得统计量以及两地区二014年全年的负荷数据变更曲线进行剖析,可以初步预判哪个地区的负荷可以获得更精确的猜测成果.2.2 对于问题二的剖析问题二请求对日最高负荷.日最低负荷与各气候身分的关系进行回归剖析,剖析回归误差,还请求用推举哪个(或哪几个)气候身分,来进步负荷猜测精度.可应用统计学常识分离对日最高负荷.日最低负荷与各气候身分的关系进行回归剖析,并经由过程回归剖析所得的一些统计学数据来进行回归误差剖析以及选出推举的气候身分.2.3 对于问题三的剖析该问题请求根据一致负荷数据,构建猜测办法,对两个地区二015年1月11日至17日共7天的电力负荷进行猜测.此问题没有说起气候身分对负荷的影响,解释请求我们经由过程负荷数据本身进行猜测,这是个时光序列猜测问题,可树立ARIMA模子就可猜测出指定7日的负荷量.2.4 对于问题四的剖析该问题请求构建计及气候身分的负荷猜测办法,并给出猜测成果.气候身分对负荷影响是很大的,我们可以测验测验构建人工建神经收集的模子,经由过程练习收集可以比较精确地找到各气候身分与负荷之间的关系,进而猜测出指定7日的负荷量.该问题还请求将经由过程气候身分猜测出的成果与问题3的猜测成果进行比较,可以从多个方面比较猜测成果的精度.2.5 对于问题五的剖析该问题请求对两地区负荷纪律性的好坏进行评价,既然是斟酌纪律性,我们可以将两地区的负荷数据进行正态拟合.Logistic拟合以及T散布拟合,比较两个地区负荷的拟合后果,就可以得出哪个地区的纪律性更好.3.模子的假设与符号解释3.1 模子的假设(1)假设2009年1月1日至2015年1月10日的电力负荷数据均为真实有用数据;(2)神经收集练习时代,“坏数据”带来的练习误差;不会使收集不克不及收敛到幻想误差.3.2 符号解释M隐层节点数F权值输入端衔接的神经节点数X第i个地区第j天第k个时刻所测量的负荷数据ijka第i个地区第j天的日最高负荷量ijb第i个地区第j天的日最低负荷量ijc第i个地区第j天的日峰谷差ijd第i个地区第j天的日平均负荷,ije第i个地区第j天的日负荷率ijY日最高负荷.日最低负荷.日平均负荷中的一种变量ANN非线性函数X最高温度1X最低温度2X平均温度3X相对湿度4X降雨量54.模子的预备4.1 回归剖析法基起源基本理回归剖析法是根据汗青数据的变更纪律和影响负荷变更的身分,查找自变量与因变量之间的相干关系及回归方程式,肯定模子参数,据此揣摸未来时刻的负荷值.回归剖析法的长处是盘算道理和构造情势简略,猜测速度快,外推机能好,对于汗青上没有消失的情形有较好的猜测.4.2 针对问题三对原始数据进行预处理在解决问题三的进程中,应用ARIMA猜测模子,起首应用SPSS软件将地区一的原始负荷数据导入,对时光点T0000构建如下的序列图.图1 数据处理前地区一T0000时光点序列图图中有明显的季候成分,是以须要做季候分化.标题请求猜测两个地区二015年1月11日至17日共7天的电力负荷,都属于春季.是以只需提取每年的前三个月的负荷数据作为输入的数据.分化后,序列图如下.图2数据处理后地区一T0000时光点序列图从上图可知,清除了季候成分.所做的猜测将会更精准,同时盘算的庞杂程度将会下降.4.3 BP神经收集基起源基本理概述4.3.1 BP神经收集基起源基本理BP收集模子处理信息的基起源基本理是:进修进程由旌旗灯号的正向传播和误差的反向传播两个进程构成.正向传播时,输入旌旗灯号经由过程中央层感化于输出层,经由非线形变换,产生输出旌旗灯号;若输出层的现实输出与期望输出不符,则转向误差的反向传播阶段.误差的反向传播是将输出误差以某种情势经由过程中央层向输入层逐层反转,并将误差分摊给各层的所有单元,从而获得各层的误差旌旗灯号作为修改各单元权值的根据.此进程周而复始,直到输出的误差降到可以接收的程度.此时经由练习的神经收集即能对相似样本的输入信息自行处理,进而输出误差最小的经由非线形转换的信息,然后可经由过程磨练神经收集的有用性.应用BP神经收集处理现实问题时分为两个步调即收集练习和收集应用.第一步收集练习采取有监视的进修,有监视的进修是指每一个练习样本都对应一个代表情形信息的教师旌旗灯号作为期望输出,练习时盘算现实输出与期望输出之间的误差,根据误差的大小和偏向重复调剂收集衔接权值,直到误差达到预订的精度为止.4.3.2 BP神经收集的构造BP神经收集是一种多层前馈收集,其神经元衔接权值的调剂规矩采取误差反传算法即BP算法.BP神经收集又是一个多层感知器,多层次感知器强调神经收集在构造上由输入层.隐含层.输出层等多层构成,BP收集则强调层间衔接权值经由过程误差反传算法进行调剂.BP 神经收集的特色是:收集由多层次构成,包含输入层.隐含层(单层或多层)和输出层;层与层之间全衔接,同层神经元之间无衔接;传递函数必须可微,经常应用的有Sifmoid 型的对数.正切函数或线性函数;采取误差反传算法进行进修,逐层向前修改收集衔接权值.BP 神经收集构造在设计时重要包含以下方面: (1)收集层数BP 神经收集至少包含一个输入层和一个输出层,可以包含一个或多个隐含层,所以收集层数的决议问题等于隐含层层数的决议问题.理论上己经证实,单个隐层可以经由过程恰当增长神经元节点数达到随意率性的非线性映射,是以大多半情形单隐层构造的神经收集足以知足需求.在样本较多的情形下,增长一个隐层可以有用减小收集范围.(2)输入层节点数输入层节点数取决于输入向量维数,具体可根据现实问题和数据类型肯定.假如输入数据为模子旌旗灯号波形,则可根据波形的采样点数量决议输入向量维数;假如输入数据为时光序列数据,则输入节点为时光点数;假如输入为图像,则输入单元可认为图像像素或经处理的图像特点.(3)隐含层节点数隐含层节点数在很大程度上影响着BP 神经收集的机能.对此一个异常重要的定理表述为对任何一个在闭区间内的中断函数都可以用三层即单隐层BP 神经收集逼近,因而单隐层BP 收集可以完成随意率性的n 维到m 维的映射.一般而言,隐含层较多节点可使收集达到更好的机能,但可能导致较长的收敛时光.实践中,平日采取以下经验公式选 择最佳节点数:第一种:0ni mi Ck=>∑,个中k 为样本数,M 为隐层节点数.假如i M>,划定i m C =0.第二种:M a =,个中n 为输入节点数,m 为输出节点数.a 是[]0,10之间的常数.第三种:2log M n =,n 为输入节点数.(4)输出层节点数输出层节点数须要根据现实问题的抽象模子进行肯定.例如在应用神经收集解决模式分类问题中,假如共有n 个类别,则输出节点数为n 或[]2log n ,[]x 表述不小于x 的最小整数.(5)传递函数根据研讨经验,一般情形下输入层和隐层的传递函数选用S 型函数或正切S 型函数输出层选用线性函数作为传递函数,用purelin 暗示.(6)练习办法BP 神经收集采取迭代调剂的方法进行权值肯定,是以在练习之前须要肯定初始值作为迭代调剂的起点.初始值的大小会影响收集的机能,平日情形将初始值定为较小的非零随机值,经验值为()2.4 2.4,F F -或⎛ ⎝之间,个中F 为权值输入端衔接的神经节点数.5.模子的树立与求解5.1 问题一的模子树立与求解对于第一问,设ijk X 为第i 个地区第j 天第k 个时刻所测量的负荷数据,可树立日最高负荷量的数学模子: 该模子中a ij 暗示第i 个地区第j 天的日最高负荷量.同样可树立最日低负荷量的数学模子: 该模子中ij b 暗示第i 个地区第j 天的日最低负荷量.对于日峰谷差,可树立如下模子:该模子中ij c 暗示第i 个地区第j 天的日峰谷差.日负荷率为日平均负荷与日最大负荷的比值,可树立如下模子:个中ij d 为第i 个地区第j 天的日平均负荷,ij e 暗示第i 个地区第j 天的日负荷率.根据上述模子可应用Excel 软件求出部分下列成果如下(详见附件1):表12014年地区二负荷量的统计量成果日期 最高负荷最低负荷日峰谷差日平均负荷日负荷率2014010120140102 20140103 20140104 …… …… …… …… …… …… 20141228 20141229 20141230 录1),可得出如下负荷中断曲线图:图3两地2014年负荷中断曲线图经由过程结合上述成果,剖析两地区负荷变更的重要差别,初步预判地区二的负荷可获得更精确的猜测成果.原因是经由过程对附件1的统计量成果的剖析,地区二的日峰谷差更小,经由过程图1也可以明显看出负荷中断摇动更小,是以地区二可获得更精确的猜测成果.5.2 问题二的模子树立与求解 5.2.1 多元线性回归模子的树立变量Y 和变量12345,,,,X X X X X 的关系:个平分12345,,X ,X ,X X X 离代表最高温度.最低温度.平均温度.相对湿度以及降雨量,Y 代表日最高负荷.日最低负荷.日平均负荷中的一种变量.ε为均值为0的随机变量.f 的函数为线性的,即全部线性模子为:01122334455Y X X X X X ββββββε=++++++.为了得到回归参数的估量值,就要对变量进行不雅测,对变量的1096n =次自力不雅测数据为:12{(,,,,),1,,}i i i im y x x x i n =,则这些不雅测数据应知足式,即有 个中),,1,(,),(,0)(2n j i Cov E ij j i i ===σδεεε, 若记Tn T m T n b b b y y y Y ),,,(,),,,(,),,,(211021εεεεβ ===, 则多元线性回归的数学模子式(4-6)可以写成矩阵情势 个中n I Var E 2)(,0)(σεε==.为了获得参β的估量,我们采取最小二乘法,即选择β,使)()()(12ββεεεβX Y X Y Q T T ni i --===∑=(4-8)达到最小.将()βQ 对β求导数并令其为零,得即Y X X X T T =β.记X X L T =,则上述方程称为正规方程,个中X 为)1(+⨯m n 阶矩阵,一般假定1)(+=m X rank ,由线性代数理论可知,X X L T =为满秩矩阵,它的秩1)(+=m L rank ,则正规方程有独一解,记作 我们来证实上式中∧β为参数向量β的最小二乘法估量量,现用矩阵情势来论述其证实步调.对随意率性的β有)()(ββX Y X Y Q T--=则有上述证实进程中应用了如下成果: 至此,在0≠L 时,证清楚明了正规方程中的∧β是β的最小二乘法估量量. 在现实工作中,常称m m x b x b b y ∧∧∧∧+++= 110为经验线性回归方程. 5.2.2 多元线性回归模子的求解起首本文应用问题一中所给模子,求出2012年1月1日至2014年12月31日的日最高负荷.日最低负荷.日平均负荷,部分成果如下表(详见附件2):表22012年到2014年地区一统计量成果日期 最高负荷最低负荷日平均负荷20120101 20120102 20120103 20120104 20120105 20120106 20120107 20120108 20120109 20120110 …… …… …… …… 20141224 20141225 20141226 20141227 20141228 20141229 20141230最低负荷.日平均负荷与各气候身分的关系进行回归剖析.将数据导入软件后,设置回归剖析办法为进入法,分离将日最高负荷.日最低负荷.日平均负荷作为因变量,进行回归剖析.例如,对地区一日最高负荷与各气候身分的关系进行回归剖析,可得以下剖析成果:表3地区一最高负荷与各气候身分回归剖析的模子汇总般.表4地区一最高负荷与各气候身分回归剖析的系数须要不雅察以下尺度化残差图:图4地区一最高负荷与各气候身分回归剖析尺度化残差图 从图中可以看出,残差图中的散布是随机的,可以看作没有消失趋向性,所以回归模子是有用的.最终的回归模子为:123455604.14033.5130.059105.83412.906 5.856y X X X X X =-++-+.用同样的剖析进程可得两个地区各个因变量的回归剖析,成果如下表:表5各个回归方程汇总表有影响.5.2.3 多元线性回归误差的剖析本文将地区二的日平均负荷作为实例进行误差剖析.我们知道两个身分之间的相干性可作为两个身分的互相影响程度的权衡尺度,是以可以经由过程下表来得出一些结论:表6地区二的日平均负荷与各身分的相干系数表与日平均负荷的相干性为.这两个相干系数都比较低,解释相对湿度和降雨量对日平均负荷的影响很少.假如将相对湿度与降雨量强行作为自变量的话,就会加大误差.是以假如将相对湿度度与降雨量这两个身分从自变量中清除,可减小回归误差.可以对回归剖析模子的汇总进行比较.表7地区二日平均负荷与各气候身分回归剖析的模子汇总表8地区二日平均负荷与部分象身分回归剖析的模子汇总固然最高的R即可决系数在去掉落两个自变量后减小了一点为,但因为原始数据的减小,我们任然可以认为降雨量与相对湿度是造成误差加大的一个比较重要的原因.5.2.4 为进步负荷猜测精度对气候身分的选择在SPSS软件中,有多种回归办法可供选择,现将回归办法改为慢慢回归法.以地区二日最高负荷与各气候身分的回归剖析为例,成果如下:表9地区二日最高负荷与部分象身分回归剖析的模子汇总合程度最高,DW 值为,经由过程磨练,解释残差项不消失一阶自相干.表9地区二日最高负荷与部分象身分回归剖析的方差剖析表明显.表10地区二的日最高负荷与各身分的相干系数表为34670.460209.531y X =+.同理,可得出其他经由筛选后的回归方程,成果如下表:表11对气候身分筛选后各个回归方程汇总表5.3 问题三的模子树立与求解 5.3.1 ARIMA 猜测模子的树立一个时光序列平日消失长期趋向变动.季候变动.周期变动和不规矩变动身分.时光序列的目标就是一一分化和测准时光序列中各项身分的变动程度和变动纪律,然后将其从新分解起来,猜测统计指标往后分解的变更的成长情形.采取ARIMA 模子对现有的数据进行建模,重要问题是肯定模子的阶数,即响应的,q p 值,对于ARIMA 模子的辨认主如果经由过程序列的自相干函数和偏自相干函数进行的.序列t y 的自相干函数器量了t y 与t k y -之间的线性相干程度,用k β暗示,界说如下:式中:()()0cov ,;cov ,k t t k t t r y y r y y -==暗示序列的方差.自相干函数描绘的是t y 与t k y -分离与它们的中央部分121,,t t t k y y y ---+之间消失关系,假如在给定121,,t t t k y y y ---+之间的前提下,对t y 与t k y -之间的前提相干关系进行描绘,则要经由过程偏自相干函数kk ϕ进行,偏自相干函数可由下面的递推公式得到:AIC 准则既斟酌拟合模子对数据底接近程度,也斟酌模子中所含待定参数的个数.关于ARIM(,)p q ,对其界说AIC 函数如下:个中2σ是拟合ARIM(,)p q 模子时残差的方差,它是(),p q 的函数.假如模子中含有常数项,则p q +被1p q ++代替.AIC 定阶的办法就是选择ARIM(,)p q 最小的(),p q 作为响应的模子阶数.模子阶数肯定后,就可以估量模子.重要办法有三种估量办法:据估量,极大似然估量和最小二乘估量.最小二乘估量和极大似然估量的精度比较高,因而一般称为模子参数的精估量. 5.3.2 ARIMA 猜测模子的求解在数据处理的基本上,同样以地区一在时光点T0000的数据为例,做自相干剖析,成果如下:图5地区一T0000的ACF图图6地区一T0000的PACF图从图中可以看出,序列的自相干图(ACF)和偏自相干图(PACF)都是拖尾的,解释序列长短安稳的.数据序列平日不是安稳序列,但一般一阶差分都是安稳的,是以可以经由过程差分做进一步剖析.将差分设为1,绘制差分序列的序列图如下:图7地区一T0000的差分序列图由图可以知道,差分序列根本平均散布在0刻度线高低两侧,是以可以认为差分序列是安稳的.图8调剂后地区一T0000的ACF图图9调剂后地区一T0000的PACF图由图可知,差分序列的ACF和PACF都是拖尾的,是以,可对序列树立ARIMA(p,1,q)模子.经由重复实验,肯定模子为ARIMA (1,1,1),模子运行如下:依次点击“剖析”,“猜测”,“创建模子”,弹出时光序列建模器.可求出最后所需的成果,下表给出了地区一猜测模子的部分统计量(详见附件3.附件4):表12地区一猜测模子统计量从上表可看出R都在以上,可证实拟合的成果比较科学.成果中给出了各个,p q的值,如下表所示:表13地区一ARIMA猜测模子参数用同样的办法可猜测出地区二的指定七天的负荷量,部分成果如下(详见附件Q3-Area1-Load.附件Q3-Area2-Load):表13地区二ARIMA猜测成果YMD T0000 T0015 T0030 T0045 ……T2300 T2315 T2330 T2345 20150111 ……20150112 ……20150113 ……20150114 (6834)20150115 ……20150116 …………5.4 问题4的模子树立与求解5.4.1 多元非线性模子当有q 个应变量1(,,)'q y y y =时,而0110(,,,)', 1p x x x x x -=≡,的是:个中()0, (()), >0n U Var vec U I ε==⊗∑∑式中Y :n×q 是应变量的n 组随机自力抽样的不雅察值矩阵,X :n×p 是对应于Y 的自变量的已知的不雅察值矩阵,B :p×q 是未知的回归系数矩阵,U :n×q 是未知的随机误差矩阵,一般称为残差阵.与一元的线性模子一样,多元方差剖析及多元协方差剖析. 一般,在线性模子中多假设有下散布: 与上假设等价的是5.4.2 基于BP 神经收集算法的多元非线性体系模子的树立 在科学研讨和临盆实践中,对具有表示体系特点或运行状况的离散数据进行建模,用于体系猜测.评价等,是科学决议计划和决议计划体系树立的重要基本.因为大多半研讨对象广泛具有多变量且依从高度非线性关系等特点,是以多元非线性体系建模极其重要.人工神经收集是由大量简略的处理单元(神经元)广泛地互相衔接形成的庞杂非线性体系.它不须要任何先验公式,可直接从练习样本(离散数据)中主动归纳规矩,提取离散数据之问庞杂的依从关系(可所以高度非线性关系),储存于收集权重之中,从而树立研讨问题的神经收集模子.个中由Rumelhart 提出的多层前馈神经收集,因为采取误差反传的进修算法,被称为BP 收集,其应用异常广泛.在理论上已经证实具有三层构造(一个隐含层)的BP 收集可以或许逼近仟何有理函数.标题中给出了5个自变量.1个因变量.有三层BP 神经收集模子逼近消失于样本数据间的函数关系,其模子为12345(x ,x ,x ,x ,x )y ANN =,这是一个非线性函数.此模子为隐含表达式,即不克不及用平日数学公式暗示,故称为“常识库”.5.4.3 基于BP 神经收集算法的多元非线性体系模子的求解 根据这个多元非线性体系模子,应用Matlab 编程可练习出响应的神经收集构造.起首照样斟酌负荷的季候性很明显,为清除季。
电力负荷预测

中国农业大学毕业设计(论文)电力负荷的预测学院(系):专业班级:学生姓名:指导教师:学位论文原创性声明本人郑重声明:所呈交的论文是本人在导师的指导下独立进行研究所取得的研究成果。
除了文中特别加以标注引用的内容外,本论文不包括任何其他个人或集体已经发表或撰写的成果作品。
本人完全意识到本声明的法律后果由本人承担。
作者签名:年月日学位论文版权使用授权书本学位论文作者完全了解学校有关保障、使用学位论文的规定,同意学校保留并向有关学位论文管理部门或机构送交论文的复印件和电子版,允许论文被查阅和借阅。
本人授权省级优秀学士论文评选机构将本学位论文的全部或部分内容编入有关数据进行检索,可以采用影印、缩印或扫描等复制手段保存和汇编本学位论文。
本学位论文属于1、保密囗,在年解密后适用本授权书2、不保密囗。
(请在以上相应方框内打“√”)作者签名:年月日导师签名:年月日摘要电力负荷预测是电力系统调度、用电、规划等管理部门的重要工作。
短期电力负荷预测圭要用来预报未来几小时,一天至几天的电力负荷,它是能量管理系统的重要组成部分,在现代电力系统的安全和经济运行中起着重要作用。
随着电力企业逐渐走向市场,对短期负荷预测提出了更高的精度要求。
由于电力负荷受政治、气候、以及电力负荷自身状况等多种因素的影响,因此负荷预测是一项十分复杂的工作。
本文首先分析了电力系统负荷的构成,阐述了国内外短期电力负荷预测的基本方法,并在此基础上对近一年来的负荷数据进行统计分析,重点介绍了数据预处理的方法、相似目的选取和灰色模型在短期电力负荷预测中的应用。
关键词:短期负荷预测精度系统设计AbstractElectrical load forecasting has important function in programming anddispatching department of power system.Short—term load forecasting,which major function is to forecast future power load several hours or several days 1ater,is themain part of the energy management system(EMS).Meanwhile,It is important to the security and economical operation in modem power systems.Gone with the powerPlant walking towards to the power market,load forecasting precision standard has become more and more strict.Because power load is influenced by multiple factors,such as politics,climate,self-status of the power load and so on,short-term load forecasting is a complexemployment.Firstly,this paper analyses constitutes of the electrical load,and then introduces the basic method for short—term load forecasting at home and abroad.Onthe basis of these theories,this analyses load data in nearly one year,and then make emphases On the method of processing the history load data ,the selection of the similar day and the applying of the gray model in short-term load forecasting.At last,this paper shows the designing procedure of the power short-term load forecasting system and then proved the validity of the gray model method.Key words:short-term load forecasting precision system design目录第一章绪论1.1 研究的背景和意义1.1.1 课题背景随着工农业的发展、人民生活水平的日益提高,社会对电力的需求量越来越大。
电力系统短期负荷预测的研究

目录中文摘要 (1)英文摘要 (2)1 电力系统负荷预测综述 (3)1.1 引言 (3)1.2 电力系统负荷预测的含义 (3)1.3 电力系统负荷预测的意义 (4)1.4 电力系统负荷预测的现状 (4)1.5 电力系统负荷预测的程序 (5)1.6 本文的主要工作 (6)2 电力系统短期负荷预测的研究方法 (7)2.1 经典预测方法 (7)2.2 现代负荷预测方法 (8)3 人工神经网络概述 (12)3.1 人工神经网络发展简史 (12)3.2 人工神经网络模型 (12)3.3 人工神经网络的工作原理 (13)3.4 人工神经网络的特点 (14)3.5 人工神经网络的发展趋势及研究热点 (15)3.6 神经网络BP算法 (15)4 电力系统短期负荷预测建模及MATLAB实现 (19)4.1 基于神经网络的电力系统短期负荷预测建模 (19)4.1.1 正向建模 (19)4.1.2 逆向建模 (19)4.2 电力系统短期负荷预测的MATLAB实现 (20)4.2.1电力系统短期负荷预测问题描述 (20)4.2.2 输入/输出向量设计 (21)4.2.3 短期负荷预测的BP网络设计 (23)4.2.4 网络训练 (24)4.3 结果分析 (29)结论 (32)谢辞 (33)参考文献 (34)附录Ⅰ:数据归一化MATLAB程序代码 (35)附录Ⅱ:BP算法MATLAB程序代码 (39)附录Ⅲ基于BP神经网络的不同隐层节点数的负荷预测结果 (41)电力系统短期负荷预测的研究摘要:随着我国电力事业的发展,电网管理日趋现代化和智能化。
电力系统负荷预测问题的研究越来越引起人们的注意,成为现代电力系统运行研究中的重要课题之一,是实现电力系统安全、经济、高效运行的基础。
对一个电力系统而言,提高电网运行的安全性和经济性,改善电能质量,无不依赖于精准的负荷预测。
在对大量历史负荷数据进行统计分析的基础上,根据电力负荷的特点,在考虑天气温度、日类型、实际历史负荷等因素对预测负荷影响的基础上,本文介绍了一种基于BP神经网络的短期负荷预测方法。
电力负荷预测

电力负荷预测
电力负荷预测是指对未来一段时间内的电力负荷进行预测分析,从而帮助能源供应商、电力系统运营商等做出合理的能源调度和运营决策。
电力负荷预测通常包括短期、中期和长期预测。
短期预测主要针对未来数小时至数天内的电力负荷进行预测,通常采用时间序列分析、回归分析等统计方法,结合历史负荷数据、天气数据等进行建模和预测。
中期预测主要针对未来数天至数周的电力负荷进行预测,除了考虑时间序列和回归分析外,还会考虑一些更复杂的因素,如经济发展、季节性变化等。
长期预测主要针对未来数月至数年的电力负荷进行预测,除了考虑时间序列和回归分析外,还会考虑更多的因素,如人口增长、城市发展规划等。
电力负荷预测对电力系统的运营和管理至关重要。
准确的预测可以帮助决策者合理安排发电计划和能源调度,避免供需不平衡,提高电力系统的稳定性和效率。
同时,电力负荷预测也对优化用能计划、提高能源利用效率有重要意义。
电力负荷预测的习题及答案

电力负荷预测的习题及答案电力负荷预测的习题及答案电力负荷预测是一个重要的领域,它对于电力行业的运营和规划起着至关重要的作用。
准确的负荷预测可以帮助电力公司合理安排发电计划,提高电力供应的效率和稳定性。
本文将通过一些习题来探讨电力负荷预测的相关问题,并提供相应的答案。
习题一:什么是电力负荷预测?答案:电力负荷预测是指通过对历史负荷数据和相关因素进行分析和建模,预测未来一段时间内的电力负荷水平。
这些相关因素包括季节性变化、天气状况、经济发展水平等。
电力负荷预测可以帮助电力公司合理调度发电设备,确保电力供应的平稳和可靠。
习题二:电力负荷预测的方法有哪些?答案:电力负荷预测的方法主要分为基于统计学的方法和基于机器学习的方法两大类。
基于统计学的方法包括时间序列分析、回归分析等,它们基于历史负荷数据的趋势和周期性进行预测。
而基于机器学习的方法则利用大量的历史负荷数据和其他相关因素,通过建立复杂的模型来进行预测。
习题三:时间序列分析在电力负荷预测中的应用是什么?答案:时间序列分析是一种基于历史数据的预测方法,它假设未来的负荷水平与过去的负荷水平有关。
时间序列分析通过分析历史负荷数据的趋势、季节性和周期性等特征,建立相应的模型来进行预测。
常用的时间序列分析方法包括移动平均法、指数平滑法和ARIMA模型等。
习题四:机器学习在电力负荷预测中的应用是什么?答案:机器学习是一种通过让计算机从数据中学习和发现规律,从而进行预测和决策的方法。
在电力负荷预测中,机器学习可以利用大量的历史负荷数据和其他相关因素,通过建立复杂的模型来进行预测。
常用的机器学习方法包括神经网络、支持向量机和随机森林等。
习题五:电力负荷预测中的天气因素有哪些?答案:天气因素对电力负荷预测有着重要的影响。
常见的天气因素包括温度、湿度、风速、日照时数等。
这些因素与人们的用电行为密切相关,例如在高温天气下,人们会使用空调等电器设备,导致负荷水平增加。
因此,在电力负荷预测中考虑天气因素是非常重要的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
报名序号:1254论文题目:电力系统短期负荷预测指导教师:参赛学校:证书邮寄地址、邮编、收件人:报名序号:电力系统短期负荷预测摘 要提高负荷预测进度是保障电力系统优化决策科学性的重要手段。
根据已有电力负荷数据及气象因素数据,文章主要建立了4个模型来解决关于短期负荷预测方面的问题。
针对问题一,建立日最高负荷量模型、日最低负荷量模型、日峰谷差模型、日平均负荷量模型以及日负荷率模型。
利用Excel 软件可将两地区014年各个负荷量的统计值求出(详见附件1),其中地区二2014年1月1日的日最高负荷量、日最低负荷量、日峰谷差、日平均负荷量以及日负荷率分别为6765.5、3748.48、3017.05、5138.23和0.76。
通过观察两地2014年负荷数据变化曲线图,考虑数据的波动性等因素可得出地区二更准确的预测结果的结论。
针对问题二,构建多元线性回归模型,利用SPSS 软件对日最高负荷、日最低负荷、日平均负荷与各气象因素进行回归分析。
通过观察标准化残差图(详见图4),认为没有趋势性,回归模型有效。
用同样的方法可得出两地区各个因变量的回归方程(详见表5)。
对多元线性方程做回归误差分析,认为将不重要的气象因素剔除可减小误差。
利用逐步回归法可进行更合理的回归分析,得出优先推荐平均温度来提高负荷预测精度。
针对问题三,构建ARIMA 预测模型,对数据进行预处理,取每年春季的负荷量作为参照数据,消除了季节成分的影响。
通过自相关方面的分析,确定模型为ARIMA (1,1,1),利用SPSS 软件可得出所需的预测结果。
例如地区一在时间点T0000的负荷量预测模型为10.9280.999t t t x x ε-=+-。
模型拟合的可决系数都在0.8以上,说明预测结果精度比较高。
针对问题四,构建基于BP 神经网络算法的多元非线性系统模型,确定模型为12345(,,,,)y ANN x x x x x =,利用Matlab 编程可训练出相应的神经网络结构,得出预测结果。
通过参照数据、模型原理这两个方面,论证了计及气象因素影响的负荷预测结果的精度得到了改善这一结论。
针对问题五,提取两地区日负荷率作为待处理数据,分别对两地区日负荷率进行正态拟合、T 分布拟合、Logistic 拟合,做出拟合曲线并对各个拟合进行拟合曲线广义似然比检验。
得出地区二的数据比地区一的数据更有规律的结论。
关键词:短期负荷预测;多元线性回归;ARIMA 预测模型;BP 神经网络;拟合1.问题的重述短期负荷预测是电力系统运行与分析的基础,对机组组合、经济调度、安全校核等具有重要意义。
提高负荷预测精度,是保障电力系统优化决策科学性的重要手段。
现代电力系统中,构成电力负荷的用电器种类繁多,空调等受气象条件影响的负荷占比持续增高,气象因素(温度、湿度、降雨量等)对电力系统负荷的影响愈显突出。
考虑气象因素成为调度中心进一步改进负荷预测精度的主要手段之一。
已知地区1、地区2从2009年1月1日至2015年1月10日的电力负荷数据(每15 min一个采样点,每日96点,量纲为MW)以及2012年1月1日至2015年1月17日的气象因素数据(日最高温度、日最低温度、日平均温度、日相对湿度以及日降雨量)。
具体要求如下:1.请分析两个地区2014年1月1日一2014年12月31日的负荷数据,统计各地区全年的日最高负荷、日最低负荷、日峰谷差、日负荷率指标的分布情况,并绘制两地区2014年全年的负荷持续曲线;结合上述结果,分析两地区负荷变化的主要差异;初步预判哪个地区的负荷可以获得更准确的预测结果,说明你的理由。
2.根据2012年1月1日至2014年12月31日的数据,分别对日最高负荷、日最低负荷、日平均负荷与各气象因素的关系进行回归分析,分析回归误差;如果要用气象因素来提高负荷预测精度,在诸气象因素中,你优先推荐哪个(或哪几个)?简要说明理由。
3.请根据已知负荷数据,构建预测方法,对两个地区2015年1月11日至17日共7天的电力负荷进行预测(间隔15min),给出负荷预测结;在不知道实际负荷数据的条件下,你对预测结果的准确度有何推断,请说明理由。
4.如果已获得2015年1月11日至17日的气象因素数据,你能否构建计及气象因素的负荷预测方法,对两个地区2015年1月11日至17日共7天的电力负荷再次进行预测(间隔15min),给出预测结果;与原有的预测结果相比,你认为计及气象因素影响的负荷预测结果精度得到改善了吗?有何证据?请说明理由。
5.综合上述计算结果,你如何评价两地区负荷规律性的优劣?你还有什么证据可以佐证两地区负荷整体规律性优劣的判断?2.问题的分析2.1 对于问题一的分析问题一要求分析两个地区二014年的负荷量数据的一些统计量,全年的日最高负荷、日最低负荷、日峰谷差、日负荷率指标的分布情况。
可以直接建立最大量最小量模型以及一些简单算数模型来解决,利用Excel软件可以很快求出答案。
题目还要求绘制出两地区二014年全年的负荷数据变化曲线,可以利用Matlab 的绘图工具来绘制出想要的结果。
最后对所得统计量以及两地区二014年全年的负荷数据变化曲线进行分析,可以初步预判哪个地区的负荷可以获得更准确的预测结果。
2.2 对于问题二的分析问题二要求对日最高负荷、日最低负荷与各气象因素的关系进行回归分析,分析回归误差,还要求用推荐哪个(或哪几个)气象因素,来提高负荷预测精度。
可利用统计学知识分别对日最高负荷、日最低负荷与各气象因素的关系进行回归分析,并通过回归分析所得的一些统计学数据来进行回归误差分析以及选出推荐的气象因素。
2.3 对于问题三的分析该问题要求根据一致负荷数据,构建预测方法,对两个地区二015年1月11日至17日共7天的电力负荷进行预测。
此问题没有提及气象因素对负荷的影响,说明要求我们通过负荷数据本身进行预测,这是个时间序列预测问题,可建立ARIMA模型就可预测出指定7日的负荷量。
2.4 对于问题四的分析该问题要求构建计及气象因素的负荷预测方法,并给出预测结果。
气象因素对负荷影响是很大的,我们可以尝试构建人工建神经网络的模型,通过训练网络可以比较准确地找到各气象因素与负荷之间的关系,进而预测出指定7日的负荷量。
该问题还要求将通过气象因素预测出的结果与问题3的预测结果进行比较,可以从多个方面比较预测结果的精度。
2.5 对于问题五的分析该问题要求对两地区负荷规律性的优劣进行评价,既然是考虑规律性,我们可以将两地区的负荷数据进行正态拟合、Logistic拟合以及T分布拟合,比较两个地区负荷的拟合效果,就可以得出哪个地区的规律性更好。
3.模型的假设与符号说明3.1 模型的假设(1)假设2009年1月1日至2015年1月10日的电力负荷数据均为真实有效数据;(2)神经网络训练期间,“坏数据”带来的训练误差;不会使网络不能收敛到理想误差。
3.2 符号说明M隐层节点数F权值输入端连接的神经节点数X第i个地区第j天第k个时刻所测量的负荷数据ijka第i个地区第j天的日最高负荷量ijb第i个地区第j天的日最低负荷量ijc第i个地区第j天的日峰谷差ijd第i个地区第j天的日平均负荷,ije第i个地区第j天的日负荷率ijY日最高负荷、日最低负荷、日平均负荷中的一种变量ANN非线性函数X最高温度1X最低温度2X平均温度3X相对湿度4X降雨量54.模型的准备4.1 回归分析法基本原理回归分析法是根据历史数据的变化规律和影响负荷变化的因素,寻找自变量与因变量之间的相关关系及回归方程式,确定模型参数,据此推断将来时刻的负荷值。
回归分析法的优点是计算原理和结构形式简单,预测速度快,外推性能好,对于历史上没有出现的情况有较好的预测。
4.2 针对问题三对原始数据进行预处理在解决问题三的过程中,利用ARIMA预测模型,首先运用SPSS软件将地区一的原始负荷数据导入,对时间点T0000构建如下的序列图。
图1 数据处理前地区一T0000时间点序列图图中有明显的季节成分,因此需要做季节分解。
题目要求预测两个地区二015年1月11日至17日共7天的电力负荷,都属于春季。
因此只需提取每年的前三个月的负荷数据作为输入的数据。
分解后,序列图如下。
图2 数据处理后地区一T0000时间点序列图从上图可知,排除了季节成分。
所做的预测将会更精准,同时计算的复杂程度将会降低。
4.3 BP神经网络基本原理概述4.3.1 BP神经网络基本原理BP网络模型处理信息的基本原理是:学习过程由信号的正向传播和误差的反向传播两个过程组成。
正向传播时,输入信号通过中间层作用于输出层,经过非线形变换,产生输出信号;若输出层的实际输出与期望输出不符,则转向误差的反向传播阶段。
误差的反向传播是将输出误差以某种形式通过中间层向输入层逐层反转,并将误差分摊给各层的所有单元,从而获得各层的误差信号作为修正各单元权值的依据。
此过程周而复始,直到输出的误差降到可以接受的程度。
此时经过训练的神经网络即能对类似样本的输入信息自行处理,进而输出误差最小的经过非线形转换的信息,然后可通过检验神经网络的有效性。
运用BP神经网络处理实际问题时分为两个步骤即网络训练和网络应用。
第一步网络训练采用有监督的学习,有监督的学习是指每一个训练样本都对应一个代表环境信息的教师信号作为期望输出,训练时计算实际输出与期望输出之间的误差,根据误差的大小和方向反复调整网络连接权值,直到误差达到预订的精度为止。
4.3.2 BP神经网络的结构BP神经网络是一种多层前馈网络,其神经元连接权值的调整规则采用误差反传算法即BP算法。
BP神经网络又是一个多层感知器,多层次感知器强调神经网络在结构上由输入层、隐含层、输出层等多层构成,BP网络则强调层间连接权值通过误差反传算法进行调整。
BP神经网络的特点是:网络由多层次构成,包括输入层、隐含层(单层或多层)和输出层;层与层之间全连接,同层神经元之间无连接;传递函数必须可微,常用的有Sifmoid 型的对数、正切函数或线性函数;采用误差反传算法进行学习,逐层向前修正网络连接权值。
BP 神经网络结构在设计时主要包括以下方面: (1)网络层数BP 神经网络至少包括一个输入层和一个输出层,可以包含一个或多个隐含层,所以网络层数的决定问题即是隐含层层数的决定问题。
理论上己经证明,单个隐层可以通过适当增加神经元节点数达到任意的非线性映射,因此大多数情况单隐层结构的神经网络足以满足需求。
在样本较多的情况下,增加一个隐层可以有效减小网络规模。
(2)输入层节点数输入层节点数取决于输入向量维数,具体可根据实际问题和数据类型确定。
如果输入数据为模型信号波形,则可根据波形的采样点数目决定输入向量维数;如果输入数据为时间序列数据,则输入节点为时间点数;如果输入为图像,则输入单元可以为图像像素或经处理的图像特征。
