14-matlab--计算数n的阶乘
matlab向量化编程基础精讲

matlab向量化编程基础精讲【原创实用版】目录一、MATLAB 简介及向量化编程概念二、MATLAB 向量化编程基础1.向量和矩阵操作2.逻辑语句3.符号变量处理4.函数5.微分方程6.积分7.图形处理8.GUI三、MATLAB 向量化编程实践1.求解 n 的阶乘2.编写脚本文件四、MATLAB 编程入门基础与应用1.MATLAB 安装和启动2.MATLAB 操作界面介绍3.MATLAB 数学运算知识4.MATLAB 工具箱简介5.MATLAB 帮助查询功能正文MATLAB 向量化编程基础精讲一、MATLAB 简介及向量化编程概念MATLAB 是一种广泛应用于科学计算、数据分析、可视化和算法开发的编程语言。
它基于矩阵计算,具有强大的向量化编程能力,使得用户可以简洁、高效地完成各种数学运算和工程任务。
向量化编程是一种基于向量和矩阵操作的编程范式,它利用 MATLAB 的内置函数和命令对数据进行处理,避免了传统的循环结构,从而提高了代码的执行效率和可读性。
二、MATLAB 向量化编程基础1.向量和矩阵操作MATLAB 中,向量和矩阵的操作非常简便。
例如,我们可以使用“*”运算符进行矩阵乘法,使用“^”运算符进行矩阵幂运算,使用“.”运算符进行向量点乘等。
2.逻辑语句MATLAB 中的逻辑语句主要包括 if、elseif、else 等,用于实现条件判断和分支结构。
3.符号变量处理MATLAB 允许用户使用符号变量进行计算。
符号变量可以表示数学表达式中的变量,用户可以通过赋值、求导、积分等操作进行处理。
4.函数MATLAB 中的函数可以通过函数文件或脚本文件实现。
函数文件以function 开头,end 结束,用于封装一系列相关操作。
脚本文件则可以直接在命令行窗口运行。
5.微分方程MATLAB 提供了一系列求解微分方程的函数,如 ode45、ode23 等。
用户可以根据需要选择合适的函数进行求解。
6.积分MATLAB 中的积分函数主要有 integral、quad 等。
Matlab与数学实验(第二版)(张志刚 刘丽梅 版) 习题答案

Matlab与数学实验(第二版)(张志刚刘丽梅版)习题答案(1,3,4,5章)第一章d1zxt1用format的不同格式显示2*Pi,并分析格式之间的异同。
a=2*pi ;disp('***(1) 5位定点表示2*pi:')format short , a % 5位定点表disp('***(2) 15位定点表示2*pi:')format long , a % 15位定点表disp('***(3) 5位浮点表示2*pi:')format short e , a % 5位浮点表示disp('***(4) 15位浮点表示2*pi:')format long e , a % 15位浮点表示disp('***(5) 系统选择5位定点和5位浮点中更好的表示2*pi:')format short g , a % 系统选择5位定点和5位浮点中更好的表示disp('***(6) 系统选择15位定点和15位浮点中更好的表示2*pi:')format long g , a % 系统选择15位定点和15位浮点中更好的表disp('***(7) 近似的有理数的表示2*pi:')format rat , a % 近似的有理数的表disp('***(8) 十六进制的表示:')format hex , a % 十六进制的表disp('***(9) 用圆角分(美制)定点表示2*pi:')format bank , a % 用圆角分(美制)定点表示d1zxt2利用公式求Pi的值。
sum=0 ;n=21;for i = 1:4:n % 循环条件sum= sum+(1/i) ; % 循环体enddiff=0 ;for j = 3:4:(n-2) % 循环条件diff= diff+(1/j) ; % 循环体endpai=4*(sum-diff)d1zxt3 编程计算1!+3!+...+25!的阶乘。
n的阶乘python代码

n的阶乘python代码n的阶乘Python代码一、什么是阶乘?阶乘是指从1到某个正整数n的所有整数相乘的积,通常用符号“!”表示。
例如,5的阶乘为5! = 1 x 2 x 3 x 4 x 5 = 120。
二、如何用Python计算n的阶乘?Python提供了多种方法来计算n的阶乘。
以下是其中两种常见的方法:1. 使用循环使用循环计算n的阶乘需要用到for或while语句。
具体实现方法如下:```def factorial(n):result = 1for i in range(1, n+1):result *= ireturn result```上述代码中,我们定义了一个名为factorial的函数,并传入一个参数n。
在函数内部,我们使用for循环遍历从1到n之间的所有整数,并将它们相乘得到结果。
2. 使用递归使用递归计算n的阶乘需要用到函数自身调用。
具体实现方法如下:```def factorial(n):if n == 0 or n == 1:return 1else:return n * factorial(n-1)```上述代码中,我们定义了一个名为factorial的函数,并传入一个参数n。
在函数内部,我们首先判断当n等于0或1时,直接返回结果为1;否则,我们将n乘以factorial(n-1)的结果,从而实现递归调用。
三、如何测试Python代码?为了验证我们编写的Python代码是否正确,我们需要进行测试。
以下是测试Python代码的方法:1. 使用assert语句assert语句可以用来判断一个表达式是否为真。
如果表达式为假,则抛出AssertionError异常,否则程序继续执行。
具体实现方法如下:```def test_factorial():assert factorial(0) == 1assert factorial(1) == 1assert factorial(5) == 120assert factorial(10) == 3628800```上述代码中,我们定义了一个名为test_factorial的函数,并使用assert语句来验证factorial函数的输出结果是否正确。
Matlab中的阶乘函数

Matlab中的阶乘函数factorial一、函数形式Matlab中的阶乘函数是factorial,其函数形式为factorial(N)当N为向量时,计算从1到N这N个数的乘积,即相当于prod(1:N);当N 是N维数组时,计算N中每个元素的阶乘。
注意:由于在Matlab中双精度浮点数的整数位数大约是15位,只有对不大于21的整数计算结果是精确的,对大于21的整数,factorial的计算结果只有前15位是准确的。
二、用法例子(1)计算6的阶乘。
在Matlab命令窗口(Command Window)中,输入y = factorial(6)运算结果为:720与在Matlab命令窗口(Command Window)中,输入y = prod(1:6)运算结果为:720。
与factorial(6) 的结果相同。
(2)同时计算5,6,7,10的阶乘。
在Matlab命令窗口(Command Window)中,输入命令y = factorial([5 6 7 10])运算结果为:120 720 5040 3628800,是数组中每个元素的阶乘。
(3)计算排列组合可以使用下面函数计算从n个元素中抽出m(m, n是自然数n≥m≥1)个元素进行组合的个数。
与在Matlab命令窗口(Command Window)中,输入Combination = @(n, m) prod(n:-1:n-m+1)/ factorial(m);Combination(4,2)运算结果为:6。
三、与factor函数的区别factorial函数与factor函数名称很相似但功能不同,factorial(n)计算自然数的阶乘;factor(n)是对n进行因数分解。
factorial(6) 的计算结果为720factor(6) 的计算结果为 2 3。
Matlab中常见数学函数的使用
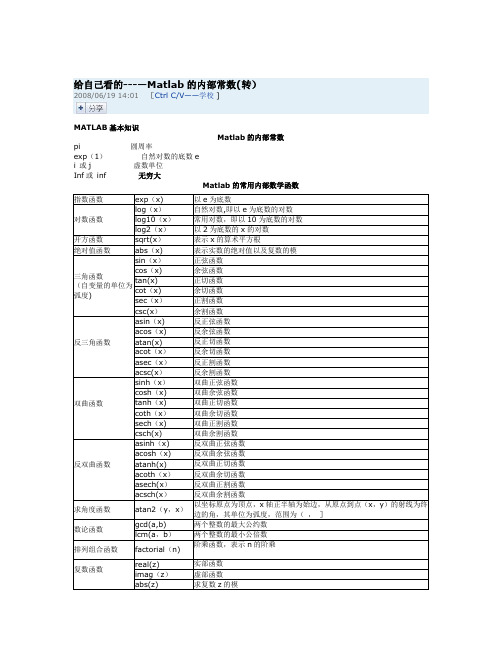
给自己看的---—Matlab的内部常数(转)2008/06/19 14:01[Ctrl C/V——学校 ]MATLAB基本知识Matlab的内部常数pi 圆周率exp(1)自然对数的底数ei 或j 虚数单位Inf或inf 无穷大Matlab的常用内部数学函数我们也可在matlab中调用maple的命令进行多项式的运算,调用格式如下:maple(’maple中多项式的运算命令')如何用matlab进行分式运算发现matlab只有一条处理分式问题的命令,其使用格式如下:[n,d]=numden(f)把符号表达式f化简为有理形式,其中分子和分母的系数为整数且分子分母不含公约项,返回结果n为分子,d为分母。
注意:f必须为符号表达式不过我们可以调用maple的命令,调用方法如下:maple('denom(f)’)提取分式f的分母maple(’numer(f)’)提取分式f的分子maple(’normal(f)’ )把分式f的分子与分母约分成最简形式maple(’expand(f)’)把分式f的分子展开,分母不变且被看成单项.maple(’factor(f)')把分式f的分母和分子因式分解,并进行约分。
如何用Matlab进行因式分解syms 表达式中包含的变量factor(表达式)如何用Matlab展开syms 表达式中包含的变量expand(表达式)如何用Matlab进行化简syms 表达式中包含的变量simplify(表达式)如何用Matlab合并同类项syms 表达式中包含的变量collect(表达式,指定的变量)如何用Matlab进行数学式的转换调用Maple中数学式的转换命令,调用格式如下:maple(‘Maple的数学式转换命令’)即:maple(‘convert(表达式,form)')将表达式转换成form的表示方式maple(‘convert(表达式,form, x)’)指定变量为x,将依赖于变量x的函数转换成form的表示方式(此指令仅对form为exp与sincos的转换式有用)如何用Matlab进行变量替换syms 表达式和代换式中包含的所有变量subs(表达式,要替换的变量或式子,代换式)如何用matlab进行复数运算a+b*i 或 a +b*j表示复数a+bi 或a+bjreal(z)求复数z的实部imag(z)求复数z的虚部abs(z)求复数z的模angle(z)求复数z的辐角,conj(z)求复数z的共轭复数exp(z)复数的指数函数,表示e^z如何在matlab中表示集合[a, b, c,…]表示由a,b, c,…组成的集合(注意:元素之间也可用空格隔开)unique(A) 表示集合A的最小等效集合(每个元素只出现一次)也可调用maple的命令,格式如下:maple(’{a, b,c,…}’)表示由a,b, c,…组成的集合下列命令可以生成特殊的集合:maple(‘{seq(f(i),i=n。
Matlab中实现阶乘算法的几种途径

Matlab中实现阶乘算法的几种途径作者:徐会艳胡鹏来源:《电脑知识与技术·学术交流》2008年第16期摘要:本文简要介绍了Matlab,阐述了阶乘的概念,并给出了阶乘算法在Matlab中的几种实现方案。
关键词:matlab;mex;阶乘;函数中图分类号:TP312文献标识码:A文章编号:1009-3044(2008)16-21258-02Several Ways of Achieving Factorial Algorithm in MatlabXU Hui-yan1,HU Peng2(1.Huaiyin Teachers College,Huaian 223300,China;2.Huaian college of Information Technology,Huaian 223003,China)Abstract:The paper introduced Matlab briefly,and illustrated the conception of factorial. It gave us Several Ways of Achieving factorial algorithm in Matlab.Key words:matlab;mex;factorial;function1 Matlab简介Matlab是由美国的Cleve Moler为了学生而用FORTRAN语言编写的关于EISPACK和LINPACK的接口程序,后经他和John Little,Steve Bangert等人一起用C语言进行了完善,并作了进一步开发。
Matlab早期是用来进行工程和科学计算的,但随着时代的变迁,自身的不断完善和充实,如今Matlab已发展成为众多行业不可缺少的软件之一,如数理统计、工程计算、图形图像处理、仿真与建模、生物遗传、控制系统设计与分析等领域。
但Matlab和其他高级语言相比,程序执行时以解释方式工作,不用编译,源程序读一句,翻译一句,执行一句,输入程序立即显示结果,从而导致程序执行速度降低。
matlab教程习题答案

matlab教程习题答案MATLAB教程习题答案MATLAB是一种广泛应用于科学计算和工程领域的高级编程语言和环境。
它的强大功能和灵活性使得许多人对其感兴趣,但对于初学者来说,掌握MATLAB 可能会有一些困难。
为了帮助大家更好地理解和掌握MATLAB,下面将给出一些常见的MATLAB教程习题的答案,希望能对大家有所帮助。
1. 编写一个MATLAB程序,计算1到100之间所有偶数的和。
答案:```matlabsum = 0;for i = 2:2:100sum = sum + i;enddisp(sum);```2. 编写一个MATLAB程序,生成一个10行10列的随机矩阵,并计算该矩阵的行和列的和。
答案:```matlabmatrix = rand(10, 10);row_sum = sum(matrix, 2);col_sum = sum(matrix);disp(col_sum);```3. 编写一个MATLAB程序,计算斐波那契数列的前20个数。
答案:```matlabfibonacci = zeros(1, 20);fibonacci(1) = 1;fibonacci(2) = 1;for i = 3:20fibonacci(i) = fibonacci(i-1) + fibonacci(i-2);enddisp(fibonacci);```4. 编写一个MATLAB程序,计算一个正整数的阶乘。
答案:```matlabnum = input('请输入一个正整数:');factorial = 1;for i = 1:numfactorial = factorial * i;end```5. 编写一个MATLAB程序,求解一个二次方程的根。
假设二次方程的形式为ax^2 + bx + c = 0,其中a、b、c为用户输入的系数。
答案:```matlaba = input('请输入二次方程的系数a:');b = input('请输入二次方程的系数b:');c = input('请输入二次方程的系数c:');delta = b^2 - 4*a*c;if delta < 0disp('该二次方程无实根。
matlab各种函数的用法详细介绍

1 Text函数的用法:用法 text(x,y,'string')在图形中指定的位置(x,y)上显示字符串stringtext(x,y,z,'string') 在三维图形空间中的指定位置(x,y,z)上显示字符串string2,plot([0,z1,z12],'-b','LineWidth',3)[ ]里面表示数组.3,x,y均为矩阵,plot命令就是画出x,y矩阵对应的二维平面的点形成的曲线。
y(:,1)中逗号前是行,逗号后是列,冒号表示从几到几。
所以y(:,1)表示第一列的所有元素。
如果是y(3:5,1)则表示第一列的第3到第5行对应的元素。
只要你的y矩阵有100列,那你当然可以将1改成100。
同理,x矩阵也可以这样。
4 sym的意思是symbol,就是后面括号里面是个代数式,要进行符号运算,class()判断对象是什么类型。
5 matlab控制运算精度用的是digits和vpa这两个函数xs = vpa(x,n)在n位相对精度下,给出x的数值型符号结果xsxs = vpa(x)在digits指定的精度下,给出x的数值型符号结果xsdigits用于规定运算精度,比如:digits(20);这个语句就规定了运算精度是20位有效数字。
但并不是规定了就可以使用,因为实际编程中,我们可能有些运算需要控制精度,而有些不需要控制。
vpa就用于解决这个问题,凡是用需要控制精度的,我们都对运算表达式使用vpa函数。
例如:digits(5);a=vpa(sqrt(2));这样a的值就是1.4142,而不是准确的1.4142135623730950488016887242097又如:digits(5);a=vpa(sqrt(2));b=sqrt(2);这样a的值是1.4142,b没有用vpa函数,所以b是1.4142135623730950488016887242097......6识别变量的指令:findsym(EXPR)确认表达式EXPR中所有自由符号变量findsym(EXPR,N)从表达式EXPR中确认出靠x最近的N个自由符号变量默认自由变量的顺序为:x y w z v.7 matlab中size函数的用法size:获取数组的行数和列数(1)s=size(A),当只有一个输出参数时,返回一个行向量,该行向量的第一个元素时数组的行数,第二个元素是数组的列数。
最新MATLAB入门及进阶教程

若对 MATLAB 函数用法有疑问, 可随时使用 help 来寻求线上支援 (on-line help) : help linspace 小整理:MATLAB 的查询命令 help:用来查询已知命令的用法。例如已知 inv 是用来计算反矩阵,键入 help inv 即可得知有关 inv 命令的用法。 (键入 help help 则显示 help 的用法,请试看看! ) lookfor:用来寻找未知的命令。例如要寻找计算反矩阵的命令,可键入 lookfor inverse,MATLAB 即会列出所有和关键字 inverse 相关的指令。找到所需的命令 後 ,即可用 help 进一步找出其用法。 (lookfor 事实上是对所有在搜寻路径下的 M 档案进行关键字对第一注解行的比对,详见後叙。 ) 将列向量转置(Transpose)後,即可得到行向量(Column vector) : z = x' z = 4.0000 5.2000 6.4000 7.6000 8.8000 10.0000 不论是行向量或列向量,我们均可用相同的函数找出其元素个数、最大值、最小 值等: length(z) % z 的元素个数 ans = 6 max(z) % z 的最大值 ans = 10 min(z) % z 的最小值 ans = 4 小整理:适用於向量的常用函数有: min(x): 向量 x 的元素的最小值 max(x): 向量 x 的元素的最大值 mean(x): 向量 x 的元素的平均值 median(x): 向量 x 的元素的中位数 std(x): 向量 x 的元素的标准差 diff(x): 向量 x 的相邻元素的差 sort(x): 对向量 x 的元素进行排序(Sorting) length(x): 向量 x 的元素个数 norm(x): 向量 x 的欧氏(Euclidean)长度 sum(x): 向量 x 的元素总和 prod(x): 向量 x 的元素总乘积 cumsum(x): 向量 x 的累计元素总和 cumprod(x): 向量 x 的累计元素总乘积 dot(x, y): 向量 x 和 y 的内 积 cross(x, y): 向量 x 和 y 的外积(大部份的向量函数也可适用於矩阵, 详见下述。 )
计算机编程算法求n!

算法:求n!对于“求n!”这个问题,高中学生不是很清楚,所以应该对n!的定义进行一个说明。
并理解用计算机来求解n!的一种算法,一、什么是n!在函数型计算器上有一个特殊的按钮,就是“n!”,称为“阶乘”,在数学上表示从1一直累乘到n,即n!=1*2*3*……*n,在高中数学的排列组合运算中会大量运用。
视窗系统附件中的“计算器”面板上也有阶乘的按钮“n!”。
在这个算法中,首先要得到n的值,然后必须对一些变量进行初始化,一般情况下用于乘法的变量初值必须为1。
试想,如果用于乘法的变量初值是0的话,那么根据乘法的一个规则,“任何数乘以0,则相乘的结果仍然是0”,因此,这个累乘的算法就没有意义了。
因此,在计算时,必须从1开始每次乘上一个递增的自然数,直到n为止。
其中每次乘上一个自然数的过程就是一个重复的过程,所以我们可以使用循环结构来实现。
二、n!的算法流程图下面的流程图就给出了用计算机程序实现阶乘的一种思路。
流程图中通过一个条件判断,如果条件成立就重复一次已经做过的语句,直至条件不成立。
实现上面流程图算法的循环语句可以用“Do....Loop While ”语句,也可以使用“For/Next ”循环语句,由于n 是确定的,即循环次数是已知的,所以用“for/Next ”较为方便。
对n!来说,计数变量的初值应该是1,终值必须为n ,由于n!中循环变量值每次增加1,所以步长值为1,而当步长值为1时,则步长这部分可以省略。
三、算法的程序实现为了实现这个算法,则需要用计算机程序设计语言来编制相应的程序,在程序中除了需要用到赋值语句、输入输出语句、其它计算语句外,还必须用到循环语句。
范例:我使用VB 来编写程序实现这个算法。
算法中用到了一条输入语句、一个循环语句、一个输出语句。
其中输入语句和输出语句与顺序结构的例题中的语句一致。
(1)建立窗体和输入、输出、命令按钮组件对象。
方法与前二节一样,注意将lable 组件对象的宽度设置得大些,以便能完整地显示阶乘的结果。
Matlab中常见数学函数的使用
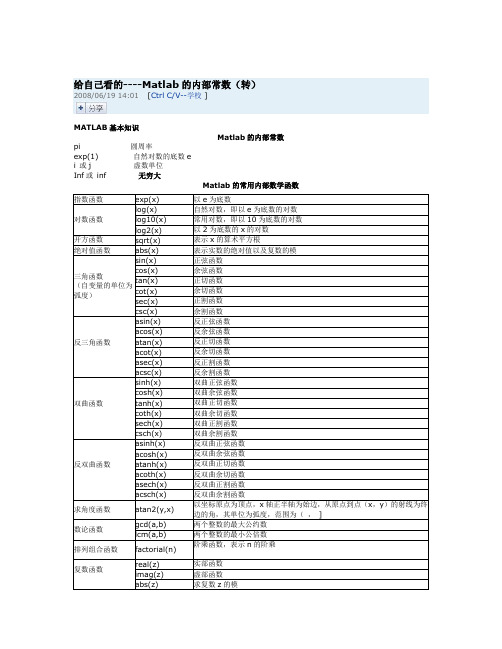
给自己看的----Matlab的内部常数(转)2008/06/19 14:01[Ctrl C/V--学校 ]MATLAB基本知识Matlab的内部常数pi 圆周率exp(1) 自然对数的底数ei 或j 虚数单位Inf或inf 无穷大Matlab的常用内部数学函数我们也可在matlab中调用maple的命令进行多项式的运算,调用格式如下:maple(’maple中多项式的运算命令’)如何用matlab进行分式运算发现matlab只有一条处理分式问题的命令,其使用格式如下:[n,d]=numden(f)把符号表达式f化简为有理形式,其中分子和分母的系数为整数且分子分母不含公约项,返回结果n为分子,d为分母。
注意:f必须为符号表达式不过我们可以调用maple的命令,调用方法如下:maple(’denom(f)’)提取分式f的分母maple(’numer(f)’)提取分式f的分子maple(’normal(f)’ ) 把分式f的分子与分母约分成最简形式maple(’expand(f)’) 把分式f的分子展开,分母不变且被看成单项。
maple(’factor(f)’) 把分式f的分母和分子因式分解,并进行约分。
如何用Matlab进行因式分解syms 表达式中包含的变量factor(表达式)如何用Matlab展开syms 表达式中包含的变量expand(表达式)如何用Matlab进行化简syms 表达式中包含的变量simplify(表达式)如何用Matlab合并同类项syms 表达式中包含的变量collect(表达式,指定的变量)如何用Matlab进行数学式的转换调用Maple中数学式的转换命令,调用格式如下:maple(‘Maple的数学式转换命令’)即:maple(‘convert(表达式,form)’)将表达式转换成form的表示方式maple(‘convert(表达式,form, x)’)指定变量为x,将依赖于变量x的函数转换成form的表示方式(此指令仅对form为exp与sincos的转换式有用)如何用Matlab进行变量替换syms 表达式和代换式中包含的所有变量subs(表达式,要替换的变量或式子,代换式)如何用matlab进行复数运算a+b*i 或 a +b*j表示复数a+bi 或a+bjreal(z)求复数z的实部imag(z)求复数z的虚部abs(z)求复数z的模angle(z)求复数z的辐角,conj(z)求复数z的共轭复数exp(z)复数的指数函数,表示e^z如何在matlab中表示集合[a, b, c,…] 表示由a, b, c,…组成的集合(注意:元素之间也可用空格隔开)unique(A) 表示集合A的最小等效集合(每个元素只出现一次)也可调用maple的命令,格式如下:maple('{a, b, c,…}')表示由a, b, c,…组成的集合下列命令可以生成特殊的集合:maple(‘{seq(f(i),i=n..m)}’)生成集合{f(n), f(n+1), f(n+2), … , f(m)}如何用Matlab求集合的交集、并集、差集和补集maple('A minus B ' ) 求差集A-Bmaple( '全集I minus A ' ) 求集合A关于全集I的补集。
matlab中符号变量的阶乘

符号变量的阶乘在Matlab中可以通过符号计算工具箱来实现。
在计算机编程中,阶乘是一个常见的数学运算,特别是在组合数学和概率论中经常用到。
符号变量的阶乘指的是将一个符号变量(通常用字母表示)的阶乘结果表示为一个符号表达式,而不是计算出一个具体的数值。
在Matlab中,可以使用符号计算工具箱来进行符号变量的阶乘运算。
1. 导入符号计算工具箱要在Matlab中进行符号计算,首先需要导入符号计算工具箱。
可以使用以下命令来导入符号计算工具箱:```matlabsyms x```这条命令会创建一个符号变量x,表示我们要进行符号计算的变量。
接下来,就可以使用这个符号变量来进行各种符号计算操作,包括阶乘运算。
2. 计算符号变量的阶乘在Matlab中,可以使用符号计算工具箱中的`factorial`函数来计算符号变量的阶乘。
如果要计算符号变量x的阶乘,可以使用以下命令:```matlabf = factorial(x)```这条命令会将计算结果保存在变量f中,f是一个表示x的阶乘的符号表达式。
需要注意的是,这里计算得到的并不是具体的数值,而是一个表示阶乘的符号表达式。
这样做的好处是可以在之后的符号计算中继续使用这个符号表达式,而不用每次都重新计算阶乘。
3. 符号变量的阶乘在符号计算中的应用符号变量的阶乘在符号计算中有着广泛的应用。
在组合数学中,阶乘是计算排列和组合的重要工具。
通过使用符号变量的阶乘,可以方便地进行排列和组合的符号计算,而不用担心数值计算的精度问题。
另外,在概率论和统计学中,阶乘也经常用到。
以二项分布为例,其概率质量函数中就包含了阶乘运算。
通过使用符号变量的阶乘,可以方便地进行二项分布的符号计算,而不用担心数值计算的误差累积。
4. 总结通过Matlab中符号计算工具箱,可以方便地进行符号变量的阶乘运算。
这对于需要进行符号计算的数学问题来说,是一个非常有用的工具。
在组合数学、概率论和统计学等领域,符号变量的阶乘都有着广泛的应用,而Matlab提供了一个便捷的符号计算环墶,使得符号变量的阶乘计算变得更加简便和高效。
递归法求n的阶乘

递归法求n的阶乘一、递归的概念递归,英文名为Recursion,指的是在函数的定义中使用函数自身的方法。
递归是一种常见的编程技术,常用于解决树形结构和分治问题。
递归包括两个部分,分别为递归基例和递归表达式。
在递归基例中,会给出一个最基本的问题,当问题比这个基例还要简单时,就不再使用递归,而是直接解决问题。
在递归表达式中,会对原问题进行拆分、递归调用函数,最终合并各个子问题的解得到答案。
二、递归求解阶乘阶乘,英文名为Factorial,是指从1到给定数n的所有数的乘积,例如5的阶乘为5! = 5×4×3×2×1 = 120。
下面利用递归的方法来求解阶乘:1、定义递归基例:当输入为1时,阶乘为1。
2、定义递归表达式:当输入为n时,先调用函数自身计算n-1的阶乘,然后乘以n,最终得到n的阶乘。
下面是求解阶乘的递归函数的Python代码:```pythondef factorial(n):if n == 1:return 1else:return n * factorial(n-1)```在这个函数中,当n等于1时,直接返回1,作为递归基例。
否则,调用函数本身计算n-1的阶乘,并将结果乘以n,得到n的阶乘。
在计算阶乘的过程中,函数会不断调用自身,直到达到递归基例,然后再一步步返回结果。
三、递归的特点递归具有以下几个特点:1、递归需要一个递归基例,即递归调用最终需要停止的条件。
2、每次递归需要进入更深层次,直到达到递归基例。
递归会在每次调用时保存一个上下文,使得每层递归调用能够完成工作。
3、递归需要有能力在返回时合并各个子问题的解,得到原问题的解。
四、递归的优缺点递归的优点是它可以简化代码,使程序易于理解。
递归同样能够解决算法中许多复杂的问题,例如树形结构和分治问题。
递归的缺点是递归需要保存大量的上下文信息,占用内存较多,而且有时递归可能会比迭代更慢。
五、总结递归是一种常见的编程技术,用于解决树形结构和分治问题等。
MATLAB实验报告_8

实验一基本操作和简单语句输入一、实验环境计算机MATLAB软件二、实验目的1.熟悉MA TLAB的命令窗口。
2、掌握MATLAB的一些基本操作, 能够进行一般的数值计算。
3.实现语句的重调和修改。
三、实验内容与步骤1.启动MA TLAB2.观察MA TLAB窗口的各个组成部分(1)了解菜单栏各窗口项的功能, 用鼠标打开MA TLAB的各个菜单, 在状态栏里显示当前鼠标所指的菜单项的含义。
(2)用鼠标指向常用工具栏的每个工具按钮, 了解各工具按钮的含义。
3.命令窗口的打开和关闭(1)查看菜单窗口中有哪些菜单命令。
(2)在命令窗口中输入命令a=3;b=4;y=a*b+a/b, 然后回车, 查看命令显示结果。
>> a=3;b=4;y=a*b+a/b,y =12.7500(3)利用MA TLAB中编辑命令时常用的按键功能, 调用上一个语句, 对它进行修改(如把分号改成逗号, 看运行结果), 并把运行结果复制到word中保存。
>> a=3,b=4,y=a*b+a/b,a =3b =4y =12.7500(4)关闭命令窗口。
(5)打开命令窗口。
4.使用MA TLAB帮助熟悉MATLAB的帮助系统, 通过帮助系统了解有关内容。
5、在命令窗口中输入demo, 将出现MA TLAB的演示窗, 通过演示窗, 对MATLAB的功能进行一次浏览。
四、练习1.计算y=x^3+(x-0.98)^2/(x+1.25)^3-5*(x+1/x), x=2, x=3时的值。
>> x=2;y=x^3+(x-0.98)^2/(x+1.25)^3-5*(x+1/x)y =-4.4697>> x=3;y=x^3+(x-0.98)^2/(x+1.25)^3-5*(x+1/x)y =10.38652.计算cos(pi/3)-sqrt(9-sqrt(2))>> cos(pi/3)-sqrt(9-sqrt(2))ans =-2.25423.已知: a=3,A=4,b=a^2,B=b^2-1,c=a+A-2*B,C=a+B+2*c, 求: C>> a=3;A=4;b=a^2;B=b^2-1;c=a+A-2*B;C=a+B+2*cC =-2234.复数z1=1+3*i,z2=1+2*i,z3=2*exp((pi/6)*i),求z=(z1*z2)/z3>> z1=1+3*i;z2=1+2*i;z3=2*exp((pi/6)*i);z=(z1*z2)/z3z =-0.9151 + 3.4151i实验二矩阵和数组的操作一、实验环境计算机MATLAB软件二、实验目的1.掌握矩阵和数组的一般操作, 包括创建、保存、修改和调用等。
pythonn的阶乘

Python的阶乘一、介绍阶乘是数学中的一个概念,指的是一个正整数及所有小于它的正整数的乘积。
在程序设计中,阶乘常常用来解决组合问题或概率问题。
Python作为一种高级编程语言,提供了多种方法来计算阶乘,本文将详细介绍Python中计算阶乘的方法和应用场景。
二、基本概念阶乘的数学符号为n!,表示从n到1的所有正整数的乘积。
例如,5的阶乘为5!= 5 * 4 * 3 * 2 * 1 = 120。
三、计算阶乘的方法1. 循环迭代法循环迭代法是计算阶乘的常见方法,通过循环将数从n乘到1,累乘的结果即为阶乘的值。
以下是使用循环迭代法计算阶乘的Python代码:def factorial_iterative(n):result = 1for i in range(1, n+1):result *= ireturn result2. 递归法递归法是另一种常见的计算阶乘的方法,它通过将问题分解为较小的子问题来解决。
以下是使用递归法计算阶乘的Python代码:def factorial_recursive(n):if n == 0:return 1else:return n * factorial_recursive(n-1)3. math库函数Python的math库中提供了一个factorial函数,可以直接计算阶乘。
以下是使用math库计算阶乘的Python代码:import mathdef factorial_math(n):return math.factorial(n)四、应用场景阶乘在实际应用中常常用来解决组合问题或概率问题。
以下是几个阶乘应用的例子:1. 组合问题组合是从一个给定的集合中选取特定数量元素的方式。
阶乘可以用来计算组合的可能性。
例如,从n个元素中选取k个元素的组合数可以通过以下公式得到:C(n, k) = n! / (k!(n-k)!)2. 概率问题阶乘也可以用来计算概率。
例如,假设一个骰子有6个面,当它投掷n次时,计算连续n次都出现相同点数的概率可以使用以下公式:P = 1 / 6^n3. 动态规划问题动态规划是解决一类有重叠子问题和最优子结构性质的问题的方法。
matlab 函数调用函数本身

MATLAB函数调用函数本身引言MATLAB(Matrix Laboratory)是一种运用于数学计算、数值分析、数据可视化以及编程的高级技术计算语言和互动环境。
其强大的功能使其成为科学、工程和金融领域常用的计算工具。
在MATLAB中,函数是一种重要的编程构件,它使得代码模块化、可重用、易读。
本文将探讨一种特殊情况,即MATLAB函数调用函数本身的概念、用法和实例。
递归函数概述递归函数是一种在定义自身的过程中调用自身的函数。
当函数调用自身时,它创建了一种递归循环,使得该函数可以反复执行某个任务,直到满足某个终止条件。
递归函数通常具有以下特点: - 一个或多个基本情况(终止条件),它们不调用函数本身。
- 一个或多个递归情况,它们调用函数本身。
MATLAB递归函数实现在MATLAB中,递归函数的实现遵循以下步骤: 1. 定义递归函数的输入参数。
2. 定义终止条件,即判断是否满足停止递归的条件。
3. 定义递归情况,即在每次递归调用中如何改变输入参数,以接近终止条件。
4. 在递归情况中,调用函数本身。
以下是一个简单的例子,展示了如何使用MATLAB实现一个计算阶乘的递归函数:function result = factorial(n)if n <= 1result = 1;elseresult = n * factorial(n-1);endend在这个例子中,factorial函数计算输入参数n的阶乘。
当n小于等于1时,函数返回1作为终止条件。
否则,函数调用自身来计算n-1的阶乘,并将结果乘以n,最终得到n的阶乘。
递归函数的应用场景递归函数在许多问题的求解中起到重要的作用。
以下是一些常见的递归函数应用场景:斐波那契数列斐波那契数列是一个经典的递归问题。
它的定义如下: - 第0项为0 - 第1项为1 - 从第2项开始,每一项都是前两项的和以下是MATLAB代码实现斐波那契数列的递归函数:function result = fibonacci(n)if n <= 0result = 0;elseif n == 1result = 1;elseresult = fibonacci(n-1) + fibonacci(n-2);endend文件/目录遍历递归函数在文件/目录遍历中也非常有用。
阶乘的相关运算公式

阶乘的相关运算公式阶乘,这个数学概念在我们的学习过程中可有着重要的地位呢!先来说说什么是阶乘。
阶乘用符号“!”表示,比如说 5 的阶乘,写作5! ,它就等于 5×4×3×2×1 。
简单来讲,就是从给定的那个数开始,依次乘以比它小 1 的数,一直乘到 1 为止。
那阶乘的运算公式都有啥呢?首先就是最基本的 n! = n×(n - 1)! 。
这个公式看起来有点绕,咱们来举个例子。
比如说算 6 的阶乘,也就是6! ,根据这个公式, 6! = 6×5! 。
而 5! 呢又等于 5×4×3×2×1 ,这样就能逐步算出 6! 的值啦。
再给大家说个有趣的事儿,我之前教过一个学生,他刚开始接触阶乘的时候,那叫一个迷糊。
有一次做作业,题目是算 4 的阶乘,他居然写成了 4×3×2 ,少乘了个 1 。
我就问他:“你咋把 1 给忘了呢?1 也是有作用的呀!”他挠挠头,不好意思地笑了。
从那以后,他就记住了阶乘的运算可不能少了最后的 1 。
还有一个重要的性质, 0! = 1 。
这可能会让一些同学感到奇怪,为啥 0 的阶乘是 1 呢?其实呀,这是为了让一些数学公式和运算能够更统一、更方便。
阶乘在数学的很多领域都有应用。
比如在排列组合中,要计算从 n 个不同元素中取出 m 个元素的排列数,就会用到阶乘。
另外,阶乘的增长速度是非常快的。
比如说 10! 就已经是 3628800 了。
随着数字越来越大,阶乘的值会变得超级大。
咱们再来说说怎么快速计算阶乘。
对于比较小的数,咱们可以直接一步一步乘。
但如果数字比较大,那可能就得借助一些数学方法或者计算机程序了。
阶乘这个概念虽然有点复杂,但只要咱们多练习、多思考,就一定能掌握它。
就像我那个迷糊的学生,后来不也搞清楚了嘛!总之,阶乘的运算公式虽然看起来有点头疼,但只要咱们耐心琢磨,多做几道题,就能轻松应对啦!希望大家都能在数学的海洋里畅游,把阶乘这个小怪兽给征服!。
