特殊角三角函数值表

三角函数特殊角值表75587

三角函数特殊值1、图示法：借助于下面三个图形来记忆，即使有所遗忘也可根据图形重新推出：sin30°=cos60°=21 sin45°=cos45°=22tan30°=cot60°=33tan 45°=cot45°=12、列表法：30˚13145˚121603说明：正弦值随角度变化，即0˚ 30˚ 45˚ 60˚ 90˚变化；值从0变化，其余类似记忆．3、规律记忆法：观察表中的数值特征，可总结为下列记忆规律：① 有界性：（锐角三角函数值都是正值）即当0°＜α＜90°时，则0＜sin α＜1； 0＜cos α＜1 ； tan α＞0 ； cot α＞0。

②增减性：（锐角的正弦、正切值随角度的增大而增大；余弦、余切值随角度的增大而减小），即当0＜A ＜B ＜90°时，则sin A ＜sin B ；tan A ＜tan B ； cos A ＞cos B ；cot A ＞cot B ；特别地：若0°＜α＜45°，则sin A ＜cos A ；tan A ＜cot A若45°＜A ＜90°，则sin A ＞cos A ；tan A ＞cot A ．4、口决记忆法：观察表中的数值特征正弦、余弦值可表示为2m 形式，正切、余切值可表示为3m 形式，有关m的值可归纳成顺口溜：一、二、三；三、二、一；三九二十七．巧记特殊角的三角函数值初学三角函数，记忆特殊角三角函数值易错易混。

若在理解掌握的基础上，经过变形，使其呈现某种规律，再配以歌诀，则可浅显易记，触目成诵。

仔细观察表1，你会发现重要的规律。

表1表1中，三角函数值的前三行，分子被开方数排列特征依次为“1，2，3，3，2，1，3，9，27”。

“一二三，三二一，三九二十七”。

记此歌诀即可。

观察表2也可发现重要的规律。

(完整版)三角函数特殊角值表

角度函数 0 30 45 60 90 120 135 150 180 270 360 角a 的弧度0 π/6 π/4 π/3 π/2 2π/3 3π/4 5π/6 π 3π/2 2π sin 0 1/2 √2/2 √3/2 1 √3/2 √2/2 1/2 0 -1 0 cos 1 √3/2 √2/2 1/2 0 -1/2 -√2/2 -√3/2 -1 0 1 tan√3/31√3-√3-1-√3/31、图示法：借助于下面三个图形来记忆，即使有所遗忘也可根据图形重新推出： sin30°=cos60°=21，sin45°=cos45°=22， tan30°=cot60°=33， tan 45°=cot45°=1正弦函数 sinθ=y/r 余弦函数 cosθ=x/r 正切函数 tanθ=y/x 余切函数 cotθ=x/y 正割函数 secθ=r/x 余割函数 cscθ=r/y2、列表法：说明：正弦值随角度变化，即0˚ 30˚ 45˚ 60˚ 90˚变化；值从02122 23 1变化，其余类似记忆．3、规律记忆法：观察表中的数值特征，可总结为下列记忆规律：① 有界性：（锐角三角函数值都是正值）即当0°＜α＜90°时，则0＜sin α＜1； 0＜cos α＜1 ； tan α＞0 ； cot α＞0。

②增减性：（锐角的正弦、正切值随角度的增大而增大；余弦、余切值随角度的增大而减小），即当0＜A ＜B ＜90°时，则sin A ＜sin B ；tan A ＜tan B ； cos A ＞cos B ；cot A ＞cot B ；特别地：若0°＜α＜45°，则sin A ＜cos A ；tan A ＜cot A 若45°＜A ＜90°，则sin A ＞cos A ；tan A ＞cot A ． 4、口决记忆法：观察表中的数值特征正弦、余弦值可表示为2m 形式，正切、余切值可表示为3m 形式，有关m 的值可归纳成顺口溜：一、二、三；三、二、一；三九二十七．30˚ 123145˚ 1212 60˚ 3函数名正弦余弦正切余切正割余割符号sin cos tan cot sec csc正弦函数sin（A）=a/c余弦函数cos（A）=b/c正切函数tan（A）=a/b余切函数cot（A）=b/a其中a为对边，b为邻边，c为斜边三角函数对照表三角函数SIN COS TAN 三角函数SIN COS TAN 0°0 1 0 90° 1 0 无1°0.0174 0.9998 0.0174 89°0.9998 0.0174 57.2899 2°0.0348 0.9993 0.0349 88°0.9993 0.0348 28.6362 3°0.0523 0.9986 0.0524 87°0.9986 0.0523 19.0811 4°0.0697 0.9975 0.0699 86°0.9975 0.0697 14.3006 5°0.0871 0.9961 0.0874 85°0.9961 0.0871 11.4300 6°0.1045 0.9945 0.1051 84°0.9945 0.1045 9.5143 7°0.1218 0.9925 0.1227 83°0.9925 0.1218 8.1443 8°0.1391 0.9902 0.1405 82°0.9902 0.1391 7.1153 9°0.1564 0.9876 0.1583 81°0.9876 0.1564 6.3137 10°0.1736 0.9848 0.1763 80°0.9848 0.1736 5.6712 11°0.1908 0.9816 0.1943 79°0.9816 0.1908 5.1445 12°0.2079 0.9781 0.2125 78°0.9781 0.2079 4.7046 13°0.2249 0.9743 0.2308 77°0.9743 0.2249 4.3314 14°0.2419 0.9702 0.2493 76°0.9702 0.2419 4.0107 15°0.2588 0.9659 0.2679 75°0.9659 0.2588 3.7320二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin 22sin cos cos 2cos 2sin 22cos 2112sin 2αααααααα==-=-=-2tan tan 21tan 2ααα=--sin 33sin 4sin 3cos34cos33cos .3tan tan 3tan 313tan 2αααααααααα=-=--=--三角函数的和差化积公式三角函数的积化和差公式sin sin 2sincos 22sin sin 2cos sin22cos cos 2cos cos22cos cos 2sin sin22αβαβαβαβαβαβαβαβαβαβαβαβ+-+=⋅+--=⋅+-+=⋅+--=-⋅[][][][]1sin cos sin()sin()21cos sin sin()sin()21cos cos cos()cos()21sin sin cos()cos()2αβαβαβαβαβαβαβαβαβαβαβαβ⋅=++-⋅=+--⋅=++-⋅=-+--化asinα ±bcosα为一个角的一个三角函数的形式（辅助角的三角函数的公式）22sin cos sin()a x b x a b x φ±=+±其中φ角所在的象限由a 、b 的符号确定，φ角的值由tan ba φ=确定六边形记忆法：图形结构“上弦中切下割，左正右余中间1”；记忆方法“对角线上两个函数的积为1；阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方；任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。

每一个角度的三角函数值表

（1）特殊角三角函数值sin0=0sin30=0.5sin45=0.7071 二分之根号2sin60=0.8660 二分之根号3sin90=1cos0=1cos30=0. 二分之根号3cos45=0. 二分之根号2cos60=0.5cos90=0tan0=0tan30=0. 三分之根号3tan45=1tan60=1. 根号3tan90=无cot0=无cot30=1. 根号3cot45=1cot60=0. 三分之根号3cot90=0（2）0°～90°的任意角的三角函数值，查三角函数表。

（见下）（3）锐角三角函数值的变化情况（i）锐角三角函数值都是正值（ii）当角度在0°～90°间变化时，正弦值随着角度的增大（或减小）而增大（或减小）余弦值随着角度的增大（或减小）而减小（或增大）正切值随着角度的增大（或减小）而增大（或减小）余切值随着角度的增大（或减小）而减小（或增大）（iii）当角度在0°≤α≤90°间变化时，0≤sinα≤1, 1≥cosα≥0,当角度在0°<α<90°间变化时，tanα>0, cotα>0.“锐角三角函数”属于三角学，是《数学课程标准》中“空间与图形”领域的重要内容。

从《数学课程标准》看，中学数学把三角学内容分成两个部分，第一部分放在义务教育第三学段，第二部分放在高中阶段。

在义务教育第三学段，主要研究锐角三角函数和解直角三角形的内容，本套教科书安排了一章的内容，就是本章“锐角三角函数”。

在高中阶段的三角内容是三角学的主体部分，包括解斜三角形、三角函数、反三角函数和简单的三角方程。

无论是从内容上看，还是从思考问题的方法上看，前一部分都是后一部分的重要基础，掌握锐角三角函数的概念和解直角三角形的方法，是学习三角函数和解斜三角形的重要准备。

附：三角函数值表sin0=0,sin15=（√6-√2)/4 ,sin30=1/2,sin45=√2/2,sin60=√3/2,sin75=(√6+√2)/2 ,sin90=1,sin105=√2/2*(√3/2+1/2)sin120=√3/2sin135=√2/2sin150=1/2sin165=（√6-√2)/4sin180=0sin270=-1sin360=0sin1=0. sin2=0. sin3=0.sin4=0.41253 sin5=0. sin6=0.sin7=0. sin8=0. sin9=0.sin10=0. sin11=0.65448 sin12=0.sin13=0. sin14=0. sin15=0.sin16=0. sin17=0.27367 sin18=0.49474sin19=0.71567 sin20=0.56687 sin21=0.sin22=0.5912 sin23=0.92737 sin24=0.sin25=0. sin26=0.90774 sin27=0.sin28=0.58908 sin29=0. sin30=0.sin31=0.00542 sin32=0.32049 sin33=0.5027 sin34=0.07468 sin35=0.1046 sin36=0.24731 sin37=0.20483 sin38=0.56583 sin39=0.98375 sin40=0.65392 sin41=0.05073 sin42=0.88582 sin43=0.24985 sin44=0.89972 sin45=0.65475 sin46=0.86511 sin47=0.91705 sin48=0.73941 sin49=0.27719 sin50=0.8978 sin51=0.69708 sin52=0.67219 sin53=0.72928 sin54=0.49474 sin55=0.89918 sin56=0.50417 sin57=0.54239 sin58=0.6426 sin59=0.21122 sin60=0.44386 sin61=0.93957 sin62=0.89269 sin63=0.83678 sin64=0.9167 sin65=0.66499 sin66=0.26009 sin67=0.24404 sin68=0.67873 sin69=0.72017 sin70=0.59083 sin71=0.93167 sin72=0.51535 sin73=0.30354 sin74=0.83189 sin75=0.90683 sin76=0.59965 sin77=0.52352 sin78=0.38057 sin79=0.7664 sin80=0.2208 sin81=0.51378 sin82=0.15704 sin83=0.1322 sin84=0.82733 sin85=0.17455 sin86=0.98242 sin87=0.45738 sin88=0.90958 sin89=0.63913sin90=1cos1=0.63913 cos2=0.90958 cos3=0.45738 cos4=0.98242 cos5=0.17455 cos6=0.82733 cos7=0.1322 cos8=0.15704 cos9=0.51378cos10=0.2208 cos11=0.7664 cos12=0.38057 cos13=0.52352 cos14=0.59965 cos15=0.90683 cos16=0.83189 cos17=0.30355 cos18=0.51535 cos19=0.93168 cos20=0.59084 cos21=0.72017 cos22=0.67874 cos23=0.24404 cos24=0.26009 cos25=0.66499 cos26=0.9167 cos27=0.83679 cos28=0.8927 cos29=0.93957 cos30=0.44387 cos31=0.21123 cos32=0.6426 cos33=0.5424 cos34=0.50417 cos35=0.89918 cos36=0.49474 cos37=0.72928 cos38=0.67219 cos39=0.69709 cos40=0.8978 cos41=0.2772 cos42=0.73942 cos43=0.91705 cos44=0.86512 cos45=0.65476 cos46=0.89974 cos47=0.24985 cos48=0.88582 cos49=0.05074 cos50=0.65394 cos51=0.98375 cos52=0.56583 cos53=0.20484 cos54=0.24731 cos55=0.10462 cos56=0.07468 cos57=0.50272 cos58=0.32049 cos59=0.00544 cos60=0.00001 cos61=0.63371 cos62=0. cos63=0.95468cos64=0. cos65=0. cos66=0.58004cos67=0.92737 cos68=0.59122 cos69=0.cos70=0.56688 cos71=0. cos72=0.cos73=0. cos74=0. cos75=0.cos76=0. cos77=0. cos78=0.cos79=0. cos80=0. cos81=0.cos82=0. cos83=0. cos84=0.cos85=0. cos86=0. cos87=0.cos88=0. cos89=0.72836cos90=0tan1=0. tan2=0. tan3=0.tan4=0. tan5=0. tan6=0.tan7=0.29046 tan8=0. tan9=0.tan10=0. tan11=0. tan12=0.00221tan13=0.55631 tan14=0. tan15=0.11227tan16=0.88079 tan17=0. tan18=0.29063tan19=0. tan20=0. tan21=0.54158tan22=0.51568 tan23=0.96047 tan24=0.85361 tan25=0.49986 tan26=0.58614 tan27=0.44288 tan28=0.14788 tan29=0.2769 tan30=0.96257 tan31=0.75604 tan32=0.93275 tan33=0.75104 tan34=0.24265 tan35=0.97097 tan36=0.53609 tan37=0.27942 tan38=0.67174 tan39=0.50072 tan40=0.72799 tan41=0.62267 tan42=0.78399 tan43=0.76618 tan44=0.70739 tan45=0.99999 tan46=1.05693 tan47=1.46826 tan48=1.91927 tan49=1.10092 tan50=1.421 tan51=1.5051 tan52=1.30785 tan53=1.04098 tan54=1.11733 tan55=1.21144 tan56=1.27403 tan57=1.45827 tan58=1.10506 tan59=1.05173 tan60=1.88767 tan61=1.14235 tan62=1.63318 tan63=1.51503 tan64=2.9296 tan65=2.95586 tan66=2.4215 tan67=2.3753 tan68=2.62946 tan69=2.38023 tan70=2.46216 tan71=2.5822 tan72=3.52526 tan73=3.41404 tan74=3.09087 tan75=3.88776 tan76=4.58455 tan77=4.4153 tan78=4.8456 tan79=5.0307 tan80=5.7707 tan81=6.5041 tan82=7.4207 tan83=8.4593 tan84=9.2587 tan85=11.132 tan86=14.1942 tan87=19.816 tan88=28.5515 tan89=57.9144tan90=无取值。

三角函数特殊角值表

若45°＜A＜90°，则sinA＞cosA；tanA＞cotA．
3、规律记忆法：观察表中的数值特征，可总结为下列记忆规律：
1有界性：（锐角三角函数值都是正值）即当0°＜＜90°时，
则0＜sin ＜1；0＜cos ＜1；tan ＞0；cot ＞0。
②增减性：（锐角的正弦、正切值随角度的增大而增大；余弦、余切值随角度的增大而减小），即当0＜A＜B＜90°时，则sinA＜sinB；tanA＜tanB；cosA＞cosB；cotA＞cotB；特别地：若0°＜＜45°，则sinA＜cosA；tanA＜cotA
三角函数
角度
函数030 Nhomakorabea4560
90
120
135
150
180
270
360
角a的弧度
0
π/6
π/4
π/3
π/2
2π/3
3π/4
5π/6
π
3π/2
2π
sin
0
1/2
√2/2
√3/2
1
√3/2
√2/2
1/2
0
-1
0
cos
1
√3/2
√2/2
1/2
0
-1/2
-√2/2
-√3/2
-1
0
1
tan
0
√3/3
1
√3
-√3
-1
-√3/3
0
0
1、图示法：借助于下面三个图形来记忆，即使有所遗忘也可根据图形重新推出：
sin30°=cos60°= sin45°=cos45°=
tan30°=cot60°= tan 45°=cot45°=1
2、列表法：

三角函数特殊角值表

三角函数特殊角函数值
只想上传这一个表下面的都是无用的话不用看了。

1、图示法：借助于下面三个图形来记忆，即使有所遗忘也可根据图形重新推出： sin30°=cos60°=
2
1
sin45°=cos45°=22
tan30°=cot60°=3
3
tan 45°=cot45°=1
2、列表法：
说明：正弦值随角度变化，即0? 30? 45? 60? 90?变化；值从0
30? 1
2
3 1
45? 1
2 1
2 60? 3
变化，其余类似记忆．
3、规律记忆法：观察表中的数值特征，可总结为下列记忆规律：
①有界性：（锐角三角函数值都是正值）即当0°＜α＜90°时，
则0＜sinα＜1； 0＜cosα＜1 ； tanα＞0 ； cotα＞0。

②增减性：（锐角的正弦、正切值随角度的增大而增大；余弦、余切值随角度的增大而减小），即当0＜A＜B＜90°时，则sin A＜sin B；tan A＜tan B； cos A＞cos B；cot A＞cot B；特别地：若0°＜α＜45°，则sin A＜cos A；tan A＜cot A
若45°＜A＜90°，则sin A＞cos A；tan A＞cot A．
4、口决记忆法：观察表中的数值特征
正弦、余弦值可表示为
2
m形式，正切、余切值可表示为
3
m形式，有关m的值可归纳成顺口溜：一、二、三；三、二、一；三九二十七．。

三角函数特殊角值表

角度函数 0 3045 60 90 120 135 150 180 270 360 角a 的弧度0 π/6 π/4 π/3 π/2 2π/3 3π/4 5π/6 π 3π/2 2π sin 0 1/2 √2/2 √3/2 1 √3/2 √2/2 1/2 0 -1 0 cos 1 √3/2 √2/2 1/2 0 -1/2 -√2/2 -√3/2 -1 0 1 tan√3/31√3-√3-1-√3/31、图示法：借助于下面三个图形来记忆，即使有所遗忘也可根据图形重新推出： sin30°=cos60°=21，sin45°=cos45°=22， tan30°=cot60°=33， tan 45°=cot45°=1正弦函数 sinθ=y/r 余弦函数 cosθ=x/r 正切函数 tanθ=y/x 余切函数 cotθ=x/y 正割函数 secθ=r/x 余割函数 cscθ=r/y2、列表法：说明：正弦值随角度变化，即0˚ 30˚ 45˚ 60˚ 90˚变化；值从021 22 23 1变化，其余类似记忆． 3、规律记忆法：观察表中的数值特征，可总结为以下记忆规律： ① 有界性：〔锐角三角函数值都是正值〕即当0°＜α＜90°时，那么0＜sin α＜1； 0＜cos α＜1 ； tan α＞0 ； cot α＞0。

②增减性：〔锐角的正弦、正切值随角度的增大而增大；余弦、余切值随角度的增大而减小〕，即当0＜A ＜B ＜90°时，那么sin A ＜sin B ；tan A ＜tan B ； cos A ＞cos B ；cot A ＞cot B ；特别地：假设0°＜α＜45°，那么sin A ＜cos A ；tan A ＜cot A 假设45°＜A ＜90°，那么sin A ＞cos A ；tan A ＞cot A ． 4、口决记忆法：观察表中的数值特征正弦、余弦值可表示为2m 形式，正切、余切值可表示为3m 形式，有关m 的值可归纳成顺口溜：一、二、三；三、二、一；三九二十七．30˚ 123145˚1212 60˚ 3函数名正弦余弦正切余切正割余割符号sin cos tan cot sec csc正弦函数sin〔A〕=a/c余弦函数cos〔A〕=b/c正切函数tan〔A〕=a/b余切函数cot〔A〕=b/a其中a为对边，b为邻边，c为斜边三角函数对照表三角函数SIN COS TAN 三角函数SIN COS TAN 0°0 1 0 90° 1 0 无1°0.0174 0.9998 0.0174 89°0.9998 0.0174 57.2899 2°0.0348 0.9993 0.0349 88°0.9993 0.0348 28.6362 3°0.0523 0.9986 0.0524 87°0.9986 0.0523 19.0811 4°0.0697 0.9975 0.0699 86°0.9975 0.0697 14.3006 5°0.0871 0.9961 0.0874 85°0.9961 0.0871 11.4300 6°0.1045 0.9945 0.1051 84°0.9945 0.1045 9.5143 7°0.1218 0.9925 0.1227 83°0.9925 0.1218 8.1443 8°0.1391 0.9902 0.1405 82°0.9902 0.1391 7.1153 9°0.1564 0.9876 0.1583 81°0.9876 0.1564 6.3137 10°0.1736 0.9848 0.1763 80°0.9848 0.1736 5.6712 11°0.1908 0.9816 0.1943 79°0.9816 0.1908 5.1445 12°0.2079 0.9781 0.2125 78°0.9781 0.2079 4.7046 13°0.2249 0.9743 0.2308 77°0.9743 0.2249 4.3314 14°0.2419 0.9702 0.2493 76°0.9702 0.2419 4.0107 15°0.2588 0.9659 0.2679 75°0.9659 0.2588 3.7320二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin 22sin cos cos 2cos 2sin 22cos 2112sin 2αααααααα==-=-=- 2tan tan 21tan 2ααα=--sin 33sin 4sin 3cos34cos33cos .3tan tan 3tan 313tan 2αααααααααα=-=--=--三角函数的和差化积公式三角函数的积化和差公式sin sin 2sincos 22sin sin 2cos sin22cos cos 2cos cos22cos cos 2sin sin22αβαβαβαβαβαβαβαβαβαβαβαβ+-+=⋅+--=⋅+-+=⋅+--=-⋅[][][][]1sin cos sin()sin()21cos sin sin()sin()21cos cos cos()cos()21sin sin cos()cos()2αβαβαβαβαβαβαβαβαβαβαβαβ⋅=++-⋅=+--⋅=++-⋅=-+-- 化asinα ±bcosα为一个角的一个三角函数的形式〔辅助角的三角函数的公式〕22sin cos sin()a x b x a b x φ±=+±其中φ角所在的象限由a 、b 的符号确定，φ角的值由tan ba φ=确定六边形记忆法：图形结构“上弦中切下割，左正右余中间1”；记忆方法“对角线上两个函数的积为1；阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方；任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。

三角函数特殊角值表

角度函数0 30 45 60 90 120 135 150 180 270 360 角a 的弧度0 π/6 π/4 π/3 π/2 2π/3 3π/4 5π/6 π3π/2 2πsin 0 1/2 √2/2 √3/2 1 √3/2 √2/2 1/2 0 -1 0 cos 1 √3/2 √2/2 1/2 0 -1/2 -√2/2 -√3/2 -1 0 1 tan 0 √3/3 1 √3 -√3 -1 -√3/3 0 01、图示法：借助于下面三个图形来记忆，即使有所遗忘也可根据图形重新推出：sin30 =°cos60 °=12，sin45 °=cos45°=22，tan30°=cot60 °=33，tan 45 °=cot45 °=122 21 3130?60?45?3 1 1正弦函数sin θ=y/r余弦函数cosθ=x/r 正切函数tan θ=y/x 余切函数cot θ=x/y正割函数secθ=r/x余割函数cscθ=r/y2、列表法：说明：正弦值随角度变化，即0? 30? 45? 60? 90?变化；值从01 222321 变化，其余类似记忆．3、规律记忆法：观察表中的数值特征，可总结为下列记忆规律：①有界性：（锐角三角函数值都是正值）即当0°＜＜90°时，则0＜sin ＜1；0＜cos ＜1 ；tan ＞0 ；cot ＞0。

②增减性：（锐角的正弦、正切值随角度的增大而增大；余弦、余切值随角度的增大而减小），即当0＜A＜B＜90°时，则sinA＜sin B；tanA＜tan B；cosA＞cosB；cotA＞cotB；特别地：若0°＜＜45°，则sinA＜cosA；tanA＜cotA若45°＜A＜90°，则sinA＞cosA；tanA＞cotA．4、口决记忆法：观察表中的数值特征正弦、余弦值可表示为m2形式，正切、余切值可表示为m3形式，有关m 的值可归纳成顺口溜：一、二、三；三、二、一；三九二十七．函数名正弦余弦正切余切正割余割符号sin cos tan cot sec csc正弦函数sin（A）=a/c余弦函数cos（A ）=b/c正切函数tan（A）=a/b余切函数cot（A）=b/a其中 a 为对边，b 为邻边， c 为斜边三角函数对照表三角函数SIN COS TAN 三角函数SIN COS TAN 0°0 1 0 90° 1 0 无1°0.0174 0.9998 0.0174 89°0.9998 0.0174 57.2899 2°0.0348 0.9993 0.0349 88°0.9993 0.0348 28.6362 3°0.0523 0.9986 0.0524 87°0.9986 0.0523 19.0811 4°0.0697 0.9975 0.0699 86°0.9975 0.0697 14.3006 5°0.0871 0.9961 0.0874 85°0.9961 0.0871 11.4300 6°0.1045 0.9945 0.1051 84°0.9945 0.1045 9.5143 7°0.1218 0.9925 0.1227 83°0.9925 0.1218 8.1443 8°0.1391 0.9902 0.1405 82°0.9902 0.1391 7.1153 9°0.1564 0.9876 0.1583 81°0.9876 0.1564 6.3137 10°0.1736 0.9848 0.1763 80°0.9848 0.1736 5.6712 11°0.1908 0.9816 0.1943 79°0.9816 0.1908 5.1445 12°0.2079 0.9781 0.2125 78°0.9781 0.2079 4.7046 13°0.2249 0.9743 0.2308 77°0.9743 0.2249 4.3314 14°0.2419 0.9702 0.2493 76°0.9702 0.2419 4.0107 15°0.2588 0.9659 0.2679 75°0.9659 0.2588 3.732016°0.2756 0.9612 0.2867 74°0.9612 0.2756 3.4874 17°0.2923 0.9563 0.3057 73°0.9563 0.2923 3.2708 18°0.3090 0.9510 0.3249 72°0.9510 0.3090 3.0776 19°0.3255 0.9455 0.3443 71°0.9455 0.3255 2.9042 20°0.3420 0.9396 0.3639 70°0.9396 0.3420 2.7474 21°0.3583 0.9335 0.3838 69°0.9335 0.3583 2.6050 22°0.3746 0.9271 0.4040 68°0.9271 0.3746 2.4750 23°0.3907 0.9205 0.4244 67°0.9205 0.3907 2.3558 24°0.4067 0.9135 0.4452 66°0.9135 0.4067 2.2460 25°0.4226 0.9063 0.4663 65°0.9063 0.4226 2.1445 26°0.4383 0.8987 0.4877 64°0.8987 0.4383 2.0503 27°0.4539 0.8910 0.5095 63°0.8910 0.4539 1.9626 28°0.4694 0.8829 0.5317 62°0.8829 0.4694 1.8807 29°0.4848 0.8746 0.5543 61°0.8746 0.4848 1.8040 30°0.5000 0.8660 0.5773 60°0.8660 0.5000 1.7320 31°0.5150 0.8571 0.6008 59°0.8571 0.5150 1.6642 32°0.5299 0.8480 0.6248 58°0.8480 0.5299 1.6003 33°0.5446 0.8386 0.6494 57°0.8386 0.5446 1.5398 34°0.5591 0.8290 0.6745 56°0.8290 0.5591 1.4825 35°0.5735 0.8191 0.7002 55°0.8191 0.5735 1.4281 36°0.5877 0.8090 0.7265 54°0.8090 0.5877 1.3763 37°0.6018 0.7986 0.7535 53°0.7986 0.6018 1.3270 38°0.6156 0.7880 0.7812 52°0.7880 0.6156 1.2799 39°0.6293 0.7771 0.8097 51°0.7771 0.6293 1.2348 40°0.6427 0.7660 0.8390 50°0.7660 0.6427 1.1917 41°0.6560 0.7547 0.8692 49°0.7547 0.6560 1.1503 42°0.6691 0.7431 0.9004 48°0.7431 0.6691 1.1106 43°0.6819 0.7313 0.9325 47°0.7313 0.6819 1.0723 44°0.6946 0.7193 0.9656 46°0.7193 0.6946 1.0355 45°0.7071 0.7071 1 45°0.7071 0.7071 1同角基本关系式倒数关系商的关系平方关系tan cot1 sin csc1 cos sec1sin sectancos csccos csccotsin sec22sin cos1221tan sec221cot csc诱导公式sin()sin cos()cos tan()tan cot()cotsin( ) cos 2 sin( ) sincos( ) cos3sin( ) cos2sin(2 ) sincos(2 ) coscos( ) sin2 t an( ) tancot( ) cot3cos( ) sin2t an(2 ) tancot(2 ) cottan( ) cot2cot( ) tan23tan( ) cot23cot( ) tan2(其中k∈Z)sin( ) cos 2cos( ) sin2 sin( ) sin3sin( ) cos2s in(2 ) sintan( ) cot 2 cos( ) costan( ) tan3cos( ) sin2cos(2 ) costan(2 ) tancot( ) tan 2 c ot( ) cot 3tan( ) cot23cot( ) tan2c ot(2 ) cot两角和与差的三角函数公式万能公式sin( ) sin cos cos sin sin( ) sin cos cos sin sin2 tan( / 2)1 tan 2( / 2)cos( ) cos cos sin sincos( ) cos cos sin sin cos 1 tan 2( / 2)1 tan 2( / 2)tan( )tan tan1 tan tantan2 tan( / 2)1 tan 2( / 2)tan( )tan tan 1 tan tan半角的正弦、余弦和正切公式三角函数的降幂公式1 cos sin( )2 22sin1 cos 221 cos cos( )2 22cos1 cos 221 cos 1 cos sintan( )2 1 cos sin 1 cos二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin33sin4sin3 sin22sin coscos34cos33cos. cos2cos2sin22cos2112sin2tan22tan1tan2tan33tan tan313tan2三角函数的和差化积公式三角函数的积化和差公式sin sin2sin cos221sin cos sin()sin()2sin sin2cos sin221cos sin sin()sin()2cos cos2cos cos221cos cos cos()cos()2cos cos2sin sin221sin sin cos()cos()2化asinα±bco为sα一个角的一个三角函数的形式（辅助角的三角函数的公式）22a sin xb cosx a b sin(x)其中角所在的象限由a、b的符号确定，角的值由b tana确定六边形记忆法：图形结构“上弦中切下割，左正右余中间1”；记忆方法“对角线上两个函数的积为1；阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方；任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。

特殊角的三角函数值表高中用(完善版)

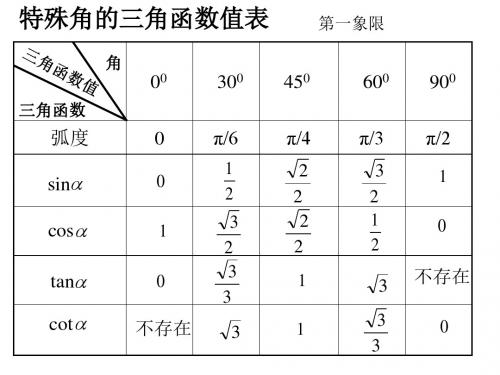
特殊角的三角函数值表
角
第二象限
1200
三角函数
1350
3π/4
2 2 2 2
1 1
1500
5π/6
1 2
1800
π
0
1
弧度 sin cos
2π/3
3 2 1 2
tan
cot
3
3 3
3 2 3 3
0
3
不存在
特殊角的三角函数值表
角
第三象限
2100
三角函数
2250
5π/4
2 2 2 2
1 1
2400
4π/3
3 2 1 2
2700
3π/2
1
弧度 sin cos
7π/6
1 2
tan
cot
3 2 3 30Fra bibliotek33 3
不存在
0
3
特殊角的三角函数值表
角
第四象限
3000
三角函数
3150
7π/4
2 2 2 2
1 1
3300
特殊角的三角函数值表
角
第一象限
00
三角函数
300
π/6
1 2
450
π/4
2 2 2 2
1 1
600
π/3
3 2 1 2
900
π/2
1
弧度 sin cos
0
0
1
tan
cot
0
3 2 3 3
0
3
3 3
不存在
0
不存在
3
sin37=3/5 sin53=4/5 cos37=4/5 cos53=3/5 tan37=3/4 tan53=4/3 cot37=4/3 cot53=3/4 注：(1）与0、30、45、60、90有关角三角函数值只需背第一象限三角函数值＋结合三角函数线法记忆即可（2）与345三角形有关角三角函数值只需背两个角度+在使用时画出345三角形现推即可

三角函数特殊角值表

角度 030456090120135150180270360函数角 a 的弧度0 π /6 π/4 π /3 π /2 2π /3 3π /4 5π /6π 3π /22πsin 0 1/2 √ 2/2 √3/2 1 √ 3/2 √ 2/2 1/2 0 -1 0cos1 √ 3/2 √ 2/2 1/2 0-1/2 -√ 2/2 -√ 3/2 -1 01tan 0√ 3/31√3-√ 3-1-√ 3/31、图示法：借助于下边三个图形来记忆，即便有所忘记也可依据图形从头推出：sin30 =cos60° °= 1 ， sin45 °=cos45°=2， tan30 °=cot60 °=3， tan 45 °=cot45 °=122 322123130?45?60? 311正弦函数sin θ=y/r 余弦函数 cos θ=x/r 正切函数 tan θ=y/x余切函数 cot θ=x/y 正割函数 sec θ=r/x 余割函数 csc θ=r/y2、列表法：说明：正弦值随角度变化，即0?30? 45? 60? 90?变化；值从 012 3 1 变化，其他近似记忆．2223、规律记忆法：察看表中的数值特点，可总结为以下记忆规律：① 有界性：（锐角三角函数值都是正当）即当0°＜＜ 90°时，则 0＜ sin ＜ 1； 0＜ cos ＜ 1 ； tan ＞ 0 ； cot ＞0。

② 增减性：（锐角的正弦、正切值随角度的增大而增大；余弦、余切值随角度的增大而减小），即当 0＜ A ＜ B ＜90°时，则 sinA ＜ sinB ；tanA ＜ tanB ； cosA ＞ cosB ；cotA ＞ cotB ；特别地：若 0°＜＜ 45°，则 sinA ＜ cosA ； tanA ＜ cotA若 45°＜ A ＜ 90°，则 sinA ＞cosA ； tanA ＞ cotA ． 4、口决记忆法：察看表中的数值特点正弦、余弦值可表示为m形式，正切、余切值可表示为m形式，相关m 的值可概括成23顺口溜：一、二、三；三、二、一；三九二十七．函数名正弦余弦正切余切正割余割符号sin cos tan cot sec csc正弦函数sin（ A） =a/c余弦函数cos（A ）=b/c正切函数tan（ A ） =a/b余切函数cot（ A ） =b/a此中 a 为对边， b 为邻边， c 为斜边三角函数比较表三角函数SIN COS TAN三角函数SIN COS TAN 0°01090°10无1°89°2°88°3°87°4°86°5°85°6°84°7°83°8°82°9°81°10°80°11°79°12°78°13°77°14°76°15°75°16°74°17°73°18°72°19°71°20°70°21°69°22°68°23°67°24°66°25°65°26°64°27°63°28°62°29°61°30°60°31°59°32°58°33°57°34°56°35°55°36°54°37°53°38°52°39°51°40°50°41°49°42°48°43°47°44°46°45°145°1同角基本关系式倒数关系商的关系平方关系tan cot1sin sec22sin cos1sin csc1tan csccos122cos sec1cos csc tan sec22cotsecsin1cot csc引诱公式sin()sin cos( ) cos tan()tan cot()cotsin() cossin( ) sin 3 cos( ) cos sin(22 cos() sintan()tan 3cos(2cot()cot2tan() cottan(322cot() tancot(322sin() cos2cos()sin sin( ) sin sin( 322cos( )costan()cot cos(3tan( ) tan 22 cot()tancot() cot3tan(223cot(两角和与差的三角函数公式sin( ) sin cos cos sin sin( ) sin cos cos sincos( ) cos cos sin sincos() cos cossin sintan()tan tan1 tan tantan()tan tan1 tantan)cos sin(2 ) sincos(2 ) cos)sin tan(2 ) tancot(2)cot)cot(此中 k ∈ Z)) tan)cos sin(2 ) sin) sincos(2 ) costan(2 ) tan) cot cot(2) cot)tan全能公式sin2 tan( / 2)tan 2( / 2)1 1 tan 2( / 2)costan 2( / 2)1 tan2 tan( / 2)tan 2( / 2)1半角的正弦、余弦和正切公式三角函数的降幂公式1 cos21 cos2sin( ) 2sin22cos(1 cos21 cos2cos)222tan( 1 cos 1 cos sin)cossin1 cos21二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin 2 2sin cossin33sin 4sin 3cos2 cos2sin 22cos 21 1 2sin 2cos3 4cos3 3cos . tan 22 tantan33tantan31 3tan 21 tan 2三角函数的和差化积公式三角函数的积化和差公式sinsin 2sincossincos 1 sin( ) sin()222sinsin2cossincos sin1 sin( ) sin()222coscos 2coscoscoscos 1 cos( ) cos()222coscos2sinsinsinsin1 cos( ) cos()222化 asin α ±bcos 为α一个角的一个三角函数的形式（协助角的三角函数的公式）a sin xb cosxa 2b 2 sin(x )ba、 b 的符号确立，tan此中角所在的象限由角的值由a 确立六边形记忆法：图形构造 “上弦中切下割，左正右余中间1”；记忆方法“对角线上两个函数的积为1；暗影三角形上两极点的三角函数值的平方和等于下极点的三角函数值的平方；随意一顶点的三角函数值等于相邻两个极点的三角函数值的乘积。

三角函数特殊角值表

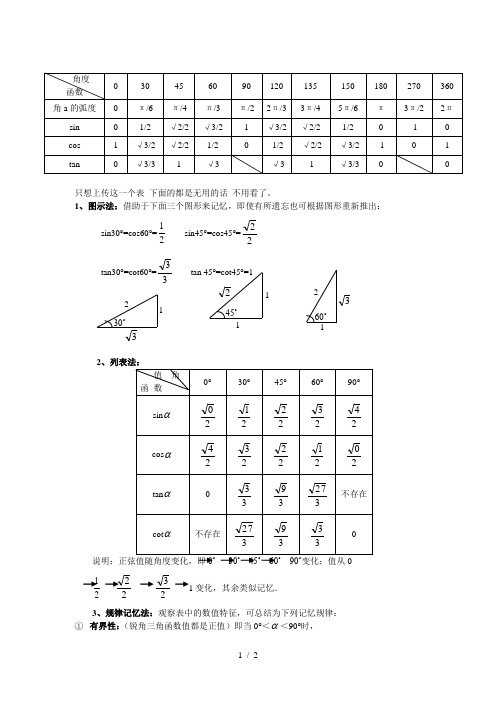
只想上传这一个表下面的都是无用的话不用看了。

1、图示法：借助于下面三个图形来记忆，即使有所遗忘也可根据图形重新推出： sin30°=cos60°=
21 sin45°=cos45°=2
2
tan30°=cot60°=3
3
tan 45°=cot45°=1
2说明：正弦值随角度变化，即0˚ 30˚ 45˚ 60˚ 90˚变化；值从0 23 1变化，其余类似记忆． 3、规律记忆法：观察表中的数值特征，可总结为下列记忆规律： ① 有界性：（锐角三角函数值都是正值）即当0°＜α＜90°时，
30˚ 1
2
3 1
45˚ 1
2 1
2 60˚ 3
则0＜sin α＜1； 0＜cos α＜1 ； tan α＞0 ； cot α＞0。

②增减性：（锐角的正弦、正切值随角度的增大而增大；余弦、余切值随角度的增大而减小），即当0＜A ＜B ＜90°时，则sin A ＜sin B ；tan A ＜tan B ； cos A ＞cos B ；cot A ＞cot B ；特别地：若0°＜α＜45°，则sin A ＜cos A ；tan A ＜cot A 若45°＜A ＜90°，则sin A ＞cos A ；tan A ＞cot A ． 4、口决记忆法：观察表中的数值特征正弦、余弦值可表示为
2m 形式，正切、余切值可表示为3
m 形式，有关m 的值可归纳成顺口溜：一、二、三；三、二、一；三九二十七．
注：资料可能无法思考和涵盖全面，最好仔细浏览后下载使用，感谢您的关注！。

三角函数特殊角值表

角度函数0 30 45 60 90 120 135 150 180 270 360 角a 的弧度0 π/6 π/4 π/3 π/2 2π/3 3π/4 5π/6 π3π/2 2πsin 0 1/2 √2/2 √3/2 1 √3/2 √2/2 1/2 0 -1 0 cos 1 √3/2 √2/2 1/2 0 -1/2 -√2/2 -√3/2 -1 0 1 tan 0 √3/3 1 √3 -√3 -1 -√3/3 0 01、图示法：借助于下面三个图形来记忆，即使有所遗忘也可根据图形重新推出：sin30 =°cos60 °=12，sin45 °=cos45°=22，tan30°=cot60 °=33，tan 45 °=cot45 °=122 21 3130?60?45?3 1 1正弦函数sin θ=y/r余弦函数cosθ=x/r 正切函数tan θ=y/x 余切函数cot θ=x/y正割函数secθ=r/x余割函数cscθ=r/y2、列表法：说明：正弦值随角度变化，即0? 30? 45? 60? 90?变化；值从01 222321 变化，其余类似记忆．3、规律记忆法：观察表中的数值特征，可总结为下列记忆规律：①有界性：（锐角三角函数值都是正值）即当0°＜＜90°时，则0＜sin ＜1；0＜cos ＜1 ；tan ＞0 ；cot ＞0。

②增减性：（锐角的正弦、正切值随角度的增大而增大；余弦、余切值随角度的增大而减小），即当0＜A＜B＜90°时，则sinA＜sin B；tanA＜tan B；cosA＞cosB；cotA＞cotB；特别地：若0°＜＜45°，则sinA＜cosA；tanA＜cotA若45°＜A＜90°，则sinA＞cosA；tanA＞cotA．4、口决记忆法：观察表中的数值特征正弦、余弦值可表示为m2形式，正切、余切值可表示为m3形式，有关m 的值可归纳成顺口溜：一、二、三；三、二、一；三九二十七．函数名正弦余弦正切余切正割余割符号sin cos tan cot sec csc正弦函数sin（A）=a/c余弦函数cos（A ）=b/c正切函数tan（A）=a/b余切函数cot（A）=b/a其中 a 为对边，b 为邻边， c 为斜边三角函数对照表三角函数SIN COS TAN 三角函数SIN COS TAN 0°0 1 0 90° 1 0 无1°0.0174 0.9998 0.0174 89°0.9998 0.0174 57.2899 2°0.0348 0.9993 0.0349 88°0.9993 0.0348 28.6362 3°0.0523 0.9986 0.0524 87°0.9986 0.0523 19.0811 4°0.0697 0.9975 0.0699 86°0.9975 0.0697 14.3006 5°0.0871 0.9961 0.0874 85°0.9961 0.0871 11.4300 6°0.1045 0.9945 0.1051 84°0.9945 0.1045 9.5143 7°0.1218 0.9925 0.1227 83°0.9925 0.1218 8.1443 8°0.1391 0.9902 0.1405 82°0.9902 0.1391 7.1153 9°0.1564 0.9876 0.1583 81°0.9876 0.1564 6.3137 10°0.1736 0.9848 0.1763 80°0.9848 0.1736 5.6712 11°0.1908 0.9816 0.1943 79°0.9816 0.1908 5.1445 12°0.2079 0.9781 0.2125 78°0.9781 0.2079 4.7046 13°0.2249 0.9743 0.2308 77°0.9743 0.2249 4.3314 14°0.2419 0.9702 0.2493 76°0.9702 0.2419 4.0107 15°0.2588 0.9659 0.2679 75°0.9659 0.2588 3.732016°0.2756 0.9612 0.2867 74°0.9612 0.2756 3.4874 17°0.2923 0.9563 0.3057 73°0.9563 0.2923 3.2708 18°0.3090 0.9510 0.3249 72°0.9510 0.3090 3.0776 19°0.3255 0.9455 0.3443 71°0.9455 0.3255 2.9042 20°0.3420 0.9396 0.3639 70°0.9396 0.3420 2.7474 21°0.3583 0.9335 0.3838 69°0.9335 0.3583 2.6050 22°0.3746 0.9271 0.4040 68°0.9271 0.3746 2.4750 23°0.3907 0.9205 0.4244 67°0.9205 0.3907 2.3558 24°0.4067 0.9135 0.4452 66°0.9135 0.4067 2.2460 25°0.4226 0.9063 0.4663 65°0.9063 0.4226 2.1445 26°0.4383 0.8987 0.4877 64°0.8987 0.4383 2.0503 27°0.4539 0.8910 0.5095 63°0.8910 0.4539 1.9626 28°0.4694 0.8829 0.5317 62°0.8829 0.4694 1.8807 29°0.4848 0.8746 0.5543 61°0.8746 0.4848 1.8040 30°0.5000 0.8660 0.5773 60°0.8660 0.5000 1.7320 31°0.5150 0.8571 0.6008 59°0.8571 0.5150 1.6642 32°0.5299 0.8480 0.6248 58°0.8480 0.5299 1.6003 33°0.5446 0.8386 0.6494 57°0.8386 0.5446 1.5398 34°0.5591 0.8290 0.6745 56°0.8290 0.5591 1.4825 35°0.5735 0.8191 0.7002 55°0.8191 0.5735 1.4281 36°0.5877 0.8090 0.7265 54°0.8090 0.5877 1.3763 37°0.6018 0.7986 0.7535 53°0.7986 0.6018 1.3270 38°0.6156 0.7880 0.7812 52°0.7880 0.6156 1.2799 39°0.6293 0.7771 0.8097 51°0.7771 0.6293 1.2348 40°0.6427 0.7660 0.8390 50°0.7660 0.6427 1.1917 41°0.6560 0.7547 0.8692 49°0.7547 0.6560 1.1503 42°0.6691 0.7431 0.9004 48°0.7431 0.6691 1.1106 43°0.6819 0.7313 0.9325 47°0.7313 0.6819 1.0723 44°0.6946 0.7193 0.9656 46°0.7193 0.6946 1.0355 45°0.7071 0.7071 1 45°0.7071 0.7071 1同角基本关系式倒数关系商的关系平方关系tan cot1 sin csc1 cos sec1sin sectancos csccos csccotsin sec22sin cos1221tan sec221cot csc诱导公式sin()sin cos()cos tan()tan cot()cotsin( ) cos 2 sin( ) sincos( ) cos3sin( ) cos2sin(2 ) sincos(2 ) coscos( ) sin2 t an( ) tancot( ) cot3cos( ) sin2t an(2 ) tancot(2 ) cottan( ) cot2cot( ) tan23tan( ) cot23cot( ) tan2(其中k∈Z)sin( ) cos 2cos( ) sin2 sin( ) sin3sin( ) cos2s in(2 ) sintan( ) cot 2 cos( ) costan( ) tan3cos( ) sin2cos(2 ) costan(2 ) tancot( ) tan 2 c ot( ) cot 3tan( ) cot23cot( ) tan2c ot(2 ) cot两角和与差的三角函数公式万能公式sin( ) sin cos cos sin sin( ) sin cos cos sin sin2 tan( / 2)1 tan 2( / 2)cos( ) cos cos sin sincos( ) cos cos sin sin cos 1 tan 2( / 2)1 tan 2( / 2)tan( )tan tan1 tan tantan2 tan( / 2)1 tan 2( / 2)tan( )tan tan 1 tan tan半角的正弦、余弦和正切公式三角函数的降幂公式1 cos sin( )2 22sin1 cos 221 cos cos( )2 22cos1 cos 221 cos 1 cos sintan( )2 1 cos sin 1 cos二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin33sin4sin3 sin22sin coscos34cos33cos. cos2cos2sin22cos2112sin2tan22tan1tan2tan33tan tan313tan2三角函数的和差化积公式三角函数的积化和差公式sin sin2sin cos221sin cos sin()sin()2sin sin2cos sin221cos sin sin()sin()2cos cos2cos cos221cos cos cos()cos()2cos cos2sin sin221sin sin cos()cos()2化asinα±bco为sα一个角的一个三角函数的形式（辅助角的三角函数的公式）22a sin xb cosx a b sin(x)其中角所在的象限由a、b的符号确定，角的值由b tana确定六边形记忆法：图形结构“上弦中切下割，左正右余中间1”；记忆方法“对角线上两个函数的积为1；阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方；任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。

三角函数特殊角值表

只想上传这一个表下面的都是无用的话不用看了。

1、图示法：借助于下面三个图形来记忆，即使有所遗忘也可根据图形重新
推出：
sin30°=cos60°=sin45°=cos45°=
tan30°=cot60°=tan 45°=cot45°=1
2、列表法：
说明：正弦值随角度变化，即0˚ 30˚ 45˚ 60˚ 90˚变化；值从0
1变化，其余类似记忆．
3、规律记忆法：观察表中的数值特征，可总结为下列记忆规律：
有界性：（锐角三角函数值都是正值）即当0°＜＜90°时，
则0＜sin＜1；0＜cos＜1 ；tan＞0 ；cot
0。

②增减性：（锐角的正弦、正切值随角度的增大而增大；xx、余切值随角度的增大而减小），即当0＜A＜B＜90°时，则sinA＜sinB；tanA＜tanB；cosA＞cosB；cotA＞cotB；特别地：若0°＜＜45°，则sinA＜cosA；tanA＜cotA
若45°＜A＜90°，则sinA＞cosA；tanA＞cotA．
4、口决记忆法：观察表中的数值特征
正弦、xx值可表示为形式，正切、余切值可表示为形式，有关m的值可归
纳成顺口溜
一、二、三
三、二、一三九二十七．。

特殊角度三角函数值表

特殊角度三角函数值表特殊角度三角函数值表三角函数特殊角值表只想上传这一个表下面的.都是无用的话不用看了。

1、图示法:借助于下面三个图形来记忆，即使有所遗忘也可根据图形重新推出:sin30°=cos60°= sin45°=cos45°=12、列表法:1变化，其余类似记忆.3、规律记忆法:观察表中的数值特征，可总结为下列记忆规律:① 有界性:(锐角三角函数值都是正值)即当0°<<90°时，则00 ; cot>0。

②增减性:(锐角的正弦、正切值随角度的增大而增大;余弦、余切值随角度的增大而减小)，即当0cosB;cotA>cotB;特别地:若0°<<45°，则sinA若45°cosA;tanA>cotA.4、口决记忆法:观察表中的数值特征正弦、余弦值可表示为形式，正切、余切值可表示为形式，有关m的值可归纳成顺口溜:一、二、三;三、二、一;三九二十七.特殊角的三角函数值表0度sina=0,cosa=1,tana=030度sina=0,cosa=√3/2,tana=√3/345度sina=√2/2,cosa=√2/2,tana=160度sina=√3/2,cosa=1/2,tana=√390度sina=1,cosa=0,tana不存在120度sina=√3/2,cosa=-1/2,tana=-√3150度sina=1/2,cosa=-√3/2,tana=-√3/3180度sina=0,cosa=-1,tana=0270度sina=-1,cosa=0,tana不存在360度sina=0,cosa=1,tana=0。